The glymphatic system: Current understanding and modeling

Summary

We review theoretical and numerical models of the glymphatic system, which circulates cerebrospinal fluid and interstitial fluid around the brain, facilitating solute transport. Models enable hypothesis development and predictions of transport, with clinical applications including drug delivery, stroke, cardiac arrest, and neurodegenerative disorders like Alzheimer’s disease. We sort existing models into broad categories by anatomical function: Perivascular flow, transport in brain parenchyma, interfaces to perivascular spaces, efflux routes, and links to neuronal activity. Needs and opportunities for future work are highlighted wherever possible; new models, expanded models, and novel experiments to inform models could all have tremendous value for advancing the field.

Graphical abstract

Neuroscience; Neuroanatomy; Systems biology

Preface

The authors of this paper came together in October 2021 for a workshop entitled “The glymphatic system: From theoretical models to clinical applications.” As the title suggests, although experiments were a common topic of discussion, our primary focus was modeling: Reconciling observations with theory to construct a broad conception of the flow of cerebrospinal fluid in the brain, along with its clinical implications. We not only shared recent research results but also engaged in extended, moderated conversations among all participants, seeking to identify topics of broad consensus in the field, topics of controversy, and future work that could settle controversies, thereby producing key knowledge to advance the field. The purpose of this article is to summarize the shared understanding we developed.

Accordingly, this article is not a broad review of cerebrospinal fluid flow in the brain or central nervous system. (We direct readers to other recent publications for excellent reviews of the glymphatic system (Rasmussen et al., 2021; Benveniste et al., 2019b; Nedergaard and Goldman, 2020; Ray and Heys, 2019; Linninger et al., 2016) and alternate perspectives on cerebrospinal fluid flow in the brain (Hladky and Barrand, 2022; Tarasoff-Conway et al., 2016; Engelhardt et al., 2016).) Rather, we focus on theoretical and mathematical modeling of the glymphatic system, especially where it might benefit clinicians and experimentalists, while also noting where future experiments are needed for improved models. It is increasingly clear that the glymphatic system, rightfully understood for the last decade as being capable of clearing brain metabolic waste, also does much more and is a fundamental facet of neurobiology. Because it seems to play an essential clinical role for degenerative disorders such as Alzheimer’s disease (Nedergaard and Goldman, 2020), stroke (Mestre et al., 2020a), and cardiac arrest (Du et al., 2022), and because of the potential as a novel route for drug delivery (Plog et al., 2018; Lilius et al., 2019), interest is growing exponentially, and new modelers are joining the field in large numbers. If you are among them, we welcome you and hope this article will prove useful. If you are an established expert, we hope that you will nonetheless find insight and a coherent vision in this article. Throughout, we have made every effort to delineate where evidence leads to broad consensus, where uncertainties leave room for current controversies, and what future work could resolve old questions and make way for new ones. For further information, we refer you to another recent, and excellent, review of glymphatic modeling (Martinac and Bilston, 2019).

The article proceeds as follows. Rapid review presents a rapid review, limited to topics necessary for the subsequent discussion, noting topics of consensus and controversy. Mechanisms continues by tabulating known and proposed mechanisms of fluid flow and solute transport in the brain, with links to neuronal activity. Modeling discusses theoretical models devised for each mechanism discussed in the prior section, and also gives an introduction to optimal mass transport, a powerful method for inferring in vivo flows in order to test theoretical models. Section Use case: Drug delivery presents one use case in which glymphatic models could have concrete impact in the near future: drug delivery. Finally, Use case: Drug delivery considers the outlook for glymphatic modeling and proposes future work to move the field forward.

Rapid review

The glymphatic model, past and present

The initial description of the glymphatic system

Throughout the body, the extracellular space is essential for cell-cell signaling, as well as the import and distribution of metabolic substrates and the export of waste. In the periphery, a steady influx of plasma ultrafiltrate drives interstitial fluid (ISF) into tissues, whereas excess fluid and metabolic waste products are exported by lymphatic vessels (Wiig and Swartz, 2012; Moore and Bertram, 2018). Fluid transport in the central nervous system (CNS) differs from peripheral tissue, first by the presence of the blood-brain barrier (BBB) that restricts fluid and solute exchange with the vascular compartment, and second by the absence of lymphatic vessels from neural tissue. It is therefore no surprise that diffusion processes traditionally are regarded as primarily responsible for solute distribution in the CNS (Abbott, 2004; Syková and Nicholson, 2008).

In a series of four studies published in 2012–2013, the anatomical organization, function, and physiological regulation of the “glymphatic” system was first described using dynamic imaging techniques. In the initial study (Iliff et al., 2012), in vivo two-photon microscopy was used to characterize the rapid unidirectional influx of cerebrospinal fluid (CSF) into and through brain tissue along perivascular spaces surrounding cerebral arteries. Interstitial solutes, in turn, were cleared from the brain along white matter tracts and large draining veins towards cisternal CSF compartments associated with dural venous sinuses. Both perivascular CSF influx and interstitial solute clearance, including that of amyloid beta, were sensitive to the deletion of the gene encoding the astroglial water channel aquaporin-4 (AQP4), demonstrating that glymphatic function is dependent on astroglial water transport. A subsequent in vivo two-photon microscopy study showed that cerebral arterial pulsation was a key driver of this perivascular exchange (Iliff et al., 2013a), whereas a study utilizing dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) documented that glymphatic exchange occurs throughout the brain and is organized macroscopically along the scaffold of the cerebral arterial vasculature (Iliff et al., 2013b). The final study of this sequence showed that perivascular CSF influx and interstitial solute efflux, including the clearance of amyloid beta, are more rapid in the sleeping compared to the waking brain (Xie et al., 2013).

Although these initial studies framed the present understanding of glymphatic function, it is important to note that several aspects of brain fluid transport had already been shown. Periarterial CSF influx and perivenous interstitial solute efflux were clearly described by Rennels et al. in studies that identified arterial pulsation as the key driver of perivascular exchange (Rennels et al., 1985, 1990). Yet, these findings were quickly rejected as an artifact of the histological procedure by their contemporaries (Abbott, 2004; Ichimura et al., 1991). Interest faded, in part because other groups could not replicate the original findings, but also because no function for perivascular flow was proposed. The novelty of the glymphatic concept stemmed from the integration of CNS perivascular exchange with clearance of amyloid beta, dependence on AQP4, and sleep-wake regulation within a single physiological framework. Another important aspect of the glymphatic studies was that they were critically enabled by the development of imaging techniques including two-photon microscopy and DCE-MRI, which permitted the processes of fluid and solute exchange to be visualized in real-time, non-invasively (without opening the skull or disrupting the meninges), and in the living brain. Indeed, it is the use of MRI that has enabled the validation of these initial findings in rodents in the primate (Goulay et al., 2017) and human brain (Ringstad et al., 2017; Eide et al., 2021c).

An evolving understanding of glymphatic biology

Based on these initial studies, the “glymphatic” system was named based on its dependence on perivascular AQP4 astroglial water channels and its similarities in function to the peripheral lymphatic system.

The initial description of the glymphatic system focused on advective periarterial CSF influx, perivenous interstitial solute efflux, and a dependence on astroglial water transport. By now, more than 1000 papers have been published on the glymphatic system, and the field is rapidly expanding. The simple model proposed in 2012 remains the cornerstone depicting glymphatic export of amyloid beta on a microscopic scale, but additional twists and refinements have been added to our understanding of how fluid transport contributes to export of waste from the metabolically active brain.

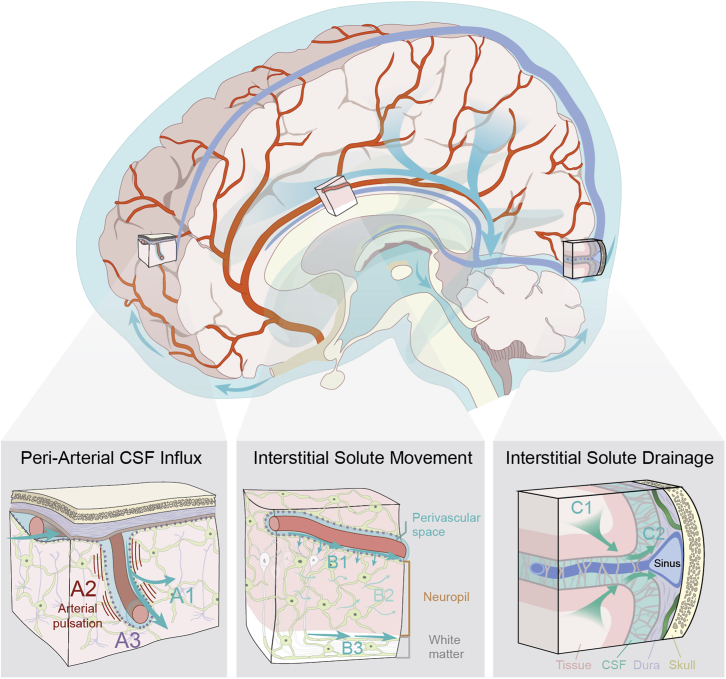
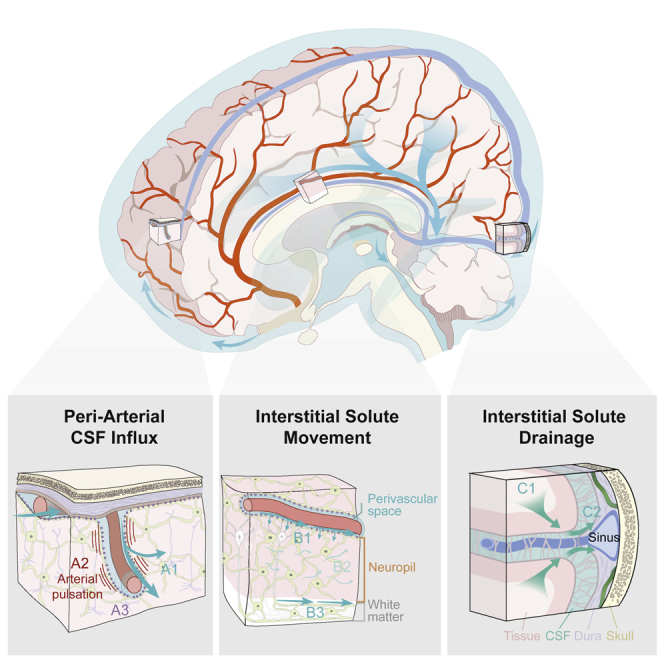
In Figure 1, we provide an updated glymphatic model in which insights collected over the past nine years have been incorporated. The most important novel aspect is that the Kipnis and Alitalo groups documented the presence and function of lymphatic vessels in the meninges surrounding the brain in 2015 (Aspelund et al., 2015; Louveau et al., 2015); more were found later (Ahn et al., 2019). Intriguingly, the initial segments of the meningeal lymphatic capillaries are in close proximity to the dural venous sinuses, towards which interstitial solutes are cleared along glymphatic perivenous pathways (Rustenhoven et al., 2021). We now understand that the glymphatic system comprises the first three segments of brain fluid transport, including periarterial CSF influx, interstitial solute movement, and efflux along the perivenous spaces and cranial and spinal nerves. Lymphatic uptake and drainage represents the fourth and final step in the clearance of brain interstitial solutes from the cranium. Another key perspective that has emerged since the initial description of the glymphatic system is that while this biology is dependent on microscopic features, such as perivascular spaces, astroglial endfeet, and meningeal lymphatic vessels, it functions at the macroscopic scale of the cranium, cerebrovascular network, CSF circulation, brain and spinal cord (Figure 1). A clear understanding of its function requires consideration of the large anatomical distances that solutes must traverse within the mammalian (and particularly the human) brain, CSF dynamics throughout the ventricular, cisternal and subarachnoid compartments, the organization of the cerebrovascular tree, including both arterial segments and venous drainage, and the manner in which intracranial pressure dynamics contribute to patterns of fluid and solute movement both within fluid-filled compartments, and through the neuropil itself.

Figure 1.

Updated schematic description of the glymphatic system (2022)

The glymphatic system supports the perivascular exchange of CSF and interstitial solutes throughout the CNS. This process occurs over macroscopic anatomical scales, within the perivascular influx of subarachnoid CSF into brain tissue organized along the scaffold of the arterial vascular network, and the efflux of interstitial solutes occurring toward cisternal CSF compartments associated with dural sinuses.

(A) CSF influx into brain tissue occurs along perivascular pathway surrounding penetrating arteries (A1) and is driven in part by arterial pulsation (A2). Perivascular bulk flow and interstitial solute clearance are dependent upon the astroglial water channel AQP4 localized to perivascular astroglial endfeet surrounding the cerebral vasculature (A3).

(B) Interstitial solute movement occurs through the combined effects of diffusion and advection. Advection is most rapid along privileged anatomical pathways, including intraparenchymal perivascular spaces (B1) and white matter tracts (B3), and supports the movement of large molecular weight solutes. Diffusion dominates the movement of small molecules, particularly within the wider interstitium (B2).

(C) Interstitial solutes drain from the parenchyma along white matter tracts and draining veins towards sinus-associated cisternal CSF compartments (C1). CSF solutes are cleared from the cranium via uptake into meningeal lymphatic vessels, by efflux through dural arachnoid granulations, or through clearance along cranial or spinal nerve sheathes (C2).

Glymphatic function and dysfunction

Biological functions of the glymphatic system

Although it has been described predominantly as “the brain’s waste clearance system”, the role of the glymphatic system in brain function extends beyond waste clearance alone. At a fundamental level, glymphatic function is understood to facilitate the exchange of fluid and solutes between the CSF and brain interstitial compartments — organized along perivascular pathways, driven by arterial pulsation and slow vasomotion, facilitated by astroglial water transport. For metabolic wastes, macromolecules and cellular debris that is not cleared by local cellular degradation or BBB transport, clearance to the CSF via glymphatic exchange and hence to the blood through lymphatic vessels reflects the principal route for elimination from the CNS. To date, no comprehensive study to define all of the solutes cleared from the CNS by the glymphatic system has been conducted. The select endogenous solutes that have been shown to be cleared by glymphatic transport include potassium (Monai et al., 2019); lactate; pathogenic peptides and proteins, including amyloid beta and tau; and soluble proteins released from damaged cells, including neuron-specific enolase and glial fibrillary acidic protein. In addition, such clearance contributes to CNS immune surveillance as perivascular exchange of soluble CNS antigens and interaction with associated peripheral immune cells (Rustenhoven et al., 2021; Plog et al., 2015; Lundgaard et al., 2017; Rasmussen et al., 2018).

In seminal work on choroid plexus function, Cserr proposed that both bulk flow and diffusion are necessary within the CNS to equilibrate solute concentrations between sources within the neuropil and the sink of the CSF, and prevent the formation of concentration gradients incompatible with neural function (Cserr, 1971). Although in the case of metabolic wastes this process can be thought of as “waste clearance”, the same process underlies the distribution of solutes from areas of local production or entry to more distant locations. Thus, glymphatic function likely contributes to such diverse processes as volume transmission by neuromodulators, growth factor distribution, and the distribution and clearance of inflammatory cytokines (Hablitz and Nedergaard, 2021). For molecules that enter the CNS primarily across the blood-CSF barrier at the choroid plexus or are produced by the choroid plexus, such as folate and apolipoprotein E, perivascular transport supports their distribution throughout the CNS (Achariyar et al., 2016).

Implications for the sleep-wake regulation of glymphatic function

A frequently overlooked element of glymphatic biology is the observation that perivascular exchange is a physiologically regulated process, and thus is not constant across different experimental conditions. Perivascular CSF influx and interstitial solute clearance are more rapid during sleep and under circadian regulation, a process that at least in part is regulated via central noradrenergic regulation of the brain extracellular space volume (Xie et al., 2013; Ding et al., 2016; Hablitz et al., 2020). Quantitative measurements of cortical extracellular space volume using the tetramethylammonium iontophoresis method (Nicholson, 1992; Nicholson and Hrabětová, 2017) showed that the extracellular space increases from $\text{∼}14\%$ to $24\%$ when awake mice transition into non-rapid eye movement (NREM) sleep or anesthesia (Xie et al., 2013). Whereas the extracellular space volume exhibited a sharp increase on loss of consciousness, the extracellular tortuosity remained unaltered (Xie et al., 2013; Ding et al., 2016). In slice preparations, beta-andrenergic receptor activation reduced ECS volume and expanded astrocyting processes, as quantified using iontophoresis (Sherpa et al, 2016). Although these observations await independent confirmation, alternative methodologies, including electron microscopy, have supported the finding that cellular structures expand during wakefulness, restricting water diffusion (Rasmussen et al., 2021). Analysis of motor and sensory cortex in mice via electron microscopy documented that cortical synapses and perisynaptic astrocytic processes expand during wakefulness, and in particular, during sleep deprivation (de Vivo et al., 2017; Bellesi et al., 2015).

Diffusion weighted MRI studies have provided mixed results. One study in human brain was not able to detect changes in the mean diffusivity between wakefulness and sleep after sleep deprivation, thereby not corroborating extracellular space volume changes (Demiral et al., 2019). However, two other studies showed that 12 h of alert wakefulness during a learning paradigm led to a decline in cortical mean diffusivity. The decrease in water diffusivity became more pronounced during sleep deprivation combined with task practice. Ventricular volume decreased, whereas subcortical volumes of gray matter and white matter increased. All reported changes reverted after recovery sleep (Bernardi et al., 2016); moreover, human brain volume decreases steadily during wakefulness (Nakamura et al., 2015). Electroencephalography studies in rodents demonstrate that slow wave activity, indicated by low-frequency oscillations between synchronous activity and inactivity, is strongly associated with glymphatic function (Hablitz et al., 2019), suggesting that slow wave sleep is the phase of sleep during which glymphatic exchange is most rapid. The evolutionary basis for sequestration of glymphatic exchange and waste clearance into periods of sleep remains speculative. One possibility is that the reduced porosity $(\text{∼}14\%)$ in the waking brain is optimized for rapid and high-fidelity neuronal network activity, but suppresses solute efflux. The sleep-associated change in porosity, in turn, supports the clearance of metabolic wastes that accumulate through the waking day. The synchronous neuronal activity of slow wave sleep may drive fluid and solute movement physio-mechanically through coupled vasomotor changes. Such coupling has been observed between k complexes (isolated slow waves) during N2 NREM sleep and CSF movement through the ventricular compartment. Conversely, the intense but asynchronous network activity characteristic of the waking brain may prevent the organized movement of fluid and solutes through brain tissue. An interesting related case is the state of hibernation, which could be explored in future studies.

Clinical relevance of glymphatic dysfunction

Neurodegenerative disease states such as Alzheimer’s disease, Parkinson’s disease, and Huntington’s disease result in cognitive impairment and dementia, and are associated with distinct neuropathology in the form of accumulation of aggregation-prone misfolded waste proteins within the cytoplasm of neurons or deposited in the interstitial space of the neuropil. For example, extracellular amyloid beta plaques and intracellular tau aggregates are the central histological feature of Alzheimer’s, whereas the abnormal accumulation and aggregation of $\alpha$-synuclein in the form of Lewy bodies are a central histological feature of Parkinson’s. (The amyloid hypothesis for Alzheimer’s disease is debated, however (Selkoe and Hardy, 2016).) The amyloid beta peptide is a normal product of amyloid precursor protein cleavage. Amyloid beta monomers can aggregate into different forms of oligomers, with sizes between 100 and 200 kD (Chen et al., 2017). Amyloid beta oligomers are soluble and can spread in the interstitial space of the CNS; however, when they convert into to a beta-sheet secondary structure, they fibrillize (Chen et al., 2017). Amyloid fibrils are insoluble and can assemble into amyloid beta plaques (Chen et al., 2017). However, there is a window of opportunity for removal of extracellular amyloid beta before it is incorporated into plaques. Stable isotope amino acid tracers in human subjects revealed that the amyloid beta turn-over rate slowed with aging. Specifically, the half-life of all amyloid beta isoforms including A$\beta$42 was reported to decrease by 60%, from 3.8 h to 9.4 h over five decades of aging (Patterson et al., 2015), suggesting that the clearance mechanisms fail with aging and calling for therapeutic action. Furthermore, increased loss of soluble A$\beta$42 was noted in subjects already positive for amyloidosis, implying rapid and irreversible aggregation in the amyloid plaques (Patterson et al., 2015; Huang et al., 2012). In contrast to amyloid beta, tau is predominantly an intracellular soluble protein. However, tau has also been reported to be passively released by cells in disease and even across synapses in a prion-like manner (Annadurai et al., 2021; Goedert et al., 2017). Approximately 75% of tau in the human brain is of the full-length type whereas the rest is truncated (Sato et al., 2018). Notably, in CSF, tau is predominantly of the truncated type which is more aggregation prone (Sato et al., 2018; Kovacech and Novak, 2010). Kinetic analysis in humans revealed that the average half-life of tau is $\text{∼}23$ days and the tau production rate is 26 pg/mL/day (Sato et al., 2018).

A key relationship between sleep disruption and Alzheimer’s-related pathology has emerged recently as well. Clinical neuroimaging studies have shown that life-long sleep disruption and short sleep duration are associated with greater amyloid beta burden in the brain of elderly subjects (Spira et al., 2013), and even one night of sleep deprivation can elevate amyloid beta levels in the hippocampus of healthy subjects (Shokri-Kojori et al., 2018). The link between sleep and brain waste disposal has been further corroborated by studies from the Holtzman group showing that the concentration of amyloid beta in CSF is lowest during sleep and increases during wakefulness (Ooms et al., 2014). The same group also showed that disruption of slow wave activity increases CSF amyloid beta levels acutely, and poorer sleep quality over several days increases tau levels (Ju et al., 2017). Recent large scale studies similarly report that shorter habitual sleep duration is associated with increased tau and amyloid beta levels (Insel et al., 2021; Winer et al., 2021). The glymphatic system contributes to the clearance of soluble amyloid beta as well as tau (Iliff et al., 2012, 2014; Patel et al., 2019) and therefore constitutes a promising and alternative therapeutic target for curbing buildup of toxic waste protein and preventing cognitive impairment. This statement is strongly supported by several studies showing that the glymphatic system clears waste solutes in a manner dependent on the brain’s state of arousal (Xie et al., 2013; Eide et al., 2021c; Eide and Ringstad, 2021), as well as cardiovascular and respiratory forces (Rennels et al., 1990; Annadurai et al., 2021; Goedert et al., 2017; Dreha-Kulaczewski et al., 2015, 2017), which are all therapeutically modifiable. More recent evidence in mouse models of Parkinson’s demonstrate that pharmacological enhancement of slow wave sleep across several months can reduce pathological $\alpha$-synuclein accumulation and increase recruitment of AQP4 to perivascular sites, suggesting a possible relevant increase of glymphatic function also in Parkinson’s (Morawska et al., 2021). Given this evidence, it is not surprising that the glymphatic system has gained tremendous interest in the neuroscience and clinical communities. As previously mentioned, the glymphatic system clears brain waste solutes — including amyloid beta and tau (Iliff et al., 2012, 2014) — in a manner dependent on the brain’s state of arousal (i.e., sleep/wake cycle (Xie et al., 2013), anesthesia (Xie et al., 2013; Hablitz et al., 2019; Benveniste et al., 2017), and circadian clock (Hablitz et al., 2020)). Specifically, glymphatic solute transport was shown to increase during sleep and with certain anesthetics compared the wakefulness, and the increase is associated with elevated prevalence of slow delta activity (Xie et al., 2013; Ding et al., 2016).

Another common form of dementia in the elderly — vascular contribution to cognitive impairment and dementia (VCID) — involves pathology of the small vessels of the brain in the form of cerebral arteriosclerosis and is the most common cause of lacunar stroke and white matter loss. VCID is associated with enlarged perivascular spaces (PVSs) on T2-or T1-weighted MRI, and clinically, these are interpreted as CSF sitting “stagnant” along the vasculature (mostly arterioles) (Brown et al., 2018; Wardlaw et al., 2020). The enlarged PVS in VCID are now thought to indicate impaired glymphatic transport for a few reasons. First, glymphatic system transport is dependent on a healthy perivascular channel network to clear waste solutes. Accordingly, if the PVS is afflicted with disease (e.g., remodeled secondary to hypertension, inflammation, or diabetes) CSF flow and glymphatic function will be adversely impacted (Benveniste and Nedergaard, 2022). Second, in rodent VCID models perivascular CSF flow is sluggish (Koundal et al., 2020). Third, VCID rat models exhibit reduced parenchymal glymphatic transport (Koundal et al., 2020; Mortensen et al., 2019).

A more recent clinical area of interest involves the increased risk of perioperative delirium and cognitive dysfunction in elderly patients undergoing surgery, which is associated with significant morbidity and mortality. The potential role of CSF flow, solute waste, and glymphatic transport underlying its pathophysiology is now an active research area (Cunningham et al., 2019; Benveniste et al., 2019a; Hov et al., 2017; Idland et al., 2017). Indeed, the dependence of glymphatic function on choice of anesthetic regimen has been well documented, and this feature is related to the anesthetic drug’s ability to induce slow wave delta activity (Hablitz et al., 2019) and also its ability to impair perivascular CSF transport by interfering with vasomotion and the physical dimensions of the PVS (e.g., vasodilation or vasoconstriction) (Ozturk et al., 2021). The various anesthetics used also have varying effects on vascular pulsatility, vascular compliance (cerebral vasoreactivity), and vasomotion, which are all key drivers of PVS CSF flow and glymphatic transport.

Glymphatic biology: Questions raised

Glymphatic modeling and experiments have raised a number of questions that are subjects of ongoing debate in the literature. In our consensus view, some of the debates stem from knowledge gaps and could be resolved by specific future work, but other debates can largely be resolved with current knowledge. A few are discussed below.

Diffusion and advection

Solutes are transported via diffusion anywhere concentrations are non-uniform and via advection anywhere fluid also flows. (We avoid the term “convection” because of ambiguity: It has sometimes been used as a synonym for advection, and sometimes to mean transport by the combined effects of advection and diffusion, which we denote “dispersion”.) Thus, both processes almost certainly act throughout the glymphatic system, but their relative importance varies. It can be quantified by the Péclet number, $\text{Pe}=UL/D$, where $U$ is a characteristic flow speed, $L$ is a characteristic length scale, and $D$ is the diffusivity. When the value is very large $(\text{Pe}\gg 1)$, advection dominates, as is typical for large molecules over long distances; when the value is very small $(\text{Pe}\ll 1)$, diffusion dominates, as is typical for small molecules over short distances (Koundal et al., 2020; Ray et al., 2019; Valnes et al., 2020). There is consensus that solute transport in the larger perivascular spaces of the subarachnoid space occurs primarily via advection. Studies using DCE-MRI in combination with small-molecular-weight Gd-based tracers in CSF found advection dominating transport not only there, but also in the larger periarterial channels along arteries penetrating into the rodent brain (Iliff et al., 2013b; Koundal et al., 2020). Advection is also known to dominate transport along privileged pathways like white matter tracts (Iliff et al., 2012). Furthermore, regularized optimal mass transport (rOMT) analysis revealed high-speed transport suggestive of advection in the cerebellum, but not in the forebrain (Koundal et al., 2020), consistent with the facts that cytoarchitecture and blood vessel architecture differ from cerebellum to cortex, and that AQP4 expression is higher in cortex (Hubbard et al., 2015). The cerebellum is also very old from an evolutionary perspective (it occurs in lampreys), and its particular features might favor fast solute transport.

Whether advection is appreciable in the interstitial compartment remains an open question. Bulk flow in the interstitium would be necessary for conserving fluid mass if net CSF motion along periarterial spaces is directed into the brain. In the original description of the glymphatic system a small molecular weight solute (A594, with molecular weight 759 Da) was reported to distribute rapidly and almost ubiquitously across the mouse brain within $\text{∼}30$ min (Iliff et al., 2012). This result, as well as other data obtained using in vivo two-photon microscopy and ex vivo optical imaging, led to the conclusion that transport of small-molecular-weight solutes in the glymphatic system, including the neuropil, was rapid and partly advective (Iliff et al., 2012; Nedergaard, 2013). However, this concept has since been challenged by several investigators (Jin et al., 2016; Smith et al., 2017; Abbott et al., 2018; Asgari et al., 2015, 2016; Holter et al., 2017). Recently it was suggested solutes move through brain parenchyma via diffusion down a concentration gradient maintained by perivascular advective flow (Thomas, 2019). Because glymphatic solute transport depends on what anesthetics are used in an experiment, comparison of results across laboratories has been difficult. We do know, however, that interstitial solute efflux depends on perivascular localization of AQP4 (Iliff et al., 2012; Mestre et al., 2018a) and is faster during sleep (Xie et al., 2013; Hablitz et al., 2019, 2020). The Cserr group showed that solute efflux occurs independently of molecular weight, which is a hallmark of advective transport (Cserr et al., 1981). Resolving the question of advective transport in the neuropil will require novel non-invasive approaches with high spatial and temporal resolution.

The role of AQP4 in glymphatic function

AQP4 is an astroglial water channel that localizes primarily to the perivascular endfeet ensheathing the cerebral vasculature. Although implicated in early studies in the formation and resolution of cerebral edema following brain injury, the physiological role for this pattern of localization remained unclear. In the initial description of the glymphatic system in 2012, the authors reported that deletion of the AQP4 gene impaired perivascular CSF tracer influx and the clearance of interstitial solutes. In a subsequent study, Verkman et al. saw no effect from gene deletion on CSF tracer influx (Smith et al., 2017). Based on these findings, the role of AQP4 in perivascular fluid and solute exchange, and indeed the glymphatic model, were proposed to be refuted. However, a subsequent collaborative study aggregating data from five different research groups utilizing four separate null mouse lines found gene deletion affected both CSF solute influx and interstitial solute efflux (Mestre et al., 2018b). In addition, in this study, glymphatic function was impaired by deletion of the Snta1 gene, which results in the loss of perivascular AQP4 localization. An included meta-analysis demonstrates consistent results across comparable studies, excepting that of Verkman et al. Verkman et al. utilized different injection approaches than the other studies and an anesthetic regime that in previous work markedly suppressed glymphatic function (Hablitz et al., 2019). These results clearly establish the key role of the astroglial water channel AQP4 in perivascular glymphatic function and highlight the importance of using experimental methods, including injection protocols and anesthesia, that perturb physiological conditions minimally. The possible mechanisms by which AQP4 affects glymphatic flow are discussed in Interfaces to perivascular spaces, below.

Directions of periarterial fluid flow and implications for cerebral amyloid angiopathy

Observing that amyloid beta accumulates in the walls of penetrating and surface arteries in cases of cerebral amyloid angiopathy (CAA), Weller et al. proposed that the intramural spaces of the walls of the arteries serve as efflux pathways for interstitial solutes (Albargothy et al., 2018). Beginning with the initial description of the glymphatic system in 2012, and in subsequent studies from multiple groups in both rodents and humans, the observed influx of CSF solutes into brain tissue along perivascular spaces surrounding arteries, and the clearance of interstitial solutes like amyloid beta along perivenous and white matter tracts towards sinus-associated cisternal CSF compartments, appeared to contradict this periarterial efflux route. More recently, Carare et al. have reported that intra-parenchymally injected tracers, including amyloid beta, localize to the basement membranes of arteries and veins as early as 30 min after injection (Albargothy et al., 2018; Carare et al., 2008). The divergent findings of amyloid beta clearance along veins versus arteries have led to controversy in the field of brain waste clearance (Abbott et al., 2018; Agarwal and Carare, 2020; Benveniste et al., 2019b; Hladky and Barrand, 2018; Mestre et al., 2020b). The periarterial clearance concept — referred to as the intramural periarterial drainage (IPAD) model — states that glymphatic influx of CSF (including soluble amyloid beta) occurs along the basement membranes on the outside of the artery walls, and the clearance of amyloid beta from the neuropil happens along the basement membrane of capillaries, continuing upstream into the basement membranes of smooth muscle cells within the walls of arterioles and arteries (Albargothy et al., 2018; Aldea et al., 2019). There are several pieces of information that are important to contextualize for understanding these two opposing viewpoints.

First, there is general consensus that small molecular weight CSF solutes and waste including tau drain via the glymphatic system from the CNS via meningeal and extracranial lymphatics (Engelhardt et al., 2016; Aspelund et al., 2015; Louveau et al., 2015; Ahn et al., 2019; Patel et al., 2019; Eide et al., 2018). Second, although the exact anatomical constructs connecting the glymphatic and lymphatic systems are still actively investigated, recent data from human brain acquired using DCE-MRI show that Gd-based tracers from CSF and brain parenchyma egress the CNS partly via a transitional hub, the parasagittal dura, which runs along the superior sagittal sinus (Ringstad and Eide, 2020), implying that waste clearance is indeed perivenous. These clinical studies are supported by data in rodents revealing the existence of an extensive network of meningeal lymphatic vessels with valves along the sigmoid and petrosquamosal venous sinuses and in the dura covering the skull base, which drain to the cervical lymph nodes (Ahn et al., 2019). Furthermore, the dorsal and ventral meningeal lymphatic vessels may serve as connective hot spots for glymphatic egress of macromolecules from the brain parenchyma or CSF (Ahn et al., 2019; Rustenhoven et al., 2021), implying that there are direct connections between the two systems. That said, the precise distribution of CSF drainage by lymph vessels is not yet known. Ahn et al. (Ahn et al. (2019) argued that basal meningeal lymphatic vessels carry more CSF than dorsal ones, and Ma et al. (Ma et al. (2017) found no tracer uptake by dorsal meningeal lymphatic vessels. Further studies will clarify the relative importance of the various vessels in clearing CSF.

Third, the IPAD model is grounded in the neuropathological signature of CAA (Albargothy et al., 2018; Carare et al., 2008; Agarwal and Carare, 2020), the rapid association of injected amyloid beta with arterial basement membranes, and an anatomical division between glymphatic influx along arterial perivascular spaces and the intramural basement membrane. CAA presents as two subtypes: CAA type 1, where amyloid beta accumulates along cerebral microvessels and capillaries, and CAA type 2, where amyloid beta accumulation occurs within the walls of small arteries and arterioles, primarily in the leptomeninges and cortex (Thal et al., 2002). At least initially, it has seemed difficult to reconcile the deposition pattern of amyloid beta in CAA type 2 with the glymphatic model including perivenous drainage. However, the clearance of a solute along a pathway is likely to preclude accumulation along that pathway. It is possible that the deposition of amyloid beta in arterial walls reflects retention because of matrix interactions or perhaps the stagnation of periarterial influx, rather than the physiological route for amyloid beta clearance. Indeed, CAA is clinically associated with greater perivascular space dilation. A similar critique applies to the studies reporting rapid association of injected amyloid beta with arterial segments. It is possible that this rapid association reflects binding and retention of amyloid beta with arterial basement membranes or is an artifact of the intraparenchymal injection technique. Because these studies were not carried out with time-resolved imaging, it is difficult to compare them with the dynamic imaging studies that have demonstrated periarterial CSF tracer influx. In addition, tracer can move great distances and enter different tissue during death (Mestre et al., 2020a) and perfusion (Mestre et al., 2018a), so postmortem imaging is unavoidably prone to significant artifacts.

Substantial intramural flows along arterioles would also seem to be prevented by fluid dynamics. Intramural spaces in arteriole basement membranes have lateral sizes on the order of 100 nm (Keith Sharp et al., 2019), whereas perivascular spaces have lateral sizes of a few microns around murine penetrating vessels (Iliff et al., 2012), 40 $\mu$m around murine pial vessels (Mestre et al., 2018a), and 300 $\mu$m around human pial vessels (Bedussi et al., 2018). For flow in any of these spaces, all else being equal, the volume flow rate scales as the lateral size to the fourth power, according to the Hagen-Poiseuille equation. Thus, estimating the size of the space in the arteriole basement membrane to be smaller than the perivascular space by a factor of ${10}^2$, we expect that, in each minute, the volume of fluid carried along the basement membrane is less than that carried along the perivascular space by a factor of ${10}^8$. Fluid flows hypothesized to occur in basement membranes, if they exist, are therefore likely to cause so much less transport than observed perivascular flows as to be negligible and probably unmeasurable.

Lastly, although the IPAD model presupposes a functional separation between arterial PVS influx routes and intramural efflux routes, its anatomical basis remains unclear. The initial study characterizing glymphatic function in the rodent brain clearly demonstrated that fixable CSF tracers entering along periarterial influx routes had relatively unrestricted access to the basement membranes between the vascular smooth muscle cells and the underlying endothelial cell layer. However, the relationship between glymphatic function and dysfunction and the occurrence of CAA remains poorly understood. One possible explanation could be that amyloid beta oligomers taken up by phagocytotic vascular smooth muscle cells act as the seeds that initiate vascular amyloidosis (Soltoff-Schiller et al., 1976). Another explanation could be that the reduction in glymphatic flow in aging (Kress et al., 2014), combined with a multitude of age-related changes, including stiffening of the arterial wall, enlargement of the perivascular spaces, reactive gliosis, and changes in intracranial pressure (Wen and Wong, 2019), may lead to stagnation of periarterial fluid, increasing the likelihood of amyloid beta aggregation. Clearly, further experiments are required to understand the underlying mechanisms for waste deposition patterns in CAA, in particular CAA type 2.

In vivo approaches that inform glymphatic modeling

Seeing that many of the outstanding questions for glymphatic modeling can be resolved only with the help of additional experimental measurements, having noted that measurements can depend sensitively on experimental technicalities like anesthesia type and injection protocols, and having pointed out that postmortem measurements may not reflect the biology of living animals, here we present practices that can help future experimental studies maximize their benefit for modeling.

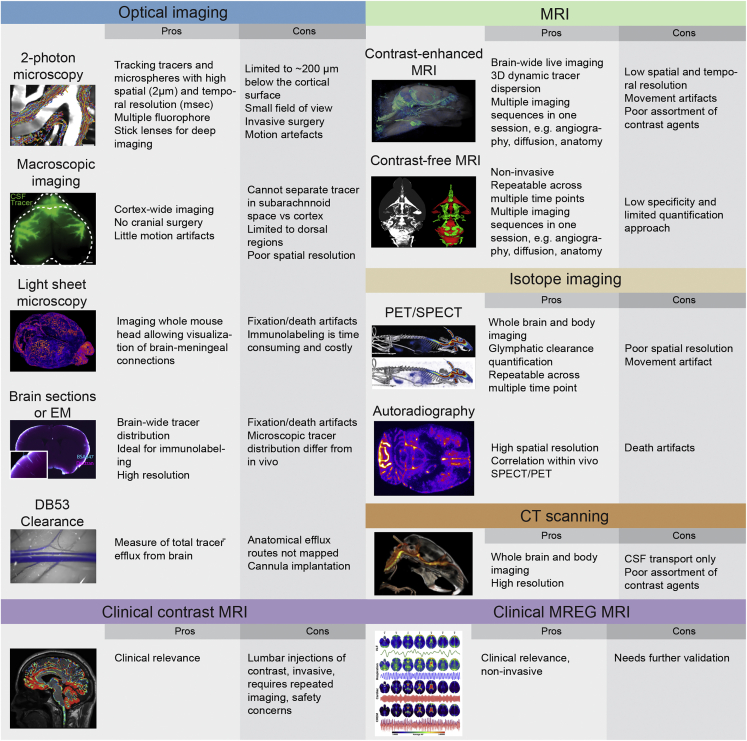
The glymphatic system relies on three steps to function: influx of CSF via perivascular spaces, mixing of CSF with ISF, and clearance of the fluid that has travelled through brain tissue. The first two steps are the focus of most glymphatic assays and have been shown to vary greatly in disease models. The initial discovery of the glymphatic system was made using dynamic two-photon imaging in vivo (Iliff et al., 2012), which has been further developed to track the movement of individual particles (Mestre et al., 2018a). Two-photon microscopy offers excellent resolution (0.5 to 1 $\mu$m in-plane, 1.5 $\mu$m out-of-plane) but with limited tissue penetration (to 200 $\mu$m or a bit more, depending on contrast), and the frequent need for a cranial window (Figure 2).

Figure 2.

Overview of experimental techniques that can inform glymphatic modeling

¹In spite of the mathematician Gelfand’s claim that “there is only one thing which is more unreasonable than the unreasonable effectiveness of mathematics in physics, and this is the unreasonable ineffectiveness of mathematics in biology”, the powerful mathematical methods developed with the understanding of inorganic matter are often surprisingly useful (Wigner, 1990).

Imaging of the entire dorsal cortex can be performed using epifluorescence microscopy through an intact skull. This approach is valuable for tracking perivascular CSF tracer influx and for studies in awake mice. The main limitation of this type of macroscopic imaging is its lack of depth information, particularly its inability to distinguish tracers in the subarachnoid space from those in cortical tissue (Plog et al., 2018).

Light sheet microscopy has allowed 3D imaging of the entire rodent brain (Bèchet et al., 2020) and parts of a pig brain (Bèchet et al., 2021), with the potential for slightly larger brains. Such imaging gives access to parameters including average influx depth and number of influx sites per cortical area, while causing little photobleaching or phototoxicity. Observing variations in time can be difficult, however, because light sheet imaging cannot be done in vivo.

Tracer influx can also be imaged in postmortem brain slices, using equipment that is readily available in many laboratories, with high resolution. However, time-lapse imaging is not possible, so death effects again complicate data interpretation, and sample collection is labor-intensive (Figure 2). Although most optical imaging is centered on studying influx of CSF tracers, assays for efflux are being developed (Iliff et al., 2013a; Lee et al., 2015; Evans et al., 2020; Stanton et al., 2021).

MRI techniques can provide global, time-lapse imaging which enables investigations of both influx and efflux rates. MRI can detect glymphatic function by measuring signal from paramagnetic (Gd³⁺) tracers or from brain water itself (phase contrast MRI, blood-oxygen-level-dependent (BOLD) MRI). Experiments show Gd³⁺ tracers are distributed brain-wide in less than 24 h, with timing varying among diseases (Ringstad et al., 2017, 2018; Eide et al., 2021b) and with sleep (Eide and Ringstad, 2021). Novel high-speed techniques can measure flow (Dreha-Kulaczewski et al., 2017) and tissue deformation (Sloots et al., 2020) on short timescales. Recent studies have used BOLD techniques to measure motions of free CSF (Posse et al., 2013; Kiviniemi et al., 2016; Fultz et al., 2019; Hennig et al., 2020). However, MRI imaging in animals that are not anesthetized can be difficult to interpret, because the loud noises made by MRI machines may induce a stress response in animals (Cai et al., 2020). Computed tomography (CT) and positron emission tomography/single-photon emission computed tomography (PET/SPECT) scans may also prove to be viable ways of measuring CSF tracer influx and clearance in vivo (2).

Recently-developed super-resolution microscopy techniques enable optical imaging with resolution well beyond the diffraction limit through the use of fluorescent tracers. Single-molecule localization microscopy (SMLM) works by inducing fluorescence in a small, isolated tracer, such as a carbon nanotube, and has been used in acute brain slices to reveal significant local variations in the spaces between cells, with implications for the porosity and tortuosity of brain tissue (Godin et al., 2017). When tracer molecules cannot be isolated, resolution can still be increased by reducing the effective size of the laser spot that excited fluorescence, as in stimulated emission depletion (STED) microscopy, which has been used to visualize neurons and glia (Arizono et al., 2020; Nägerl et al., 2008) as well as the structure of the extracellular space surrounding them (Tønnesen et al., 2018). Technical challenges have so far prevented in vivo use of these super-resolution techniques but may soon be overcome.

Beyond the question of imaging techniques, accurate study of the glymphatic system requires carefully avoiding creation or alteration of pressure gradients in the brain, because even small gradients can drive substantial flow. For example, craniectomy without penetration of the dura mater impairs glymphatic circulation (Borha et al., 2020; Plog et al., 2020). In one study, preparation of a cranial burr hole and insertion of a glass pipette through the dura mater and into the brain parenchyma suppressed CSF tracer influx by $40\%$ (Mestre et al., 2018b). Many imaging methods involve invasive injection of tracer into the cisterna magna. Leaving the needle in place during experiments reduces acute trauma. Still, tracer injection can increase the intracranial pressure (ICP), and many researchers have noted the potential for that increase to drive artifactual flows (Smith et al., 2017; Keith Sharp et al., 2019; Smith and Verkman, 2018; Croci et al., 2019; van Veluw et al., 2020; Vinje et al., 2020; Kedarasetti et al., 2020b; Faghih and Keith Sharp, 2021). One recent study found that after injecting 10 $\mu$L of fluid at a rate of 2 $\mu$L/min into the cisterna magnas of mice, ICP increased by 2 mmHg (Raghunandan et al., 2021). Theoretical estimates predict that if the pressure were 2 mmHg higher in one region of the murine skull than in another, robust fluid flow would ensue. On the other hand, a spatially uniform ICP change would cause no flow at all. Moreover, ICP variations greater than 2 mmHg occur when mice change their body position or sneeze (Lee et al., 2015). In further experiments in the same study, 20 $\mu$L was injected at 2 $\mu$L/min while fluid was simultaneously withdrawn at the same rate through a second cannula. In those experiments, ICP did not change over time, but flow in pial PVSs were statistically indistinguishable from the earlier experiments, suggesting that injecting 10 $\mu$L into the murine cisterna magna at 2 $\mu$L/min perturbs flows minimally (Raghunandan et al., 2021). More broadly, since flow is driven not by ICP but by its spatial variation, and because in vivo measures of that spatial variation have been achieved only twice (Eide et al., 2012; Young et al., 2021), using future models to estimate pressure variation could substantially advance the field.

That said, pressure changes are not the only perturbations that can be caused by invasive imaging techniques, and we urge the use of noninvasive techniques whenever possible.

Mechanisms

Because the glymphatic system comprises a brain-wide, coordinated network for fluid and solute transport, modeling it meaningfully requires considering both global and local effects and accounting for a wide variety of mechanisms. Although an exhaustive discussion of all mechanisms would be impossible until much ongoing and future work is completed, we highlight key mechanisms. The discussion in this section is about the mechanisms themselves, their implications, and what we know about them from prior work; actually modeling them is the topic of the next section. The mechanisms comprise the entire glymphatic pathway: flow in PVSs, transport in brain parenchyma, links between PVSs and parenchyma, and brain efflux routes. The section concludes with a discussion of mechanistic links to neuronal activity.

Perivascular flow

In the glymphatic model, CSF enters the brain along periarterial spaces, so our discussion of drivers and modulators begins there. Given decades of in vivo evidence of flow in perivascular spaces, it is natural to wonder what fluid dynamical mechanisms propel CSF and set its net flow direction. Pumping mechanisms are known most clearly for the pathological cases of stroke and cardiac arrest, in which in vivo flow measurements can be matched reasonably closely, at both local and global scales, by assuming that flow is driven by the contraction of arteries with the passing of a wave of spreading depolarization (Mestre et al., 2020a; Du et al., 2022).

Physiological pumping mechanisms are less certain, and many have been proposed. Although respiration modulates lymphatic flow and is expected to influence CSF flow in perivenous spaces (Santisakultarm et al., 2012) and ventricles (Fultz et al., 2019; Vinje et al., 2019), flow in periarterial spaces evidently pulses in synchrony with the heart (Mestre et al., 2018a; Bedussi et al., 2018); respiration seems to play a role only incidentally, when it occurs in step with the heartbeat (Mestre et al., 2018a). Similarly, another recent study found that strong respiratory pulsations in the human brain modulate cardiac pulsations in central CSF spaces (Raitamaa et al., 2021). Given the synchrony between periarterial flow and the heart, it has long been hypothesized that the waves of constriction and dilation that travel down artery walls with each heartbeat (now detectable with MRI (Rajna et al., 2021; Tuovinen et al., 2020)) might drive not only CSF oscillation but also a net motion of CSF in periarterial spaces, parallel to the blood (Hadaczek et al., 2006; Wang and Olbricht, 2011), in a mechanism dubbed “perivascular pumping”. Experiments have demonstrated that in physiological conditions, artery wall velocities closely match CSF velocities in pial perivascular spaces, and that altering artery wall motion (by raising the blood pressure to cause arterial stiffening) significantly reduces CSF flow (Mestre et al., 2018a), suggesting that artery wall motion at the cardiac frequency plays an important role. On the other hand, one team has also pointed out that net CSF flow antiparallel to blood could occur in certain cases of wave reflection (Coloma et al., 2016, 2019). Net flow might also be driven in part or entirely by the global change in cranial blood volume with each heartbeat, which would likewise produce lock-step synchrony with the heart, as observed in vivo. To the extent that cardiac pulsations cause CSF flow, arrhythmia might lead to pathological glymphatic function; future studies should address this possibility.

Another alternative is that cardiac pulsation and blood volume change drive oscillations but not the observed net flow, which is caused by other mechanisms. Even small pressure gradients, on the order of 1.5 mmHg/m, would be sufficient (Kedarasetti et al., 2020b; Daversin-Catty et al., 2020). Actual pressure gradients are not well-known. Eide et al. (2012) measured ICP simultaneously at two locations in the human skull, finding differences of a few mmHg. Young et al. (2021) measured ICP simultaneously in the cranial and spinal subarachnoid spaces of alligators, finding differences of similar magnitude. To our knowledge, no other studies have measured ICP at more than one location simultaneously, so making accurate estimates of pressure gradients is difficult. Linninger et al. (2009) used temporal pressure variations and model parameters to estimate that pressure differences among brain CSF compartments might be as large as 1 mmHg, agreeing with the experimental measurements (Eide et al., 2012; Young et al., 2021). If present in a $\text{∼}10$ mm mouse brain, such pressure differences would imply pressure gradients significantly larger than the 1.5 mmHg/m required to drive observed flows. Thus, it is useful to consider mechanisms that might cause steady pressure gradients.

One such mechanism is functional hyperemia, the process by which additional blood is routed to active regions of cortex, depending on brain state (Fultz et al., 2019; Kedarasetti et al., 2020a). The corresponding vasodilation would displace CSF in perivascular spaces unless the outer boundaries expand by the same amount, which is unlikely. However, like cardiac pulsation, functional hyperemia could drive oscillations without net flow, albeit on longer timescales. Early work proposed that fluid secretion across the blood-brain-barrier could drive flow (Cserr et al., 1981; Bradbury and Cole, 1980) in the parenchyma, and secretion has recently been measured via MRI, suggesting CSF is produced not only near choroid plexus but also in the subarachnoid space (Petitclerc et al., 2021). By extension, secretion might drive flow in perivascular spaces as well, but it has not been measured directly and can be estimated only roughly (Hladky and Barrand, 2014, 2018), so we will not discuss it further. However, a recent study based on direct measurements of CSF production in mice found that production and glymphatic fluid transport are regulated differently and can change independently (Liu et al., 2020). In any case, the relative importance of flow drivers almost certainly varies by location and depends on brain state.

Another mechanism is CSF production by the choroid plexus, which presumably involves an osmotic pressure sufficient to drive some flow. Osmotic (Starling) forces are considered in (Buishas et al., 2014; Linninger et al., 2017), which make ambitious attempts at global modeling of the water and solute transport through the brain. Osmotic forces require membranes over which they can act, and the membranes considered are in choroid plexus, blood brain barrier, extracellular spaces, pia mater, and the lining around the ventricles.

The characteristics of perivascular spaces affect flows there and can inform models of potential pumping mechanisms. Because veins lack smooth muscle cells and are compliant, they seem less likely to pump perivenous fluid, although blood volume changes might still play a role; additional experimental study is needed. Crucially, the porosity of perivascular spaces likely varies from proximal to distal parts of the glymphatic system; pial periarterial spaces are known to be open (not porous) (Min Rivas et al., 2020), but elsewhere, the porosity is unknown. Shapes also matter. Pial periarterial spaces typically have elliptical cross-sections (Mestre et al., 2018a; Bedussi et al., 2018; Schain et al., 2017), whereas penetrating periarterial spaces typically have nearly circular cross-sections with their arterioles placed eccentrically to one side. Both shapes have lower hydraulic resistance (pressure drop per volume flow rate) than circular concentric annuli of the same size (Tithof et al., 2019). With perivascular pumping, elliptical cross-sections would cause azimuthal flow — pulsatile fluid motions along orbits around the axis of the artery (Thomas, 2019; Carr et al., 2021; Coenen et al., 2021). Also, pial periarterial spaces can communicate directly with pial perivenous spaces (Bedussi et al., 2017), are connected via more anastomoses, and are larger than penetrating periarterial spaces. Periarterial spaces are commonly thought to attenuate and end before reaching the capillaries, but pericapillary spaces have been speculated to exist (Hannocks et al., 2018; Ferris, 2021) and would presumably have characteristics different from either pial or penetrating periarterial spaces.

Transport in brain parenchyma

If tissues throughout the brain rely on fluid transport to eliminate waste and deliver nutrients, then much of that transport must occur in brain parenchyma, and particularly, in the extracellular space (ECS). Transport there has often been measured using radiotracers, and more recently using two “point-source paradigms”. The latest technical approach utilizes single particle tracking of carbon nanotubes. A review of transport in the ECS appeared in 2008 (Syková and Nicholson, 2008), and more recent ones are now available (Nicholson and Hrabětová, 2017; Soria et al., 2020; Sun and Sun, 2021).

These measures typically presume that diffusion dominates transport in the ECS, consistent with the fact that advection is relatively weak for transport of small molecules over short distances (see Section Rapid review). Diffusion analysis provides three pieces of information. The first is an effective diffusivity in the brain for a given molecule, such as a metabolic waste product, drug, or probe molecule (see (Syková and Nicholson, 2008; Fenstermacher and Kaye, 1988) for selected values). The second is the porosity (volume fraction) of the ECS, defined as $\alpha =V_{\text{ECS}}/V_{\text{total}}$, the ratio of the ECS volume $V_{\text{ECS}}$ to the total tissue volume $V_{\text{total}}$. The third is the tortuosity, which is a measure of the hindrance that a molecule experiences because of the structure of the brain. Tortuosity is defined as $\lambda =\sqrt{D/D^{\ast }}$, where $D$ is the free diffusivity of a molecule and $D^{\ast }$ is the effective diffusivity in brain tissue. Both porosity and tortuosity are characteristics of the ECS structure.

The radiotracer method was developed by Rall, Fenstermacher and Patlak in the 1970s (Fenstermacher and Kaye, 1988). In it, the ventricles of an anesthetized animal are perfused with a radiotracer that spreads into adjacent brain regions. After a chosen time, the animal is euthanized and the brain fixed. Then, small samples of tissue are taken along a path normal to the surface of the brain, and the radiotracer content is counted in each sample and analyzed using a solution to the diffusion equation. Studies with sucrose and inulin showed that $\alpha$ was 18% to 20% in the cerebral cortex in several species (Levin et al., 1970) and $\lambda$ was $\text{∼}1.5$ in the dog caudate nucleus (Fenstermacher and Patlak, 1976). The major disadvantages of this method are that there is only one time point per animal and tissue samples are 0.5 mm to 1 mm thick, so spatial resolution is low.

In the context of the glymphatic system, Rosenberg et al. (Rosenberg et al. (1980) used the radiotracer paradigm to look for bulk flow in the ECS in cat caudate nucleus. They concluded that there was flow in white matter bundles with a velocity of 10.5 $\mu$m/min but zero flow velocity in gray matter. The gray matter measurements were criticized by Cserr et al. (Cserr et al. (1981) because they did not account for the vectorial nature of flow. Ultimately, the radiotracer method is unlikely to be sensitive enough to reveal reliable flow data.

The “point-source paradigm” was first realized in the real time iontophoresis (RTI) method introduced by Nicholson and Phillips (Nicholson and Phillips, 1981). A small extracellular probe ion, typically tetramethylammonium, was released from a micropipette by iontophoresis and the concentration measured $\text{∼}100\mu$m away using an ion-selective microelectrode. The parameters $\alpha$ and $\lambda$ were extracted by fitting a solution of the diffusion equation to the concentration verses time curves. Measurement time was of the order of a minute, enabling real-time changes in brain environment to be monitored. The RTI technique confirmed that $\alpha$ was about 20% and $1.5\le \lambda \le 1.6$ in several brain regions in rats, mice, and other species (Syková and Nicholson, 2008). These results were obtained in anesthetized animals or brain slices. When measurements were made in awake mice $\alpha$ was found to be only 14% (Xie et al., 2013). In contrast, in ischemia or anoxia, $\alpha$ fell to about 5% (Syková and Nicholson, 2008), which is typically the value seen in classical electron microscopy, where the ECS is known to be largely obliterated. Limitations of the RTI method include the fact that it can only be used with a few small charged molecules and requires an invasive procedure that may alter transport.

The point-source paradigm was extended to macromolecules with the introduction of the integrative optical imaging (IOI) method (Nicholson and Tao, 1993). A micropipette was again used as a source and a small volume of fluorescently labeled molecules pressure injected into brain tissue. The resulting cloud was imaged, and the intensity distribution fitted to a solution to the diffusion equation enabling $\lambda$ to be extracted. An important finding was that $\lambda$ increased with molecular size. This increase was attributed to interaction with the “walls” of the ECS, an interpretation bolstered by applying restricted diffusion theory, which also indicated an ECS average width of about 40 nm (Nicholson and Hrabětová, 2017; Thorne and Nicholson, 2006).

Ray et al. (Ray et al. (2019) showed that variation in a set of in vivo RTI measurements could be matched more accurately with a model that included, in addition to diffusion, advective transport with superficial flow speeds as high as 50 $\mu$m/min. However, similar experimental variability occurs in RTI measurements in brain slices, where no flow is expected. If such flows do occur, we would expect advection to cause solute transport at rates similar to diffusion, if a bit less, as evidenced by the Péclet number: taking $U=250\mu$m/min ($=U_s/\alpha$, with superficial speed $U_s=50\mu$m/min and porosity $\alpha =0.2$), $L=250\mu$m (a typical separation distance between penetrating vessels in the cortex) and $D=0.18\mu {\text{m}}^2$/ms for A$\beta$42 (Waters, 2011) gives $\text{Pe}=5$. Thus, both diffusion and advection would contribute significantly to A$\beta 42$ transport in the ECS. Of the point-source measurement methods, IOI would be more likely to detect advection effects because it uses larger molecules (hence, smaller $D$ and larger Pe). RTI, which uses small molecules, would be affected much less. MRI, perhaps in combination with rOMT, may be a more promising method for quantifying flow in the ECS (see Section Quantifying and defining glymphatic transport with optimal mass transport).

The idea that osmotic pressure differences could be a basic mechanism for transport in the brain parenchyma has been explored recently by Halnes et al. (Halnes et al. (2019). Previously, some of the same authors developed a scheme for the quantifying concentrations of Na⁺, K⁺ and Cl^- in the ECS (Halnes et al., 2013). The more recent paper considered how ion dynamics could drive flow by osmosis across astrocyte membranes, which have high permeability thanks to AQP4 channels. With concentration differences around 60 mM, osmotic pressure differences were predicted to reach 1000 mmHg, which would dominate all other pressure differences in the ECS. Thus, osmotic flows might play a key role in the glymphatic system, and further study is warranted.

Recent studies show that ECS volume can change dynamically during physiological and pathological events on multiple time scales: over a day (sleep-wake cycle), over minutes (spreading depolarization), and in seconds (epilepsy). The volume fraction $\left(\alpha \right)$ is about 20% in anesthetized animals and brain slices so it was a surprise when Xie et al. (Xie et al. (2013), using the RTI-TMA method in mouse cortex, found that $\alpha$ changed from 23% to 14%, as the sleeping animal awoke. This state transition is mediated by noradrenergic innervation (Constantinople and Bruno, 2011), and Sherpa et al. (Sherpa et al, 2016) confirmed that activation of adrenergic receptors in brain slices reduced $\alpha$ from 22% to 18%. Spreading depolarization (SD; also known as spreading depression) is an abnormal transient depolarization of a population of brain cell that propagates at about $3\text{mm}\cdot {\text{min}}^{-1}$ in the cortex and elsewhere (Somjen, 2001; Lauritzen and Strong, 2017). SD-like events can occur in migraine headaches, ischemia, trauma, and seizures (Somjen, 2001; Lauritzen and Strong, 2017; Hartings et al., 2017). The ECS shrinks dramatically during SD (Van Harreveld and Khattab, 1967; Phillips and Nicholson, 1979) and Hrabe and Hrabetova (Hrabe and Hrabetova, 2019) introduced time-resolved IOI and showed that diffusion of a small extracellular marker (3000 Da) briefly ceased at the peak of SD. Epileptic seizures represent abnormal synchronous excitatory activity in neurons. Colbourn et al. (Colbourn et al. (2021) infiltrated the ECS with tetramethylammonium and used ion-selective microelectrodes to reveal a new phenomenon they called rapid volume pulsation (RVP). This transient reduction of $\alpha$ coincided with the local field potential spikes of epileptic activity. The studies of sleep, SD, and seizure demonstrate that the volume of the ECS compartment can change in response to brain activity over a range of timescales.

Super-resolution fluorescence microscopy enables live imaging of fluorescent probes beyond the classic diffraction limit of light microscopy. Two implementations are especially relevant to the ECS. The first is single molecule light microscopy exemplified by the use of single-walled carbon nanotubes (Godin et al., 2017; Paviolo et al., 2020) that are intensely luminescent, photostable, and work in the near-infrared. The nanotubes are highly elongated and diffuse slowly, enabling single-molecule tracking. Application in acute brain slices reveals local ECS to be very heterogeneous, with many inter-cellular gaps greater than 100 nm. In addition, nanotube imaging can distinguish the geometric and viscous components of diffusion and look at structural changes (Godin et al., 2017; Soria et al., 2020; Paviolo et al., 2020). The second super-resolution implementation is point-spread function engineering that optically shrinks the fluorescent spot, achieving a spatial resolution of tens of nanometers, exemplified by STED microscopy (Arizono et al., 2020; Nägerl et al., 2008). To apply this to the ECS, Nägerl et al. combined 3D-STED microscopy with a diffusible, membrane-impermeable, fluorescent dye in the ISF, and called the method super-resolution shadow imaging (SUSHI) (Tønnesen et al., 2018). This technique enabled visualization of ECS structure in organotypic slices derived from mouse hippocampus (Arizono et al., 2020; Tønnesen et al., 2018; Paviolo et al., 2020). The width of the local ECS measured by SUSHI was highly heterogeneous, ranging from below the 50 nm resolution limit of SUSHI to above 1 $\mu$m. Most gaps exceed 100 nm, in agreement with electron microscopy of cryofixed tissue (Korogod et al., 2015) and nanotube imaging. Local ECS volume fraction averaged around 20%. After technical limitations are overcome, these two super-resolution techniques should work in the intact brain in vivo; already, however, they reveal heterogeneity of the ECS on a nanoscopic scale that may impact glymphatic models.

Interfaces to perivascular spaces

Meaningfully modeling solute transport in the parenchyma requires accounting for phenomena at the interfaces between parenchyma and perivascular spaces. Likewise, meaningfully modeling flow (and transport) in PVSs requires accounting for phenomena at those same interfaces, as well as the proximal interfaces between PVSs and other fluid compartments. A few mechanisms are known to have important implications.

First, consider interfaces between PVSs and other fluid compartments. In experiments, tracer is often injected into the cisterna magna, but not all CSF there, or in subarachnoid spaces, is drawn into PVSs. Rather, two studies found that for small tracers, approximately 20% enters the brain (Xie et al., 2013; Lee et al., 2018). The percentage is probably smaller for larger tracers because influx of a CSF tracer is an inverse function of its molecular weight. A more recent study used a heavy isotope of water, ${\text{H}}_2^{17}$O, with molecular weight just 19 Da, orders of magnitude less than common contrast agents or fluorescent dyes, and found much more than 20% influx (Alshuhri et al., 2021). Small molecular weight, however, may not be the sole cause of the observed difference because many membranes pass water but block other molecules, e.g., via AQP4. Moreover, subarachnoid CSF is not the only source of ISF: Vascular fluid crosses the blood-brain-barrier to form additional ISF (Petitclerc et al., 2021). This idea is debated, and albeit no definitive proof has been presented, it is estimated that the contribution of vascular fluid to ISF is in the range of 20 to 100% (Rasmussen et al., 2021). Based on these lines of evidence, it can be concluded that ISF is not static but rather constantly being exchanged with surrounding fluid compartments, both CSF and blood.

Second, consider interfaces between PVSs and parenchyma. AQP4 water channels are known to cover much of the endfoot surfaces that separate PVS from parenchyma (Nagelhus et al., 1998), and eliminating that localization or knocking out AQP4 altogether is known to reduce glymphatic flow (Iliff et al., 2012; Mestre et al., 2018b), but the neurological mechanism by which AQP4 regulates glymphatic flow is a topic of ongoing study. One hypothesis is that water passes from periarterial spaces, into astrocyte bodies via AQP4 channels, through the cells, and out again to perivenous spaces and/or nerve sheaths. A second (and not exclusive) hypothesis is that water and solutes pass from periarterial spaces into parenchyma through the gaps between astrocyte endfeet, with flow in the gaps being somehow controlled by AQP4. (Because AQP4 is specifically a water channel, solute molecules cannot pass through it directly.) Both of these hypotheses depend sensitively on the size, arrangement, composition, and biological activity of the endfeet, which are difficult to image in vivo. Furthermore, AQP4 is highly polarized, with a high localization at the endfeet, where a high percentage of the surface is covered by AQP4 (Nagelhus et al., 1998; Nielsen et al., 1997). However, the endfeet comprise only a fraction of the astrocyte membrane area. In fact, more than 90% of the total surface area of the astrocyte is estimated to be in the processes. As such it is hard to assess the relative importance of endfoot resistance, compared to that of the intra-cellular pathway. Although AQP4 is a highly selective water channel, the endfoot gaps are $\text{∼}20$ nm wide and allow for the passage of a range of small molecules as well. For example, amyloid beta typically has diameter of a few nm and could pass, although its oligomerized length may be $\text{∼}100$ nm. As such, the perivascular-parenchyma interface can be understood as a semi-permeable membrane involving both intra- and extra-cellular compartments, where both hydrostatic and osmotic pressure gradients may play crucial roles (Asgari et al., 2015), dependent on the astrocyte geometry and AQP4 localization. Furthermore, it has recently been shown that the size of astrocyte endfeet varies along the vasculature (Wang et al., 2021), correlating with vessel diameter. In simulations, that variation allowed near-constant flux through the endfoot gaps across the vascular generations.

Alternatively, if pericapillary spaces exist (Hannocks et al., 2018; Ferris, 2021), they might provide a continuous fluid pathway from periarterial spaces to perivenous spaces without entering the ECS. Further anatomical studies could clarify the situation.

Efflux routes

CSF influx routes have been extensively studied by optical or MR imaging approaches, yet only a few studies have dissected the path by which ISF exits the CNS (Rasmussen et al., 2021; Steven, 2021). Taking the law of conservation of mass into consideration, however, we can deduce that a large volume of fluid must be leaving the CNS: efflux must match influx. Multiple paths for fluid efflux exist, including the perivenous spaces, spaces along cranial and spinal nerves, subarachnoid granulations, and more (Rasmussen et al., 2021; Steven, 2021). The exported fluid is ultimately collected by lymphatic vessels and returned to the general circulation close to the subclavian veins. Very few studies have attempted to quantify the relative importance of the different efflux paths. In fact, it is likely that the relative volume of fluid leaving CNS by any of the efflux routes constantly changes in response to body position (Lee et al., 2015), state of brain activity, and changes in ICP. Efflux is also likely to vary in the long term, depending on age, cardiovascular health, and disease. Classical studies concluded, based on injection of radiolabeled compounds, that only a minor fraction of ISF mixes with CSF before leaving CNS (Cserr et al., 1981), but these studies await confirmation using less invasive approaches. The importance of efflux via subarachnoid granulations is also debated, as the granulations do not exist in early childhood and might be absent in most experimental animal models, including rodents.

Links to neuronal activity and vasomotion

Accurate glymphatic modeling almost certainly requires considering neuronal activity. NREM slow waves, which consist of highly synchronized neuronal up and down states (Vyazovskiy and Harris, 2013), appear to regulate glymphatic function and correlate with glymphatic activity (Xie et al., 2013; Hablitz et al., 2019). Pharmacological enhancement of slow wave sleep, e.g., via $\alpha$2-adrenergic agonists, promote glymphatic brain delivery (Lilius et al., 2019), whereas long-term slow wave sleep promotion by sodium oxybate in mouse models of Parkinson’s disease can reduce the accumulation of $\alpha$-synuclein and promote perivascular AQP4 expression (Morawska et al., 2021). Inversely, the disruption of slow waves causes A$\beta$ accumulation (Ju et al., 2017), detailing a likely causal relationship between sleep slow waves and glymphatic function. One mechanism that could explain the link is functional hyperemia: increased neuronal activity draws additional blood (Turner et al., 2020), causing arteries to expand and therefore displace CSF in the surrounding perivascular spaces. Changes in blood volume are of highest magnitude during sleep, when slow waves cause global, oscillatory changes in blood volume. Their magnitude might explain why glymphatic clearance is faster during NREM sleep than during wakefulness. In fact, one recent study observed that slow wave modulations were immediately followed by hemodynamic oscillations coupled to CSF flow in humans (Fultz et al., 2019). Another study found that increasing vasomotion in awake mice by offering visual stimulus caused increased solute clearance in the visual cortex (van Veluw et al., 2020). It is also important to note that neuronal activity, especially sleep dependent synchronized neuronal activity, is coupled to substantial transmembrane ion transport (Ding et al., 2016) that also might drive glymphatic flow directly, without vasomotion as intermediary. In any case, because synchronized neuronal activity during NREM slow wave sleep is homeostatically regulated, increases in intensity as a function of prior sleep and wakefulness (Borbély et al., 2016), and shows distinct spatiotemporal spreading across the brain (Massimini et al., 2004; Kurth et al., 2017), it is intriguing to speculate that sleep could be actively directing cellular clearance toward relevant areas of the CNS.

Modeling

Having introduced some key mechanisms known or hypothesized to be at play in the glymphatic system, we now review existing models of those mechanisms. This section is organized parallel to Section Mechanisms, with subsections focused on flow in PVSs, transport in brain parenchyma, links between PVSs and parenchyma, brain efflux routes, and links to neuronal activity. We then discuss rOMT, which may go far to inform glymphatic models. This section closes with a few comments on the inherent utility and limits of modeling, and the modeling approaches that seem most productive for advancing the field.

Perivascular flow

As discussed in Section Perivascular flow, a large number of possible drivers and modulators could affect perivascular flow and therefore deserve to be modeled. Among the mechanisms are perivascular pumping, functional hyperemia driven by neural activity, and osmotic effects.

Several papers have investigated perivascular pumping in idealized and localized geometries. An early model studied how CSF-filled cavities associated with syringomyelia formed in the spinal cord because of peristaltic pumping (Bilston et al., 2003). However, the wavelength of the vascular deformation was unreasonably short, and although the wavelength has not been measured, it is generally assumed to be in the range 20 cm to a couple of meters (Martinac and Bilston, 2019; Thomas, 2019; Daversin-Catty et al., 2020). Later, a pumping mechanism was proposed to be the offset between the cardiac and CSF pulsation, but this was deemed unlikely in (Martinac et al., 2021). Another early model asked how perivascular pumping might transport proteins in the direction antiparallel to blood, and hypothesized that surface chemistry could provide a valve-like effect for amyloid beta transport (Schley et al., 2006). The fluid motions (as opposed to amyloid motions) predicted by that model, however, are similar to those predicted by others, proceeding parallel to blood, on average, in most cases. Motivated by the model of Bilston et al. (Bilston et al. (2003), Wang and Olbricht (Wang and Olbricht, 2011) derived an analytical model of perivascular flow capable of explaining both influx and efflux, depending on the parameters in use. Their model predicts velocities around 20 $\mu$m/s, as seen in vivo (Mestre et al., 2018a; Bedussi et al., 2018), in reasonably sized perivascular spaces (Thomas, 2019). Still, the model involves simplifying assumptions: a circular cross-section, a sinusoidal wave pattern, and a very long annulus. Elliptical cross-sections observed in vivo reduce the resistance to flow and may constitute an evolutionary adaptation (Tithof et al., 2019). Yokoyama et al. (Yokoyama et al. (2021) observed that the ratio of wave amplitude to wavelength must be $\text{∼}{10}^{-4}$ in order to produce flows at 20 $\mu$m/s without a net pressure gradient. Localized computational studies have produced similar insights (Kedarasetti et al., 2020b; Daversin-Catty et al., 2020).

Boundary conditions should be considered carefully when modeling flows in perivascular spaces. If the surrounding tissue is soft enough to be deformed significantly when artery walls dilate or contract, we expect its deformation to remove kinetic energy from CSF and thereby reduce the flow speed. Kedarasetti et al. (2020a) imaged fluorescent neurons near a penetrating perivascular space, finding that the neurons moved in concert with artery walls, then went on to show slower flows in simulations with soft outer boundaries. However, other groups have observed no significant deformation (Mestre et al., 2020a), so further in vivo measurements are warranted.

There are other considerations in addition to side boundaries. Prior studies modeling perivascular spaces have frequently used periodic end boundaries (Wang and Olbricht, 2011) or zero-pressure end boundaries, which neglect effects of the fluid pathway beyond the modeling domain, such as resistance and compliance. Including them can change predictions significantly (Ladrón-de Guevara et al., 2020). The length of the modeling domain is also important. In perivascular pumping, the net flow direction is set by the travel direction of artery wall deformations. Therefore, in the limit of a domain that is infinitesimally short compared to the deformation wavelength, where the entire wall would deform simultaneously, perivascular pumping could produce no net flow. Although models have agreed closely with in vivo flow measurements (Mestre et al., 2018a), typical segments of real perivascular networks are shorter than a cardiac pulsation wavelength by a factor of $\text{∼}{10}^4$, bringing the mechanism into question. Daversin-Catty et al. (Daversin-Catty et al. (2020) simulated shorter domains, finding much slower flows, and suggested that pulsation is accompanied by a small ($\approx {10}^{-2}$ mmHg/cm) and steady pressure gradient of uncertain origin.

Recent studies have asked whether CSF flow in perivascular spaces could be driven by functional hyperemia, the local variation of blood volume in response to neuronal activity. Kedarasetti et al. (2020a) simulated slow, large artery dilations as expected during functional hyperemia, finding significant displacement of CSF. With additional simulations, Kedarasetti et al. (2021) found that functional hyperemia drove more periarterial flow than cardiac pulsation, in part because vasodilations associated with functional hyperemia have less temporal symmetry than those associated with cardiac pulsation. However, functional hyperemia typically propagates antiparallel to blood flow (Tian et al., 2010; Rungta et al., 2018) and would drive CSF in the same direction, if it imposes any net flow direction at all, but in vivo observations of CSF in perivascular spaces almost always show it moving parallel to blood. Also, although glymphatic transport occurs primarily during sleep, functional hyperemia is stronger during wakefulness (Turner et al., 2020). Further studies are required and should consider not only functional hyperemia, but also vasomotion linked to autonomic activity (Gu et al., 2022).

A few studies have argued that purely oscillatory flow, without net motion of fluid over time, could produce the rapid transport observed in experiments because of Taylor dispersion (Asgari et al., 2016; Smith and Verkman, 2018; Kedarasetti et al., 2020b; Faghih and Keith Sharp, 2021; Rey and Sarntinoranont, 2018). Taylor dispersion (also called shear-enhanced dispersion) occurs when shear in a narrow channel, such as a PVS, spreads solute along the channel axis whereas diffusion spreads solute laterally, resulting in greater effective axial diffusivity. However, recent theoretical arguments (Thomas, 2019) and numerical simulations (Troyetsky et al., 2021) concluded that Taylor dispersion in PVSs could speed transport only slightly, and much less than even weak net flows, resulting in far slower transport than those observed in vivo.

Most studies of perivascular spaces have avoided the complexities of bifurcations and of interactions among the many PVS segments that comprise the glymphatic system. Although the computational costs of simulating those complexities are daunting, flow and transport are surely affected by bifurcations and interactions, which are routinely simulated in studies of blood flow (e.g., see Goirand et al. (Goirand et al. (2021)). Daversin-Catty et al. (2020) simulated flow in a bifurcation, concluding that in vivo flow characteristics could most easily be reproduced via a combination of arterial pulsation and a steady pressure gradient of unknown source. Many studies have likewise pointed out that a small pressure gradient could drive the observed mean flows, but testable hypotheses about the source of that gradient are less common — and are an important topic for future work. Daversin-Catty et al. (Daversin-Catty et al. (2021) demonstrated that flow in bifurcations could be predicted with reasonable accuracy and substantially lower computational cost by solving the mass and Navier-Stokes equations in a single spatial dimension, by averaging radially and azimuthally. Coenen et al. (Coenen et al. (2021) produced analytic approximations for flow in non-axisymmetric annuli and suggested methods for solving PVS networks using those approximations, which are promising because they would be computationally feasible even for large networks. Interactions among segments have also been captured in hydraulic network models (Mestre et al., 2020a; Rey and Sarntinoranont, 2018; Faghih and Sharp, 2018; Tithof et al., 2022), discussed further below.

Transport in brain parenchyma

Because of the tortuous and complex shape of the ECS, brain parenchyma is typically modeled as an unconsolidated porous medium. Numerical studies have often made the simplifying assumption that diffusion alone can predict solute motion. Such studies simulated random walks of individual molecules repeatedly (a Monte Carlo method), often using the MCell software package (Tao and Nicholson, 2004; Hrabe et al., 2004), making predictions that can be compared directly to RTI measurements. The typical tortuosity measured in vivo, $\lambda =1.6$, is higher than that expected for simple diffusion around uniformly spaced convex objects, such as cell bodies or dendrites (Tao and Nicholson, 2004; Hrabe et al., 2004; Nicholson and Kamali-Zare, 2020). The discrepancy can be explained partially, but not completely, by interstitial viscosity (Zheng et al., 2017). However, adding dead spaces to the ECS has reproduced $\lambda =1.6$ in Monte Carlo models (Hrabe et al., 2004; Tao et al., 2005; Nicholson, 2018). Dead spaces are local enlargements of the ECS, where diffusing molecules spend extra time, causing delays that increase the tortuosity $\lambda$ (see Section Mechanisms). Dead spaces have been visualized in living organotypic brain slices (Tønnesen et al., 2018) and inferred from diffusion measurements with carbon nanotubes (Godin et al., 2017; Nägerl et al., 2008). There is also other experimental evidence (Hrabetová et al., 2003). Combining three-dimensional electron microscopy data with MCell showed that the ECS consisted of “tunnels” and “sheets” (Kinney et al., 2013), again implying a non-uniform ECS containing dead-spaces.

Some models of the parenchyma have also considered flow and advection effects. Again taking the tissue to be a porous medium, they typically model flow dynamics with Darcy’s equation. Holter et al. (Holter et al., 2017), using a three-dimensional geometry of the neuropil based on (Kinney et al., 2013), predicted that advective transport could indeed be neglected with good accuracy, as long as ample flow in perivascular spaces maintains steep concentration gradients in the parenchyma. The same study found that the relative fraction of tunnels and sheets did not significantly affect the extracellular diffusion process. Ray et al. (Ray et al. (2019) found that RTI measurements might be explained more accurately by accounting for advection (see Section Mechanisms). Linninger et al. (Linninger et al. (2008) simulated parenchymal drug delivery, finding that using the injection to drive a flow caused penetration depths greater by a factor of 15 than with diffusion alone. Schreder et al. (Schreder et al. (2022) asked how parenchymal resistance depends on the spacing and arrangement of penetrating blood vessels, finding that, when considering regions large enough to contain many vessels, the per-arteriole conductance is approximately constant. Altogether, the role of advection in transport through brain parenchyma, during physiological conditions, pathological conditions, or clinical interventions, remains a topic of ongoing study.

Thomas (Thomas (2022) modeled effects on solute transport in the parenchyma caused when its porosity increases during the transition from wake to sleep (Xie et al., 2013). Greater porosity implies larger ECS spaces with lower hydraulic resistance, allowing more flow and stronger advection. Meanwhile, because enlarged ECS spaces are filled with fluid ejected from astrocytes and therefore low in substances like amyloid beta, solutes would be diluted in the ECS, weakening diffusion. Although the model is idealized, its prediction of strengthened advection and weakened diffusion is consistent with the simulation results of Jin et al. (Jin et al. (2016). Thus, observations that transport is stronger during sleep or sleep-like states than during wakefulness or wake-like states (Xie et al., 2013; Hablitz et al., 2019, 2020) suggest that advection plays an important role. If diffusion alone transported solutes from the deep brain to the cortical surface, concentrations would vary spatially to an unrealistic degree.

Interfaces to perivascular spaces

The mechanisms that control influx at interfaces between PVSs and other fluid compartments are not well understood and are ripe for future modeling, although we will not discuss them further here. Mechanisms at the interfaces between perivascular spaces and parenchyma, on the other hand, have been an active topic of recent modeling.

It has been suggested that CSF might not leave perivascular spaces at all, with periarterial spaces connecting to perivenous spaces via pericapillary spaces. However, when Tithof et al. (Tithof et al. (2022) allowed for this pathway in a brain-wide hydraulic network model, they found flow there to be negligible for reasonable parameter values. Asgari et al. (Asgari et al. (2015) estimated the hydraulic resistances of two alternate pathways — one through AQP4 and astrocyte cell bodies, another through endfoot gaps — concluding that a large fraction of the water flow is intracellular because of the high AQP4 concentration and small gap size. In vivo gap size, however, is not known precisely. A further difficulty of this conclusion is that AQP4 admits only water molecules, prohibiting waste or nutrient transport through cell bodies.

Models have often focused on the pathway through endfoot gaps, and consequently, the arrangement and properties of astrocytes and their endfeet. Wang et al., 2021) observed that endfeet surrounding smaller vessels are themselves smaller, implying greater gap length per unit interface area. Continuing, the authors simulated flow through a network of PVSs and gaps modeled on images from super-resolution microscopy, finding that the observed variation in endfoot size allowed flow from PVSs to parenchyma to be more uniform than it otherwise would have been. That result is consistent with the conclusions of Romanò et al. (Romanò et al., 2020), who found PVS flows to depend sensitively on the porosity of the parenchyma at its interfaces with PVSs. Kedarasetti et al. (2021) modeled the parenchyma around periarterial spaces as a poro-elastic medium, that is, a porous medium in which the solid phase (here, cells and other tissue) is soft enough to be deformed appreciably by the flow of fluid through pores. The authors found that poro-elasticity acted like a rectifier, favoring flow into the parenchyma, and therefore parallel to blood, over flow out of the parenchyma. Thus, poro-elasticity might answer a key question: what mechanism sets the glymphatic flow direction? However, at the interfaces between perivenous spaces and parenchyma, the same mechanism would favor flow anti-parallel to blood, so further modeling is needed.

Efflux routes

Few glymphatic modeling studies include efflux, and those typically account only for perivenous spaces. Asgari et al. (Asgari et al. (2016) simulated transport from a periarterial space, through parenchyma, to a venous PVS, and characterized solute concentrations over time for different boundary conditions. Rey and Sarntinoranont (Rey and Sarntinoranont, 2018) devised a lumped parameter model of flow near one arteriole and one vein, finding that flow was purely oscillatory, but that conclusion is unsurprising because flow was driven using standing (not traveling) vasodilations; no mechanisms were simulated that favored flow in one direction over the other. Faghih and Sharp (Faghih and Sharp, 2018) modeled perivascular flow — including efflux through perivenous spaces — using idealized branching based on Murray’s law. They found the total resistance of the perivenous tree ($1.75\times {10}^{-3}$ mmHg$\cdot$min/mL) to be smaller than that of the periarterial tree by a factor of ${10}^3$. Tithof et al. (2022) performed lumped parameter simulations to investigate uncertain parameters; they modeled the entire glymphatic CSF efflux as a single resistor with negligible resistance, based on the finding of Faghih and Sharp (Faghih and Sharp, 2018).

Some studies have explored glymphatic efflux in more detail. Vinje et al. (2021) concluded from solute transport simulations that tracer moves faster through pial periarterial than in perivenous spaces, which may explain experimental observations without the need for parenchymal flow. However, that conclusion depends strongly on the applied pressure differences, which were chosen to be identical for periarterial and perivenous spaces, although their values in vivo are unknown. Vardakis et al. (Vardakis et al. (2020) devised a novel brain-wide finite element model with six transport compartments, accounting for perivenous efflux. Davoodi-Bojd et al. (Davoodi-Bojd et al., 2019) analyzed MRI measurements using two-compartment models for each of a collection of brain regions, finding that tracer transport was different in a rat model of diabetes than in wild-type rats. Elkin et al. (2018) implemented an OMT-based approach and identified differences in glymphatic transport — including efflux to lymphatic vessels — for rats under two different anesthetics (see Section Quantifying and defining glymphatic transport with optimal mass transport for an in-depth discussion of OMT). Vinje et al. (Vinje et al. (2020) developed a compartmental model and demonstrated that elevated ICP may alter the proportion of CSF that exits the subarachnoid space via different efflux routes (including the glymphatic pathway with perivenous spaces). However, that conclusion follows directly from the authors’ specification of a pressure-dependent compliance that varies inversely with ICP, which may require further validation.

Ample opportunities remain for exploring glymphatic efflux via computational approaches. Future studies should explore the relative proportion of fluid efflux via perivenous spaces versus white matter tracts; no models of the latter route exist, to the best of our knowledge. Modeling may also provide important evidence for the role of respiration as a glymphatic driving mechanism in perivenous spaces (Abbott, 2004; Kiviniemi et al., 2016; Santisakultarm et al., 2012) and CSF in general (Vinje et al., 2019; Helakari et al., 2022). Finally, future experimental studies could help illuminate whether there is direct efflux from the glymphatic system to the meningeal lymphatics; if so, techniques developed for modeling peripheral lymphatic vessels (Moore and Bertram, 2018; Margaris and Black, 2012) can be adapted to investigate glymphatic-lymphatic efflux.

Links to neuronal activity and vasomotion

Although many models have been developed for the hemodynamic link between neuronal activity and local blood volume, often with application to functional MRI (Polimeni and Lewis, 2021), there is a lack of models explicitly linking neuronal activity to CSF flow in physiological conditions. Existing models that are closely related are those that predict CSF flow driven by spreading depolarization during ischemic stroke (Mestre et al., 2020a) and cardiac arrest (Du et al., 2022).

Models linking neuronal activity and vasomotion to CSF flow in physiological conditions are an important topic for future work. The link acts on millisecond timescales and can be understood as one sort of dynamic effect that changes over time and affects the perivascular transport network. Dynamic effects can influence connectivity and thickness of vessels, affecting local and global resistance to flow (Gross and Blasius, 2008; Porter and Gleeson, 2016; Martens and Klemm, 2017; Hu and Cai, 2013). Other dynamic effects take place over other timescales, including vascular remodeling in disease (weeks to months) (Jacobsen et al., 2009), circadian rhythms (hours) (Hablitz et al., 2020), and vasomotion (seconds) (Carmignoto and Gómez-Gonzalo, 2010). Vasomotion has been modeled as local response mechanism in smooth muscle cells (Jacobsen et al., 2008), but also as the coupling of smooth muscle cells leading to electric signals propagating along vessel walls (Jacobsen et al., 2007; Hald et al., 2014). Alternating vessel responses due to cerebral autoregulation may even induce pressure gradients, leading to pumping across the network.

Quantifying and defining glymphatic transport with optimal mass transport

In the glymphatic model, perivascular CSF transports solutes and clears wastes from brain tissue. However, the presence of bulk flow (i.e., advection) in neuropil is uncertain, as discussed in Section Mechanisms. Recent work has addressed the relative importance of advective and diffusive transport via data-driven methods, in which measurements (often from MRI) are combined with a mathematical model in order to make inferences about quantities that cannot be measured directly, such as fluid velocity (Koundal et al., 2020; Valnes et al., 2020; Elkin et al., 2018; Ray et al., 2021; Chen et al., 2022). To illustrate the requirements and capabilities of data-driven methods, we will discuss one in more detail: regularized optimal mass transport (rOMT). Given noisy, uncertain data — for example, dynamic contrast enhanced MRI (DCE-MRI) measurements — the rOMT algorithm determines the lowest-energy flow that could carry tracer from its initial spatial distribution to its final spatial distribution, subject to the constraint that the flow velocity and tracer concentrations satisfy the advection-diffusion equation. The resulting lowest-energy flow is an estimate of the fluid velocity as it varies through space and time. Knowing that velocity is useful because it allows one to quantify the relative importance of advection and diffusion in the observed tracer transport via its Péclet number, which may likewise vary over space and time. In addition, knowing the velocity allows predicting transport and the Péclet number for any other solute whose diffusivity is known, including endogenous proteins like amyloid beta and tau, which are difficult to isolate but have profound implications for neurodegeneration. rOMT also has potential for improving image registration (Elkin et al., 2018).

In recent work, rOMT revealed that solute speed is faster in CSF than in gray or white matter (Koundal et al., 2020; Elkin et al., 2018) and found two-fold differences in regional solute speed within the brain, which might imply varying importance of advection and diffusion across brain regions. These results suggest that advective transport dominates in CSF whereas diffusion and advection both contribute to glymphatic transport in the parenchyma. The analytical framework of rOMT provides novel insights in the local dynamics of glymphatic transport that may have implications for understanding pathophysiology of neurodegenerative diseases. Chen et al. (Chen et al. (2022) used rOMT and other tools to conclude that, in a rat model of cerebral amyloid angiopathy, compared to wild-type rats, flow and solute transport through brain tissue are significantly decreased, efflux along neck arteries is delayed, and efflux to the olfactory bulb is accelerated. The implication is that both glymphatic transport and lymphatic drainage are impaired and could be targets for future clinical interventions (Table 1)

Table 1.

Acronyms used in this paper

Acronym	Meaning
AQP4	aquaporin-4
BBB	blood-brain barrier
BOLD	blood-oxygen-level-dependent
CAA	cerebral amyloid angiopathy
CNS	central nervous system
CSF	cerebrospinal fluid
CT	computed tomography
DCE	dynamic contrast-enhanced
ECS	extracellular space
ICP	intracranial pressure
IOI	integrative optical imaging
IPAD	intramural periarterial drainage
ISF	interstitial fluid
MRI	magnetic resonance imaging
NREM	non-rapid eye movement
PET	positron emission tomography
PVS	perivascular space
rOMT	regularized optimal mass transport
RTI	real time iontophoresis
SAS	subarachnoid space
SB	Schrödinger bridge
SD	spreading depolarization
SLML	single-molecule localization microscopy
SPECT	single-photon emission computed tomography
STED	stimulated emission depletion
SUSHI	super-resolution shadow imaging
VCID	vascular contribution to cognitive impairment and dementia

Key points to remember when modeling

Happily, mathematical modeling has proved to be “unreasonably effective” in a wide variety of physical and biological systems1. Still, neither the practice of modeling nor any single model is a panacea, and the glymphatic system — in which many material properties are inaccurately known, mechanisms interact, and novel phenomena emerge collectively — poses a substantial challenge. Thus, we encourage ongoing and expanded modeling efforts while also urging caution and rigor. Great models are built on stated hypotheses, make falsifiable clinical predictions, and are open to future improvements. Great models, although necessarily less realistic than in vivo observations, are a crucial complement because they allow counterfactuals to be tested and thereby raise new questions for future experiments. To enable this virtuous cycle, models should be presented with their assumptions and range of applicability stated as clearly as possible; some models apply more broadly than first expected, but many apply more narrowly than initially perceived. With models as with any scientific inquiry, we urge that results and data be distinguished from conclusions and interpretations, which are and should be more speculative. Categorizing existing models can help not only to organize prior results but also to reveal opportunities for impactful future studies. With Table 2, we attempt to do so.

Table 2.

Many models have been developed, with application to different parts of the glymphatic system, and using different modeling approaches, with strengths and limitations varying accordingly

Perivascular flow
Type	Strengths	Limitations	Examples
Lubrication theory	Analytic approach makes scaling clear.	Highly idealized geometry. Single mechanism.	(Wang and Olbricht, 2011; Coenen et al., 2021; Bilston et al., 2003; Schley et al., 2006)
Numerical Navier-Stokes solution, 2D or 3D	Applicable to complicated geometry.	Prohibitively expensive if PVS length and cardiac wave speeds are realistic. Bifurcations studied only rarely; networks currently too expensive.	(Kedarasetti et al., 2020b; Daversin-Catty et al., 2020; Kedarasetti et al., 2020a; Yokoyama et al., 2021; Vinje et al., 2021)
Numerical Navier-Stokes solution, 1D	Low computational cost accommodates whole PVS networks.	Neglects sometimes-important details like PVS shape.	(Daversin-Catty et al., 2021)
Numerical advection-diffusion solution	Predict solute transport.	Requires knowledge of velocity fields. Highly idealized or prohibitively expensive.	(Keith Sharp et al., 2019; Troyetsky et al., 2021)
Hydraulic resistance modeling	Inexpensive calculations can inform brain-wide models.	Idealized: typically assumes parallel, steady flow and simple geometry.	(Tithof et al., 2019; Rey and Sarntinoranont, 2018; Faghih and Sharp, 2018)
Transport in brain parenchyma
Type	Strengths	Limitations	Examples
Monte Carlo molecular random walks	Direct calculation of porosity, tortuosity, and effective diffusivity from microscale ECS geometry	Requires knowledge of microscale geometry. Prohibitively expensive for large regions.	(Tao and Nicholson, 2004; Hrabe et al., 2004; Nicholson and Kamali-Zare, 2020; Tao et al., 2005; Nicholson, 2018; Kinney et al., 2013)
Numerical advection-diffusion solution	Predict transport via flow and diffusion	Required inputs (e.g., permeability, porosity, tortuosity) often poorly characterized or derived from measurements subject to fixation artifacts.	(Ray et al., 2019; Asgari et al., 2016; Holter et al., 2017)
Analytic advection solution	Predict flow	Required inputs (e.g., permeability, porosity, tortuosity) often poorly characterized or derived from measurements subject to fixation artifacts.	(Schreder et al., 2022)
Interfaces to perivascular spaces
Type	Strengths	Limitations	Examples
Numerical Navier-Stokes solution with porous boundaries	Pioneering models of PVS-parenchyma interface.	Tissue properties poorly characterized. Expensive, depending on PVS flow parameters. Networks currently too expensive.	(Kedarasetti et al., 2021; Wang et al., 2021; Romanò et al., 2020)
Efflux routes
Type	Strengths	Limitations	Examples
Hydraulic network models	Based on hypothesized flow mechanisms. Can span brain-wide, incorporate efflux. Computationally inexpensive.	Many simplifications, many poorly-characterized parameters. No solute transport.	(Mestre et al., 2020a; Asgari et al., 2015; Rey and Sarntinoranont, 2018; Faghih and Sharp, 2018; Tithof et al., 2022)
Compartment models	Easily compared to in vivo clearance measurements. Can span brain-wide, incorporate efflux. Less computationally expensive than most other techniques.	Many simplifications, many poorly-characterized parameters, flow mechanisms stated less explicitly.	(Vardakis et al., 2020)
Links to neuronal activity
Type	Strengths	Limitations	Examples
Numerical continuity solution, with artery constriction set by spreading depolarization	Pioneering models of links to neuronal activity	Applied only to pathological cases of stroke and cardiac arrest. Neglect drivers other than constriction.	(Mestre et al., 2020a; Du et al., 2022)

Many mathematical models have been and will continue to be devised for mice, rats, and other animals, although human clinical applications are usually the ultimate goal. Translating models from other brains to human brains therefore requires careful consideration. Scaling laws based on dimensionless parameters like the Péclet number can help guide our intuition about how biophysical mechanisms vary with physical and geometrical constraints (Thomas, 2022; West et al., 1997). That said, humans are set apart from rodents by more than just their size. Body posture, sleep patterns, and cortical arteriole-to-venule ratio all differ significantly and seem relevant to the glymphatic system. Gyrencephalic (folded) and lissencephalic (smooth) brains may host substantially different glymphatic systems. Even small-scale biochemistry could vary. Successful translation from rodents to humans will require models cognizant of these and other considerations.

Use case: Drug delivery

Neurobiology is often beautiful, but we aspire to make models that are practical, as well. As an example of one practical, clinical application, we consider in this section one use case: delivery of drugs directly to the CNS, unimpeded by the BBB, via CSF flow in the glymphatic system.

Delivery of drugs and diagnostic agents to the CNS is particularly difficult because of the BBB that protects the CNS from exogenous substances by both passive and active mechanisms, requiring that intravenously or orally administered CNS-targeted drugs be given in excessive doses that often cause adverse systemic effects. Several noninvasive and invasive techniques have been utilized to overcome the BBB (Terstappen et al., 2021). Of the invasive procedures, direct administration to the CSF allows therapeutics to bypass the BBB endothelium. In particular, the lumbar intrathecal route (Kevin et al., 2018) is used widely to deliver small-molecule drugs, and also larger therapeutics such as polypeptides (Staats et al., 2004), proteins (Schulz et al., 2018), oligonucleotides (Finkel et al., 2017), and diagnostic agents such as gadolinium-labeled (Ringstad et al., 2018) and radionuclide-labeled (Verma et al., 2020) CSF tracers. However, the slow diffusion rate of large solutes from the subarachnoid CSF to deep CNS structures restricts the efficacy and utility of intrathecal therapeutics (Wolak and Thorne, 2013). For example, a recent study of intrathecal administration of iron-based nanoparticles (Venugopal et al., 2017) found uptake into the parenchyma occurring mainly near perivascular spaces, not across the cortical surface elsewhere. Advective glymphatic CSF influx in periarterial spaces could be harnessed to deliver intrathecal therapeutics widely to the deep CNS structures.

In clinical practice, intrathecal drugs are usually administered at the outpatient clinic in the awake state, when the glymphatic system is nearly inactive. Enhanced glymphatic flow facilitated by deep sleep or other interventions enhancing glymphatic CSF influx could theoretically improve drug delivery to the brain and spinal cord parenchymas. Preclinical rodent studies have found that dexmedetomidine, a clinically used ${\alpha }_2$-adrenergic agonist sedative that enhances both glymphatic influx and efflux (Benveniste et al., 2017), increased the brain and spinal cord exposure to intracisternally administered small-molecular opioids oxycodone and naloxone and increases the delivery of an IgG-sized amyloid-beta antibody to the rat brain (Lilius et al., 2019). Whereas dexmedetomidine-induced controlled sedation mimics NREM sleep, another clinically intriguing option to transiently enhance periarterial CSF influx without affecting consciousness is the systemic administration of hypertonic solutions. Systemic hyperosmolality leads to movement of water from the CNS to peripheral circulation, replaced by rapid influx of CSF from the subarachnoid space, possibly driven by the osmotic pressure gradient (Buishas et al., 2014; Linninger et al., 2017). In a study in mice, hypertonicity induced by intraperitoneal mannitol or hypertonic saline enhanced the penetration of intracisternally infused IgG-sized amyloid-beta antibody to the brain and its binding to amyloid-beta plaques manifold (Plog et al., 2018). The results suggest not only that hypertonicity could be used to enhance drug delivery, but also that solutes in the extracellular space are transported, at least in part, by advection, because diffusive transport would typically decrease after water moves from brain cells to ECS (Thomas, 2022). In rats, systemic hypertonic saline enhanced the delivery of morphine to the spinal cord after lumbar intrathecal administration, resulting in enhanced antinociception (Blomqvist et al., 2022).

Although there are several suitable potential interventions available for glymphatic-enhanced drug delivery, they have not yet been tested in randomized controlled clinical trials. Recent work by Eide et al. has highlighted the possibility for modeling studies to measure CSF clearance with very limited data. The small-molecule MRI contrast agent gadobutrol — sharing properties with typical CNS-targeted drugs such as low BBB permeability — was infused intrathecally, and its CNS distribution over time was assessed using MRI in different patient populations (Ringstad et al., 2018). Eide et al. measured gadobutrol concentrations in the systemic circulation and used pharmacokinetic models (also known as compartment models or control volume models) to estimate clearance of the intrathecally administered tracer (Eide et al., 2021a). Because repeated blood sampling is readily available in the clinic, pharmacokinetic modeling could provide rough estimates of efficacy of CNS delivery. Drug-specific clearance is typically assessed with multimodal imaging studies (Tangen et al., 2020). The Linninger lab has developed a framework to combine dynamic imaging data with detailed modeling of CSF dynamics (Tangen et al., 2017) to predict biodispersion to target spinal or cerebral delivery sites and clearance routes as a function of infusion setting. Future work will define the optimal characteristics of drugs to be delivered through CSF administration possibly aided by the glymphatic pathway and the potential clinical utility of this delivery route.

Outlook and future work

Recent modeling of CSF / ISF flow and solute transport in the brain has produced discoveries and insights which are often subjects of widespread consensus. Meanwhile, controversies continue, and although some can be resolved with existing knowledge, others point helpfully to important future work.

Perivascular flow

The mechanisms that drive flow, especially in perivascular spaces, still deserve further study. Models of vasoconstriction caused by spreading depolarization can reproduce flows and transport observed during stroke and cardiac arrest, but in physiological situations, the story is less clear. Arterial pulsation with the cardiac cycle induces CSF oscillations and increases effective diffusivity modestly; whether it also drives net flow is debated. Many researchers have noted that net flow could be driven by a small, steady pressure gradient, but few mechanisms have been suggested for maintaining such a gradient. (Artifactual gradients from tracer injection do not seem to explain the observed flows (Raghunandan et al., 2021).) The idea is fraught: both influx and efflux routes connect to the subarachnoid space, so a pressure difference between parenchyma and subarachnoid space (SAS) would not alone cause circulation. Future experiments might explore whether the SAS is segregated into influx and efflux regions. Experiments should also determine the stiffness of tissue around pial and penetrating perivascular spaces, which is currently debated and affects models greatly; acoustic methods hold promise. Future models might make progress by considering PVSs of realistic lengths and accounting for interactions of multiple PVSs segments, with careful attention to bifurcations, boundary conditions and dynamic interactions.

Functional hyperemia almost certainly plays an important role in perivascular flows but is unlikely to be the sole driver, because flow has been observed in experiments where the slow, large-amplitude vasomotion characteristic of functional hyperemia was absent, particularly during anesthesia (Hablitz et al., 2019). Future experiments and models could quantify the effects of functional hyperemia, characterize its variation with brain state, and determine whether low-frequency flows in SAS and ventricles link to PVSs, as suggested by a recent anatomical study (Magdoom et al., 2019). Experiments might also determine the porosity and permeability of penetrating perivascular spaces, which are essentially unknown and have profound implications for model predictions.

Transport in brain parenchyma

In brain parenchyma, solute transport almost certainly occurs via both diffusion and advection, with diffusion likely making the greater contribution, except possibly for large solutes (e.g., tau). The relative importance of diffusion and advection vary spatially and with brain state. Some fluid flow through the parenchyma is implied by the model of glymphatic circulation; flow closes the circuit, because fluid must be conserved. That flow may pass through the extracellular space, through astrocyte bodies, and/or through pericapillary spaces (if they exist). Besides completing the circuit, that flow would also maintain the concentration gradients necessary for diffusive transport. Future experiments could reveal much about transport and flow in the parenchyma by determining the permeability of the extracellular space, the magnitudes of solute concentration gradients, and whether or not pericapillary spaces exist. MRI, rOMT, and super-resolution in vivo imaging via carbon nanotubes all seem particularly promising.

Interfaces to perivascular spaces

Interfaces between perivascular spaces and parenchyma are an important control site for the glymphatic system, as evidenced by flow modulation via the AQP4 that decorates endfeet at those interfaces. But the control mechanism is unknown, and future models should probe it. Poro-elasticity at that interface may play an important role, perhaps setting the circulation direction in lieu of valves. Future models should explore poro-elasticity further, and future experiments should measure tissue stiffness (see above). Interfaces between perivascular spaces and other fluid compartments control the origins and amounts of fluid in PVSs, setting flow rates, recirculation rates, and bypass rates. These effects, often osmotic, have been modeled little and warrant future study.

Efflux routes

Efflux routes are poorly characterized. Models can make better efflux predictions only after experiments provide more ground truth. Mapping efflux routes is essential, although tricky because concentrations are smaller than in influx routes. Future experiments could reveal how efflux routes link to meningeal lymph vessels or other skull exits. Determining whether the SAS is segregated into influx and efflux regions is also important (see above). Because large tracer particles cannot access efflux routes, PET/SPECT, MRI, and perhaps light sheet microscopy are the most promising tools. Experiments would also do well to explore effects of respiration and the intrinsic pumping of lymph vessels. Brain-wide models (hydraulic networks, 1D simulations, and compartment models) can suggest which parameters most need measurement and make improved efflux predictions once measurements are done.

Links to neuronal activity and vasomotion

Opportunities abound for modeling glymphatic links to neuronal activity, which has rarely been explored in the past. Slow wave activity and slow wave modulation both seem important and may influence flows directly or indirectly (via vasomotion / functional hyperemia). Future experiments can contribute by measuring neuronal activity, fluid flow, and vasomotion simultaneously, e.g., with two-photon imaging of GCaMP mice (which are genetically modified such that neuronal activity causes fluorescence).

Conclusion

Many models have been developed for the mechanisms of the glymphatic system (Table 2). As these tools are expanded and refined, we urge that each be applied where most useful, with strengths and limitations made clear, and in combination with other models when necessary. Models are essential for their flexibility, tendency to produce new hypotheses, and capacity for testing counterfactuals that cannot be addressed in physiological conditions. Models must be validated experimentally — in vivo if possible — where discrepancies can lead to key insights. Open conversation is essential and can be facilitated through more workshops like the one that inspired this paper.