Abstract
Membrane reshaping is an essential biological process. The chemical composition of lipid membranes determines their mechanical properties and thus the energetics of their shape. Hundreds of distinct lipid species make up native bilayers, and this diversity complicates efforts to uncover what compositional factors drive membrane stability in cells. Simplifying assumptions, therefore, are used to generate quantitative predictions of bilayer dynamics based on lipid composition. One assumption commonly used is that “per lipid” mechanical properties are both additive and constant—that they are an intrinsic property of lipids independent of the surrounding composition. Related to this is the assumption that lipid bulkiness, or “shape,” determines its curvature preference, independently of context. In this study, all-atom molecular dynamics simulations on three separate multilipid systems were used to explicitly test these assumptions, applying methodology recently developed to isolate properties of single lipids or nanometer-scale patches of lipids. The curvature preference experienced by populations of lipid conformations were inferred from their redistribution on a dynamically fluctuating bilayer. Representative populations were extracted by both structural similarity and semi-automated hidden Markov model analysis. The curvature preferences of lipid dimers were then determined and compared with an additive model that combines the monomer curvature preference of both the individual lipids. In all three systems, we identified conformational subpopulations of lipid dimers that showed non-additive curvature preference, in each case mediated by a special chemical interaction (e.g., hydrogen bonding). Our study highlights the importance of specific chemical interactions between lipids in multicomponent bilayers and the impact of interactions on bilayer stiffness. We identify two mechanisms of bilayer softening: diffusional softening, driven by the dynamic coupling between lipid distributions and membrane undulations, and conformational softening, driven by the inter-conversion between distinct dimeric conformations.
Significance
Cells must expend energy to deform and reshape membranes for necessary biological functions. The work required to accomplish these tasks is directly dependent on the molecular composition of the target membranes. Additionally, many biologically important lipids form multimeric complexes within the bilayer. Knowing how inter-molecular association alters the curvature preference of lipids is crucial to understanding the impact of complex biological lipid composition on the shapes of lipidic structures in cells.
Introduction
Compositional heterogeneity in cellular membranes is necessary for function (1). The bilayer and its constituent lipids are important for many essential functions including signaling (2, 3, 4), chemical separation (5), intracellular sorting (6), metabolism (7), and biogenesis (8). In eukaryotic cells, different organelles have well-defined lipid compositions (1), and deviations from normal lipid composition indicate stress or pathology. Membranes also show compositional asymmetry in their leaflets (9), enriching the possibilities for functional roles of lipid composition. Finally, bilayers are not well mixed within the leaflet and frequently display enrichment of particular lipid types in specific regions and shapes (10,11). For example, lipid-dependent spatial correlations of surface receptors directly tie compositional affinity to cellular signaling processes (12). Stresses due to lipid chemistry (i.e., deviation from preferred geometry) not only influence local mechanics but also protein function (13, 14, 15). Because of the extensive physiological role and great chemical diversity of lipids in the cell, it is imperative to understand how the energetics of native bilayers depend on its many components.
More work is required to relate findings from model membranes (typically one to three lipid species) to biological membranes (hundreds of lipid species). It is often assumed that membrane properties are directly proportional to relative amounts of different lipids, but this is not always the case. For example, cell-extracted giant plasma membrane vesicles have lower bending moduli than their model counterparts. The bending modulus of cell-extracted giant plasma membrane vesicles was measured to be ∼20 (16). This is considerably lower than giant vesicles of fluid membranes like 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) (26 (17)) and a liquid-disordered phase mixture of DOPC, cholesterol, and sphingomyelin (46 (18)). Similar observations have been seen when comparing the area compressibility modulus of red blood cell extract to model membrane mixture representative of the major lipid types (19). The bending stiffness is of fundamental interest to membrane remodeling events, as it controls the overall energetic scale. The mechanism behind reduction is important for understanding the forces that drive many cellular processes.
To address the discrepancies between biological systems and their simplified models, it is necessary to understand how lipid mixtures differ from homogeneous bilayers. Leibler has previously described how bilayers will soften as a result of the dynamic redistribution of curvature-sensitive inclusions (20). In the supporting material, we derive (using the Helfrich/Canham model modified for local lipid energetics (21)) the softening factor yielding the apparent bending modulus in our own notation:
| (1) |
| (2) |
where is the difference of spontaneous curvature of the inclusion compared with the bulk, is the inclusion mole fraction, is the bilayer bending modulus, and is the area of the inclusion. Consider, for example, a mixture of PE and PC lipids, with Å−1, Å2, , and kcal/mol, yields an 8% reduction in the bending modulus. For additional discussion of softening in lipid bilayers with mixed composition, refer to refs. (22, 23, 24, 25).
The correct identification of both the temporal and spatial scale driving softening is necessary for identifying the softening mechanism. As such, we have defined two possible mechanisms of softening that rely on differences in the spontaneous curvature of lipids: diffusional and conformational. Our proposed mechanisms differ in two major ways: origin of , and timescale of redistribution. Diffusional softening is caused by the lateral distribution of lipids with different curvature preferences to membrane undulations. The timescale for this softening depends on both the timescales of lipid diffusion and the membrane undulations (21). For example, a bilayer composed of minor species lipid A (non-zero curvature) and matrix lipid B (zero curvature) would exhibit this softening. Alternatively, conformational softening is due to the dynamic inter-conversion between curvature sensitive lipid conformations. This mechanism depends on the timescale governing inter-conversion between these curvature sensitive states. Importantly, knowledge of curvature-dependent lipid conformations is needed for this mechanism and is at odds with some common assumptions used in continuum membrane models. Both mechanisms result in softening described by Eq. 2.
Continuum models, like the Helfrich/Canham formalism (26,27), use simplifying assumptions to calculate the energetics of membrane deformations. One such assumption is that per-lipid continuum properties (i.e., spontaneous curvature, bending modulus, and area compressibility) are additive, i.e., the properties of the whole system are the linear sum of its parts. Employing the additive assumption dramatically reduces the complexity of heterogeneous membrane energetics, and indeed the assumption is supported experimentally in many cases. For example, the spontaneous curvature of cholesterol is similar in both PE and PC matrices (28). This is, however, not always the case. Experiments on hexagonal phases indicate non-additive curvature preferences of palmitoyl sphingomyelin (PSM) mixtures with certain ceramides (29). In cholesterol-rich bilayers, simulations indicate curvature energetics vary non-linearly with tail saturation (30). Additionally, the formation of specific molecular interactions (in this case, hydrogen bonds) leads to a non-linear relationship between lipid content and curvature preference (30). These exceptions highlight the importance of understanding how complex formation between lipid components alters the additive assumption for the continuum description of the bilayer. Current molecular simulation methods provide unparalleled resolution for identifying the molecular underpinnings of bilayer energetics. To take advantage of these simulations, new tools must be generated to efficiently identify novel lipid pairs and analyze their per-lipid continuum properties.
To accomplish this, we developed a novel analysis that uncovers the properties of collections of lipids, including dimers. The analysis takes two approaches to isolating important dimer structures. The first directly identifies dimers that contained features suspected to be strong, such as salt-bridged interactions and hydrogen bonding. The second, a hidden Markov model (HMM), allows for the emergence of structural features based on their similarity in space and time. We consider this approach to be “semi-automated” in that the important lipid sites were chosen (e.g., charged moieties, hydrogen-bond donors) as structural information but were not enforced to map to states.
Markov models have shown promise in being able to extract mechanistic insight and timescale information from molecular simulations. The Markov model framework provides a formalism for defining timescales for processes (31). It typically relies on a discrete assignment of state such that transitions between states can be counted. They have been successfully employed to study several problems in molecular biophysics, including protein folding (32, 33, 34, 35, 36), ligand binding (37), protein-protein associations (38), and phase identification in lipid bilayers (39).
HMMs allow for a weak association of an observable and the state of interest. In an HMM, there is not a one-to-one mapping of an observation to state. Rather, observed configurations are assigned to a state based on the time sequence of observations. Applications to lipid bilayers are particularly amenable to HMM analysis. First, the large number of target molecules in a simulation is directly proportional to the sampling statistics that can be obtained through simulation. In simulation systems containing hundreds of lipid molecules, even somewhat rare states can be sampled. Second, the molecular environment around a lipid relaxes much more slowly than for material solvated by water. This strongly suggests a hidden contextual influence on lipid configuration.
In this work, we use three unique test cases to examine varied effects of lipid-lipid interaction on the preferred curvature (spontaneous curvature) of lipid dimers. In order to better control for bilayer effects, we have chosen to simulate only symmetric bilayers. We introduce the additive model as the null hypothesis to which we compare dimer curvature preference. Subconformations of lipid dimers that exhibit non-additive spontaneous curvatures are then identified as curvature-sensitive states. In all cases, curvature-sensitive states were most easily identified by standard interaction metrics (e.g., hydrogen-bond formation and divalent-cation binding). These were predominantly distance-based cutoffs for chemical sites known to form relatively strong interactions. The three systems studied with the approach were 1) a tertiary mixture of DOPC, 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE), and 1,2-dioleoyl-sn-glycero-3-phospho-L-serine (DOPS), 2) a mixture of phosphatidyl-inositol-4,5-bisphosphate (PIP2) and 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (POPC), and 3) binary mixtures of PSM and POPC. These three mixtures highlight three unique mechanisms that can alter the spontaneous curvature of a dimer conformation. Specifically, the DOPC, DOPE, and DOPS system illustrates the impact of hydrogen-bond formation on the negative spontaneous curvature of PE. The more physiologically relevant systems (2 and 3) help to provide mechanistic insights into lipid-lipid interactions that are important for cellular function. We observed that -meditated heterodimers between PIP2 and POPC have highly negative spontaneous curvature. The implication is that curvature generation by PIP2 does not require clustering. Additionally, the PSM and POPC mixtures reveal a complicated role for hydrogen bonding that alters dimer spontaneous curvature in a way that appears to depend on the lipid matrix. As PSM is a major component in the plasma membrane and has been observed in nanometer-scale domains in cells (40), this finding has potentially broad-reaching implication for a number of membrane trafficking processes that depend on membrane mechanics.
Methods
Molecular dynamics
Build and simulation parameters
All simulations used the CHARMM C36 lipid force field (41). Both PC/PE/PS and PSM/POPC simulations were built to be oblong, with one lateral dimension four times larger than the other, to capture long wavelength undulations. Simulations of PIP2/POPC were built square. While the simulations made with oblong geometries provide access to longer wavelengths, the differences in geometry of these systems do not impact the mechanical properties extracted from our simulations. Four replicas of PC/PE/PS each had 1272 total lipids. One replica each of 10%, 20%, or 30% PSM in POPC had 1320 total lipids. One simulation of 10:1 PIP2:POPC had total 484 lipids, with 129 ions. When simulating PIP2, the CHARMM residues SAPI24 and SAPI25 were used in equal amounts. The residues only vary by the protonation state of either the fourth or fifth position phosphate group. These lipids both possess one stearoyl (18 carbon, fully saturated) and one arachidonic (20 carbon, 4 unsaturated bonds) acyl tail each. All systems were simulated for at least one microsecond (summing all replicas) with a constant temperature of 310.15 K and pressure of 1 bar. A summary of components and durations for each of the simulation systems is listed in Table S5.
Using NAMD (42), systems were minimized and initially relaxed as prescribed by CHARMM-GUI. After these steps, the systems were converted into AMBER format (43,44) using ParmEd. All analyzed data was simulated with AMBER. Constant temperature was targeted and regulated by a Langevin thermostat with a friction coefficient of 1 ps−1, and constant pressure was anisotropically ( and coupled; zero surface tension) maintained by a Monte Carlo barostat. Note that there was no apparent static buckling of the membrane as observed in ref. (45). Non-bonded interactions were switched off between 10 and 12 Å using force-based switching. Long-range electrostatics were handled by the PME implementation for GPUs by Salomon-Ferrer et al. (46). The PME grid was constructed with a spacing of less than 1 Å (tolerance = ; Ewald coefficient = 0.22664; inter-polation order = 4). Bond lengths involving hydrogen were constrained by SHAKE (47); water was kept rigid using SETTLE (48). A 2 fs time step was used, and coordinates were saved every 200 ps for analysis.
Dimer identification
Lipid structures were characterized by a subset of atoms, defined for each type below. Pairs of lipids were selected if the center of geometry of the subset was within 14 Å. Atom names are listed below in the C36 lipid force field naming scheme.
Hydrogen bonding from DOPE
The atom selections for DOPE, DOPC, and DOPS were {P, N, C1, C3, C24, and C34}. Hydrogen bonds between lipids were identified when a PE hydrogen was within 2.5 Å of a hydrogen-bond acceptor, here either the phosphate oxygens or the carbonyl oxygens.
Divalent-cation mediation of PIP2
Both SAPI24 and SAPI25 PIP2 residues were treated identically in lipid-pair detection. The atom selections for PIP2 were {C11, C12, C13, C14, C15, C16, P4, P5, P, C1, C2, C3, C21, and C31}, while POPC used {P, N, C1, and C11}. Divalent-cation-mediated dimers were identified when a (or ; see supporting material) ion was within 4 Å of the center of geometry of a lipid dimer.
Hydrogen bonding of PSM
The atom selections for PSM were {N, P, NF, HNF, O3, HO3, and OF}. Hydrogen bonds between lipids were identified when either the HNF or HO3 atom was within 2.5 Å of a hydrogen-bond acceptor, here a phosphate oxygen, OF, or O3.
General state identification with an HMM
The full description of the HMM methodology for dimer state extraction is described in the supporting material. Briefly, a subset of dimer states was extracted using the atom selections and cutoffs above, yielding between 104 and structures for a dimer type. Fifty-two clusters were formed by K-medoid clustering, which chooses clusters based on representative structures from a set, associating each member of the whole set with a cluster center to minimize the summed root-mean-square deviation of the clusters. These clusters formed the observable in the HMM. Following the definition of the clusters, all time-ordered sequences of dimers were extracted from the simulation, assigning each instance of a dimer to a cluster based on root-mean-square deviation. An HMM describing the observed sequences of dimer clusters was created by optimizing the transition and observation probabilities of the HMM such that the probability of observing the ordered sequences was maximized. State was then assigned to each dimer configuration based on the optimized HMM.
Computation of dimer curvature preference
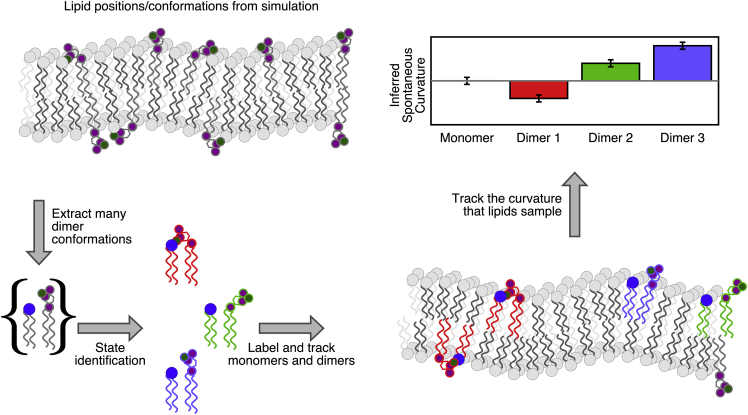
We define here the curvature-coupled redistribution (CCR) method, which extracts the curvature experienced by lipids, implying the spontaneous curvature (21). A cartoon illustrating the overall approach is shown in Fig. 1.
Figure 1.
A cartoon illustrating the curvature-coupled redistribution method. Beginning at the top left and proceeding counter-clockwise, a patch of multicomponent bilayer is simulated (represented above by purple and gray lipids in the top left). A set of dimer conformations are extracted and collected into states with common properties. Here, the cartoon represents divalent-cation-mediated interactions between an anionic lipid and its neighbors. The correlation of state (i.e., molecular structure) and curvature is recorded and compared with Helfrich/Canham theory. The mechanism of curvature sensitivity of a state is inferred from the correlation of structure and sampled curvature. To see this figure in color, go online.
The instantaneous (i.e., per frame) discrete Fourier spectrum is computed on a grid with maximum spacing of 15 Å. The height is computed first for each leaflet; the bilayer height is the mean of the two. The coefficient of mode q is
| (3) |
where here is the height of the grid point located at lateral coordinates . For each frame in the trajectory, the set is recorded, along with the lateral positions for each lipid.
The instantaneous curvature a lipid experiences is computed as :
| (4) |
which is real as . The upper cutoff, , determines the highest frequency mode used to compute curvature. In this analysis, lower q modes are less well sampled because they occur more slowly. Conversely, higher q modes are more readily sampled, helping to reduce error in the calculations. The cost of including these high q modes is the potential biasing of the analysis to only describe these short wavelength fluctuations instead of the whole bilayer. The used in our analysis 0.08 attempts to balance these considerations. The average curvature, , experienced by a lipid is then the average of over the trajectory.
Lipids can be analyzed as monomers to determine single-lipid spontaneous curvature as pairs (e.g., DOPE-DOPE homodimers or POPC-PIP2 heterodimers) or as subsets of lipid pairs differentiated by a specific chemical interaction (e.g., hydrogen-bond formation or ion binding). Lipid populations will be compared in terms of their experienced curvature, , calculated using Eq. 4 and averaged over the duration of the simulation. The quantity is directly proportional to spontaneous curvature . The benefit of using is that it can be directly calculated from simulation and does not rely on knowledge of the area per lipid in a complex. An additive model is useful as the null hypothesis of a single-lipid ; it accounts for the likelihood of finding two curvature-sensitive lipids co-localized. Subpopulation can then be compared with each other as well as with the additive model.
The additive model for lipid dimers
A simple hypothesis for the spontaneous curvature of dimers is that their spontaneous curvature is the area-weighted average of the two species and that the total area of the dimer is the sum of the monomer areas:
| (5) |
From the Helfrich/Canham model (26,27) and assuming a localized lipid mechanical extent (21), the experienced curvature of some embedded molecule on mode is proportional to its area fraction (, where is the area of the embedded object and is the area of the bilayer patch) times its spontaneous curvature difference with the background, (21):
| (6) |
The additive model of two interacting lipids is that the experienced curvature for a dimer is the sum of the observed monomer curvatures:
| (7) |
Our methodology distinguishes the case that interacting lipids (e.g., hydrogen-bonded PE lipids) have a unique spontaneous curvature from the null hypothesis that random co-localization of curvature sensitive lipids doubles the monomer effect. In both cases, the background is the average of the complete bilayer, where is the difference of the target lipid (e.g., a PE monomer or dimer) relative to all the lipids, including PE. The additive model assumes that the spontaneous curvature of the PE lipids is constant, regardless of its environment. To characterize interacting lipids, we compare the experienced curvature of all PE-PE pairs that form a hydrogen bond between lipid headgroups with the additive model. This comparison is possible because the CCR method can track lipids that have been tagged in specific states. If the formation (or lack of) hydrogen bonds influences the curvature preference of interacting lipids, it will manifest as the lipid subpopulation having a significantly different experienced curvature than that of non-interacting lipids. These two cases illustrate how the CCR method can be used to investigate the molecular mechanisms that drive spontaneous curvature.
The additive model may overestimate the spontaneous curvature of a monomer due to attractive interactions between lipids. That is, the monomer may appear to have a stronger influence on curvature because its effect is amplified by co-localization.
The additive model as the null hypothesis
All three test systems described above are analyzed using the same relative reference state: the additive model. The used to construct the model comes from the bulk lipid redistribution analysis and are reported as the single lipid species differences in spontaneous curvature. Values of for each monomer in this paper are reported in Table 1. Use Eq. 7 to translate between and experienced curvature, .
Table 1.
values used in the additive model
| Lipid | (Å−1) | Simulation |
|---|---|---|
| DOPE | 30% DOPE 25% DOPC +45% DOPS | |
| DOPC | ||
| DOPS | ||
| PIP2 | 10% PIP2 90% POPC | |
| POPC | ||
| PSM | 10% PSM 90% POPC | |
| POPC | ||
| PSM | 20% PSM 80% POPC | |
| POPC | ||
| PSM | 30% PSM 70% POPC | |
| POPC |
These values are calculated from a bulk analysis of spontaneous curvature values for individual lipid species subtracted from the spontaneous curvature of the entire membrane. Error bars represent one standard error of the mean (SEM).
Dimer spontaneous curvature is distinguished by comparison with lipid monomers. Monomers are defined as those lipids that do not meet the criteria for a dimer. For example, when classifying PIP2-PIP2 dimers, PIP2 lipids as members of PIP2--POPC complexes would be classified as monomers if they are not in complex with other PIP2 lipids. When identifying PIP2--POPC complexes, PIP2 lipids as members of PIP2-PIP2 complexes would be classified as monomers if they are not bridged by to POPC.
Results
Hydrogen-bond donation from DOPE lipids induces negative curvature
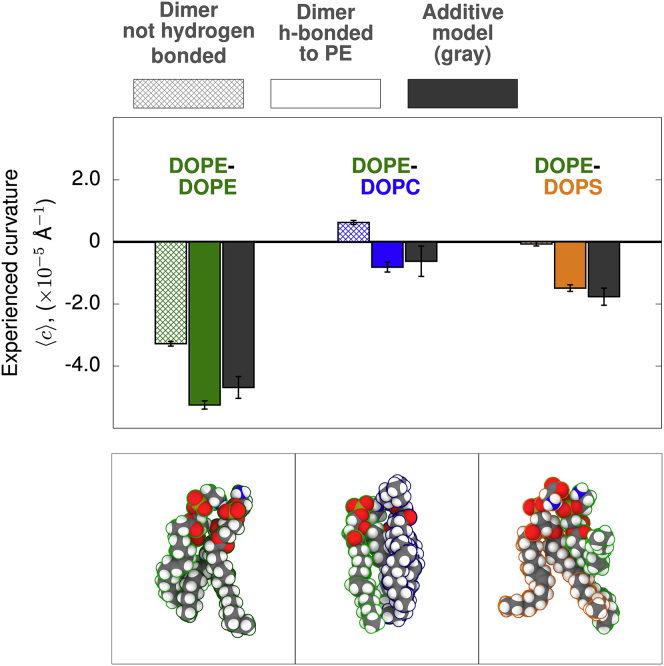
Fig. 2 reports the average curvature experienced by dimers of DOPE with DOPE, DOPC, or DOPS. The simulations in this work have been previously used in ref. (21) to establish the equivalence between the lateral pressure profile and CCR methodology. It is clear that DOPE modeled with the CHARMM C36 force field has a negative spontaneous curvature, consistent with experiment (28). Also apparent from this analysis is the observation that complex formation with DOPE leads to significant deviations from the additive approximation.
Figure 2.
Hydrogen-bond donation from PE headgroups enhances negative curvature in lipid dimers. Legend above figure (in gray) shows the crosshatched bars that represent the non-hydrogen-bonded complexes, the colored bars represent the hydrogen-bonded dimers, and the gray bar represents the theoretical, additive model. Experienced curvature is plotted for lipids as monomers or as in complex. Lipids (DOPE, green; DOPC, blue; DOPS, gold) are colored by type. The additive model is shown in gray. The bottom panels are representative molecular configurations of hydrogen-bonded dimers. To see this figure in color, go online. Error bars represent one SEM.
The spontaneous curvature of lipid dimers containing DOPE depends on variations of the intra-complex conformations of interacting lipids. Two mechanisms are proposed to influence the spontaneous curvature of DOPE: headgroup size and hydrogen-bond formation (49, 50, 51). The small PE headgroup suggests that it is a predominant factor in determining its negative spontaneous curvature. The present analysis indicates, however, this is not the complete story. A comparison of dimers in which DOPE forms a hydrogen bond (Fig. 2, middle column, solid) or does not (Fig. 2, left column, hashed) indicates substantially increased negative spontaneous curvature for configurations with hydrogen bonding. In all three cases, the statistical significance of experienced curvature differences between the states as determined by pairwise comparison indicates a significant difference between the non-hydrogen-bonded and hydrogen-bonded dimer states: DOPE-DOPE (p = 0.000077), DOPE-DOPC (p = 0.0011), and DOPE-DOPS (p = 0.000083). Complete tables of p values can be found in the supporting material. This highlights the importance of specific molecular interactions when relating lipid content to curvature.
Following theory (Eq. 1), this system should undergo both diffusional and conformational softening. DOPE can form complexes between all three types of lipids in the system, each with a different bulk curvature preference. The dynamic, diffusional coupling of these complexes to membrane undulations will lower the apparent bending modulus. Likewise, formation of a hydrogen bond in each of these complexes significantly changes to become more negative. Rapid inter-conversion between these states then leads to a softer bilayer. Even in a system with only three components, lipid heterogeneity and molecular details complicate the traditional continuum interpretation of bilayer mechanics.
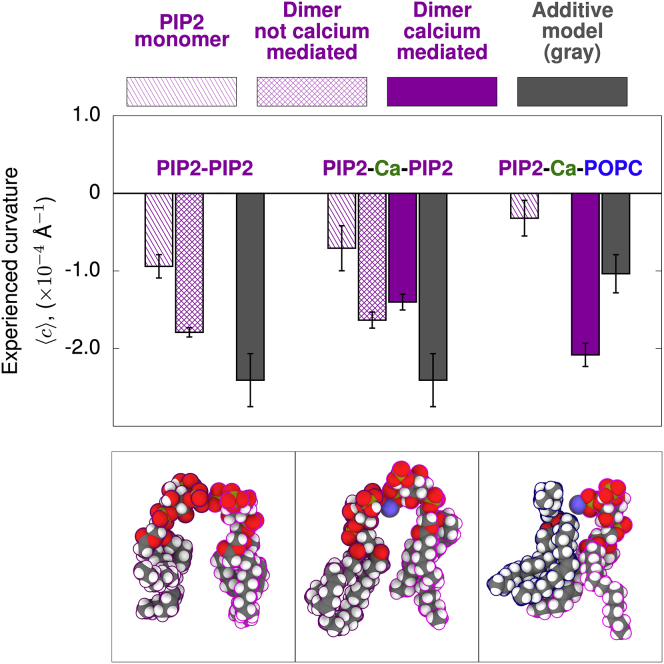
Divalent-cation-mediated interactions of PIP2 induce negative curvature independent of clustering
Three PIP2 dimer schemes were analyzed. In the first, a dimer is defined by its interactions with neighboring PIP2 (Fig. 3, left column). Redistribution analysis indicated dimers were consistent with twice the monomer model (compare twice the value of the striped bar and the crosshatched bar, when compared at p = 0.05). Thus, PIP2-PIP2 interactions did not appear to influence curvature. Second, PIP2-PIP2 dimers were isolated if their interaction was mediated by (Fig. 3, center column). interactions within the dimer showed no significant changes in negative curvature (Fig. 3, solid purple and crosshatched bars; p = 0.15). Third, the dimer state was defined as a -mediated interaction with neighboring POPC (Fig. 3, right column). Here, a significant, non-additive negative curvature preference was detected (Fig. 3, solid purple to gray; p = 0.0093). Note that -mediated clustering of PIP2 has likely led to an overestimate of the PIP2 monomer spontaneous curvature, yielding a dimer additive model that overestimates the effect of a dimer (Fig. 3, first and second columns).
Figure 3.
Calcium-bridged interactions between PIP2 and POPC show strong negative curvature. Experienced curvature is plotted for lipids as monomers or as in complex. The additive model is shown in gray, and monomers are striped. Dimers are crosshatched. -mediated dimers are solid. The bottom panels are representative molecular configurations of each type (PIP2-PIP2, PIP2--PIP2, and PIP2--POPC). To see this figure in color, go online. Error bars represent one SEM.
These results support current models of PIP2 cluster curvature preference and highlight the need to better understand the role of divalent cations in mediating PIP2 heterodimer formation. While in native membranes PIP2 is a minor lipid species (52), it can form clusters that enhance local concentration (53). In this case, the PIP2 clusters should act as a slowly diffusing curvature-sensitive inclusion that contributes to softening. While the PIP2-PIP2 interactions within the clusters may not show a strong preference for negative curvature, these clusters are also surrounded by a myriad of other lipids. Our results suggest that further analysis of PIP2 clustering would show that curvature is affected by the boundary of a PIP2 domain, where conformations would more closely resemble the PIP2--POPC interaction we identify. These types of ion-mediated heterodimers present a potentially important case for conformational softening near PIP2 clusters that may have functional relevance for curvature-influencing proteins that bind PIP2 (4).
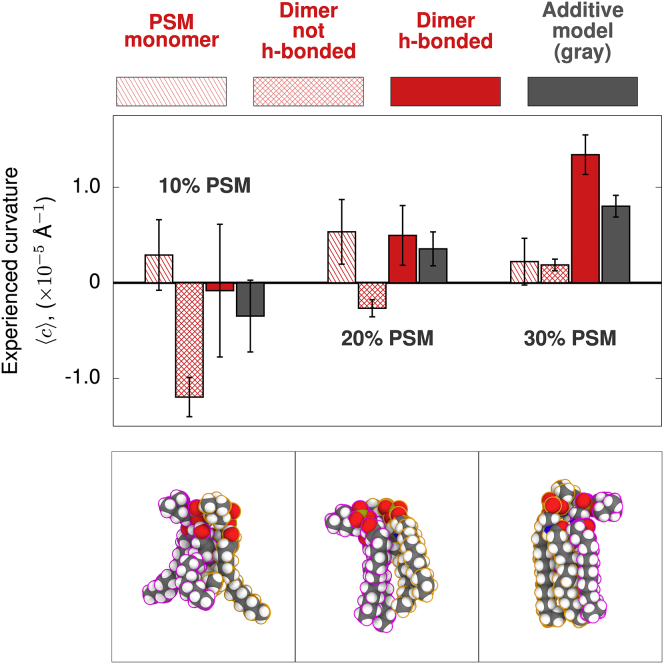
PSM complex formation promotes positive curvature
Fig. 4 shows that the monomeric state of PSM exhibits similar curvature preferences to POPC (little net curvature preference). Neighboring PSM lipids without hydrogen bonds do not show a positive curvature preference (Fig. 4, crosshatched bars). By comparison, PSM lipids that form amide-mediated hydrogen-bonded states exhibit a positive spontaneous curvature (Fig. 4, solid bars). This shift to a more positive spontaneous curvature becomes more pronounced as the mole fraction of PSM is increased. At 30 mol % fraction of PSM, the experienced curvature difference between dimer states with and without hydrogen bonds becomes statistically significant (p = 0.0038). The p values comparing the other states in this analysis can be found in Table S4. The relationship between the increased positive curvature preference of the hydrogen-bonded state and the mol fraction of PSM suggests that formation of the amide hydrogen bond helps to drive shift to more positive spontaneous curvature at higher concentrations of PSM.
Figure 4.
Curvature sensitivity of PSM dimers changes with hydrogen-bond formation and concentration. Experienced curvature is plotted for lipids as monomers or as in complex. The additive model is shown in gray, and monomers are striped. Dimers are crosshatched. Hydrogen-bond-mediated dimers are solid. The bottom panels are representative molecular configurations of the amide-hydrogen-bonded configuration. To see this figure in color, go online. Error bars represent one SEM.
It is important to highlight that hydrogen-bond formation in the PSM systems has the opposite effect (i.e., biasing the complex to more positive curvatures) that what was seen in the DOPE system (more negative curvature bias). The positioning of the PSM amide hydrogen bond within the leaflet is likely important for determining the sign of the curvature. Hydrogen-bond formation occurs closer to the bilayer mid-plane in the PSM lipids than the hydrogen bonds made by lipids PE headgroups. In the case of DOPE, attractive forces near the headgroup surface lead to negative curvature (54). We propose that amide HB formation observed in the PSM system helps to reduce tail entropy and, therefore, shift the curvature preference more positive (further explained in the discussion).
PSM exhibits a concentration-dependent positive curvature preference, yet it is unclear whether the amide-hydrogen-bonded dimer is sufficient to completely explain the trend. We speculate that the increasing positive curvature of PSM is also due to higher-order effects beyond dimerization. For example, with sufficient PSM nearby, cohesive hydrogen bonding supports chain ordering, further lessening entropic tail repulsion and thus its contribution to positive curvature. A similar effect was observed with the chain-ordering ability of cholesterol (30). The possibilities for extending the CCR analysis to higher-order complexes are discussed below.
This system shows an additional way that heterogeneous lipid composition can complicate the traditional continuum view of mixed bilayers. In this case, changes in the lipid matrix composition influence both the sign of different PSM-PSM complex curvature preference and the magnitude of hydrogen-bond formation on the curvature. By making the difference in curvature preferences between the hydrogen-bonded and non-hydrogen-bonded states larger, the anticipated magnitude of conformational softening will increase. Further, as matrix PSM increases, PSM-PSM dimers prefer more positive curvature, which changes where these structures will diffuse to and will alter the impact of diffusional softening.
Discussion
Curvature preference is a balance of repulsive and cohesive forces along the bilayer normal
Curvature preference is typically described using the heuristic of “lipid shape” that conveniently describes lipids as cones or cylinders (55). Needless to say, specific interactions between lipids are incompatible with shape. Thus, identification of the curvature sensitivity of specific interactions coupling to curvature refutes the ubiquity of the shape model. In contrast, CCR provides the required framework for distinguishing the molecular mechanisms of spontaneous curvature quantitatively.
It is the balance of repulsive and attractive forces that determines the curvature stresses of a leaflet and thus its spontaneous curvature. Qualitatively, repulsive forces originating from bulky headgroups and tail entropy are the essence of the shape model. Attractive forces, such as hydrogen bonding and Coulombic interactions, are better described by specific interactions. Both are quantified in the lateral pressure profiles (54) that are typically used to infer . The lateral pressure profile of PE, for example, has a cohesive stress at the depth of the hydrogen bond (56), relative to PC. There is currently no method to determine, from the pressure profile, whether this is due to the size of the headgroup or hydrogen bonding.
Applying the CCR method allows us to correlate molecular interactions with curvature and make connections to the transverse positions of interactions. In the cases of both DOPE and -mediated interactions of PIP2, attractive interactions near the level of the glycerophospholipid phosphate induce strong negative curvature. In contrast, the amide hydrogen bond is formed deeper in the membrane for PSM-PSM dimers. By anchoring the two lipids closer to the tails, we speculate that the hydrogen bond restricts the tail entropy and, therefore, reduces the repulsive forces on that region of the lipid. Lessening the tail repulsion would then give rise to the positive curvature preference of these PSM dimers. Additionally, positive curvature coincides with ordering of the surrounding matrix. That is, is more positive at 30% PSM, and ordered configurations are likely.
Curvature-dependent lipid configurations determine the bending modulus
The bending modulus is the elastic constant describing the second-order variation in the curvature energy. The magnitude of is related to the conformational plasticity of the lipids. An example of this is the stiffening (∼5 times (57)) of ordered phase bilayers compared with disordered bilayers. In the liquid disordered phase, lipids are less tightly packed and can adopt a greater range of conformations, presumably leading to a smaller bending modulus. Conversely, the liquid-ordered phase restricts lipid dynamics and increases packing, increasing the bending modulus. The differences between these two phases highlights the importance of molecular details when interpreting a bulk phenomenon like bending energy. We relate two mechanisms of bilayer softening that are displayed on very different timescales. First, consider diffusional softening, the change in the undulation relaxation spectrum due to dynamic lateral fluctuations of a mixture of lipids with varied . The second mechanism shows how membrane bending rigidity can be reduced through the inter-conversion between lipid pairs with distinct, curvature-dependent states, which we refer to as conformational softening. The observed softening generated by both mechanisms is described by Eq. 2. For clarity, we will the specify softening mechanism by denoting as either or .
Diffusional softening
A bilayer is assembled with symmetrical leaflet composition: a small molecular fraction of a lipid species A with spontaneous curvature amid a background of lipids with zero spontaneous curvature. Further assume that there is a well-defined bending modulus that is the same for the background as well as that of . The bending modulus of the entire mixture will appear to be
| (8) |
with having the same form defined in Eq. 2. Here is the difference of spontaneous curvature between and the spontaneous curvature of the background lipid composition. The softening factor arises from the coupling of the lateral distribution of lipids to bilayer undulations. Note that the lateral distribution of lipids relaxes slowly (as , where is the diffusion constant, and , where is the undulation wavelength) for submicron wavelength undulations. This introduces kinetics as an important consideration when investigating softening mechanisms.
Conformational softening
Consider now softening due to (perhaps rapidly) inter-changing curvature-dependent conformations. Our results show that different conformations can exhibit different curvature preferences. We have introduced the softening factor in Eq. 2 that shows mathematically how different curvature-sensitive conformations can soften bilayers. Below, we will provide an additional way to understand this mechanism by how can alter the energy required to bend membranes. We propose a simple model in which mechanical properties (spontaneous curvature and bending modulus) are altered by adding in a specific interaction. The hydrogen bond donated by a PE lipid to a neighbor adds negative curvature preference that appears to be largely independent of the acceptor (Fig. 2). The -mediated interaction between PIP2 and POPC dramatically shifts curvature to be negative (Fig. 3). We model the interacting state as being “added on” by shifting the spontaneous curvature of a reference lipid, such as POPC, by . The reference lipid has area per lipid , spontaneous curvature , and bending modulus . The likelihood of the interacting state is further characterized by its curvature-independent mole fraction, .
Apply separate local Helfrich models and for the curvature energy of the reference and interacting states, respectively:
| (9) |
and
| (10) |
where is the area per lipid for the reference, is the curvature local to the lipid, and is the monolayer bending modulus. The free energy is
| (11) |
can be restructured in a form resembling the Helfrich Hamiltonian. Consider the case in which is small. Expanding to second order in
| (12) |
where has the same form outlined in Eq. 2. Because both conformational and diffusional softening have the same factor, , compositional and conformational heterogeneity have a similar effect on bilayer properties. For Å−1, Å−2, , and kcal/mol, the lipid patch has 83% the stiffness. This is a substantial decrease in the apparent stiffness of the bilayer and can be directly attributed to the ability of specific states to stabilize different curvatures.
Unlike chemical composition, the conformational composition fluctuates rapidly. Furthermore, the inter-change of conformations is typically much faster than the lateral rearrangement of lipids. An intuitive example is conformational isomerization of acyl chains, which occurs on the subnanosecond timescale (58), whereas lipids require tens of nanoseconds to change neighbors and for a fluctuation with wavenumber to relax (microseconds for a tens of nanometers lengthscale).
Molecular configurations of lipids are a continuum, not discrete. The reasoning in this section thus only forms a rationale for how curvature sensitivity of conformational sets determines softening rather than for predicting ab initio. We have implicitly chosen to represent the bending modulus of some idealized simple lipid, for example, POPC, that serves as a base value. Stiffening, on the other hand, may result in the removal of conformational space, for which the base of of POPC, and the treatment here would be inadequate.
Impact of timescale on membrane elasticity measurements
The impact of two complementary but temporally distinct mechanisms for bilayer softening should be observable by techniques that measure . Equilibrium measurements that report the entire distribution of undulation amplitudes (diffusive x-ray studies and fluctuation analysis) will show the effects of both diffusion and conformational softening. The apparent bending modulus measured using these techniques likely best models the average work required to deform a membrane.
By comparison, experiments that infer mechanical properties from relaxation kinetics can shed light on complex mechanisms that underly mechanics. Neutron spin echo (NSE) and nuclear magnetic resonance spectroscopies will be influenced by the fast relaxation processes that determine conformational softening. Where only the faster relaxation times of short wavelength undulations are probed, mechanical properties will be insensitive to diffusional softening.
How these two softening mechanisms intersect and impact membrane mechanics highlights the importance of considering timescales and length scales when measuring membrane elasticity. Consider the NSE and nuclear magnetic resonance experiments on mixtures of DOPC and cholesterol in ref. (59), which find that a DOPC bilayer is stiffened by cholesterol. Diffusional softening is expected by cholesterol, a lipid that induces high negative curvature (28), yet this would only be clear from techniques able to probe long timescales in which lateral fluctuations of cholesterol concentration are relaxed. This is a plausible explanation for the disagreement between diffusive x-ray studies and NSE techniques (60,61). Combining the two techniques would isolate mechanisms of softening that are important at separate timescales and increase clarity into the molecular impact of cholesterol on membrane mechanics.
Impact on bilayer viscosity
The undulation of a simple bilayer relaxes with rate at low , where is the solvent viscosity (62). For higher frequency undulations occurring on the submicrometer length scale and submicrosecond timescale, inter-leaflet friction and surface viscosity slow the relaxation rate (63). Experimental work using homogeneous PC lipid bilayers suggest that acyl chain dynamics are important determinants of viscosity (64). Extending insights drawn from bulk alkane systems (65), the authors speculate that both internal dynamics controlled by factors such as tail saturation and external factors (e.g. lipid-lipid coupling) control different timescale relaxation phenomena (64).
In addition to acyl chain dynamics, ensembles of curvature-sensitive conformations must also relax; we hypothesize that the lipids studied herein, as well as others with similar chemistry, should contribute to the viscosity. The lifetimes of complexes studied here (many nanoseconds for PIP2--POPC bridging) are on the same order of magnitudes for the slow relaxation times reported in studies of alcohol and alkane systems (65) and DMPC bilayers (64). Plausibly, long-lived lipid dimers would increase the lipid-lipid couplings that are proposed to dominate at higher . In this way, we identify two competing ways that viscosity can be altered by headgroup dynamics and heterogeneity in multicomponent bilayers (diffusional and conformational). In lieu of the additional molecular mechanism implicated in determining bilayer viscosity, new whole-lipid approaches are needed for investigating the viscoelastic properties of multicomponent bilayers.
Importance of divalent-cation-mediated heterodimers in PIP2 membrane mechanics
The unique chemistry of PIP2 allows it to play an outsized role in healthy cell physiology. Despite being 1% of cellular membrane composition (66), it is an essential part of cellular pathways including actin dynamics, cell adhesion, endocytosis, signaling, and organelle trafficking (67,68). In these processes, PIP2 binds various effector proteins that can either be peripheral membrane proteins (e.g., BAR proteins, kinases, etc.) or integral membrane proteins (e.g., voltage-gated potassium channels). PIP2 function is tied to cellular localization that depends intimately on the physical chemistry of the lipid. It is a negatively charged lipid due to the addition of phosphate groups and, as a result, can make a strong complex with divalent cations but only if the cation is present at sufficient concentration (69).
Divalent-cation binding is important to PIP2 membrane biophysics. Studies have shown that PIP2 organization in lipid bilayers is altered by the presence of divalent cations (70). Namely, PIP2 is suggested to form microdomains within the native membrane and thereby increase its effective local concentration (70). While calcium is a physiologically important ion, clustering also is induced by magnesium and zinc (53). Computational studies have used graph theory and network analysis to describe the differences these various ions have on inter-connectivity induced by these ions (71). Simulations of PIP2 indicate it has negative spontaneous curvature, with divalent-cation binding increasing the coupling to negative curvature (72). This adds an additional layer of complexity to understanding microdomain formation in PIP2. In addition to knowing that PIP2 can exist at high effective concentrations, it is also important to consider the local bilayer structure of PIP2 microdomains.
In ref. (72), the negative curvature of -bound PIP2 is studied in pure PIP2 bilayers. The authors found that high calcium concentrations (2:1 :PIP2) are necessary to induce the strongest negative curvature. In contrast, we find that at 10% coverage, it is the simple -mediated interactions with neighboring POPC that induce negative curvature, an effect that would not be apparent in a bilayer saturated with PIP2. According to our analysis, domains of PIP2 are not required for a profound mechanical effect. Rather, it is the strong connection to neighboring lipids by divalent cations that is required.
Conclusions
This study introduces methodology for linking molecular interactions to lipid spontaneous curvature. The negative spontaneous curvature of PE lipids is partly explained by its ability to donate hydrogen bonds to neighboring lipids. Divalent-cation-mediated interactions between PIP2 and neighboring glycerophospholipids show a strong trend to negative curvature, indicating that domains of PIP2 are not required for its negative curvature preference. In a third case, hydrogen-bond-linked conformations of PSM showed a strong positive curvature preference only at higher PSM concentrations, suggesting the ordered lipid matrix is part of the mechanism.
The shape of membranes is typically interpreted in terms of the average, or monomer, mechanical properties of lipids, assuming static or uniform distributions of lipids. Biological membranes, however, are neither static nor uniform. By ignoring the possibility of substates with different curvature preferences or averaging over these substates, it is likely that important mechanistic insights into physiological process are being missed. The simulation methodology here presents a path to understanding this complexity, with the mechanism testable by scattering and membrane-fluctuation analysis techniques. In our judgment, the modeling of with diffusional and conformational softening, the characterization of the spatial mechanical extent of lipids and multilipid complexes (21), and the understanding of the effects of differential stresses between leaflets (73) are forging a clear path to characterization of the bending modulus and curvature stresses of biological membranes with complex composition.
Author contributions
H.J.L., K.C.S., and A.J.S designed the research. H.J.L. and A.H.B. performed the simulations. H.J.L., K.C.S., A.H.B., R.A., and A.J.S. wrote the paper.
Acknowledgments
This work was supported by the intramural research program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) at the National Institutes of Health. A.H.B. was supported by a Postdoctoral Research Associate (PRAT) fellowship from the National Institute of General Medical Sciences, award number 1Fi2GM137844-01. R.A. acknowledges support from the National Science Foundation under award number MCB-2137154. Molecular rendering was performed with Tachyon software written by John E. Stone. Simulations were performed on computational resources provided by the NICHD.
Declaration of interests
The authors declare no competing interests.
Editor: Michael F. Brown.
Footnotes
Henry J. Lessen and Kayla C. Sapp contributed equally to this work.
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.07.036.
Supporting material
References
- 1.Harayama T., Riezman H. Understanding the diversity of membrane lipid composition. Nat. Rev. Mol. Cell Biol. 2018;19:281–296. doi: 10.1038/nrm.2017.138. [DOI] [PubMed] [Google Scholar]
- 2.Dennis E.A., Norris P.C. Eicosanoid storm in infection and inflammation. Nat. Rev. Immunol. 2015;15:511–523. doi: 10.1038/nri3859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fernandis A.Z., Wenk M.R. Membrane lipids as signaling molecules. Curr. Opin. Lipidol. 2007;18:121–128. doi: 10.1097/MOL.0b013e328082e4d5. [DOI] [PubMed] [Google Scholar]
- 4.Mandal K. Review of PIP2 in cellular signaling, functions and diseases. Int. J. Mol. Sci. 2020 doi: 10.3390/ijms21218342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Van Meer G., Voelker D.R., Feigenson G.W. Membrane lipids: where they are and how they behave. Nat. Rev. Mol. Cell Biol. 2008;9:112–124. doi: 10.1038/nrm2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lujan P., Campelo F. Should I stay or should I go? Golgi membrane spatial organization for protein sorting and retention. Arch. Biochem. Biophys. 2021;707:108921. doi: 10.1016/j.abb.2021.108921. [DOI] [PubMed] [Google Scholar]
- 7.Nakamura M.T., Yudell B.E., Loor J.J. Regulation of energy metabolism by long-chain fatty acids. Prog. Lipid Res. 2014;53:124–144. doi: 10.1016/j.plipres.2013.12.001. [DOI] [PubMed] [Google Scholar]
- 8.Deevska G.M., Nikolova-Karakashian M.N. The expanding role of sphingolipids in lipid droplet biogenesis. Biochim. Biophys. Acta. Mol. Cell Biol. Lipids. 2017;1862:1155–1165. doi: 10.1016/j.bbalip.2017.07.008. [DOI] [PubMed] [Google Scholar]
- 9.Lorent J.H., Levental K.R., et al. Levental I. Plasma membranes are asymmetric in lipid unsaturation, packing and protein shape. Nat. Chem. Biol. 2020;16:644–652. doi: 10.1038/s41589-020-0529-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Levental I., Veatch S. The continuing mystery of lipid rafts. J. Mol. Biol. 2016;428:4749–4764. doi: 10.1016/j.jmb.2016.08.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cheng X., Smith J.C. Biological membrane organization and cellular signaling. Chem. Rev. 2019;119:5849–5880. doi: 10.1021/acs.chemrev.8b00439. [DOI] [PubMed] [Google Scholar]
- 12.Stone M.B., Shelby S.A., et al. Veatch S.L. Protein sorting by lipid phase-like domains supports emergent signaling function in b lymphocyte plasma membranes. Elife. 2017;6:e19891. doi: 10.7554/eLife.19891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Soubias O., Teague W.E., et al. Gawrisch K. Contribution of membrane elastic energy to rhodopsin function. Biophys. J. 2010;99:817–824. doi: 10.1016/j.bpj.2010.04.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Beaven A.H., Maer A.M., et al. Im W. Gramicidin A channel formation induces local lipid redistribution I: experiment and simulation. Biophys. J. 2017;112:1185–1197. doi: 10.1016/j.bpj.2017.01.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brown M.F. Curvature forces in membrane lipid-protein interactions. Biochemistry. 2012;51:9782–9795. doi: 10.1021/bi301332v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Steinkühler J., Sezgin E., et al. Dimova R. Mechanical properties of plasma membrane vesicles correlate with lipid order, viscosity and cell density. Commun. Biol. 2019;2:337. doi: 10.1038/s42003-019-0583-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gracià R.S., Bezlyepkina N., et al. Dimova R. Effect of cholesterol on the rigidity of saturated and unsaturated membranes: fluctuation and electrodeformation analysis of giant vesicles. Soft Matter. 2010;6:1472–1482. [Google Scholar]
- 18.Semrau S., Idema T., et al. Storm C. Accurate determination of elastic parameters for multicomponent membranes. Phys. Rev. Lett. 2008;100:088101. doi: 10.1103/PhysRevLett.100.088101. [DOI] [PubMed] [Google Scholar]
- 19.Needham D., Nunn R.S. Elastic deformation and failure of lipid bilayer membranes containing cholesterol. Biophys. J. 1990;58:997–1009. doi: 10.1016/S0006-3495(90)82444-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Leibler S. Curvature instability in membranes. J. Phys. France. 1986;47:507–516. [Google Scholar]
- 21.Sapp K.C., Beaven A.H., Sodt A.J. Spatial extent of a single lipid’s influence on bilayer mechanics. Phys. Rev. E. 2021;103:042413. doi: 10.1103/PhysRevE.103.042413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kozlov M.M., Helfrich W. Effects of a cosurfactant on the stretching and bending elasticities of a surfactant monolayer. Langmuir. 1992;8:2792–2797. [Google Scholar]
- 23.Bivas I., Méléard P. Bending elasticity and bending fluctuations of lipid bilayer containing an additive. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;67:012901. doi: 10.1103/PhysRevE.67.012901. [DOI] [PubMed] [Google Scholar]
- 24.Tian A., Capraro B.R., et al. Baumgart T. Bending stiffness depends on curvature of ternary lipid mixture tubular membranes. Biophys. J. 2009;97:1636–1646. doi: 10.1016/j.bpj.2009.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bashkirov P.V., Kuzmin P.I., et al. Frolov V.A. Molecular shape solution for mesoscopic remodeling of cellular membranes. Annu. Rev. Biophys. 2022;51:473–497. doi: 10.1146/annurev-biophys-011422-100054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 27.Canham P.B. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theor. Biol. 1970;26:61–81. doi: 10.1016/s0022-5193(70)80032-7. [DOI] [PubMed] [Google Scholar]
- 28.Chen Z., Rand R.P. The influence of cholesterol on phospholipid membrane curvature and bending elasticity. Biophys. J. 1997;73:267–276. doi: 10.1016/S0006-3495(97)78067-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kaltenegger M., Kremser J., et al. Pabst G. Intrinsic lipid curvatures of mammalian plasma membrane outer leaflet lipids and ceramides. Biochim. Biophys. Acta Biomembr. 2021;1863:183709. doi: 10.1016/j.bbamem.2021.183709. [DOI] [PubMed] [Google Scholar]
- 30.Sodt A.J., Venable R.M., et al. Pastor R.W. Nonadditive compositional curvature energetics of lipid bilayers. Phys. Rev. Lett. 2016;117:138104. doi: 10.1103/PhysRevLett.117.138104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chodera J.D., Noé F. Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 2014;25:135–144. doi: 10.1016/j.sbi.2014.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Voelz V.A., Jäger M., et al. Pande V.S. Slow unfolded-state structuring in acyl-CoA binding protein folding revealed by simulation and experiment. J. Am. Chem. Soc. 2012;134:12565–12577. doi: 10.1021/ja302528z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Voelz V.A., Bowman G.R., et al. Pande V.S. Molecular simulation of ab initio protein folding for a millisecond folder NTL9(1-39) J. Am. Chem. Soc. 2010;132:1526–1528. doi: 10.1021/ja9090353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Noé F., Schütte C., et al. Weikl T.R. Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations. Proc. Natl. Acad. Sci. USA. 2009;106:19011–19016. doi: 10.1073/pnas.0905466106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lane T.J., Bowman G.R., et al. Pande V.S. Markov State model reveals folding and functional dynamics in ultra-long MD trajectories. J. Am. Chem. Soc. 2011;133:18413–18419. doi: 10.1021/ja207470h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bowman G.R., Pande V.S. Protein folded states are kinetic hubs. Proc. Natl. Acad. Sci. USA. 2010;107:10890–10895. doi: 10.1073/pnas.1003962107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Paul F., Wehmeyer C., et al. Noé F. Protein-peptide association kinetics beyond the seconds timescale from atomistic simulations. Nat. Commun. 2017;8:1095. doi: 10.1038/s41467-017-01163-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Plattner N., Doerr S., et al. Noé F. Complete protein-protein association kinetics in atomic detail revealed by molecular dynamics simulations and Markov modelling. Nat. Chem. 2017;9:1005–1011. doi: 10.1038/nchem.2785. [DOI] [PubMed] [Google Scholar]
- 39.Sodt A.J., Sandar M.L., et al. Lyman E. The molecular structure of the liquid-ordered phase of lipid bilayers. J. Am. Chem. Soc. 2014;136:725–732. doi: 10.1021/ja4105667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Frisz J.F., Klitzing H.A., et al. Kraft M.L. Sphingolipid domains in the plasma membranes of fibroblasts are not enriched with cholesterol. J. Biol. Chem. 2013;288:16855–16861. doi: 10.1074/jbc.M113.473207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Klauda J.B., Venable R.M., et al. Pastor R.W. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J. Phys. Chem. B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Phillips J.C., Braun R., et al. Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Case D.A., Cheatham T.E., et al. Woods R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Case D.A., Ben-Shalom I.Y., et al. Gilson M.K. University of California; 2018. Amber 2018. [Google Scholar]
- 45.Gomez Y.K., Natale A.M., et al. Grabe M. Taking the Monte-Carlo gamble: how not to buckle under the pressure! J. Comput. Chem. 2022;43:431–434. doi: 10.1002/jcc.26798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Salomon-Ferrer R., Götz A.W., et al. Walker R.C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh ewald. J. Chem. Theory Comput. 2013;9:3878–3888. doi: 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
- 47.Ryckaert J.P., Ciccotti G., Berendsen H.J. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 48.Miyamoto S., Kollman P.A. Settle: an analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992;13:952–962. [Google Scholar]
- 49.Gruner S.M. Intrinsic curvature hypothesis for biomembrane lipid composition: a role for nonbilayer lipids. Proc. Natl. Acad. Sci. USA. 1985;82:3665–3669. doi: 10.1073/pnas.82.11.3665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hamai C., Yang T., et al. Musser S.M. Effect of average phospholipid curvature on supported bilayer formation on glass by vesicle fusion. Biophys. J. 2006;90:1241–1248. doi: 10.1529/biophysj.105.069435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sodt A.J., Pastor R.W. Molecular modeling of lipid membrane curvature induction by a peptide: more than simply shape. Biophys. J. 2014;106:1958–1969. doi: 10.1016/j.bpj.2014.02.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Mitchell K.T., Ferrell J.E., Huestis W.H. Separation of phosphoinositides and other phospholipids by two-dimensional thin-layer chromatography. Anal. Biochem. 1986;158:447–453. doi: 10.1016/0003-2697(86)90574-9. [DOI] [PubMed] [Google Scholar]
- 53.Wen Y., Vogt V.M., Feigenson G.W. Multivalent cation-bridged PI(4, 5)P2 clusters form at very low concentrations. Biophys. J. 2018;114:2630–2639. doi: 10.1016/j.bpj.2018.04.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Szleifer I., Kramer D., et al. Safran S.A. Molecular theory of curvature elasticity in surfactant films. J. Chem. Phys. 1990;92:6800–6817. [Google Scholar]
- 55.Frolov V.A., Shnyrova A.V., Zimmerberg J. Lipid polymorphisms and membrane shape. Cold Spring Harb. Perspect. Biol. 2011;3:a004747. doi: 10.1101/cshperspect.a004747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Sodt A.J., Pastor R.W. Bending free energy from simulation: correspondence of planar and inverse hexagonal lipid phases. Biophys. J. 2013;104:2202–2211. doi: 10.1016/j.bpj.2013.03.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Baumgart T., Das S., et al. Jenkins J.T. Membrane elasticity in giant vesicles with fluid phase coexistence. Biophys. J. 2005;89:1067–1080. doi: 10.1529/biophysj.104.049692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Venable R.M., Zhang Y., et al. Pastor R.W. Molecular dynamics simulations of a lipid bilayer and of hexadecane: an investigation of membrane fluidity. Science. 1993;262:223–226. doi: 10.1126/science.8211140. [DOI] [PubMed] [Google Scholar]
- 59.Chakraborty S., Doktorova M., et al. Ashkar R. How cholesterol stiffens unsaturated lipid membranes. Proc. Natl. Acad. Sci. USA. 2020;117:21896–21905. doi: 10.1073/pnas.2004807117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Nagle J.F., Evans E.A., et al. Dimova R. A needless but interesting controversy. Proc. Natl. Acad. Sci. USA. 2021 doi: 10.1073/pnas.2025011118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ashkar R., Doktorova M., et al. Brown M.F. Reply to Nagle et al.: the universal stiffening effects of cholesterol on lipid membranes. Proc. Natl. Acad. Sci. USA. 2021 doi: 10.1073/pnas.2102845118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Brochard F., Lennon J. Frequency spectrum of the flicker phenomenon in erythrocytes. J. Phys. France. 1975;36:1035–1047. [Google Scholar]
- 63.Seifert U., Langer S.A. Viscous modes of fluid bilayer membranes. Europhys. Lett. 1993;23:71–76. [Google Scholar]
- 64.Nagao M., Kelley E.G., et al. Butler P.D. Relationship between viscosity and acyl tail dynamics in lipid bilayers. Phys. Rev. Lett. 2021;127:078102. doi: 10.1103/PhysRevLett.127.078102. [DOI] [PubMed] [Google Scholar]
- 65.Yamaguchi T., Faraone A. Viscoelastic relaxations of high alcohols and alkanes: effects of heterogeneous structure and translation-orientation coupling. J. Chem. Phys. 2017;146:244506. [Google Scholar]
- 66.Van Den Bogaart G., Meyenberg K., et al. Jahn R. Membrane protein sequestering by ionic protein-lipid interactions. Nature. 2011;479:552–555. doi: 10.1038/nature10545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Dickson E.J., Hille B. Understanding phosphoinositides: rare, dynamic, and essential membrane phospholipids. Biochem. J. 2019;476:1–23. doi: 10.1042/BCJ20180022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Krajnik A., Brazzo J.A., et al. Bae Y. Phosphoinositide signaling and mechanotransduction in cardiovascular biology and disease. Front. Cell Dev. Biol. 2020;8:595849. doi: 10.3389/fcell.2020.595849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Toner M., Vaio G., et al. McLaughlin S. Adsorption of cations to phosphatidylinositol 4, 5-bisphosphate. Biochemistry. 1988;27:7435–7443. doi: 10.1021/bi00419a039. [DOI] [PubMed] [Google Scholar]
- 70.Levental I., Byfield F.J., et al. Janmey P.A. Cholesterol-dependent phase separation in cell-derived giant plasma-membrane vesicles. Biochem. J. 2009;424:163–167. doi: 10.1042/BJ20091283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Han K., Gericke A., Pastor R.W. Characterization of specific ion effects on PI(4, 5)P2 clustering: molecular dynamics simulations and graph-theoretic analysis. J. Phys. Chem. B. 2020;124:1183–1196. doi: 10.1021/acs.jpcb.9b10951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Allolio C., Harries D. Calcium ions promote membrane fusion by forming negative-curvature inducing clusters on specific anionic lipids. ACS Nano. 2021;15:12880–12887. doi: 10.1021/acsnano.0c08614. [DOI] [PubMed] [Google Scholar]
- 73.Hossein A., Deserno M. Spontaneous curvature, differential stress, and bending modulus of asymmetric lipid membranes. Biophys. J. 2020;118:624–642. doi: 10.1016/j.bpj.2019.11.3398. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.