Generalized infinite factorization models

Summary

Factorization models express a statistical object of interest in terms of a collection of simpler objects. For example, a matrix or tensor can be expressed as a sum of rank-one components. However, in practice, it can be challenging to infer the relative impact of the different components as well as the number of components. A popular idea is to include infinitely many components having impact decreasing with the component index. This article is motivated by two limitations of existing methods: (1) lack of careful consideration of the within component sparsity structure; and (2) no accommodation for grouped variables and other non-exchangeable structures. We propose a general class of infinite factorization models that address these limitations. Theoretical support is provided, practical gains are shown in simulation studies, and an ecology application focusing on modelling bird species occurrence is discussed.

1. Introduction

Factorization models are used routinely to express matrices, tensors or other statistical objects based on simple components. The likelihood for data y under a general class of factorization models can be expressed as L(y; Λ, Ψ, Σ), with Λ = (Λ_h, h = 1, …, k} a p × k matrix, Λ_h = (λ_1h, …, λ_ph)^T the hth column vector of Λ, Ψ and Σ additional parameters, and k a positive integer. This class includes Gaussian linear factor models (Roweis & Ghahramani, 1999), exponential family factor models (Jun & Tao, 2013), Gaussian copula factor models (Murray et al., 2013), latent factor linear mixed models (An et al., 2013), probabilistic matrix factorization (Mnih & Salakhutdinov, 2008), underlying Gaussian factor models for mixed scale data (Reich & Bandyopadhyay, 2010), and functional data factor models (Montagna et al., 2012). A fundamental problem is how to choose weights for the components and the number of components k. This article proposes a general class of Bayesian methods to address this problem.

Although there is a rich literature, selection of k is far from a solved problem. In unsupervised settings, it is common to fit the model for different choices of k and then choose the value with the best goodness-of-fit criteria. For likelihood models, the Bayesian information criteria is particularly popular. It is also common to use an informal elbow rule, selecting the smallest k such that the criteria improves only a small amount for k + 1. In specific contexts, formal model selection methods have been developed. For example, taking a Bayesian approach, one can choose a prior for k and attempt to approximate the posterior distribution of k using Markov chain Monte Carlo; see Lopes & West (2004) for linear factor models, Miller & Harrison (2018) for mixture models and Yang et al. (2018) for matrix factorization. Although such methods are conceptually appealing, computation can be prohibitive outside of specialized settings.

Due to these challenges it has become popular to rely on over-fitted factorization models, which include more than enough components, but with shrinkage priors adaptively removing unnecessary ones by shrinking their coefficients close to zero. Such approaches were proposed by Rousseau & Mengersen (2011) for mixture models and Bhattacharya & Dunson (2011) for Gaussian linear factor models. The latter approach specifically assumes an increasing shrinkage prior on the columns of the factor loadings matrix Λ. Legramanti et al. (2020) recently modified this approach using a spike and slab structure (Mitchell & Beauchamp, 1988) that increases the mass on the spike for later columns.

Although over-fitted factorizations are widely used, there are two key gaps in the literature. The first is a careful development of the shrinkage properties of increasing shrinkage priors (Durante, 2017). Outside of the factorization context and mostly motivated by high-dimensional regression, there is a rich literature recommending specific desirable properties for shrinkage priors. These include high concentration at zero to favor shrinkage of small coefficients and heavy tails to avoid over shrinking large coefficients. Motivated by this thinking, popular shrinkage priors have been developed including the Dirichlet-Laplace (Bhattacharya et al., 2015) and horseshoe (Carvalho et al., 2010). Current increasing shrinkage priors, such as those of Bhattacharya & Dunson (2011), were not designed to have the desirable shrinkage properties of these priors. For this reason, ad hoc truncation and use of the horseshoe/Dirichlet-Laplace can outperform increasing shrinkage priors in some contexts; for example, this was the case in Ferrari & Dunson (2020).

A second gap in the literature on over-fitted factorization priors is the lack of structured shrinkage. The focus has been on priors for Λ that are exchangeable within columns, with the level of shrinkage increasing with the column index. However, it is common in practice to have meta covariates encoding features of the rows of Λ. For example, the rows may correspond to different genes in genomic applications or species in ecology. There is a rich literature on incorporating gene ontology in statistical analyses of genomic data; refer, for example to Thomas et al. (2009). In ecology it is common to include species traits in species distribution models (Ovaskainen & Abrego, 2020). Beyond the Bayesian literature, it is common to include structured penalties, with the grouped Lasso (Yuan & Lin, 2006) a notable example.

Motivated by these deficiencies of current factorizations priors, this article proposes a broad class of generalized infinite factorization priors, along with corresponding theory and algorithms for routine Bayesian implementation.

2. Generalized infinite factor models

2.1. Model specification

Suppose that an n × p data matrix y is available. In our motivating application, y_ij is a binary indicator of occurrence of bird species j (j = 1, …, p) in sample i (i = 1, …, n). Consider the following general class of models,

$$y_{ij}=t_j\left(z_{ij}\right),z_i=\text{Λ}{\eta }_i+{ϵ}_i,{ϵ}_i\sim f_{ϵ},$$ (1)

with Λ a p × k loadings matrix, η_i a k dimensional factor with diagonal covariance matrix Ψ = diag(ψ₁₁, …, ψ_kk), ϵ_i a p-dimensional error term independent of η_i, and the function $t_j:\mathcal{R}\to \mathcal{R}$, for j = 1 …, p. We refer to this class as generalized factorization models. Class (1) includes most of the cases mentioned in Section 1. When ϵ_i and η_i are Gaussian random vectors and t_j is the identity function, model (1) is a Gaussian linear factor model. With similar assumptions for ϵ_i and η_i, and assuming $t_j=F_j^{-1}\left\{\text{Φ}\left(z_{ij}\right)\right\}$, with Φ(z_ij) the Gaussian cumulative distribution function, model (1) is a Gaussian copula factor model (Murray et al., 2013). Exponential family factor models (Jun & Tao, 2013), probabilistic matrix factorization (Mnih & Salakhutdinov, 2008) and underlying Gaussian models for mixed scale data (Reich & Bandyopadhyay, 2010) can be obtained by appropriately defining the elements in (1), whereas multivariate response regression models belong to this framework when η_i is known.

The matrix Ω = var(z_i) can be expressed as Ω = ΛΨΛ^T + Σ, where Σ = var(ϵ_i). Following common practice in Bayesian factor analysis (Bhattacharya & Dunson, 2011), we avoid imposing identifiability constraints on Λ and assume Ψ is pre-specified. Our focus is on a new class of generalized infinite factor models induced through a novel class of priors for Λ that allows infinitely many factors, k = ∞. In particular, we let

$${\lambda }_{jh}|{\theta }_{jh}\sim N\left(0,{\theta }_{jh}\right),{\theta }_{jh}={\tau }_0{\gamma }_h{\varphi }_{jh},{\tau }_0\sim f_{{\tau }_0},{\gamma }_h\sim f_{{\gamma }_h},{\varphi }_{jh}\sim f_{{\varphi }_j},$$ (2)

where f_τ0, f_γh, and f_ϕj are supported on [0, ∞) with positive probability mass on (0, ∞). The local ϕ_jh, column-specific γ_h, and global τ₀ scales are all independent a priori. We let N(0, 0) denote a degenerate distribution with all its mass at zero. Expression (2) induces a class of scale-mixture of Gaussian shrinkage priors (Polson & Scott, 2010) for the loadings. Although we allow infinitely many columns in Λ, (2) induces a prior for Ω supported on the set of p × p positive semi-definite matrices under mild conditions reported in Proposition S1 in the Supplementary Material.

Differently from most of the existing literature on shrinkage priors, we want to define a non-exchangeable structure that includes meta covariates x informing the sparsity structure of Λ. In our context, meta covariates provide information to distinguish the p different variables as opposed to traditional covariates that serve to distinguish the n subjects. Letting x denote a p × q matrix of such meta covariates, we choose f_ϕj not depending on the index h and such that

$$E\left({\varphi }_{jh}|{\beta }_h\right)=g\left(x_j^T{\beta }_h\right),{\beta }_h={\left({\beta }_{1h},\dots ,{\beta }_{qh}\right)}^{\text{T}},{\beta }_{mh}\sim f_{\beta }\left(m=1,\dots ,q\right)$$ (3)

where $g:\mathcal{R}\to \mathcal{A}\subset {\mathcal{R}}_{+}$ is a known smooth one-to-one differentiable link function, x_j = (x_j1, …, x_jq)^T denotes the jth row vector of x, and β_h are coefficients controlling the impact of the meta covariates on shrinkage of the factor loadings in the hth column of Λ.

To illustrate the usefulness of (3), consider the previously introduced ecological study and suppose $x_j={\left\{1,\mathbb{1}\left({\kappa }_j=2\right),\dots ,\mathbb{1}\left({\kappa }_j=q\right)\right\}}^T$, where κ_j ∈ {1, …, q} denotes the phylogenetic order of species j. Species of the same order may tend to have similarities that can be expressed in terms of a shared pattern of high or low loadings on the same latent factors. To illustrate this situation, we simulate a loadings matrix, displayed in Fig. 1, sampling from the prior introduced in Section 3 where pr(λ_jh = 0) > pr(ϕ_jh = 0) > 0. The loadings within each column are penalized basing on the group structure identified by the q = 3 phylogenetic orders (Passeriformes, Charadriiformes, and Piciformes) of the p = 10 birds species considered. Our proposed prior allows for the possibility of such structure while not imposing it. In the bird ecology application, x can be defined to include not just phylogenetic placement of each bird species but also species traits, such as size or diet (Tikhonov et al., 2020). Related meta covariates are widely available, both in other ecology applications (Miller et al., 2019) and in other fields such as genomics (Thomas et al., 2009).

Fig. 1:

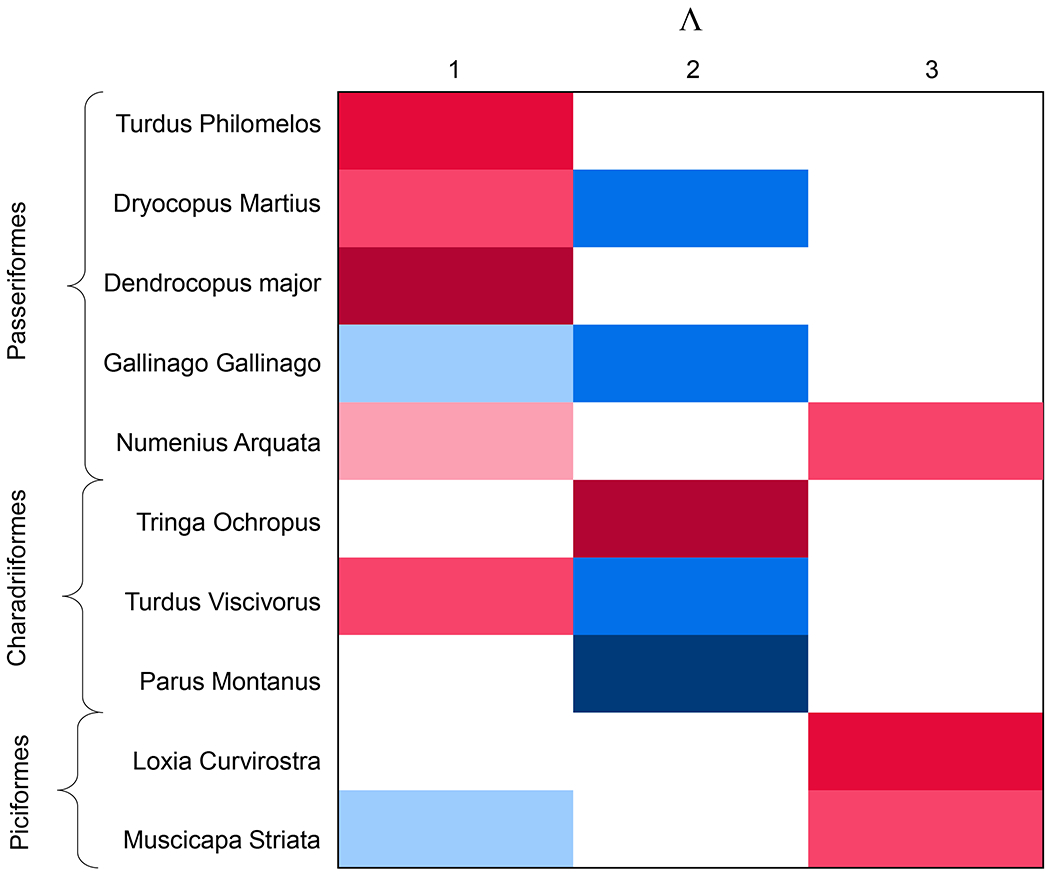
Illustrative loadings matrix of an ecology application, where the rows refer to ten bird species belonging to three phylogenetic orders. White cells represent the elements of Λ equal to zero, while blue and red cells represent negative and positive values, respectively.

2.2. Properties

In this section we present some properties motivating the shrinkage process in (2) and provide insight into prior elicitation. It is important to relate the choice of hyperparameters to the signal-to-noise ratio, expressed as the proportion of variance explained by the factors. Section S2.4 of the Supplementary Material provides a study of the posterior distribution of the proportion of variance explained; the posterior tends to be robust to hyperparameter choice. Below we study key properties of our prior, including an increasing shrinkage property, the ability of the induced marginal prior to accommodate both sparse and large signals, and control of the multiplicity problem in sparse settings. Proofs are included in the Appendix and in Section S1 of Supplementary Material. This theory illuminates the role of hyperparameters; specific recommendations of hyperparameter choice in practice are illustrated under the model settings of Section 3.1.

To formalize the increasing shrinkage property, we introduce the following definition.

Definition 1. Letting Π_Λ denote a shrinkage prior on Λ, Π_Λ is a weakly increasing shrinkage prior if var(λ_j(h–1)) > var(λ_jh) for j in 1, …, p and h = 2, …, ∞. Π_Λ is a strongly increasing shrinkage prior if var(λ_s(h–1)) > var(λ_jh), for j, s in {1, …, p} and h = 2, …, ∞.

Weakly increasing shrinkage corresponds to the prior variance increasing across columns within each row of Λ, while strongly increasing shrinkage implies that the prior variance of any loading element is larger than all elements with a higher column index. In the following Theorem, we show that the process in (2) induces weakly increasing shrinkage under a simple sufficient condition.

Theorem 1. Expression (2) is a weakly increasing shrinkage prior under Definition 1 if E(γ_h) > E(γ_h+1) for any h.

Increasing shrinkage priors favor a decreasing contribution of higher indexed columns of Λ to the covariance Ω. In addition to inducing a flexible shrinkage structure that allows different factors to have a different sparsity structure in their loadings, this allows one to accurately approximate the likelihood L(y; Λ, Ψ, Σ) by L(y; Λ_H, Ψ_H, Σ), with Λ_H containing the first H columns of the infinite matrix Λ and Ψ_H the first H rows and columns of Ψ. To measure the induced truncation error of ${\text{Ω}}_H={\text{Λ}}_H{\text{Ψ}}_H{\text{Λ}}_H^{\text{T}}+\text{Σ}$, we use the trace of Ω. The trace is justified by the fact that the maximum error occurring in an element of Ω due to truncation always lies along the diagonal and by the relation between difference of traces and the nuclear norm, routinely used to approximate low rank minimization problems (Liu & Vandenberghe, 2010). The following Proposition provides conditions on prior (2) so that the under-estimation of Ω that occurs by truncating decreases exponentially fast as H increases.

Proposition 1. Let E(τ₀) and E(ϕ_jh) be finite for j = 1, …, p and h = 1, …, ∞ and E(γ_h) = ab^h−1 with a > 0 and b ∈ (0, 1) for all h = 1, …, ∞. Let c > 0 be a sufficiently large number such that $c\ge {\max }_{h=1,\dots ,\infty }{\psi }_{hh}$. If

$$m_{\text{Ω}}=\underset{j=1,\dots ,p}{\min }\left[E\left({\sigma }_j^{-2}\right),E\left\{{\left(\sum _{h=1}^{\infty }{\psi }_{hh}{\lambda }_{jh}^2\right)}^{-1}\right\}\right]<\infty ,$$

then for any T ∈ (0, 1),

$$\text{pr}\left\{\frac{\text{tr}\left({\text{Ω}}_H\right)}{\text{tr}\left(\text{Ω}\right)}\le T\right\}\le \left(\frac{1}{1-T}\right)ac\frac{b^H}{1-b}{m}_{\text{Ω}}E\left({\tau }_0\right)\sum _{j=1}^{p}E\left({\varphi }_{j1}\right).$$

The above increasing shrinkage properties can be satisfied by naive priors that over-shrink the elements of Λ. It is important to avoid such over-shrinkage and allow not only many elements that are ≈ 0 but also a small proportion of large coefficients. A similar motivation applies in the literature on shrinkage priors in regression (Carvalho et al., 2010). Borrowing from that literature, the marginal prior for λ_jh should be concentrated at zero to reduce mean square error by shrinking small coefficients to zero but with heavy tails to avoid over-shrinking the signal.

To quantify the prior concentration of (2) in an ϵ neighbourhood of zero, we can obtain

$$\text{pr}\left(|{\lambda }_{jh}|>ϵ\right)\le \frac{E\left({\tau }_0\right)E\left({\gamma }_h\right)E\left({\varphi }_{jh}\right)}{{ϵ}^2}$$ (4)

as a consequence of Markov’s inequality. Common practice in local-global shrinkage priors chooses E(τ₀) small while assigning a heavy-tailed density to the local or column scales. In our case, (3) allows the bound in (4) to be regulated by meta covariates x, while, under the condition in Theorem 1, decreasing E(γ_h) with column index causes an increasing concentration near zero, since E(ϕ_jh) = E(ϕ_jl) for every h, l ∈ {1, …, ∞}. The means of the column and the local scales control prior concentration near zero, while over-shrinkage can be ameliorated by choosing f_ϕj or f_γh (h = 1, …, ∞) heavy tailed. The following Proposition provides a condition on the prior to guarantee a heavy tailed marginal distribution for λ_jh. A random variable has power law tails if its cumulative distribution function F has 1 − F(t) ≥ ct^−α for constants c > 0, α > 0, and for any t > L for L sufficiently large.

Proposition 2. If at least one scale parameter among τ₀, γ_h or ϕ_jh is characterized by a power law tail prior distribution, then the prior marginal distribution of λ_jh has power law tails.

An important consequence of the heavy tailed property is avoidance of over-shrinkage of large signals. This is often formalized via a tail robustness property (Carvalho et al., 2010). As an initial result, key to showing sufficient conditions for a type of local tail robustness, we provide the following Lemma on the derivative of the log prior in the limit as the value of λ_jh → ∞.

Lemma 1. If at least one scale parameter among τ₀, γ_h or ϕ_jh has a prior with power law tails for any possible prior distribution of β_h, then for any finite truncation level H,

$$\underset{\lambda \to \infty }{\lim }\frac{\partial \log \left\{f_{{\lambda }_{jh}|{\text{Λ}}_{-jh}}\left(\lambda \right)\right\}}{\partial \lambda }=0$$

where $f_{{\lambda }_{jh}|{\Lambda }_{-jh}}\left(\lambda \right)$ is the conditional distribution of λ_jh given the other elements of Λ_H.

The following definition introduces a type of local tail robustness property.

Definition 2. Consider model (1) with factors η known. Let $f_{{\lambda }_{jh}|y,\eta ,{\text{Λ}}_{-jh}\left(\lambda \right)}$ denote the posterior density of λ_jh, given the data, conditional on any possible value of the other elements of Λ_H for any finite H, and let ${\widehat{\lambda }}_{jh}$ denote the conditional maximum likelihood estimate of λ_jh for any possible value of the other elements of Λ_H. We say that the prior on λ_jh is tail robust if

$$\underset{{\widehat{\lambda }}_{jh}\to \infty }{\lim }|{\widehat{\lambda }}_{jh}-\arg \underset{\lambda }{\max }{f}_{{\lambda }_{jh}|y,\eta ,{\text{Λ}}_{-jh}}\left(\lambda \right)|=0.$$

For a given sample, ${\widehat{\lambda }}_{jh}$ is a fixed quantity; the above limit should be interpreted as what happens as the data support a larger and larger maximum likelihood estimate. In order for tail robustness to hold, we need the data to be sufficiently informative about the parameter λ_jh and the likelihood to be sufficiently regular; this is formalized as follows.

Assumption 1. Let L(y; Λ, η, Σ) denote the likelihood for data y conditionally on latent variables η, let l_s(λ) denote the derivative function of the log-likelihood with respect to λ_jh, and let $\mathcal{J}\left({\widehat{\lambda }}_{jh}\right)$ denote the negative of the second derivative of the log-likelihood with respect to λ_jh, evaluated at the conditional maximum likelihood estimate ${\widehat{\lambda }}_{jh}$. Then l_s(λ) is a continuous function for every $\lambda \in \mathcal{R}$ and $\mathcal{J}\left({\widehat{\lambda }}_{jh}\right)\ge \nu \left({\widehat{\lambda }}_{jh}\right)$, where $\upsilon \left({\widehat{\lambda }}_{jh}\right)$ is of order O(1) as ${\widehat{\lambda }}_{jh}\to \infty$.

This assumption can be verified for most of the cases mentioned in Section 1; for example, for Gaussian linear factor models $\mathcal{J}\left({\widehat{\lambda }}_{jh}\right)$ is of order O(1) with respect to ${\widehat{\lambda }}_{jh}$.

Theorem 2. Under Assumption 1, if at least one scale parameter among τ₀, γ_h or ϕ_jh is power law tail distributed for any possible prior distribution of β_h, then the prior on λ_jh is tail robust under Definition 2.

As an additional desirable property, we would like to control for the multiplicity problem within each column λ_h of the loadings matrix, corresponding to increasing numbers of false signals as dimension p increases. This can be accomplished by imposing an asymptotically increasingly sparse property on the prior, which is defined as follows.

Definition 3. Let $|{\text{supp}}_{ϵ}\left({\lambda }_h\right)|$ denote the cardinality of ${\text{supp}}_{ϵ}\left({\lambda }_h\right)=\left(j:|{\lambda }_{jh}|>ϵ\right)$. Let s_p = o(p) such that $s_p\ge c_s\log \left(p\right)/p$ for some constant c_s > 0. We say that the prior on Λ defined in (2) is an asymptotically increasingly sparse prior if

$$\underset{p\to \infty }{\lim }\text{pr}\left\{|{\text{supp}}_{ϵ}\left({\lambda }_h\right)|>a{s}_p|{\gamma }_h,{\tau }_0\right\}=0,forsomeconstanta>0.$$

The quantity |supp_ϵ(λ_h)| represents an approximate measure of model size for continuous shrinkage priors and, conditionally on β_h, γ_h, and τ₀, it is a priori distributed as a sum of independent Bernoulli random variables Ber(ζ_ϵjh), where

$${\zeta }_{ϵjh}=\text{pr}\left(|{\lambda }_{jh}|>ϵ|{\beta }_h,{\gamma }_h,{\tau }_0\right)\le \frac{{\tau }_0{\gamma }_{h}g\left(x_j^{\text{T}}{\beta }_h\right)}{{ϵ}^2}.$$

We now provide sufficient conditions for an asymptotically increasingly sparse prior, allowing regulation of the sparsity behaviour of the prior of the columns of Λ for increasing dimension p.

Theorem 3. Consider prior (2) with ϕ_jh (j = 1, …, p) a priori independent given β_h. If $\text{pr}\{g\left(x_j^{\text{T}}{\beta }_h\right)\le {\nu }_j(p)\}=1$, with ν_j(p) = O{log(p)/p}, (j = 1, …, p), then the prior on Λ is asymptotically increasingly sparse under Definition 3.

The condition of the theorem is easily satisfied, for example, if g is the multiplication of a bounded function and a suitable offset depending on p as assumed in Section 3.1. The multiplicative gamma process (Bhattacharya & Dunson, 2011) and cumulative shrinkage process (Legramanti et al., 2020) do not satisfy the sufficient conditions of Theorem 3, and, furthermore, the following lemma holds.

Lemma 2. The multiplicative gamma process prior (Bhattacharya & Dunson, 2011) and the cumulative shrinkage process prior (Legramanti et al., 2020) are not asymptotically increasing sparse under Definition 3.

Although this Section has focused on properties of the prior, we find empirically that these properties tend to carry over to the posterior, as will be illustrated in the subsequent sections. For example, the posterior exhibits asymptotic increasing sparsity; refer to Table 2 of Section 4, which shows results for a novel process in our proposed class that is much more effective than current approaches in identifying the true sparsity structure, particularly when p is large.

Table 2:

Median and interquartile range of the mean classification error computed in 25 replications assuming Scenario b and several combinations of (p, k, s)

MCE	(p, k, s)	MGP		CUSP		SIS
		Q0.5	IQR	Q0.5	IQR	Q0.5	IQR
	(16,4,0.6)	1.06	0.16	0.38	0.01	0.24	0.09
	(32,8,0.4)	0.70	0.07	0.48	0.08	0.16	0.09
	(64,12,0.3)	0.61	0.07	0.58	0.01	0.09	0.06
	(128,16,0.2)	0.49	0.03	0.52	0.08	0.04	0.01

MCE, mean classification error; MGP, multiplicative gamma process; CUSP, cumulative shrinkage process; SIS, structured increasing shrinkage process; Q_0.5, median; IQR, interquartile range.

3. Structured increasing shrinkage process

3.1. Model specification

In this section we propose a structured increasing shrinkage process prior for generalized infinite factor models satisfying all the sufficient conditions in Propositions 1–2 and Theorems 2–3. Let Ga(a, b) denote the gamma distribution with mean a/b and variance a/b². Following the notation of Section 2.1, we specify

$${\tau }_0=1,{\gamma }_h={\vartheta }_h{\rho }_h,{\varphi }_{jh}|{\beta }_h\sim \text{Ber}\left\{{\text{logit}}^{-1}\left(x_j^{\text{T}}{\beta }_h\right)c_p\right\},$$ (5)

$${\vartheta }_h^{-1}\sim \text{Ga}\left(a_{\theta },b_{\theta }\right),a_{\theta }>1,{\rho }_h=\text{Ber}\left(1-{\pi }_h\right),{\beta }_h\sim N_q\left(0,{\sigma }_{\beta }^2{I}_q\right),$$

where we assume the link g(x) = logit⁻¹(x)c_p, with logit⁻¹(x) = e^x/(1 + e^x) and c_p ∈ (0, 1) a possible offset. The parameter π_h = pr(γ_h = 0) follows a stick-breaking construction,

$${\pi }_h=\sum _{l=1}^h{w}_l,w_l=v_l\prod _{m=1}^{l-1}\left(1-{\upsilon }_m\right),{\upsilon }_m\sim \text{Be}\left(1,\alpha \right),$$

with Be(a, b) the beta distribution with mean a/(a + b), such that ${\pi }_{h+1}>{\pi }_h$ is guaranteed for any h = 1, …, ∞ and ${\lim }_{h\to \infty }{\pi }_h=1$ almost surely. The prior expected number of non degenerate Λ columns is $E\left({\sum }_{h=1}^{\infty }{\rho }_h\right)=\alpha$ (Legramanti et al., 2020), suggesting setting α equal to the expected number of active factors. The prior specification is completed assuming $\text{Σ}=\text{diag}\left({\sigma }_1^2,\dots ,{\sigma }_p^2\right)$ with ${\sigma }_j^{-2}\sim \text{Ga}\left(a_{\sigma },b_{\sigma }\right)$ for j = 1, …, p, consistently with the literature. The hyperparameters can be chosen based on one’s prior expectation of the signal-to-noise ratio, as ${\sigma }_j^2$ is the contribution of the noise component to the total variance of the jth variable. A sensitivity study in Section S2.4 of the Supplementary Material, however, shows that posterior distributions tend to be robust to the specification of a_σ, b_σ. Regarding prior elicitation, we recommend setting b_θ ≥ a_θ to induce a high enough proportion of variance explained by the factor model. In Section S2.4 in the Supplementary Materials we report empirical evidence of the effect of different prior parameters on this quantity.

The above specification respects (2) and, consequently, the following corollary holds.

Corollary 1. The structured increasing shrinkage process defined in (5)

1. is a strongly increasing shrinkage prior under Definition 1;

2. for any T ∈ (0, 1),

   $$\text{pr}\left\{\frac{\text{tr}\left({\text{Ω}}_H\right)}{\text{tr}\left(\text{Ω}\right)}\le T\right\}\le \left(\frac{1}{1-T}\right)\frac{b^H}{1-b}{\theta }_0\frac{a_{\sigma }}{b_{\sigma }}\sum _{j=1}^{p}E\left({\varphi }_{j1}\right),$$

   with b = {α(1 + α)}⁻¹ and ${\theta }_0=E\left({\vartheta }_h\right)$.

We conducted a simulation study on the posterior distribution of {tr(Ω_H)/tr(Ω) ≤ T} for varying hyperparameters, and found that the results, reported in Section S2.4 of the Supplementary Material, were quite consistent with our prior truncation error bounds.

The prior concentration of the structured increasing shrinkage process in (5) follows from (4):

$$\text{pr}\left(|{\lambda }_{jh}|>ϵ\right)\le \frac{E\left({\vartheta }_h\right)\{1-E\left({\pi }_h\right)E\left({\varphi }_{jh}\right)\}}{{ϵ}^2}=\frac{{\theta }_0{\left\{\alpha /\left(1+\alpha \right)\right\}}^h}{{ϵ}^2}\frac{c_p}{2}.$$

In addition, the inverse gamma prior on ${\vartheta }_h$ implies a power law tail distribution on γ_h inducing robustness properties on λ_jh as formalized by the next corollary of Proposition 2 and Theorem 2.

Corollary 2. Under the structured increasing shrinkage process defined in (5)

1. the marginal prior distribution on λ_jh (j = 1, …, p; h = 1, 2, …) has power law tails;

2. under Assumption 1, the prior on λ_jh (j = 1, …, p; h = 1, 2, …) is tail robust under Definition 2.

Finally, it is important to assess the joint sparsity properties of the prior on each column of Λ. This is formalized in the following corollary of Theorem 3.

Corollary 3. If c_p = O{log(p)/p} the structured increasing shrinkage process defined in (5) is asymptotically increasingly sparse under Definition 3.

3.2. Posterior computations

Posterior inference is conducted via Markov chain Monte Carlo sampling. Following common practice in infinite factor models (Bhattacharya & Dunson, 2011; Legramanti et al., 2020; Schiavon & Canale, 2020) we use an adaptive Gibbs algorithm, which attempts to infer the best truncation level H while drawing from the posterior distribution of the parameters. The value of H is adapted only at some Gibbs iterations by discarding redundant factors and, if no redundant factors are identified, by adding a new factor by sampling its parameters from the prior distribution. Convergence of the Markov chain is guaranteed by satisfying the diminishing adaptation condition in Theorem 5 of Roberts & Rosenthal (2007), by specifying the probability of occurrence of an adaptive iteration t as equal to p(t) = exp(α₀ + α₁t), where α₀ and α₁ are negative constants, such that frequency of adaptation decreases.

The decomposition of γ_h into two parameters ρ_h and ${\vartheta }_h$ allows one to identify the inactive columns of Λ, corresponding to the redundant factors, as those with ρ_h = 0, while H_a indicates the number of active columns of Λ. Consequently, at the adaptive iteration t + 1, the truncation level H is set to $H^{\left(t+1\right)}=H_a^{\left(t\right)}+1$ if $H_a^{\left(t\right)}<H^{\left(t\right)}-1$, and H^(t+1) = H^(t) + 1 otherwise. Given H^(t+1), the number of factors of the truncated model at iteration t + 1, the sampler draws the model parameters from the corresponding posterior full conditional distributions. The detailed steps of the adaptive Gibbs sampler for the structured increasing shrinkage prior in case of Gaussian or binary data are reported in the Supplementary Material, as well as trace plots of the posterior samples for some parameters of the model in Section 5 (see Section S3.2), showing good mixing.

3.3. Identifiability and posterior summaries

Non-identifiability of the latent structure creates problems in interpretation of the results from Markov chain Monte Carlo samples. Indeed, both Λ and η are only identifiable up to an arbitrary rotation P with PP^T = I_k. This is a well known problem in Bayesian factor models and there is a rich literature proposing post-processing algorithms that align posterior samples Λ^(t), so that one can then obtain interpretable posterior summaries. Refer to McParland et al. (2014), Aßmann et al. (2016), and Roy et al. (2019) for alternative post-processing algorithms in related contexts.

Unfortunately, such post-hoc alignment algorithms destroy the structure we have carefully imposed on the loadings in terms of sparsity and dependence on meta covariates. Therefore, we propose a different solution to obtain a point estimate of Λ based on finding a representative Monte Carlo draw Λ^(t) consistently with the proposals of Dahl (2006) and Wade et al. (2018) in the context of Bayesian model-based clustering. Specifically, we summarize Λ and β = (β₁, β₂, …) through Λ^(t*) and β^(t*) sampled at iteration t*, characterized by the highest marginal posterior density function f (Λ, β, Σ | y) obtained by integrating out the scale parameters τ₀, γ_h, ϕ_jh (j = 1, …, p, h = 1, …) and the latent factors η_i (i = 1, …, n) from the posterior density function. Formally, we select the iteration t* ∈ {1, …, T} such that

$$f\left({\text{Λ}}^{\left(t*\right)},{\beta }^{\left(t*\right)},{\text{Σ}}^{\left(t*\right)}|y\right)>f\left({\text{Λ}}^{\left(t\right)},{\beta }^{\left(t\right)},{\text{Σ}}^{\left(t\right)}|y\right)\left(t=1,\dots ,T\right),$$

where t = 1, …, T indexes the posterior samples. Under the structured increasing shrinkage prior described in Section 3.1, these computations are straightforward. The matrices Λ^(t*), β^(t*), Σ^(t*) are Monte Carlo approximations of the maximum a posteriori estimator, which corresponds to the Bayes estimator under L_∞ loss. Although one can argue that L_∞ is not an ideal choice of loss philosophically in continuous parameter problems, it nonetheless is an appealing pragmatic choice in our context and is broadly used in other sparse estimation contexts, as in the algorithm proposed by Ročková & George (2016) that similarly aims to recover a strongly sparse posterior mode of an over-parameterized factor model.

4. Simulation experiments

We assess the performance of our structured increasing shrinkage prior compared with current approaches (Bhattacharya & Dunson, 2011; Ročková & George, 2016; Legramanti et al., 2020) through a simulation study. We have a particular interest in inferring sparse and interpretable loadings matrices Λ, but also assess performance in estimating the induced covariance matrix Ω and number of factors. We generate synthetic data from four scenarios based on different loadings structures. For each scenario we simulate R = 25 data sets with n = 250 observations from $y_i\sim N_p\left(0,{\text{Λ}}_0{\text{Λ}}_0^T+I_p\right)$ (i = 1, …, n). In Scenario a, we assume non sparse Λ₀, sampling the loadings λ_jh from a Gaussian distribution with mean zero, variance equal to ${\sigma }_{\lambda }^2=1$ and ordering them to obtain decreasing variance over the columns. To ensure that each element λ_jh represents a signal, we shifted them away from zero by ${\sigma }_{\lambda }^2/3$. In Scenario b we remove the decreasing behaviour and introduce a random sparsity pattern characterized by an increasing number of zero entries over the column index. The loadings matrix for Scenario c is characterized by both the decreasing behaviour over the columns of Scenario a and the random sparsity structure of Scenario b. Finally, in Scenario d, while the decreasing behaviour is kept, we induce a sparsity pattern dependent on a categorical and two continuous meta covariates x₀. Details are reported in Section S2.2 of the Supplementary Material.

For each scenario we consider four combinations of dimension and sparsity level of Λ₀. We let (p, k, s) ∈ {(16, 4, 0.6), (32, 8, 0.4), (64, 12, 0.3), (128, 16, 0.2)}, where s is the proportion of non-zero entries of Λ, with the exception of Scenario a where s = 1. In these settings the algorithm takes from 0.07 to 0.73 seconds of computational time per iteration depending on the dimension p and considering an R implementation on an Intel Core i5-6200U CPU laptop with 15.8 GB of RAM. To estimate the structured increasing shrinkage model, we set x equal to the p-variate column vector of 1s, σ_β = 1 and, consistently with Corollary 3, c_p = 2e log(p)/p. In Scenario d we also estimate and compare a correctly specified structured increasing model with x = x₀. For the method proposed by Ročková & George (2016), we set the hyperparameters as suggested by the authors, while for the remaining approaches, we follow the hyperparameter specification and factor selection guidelines in Section 4 of Schiavon & Canale (2020).

Scenario a is a worst case for the proposed method since there is no sparsity, no structure, and the elements of the loadings matrix are similar in magnitude. However, even in this case, structured increasing shrinkage performs essentially identically to the best competitor, as illustrated by the results in Table 1. The results of Ročková & George (2016) are not reported as they are not competitive, as can be seen in table S2 in the Supplementary Material. We report the median and interquartile range over the R replicates of the logarithm of the pseudo-marginal likelihood (Gelfand & Dey, 1994) and of the estimated posterior mean of the number of factors E(H_a | y).

Table 1:

Median and interquartile range of LPML and E(H_a | y) in 25 replications of Scenario a for different combinations of (p, k); Scenario a is a worst case for the proposed SIS method.

	(p, k)	MGP		CUSP		SIS
		Q0.5	IQR	Q0.5	IQR	Q0.5	IQR
LPML	(16,4)	−28.68	0.42	−28.68	0.43	−28.65	0.41
	(32,8)	−60.08	0.45	−60.09	0.45	−60.07	0.49
	(64,12)	−117.68	0.56	−117.75	0.53	−117.88	0.56
	(128,16)	−225.04	1.04	−225.13	1.04	−228.76	1.47
E(Ha | y)	(16,4)	8.17	1.44	4.00	0.00	4.00	0.00
	(32,8)	10.68	0.33	8.00	0.00	8.00	0.00
	(64,12)	14.16	1.09	12.00	0.00	12.00	0.00
	(128,16)	17.03	0.47	16.00	0.00	18.00	0.02

LPML, logarithm of the pseudo-marginal likelihood; CUSP, cumulative shrinkage process; MGP, multiplicative gamma process; SIS, structured increasing shrinkage process; Q_0.5, median; IQR, interquartile range.

Scenario b judges performance in detecting sparsity. The proposed approach shows better performance in the logarithm of the pseudo-marginal likelihood and mean squared error of the covariance matrix, particularly as sparsity increases, as displayed in Fig. 2. Consistently with (Legramanti et al., 2020), the covariance mean squared error is estimated in each simulation by ${\sum }_{j,l}^p{\sum }_{t=1}^S{\left({\omega }_{jl}^{\left(t\right)}-{\omega }_{jl0}\right)}^2/\left\{p\left(p+1\right)/2\right\}$, where ω_jl0 and ${\omega }_{jl}^{\left(t\right)}$ are the elements jl of ${\text{Ω}}_0={\text{Λ}}_0{\text{Λ}}_0^{\text{T}}+I_p$ and ${\text{Ω}}^{\left(t\right)}={\text{Λ}}^{\left(t\right)}{\text{Λ}}^{\left(t\right)\text{T}}+I_p$, respectively. The proposed approach allows exact zeros in the loadings, while the competitors require thresholding to infer sparsity. Following the thresholding approach described in Section S2.2 of the Supplementary Material, we evaluate performance in inferring the sparsity pattern via the mean classification error:

$$MCE=\frac{1}{S}\sum _{t=1}^S\frac{{\sum }_{j=1}^p{\sum }_{h=1}^{k^{*\left(t\right)}}|\mathbb{1}\left({\lambda }_{jh0}=0\right)-\mathbb{1}\left({\lambda }_{jh}^{\left(t\right)}=0\right)|}{pk},$$

where k^*(t) is the maximum between the true number of factors k and $H_a^{\left(t\right)}$, and λ_jh0 and ${\lambda }_{jh}^{\left(t\right)}$ are the elements jh of Λ₀ and Λ^(t), respectively. If $H_a^{\left(t\right)}$ or k are smaller than k*, we fix the higher indexed columns at zero, possibly leading to a mean classification error bigger than one. The results reported in Table 2 show that the proposed structured increasing shrinkage prior is much more effective in identifying sparsity in Λ, maintaining good performance even with large p and in strongly sparse contexts. Also, more accurate estimation of the number of factors is obtained, as reported in Table S1 in the Supplementary Material.

Fig. 2:

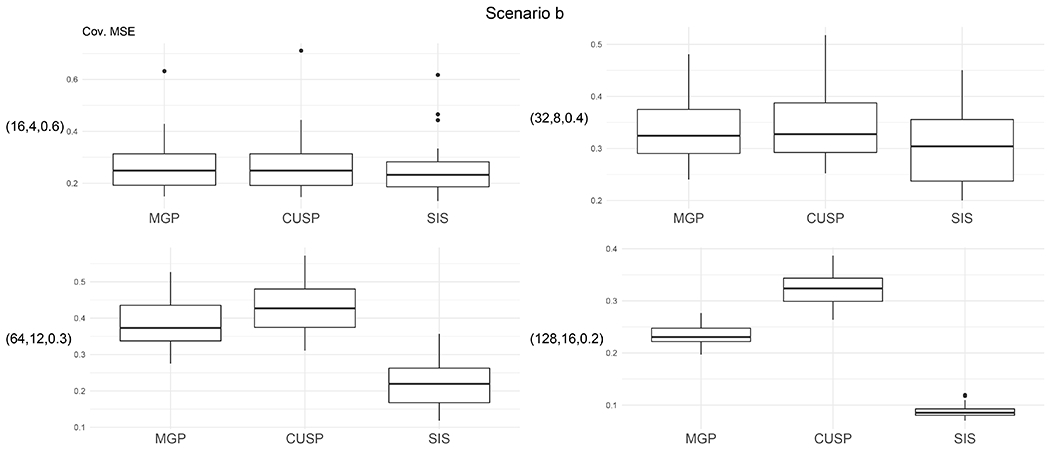
Boxplots of mean squared error of the covariance matrix of each model for different combinations of (p, k, s) in Scenario b. Cov. MSE, covariance mean squared error; CUSP, cumulative shrinkage process; MGP, multiplicative gamma process; SIS, structured increasing shrinkage process.

Similar comments apply in Scenarios c and d reported in Fig. S2 in the Supplementary Material. The superior performance of the structured increasing shrinkage model is only partially mitigated in Scenario c for large p for the logarithm of the pseudo-marginal likelihood. In Scenario d, the use of meta covariates has a mild benefit in identifying the sparsity pattern. In lower signal-to-noise settings, meta covariates have a bigger impact, and they also aid interpretation, as illustrated in the next section. Additional details, tables, and plots for all scenarios are reported in Section S2.3 of the Supplementary Material.

5. Finnish bird co-occurrence application

We illustrate our approach by modelling co-occurrence of the fifty most common bird species in Finland (Lindström et al., 2015), focusing on data in 2014. Response y is an n × p binary matrix denoting occurrence of p = 50 species in n = 137 sampling areas. An n × c environmental covariate matrix w is available, including a 5-level habitat type, ‘spring temperature’ (mean temperature in April and May), and (spring temperature)², leading to c = 7. We consider a meta covariate p × q matrix x of species traits: logarithm of typical body mass, migratory strategy (short-distance migrant, resident species, long-distance migrant), and a 7-level superfamily index. We model species presence or absence via a multivariate probit regression model:

$$y_{ij}=\mathbb{1}\left(z_{ij}>0\right),z_{ij}=w_i^T{\mu }_j+{ϵ}_{ij},{ϵ}_i={\left({ϵ}_{i1},\dots ,{ϵ}_{ip}\right)}^T\sim N_p\left(0,\text{Λ}{\text{Λ}}^T+I_p\right),$$ (6)

where μ_j characterizes impact of environmental covariates on species occurrence probabilities, and covariance in the latent z_i vector is characterized through a factor model. To borrow information across species while incorporating species traits, we let

$${\mu }_j\sim N_c\left(b{x}_j,{\sigma }_{\mu }^2{I}_c\right),b\text{=}\left(b_1,\dots ,b_q\right),b_m\sim N_c\left(0,{\sigma }_b^2{I}_c\right),$$ (7)

where b is a c × q coefficient matrix with column vectors b_m given Gaussian priors.

Model (6)–(7) is consistent with popular joint species distribution models (Ovaskainen et al., 2016; Tikhonov et al., 2017; Ovaskainen & Abrego, 2020), with current standard practice using a multiplicative gamma process for Λ. We compare this approach to an analysis that instead uses our proposed structured increasing shrinkage prior to allow the species traits x to impact Λ and hence the covariance structure across species. After standardizing w and x, we set α = 4, a_θ = b_θ = 2 and σ_μ = σ_b = 1. Posterior sampling is straightforward via a Gibbs sampler reported in Section S3.1 of the Supplementary Material.

Figure S8 in the Supplementary Material displays the posterior means of μ and b. A first investigation shows large heterogeneity of the habitat type effects across different species. Matrix b shows that covariate effects tend to not depend on migratory strategy or body mass, with the exception of urban habitats tending to have more migratory birds.

The estimated Λ and meta covariate coefficients β, following the guidelines of Section 3.3, are displayed in Fig. 3. The loadings matrix is quite sparse, indicating that each latent factor impacts a small group of species. Positive sign of the loadings means that high levels of the corresponding factors increase the probability of observing birds from those species. Lower elements of β^(t*), represented with light cells on the right panel, induce higher shrinkage on the corresponding group of birds. To facilitate interpretation, we re-arrange the rows of Λ^(t*) according to the most relevant species traits in terms of shrinkage, which are migration strategy and body mass. The species influenced by the first factor are fairly homogeneous, characterized by short distance or resident migratory strategies and a larger body mass. The strongly negative value of β_(t*)42 suggests heavier species of birds tend to have loadings close to zero for the second factor. This is also true for the third factor, which also does not impact short-distance migrants.

Fig. 3:

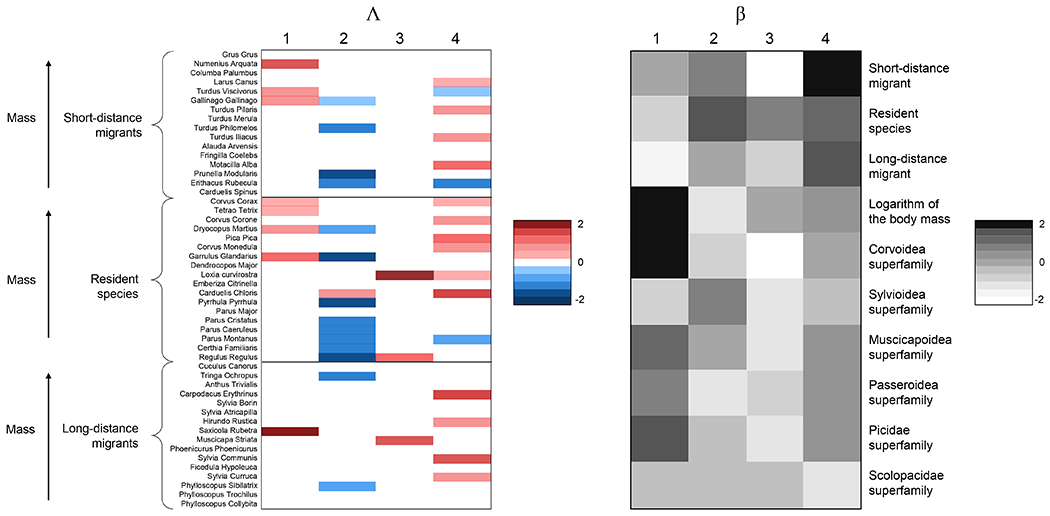
Posterior summaries Λ^(t*) and β^(t*) of the structured increasing shrinkage model; rows of left matrix refer to 50 birds species, and rows of right matrix to ten species traits. Light coloured cells of β^(t*) induce shrinkage on corresponding cells of Λ^(t*).

Figure S9 in the Supplementary Material shows a spatial map of the sampling units coloured accordingly to the values of the first and the third latent factors. We can interpret these latent factors as unobserved environmental covariates. We find that the species traits included in our analysis only partially explain the loadings structure; this is as expected and provides motivation for the proposed approach. Sparsity in the loadings matrix helps in interpretation. Species may load on the same factor not just because they have similar traits but also because they tend to favor similar habitats for reasons not captured by the measured traits.

The induced covariance matrix Ω = ΛΛ^T + I_p across species is of particular interest. We compare estimates of Ω under the multiplicative gamma process, estimated using the R package hmsc (Tikhonov et al., 2020), and our proposed structured increasing shrinkage model. Figure 4 reports the posterior mean of the correlation matrices under the two competing models. The network graph based on the posterior mean of the partial correlation matrices, reported in Fig. 5, reveals several communities of species under the proposed structured increasing shrinkage prior that are not evident under the multiplicative gamma.

Fig. 4:

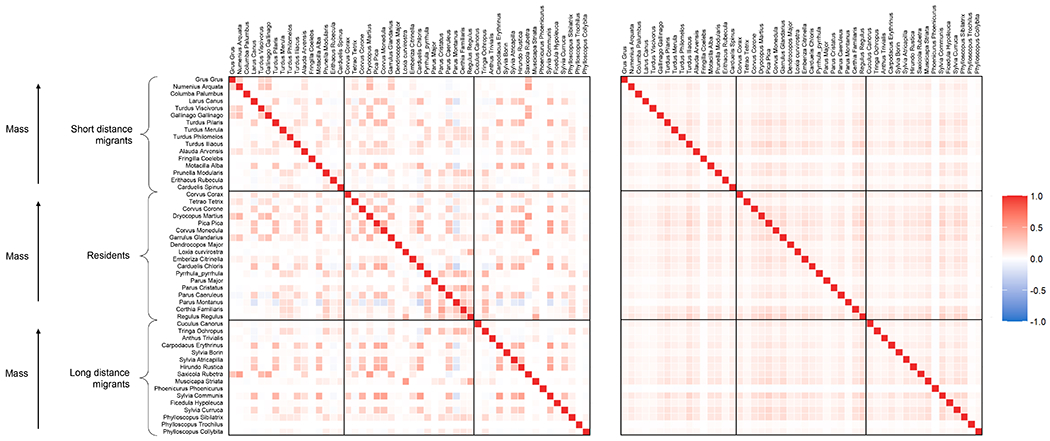
Posterior mean of the correlation matrices estimated by the structured increasing shrinkage model (on the left) and the multiplicative gamma process model (on the right).

Fig. 5:

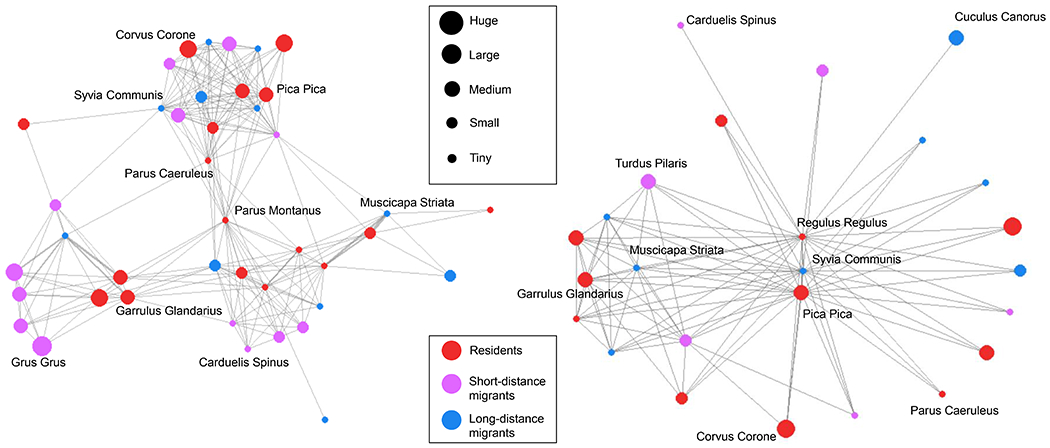
Graphical representation based on the inverse of the posterior mean of the correlation matrices estimated by the structured increasing shrinkage model (on the left) and the multiplicative gamma process model (on the right). Edge thicknesses are proportional to the latent partial correlations between species. Values below 0.025 are not reported. Nodes are positioned using a FruchtermanReingold force-direct algorithm.

We also find that the multiplicative gamma process provides a slightly worse fit to the data. The logarithm of the pseudo marginal likelihood computed on the posterior samples of the structured increasing shrinkage model is equal to −21.06, higher than that achieved by the competing model, which is −21.36. Using 4-fold cross-validation, we compared the log-likelihood evaluated in the held-out data, with μ and Ω estimated by the posterior mean in the training set. The mean of the log-likelihood was −22.62 under the structured increasing shrinkage and −23.22 under the multiplicative gamma process prior.

Appendix. Lemmas and proofs

Proof of Theorem 1. The variance of λ_jh is

$$\mathrm{var}\left({\lambda }_{jh}\right)=E\left\{E\left({\lambda }_{jh}^2|{\varphi }_{jh},{\gamma }_h,{\tau }_0\right)\right\}=E\left\{E\left({\theta }_{jh}|{\varphi }_{jh},{\gamma }_h,{\tau }_0\right)\right\}.$$

By construction, $E\left({\theta }_{jh}|{\varphi }_{jh},{\gamma }_h,{\tau }_0\right)={\varphi }_{jh}{\gamma }_h{\tau }_0$. Then,

$$\mathrm{var}\left({\lambda }_{jh}\right)=E\left({\varphi }_{jh}{\gamma }_h{\tau }_0\right)=E\left({\varphi }_{j1}\right)E\left({\gamma }_h\right)E\left({\tau }_0\right)>E\left({\varphi }_{j1}\right)E\left({\gamma }_{h+1}\right)E\left({\tau }_0\right)=\mathrm{var}\left({\lambda }_{jh+1}\right),$$

since the scale parameters are independent and the local scale ϕ_jh is equally distributed over the column index h. □

To prove Proposition 2 we need to introduce the following Lemma.

Lemma 3. Let u, v denote two real positive random variables. If at least one among (u | v) and (v | u) is power law tail distributed, then the product uv is power law tail distributed.

Proof. For a positive value w, we can write

$$\text{pr}\left(uv>w\right)={\int }_0^{\infty }\text{pr}\left(u>w/v|v\right)f\left(v\right)\text{d}v=E\left\{F_{u|v}^C\left(w/v\right)\right\},$$

where $F_{u|v}^C\left(w\right)=\text{pr}\left(u>w|v\right)$ and f(v) is the probability density function of v. If $F_{u|v}^C\left(w\right)\ge c{w}^{-\alpha }$ with c, α positive constants and w greater than a sufficiently large number L, then

$$\text{pr}\left(uv>w\right)\ge E\left\{c{\left(w/v\right)}^{-\alpha }\right\}=c{w}^{-\alpha }E\left(v^{\alpha }\right)w>L\gg \text{0}.$$

If E(v^α) = ∞, then pr(uv > w) > cw^−α = O(w^−α), otherwise pr(uv > w) ≥ v(w) for w > L, with v(w) a function of order O(w^−α) as w goes to infinity. This shows that the right tail of the distribution of the random variable uv follows a power law behaviour. □

Proof of Proposition 2. Consider the strictly positive random variables ${\theta }_{jh}^{*}=\left({\theta }_{jh}|{\theta }_{jh}>0\right)$, ${\tau }_0^{*}=\left({\tau }_0|{\tau }_0>0\right)$, ${\gamma }_h^{*}=\left({\gamma }_h|{\gamma }_h>0\right)$, and ${\varphi }_{jh}^{*}=\left({\varphi }_{jh}|{\varphi }_{jh}>0\right)$. Since ${\theta }_{jh}^{*}$ is equal to the product ${\tau }^{*}{\gamma }_h^{*}{\varphi }_{jh}^{*}$ of independent positive random variables, Lemma 3 ensures that if at least one of those scale parameters follows a power law tail distribution, then ${\theta }_{jh}^{*}$ is power law tail distributed, so that $\text{pr}\left({\theta }_{jh}^{*}>\theta \right)\ge c{\theta }^{-\alpha }$ for c, α positive constants and θ > L. Without loss of generality, we focus on the right tail of λ_jh. Let

$$\text{pr}\left({\lambda }_{jh}>\lambda \right)=\text{pr}\left({\lambda }_{jh}>\lambda |{\theta }_{jh}>0\right)\text{pr}\left({\theta }_{jh}>0\right)+\text{pr}\left({\lambda }_{jh}>\lambda |{\theta }_{jh}=0\right)\text{pr}\left({\theta }_{jh}=0\right).$$ (1)

It is straightforward to observe that λ_jh marginally has a power law tail if and only if (λ_jh | θ_jh > 0) is power law tail distributed and pr(θ_jh > 0) is strictly positive. Since pr(τ₀ > 0) > 0, pr(γ_h > 0) > 0, and pr(ϕ_jh > 0) > 0, then pr(θ_jh > 0) > 0, given independence between the scale parameters. Focusing on θ_jh > 0 in the first term of the right hand side of (1), we have

$$\text{pr}\left({\lambda }_{jh}>\lambda |{\theta }_{jh}^{*}\right)=1-\text{Φ}\left(\lambda {\theta }_{jh}^{*-0.5}\right),$$

and we want to prove that the marginal $F_{{\lambda }_{jh}}^c\left(\lambda \right)=\text{pr}\left({\lambda }_{jh}>\lambda \right)$ is sub-exponential as λ → ∞. Using the lower bound for the right tail of the standard Gaussian of Abramowitz & Stegun (1948),

$$1-\text{Φ}\left(\lambda {\theta }_{jh}^{*-0.5}\right)\ge {\left(\frac{2}{\pi }\right)}^{0.5}\frac{{\theta }_{jh}^{*0.5}}{\lambda +{\left({\lambda }^2+4{\theta }_{jh}^{*}\right)}^{0.5}}{e}^{-{\lambda }^2/\left(2{\theta }_{jh}^{*}\right)}.$$

Marginalizing over ${\theta }_{jh}^{*}$, we obtain

$$\text{pr}\left({\lambda }_{jh}>\lambda |{\theta }_{jh}^{*}\right)\ge E\left\{{\left(\frac{2}{\pi }\right)}^{0.5}\frac{{\theta }_{jh}^{*0.5}}{\lambda +{\left({\lambda }^2+4{\theta }_{jh}^{*}\right)}^{0.5}}{e}^{-{\lambda }^2/\left(2{\theta }_{jh}^{*}\right)}\right\}=E\left\{t_{\lambda }\left({\theta }_{jh}^{*}\right)\right\},$$

where $t_{\lambda }\left({\theta }_{jh}^{*}\right)$ is a monotonically increasing nonnegative function defined on the positive real line. Applying Markov’s inequality, we have $E\left\{t_{\lambda }\left({\theta }_{jh}^{*}\right)\right\}>\text{pr}\left({\theta }_{jh}^{*}>ϵ\right)t_{\lambda }\left(ϵ\right)$, and letting ϵ = λ²

$$E\left\{t_{\lambda }\left({\theta }_{jh}^{*}\right)\right\}>\text{pr}\left({\theta }_{jh}^{*}>{\lambda }^2\right)\frac{e^{-0.5}}{1+5^{0.5}}{\left(\frac{2}{\pi }\right)}^{0.5}.$$

If $\text{pr}\left({\theta }_{jh}^{*}>\lambda \right)\ge c{\lambda }^{-\alpha }$ for certain α, c positive constants and λ sufficiently large, then

$$\text{pr}\left({\lambda }_{jh}>\lambda |{\theta }_{jh}^{*}\right)\ge \frac{e^{-0.5}}{1+5^{0.5}}{\left(\frac{2}{\pi }\right)}^{0.5}c{\lambda }^{-2\alpha }=\tilde{c}{\lambda }^{-\tilde{\alpha }},$$

where $\tilde{c}=e^{-0.5}{\left(1+5^{0.5}\right)}^{-1}{\left(2/\pi \right)}^{0.5}c>0$ and $\tilde{\alpha }=\alpha /2>0$. By symmetry, $\text{pr}\left({\lambda }_{jh}<-\lambda |{\theta }_{jh}>0\right)\ge \tilde{c}{\lambda }^{-\tilde{\alpha }}$ for λ > L sufficiently large. It is sufficient that the marginal distribution of ${\theta }_{jh}^{*}$ has power law right tail to guarantee that $\left({\lambda }_{jh}|{\theta }_{jh}>0\right)$ has power law tail and then that marginally λ_jh has power law tail. □

Proof of Theorem 2. The mode of the conditional posterior density of λ_jh is ${\tilde{\lambda }}_{jh}$ such that

$$l_s\left({\tilde{\lambda }}_{jh};y,\eta \right)+\frac{\partial }{\partial \lambda }{\log \left\{f_{{\lambda }_{jh}|{\text{Λ}}_{-jh}}\left(\lambda \right)\right\}|}_{\lambda ={\tilde{\lambda }}_{jh}}=0,$$ (2)

where $l_s\left({\tilde{\lambda }}_{jh};y,\eta \right)$ is the jhth element of the score function of the likelihood for the data y conditionally on the latent variables η, and $f_{{\lambda }_{jh}|{\text{Λ}}_{-jh}}$ is the conditional prior density function of $\left({\lambda }_{jh}|{\text{Λ}}_{-jh}\right)$. Given prior symmetry, without loss of generality, we focus on ${\widehat{\lambda }}_{jh}>0$. In a neighbourhood $\left({\widehat{\lambda }}_{jh}-\epsilon ,{\widehat{\lambda }}_{jh}+\epsilon \right)$ of the conditional maximum likelihood estimate ${\widehat{\lambda }}_{jh}$ of λ_jh, we can approximate the score function using a Taylor expansion: $l_s\left(\lambda ;y\right)=-\mathcal{J}\left({\widehat{\lambda }}_{jh}\right)\left(\lambda -{\widehat{\lambda }}_{jh}\right)+{ϵ}_{\epsilon }$, where $\mathcal{J}\left({\widehat{\lambda }}_{jh}\right)>0$ is the negative of the derivative of l_s (λ; y) evaluated at $\lambda ={\widehat{\lambda }}_{jh}$, and ϵ_ε is an approximation error term such that ${\lim }_{\epsilon \to 0}{ϵ}_{\epsilon }/\epsilon =0$. For ${\widehat{\lambda }}_{jh}$ large enough, such that ${\widehat{\lambda }}_{jh}-\epsilon >L$ with $L\gg 0$, Lemma 1 holds for every λ in $\left({\widehat{\lambda }}_{jh}-\epsilon ,{\widehat{\lambda }}_{jh}+\epsilon \right)$, leading to the lower bound

$$-\mathcal{J}\left({\widehat{\lambda }}_{jh}\right)\left(\lambda -{\widehat{\lambda }}_{jh}\right)+{f^{\prime }}_{lb}\left(\lambda \right)+{ϵ}_{\epsilon }\le l_s\left(\lambda ;y\right)+\frac{\partial }{\partial \lambda }\log \left\{f_{{\lambda }_{jh}|{\text{Λ}}_{-jh}}\left(\lambda \right)\right\},$$

where ${f^{\prime }}_{lb}\left(\lambda \right)$ is a non positive continuous function for every λ > 0, ${\lim }_{\lambda \to +\infty }{f^{\prime }}_{lb}\left(\lambda \right)=0$. Let ε be a function of ${\widehat{\lambda }}_{jh}$ such that ${\lim }_{{\widehat{\lambda }}_{jh}\to \infty }\epsilon =0$ and ${\lim }_{{\widehat{\lambda }}_{jh}\to \infty }{f^{\prime }}_{lb}\left({\widehat{\lambda }}_{jh}\right)/\epsilon =0$. The limit for ${\widehat{\lambda }}_{jh}\to \infty$ of the lower bound evaluated in ${\widehat{\lambda }}_{jh}-\epsilon$ is

$$\underset{{\widehat{\lambda }}_{jh}\to \infty }{\lim }\mathcal{J}\left({\widehat{\lambda }}_{jh}\right)\epsilon +{f^{\prime }}_{lb}\left({\widehat{\lambda }}_{jh}-\epsilon \right)+{ϵ}_{\epsilon }=\underset{{\widehat{\lambda }}_{jh}\to \infty }{\lim }|\epsilon |\left\{\mathcal{J}\left({\widehat{\lambda }}_{jh}\right)+{f^{\prime }}_{lb}\left({\widehat{\lambda }}_{jh}-\epsilon \right)/|\epsilon |+{ϵ}_{\epsilon }/|\epsilon |\right\}.$$

Under Assumption 1, ${\lim }_{{\widehat{\lambda }}_{jh}\to \infty }\mathcal{J}\left({\widehat{\lambda }}_{jh}\right)+{f^{\prime }}_{lb}\left({\widehat{\lambda }}_{jh}-\epsilon \right)/|\epsilon |+{ϵ}_{\epsilon }/|\epsilon |\ge 0$, which guarantees ${\widehat{\lambda }}_{jh}-\epsilon \le {\tilde{\lambda }}_{jh}\le {\widehat{\lambda }}_{jh}$, and, hence ${\lim }_{{\widehat{\lambda }}_{jh}\to \infty }|{\tilde{\lambda }}_{jh}-{\widehat{\lambda }}_{jh}|=0$, which proves the theorem. □

Proof of Theorem 3. Since the local scales are independent, conditionally on β, we can apply the Chernoff’s method and obtain the following upper bound

$$\text{pr}\left\{|{\text{supp}}_{ϵ}\left({\lambda }_h\right)|>a{s}_p|{\beta }_h,{\gamma }_h,{\tau }_0\right\}\le \exp \left(-s_{p}at\right)\exp \left\{\left(e^t-1\right)\sum _{j=1}^p{\zeta }_{ϵjh}\right\},$$

for every t > 0 and ${\zeta }_{ϵjh}=\left\{{\tau }_0{\gamma }_{h}g\left(x_j^{\text{T}}{\beta }_h\right)\right\}/{ϵ}^2$ a function of β_h. Since $g\left(x_j^{\text{T}}{\beta }_h\right)$ is of order $\le O\left(\log \left(p\right)/p\right)$ by assumption and is limited above with respect to β_h, we can deduce $g\left(x_j^{\text{T}}{\beta }_h\right)\le c_j\log \left(p\right)/p$ for p sufficiently large and for some constant c_j > 0 that does not depend on β_h and is asymptotically of order O(1) with respect to p. Then, for $p\gg 0$,

$$\sum _{j=1}^{p}g\left(x_j^{\text{T}}{\beta }_h\right)\le \sum _{j=1}^p{c}_j\log \left(p\right)/p\le p\log \left(p\right)/p\underset{1\le j\le p}{\max }{c}_j=m\log \left(p\right),$$

where $m={\max }_{1\le j\le p}{c}_j$ does not depend on β_h. Then, the upper bound is

$$\text{pr}\left\{|{\text{supp}}_{ϵ}\left({\lambda }_h\right)|>a{s}_p|{\beta }_h,{\gamma }_h,{\tau }_0\right\}\le \exp \left\{-s_{p}at+\left(e^t-1\right)\frac{{\tau }_0{\gamma }_h}{{ϵ}^2}m\log \left(p\right)\right\}.$$

Let us choose $t=\log \left\{{ϵ}^2/\left({\tau }_0{\gamma }_{h}m\right)+1\right\}$. Since $s_p\ge \log \left(p\right)c_s$ for a certain c_s > 0, then, for any $a>{\left(c_{s}t\right)}^{-1}$, we can write

$$\text{pr}\left\{|{\text{supp}}_{ϵ}\left({\lambda }_h\right)|>a{s}_p|{\beta }_h,{\gamma }_h,{\tau }_0\right\}\le \exp \left\{-\log \left(p\right)\tilde{a}\right\},$$

where $\tilde{a}$ is a positive constant such that $a=\left(1+\tilde{a}\right){\left(c_{s}t\right)}^{-1}$. The upper bound does not depend on β_h, so

$$\text{pr}\left\{|{\text{supp}}_{ϵ}\left({\lambda }_h\right)|>a{s}_p|{\gamma }_h,{\tau }_0\right\}\le v\left(p\right)$$

with ν(p) of order O(p⁻¹) that goes to zero. □