Log-ratio lasso: Scalable, sparse estimation for log-ratio models

Abstract

Positive-valued signal data is common in the biological and medical sciences, due to the prevalence of mass spectrometry other imaging techniques. With such data, only the relative intensities of the raw measurements are meaningful. It is desirable to consider models consisting of the log-ratios of all pairs of the raw features, since log-ratios are the simplest meaningful derived features. In this case, however, the dimensionality of the predictor space becomes large, and computationally efficient estimation procedures are required. In this work, we introduce an embedding of the log-ratio parameter space into a space of much lower dimension and use this representation to develop an efficient penalized fitting procedure. This procedure serves as the foundation for a two-step fitting procedure that combines a convex filtering step with a second non-convex pruning step to yield highly sparse solutions. On a cancer proteomics data set, the proposed method fits a highly sparse model consisting of features of known biological relevance while greatly improving upon the predictive accuracy of less interpretable methods.

1 |. INTRODUCTION

In biological and medical sciences, imaging techniques are a common tool for investigating the molecular composition of a sample of interest. These methods give intensity values across a range of frequency values, and a data processing step translates the raw spectrum into intensity values for many molecules of interest. With such data, meaningful standardization of the resulting features is difficult, so it is desirable to treat this as compositional data. In a medical imaging setting, a common task of interest is to predict disease status from a tissue sample. Recent results by Banerjee et al. (2017) show that such data can be used to detect the presence of prostate cancer from tissues samples with high accuracy. It is desirable to have a model that combines high predictive accuracy with interpretability and parsimony, since parsimonious models can lead to (i) novel scientific insights and (ii) increased ease of model checking and confidence in the model. This second point is of particular importance for clinical applications. Model interpretability allows domain experts to add another layer of validation, making such methods more trustworthy and appealing to safety advisory boards.

Variable selection in regression models is a well-studied topic in the statistical literature. Classically, best subset selection, forward stepwise selection, and backward stepwise selection are commonly used methods for variable selection, see, for example, Hastie et al. (2001), with the size of the model selected using Mallow’s Cp/AIC (Mallows, 1973; Akaike, 1974), BIC (Schwarz, 1978), or cross-validation. A more modern approach that has enjoyed widespread success is the lasso estimator introduced by Tibshirani (1996), which uses L₁-penalization to induce sparse models.

Similarly, methods for compositional data have a long history in the statistical literature (Aitchison, 1982). Compositional data is typically transformed to real-valued data using a logarithmic transform after either (i) transforming all features to their relative intensity to an arbitrarily chosen baseline feature (Aitchison and Bacon-shone, 1984) or (ii) standardizing each observation by the geometric mean of the features (Aitchison, 1983). A flurry of recent work has introduced variable selection methods for composition data. Lin et al. (2014) use L₁-penalization to select sparse log-contrasts for compositional data, and a related class of optimization problems is studied in James et al. (2013). For increased interpretability and the inclusion of prior information regarding feature structure, Shi et al. (2016) develop a method for selecting small groups of compositional features. With similar motivation, Wang and Zhao (2017) introduce a method for selecting small groups of compositional features based on a known binary tree-structure on the features. These latter two methods are particularly motivated by the analysis of microbiome data, where the features are the relative abundances of bacteria species with a known phylogenetic structure.

1.1 |. Our contribution

In this work, we introduce a new notion of sparsity for compositional data based on a linear model containing all pairwise log-ratios. For sparse estimation, we use L₁-penalized regression, and prove the equivalence of our method with that of a modified lasso estimator in a lower-dimensional space. We then introduce a second pruning step to fit even sparser models, giving a mathematical argument for why this additional step is required. Our mathematical characterization of the log-ratio feature space also gives rise to an approximate forward stepwise algorithm for this same setting. To the best of the authors’ knowledge, there are no existing efficient fitting algorithms for these models. We further use the low-dimensional characterization to develop a novel post-selective goodness-of-fit test. In a simulation study, we find that when the true underlying model has sparse log-ratio structure, our estimator greatly improves upon generic approaches. When applied to a medical proteomics data set, the method improves the predictive performance relative to baseline methods and discovers features of biological importance.

1.2 |. Outline

This paper proceeds as follows. In Section 2, we introduce the all-pairs log-ratio model. In Section 3, we propose an estimator for this family of models, and formally establish the relationship between our estimator and a modified lasso estimator in a smaller space. We then develop an additional pruning stage which leads to much sparser model fits. In Section 4, we propose an approximate forward stepwise algorithm as an additional scalable estimator for this family of models. In Section 5, we explain how to test the appropriateness of a log-ratio model using classical testing and develop a novel post-selective test of model fit. In Section 6, we examine these estimators in simulation experiments. In Section 7, we apply these estimators to a proteomics data set to diagnose cancer from metabolite intensity. Lastly, we offer a few concluding remarks in Section 8.

2 |. ALL-PAIRS LOG-RATIO MODEL

We begin by introducing the all-pairs log-ratio model and briefly explain its appeal. Let Y = (y₁, ... , y_n)^⊤ be the response variable and let X be the n × p matrix of positive features, which does not include an intercept term. In the remainder of this work, we will be interested in models of the form

$$y_i=\mu +\sum _{1\le j<k\le p}{\theta }_{j,k}\log \left(x_{i,j}/x_{i,k}\right)+{ϵ}_i$$ (1)

for i = 1, ... , n. The ϵ_i are mean zero noise terms with common variance. In particular, we are interested in fitting such models under the assumption that most of the entries θ_j,k for 1 ≤ j < k ≤ p are zero. If we let Z be the $n\times \left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$ matrix with columns given by enumerating all log-ratio features log(x_j/x_k) for 1 ≤ j < k ≤ p and take ϵ = (ϵ₁, ... , ϵ_n)^⊤ then we see that Equation 1 is a linear model in Z:Y = μ1 + Zθ + ϵ. Such models are attractive for several reasons:

1. Compositionality. In his seminal work on the multivariate analysis of compositional data, Aitchison (1982) introduced the notion of subcompositional coherence: any analysis of subcompositional data should have the property that the analysis is unchanged whether we are analyzing the entire data set or a subcomposition. In our case, we are using compositional variables as features in a regression procedure, and the analogous property is invariance to the multiplicative scale of each observation. This invariance implies that when we run our procedure on a data set, whether or not the data set is a subcomposition of a larger set of compositional predictors has no effect on the result.

2. Predictive accuracy. In settings such as medical imaging, we may expect that only the relative intensity of a small number of raw features carry information about the response variable. Furthermore, in such imaging settings, the distribution of the raw features is often very skewed with values spanning many orders of magnitude. Enforcing compositional structure and taking a logarithmic transformation serves to reduce the variance of the procedure, improving predictive accuracy.

3. Interpretability and scientific relevance. In some fields such as biochemistry it is standard for scientists to work with log-ratio quantities in the course of a scientific investigation. Formulating the statistical model in the scientifically natural basis allows researchers to more effectively use and interpret the model.

There are two main challenges considering the all-pairs log-ratio model. The first is computation; the expanded feature space has dimensions $\left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$, which can be computationally unwieldy. Much of this paper is devoted the development of a novel method for overcoming this challenge. The second challenge is identifiability. There are many coefficients θ which lead to identical predictions. With a model of the form (1), one chooses representative θ from a class of mathematically equivalent choices. We urge the practitioner to keep this in mind when evaluating the coefficients of a model of this form. Not all choices of representation are equally attractive, however. Sparser models are preferable because they allow the user to more easily understand the model and verify that the directions of the effects are sensible in the given context. This paper develops a method for selecting a highly sparse model of the form (1), which will very often be the most desirable representation for the practitioner.

3 |. THE LOG-RATIO LASSO ESTIMATOR

Motivated by the linear model formulation in (1), we next propose an estimator for the sparse log-ratio model setting and examine its properties.

Definition 1 (Log-ratio lasso).

The log-ratio lasso estimator is defined to be

$$\theta \in \underset{\theta }{\mathrm{argmin}}\frac{1}{2}\sum _{i=1}^n{\left\{y_i-\mu -\sum _{1\le j<k\le p}{\theta }_{j,k}\log \left(\frac{x_{i,j}}{x_{i,k}}\right)\right\}}^2+\lambda \Vert \theta {\Vert }_1.$$ (2)

Here θ_i,j is defined only for i < j, so this can be represented as a vector in ${ℝ}^{\left(\frac{p}{2}\right)}$. λ is a tuning parameter. This is the usual lasso estimator with the expanded feature matrix Z, and so the solutions θ will be sparse for appropriate values of λ. Lasso estimators are firmly established in the statistical literature, making this a natural starting point for the log-ratio model (1), but solving this optimization problem is challenging because it is an optimization in $\left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$ variables and requires explicit construction of the $n\times \left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$ matrix of predictors Z. For even moderate values of p, this would require a large amount of memory and computation time. For large values of p, this becomes intractable.

3.1 |. Low-dimensional characterization of the log-ratio lasso

The log-ratio lasso is an appealing variable selection technique for our setting, but in its original form it is not practical for large p because solving such an optimization problem in $\left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$ variables will have prohibitively large running time and memory requirements. A major component of our contribution is to show that this estimator can be recovered from the solution of a much simpler optimization problem in only p variables that does not require the construction of the expanded feature matrix Z. We proceed by defining this simpler optimization problem and connecting it to the log-ratio lasso estimator.

Definition 2 (Linearly constrained lasso).

The linearly constrained lasso fit is defined to be

$$\mathit{\beta }=\underset{\left\{\mathit{\beta }:1^{\top }\mathit{\beta }=0\right\}}{\mathrm{argmin}}\frac{1}{2}\sum _{i=1}^n{\{y_i-\mu -\sum _{j=1}^p{\beta }_j\log \left(x_{i,j}\right)\}}^2+\gamma \Vert \mathit{\beta }{\Vert }_1.$$ (3)

Notice this is the lasso estimator on the logarithmically transformed variables, with the additional constraint that the sum of the coefficients is zero. This is a convex optimization problem with p variables and 1 linear constraint, and it can be solved efficiently. We provided details about how to efficiently solve this optimization problem using any lasso solver in the Supplementary Material. This estimator was first studied in Lin et al. (2014), also in the context of compositional data. In that work, however, the authors were not interested in the log-ratio models (1). This work develops a different notion of sparsity. We now turn to the relationship between this estimator and the log-ratio lasso estimator.

Theorem 1.

The log-ratio lasso problem and the linearly constrained lasso problem are equivalent for λ = 2γ.

This theorem is important because implies that we can fit the log-ratio lasso efficiently, even for large values of p.

We must explain in detail what we mean by “equivalent” in the statement of the previous theorem. Let W = log(X) be the matrix obtained by taking the element-wise logarithm of X. Let $b:{ℝ}^{\left(\begin{array}{c}p\\ 2\end{array}\right)}\to {ℝ}^p$ be the linear map that takes a θ from a log-ratio lasso feature space to the corresponding β in the standard feature space:

$$b{(\theta )}_k=\sum _{j=1}^{k-1}-{\theta }_{j,k}+\sum _{j=k+1}^p{\theta }_{k,j}.$$

This definition implies Zθ = W{b(θ)}. The log-ratio lasso fit is not unique, so “equivalence” in the preceding theorem means that the same minimum value of the objective function is achieved for both problems, and for any solution θ of the log-ratio lasso optimization, β = b(θ) is a solution of the linearly constrained lasso optimization and vice-versa. By the following corollary, the solution to the linearly constrained lasso optimization will typically be unique when n > p.

Corollary 1.

The minimizer of the constrained lasso is unique if the matrix W has full rank.

Proofs are provided in the Supplementary Material.

To fit the log-ratio lasso, we solve the constrained lasso optimization (3) to obtain the solution β. By the preceding theorem, the solutions to the log-ratio lasso (2) are all θ such that b(θ) = β and 2 ∥θ∥ = ∥β∥. There will typically be multiple solutions θ to the log-ratio lasso optimization problem (2), but we emphasize that we will never need to explicitly construct the full set of such solutions. Subsection 3.4 develops a procedure for taking the solution of the constrained lasso β and selecting an approximate solution θ from the set of all solutions to the optimization problem (2), giving preference to sparser solutions.

3.1.1 |. Extensions beyond the linear model

We note in passing that this theorem also applies to L₁-penalized GLMs (Nelder and Wedderburn, 1972) and the L₁-penalized Cox proportional hazards model (Cox, 1972; Tibshirani, 1997), which can be seen from the argument in the Supplementary Material. It would be of great interest to further pursue the case of logistic regression, which is the natural model when dealing with binary outcome data such as disease status. Similarly, the Cox model is of great interest because survival time outcomes are common in medical contexts. For the remainder of this work, however, we limit ourselves to L₁-penalized linear regression.

3.1.2 |. Mathematical intuition

We now give some intuition for the preceding theorem. A formal proof is provided in the Supplementary Material. Notice that any model Y = Zθ + ϵ corresponds to a model Y = Wβ + ϵ with the mapping β = b(θ). Furthermore, we have that ${\sum }_{k=1}^p{\beta }_k={\sum }_{k=1}^p\{{\sum }_{j=1}^{k-1}-{\theta }_{j,k}+{\sum }_{j=k+1}^p{\theta }_{k,j}\}=0$, since each term θ_j,k for j < k appears once with a positive sign and once with a negative sign. Thus when searching for a model in the form Wβ, we can restrict our attention to vectors β such that ${\sum }_{k=1}^p{\beta }_k=0$.

Take β = b(θ). We now turn to the connection between ∥θ∥₁ and ∥β∥₁. It is not true that 2 ∥θ∥₁ = ∥β∥₁ in general, but it does hold in some cases. Loosely speaking, this relationship holds whenever θ does not lead to redundant linear combinations of columns. In the Supplementary Material we show that among the vectors θ′ such that Zθ = Zθ′, the minimum L₁-norm solution satisfies 2 ∥θ′∥₁ = ∥β∥₁. For other choices of θ′, the L₁ norm can be reduced without changing the model fit, and those values of θ′ will not be selected by the log-ratio lasso procedure. We then show that for relevant β, there exists a corresponding θ with this property, and the theorem follows.

3.2 |. Relationship with the lasso

From this formulation of the problem, we can see that the log-ratio lasso is finding a model of the form

$${\widehat{y}}_i=\mu +\sum _{j=1}^p{\beta }_j\log x_{i,j}(i=1,...,n).$$ (4)

The log-ratio lasso differs from the standard lasso in that it is searching for models that can be represented as a sparse collection of ratios, rather than only a sparse coefficient vector β. The standard lasso on the transformed set of features (logx_i,j)_{j=1, ... , p} and the log-ratio lasso are both fitting models within this family, but they differ in the way that they search among the candidate models. We will see in simulation experiments that when the true model consists of a few log-ratios, the specialized log-ratio lasso has better performance.

3.3 |. Non-uniqueness of solution

There are linear dependencies among the features in the expanded feature matrix Z because there are $\left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$ features takes of form log(x_i) − log(x_j), which together have a linear span of only dimension p − 1. Since Z is not full rank, the OLS solution regressing Y onto Z is not well-defined. A standard way to fix such non-identifiability is to add a penalty term. Interestingly, in the model Y = Zθ + ϵ, the addition of L₁-penalization is not sufficient to make the model fit unique.

3.3.1 |. Explicit example

To demonstrate the non-uniqueness in the solutions θ, suppose we have fit the following model:

$$\widehat{\mathbf{y}}=2\log \left({\mathbf{x}}_{\mathbf{1}}\right)+1\log \left({\mathbf{x}}_{\mathbf{2}}\right)-2\log \left({\mathbf{x}}_{\mathbf{3}}\right)-1\log \left({\mathbf{x}}_{\mathbf{4}}\right).$$

We can represent this as y = Zθ for several different values of θ with equivalent L₁ norm:

1. $\widehat{\mathbf{y}}=2\left\{\log \left({\mathbf{x}}_{\mathbf{1}}\right)-\log \left({\mathbf{x}}_{\mathbf{3}}\right)\right\}+1\left\{\log \left({\mathbf{x}}_{\mathbf{2}}\right)-\log \left({\mathbf{x}}_{\mathbf{4}}\right)\right\}$. Here ∥θ∥₁ = 2.

2. $\widehat{\mathbf{y}}=1.5\left\{\log \left({\mathbf{x}}_{\mathbf{1}}\right)-\log \left({\mathbf{x}}_{\mathbf{3}}\right)\right\}+.5\left\{\log \left({\mathbf{x}}_{\mathbf{1}}\right)-\log \left({\mathbf{x}}_{\mathbf{4}}\right)\right\}+.5\left\{\log \left({\mathbf{x}}_{\mathbf{2}}\right)-\log \left({\mathbf{x}}_{\mathbf{3}}\right)\right\}+.5\left\{\log \left({\mathbf{x}}_{\mathbf{2}}\right)-\log \left({\mathbf{x}}_{\mathbf{4}}\right)\right\}$. Here ∥θ∥₁ = 2.

3. $\widehat{\mathbf{y}}=1.7\left\{\log \left({\mathbf{x}}_{\mathbf{1}}\right)-\log \left({\mathbf{x}}_{\mathbf{3}}\right)\right\}+.3\left\{\log \left({\mathbf{x}}_{\mathbf{1}}\right)-\log \left({\mathbf{x}}_{\mathbf{4}}\right)\right\}+.3\left\{\log \left({\mathbf{x}}_{\mathbf{2}}\right)-\log \left({\mathbf{x}}_{\mathbf{3}}\right)\right\}+.7\left\{\log \left({\mathbf{x}}_{\mathbf{2}}\right)-\log \left({\mathbf{x}}_{\mathbf{4}}\right)\right\}$. Here ∥θ∥₁ = 2.

This ambiguity in θ occurs whenever there are at least 2 disjoint log-ratios that are nonzero. The solution θ may not be unique, but we noted earlier that b(θ) is unique unless the matrix W is not of full rank. Although there may exist many equivalent solutions θ with the same L₁-norm, we see that some of these solutions may be sparser than others. Since even L1-penalization is not enough to enforce the desired sparsity in θ, a more demanding selection criterion is needed. We now turn to a method for finding a highly sparse solution θ.

3.4 |. Two-stage procedure

Our goal is to find a succinct model of the form (1) that explains the data well. In the preceding section, we saw that there is some ambiguity resulting from the solution to the log-ratio lasso optimization problem. We now turn to a method for finding a highly sparse parameter θ. We will use the log-ratio lasso solution as a baseline solution, followed by a secondary sparse regression procedure.

Algorithm 1.

Two-stage Log-ratio Lasso

1.	Fit the log-ratio lasso with tuning parameter λ.
2.	Using variables in the support from step one, enumerate all log-ratios into a matrix $\tilde{\mathbf{Z}}$.
3.	Use a sparse regression procedure to fit y onto $\tilde{\mathbf{Z}}$, with tuning paramemter γ.

Examples of such procedures include forward stepwise, backward stepwise, or best subset selection. There are several other sub-L₁ methods explored in the literature such as the MC+ (Zhang et al., 2010) and SCAD (Fan and Li, 2001) penalties. In Algorithm 3.4, the parameters λ and γ should be chosen by joint cross-validation over a grid of values. Using warm-starts for the solutions of the two optimization problems in step 1 and step 3 means that this takes much less time than fitting the model from scratch at each value of the parameter. When using forward-stepwise regression in step 3, the model fitting is particularly fast. In this paper, we concentrate on forward-stepwise regression, because it works in the GLM case and scales to large data sets.

We can view this as a class of computationally feasible sparse regression procedures for log-ratio models (1). Due to the size of predictor space ($\left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$ variables) we use log-ratio lasso (2) as a screening step, which by theorem 1 can be fit using a much simpler optimization problem (3). The screening step is followed by a “sparser” regression procedure. This allows us to fit log-ratio models (1) without ever explicitly constructing the expanded feature matrix Z. In some cases fitting something as simple as a forward stepwise regression of y onto the expanded feature matrix Z would be computationally expensive, so this screening step is necessary. This algorithm can provide both a statistical and computational improvement over forward stepwise selection for large p.

4 |. APPROXIMATE FORWARD STEPWISE SELECTION

In previous sections, we introduced a procedure to efficiently fit large log-ratio models based on the lasso. We now introduce an alternative greedy fitting procedure that also takes advantage of the unique log-ratio structure of our setting. An obvious first candidate for a greedy algorithm for the all-pairs log-ratio model (1) is forward stepwise selection on the expanded feature matrix of all log-ratios Z of dimension $n\times \left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$, but this quickly becomes infeasible for large p. In this section, we use the log-ratio structure to develop an efficient stepwise selection procedure for fitting log-ratio models.

Algorithm 2.

Approximate Forward Stepwise Selection

Standardize the features to have mean 0 and variance 1. Begin with $\mathcal{S}=\varnothing$ and $\mathbf{r}=\mathbf{y}-\overline{y}\mathbf{1}$.
for j = 1 to k do
1.	Fit a single-variable linear regression on features 1 to p using residual r as the response.
2.	Select the feature log(xi/xj) where i corresponds to the feature with largest positive coefficient and j corresponds to the feature with largest negative coefficient. Add this ratio to the set of selected ratios $\mathcal{S}$.
3.	Regress out the log-ratio features in $\mathcal{S}$ together with an intercept from y to obtain a new residual vector r.
end

This procedure approximates forward stepwise selection for log-ratio models but is much faster. The connection between the two procedures is the following, when regressing onto all log-ratio terms, at each step forward stepwise selection will choose i and j to maximize

$$\frac{{\mathbf{r}}^{\top }\left(\log \left({\mathbf{x}}_{\mathbf{i}}\right)-\log \left({\mathbf{x}}_{\mathbf{j}}\right)\right)}{\sqrt{{\Vert \log \left({\mathbf{x}}_{\mathbf{i}}\right)\Vert }^2+{\Vert \log \left({\mathbf{x}}_{\mathbf{j}}\right)\Vert }^2-2\log {\left({\mathbf{x}}_{\mathbf{i}}\right)}^{\top }\log \left({\mathbf{x}}_{\mathbf{j}}\right)}}$$ (5)

whereas approximate forward stepwise will choose i _and j to maximize

$$\frac{{\mathbf{r}}^{\top }\left(\log \left({\mathbf{x}}_i\right)-\log \left({\mathbf{x}}_j\right)\right)}{\sqrt{{\Vert \log \left({\mathbf{x}}_i\right)\Vert }^2+{\Vert \log \left({\mathbf{x}}_j\right)\Vert }^2}}$$ (6)

where r denotes the residual at that step. The approximate forward stepwise procedure selects a log-ratio with high explanatory power at each step, ignoring correlation among the features to make the computation feasible. When the vectors log(x_i) are mutually orthogonal for i = 1, ... , p, the proposed approximate stepwise procedures coincides with the exact forward stepwise solution on the expanded feature set Z.

Comparing Equations 5 and 6 shows that we can fit approximate forward stepwise faster than exact forward stepwise selection. Exact forward stepwise requires the computation of the $\left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$ inner products among the features, whereas approximate forward stepwise selection only requires the computation of p inner products at each step. When the total number of steps k is small relative to p, the complexity of approximate forward stepwise selection is O(npk) and of forward stepwise selection is O(np²). We examine the statistical and computational performance of this procedure in simulations in Section 6 and on real data in Section 7.

5 |. MODEL VERIFICATION VIA HYPOTHESIS TESTING

In the preceding sections, we developed variable selection methods for the all-pairs log-ratio model (1). For a practitioner applying such methods, it is essential to have model diagnostics for evaluating the plausibility of resulting model fits. In Section 3 and the associated proofs in the Supplementary Material, it is shown that a linear model in the logarithmically transformed variables (4) corresponds to an all-pairs log-ratio model (1) if and only if

$$\sum _{i=j}^p{\beta }_j=0.$$ (7)

As a goodness-of-fit test of the log-ratio model, a practitioner can conduct a formal hypothesis test of (7). We present two tests, a classical test and a modern selective inference test.

5.1 |. Classical testing

If p < n and the model matrix of the logarithmically transformed variables is of full rank, then we can use OLS to fit a linear model of the form (4). Under the assumption that the errors ϵ are i.i.d. normally distributed, we can test the linear hypothesis given by (7) using the F-test.

5.2 |. Selective inference

When doing model selection, classical hypothesis testing no longer applies since the object of inference is based on the (random) data. The selective inference formalism has been developed in recent years to address the problem of inference in the presence of model selection (Lee et al., 2016; Tibshirani, Ryan J. et al., 2016). We will use results from selective inference theory to compare the one-step log-ratio lasso estimator to the standard lasso estimator on the feature (logx_j)_{j=1, ... , p}. Our proposed test considers the sparse model selected by the lasso rather than the less relevant full model consider by the classical F-test, and applies even when p > n. The proposed test does not assume correctness of the linear model, but does require that y ~ N(μ, σ²I) for some μ and σ₂.

Let M be a subset of features together with signs for each, and let X_M be the feature matrix containing only the selected features. Let ${\beta }^{(\mathbf{M})}:=\mathbb{E}\{{\left({\mathbf{X}}_M^{\top }{\mathbf{X}}_M\right)}^{-1}{\mathbf{X}}_M^{\top }y\}$ be the partial regression coefficients in a model consisting only of features in M. Let ${\eta }_M={\mathbf{1}}^{\top }{\left({\mathbf{X}}_M^{\top }{\mathbf{X}}_M\right)}^{-1}{\mathbf{X}}_M^{\top }$. We will test the hypothesis that

$$\sum _{j\in M}{\beta }_j^{(M)}=0,$$ (8)

where M is the support set identified by the lasso. With this hypothesis we are asking the question: given the selection of the lasso, is there any log-ratio model in the selected variables consistent with the data? If there is sufficient resolution in the data to reject this hypothesis, this indicates to the researcher that the log-ratio model is not appropriate.

Proposition 1 (Post-selective test of the log-ratio model).

Let $F_{\mu ,{\sigma }^2}^{𝒮}$ be the CDF of a N(μ, σ²) random variable truncated to have support only on the set $𝒮$. Then there exist quantities a(y) and b(y) independent of η_M^⊤y such that with $𝒮\text{=[}a\text{(}y\text{),}b\text{(}y\text{)]}$, $\mu ={\mathbf{1}}^{\top }{\beta }^{(\mathit{M})}$, and ${\sigma }^2={\Vert {\eta }_M\Vert }^2$,

$$F_{\mu ,{\sigma }^2}^{𝒮}\left({\eta }_{\mathbf{M}}^{\top }\mathbf{y}\right)\mid \{\widehat{M}=M\}~\mathrm{Unif}(0,1).$$ (9)

This proposition gives a conditional P-value for the post-selective hypothesis given in (8):

$$p_0=F_{0,{\sigma }^2}^{𝒮}\left({\eta }_{\mathbf{M}}^{\top }\mathbf{y}\right).$$

The pivotal quantity from (9) is monotone decreasing in the Gaussian mean parameter 1^⊤β^(M), so this is a one-sided P-value. For our context, we usually prefer the two-sided P-value given by $p_0^{\prime }=1-2\left|p_0-1/2\right|$. Technical details are provided in the Supplementary Material.

We now examine the post-selective test in a simple setting. We take n = 100, p = 30 and $X_{i,j}\stackrel{iid}{~}N(0,1)$. We use the feature matrix Z_i,j = log(|X_i,j|) and generate y = Zβ + ϵ with ϵ ~ N(0, I_n). We examine the results with β = (2, −2, 0, ... , 0)^⊤ which corresponds to a model with a single large log-ratio signal log(x₁/x₂) and β = (2, 0, ... , 0)^⊤ which is not equivalent to any log-ratio model. The signals are large enough that the true support is always contained in the selected support. One-sided P-values are computed using Proposition 1. We present the result of 2000 repetitions in Figure 1. We observe close agreement with the theory; when the log-ratio model holds the P-values appear to be uniform and when the log-ratio model does not hold the P-values are noticeably sub-uniform.

FIGURE 1.

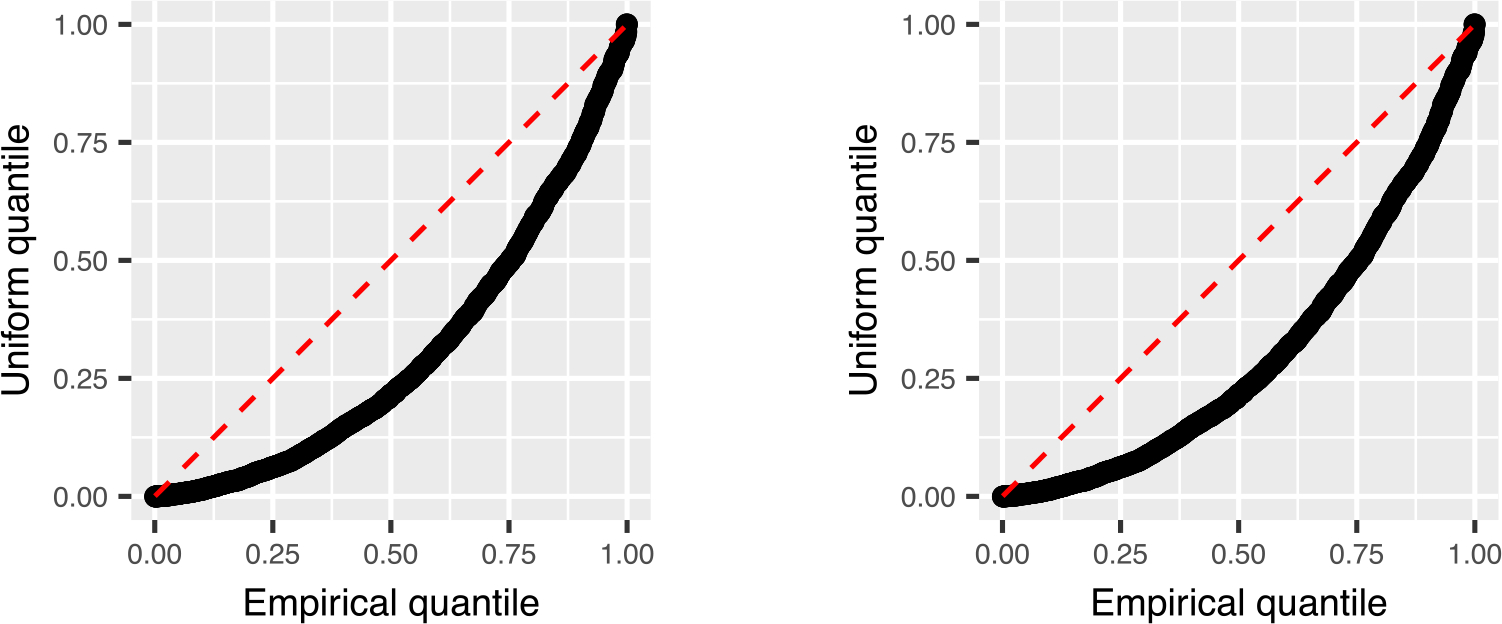
Results from the numerical example of Subsection 5.2. The left panel corresponds to the log-ratio model with one signal, in which case the null hypothesis holds whenever the first two features are both selected. The right panel corresponds to a single unpaired signal, in which case the null hypothesis does not hold.

6 |. SIMULATION EXPERIMENTS

We now examine the performance of our proposed methods for fitting log-ratio models with simulation experiments. We examine the following five methods:

1. Approximate forward stepwise (approx-fs): the approximate forward stepwise procedure described in Algorithm 2.

2. Forward stepwise selection (fs): forward stepwise selection applied on the logarithmically transformed features.

3. Single-stage log-ratio lasso (single-stage): the method described in (2), which we showed is equivalent to the constrained lasso method of Lin et al. (2014). The solution is computed using (3).

4. Two-stage log-ratio lasso (two-stage): Algorithm 3.4 using forward stepwise selection for the pruning stage.

5. Lasso (vanilla-lasso): the usual lasso estimator on the logarithmically transformed raw features.

All tuning parameters are chosen by cross-validation. Methods 2 and 5 are fitting linear models in the logarithmically transformed feature space of the form (4) whereas methods 1,3, and 4 are fitting log-ratio models of the form (1). A more comprehensive simulation study which includes ridge regression and a variant of the two stage procedure incorporating shrinkage are available in the Supplementary Materials.

6.1 |. Experiment 1: Two log-ratio signals

We first examine the performance of our estimator when the data is generated from a log-ratio model. We consider the following model, consisting of two log-ratio terms of different amplitudes:

$$y_i=2s\log \left(x_{i,1}/x_{i,2}\right)+s\log \left(x_{i,3}/x_{i,4}\right)+{ϵ}_i\text{for}i=1,...,n.$$

We take ${ϵ}_i\stackrel{iid}{~}N(0,1)$. In the following simulations we use n = 100, p = 30, $X_{i,j}\stackrel{iid}{~}|N(0,1)|$. The signal strength s is taken across a grid of values from 0 to 3. We present the result in Figure 2.

FIGURE 2.

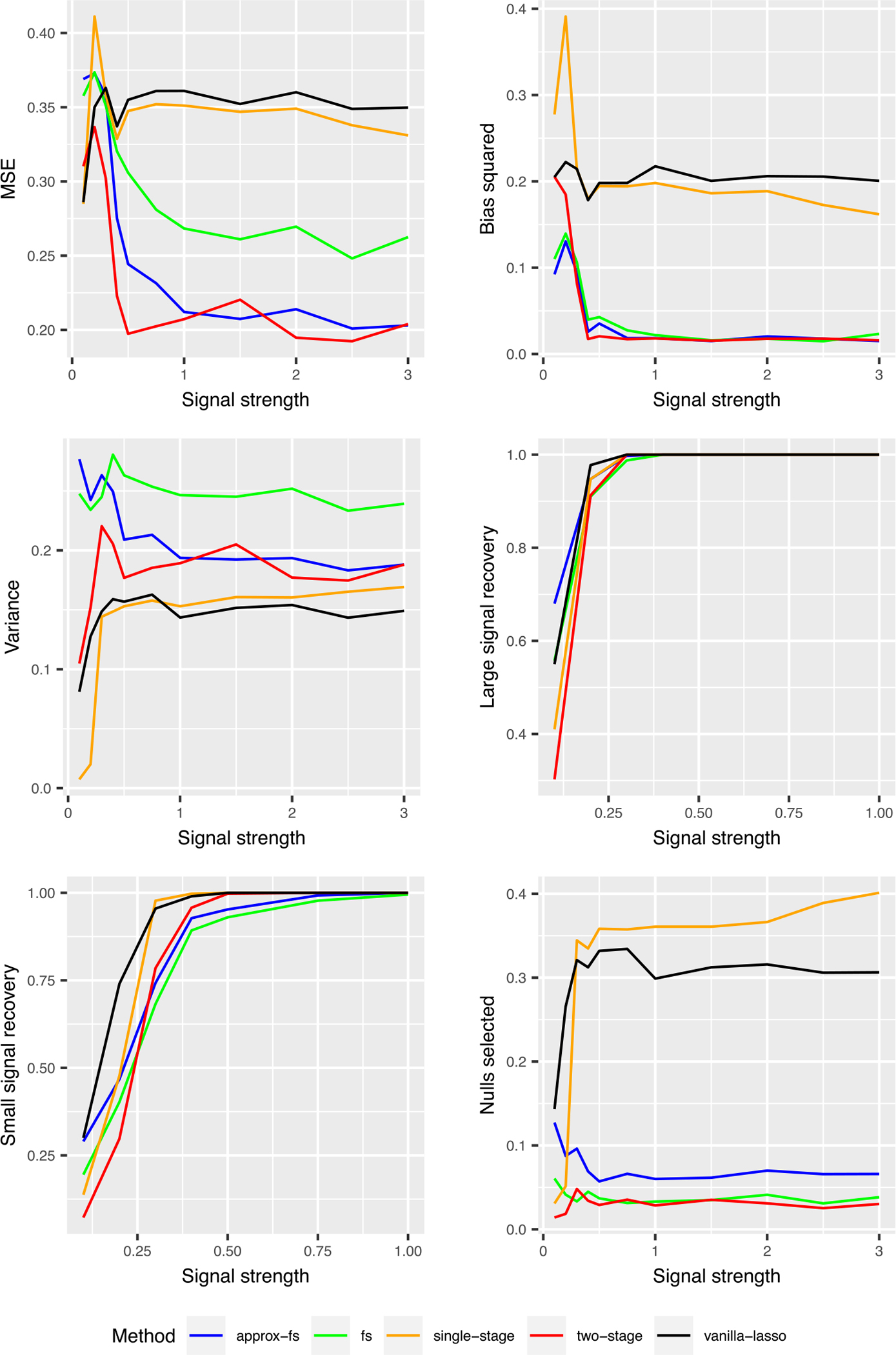
Results of experiment 1: MSE and support recovery of log-ratio lasso in the sparse log-ratio model. The “large signal recovery” and “small signal recovery” graphs report the proportion of times that the true large signal and true small signal are selected, respectively. The “nulls selected” graph shows the average fraction of null variables that are selected.

6.1.1 |. MSE, bias, and variance

We find that there is a large regime of signal strengths where the two-step procedure significantly outperforms the original lasso. For coefficients from 0.5 to about 3, there is a MSE reduction of about 40% relative to the lasso. The two-stage procedure has very low bias in the sparse setting, because it sets many coefficients to zero. It has slightly more variance than lasso, due to its discontinuous nature. We also note that the lasso and the single-stage log-ratio lasso are quite close, with the single-stage log-ratio lasso performing slightly better. Approximate forward stepwise selection has competitive MSE to the two-stage procedure. Overall, the two-stage procedure has the best MSE.

6.1.2 |. Support recovery

We next consider the support recovery properties of these procedures. The lasso and single-stage procedure recovers the signals slightly more often than the two-stage procedure. This is expected, because the two-stage procedure is a pruning of the single stage procedure. The two-stage procedure selects very few null variables. This explains why this procedure has much better MSE and is an appealing aspect of this procedure in scientific contexts. Overall, the two-stage procedure has the best support recovery properties; it recovers the true signals very frequently and rarely selects null variables.

Additional simulation experiments in the Supplementary Material show that the procedure maintains this good performance even in the presence of moderate model misspecification.

6.2 |. Experiment 2: Computational efficiency

We compare the computational efficiency of the methods. The results are presented in Figure 3. We find that approximate forward stepwise selection offers a significant speedup over standard forward stepwise selection. Our R implementation of the approximate forward stepwise procedure runs in less than 1 s on a notebook computer for a log-ratio model with 500 observations and 500 raw features, whereas standard forward stepwise regression in R on all log-ratios becomes computationally infeasible for problems of this size.

FIGURE 3.

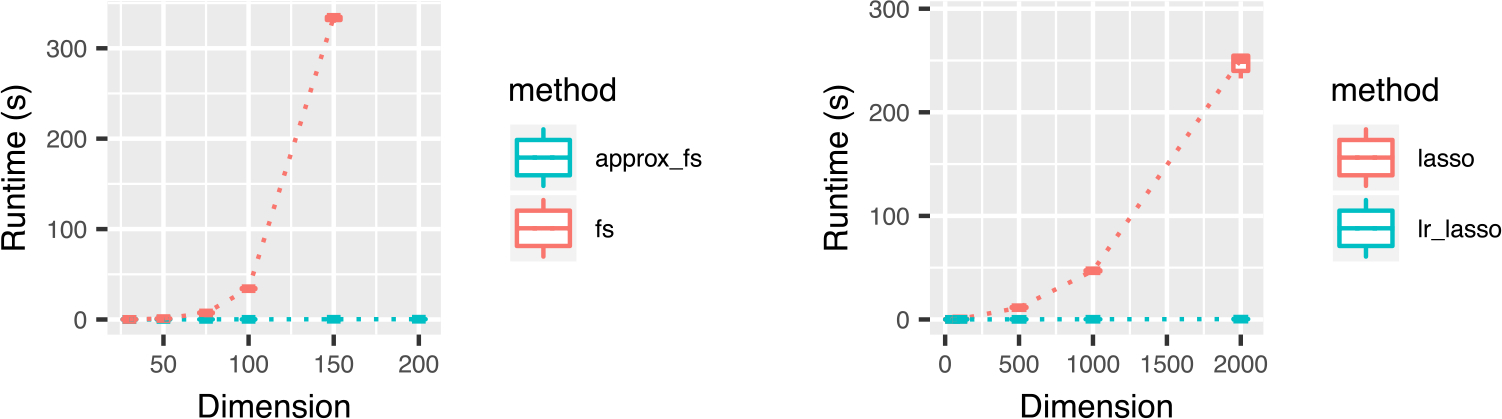
Results of experiment 3, a comparison of the runtime of 10 steps of the approximate forward stepwise selection and standard forward stepwise procedure (left) and naïve lasso versus constrained lasso fitting (right). Fitting for forward stepwise selection and naïve lasso are done on the expanded feature set of all log-ratios, which is of size $\left(\begin{array}{c}\text{dimension}\\ 2\end{array}\right)$. Runtimes are from a Macbook pro with 3.3 GHz Intel Core i7 processor. Forward stepwise selection was fit using the leaps(Lumley, 2017) R package and lasso was fit with the glmnet(Friedman et al., 2010) R package. We note that glmnet is internally running FORTRAN code, which accounts for the large difference in runtime among the methods in the left versus right panels.

We also observe that constrained lasso offers a significant speedup over a naïve lasso fitting procedure applied to all log-ratio terms. Recall that by the results in Section 3, the solution to these two optimization problems are equivalent. For a model with d predictors with d ≫ n, lasso has computational complexity approximately O(nd²). For a log-ratio model with p raw features and $\left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$ log-ratio features, the naïve lasso fitting scales as O(np⁴) whereas constrained lasso fitting (3) scales as O(np²).

7 |. REAL DATA EXAMPLE: CANCER PROTEOMICS

We now apply the log-ratio lasso methods to a proteomics data set collected and analyzed in Banerjee et al. (2017). The data consist of measurements from 54 patients, each of whom has either a healthy prostate or prostate cancer. For each individual 5 to 18 locations on a tissue sample are examined, and for each location the intensity of 53 chemical markers is measured using mass spectrometry. The resulting data set has 618 observations of 53 features. Researchers are working to use data sets like this to classify tissue samples as healthy or cancerous in minutes, so that they can be used by physicians in the middle of a surgery. In this data set, observations from the same patient are not independent, and the cross-validation process is done block-wise so that each patient falls entirely in the training fold or test fold. A validation set of 202 observations from 18 patients is put aside for assessing the accuracy of the final model. Many of the features are zero, so a small constant was added to each entry to allow for subsequent logarithmic transformations, see the Supplementary Materials for a brief discussion.

7.1 |. Baseline models

We perform lasso logistic regression, approximate forward stepwise, and ridge regression on this data set, using the logarithmically transformed feature matrix. Performance is reported in Table 1. Based on previous scientific knowledge, Banerjee et al. (2017) found that glucose/citrate ratio is a highly predictive feature. Logistic regression using only this feature and intercept gives 94% validation set accuracy. We will refer to this model as oracle logistic regression since it is based on external information. From this regression model, we see that there is a strong predictive model consisting of only one log-ratio term. This model is inside the span of the lasso and ridge regression models, but these fitting techniques have very poor predictive performance compared to the oracle model. Furthermore, lasso logistic regression, does not find this log-ratio in the sense that glucose and citrate do not have the largest positive and smallest negative coefficients. This is visually represented by the lasso path in Figure 4. A researcher interpreting the fit of the lasso model would not be led to the conclusion that the log-ratio of glucose to citrate is highly important.

TABLE 1.

A comparison of predictive accuracy and parsimony of various models

Method	Classification accuracy	Support size	Selects glucose and citrate?
Oracle logistic regression	0.94	2	Yes
Ridge regression	0.71	53	Yes
Approximate FS	0.72	6	No
Lasso	0.73	20	Yes
LR lasso (single stage)	0.74	27	Yes
LR-lasso (two-stage)	0.90	4	Yes

Note: The oracle model is constructed on the bases of external scientific information.

FIGURE 4.

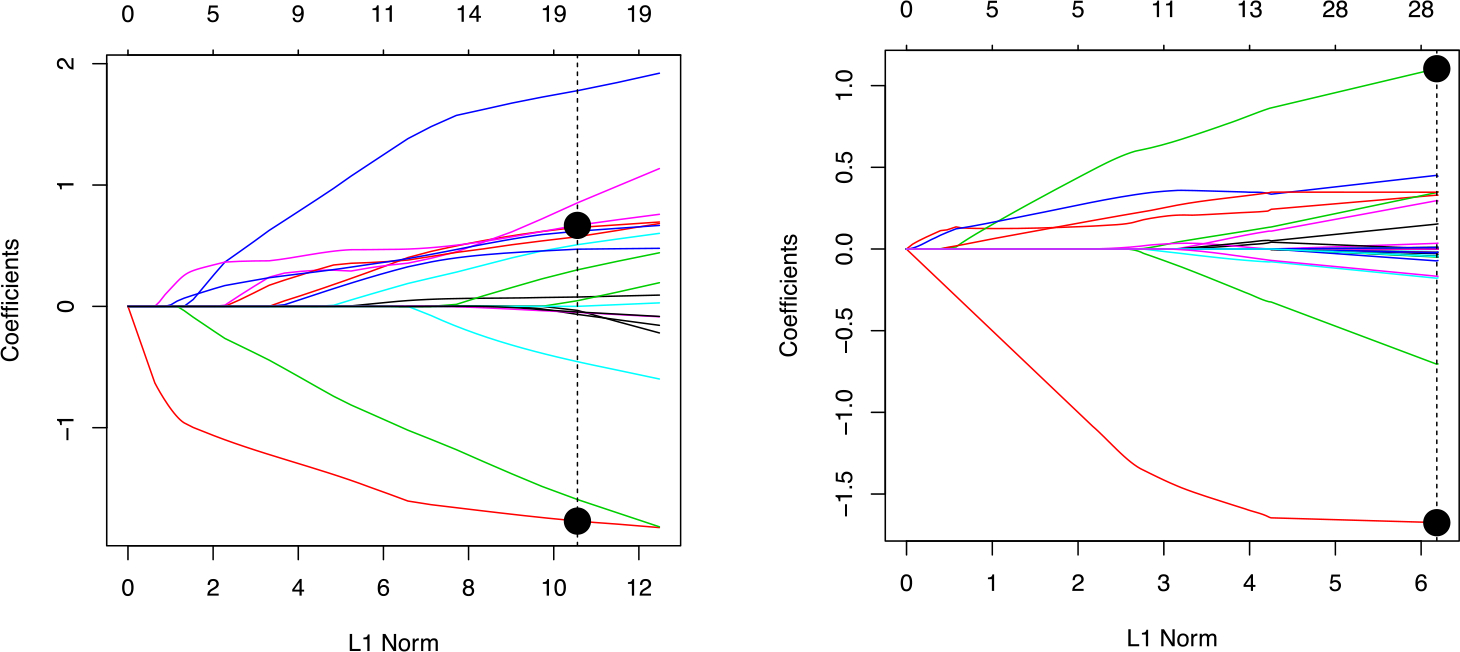
A comparison of the selection paths from lasso logistic regression (left) and the single stage log-ratio lasso (right). The top horizontal labels indicate how many variables are in the model at each point along the path. Dashed vertical lines indicate the tuning parameter selected by cross-validation. The coefficients of glucose and citrate for the optimal value of the tuning parameter are marked with large circles. Notice that citrate is not easily picked out on the left plot, but it is easily picked out on the right.

7.2 |. Log-ratio lasso

We next fit the single-stage logistic log-ratio lasso, which we have seen is equivalent to the constrained lasso of Lin et al. (2014). The log-ratio lasso results in 74% validation set accuracy. In Figure 4 we see that the lasso path from the single stage log-ratio lasso procedure. A researcher using this method would clearly see that the ratio of glucose to citrate is highly important, and we will soon see the two stage procedure easily picks this out as the most important feature.

Lastly, we fit the two-stage log-ratio lasso. The fitted model is remarkably simple:

$$\begin{gathered} y=0.24\log \left(x_{glucose}/x_{citrate}\right) \\ -0.09\log \left(x_{[gluc/fruct]Cl-}/x_{oleicaciddimer}\right). \end{gathered}$$

The first term is the log-ratio term from the oracle model previously reported in the literature: the logarithm of glucose divided by citrate. In addition to being highly parsimonious, the predictive performance of the model is close to that of the oracle model, and much better than that of the baseline methods, see Table 1. Figure 5 shows that the predictions from the log-ratio lasso on the validation set. The two-stage log-ratio lasso procedure nicely separate the two classes, and the ROC curve shows that the predictive performance is much better for any choice of the false positive rate. The model rivals that of the oracle model in both model parsimony and predictive accuracy. It is highly appealing the log-ratio lasso is able to systematically find such a model fit without requiring prior information.

FIGURE 5.

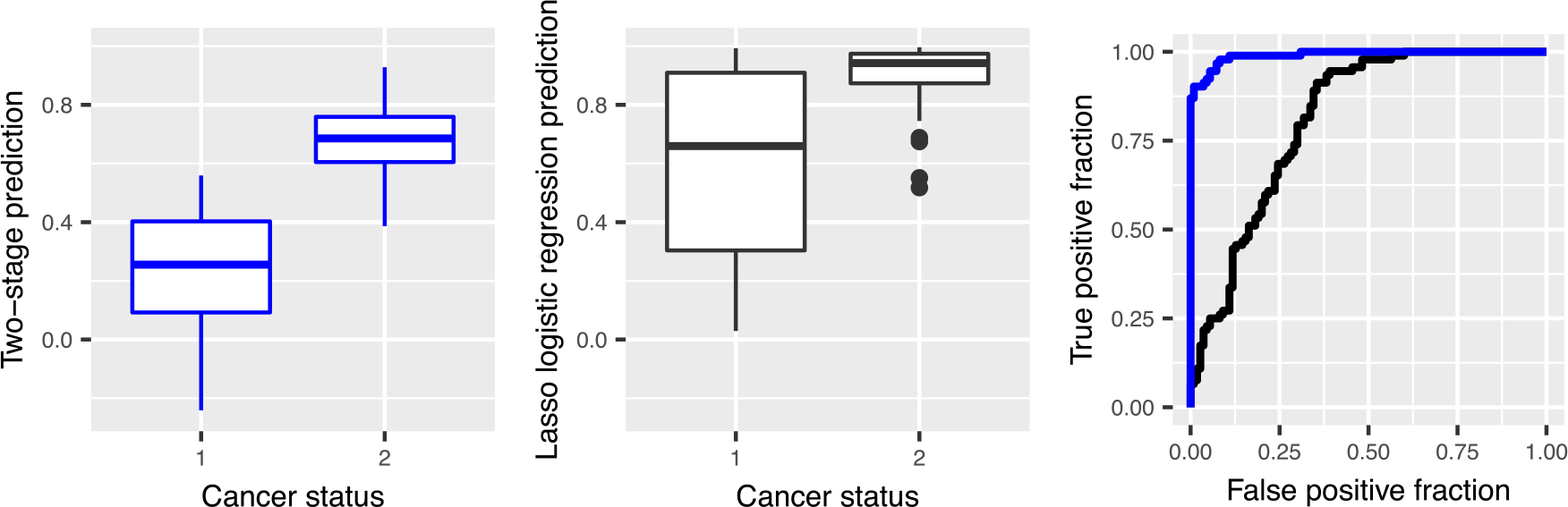
A comparison of the predictions on a validation set generated by lasso logistic regression (black) and two-stage log-ratio lasso (blue) using box plots and ROC curves. The AUC is 0.81 for lasso logistic regression and 0.99 for two-stage log-ratio lasso.

8 |. DISCUSSION

We have formulated a new and useful notion of sparsity for compositional data based on the all-pairs log-ratio model (1). We have introduced a novel, principled variable selection procedure for this model. We proved the equivalence of our method to a constrained lasso problem with a small number of variables. To the best of our knowledge, there are no existing specialized variable selection procedures for this model, and the naïve application of standard techniques would require the creation of $\left(\begin{array}{l}p\hfill \\ 2\hfill \end{array}\right)$ additional features, which quickly makes the runtime and storage requirements prohibitively large. In contrast, the method introduced in this work only requires solving a modified lasso optimization with p features, which enjoys favorable runtime and storage even for very large p. We extend this method with a second pruning step which leads to highly sparse models and greatly improves the performance in simulation experiments and on a real data set. On real data, the method recovers a very sparse model containing features of known relevance and with high predictive accuracy. The method appears to be very well-suited for imaging data in biological and medical domains, where the relative intensity of the raw features are the scientifically meaningful quantities, and where researchers are often jointly interested in predictive accuracy and model parsimony.

Unlike previous approaches to variable selection in compositional models, our approach deals directly with all pairwise log-ratios. Shi et al. (2016) and Wang and Zhao (2017) were also interested in creating small groups of log-constrasts, but the authors take a different approach, relying on known prior structure to group the predictors. In many interesting cases such as our proteomics example, prior knowledge of the groups of features is not available. Rather than using prior knowledge, our proposed method finds a highly sparse collection of pairwise log-ratio features.

We conclude by pointing to a few directions for further work.

• Extensions beyond the linear model. In Section 3, we mentioned that the low-dimensional characterization of the log-ratio lasso holds for other models such as GLMs and the Cox model. Extending the proposed methodology to these cases would be of interest.

• Combining compositional and non-compositional features. This work only addressed the case with only compositional features. In many applications the practitioner may have a combination of compositional features and non-compositional features, so extending the techniques of this work to the mixed setting would be desirable.

• Selective inference. Methods for post-selective confidence intervals have recently been introduced. Similar techniques can likely be used to develop post-selective confidence intervals for both the single-stage and two-stage log-ratio lasso estimator.