Brain-wide neural co-activations in resting human

Abstract

Spontaneous neural activity in human as assessed with resting-state functional magnetic resonance imaging (fMRI) exhibits brain-wide coordinated patterns in the frequency of < 0.1 Hz. However, understanding of fast brain-wide networks at the timescales of neuronal events (milliseconds to sub-seconds) and their spatial, spectral, and transitional characteristics remain limited due to the temporal constraints of hemodynamic signals. With milli-second resolution and whole-head coverage, scalp-based electroencephalography (EEG) provides a unique window into brain-wide networks with neuronal-timescale dynamics, shedding light on the organizing principles of brain functions. Using the state-of-the-art signal processing techniques, we reconstructed cortical neural tomography from resting-state EEG and extracted component-based co-activation patterns (cCAPs). These cCAPs revealed brain-wide intrinsic networks and their dynamics, indicating the configuration/reconfiguration of resting human brains into recurring and transitional functional states, which are featured with the prominent spatial phenomena of global patterns and anti-state pairs of co-(de)activations. Rich oscillational structures across a wide frequency band (i.e., 0.6 Hz, 5 Hz, and 10 Hz) were embedded in the nonstationary dynamics of these functional states. We further identified a superstructure that regulated between-state immediate and long-range transitions involving the entire set of identified cCAPs and governed a significant aspect of brain-wide network dynamics. These findings demonstrated how resting-state EEG data can be functionally decomposed using cCAPs to reveal rich dynamic structures of brain-wide human neural activations.

1. Introduction

Spontaneous fluctuations are a hallmark of neural signals, which have been observed in electrophysiological (Leopold et al., 2003; Hipp et al., 2012), hemodynamic (Biswal et al., 1995; Fox et al., 2005), and optical imaging studies (Arieli et al., 1996), in various species under different behavioral conditions (Fox et al., 2006; Larson-Prior et al., 2009). These spontaneous fluctuations exhibit inter-regional functional connectivity at multiple spatial scales ranging from function-specific resting state networks (RSNs) (Smith et al., 2009) to functional network connectivity (FNC) (Allen et al., 2014) to whole-brain networked activities (Yousefi et al., 2018; Raut et al., 2020; Takeda et al., 2021) defining a collection of distinctly structured brain-wide patterns. Spatial and dynamic structures of these brain-wide intrinsic networks have been observed with abnormalities in almost all major neuropsychiatric disorders (Greicius 2008), indicating their significant clinical value.

Brain-wide functional networks have been predominantly probed through noninvasive measurement of spontaneous hemodynamic signals using functional magnetic resonance imaging (fMRI) (Fox and Raichle 2007; Logothetis 2008). It has been assumed that inter-regional correlations observed in hemodynamic signals, reflecting spatial organizations of brain-wide intrinsic networks and their state-dependent changes, are converted from coordinated large-scale spatiotemporal dynamics of spontaneous neural activity via neurovascular coupling (Logothetis et al., 2001; Shmuel and Leopold 2008). Numerous studies have reported the linkage between individual fMRI RSNs and electroencephalography (EEG) oscillations (Sadaghiani et al., 2022), e.g., the attention network with EEG alpha power and the default mode network with EEG beta power (Laufs et al., 2003). More recently, all major RSNs reported previously with fMRI data have been independently identified in magnetoencephalography (MEG) (Brookes et al., 2011) and EEG data (Britz et al., 2010; Yuan et al., 2016), which show spatial similarities to fMRI RSNs. Simultaneous EEG-fMRI studies have further demonstrated strong temporal correlations between corresponding RSNs revealed in EEG and fMRI beyond their spatial similarities (Yuan et al., 2016). While the evidence of neural origins for fMRI RSNs are accumulating, the knowledge of neural underpinnings for more brain-wide functional networks, e.g., FNC and whole-brain networks, are scarce, especially in human. To date, multiple heterogeneous dynamics of large-scale spontaneous neural networks have been reported in animals using optical imaging (Huang et al., 2010; Stroh et al., 2013) and neurophysiological studies (Steriade et al., 1993; Luczak et al., 2007), based on observations of propagational patterns from recordings of limited spatial coverage, i.e., restricted imaging areas (Ferezou et al., 2007; Stroh et al., 2013) and/or a few selected but largely-separated recording sites (Crunelli and Hughes 2010). In human, a scalp-based EEG study has suggested a long-range anteroposterior propagation (Massimini et al., 2004). These studies, while indirect and limited, attest to the existence of brain-wide neural networks, beyond RSNs, in humans that underlie brain-wide hemodynamic networks. More importantly, while brain networks may be best defined spatially by fMRI in terms of their anatomy, to investigate their temporal organization patterns, it requires high temporal resolution data such as EEG or MEG (e.g., 1000 Hz) over fMRI (~1 Hz).

The gap between brain-wide neural and hemodynamic networks is intrinsically tied to the difference between neuronal and vascular structures. It is largely unknown how observed large-scale heterogeneous dynamics among neurons, e.g., traveling wave (Massimini et al., 2004; Stroh et al., 2013) and spiral wave (Huang et al., 2010), are converted into the dynamics of vascular networks (Allen et al., 2014). Motivated to understand this gap, a strategy shift of fMRI data analysis from traditional correlation-based approaches to the ones integrating amplitudes has revealed several new brain-wide network patterns. This includes transient co-activation patterns (CAPs) (Liu and Duyn 2013; Karahanoglu and Van De Ville 2015; Liu et al., 2018; Gutierrez-Barragan et al., 2019) among a subset of anatomically connected cortical areas, i.e., a prominent feature similarly observed in hemodynamic correlation structures, and brain-wide propagational transitions (Mitra et al., 2015; Matsui et al., 2016; Gutierrez-Barragan et al., 2019), bridging more toward neuronal waves. A novel wide-field optical imaging study concurrently monitoring calcium signals reflecting neuronal spiking activity and hemodynamic signals in mice (Matsui et al., 2016) indicates that transient neural CAPs, representing instantaneous brain states, are embedded in brain-wide propagations, characterizing dynamic transitions among various brain states. This observation suggests that these two new brain-wide patterns are associated, and brain-wide transitions might play a critical role in formulating hemodynamic correlation structures of brain-wide patterns.

Currently, optical imaging systems sensitive to neural activities cannot effectively penetrate human skulls (Grienberger and Konnerth 2012), preventing human studies from directly reporting and visualizing cortical-level brain-wide coordinated neural electrical phenomena and dynamics. The present study was conducted to identify such patterns on the human cortex from classical EEG data using an advanced computational framework developed based on the state-of-the-art signal processing techniques. Our data indicate that brain-wide CAPs could be probed from high-density scalp-based EEG data, and their cortical constructs could be directly visualized in the form of reconstructed tomographies. Our data further indicate rich dynamic structures in identified brain states, i.e., CAPs, at multiple time scales, including recurring, transitional, and oscillatory patterns. Finally, we report a superstructure involving all identified brain states that regulates between-state spatial, temporal, and transitional relationships and leads to the characteristic long-range transitional patterns coordinated by a pair of global co-(de)activation brain states identified in all individuals.

2. Methods

2.1. Dataset and preprocessing

The experiment of the main dataset was approved by the Institutional Review Board at the University of Oklahoma Health Science Center (OUHSC), and written informed consents were obtained from all healthy participants. Resting-state EEG data (Dataset 0: 10 min long, n = 34, 10 females, age: 24±5 years) with eye-closed were recorded at a sample frequency of 1000 Hz using the 128-channel Amps 300 amplifier (Electrical Geodesics Inc., OR, USA). No sleep was noted as monitored by experimenters and/or reported by participants. Structural MRI was collected for each participant on a GE MR750 scanner at OUHSC MRI facility, using GE’s “BRAVO” sequence: FOV = 240 mm, axial slices per slab = 180, slice thickness = 1 mm, image matrix = 256 × 256, TR/TE = 8.45/3.24 ms. In addition, EEG sensor positions and three landmark fiducial locations (i.e., nasion, left and right pre-auricular points) were digitized by the Polhemus Patriot system. Two other datasets (see details in Supplementary Note 1) from healthy participants of our previous studies were included to validate the findings from Dataset 0. Briefly, dataset 1 (Shou et al., 2017) had eye-closed resting-state EEG data (5 min long, 128 channels, and sampled at 512 Hz; n = 19, 13 females, age: 13±6 years) and no individual structural MRI, where age-appropriate MRI templates were used (Richards et al., 2016). Dataset 2 (Ding et al., 2014) had eye-closed resting-state EEG data (5 min long, 126 channels, and sampled at 1000 Hz; n = 20, all females, age: 49±7 years) and individual structural MRI data. These three datasets exhibited a significant age difference across groups (F₍₂₎ = 208, p < 1e-6). All three EEG datasets were first filtered by a notch filter at 58 to 62 Hz and a band-pass filter at 0.5–100 Hz. Noisy channels interpolation and ICs removal related to ocular, muscular and cardiac activities were conducted using the EEGLAB toolbox (Delorme and Makeig 2004). Finally, EEG data were down-sampled to 250 Hz and re-referenced to the common average. It is noted that no EEG segments were rejected to maintain the continuity of data for subsequent dynamic analysis.

2.2. Cortical source imaging: cortical current tomography

Cortical source imaging was performed individually to reconstruct cortical sources from scalp-level EEG signals (Fig. 1A). FreeSurfer (Fischl 2012) was used to segment individual MRI data to extract the surfaces of the scalp, skull, and brain for volume conduction model, and the interface between white and gray matters for cortical current density (CCD) source model. The surfaces of volume conduction model were each tessellated into triangular elements of 10,242 nodes and 20,480 triangles, while the surface of the CCD model was tessellated into triangular elements of 20,484 nodes and 40,960 triangles. On the CCD model, the nodes on the medial wall adjoining the corpus callosum, basal forebrain, and hippocampus were excluded, and the total number of source nodes was reduced to 18,715. Each of these nodes was assigned with a dipole with its orientation set as the normalized vector sum of the normal directions of all triangles sharing the node. The electrical conductivities of the scalp, skull, and brain were assigned as 0.33/Ωm, 0.0165/Ωm, and 0.33/Ωm, respectively. EEG sensor locations were registered on the scalp surface by aligning three landmark fiducial points from both EEG and MRI recordings. Based on these models, the boundary element method (Hamalainen and Sarvas 1989) was used to build the forward relationship: Φ(t) = L·S (t), where L is the lead field matrix; Φ(t) and S(t) are functions of time for scalp EEGs and dipole amplitudes, respectively. The minimum-norm estimate (Hamalainen and Ilmoniemi 1994) was used to reconstruct dipole amplitudes on the cortical surface: S(t) = L^T ·(L·L ^T + λ·I)⁻¹ ·Φ(t), where λ was the regularization parameter and selected via the generalized cross validation method (Golub et al., 1979) and I was the identity matrix. To control the quality of reconstructed cortical sources, the selected λ values beyond three standard deviations of all values in each participant were considered as outliers and interpolated with the neighboring ones. Based on these adjusted λ values, cortical current tomography was reconstructed as a function of time for each participant for subsequent analysis.

Fig. 1.

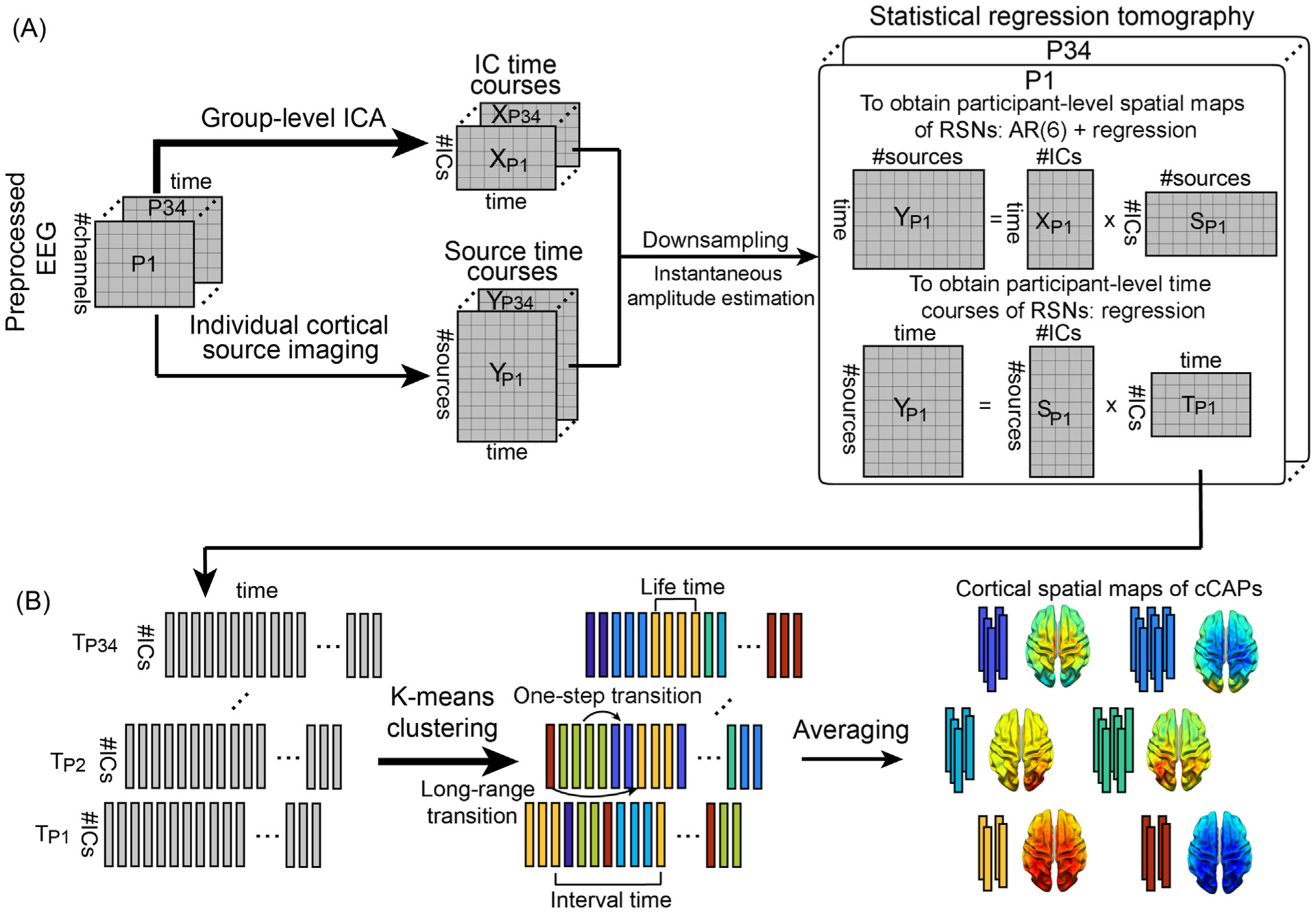
Schematic illustration of the method. (A) Spatial definitions of cortical RSNs and their dynamics calculated using a statistical dual-regression analysis between the instantaneous amplitudes of sensor-level IC time courses and cortical-level source time courses. IC time courses are calculated from a group-level ICA on preprocessed EEG data temporally concatenated across all participants. Cortical source time courses are calculated by cortical source imaging from EEG and MRI data of individual participants. (B) Recurring brain states and their dynamic transitions captured and classified by clustering timeframe data of cortical RSNs into short-lived spatially congruent patterns (i.e., cCAPs) using the k-means algorithm. Four temporal and transitional measures, i.e., lifetime, interval time, one-step transition, and long-range transition, are illustrated. P: participant; T: timecourse.

2.3. Group-level ICA: scalp-level representations of RSNs

A group-level ICA was used to decompose preprocessed scalp EEG data into multiple ICs (Ding et al., 2014; Shou et al., 2017). Briefly, individual EEG data were normalized to z values and temporally concatenated. A short-time Fourier transform was then performed on segmented 1-s epoch data without overlap to obtain time-frequency representations of EEG data on channels, which were the input for the time-frequency ICA model (Bingham and Hyvarinen 2000; Shou et al., 2012). The Fourier transform modulated rhythmic neural activities that were usually Gaussian distributed into more super-Gaussian to be better detected from artifacts (Bingham and Hyvarinen 2000; Shou et al., 2012). Here, the Fourier spectrum data were selected in the range of 1 to 100 Hz at a resolution of 1 Hz, which were individually normalized to account for the 1/f distribution over the spectrum. The ICA model was run for each model order from 25 to 64 with 64 finally being selected as the order of the ICA model for subsequent analyses, as it gave the best spatial patterns in identifying major RSNs. To obtain IC time courses, original EEG data were projected using the demixing matrix calculated from the group-level ICA. Thereafter, ICs showing neural activation characteristics in both of their spatial and spectral patterns, as compared to the ones reported in the literature (Brookes et al., 2011; Shou et al., 2012; Yuan et al., 2016; Shou et al., 2020), were selected as the scalp-level representations of cortical RSNs.

2.4. Statistical regression tomography: cortical representations of RSNs

For each participant, the cortical representation of each RSN was estimated via a statistical dual-regression analysis between time courses of individual cortical dipoles and the time courses of the selected ICs (Fig. 1A). First, both time courses were down-sampled to 100 Hz and their instantaneous amplitudes (Sandoval and De Leon 2015) were calculated via the Hilbert transform (Baker et al., 2014; Coquelet et al., 2022). Second, to obtain cortical maps of RSNs, the first regression was performed with amplitude time courses of all selected ICs as the regressors and amplitude time courses of individual cortical dipoles as the response data. Considering highly autocorrelated nature of EEG signals (Nunez 1981), an autoregression (AR) model with the order of 6 was used to reduce the autocorrelation effect on regression, similar to the practice in reported fMRI studies (Woolrich et al., 2001). The order of the AR model was selected after testing three different values (i.e., 1, 6, and 15), which found that the AR (6) model could significantly reduce the autocorrelation effect to the similar level as the AR (15) model more than the AR (1) model. Third, the second regression was performed to reconstruct time courses of cortical RSNs with cortical RSN maps obtained from the first regression analysis as the regressors and timeframe-wise spatial maps of cortical dipoles as the response data. As a result, cortical tomographies of RSNs were defined with their corresponding spatial and temporal patterns in individuals.

2.5. Identifying component-based CAPs: a K-means clustering analysis

Time courses of cortical RSNs obtained above were subject to a K-means clustering analysis to identify distinct recurring patterns that were characterized by different levels of co-(de)activations among different ICs (Fig. 1B), which was termed as component-based CAPs (cCAPs). The clustering analysis was performed at the group level on matrix data, i.e., number of time points from all participants × number of RSNs. To account for different variances in different RSNs and participants, each time course was normalized as zero-mean and unit-variance per participant before the clustering analysis. In the clustering model, the L1-norm distance was used as the metric to measure the similarity among timeframe-wise data and, therefore, the co-activation here was defined on amplitudes (rather than temporal correlation) similar to reported fMRI CAP studies (Allen et al., 2014; Karahanoglu and Van De Ville 2015; Gutierrez-Barragan et al., 2019). After calculating the model order in a range from 2 to 20 for clustering, we chose the model order of 8 using the metrics of percentage of variance explained and average within-cluster sum of squares (see Supplementary Fig. 2) to report our results. We further examined the spatial patterns of cCAPs obtained for the model orders between 6 and 10, which were highly similar (Supplementary Fig. 2C). The output of the clustering analysis labeled each timeframe data of cortical RSNs to a unique cCAP (Fig. 1B). Thereafter, the cluster centers of individual cCAPs were obtained as the vectors of weights of selected RSNs via averaging original values of cortical RSN timeframe data (before normalization) with the same corresponding labels (Fig. 1B). The weights in these center vectors were further numerically ranked, i.e., from 1 to 8 in their absolute values, for each RSN across all eight cCAPs to illustrate relative activation levels of each RSN among all cCAPs. The distances between these center vectors were calculated and projected into a 3D space (Fig. 2C) using a multidimensional scaling tool from MATLAB (i.e., cmdscale.m) to examine the spatial relationship among all cCAPs. Finally, the cortical tomography of each cCAP was built for individual participants as the weighted sum of cortical tomographies of RSNs from individual participants with the corresponding center vector (Fig. 1B). Using the same means, cortical tomographies of all cCAPs at each timeframe were similarly reconstructed with instantaneous weights of RSNs from their time courses (Fig. 5 and Supplementary Movies 1–4).

Fig. 2.

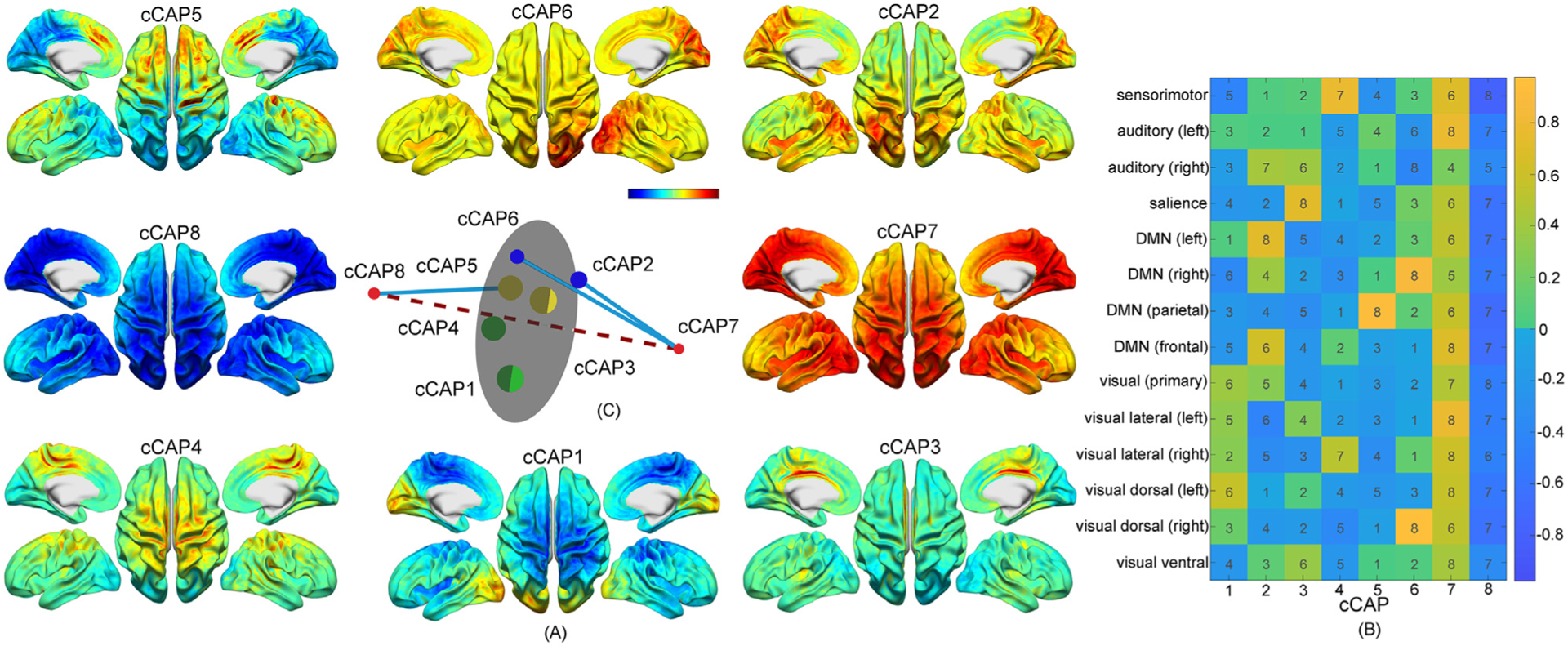
A set of spatially-structured functional states with brain-wide patterns, i.e., cCAPs, from the resting human brain. (A) Cortical maps of the cCAPs identified at the group level in which both cCAPs 7 and 8 show global co-(de)activation patterns. Red-yellow colors indicate co-activations (i.e., high neuronal currents), and blue indicates co-deactivations (i.e., low neuronal currents). (B) The weight vectors, i.e., columns, of the cluster centers of all cCAPs. Colors indicate weight amplitudes (with±signs) of individual RSNs at the cluster centers of cCAPs and numbers indicates the amplitude ranks (no signs) of same individual RSNs across all cCAPs. DMN: Default mode network. (C) The distance map of the weight vectors of all cCAPs projected into a 3D space. Same-color dots: anti-state pairs and hemisphere-symmetric pair; red dots: two polarized states, i.e., cCAPs 7 and 8, connected by the dashed line; blue lines: connecting brain states that are structurally closest to two polarized states (see more in Supplementary Fig. 3A); gray circular plane: halfway between two polarized states.

Fig. 5.

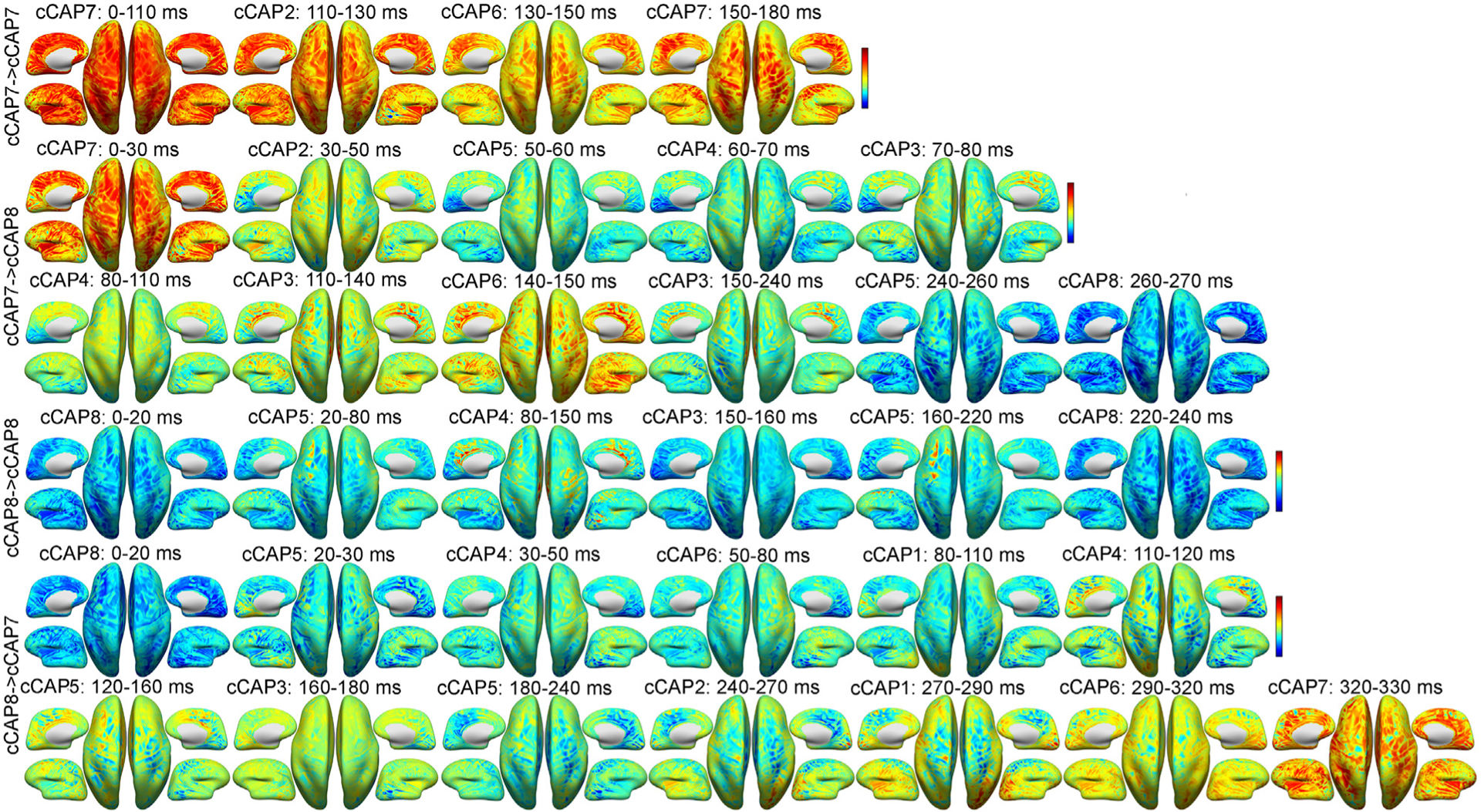
Representative occurrences for two long-range transitions and two reference transitions between two polarized functional brain states (Fig. 2) on the inflated cortical surface from a participant: cCAP 7→7, cCAP 7→8, cCAP 8→8 and cCAP 8→7. Each map represents the averaged cortical pattern of an occurred cCAP over all timeframes within its lifetime window (labeled above) during the sequenced transition. See Supplementary Movies 1–4 for corresponding videos in continuous timeframes.

2.6. Temporal metrics of cCAPs

Multiple temporal metrics (Fig. 1B) were calculated on data from individuals and then summarized to generate group-level statistics, e.g., means, standard deviations, and histograms. The metric of lifetime was defined as the duration of each occurrence of a cCAP. A transition happened when two neighboring timeframes were labeled with different cCAPs. The interval time of a cCAP was defined as the time difference between its two consecutive occurrences from the end of the early one to the beginning of the late one. To probe temporal long-scale relationship between the occurrences among all eight cCAPs, an alignment analysis was developed, where one cCAP was selected as a reference cCAP and then the occurrence probabilities of all cCAPs at certain distances in the time axis were calculated with respect to the reference cCAP. Specifically, the epochs of all occurrences of the reference cCAP were extracted with 5 s before the start of and 5 s after the end of an occurrence. Within the total 10 s for each epoch, the occurrences of all eight cCAPs at each time instant were calculated in individual participants and then divided by the total number of epochs to obtain their occurring probabilities, each presented as a function of time centered toward the reference cCAP (see Fig. 3D).

Fig. 3.

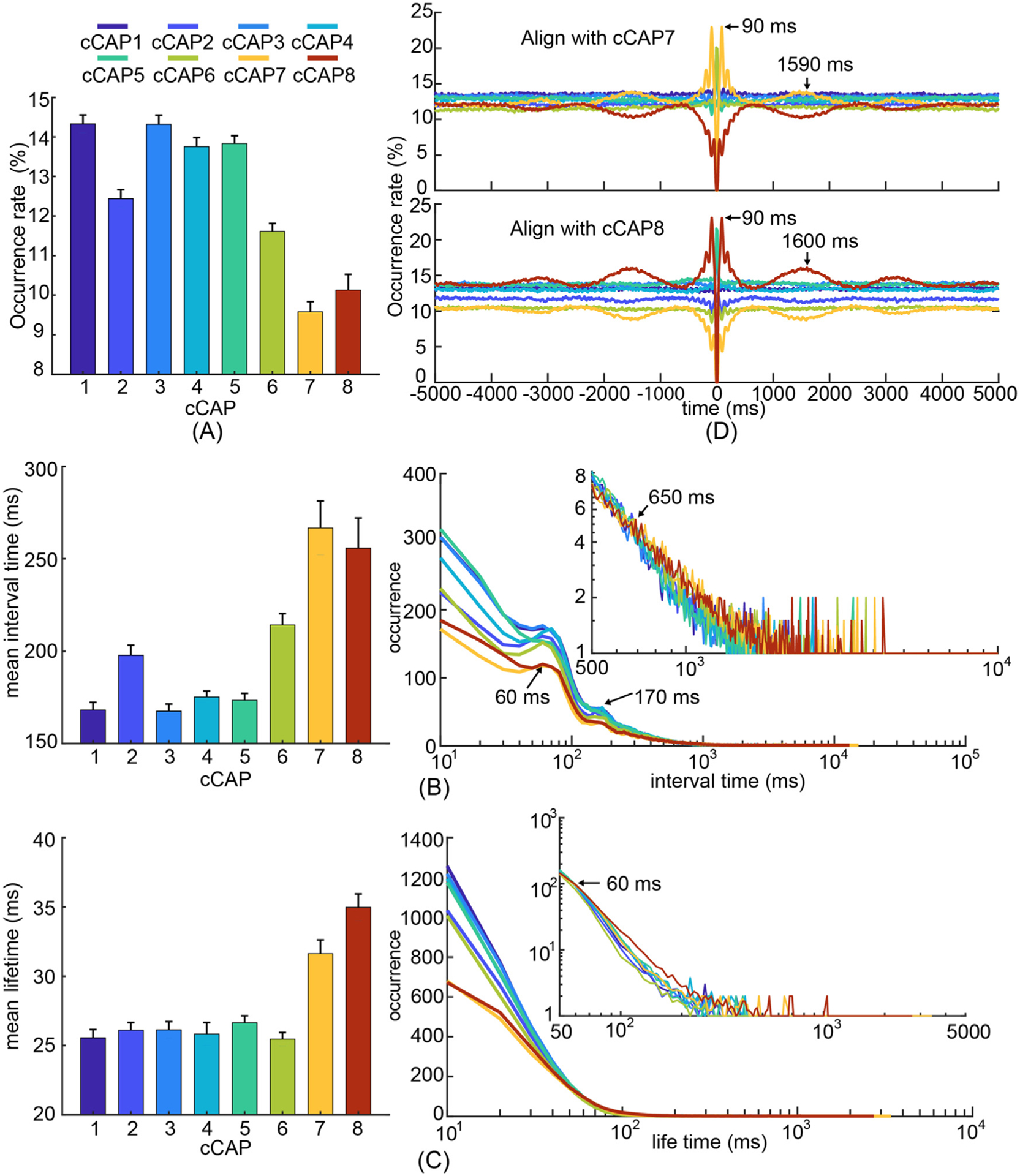
Temporal characteristics of recurring functional brain states, i.e., cCAPs. (A) Occurrence rates of cCAPs (mean±SEM) where cCAPs 7 and 8 show significantly lower occurrences than others (p < 0.05, FDR corrected). (B) Mean (±SEM) values (left) and histograms (right) of interval times of cCAPs. Note that cCAPs 7 and 8 have significantly longer mean interval time than others (p < 0.05, FDR corrected). All histograms show two peaks (around 60 ms and 170 ms) and the occurrences of cCAPs 7 and 8 become higher than other cCAPs beyond the interval time of 650 ms (the inset). (C) Mean (±SEM) values (left) and histograms (right) of lifetimes of cCAPs. Note that cCAPs 7 and 8 have significantly longer mean lifetime than others (p < 0.05, FDR corrected). The occurrences of cCAPs 7 and 8 become higher than other cCAPs beyond the lifetime of 60 ms (the inset). (D) Occurrence probabilities of all cCAPs as functions of time distances toward all occurrences of the target cCAP 7 (top) and cCAP 8 (bottom). See other cCAPs as the target cCAP in Supplementary Figs. 5B–C. SEM: standard error of mean.

2.7. Transitional patterns among cCAPs

To investigate the transition structures among cCAPs, two analyses focusing on different time scales were performed on individual participant data. First, one-step transition probabilities of a cCAP (at time t) to other cCAPs (at time t + 1) defined as the numbers of transitions from the cCAP to other cCAPs (i.e., outflow) or from other cCAPs to the cCAP (i.e., inflow), divided by the total number of occurrences of the cCAP. These probability data were used to form the outflow/inflow matrices with the current cCAP state at time t in the vertical direction and the next cCAP state at time t + 1 in the horizontal direction, in which the entries in any row of the outflow matrices summed to one and the entries in any column of the inflow matrices summed to one, known as percentage outflow/inflow rates of cCAPs (see Fig. 4). Second, we studied the transitions between two polarized brain states (i.e., cCAPs 7 & 8), which exhibit distinct spatial, temporal, and transitional patterns as compared to all other cCAPs (see Figs. 2–4). The 3D distance map (Fig. 2C) further indicates that cCAPs 7 & 8 represent two polarized brain states on the opposite boundary of the entire repertoire of brain states identified in the present study. Therefore, the events of visiting one polarized brain state (e.g., cCAP 7) after visiting another (then cCAP 8) and vice versa via other non-polarized brain states (from cCAP 1 to cCAP 6) were of investigational interests, termed as the long-range transitions and noted as cCAP 7→8 and cCAP 8→7, respectively. Multiple temporal metrics were calculated on long-range transition data per participant and statistically compared using repeated measures ANOVA (rmANOVA) and t-test when appliable (Fig. 6) with all participants as metric data samples. These temporal metrics include occurrences (Fig. 6A), means and histograms of transition durations in continuous timeframes (Fig. 6B), numeric counts of total non-polarized cCAPs visited (counting repeated visits) and different non-polarized cCAPs visited (not counting repeated visits) during long-range transitions (Fig. 6C), and occurrence rate histograms of two types of transitions (i.e., cCAP 7→8 and cCAP 8→7) as a function of number of different cCAPs visited (Fig. 6C). To study the roles of the six non-polarized cCAPs in each type of long-range transitions, we calculated the occurrence rates of the transitions with the visit to a specific non-polarized cCAP (i.e., cCAPs 1–6) out of total number of the same-type long-range transitions (Fig. 6D). We also broke down total occurrence data according to the number of different non-polarized cCAPs visited in each type of long-range transitions and calculated the occurrence rates of the transitions involving a specific non-polarized cCAP at different numeric counts of brain states visited during each type of long-range transitions (Fig. 6E). After that, two reference transitions (i.e., cCAP 7→7 and cCAP 8→8) involving cCAP 7 or 8 only (i.e., successive visits of one of two polarized states without visiting another) were introduced and their temporal metrics were assessed similarly. Note that these two reference transitions were not the long-range transitions defined in the present study, but their temporal metric values were used as references to evaluate distinct patterns of the same metric values from two long-range transitions. To investigate whether the long-range transition patterns coordinated by cCAPs 7 and 8 were unique, similar long-range transitions and reference transitions based on two pseudo-polarized states made by all other possible pairs (total 27 pairs) of the eight cCAPs were examined and all above-mentioned calculations were repeated. Unless specified, p values were corrected by Bonferroni method.

Fig. 4.

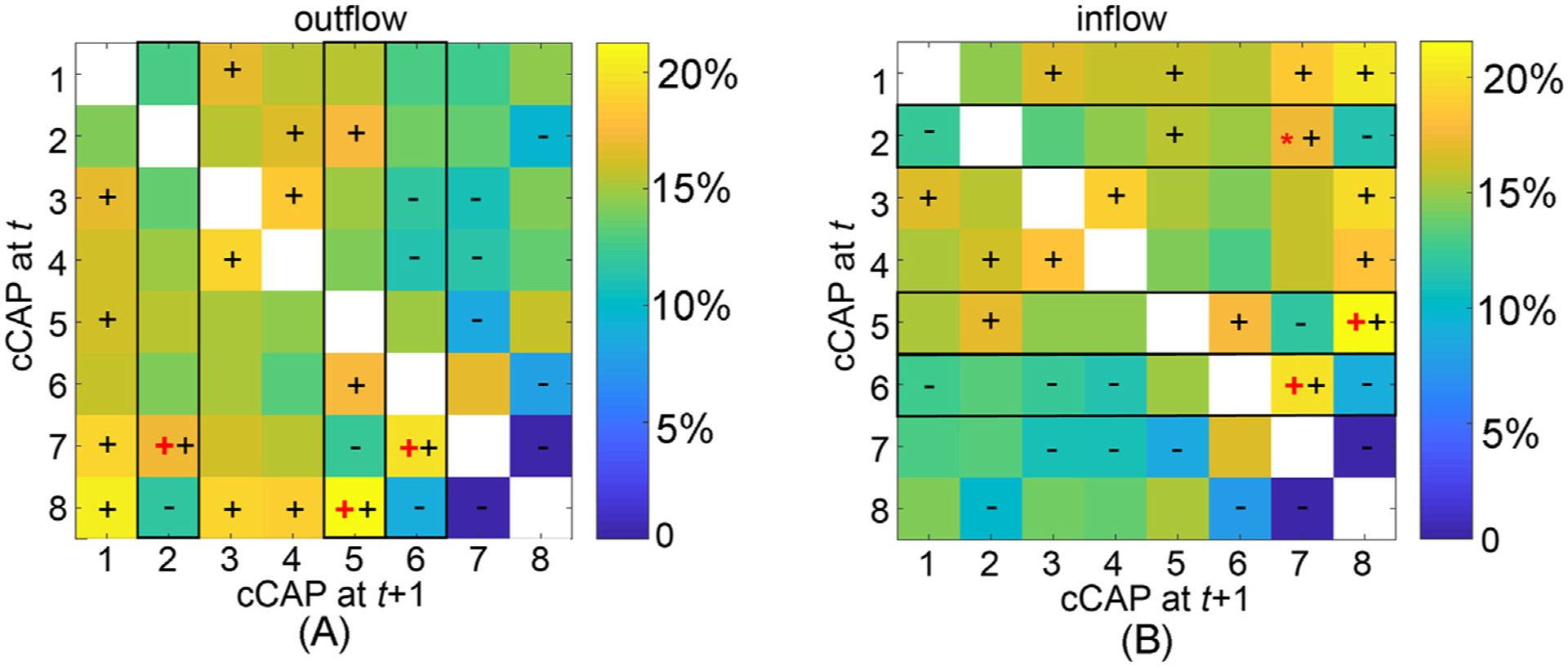
The immediate transition probability (one-step from time t to time t + 1) among functional brain states: (A) the outflow matrix (normalized in rows) and (B) the inflow matrix (normalized in columns). The signs ‘+’ and ‘−’denote significantly higher or lower transition probability values, respectively, than the equal probability value (i.e., 1/7, p < 0.05, Bonferroni adjusted). The black rectangles highlight the columns (in A) and rows (in B), in which the cCAPs with the largest outflow or inflow values that are significantly higher than the second largest values are labeled (‘+’: p < 0.001, Bonferroni adjusted, ‘*’: p < 0.05, unadjusted). These identified cCAPs (labeled as ‘+’ or ‘*’) appear only to be the ones that are spatially close to two polarized states (Fig. 2C).

Fig. 6.

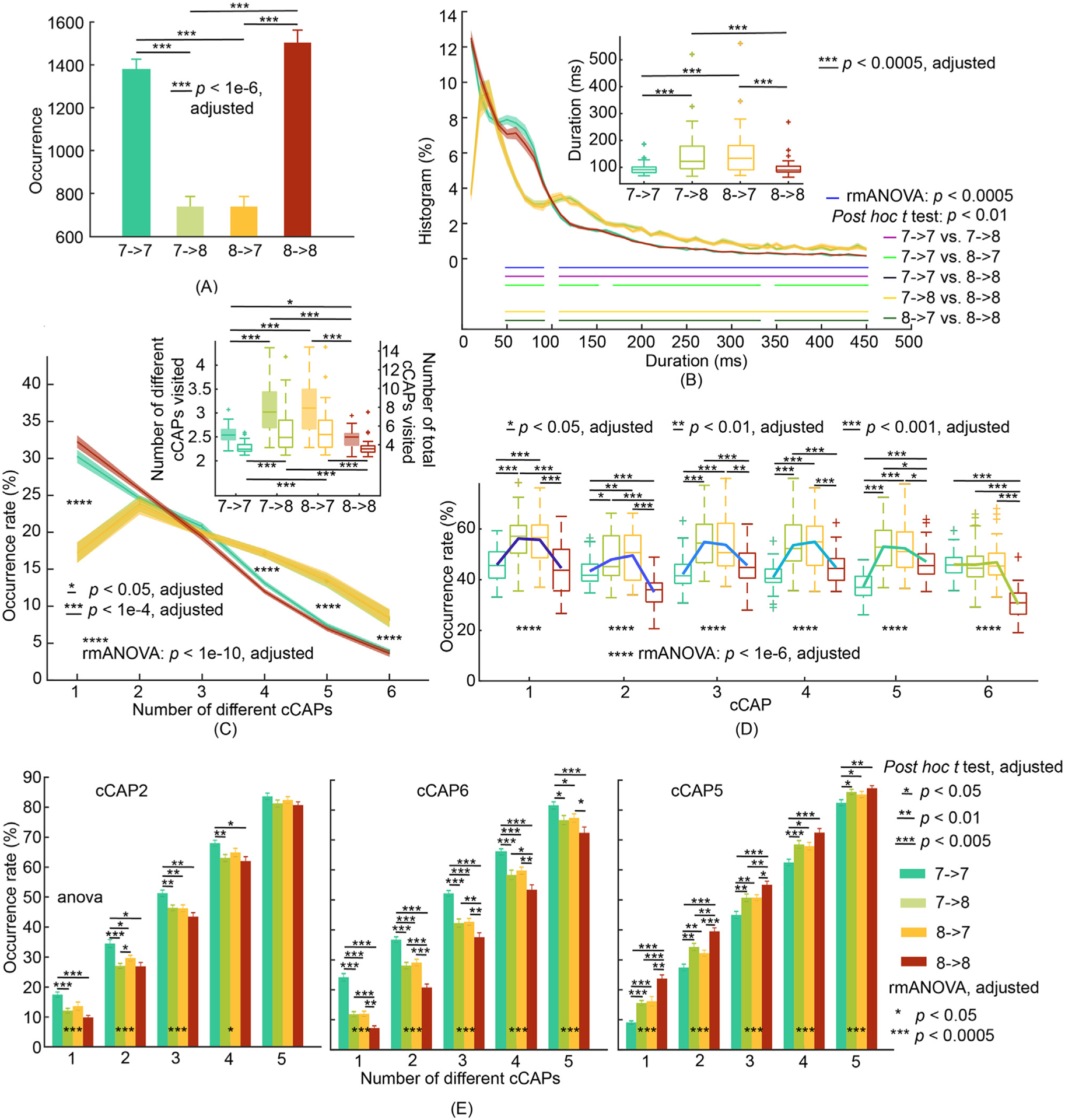
Patterns of transitions between two polarized functional brain states of cCAPs 7 and 8. (A) Occurrences of two long-range transitions: cCAP 7→8 and cCAP 8→7, and two reference transitions: cCAP 7→7 and cCAP 8→8. (B) Boxplots (inset) of mean durations and histograms of durations (SEM: shaded areas) as functions of time for four types of transitions. (C) Occurrence rates of four types of transitions (SEM: shaded areas) as functions of the number of different cCAPs (the six non-polarized cCAPs) visited per occurrence. Inset: Participant-level means (±SEM) of numbers of different cCAPs (left y-axis and boxplots with solid-fills) and total numbers of cCAPs (right y-axis and boxplots with no-fills) visited per occurrence. Post-hoc t tests indicate significant differences (p < 0.01, adjusted) when the number of different cCAPs equals to 1, 4, 5, and 6 between two long-range transitions and two reference transitions. (D) Occurrence rates of the six non-polarized cCAPs within each type of transition. (E) Occurrence rates of cCAPs 2, 6 and 5 within each type of transition as functions of number of different cCAPs visited per occurrence. See Supplementary Fig. 7 for cCAPs 1, 3, and 4. The condition of number of cCAPs as 6 is omitted since all occurrence rates are 100% by the definition of this metric.

3. Results

3.1. Brain-wide EEG component clustering analysis reveals a set of spatially-structured functional brain states

Using concatenated high-density EEG resting-state data from 34 participants (128 channels, sampled at 1000 Hz, Dataset 0), mapped onto participant-specific models of cortical surfaces from FREESURFER (Fischl 2012) by our newly developed computational framework (Fig. 1), we identified eight reproducible CAP patterns from EEG component signals (component-based CAPs, cCAPs, Fig. 2A), where these component signals have been related to the definitions of electrophysiological resting state networks (RSNs, Supplementary Fig. 1A) in previous studies (Brookes et al., 2011; Yuan et al., 2016; Shou et al., 2020). Essentially, this framework finds, in a completely data-driven way, recurrent states of networked activities (i.e., cCAPs) in human brains with structured spatiotemporal properties. Spatially, almost all cCAPs (with the exception of cCAP 3 relatively focusing on the cingulate cortex) suggest brain-wide patterns of co-(de)activations in both their cortical maps (Fig. 2A) and activity levels of involved RSNs (Fig. 2B and Supplementary Note 2). These facts indicate that identified cCAPs activate anatomically connected and functionally related neural substrates in the dynamic behaviors of the resting human brain. Two cCAPs (cCAPs 7 and 8) indicate global co-activation and co-deactivation patterns, respectively, as all RSNs reach their own top (or close to top) levels of positive or negative magnitude of activity, which are further supported by their cortical maps. Moreover, default mode networks (DMNs, Supplementary Fig. 1A) and task-positive networks (TPNs, RSNs other than DMNs) reveal opposite co-activation patterns where high-magnitude DMN activations are accompanied by relatively low-magnitude TPN activations in cCAPs 2, 5 and 6 (Fig. 2B) and vice versa in cCAPs 1, 3, and 4. As a notable feature of CAPs identified in fMRI, the configuration into anti-state pairs is characterized by opposing patterns of functional co-(de)activations (Gutierrez-Barragan et al., 2019). We conducted a sequential search for such pairs based on the metric of vectorized spatial correlation coefficients. Apart from the hemisphere-mirrored pair (cCAP 2–6), the anti-state characteristic is especially prominent in the cCAP 7–8 pair (r = −0.90±0.05), but also apparent in the cCAP 1–4 pair (r = −0.41±0.23) and the cCAP 3–5 pair (r = −0.27±0.18). The spatial distances among all eight cCAPs in the 3D space (see Methods) reveal a well-structured spatial relationship among the entire set of cCAPs (Fig. 2C), in which cCAPs 7 and 8 are positioned as two poles with the longest distance and the other six cCAPs are clustered halfway between them. Furthermore, cCAP 5 is significantly closer to cCAP 8 while both cCAPs 2 and 6 are significantly closer to cCAP 7 than other cCAPs (Supplementary Note 2). The vectorized spatial correlation coefficients of eight cCAPs between those identified in individual participants and the group-level ones indicate that these cCAPs can be reliably detected in individual participants (Supplementary Fig. 3C). In particular, cCAPs 7 and 8 have the highest spatial correlations (only two r > 0.5) (Supplementary Fig. 3B).

3.2. Recurring patterns of cCAPs support the spatial structure formulated by the set of brain states

We then investigated cCAP dynamics with the goal of finding evidence to support the observation of multi-level spatial structures formulated by the eight cCAPs. We report the occurrence rates of individual cCAPs that are within a range of 9% and 15% (Fig. 3A), close to the equal opportunity of occurrence (i.e., 12.5% for eight cCAPs). The lifetime of each cCAP occurrence was in the range between 25 and 35 milliseconds for mean values (Fig. 3C). Both data suggest all cCAPs are recurring states that can be reliably detected at both group and individual levels as their variabilities among individuals are low comparing with their group-level mean values, which are consistent with individually reproducible cCAP spatial patterns discussed above. The cCAPs 7–8 pair reveals significantly lower occurrence rate (p < 0.0005, FDR corrected), longer lifetime (p < 0.00005, FDR corrected), and longer interval time between successive occurrences (p < 0.005, FDR corrected) than all other cCAPs. The two anti-state pairs (cCAP 1–4 and cCAP 3–5) that are spatially close (Fig. 2C) share similar data for these temporal metrics. The hemisphere-mirrored cCAP pair (cCAP 2–6) have occurrence rates higher than the two polarized states (p < 0.005, FDR corrected) but lower than the four anti-states (p < 0.0005, FDR corrected). Their interval times are lower than the two polarized states (p < 0.05, FDR corrected) but higher than the four anti-states (p < 0.0005, FDR corrected). The lowest occurrence rates and longest interval times of cCAPs 7 and 8 are consistent with these two states being at the boundaries of distance maps (Fig. 2C), exhibiting low chances to be visited during between-state transitions (see Figs. 4 and 5). Other states are more likely to be visited since they are closer to each other. In summary, the consistencies observed between cCAP spatial and temporal patterns at three different levels, i.e., individual cCAPs, cCAP pairs, and the entire set of all eight cCAPs, suggest that these observations are manifested from the same underlying source, i.e., dynamically coordinated and networked brain-wide activations.

3.3. Individual cCAPs show intrinsic temporal dynamics and cCAPs 7–8 further indicate coordinated large-scale fluctuations

The histograms of cCAP interval times (Fig. 3B) exhibit two characteristic peaks (~10 Hz and ~5 Hz, Supplementary Note 2) on top of exponentially decreasing curves. The wide ranges of interval times illustrated in the decreasing curves indicate that the occurrences of these recurring brain states are nonstationary, while two peaks reveal weak but observable intrinsic dynamic rhythms in cCAPs. These are consistently detected in data from individual participants (Supplementary Fig. 4A). Note that the significantly longer interval times of cCAP 7–8 are achieved via having fewer short intervals and more long intervals (the inset, Fig. 3B) without lengthening the characteristic peaks. The same mechanism is also observed in cCAP 2–6 for their moderately but statistically significantly longer interval times (p < 0.0005, FDR corrected), as well as for longer lifetimes of cCAPs 7, 8, 2, and 6 (Fig. 3C). These observations suggest that both lifetimes and interval times of cCAPs are potentially modulated by some unrevealed mechanisms with longer temporal scales (Gutierrez-Barragan et al., 2019). To this end, we next examined long-scale temporal dynamics beyond interval times using an alignment analysis on occurrences of a target cCAP at different time distances toward all occurrences of a reference cCAP (see Methods). We observe two oscillatory phenomena elevated from the baseline of 12.5% (i.e., equal opportunity for eight cCAPs) that are exponentially decayed over the distance to the reference cCAP (Fig. 3D and Supplementary Fig. 5A). The short-scale oscillations have an inter-peak distance of ~100 ms, corresponding to the 10 Hz frequency component in Fig. 3B. The long-scale oscillations show an inter-peak distance of ~1.6 s, corresponding to a frequency of < 1 Hz. These elevated oscillatory phenomena could be reliably detected at both the group and individual participant levels (Supplementary Fig. 5B) but mainly when the target and reference cCAPs are same. One notable exception is the cCAPs 7–8 pair, in which elevated oscillations in one of them lead to symmetric but depressed oscillations in the other. This coordination between cCAPs 7 and 8, together with other data distinguishing them from the other cCAPs (Figs. 2 and 3A–C), suggests their important roles in modulating temporal dynamics of the resting human brain activity encoded in all cCAPs of brain-wide spatial patterns.

3.4. Immediate transition patterns across cCAPs support spatial structures formulated by cCAPs

We then moved on to study between-state transitions via firstly investigating one-step transitions among cCAPs. The outflow matrix indicates patterns of lower transitions from all cCAPs to cCAPs 7 and 8 (last two columns, Fig. 4A) than to the other 6 cCAPs. Similarly, the inflow matrix indicates lower transitions from cCAPs 7 and 8 to all other cCAPs (last two rows, Fig. 4B). More prominently, the immediate transitions between cCAP 7 and 8 for both outflow and inflow are almost zero (<0.5%). All these observations support cCAP 7/8 as a polarized state similarly suggested in their distance maps and recurring patterns (Figs. 2–3). To find which one(s) from other six cCAPs have more immediate transitions to cCAP 7/8, percentage outflow rates (i.e., elements of a column, Fig. 4A) and percentage inflow rates (i.e., elements of a row, Fig. 4B) for each of these six cCAPs were compared, respectively, as actual outflow/inflow data biased by their occurrence rates (Fig. 3). cCAPs 2 and 6 show the maximal and significantly higher (as compared with the corresponding second largest) outflow rates (9% and 23% larger, respectively, both p < 0.05, corrected) and inflow rates (14%, p < 0.05, and 41% larger, p < 0.05, corrected, respectively) towards cCAP 7. cCAP 5 shows the maximal and significantly higher outflow rates (15% larger, p < 0.05, corrected) and inflow rates (24% larger, p < 0.05, corrected) towards cCAP 8. All other three cCAPs (i.e., 1, 3, and 4) show no significant differences between the largest and second largest outflow/inflow rates. These observations are consistent with the distance map (Supplementary Note 2) where cCAPs 2/6 are closest to cCAP 7 and cCAP 5 is closest to cCAP 8.

3.5. Unique characteristic patterns in long-range transitions between global co-activation and co-deactivation states

Driven by the observations in above results about the existence of large-scale spatial (Fig. 2C) and temporal structures (Fig. 3D and Supplementary Fig. 5A) among the entire set of CAPs, we further investigated large-scale dynamics of transitional structures, beyond a pair of CAPs (Fig. 4), involving the entire set of CAPs. When visually inspecting movies of spontaneous cCAPs (Supplementary Movies 1–4 in continuous timeframes), we noticed that the long-range transitions usually took longer times and visited more non-polarized brain states (as well as more different non-polarized brain states) than the reference transitions. Quantitatively, we observe that the long-range transitions between cCAPs 7 and 8 occur significantly lower (>85% lower, p < 1e-6, corrected, Fig. 6A), take about 1.6 times longer (p < 0.0005, corrected, the inset in Fig. 6B), and visit over 1.2 times more states (p < 1e-4, corrected, the inset in Fig. 6C) than the reference transitions (see more in Supplementary Note 3). The breakdown data according to the transition duration (Fig. 6B) showed exponential decreasing patterns for both long-range and reference transitions and more occurrences of cCAP 8→7 and 7→8 for the durations over 100 ms (post-hoc t tests: p < 0.01 and consecutive durations>5), and less occurrences for the durations below 100 ms than the reference transitions (post-hoc t tests: p < 0.01 and consecutive durations>5). A characteristic peak for both cCAP 8→7 and 7→8 appears around this point of separation (i.e., 100 ms) indicating that the shift towards longer durations is needed in order to visit more brain states (the inset in Fig. 6C). The extremely low short-duration transitions (i.e., 10 ms and 20 ms) in cCAP 8→7 and 7→8 is consistent with the largest distance (Fig. 2) and almost zero one-step transitions (Fig. 4) between cCAPs 7 and 8.

It is further suggested that the long-range transitions between cCAPs 7 and 8 not only visit more other states, but also visit more different states (Fig. 6C). Percentage-wise, significantly more cCAP 8→7 and 7→8 than the reference transitions (rmANOVA: p < 1e-10, corrected; post-hoc t tests: p < 0.001, corrected) happen when the numbers of different states visited are high (i.e., 4, 5, and 6). When only one other state is visited, significantly less cCAP 8→7 and 7→8 (p < 1e-10, corrected) happen than the reference transitions. We further studied the occurrence rates of other six non-polarized cCAPs in these four transitions (Fig. 6D). It appears that these six cCAPs are visited significantly more during most long-range transitions than the reference transitions (p < 0.01, corrected). Moreover, cCAPs 1, 3, and 4 show similar occurrences between two reference transitions, while cCAPs 2, 5, and 6 show different patterns. High occurrences of cCAP 2/6 during cCAP 8→8 and cCAP 5 during cCAP 7→7 once again confirm the affinities of cCAP 2/6 toward cCAP 8 and cCAP 5 towards cCAP 7 as in Figs. 2–4. On the other hand, significantly lowered occurrences of cCAP 5 during cCAP 8→8 and cCAP 2/6 during cCAP 7→7 (p < 0.001, corrected) as compared with occurrences of other non-polarized cCAPs in either cCAP 8→8 or cCAP 2/6 during cCAP 7→7 suggest that these lowered occurrences might be the reasons behind no transition between cCAPs 7 and 8 during time windows of two reference transitions. When the occurrence data of long-range transitions involving a specific non-polarized cCAP are broken down according to the number of different states visited (Fig. 6E), significantly lowered occurrences of cCAP 5 in cCAP 8→8 and cCAP 2/6 in cCAP 7→7 (at least p < 0.05, corrected) than two reference transitions in all conditions are similarly observed. No other cCAPs show consistently significant different occurrences over five different numbers of different states visited (Supplementary Fig. 7).

Long-range transition data based on 27 pairs of pseudo-polarized states (Supplementary Note 4) reveal, in comparison to similarly generated reference transition data, no similar patterns to the cCAP 7–8 pair on metrics of occurrence (Supplementary Fig. 8), duration (Supplementary Figs. 9–10), state visit (Supplementary Figs. 11–12), and state-specific occurrence (Supplementary Fig. 13). The long-range transitions between the two global co-(de)activation states were thus unique.

3.6. Reproducibility

We repeated the exact same analyses on other two datasets, which were independently collected (i.e., Datasets 1 and 2), and reproduced almost all phenomena reported from Dataset 0 (see Supplementary Note 1). These phenomena include a set of cCAPs each showing distinct hemispherically-symmetric spatial pattern, a pair of polarized cCAPs with global co-(de)activation patterns, anti-state cCAP pairs (Fig. 7A), recurring temporal patterns and their differences among different cCAPs (especially the significantly lower occurrences in two polarized cCAPs, Fig. 7B), oscillations at <1 Hz, 5 Hz, and 10 Hz, one-step transition patterns, and long-range transition patterns coordinated by two polarized cCAPs (Fig. 7C). The only exception is the <1 Hz oscillation, which was detected in both Datasets 0 and 1, but not obvious in Dataset 2 (having the oldest participants out of three datasets). It is important to note that the superstructure among the entire set of cCAPs is identified in both Datasets 1 and 2. This superstructure is spatially supported by the distance map (Fig. 7A), where brain states closer to two polarized cCAPs are also identified similarly as in Dataset 0 (i.e., cCAPs 1 and 5 close to the polarized cCAP 2, and cCAP 6 close to the polarized cCAP 7 in Dataset 1; cCAP 1 close to the polarized cCAP 2 and cCAP 4 close to the polarized cCAP 8 in Dataset 2), revealing the fine spatial constructs within eight cCAPs beyond two polarized cCAPs. The superstructure and its fine spatial constructs are then supported by one-step transition data and long-range transition patterns (Fig. 7C).

Fig. 7.

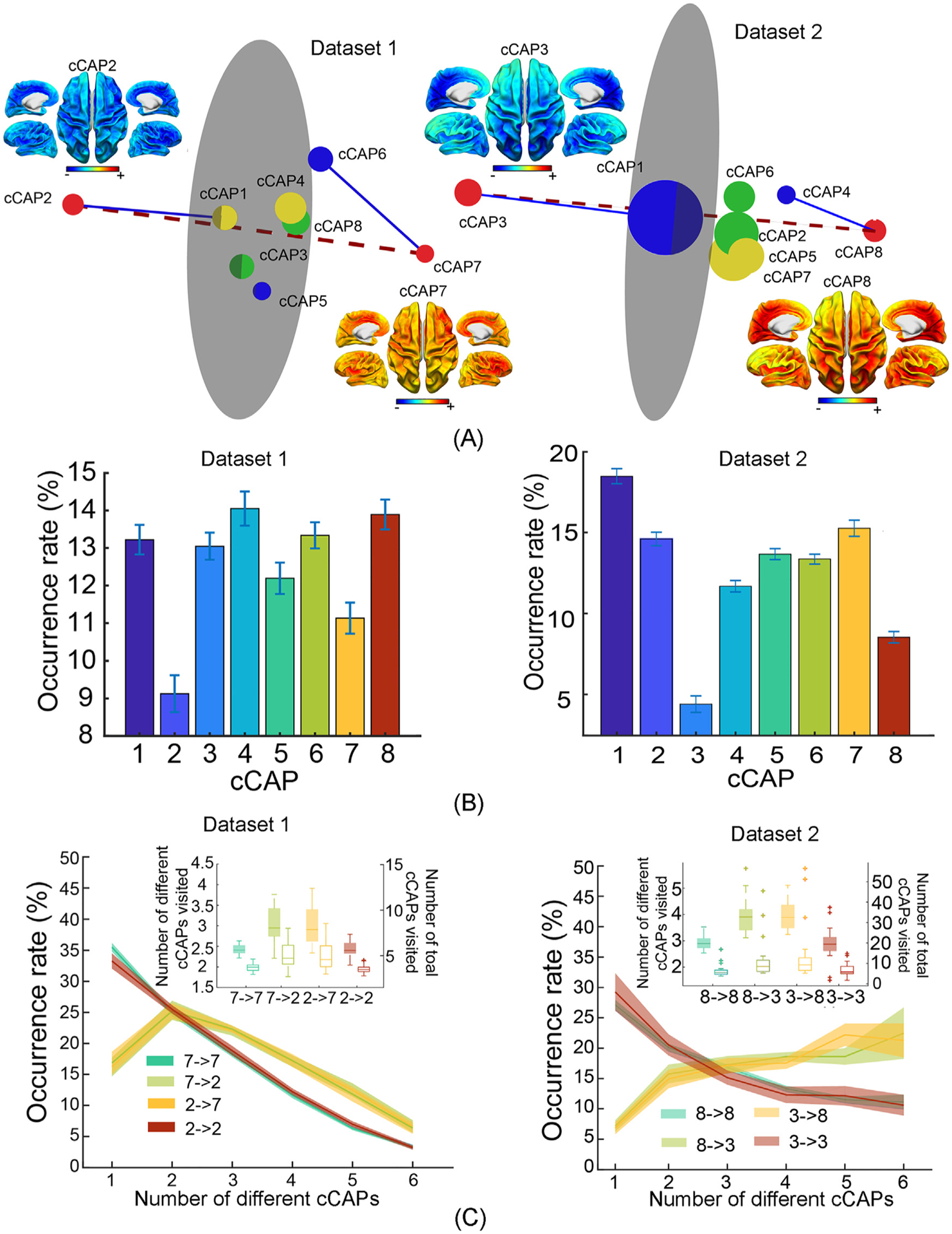
Reproduced key results of brain-wide functional states and their spatial, temporal, dynamic patterns from Datasets 1 and 2. (A) Spatial maps of two polarized global co-(de)activation brain states, i.e., cCAPs 2 and 7 in Dataset 1 and cCAPs 3 and 8 in Dataset 2, and the 3D distance maps among all cCAPs. Same-color dots: anti-state pairs; red dots: two polarized states connected by the dashed line; blue lines: connecting brain states that are structurally closest to two polarized states; gray circular plane: halfway between two polarized states (see Fig. 2). (B) Occurrence rates of cCAPs (see Fig. 3). (C) Occurrence rates of four types of transitions as a function of the number of cCAPs visited per occurrence (see Fig. 6 for more details).

4. Discussion

Using an advanced computational framework, we reconstructed and visualized spatial maps of brain-wide intrinsic functional states and their dynamics in resting human brains from electrophysiological signals. Our results collectively indicate that spontaneous human brain neural activity is a nonstationary phenomenon, involving reconfiguration into recurring and dynamically transitional functional states, which replicate and extend previous discoveries from optical imaging studies in animals (Matsui et al., 2016; Gutierrez-Barragan et al., 2019). Such recurring and transitional spontaneous neural activity results in synchronous neural co-(de)activations across hemispherically-symmetric and functionally-connected brain areas, including the prominent phenomena of global patterns (Mitra et al., 2015; Yousefi et al., 2018) and anti-state pairs of co-(de)activations (Liu and Duyn 2013; Karahanoglu and Van De Ville 2015; Gutierrez-Barragan et al., 2019) in their spatial tomographies. This view is further expanded by reporting that time-varying patterns of spontaneous resting-state EEG signals are governed by a limited number of functional states showing rich organized dynamic structures across a wide frequency band, i.e., multi-scale oscillations from fast (5 Hz and 10 Hz) to slow (0.6 Hz) rates. In parallel to oscillatory structures, we further found a superstructure among the identified entire set of functional states that regulates between-state one-step transitions and long-range transitions mediated by two unique states with opposite global co-(de)activation spatial patterns.

These findings advance our understanding of the principles underlying spontaneous neural networks in multiple directions. First, our results directly visualize large-scale brain-wide intrinsic functional states on the cortex based on electrical signals generated by the human brain, which have been mainly reported in human hemodynamic signals (Allen et al., 2014; Karahanoglu and Van De Ville 2015; Yousefi et al., 2018) but limited in EEG/MEG signals (Baker et al., 2014; Vidaurre et al., 2018; Coquelet et al., 2022). Such visual constructs confirm hypothesized brain-wide networked dynamics based on electrical recordings from a limited number brain sites (Massimini et al., 2004). As several cortical-level spatial prominent features of identified functional states resemble those from recent reports of human fMRI data (Karahanoglu and Van De Ville 2015; Yousefi et al., 2018), our greater temporal resolution of electrophysiological recordings extends those observations and provides novel mechanistic understanding of neural determinants of brain-wide hemodynamic structures. Second, the use of signal amplitude as the basis for clustering similarities and identifying differences among moment-to-moment cortical activation tomographies provides a means to discover brain-wide co-activation patterns in population-level electrical signals. In contrast, correlation-based methods applied to resting-state EEG/MEG signals have led to largely regionally activated neural patterns (Brookes et al., 2011; Hipp et al., 2012; Shou et al., 2020) as compared to distributed network patterns seen in corresponding correlation-based fMRI studies. Finally, in contrast to the slow response in hemodynamic signals to be <0.1 Hz (Logothetis et al., 2001; Shmuel and Leopold 2008; Gutierrez-Barragan et al., 2019), our present results have revealed rich frequency-specific phenomena in the classical range of EEG between 0.1 Hz and 50 Hz (Fig. 3), similar to previous EEG/MEG based brain state studies (Britz et al., 2010; Baker et al., 2014; Michel and Koenig 2018). Future studies can expand observations on both ends of the spectrum (i.e., <0.1 Hz and >50 Hz) to investigate more frequency-specific neuronal communications as well as cross-frequency mechanisms (Canolty and Knight 2010).

Our results indicate that the number of functional states (i.e., 8) that explain most resting-state EEG temporal dynamics is considerably lower than the common number of RSNs (e.g., 15–50) identified as spatial independent sources (ICs) using ICA from resting-state fMRI (Damoiseaux et al., 2006). Meanwhile, the dynamic states arising from these spatial sources have been suggested to be typically small (e.g., 4–8) in resting-state fMRI from both humans (Calhoun et al., 2014) and animals (Gutierrez-Barragan et al., 2019). Our eight recurring functional states (Fig. 2) are in fact constructed from 14 RSN components (Supplementary Fig. 1). This is consistent with the suggestion that ICs present a spatial parcellation of the brain rather than distinct states of functional connectivity (Liu et al., 2013), which has been used to identify function-based parcellations of the human brain (Smith et al., 2013). Therefore, our observations suggest, together with previous studies on dynamic states (Shou et al., 2020), that, under resting conditions, most of these spatial independent sources may be concomitantly engaged in coordinated patterns of co-(de)activations. Co-(de)activations of these distinct spatial sources then inevitably generate brain-wide cortical patterns indicating involvement of distributed neural network systems that generate moment-to-moment dynamics as suggested by fMRI data (Fox et al., 2005; Allen et al., 2014), which reveal phenomena that have or have not been revealed via exploring data correlation structures before as discussed below.

First, the identified states exhibit brain-wide co-activations both across anatomically homologous areas between hemispheres and across functional brain regions that are spatially separated, e.g., along the anterior-posterior direction. Strong hemisphere-mirrored symmetries (observed in cCAPs 1, 3, 4, 5, 7, 8, and the cCAP 2–6 pair) are the hallmark of RSNs (Smith et al., 2009) and resting-state functional connectivity in fMRI (Gutierrez-Barragan et al., 2019). Electrophysiological and optical studies have also suggested such hemispheric symmetries during the propagation of brain waves in both animals (Stroh et al., 2013) and humans (Mitra and Raichle 2016; Raut et al., 2020; Takeda et al., 2021). The pattern in cCAP 2 recapitulates the cardinal feature of DMN organization from the anterior brain, i.e., medial prefrontal cortex, to the posterior brain, i.e., posterior cingulate cortex and temporo-parietal junction (Buckner et al., 2008). These anterior-posterior structured activations, together with temporal lobe activations, reflect a full distributed membership of cortical nodes for DMN as established in human fMRI data. Similar DMN patterns have been revealed in human MEG data but with missing posterior nodes using spatial ICA (Brookes et al., 2011) or more lateralized distributions using seed-based correlation methods (de Pasquale et al. 2010; Hipp et al., 2012). As spatial ICs are more relevant to anatomic parcellations and correlation methods are stationary, the differences in characterizing DMN of our present results and previous EEG/MEG studies support the prevailing notion of time-varying functional connectivity across brain regions reported in previous studies (Allen et al., 2014; Calhoun et al., 2014; Liu et al., 2018; Gutierrez-Barragan et al., 2019). Second, the opposing co-activations between DMN and various constituents of TPN revealed in cCAPs 1, 2, 3, 4, and 5 (Fig. 2B) corroborate the presence of a tight inverse coupling between these two systems (Popa et al., 2009). The widely reported brain-wide anticorrelated functional networks characterized using hemodynamic signals (Fox et al., 2005) are believed to be manifestations of this inverse coupling at the spatial scale of the entire cortex, while no studies, to the best of our knowledge, have reported their brain-wide presence in neural electrical signals. This phenomenon supports the notion that large-scale hemodynamic correlation-based network structures are converted from large-scale spatiotemporal dynamics of spontaneous neural activity (Tagliazucchi et al., 2012). Finally, global co-activations as indicated in cCAPs 7 and 8 in our results have only been reported when human hemodynamic signals are analyzed beyond the correlation structure (Mitra et al., 2015; Yousefi et al., 2018). For example, the presence of strong correlated DMN and TPN, that usually lead to global co-activation patterns, has been discovered in human hemodynamic signals under the influence of global signal (Liu et al., 2017) using a quasiperiodic pattern searching algorithm (Yousefi et al., 2018). Transient global co-activations have been observed in searching globally propagating waves in both hemodynamic and neural signals from rodents (Matsui et al., 2016). Furthermore, slow oscillations (<1 Hz) of membrane potential are characterized with global traveling waves of both depolarizing and hyperpolarizing components (Stroh et al., 2013), which support the existence of transient global co-activations with opposite patterns.

Lifetimes and interval times between visits of these short-lived brain states exhibit large value ranges (Fig. 3B–C), which suggest that cortical networks in wakefulness are predominantly asynchronous. As a matter of fact, awake behaving states are traditionally called “desynchronized EEG” in contrast to large-amplitude slow oscillations observed in quiet sleep (Steriade et al., 1993). These asynchronous behaviors follow exponentially decreasing patterns as the scale increases, suggesting scale-free properties (Van de Ville et al. 2010), which are consistent with observations in brain states reported from microstate (Michel and Koenig 2018; Coquelet et al., 2022) and hidden Markov model (HMM) studies (Baker et al., 2014; Vidaurre et al., 2018). On top of scale-free phenomena, weak and selective coherences are presented with evidence for both slow (0.6 Hz) and fast oscillations (5 Hz and 10 Hz). Frequency-specific oscillatory synchronizations are essential mechanisms for efficient neuronal coordination across the entire brain (Siegel et al., 2012). Both 5 Hz and 10 Hz oscillations have been well established in EEG literature as theta (Kahana et al., 1999) and alpha rhythms (Halgren et al., 2019). The <1 Hz oscillation has been discovered as an overriding EEG pattern during non-REM sleep (Steriade et al., 1993; Crunelli and Hughes 2010), while recent experimental evidence indicates that slow-wave-like activity is also present in awake animals (Vyazovskiy et al., 2011). These intermittently recurring oscillations are similarly manifested in all identified brain states, although their occurrence patterns (e.g., occurrence rates) indicate statistically significant differences. Therefore, our observations suggest, on top of largely nonstationary dynamics, the presence of rich multi-scale ongoing intrinsic neural rhythms under awake resting conditions, which are independent from each other and not constrained towards specific brain states. It is important to note that several recent studies have started to investigate brain states defined with spectral parameters (Vidaurre et al., 2018) and on band-specific signals (Li et al., 2022) (rather than wideband signals considered in the present study), while asynchronous behaviors have not been separately considered. Future studies are needed to further clarify whether such brain-wide states are of both scale-free and poly-rhythmic nature or asynchronous and various oscillatory signals should be characterized separately with different brain-wide states.

Beyond asynchronous and oscillatory temporal behaviors, brain-wide functional states characterized by cCAPs in the present study further share other similarities in dynamic parameters to brain states obtained from microstate (Michel and Koenig 2018; Coquelet et al., 2022) and hidden Markov model (HMM) analyses (Baker et al., 2014; Vidaurre et al., 2018) in EEG/MEG literature, which include small number of brain states (~10) and transient nature (tens to hundreds milliseconds). It is therefore tempting to know whether the brain states from cCAPs in the present study are same as classical sensor-based microstates. Our results of reconstructed sensor-level EEG topographies based on timeframes for individual cCAP brain states (see Supplementary Fig. 14) indicate that they are different from classical microstate topographies reported in literature (Michel and Koenig 2018; Coquelet et al., 2022), despites their similarities in several dynamic features. These dynamic similarities might be explained due to universal features of transient brain events, where, for example, small number of brain states and scale-free dynamics have been observed in different neuroimaging data (Tagliazucchi et al., 2012; Calhoun et al., 2014) and in different species (Gutierrez-Barragan et al., 2019). On the contrary, several steps in our proposed computational framework (Fig. 1) might alter the variance spatial structure of data for clustering, as compared with the data on the sensor domain, leading to the identifications of brain states different from microstates. For example, cortical source imaging deconvolutes the volume conductor effect on mixing and altering brain signals from different brain regions, and normalizing time courses of ICA latent variables reduces the bias on clustering due to their potential different strength levels. In the literature, spatial sources of EEG microstates have been reported with regional patterns (Custo et al., 2017) (rather than brain-wide spatial patterns) and show similar spatial distributions as individual RSNs (similar to those in Supplementary Fig. 1) as compared with fMRI RSNs (Britz et al., 2010; Yuan et al., 2016) and MEG RSNs obtained via ICA (Brookes et al., 2011). It is also noted that brain states identified with microstate and HMM analyses have been indicated with significantly different spatial patterns (Coquelet et al., 2022). The use of different analytic approaches leading to different definitions of brain states have been widely reported in other neuroimaging data, e.g., fMRI (Calhoun et al., 2014). It remains to be seen in future studies about the relationship between different sets of brain states identified with different analytic choices since they are from same raw data of same human brains and if “optimal” analytics are available in defining brain states or the selection of analytics is problem dependent.

One of the most intriguing and novel findings of our present is the identification of a superstructure that governs the spatial, temporal, and transitional relationships among the identified brain states, which describes an important aspect in the dynamic control of states of brain functions under wakeful resting conditions. The superstructure, built with two polarized states and six intermediate states, is first established via visualizing spatial distances (Fig. 2C) among these states and then supported by the occurrence data, which indicate statistically significantly fewer visits to two polarized states (Fig. 3A). Single-step transition data (Fig. 4) further suggest close-to-zero direct transitions between two polarized states. Finally, long-range transitions between two polarized states, mediated by other states, take statistically longer times (Fig. 6A) and more visits to intermediate states (Fig. 6C) than no transitions between two polarized states. These consistent data from multiple different facets support the genuine existence of such a superstructure, which have been replicated in two independently collected datasets (Fig. 7), and no similarly structured transitional patterns exist in simulations using pseudo-polarized states (Supplementary Figs. 8–13). The generation of the superstructure is believed to be driven by structured brain-wide transitions among identified brain states coordinated by two polarized states with global co-(de)activation patterns. Beyond them, six intermediate states further exhibit layered structures in which some states are more affined to two polarized states (i.e., cCAP 5 to cCAP 8; cCAP 2/6 for cCAP 7) than others in terms of both spatial distance and transition probability.

The cellular mechanism and physiological significance of this superstructure of co-activations remains an open question. Our results indicate many similarities between the identified superstructure and the slow-wave oscillation of membrane potentials (Steriade et al., 1993), including their transitional nature, occurring frequency, and correspondence between the pairs of global co-activations and the UP and DOWN states of slow-wave oscillations (Jercog et al., 2017). Moreover, the mean lifetimes of identified brain states forming the superstructure are in the similar time scale of atomic wavelet events on membrane potentials during both slow-wave depolarization and hyperpolarization (i.e., 20–35 ms) (Steriade et al., 1993). However, there are still significant gaps of knowledge in how these cellular neuronal phenomena are manifested in the phase-locked behaviors of neural populations recorded in EEG (Wang 2010), and how neuronal waves recorded at spatially discrete locations are converted into structured dynamics of brain-wide spatial patterns (He et al., 2008). It is possible that other types of neuronal processes underlie such structured co-activations, such as, massive activations of cortical regions during episodic high-frequency field-potential oscillations in hippocampus (Logothetis et al., 2012) and potential neural activity associated with certain conscious processes, e.g., mind wandering, occurred during wakefulness. As animal studies (Matsui et al., 2016; Schwalm et al., 2017) have convincingly linked the transitions among brain-wide functional states from concurrent hemodynamic and neural recordings, future concurrent EEG and fMRI studies in humans (Yuan et al., 2016) to directly study such a linkage might provide evidence on the cellular mechanisms of the identified superstructure, and shed new light on the link between fast, sub-second EEG brain-wide dynamics and infra-slow fMRI brain-wide dynamics (Wirsich et al., 2020). Regarding its physiological significance, a close relationship to RSNs and slow-wave oscillations may already indicate its importance to understanding brain-wide memory consolidation (Tambini et al., 2010). As several fMRI studies have reported functional connectivity changes after task learning (Lewis et al., 2009) and the relationship between global co-activations and global BOLD signals, it is of great interest for future works to study how behavioral context influences the dynamics of these structured co-activations.

A methodological advancement that needs further innovative ideas is how to best compare tomographic, dynamic, and transitional co-activation patterns across different datasets, different conditions, and/or different brain signals. Leveraging the reproducibility of our identified co-activations, we have demonstrated its detections in three independent EEG datasets. However, linking co-activation patterns identified from different brain signals, e.g., EEG and fMRI, will require other algorithms. For example, the clustering algorithm used in our present study assumes all snapshots from individual time points belong to one of eight clusters, which is different from assumptions made in searching algorithms for transient events in fMRI (Liu et al., 2013; Karahanoglu and Van De Ville 2015). The adoption of our current algorithm is due to the noisy nature of EEG recordings, the complexity of computational processes in reconstructing brain-wide co-activations (see Methods), and the potential of much more complicated dynamic patterns in humans compared to small animals (Mitra and Raichle 2016). The important aspects of future research are to develop more advanced computational processes on potentially less noisy data from new sensors (Boto et al., 2018; Aghaei-Lasboo et al., 2020) to perform such comparisons and design analytical approaches accordingly. Finally, while the present study examined brain-wide functional states on wideband signals (i.e., 0.5–50 Hz), investigations of brain-wide states on narrow-band oscillatory signals and even asynchronous signals are needed in future studies as discussed above. One challenge (and the limitation of the present cCAP study) is to accurately estimate instantaneous amplitude of wideband signals, which would need more advanced algorithms (Nakhnikian et al., 2016; Munia and Aviyente 2019) than the Hilbert transform.

Abbreviations:

cCAP

component-based co-activation pattern

EEG

electroencephalography

Data and code availability statement

The data that support the findings of this study are available on request from the corresponding author (L.D.) through a data use agreement. The data are not publicly available due to them containing information that could compromise research participant privacy or consent. EEG preprocessing was performed using EEGLAB toolbox (https://eeglab.org) and FASTER plugin (https://sourceforge.net/projects/faster/). The segmentation and modeling were performed using FREESURFER (https://surfer.nmr.mgh.harvard.edu). Clustering analysis was conducted using the MATLAB kmeans function (https://www.mathworks.com/help/stats/kmeans.html). Group independent component analysis was performed using Fourier ICA code (https://www.cs.helsinki.fi/group/neuroinf/code/fourierica/html/fourierica.html). Codes for minimum-norm estimate in cortical source imaging and regression analysis in statistical regression tomography were implemented using MATLAB and are available from the corresponding author on reasonable request.