Open Reimplementation of the BIS Algorithms for Depth of Anesthesia

Abstract

Background

BIS scores have become interwoven into clinical anesthesia care and research. Yet, the algorithms used by such monitors remain proprietary. We do not actually know what we are measuring. If we knew, we could better understand the clinical prognostic significance of deviations in the score and make greater research advances in closed-loop control or avoiding post-operative cognitive dysfunction or juvenile neurological injury.

In previous work, an A-2000 BIS monitor was forensically disassembled and its algorithms (the BIS Engine) retrieved as machine code. Development of an emulator allowed BIS scores to be calculated from arbitrary EEG data for the first time. We now address the fundamental questions of how these algorithms function and what they represent physiologically.

Methods

EEG data were obtained during induction, maintenance and emergence from twelve patients receiving customary anesthetic management for orthopedic, general, vascular and neurosurgical procedures. These data were used to trigger the closely-monitored execution of the various parts of the BIS Engine, allowing it to be reimplemented in a high-level language as an algorithm entitled ibis. Ibis was then rewritten for concision and physiological clarity to produce a novel completely clear-box depth-of-anesthesia algorithm entitled openibis.

Results

The output of the ibis algorithm is functionally indistinguishable from the native BIS A-2000, with r = 0.9970 (0.9970-0.9971) and Bland-Altman mean difference between methods of −0.25 ± 2.6 on a unitless 0-100 depth-of-anesthesia scale. This precision exceeds the performance of any earlier attempt to reimplement the function of the BIS algorithms. The openibis algorithm also matches the output of the native algorithm very closely (r = 0.9395 (0.9390-0.9400), Bland-Altman 2.62 ± 12.0) in only 64 lines of readable code whose function can be unambiguously related to observable features in the EEG signal. The operation of the openibis algorithm is described in an intuitive, graphical form.

Conclusions

The openibis algorithm finally provides definitive answers about the BIS: the reliance of the most important signal components on the low-gamma waveband, and how these components are weighted against each other. Reverse engineering allows these conclusions to be reached with a clarity and precision that cannot be obtained by other means. These results contradict previous review articles that were believed to be authoritative: the BIS score does not appear to depend on a bispectral index at all. These results put clinical anesthesia research using depth-of-anesthesia scores on a firm footing by elucidating their physiological basis, and enable comparison to other animal models for mechanistic research.

Introduction

The use of processed EEG monitors during anesthesia or critical care has become commonplace over the last twenty years. In 2020, for example, Brigham & Women’s Hospital used approximately 7,800 sets of BIS electrodes (Medtronic, Minneapolis, MN) for the management of approximately 35,000 Main OR cases: approximately 22% of all-comers. Processed EEG monitoring is by far the most common monitoring technique that is not a mandated ASA standard. Yet, the BIS monitor is a black box for the monitoring of depth of anesthesia; its algorithms have remained proprietary. This demands our continued professional scrutiny, especially when measurements for depth-of-anesthesia are considered as prognostic measures for clinical management, or used as guides or endpoints in current clinical trials, or for use in the closed-loop control of anesthetic administration.^1-8

Previously, an A-2000 BIS monitor was forensically disassembled and its algorithms, known collectively as the BIS Engine, were retrieved in machine code from the motherboard.⁹ An emulator was then developed, which allowed the BIS Engine to be executed on arbitrary EEG data on a desktop computer to produce depth-of-anesthesia scores.¹⁰ Nevertheless, this is only an incomplete solution for three reasons:

1. Emulation simulates foreign processor instructions strictly in sequence, which is hard to parallelize on modern hardware. When hours of EEG data take hours to process, even real-time is too slow for research purposes.

2. Emulation requires legitimate access to the embedded software, either by obtaining it from the manufacturer, which is implausible, or by extracting it from a legally-owned device oneself, which is labyrinthine. This limits its use as a practical research tool.

3. Emulation allows the code to be run on an arbitrary EEG signal - but it is still a black box. We are otherwise none the wiser. The fundamental questions of how the EEG signal is converted into a depth-of-anesthesia score and what that conversion represents physiologically are not addressed by this technique.

A medical device is ultimately no more and no less than whatever its hardware and software implement, and so a device can be reverse engineered to provide a statement of its own function.

The task now is to produce a reimplementation of the BIS algorithms in a high-level language so their operation can be clearly understood and the original machine code is no longer required. Determining the actual mathematical operations that are performed on the EEG to produce the BIS score finally opens the black box.

Methods

Acquisition of Exemplar EEG Data for Analysis

Approval was obtained from the Massachusetts General Brigham IRB to capture and perform post-hoc analysis on raw EEG data obtained by the BIS monitor from surgical patients in whom BIS monitoring was performed. The proposed work was determined to be IRB-exempt as it involves only the analysis of de-identified samples that would otherwise be discarded that were acquired in the course of the patient’s usual customary care. Adult patients were recruited on an as-available basis across a range of surgical indications (orthopedic, general, vascular and neurosurgical). Customary anesthetic management was performed, as appropriate for each patient and indication, producing a broad invocation of techniques including general anesthesia (with/without volatile agents, with/without prolonged neuromuscular blockade), regional anesthesia, and the use common sedatives and analgesics (e.g. midazolam, propofol, fentanyl, sufentanil, remifentanil and hydromorphone). EEG data were obtained as a continuous stream from a total of 12 patients, spanning pre-induction, intraoperative management and emergence. Raw EEG data were exported from a BIS Vista monitor onto a USB drive under an anonymized alphanumeric key for each patient.¹⁰ A total of 36 hours and 16 minutes of EEG data was acquired at 128 Hz, producing an exemplar dataset of 16.7 million EEG voltage samples. These raw EEG data were used as inputs to emulations of the BIS A-2000 monitor to produce native BIS A-2000 depth-of-anesthesia scores and recordings of internal calculations for each patient.¹⁰

Reverse Engineering and Algorithm Reimplementation

Machine code is extraordinarily granular in its operation: shunting individual items of numerical data around in memory and performing seemingly endless trivial operations upon them. Only the totality of these operations produces meaningful functions. The conceptual task in reverse engineering is to see the forest through the trees, and to reimplement those functions in a high-level, expressive, readable form rather than simply executing the code as-is by emulation. However, emulation is an essential tool in this process, because it allows the machine code to be executed on real data in a controlled environment with perfect repeatability so that its behavior can be tracked, rewound, and analyzed step-by-step whenever an informative event occurs, until it is understood.¹¹

MATLAB (The Mathworks, Natick, MA) was selected as the high-level reimplementation language for this project. It is broadly available to academic researchers and has an open-source compatible alternative, Octave. MATLAB is concise, and the availability of a rich library of standard functions avoids reinventing the wheel. For example, the BIS Engine performs Fast Fourier Transforms to convert the time-sequence EEG data into frequency spectra, requiring hundreds of machine code instructions and several precomputed tables. In MATLAB, that operation is simply fft. As an expressive lingua franca, MATLAB can be translated into other programming languages with relative ease.

The practical work of reimplementing the BIS algorithm was undertaken under the project name ibis. Fittingly, the ibis is the head of the Egyptian deity Thoth - the god of science, medicine and mathematics who weighs in judgement the spirits of those near death. The explanatory power of ibis is maximized by these constraints:

• The sole function of the code should be to accept an input EEG in microvolts (μV) for conversion into an output depth-of-anesthesia score (0-100).

• All EEG data should be already available rather than live-streaming, avoiding the technical complexity of buffering, and allowing many calculations to be parallelized.

• The EEG data should be free of artifact, such as electrical interference or disconnections. Appropriately correcting or managing these issues depends on the device hardware, about which an open algorithm reimplementation should be agnostic.

The reimplementation was performed in three stages:

1. By carefully monitoring and stepping through the action of the BIS Engine code on the exemplar EEG data under emulation, the algorithm ibis was written to mimic the actions of the BIS depth-of-anesthesia algorithm indistinguishably.

2. By paring away rarely-used code and code dependent on large numbers of empirically-fit parameters (i.e. grey box functions), a much-abbreviated but functionally similar algorithm ezibis was produced.

3. By trading off deviations in the output unlikely to be clinically significant to keep only streamlined implementations of functions whose operation can be related to known anesthetic physiology, openibis was produced.

Statistical Methods

The BIS Engine recalculates a depth-of-anesthesia value after every half-second of EEG data. The first 120 seconds of data for each patient were excluded to avoid any potential artifacts arising from buffer run-in. For twelve patients spanning in excess of 36 hours of anesthesia care, this produced n ≈ 260,000 paired measurements between the reference BIS measurement and each of the ibis reimplementations. This dataset provides abundant statistical power and allows a range of clinically relevant anesthesia techniques to be explored. The native BIS A-2000 depth-of-anesthesia was taken as the reference “gold standard” for each patient, and compared to the ibis, ezibis and openibis algorithms. The agreement between two measurement techniques was tested statistically with Lin’s concordance correlation coefficient¹² r_c and also estimation of the Bland-Altman limits of agreement as mean difference ± 1.96 SD of the difference with confidence intervals for the lower and upper limits of agreement.¹³ Correction for repeated measures was applied to both the Lin and Bland-Altman techniques. The estimated limits of agreement for r_c were determined by 10,000 iterations of bootstrap resampling. Significance was defined as p < 0.05, and very highly significant as p < 10⁻¹².

The Pearson correlation coefficient r was also calculated between the BIS measurement and the ibis reimplementations. Use of the classical Pearson correlation coefficient as a test of agreement is statistically flawed; Lin’s coefficient and Bland-Altman analysis are the appropriate tests instead. However, previous studies and manufacturer data have been reported using the Pearson correlation coefficient,¹⁰ and so this value was additionally calculated here to allow for necessary historical comparison. The Pearson r value can be calculated with a resolution down to r = 0.01 for Type I and Type II error limits at 0.05 with n ≈ 130,000 observations.

Results

Quantitative Tests of Agreement in Depth-of-Anesthesia Output

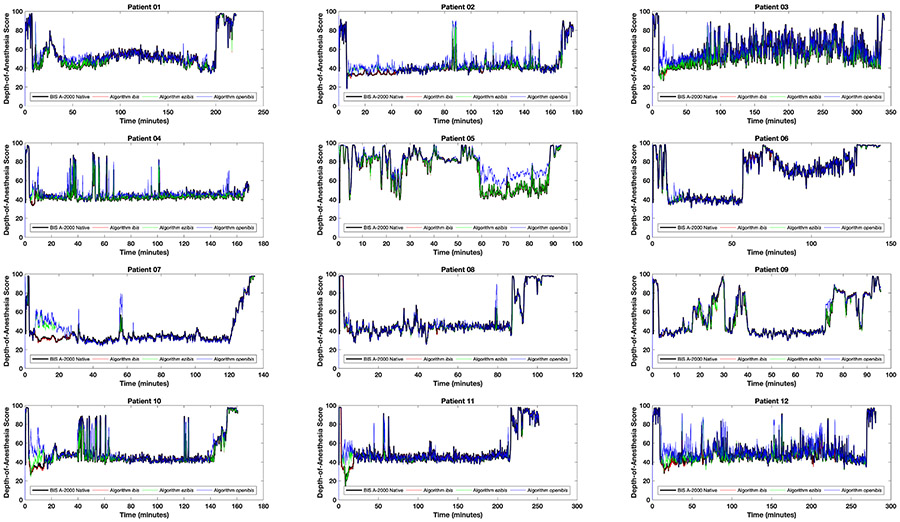
By visual inspection, the agreement between the BIS, ibis, ezibis and openibis algorithms is generally excellent across the complete time-courses of all twelve patients (Figure 1). The scores of the ibis algorithm match the scores of the native BIS A-2000 algorithm with Pearson correlation coefficient r = 0.9970 (0.9970-0.9971) and linear gradient 1.00. The Lin concordance correlation r_c = 0.9967 (0.9964-0.9969). The Bland-Altman mean difference between methods and limits of agreement are −0.25 ± 2.6 (mean difference ± 1.96 SD of the difference), i.e. when calculating a depth-of-anesthesia score between 0 and 100, the average difference between the two algorithms is −0.25 (less than one point!) and 95% of values agree within 2.6 points. The upper and lower 95% confidence intervals on the Bland-Altman limits of agreement are −2.99 to −2.79 and 2.29 to 2.49 respectively. The ibis algorithm is therefore functionally indistinguishable from the native algorithm, and requires only 180 lines of code to thoroughly outperform all previously published attempts including, notably, a neural network trained retrospectively on data from 5,427 patients under general anesthesia.^14-17 Furthermore, reverse engineering is not machine learning: there is no optimization process whereby the resultant algorithm might become overtrained to the available data or otherwise memorize it.

Figure 1:

Comparative performance in time of the ibis (red), ezibis (green) and openibis (blue) algorithms with respect to the reference BIS A-2000 native depth-of-anesthesia algorithm (black), over the twelve patients studied. The black line is plotted thicker as otherwise it would be obscured by the accuracy of the other algorithms.

The simplified ezibis algorithm requires 90 lines of code to produce r = 0.9850 (0.9849-0.9851) with linear gradient 0.97, r_c = 0.9836 (0.9831-0.9840) and Bland-Altman agreement of 0.30 ± 5.9 with upper and lower limit of agreement confidence intervals of −6.01 to −5.24 and 5.84 to 6.61; it remains in the most part indistinguishable. Openibis is the most readable and clinically intuitive of the new algorithms. The openibis algorithm requires only 64 lines of code (as shown in Table 1) and produces r = 0.9395 (0.9390-0.9400) with linear gradient 0.93, r_c = 0.9174 (0.9162-0.9186) and Bland-Altman agreement of 2.62 ± 12.0 with upper and lower limit of agreement confidence intervals of −10.90 to −8.29 and 13.53 to 16.14. A manufacturer-reported r value for consistency between the outputs of BIS Platform 3.4 and BIS Platform 4.0 is r = 0.96.¹⁰ Consequently, all three algorithms developed for this project have r values comparable to or even better than different versions of the official BIS monitor. On an unremarkable desktop computer, openibis processed the entire EEG dataset in 91 seconds, reduced to 38 seconds with explicit parallelization.

Table 1:

The MATLAB code for the openibis algorithm, accompanied by detailed line-by-line commentary. Openibis is an approximate and open reimplementation of the A-2000 BIS Engine depth-of-anesthesia algorithm.

Openibis, an approximate and open reimplementation of the BIS depth-of-anesthesia algorithm.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64

function depthOfAnesthesia = openibis(eeg) % The input eeg is a column vector, units of uV. Outputs one score per EEG epoch. [Fs,stride] = deal(128,0.5); % The EEG sampling frequency Fs must be 128 Hz, and each EEG window advances 0.5 seconds. [BSRmap,BSR] = suppression(eeg,Fs,stride); % Identify burst suppressed segments and calculate Burst Suppression Rates. components = logPowerRatios(eeg,Fs,stride,BSRmap); % Calculate the other components for the depth-of-anesthesia. depthOfAnesthesia = mixer(components,BSR); % Mix the components and BSR together to generate the depth-of-anesthesia scores. function [BSRmap,BSR] = suppression(eeg,Fs,stride) % Determines whether an EEG segment is burst-suppressed and calculates BSR. [N,nStride] = nEpochs(eeg,Fs,stride); % Calculate the total number of epochs N and the number of samples per stride. BSRmap = zeros(N,1); % Allocate space to store a true/false map of whether epochs are burst suppressed. for n = 1:N % Evaluate over the available epochs. x = segment(eeg,n+6.5,2,nStride); % Obtain two half-second strides (1 second). BSRmap(n) = all(abs(x - baseline(x)) <= 5); % Define this epoch as suppressed if all samples are within 5 uV of baseline. end BSR = 100 * movmean(BSRmap,[(63/stride)−1,0]); % BSR is the percentage of burst suppression in the previous 63 sec. function components = logPowerRatios(eeg,Fs,stride,BSRmap) % Calculates a family of components, based on log-power ratios. [N,nStride] = nEpochs(eeg,Fs,stride); % Calculate the total number of epochs and the number of samples per stride. [B,A] = butter(2,0.65/(Fs/2),'high'); % Create a second order high-pass Butterworth filter at 0.65 Hz. eegHiPassFiltered = filter(B,A,eeg); % … and filter out very low frequencies from the input EEG. psd = nan(N,4*nStride/2); % Allocate space to store power spectral densities, 0 to 63.5 Hz with 0.5 Hz bins. suppressionFilter = piecewise(0:0.5:63.5,[0,3,6],[0,0.25,1]).^2; % Define a suppression filter in the range of 0 - 6 Hz. components = nan(N,3); % Allocate space to store output signal components, 3 components for each epoch. for n = 1:N % Evaluate over the available epochs. Epochs are 2 seconds long, and the stride is 0.5 s, hence 75% overlap. if isNotBurstSuppressed(BSRmap,n,4) % If this EEG epoch (4 strides = 2 seconds) does not contain any burst suppression … psd(n,:) = powerSpectralDensity(segment(eegHiPassFiltered,n+4,4,nStride)); % then calculate Power Spectral Densities. if sawtoothDetector(segment(eeg,n+4,4,nStride),nStride) % If sawtooth-shaped K-complexes are detected … psd(n,:) = suppressionFilter .* psd(n,:); % then suppress low frequencies accordingly. end end thirtySec = timeRange(30,n,stride); % Consider data from the most recent thirty seconds. vhighPowerConc = sqrt(mean(psd(thirtySec,bandRange(39.5,46.5,0.5)).*psd(thirtySec,bandRange(40,47,0.5)),2)); wholePowerConc = sqrt(mean(psd(thirtySec,bandRange( 0.5,46.5,0.5)).*psd(thirtySec,bandRange( 1,47,0.5)),2)); midBandPower = prctmean(nanmean(10*log10(psd(thirtySec,bandRange(11,20,0.5))),1),50,100); % 11 - 20Hz band power in dB. components(n,1) = meanBandPower(psd(thirtySec,:),30,47,0.5) - midBandPower; % Used for sedation depth-of-anesthesia. components(n,2) = trimmean(10*log10(vhighPowerConc./wholePowerConc),50); % Used for general depth-of-anesthesia. components(n,3) = meanBandPower(psd(thirtySec,:),0.5,4,0.5) - midBandPower; % For weighting between sedation and general. end function y = powerSpectralDensity(x) % Calculates the Blackman-windowed Power Spectral Density. f = fft(blackman(length(x)) .* (x - baseline(x))); % Perform a Blackman-windowed FFT, removing baseline signal drift. y = 2*abs(f(1:length(x)/2)').^2 / (length(x)*sum(blackman(length(x)).^2)); % Convert frequency amplitudes to frequency powers. function y = sawtoothDetector(eeg,nStride) % Determines if this EEG segment contains a strong sawtooth-shaped K-complex. saw = [zeros(1,nStride-5) 1:5]'; saw = (saw-mean(saw))/std(saw,1); % Construct a normalized sawtoothed waveform. r = 1:(length(eeg)-length(saw)); v = movvar(eeg,[0 length(saw)−1],1); m = ([conv(eeg,flipud(saw),'valid') conv(eeg,saw,'valid')]/length(saw)).^2; % Match the sawtooth to the EEG by convolution. y = max([(v(r)>10).*m(r,1)./v(r) ; (v(r)>10).*m(r,2)./v(r)]) > 0.63; % Return a true value if there are any strong matches. function y = mixer(components,BSR) % Generates the output depth-of-anesthesia by converting and weighting components, BSRs. sedationScore = scurve(components(:,1),104.4,49.4,−13.9,5.29); % Map component 1 to a sedation score on a logistic S-curve. generalScore = piecewise(components(:,2),[−60.89,−30],[−40,43.1]); % Map component 2 to a general score, linear region … generalScore = generalScore + scurve(components(:,2),61.3,72.6,−24.0,3.55).*(components(:,2)>=−30); % and S-curved region. bsrScore = piecewise(BSR,[0,100],[50,0]); % Convert the BSR to a BSR score using a piecewise linear function. generalWeight = piecewise(components(:,3),[0,5],[0.5,1]) .* (generalScore<sedationScore); % Convert component 3 to a weight. bsrWeight = piecewise(BSR,[10,50],[0,1]); % Convert the BSR to a weight. x = (sedationScore .* (1-generalWeight)) + (generalScore .* generalWeight); % Weight the sedation and general scores together. y = piecewise(x,[−40,10,97,110],[0,10,97,100]).*(1-bsrWeight) + bsrScore.*bsrWeight; % Compress and weight these with the BSR. % --- Helper functions. --- function [N,nStride] = nEpochs(eeg,Fs,stride), nStride = Fs*stride; N=floor((length(eeg)-Fs)/nStride)−10; % Number of epochs. function y = meanBandPower(psd,from,to,bins), v = psd(:,bandRange(from,to,bins)); y = mean(10*log10(v(~isnan(v)))); % in dB. function y = bandRange(from,to,bins), y = ((from/bins):(to/bins))+1; % Indices of bins for a given frequency band. function y = baseline(x), v = (1:length(x))'.^(0:1); y = v * (v\x); % Fits a baseline to the input. function y = bound(x,lowerBound,upperBound), y = min(max(x,lowerBound),upperBound); % Fixes the input between bounds. function y = segment(eeg,from,number,nStride), y = eeg(from*nStride+(1:number*nStride)); % Extracts a segment of the EEG data. function y = isNotBurstSuppressed(BSRmap,n,p), y = ~((n<p) ∥ any(BSRmap(n+((1-p):0)))); % Checks if not burst suppressed. function y = timeRange(seconds,n,stride), y = max(1,n-(seconds/stride)+1):n; % Indices for the most recent time points. function y = prctmean(x,lo,hi), v = prctile(x,[lo hi]); y = mean(x(x>=v(1) & x<=v(2))); % Percentile-band mean. function y = piecewise(x,xp,yp), y = interp1(xp,yp,bound(x,xp(1),xp(end))); % Response on a piecewise-linear fn. function y = scurve(x,Eo,Emax,x50,xwidth), y = Eo - Emax./(1+exp((x-x50)/xwidth)); % Response on a logistic S-curve fn.

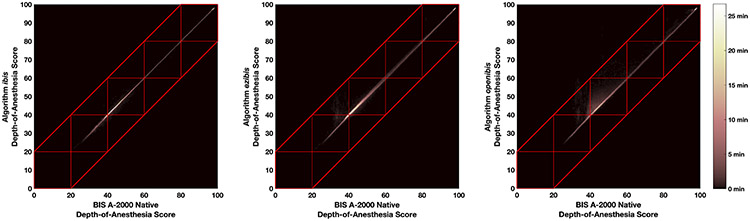
Ezibis and openibis err on the side of caution and produce slightly higher depth-of-anesthesia scores than the reference native algorithm when they diverge, as noted by their positive Bland-Altman mean values. This difference can be seen in Figure 1, for example patients 05 and 07, where depth-of-anesthesia scores for these algorithms hover occasionally above the others. Figure 2 shows heatmaps of the “gold standard” native algorithm versus this project’s algorithms. Essentially perfect agreement between algorithms results in datapoints only on the diagonal (Figure 2A, ibis). Figures 2B (ezibis) and 2C (openibis) show faint blooms above the diagonal line, but not below the line, consistent with Figure 1. The red boxes in Figures 2 delineate the customary depth-of-anesthesia regions of 0 - 20, 20 - 40, 40 - 60, 60 - 80 and 80 - 100. If a clinical agreement in prediction is represented as the closest boundary that incorporates these boxes, as marked by the red tramlines, then 99.96% of observations are inbounds for ibis, 99.6% for ezibis, and 96.9% for openibis.

Figure 2:

Heatmap of the overall agreement between the depth-of-anesthesia algorithms. The red boxes indicate the customary clinical depth-of-anesthesia regions of burst suppression (0 – 20), deep hypnosis (20 – 40), general anesthesia (40 – 60), mild/moderate sedation (60 – 80) and awake (80 – 100). The red tramlines minimally bound these regions.

(A) Agreement of the BIS A-2000 native algorithm with the ibis algorithm.

(B) Agreement of the BIS A-2000 native algorithm with the ezibis algorithm.

(C) Agreement of the BIS A-2000 native algorithm with the openibis algorithm.

The Openibis Algorithm: Implementation and Physiologic Rationale

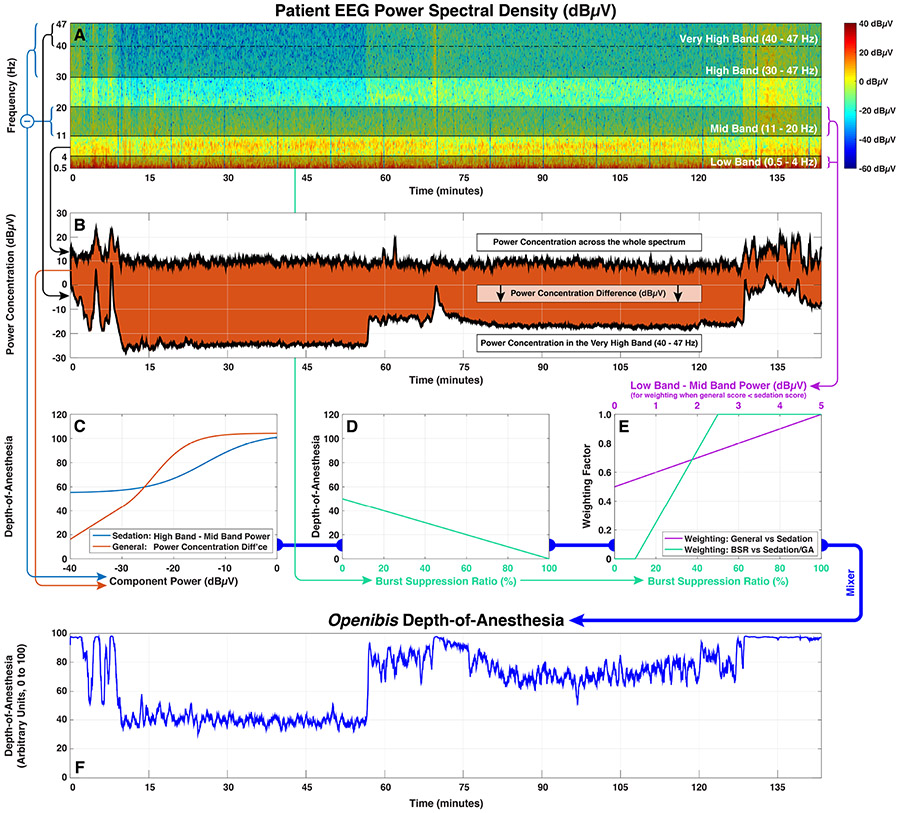
The complete MATLAB code for the openibis algorithm along with heavy line-by-line commentary is presented in Table 1. The compelling advantage of this approach over, for example, fitting a black-box neural network model¹⁸ is that the operation of the algorithm is made wholly explicit, and one can speculate constructively about what it means and how it might be modified or improved. Figure 3 shows a simplified graphical roadmap of the algorithm, but the code of the algorithm itself should be taken as definitive.

Figure 3:

A graphical roadmap of EEG processing in the openibis algorithm, using data from patient 09 in Figure 1.

(A) EEG epochs are converted into a power spectral density by Fourier transform. Subsequent calculations depend upon the relative power distributions across the whole frequency range, and across sub-bands spanning 0.5 – 4 Hz (low), 11 – 20 Hz (mid), 30 – 47 Hz (high) and 40 – 47 Hz (very high).

(B) A component related to general anesthesia is derived from the difference in power concentration between the very high band and the spectrum as a whole.

(C) The components related to sedation and general anesthesia are converted into depth-of-anesthesia scores using curvilinear logistic response functions.

(D) The burst suppression rate (BSR) is converted linearly into a depth-of-anesthesia score.

(E) The lower value of the sedation and general anesthesia scores predominates. Some transitional averaging between sedation and general occurs if the general score is lower and the difference between the low and mid band power is equivocal (≤ 5 dBμV). This score, representing the combination of sedation and general, is then weighted against the BSR score to produce a provisional final score.

(F) Extreme values in the provisional score (≤ 10 or ≥ 97) are compressed into the allowable range of 0 – 100 to produce the final score.

The openibis algorithm models the effect of anesthetic agents on the brain by generating depth-of-anesthesia components based on the EEG that respectively estimate the magnitudes of the effects of burst suppression, sedation and general anesthesia to produce corresponding depth-of-anesthesia scores. Weights are estimated to control how these different scores should be mixed to produce the single output score for each timepoint.

Burst Suppression Rate

The design of algorithms to detect burst suppression reliably remains an active area of research.^19,20 The BIS monitor, ibis and ezibis employ a proprietary algorithm called QUAZI to estimate EEG burst suppression, whereas the classical approach is to detect intervals in which the EEG voltage does not exceed 5 μV.²¹ Openibis implements a baseline-compensated version of the simple 5 μV threshold which, over the EEG dataset studied, nevertheless produced very comparable results to QUAZI (r = 0.996, Bland-Altman −0.40 ± 4.0, p very highly significant). At high levels of burst suppression, the depth-of-anesthesia score becomes linear with regard to BSR: the output score is given exactly by 50 – BSR/2 when the BSR is at least 50%. However, low scores can be generated without any burst suppression.^9,22 Epochs containing burst suppression are excluded when calculating time-averages for the other depth-of-anesthesia components. Of the total 36 hours and 16 minutes of EEG data analyzed, 4.1% were so excluded.

Sedation

Openibis imputes a sedation depth-of-anesthesia score using a time-windowed average of the difference in power in dBμV between the 11 – 20 Hz and 30 – 47 Hz frequency bands (shown in Figure 3 as the mid and high bands), approximately equal to:

$$\overline{10{\log }_{10}(P_{30-47\text{Hz}})}-\overline{10{\log }_{10}(P_{11-20\text{Hz}})}$$ (Eq 1)

This is similar to the property described as the BetaRatio by Rampil.²¹

General Anesthesia

Openibis imputes a general anesthesia depth-of-anesthesia from the difference in power concentration between the 40 – 47 Hz band and the power concentration over the entire spectrum. Figure 3B shows a dramatic drop in power concentration in the 40 – 47 Hz band (i.e. very high band) coincident with the induction of general anesthesia. Occasionally, large sawtooth-shaped K-complexes appear in the cortical EEG, especially in frontal locations.²³ These are a form of physiologic interference to this form of EEG interpretation. Openibis detects and then suppresses frequencies associated with these complexes.

Power concentration is defined as follows: the signal power P in each frequency bin is multiplied by the power in the preceding bin, a time-windowed average of these results is taken, and the square root obtained. The power concentration is stated in dBμV, approximately as:

$$PowerConcentration\approx 10{\log }_{10}\left({}^2\sqrt{\overline{P_{n-1}.P_n}}\right)\text{over the range of interest}$$ (Eq 2)

For a certain amount of power in a frequency range, the power concentration will be maximized if all of the power is divided equally between only two adjacent bins, producing a sharp peak. A simple thought experiment demonstrates this result. Imagine that we are homesteaders, and that we possess 20 units of fence with which we may construct any number of rectangular fields. We wish to enclose the largest area of land possible. The outcome depends on the quantity of fence we possess and how it is arranged. The obvious solution is that all the fence should be committed to construct only one large square field: a 5x5 field, rather than a 1x9 field or multiple smaller fields. This is, essentially, the same result. The power concentration favors greater signal power in peaked concentrations, and falls dramatically otherwise.

Mixing

The scores related to sedation, general anesthesia and burst suppression are combined. Approximately, it is the lowest score that wins. However, in transitioning to general anesthesia from sedation, a relative weighting is calculated based on the power in the 0.5 – 4 Hz band compared to the 11 – 20 Hz band (Figure 3E). Higher power in the low band is associated with a shift towards general anesthesia. This combination of the sedation and general anesthesia depth-of-anesthesia scores is then subsequently also mixed with a score produced from the burst suppression rate to produce the final, single value for depth-of-anesthesia for that timepoint (Figure 3F).

Discussion

The reliance of the power concentration on readings in the 40 – 47 Hz band is evocative of a detector for the “traveling peak” theory of anesthetic action, in which the frequency of a prevailing thalamocortical rhythm in the low gamma (γ) EEG band at around 40Hz becomes progressively lowered^24,25 by the action of inhibitory agents until the point where unconsciousness occurs. The EMG frequency response overlaps the gamma band, and this most likely explains the well-known clinical observation that neuromuscular blockade tends to decrease the BIS score²⁶, even in fully awake experimental volunteers.²⁷ Gamma waves are linked to cognitive function, information processing and memory, and dysregulated gamma band activity appears to be a marker for cognitive impairment. It may be possible to extract better prognostic markers for post-operative cognitive dysfunction intraoperatively from this frequency band.^28,29 Other authors have proposed more complex stochastic EEG measures to personalize depth-of-anesthesia.^30,31 In order to design or assess these more advanced depth-of-anesthesia metrics, it would be of foundational utility to understand how a current device functions.

The power concentration is also similar to Wiener Entropy, a metric for estimating information content from a frequency spectrum. Efficiently compressed data transmissions should use their assigned frequency space approximately evenly. For a power spectrum P in n frequency bins, the Wiener Entropy is the geometric mean (i.e. the n^th root of P_n terms multiplied together) divided by the arithmetic mean (i.e. the sum of P_n terms divided by n). Wiener Entropy is maximized when the signal power is evenly distributed and falls as the power becomes concentrated more tightly. For this EEG dataset, the Wiener Entropy and the power concentration are inversely proportional (r = 0.94, p very highly significant). The effect of volatile anesthetics is broadly conserved across all multicellular creatures.³² That a metric directly from information theory could evidently be used to construct a clinically-relevant measure of depth-of-anesthesia in humans provides great conceptual support for the idea of using information theory in simpler and more observable animal model systems, such as C. elegans, to determine the fundamental basis of volatile anesthetics in suppressing consciousness.^33,34

Reverse engineering is a legally acceptable means for learning the function of a device that one owns,³⁵ and it affords results that are obtained with a clarity and precision that is otherwise unachievable by machine learning or observation.^15,18,22 Nevertheless, a whiff of impropriety clings to the practice. Perhaps this is because we are socialized that it is impolite to enquire too pointedly into the secrets of others? A recent editorial in this journal on the subject of medical devices, proprietary algorithms and the legitimate scope of interest of clinicians referred to the long-held trade secret of the Coca-Cola recipe.³⁶ This is a correct example, but it is not medically salient. The Coca-Cola recipe is of no interest to medical professionals, excepting possibly the oral administration of caffeine in the conservative management of post-dural puncture headache and that’s not a secret: it’s 34 mg per can.³⁷ Consider instead the history of the obstetric forceps, maintained by all manner of obfuscation as a trade secret for over 100 years.³⁸ Laboring women were blindfolded in locked rooms before the forceps were applied, in order that the secret should not escape. How do we count the cost of medical secrets?

The professionalization of anesthesiology was borne from an act of reverse engineering. As Bigelow wrote in his landmark manuscript in 1846, “I subsequently undertook a number of experiments with the view of ascertaining the nature of this new agent… The first experiment was with sulphuric ether, the odor of which was readily recognized in the preparation employed by Dr. Morton.”³⁹

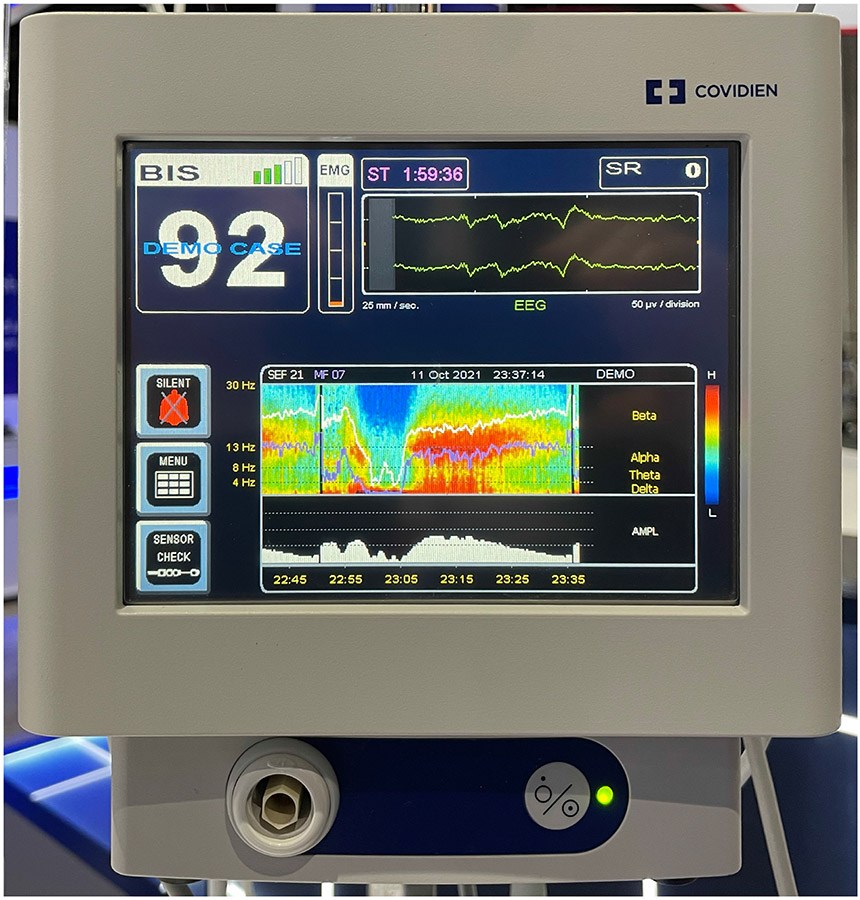
Let us finish where we began by considering the effect of the design of anesthetic monitoring equipment on both the practice and knowledge of the specialty. Firstly, it was previously demonstrated that a coding error in the A-2000 BIS Engine could cause it to miscalculate the Spectral Edge Frequency (SEF) under certain conditions.⁹ At the ASA annual meeting in 2021, the latest version of the BIS Platform was exhibited (Figure 4), which now shows SEF on a new spectral density display along with delineations for the classical β, α, θ, and δ EEG bands. These bands are all below 30 Hz. However, it is now readily apparent that it is the bands in the low γ range (30 – 47 Hz and 40 – 47 Hz) that primarily control the depth-of-anesthesia score (absent appreciable burst suppression, as discussed). Why would the manufacturer appear to show - but then actually cut off! - that part of the spectrum that a clinical anesthesiologist would need to see in order to interpret it as the machine does? Secondly, it is current and commonplace to describe the BIS as a bispectral index^21,40; a search for “bispectral index” on PubMed returns over 3,400 results. The ibis, ezibis and openibis algorithms never calculate a bispectral index. Furthermore, it does not appear that the A-2000 BIS monitor itself calculates a bispectral index, even internally. To calculate a bispectrum requires that the difference in phase be calculated between signals at various frequencies. However, all discernable execution paths in the BIS Engine that perform a Fast Fourier Transform to calculate signal amplitude and phase immediately convert those measurements to signal power, discarding the phase information. Consequently, one is inevitably led to the conclusion that the BIS score does not depend upon, and probably for twenty years has not depended upon, a bispectral index at all. This contradicts essentially all published material on the subject. This does matter. When anesthesia researchers use a BIS score as a surrogate endpoint for neurological function in a large clinical trial, it is entirely correct and appropriate that we should know the foundation of what that endpoint is and what it represents. We are the medical specialty that manipulates consciousness: what possible reason is there for us to allow ourselves to be misinformed as to how it is clinically measured?

Figure 4:

Public exhibition and demonstration of a new power spectral density display on the BIS monitor at the annual meeting of the ASA. (Photographed by the author, October 11^th 2021, San Diego, CA.)

Key Points (Question, Findings, and Meaning, each in one sentence).

• What algorithms are used to calculate BIS depth-of-anesthesia scores from EEG signals in clinical and research use, and what do these algorithms represent physiologically?

• Reliable reimplementation of the BIS algorithms in a clear-box form uncovered a strong dependence on EEG signal content in the low gamma band but, astonishingly, no calculations based upon the bispectrum or any sort of bispectral index.

• The openibis algorithm, finally, settles longstanding questions on the functional behavior of the BIS monitor, and can serve as a foundational tool both for clinical anesthesia research and for the study of anesthetic mechanisms in comparative animal models.

Glossary and Abbreviations

ASA

American Society of Anesthesiologists.

BIS

A brand of processed EEG depth-of-anesthesia monitor.

BSR

Burst suppression rate.

CI

Confidence interval.

dBμV

Decibels, a unit of signal power, normalized against 1 microvolt.

EEG

Electroencephalogram.

FFT

Fast Fourier Transform.

EMG

Electromyogram.

IRB

Institutional Review Board.

OR

Operating Room.

QUAZI

A proprietary algorithm for burst suppression.

SD

Standard Deviation.

SEF

Spectral Edge Frequency.

USB

Universal Serial Bus.