Comparative evaluation of spin-label modeling methods for protein structural studies

Abstract

Site-directed spin-labeling electron paramagnetic resonance spectroscopy is a powerful technique for the investigation of protein structure and dynamics. Accurate spin-label modeling methods are essential to make full quantitative use of site-directed spin-labeling electron paramagnetic resonance data for protein modeling and model validation. Using a set of double electron-electron resonance data from seven different site pairs on maltodextrin/maltose-binding protein under two different conditions using five different spin labels, we compare the ability of two widely used spin-label modeling methods, based on accessible volume sampling and rotamer libraries, to predict experimental distance distributions. We present a spin-label modeling approach inspired by canonical side-chain modeling methods and compare modeling accuracy with the established methods.

Significance

Understanding protein structure and dynamics is critical to the investigation of diseases and the development of novel therapeutics. Site-directed spin-labeling electron paramagnetic resonance is a powerful tool for the study of protein structure and dynamics. Quantitative application of site-directed spin-labeling electron paramagnetic resonance data to the modeling of proteins and their conformational heterogeneity require accurate computational spin-label modeling methods. This work compares the accuracy of two widely used spin-label modeling methods and builds upon them to propose an improved spin-label modeling method.

Introduction

Site-directed spin-labeling (SDSL) (1) electron paramagnetic resonance (EPR) spectroscopy is a useful technique to study the structure and dynamics of large, flexible, and membrane-associated proteins (2,3). SDSL EPR can be used to study local protein dynamics using continuous-wave (CW) EPR and structure and conformational change using pulse dipolar EPR methods like double electron-electron resonance (DEER) (4, 5, 6). One of the major advantages of using EPR techniques like DEER is that they provide information about full ensemble spin-spin distance distributions rather than single or average distances (7,8). For protein structure determination, these distributions can reveal multiple conformations and their relative populations. When combined with computational techniques, these data can be used to understand and model conformational states that are often inaccessible using other structural techniques. SDSL EPR has been used to model protein conformational changes (9, 10, 11, 12, 13, 14, 15), protein-protein interactions (16, 17, 18, 19), dynamic loops (11,20, 21, 22), and even entire proteins and protein domains de novo (23, 24, 25).

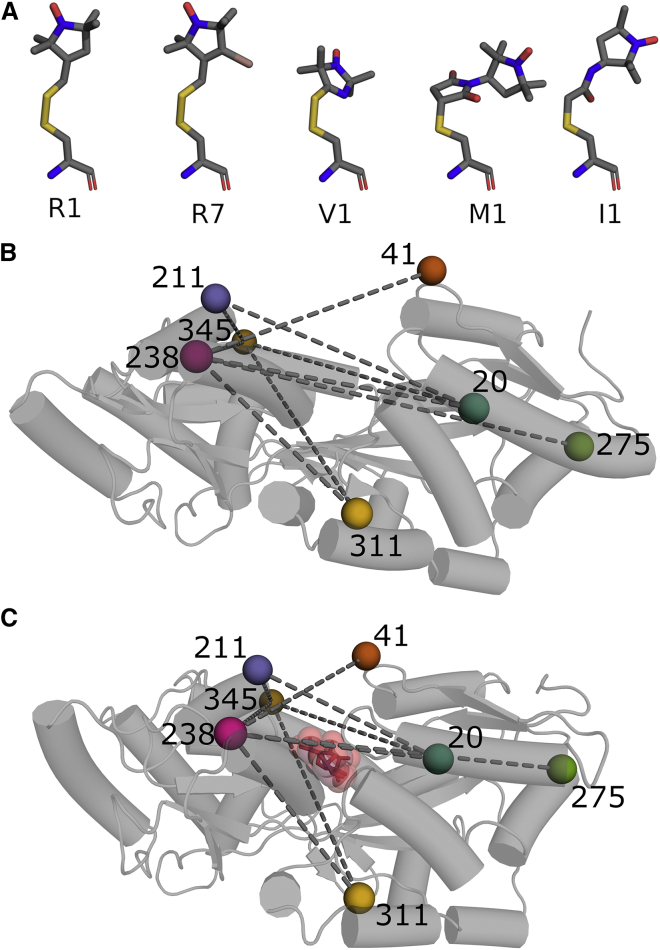
One challenge in using DEER-derived distance distributions as quantitative structural restraints is the fact that they represent spin-spin distances rather than backbone distances. Pulse dipolar EPR techniques measure the dipolar interaction between the spin centers of the labels, usually located on a nitroxide moiety attached as a side chain. Spin-label side chains are often relatively long and flexible (Figs. 1 A and S1), and their conformational ensembles can vary drastically as a function of their local environment (26, 27, 28, 29, 30, 31). For DEER, a protein is typically labeled at two sites, further increasing the uncertainty in label distance and orientation with respect to the protein backbone. Due to this uncertainty, it is often difficult to infer accurate protein backbone C_β-C_β distances directly from the measured spin-spin distributions or distinguish changes in label conformations from biologically relevant backbone conformational changes.

Figure 1.

Spin labels and maltodextrin-binding protein. (A) Cysteine-reactive nitroxide spin labels used in this study. Atom types are colored as follows: nitrogen (blue), oxygen (red), carbon (gray), sulfur (yellow), and bromine (salmon). Lewis structures are provided in Fig. S1. (B) Maltodextrin-binding protein in the unbound state (PDB: 1OMP). Color-labeled spheres indicate spin-labeled residues. Dashed lines indicate site pairs used in DEER experiments. (C) Same as (B) for the maltose-bound state of MBP (PDB: 1ANF). Maltose is shown as spheres with raspberry carbon atoms and red oxygen atoms. To see this figure in color, go online.

To address this uncertainty, several methods have been introduced that model spin-label conformations in a given protein environment. These methods are used to guide hypothesis development, experimental design, and computational protein modeling. Spin-label modeling methods include the rotamer library approach (24,32), Monte Carlo sampling of the accessible volume (33, 34, 35), empirical potentials (23,36), molecular dynamics simulations (37, 38, 39), and advanced sampling methods (40, 41, 42). The quality of protein structure models, as well as hypotheses and experimental designs based on their predictions, is dependent on the accuracy of the label modeling method. Unlike canonical side chains, there is not a wealth of experimental structural information available for benchmarking spin-label modeling methods, making the assessment of modeling performances difficult.

In addition to limited experimental validation, most of these methods only support one label, S-(1-oxyl-2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-3-yl)methyl methanesulfonothioate (MTSL), which produces the R1 side chain. While most SDSL experiments are conducted using R1, several alternative labels have been developed for various purposes. These labels have different advantages (43), including resistance to reduction in the cellular environment (44), bio-orthogonality (45), decreased label size and flexibility (46), and more stable ligation chemistries via maleimide or iodoacetamide. Some modeling methods have been expanded to include additional labels, though they are usually not thoroughly validated due to the severe paucity of experimental structural data.

Here, we seek to evaluate the performance of popular spin-label modeling methods against a large experimental data set and assess improvements that can be made by using canonical amino acid modeling methods. We construct and label nine different site pairs of the highly stable and well-characterized maltodextrin/maltose-binding protein (MBP) with MTSL (R1), bromo-MTSL (R7), bis-(2,2,5,5-tetramethyl-3-imidazoline-1-oxyl-4-yl) (V1), 3-maleimido-2,2,5,5-tetramethyl-1-pyrrolidinyloxy (M1), and 3-(2-iodoacetamido)-2,2,5,5-tetramethyl-1-pyrrolidinyloxy (I1) labels (Figs. 1 A and S1). We perform Q-band DEER spectroscopy in the presence and absence of maltose, resulting in 90 DEER distance distributions. We prune to a subset of 70 distributions that we then use to compare the performance of the rotamer library and the accessible-volume approach, both of which support all the labels used in this study. We find that the accessible-volume approach makes more accurate predictions of our experimental data despite producing unrealistic spin-label models. We then introduce an extended rotamer library approach that utilizes off-rotamer sampling inspired by canonical side-chain modeling methods. For our experimental dataset, this approach shows improved predictions while maintaining realistic spin-label models.

Materials and methods

Cloning, purification, and spin labeling

Wild-type (WT) MBP DNA in the pETM-11 vector was used as the template DNA for all constructs. Mutagenesis was performed with a modified hot-start PCR protocol (47). All constructs were double-strand-sequence verified. All sequencing was performed by Genewiz, and the sequence analysis was performed using SDMCheck (https://gitlab.com/mtessmer/SDMCheck). Sequence-verified plasmids were transformed into chemically competent BL21 (DE3) E. coli cells (NEB C2527) using the manufacturer’s recommended heat-shock protocol. Isolated colonies were used to inoculate 5–25 mL starter cultures in lysogeny broth with 50 μg/mL kanamycin (Gibco 15160054). Starter cultures were grown overnight at 30–37°C and used to inoculate 250–1000 mL induction cultures (lysogeny broth, 50 μg/mL kanamycin). Protein expression was induced at optical density at 600 nm of 0.4–0.6 using 0.5 mM isopropylthio-β-galactoside. The protein was purified using standard immobilized metal affinity chromatography with NiNTA agarose beads (QIAGEN 30210) per the manufacturer’s recommended protocol. The purified protein was spin-labeled overnight at 4°C with a 10-fold molar excess of the label. MTSL was purchased from Santa Cruz Biotech (sc-208677), bromo-MTSL was purchased from Toronto Research Chemicals (B686290), V1 was purchased from Enzo Life Sciences (ALX-430-102-M025), and M1 and I1 were purchased from Sigma-Aldrich (253375, 253421). All spin-label stock solutions were prepared in acetonitrile at 100 (R1 and V1), 40 (I1 and M1), and 20 mM (R7). The three constructs containing L20I1 labels were spin labeled in the presence of 4 M urea to improve label site accessibility. All labeled constructs were buffer exchanged by performing 20-fold dilutions or greater and concentrating and repeating a minimum of five times. Protein concentration was carried out in an Amicon Ultra-4 centrifugal concentrator with a 30 kDa molecular weight cutoff (Millipore-Sigma). All spin-labeled constructs were checked for free label with CW EPR.

CW EPR

All CW EPR experiments were performed at room temperature on an X-band Bruker EMX EPR spectrometer with a Bruker ER 4123D dielectric resonator. Samples were prepared in 20 mM tris buffer (pH 7.5) with 150 mM NaCl. Samples were diluted to 20 μM protein, and 500 mM maltose was added when appropriate (MBP-maltose K_d ≈ 1 μM) (48). Samples were transferred to 1.0 mm OD 0.70 mm ID quartz capillaries (Sutter Instrument, Q100-70-10). All experiments were performed using a microwave power of 2 mW, a 100 kHz field modulation with 0.1 mT peak-to-peak amplitude, 10 scans, and a sweep rate of 0.12 mT/s. CW EPR spectra were analyzed using Python. All spectra were baseline corrected by subtracting the mean of the spectrum and normalized to the double integral of the spectrum.

DEER

Before DEER, all constructs were exchanged into a deuterated buffer of 20 mM tris (pH 7.5) and 150 mM NaCl with 20%–50% (w/w) d₈-glycerol as a cryoprotectant. Fig. S5 shows that the glycerol concentration causes little to no difference in the DEER trace and the respective distance distribution. Samples containing 20 μM MBP were supplemented with 5 mM maltose when applicable (MBP-maltose K_d ≈ 1 μM). Samples were transferred into a 1.5 mm OD, 1.1 mm ID quartz capillary (Sutter Instrument), flash frozen in liquid nitrogen, and stored at −80°C until measurement. DEER measurements were performed at 34 GHz and 50 K in a Bruker EleXsys E580 EPR spectrometer, in an MD2 resonator, equipped with a SpinJet AWG, a 390 W TWT amplifier (Applied Systems Engineering), and a cryogen-free cooling system (ColdEdge). DEER experiments were all performed with 60 ns Gaussian observer pulses (full width at half maximum ≈ 30 ns) with power amplitudes corresponding to π/2 and π flip angles and a 150 ns sech/tanh pump pulse (beta parameter 10). The sech/tanh pulse had an 80 MHz wide excitation bandwidth 40–120 MHz above the observer pulse frequency. All DEER experiments utilized 8-step phase cycling and a shot repetition time of 2040 μs. τ₁ averaging was used to reduce the effect of nuclear modulations, with τ₁ ranging from 400 to 528 ns in 16 ns increments. Values for τ₂, Δt, number of averages, and t₀ offset are reported in Table S1. Pulse shapes were generated and compensated for the resonator transfer function using EasySpin 6.0.0-dev (49) or PulseShape (https://gitlab.com/mtessmer/PulseShape). All DEER data were analyzed with DeerLab (50) using Tikhonov regularization and compactness regularization (51). Tikhonov regularization was performed using the second-derivative operator, and the smoothing parameter was selected using generalized cross-validation as described previously (52). The compactness regularization parameter was chosen using the informational complexity criterion (51). Single-step fitting was performed using separable non-linear least squares (50).

Rotamer modeling

Spin-label rotamers for all methods were modeled using an in-house Python package (https://github.com/mtessmer/chiLife). The rotamer library method was implemented to reproduce MMM (53) functionality using the default settings for R1, R7, and V1 from MMM v.2021.2. Notably, MMM uses different default clash evaluation functions for R1, R7, and V1 versus I1 and M1. We chose to use the defaults for R1/R7/V1 for all labels for consistency. Rotamers from the default MMM rotamer libraries (32) were attached to the protein backbone by aligning two local coordinate frames defined by the N, CA, and C atoms of the protein and of the label. The CA atom was defined as the origin, the X axis defined as the unit vector along the CA-N bond, the Y axis as the unit vector along the projection of the CA-C bond onto the axis orthogonal to the X axis in the N-CA-C plane, and the Z axis as the cross product of the X and Y axes. Due to variations of the N-CA-C bond angle, the choice of the principal axes can have a significant effect on the N-CA-CB bond angle of the attached spin label, resulting in different clash energies for spin-label side-chain atoms. Clashes were evaluated for each rotamer in the library by summing the pairwise Lennard-Jones potential for each atom i of the label and j of the protein within a label-specific radius defined by the calibration.maxdist field of the rot_lib structure of MMM plus 4 Å, giving the total energy

$$E=\sum _{ij}{\epsilon }_{ij}\left[{\left(\frac{f{R_{\text{min}}}_{ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{f{R_{\text{min}}}_{ij}}{r_{ij}}\right)}^6\right]\text{,}$$ (1)

where r_ij is the distance between atoms i and j, $R_{{\text{min}}_{ij}}$ and ${ϵ}_{ij}$ are the optimal van der Waals distance and potential well depth as parameterized by the Towhee universal force field (54) respectively, and f is a forgive factor set to 0.5 as it is in MMM 2021.2 (32,53). Rotamer weights $w_{\text{site}}$ were calculated using Boltzmann reweighting

$$w_{\text{site}}=w_{\text{internal}}\frac{{\text{e}}^{-\frac{E}{kT}}}{Z}\text{,}$$ (2)

where w_internal is the internal weight of the precalculated rotamer library, Z is the partition function, k is the Boltzmann constant, and T is the temperature set to 298 K.

The accessible-volume method was implemented to reproduce the behavior of MTSSLWizard (33,34,55). Single spin-label structures were superimposed on the labeling site using the same method as above. All side-chain dihedral angles were sampled uniformly, and any rotamer with internal clashes was discarded. Internal clashes were defined as any two non-bonded atoms of the spin label within 2 Å. Any rotamer atom within 2.5 Å of a protein atom was counted as an external clash, and rotamers with 5 or more external clashes were discarded. This process was repeated until either 2000 rotamers were successfully sampled or 10,000 rotamer samples were attempted. These settings correspond to the “loose” clash evaluation setting and the “thorough” search setting of the R1 label in MTSSLWizard. In the rare event that no rotamers were found for a site, the clash radius was iteratively reduced by 0.01 Å until at least one rotamer could be successfully modeled. No label required the clash radius to be reduced below 2.39 Å.

The off-rotamer sampling approach proposed in this work utilizes the MMM rotamer library as described above, with added stochasticity. For 10,000 iterations, new dihedral angles were sampled from von Mises distributions with means chosen from one random rotamer of the rotamer library and the concentration parameter $\kappa =s^{-2}$ with $s=35°$, where $s$ is the approximate standard deviation. This value was chosen by grid searching $s$ between 5° and 100° and choosing the smallest value at which the total overlap between the experimental and simulated distance distributions, over the whole data set including all labels and all conditions, stopped improving. This distribution width is reasonably close to the one required to reproduce fluctuations about R1 rotamers computationally observed by Sezer, Freed, and Roux (37). Energetic contributions of clashes were evaluated using only the repulsive terms of the Lennard-Jones potential capped at $10{\epsilon }_{ij}$ with a forgive factor of 0.9 (Eq. 3). This has previously been shown to be the optimal forgive factor for several clash evaluation potentials (56).

$$E=\sum _{ij}{\epsilon }_{ij}\min \left({\left(\frac{f{R_{\text{min}}}_{ij}}{r_{ij}}\right)}^{12},10\right)$$ (3)

The attractive term was neglected because without a solvent model, it introduces a bias to solvent-exposed residues (57).

Distance distributions were calculated by creating histograms over the experimental distance range with a 0.5 Å resolution for the accessible-volume approach and 0.25 Å in the case of the rotamer library and the off-rotamer sampling approach. Rotamer library and off-rotamer sampling method histograms were convolved with a Gaussian distribution with a standard deviation of 1 Å to match MMM behavior. Histograms generated from the accessible-volume approach were not convolved so as to match MTSSLWizard behavior. As a final step, all simulated distance distributions were normalized and interpolated to match the distance domain of the experimental distribution.

Results

MBP variant construction, spin labeling, and CW EPR

To compare spin-label modeling methods, we acquired a data set of DEER distance distributions using MPB. This protein was chosen for several reasons. First, it is known to have two well-defined conformations. The apo state is open, and, upon binding of maltodextrins, the protein closes in a clam-shell fashion via a hinge-and-twist motion between the two lobes flanking the binding site (Fig. 1 B and C). Second, these states have been studied extensively, and a plethora of structures determined by different methods exist (58, 59, 60, 61, 62, 63, 64, 65, 66). Third, MBP does not have native cysteine residues. This prevents off-target labeling by the cysteine-reactive spin labels used in this study. Thus, we minimize functional and structural perturbations by only mutating cysteines at the sites of interest. Finally, MBP is highly stable and resilient to point mutations.

To include a diverse set of secondary and tertiary environments and spin-label orientations as well as a range of expected distance changes, nine site pairs were selected based on the published crystal structures of MBP (Fig. 1 B and C). Each construct was expressed and labeled with five different labels (Figs. 1 A and S1), as described in the materials and methods section.

To qualitatively assess labeling efficiency and functional competence of all constructs, X-band CW EPR spectra in the absence and presence of saturating levels of maltose were recorded (Fig. S2). These experiments showed that all constructs were labeled. To control for off-target labeling, we attempted to label WT MBP with all five labels. Fig. S3 compares the lowest signal CW EPR spectrum for each label with the WT MBP control, showing negligible off-target labeling; however, there does appear to be residual free label in the R7 sample. Nearly all V1-labeled constructs showed signs of varying levels of free label, manifesting as sharp peaks (Fig. S2, column 3). This likely comes from the V1 detaching from the protein, as has been previously observed (46). On a much smaller scale, R7-labeled constructs also exhibited signs of free label, which may be a sign of detachment or residual free label as mentioned above. Nearly all spectra exhibited at least a small change upon the addition of maltose, generally broadening the spectra, suggesting a reduction in label mobility that might be indicative of conformational change. Alternatively, an increase in viscosity of the sample caused by adding large amounts of maltose also could cause a reduction in the tumbling rate of MBP or the label, obscuring potential spectral changes caused by conformational changes.

DEER distance distributions and comparison of spin labels

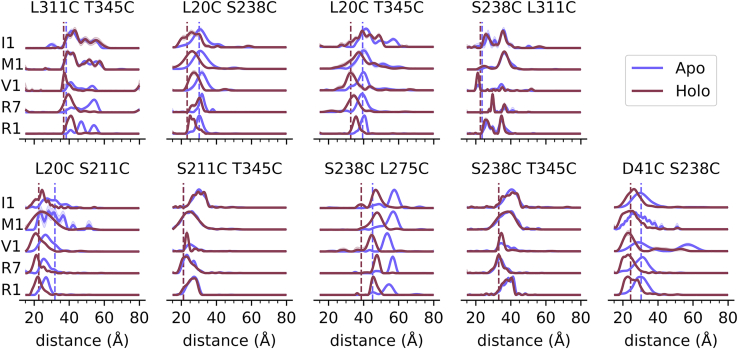
Next, DEER was performed on 20 μM MBP for all constructs in the absence and presence of 5 mM maltose to saturate MBP (K_d ≈ 1 μM). The results are shown in Fig. 2 (see also Fig. S4). All five of the nine site pairs expected to exhibit a distance change upon the addition of maltose did so for all five spin labels used. The direction and magnitude of the observed changes are consistent with the published crystal structures, suggesting that spin labeling did not abrogate MBP folding, ligand binding, or conformational change. Two of the four remaining constructs, S211C T345C and S238C T345C, exhibited distance distributions consistent with the published crystal structures and no distance change, as expected. Furthermore, each of these sites from these constructs was present in at least one of the five constructs that exhibited the expected conformational changes, suggesting that these two constructs are not significantly perturbed by spin labeling. The two constructs labeled at L311 had distance distributions inconsistent with the crystal structures. Many of these distributions had sporadic peaks, and several showed conformational changes far larger than expected. Since L311 is a partially buried site at the hinge of MBP and may be important for stability and conformational change, we decided to exclude the constructs containing L311 labels from further analysis.

Figure 2.

DEER distance distributions for all nine site pairs and all five spin labels for the apo state (blue) and the maltose-bound state (red). Vertical lines indicate the C_β-C_β distance calculated from published crystal structures (PDB: 1OMP [apo] and 1ANF [holo]). Shaded areas indicate 95% confidence interval. To see this figure in color, go online.

Notably, none of the L20C constructs exhibited DEER when labeled with I1 under standard conditions and had to be repurified and labeled under denaturing conditions to detect DEER. Analysis of this site on apo- and maltose-bound crystal structures (PDB: 1OMP and 1ANF, respectively) suggests that the bulky iodoacetamide group might not be able to access the somewhat buried cysteine residue when labeling folded protein. Despite the need for labeling under denaturation, all L20I1 constructs exhibited conformational changes with the expected magnitude and direction, again suggesting that labeling did not significantly perturb MBP structure and function.

One construct, D41V1 S238V1, contained additional long-distance peaks in both the apo and holo states. These peaks are likely protein dimers that have previously been observed when spin labeling with V1 at low label-to-protein ratios (43). We did not see this effect with any other construct or spin label, suggesting that this phenomenon was specific to both the label and the site pair.

Previous publications have observed incomplete conformational change of MBP attributed to the presence of cryoprotectants such as ethylene glycol and, to a lesser extent, glycerol (67). We did not detect any residual apo MBP after the addition of maltose, likely due to the use of glycerol instead of ethylene glycol, a lower cryoprotectant concentration, and a higher maltose concentration. We did, however, observe a small population of the maltose-bound conformation in the apo samples, which was most noticeable for S238C L275C. For most constructs, the relative population of bound conformation is small and is consistent with previous observations that a small population of MBP samples closed conformation in the absence of maltose (68).

Comparison of spin-label modeling methods

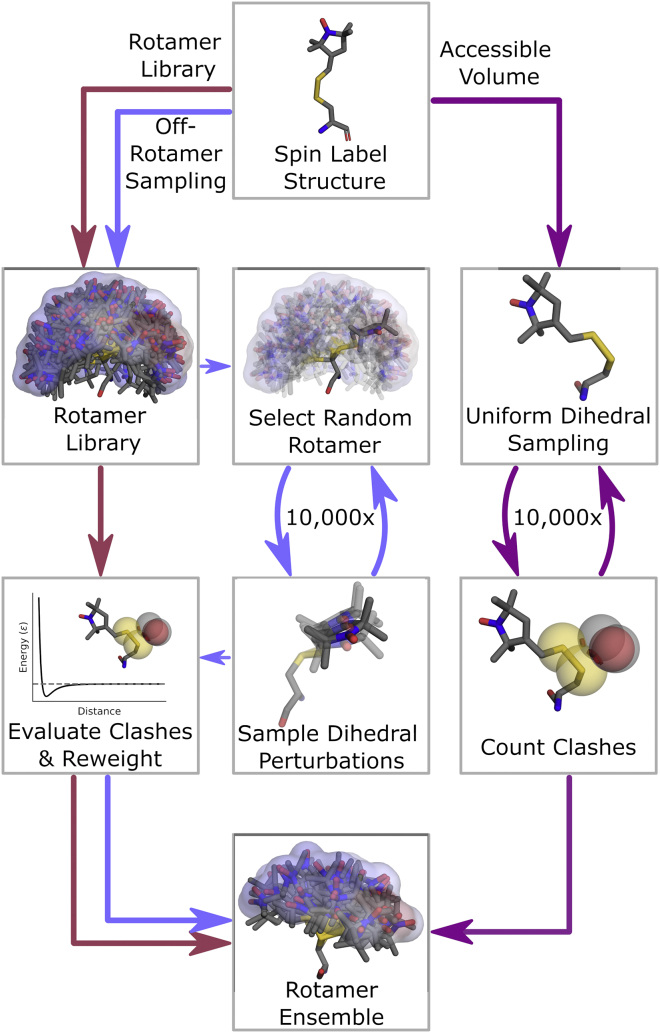
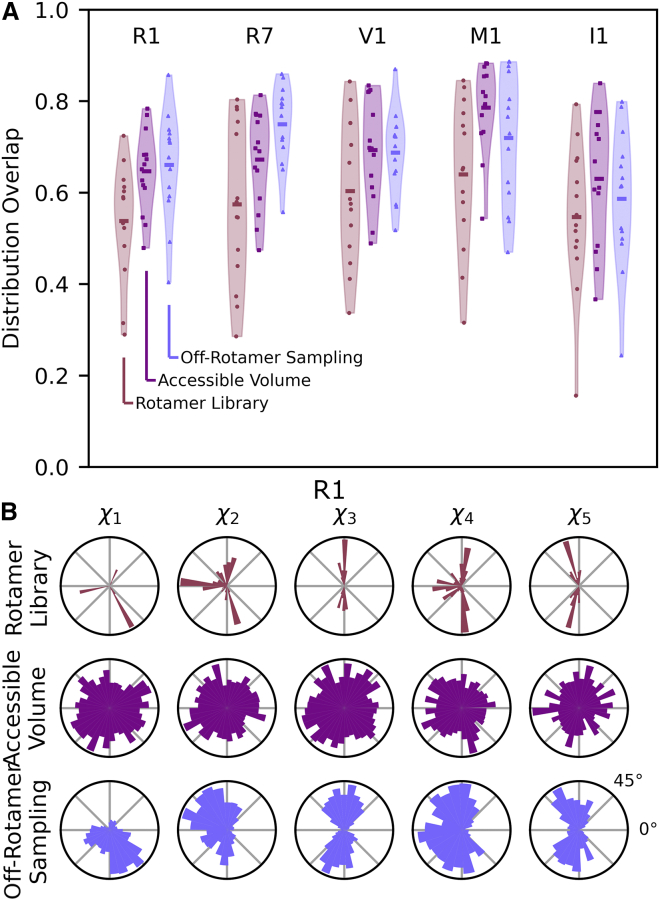
For each site pair and each label type, we simulated DEER distance distributions (Fig. S6–S10) in both the apo- (PDB: 1OMP) and maltose-bound states (PDB: 1ANF) using two of the most popular spin-label modeling methods: the rotamer library approach (as implemented in MMM (32,53)) and the accessible-volume approach (as implemented in MTSSLWizard (33)). The approaches are summarized in Fig. 3, and detailed descriptions can be found in the materials and methods section. Fig. 4 A summarizes how well the two modeling approaches recover the experimentally determined distance distributions. We used distribution overlap as the primary metric to quantify the agreement between simulated and experimental distributions as it captures both differences in mean density and in distribution shape. We also utilized the Kullback-Leibler divergence, earth mover’s distance, and absolute difference in mean distance (Figs. S11–14; see description of metrics in the supporting material). All metrics indicate that, for our data set, the accessible-volume sampling method produces distance-distribution predictions that are in better agreement with experiment than those predicted by the rotamer library method. This result came as a surprise due to the less quantitative clash evaluation of the accessible-volume method and the lack of consideration of the internal energy of the spin label.

Figure 3.

Flow chart illustrating the three spin-label ensemble modeling protocols used in this work. To see this figure in color, go online.

Figure 4.

Comparison of model predictions to experimental DEER data. (A) Violin plot of experimental and simulated distance distribution overlap over the DEER data set for each spin label. Scattered points indicate overlap of individual samples. The horizontal line indicates the mean overlap of the group. Shaded bands are a density estimate of all data points in the group, indicating the characteristics of the distribution of the data. (B) Side-chain dihedral angle histograms of the R1 spin label over apo and holo samples. To see this figure in color, go online.

Fig. 4B plots histograms of the R1 side-chain dihedrals and shows a more realistic distribution of side-chain conformations for R1 labels modeled using the rotamer library approach, with the accessible-volume approach exhibiting major deviations from canonical side-chain dihedral conformations. In particular, the dihedral angle around the S-S bond, χ₃, exhibits an unrealistic, approximately uniform distribution in spin labels modeled using the accessible-volume approach, while it is well known to be highly energetically restricted to ±90° (69). Thus, while the accessible-volume method appears to make more realistic distance-distribution predictions, the rotamer library method seems to produce more realistic spin-label models. Analogous dihedral histograms for the other labels can be found in the supporting material (Figs. S16–S20).

A common issue with modeling side chains with static rotamer libraries is the large repulsion penalties between the rotamer and its environment that would otherwise be avoided by small adjustments to the label conformation or neighboring side chains (56). We refer to these kinds of clashes as rigid-body artifacts. Canonical amino acid modeling methods have shown that rigid-body artifacts can be mitigated by energy minimizations over the rotamer dihedral space (70), increasing the number of rotamers in a library (71), probabilistic side-chain sampling (72) and using modified Lennard-Jones potentials (56). Notably, the rotamer library approach modifies the Lennard-Jones potential with a “forgive factor” (Eq. 1) intended to alleviate this kind of artifact (32,53). The forgive factor f reduces the optimal van der Waals radius between two atoms, resulting in real clashes being energetically favored (Fig. S15). The rotamer library approach used in previous implementations and replicated here uses a forgive factor of 0.5; however, recent work uses forgive factors as low as 0.175 (73). Forgive factors below 0.85 have been shown to perform very poorly for canonical amino acid side-chain modeling (56).

To overcome the obstacles of rigid-body artifacts, we implemented an off-rotamer sampling scheme, which is schematically illustrated in Fig. 3. It uses a capped Lennard-Jones potential softened with a forgive factor of 0.9 (56) with only the repulsive term (Eq. 3; see materials and methods). For 10,000 iterations, a rotamer is sampled from the rotamer library at random. New off-rotamer conformations are generated by sampling dihedral angle perturbations from a von Mises distribution with a concentration parameter chosen to generate a standard deviation of approximately 35°. All rotamers with any non-bonded pairs of atoms closer than their joint van der Waals radius are discarded. External clashes are evaluated with Eq. 3, and all sampled rotamers are reweighted using Eq. 2. Similar off-rotamer sampling schemes have been shown to work well for modeling canonical amino acid side chains (72,74). Our approach combines some aspects of the rotamer library approach and the accessible-volume approach by introducing the rotamer library as a sampling prior and applying a more quantitative clash evaluation method than the accessible-volume approach.

We performed the same evaluation of the off-rotamer sampling approach using our MBP data set. As shown in Fig. 4 A, the off-rotamer sampling approach improves upon the rotamer library approach for all labels. In the cases of R1 and R7, it even shows a modest improvement on the accessible-volume approach (see also Figs. S11–S14). For the M1 and I1 labels, the off-rotamer sampling approach does not quite achieve the accuracy of the accessible-volume approach. Because both M1 and I1 have longer side chains, it is possible that the label conformations are dominated by external interactions resulting in conformations that could not be sampled from the rotamer library. In this case, off rotamers of M1 and I1 may not be sufficiently sampled, or the sampling standard deviation of 35° is too restrictive. Alternatively, the rotamer libraries used for I1 and M1 might not accurately represent the label conformational landscapes due to limitations in computational rotamer library development, such as errors in energy functions, lack of ergodic sampling, or because the libraries do not account for label modifications such as ring openings known to affect labels like M1 (75).

The off-rotamer sampling approach produces realistic spin-label conformations, as illustrated by the R1 dihedral histograms in Fig. 4 B. Unlike the accessible-volume approach, the off-rotamer sampling approach results in dihedrals clustered around the canonical torsion angle minima, gauche positive (60°), negative (−60°), and trans (±180°) for dihedral angles ${\chi }_1$, ${\chi }_2$, ${\chi }_4$, and ${\chi }_5$ and ±90° for ${\chi }_3$. These clusters are broader than those observed in the rotamer library approach but are still consistent with computational and experimental descriptions of the R1 spin label (37,69). Similar patterns are observed for R7, V1, M1, and I1 (Figs. S16–S20). Interestingly, V1 conformations where nitrogen 3 of the imidazoline ring can interact with the S_γ sulfur (${\chi }_4$ ≈0°) are not in abundance in either the rotamer library or off-rotamer sampling models (Fig. S18). Notably, this is the only conformation experimentally observed and has been computationally predicted to be about 4 kcal/mol more favorable than other conformations (46).

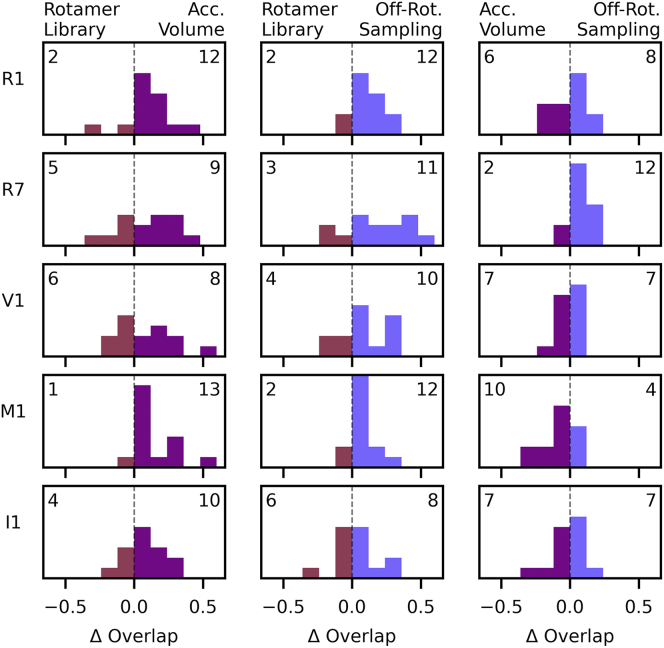
Fig. 5 shows the difference in overlap scores between all methods for all site pairs. The off-rotamer sampling and accessible-volume methods perform similarly, and they both predominantly show improvements over the rotamer library approach for our data set. Only in two cases out of 70 did the off-rotamer sampling method perform significantly worse (>5% difference in overlap) than both other methods (Fig. S8). These cases were L20I1 S211I1 holo (6% difference in overlap) and D41I1 S238I1 holo (25% difference in overlap). Both cases used the I1 label, which has the largest number of rotatable dihedrals, suggesting that the dihedral space may not be sufficiently sampled in either the generation of the rotamer library or the off-rotamer sampling method. These analyses were performed for all metrics (Figs. S8–S11) yielding similar results.

Figure 5.

Histograms of the difference in overlap score between modeling methods for each site pair. Bars are colored by which method the difference favors, i.e., by which side they are on. Numbers track the number of samples for which a method performed better and are placed on the corresponding side of the figure. To see this figure in color, go online.

Comparison of models

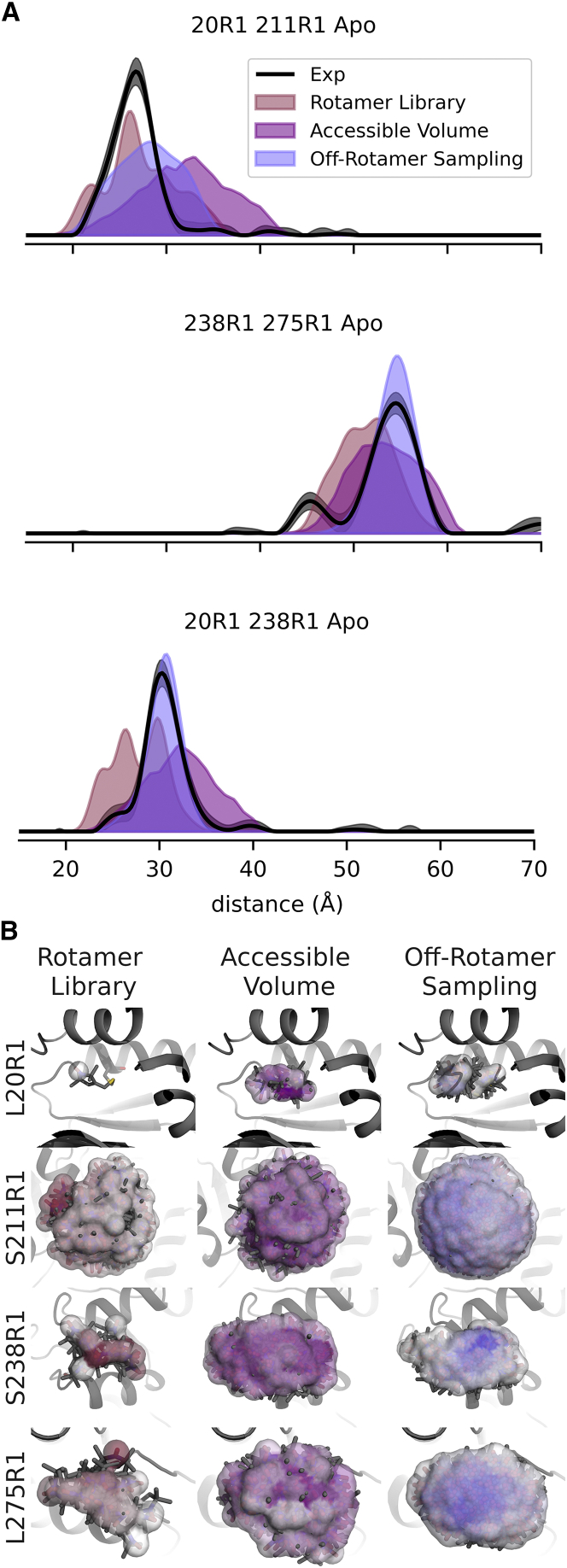
Fig. 6 shows three representative examples of simulated distance distributions over the R1 data set. Examples were selected to share sites on a single structure and to cover situations where the rotamer library method excelled, the accessible-volume method excelled, and where neither excelled. These examples illustrate how the off-rotamer sampling method can lead to more realistic spin-label models.

Figure 6.

Selected examples of simulated site pairs. Three examples illustrate the similarities and differences between the modeling methods. (A) Comparison of simulated (colored shaded areas) and experimentally determined (black traces) DEER distance distributions and 95% confidence intervals (gray shaded areas). (B) Comparison of spin-label ensemble models for each site used in the selected examples above. Surfaces indicate the locations of the N–O midpoints of the sampled rotamers, with color saturation indicating relative weight. To see this figure in color, go online.

In the first example (Fig. 6 A, top), L20R1 S211R1, the rotamer library approach seems to correctly predict the mode distance, while the accessible-volume approach predicts a more diffuse distribution of labels. Using the rotamer library as a prior allows the off-rotamer sampling approach to capture conformational preferences of R1 that lead to a more accurate distance-distribution prediction than the accessible-volume approach. In this case, the off-rotamer sampling method did not perform as well as the rotamer library. As one of the most solvent-exposed sites, the S211R1 rotamer ensemble has the largest number of rotamers (Fig. 6 B, S211R1 rotamer ensembles). These data suggest that the off-rotamer sampling method likely overestimates the conformational freedom of the R1 label in the absence of tertiary contacts.

In the second example (Fig. 6 A, middle), S238R1 L275R1, the rotamer library approach underpredicts the major mode of the experimental distribution, likely due to erroneous redistribution of weights caused by rigid-body artifacts and the significant forgive factor. Sampling off-rotamer conformations at sites S238 and L275 reveals that minor changes to the side-chain dihedrals can reduce these artifacts, resulting in a more accurate prediction of the primary mode of the experimental distribution. This is visualized in the spin-label ensembles of L275R1 (Fig. 6 B), where the off-rotamer sampling method places most of the label density near the center of the ensemble and the rotamer library approach places most of the density on one rotamer near the top of the ensemble. The accessible-volume method accurately predicts the mode of the experimental distribution and has the best overlap score overall, although this is likely due to the broad nature of the distribution adding overlap with the lower-distance peak. This peak is likely a subpopulation of the closed form of MBP; since MBP is known to sample the holo conformation in the absence of ligand (68), the peak in question appears in roughly the same location as the holo peak of the same construct (Fig. 2), and all other labels of the same site pair exhibit a similar trend. These data suggest that the accessible-volume method is oversampling the conformational space of the R1 spin label compared with the rotamer library and off-rotamer sampling approaches, as is evident by having more rotamers than any other ensemble.

In the third example (Fig. 6 A, bottom), L20R1 S238R1, neither the rotamer library approach nor the accessible-volume approach accurately model the distance distribution as well as the off-rotamer sampling approach. The S238R1 rotamer library ensemble is constrained to a very small region, and most of the spin density is assigned to one or a small number of rotamers. The off-rotamer sampling ensemble also places most of the ensemble density at one location but more completely samples the surrounding region. The location of the primary density is different from the rotamer library ensemble, suggesting that the rotamer library has rotamers that occupied this location, but they were eliminated by clash evaluation. In contrast, the accessible-volume ensemble predicts a broad ensemble of spin labels with no clear preferred conformations, resulting in a broad distribution.

Discussion

We have constructed, labeled, and performed DEER on nine site pairs of MBP with five spin labels under two different conditions. Our data illustrate the different qualities of each label and highlight limitations, such as label accessibility and stability, that should be considered when designing DEER experiments. We then used a subset of our DEER data to test two widely used modeling methods, the rotamer library method and the accessible-volume method. We showed that the accessible-volume method made more accurate distance distribution predictions for our data set and that the rotamer library method produced more realistic dihedral angle distributions. With these insight regarding the strengths and weaknesses of each method, we developed a spin label modeling method based on canonical side-chain modeling methods that combines aspects of the two approaches. The addition of off-rotamer sampling to the rotamer library, combined with a strictly repulsive clash evaluation function with less softening, improved the ability to accurately predict distributions while still producing spin-label models with more realistic dihedral angle distributions.

Notably, the off-rotamer modeling approach barely outperformed the accessible-volume approach over all labels, with 38/70 of the off-rotamer distributions having better overlap compared with 32/70 of the accessible-volume approach. Most of the off-rotamer predictions that outperformed the accessible-volume approach were for the R1 and R7 labels. The lack of improvement on the V1, M1, and I1 predictions is likely due to inaccuracies in the rotamer libraries as discussed below. Additionally, the accessible-volume approach often results in significantly broader distributions than the other two methods, making it more likely to overlap the experimental distributions. While broader distributions may result in improved overlap, they also make modeling small changes in distance distributions more difficult. The effect of this limitation may be more evident in data sets with more stringent features such as multiple correlated distances as observed in homooligomers (10,76). Taken together with the lack of physically realistic spin label conformations, we believe that the accessible-volume approach is limited in its applications for spin-label and protein modeling with EPR and that the off-rotamer modeling approach offers several improvements despite the seemingly comparable performance with the accessible-volume approach.

The primary consideration when developing the off-rotamer sampling approach was the reduction of rigid-body artifacts inherent in the rotamer library approach (56). The data presented here suggest that the use of a rigid rotamer library is prone to these kinds of artifacts, even when utilizing a substantial forgive factor. Alternative methods for avoiding rigid-body artifacts include increasing the library size (71) and minimizing side-chain clashes in dihedral space (77). Ideally, effective side-chain modeling methods developed for canonical amino acids can be adopted for spin-label and other non-canonical side chains. Motivated by homology modeling and protein design and supported by an abundance of high-resolution data in the Protein Data Bank, the development of accurate modeling methods for canonical side chains has been an active field with much success (72,78, 79, 80, 81, 82).

In addition to rigid-body artifacts, we also identified several potential limitations of the existing spin-label rotamer libraries. In particular, the V1 rotamer library, and consequently the off-rotamer sampling method, did not reflect the expected conformations from previous experiments and theoretical computations (46). Utilization of the I1 and M1 rotamer libraries did not improve modeling accuracy as well as was observed for R1 and R7. Unfortunately, these labels are not as well studied as R1 and V1, making assessment of their rotamer libraries difficult. Naturally, as the most widely used and well-studied spin label, the R1 rotamer libraries have been the most thoroughly developed and tested. By extension, the R7 libraries are likely just as performant, as they have all the same dihedrals and only differ by one atom. While the accessible-volume method may be a suitable approximation for most applications, careful parameterization, sampling, and statistical analysis of other spin labels would likely lead to more accurate spin-label modeling. Even though the R1 and R7 rotamer libraries appeared to be accurate, they may also benefit from further development to include dihedral variance estimates of individual rotamers to improve sampling accuracy. Developing accurate computational methods for rotamer library development would also be beneficial for side-chain modeling of other non-canonical side chains like those used in fluorescent resonance energy transfer (67,73).

Another avenue for improvements would be the development of more accurate score functions. All three of the methods presented here only make use of clash evaluations; however, the inclusion of bonded forces, electrostatics, and solvent models are likely critical to accurate spin-label modeling. While methods like molecular dynamics and Rosetta have more accurate score functions, they only implement a few spin labels, and adding new labels is a highly technical and laborious task. That being said, recent developments in universal force fields (41,83) may be paving the way for more accurate score functions for a wider range of labels. Such advancements should enable easy inclusion of labels that are difficult to parameterize such as trityl- (84,85), gadolinium- (86), and copper-based labels (87, 88, 89).

There are still several limitations to the off-rotamer sampling approach. The first major limitation is the use of the same variance across all dihedrals and all labels. It is well known that ${\chi }_4$ and ${\chi }_5$ of the R1 label exhibit significantly more mobility than ${\chi }_1$, ${\chi }_2$, and ${\chi }_3$ (29, 30, 31,69,90). Similar anisotropies in dihedral variances likely exist in other labels, suggesting that the use of different variances or even covariances may enhance modeling accuracy. A second limitation is the inability to use this approach on bifunctional labels like Rx (91) and di-histidine copper (87, 88, 89) because the dihedral angles are strongly constrained by the cyclic nature of these labels. These labels are particularly attractive for protein structure investigations because they limit label flexibility and reduce the distance of the spin label from the protein backbone (87, 88, 89). Another major limitation shared by all the methods discussed here is the lack of repacking, i.e., resampling neighboring amino acids. Presently, all spin-label modeling applications known to the authors, except Rosetta (36) and molecular dynamics (37,39,41) methods, keep neighboring side chains and backbone atoms fixed. The lack of local repacking introduces another avenue for rigid-body artifacts.

Author contributions

This study and methods were conceived by M.T., E.R.C., and S.S.; novel software used was developed by M.T.; data collection and analysis were performed by M.T. and E.R.C.; article was written by M.T., E.R.C., and S.S.

Data availability

The raw DEER data collected and used here are available through the University of Washington ResearchWorks archive at https://doi.org/10.6069/S9MT-2J06.

Editor: H. Raghuraman.