Skip to main content
PMC home page
JACS Au logoLink to JACS Au
. 2022 Sep 1;2(9):2029–2037. doi: 10.1021/jacsau.2c00306

Multiconfiguration Pair-Density Functional Theory for Chromium(IV) Molecular Qubits

Arturo Sauza-de la Vega †, Riddhish Pandharkar †,, Gautam D Stroscio †, Arup Sarkar †, Donald G Truhlar ‡,*, Laura Gagliardi †,¶,*
PMCID: PMC9516709  PMID: 36186551

Abstract

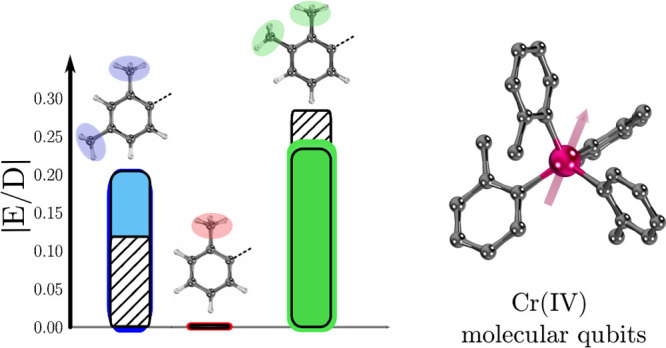
graphic file with name au2c00306_0006.jpg

Pseudotetrahedral organometallic complexes containing chromium(IV) and aryl ligands have been experimentally identified as promising molecular qubit candidates. Here we present a computational protocol based on multiconfiguration pair-density functional theory for computing singlet–triplet gaps and zero-field splitting (ZFS) parameters in Cr(IV) aryl complexes. We find that two multireference methods, multistate complete active space second-order perturbation theory (MS-CASPT2) and hybrid multistate pair-density functional theory (HMS-PDFT), perform better than Kohn–Sham density functional theory for singlet–triplet gaps. Despite the very small values of the ZFS parameters, both multireference methods performed qualitatively well. MS-CASPT2 and HMS-PDFT performed particularly well for predicting the trend in the ratio of the rhombic and axial ZFS parameters, |E/D|. We have also investigated the dependence and sensitivity of the calculated ZFS parameters on the active space and the molecular geometry. The methodologies outlined here can guide future prediction of ZFS parameters in molecular qubit candidates.

Keywords: Multiconfigurational calculations, Molecular qubits, Chromium(IV) aryl complexes, Zero-field splitting, Singlet−triplet gap, Optically addressable qubits

Introduction

Advances in quantum computing, quantum sensing, and high-density data storage require fine control of the superposition states in qubits—the fundamental building units of quantum information.1−4 A variety of different materials have been proposed to actualize these qubits, including superconducting circuits,5 trapped ions,6 silicon-based qubits,7 rare-earth ions in crystals,8 and nitrogen-vacancy (NV–) defects in diamond.9,10 Each of these materials have physical properties and features that can be synthetically controlled, making them potentially promising qubit candidates.

Some paramagnetic transition metal complexes have also been proven to be reliable spin qubits. They are optically addressable for photoluminescence readout, and they can be coherently manipulated with microwave radiation. Also, they can display coherence times longer than 100 μs; it is possible to increase their coherence times through the modification of the molecular environment.9,11,12 These features make them promising spin qubits with properties tunable by chemical synthesis.11,13−16

Among these paramagnetic transition metal complexes, molecules with a triplet ground-state and small zero-field splitting (ZFS) provide two-level quantum systems addressable via microwave frequencies.11,14,17 Strikingly, Bayliss et al.17 showed that the ZFS parameters of pseudotetrahedral chromium(IV) aryl complexes can be tuned by modifying their organic ligands. In order to design new, better qubits, a very large chemical space of possible ligands needs to be explored. It is not feasible to achieve this by purely synthetic approaches. Therefore, a reliable computational methodology to predict the properties of target compounds needs to be developed.

Several quantum-mechanical theoretical models based on multireference methods or Kohn–Sham density functional theory (KS-DFT) have been used to predict molecular properties.18,19 It is possible to calculate the ZFS parameters with a coupled-perturbed response treatment using density functional theory.20 When dealing with open-shell transition metal complexes, KS-DFT performance can be questionable and is functional-dependent.18,21−23 Due to close-lying excited states and the importance of the proper account of electron correlation of the d-orbitals in transition metal complexes, multireference methods are preferred. Multiconfiguration perturbation theory methods perform better than KS-DFT, but they are computationally expensive when dealing with large molecular systems.24 In the present work, we used multiconfigurational pair-density functional theory (MC-PDFT) to investigate the spin-state gaps and ZFS parameters of three Cr(L)4 compounds with different aryl ligands, L = 2-methylphenyl, 2,3-dimethylphenyl, or 2,4-dimethylphenyl (Figure 1). We refer to these Cr(IV) complexes as 1, 2, and 3, respectively. Multireference methods have been shown to be useful for understanding the electronic structure of these molecular qubits.25−30

Figure 1.

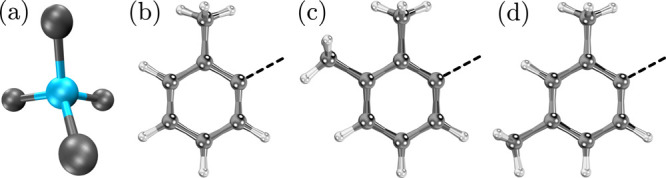
Figure 1

Open in a new tab

Potential molecular spin-qubits based on Cr(IV) aryl complexes. (a) Distorted tetrahedral environment with the Cr(IV) center (blue) and the ligating ligand atoms (gray). The organic ligands are based on (b) toluene, (c) o-xylene, and (d) m-xylene molecules. The dashed line indicates the carbon atom bonded to the metal center.

The ZFS parameters and the triplet-singlet gap are crucial descriptors for determining whether molecular qubit candidates can be initialized and addressed. In this paper, we use multireference calculations to study the ZFS parameters and vertical excitation energies of the chromium(IV) aryl complexes shown in Figure 1. Because the ground triplet state is orbitally nondegenerate, its zero-field spin–orbit splitting only becomes nonzero at second order, and therefore, it is small and depends strongly on the spin–orbit couplings to the excited states. Janicka et al.31 showed that the spin–spin contribution to the ZFS is negligibly small, and we shall not consider it here. Our paper differs from their in that they used perturbation theory, whereas we demonstrate the applicability of the MC-PDFT method, which, due to its lower cost, may be used efficiently in future work to study large chemical spaces of ligands. Another difference from previous work is that, in order to better understand the multiconfigurational character of the ZFS parameters, we examine the dependence of the calculated ZFS parameters on the choice on active space; we consider a wide range of choices.

We investigate changes in the ZFS parameters with respect to (i) molecular geometry, (ii) the choice of active space, and (iii) the choice of multireference method. We also study the origin of the small ZFS values in the examined complexes. Overall, the analysis reported here demonstrates the remarkable performance of hybrid multistate pair-density functional theory (HMS-PDFT) for the computation of triplet-singlet gaps and ZFS parameters with accuracy comparable to the well-established multistate multiconfiguration complete active space second-order perturbation theory (MS-CASPT2).

Theoretical Framework

The quantum mechanical treatment of the ZFS relies on the phenomenological Hamiltonian:

graphic file with name au2c00306_m001.jpg 1

where Ŝ is the pseudospin operator, and D is a real symmetric tensor that characterizes the ZFS.32,33 After diagonalization, the Hamiltonian in eq 1 can be rewritten as34

graphic file with name au2c00306_m002.jpg 2

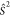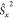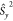By using the relation Inline graphic = Inline graphic + Inline graphic + Inline graphic and using the standard convention that the trace of D is zero, the Hamiltonian can be expressed as,34

graphic file with name au2c00306_m007.jpg 3

where the axial (D) and rhombic (E) ZFS parameters are defined to be

graphic file with name au2c00306_m008.jpg 4

Different quantum technology applications place different demands on the value of D. For example, D needs to be large and negative in single-molecule magnets used for data storage applications.1,35−37 However, for optically addressable molecular qubits, D should be small, allowing for control of the electron spin by microwave radiation.11,17 One can try to design molecules with small D by changing the ligand field; the magnitude of D can then be measured in EPR experiments.11

We use multiconfiguration wave functions based on active spaces, and choosing an active space requires the selection of a set of n active electrons in m active orbitals; the resulting active space is denoted (n, m). Active space selection is not a black box operation; there are several procedures for active space selection,38−43 and specialized considerations may be advisible when dealing with magnetic properties.44−46 Following the protocol of ref (47), a basis of states computed without including spin–orbit coupling (called spin–orbit-free states or spin–orbit-free roots) are computed first. The spin–orbit-free states include the ground-state and various excited states with different spin multiplicities. For transition metal systems, the valence 3d orbitals are an obvious choice for inclusion in the active space; however, the resulting minimal active space is not large enough to capture a sufficient portion of the multiconfigurational character when the covalency of the metal–ligand bonds become significant. Alternately, inclusion of too many metal-to-ligand or ligand-to-metal charge transfer states may result in an unaffordable state-averaged CASSCF calculation. Thus, it is necessary to fine-tune the number of excited states used to compute the ZFS parameters.44 The spin–orbit matrix elements are computed under the restricted active space state interaction spin–orbit (RASSI-SO) formalism.47−49 The resulting matrix elements allow the calculation of the magnetic properties.

We calculate the spin–orbit-free state energies with the state-averaged complete active space self-consistent field method (SA-CASSCF).50 This method provides a good qualitative description of systems with static correlation. To quantitatively describe dynamic electron correlation in chemical systems, a post-SA-CASSCF calculation is performed, using multistate complete-active-space second-order perturbation theory (MS-CASPT2),51 multiconfiguration pair-density functional theory (MC-PDFT), or multistate pair-density functional theory (MS-PDFT). MC-PDFT and MS-PDFT are methods that provide CASPT2-quality and MS-CASPT2-quality accuracy at reduced computational cost.52−57 The MC-PDFT or MS-PDFT computational cost is similar to that of computing the reference wave function.58 MS-PDFT has recently been successfully used to study the g tensor59 and the ZFS46 of several transition metal complexes.

The MC-PDFT and MS-PDFT performance can be further improved by using a hybrid MC-PDFT (HMC-PDFT) and hybrid MS-PDFT (HMS-PDFT).60 Similarly to Kohn–Sham DFT, in which local functionals are combined with Hartree–Fock exchange, the HMC-PDFT energy can be expressed as

graphic file with name au2c00306_m009.jpg 5

where the parameter λ indicates the amount of CASSCF energy included in the hybridization. In the present work, we consider the hybrid translated functional tPBE0 defined previously,60 for which the λ parameter is set equal to 0.25.

Computational Methods

We performed various kinds of calculations, which we now describe in turn. All calculations were performed without imposing any symmetry.

Crystal Calculations

We optimized the geometries of the chromium(IV) aryl complexes (Figure 1) in periodic calculations on the molecular crystals to consider the experimental environment. These calculations were carried out using the VASP package61−64 with the PBE exchange-correlation functional65 and the D3 dispersion term damped by the Becke–Johnson damping factor.66 A plane wave kinetic energy cutoff of 600 eV was used along with the PAW pseudopotential.67,68 A triplet spin multiplicity was considered since all the complexes studied herein have triplet ground states. The Brillouin zone was sampled only at the Γ point. The experimental crystal structure17 was used as an initial guess, and the ionic positions and the lattice coordinates were allowed to relax without any space group symmetry imposed.

Subsequent calculations (described below) were out for a single molecule using both the molecular structure extracted from this optimized crystal and the molecular structure extracted from the experimental crystal structure.

Gas-Phase Calculations

Using the crystal structure as input, we optimized the molecular geometries for the triplet state of the complexes studied herein. The calculations were done using Orca 5.0.69 To be consistent with the crystal calculations, we used the PBE Kohn–Sham functional and the D3 dispersion model with Becke–Johnson damping factor,66 and Def2-TZVPP basis set.70

The optimized geometries were used as inputs for the following multiconfigurational calculations.

SA-CASSCF Calculations

The optimized and crystal structures were used as inputs for SA-CASSCF calculations of the triplet ground state and first singlet excited state energy. Calculations for both spin states were performed at the ground-state (triplet) geometries without spin–orbit coupling. These calculations were performed using OpenMolcas v21.10.71 We used the ANO-RCC-VTZP basis set for the chromium atom and the ANO-RCC-VDZ basis set72 for the carbon and hydrogen atoms. The second-order Douglas–Kroll–Hess Hamiltonian to was used to account for scalar relativistic effects.73,74 We used the resolution of the identity and the Cholesky decomposition to speed up the two-electron integral calculations.75

We considered several active spaces (Figure 2). The Cr(IV) ion has a 3d2 electron configuration; the minimal active space for the ion in tetrahedral geometry would be (2,2), consisting of a doubly degenerate e orbital. A (2,5) active space is constructed by adding the empty t2* orbitals. Adding a correlating subshell of d orbitals yields a (2,10) active space. Alternatively, one can add Cr–ligand occupied molecular orbitals, t2, to the to the (2,5) active space to construct the (8,8) active space that accounts better for metal–ligand covalency. Finally, for the largest active space, we added the correlating d subshell and the chromium s bonding and antibonding orbitals to the (8,8) active space to obtain the (10,15) active space. (See Figures 2 and S7–S11. Figures and tables with a prefix S are given in the Supporting Information.)

Figure 2.

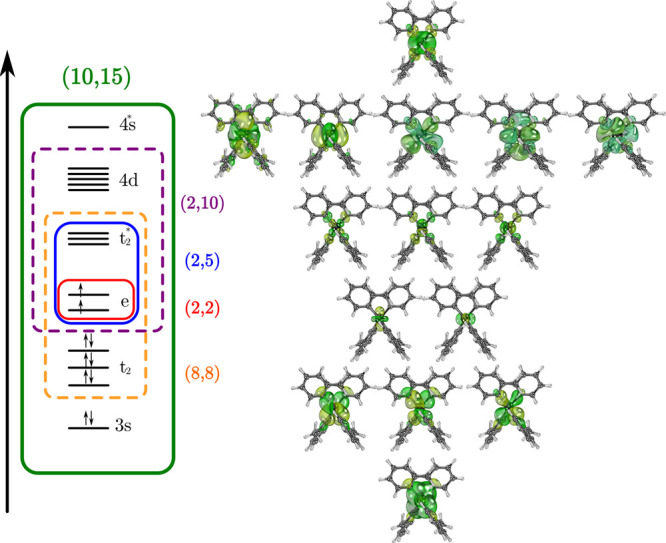
Figure 2

Open in a new tab

Molecular orbitals of molecule 1 are included in the different active spaces considered for the multireference calculations. Left: In the diagram, the red, blue, purple, orange, and green boxes correspond to the (2,2), (2,5), (2,10), (8,8), and (10,15) active spaces. Right: Drawings of all the molecular orbitals considered for the aforementioned active spaces. The orbitals are displayed in the same order as in the diagram on the left.

The number of states averaged was 10 triplets and 15 singlets for the (2,5) and (2,10) active spaces and 7 triplets and 9 singlets for the (8,8) and (10,15) active spaces. Equal weights were used for all averaged energies.

Multiconfiguration Calculations of the Singlet–Triplet Splitting

The first excited singlet state is nearly doubly degenerate due to the near-tetrahedral geometry. Using the optimized spin-triplet structures, we calculated the vertical excitation energies to the lower of the two states. These excitation energies were calculated without spin–orbit coupling by SA-CASSCF (described above), MS-CASPT2, single-state MC-PDFT, and single-state hybrid MC-PDFT (HMC-PDFT). The reference functions for the latter three kinds of calculation were the SA-CASSCF calculations described above. The MS-CASPT2 calculations employed an imaginary shift of 0.3 au and an ionization-potential electron-affinity shift of 0.25 au;59 the model space sizes were the same as the numbers of states averaged in the SA-CASSCF steps. The MC-PDFT calculations employed the tPBE on-top functional.52 The HMC-PDFT calculations employ the tPBE0 functional,60 which combines 25% CASSCF nonclassical energy with 75% tPBE nonclassical energy. A fine grid was used for the MC-PDFT and HMC-PDFT calculations.

Inclusion of Spin–Orbit Coupling

The ZFS parameters were calculated for all mentioned active spaces except for the minimal one. The ZFS calculations include spin–orbit coupling by methods describe previously;46,49,59,76 in particular, spin–orbit coupling was included in SA-CASSCF, MS-CASPT2, MS-PDFT,77 and HMS-PDFT calculations by using the atomic-mean field approximation to the Breit–Pauli Hamiltonian, where the spin–orbit coupling operator is diagonalized using the eigenstates obtained with the multiconfiguration methods aforementioned, to obtain the spin–orbit coupled eigenstates and energies. This procedure was widely discussed in ref (59), and the available implementation on the RASSI module48,49 of OpenMolcas. This allows us to use molecular orbitals optimized separately for the singlet and triplet manifolds. For the latter three kinds of calculation, the states included in the model space were the same as the states averaged in the SA-CASSCF calculations. In the MS-PDFT and HMS-PDFT calculations, the basis for the model space calculations was the set of SA-CASSCF eigenvectors (i.e., we did not transform to an intermediate basis). Additional data for the on-top functionals tested is available in the Supporting Information (Figures S15–S17).

NEVPT2 Calculations

For comparison, we also performed SA-CASSCF calculations and N-electron valence-state second-order perturbation theory78−80 (NEVPT2) calculations (with these SA-CASSCF calculations providing the reference states) using the Orca 5.0 code.69 In these calculations, the orbitals are optimized simultaneously for the singlets and triplets, resulting in a single set of molecular orbitals. Ten triplets and 15 singlets were included in the state averaging with equal weights. We used an active space of 2 active electrons in 5 active orbitals (the 3d orbitals). Representative active space orbitals are shown in Figure S2. The Douglas–Kroll–Hess73,74,81−83 scalar relativistic Hamiltonian and the DKH-def2-TZVP basis set were used. SCF convergence criteria with an energy tolerance of 10–7 hartrees were applied. The NEVPT2 calculations were performed on the experimental and periodic optimized Cr(IV) structures (see Tables S7 and S8).

Kohn–Sham Density Functional Calculations

The Orca 5.0(69) package was used to determine the ZFS parameters with various Kohn–Sham functionals. Details are in the Supporting Information.

Spin–Spin Coupling

We also considered the effect of spin–spin coupling (SSC) in the SA-CASSCF/NEVPT2 calculations and Kohn–Sham density functional calculations. The SA-CASSCF/NEVPT2 calculations were done without and with SSC, and this showed that SSC has only a small effect on the results (see Tables S7 and S8). SSC was not included in the OpenMolcas calculations.

Results and Discussion

Structures

It is well-known that the spin properties of the metal ion depend significantly on its coordination environment.16,17,28,84−88 In order to study the sensitivity of the results to the geometry, we compared calculations with (i) the experimental crystal structures (measured at 100 K) from ref (17), (ii) the structures optimized with periodic boundary conditions on the unit cell, and (iii) the gas-phase optimized structures. The optimized structures differ from the former by lack of the zero-point and temperature effects.

The experimental and optimized structures showed slight differences in the structural parameters. The four Cr–ligand bond lengths in the periodic optimized complex 1 structure are 1.97 Å, in the gas-phase structure are 1.98 Å, while the bond lengths range from 1.98 to 2.00 Å in the structure obtained from the crystallographic data. The Cr–ligand bond distances are 1.98 Å in the complex 2 optimized geometries, whereas the two bond distances are 2.02 and 2.00 Å in the crystal structure. For 3, there are two different Cr–ligand bond lengths, 1.98 and 1.97 Å in the optimized geometries as compared to 2.00 and 1.99 Å in the experimental structure. The geometric parameters differ the most in the compound 1, where the largest difference in the Cr–ligand bond distances is 0.03 Å, and the largest difference in the R–Cr–R bond angles is 2.8°. For the complexes 2 and 3, the corresponding values between the experimental and periodic optimized structures are 0.04 Å and 0.1°, and 0.03 Å and 1.4°, respectively. However, between the gas-phase and experimental structures, the differences between the bond angles increase up to 5°. The experimental structures and those optimized with periodic calculations show more similarity between them (see Figures S4–S7).

Triplet–Singlet Gaps

Bayliss et al. reported for complexes 1, 2, and 3 the experimental zero-phonon lines ranging from 1.20 to 1.22 eV (1009 to 1025 nm).17 We evaluated the capability of the methods explored herein to reproduce these reported experimental singlet–triplet gaps.

According to our calculations, the first singlet excited state is double degenerate, and the optimization of such structure is complicated with Kohn–Sham DFT based methods. Thus, we approximate the triplet-singlet gap as a vertical excitation. Table 1 reports the triplet–singlet energy differences (ΔET-S) for the molecule 1 using the experimental, and periodic optimized geometries. We computed the vertical excitation energy at the ground (triplet) state geometry. The experimental gap from the zero-phonon line would correspond to a difference between the lowest vibrational levels of the two different spin states, which have different geometries. In Table 1, the MC-PDFT and HMC-PDFT results are labeled tPBE and tPBE0, respectively. The close agreement between the (2,2) MS-CASPT2 gap and the experimental value may be attributed to some cancellation of errors. When virtual orbitals are added to form the (2,5) and (2,10) active spaces, the triplet-singlet MS-CASPT2 energy gap is reduced by about 0.2–0.3 eV, with respect to the minimal active space. In contrast, tPBE0 is less affected by adding empty orbitals. Further inclusion of Cr–ligand bonding and antibonding orbitals causes both the MS-CASPT2 and tPBE0 gaps to increase. However, the tPBE0 value displays a better agreement with the experimental findings when using the (10,15) active space. With the largest active space, SA-CASSCF overestimates the gap by 0.29–0.46 eV, depending on the geometry, MS-CASPT2 overestimates it by 0.21–0.31 eV, MC-PDFT underestimates it by 0.18 or 0.04 eV, and HMC-PDFT is accurate within 0.04 eV at either geometry.

Table 1. Calculated Triplet–Singlet Gaps (ΔET-S, in eV) Using the Periodic Optimized Structure of Molecule 1 with the SA-CASSCF, MS-CASPT2, tPBE, and tPBE0 Methods.

ΔET-S for optimized geometry
active space SA-CASSCF MS-CASPT2 tPBE tPBE0 expt.
(2,2) 1.87 1.23 0.55 0.88  
(2,5) 1.89 0.94 0.48 0.83  
(2,10) 1.81 0.98 0.51 0.83  
(8,8) 1.83 1.41 0.94 1.16  
(10,15) 1.66 1.41 1.02 1.18 1.20
ΔET-S for experimental geometry
active space SA-CASSCF MS-CASPT2 tPBE tPBE0 expt.
(2,2) 1.75 1.20 0.64 0.92  
(2,5) 1.89 0.92 0.49 0.84  
(2,10) 1.81 0.97 0.52 0.98  
(8,8) 1.83 1.43 0.97 1.18  
(10,15) 1.49 1.51 1.15 1.24 1.20
Open in a new tab

The ΔET-S values for 1, 2, and 3 are very similar, 1.18, 1.22, and 1.21 eV, respectively, as indicated in Tables 1, 2, and S9–S11. In agreement with this trend, our HMC-PDFT calculations also show only slight differences among the three complexes, as shown in Table 2. This table also shows Kohn–Sham density functional calculations from the literature88 that are consistently larger than experiment and show much larger variation with changing ligands. We performed additional Kohn–Sham theory with several functionals; the results are given in Tables S1–S3, and they show systematic overestimation of the energy gap for all functionals tested. We conclude that it is better to use multireference methods to study this kind of problem. Table 2 also shows the MS-CASPT2 for all three complexes. MS-CASPT2 agrees that the variations in the gap with the changes of ligands are small, but it systematically overestimates the magnitudes of the gaps. The finding that HMC-PDFT agrees better with experiment than does MS-CASPT2 is very encouraging, since HMC-PDFT has a lower computational cost with respect to MS-CASPT2.

Table 2. Calculated Triplet–Singlet Gaps (ΔET-S) with the (10,15) Active Space for the Periodic Optimized Geometry of Molecules 1, 2, and 3 Using MS-CASPT2, tPBE0, and B3LYP+D3(BJ) Methodsa.

complex MS-CASPT2 tPBE0 B3LYP+D3(BJ)b expt.
1 1.41 1.18 1.63 1.20
2 1.46 1.22 1.47 1.22
3 1.46 1.21 1.31 1.20
Open in a new tab
a

The energy gaps are reported in eV.

b

The DFT values were obtained from ref (88).

Zero-Field Splittings

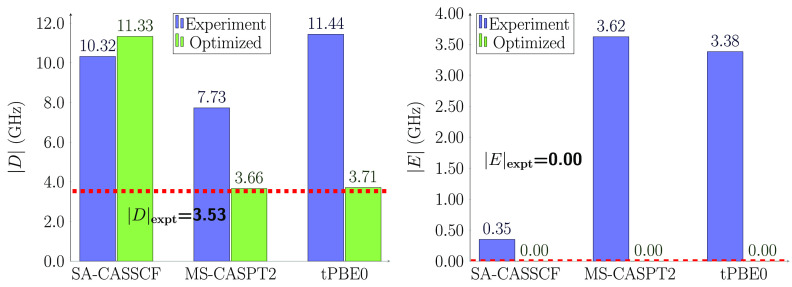
Figure 3 shows the |D| and |E| parameters of the complex 1, in blue for the experimental structure and in green for the structure optimized in the crystal, with both employing the (2,5) active space. The HMS-PDFT results are labeled tPBE0 in the figures. To put the size of the splitting into perspective, we note that the experimental |D| value of 3.53 GHz is only 0.118 cm–1 = 0.0146 meV.

Figure 3.

Figure 3

Open in a new tab

Computed ZFS parameters |D| and |E| of the complex 1 using the (2,5) active space and the SA-CASSCF, MS-CASPT2, and HMS-PDFT(tPBE0) methods. The vertical bars represents the absolute magnitude of the parameters for the experimental structure (blue) and the optimized one (green). The horizontal line represents the experimental values.17

The rhombic parameter (E) is zero by tensorial symmetry for a system with a 3-fold or higher rotation axis. The present system is slightly distorted, and we calculate a small but nonzero E parameter with the experimental structure, although the result reported experimentally17 is zero. However, when we use the optimized geometry, our calculated E value is indeed zero. This shows the importance of the geometry.

The results Figure 3 also indicate that |D| is also closer to experiment when calculated at the optimized geometry. The SA-CASSCF calculations overestimate |D| by more than a factor of 2, but MS-CASPT2 and HMS-PDFT are accurate within 5%. In ref (17), the authors were not able to obtain the sign of D. However, our calculations consistently predict that D is negative, meaning that for the triplet ground-state, the MS = 0 level is above the MS = ± 1 levels).

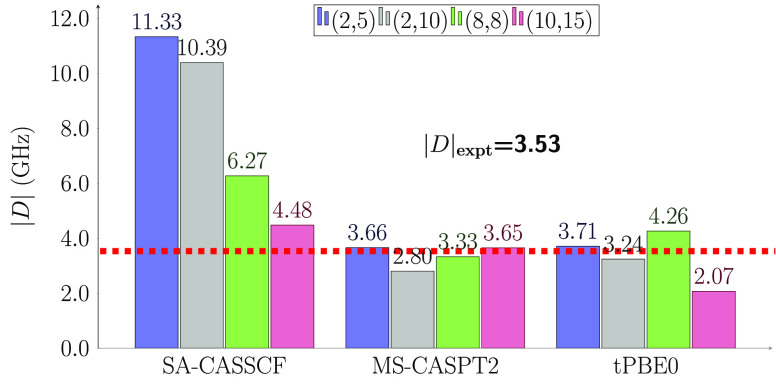
Figure 4 shows the computed |D| parameter for the system 1 at the optimized geometry with different active spaces. We see that the value of |D| is not sensitive to the change of active space for MS-CASPT2 and for three of the four active spaces for HMS-PDFT, even though the SA-CASSCF results differ from one another by as much a factor of 2.5. Although the crystallographic data suggest the complex 1 has a S4 symmetry, we obtained nonzero |E| values when using the experimental structure (Figure 3). This can be attributed to the disorder in the crystal structure. When using the optimized structure, all active spaces in Figure 4, yield an |E| value of zero–matching the experimental observations.

Figure 4.

Figure 4

Open in a new tab

Calculation of |D| parameter of optimized complex 1 geometry with the SA-CASSCF, MS-CASPT2, and HMS-PDFT(tPBE0) methods. The active spaces used are (2,5) in blue, (2,10) in gray, (8,8) in green, and (10,15) in purple. The dashed line corresponds to the experimental data.17

The inclusion of more triplets and singlets in the RASSI calculation does not improve the computed value of the axial parameter |D| of molecule 1, as shown in Tables S12–S15. The (8,8) MS-CASPT2 value for |D| is 3.33 GHz when using an energy cutoff of 4.3 eV and including 7 triplets and 9 singlets. When the cutoff is increased to 5.0 eV, thereby including 18 triplets and 16 singlets, there is a decrease in the magnitude of D, resulting in worse agreement with experiment. This behavior is also found for HMS-PDFT. This is also true for the (10,15) active space; when using more triplet and singlet excited states there is a decrease of the magnitude of |D|. For both active spaces, the computed |E| parameter is always zero regardless of the number of spin–orbit-free states included.

For the compounds 2 and 3, there is also a decrease in the quality of the calculated ZFS parameters when going beyond 7 triplets and 9 singlets in the RASSI calculation (Tables S16–S23). Because these 7 triplets and 9 singlets are mostly metal-to-ligand charge transfer (MLCT) states, we conclude that the MLCT states rather than ligand-to-ligand or ligand-to-metal charge transfer states are most useful to obtain a qualitative and semiquantitative description of the axial parameter.

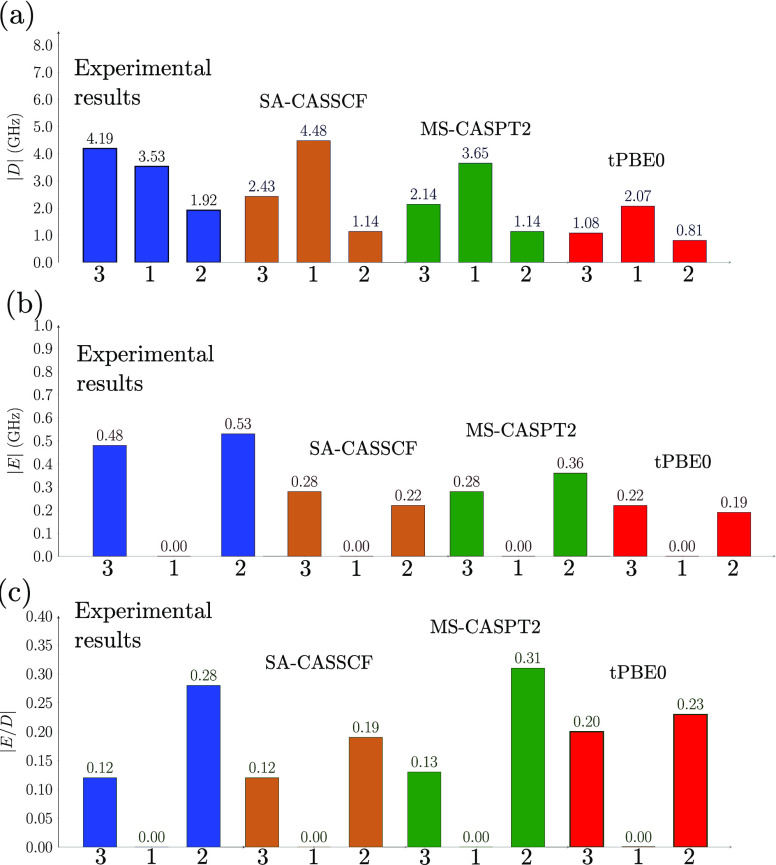
According to the experimental data, the axial ZFS parameter values are in the following order: |D|3 > |D|1 > |D|2. However, when using the optimized geometry in the crystal, all of the theoretical methods showed a trend of |D|1 > |D|3 > |D|2, as shown in Figure 5a. The figure shows that all theoretical methods correctly predict that D is smallest for 2, but they incorrectly predict the order for 1 and 3. Since D is inversely related to the energy gaps between the ground and excited states, a possible rationalization of the trend in the computed D values of the three complexes might be based on the calculated values of the spin–orbit-free energies. The calculated spin–orbit-free triplet spectrum is given in Tables S24–S27, and we observe that the order of the |D| for the three complexes is opposite to the order of the calculated energy difference between the ground state and the first triplet excited state.

Figure 5.

Figure 5

Open in a new tab

Comparison of experimental and calculated values using the (10,15) active space for (a) the axial ZFS parameter |D|, (b) the rhombic ZFS parameter |E|, and (c) the ratio |E/D|. The blue bars correspond to the experimental measurements, and the other bars are for the following electronic structure methods: SA-CASSCF (brown), MS-CASPT2 (green), and HMS-PDFT(tPBE0) (red).

Figure 5b shows that none of theoretical calculations reproduces the experimentally observed trend that 2 has a larger rhombic parameter than 3, although they all correctly predict that |E| = 0 for compound 1.

Figure 5c compares the ratios |E/D|. The experimental trend |E/D|2 > |E/D|3 > |E/D|1 is reproduced by all methods when using (10,15) active space. The figure shows that the ratio |E/D|2/|E/D|3 is 2.4 experimentally, 1.6 by SA-CASSCF, 2.4 by MS-CASPT2, and 1.2 by HMS-PDFT(tPBE0); thus, the HMS-PDFT value is semiquantitative. For the (2,5) and (2,10) active spaces, the MS-CASPT2 method shows an opposite trend (ratio less than 1). Figures S21–S24 show that there is no major change upon varying the active space; in particular, we obtain similar qualitative results when using either the (2,5) or (10,15) active spaces with HMS-PDFT(tPBE0) and MS-CASPT2. This observation may indicate some error cancellation while computing the quotient |E/D|, which allows HMS-PDFT to obtain a good estimate of this ratio. This result is important because knowledge of |E/D| and the g tensor is useful to recognize important spin systems37,89−91 Thus, using the (2,5) active space and MS-CASPT2 or the HMS-PDFT(tPBE0) method can provide a good initial exploration of molecular qubit candidates. It is encouraging that HMS-PDFT(tPBE0) provides the same qualitative information as MS-CASPT2, but at a lower computational cost as observed in several studies for a wide range of molecules and properties (more information available in ref (58)). Hence, it may be affordable to explore larger molecular systems with this method.

In addition, when the gas-phase optimized geometries are used to compute the ZFS parameters, we find the experimental trend for |D| is satisfied for all methods when using (8,8) and (10,15) active spaces. However, the values for the rhombic parameter, |E|, are approximately zero (Figures S25–S28). Therefore, we obtain slightly different structures depending on the approximation used to optimize the molecular structures. Still, these differences significantly affected the ZFS parameters due to their small magnitude.

Tables S4–S6 shows that Kohn–Sham density functional calculations of the ZFS parameters using the coupled-perturbed method20 do not improve over the results we obtained with multiconfigurational methods. Moreover, Figure S1 shows that the Kohn–Sham density functional calculations show strong dependence on the choice of functional, which would lead to uncertainty in using calculations to guide the synthesis of molecular qubit candidates. In contrast, the tested multiconfigurational methods do not show such a strong strong method dependence for the computation of the axial and rhombic parameters (Figures S18–S20).

Concluding Remarks

We have presented the results of multireference calculations for the axial and rhombic ZFS parameters, |D| and |E|, of three Cr(IV) aryl complexes.

The accurate prediction of ZFS parameters is a challenge for electronic structure theory. Our calculations show that the molecular geometry plays a vital role in obtaining values for |D| and |E|; small changes in the molecular geometry generate significant changes in these ZFS parameters. Gas-phase methods are useful to obtain molecular geometries. Still, periodic methods may be needed because of the geometric distortions resulting from crystal packing that may play a major role in tuning |D| and |E|. Therefore, we recommend the optimization of molecular geometries using periodic calculations followed by multireference calculations of the spin properties of molecular qubit candidates.

The HMS-PDFT(tPBE0) and MS-CASPT2 zero-field splitting values do not show a significant dependence on the active space. Furthermore, since it is impossible to consider all the spin–orbit-free roots for active spaces larger than (2,5), one has to choose a cutoff for the included excited states. The choice of cutoff for the studied complexes should consider the MLCT character of the excited states. For the compounds studied here, the energy cutoff was taken as 4.3 eV; the inclusion of higher-energy roots in the RASSI calculations did not improve in the results.

An appropriate singlet–triplet gap is essential for achieving photoluminescence readout of molecular spin qubits. The tPBE0 hybrid on-top functional with the (10,15) active space accurately reproduces the energy difference between the triplet ground state and first excited singlet state. Furthermore, all the examined multireference methodologies qualitatively reproduced the general magnitudes of |D| and |E|, although not all the trends between complexes; however, the |E/D| trend is in agreement with experiment. Hence, we expect that hybrid multistate pair-density functional theory will be useful to predict the optical and microwave addressability of unsynthesized molecular qubits via the accurate prediction of ZFS parameters at an affordable computational cost.

Acknowledgments

We thank Prof. David Awschalom, Dr. Samuel Bayliss, and Pratiti Deb for helpful suggestions regarding the data analysis and Dr. Dihua Wu for contiunuing discussions of magnetic applications of PDFT. This material is based upon work supported by the U.S. Department of Energy Office of Science National Quantum Information Science Research Centers. The calculations performed in this study made use of the Research Computing Center (RCC) resources from the University of Chicago. The development of PDFT methods is supported in part by the Air Force Office of Scientific Research by Grant FA9550-20-1-0360.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.2c00306.

  • Triplet-singlet gaps and zero-field splitting parameters calculated using different active spaces and different methods: MC-PDFT; HMC-PDFT, SA-CASSCF, MS-CASTP2, and NEVPT2 methods; MS-CASPT2 electronic spectra; Orca and OpenMolcas input files; and Cartesian coordinates of periodic optimized structures (PDF)

The authors declare no competing financial interest.

Supplementary Material

au2c00306_si_001.pdf (20.7MB, pdf)

References

  1. Jackson c. E.; Moseley I. P.; Martinez R.; Sung S.; Zadrozny J. M. A reaction-coordinate perspective of magnetic relaxation. Chem. Soc. Rev. 2021, 50, 6684–6699. 10.1039/D1CS00001B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Browne D.; Bose S.; Mintert F.; Kim M. S. From quantum optics to quantum technologies. Prog. Quantum Electron 2017, 54, 2–18. 10.1016/j.pquantelec.2017.06.002. [DOI] [Google Scholar]
  3. Gill S. S.; Kumar A.; Singh A.; Singh H.; Singh M.; Kaur K.; Usman M.; Buyya R. Quantum computing: A taxonomy, systematic review and future directions. Softw: Pract. Exp. 2022, 52, 66–114. 10.1002/spe.3039. [DOI] [Google Scholar]
  4. Degen C. L.; Reinhard F.; Cappellaro P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. 10.1103/RevModPhys.89.035002. [DOI] [Google Scholar]
  5. Wendin G. Quantum information processing with superconducting circuits: A review. Rep. Prog. Phys. 2017, 80, 106001. 10.1088/1361-6633/aa7e1a. [DOI] [PubMed] [Google Scholar]
  6. Bruzewicz C. D.; Chiaverini J.; McConnell R.; Sage J. M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. 10.1063/1.5088164. [DOI] [Google Scholar]
  7. Kane B. E. A silicon-based nuclear spin quantum computer. Nature 1998, 393, 133–137. 10.1038/30156. [DOI] [Google Scholar]
  8. Ichimura K. A simple frequency-domain quantum computer with ions in a crystal coupled to a cavity mode. Opt. Commun. 2001, 196, 119–125. 10.1016/S0030-4018(01)01394-3. [DOI] [Google Scholar]
  9. Wolfowicz G.; Heremans F. J.; Anderson C. P.; Kanai S.; Seo H.; Gali A.; Galli G.; Awschalom D. D. Quantum guidelines for solid-state spin defects. Nat. Rev. Mater. 2021, 6, 906–925. 10.1038/s41578-021-00306-y. [DOI] [Google Scholar]
  10. Gruber A.; Dräbenstedt A.; Tietz C.; Fleury L.; Wrachtrup J.; von Borczyskowski C. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 1997, 276, 2012–2014. 10.1126/science.276.5321.2012. [DOI] [Google Scholar]
  11. Fataftah M. S.; Freedman D. E. Progress towards creating optically addressable molecular qubits. Chem. Commun. 2018, 54, 13773–13781. 10.1039/C8CC07939K. [DOI] [PubMed] [Google Scholar]
  12. Anderson C. P.; Glen E. I.; Zeledon C.; Bourassa A.; Jin Y.; Zhu Y.; Vorwerk C.; Crook A. L.; Abe H.; Ul-Hassan J.; Ohshima T.; Son N. T.; Galli G.; Awschalom D. D. Five-second coherence of a single spin with single-shot readout in silicon carbide. Sci. Adv. 2022, 8, eabm5912 10.1126/sciadv.abm5912. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Bader K.; Dengler D.; Lenz S.; Endeward B.; Jiang S.-D.; Neugebauer P.; van Slageren J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. 10.1038/ncomms6304. [DOI] [PubMed] [Google Scholar]
  14. Timco G. A.; Carretta S.; Troiani F.; Tuna F.; Pritchard R. J.; Muryn C. A.; McInnes E. J. L.; Ghirri A.; Candini A.; Santini P.; Amoretti G.; Affronte M.; Winpenny R. E. P. Engineering the coupling between molecular spin qubits by coordination chemistry. Nat. Nanotechnol. 2009, 4, 173–178. 10.1038/nnano.2008.404. [DOI] [PubMed] [Google Scholar]
  15. Balasubramanian G.; Neumann P.; Twitchen D.; Markham M.; Kolesov R.; Mizuochi N.; Isoya J.; Achard J.; Beck J.; Tissler J.; Jacques V.; Hemmer P. R.; Jelezko F.; Wrachtrup J. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 2009, 8, 383–387. 10.1038/nmat2420. [DOI] [PubMed] [Google Scholar]
  16. Zadrozny J. M.; Niklas J.; Poluektov O. G.; Freedman D. E. Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit. ACS Cent. Sci. 2015, 1, 488–492. 10.1021/acscentsci.5b00338. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Bayliss S. L.; Laorenza D. W.; Mintun P. J.; Kovos B. D.; Freedman D. E.; Awschalom D. D. Optically addressable molecular spins for quantum information processing. Science 2020, 370, 1309–1312. 10.1126/science.abb9352. [DOI] [PubMed] [Google Scholar]
  18. Neese F. Prediction of molecular properties and molecular spectroscopy with density functional theory: From fundamental theory to exchange-coupling. Coord. Chem. Rev. 2009, 253, 526–563. 10.1016/j.ccr.2008.05.014. [DOI] [Google Scholar]
  19. Neese F.; Schwabe T.; Grimme S. Analytic derivatives for perturbatively corrected double hybrid density functionals: Theory, implementation, and applications. J. Chem. Phys. 2007, 126, 124115. 10.1063/1.2712433. [DOI] [PubMed] [Google Scholar]
  20. Neese F. Calculation of the zero-field splitting tensor on the basis of hybrid density functional and Hartree-Fock theory. J. Chem. Phys. 2007, 127, 164112. 10.1063/1.2772857. [DOI] [PubMed] [Google Scholar]
  21. Luo S.; Averkiev B.; Yang K. R.; Xu X.; Truhlar D. G. Density Functional Theory of Open-Shell Systems. The 3d-Series Transition-Metal Atoms and Their Cations. J. Chem. Theory Comput. 2014, 10, 102–121. 10.1021/ct400712k. [DOI] [PubMed] [Google Scholar]
  22. Duboc C.; Ganyushin D.; Sivalingam K.; Collomb M.-N.; Neese F. Systematic Theoretical Study of the Zero-Field Splitting in Coordination Complexes of Mn(III). Density Functional Theory versus Multireference Wave Function Approaches. J. Phys. Chem. A 2010, 114, 10750–10758. 10.1021/jp107823s. [DOI] [PubMed] [Google Scholar]
  23. Kubica A.; Kowalewski J.; Kruk D.; Odelius M. Zero-field splitting in nickel(II) complexes: A comparison of DFT and multi-configurational wavefunction calculations. J. Chem. Phys. 2013, 138, 064304. 10.1063/1.4790167. [DOI] [PubMed] [Google Scholar]
  24. Pulay P. A perspective on the CASPT2 method. Int. J. Quantum Chem. 2011, 111, 3273–3279. 10.1002/qua.23052. [DOI] [Google Scholar]
  25. Neese F. Importance of direct spin-spin coupling and spin-flip excitations for the zero-field splittings of transition metal complexes: A case study. J. Am. Chem. Soc. 2006, 128, 10213–10222. 10.1021/ja061798a. [DOI] [PubMed] [Google Scholar]
  26. Juráková J.; Dubnická Midlíková J.; Hrubý J.; Kliuikov A.; Santana V. T.; Pavlik J.; Moncol J.; Cizmár E.; Orlita M.; Mohelský I.; Neugebauer P.; Gentili D.; Cavallini M.; Salitros I. Pentacoordinate cobalt (II) single ion magnets with pendant alkyl chains: shall we go for chloride or bromide?. Inorg. Chem. Front. 2022, 9, 1179–1194. 10.1039/D1QI01350E. [DOI] [Google Scholar]
  27. Liakos D. G.; Ganyushin D.; Neese F. A multiconfigurational ab initio study of the zero-field spliting in the di- and trivalent hexaquo-chromium complexes. Inorg. Chem. 2009, 48, 10572–10580. 10.1021/ic901063y. [DOI] [PubMed] [Google Scholar]
  28. Hay M. A.; Sarkar A.; Craig G. A.; Bhaskaran L.; Nehrkorn J.; Ozerov M.; Marriott K. E. R.; Wilson C.; Rajaraman G.; Hill S.; Murrie M. In-depth investigation of large axial magnetic anisotropy in monometallic 3d complexes using frequency domain magnetic resonance and ab initio methods: a study of trigonal bipyramidal Co(II). Chem. Sci. 2019, 10, 6354–6361. 10.1039/C9SC00987F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hakey B. M.; Leary D. C.; Xiong J.; Harris C. F.; Darmon J. M.; Petersen J. L.; Berry J. F.; Guo Y.; Milsmann C. High magnetic anisotropy of a square-planar iron-carbene complex. Inorg. Chem. 2021, 60, 18575–18588. 10.1021/acs.inorgchem.1c01860. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Campanella A. J.; Ozvat T. M.; Zadrozny J. M. Ligand design of zero-field splitting in trigonal prismatic Ni (II) cage complexes. Dalton Trans 2022, 51, 3341–3348. 10.1039/D1DT02156G. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Janicka K.; Wysocki A. L.; Park K.. Computational insights into electronic excitations, spin-orbit coupling effects, and spin decoherence in Cr(IV)-based molecular qubits. arxiv(Condensed Matter, Materials Science) 2022, May 1, 2022, 10.48550/ARXIV.2205.00375, https://arxiv.org/abs/2205.00375 (accesssed May 5, 2022). [DOI] [PubMed]
  32. Maurice R.; Bastardis R.; de Graaf C.; Suaud N.; Mallah T.; Guihéry Universal theoretical approach to extract anisotropic spin hamiltonians. J. Chem. Theory Comput. 2009, 5, 2977–2984. 10.1021/ct900326e. [DOI] [PubMed] [Google Scholar]
  33. Ma H.; Govoni M.; Galli G. PyZFS: A Python package for first-principles calculations of zero-field splitting tensors. J. Open Source Softw. 2020, 5, 2160. 10.21105/joss.02160. [DOI] [Google Scholar]
  34. Gatteschi D.; Sessoli R.; Villain J.. Molecular Nanomagnets: Mesoscopic Physics and Nanotechnology; Oxford University Press: pp 15–18. [Google Scholar]
  35. Sessoli R.; Gatteschi D.; Caneschi A.; Novak M. A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. 10.1038/365141a0. [DOI] [Google Scholar]
  36. Sutter J. P.; Béreau V.; Jubault V.; Bretosh K.; Pichon C.; Duhayon C. Magnetic anisotropy of transition metal and lanthanide ions in pentagonal bipyramidal geometry. Chem. Soc. Rev. 2022, 51, 3280–3313. 10.1039/D2CS00028H. [DOI] [PubMed] [Google Scholar]
  37. Neese F.Calculation of NMR and EPR Parameters; John Wiley and Sons, Ltd.: 2004; Chapter 34, pp 541–564. [Google Scholar]
  38. Tishchenko O.; Zheng J.; Truhlar D. G. Multireference Model Chemistries for Thermochemical Kinetics. J. Chem. Theory Comput. 2008, 4, 1208–1219. 10.1021/ct800077r. [DOI] [PubMed] [Google Scholar]
  39. Keller S.; Boguslawski K.; Janowski T.; Reiher M.; Pulay P. Selection of active spaces for multiconfigurational wavefunctions. J. Chem. Phys. 2015, 142, 244104. 10.1063/1.4922352. [DOI] [PubMed] [Google Scholar]
  40. Bao J. J.; Truhlar D. G. Automatic Active Space Selection for Calculating Electronic Excitation Energies Based on High-Spin Unrestricted Hartree-Fock Orbitals. J. Chem. Theory Comput. 2019, 15, 5308–5318. 10.1021/acs.jctc.9b00535. [DOI] [PubMed] [Google Scholar]
  41. Khedkar A.; Roemelt M. Extending the ASS1ST active space selection scheme to large mcecules and excited states. J. Chem. Theory Comput. 2020, 16, 4993–5005. 10.1021/acs.jctc.0c00332. [DOI] [PubMed] [Google Scholar]
  42. Jeong W.; Stoneburner S. J.; King D.; Li R.; Walker A.; Lindh R.; Gagliardi L. Automation of active space selection for multireference methods via machine learning on chemical bond dissociation. J. Chem. Theory Comput. 2020, 16, 2389–2399. 10.1021/acs.jctc.9b01297. [DOI] [PubMed] [Google Scholar]
  43. King D. S.; Gagliardi L. A Ranked-Orbital Approach to Select Active Spaces for High- Throughput Multireference Computation. J. Chem. Theory Comput. 2021, 17, 2817–2831. 10.1021/acs.jctc.1c00037. [DOI] [PubMed] [Google Scholar]
  44. Cahier B.; Maurice R.; Bolvin H.; Mallah T.; Guihéry N. Tools for predicting the nature and magnitude of magnetic anisotropy in transition metal complexes: Application to Co(II) complexes. Magnetochemistry 2016, 2, 31. 10.3390/magnetochemistry2030031. [DOI] [Google Scholar]
  45. Atanasov M.; Aravena D.; Suturina E.; Bill E.; Maganas D.; Neese F. First principles approach to the electronic structure, magnetic anisotropy and spin relaxation in mononuclear 3d-transition metal single molecule magnets. Coord. Chem. Rev. 2015, 289–290, 177–214. 10.1016/j.ccr.2014.10.015. [DOI] [Google Scholar]
  46. Wu D.; Zhou C.; Bao J. J.; Gagliardi L.; Truhlar D. G. Zero-field splitting calculations by multiconfiguration pair-density functional theory. J. Chem. Theory Comput. 2022, 18, 2199–2207. 10.1021/acs.jctc.1c01115. [DOI] [PubMed] [Google Scholar]
  47. Roos B. O.; Malmqvist P. Relativistic quantum chemistry: the multiconfigurational approach. Phys. Chem. Chem. Phys. 2004, 6, 2919–2927. 10.1039/b401472n. [DOI] [Google Scholar]
  48. Heß B.; Marian C. M.; Wahlgren U.; Gropen O. A mean-field spin-orbit method applicable to correlated wavefunctions. Chem. Phys. Lett. 1996, 251, 365–371. 10.1016/0009-2614(96)00119-4. [DOI] [Google Scholar]
  49. Malmqvist P.; Roos B.; Schimmelpfennig B. The restricted active space (RAS) state interaction approach with spin-orbit coupling. Chem. Phys. Lett. 2002, 357, 230–240. 10.1016/S0009-2614(02)00498-0. [DOI] [Google Scholar]
  50. Roos B. O. The complete active space self-consistent field method and its applications in electronic structure calculations. Adv. Chem. Phys. 1987, 69, 399–445. 10.1002/9780470142943.ch7. [DOI] [Google Scholar]
  51. Andersson K.; Malmqvist P.; Roos B. O. Second-order Perturbation Theory with a Complete Active Space Self-consistent Field Reference Function. J. Chem. Phys. 1992, 96, 1218–1226. 10.1063/1.462209. [DOI] [Google Scholar]
  52. Li Manni G.; Carlson R. K.; Luo S.; Ma D.; Olsen J.; Truhlar D. G.; Gagliardi L. Multiconfiguration pair-density functional theory. J. Chem. Theory Comput. 2014, 10, 3669–3680. 10.1021/ct500483t. [DOI] [PubMed] [Google Scholar]
  53. Gagliardi L.; Truhlar D. G.; Li Manni G.; Carlson R. K.; Hoyer C. E.; Bao J. L. Multiconfigurational pair-density functional theory: A new way to treat strongly correlated systems. Acc. Chem. Res. 2017, 50, 66–73. 10.1021/acs.accounts.6b00471. [DOI] [PubMed] [Google Scholar]
  54. Stoneburner S. J.; Truhlar D. G.; Gagliardi L. MC-PDFT can calculate singlet-triplet splittings of organic diradicals. J. Chem. Phys. 2018, 148, 064108. 10.1063/1.5017132. [DOI] [PubMed] [Google Scholar]
  55. Sharma P.; Bernales V.; Knecht S.; Truhlar D. G.; Gagliardi L. Density matrix renormalization group pair-density functional theory (DMRG-PDFT): singlet-triplet gaps in polyacenes and polyacetylenes. Chem. Sci. 2019, 10, 1716–1723. 10.1039/C8SC03569E. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Sharma P.; Bernales V.; Truhlar D. G.; Gagliardi L. Valence ππ* excitations in benzene studied by multiconfiguration pair-density functional theory. J. Phys. Chem. Lett. 2019, 10, 75–81. 10.1021/acs.jpclett.8b03277. [DOI] [PubMed] [Google Scholar]
  57. Stoneburner S. J.; Truhlar D. G.; Gagliardi L. Transition metal spin-state energetics by MC-PDFT with high local exchange. J. Phys. Chem. A 2020, 124, 1187–1195. 10.1021/acs.jpca.9b10772. [DOI] [PubMed] [Google Scholar]
  58. Zhou C.; Hermes M. R.; Wu D.; Bao J. J.; Pandharkar R.; King D. S.; Zhang D.; Scott T. R.; Lykhin A. O.; Gagliardi L.; Truhlar D. G. Electronic structure of strongly correlated systems: recent developments in multiconfiguration pair-density functional theory and multiconfiguration nonclassical-energy functional theory. Chem. Sci. 2022, 13, 7685. 10.1039/D2SC01022D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Zhou C.; Wu D.; Gagliardi L.; Truhlar D. G. Calculation of the Zeeman effect for transition-metal complexes by multiconfiguration pair-density functional theory. J. Chem. Theory Comput. 2021, 17, 5050–5063. 10.1021/acs.jctc.1c00208. [DOI] [PubMed] [Google Scholar]
  60. Pandharkar R.; Hermes M. R.; Truhlar D. G.; Gagliardi L. A new mixing of nonlocal exchange and nonlocal correlation with multiconfiguration pair-density functional theory. J. Phys. Chem. Lett. 2020, 11, 10158–10163. 10.1021/acs.jpclett.0c02956. [DOI] [PubMed] [Google Scholar]
  61. Kresse G.; Hafner J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. 10.1103/PhysRevB.48.13115. [DOI] [PubMed] [Google Scholar]
  62. Kresse G.; Hafner J. Ab initio molecular-dynamics simulation of the liquid-metalamorphous- semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
  63. Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  64. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  65. Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  66. Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
  67. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  68. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  69. Neese F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]
  70. Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  71. Fdez. Galván I.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. 10.1021/acs.jctc.9b00532. [DOI] [PubMed] [Google Scholar]
  72. Pierloot K.; Dumez B.; Widmark P. O.; Roos B. O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. IV. Medium size basis sets for the atoms H-Kr. Theor. Chim. Acta 1995, 90, 87–114. 10.1007/BF01113842. [DOI] [Google Scholar]
  73. Peng D.; Reiher M. Exact decoupling of the relativistic Fock operator. Theor. Chem. Acc. 2012, 131, 1081. 10.1007/s00214-011-1081-y. [DOI] [Google Scholar]
  74. Peng K.; Hirao D. An arbitrary order Douglas-Kroll method with polynomial cost. J. Chem. Phys. 2009, 130, 044102. 10.1063/1.3068310. [DOI] [PubMed] [Google Scholar]
  75. Aquilante F.; Pedersen T. B.; Lindh R. Low-cost evaluation of the exchange Fock Matrix from Cholesky and density fitting representations of the electron repulsion integrals. J. Chem. Phys. 2007, 126, 194106. 10.1063/1.2736701. [DOI] [PubMed] [Google Scholar]
  76. Chibotaru L. F.; Ungur L. Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation. J. Chem. Phys. 2012, 137, 064112. 10.1063/1.4739763. [DOI] [PubMed] [Google Scholar]
  77. Bao J. J.; Zhou C.; Varga Z.; Kanchanakungwankul S.; Gagliardi L.; Truhlar D. G. Multi-State Pair-Density Functional Theory. Faraday Discuss. 2020, 224, 348–372. 10.1039/D0FD00037J. [DOI] [PubMed] [Google Scholar]
  78. Angeli C.; Cimiraglia R.; Evangelisti S.; Leininger T.; Malrieu J. P. Introduction of N-Electron Valence States for Multireference Perturbation Theory. J. Chem. Phys. 2001, 114, 10252–10264. 10.1063/1.1361246. [DOI] [Google Scholar]
  79. Angeli C.; Cimiraglia R.; Malrieu J. P. N-Electron Valence State Perturbation Theory: A Fast Implementation of the Strongly Contracted Variant. Chem. Phys. Lett. 2001, 350, 297–305. 10.1016/S0009-2614(01)01303-3. [DOI] [Google Scholar]
  80. Angeli C.; Cimiraglia R.; Malrieu J. P. N-Electron Valence State Perturbation Theory: A Spinless Formulation and an Efficient Implementation of the Strongly Contracted and of the Partially Contracted Variants. J. Chem. Phys. 2002, 117, 9138–9153. 10.1063/1.1515317. [DOI] [Google Scholar]
  81. Reiher M.; Wolf A. Exact decoupling of the Dirac Hamiltonian. I. General theory. J. Chem. Phys. 2004, 121, 2037–2047. 10.1063/1.1768160. [DOI] [PubMed] [Google Scholar]
  82. Reiher M.; Wolf A. Exact decoupling of the Dirac Hamiltonian. II. The generalized Douglas-Kroll-Hess transformation up to arbitrary order. J. Chem. Phys. 2004, 121, 10945–10956. 10.1063/1.1818681. [DOI] [PubMed] [Google Scholar]
  83. Reiher M. Douglas-Kroll-Hess theory: a relativistic electrons-only theory for chemistry. Theor. Chem. Acc. 2006, 116, 241–252. 10.1007/s00214-005-0003-2. [DOI] [Google Scholar]
  84. Ivaniková R.; Boča R.; Dlháň L.; Fuess H.; Mašlejová A.; Mrázová V.; Svoboda I.; Titiš J. Heteroleptic nickel(II) complexes formed from N-donor bases, carboxylic acids and water: Magnetostructural correlations. Polyhedron 2006, 25, 3261–3268. 10.1016/j.poly.2006.05.040. [DOI] [Google Scholar]
  85. Bar A. K.; Pichon C.; Sutter J.-P. Magnetic anisotropy in two- to eight-coordinated transition–metal complexes: Recent developments in molecular magnetism. Coord. Chem. Rev. 2016, 308, 346–380. 10.1016/j.ccr.2015.06.013. [DOI] [Google Scholar]
  86. Böhme M.; Ziegenbalg S.; Aliabadi A.; Schnegg A.; Görls H.; Plass W. Magnetic relaxation in cobalt(ii)-based single-ion magnets influenced by distortion of the pseudotetrahedral [N2O2] coordination environment. Dalton Trans 2018, 47, 10861–10873. 10.1039/C8DT01530A. [DOI] [PubMed] [Google Scholar]
  87. Zahradníková E.; Herchel R.; Šalitroš I.; Císařová I.; Drahoš B. Late first-row transition metal complexes of a 17-membered piperazine-based macrocyclic ligand: Structures and magnetism. Dalton Trans 2020, 49, 9057–9069. 10.1039/D0DT01392G. [DOI] [PubMed] [Google Scholar]
  88. Laorenza D. W.; Kairalapova A.; Bayliss S. L.; Goldzak T.; Greene S. M.; Weiss L. R.; Deb P.; Mintun P. J.; Collins K. A.; Awschalom D. D.; Berkelbach T. C.; Freedman D. E. Tunable Cr4+ molecular color centers. J. Am. Chem. Soc. 2021, 143, 21350–21363. 10.1021/jacs.1c10145. [DOI] [PubMed] [Google Scholar]
  89. Hagen W. R. EPR spectroscopy of iron—sulfur proteins. Adv. Inorg. Chem. 1992, 38, 165–222. 10.1016/S0898-8838(08)60064-1. [DOI] [Google Scholar]
  90. Roessler M. M.; Salvadori E. Principles and applications of EPR spectroscopy in the chemical sciences. Chem. Soc. Rev. 2018, 47, 2534–2553. 10.1039/C6CS00565A. [DOI] [PubMed] [Google Scholar]
  91. Hagen W. R.Biomolecular EPR Spectroscopy; CRC Press: 2009. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

au2c00306_si_001.pdf (20.7MB, pdf)

Articles from JACS Au are provided here courtesy of American Chemical Society

RESOURCES