Discrimination of RNA Fiber Structures Using Solid-State Nanopores

Abstract

RNA fibers are a class of biomaterials that can be assembled using HIV-like kissing loop interactions. Because of the programmability of molecular design and low immunorecognition, these structures present an interesting opportunity to solve problems in nanobiotechnology and synthetic biology. However, the experimental tools to fully characterize and discriminate among different fiber structures in solution are limited. Herein, we utilize solid-state nanopore experiments and Brownian dynamics simulations to characterize and distinguish several RNA fiber structures that differ in their degrees of branching. We found that, regardless of the electrolyte type and concentration, fiber structures that have more branches produce longer and deeper ionic current blockades in comparison to the unbranched fibers. Experiments carried out at temperatures ranging from 20–60 °C revealed almost identical distributions of current blockade amplitudes, suggesting that the kissing loop interactions in fibers are resistant to heating within this range.

Therapeutic nucleic acids (TNAs) have emerged as new treatment for a broad range of diseases, with a variety of TNAs recently approved by the U.S. Food and Drug Administration (FDA)^1,2. When targeting several pathways is beneficial for the therapeutic outcome^3–5, nucleic acid nanoscaffolds can ensure simultaneous codelivery of multiple TNAs, increasing the effective dosage or enabling synergistic effects. In addition to TNAs, other functional moieties, such as fluorophores for imaging or small molecules or aptamers for targeting, can be introduced on the same nanoscaffold to enhance the formulation⁶. Nucleic acid nanoparticles (NANPs) that vary in size, shape, composition, and immunostimulation can be chosen as optimal nanoscaffolds for various applications^7–12. Among the variety of available NANPs are RNA fibers, an A-B assembly system, the formation of which relies on intermolecular interactions between HIV-like kissing loop complexes adopting a 180° geometry¹³. Fibrous NANPs have been shown to be the least immunostimulatory when compared to planar or globular analogs, though the extent of immunostimulation depends on the extent to which they are functionalized with TNAs⁸. When assembled, however, no current approach to characterization, i.e., electrophoretic mobility shift assays (EMSA), atomic force microscopy (AFM), or dynamic light scattering, allows for minor structural differences to be observed in the way that the immune system can differentiate. Therefore, new approaches for characterization of TNA assembly on fibrous scaffolds are needed for further development of the TNA-based therapeutic technologies.

As one such approach, solid-state nanopores offer the ability to detect and differentiate molecules by measuring them one at a time. Solid-state pores have been previously used to differentiate at pM levels between NANP ring and cube scaffolds¹⁴, as well as various other structured nucleic acids^15–19. By measuring the differences in the reduction of ionic current brought about by the translocation of molecules through the nanopore, the nanopore approach provides a platform for the high-throughput characterization of samples of complex heterogenicity. Solid-state nanopores have also been used to discriminate between chromatin sub-structures such as histone monomers, tetramers, and octamers²⁰. Nanopores have been used to perform force spectroscopy of histone-DNA interactions in individual nucleosomes²¹,protein-DNA interactions^{22, 23}, study DNA modifications²⁴, study folded²⁵, decorated molecules²⁶ and map DNA sequence ¹⁷.

Here, we used solid-state nanopores (Fig. 1A) to characterize three different structures of RNA fibers (Fig. 1B): non-functionalized (NF) fibers without any branching and fibers with branching resulting from functionalization with dicer substrate RNAs either at every other monomer (EOM) or at every monomer (EM). We performed characterization of these three different NANPs at different electrolyte conditions varying both the monovalent cation type (KCl and LiCl) and electrolyte concentration (0.2 – 4 M), using nanopores of different diameters (4.5 – 7 nm), and at different temperatures (23 ― 60°C). We found that EOM and EM fibers produce longer, and deeper current blockades compared to the NF fibers and can be distinguished from each other regardless of the large heterogeneity present in the samples (Fig. 1C), while neither gel electrophoresis nor AFM techniques could clearly resolve the two fiber types (Fig. 1D). Surprisingly, the NANPs appear to be intact even at higher temperatures (60°C), thus suggesting possible applications of these nanomaterials at extreme conditions.

Figure 1.

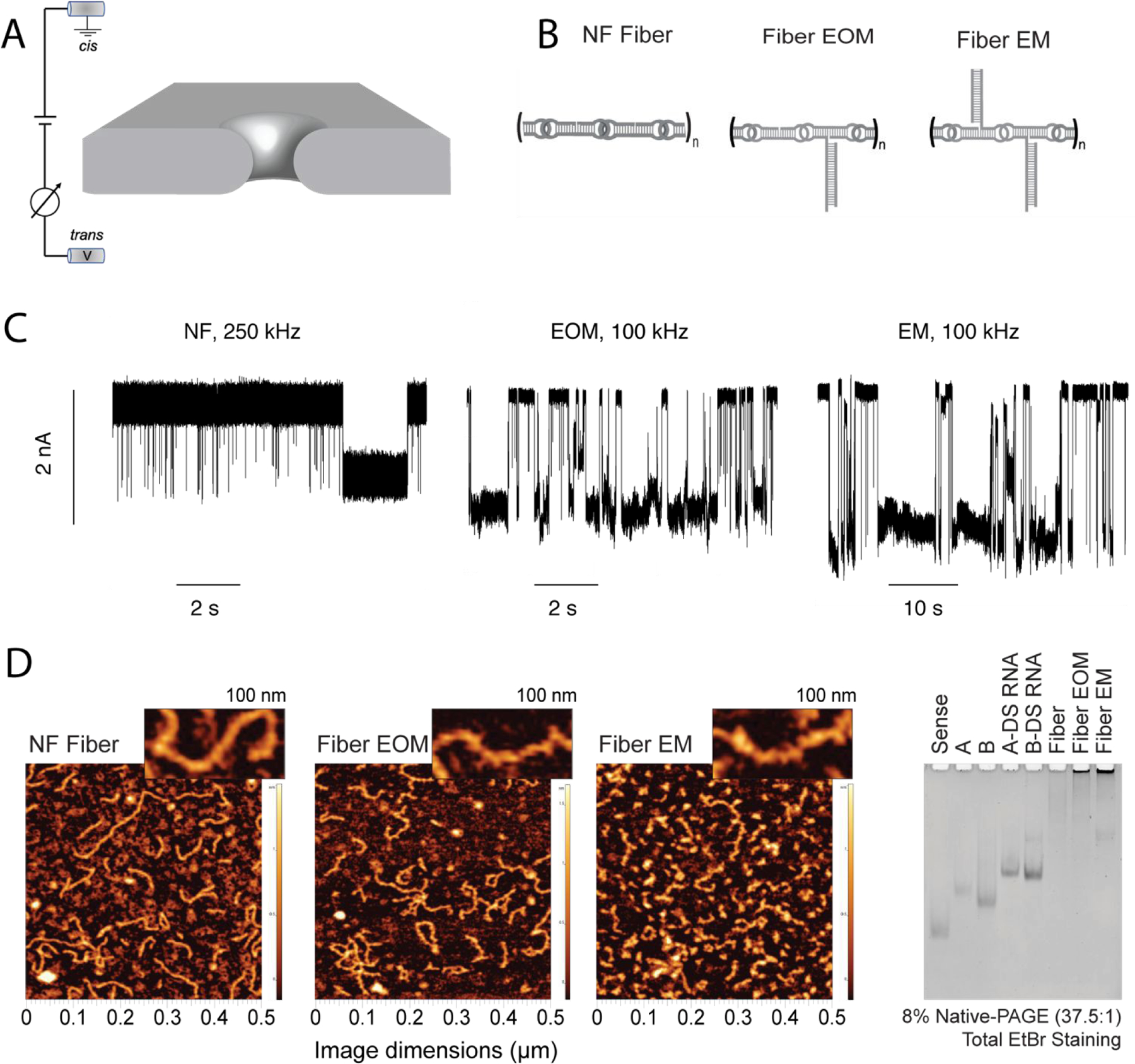
Differentiation of RNA fibers using a solid-state nanopore. (A) Schematic representation of experimental set-up, wherein the application of positive transmembrane voltages electrophoretically captures NANPs at the pore vicinity. (B) Sketches of the different RNA fibers studied in this work: non-functionalized (NF) fibers; fibers with a branch at every other monomer (EOM); fibers with a branch at every monomer (EM). (C) Representative fragments of ionic current traces obtained using a 4.5 nm diameter nanopore at 300 mV (in 1 M KCl, 10 mM HEPES, 2 mM MgCl₂, pH 7.5) for NF, EOM, and EM fibers. The traces from the NF fiber sample were recorded at a sampling rate of 4,167 kHz and low-pass filtered at 250 kHz, whereas traces from the EOR and EM fiber samples (concentration of 25–100 nM) were recorded at a sampling rate of 250 kHz and low-pass filtered at 100 kHz. These traces clearly demonstrate that the fibers can be identified by solid-state nanopore according to their branching, which is difficult to achieve using other methods such as AFM and gel electrophoresis as shown in (D). (D) AFM images and gel electrophoresis of each fiber, suggesting large heterogeneity in the fibers lengths.

Results:

We first performed experiments in 1 M KCl using a 4.5 nm diameter pore, which was expected to allow for rapid passage of NF fibers but hinder the translocation of EOM and reject the passage of EM fibers because of the steric constraints imposed by the side branches. We measured the perturbation in ionic current produced by the translocations of the three fiber structures. As can be seen from the current traces in Fig 1C and scatter plots in the SI: Fig. S1, we found that the NF fibers produced <50 % blockade of ionic current. The decrease in the dwell time with the voltages suggests a more rapid translocation of fiber as voltage is increased. In contrast, EOM fibers produce events characterized by >50% blockade amplitude and much longer lifetime (in some cases >10 s). We attribute these deeper current blockades to the presence of branches inside the pore, and the longer dwell times to additional friction produced by the interaction of the fiber with the pore walls. We expected that placing the EM fibers in the cis chamber would produce even longer and deeper blockades of ionic current because of the higher density of “bristles” in the molecular brush. Indeed, when we cleaned the pore with fresh buffer and added EM fibers, we observed events with even deeper and longer blockades of the ionic current, even as there was a slight increase in the baseline current (see SI: Fig. S1). We also observed events during the experiments with EM and EOM fibers in which the pore was blocked for longer durations and required voltage reversal or replacement of the buffer solution in the cis chamber to recover the baseline current. An example of such an event is shown in Fig. S2. These results clearly demonstrate the ability of solid-state nanopore to discern different RNA fiber structures by means of their ionic current signatures.

For all fiber structures, we found the interevent-time distribution to be exponentially distributed (SI: Fig S1), with the time constant decreasing as the voltage increased. This suggests a faster capture of fiber molecules at higher voltages. For bare fiber structures, we found the dwell time to decrease with the voltage as well, suggesting successful translocation of the fibers through the pore. For EOM and EM fibers, we found only a slight decrease in the dwell time as the voltage increased. We attribute this weaker dependence on the voltage to a possibility that only a fraction of the EOM and EM fibers completely translocate through the nanopores, which in turn is caused by the pore diameter being smaller than the cross-section of the branched fiber. AFM images and gel electrophoresis of each of the fiber samples indicate the heterogeneity in the sample lengths (Fig. 1D).

To characterize the process of RNA fiber translocation at the microscopic level, we constructed a coarse-grained Brownian dynamics (BD) model of the experimental systems containing a grid-based potential representation of a solid-state nanopore and a bead-model of the RNA fibers. The RNA nanostructure was represented within the framework of the mrDNA model²⁷ with one bead per nucleotide resolution, see ref²⁸ and Methods for details. The local distribution of the electrostatic potential was determined using COMSOL corresponding to a 200-mV transmembrane bias. Starting with a fully extended configuration, Fig. 2A, we run BD simulations of the RNA fibers with the electrostatic potential of the transmembrane bias and the steric potential of the nanopore surface guiding the translocation. The resulting microscopic conformations were used to compute the nanopore ionic current using the steric exclusion model (SEM) and 1M KCl bulk conductivity as described previously^{29, 30}.

Figure 2.

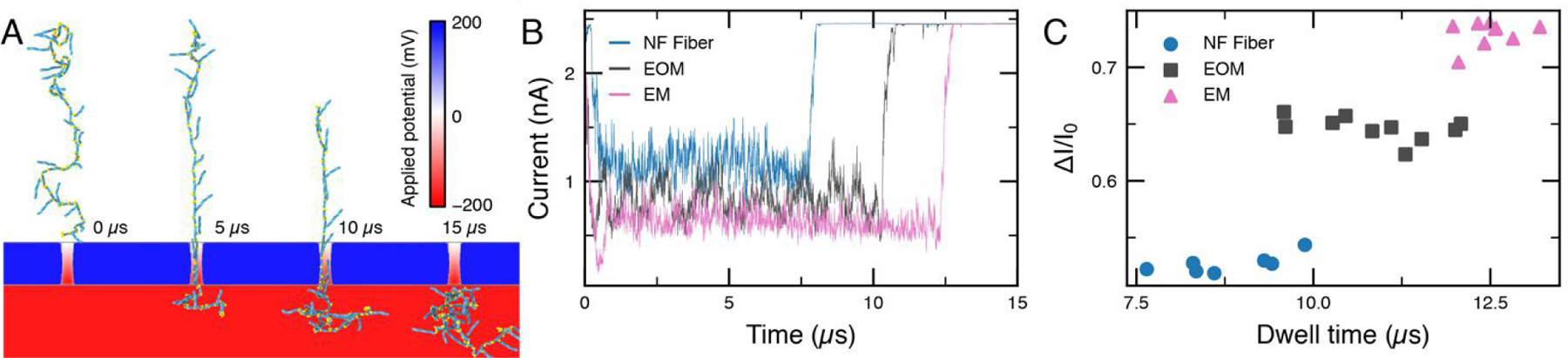
Coarse-grained Brownian dynamics simulation of RNA fibers passing through a 4.5 nm diameter nanopore. (A) Snapshots depicting a typical translocation trajectory of an EM fiber. COMSOL Multiphysics was used to determine the distribution of the electrostatic potential in and around the nanopore. The membrane containing a nanopore was represented as a steric (repulsive) potential²⁸. (B) Typical ionic current traces calculated from the translocation trajectories using SEM^{29, 30}. (C) Average relative blockade current amplitude versus dwell time for each translocation trajectory. The different fiber types are readily distinguished.

Fig. 2A illustrates a typical permeation trajectory of an EM fiber; Supplementary Movies 1–3 illustrate typical permeation trajectories of all three fiber types. The SEM analysis of the permeation trajectories, Fig. 2B, clearly show that branching of the nanostructures reduces the nanopore ionic current, i.e., increases the blockade current amplitude, in agreement with the experiments. A periodic oscillation of the current was observed as the EOM fiber translocated, with decreases in the current induced by the presence of branched monomers in the central region of the pore. A closer look at the experimentally measured current blockade events with EOM (SI: Fig. S1ii) shows the fluctuations resembling some of the oscillatory features in the simulation. Since these oscillations occur on a time scale (~1 μs as shown in Fig.2B) faster than the sampling rate of the measurement, full resolution of such oscillations could not be observed in the experiments. Repeating the translocation simulations using different initial conformations of the fibers produced rather reproducible values of ionic current blockade and the dwell time, suggesting that the large scatter in the experimental data likely originates from heterogeneity in the fiber length which can lead to incomplete translocation events, such as partial occlusions of the nanopore with or without subsequent transmembrane permeation. To further understand the origin of oscillation observed in the simulation, we analyzed (Figure. S10) the branch thickness (L_b) and spacing (L_s) distributions in bulk and inside the pore. Our analysis suggests that in computer simulation L_s increases substantially during the translocation as the helical axis across the kissing loop junction adopts 180 ° angle when RNA is at the pore. We note, however, that our microscopic analysis represents an idealized version of the experimental system devoid of heterogeneity in the fiber length and friction between the RNA fibers and the nanopore surface, which makes the translocation both slower and less regular.

Our characterization of bare fiber translocation through a 6 nm pore in 1 M KCl (Fig. 3A–B) showed shallower blockades of the current with an average value of ∆I/I_o < 0.3 and with sub-100 μs lifetime. Due to our 100 kHz bandwidth limitation, we could not accurately capture the voltage dependence on translocation lifetimes, as some of the NF fibers passed through the pore too fast for the current blockades to be accurately recorded. On the other hand, experiments conducted with the EOM and EM fibers showed two populations, (i) one population with sub-100 μs lifetimes, which we attribute to unassembled fiber, and longer events with average blockade fractions of ∆I/I_o > 0.4, which we attribute to the translocation of EOM and EM fibers. The lifetime of the latter population decreased exponentially as the voltage was increased, indicating rapid nanopore translocation (Fig. 3C). A simple statistical analysis (SI: Fig.S9) suggests that at 99% confidence EM block 1.5–2.9% (75–150 pA) more current in comparison to EOM. To confirm the differences in blockade current signals between EOM and EM, we performed supported vector machine learning analysis^31–33 using features described in methods (and SI: Fig S12–S14). Our analysis discriminates between EOM and EM current signals (Fig. 3D) with 85.8% accuracy, confirming that the solid-state nanopore can distinguish between different fiber structures based on the nature of their branching.

Figure 3.

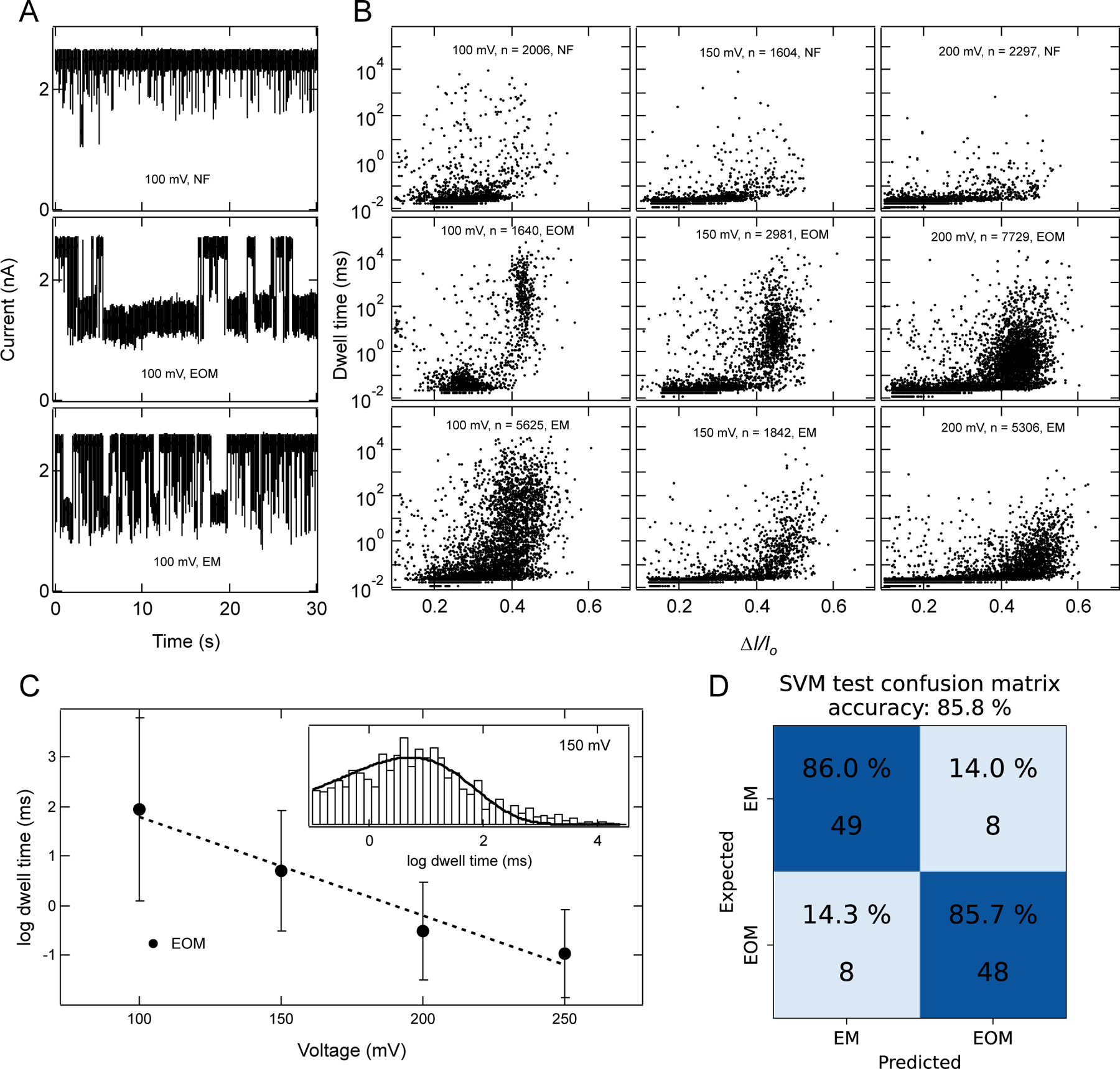
Characterization of RNA fibers using a 6 nm diameter pore. (A) Example ionic current traces for 100nM of NF, EOM, and EM fibers. Traces shown here were recorded in 1 M KCl, 10 mM HEPES, 2 mM MgCl₂, pH 7.5, with a sampling rate of 250 kHz, and 100 kHz filter. (B) Scatter plots of each fiber at different voltages and number of events (n) collected for each scatter plot are indicated in each panel. These plots clearly distinguish between three fiber structures and indicate the rapid passage of fibers as voltage is increased. At 100 mV, a wider distribution of blockade events for EM fibers indicates the mixture of populations of events which corresponds to partial translocations and full translocation. Upon increasing the voltage bias, the distribution shifts towards a higher value of ∆I/I_o and faster dwell time, suggesting more fractions of event with full translocation, as full translocation causes more current blockades. (C) log dwell time of EOM as a function of voltage. Dotted line is linear fit of the data suggesting exponential dependence of translocation time with voltage. Inset is representative histogram (excluding events faster than 100 μs) at 150 mV and a fit to a Gumbel-like distribution function having form $f\left(x\right)=a\times \mathit{exp}\hspace{0.17em}(\left(\frac{x-x0}{w}\right)-\mathit{exp}\hspace{0.17em}\left(\frac{x-x0}{w}\right))$. Error bars in C represents width of the distribution. (D) SVM analysis of current blockade signals identify EOM and EM with 85.8 % accuracy using features described in methods (also see SI: Fig. S12–S14).

To further tune the ability of solid-state nanopores to distinguish unbranched from branched fibers we performed experiments using a 6 nm diameter pore at lower ionic strength conditions (0.4 M KCl), where we expected the decreased electrostatic shielding to influence the translocation kinetics between branched and unbranched fibers. We found that despite the lower signal-to-noise ratios at lower ionic strengths, the ionic current blockades clearly differ for EM and EOM. Examples of ionic current traces for each fiber and their mixtures are presented in supporting Fig. S3. As shown in Fig. 4A, NF fiber alone produces mean fractional current blockades of ~ 15%, whereas for EM and EOM fibers mean values are ~20%. We found that NF and EOM fibers produce current blockades of similar dwell times with a mean value of ~100 μs (Fig. 4B), whereas EM fibers produce blockades with a mean dwell time of ~1 ms. These results suggest that ion current signals can be used to discriminate NF from EOM and EM fibers, whereas dwell time data can be used to discriminate between EM and EOM fibers, according to the molecular architecture of the NANPs. The longer dwell times of EM fibers than EOM fibers are likely due to relatively higher friction between pore walls and the branched fibers, as well as due to the slower axial diffusion of the EM molecules.

Figure 4.

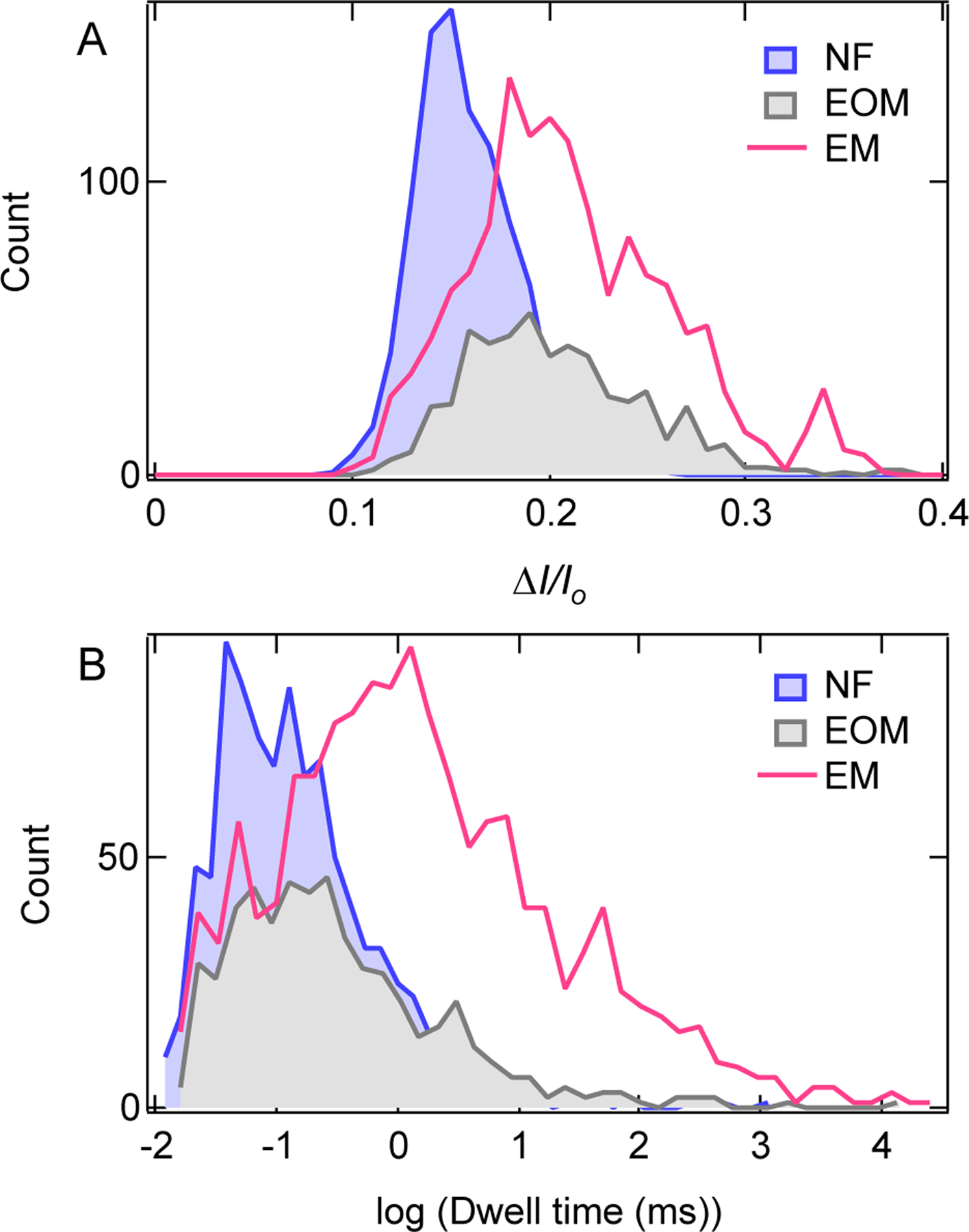
Distribution of (A) current blockade ratio and (B) dwell time for NF, EOM and EM fibers, measured at 200 mV, in 0.4 M KCl, 10 mM HEPES, pH 7.5. Number of events collected for each fiber in the distributions are following for NF, n = 936; for EOM, n = 536; and for EM, n = 1395.

We further investigated the voltage dependence of translocation lifetimes of EOM and EM fibers, in 2 M KCl for a 5 nm pore. As shown in SI: Fig. S4, we observed smooth ionic current blockades and a clear signature of translocation as judged by decreases in dwell time as voltage is increased (Fig. 5). Example ionic current traces for 2 M KCl are presented in supporting Fig. S4. Inter-event times between the events can be described by a single exponential distribution and time constants become faster as voltage is increased (SI: Fig. S4), indicating rapid capture of fibers upon increasing the voltage. As can be seen in the current blockade vs. dwell time scatter plots (Fig. 5), dwell times decrease with increasing voltage in the range 100 – 200 mV for EOM and 200 – 300 mV for EM fibers, thus suggesting that the observed current blockade events are due to the successful translocation of both EOM and EM fibers. Furthermore, we observed that at 200 mV, EM has longer dwell times than the EOM fibers. These results are consistent with the experiments in 0.4 M KCl and 1 M KCl and reinforce our hypothesis that EM fibers take longer time to pass through the pores because more branches increase friction with the pore walls and reduce molecular diffusion. However, the current blockade ratio was observed to be almost identical for both EM and EOM fibers. These results suggest that for a pore diameter greater than > 5 nm, mean blockade fractions for EM and EOM are nearly identical, whereas for a pore diameter < 5 nm mean blockade fractions are higher for EM than for EOM fibers. Power spectral density analysis (SI: Figure S11) suggests that the relative differences between current noise for EM and EOM are dependent on salt concentration. Such behavior is also found in recent studies where current fluctuation due to interaction of PEG with pore wall was salt concentration dependent³⁴.

Figure 5.

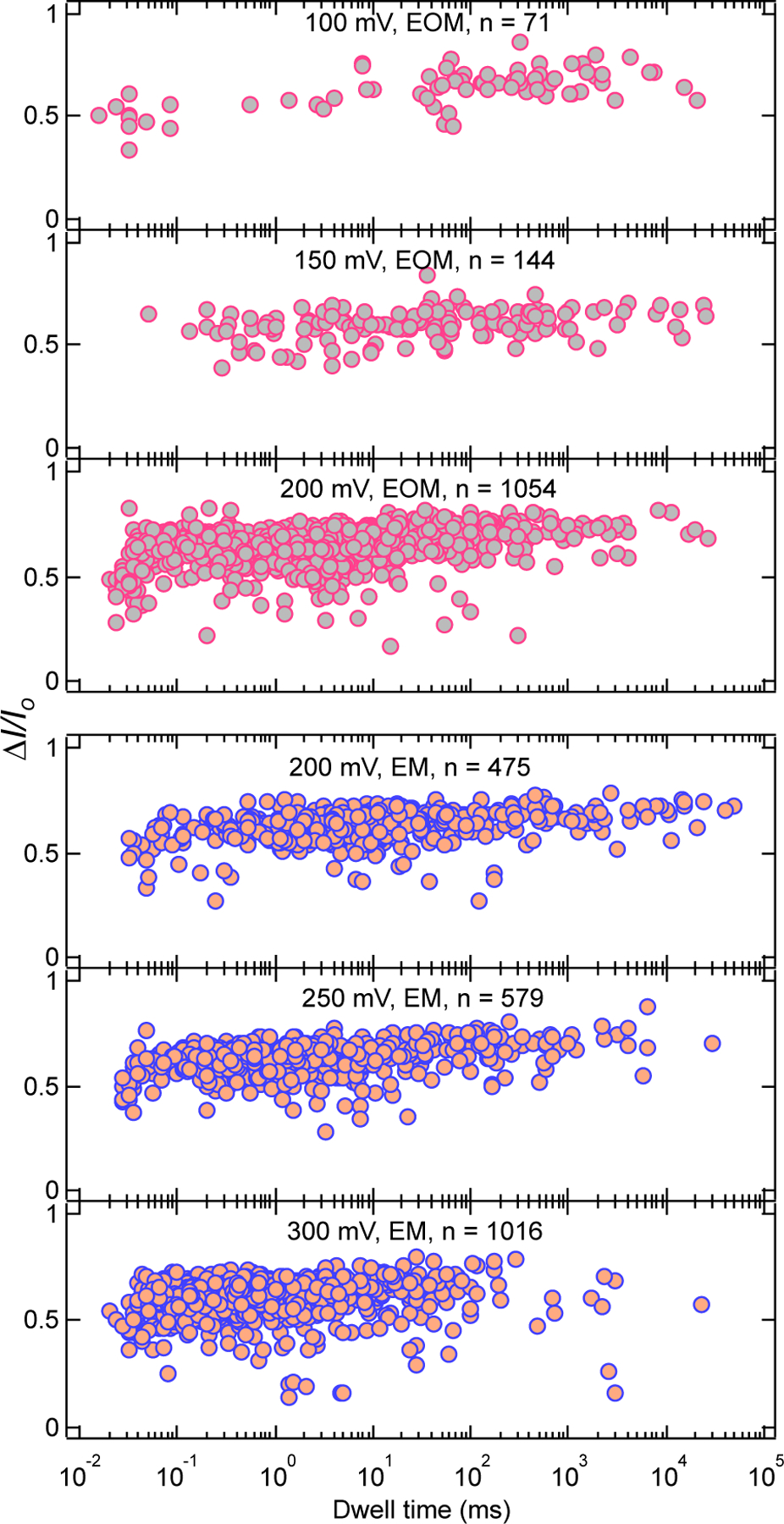
Scatter plots of EOM and EM fibers for experiments with a 5 nm pore in 2 M KCl, 10 mM HEPES, 2 mM MgCl₂, pH 7.5. Number of events (n) collected in each plot are indicated.

To test the structural integrity of the kissing loop interactions in the fiber structures, we performed experiments in 4 M LiCl solution (while maintaining 2mM MgCl₂, 10 mM HEPES, pH 7.5 buffer) at 500 mV and 750 mV and found that EM and EOM fibers produce deeper mean fractional current blockades compared to the NF fibers (Fig. 6, SI: Figs. S5–S6). Surprisingly, we found that there are two modes in dwell time distribution of EM and EOM fibers (Fig. 6, SI: Fig. S6), and dwell time distributions of both modes shift towards lower values as we increased the voltage to 750 mV. Inter-event time distributions (Figs. 6C, SI: S5B and S6B) in the experiments were found to be exponentially distributed for all three fibers at each voltage, with a time constant that decreases with increasing voltage, indicating the role of electric field on molecular capture. The observed two distinct time scales in the dwell time distribution for EOM and EM are either due to presence of two distinct length scales in the EOM and EM samples which could not be resolved in KCl solution or due to distinct initial configuration of the Fiber molecules (either branches getting captured first or main strand) at the beginning of the translocation.

Figure 6.

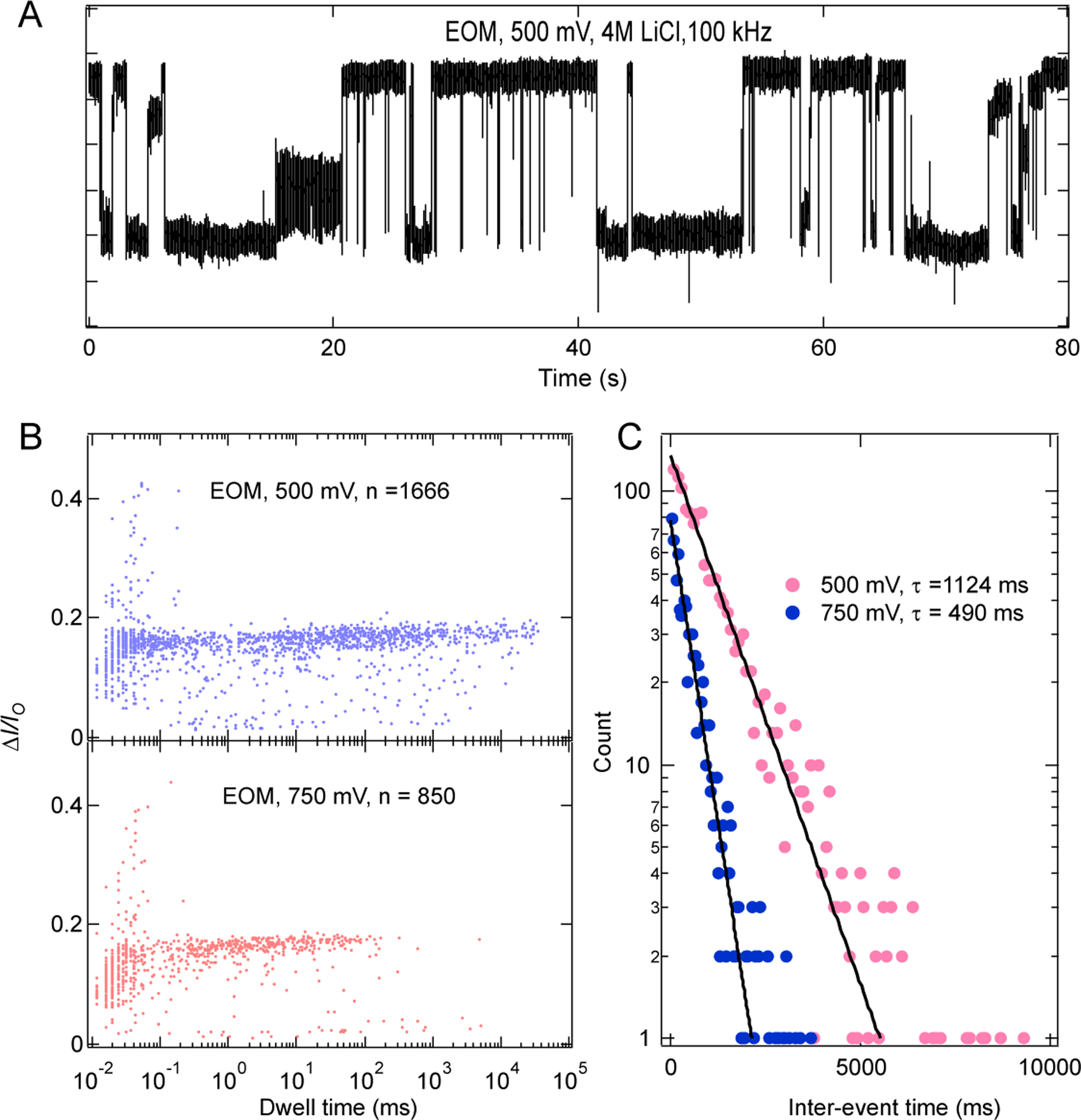
High voltage translocation of EOM in 4 M LiCl. (A) Example ionic current trace recorded at 500 mV, 4 M LiCl, 2 mM MgCl₂, 10 mM HEPES, pH 7.5. (B) Scatter plots for the translocation events at 500 mV and 750 mV. Number of events collected are shown in each plot. (C) Interevent-time distribution at 500 mV and 750 mV respectively. Solid lines are the exponential fit to the distribution.

To check the thermal stability of kissing loop interactions in these RNA fiber structures we performed nanopore measurements of EM fibers at different temperatures. As shown in Fig. 7 (and SI: Fig S7, S8), we found no appreciable change in the current blockade ratio upon heating at different voltages. Only a slightly faster dwell time can be observed, and which is consistent with our intuition as higher temperature can lead to faster movement of the molecules. Example ionic current traces for 250 mV at different temperatures are shown in supporting Fig. S7. Identical distributions of the current blockade ratio indicates that the kissing loop interactions are stable up to ~60°C. These observations are in agreement with previously reported melting temperature (T_m = 59.5 °C) of RNA fibers³⁵.

Figure 7.

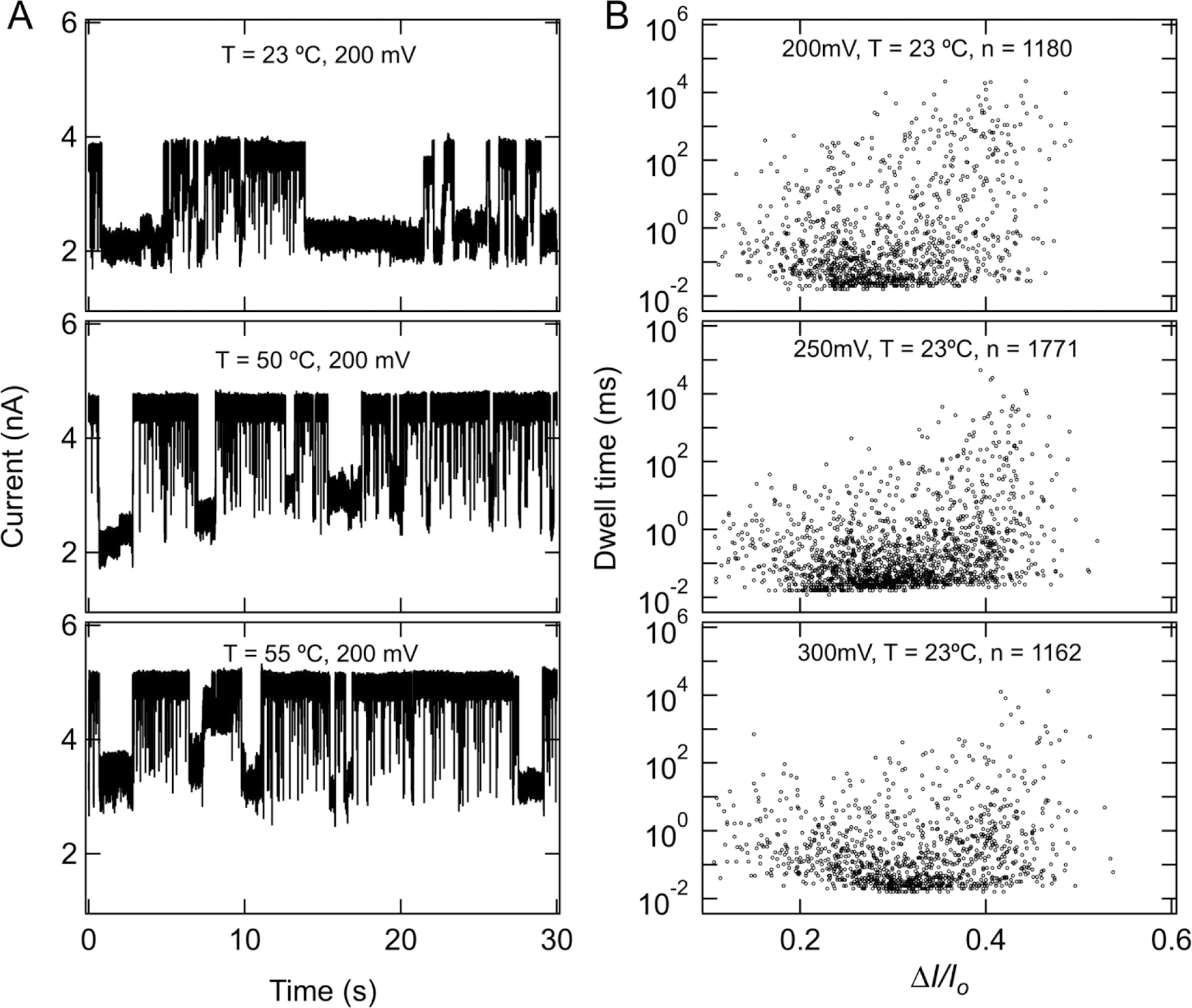
No significant effect of temperature on kissing loop interactions. (A) Example ionic current traces for 100 nM EM measured at 200 mV and at different temperatures. (B) Scatterplots as a function of voltage measured at 23 °C. There is no appreciable change in blockade ratio upon increasing the temperature up to 60 °C (see SI: Fig. S8); only dwell time becomes faster, suggesting that the kissing loop interactions in these fiber structures are resistant to heating at this temperature.

In summary, we have shown that solid-state nanopores can be used to discriminate among RNA fiber structures that differ in their branching architecture, despite their large heterogeneity in length that complicates their analysis using gel electrophoresis and/or AFM. Fiber molecules which contain more branches produce longer and deeper current blockades regardless of the nature and concentration of the electrolyte solution. Brownian dynamics simulations reproduce the trend observed in our experiments. Experiments at different temperatures appear to suggest that the kissing loop interactions in these fibers are resistant to heating, suggesting possible application of these biomaterials at extreme conditions.

Materials and Methods:

Nanopore fabrication:

We used high-stress SiN (250 MPa) membranes supported by a Si chip as substrates for nanopore fabrication as described previously^36–38. Nanopores were cleaned in hot piranha (3:1 H₂SO₄:H₂O₂) for 30 minutes, followed by hot deionized water, before each experiment. After cleaning, nanopore chips were assembled in a custom flow cell equipped with Ag/AgCl electrodes, and a quick-curing silicone elastomer was applied between the chip and the cell to seal the device and thereby reduce the noise by minimizing the chip capacitance.

Electrical detection and data acquisition:

The ionic current through nanopores was measured using an Axopatch 200B amplifier (Molecular Devices) and low pass filtered to indicated bandwidth using the internal Bessel filter of the Axopatch. Data points were digitized and sampled at 250 kHz sample rates on a National Instruments DAQ card using custom LabVIEW software. We have performed high-bandwidth measurements of ionic current (for fiber) using a Chimera instruments VC100 amplifier. Data were processed and events were detected using Pythion (https://github.com/rhenley/Pyth-Ion/) and plotted in Igor Pro software.

Preparation and assembly of NF, EOM, and EM fibers:

All RNA sequences are available in the Supporting Information. DNA primers and templates were purchased from Integrated DNA Technologies, Inc., and amplified using MyTaq Mix (Bioline). The reactions were purified using DNA Clean & Concentrator (Zymo) for the isolation of produced double-stranded DNA templates containing T7 RNA polymerase promoters, which then underwent in vitro run-off transcription using T7 RNA polymerase in the presence of 80 mM HEPES-KOH (pH 7.5), 2.5 mM spermidine, 50 mM DTT, 25 mM MgCl₂, and 5 mM of each rNTP. After 3.5 hours at 37 °C, reactions were stopped with the addition of RQ1 RNase-Free DNase (Promega) for a further 30-minute incubation at 37 °C. RNA products were then purified using denaturing polyacrylamide gel electrophoresis (PAGE, 15%) with 8 M urea which was run in TBE buffer (89 mM tris-borate (pH 8.2), 2 mM EDTA) at 70 mA. RNA was isolated via UV shadowing, cut, and eluted overnight at 4 °C in TBE with 300 mM NaCl. For precipitation, RNA was transferred into 2 volumes of EtOH for 3 hours at −20 °C and centrifuged at 10.0 G for 30 minutes at 4 °C. The sample was washed and centrifuged again at 10.0 G for 10 minutes at 4 °C twice, then dried on a Labconco CentriVap. Samples were resuspended in HyClone Molecular Biology Grade Water, Cytiva (Fisher Scientific).

NF, EOM, and EM fibers were assembled each in one pot with all component strands added in an equimolar ratio. For NF fibers, two non-functionalized strands corresponding to the AB fiber system were combined. For the EOM fibers, one functionalized fiber strand was combined with one non-functionalized fiber strand, plus one complementary RNA. For the EM fibers, two functionalized strands of the AB fiber system were combined, plus two parts complementary RNA. Samples were heated to 95 °C for 2 minutes, snap-cooled on ice for 2 minutes, and assembly buffer was added to a final concentration of 89 mM tris-borate (pH 8.2), 2 mM MgCl₂, 50 mM KCl. Samples were incubated at 30 °C for 30 minutes and were kept on ice afterwards.

Gel electrophoresis:

Fibers were visualized via 8% non-denaturing native-PAGE (37.5:1) on a Mini-PROTEAN Tetra System (Bio-Rad). Gels were run at 4 °C for 30 minutes at 300 V in 89 mM tris-borate, 2 mM MgCl₂. Afterwards, gels were stained with ethidium bromide (0.5 µg/mL) and visualized using a ChemiDoc MP system (Bio-Rad).

AFM:

Fibers were analyzed on a freshly cleaved 1-(3-aminopropyl)-silatrane-modified mica surface with a MultiMode AFM Nanoscope IV system (Bruker Instruments) in tapping mode.

Coarse-grained BD simulations:

Simulations of the RNA fibers were set up and performed using a custom version of the multiresolution modeling framework, mrDNA ²⁷, modified to employ polymer properties appropriate for dsRNA. Specifically, the helical rise was increased to 11.6 Å, the contour length per nucleotide was decreased to 2.77 Å, the stretch modulus was decreased to 560 pN, and the persistence length was increased to 60 nm. The solution for the electric field in and around the pore was obtained using COMSOL multiphysics with “Creeping flow”, “Transport of dilute species”, and “Electrostatics” modules to solve the coupled equations for incompressible Stokes’s flow, electrostatics, and Fick’s diffusion of ions. The 2D axisymmetric solution for the electrostatic potential was exported and discretized to a 3D grid with a scaling factor of 0.25 to account for the reduction of force due to elecroosmotic flow in 1M KCl observed for DNA ³⁹. Regions outside the solution domain (i.e. within the membrane) were assigned a potential value of −10 kcal mol⁻¹ e⁻¹ for subsequent inclusion in BD simulations. The model of the fibers was generated using a custom Python script to assemble monomers into a single chain. Kissing loops are not supported by the mrDNA model and were represented by a six bp dsRNA fragment that was separated from the helical portion of each monomer by a 2 nt ssRNA fragment on one strand and 1 nt fragment on the other. Models were generated at single bp/nt resolution with an extra orientation bead for each dsRNA bead. Simulations were performed using the engine ARBD⁴⁰ as described previously for mrDNA with BD integration scheme with the temperature set to 291 K and 50 fs timestep. Trajectory frames were written every 100,000 steps.

SVM analysis:

For use in machine-learning analysis and supervised classification³¹ of the two branched samples, the data from 100 mV recordings using a 6 nm pore were used. The events were re-parsed using a filter-derivative parsing algorithm (adapted and modified library from Schreiber & Karplus)³², which recognizes events by detecting signal falls and rises based on the slope of a low-pass filtered mask of it. This parsing method allows for an almost complete isolation of the event current from the start drop and end pickup transition current, which makes it possible to obtain a global maximum current value during the event. After event detection and extraction, each event was divided into five equal-duration segments. Only those events with durations between 500us and 2s, and normalized minima of under 0.63 were kept. The features used in the SVM analysis include: Log₁₀ duration, and current parameters (event mean, standard deviation, minimum, maximum, and the mean of five equal-duration segments), all of which were divided by the open pore current I₀ for normalization³³. This particular selection of features was done as an attempt to demonstrate that such basic properties of signature ionic current of these RNA brush samples can provide sufficient information for a non-linear classifier to discriminate among the two samples with good accuracy, even if sufficient separation is not apparent in univariate analyses (histograms) or pairwise comparisons (as shown in SI: Fig S12). All features and the normalized trace of an example event are illustrated in SI: Fig S13. The EM events were randomly sampled down to the same number as EOM, for a balanced selection of 187 events per analyte. The selected events were randomly split into train/test groups with a ratio of 70% / 30%. The random splitting, followed by a standard scaler normalization step (blind to the test set) and fresh training and testing of the model were repeated 9 times (SI: Fig S14). The accuracy score, defined as the fraction of correct predictions over all predictions (in the test set) showed an average of 85.8% with a standard deviation of 2.5% in those 9 repeats. All SVM classification analyses were performed using the radial basis function (RBF) kernel model, through the sci-kit learn library (sk-learn v 0.24.2)³¹.