Molecular Dynamics Simulations of Protein RNA Complexes by Using an Advanced Electrostatic Model

Abstract

Protein-RNA interactions are integral to the biological functions of RNA. It is well recognized that molecular dynamics (MD) simulations of protein-RNA complexes are more challenging than those of each component. The difficulty arises from the strong electrostatic interactions and the delicate balance between various types of physical forces at the interface. Previously MD simulations of protein-RNA complexes have predominantly employed fixed-charge force fields. Although force field modifications have been developed to address problems identified in the simulations, some protein-RNA structures are still hard to reproduce by simulations. Here we present MD simulations of two representative protein-RNA complexes using the AMOEBA polarizable force field. The van der Waals parameters were refined to reproduce accurate quantum-mechanical data of base-base and base-amino acid interactions. It was found that the refined parameters produced a more stable hydrogen-bond network in the interface. One of the complexes remained stable during the short simulations, whereas it could quickly break down in previous simulations using fixed-charge force fields. There were reversible breaking and formation of hydrogen bonds that are observed in the crystal structure, which may indicate the difference in solution and crystal structures. While further improvement and validation of the force fields are still needed, this work demonstrates that polarizable force fields are promising for the study of protein-RNA complexes.

Graphical Abstract

1. Introduction

RNA is essential for many biological activities including gene expression and regulation and catalysis. RNA also has tremendous therapeutic potential for gene therapy, immunotherapy, and vaccines.^1–3 Most of biologically active RNAs interact with proteins. The interactions with proteins are crucial for the folding, stability, regulation, transport and localization of RNAs.^4–6 Therefore, understanding of the principles of RNA-protein interactions is useful for both fundamental research and practical applications. The mechanisms of protein-RNA recognition are highly diverse. Various types of interactions can be found at the protein-RNA interface, such as electrostatic interactions, hydrogen-bonding, salt bridge, pi-pi interactions and hydrophobic interactions.^{7, 8} In protein-RNA complexes, proteins either exclusively interact with RNA backbone or have specific interactions with nucleobases. In addition, protein-RNA interactions often involve large conformation changes of RNAs.

Experimental techniques including X-ray crystallography and nuclear magnetic resonance (NMR) have been valuable for the study of protein-RNA complexes. The data generated by such experiments have enabled the development of software tools for the prediction of protein-RNA binding. Structural analyses have shown van der Waals (vdW) interactions are more prevalent than hydrogen bonds,⁹ and interactions with the RNA backbone are more frequent than interactions with nucleobases.¹⁰ There are also limitations in experimental studies of protein-RNA complexes. The biomolecules in solution may have more than one conformation, and they may be different from the crystal structure. NMR experiments are usually conducted in solution, but they are more ambiguous to interpret than X-ray crystallography.¹¹

Molecular dynamics (MD) simulations have been widely used to study biomolecular structures and dynamics as they complement experiments by providing detailed pictures of the molecules and connecting microscopic structures with macroscopic observations. Some notable examples include protein structure prediction¹² and protein-ligand binding.^{13, 14} However, MD simulations of protein-RNA complexes are still challenging. The simulation results are very sensitive to force field parameters¹⁵ because of the conformational flexibility of RNAs and the intricate network of interactions in the protein-RNA interface. There have been a lot of progress in nucleic acid force fields. Two major families of force fields for proteins and nucleic acids are AMBER and CHARMM.^15–17 AMBER force fields were first developed in the 1990s¹⁸ and have been continuously refined.^19–23 A major focus has been on torsion parameters because the conformations of nucleic acids are sensitive to torsion parameters and the non-bonded parameters were found to be sufficient for describing gas-phase interaction energies and hydration free energies.¹⁹ Recently, there have been more studies on refining non-bonded parameters to improve intramolecular hydrogen bonds, base stacking, protein-nucleic acid binding and other thermodynamics properties.^24–32 The revised non-bonded parameter for phosphate of Steinbrecher et al.³³ in combination with the OPC water model could alleviate the excessive binding excessive binding between 2’-hydroxyl groups and phosphate, while it has issues for other systems.^{25, 34} Šponer and coworkers proposed hydrogen-bond terms (HBfix and gHBfix)^23–25 to selectively fine-tune the non-bonded interactions, which leads to general improvement for RNA simulations. Shaw and coworkers developed revised versions of AMBER force fields that include new parameters for nucleobase charge and vdW to improve base pairing and stacking interactions and the phosphate vdW parameters of Steinbrecher et al.,³³ which necessitates adjustments of torsion parameters. The parameters were used with the TIP4P-D water model developed by the same group.²⁷ Subsequently the phosphate charges and vdW parameters were modified to be compatible with the DES-Amber protein force field which includes rescaling of ionic charges.^{35, 36} CHARMM force fields^{37, 38} have also been improved over the years.¹⁷ The latest version CHARMM36³⁷ improved the stability of base pairs by tuning 2’-OH torsion parameters. Common problems for standard fixed-charge force fields such as AMBER and CHARMM are the over-stabilization of protein-nucleic acid interactions and the difficulty in modeling ion-specific effects.²⁹ These problems have been partially addressed by special vdW parameters.^{29, 30, 39}

Polarizable force fields provide more accurate description of electrostatics and balanced interactions in heterogenous environments, so they are promising in addressing the problems of fixed-charge force field for protein-RNA complexes.^40–42 CHARMM-Drude force field^43–48 and AMOEBA^49–52 are two popular polarizable force fields. AMOEBA showed good accuracy for various nucleic acid systems, including DNA duplexes in different environment, RNA tetranucleotide, RNA tetraloops, RNA duplexes, and HIV-TAR.⁴⁹ There have been very few published studies on MD simulations of protein-RNA interfaces using polarizable force fields, which is likely due to the computational cost of polarizable force field and the difficulty in conformational sampling.

In this work, the vdW parameters in AMOEBA nucleic acids force field were refined by using high-quality quantum-mechanical data. MD simulations for representative protein-RNA systems were performed with both the original and the refined AMOEBA force field parameters.

2. Methods

2.1. Molecular dynamics simulations

Two protein-RNA complex systems were selected for molecular dynamics simulations: U1A protein bound to RNA hairpin⁵³ (PDB code: 1urn) and C. elegans Pumilio FBF-2 protein bound to gld-1 FBEa RNA⁵⁴ (PDB code: 3k5y). The PDB structure of 1urn contains three copies of the complex. The complex formed by chain B and chain Q was selected for simulations since it is the only one without missing residues. Both systems have been studied by Krepl et al,⁵ and more recently by Tucker et al.³⁶ The crystal structure of U1A contains a 21-nucleotide RNA sequence. The FBF protein is responsible for the regulation of messenger RNA.⁵ The FBF interface is composed of interaction between nucleobases and protein, while the RNA backbone is exposed to the solvent.⁵

The systems were prepared by using the tleap program in AmberTools.⁵⁵ All systems were neutralized and solvated in isometric truncated octahedron boxes with a minimum distance between solute and box edge of 15 Å. KCl ions were added to give a concentration of 150 mM. The solvated systems were minimized, gradually heated up from 50 K to 300 K in 500 ps NVT simulations with harmonic position restraint on protein and RNA, and equilibrated at the NPT ensemble with 300 K and 1 bar for 4 ns, and then the force constant of the position restraints was gradually reduced from 25 kcal/mol/Ų to zero in 6 ns NVT simulations. The production simulations were NVT simulations at 300 K. The RESPA integrator⁵⁶ was used with an outer time step of 2.0 fs. Temperature and pressure were maintained by Bussi thermostat⁵⁷ and Monte Carlo barostat,⁵⁸ respectively. The electrostatics was treated by PME with a real-space cutoff of 7.0 Å. The van der Waals (vdW) was truncated at 12.0 Å. Tinker-OpenMM program⁵⁹ was used for the simulations. Proteins and nucleic acids were modeled by the original amoebabio18 parameter and refined parameters as detailed below. Water and ions were modeled by the default parameters as described by Ren et al.⁶⁰ and Wang.⁶¹

2.2. Quantum mechanical calculations

Quantum mechanical (QM) calculations were used to generate reference data to refine the non-bonded interaction parameters for RNA and torsion parameters for protein. The choice of QM methods for force field parametrization significantly affects the performance of the resulting force field. Usually more accurate QM methods lead to better force fields (e.g. the DESRES RNA force field²⁷), although due to error cancelation, lower-level QM methods could be better choices in some cases (e.g. AMBER RNA force fields parmbsc0,²² OL3,⁶² OL15²¹). Since AMOEBA incorporated more physical terms including polarization and atomic multipoles, it is less prone to error cancelation than non-polarizable force fields, and the parameterization of AMOEBA has relied on high-level QM methods such as MP2 with relatively large basis sets. MP2 with cc-pVTZ or aug-cc-pVTZ was used in the parameterization of the AMOEBA RNA force field. However, recent benchmark studies have found that MP2 suffers from large errors for dispersion interactions,^{63, 64} which are prominent in base-base stacking. Various MP2-based method and DFT methods have been developed to address this issue. Based on results from previous work,^{63, 65} DSD-BLYP-D3BJ, a double-hybrid DFT method with empirical dispersion correction, was chosen for QM calculations due to its excellent accuracy and computational efficiency.

2.3. Optimization of vdW parameters

Nucleobase vdW parameters

Model compounds based on ideal geometries were generated for fitting nucleobase vdW parameters, and models based on PDB geometries were used for testing. The workflow is demonstrated in Scheme 1. The model compounds include model compounds including methylated nucleobases (A, T, U, G and C), N-methyl amide (NMA), ethanol (EtOH), acetate, methylammonium (MeNH3), imidazole and benzene. All interaction energies were calculated at the DSD-BLYP-D3BJ/def2-QZVP level of theory. The ideal geometries include canonical and noncanonical base pairing, base-base stacking and base-water dimers. The starting structures were taken from our previous work⁵⁰ with the addition of A-G cis-Watson-Crick/sugar-edge pair⁶⁶ from the JSCH benchmark database for non-covalent interactions (designated as “G…A 4”).⁶⁷ The geometries were re-optimized by using TPSS-D3BJ/def2-TZVP. For each ideal geometry, additional structures were generated by translation or rotation, as shown in Figure 1. The x-axis was defined by the closest atom pair; the y-axis represents the principal axis of the interface, which was chosen manually for base pairing and defined by three atoms in each monomer that are closest to the interface; the z-axis is orthogonal to the xy-plane.

Scheme 1.

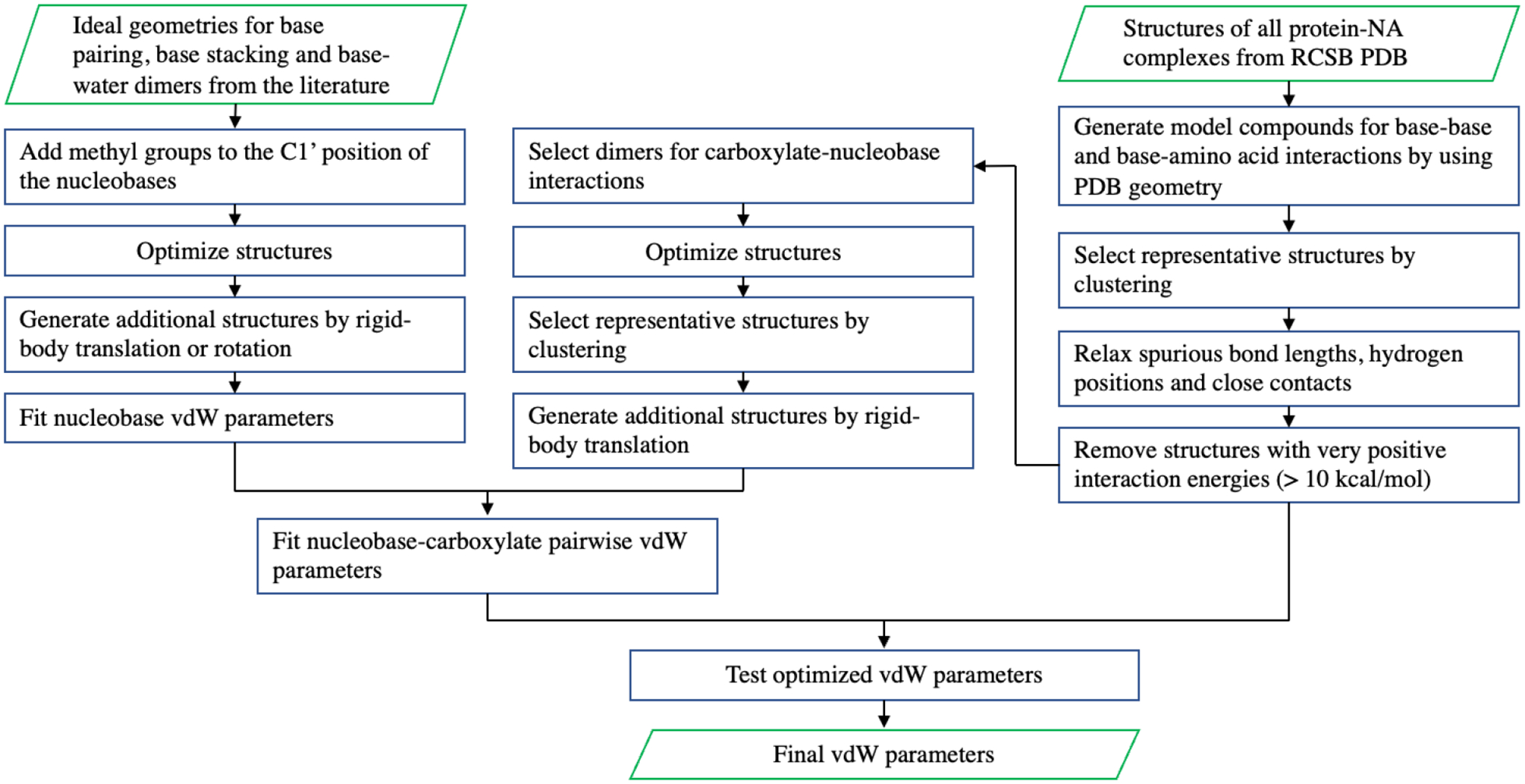
Workflow for the refinement of nucleobase and nucleobase-carboxylate vdW parameters.

Figure 1.

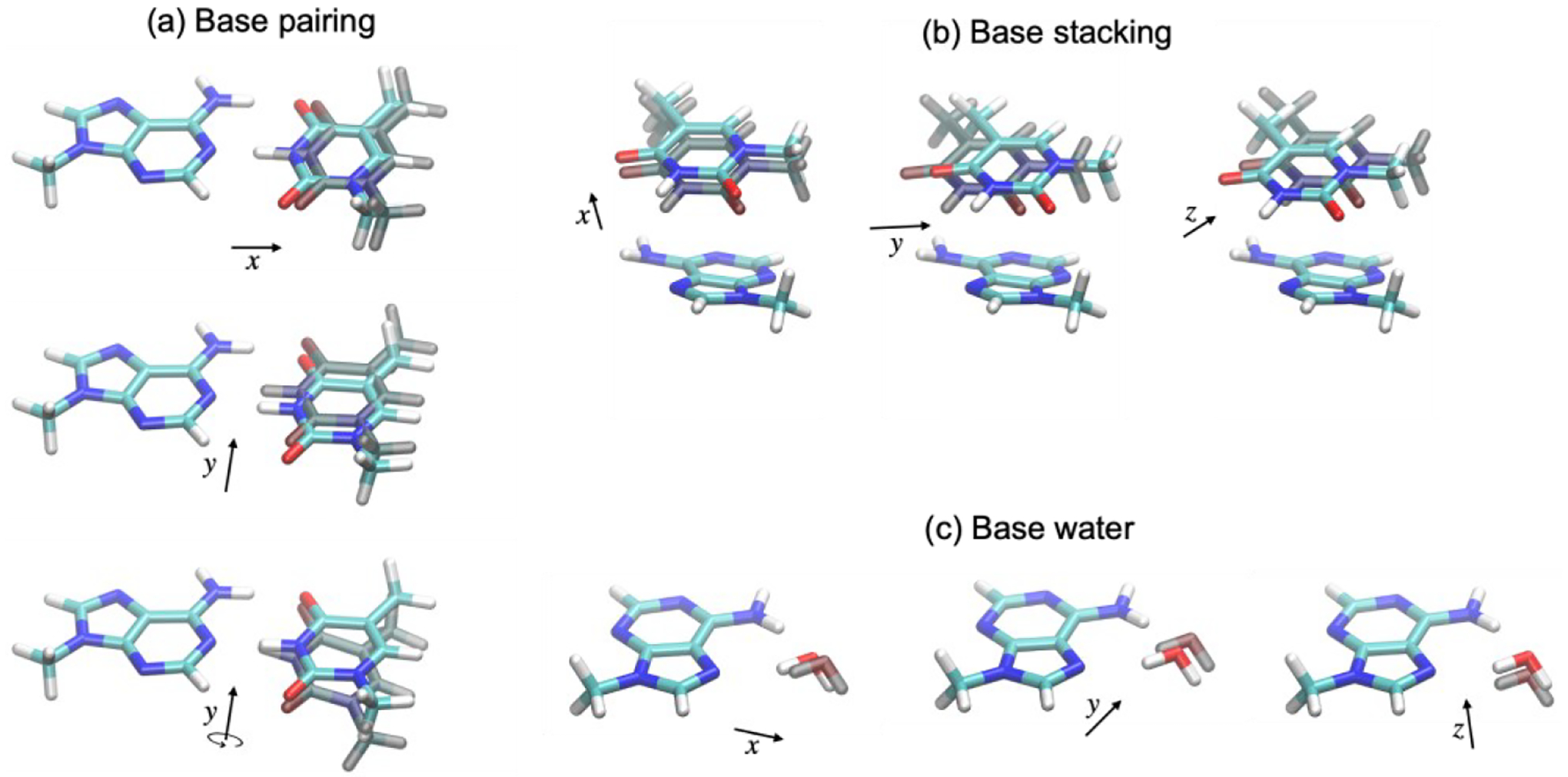
Illustration of additional structures for model compounds based on ideal geometry. (a) for base pairing, Δx = ±0.20, ±0.10, ±0.05 r₀, Δy = ±0.4 Å, and Δθ_y = ±20°, where r₀ is the equilibrium distance; (b) for base stacking, Δx = ±0.20, ±0.10 r₀, Δy = Δz = ±0.6, ±0.3 Å; (c) for base water dimer, Δx = ±0.20, ±0.10, ±0.05 r_0, Δy = Δz = ±0.6, ±0.3 Å.

The PDB geometries include base-base and base-amino acid interactions. The procedure for selecting representative structures is shown in Scheme 1. A hierarchical clustering algorithm with average link and a RMSD cutoff distance of 2.5 Å was used in the clustering. Spurious bond lengths, as defined by AMOEBA bond energy greater than 10 kcal/mol, were relaxed by optimization using AMOEBA with position restraint. Short intermolecular distances (< 1.8 Å) were relaxed by rigid-body distance scan with TPSS-D3BJ/def2-TZVP/PCM. Hydrogen positions were optimized by TPSS-D3BJ/def2-TZVP/PCM or PM6/PCM. Starting from 5334 PDB structures of protein-NA complexes, 657 structures for 45 types of dimers were generated.

The interaction energies based on the ideal geometries were used to refine the nucleobase vdW parameters, while the PDB geometries were used for validation. The data points were assigned Boltzmann weights at 1000 K relative to the corresponding lowest energy points. The Trust Region Reflective algorithm in SciPy with bounds and quadratic restraint was used for the parameter fitting. The bounds were ±5% for vdW diameter and i) ±20% for well depth within the initial parameters. The restraint was chosen based on 5-fold cross validation. Two sets of optimized vdW parameters were obtained: param1, in which the atom types are the same as in amoebabio18, and param2, in which Guanine does not share parameters with other nucleobases. The RMSEs of these parameters as well as the original amoebabio18 are summarized in Table 1. A breakdown of the mean error and root mean squared error (RMSE) to different types of base pairs is shown in Figure 2 and Figure 3. For both base-pairing and base-stacking interactions, amoebabio18 has generally positive errors. This is in part due to the deficiency of the MP2 method which was used in the parameterization of amoebabio18. The mean errors are significantly reduced in the param1 and param2 results. The improvement in RMSEs can be found in most types of base pairing and only a few types of base stacking (namely CU and GG), since the RMSEs of base stacking energy were relatively small. For param1, base pairs involving guanine have more positive errors than other base pairs, which was a motivation for the additional atom types for guanine in param2. Indeed, param2 has overall better accuracy than param1 for the training set (Table 1).

Table 1:

Weighted RMSE of AMOEBA parameters on base-base and base-amino acids interactions (kcal/mol).

Model	Training set		Test set
	Base stacking	Base pairing	Base	Base-Amino Acid
Amoebabio18	1.466	3.775	1.895	1.309
Param1	0.860	1.317	0.829	1.193
Param2	0.887	1.033	0.856	1.194

Figure 2.

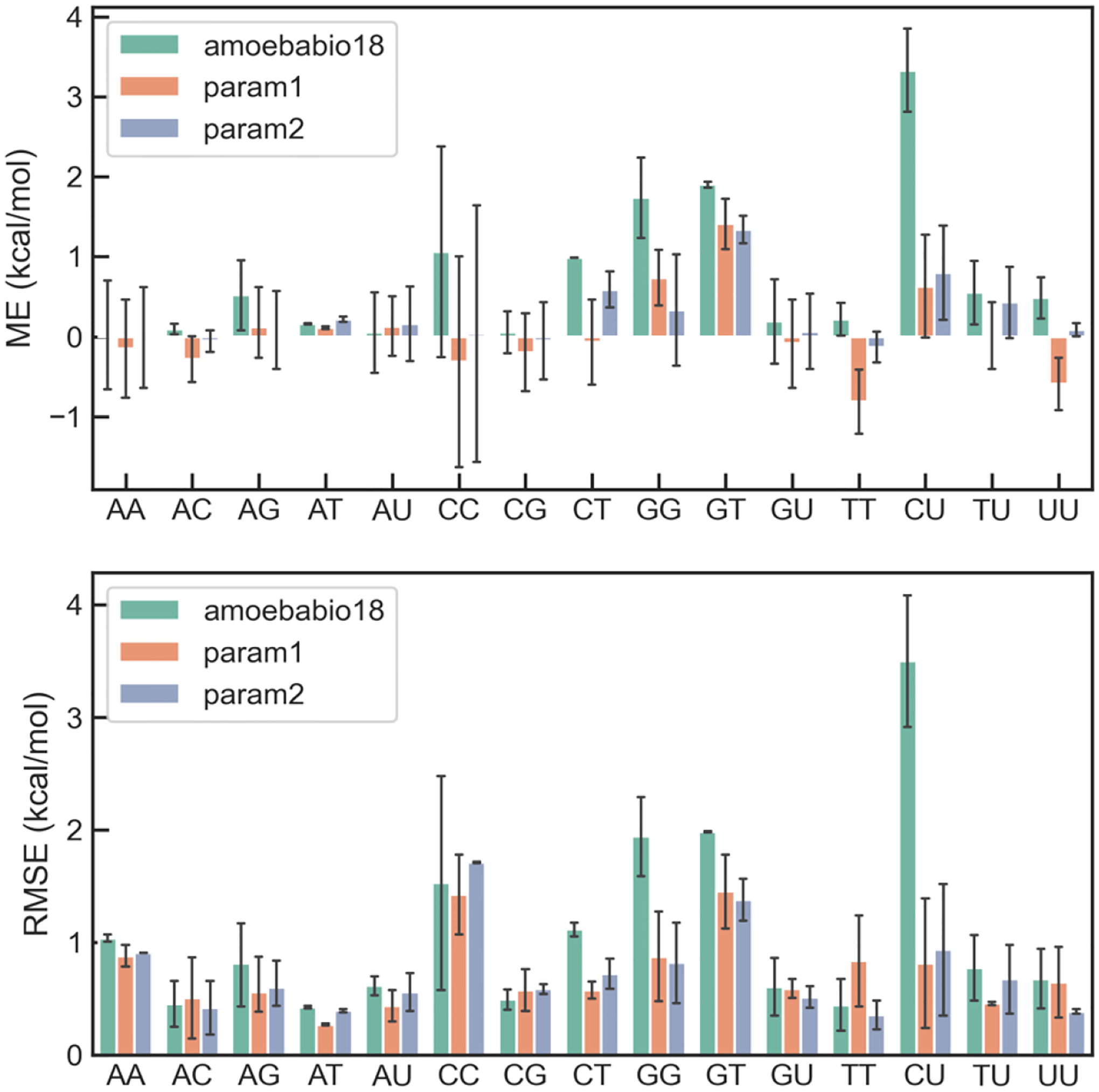
Distribution of errors of AMOEBA force fields for base stacking interaction in each type of base-stacking pairs.

Figure 3.

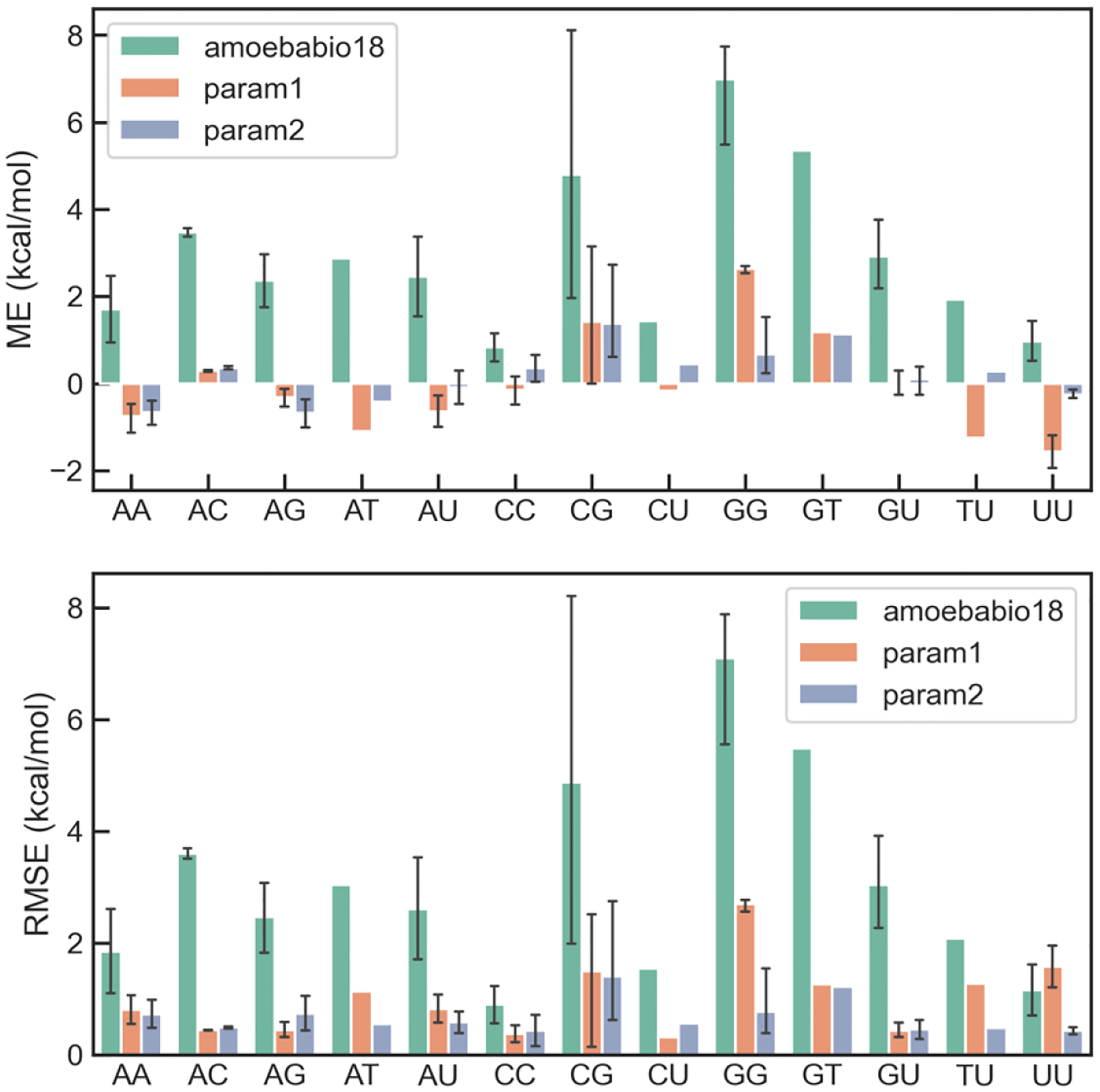
Distribution of errors of AMOEBA force fields for base pairing interaction in each type of base pairs.

The two sets of parameters were evaluated on the interaction energy from the PDB geometries (Table 1), which was not used in the parameter fitting. The accuracy for base-base interactions were significantly improved in both sets of parameters. The accuracy for base-amino acid interactions were also improved, although the training set contains no amino acids. Contrary to the performance for the training set, param2 has slightly larger errors than param1 for the test set, despite having more adjustable parameters. The combination of small training error and large test error is characteristic of overfitting. Therefore, param1 was chosen for simulations.

The optimized vdW parameters are listed in Table 2. The changes in parameters are less than 5% from amoebabio18. The vdW radii are smaller in all optimized parameters than in amoebabio18, since the base-pair interactions in amoebio18 are too weak. In param2, the vdW radii of guanine are also smaller than those of the corresponding atoms in other nucleobases.

Table 2:

Nucleobase vdW sigma (Å) and epsilon (kcal/mol) in amoebabio18 and optimized parameters.

Vdw type	Atom	amoebabio18	Param1	Param2
54 (154)	U/T N3, C N1 G N1	3.700 0.127	3.600 0.124	3.700 0.127 3.560 0.127
50 (150)	A N3/N1, C N3 G N3	3.640 0.127	3.530 0.124	3.560 0.120 3.500 0.125
49 (149)	A N7 G N7	3.640 0.127	3.530 0.124	3.560 0.120 3.500 0.125
58 (158)	C O2, U/T O2/O4 G O6,	3.350 0.129	3.250 0.124	3.250 0.124 3.200 0.120
53 (153)	A H6, C H4 G H2	2.650 0.020	2.620 0.018	2.650 0.020

Nucleobase-protein vdW parameters

The hydrogen bonds between Asp/Glu side chains and nucleobases are a common motif in protein-nucleic acid interfaces. It was found that even with the optimized nucleobase vdW parameters, some of these hydrogen bond interactions still have relatively large errors. This may be attributed to the partial covalent bonding nature of these interactions. As in our previous work on phosphate-binding proteins,⁶⁸ pairwise vdW parameters between carboxylate O and NH were included to improve the accuracy for these interactions. The training set structures were obtained by geometry optimization (TPSS-D3BJ/def2-TZVP) of model compounds from the PDB geometries (Scheme 1). For each optimized structure, two additional structures were generated by rigid-body translation, resulting in intermolecular distances of 0.9 and 1.1 times the equilibration distance. The performance for the training set and the test set are shown in Figure 4.

Figure 4.

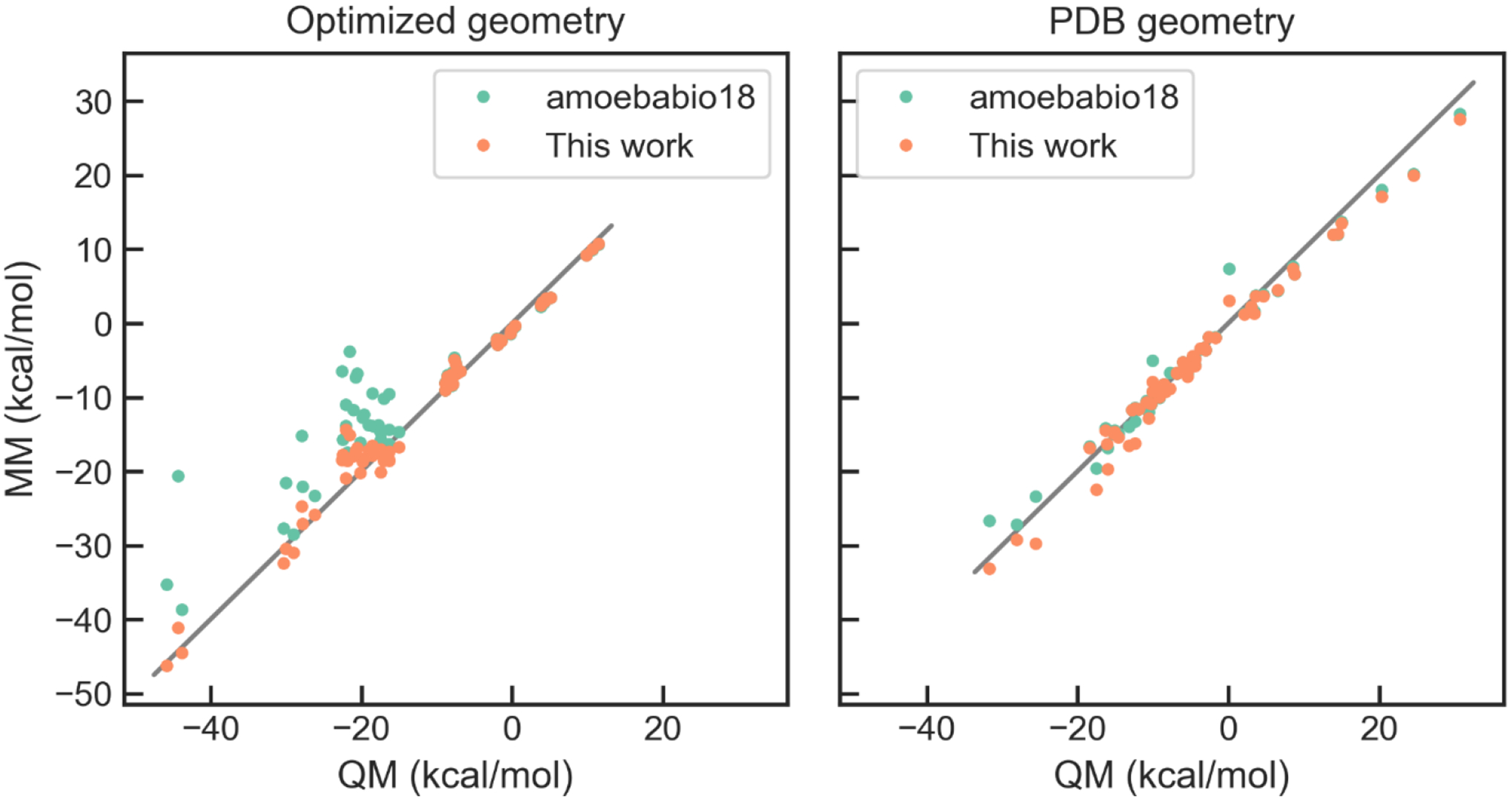
Correlation between QM and MM interaction energies for nucleobase-carboxylate interactions.

2.4. Optimization of Asn torsion parameters

During initial MD simulations of the U1A protein-RNA interface using amoebabio18, it was found that the rotamer conformation of some Asn residues in the interface was different from those in the crystal structures, which disrupted the hydrogen-bond network. Therefore, the torsion parameters of Asn were revisited. Conformations were generated by (1) one-dimensional torsion scan of Asn χ1 and χ2 torsions at 30 deg interval, with backbone torsion fixed at either alpha-helix or beta-sheet conformation, which leads to 48 conformations in total, and (2) 3-by-3 two-dimensional scan of χ1 and χ2 torsions at −30, 0 and 30 deg based on each of the 11 rotamers from the backbone dependent rotamer library,⁶⁹ for a total of 99 conformations. All the conformations were optimized at the ωB97Xd/6–311++g(2d,2p) level of theory with backbone and side chain torsions frozen, and the energies were calculated by DSD-BLYP-D3BJ/def2-QZVP. The Trust Region Reflective algorithm was used in the least-square fitting. The RMSE was reduced from 2.06 kcal/mol for amoebabio18 to 1.60 kcal/mol for the optimized parameters (param1). The improvement is more noticeable when tested on the conformations sampled from the initial MD simulations of U1A. As shown in Figure 5, amoebabio18 has large errors in the relative energies of these conformations; specifically, it predicted similar energies for the low-energy and high-energy conformers, while the two conformers differ by about 4 kcal/mol according to QM (DSD-B3LYP-D3BJ/def2-QZVP). The optimized parameters could correctly rank the low-energy and high-energy conformers. The side chain torsion parameters of the original AMOEBA protein force field were fitted to MP2/CBS energy of one-dimensional torsion, with backbone fixed at alpha-helix and beta-sheet conformations.⁷⁰ Both MP2 and DSD-B3LYP-D3BJ are very accurate for conformation energies.^{63, 65} The main difference between this work and the original parameterization is in the conformers. The training set structures were generated by using a general procedure rather than tailored to the issue of U1A simulations, so the optimized parameters are expected to be a general improvement over the original parameters.

Figure 5.

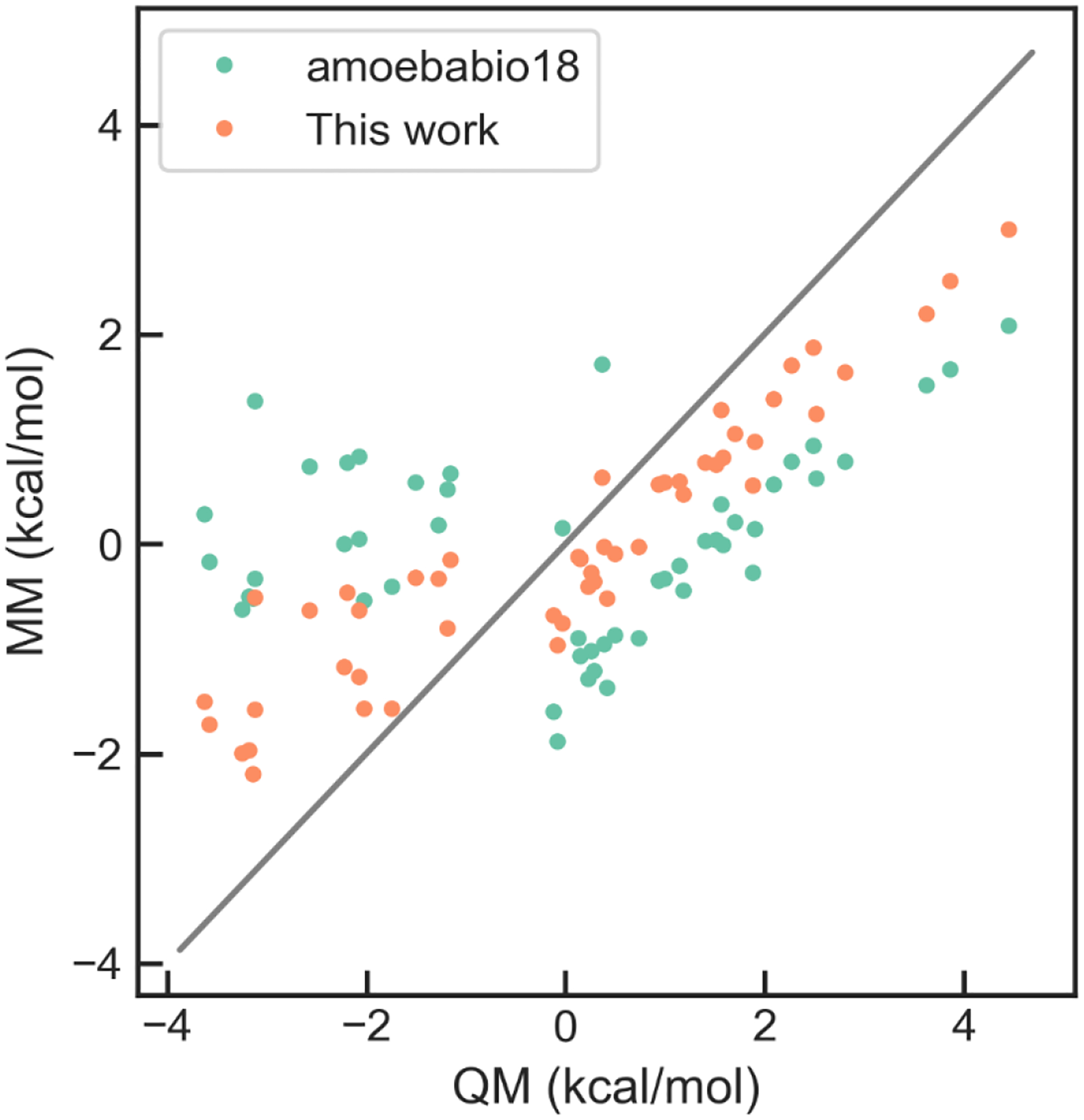
Correlation between QM and MM relative energies for the Asn conformers sampled from MD simulations of U1A.

3. Results and Discussions

3.1. U1A simulations

The U1A protein-RNA complex has been well studied by experiments and MD simulations.^{53, 71–73} Its interface consists of two parts, one between the stem region of the RNA hairpin (including U7, U8, G9 and G16) and two loops of the protein, and the other between the loop region of the RNA (including C10, A11 and C12) and a loop of the protein. The stability of the protein-RNA interface during the simulations is measured through the distances between several hydrogen-bond donor and acceptors (Figure 7), and the hydrogen bond is considered to be maintained if the distance is below 4 Å. During the simulations using the amoebabio18 parameters, the hydrogen bond between U8(N3) and Asn16(OD1) was quickly lost within 20 ns in four out of five simulations. This is accompanied by the rotation of the Asn16 χ1 torsion and the loss of the hydrogen bond between U8(O4) and Lys80. This can be clearly seen in Figure 7 where the average distance for the two hydrogen bonds in the last 20 ns of 60 ns simulations are around 6 Å. The two hydrogen bonds with U8 could reform briefly and then break multiple times during extended 100-ns simulations (Figure 8), which indicates that there is only a small free energy difference between the native structure and the disrupted structures. Among the conformations with disrupted hydrogen bond between U8(O4) and Lys80(NZ), there are water-mediated interactions when the distance is between 4 and 5 Å. The other part of the protein-RNA interface represented by the hydrogen bond between A11(N1) and Ser91(OG) remained relatively stable in the simulations. Preliminary simulations using the optimized vdW parameters suffered from similar issues for the hydrogen bonds around Asn16 (see Supporting Information). The stability of the interface was significantly improved after the introduction of the optimized Asn torsion parameters. The two hydrogen bonds with U8 were well maintained in all five simulations (Figure 7). The hydrogen bond between A11(N1) and Ser91(OG) was also stable in the majority of simulations, although there was a larger variation between simulations compared to the simulations with amoebabio18. The variations in the hydrogen bonds with A11 was largely due to the conformations of the C-terminal residues. The C-terminal of the U1A protein consists of a short five-residue alpha-helix, followed by unstructured residues Met97 and Lys98. Short alpha-helices are generally not very stable in aqueous solution. In addition, the last residue Lys98 is missing in the crystal structure, and is not included in this work and previous work.⁷⁴ The C-cap residue could affect the electrostatic interactions with RNA.

Figure 7.

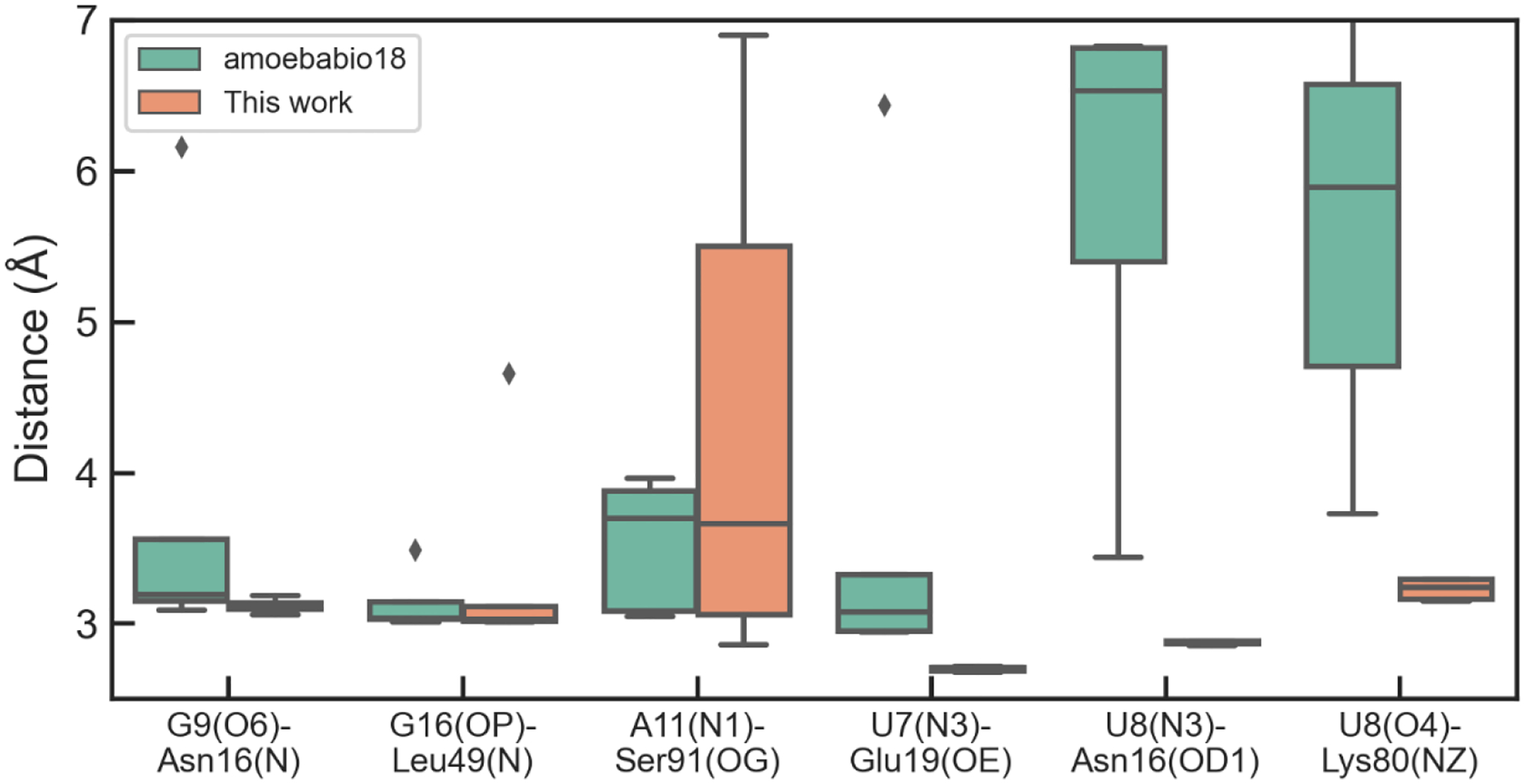
Average distances between selected hydrogen-bonds donors and acceptors in the U1A complex during MD simulations. The average is calculated over the last 20 ns of each of the five 60-ns simulations.

Figure 8.

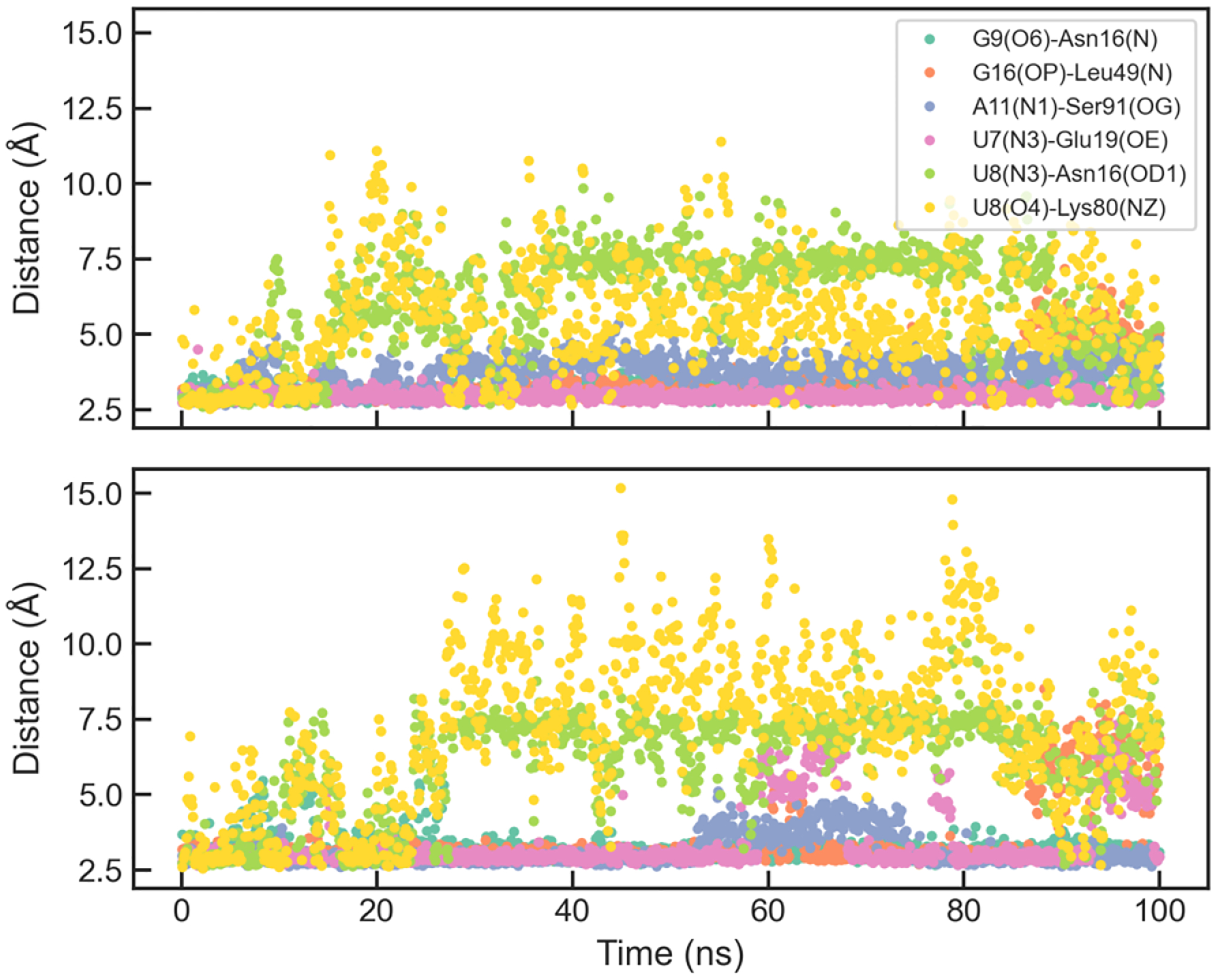
Evolution of selected hydrogen-bond distances in two extended simulations of U1A with the original AMOEBA parameters.

Previous simulations had difficulty in keeping all the native hydrogen bonds in the U1A interface. Simulations with AMBER ff99bsc0χOL3 for RNA and ff99SB or ff12SB for protein led to an altered hydrogen-bond network.⁵ Simulations with ff99SB did not maintain several hydrogen bonds with U7, U8, G9 and G16. Simulations with ff12SB which includes a reparameterization of side-chain torsion parameters did not bring significant differences in the simulations. It is worth noting that four simulations with ff12SB behaved similarly as those with ff99SB; in two other simulations, the disruption of hydrogen bonds with U8, G9 and G16 were reversible and the A11(N1)-Ser91(OG) bond was disrupted.⁵ Coincidently, the two ff12SB simulations were similar to the AMOEBA param1 simulations (Figure 7), except that U7(N3)-Glu19(OE) bond was very stable in AMOEBA simulations. Šponer and coworkers identified some deficiencies of the AMBER force fields through QM/MM calculations, especially for the solvent-exposed hydrogen bonds G9(N7)-Asn15(ND) and U8(O4)-Lys80(NZ).⁷⁴ A structure-specific force field term for the hydrogen bonds (HBfix) could help stabilize the interface.²⁴ This idea was further explored for simulations of other RNA systems.^{23, 25} In the simulations using AMBER ff12SB χOL3 with HBfix, the overall interface remained stable during 1000-ns simulations, and there were reversible breaking of G9(N7)-Asn15(ND), U7(N3)-Glu19(OE) and U8(O4)-Lys80(NZ), which were also observed in some of the AMOEBA simulations.

Tucker et al. reported 50-microsecond simulations of several protein-nucleic acid complexes including U1A and FBF, using modified versions of AMBER force field.³⁶ It was found that a reparameterization of nonbonded parameters for the nucleic acid backbone (mainly 2’-hydroxyl and phosphate oxygen) based on experimental data substantially improved the simulations of some protein-nucleic acid complexes. However, the re-parameterized force field (DES-Amber 3.20) and their previous force field (DES-Amber) have similar results for U1A. The overall RMSD went up to 4–5 Å after a few microseconds, indicating that some hydrogen bonds were possibly disrupted at a very long timescale.

Electrostatic interactions also play roles in the association and stability of the U1A complex. It was shown by mutagenesis experiments that while Lys20, Lys22 and Lys23 all affect the association rate, Lys20 has minimal effect on the complex stability.⁷³ In the crystal structure, Lys22 has a salt bridge with the backbone phosphate group, and Lys20 and Lys23 have no direct contact with the RNA. The interactions of these Lys residues during the AMOEBA simulations are generally consistent with the crystal structure: Lys20 had transient salt bridges with the phosphate group of U3 or G4, and Lys23 remained away from the RNA. In a previous simulation with AMBER ff99 force field, Lys20 and Lys23 formed stable salt bridges with phosphate groups.⁷⁵ So the fixed-charge force field seems to overestimate the electrostatic interactions between Lys and phosphate, while AMOEBA has more balanced electrostatic interactions.

3.2. FBF simulations

The FBF protein-RNA complex has an elongated interface composed of interactions between nucleobases and protein, while the RNA backbone is exposed to the solvent (Figure 6). The distances between hydrogen bond donors and acceptors at the two ends (U1, G2 and A9) during the simulations are shown in Figure 9. The optimized AMOEBA parameter has a significant improvement over amoebabio18 for the hydrogen bonds at the 5’-terminal of the RNA strand, including U1(N3)-Asn500(OD1), U1(O2)-Asn500(ND2), U1(O4)-Gln504(NE2), U1(O4)-Lys557(NZ) and G2(N2)-Ser453(OG). Even with the optimized parameters, there were rapid reversible breaking of the terminal hydrogen bonds, particularly U1(O4)-Lys557(NZ) and A9(O2’)-Lys201(NZ) (Figure 10). Both hydrogen bonds are solvent-exposed and associated with flexible Lys side-chains, so their existence in the crystal structure might be due to the crystal packing effect. Apart from the two hydrogen bonds with Lys, other hydrogen bonds were fairly stable during simulations with the optimized parameters. For both the original and optimized parameters, the 5’-terminal (U1) interface is less stable than the 3’-terminal (A9) interface. An explanation is that the A9(O2’)-Lys201(NZ) bond is stronger than the U1(O4)-Lys557(NZ) bond due to the electrostatic interaction between Lys201 and the RNA backbone, and the stacking between A9 and Tyr245 is also stronger than the stacking between U1 and Tyr501.

Figure 6.

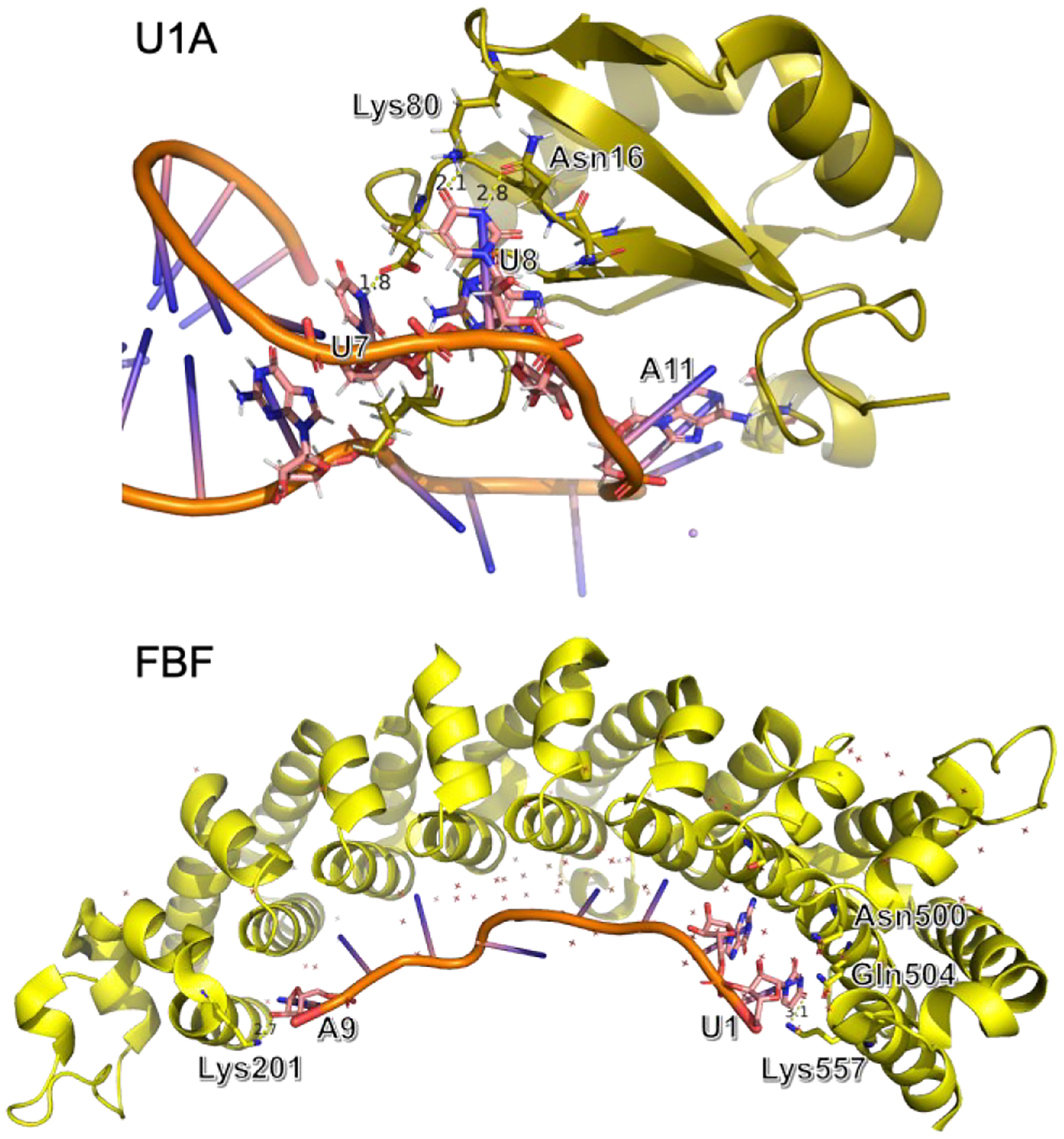
Crystal structure of the U1A (PDB code: 1urn) and FBF (PDB code: 3k5y) protein-RNA complexes.

Figure 9.

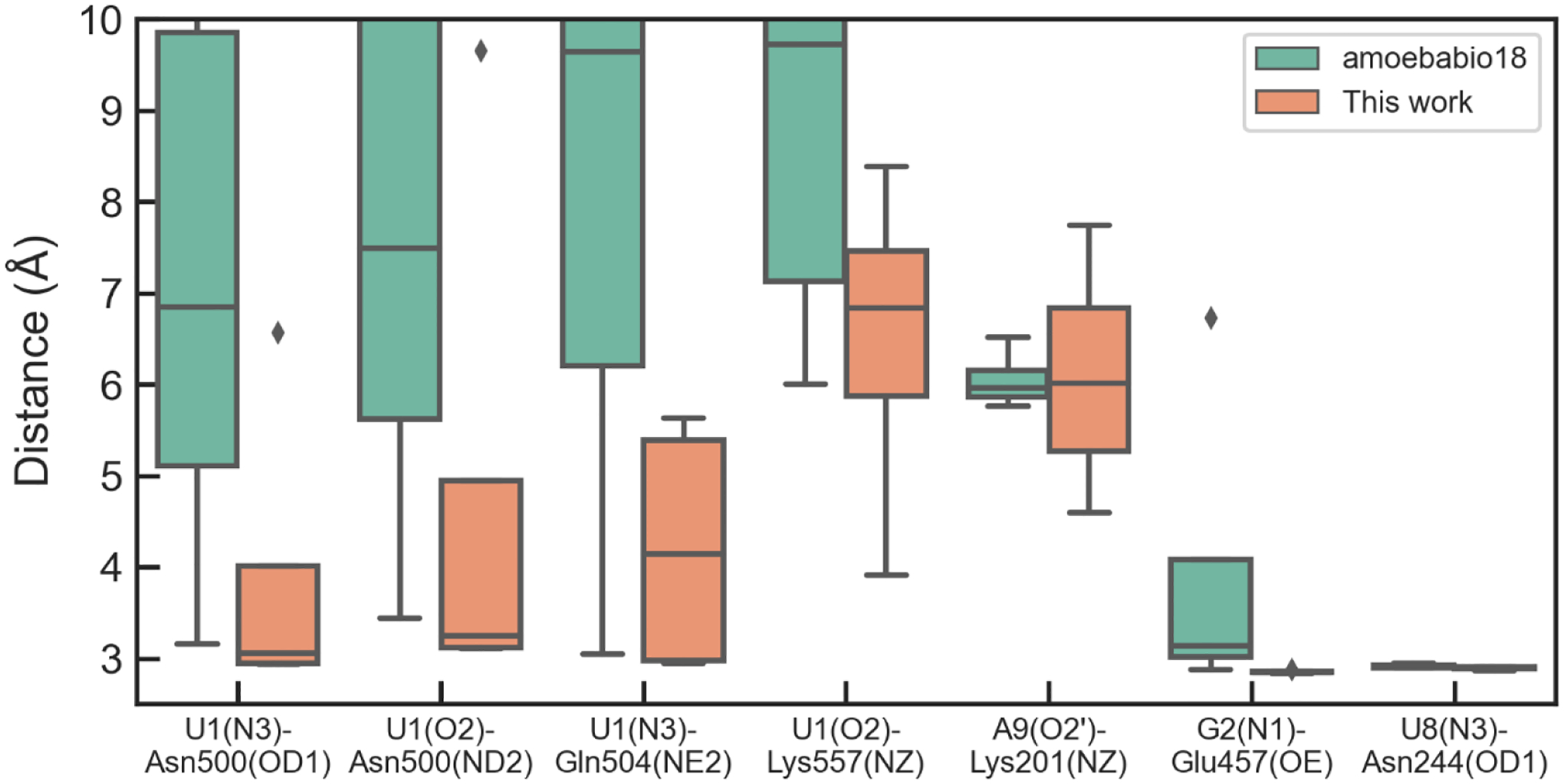
Average distances between selected hydrogen-bonds donors and acceptors in the protein-RNA interface during MD simulations of FBF. The average is calculated over the last 40 ns of each of the four 120-ns simulations.

Figure 10.

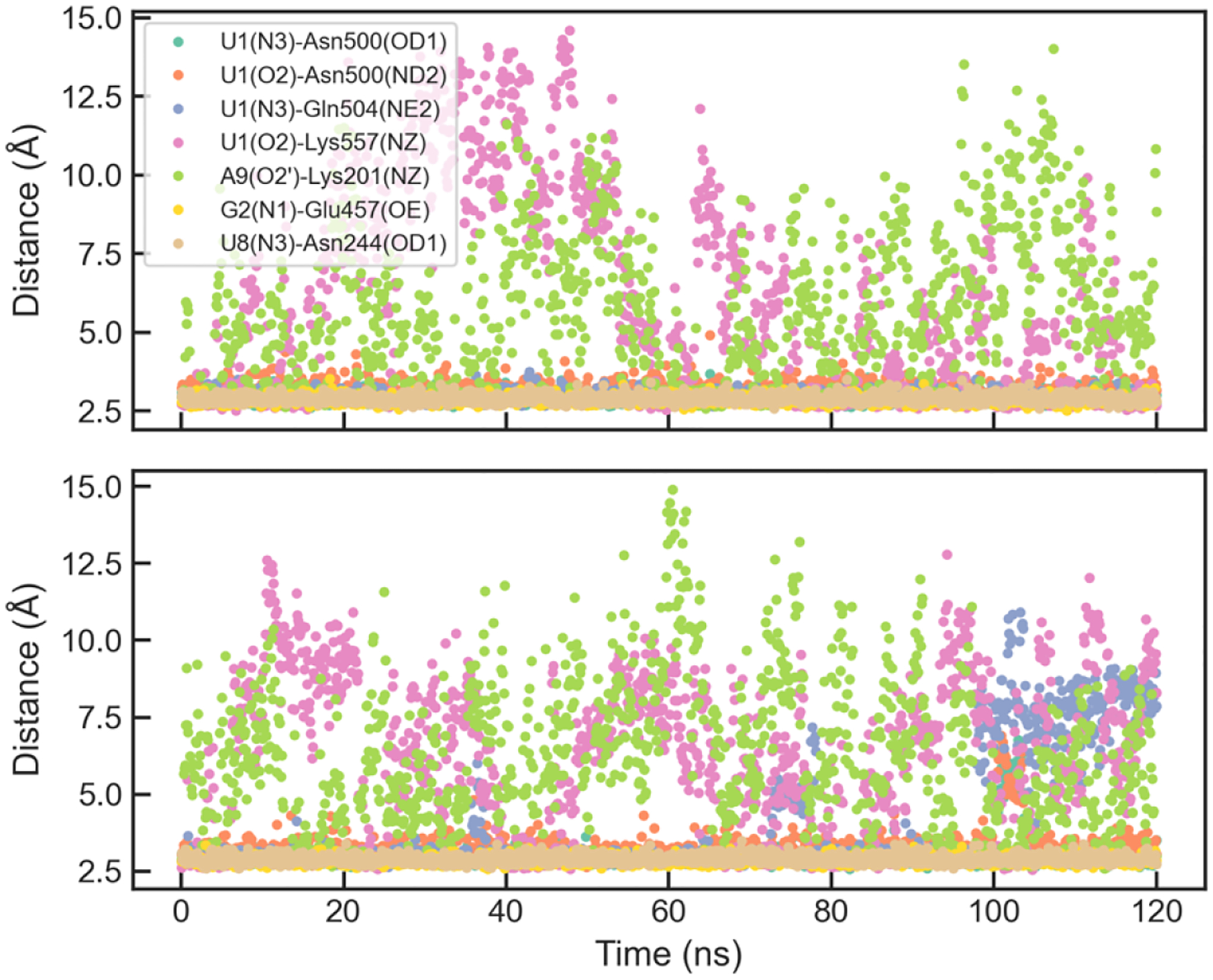
Evolution of selected hydrogen-bond distances in two representative simulations of FBF with the optimized parameters.

Previous simulations with AMBER ff99bsc0χOL3 for RNA and ff99SB or ff12SB for protein could not stabilize the interface.⁵ The terminal hydrogen bonds with U1 and A9 were lost within 50 ns, followed by the loss of hydrogen bonds with G2 and U8 after 300 ns. The interruption of the interface was mainly caused by the conformational changes of the RNA.⁵ Furthermore, the interface could not be stabilized by simulations with distance restraints on hydrogen bonds with U1 and U8. Based on these results, Krepl et al.⁵ concluded that crystal packing might play a role in the stabilization of the structure. In the simulations with DES-Amber and DES-Amber 3.20 force fields, the FBF complex was stable throughout 50-microsecond simulations. The backbone RMSDs were between 2–3 Å and there was no sign of dissociation. Since the optimized AMOEBA parameters and DES-Amber 3.20 achieved higher stability of the protein-RNA interface compared to previous versions of force fields, the crystal structure of the FBF complex could be either stable or metastable in solution.

4. Conclusions

The AMOEBA RNA force field was refined to improve the accuracy for modeling protein-RNA interfaces. Accurate DFT methods were chosen as a reference for the intermolecular interactions between nucleobases, water and small organic molecules. The nucleobase parameters were optimized by fitting to a large QM dataset including both optimized and non-ideal geometries and validated by cross-validation and separate test sets. Special vdW pair parameters were included to better represent hydrogen-bond interactions between nucleobases and carboxylate groups. The Asn torsion parameters were optimized based on conformations from torsional scan and rotamer library. The optimized AMOEBA parameters achieved better accuracy for the problematic protein-RNA interfaces identified in previous work. Since the reparameterization was based on a large QM dataset, the optimized parameters should represent a general improvement in describing protein-RNA interactions. Nevertheless, further tests on more systems are needed. Adjustment in torsion parameters might also be necessary to be compatible with the new vdW parameters.

Simulations with the optimized parameters correctly reproduced the important hydrogen bonds in the U1A protein-RNA interface, which was recently achieved by using AMBER force field with a structure-specific force field term. The AMOEBA simulations are also more realistic for the interactions between Lys side-chains and backbone phosphate groups. For the FBF protein-RNA complex, the AMOEBA simulations produced a stable binding interface except for reversible disruptions of some solvent-exposed hydrogen bonds between terminal nucleotides and Lys side-chains. Overall, the AMOEBA force field is promising for modeling the complex hydrogen-bond network and electrostatic interactions in protein-RNA interfaces.