Abstract
Distributing scarce resources such as COVID‐19 vaccines is often a highly time‐sensitive and mission‐critical operation. Our research was prompted by a significant obstacle that the United States and other nations encountered during the early months of the COVID‐19 vaccination campaign: Most COVID‐19 vaccines require two doses given 3 or 4 weeks apart. Given the severely limited supply and mounting pressure on many countries to reduce hospitalizations and mortality, how to effectively roll out two‐dose vaccines was a critical policy decision. In this paper, we first model and analyze inventory dynamics of the rollout process under three rollout strategies: (1) holding back second doses, (2) releasing second doses, and (3) stretching the lead time between doses. Then we develop an SEIR (susceptible, exposed, infectious, recovered) model that incorporates COVID‐19 asymptomatic and symptomatic infections to evaluate these strategies in terms of infections, hospitalizations, and mortality. Among our findings, we show releasing second doses reduces infections but creates uneven vaccination patterns. In addition, to ensure second doses are given on time without holding back inventory, strictly less than half of the supply can be allocated to first‐dose appointments. Stretching the between‐dose lead time flattens the infection curve and reduces both hospitalizations and mortality compared with the strategy of releasing second doses. We also consider an alternative single‐dose vaccine with lower efficacy and show that the vaccine can be more effective than its two‐dose counterparts in reducing infections and mortality. We conduct extensive sensitivity analyses related to age composition, risk‐based prioritization, supply disruptions, and disease transmissibility. Our paper provides important implications for policymakers to develop effective vaccine rollout strategies in developed and developing countries alike. More broadly, our paper sheds light on how to develop effective operations strategies for distributing time‐sensitive resources in times of crisis.
Keywords: COVID‐19 vaccine rollout, healthcare operations management, public health operations, SEIR model, vaccine inventory
1. INTRODUCTION
This research was motivated by a major challenge that COVID‐19 vaccination campaigns faced during the first half of 2021. One year after the onset of the COVID‐19 pandemic, global efforts aimed at ending the pandemic had evolved from developing vaccines at a record pace to rapidly putting doses into people's arms. Experts predicted that manufacturing or deployment delays will cause the benefit of vaccination to “decline substantially” (Paltiel et al. 2021, p. 42). Adding to the urgency of distributing vaccines, SARS‐CoV‐2, the virus underlying the disease, continued to rapidly spread and mutate. Racing against time, the mass vaccination effort was arguably “the biggest logistics challenge in history” (Arnold, 2020, p. 36), requiring vaccine manufacturers to produce billions of doses of newly developed vaccines in a matter of months.
Yet, expanding vaccine supply was challenging for two reasons. First, the vaccine production rate is limited by physical infrastructure, requisite raw materials (e.g., enzymes for converting DNA to mRNA for both the Pfizer and Moderna vaccines), 1 and packaging materials (e.g., glass vials and rubber stoppers). Second, the production yield can be uncertain. For example, uncertainty in AstraZeneca's vaccine production process, which requires the growth of cells inside bioreactors, caused major delays in its delivery to the E.U. in January 2021. In addition, developed countries have locked up much of the vaccine supply through 2023, leaving developing countries struggling with stringent supply constraints (Hopkins, 2021). Specifically, the vaccine shortage was particularly salient in Africa, which accounts for 18% of the world's population but has only received 2% of global COVID‐19 vaccine supply by June 2021 (Muhumuza & Mutsaka, 2021).
In addition to limited supply, the authorization of three major COVID‐19 vaccines (AstraZeneca, Moderna, and Pfizer) was for two‐dose regimens, creating unprecedented timing and inventory planning issues. For example, the Pfizer vaccine required two doses with a recommended 3‐week interval between them. 2 To ensure adherence to the two‐dose regimen, the United States initially (from December 2020) followed a “hold‐back policy” for each dose offered to a first‐time recipient; that is, one extra dose is held in reserve until the recipient returns for the second dose (Gottlieb, 2021).
The hold‐back policy ensures that two doses are reserved for each recipient. However, when facing severely limited vaccine supplies and rapidly rising COVID‐19 case counts, the hold‐back policy can cause a delay for other individuals to receive their first doses. To accelerate the vaccination process in order to reach herd immunity sooner, the United States and the United Kingdom had proposed unconventional solutions intended to address the logistical requirement of offering two doses of the COVID‐19 vaccine for each recipient.
In the United States, then‐President‐elect Joe Biden proposed on January 8, 2021, that he would order a switch from the hold‐back policy to a stock “release policy,” which means that (1) no vaccine inventory would be held for future vaccine recipients who return to receive their second doses and (2) all vaccine inventory is used as either first doses for new recipients or second doses for returning recipients (O'Donnell & Spalding, 2021). Unlike the hold‐back policy that can guarantee that the two‐dose regimen is administered according to the recommended time interval, the release policy can increase access of the first doses to more recipients. However, without dedicated inventory for the second doses, shortages may arise when vaccine supply remains limited.
Across the Atlantic, the U.K. government announced a related and somewhat controversial policy on December 30, 2020. Instead of administering two vaccine doses 3 weeks apart as recommended (in the case of the Pfizer vaccine), the lead time would be stretched to 12 weeks. Logistically, this “stretching policy” defers the required demand from second‐dose recipients and frees up more stock to cover first‐dose recipients. Hence, the stretching policy generates an effect similar to that of the release policy: It can expand the access to the first dose for more recipients, but it will delay the administration of the second dose, especially when the vaccine supply is limited. Delaying the time for recipients to receive their required second doses can increase the chance of infection for these recipients during the delay.
Both the U.S. and U.K. policies aimed to maximize the number of people developing at least partial immunity. As The Guardian reported, prioritizing the first dose “would mean each vulnerable person who has received the vaccine would be afforded less protection, [while] the number of people given at least some protection would double” (Rawlinson, 2020). Because clinical data suggest the marginal gain in protection of the first dose is significantly larger than that of the second dose, the U.K.'s approach appeared to increase overall protection to the population.
On the other hand, both policies were controversial for myriad reasons (Mancini & Gross, 2021). In particular, the issue of whether to hold back second doses garnered significant public attention in the United States: Some experts are in favor of holding back second doses, citing the risk of insufficient protection of single‐dose inoculations in times of potential disruptions (Mak & Tang, 2021); others believe the supply rate of COVID‐19 vaccines is expected to grow over time, at least in the United States, so holding back second doses is unnecessary (Dai & Yadav, 2021). These diverging views motivated us to model and compare the release and stretching policies against the benchmark hold‐back policy. Essentially, both the release and stretching policies were intended to address the challenge of limited vaccine supply through an operational approach: Both policies call for shifts in inventory‐control policies for vaccine stocks. Therefore, debates over these policies must involve the operations management perspective, which has been largely absent in the public discourse, in addition to the clinical, public health, and political perspectives. To facilitate such discussions, we developed a modeling framework to examine and compare these policies.
Due to limited vaccine supply (especially in many developing countries), allocating vaccines has become a time‐sensitive and mission‐critical issue. In our context, these rollout policies of a vaccine with a two‐dose requirement involve the following trade‐offs: (i) The hold‐back policy can secure two doses for fewer recipients with high efficacy, yet it delays other recipients' access to the first doses (which can give them some immunity); (ii) the release policy can increase access to the first doses, but it may cause shortages or delays for administering the required second doses for returning recipients; and (iii) the stretching policy can also vaccinate more recipients, but it can cause even longer delays for the recipients receiving their required second doses.
Critically, through modeling the rollout process under the alternative policies, we point out that the popular belief that “the number of people vaccinated would double” (Rawlinson, 2020) is incorrect. In particular, the clinical requirement to administer the second dose imposes an intertemporal constraint on the rollout problem: As more first doses are given early on, supplies in later periods become more tightly constrained.
In light of these trade‐offs, the limited supply of vaccines, and how the required second dose can boost immunity against COVID‐19, the implications of these policies are not immediately clear, especially when the timing for individuals to receive the first and second doses would vary for each policy. These observations motivated us to develop a dynamic model to examine the following questions arising from the rollout process of a COVID‐19 vaccine with a two‐dose requirement:
-
(i)
Given the production rate of vaccines (constant or linearly increasing), what are the cumulative inoculation rates for the first and second doses under the hold‐back policy, the release policy, and the stretching policy?
-
(ii)
Relative to the hold‐back policy, will the release and stretching policies generate higher cumulative inoculation rates?
-
(iii)
In light of an age‐stratified SEIR (susceptible, exposed, infectious, recovered) model that predicts the infection process under different vaccination policies, which policy is the most effective in reducing infections, hospitalizations, and mortality?
-
(iv)
How would a single‐dose vaccine with a lower efficacy (e.g., the Johnson & Johnson COVID‐19 vaccine) perform relative to its two‐dose counterparts?
As an initial attempt to examine the above questions arising from the two‐dose regimen of all approved vaccines and the limited supply of vaccines, we developed a dynamic model by examining the first‐ and second‐dose inoculation rates of a single vaccine under all three policies (hold‐back, release, and stretching). We also extend our model to capture the case of rolling out a new single‐dose vaccine with a lower efficacy.
Through analytical comparisons, we find that under a constant or linearly increasing vaccine production rate, both release and stretching policies generate a higher cumulative vaccination population than the hold‐back policy. Somewhat counterintuitively, we show that even if one intends to release all second doses, no more than half of the available doses can be allocated to first‐dose appointments, in order to avoid any delays in administering those required second doses for returning recipients, no matter how quickly supply grows over time.
One can view the single‐dose regimen as an extreme case of a stretching policy in which the timing of the required second dose is extended to the infinite future. Using this logic, we show that the single‐dose regimen can generate a higher cumulative vaccinated population than the hold‐back policy and the release policy.
We also developed a compartmental SEIR model that incorporates COVID‐19 asymptomatic and symptomatic infections in a population that consists of high‐ and low‐risk groups. Our SIER model captures the evolution of the COVID‐19 pandemic among these two groups who receive zero, one, or two doses of vaccine under different rollout strategies over time. We also calibrate our parameter values using the latest vaccine effectiveness studies (e.g., Haas et al., 2021). Our simulation study of our SEIR model reveals that both release and stretching policies can generate lower disease transmissions than the hold‐back policy; however, these two policies create uneven vaccination patterns. Stretching the between‐dose lead time flattens the infection curve, and reduces hospitalization and mortality (more than under the strategy of releasing second doses). We also consider an alternative single‐dose vaccine (e.g., J&J vaccine) with a lower overall efficacy and show that it can be more effective than its two‐dose counterparts in reducing infections, hospitalizations, and deaths. We conduct extensive sensitivity analyses related to age composition, risk‐based prioritization, supply disruptions, and the basic reproduction number R 0.
Although our work was motivated by the initial months of COVID‐19 vaccination efforts in the E.U., United Kingdom, and United States, it has broader policy implications. Developing countries are set to face limited vaccine supply as developed countries have locked up most of the vaccine supply up to 2023 (Hopkins, 2021). This is the latest episode of the longstanding ineffectiveness of global health supply chains that calls for better operations management practices (Gallien et al., 2017; Kraiselburd & Yadav, 2013). Our results can help policymakers in various developing countries understand the pros and cons of different rollout policies. Furthermore, our modeling framework and our SEIR model can be applied to a variety of vaccination environments (when relevant data become available), including different variants and different vaccines with varying administration regimens and levels of efficacy.
The remainder of the paper is organized as follows. We review the relevant literature in Section 2. Section 3 describes our model and the three rollout policies. Using the hold‐back policy as a benchmark, we examine the implications of the release policy in Section 4 and the stretching policy in Section 5. In Section 6, we examine an alternative single‐dose vaccine. In Section 7, we develop an SEIR model to evaluate the three policies and the single‐dose regimen. We conclude our paper in Section 8. All proofs are provided in Section OA1 of the Supporting Information.
2. LITERATURE REVIEW
Vaccine distribution is a vibrant line of research that has attracted substantial interest from the healthcare operations management community. Most of this stream of literature focuses on the influenza vaccine (for exceptions, see, e.g., Cummings et al., 2021; Hall et al., 2008). Whereas several papers in this literature (e.g., Arifoğlu et al., 2012; Arifoğlu & Tang, 2022; Chick et al., 2008, 2017; Yamin & Gavious, 2013) study governments' vaccine contracting, procurement, and subsidies decisions, others (e.g., Cho & Tang, 2013; Dai et al., 2016) examine optimal contract design between vaccine manufacturers and healthcare providers who administer vaccines. Duijzer et al. (2018) use a susceptible–infectious–recovered (SIR) model to study the critical vaccine coverage leading to herd effect for a pandemic and consider the optimal allocation of vaccine doses across different populations. Unlike this literature, which focuses primarily on distributing single‐dose vaccines, we study a unique problem of distributing a two‐dose vaccine during a pandemic in which whether to hold back second doses becomes a consequential national policy. In doing so, our paper speaks to a number of related public health papers on various rollout strategies, including, for example, Paltiel et al. (2021a), Paltiel et al. (2021b), Tuite et al. (2021), and Voysey et al. (2021).
Another related stream of literature studies inventory management—a classical theme of the operations research and management science community. This literature emerges from the seminal work by Arrow et al. (1951), Dvoretzky et al. (1953), and Scarf (1960), and has become the foundation of much of today's work in manufacturing and supply chain operations (Porteus, 1990; Song et al., 2020). Despite the immense breadth and depth of the extant inventory literature, our paper represents a first attempt to address a novel time‐sensitive resource allocation problem in which each customer requires exactly two units of the product at a specified timing. In addition, unlike the literature that focuses on a single organization's decision, we examine a national policy with public health implications. The only other work in the inventory literature that shares similar characteristics, to the best of our knowledge, is the paper by Natarajan and Swaminathan (2017), which considers the dynamic allocation of inventory of treatment drugs among patients with different (and evolving) health states. Compared with this work, which considers patients' health conditions in each state to evolve exogenously over time, our vaccine rollout problem involves the evolution of a pandemic that is governed by an epidemiology model.
Our paper also contributes to the rapidly growing operations management literature that addresses the COVID‐19 pandemic. For example, Kaplan (2020) documents a number of basic mathematical models to support local‐level COVID‐19 decisions ranging from event crowd control to hospital capacity planning. As another example, Chen et al. (2020) use mobility data around nursing homes to establish the relationship between cross‐facility staff movement and COVID‐19 infections. Shumsky et al. (2021) study a healthcare provider's COVID‐19 vaccine inventory management problem. We enrich this literature by studying a novel problem relevant to how health policymakers roll out COVID‐19 vaccines—the endgame of the COVID‐19 pandemic—and our findings have important implications for vaccination policies in future pandemics.
3. MODELING A TWO‐DOSE VACCINE ROLLOUT PROCESS
In this section, we present a parsimonious model of the vaccine rollout process in the spirit of scratch models as articulated by Kaplan (2020). To examine the implications of the three aforementioned policies—including (1) holding back second doses, (2) releasing second doses, and (3) stretching the between‐dose lead time—our model focuses on the dynamic first‐ and second‐dose inoculation rates over time by taking into consideration the limited availability of vaccine supply. Specifically, our model involves the following elements.
Vaccine supply rate
Consider a time horizon with a length of T (e.g., a year) during which the vaccine is rolled out. For any , let be the deterministic supply rate of vaccine doses available at t 3 ; is exogenously determined by the rate of manufacturing, quality and safety checks, and transportation. We assume is (weakly) increasing in t; that is, the supply ramps up over time. Let be the cumulative supply up to time t, where .
Vaccination rate and cumulative vaccination
We denote by and the instantaneous rates of the first‐ and second‐dose inoculations at time t, respectively. Thus, the cumulative vaccinations completed by time t, denoted by , satisfies
| (1) |
The cumulative vaccinations (and ) can be interpreted as the partially (and fully) protected populations who have received the first dose (and the second dose) by time .
Lead time L
A parameter of key concern is the lead time L; that is, the recommended time interval between the two doses of the same vaccine. The lead time L depends on the specific vaccine and the vaccination policy. In the United States, Pfizer recommends weeks and Moderna recommends . For simplicity of our analysis, we assume the second dose must be received exactly L periods after the first dose. 4 However, in the United Kingdom, weeks for the AstraZeneca, Moderna, and Pfizer vaccines under the dose‐stretching policy.
Vaccination rollout policy
As we will explain later, the hold‐back, release, and stretching policies correspond to a particular choice of functions , , and the lead time L. In general, a feasible policy must satisfy the following constraints at any time t 5 :
| (2) |
| (3) |
| (4) |
Due to limited vaccine supply, constraint (2) suggests cumulative first‐ and second‐dose vaccinations offered are bounded by the cumulative supply at every instant t. In addition, to comply with the two‐dose regimen requirement, constraints (3) and (4) indicate second doses cannot be offered until L time units have elapsed after first‐dose inoculations. (If there is sufficient supply of vaccine at all times, then (4) will hold as equality; i.e., .)
Cumulative protection
Building on the (partially and fully) protected population sizes ( and ), we now define the cumulative partial protection rate (due to the first dose) and full protection rate (due to both doses) up to time t (in person‐weeks):
| (5) |
The cumulative protection levels keep track of the number of people protected by vaccination and the duration over which protection has been developed. Hence, this measure reflects the amount of protection offered to the population as a whole. To elaborate, consider the following example.
Example 1
Consider two hypothetical scenarios: (i) One million people are given the first dose instantaneously at time and none thereafter; and (ii) 50,000 people are given the first dose per day at a continuous rate over 20 days and none thereafter. In both cases, the cumulative first‐dose vaccinated population sizes by Day 20 are the same at million when . However, the cumulative protection levels are different: is equal to 20 million person‐days in scenario (i), and is equal to 10 million person‐days in scenario (ii). Thus, the amount of protection in scenario (i) is double that under scenario (ii).
The functions , and are meaningfully defined only for ; for notational brevity, we adopt the convention that their values equal zero when . In addition to these measures, we further consider a broader class of performance metrics, including symptomatic infections, hospitalizations, and mortality, based on an SEIR model in Section 7 and Section OA2 of the Supporting Information. This involves a system of differential equations that utilizes and for .
3.1. Stock hold‐back policy
As explained in Section 1, the U.S. government followed the manufacturer's recommended lead time of L weeks by adopting the hold‐back policy as follows. Specifically, each facility only administers half of the vaccine stock received for first doses, and holds back the other half for L weeks to ensure recipients will have guaranteed stock when they return for the second dose. By considering the supply rate , the hold‐back policy stipulates the following 6 :
| (6) |
This policy ensures constraints (2)–(4) are satisfied at all time.
We now represent the cumulative protection functions using the external supply function . First, by the definition of , we have
| (7) |
Then, the amount of protection by time t can be given by
| (8) |
3.2. Stock‐release policy
Under the stock‐release policy, vaccine stock is no longer put on reserve for second doses. 7 The intention of the release policy is to maximize the rate of first‐dose inoculations to accelerate the build‐up of partial protection. Using our notation, the release policy stipulates that , such that all available stock is offered (as first or second doses) without delay. However, if the supply rate does not increase fast enough over time, then increasing the number of first‐dose recipients earlier would constrain the number of first‐dose recipients later.
To illustrate different rollout dynamics under the hold‐back and the release policies with limited vaccine supply, let us consider a simple example.
Example 2
Consider a constant supply rate of 100 doses per day (i.e., ) and a lead time of 21 days (i.e., 3 weeks between dose time interval for the Pfizer vaccine).
- (i)
Hold‐back policy. Under the hold‐back policy, 50 first doses will be offered per day, whereas the remaining 50 doses of supply will be reserved for the same 50 recipients who return 21 days later for their second doses. This pattern repeats every day.
- (ii)
Release policy. Under the release policy, from Day 1 to Day 21, 100 doses per day (i.e., the entire supply for each day) are administered to 100 people as their first doses. However, on Day 22, those 100 recipients who received the first doses on Day 1 are now due for their second doses. To adhere to the required dosage schedule, it is necessary to allocate all 100 doses (i.e., the entire supply) on Day 22 for those 100 returning second‐dose recipients. In doing so, the provider has no vaccine to offer to any first‐dose recipient on Day 22. This situation will continue until Day 43, when there are no more recipients who are due for the second dose (because no first‐dose recipient received a first dose from Day 22 to Day 42). Therefore, on Day 43, all 100 doses will be released to 100 first‐dose recipients, and the pattern repeats as on Day 1. Overall, this “alternating pattern” repeats in 42‐day (i.e., twice of the lead time 21 days) intervals. 8
We now define the stock‐release policy more formally. Initially, all available supply is released as first‐dose vaccination over so that satisfy
| (9) |
When , the available supply will be split between first‐ and second‐dose appointments. Let denote the amount of backlog by time t; that is, the difference between the number of people who have received their first doses L weeks ago and the number of people who have received their second doses. For clinical reasons, the backlog should be minimized. Therefore, the rate of second doses offered should match as closely as possible the rate of first doses completed L periods ago. To capture this preference, the release policy for must satisfy:
| (10) |
That is, when the backlog of second‐dose appointments exists (i.e., , or, equivalently, ), the entire supply will be allocated for the second dose. In the absence of a backlog, the second‐dose inoculation rate follows the first‐dose rate lagged by lead time L, up to the available capacity.
The backlog of second‐dose appointments will build up if the rate of recipients due for second doses, , exceeds the available supply, . When the supply rate ramps up slowly, most (or all) of the available supply might be allocated for second doses in order to avoid backlog. This scenario is not desirable for the purpose of steadily increasing the protected population.
The next result evaluates the fraction of supply that can be allocated for first‐dose appointments. In preparation, let us define β as the minimum fraction of available supply that is allocated for first‐dose appointments at all times, that is, .
Lemma 1
No backlogs exist if and only if β satisfies
(11)
Lemma 1 suggests that, to ensure a minimum fraction (β) of supply to be allocated for first doses (in order to continuously build up the protected population) at all times, the supply rate must grow sufficiently quickly. The first two conditions of Lemma 1 hold when , the proportion of supplies made available for second doses, is high and/or supply accelerates quickly in the initial weeks (especially during the first L periods). To illustrate the third condition, consider the case in which ; that is, when at least half of the available supply is to be used on first doses. In that case, the third condition holds if is convex.
If vaccine supply does not accelerate sufficiently quickly, the rate of first‐dose inoculations cannot be sustained. To avoid backlogs for second‐dose inoculations, first‐dose offerings must be temporarily reduced. As we show in the next section, this reduction gives rise to an alternating pattern between offering first and second doses (see Example 2).
3.3. Dose‐stretching policy
The dose‐stretching policy is intended to optimize the use of vaccine supply and maximize first‐dose inoculations. We define the dose‐stretching policy by focusing on the effect of stretching the lead time from the recommended L to , where is an integer. 9 Using this definition, we may view the stretching policy as a generalization of the stock‐release policy with a longer lead time , where . Thus, we omit the analysis of the policy for brevity.
4. IS RELEASING SECOND DOSES THE RIGHT MOVE?
We now compare the performance between the hold‐back policy and release policy . To do so, we first derive the cumulative vaccinated population and the cumulative protection associated with these policies, by considering the case in which the supply rate grows linearly over time. 10 In particular, we assume, without loss of generality, that , where and the initial supply rate is normalized to one (i.e., ).
4.1. Benchmark: Hold‐back policy
By using the supply rate and the hold‐back policy as defined in Section 3.1, we derive the corresponding performance measures and for below.
Lemma 2
Under the hold‐back policy and a linear supply growth, the cumulative vaccinations and protection evolve over time as follows:
(12)
The measures characterized in Lemma 2 later serve as the benchmark for ensuing comparisons.
4.2. Implications of the release policy
Using the same approach as in Lemma 2, we can derive the expressions of the performance measures and associated with the stock‐release policy as defined in Section 3.2. We omit the details for conciseness.
By considering the cumulative vaccinated population associated with the release policy, we can determine the backlog as defined in Section 3.2, where . The next result follows from Lemma 1 and highlights the conditions under which the backlog so that a smooth rollout of first‐dose appointments (without causing delays in administering the second dose) can be guaranteed under the linear‐supply‐growth scenario .
Proposition 1
Under a linearly growing supply, the stock‐release policy can allocate β fraction of supply to first‐dose appointments without incurring backlogs for second‐dose appointments if and only if .
To avoid backlogs at any time t (i.e., for any t) so that enough second doses are available in stock for those who have received the first dose L weeks ago, Proposition 1 suggests the stock‐release policy can never guarantee half of available supplies are allocated to first‐dose appointments (i.e., ), no matter how quickly the supply rate grows (i.e., for any value of α). The minimum guaranteed fraction available for first‐dose appointments is, intuitively, increasing in α. (Furthermore, as part of the proof of Proposition 1 in the Supporting Information, (OA2)‐(OA3) suggest that when α approaches zero, that is, when supply grows slowly, first‐ and second‐dose appointments will have to be almost shut down in alternating periods of lead time (L), in order to avoid backlogs.)
Next, through direct comparison between the performance measure associated with the hold‐back (i.e., and as stated in Lemma 2) and the release policies, we have the following proposition.
Proposition 2
Under linear supply growth, the stock‐release policy can generate higher cumulative vaccinated populations than the stock hold‐back policy by:
(13) Furthermore, over a full cycle , where , the stock‐release policy achieves better cumulative protection than the stock hold‐back policy by
(14)
From Proposition 2, we can verify that and for . Hence, the net changes in cumulative inoculations as well as cumulative protection due to switching from the stock hold‐back policy to the stock‐release policy are all strictly positive. Therefore, releasing second doses accelerates the buildup of protection, as long as the supply rate is (weakly) growing.
This improvement from releasing second doses, however, comes at the expense of potentially uneven offering patterns that alternate between first and second doses (Proposition 1) and the associated scheduling complexity, especially when the supply rate grows sluggishly. In practice, without assurance that second doses are reserved, many healthcare providers struggle with the uncertainty of scheduling second‐dose appointments. In the state of Maryland, as recently as in February 2021, despite the Biden administration's decision not to hold back second doses at the federal level, Dennis Schrader, Acting Maryland Health Secretary, urged healthcare providers to hold back second doses (Miller & Cohn, 2021). In other words, the impact of the stock‐release policy on infection control is dampened by its complexity in implementation.
Proposition 2 reveals that the release policy dominates the hold‐back policy. Will the stretching policy create additional value over the release policy by extending the lead time? We analytically examine this issue in the section that follows.
5. WILL STRETCHING THE DOSE TIME INTERVAL HELP?
We now examine the implication of the dose‐stretching policy . Recall from Section 3.3 that the stretching policy is essentially a stock‐release policy with a longer lead time that has , where . Hence, we can extend our analysis presented in Section 4.2 to determine the corresponding performance measures and when with . We omit the details to avoid repetition. In addition, through direct comparison between the performance measure associated with the release (i.e., and as examined in Section 4.2) and the stretching policies, we obtain the following result:
Proposition 3
Over a cycle , the dose‐stretching policy with can increase the cumulative first‐dose inoculations and reduce the second‐dose inoculations over the stock‐release policy by
(15) In addition, the dose‐stretching policy offers higher cumulative partial and lower full protection than the stock‐release policy by
(16)
Proposition 3 highlights the trade‐off between prioritizing the first and second doses. Through stretching the lead time (i.e., by increasing m), more supplies are made available for the first dose; thus, the cumulative population having completed the first dose and the cumulative partial protection both increase. However, deferring the second dose leads to lower levels of cumulative second‐dose completions and the level of full protection.
To better explore the trade‐off between first and second doses, let us consider the case when the first and second doses lead to efficacy levels of and , respectively, that is, the rate that an otherwise unimmunized person being infected by COVID‐19 drops from λ without vaccination to after the first dose, and after the second. 11 For notational brevity, let . If the first dose provides most of the protection, we have (e.g., for the case of Pfizer, where the efficacy rates are and after the first and second doses, we have ). Then, the efficacy‐weighted protection level measures the amount of protection provided by the vaccination program weighted by the strength of protection:
| (17) |
Proposition 4
Switching from the stock‐release policy to the dose‐stretching policy () can increase the efficacy‐weighted protection over the cycle if .
Proposition 4 suggests dose stretching (i.e., by increasing m) increases efficacy‐weighted protection as long as ζ is below the threshold value . The threshold value drops as m increases, indicating dose stretching becomes less favorable as m increases. Recall from Section 3.3 that under the stretching policy for the Pfizer vaccine when the U.K. government stretched the lead time from 3 weeks to 12. The threshold value in Proposition 4 is when . Combine this observation with the fact that for the Pfizer vaccine, the condition is satisfied so that the stretching policy adopted by the U.K. government can generate a higher efficacy‐weighted protection over the release policy.
6. IMPLICATIONS OF AN ALTERNATIVE SINGLE‐DOSE VACCINE
Thus far, our model and analysis have been motivated by three approved vaccines developed by Pfizer, Moderna, and AstraZeneca that require two doses. Another COVID‐19 vaccine, developed by Johnson & Johnson, was approved for emergency use on February 27, 2021. Unlike Pfizer, Moderna, and AstraZeneca, Johnson & Johnson ran its Phase III trials based on a single‐dose regimen, which achieved an efficacy rate of 66%. 12 Without the need to deal with the second‐dose timing issue, how would the single‐dose vaccine perform relative to those two‐dose vaccines? Clearly, if the single‐dose vaccine has a higher efficacy, it will dominate the two‐dose vaccine. However, the relative performance becomes unclear when the single‐dose vaccine (e.g., the Johnson & Johnson vaccine) has a lower efficacy than the two‐dose vaccine.
We now compare the rollout dynamics and of the single‐dose regimen against the hold‐back and stock‐release policies in this section. In preparation, observe that when offered as a single‐dose vaccine, all stock can be immediately released (because the second dose is no longer needed). Hence, this single‐dose regimen can be viewed as an extreme case of the stretching policy with lead time , where . Hence, we can apply the analysis of the stretching policy (see Section 5) to examine the performance of a single‐dose vaccine.
Under linear supply growth, the vaccination rate associated with a single‐dose regimen satisfies . Using the same approach as presented in Sections 4 and 5 to compare the vaccinated population and protection levels for the single‐dose regimen with the hold‐back and stock‐release policies under the two‐dose regimen, we obtain the following proposition.
Proposition 5
Compared with the stock hold‐back policy under a two‐dose regimen, the single‐dose regimen increases the cumulative first‐dose inoculations and cumulative first‐dose protection over a full cycle by:
(18) Compared with the stock‐release policy, the single‐dose regimen increases the cumulative first‐dose inoculations and cumulative first‐dose protection over a full cycle by:
(19)
From Proposition 5, we can see that the single‐dose regimen speeds up the buildup of protection. (Because only one dose is administered under the single‐dose regimen, our results focus only on pertinent measures and .)
However, as articulated above, when the single‐dose vaccine has a lower efficacy rate than its two‐dose counterparts, the performance of the single‐dose vaccine over the two‐dose vaccine is unclear. Specifically, even though the two‐dose regimen builds up protection more slowly, it can reach a higher level of protection due to its higher efficacy. To evaluate this trade‐off, we use the “efficacy‐weighted” protection level for the two‐dose vaccine as defined in (17) in Section 5 to define the corresponding for the single‐dose vaccine.
Recall from Section 5 that for the two‐dose regimen, one and two doses reduce the risk of infection by factors of and , respectively, and reflects the relative contribution of the first dose. Let be the efficacy rate of the single‐dose vaccine. To make a fair comparison with a two‐dose vaccine, we define . (For example, the Pfizer vaccine has and the Johnson & Johnson vaccine has so that .) In addition, by using the results presented in Proposition 5, we can define the corresponding for the single‐dose vaccine. The next proposition follows from direct comparisons.
Proposition 6
Switching from the two‐dose regimen under the stock‐release policy to the single‐dose regimen can increase the efficacy‐weighted protection over the cycle by
(20) A sufficient condition for this improvement to be nonnegative is that and .
Recall from above that for the two‐dose regimen of the Pfizer vaccine, we have , and for the single‐dose regimen of the Johnson & Johnson vaccine, . Even though these values do not satisfy the sufficient condition in Proposition 6, we can compute:
| (21) |
We can check that the first term is positive for all and that the second term is negative when and positive for . When , the overall expression is positive when . Because the supply rate is unlikely to grow more than 5.36 times over lead time L, we are more likely to observe that the Johnson & Johnson single‐dose regimen offers better cumulative efficacy‐weighted protection than the Pfizer vaccine under the stock‐release policy for any n. Overall, the above analysis suggests that the single‐dose regimen can underperform in the short run, but will eventually outperform the higher efficacy two‐dose regimen.
So far, we have obtained three key analytical results. First, we show that the release policy can improve the cumulative vaccination population and the cumulative protection in Proposition 2. Second, we prove that the stretching policy can generate a higher efficacy‐weighted protection than the release policy in Proposition 4 when . Third, we show that a single‐dose vaccine with a lower efficacy can outperform a two‐dose vaccine in terms of a higher efficacy‐weighted protection when and in Proposition 6. Besides the performance measures and , one should evaluate and compare the symptomatic infection rate, hospitalization rate, and the mortality rate of different groups of people across all policies over time. To do so, we present a variant of the SEIR epidemic model to examine these issues numerically in the next section.
7. EVALUATING ROLLOUT POLICIES VIA AN SEIR MODEL
In this section, we simulate the pandemic trajectories under the four rollout policies: (1) the stock hold‐back policy , (2) the stock‐release policy , (3) the dose‐stretch policy ( with ), and (4) the alternative single‐dose vaccine. We begin by presenting our SEIR epidemic model in Section 7.1. In Section 7.2, we simulate the rollout policies for the “baseline case” in which the parameter values are listed in Table OA1 of the Supporting Information. To analyze the robustness of our simulation results, we conduct sensitivity analyses with respect to age composition in Section 7.3, risk‐based vaccine prioritization in Section 7.4, vaccine supply disruption in Section 7.5, and the basic reproductive number (R 0) in Section 7.6. We caution that, as our simulation parameters are calibrated to data obtained on the original strain of the vaccines and the earlier (e.g., Alpha) variants, the results do not necessarily reflect the effects of future variants. Yet, the same methodology developed in our paper supports new analysis using actual or estimated parameters associated with future variants.
7.1. SEIR model
We present a compartmental SEIR epidemic model to capture the evolution of the COVID‐19 pandemic and the vaccine rollout dynamics. Using this SEIR model, we evaluate different rollout policies by comparing three performance metrics, including symptomatic infections, hospitalizations, and mortality. These metrics provide an epidemiological perspective and complement the operational perspective presented in Sections 4 to 6.
7.1.1. Risk groups and vaccination states
To capture various age‐dependent factors such as hospitalization rate, mortality rate due to COVID, and frequencies of social contact, we consider a population of size N (e.g., the U.S. adult population) that consists of a high‐risk group H (e.g., the population aged 65 and above) of size and a low‐risk group L (e.g., the population under the age of 65) of size ; this setting is consistent with the literature on modeling compartments with age groups (e.g., Longini et al., 1978). Based on the U.S. demographics, we normalize the adult population to 100 and set and to 13 and 87 (according to the profile of the adult population in the United States), respectively. To incorporate the vaccination status of the two‐dose regimen, we denote by each individual's type, where is the risk group and is the number of vaccine doses that the individual has received.
7.1.2. Compartments
In line with Keskinocak et al. (2020), an individual of type is in one of the following eight compartments at any time t: susceptible (), exposed (), infectious and presymptomatic (), infectious and asymptomatic (), infectious and symptomatic (), hospitalized (), recovered (), or deceased (). By considering this expanded set of states instead of the standard infectious and recovered compartments, our model captures key features of the COVID‐19 pandemic such as asymptomatic transmission and the demand on the healthcare system due to hospitalization. With two risk groups (i), three vaccination states (k), and eight compartments for each individual type , our SEIR model comprises a total of 48 compartments. Figure 1 illustrates our SEIR model for group . 13
FIGURE 1.
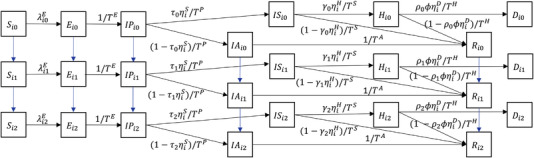
An expanded SEIR model for group . The downward arrows (in blue) indicate the change in vaccination status. if and otherwise.
7.1.3. Transition between compartments
For each individual of type , we explain in Section OA2 of the Supporting Information about how we determine the transition rate from one compartment to a different compartment as depicted in Figure 1. In particular, COVID transmissions depend on the numbers of infectious and susceptible individuals, their transmissibility and susceptibility (which depend on their vaccination status), and the frequencies of social contact between the two age groups as governed by a “contact matrix” (Bubar et al. 2021).
After contracting the virus, individuals will go through the exposed and presymptomatic stages, at the end of which they will either develop symptoms or remain asymptomatic, governed by the age‐ and vaccination‐dependent probabilities. Those who are symptomatically infected will be hospitalized (and if so, recover or die) according to the age‐ and vaccination‐dependent probabilities. We calibrate different age‐ and vaccination‐dependent parameter values using the CDC data and the recent literature and summarize the values in Table OA1 of the Supporting Information.
In addition to the transition rates among different compartments, our SEIR model depicted in Figure 1 captures the impact of the healthcare system utilization on mortality rate. Specifically, as more patients are hospitalized, critical facilities (e.g., intensive care units) become overloaded and mortality rates increase substantially (Wilde et al., 2021). Details of our mortality rate formulation are provided in Section OA2 of the Supporting Information.
7.1.4. The role of vaccination
To evaluate different vaccine rollout policies via the SEIR model for an individual type as depicted in Figure 1, we can use the vaccination rates () under each rollout policy presented in Section 4 to 6 as the key inputs for our SEIR model. In doing so, we can determine the corresponding transition rates between compartments associated with different vaccination status (e.g., from to after receiving the first vaccine dose). Based on the system dynamics captured by our SEIR model, we simulate the following three performance metrics for each risk group , under all four aforementioned rollout policies: (1) the number of active symptomatic infections: , (2) the number of active hospitalizations: , and (3) the cumulative number of deaths: . In the following subsections, we compare the simulated performance metrics , , and via our SEIR model across all four rollout policies.
We simulate our SEIR model over a 1‐year horizon. The parameter values and the settings of the simulation are summarized in S. Consistent with our theoretical analysis in the previous sections, we consider a supply function that is growing linearly unless otherwise specified.
7.2. Baseline case
We begin our numerical examples by simulating the performance of the rollout policies under the baseline case; all the parameter values are listed in Table OA1 of the Supporting Information.
Recall from Section 4 to 6 that and denote the rate of vaccine doses to be given as first and second doses at time t, under the hold‐back, release, stretch, or single‐dose policies. To determine who receives the vaccines, we consider a simple proportional allocation rule between the high‐ and low‐risk groups, for example, and of dose‐k supplies () are allocated to the high‐ and low‐risk groups at any time t, respectively. In the baseline case, we have (i.e., 100% of supply is given to eligible high‐risk individuals until they have all been vaccinated). This is consistent with the strict age‐based rollout practice in countries such as the United States and the United Kingdom. In Section 7.3, we shall consider an alternative case with a lower value of π for comparison.
Figure 2 shows the SEIR simulation results for the baseline case when we scale the population size . The panels plot the number of active symptomatic cases (left), hospitalizations (middle), and cumulative deaths (right), for the high‐risk group (top), low‐risk group (middle), and total population (bottom). Because the size of the population is normalized to 100, the vertical axes represent the percentage of the total population in each status of interest. In each panel, the four rollout policies are compared against the no‐vaccination benchmark (solid line in black).
FIGURE 2.
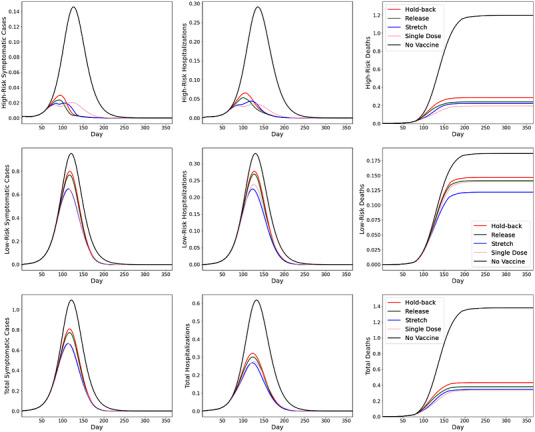
SEIR simulation results under baseline case
From the top panels of Figure 2, we find that vaccination is highly effective in reducing symptomatic cases, hospitalizations, and deaths for the high‐risk group. Under all four rollout policies, each of these key metrics are reduced by at least 75%, compared with the no‐vaccination benchmark. In comparison, the corresponding reductions are smaller for the low‐risk group, due to prioritizing the high‐risk group and the overall larger population of the low‐risk group (thus taking longer to get vaccinated). For the whole population, due to strict priority of vaccinating the high‐risk group (i.e., ), the reduction in deaths (i.e., 69%, 72%, 75%, and 76% for the hold‐back, release, stretch, and single‐dose policies, respectively) are more substantial than the reductions in hospitalizations (i.e., 48%, 51%, 57%, and 51%, respectively) and in symptomatic infections (i.e., 26%, 29%, 39%, and 39%, respectively).
Consistent with the implications from our analytical findings, Figure 2 shows that both the stretching policy and the single‐dose regimen are effective in accelerating vaccine impact and reducing symptomatic infections, hospitalizations, and mortality. The release policy also outperforms the hold‐back policy in all three metrics, although the difference is modest in the baseline case.
7.3. Age composition
We now evaluate how the demographic composition may influence the choice of rollout policies. Since hospitalization and mortality risks of COVID are highly dependent on age, the pandemic impact on relatively younger (e.g., in India and South Africa, with a median ages of about 28) and older (e.g., in the United States, with median age of about 38) populations can differ significantly. All else being the same, we now change to half as in the baseline case (so that 6.5% of the total population is above 65, compared with 93.5% below 65) so that the resulting population is younger. Figure 3 depicts our results.
FIGURE 3.
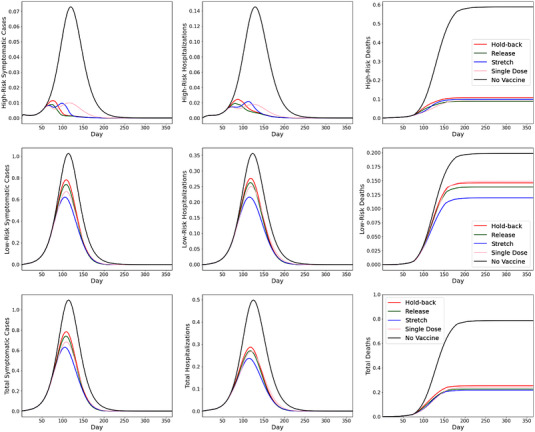
SEIR simulation results with younger population
Figure 3 resembles the baseline case as reported in Figure 2 in terms of, for example, the effectiveness of the stretching policy and the single‐dose regimen. Observe from Figure 3 that even in a younger population with a 6.5% high‐risk population, vaccination reduces mortality significantly—the four policies achieve a mortality reduction from 68% (hold‐back policy) to 72% (stretching policy). Despite similar percentage reductions in mortality compared to the baseline case (Figure 2), the absolute number of deaths is considerably lower because we consider a younger population. However, this is not the case for the other two key metrics, as the younger population records similar absolute levels of symptomatic cases and hospitalizations as the older population. This is due to the fact that most symptomatic cases and about half of hospitalizations are associated with the low‐risk group due to its higher transmission rate (albeit lower mortality rate).
Interestingly, Figure 3 shows that, relative to the stretching policy, the single‐dose regimen does not perform as well when the population is younger. Specifically, the single‐dose regimen reduces peak symptomatic cases, peak hospitalizations, and cumulative mortality by 38%, 46%, and 69%, respectively. However, it is outperformed by the stretching policy, which reduces the three key metrics by 43%, 52%, and 72%, respectively. In terms of preventing mortality, the single‐dose regimen performs worse than the release policy (71% reduction) and is similar to the hold‐back policy (68% reduction). The reason is that, when the high‐risk group is relatively small, the main advantage of the single‐dose regimen (i.e., rollout speed) becomes less appealing, whereas its weakness (i.e., lower efficacy, especially in preventing infections) becomes more pronounced.
This observation has important practical implications. Prior to the halt of the Johnson & Johnson vaccine in the United States due to blood clot concerns, its “one‐and‐done” logistical convenience was considered highly promising for younger age groups (Dai et al., 2021). Various countries have since refocused the rollout of Johnson & Johnson to older age groups on the basis of lower blood clot risks (Strauss, 2021). Our findings suggest that doing so is sensible logistically and epidemiologically as well, since the single‐dose regimen would perform better in an older population.
7.4. Risk‐based prioritization
In the baseline case (Figure 2), we have set (i.e., 100% of supply is given to eligible high‐risk individuals until they have all been vaccinated). In this subsection, we compare this with an alternative case that has (i.e., half of the supply is allocated to the high‐risk group of age above 65 and the remaining half is allocated to the low‐risk group of age below 65). Because the low‐risk group has higher frequencies of social contacts than the high‐risk group, the alternative case is intended to examine the impact of allocating some vaccine to the low‐risk group earlier as a mechanism to curb the infection rates.
Figure 4 plots the simulation results for the alternative case with priority for the high‐risk group. Despite a different vaccine priority rule, Figure 4 resembles Figure 2 in that the single‐dose regimen and stretch policies are the most effective in reducing symptomatic infections, hospitalizations, and mortality. In addition, we observe from Figure 4 that the effects of vaccination are abated for the high‐risk group and improved for the low‐risk group under 50% priority, compared with the baseline case (Figure 2), which strictly prioritizes the high‐risk group. Because most deaths arise from the high‐risk group, this leads to higher overall mortality (bottom‐right panel) under the release and hold‐back policies. On the other hand, because most symptomatic cases arise from the low‐risk group that has a larger population size and more social contacts, a less stringent risk‐group priority leads to fewer symptomatic cases, and a similar or lower number of hospitalizations.
FIGURE 4.
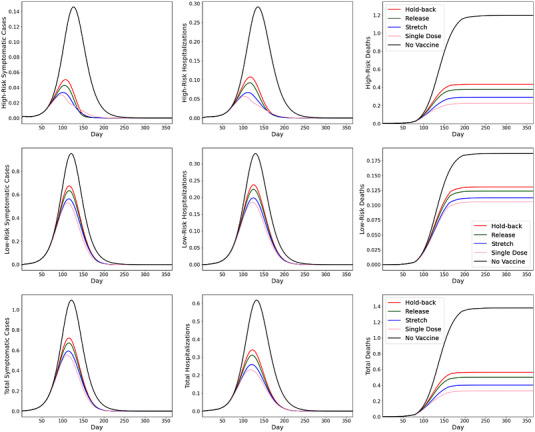
SEIR simulation results with
Our findings reflect an important trade‐off. Notwithstanding the importance of protecting the most vulnerable people by prioritizing the high‐risk group, a strict priority (e.g., the appointment system in the United Kingdom, where younger age groups cannot make bookings until the majority of older age groups receive their vaccines) can be inefficient in containing the spread of the pandemic due to the more frequent social contacts of younger age groups. This is because the vaccines (e.g., Pfizer and AstraZeneca) have significant effects on not only preventing infections, but also reducing infectiousness of those who get infected despite vaccinations, as found by Public Health England (Harris et al. 2021) in the U.K. rollout. Many countries and regions, including various states of the United States, also prioritize the vaccination of younger individuals in high‐contact essential professions, such as public transit drivers, delivery drivers, and postal service workers, together with the elderly; vaccinating them helps prevent secondary infections.
Furthermore, we notice that the differences (in all three key metrics) between the rollout policies become more pronounced under less stringent (50%) priority. In particular, the single‐dose regimen and the stretching policy, which are effective in accelerating vaccine coverage, become relatively more beneficial when supply is split between the risk groups. This is intuitive, because splitting supply leads to fewer doses available for the high‐risk group, which in turn heightens the importance of rollout efficiency. On the whole, we find that both the stretching policy and single‐dose regimen offer good trade‐offs under the 50% priority case: These policies lead to lower symptomatic cases (46% and 50% reduction from the no‐vaccination benchmark, respectively, compared with 39% and 39% under strict priority), and a similar number of hospitalizations (58% and 63% reduction from the no‐vaccination benchmark, respectively, compared with 57% and 55% under strict priority) through preventing transmissions, and record similar mortality figures (71% and 76% reduction from the no‐vaccination case, compared with 75% and 76% under strict priority) thanks to accelerated build‐up of protection for the high‐risk group.
7.5. Supply disruptions
So far, our analytical model and simulation analysis are based on the assumption that the supply process is smooth. However, the supply of the COVID‐19 vaccines is subject to disruptions to the production 14 or distribution process. 15 We conduct additional simulations to examine the performance of all four rollout policies in the presence of potential supply disruptions.
We simulate a scenario with production hiccups occurring at the initial stage of vaccine rollouts. In particular, the supply rate is assumed to be growing linearly, as explained earlier. However, the supply rate suffers from two disruptions occurring on Days 81–110 and Days 141–170, during which the supply rate is decreased to half of the initial rate. Figure 5 depicts our simulated results.
FIGURE 5.
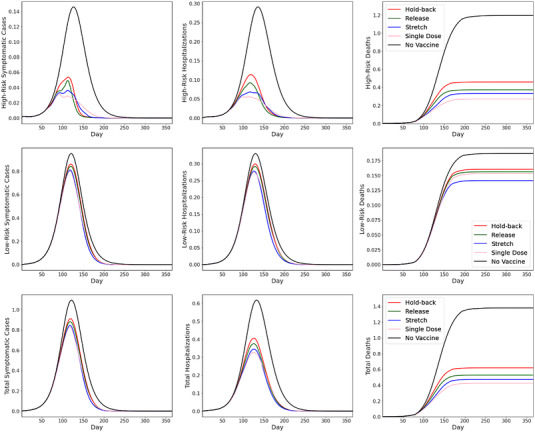
SEIR simulation results with supply disruptions
Figure 5 shows that under supply disruptions, the results obtained from the baseline case continue to hold: The single‐dose regimen and stretch policies are most effective. Because rollouts prioritize the high‐risk group, it is natural that the improvements for the low‐risk group are limited with lumpy supply. Overall, substantial reduction in mortality can still be achieved, especially under the stretching policy or the single‐dose regimen policy.
We also observe that the qualitative insights from the baseline case with smooth supply (Figure 2) remain intact; that is, the single‐dose regimen and stretch policies help prevent mortality better (by 47% and 44% compared with the no‐vaccination case) than do the release and hold‐back policies (39% and 34% reductions, respectively). These figures suggest that the performance gaps between the policies become more pronounced during supply disruptions, because making full use of the limited (and unreliable) supply to build up protection becomes more essential.
7.6. Basic reproduction number (R 0)
Finally, we evaluate the impact of the speed at which the pandemic propagates, as measured by the basic reproduction number R 0. In the COVID‐19 pandemic, the R 0 number could change due to the rise of more transmissible variants or the relaxation of social distancing measures. In Figure 6, we conduct our simulation based on the case when , which is higher than the baseline case that has (Figure 2).
FIGURE 6.
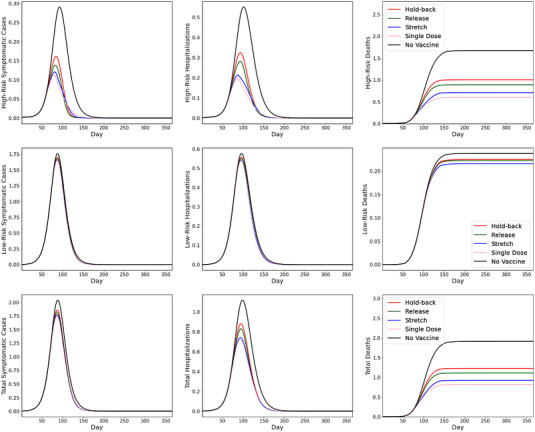
SEIR simulation results with
Figure 6 reveals that whereas all key metrics have worsened under faster transmissions, the results obtained from the baseline case continue to hold qualitatively. Figure 6 also offers insights similar to those from the case with supply disruptions (Figure 5). In particular, vaccine rollouts mostly improve the key metrics for the high‐risk group and show limited benefits for the low‐risk group. Overall, we observe significant improvements in mortality reduction—by 57%, 52%, 42%, and 36% under the single‐dose, stretch, release, and hold‐back policies, respectively. Comparing these figures with those in the baseline case (which range from 69% to 76% reduction across the policies), we observe that under a higher R 0, choosing the right rollout policy has a greater impact on reducing mortality.
The reason that the high R 0 and the supply disruption cases are qualitatively similar is that vaccination outcomes depend on the relative speeds of the pandemic and of vaccine rollout. When supply is lumpy or when R 0 is high, vaccination rollout lags behind the pandemic spread, and thus the rollout policies that accelerate protection (i.e., single‐dose and stretching policies) perform relatively better in preventing mortality of the high‐risk group and thus the total population.
8. CONCLUSIONS
Rolling out a two‐dose COVID‐19 vaccine such as that developed by Pfizer offers a rare and compelling research context for examining the impact of different inventory control policies (i.e., hold‐back, releasing, and stretching) on public health. We develop a modeling framework of a vaccine rollout process and complement it with an SEIR model to capture the disease transmission process. We compare—both analytically and numerically—various vaccine rollout policies, including (1) holding back all the second doses, (2) releasing all the doses, and (3) stretching the lead time between two doses. We also examine the rollout of a single‐dose vaccine with a lower efficacy level than its two‐dose counterparts.
Our key findings are threefold. First, one might expect releasing all the second doses would lead to an oversized effect in slowing down the pandemic. Our analytical results show that compared with the hold‐back policy, releasing doses does help slow down infections and end the pandemic sooner; we numerically show that such an impact can be modest. This result is in part due to the fact that releasing more first doses also necessitates more second doses in the future; we show that even if one intends to release all second doses, fewer than half of the available doses can be used for first‐dose appointments to avoid delays in administering the required second doses, regardless of how fast supply grows over time. Second, stretching the between‐dose lead time helps reduce mortality as well as infections and hospitalizations (more than under the strategy of releasing second doses). Third, a single‐dose vaccine, even with an overall efficacy significantly lower than its counterparts, can be more effective in infection control.
It should be acknowledged that the logistics parameters of vaccine regimens (i.e., one or two doses, recommended lead time) depend on the design of trials and the data presented for regulatory approval. For instance, the fact that Pfizer requires two doses but Johnson & Johnson requires only one is primarily due to how the respective trials were designed and thus how the specific regimens were approved, but is not necessarily reflective of the differences in the science of the vaccines. 16 In this sense, our results underline the importance of taking the operational aspect of the rollout process into consideration when designing clinical trials.
Our model has several limitations that can serve as subjects for future research. First, COVID‐19 vaccine rollouts inspire future research into a wide range of operational and logistics issues specific to vaccine administration, including cold chain management, inventory management, and manufacturing capacity planning (Dai & Song, 2021). One particularly interesting area of research entails incorporating and managing the uncertainty associated with the number of doses that can be extracted from each vial. Second, as Mak and Tang (2021) note, no‐shows for second‐dose appointments may worsen when the time interval between two doses is stretched from 3 weeks to 12 weeks for a variety of reasons, including, for example, the perception that the second dose provides limited incremental benefit due to the stretching. To incorporate potential no‐shows, one may extend our SEIR model by adding a new parameter capturing the reduction in the second‐dose vaccination rate. Third, we consider in this paper a time horizon long enough that the pandemic subsides. One related matter that we do not consider is the possibility of waning vaccine effects, which could affect infections beyond the time horizon. Lastly, several highly contagious new variants of SARS‐CoV‐2, the virus causing COVID‐19, have been found in various countries. Examining other rollout policies that can expedite herd immunity even more quickly to reduce the spread and mutation of the virus would be of interest.
Our modeling framework represents an initial attempt to examine different vaccine rollout policies under limited supply. In addition to helping inform vaccine rollout policymaking, our modeling framework can be applied to analyze similar issues facing local vaccination planners and health systems leadership in both the current and future epidemics. At the global level, our work draws from the experience of the E.U., the United Kingdom, and the United States. Yet, our results have important implications for vaccine planning in various countries, especially because developing countries are expected to face extremely limited vaccine supply up to 2023 (Hopkins, 2021). More broadly, our paper sheds light on how to develop effective operations strategies for distributing time‐sensitive resources in times of crisis.
Supporting information
Supporting Information.
ACKNOWLEDGMENTS
The authors are grateful to Stephen Chick, Eric Denardo, Edward Kaplan, Steven Lippman, Elisa Long, John Mamer, David Paltiel, Andrew Pollard, Prashant Yadav, seminar and session participants at INFORMS 2021 Annual Meeting, INSEAD, The 3rd Johns Hopkins Symposium on Healthcare Operations, McGill University, and Rutgers University for their helpful comments and suggestions.
Mak, H.‐Y. , Dai, T. , & Tang, C. S. (2022). Managing two‐dose COVID‐19 vaccine rollouts with limited supply: Operations strategies for distributing time‐sensitive resources. Production and Operations Management, 00, 1–19. 10.1111/poms.13862
Handling Editor: Kalyan Singhal
Accepted by Kalyan Singhal, after one revision.
ENDNOTES
Throughout the paper, for brevity, we refer to the Pfizer/BioNTech vaccine as the Pfizer vaccine. Similarly, we refer to the AstraZeneca/Oxford vaccine as the AstraZeneca vaccine.
The U.S. Food and Drug Administration (FDA) has only authorized the use of two specified doses of both Pfizer and Moderna vaccines at specified intervals—a 3‐week interval for the Pfizer vaccine and a 4‐week interval for the Moderna vaccine. See https://www.fda.gov/news‐events/press‐announcements/fda‐statement‐following‐authorized‐dosing‐schedules‐covid‐19‐vaccinesfor details.
Besides tractability, the deterministic production rate is a reasonable assumption for the following reason: The production process for the Pfizer and the Moderna vaccines is relatively stable, because the process involves converting DNA into mRNA rather than growing cells in a bioreactor (Boseley, 2021).
The recommended lead time days for the Pfizer vaccine, and CDC guidelines in 2021 allow for a grace period of 4 days earlier than the recommended date, see https://www.cdc.gov/vaccines/covid‐19/info‐by‐product/clinical‐considerations.htmlfor details. In February 2022, the CDC modified its recommended lead time to 8 weeks for 12‐ to 64‐year‐olds, particularly males aged 12 to 39 (https://khn.org/morning‐breakout/cdc‐advising‐some‐to‐wait‐8‐weeks‐between‐doses‐of‐mrna‐vaccines/). Despite these new guidelines, our modeling framework and approach are applicable to any lead time L and any number of doses.
To isolate the effect of different vaccine rollout policies, we do not model the issue of setting up a physical infrastructure (i.e., location and the size of vaccination sites) or mobilizing personnel (controlled by FEMA, state/county governments, or local healthcare providers) to administer vaccines. Instead, we abstract away those issues and assume all policies will be operated under the same environment.
We use the superscripts h, r, and s to denote the hold‐back, release, and stretching policies, respectively.
Though small amounts of smoothing stock will still be kept in reality, we ignore this fact in our model for simplicity.
This alternating pattern has been observed in various parts of the world. For example, in early February 2021, COVID‐19 vaccine sites in Los Angeles County postponed first‐dose appointments and only administered second doses to returning recipients; see http://cbsloc.al/3bo5uiSfor details.
In the case in which , the stretching policy reduces to the release policy. For practicality of implementation, we restrict m to being integer‐valued. For example, the U.K.'s dose‐stretching policy increases the lead time from weeks to weeks, that is, .
For tractability, we consider the linear case. However, one can use the same approach to examine the case of a nonlinear production rate numerically.
For example, the Pfizer vaccine offers 57.7% and 95.3% efficacy levels after the first and second doses; thus, and (Haas et al., 2021).
In late January 2021, Johnson & Johnson announced the Phase III trial results of its single‐dose COVID‐19 vaccine with a relatively lower efficacy (66% worldwide and 72% in the U.S. trial). However, this vaccine has major operational advantages. In particular, it has a less stringent temperature requirement than the Pfizer vaccine and only requires a single dose. Thus, it circumvents the trade‐off between offering first and second doses.
We assume the time horizon to be short enough so that individuals do not move from the low‐ to high‐risk group and vice versa (their underlying health status does not change). Therefore, the two groups interact only through sharing the same vaccine supply and hospitalization capacity.
For example, the AstraZeneca vaccine faces an uncertain yield due to uneven cell growth in bioreactors.
Disruption can occur due to weather conditions as experienced in the United States during the snow storm in February.
The authors acknowledge Andrew Pollard of the University of Oxford for this important insight.
REFERENCES
- Arifoğlu, K. , Deo, S. , & Iravani, S. (2012). Consumption externality and yield uncertainty in the influenza vaccine supply chain: Interventions in demand and supply sides. Management Science, 58(6), 1072–1091. [Google Scholar]
- Arifoğlu, K. , & Tang, C. S. (2022). A two‐sided incentive program for coordinating the influenza vaccine supply chain. Manufacturing & Service Operations Management, 24(1), 235–255. [Google Scholar]
- Arnold, C. (2020). The biggest logistics challenge in history. New Scientist, 248(3309), 36–40. [Google Scholar]
- Arrow, K. J. , Harris, T. , & Marschak, J. (1951). Optimal inventory policy. Econometrica, 19(3), 250–272. [Google Scholar]
- Boseley, S. (2021). Why has AstraZeneca reduced promised vaccine supply to EU and is UK affected? Guardian (Jan 26). http://bit.ly/azredeuuk
- Bubar, K. M. , Reinholt, K. , Kissler, S. M. , Lipsitch, M. , Cobey, S. , Grad, Y. H. , & Larremore, D. B. (2021). Model‐informed COVID‐19 vaccine prioritization strategies by age and serostatus. Science, 371(6532), 916–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, M. K. , Chevalier, J. A. , & Long, E. F. (2020). Nursing home staff networks and COVID‐19. Proceedings of the National Academy of Sciences, 118(1), e2015455118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chick, S. E. , Mamani, H. , & Simchi‐Levi, D. (2008). Supply chain coordination and influenza vaccination. Operational Research, 56(6), 1493–1506. [Google Scholar]
- Chick, S. E. , Hasija, S. , & Nasiry, J. (2017). Information elicitation and influenza vaccine production. Operational Research, 65(1), 75–96. [Google Scholar]
- Cho, S.‐H , & Tang, C. S. (2013). Advance selling in a supply chain under uncertain supply and demand. Manufacturing & Service Operations Management, 15(2), 305–319. [Google Scholar]
- Cummings, K. , Behzad, B. , & Martonosi, S. (2021). Centers for Disease Control and Prevention as a strategic agent in the pediatric vaccine market: An analytical approach. Manufacturing & Service Operations Management, 23(6), 1398–1412. [Google Scholar]
- Dai, T. , Cho, S.‐H , & Zhang, F. (2016). Contracting for on‐time delivery in the US influenza vaccine supply chain. Manufacturing & Service Operations Management, 18(3), 332–346. [Google Scholar]
- Dai, T. , Mak, H. Y. , & Tang, C. S. (2021). The great promise of a one‐dose vaccine. Barron's (February 26, 2021). http://bit.ly/barronsjnj
- Dai, T. , & Song, J. S. (2021). Transforming COVID‐19 vaccines into vaccination: Challenges and opportunities for management scientists. Health Care Management Science, 24(3), 455–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai, T. , & Yadav, P. (2021). Release second doses to speed vaccinations. USA Today (January 13) 7A.
- Duijzer, L. , van Jaarsveld, W. , Wallinga, J. , & Dekker, R. (2018). Dose‐optimal vaccine allocation over multiple populations. Production and Operations Management, 27(1), 143–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dvoretzky, A. , Kiefer, J. , & Wolfowitz, J. (1953). On the optimal character of the policy in inventory theory. Econometrica, 21(4), 586–596. [Google Scholar]
- Gallien, J. , Rashkova, I. , Atun, R. , & Yadav, P. (2017). National drug stockout risks and the global fund disbursement process for procurement. Production and Operations Management, 26(6), 997–1014. [Google Scholar]
- Gottlieb, S. (2021). Pharmacies can get shots in arms. Wall Street Journal (January 3). http://on.wsj.com/3aim4Be
- Hall, S. N. , Jacobson, S. H. , & Sewell, E. C. (2008). An analysis of pediatric vaccine formulary selection problems. Operational Research, 56(6), 1348–1365. [Google Scholar]
- Harris, R. J. , Hall, J. A. , Zaidi, A. , Andrews, N. J. , Dunbar, J. K. , & Dabrera, G. (2021). Effect of vaccination on household transmission of SARS‐CoV‐2 in England. New England Journal of Medicine, 385(8), 759–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas, E. J. , Angulo, F. J. , McLaughlin, J. M. , Anis, E. , Singer, S. R. , Khan, F. , Brooks, N. , Smaja, M. , Mircus, G. , Pan, K. , Southern, J. , Swerdlow, D. L. , Jodar, L. , Levy, Y. , & Alroy‐Preis, S. (2021). Impact and effectiveness of mRNA BNT162b2 vaccine against SARS‐CoV‐2 infections and COVID‐19 cases, hospitalisations, and deaths following a nationwide vaccination campaign in Israel: An observational study using national surveillance data. Lancet, 397(10287), 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopkins, J. S. (2021). Developed countries lock up Covid‐19 vaccines through 2023. Wall Street Journal (June 2). https://on.wsj.com/3pL3qbh
- Kaplan, E. H. (2020). OM Forum—COVID‐19 scratch models to support local decisions. Manufacturing & Service Operations Management, 22(4), 645–655. [Google Scholar]
- Keskinocak, P. , Oruc, B. E. , Baxter, A. , Asplund, J. , & Serban, N. (2020). The impact of social distancing on COVID19 spread: State of Georgia case study. PLoS One, 15(10), e0239798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraiselburd, S. , & Yadav, P. (2013). Supply chains and global health: An imperative for bringing operations management scholarship into action. Production and Operations Management, 22(2), 377–381. [Google Scholar]
- Longini, I. M. , Ackerman, E. , & Elveback, L. R. (1978). An optimization model for Influenza A epidemics. Mathematical Biosciences, 38(1–2), 141–157. [Google Scholar]
- Mak, H. Y. , & Tang, C. S. (2021). More vaccine supplies are being released. It's a gamble. Barron's (Jan 12, 2021). http://bit.ly/2ndvaxgamble
- Mancini, D. P. , & Gross, A. (2021). UK decision to space vaccination doses sparks fierce debate over risk. Financial Times (January 8). http://on.ft.com/3pgBRVr
- Miller, H. , & Cohn, M. (2021). Maryland facing shortage of second COVID vaccine doses, health secretary says. Baltimore Sun (February 1). http://bit.ly/md2dosehb
- Muhumuza, R. , & Mutsaka, F. (2021). In poorest countries, surges worsen shortages of vaccines. Associated Press (June 17). http://bit.ly/africavaxap
- Natarajan, K. V. , & Swaminathan, J. M. (2017). Multi‐treatment inventory allocation in humanitarian health settings under funding constraints. Production and Operations Management, 26(6), 1015–1034. [Google Scholar]
- O'Donnell, C. , & Spalding, R. (2021). U.S. releases millions of COVID‐19 doses, urges states to broaden vaccine access. Reuters News (Jan 12, 2021). http://reut.rs/3rBPJv1
- Paltiel, D. , Schwartz, J. , Zheng, A. , & Walensky, R. P. (2021a). Clinical outcomes of a COVID‐19 vaccine: Implementation over efficacy. Health Affairs, 40(1), 42–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paltiel, A. D. , Zheng, A. , & Schwartz, J. L. (2021b). Speed versus efficacy: Quantifying potential tradeoffs in COVID‐19 vaccine deployment. Annals of Internal Medicine, 174(4), 568–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porteus, E. L. (1990). Stochastic inventory theory. In Heyman D. P., & Sobel M. J. (Eds.), Handbooks in operations research and management science (pp. 605–652). Elsevier. [Google Scholar]
- Rawlinson, K. (2020). More data needed before giving just one vaccine dose, says Covid adviser. The Guardian . https://bit.ly/3aEz6tj
- Scarf, H. (1960). The optimality of policies in the dynamic inventory problem. In Arrow K. J., Karlin S., & Suppes P. (Eds.), Mathematical methods in the social sciences (pp. 196–202). Stanford University Press. [Google Scholar]
- Shumsky, R. A. , Smith, J. , Hoen, A. , & Gilbert, M. (2021). Allocating COVID‐19 vaccines: Save one for the second dose? Dartmouth College Working Paper. [Google Scholar]
- Song, J. S. , van Houtum, G. J. , & Van Mieghem, J. A. (2020). Capacity and inventory management: Review, trends, and projections. Manufacturing & Service Operations Management, 22(1), 36–46. [Google Scholar]
- Strauss, M. (2021). Belgium halts J&J COVID vaccine for under 41s after first EU death. Reuters (May 26). https://reut.rs/3gsfKJl
- Tuite, A. R. , Zhu, L. , Fisman, D. N. , & Salomon, J. A. (2021). Alternative dose allocation strategies to increase benefits from constrained COVID‐19 vaccine supply. Annals of Internal Medicine, 174(4), 570–572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voysey, M. , Costa Clemens, S. A. , Madhi, S. A. , Weckx, L. Y. , Folegatti, P. M. , Aley, P. K. , Angus, B. , Baillie, V. L. , Barnabas, S. L. , Bhorat, Q. E. , Bibi, S. , Briner, C. , Cicconi, P. , Clutterbuck, E. A. , Collins, A. M. , Cutland, C. L. , Darton, T. C. , Dheda, K. , Dold, C. , … Pollard, A. J. (2021). Single‐dose administration and the influence of the timing of the booster dose on immunogenicity and efficacy of ChAdOx1 nCoV‐19 (AZD1222) vaccine: A pooled analysis of four randomised trials. Lancet, 397(10277), 881–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilde, H. , Mellan, T. , Hawryluk, I. , Dennis, J. M. , Denaxas, S. , Pagel, C. , Duncan, A. , Bhatt, S. , Flaxman, S. , Mateen, B. A. , & Vollmer, S. J. (2021). The association between mechanical ventilator availability and mortality risk in intensive care patients with COVID‐19: A national retrospective cohort study. BMJ Medcine, 19(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamin, D. , & Gavious, A. (2013). Incentives' effect in influenza vaccination policy. Management Science, 59(12), 2667–2686. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information.


