The Impact of Basal Roughness on Inland Thwaites Glacier Sliding

Abstract

Swath radar technology enables three‐dimensional mapping of modern glacier beds over large areas at resolutions that are higher than those typically used in ice‐flow models. These data may enable new understanding of processes at the ice‐bed interface. Here, we use two densely surveyed swath‐mapped topographies (<50 m² resolution) of Thwaites Glacier to investigate the sensitivity of inferred basal friction proxies to bed roughness magnitude and orientation. Our work suggests that along‐flow roughness influences inferred friction more than transverse‐flow roughness, which agrees with analytic form‐drag sliding theory. Using our model results, we calculate the slip length (the ratio of internal shear to basal slip). We find excellent agreement between the numerically derived slip lengths and slip lengths predicted by analytic form‐drag sliding theory, which suggests that unresolved short wavelength bed roughness may control sliding in the Thwaites interior.

Key Points

• We infer high‐resolution basal resistance on Thwaites Glacier using a 3D, full‐stress model with 3D radar swath‐mapped basal topographies

• Drag due to material properties and flow around obstacles remain entangled below the spatial resolutions of standard models

• High‐wavenumber (short wavelength) basal roughness parallel to ice flow has the largest effect on the model inferred basal flow resistance

1. Introduction

A primary question driving glaciological research today is: how much and how fast will global sea‐level rise due to Antarctic Ice Sheet mass loss (Scambos et al., 2017)? The Amundsen Sea Embayment in West Antarctica has long been considered geometrically prone to collapse (Clarke & Lingle, 1977; Hughes, 1981). Thwaites Glacier (Figure 1), the largest glacier in the Amundsen Sea Embayment and the glacier projected to contribute the most to sea‐level rise in West Antarctica beyond the next century, is likely in the early stages of this marine ice‐sheet instability (Joughin et al., 2014; Rignot et al., 2014; Shepherd et al., 2012). The pacing of Thwaites Glacier retreat remains uncertain in part due to poorly constrained solutions for the parameters that control glacier sliding. Assumptions underlying the mechanics that define the boundary condition at the ice‐bed interface affect the glacier's modeled response to ocean forcing, increasing glaciological sources of uncertainty in predictions of the West Antarctic Ice Sheet's contribution to sea level over decadal timescales (Brondex et al., 2019).

Figure 1.

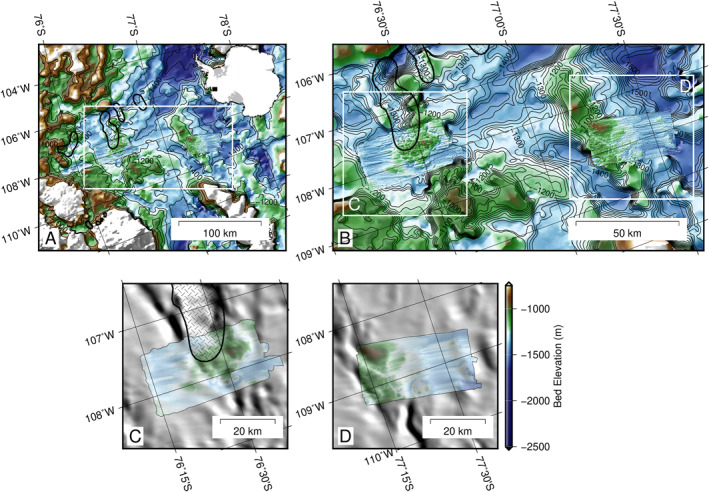
Overview map of Thwaites Glacier showing locations of the two model domains. (a) Thwaites Glacier regional subglacial topography from BedMachine Antarctica (Morlighem et al., 2020) with swath radar topography (Holschuh et al., 2020) superimposed for both model domains. Inset shows map location in Antarctica. (b) Local subglacial topography (white box in A) in the vicinity of the model subdomains. Radar swath‐mapped topographies are plotted on MODIS image mosaic of Antarctica (Haran et al., 2018, updated 2019) for the (c) lower Thwaites grid and (d) upper Thwaites grid, which highlights influence of bed topography on ice surface geometry. Positions of active subglacial lakes, most recently observed to be active in 2017 (Hoffman et al., 2020; Smith et al., 2017), are marked by hashed polygons. Projection is polar stereographic (EPSG: 3031) and contours denote bed elevation relative to WGS84 ellipsoid.

To simulate catchment‐scale glacier discharge and retreat, time‐evolving prognostic ice‐flow simulations must define the boundary condition at the ice‐bed interface, usually as part of a diagnostic optimization experiment. It is customary to assume the velocity normal to the bed is zero–ice cannot penetrate the bed. The form of the friction law, also described as the sliding law, or sliding relation in the literature, is then typically defined to condition the tangent component of the sliding velocity, relating the bed‐parallel basal velocity, ${\mathit{u}}_{\mathit{b}}^{\Vert }$, to the shear stress at the interface, ${\mathit{T}}_{\mathit{b}}^{\Vert }=\mathit{f}\left({\mathit{u}}_{\mathit{b}}^{\Vert }\right)$.

Assuming some sliding relation, $\mathit{f}\left({\mathit{u}}_{\mathit{b}}^{\Vert }\right)$, ice‐sheet models can be used with inverse methods (e.g., Joughin et al., 2004; Morlighem, 2011; Riel et al., 2021; Seroussi et al., 2014) to solve for the glacier sliding velocity and the parameters that define the sliding relation. An example sliding parameter is the friction coefficient, β, in the linear law proposed by MacAyeal (1989), ${\mathit{T}}_{\mathit{b}}^{\Vert }=\mathit{\beta }{\mathit{u}}_{\mathit{b}}^{\Vert }$, built on the work of Weertman (1964). The domain geometry defined by the ice thickness and elevation is often assumed to be known perfectly in the ice‐sheet model inversion. The result is a velocity and parameter solution consistent with surface observations that relies on assumptions made about the bed geometry, defined, crucially, by ice penetrating radar data and the resolution of the model domain.

Theoretical descriptions of the basal boundary condition often separate the contributions from the material friction at the ice‐bed interface (skin drag) and the enhanced stresses within the ice required to overcome geometric obstacles to flow (form drag; Kyrke‐Smith et al., 2018). Models that lack sufficient resolution to capture small‐scale features of the ice‐sheet bed have no way to disentangle these two controls on ice flow. The result is a basal friction proxy that misrepresents sources of stress at the ice‐bed interface.

Because the sliding law is poorly understood, it is customary to use the shear stress associated with an inferred friction proxy field (for instance, β) to initialize simulations with alternative representations of sliding physics. Some sliding relations that parameterize skin‐drag are fundamentally based on assumptions for unresolved bed‐roughness and depend strongly on flow speed (Weertman, 1957). Other sliding relations include linkages to independent fields such as effective pressure (i.e., de Fleurian et al., 2018), subglacial temperature (i.e., McCarthy et al., 2017), and till porosity (i.e., Minchew & Meyer, 2020) that evolve independently in time and produce different glacier responses in prognostic simulations driven by the same climate forcing. Even for models wherein the total drag is made to be rate‐dependent–governed by form drag at slow speeds and effective‐pressure‐dependent skin drag at faster speeds (i.e., Zoet & Iverson, 2020)–skin drag and form drag may remain mis‐partitioned in inferred resistance proxies due to the prescribed model geometry. The inability to accurately partition basal drag into form drag and time‐variable skin drag is a major challenge for prognostic ice‐flow modeling that remains understudied.

Higher resolution models should theoretically better constrain form drag and thus improve estimates for skin drag (Kyrke‐Smith et al., 2018). In this study, we use a series of smoothed swath‐mapped topographies for two subdomains of Thwaites Glacier (Holschuh et al., 2020) to determine the influence of the bed roughness wavenumber, which describes both the spatial frequency of the roughness and roughness orientation on the inferred friction proxy. We first describe the model physics and the equations solved in the inversion. Then, we introduce the data and describe the experimental framework used to explore the convolution of form drag and skin drag before interpreting the resulting friction proxies in the context of analytic form‐drag theory.

2. Methods

2.1. Ice‐Flow Model

Ice flow can be modeled using the Stokes equations by introducing a non‐Newtonian constitutive law (Glen's flow law) that describes the non‐linear deformation of ice under an applied stress (Cuffey & Patterson, 2010). In our study, we use the full‐Stokes solver implemented in Elmer/Ice (Gagliardini et al., 2013) to interrogate stresses at the ice‐bedrock interface (see Table S1 in Supporting Information S1 for all parameters used in the inversion). The sliding relation defines the boundary condition at the bed interface and relates the basal shear stress, τ _b , along flow to the glacier's sliding speed. In this study, we assume a sliding relation of the form

$${\mathit{\tau }}_{\mathit{b}}^{\left|\right|}=\mathit{\beta }{\left|{\mathit{u}}_{\mathit{b}}^{\left|\right|}\right|}^{\frac{1}{\mathit{m}}},$$ (1)

where u _b is the sliding velocity at the bed, β is the friction coefficient, and m is the glacier sliding exponent (Weertman, 1964). Solutions for β and m are not unique and cannot be distinguished from snapshot inversions of a single bed‐friction proxy. In many studies, m is assumed to be uniformly 3, though spatially variable values for the glacier slip coefficient and the sliding exponent have been inferred using time‐dependent data assimilation from time series of ice surface elevation and velocity (Goldberg et al., 2015). Here, we set m  = 1 but focus analysis on the inferred patterns of the shear stress, τ _b , which, in the limit of plug flow, theoretically does not depend on the coupled assumptions made for β and m .

2.1.1. Robin Inverse Method

We use the Robin inverse method, described by Arthern and Gudmundsson (2010) and implemented in Elmer/Ice, to infer the value of the friction coefficient, β , by solving the constrained optimization problem defined by the objective functional,

$$\mathit{J}\left(\mathit{\kappa }\right)=\frac{1}{2}{{\displaystyle \int }}_{{\mathbf{\Gamma }}_{\mathbf{s}}}\widehat{\mathit{n}}\cdot \left({\mathit{\sigma }}^{\mathit{N}}-{\mathit{\sigma }}^{\mathit{D}}\right)\cdot \left({\mathit{u}}^{\mathit{N}}-{\mathit{u}}^{\mathit{D}}\right)\mathit{dA}+\mathit{\lambda }\frac{1}{2}{{\displaystyle \int }}_{{\mathbf{\Gamma }}_{\mathbf{b}}}{\left(\frac{\partial \mathit{\kappa }}{\partial \mathit{x}}\right)}^2+{\left(\frac{\partial \mathit{\kappa }}{\partial \mathit{y}}\right)}^2\mathit{dA},$$ (2)

where $\widehat{\mathit{n}}$ is the unit outward normal vector, σ ^N and σ ^D are the full Cauchy stress tensors for the velocity solutions, u ^N and u ^D , which are constrained by Neumann and Dirichlet conditions at the ice‐sheet surface, respectively, and κ is the friction proxy varied in each inversion across the ice‐sheet base. An exponential map relating the friction coefficient and the control parameters, β(κ) = 10 ^κ , is used to ensure the inferred friction coefficient is strictly positive.

2.2. Observational Data

The model‐data misfit and resulting inference of the spatially distributed friction proxy is limited by the assumptions made about the ice viscosity, as well as the accuracy of surface velocity, surface elevation, and ice‐thickness observations. The ice viscosity was calculated from the Arrhenius relation described by Cuffey and Patterson (2010) using the temperature profile from the WAIS Divide borehole assuming a thawed bed (Osri et al., 2012). The surface velocities used to constrain the inversions are averaged from the first quarter of 2016 and were computed using synthetic aperture radar (SAR) data from the European Space Agency's (ESA) Copernicus Sentinel‐1A and Sentinel‐1B satellites following the methods of Joughin (2018, updated 2019; Joughin et al., 2021). The surface elevation used in the model was derived from the spatiotemporal least squares fitting procedure described by Smith et al. (2017) applied to Cryosat‐2 radar altimetry, optical satellite stereo‐imagery, and IceBridge airborne laser altimetry from the first quarter of 2016 when subglacial lakes beneath Thwaites Glacier were inactive (Hoffman et al., 2020).

To test the sensitivity of model‐derived friction proxies on the resolution of the basal topography, we produce 15 topographic datasets of varying resolutions from each original swath topography (Holschuh et al., 2020) for a total of 30 different topographies, which we use in 15 simulations of the upper Thwaites grid and 15 simulations of the lower Thwaites grid (Figure 1). For each swath grid, 13 topographies were smoothed isotropically using smoothing kernels that filtered wavenumbers (inverse of wavelength) from 1/1,300 m⁻¹ to 1/200 m⁻¹. Roughness is often anisotropic in areas of elongated bed features, which are present in both swath‐mapped subdomains of Thwaites Glacier. To test the influence of roughness orientation on the inferred friction proxy, two additional topographies were smoothed preferentially along and across flow. The anisotropically smoothed topographies were filtered relative to the flow direction, as defined by the reference surface velocities, using a weighted Gaussian kernel. The ratio of the Gaussian kernel smoothing in the along‐flow and across‐flow directions was varied between 1:1 and 4:1 to preserve the total spectral power relative to grids smoothed in the transverse flow direction. All 30 smoothed topographies are included in the supplement along with the surface elevation model and surface velocities used to constrain the inversion (Figures S1–S3 in Supporting Information S1).

3. Results

The inferred distributed basal drag (the bed‐parallel shear) is shown in Figure 2 for selected isotropically filtered grids. These results represent the best fit to the surface velocity data filtered by the surface‐to bed transfer function we solve in our inversion. We also plot the distributed normal pressure and the domain average normal pressure. The Tikhonov regularization curves used to select these shear stress fields are included in the Supplement (Figure S6 in Supporting Information S1; Shapero et al., 2016). For both the lower and upper Thwaites Glacier model domains, the misfit between the observed and modeled horizontal surface velocity was reduced as the resolution of the bed topography increased.

Figure 2.

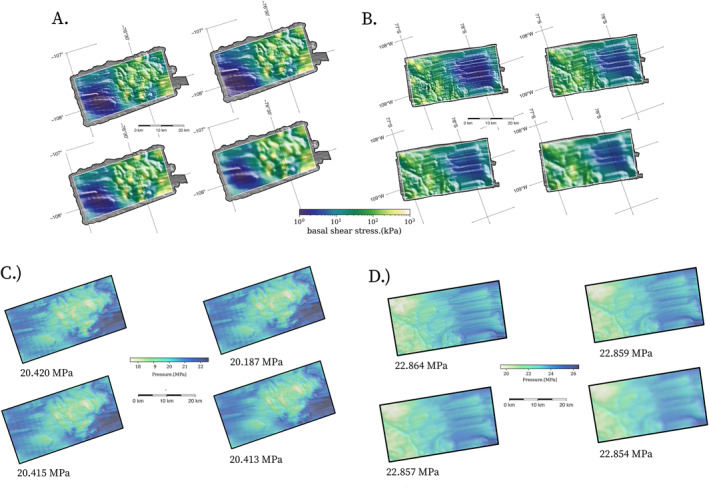
Inferred basal shear stress for the 1/200 m⁻¹, 1/400 m⁻¹, 1/600 m⁻¹, and 1/1,000 m⁻¹ wavenumber isotropically filtered grids, overlaying the filtered topography (hillshade) used in each experiment for the (a) lower Thwaites grid and (b) upper Thwaites grid. Also, shown is the normal pressure at the ice‐bottom boundary for the (c) lower Thwaites and (d) upper Thwaites grids with the mean normal pressure solution printed below each grid.

To better isolate the relationship between bed roughness (see Section S4 in Supporting Information S1) and the inferred friction coefficient, we interpolate the inferred friction proxy to a regularly spaced grid and correlate the friction coefficient with the total spectral roughness energy for the suite of isotopically smoothed grids. The windowed power spectral roughness for the native 25 m² resolution grids is shown in Figure 3. The regression slope of the inferred friction proxy is shown in Figure 4. From the regression slopes, we can identify regions where smoothing the basal topography has a strong effect on the magnitude of the inferred friction coefficient (relationship indicated by sign of slope).

Figure 3.

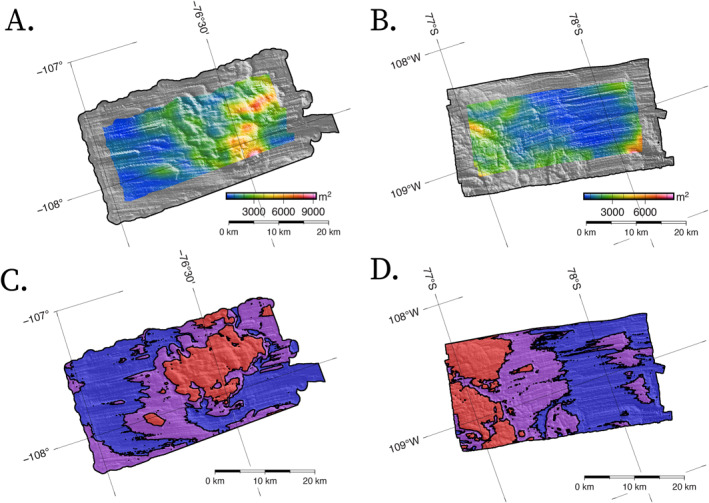
Total two‐dimensional spectral variance of 6.0 km windowed bed topography for the (a) lower and (b) upper Thwaites grids with the (c), (d) k‐means clustered regions, which we use to identify lineations (blue), ridges (red), and intermediary classes of bedforms and subglacial canyons (purple).

Figure 4.

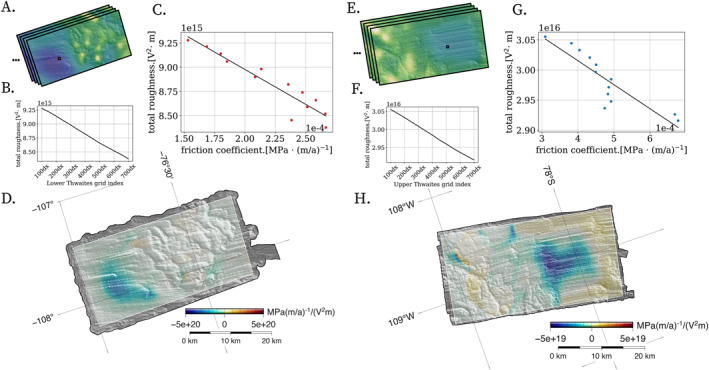
Grids of (a, e) the friction coefficient ordered by filtered roughness were correlated with the (b, f) total spectral roughness of each grid. The grid index label (x‐axis of (b, f) indicates the approximate scale of quarter wavelength features preserved in the smoothed topography. Sample correlations (c, g) are shown for two indices in regions of the lineations. Regression slope of the inferred friction coefficient with the total power spectral energy of the bed topography used in each simulation for all thirteen isotropically filtered grids for (d) lower Thwaites and (h) upper Thwaites grid.

4. Discussion

Our discussion is organized into four parts. We first discuss the normal pressure and quantify the impact of topographic smoothing on form drag. We then characterize the general patterns in the inferred friction fields, which remain largely unchanged across degrees of topographic smoothing. Finally, we discuss the effect of anisotropic smoothing on the inferred resistance field and compare the numerically derived slip lengths with predictions from analytic theory along flow lines.

4.1. Normal Pressure, a Measure of Form Drag

Using a full‐Stokes model that resolves all components of the stress tensor, we can determine the influence of form drag directly by integrating the normal pressure. Following Schoof (2002), stress at the ice‐bed interface can be broken down into the sum of form drag exerted by the undulating topography and tangential stress associated with skin drag

$$-{{\displaystyle \int }}_{{\mathbf{\Gamma }}_{\mathbf{b}}}\mathit{\sigma }\widehat{\mathit{n}}\mathit{dA}=-{{\displaystyle \int }}_{{\mathbf{\Gamma }}_{\mathbf{b}}}\widehat{\mathit{n}}\cdot \mathit{\sigma }\widehat{\mathit{n}}\mathit{dA}-{{\displaystyle \int }}_{{\mathbf{\Gamma }}_{\mathbf{b}}}\widehat{\mathit{t}}\cdot \mathit{\sigma }\widehat{\mathit{n}}\mathit{dA},$$ (3)

where σ is the stress tensor, $\widehat{\mathit{n}}$ is the unit vector normal to the bed and $\widehat{\mathit{t}}$ is the unit vector tangent to the bed in the direction of flow. In Weertman's original formulation, the tangent stress is assumed to be zero, and this assumption is invoked in many subsequent framings of basal sliding (i.e., Schoof, 2002). The influence of form drag can therefore be measured by comparing the solutions for normal pressure at the glacier bed. Our simulations show that the normal pressure decreases as the bed topographies are progressively smoothed, changing on average by 10 kPa as the maximum bed roughness wavenumber (minimum wavelength) is filtered from 1/100 m⁻¹ to 1/1,000 m⁻¹ (Figure 2). We next turn to the patterns of skin drag that remain unchanged across degrees of smoothing to understand the resistance from features that are not resolved in the radar data.

4.2. Patterns of Basal Friction Inferred for Swath Mapped Topographies

The bed topography of each swath mapped grid can be clustered into two subdomains based on the roughness characteristics of the basal topography (Figure 4). One subdomain includes ridge‐like features with roughness oriented equally in all directions with roughness wavelengths that span the width of the grid. The other includes lineated features with roughness oriented primarily orthogonal to flow with roughness anisotropy that is well captured by the swath topographies.

The spatial coverage of these clustered domains aligns with the unchanging patterns of skin drag we solve in our inversions. The lineated regions of each domain provide less resistance than the rest of the glacier bed and isolated patches of high resistivity control cumulative basal drag (Figures S4 and S5 in Supporting Information S1). In the lower Thwaites grid, we infer a two‐order reduction in basal resistance in the lineated basin where we observe ongoing thinning in satellite altimetry time series referenced to the upstream ridge (Hoffman et al., 2020). The combined observations of significant inland thinning, low inferred basal drag that is independent of basal velocity, and independent measurements of low acoustic impedance (Clyne et al., 2020; Muto et al., 2020) consistent with water‐saturated till suggest that the strength of the bed is relatively independent of the rate of deformation, or that the bed deforms more plastically in these regions (Clyne et al., 2020; Muto et al., 2020).

4.3. The Effects of Smoothing on the Skin Drag

From the friction coefficients inferred for the anisotropically filtered grids, we find that along‐flow smoothing increases the inferred skin drag at the ice‐sheet bed. Smoothing the bed along‐flow reduces form‐drag induced stresses in the ice, which are subsequently mapped into the friction proxy (skin drag). To quantify this, we compare the difference in inferred basal friction coefficient for along‐versus across‐flow‐smoothed beds. The difference between the average friction coefficient for the transverse‐flow filtered roughness and the along‐flow filtered roughness is 203  Pa ⋅( m / a )⁻¹ and 217  Pa ⋅( m / a )⁻¹ for the lower Thwaites and upper Thwaites grids, respectively (transverse‐flow filtered–along‐flow filtered).

A similar relationship might be expected to manifest in the isotropic smoothing experiment: an increase in inferred basal friction coefficient in grids with reduced spectral roughness power. The relative magnitude of this relationship should be controlled by changes in unresolved form drag across the smoothed topographies, which would present as significant and negative regression slopes after correlating total spectral power of each grid with each pixel of inferred friction coefficients. Instead, we found weak and variable relationships between roughness and inferred basal drag across the domains (Figure 4). The regression slopes are steepest in the lineated regions of each basin, as identified from k‐means clustering of the unfiltered bed topography (Figure 2). In these areas, the friction coefficient increases by a factor of two as the roughness of the bed topography decreases across the 13 isotropically filtered simulations. But over the ridges where the overall inferred basal drag was high, the relationship between roughness reduction and inferred drag was weak, with very small changes in inferred values across the suite of topographies tested. The insensitivity to smoothing could imply that form drag is dominated by features smaller than <100 m wavelength (the highest resolution grid tested). To evaluate this hypothesis, we examine analytic theory for form drag and its agreement with the numerically inferred friction field.

4.4. Agreement Between Numerical Results and Analytic Theory of Form Drag

The Weertman sliding relation we use to map distributed resistance assumes that a film of water between the ice and bedrock facilitates free slip at the microscopic scale, ${{\mathit{\tau }}_{\mathit{b}}}_{\mathit{micro}}=0$, which can be used to derive relationships between area‐averaged shear stress and unresolved roughness at larger scales, ${{\mathit{\tau }}_{\mathit{b}}}_{\mathit{micro}}=\mathit{f}\left({\mathit{u}}_{\mathit{b}}\right)$. Based on this area‐averaged assumption, analytic descriptions of ice flow over a spatially variable ice‐sheet bed can be used to understand the influence of roughness at different spatial scales on basal resistance to ice motion.

We apply analytic theory first described by Fowler (1986) and expanded by Schoof (2002) and Hogan et al. (2020) that formulates form drag as a function of topographic roughness. Assuming a linear friction law of the form τ _b  =  β u _b , consistent with the law used to infer the basal resistance field in our model experiments and assuming that bed roughness is dominated by small wavelength features, the friction coefficient ( β ) can be expressed as the sum of contributions ( β _n ) from features of angular wavenumber ( k _n  = 2 πf _n ) as:

$${\mathit{\beta }}_{\mathit{n}}=4\frac{\mathit{\eta }}{\mathit{H}}{\left(\frac{{\mathit{k}}_{\mathit{n}}}{{\mathit{k}}^{\ast }}\right)}^3\mathit{F}\left(\frac{{\mathit{k}}_{\mathit{n}}}{{\mathit{k}}^{\ast }}\right)\frac{{\left|{\widehat{\mathit{h}}}_{\mathit{n}}\right|}^2}{{\mathit{H}}^2}$$ (4)

where k _n is the integer wavenumber corresponding to the frequency f _n  =  n / a , ${\widehat{h}}_n$ is the Fourier component of the bed topography at spatial frequency f _n , η is the ice viscosity, k*  = 1/ H is the inverse characteristic thickness, H , taken to be the mean thickness over the window length, a , and F ( k _n / k* ) is a transfer function that relates the surface expression of basal drag to the friction coefficient (Schoof, 2002).

Following Hogan et al. (2020), we use periodogram coefficients as an approximation to Fourier coefficients as the glacier's bed includes substantial spatial variability in frequency content over the length of a flowline. Using frequency bins of width 1/ a  centered at f _n  =  n / a from n = 1 to n = 256, we use an inverse‐square law to fit periodogram coefficients to the power spectrum periodogram of the swath topography along flowlines. Like other studies (Hogan et al., 2020; Jordan et al., 2017; MacGregor et al., 2013), we find that the power spectrum (periodogram, P _n ) can be fit well by an inverse‐square law as a function of frequency ( P _n  =  Af _n correlation coefficient r  = 0.78 for the upper Thwaites grid and r  = 0.73 for the lower Thwaites grid). Assuming this relationship holds for all frequencies, total drag would be unbounded unless the bed becomes smooth at some scale smaller than a given wavelength ( λ _N , here assumed to be the limit of the radar resolution, 25m), and the basal friction coefficient can be approximated by a truncated sum that simplifies to β  = 8 ηπ ³ Aλ _N ⁻².

The slip length is defined as the effective ice viscosity divided by the basal friction coefficient (L = η/β). For slip lengths much greater than the ice thickness, the basal drag is too small compared to the ice viscosity to induce substantial shear in the ice column, and the ice slides over its base in plug flow. For slip lengths much smaller than the ice thickness, drag is large enough compared to the viscosity to induce shearing throughout the ice column. We calculated slip lengths from the analytic linear sliding coefficients and use the full‐Stokes solutions to calculate the modeled slip lengths from the friction coefficient and the effective ice viscosity determined from modeled strain rates at the ice‐sheet bed (Figure 5). The effective viscosity

$$\mathit{\eta }=2{\mathit{A}}^{-\frac{1}{\mathit{n}}}{\dot{{ϵ}_{\mathit{e}}}}^{-\frac{\mathit{n}-1}{\mathit{n}}}$$ (5)

was computed using modeled effective strain rates, ${\dot{\mathit{\epsilon }}}_{\mathit{e}}=\sqrt{{\mathit{\epsilon }}_{\mathit{i}\mathit{j}}{\mathit{\epsilon }}_{\mathit{i}\mathit{j}}/2}$, and modeled enhancement factor A  =  A ₀ e ^{− Q / RT} (see Table S1 in Supporting Information S1 for parameters used in the inversion). The agreement between analytically and numerically derived slip lengths suggests:

• Bed roughness resolved by the swath radar is well characterized by a power‐law fit, indicating roughness resolved by swath radar may provide information about roughness below the swath radar measurement resolution.

• Analytical predictions of basal resistance associated with form drag are consistent with the flow dynamics at Thwaites Glacier.

Figure 5.

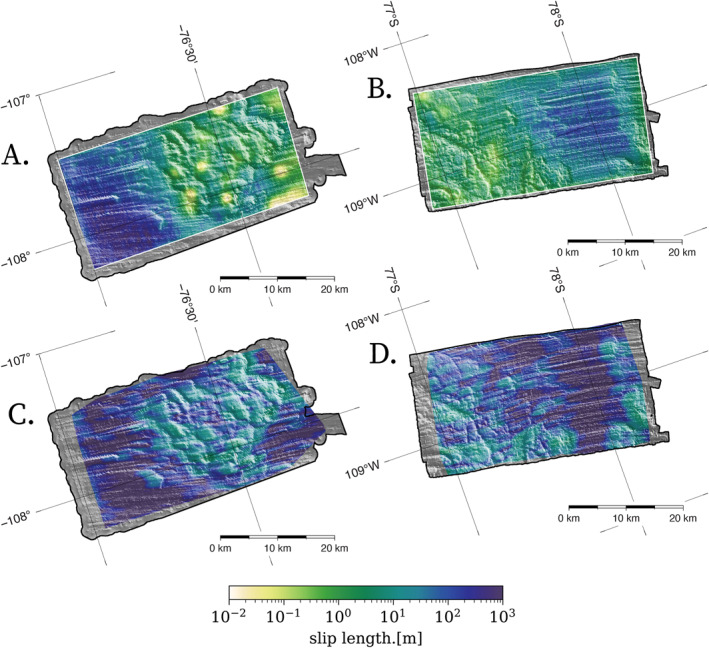
Numeric slip lengths calculated for the (a) lower and (b) upper Thwaites grids shown with (c), (d) analytic slip lengths calculated with 6 km moving windows (see appendix for details).

Our isotropic smoothing experiment shows that in the lineated regions of Thwaites, form drag remains at scales captured by the swath radar, and the inferred basal drag falls with smoothing. The roughest regions of the bed (the ridges) provide the most resistance to flow. In these regions (identified in red; Figure 4), the patterns and magnitude of the inferred friction coefficient remain unchanged across degrees of smoothing, and the ratio of the bed tangent stress to normal pressure is high. This could suggest that fine‐scale roughness that is unresolved in the highest resolution swath radar topographies controls the total basal drag budget. The static drag budget associated with the ridge surrounding the largest subglacial Thwaites lake (hashed region Figure 1, Thw₁₂₄) provides much of the resistance we observe in static inversions for basal shear stress. This may also explain why local ice dynamics are relatively insensitive to changes in effective pressure inferred from satellite altimetry time series of the lake fill‐drain cycle (Hoffman et al., 2020).

5. Conclusion

Our analysis shows that form drag and skin drag remain convolved in ice‐sheet model inversions for basal shear stress at resolutions finer than the limits prescribed in most ice‐sheet models and new radar swath‐mapped bed topography (the highest resolution mapping currently possible). High resolution radar mapping cannot yield a topography that captures all of the form drag, and thus it seems likely that form and skin drag will always be blurred in numerical models. However, going forward, self‐similarity in the basal roughness and the inferred basal resistance field may allow for a parameterization of form drag from swath radar.

The results of our study also have implications for controlled analog experiments (i.e., ring shears; Zoet & Iverson, 2020) that aim to partition total drag into form drag (for slow basal slip rates) and skin friction (at faster slip rates). The application of these models is always going to be limited by the reality that sliding relations in ice‐sheet models must also capture the effects of sub‐resolved bed morphology. Consistency between the numerically and analytically calculated slip lengths suggests that high‐frequency (<∼100 m wavelength) roughness controls bed resistance across inland portions of Thwaites Glacier; however, the feature size of the flow‐controlling obstacles remains unknown. Our results suggest that the controlling behavior and empirical form of the sliding relation associated with cm‐scale clasts at low‐slip speeds should be evaluated with larger‐scale features that are still unresolved in modern ice‐sheet topography. Idealized prognostic model experiments are also needed to better understand the sensitivity of glacier retreat and mass change due to the convolution of form drag and skin drag from the effects of unresolvable roughness.

Conflict of Interest

The authors declare no conflicts of interest relevant to this study.

Supporting information

Supporting Information S1

Hoffman, A. O. , Christianson, K. , Holschuh, N. , Case, E. , Kingslake, J. , & Arthern, R. (2022). The impact of basal roughness on inland Thwaites Glacier sliding. Geophysical Research Letters, 49, e2021GL096564. 10.1029/2021GL096564

Data Availability Statement

The bed topography, velocity and surface elevation data used in the paper are presented in the supplement and are available from the University of Washington's Research Works Archive https://doi.org/10.6069/EAZQ-XJ59. The code constituting the 3‐D inverse model framework is available with the Elmer/Ice source code at https://github.com/ElmerCSC/elmerfem.