Brain age as a surrogate marker for cognitive performance in multiple sclerosis

Abstract

Background and purpose

Data from neuro‐imaging techniques allow us to estimate a brain's age. Brain age is easily interpretable as ‘how old the brain looks’ and could therefore be an attractive communication tool for brain health in clinical practice. This study aimed to investigate its clinical utility by investigating the relationship between brain age and cognitive performance in multiple sclerosis (MS).

Methods

A linear regression model was trained to predict age from brain magnetic resonance imaging volumetric features and sex in a healthy control dataset (HC_train, n = 1673). This model was used to predict brain age in two test sets: HC_test (n = 50) and MS_test (n = 201). Brain‐predicted age difference (BPAD) was calculated as BPAD = brain age minus chronological age. Cognitive performance was assessed by the Symbol Digit Modalities Test (SDMT).

Results

Brain age was significantly related to SDMT scores in the MS_test dataset (r = −0.46, p < 0.001) and contributed uniquely to variance in SDMT beyond chronological age, reflected by a significant correlation between BPAD and SDMT (r = −0.24, p < 0.001) and a significant weight (−0.25, p = 0.002) in a multivariate regression equation with age.

Conclusions

Brain age is a candidate biomarker for cognitive dysfunction in MS and an easy to grasp metric for brain health.

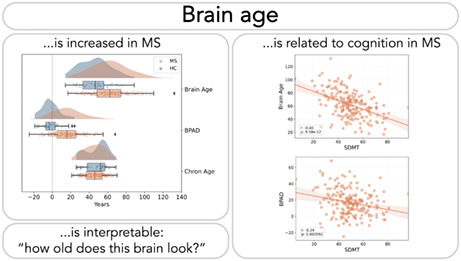
Brains of people with multiple sclerosis (MS) tend to look older than they are in reality. This brain age, as well as the overestimation compared to chronological age, correlates with cognitive performance (Symbol Digit Modalities Test) in MS (respectively r = −0.46 and r = −0.24). Given the simplicity of the linear brain age model presented in this paper, along with the interpretation of brain age as ‘how old the brain looks’, brain age could be a useful tool in clinical practice.

INTRODUCTION

About half of the people with multiple sclerosis (MS) experience cognitive impairment [1], aggravating the impact of MS on their daily life and that of their caregivers [2]. Susceptibility to cognitive impairment should be assessed holistically, as it depends on clinical factors such as age [3], disability [3], premorbid intelligence [3] and disease duration [4] but also on findings in other domains such as brain imaging [5]. The most prominent of these cognitive difficulties is a slowing of information processing abilities [6], which literature suggests to be the key driver for deficits in other cognitive domains in MS [7]. Timely identification of cognitive difficulties is imperative, as it allows for early treatment planning (in particular cognitive rehabilitation appears to be effective, although other methods exist [8]) to both prevent and address patient‐specific difficulties associated with cognitive impairment. These include falling, reduced quality of life and employment issues [7], but their impact extends to the mental health of caregivers [9]. Early detection requires regular and consistent follow‐up in standard clinical care. Currently, neuropsychological testing remains the gold standard to detect cognitive problems [10], the most popular test in clinical practice being the Symbol Digit Modalities Test (SDMT) [11]. Although the SDMT is a brief screening test [12], it is prone to practice effects [13].

An objective biomarker to diagnose cognitive deficits might circumvent the aforementioned problem. Currently, predominantly structural brain characteristics, extracted from brain imaging techniques such as magnetic resonance imaging (MRI), were found to be related to cognitive performance [14]. Yet more information can be extracted from an MRI than meets the eye. By using large datasets of brain images of healthy individuals, a machine learning model can be trained to estimate the age of a given brain. For a new brain image, the model will output the best guess of the age of that person's brain, that is, the ‘brain age’, which can look older or younger than the actual, chronological age of that person. The elegance of brain age lies in its interpretable nature; it is easily graspable how old a brain appears to be. In several brain disorders [15], including MS [15, 16, 17], brains typically look older than those of their healthy peers.

On top of being an interpretable metric, recent evidence indicates that brain age could explain clinical symptomatology in MS, reflected by statistically significant, albeit weak, correlations. More specifically, increased brain age is associated with physical disability as quantified by the Expanded Disability Status Scale (EDSS, r = 0.23) [15] and the nine‐hole peg test (r = 0.36) [16]. Beyond physical disability, recent findings by Kaufmann et al. [15] in dementia suggest that increased brain age could explain cognitive disability as well, namely by being associated with lower scores on the Mini Mental State Examination (r = −0.30), independent of chronological age.

In summary, brain age is an interpretable imaging‐derived metric that is sensitive to MS‐related pathology. However, it is currently unknown how brain aging is related to MS‐specific cognitive dysfunction. So far, efforts have mostly uncovered anatomical correlates by directly linking brain volumetry to cognitive performance. Yet, people might be more easily capable of imagining ‘how old a brain looks’ compared to ‘how voluminous a brain is’, posing an opportunity for a new communication tool in clinical practice that avoids medical jargon, which answers the desire of patients to be informed in plain language [18]. In this study, brain age is explored as a tool for studying cognitive dysfunction in MS on an international, multi‐centre dataset.

METHODS

Data description

Data are described by subdividing them into HC_train, HC_test and MS_test, used to train and test the brain age decoding model, as shown in Figure 1. HC_train was constructed from a large sample of 1673 healthy control (HC) subjects from online publicly available repositories (only subjects of 18 years or older were included, consistent with the training dataset of Cole et al. [19]). Refer to Table S1 and Figure S1 for a more detailed description. For the test datasets, two centres contributed retrospective data to this study. First, in Brussels, both HC (n = 50) and MS (n = 97) subjects were assessed as part of a study [20, 21] on understanding the neural origins of cognitive disturbances in MS. The MS subjects of this study were recruited at the National Multiple Sclerosis Center of Melsbroek. Second, the Universitätsmedizin Greifswald contributed data from 104 MS subjects to this study. Altogether, this resulted in 50 subjects for the HC_test and 201 subjects for the MS_test. For all data, T1‐weighted MRI, sex and age at image acquisition were available. For the test datasets, fluid attenuated inversion recovery (FLAIR) MRI and results from the SDMT [11] were available. The SDMT is a brief test, designed to measure information processing speed, that is attractive for its psychometric properties [22], quick administration [12] and its capability of predicting scores on other cognitive tests [23]. As a recent study by Sandry et al. [24] found that SDMT performance is not solely determined by one single cognitive process, that is, information processing speed, its results were interpreted as measuring global cognitive performance. Finally, MS_test data also contained EDSS, disease duration and type of MS. A summary of all data is available in Table 1.

FIGURE 1.

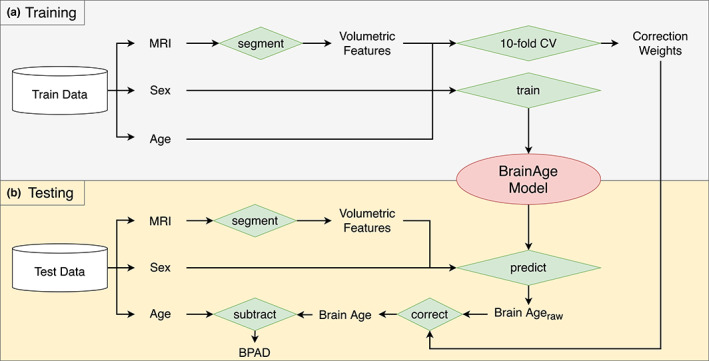
Brain age pipeline. The pipeline is subdivided into (a) a training phase and (b) a testing phase, where ‘Train Data’ refers to the HC_train data and ‘Test Data’ represents either the HC_test dataset or the MS_test dataset. A silo‐like shape represents a dataset, whereas green diamonds represent some kind of operation, specified by the text. Other text represents either variables or images [Color figure can be viewed at wileyonlinelibrary.com]

TABLE 1.

Data characteristics

Dataset	HC_train	HC_test	MS_test
Source	Public	Brussels	Brussels	Greifswald	Total
Data description
N	1673	50	97	104	201
Age
Mean ± SD	41.9 ± 19.5	48.0 ± 11.9	48.1 ± 9.6	43.1 ± 12.0	45.5 ± 11.2
Range (min–max) b	18–94	26–68	26–70	20–69	20–70
Gender (M:F)	673:1000	19:31	29:68	35:69	64:137
EDSS (median; IQR)	–	–	3.0; 2.0	1.5; 2.0	2.5; 2.5
Disease duration (years)	–	–	15.7 ± 8.4	8.4 ± 6.2	11.9 ± 8.2
MS subtype	–	–	CIS: 2 RRMS: 82 SPMS: 6 PPMS: 7	CIS: 0 RRMS: 100 SPMS: 1 PPMS: 3	CIS: 2 RRMS: 182 SPMS: 7 PPMS: 10
SDMT (mean ± SD)	–	53.8 ± 9.6	48.0 ± 11.4	51.2 ± 15.0	49.6 ± 13.5
Scanner description
Field strength (T)	1.5 and 3 a	3	3	3	3
Sequences	T1	T1 + FLAIR	T1 + FLAIR	T1 + FLAIR	T1 + FLAIR
Scanner	Various a	Philips Ingenia: 36 Philips Achieva: 14	Philips Ingenia: 68 Philips Achieva: 29	Siemens Verio	Philips Ingenia: 68 Philips Achieva: 29 Siemens Verio: 104

Abbreviations: CIS, clinically isolated syndrome; EDSS, Expanded Disability Status Scale; F, female; FLAIR, fluid attenuated inversion recovery; IQR, interquartile range; M, male; MS, multiple sclerosis; PPMS, primary progressive MS; RRMS, relapsing–remitting MS; SDMT, Symbol Digit Modalities Test; SPMS, secondary progressive MS.

^a Refer to Table S1 for more details.

^b Values displayed as integer ages (rounded down).

Ethics

All participants of the BRUMEG study, Brussels, provided their written informed consent prior to MRI assessment. The study protocol (B.U.N. 143201423263) was approved by the ethical committee of the UZ Brussel (Commissie Medische Ethiek [O.G. 016], Reflectiegroep Biomedische Ethiek) on 25 February 2015. For the patients from Greifswald, Germany, the study was approved by the ethics committee of the Medical Faculty of the University of Greifswald (BB159/18), and all participants gave their written informed consent. HC_train data consist of publicly available data originating from other projects, listed in Table S1. Ethical approval was received by each project separately.

Magnetic resonance imaging preprocessing and brain age pipeline

Several preparatory steps were involved in the construction of our brain age model. They are summarized below.

1. Brain MRI segmentation. From the HC_train dataset, 3D T1‐weighted MRI, sex and chronological age were extracted. Next, the T1‐weighted MR images were evaluated by the FDA cleared icobrain software (version 4.4) of icometrix NV (Leuven, Belgium). This is an end‐to‐end automatic software that segments and subsequently quantifies distinct regions of the brain, which was originally published in Jain et al. [25]. The pipeline relies on T1‐weighted MR images and, when available, also uses FLAIR images to segment white matter lesions in the brain. These lesions are filled in the T1 image with white matter intensities, and the T1 image is subsequently segmented by fitting a probabilistic model for grey matter, white matter and cerebrospinal fluid image intensities. Ultimately, the pipeline generates volumes of the segmented regions, yielding a set of features, normalized for head size, that describe the brain's morphology. These can be subdivided into general volumes (grey matter, white matter, lateral ventricles), lobe‐specific cortical grey matter (frontal, temporal, parietal, occipital) and subcortical volumes (hippocampus [left and right] and thalamus [left and right]). Together with the subjects' sex, this forms the total set of features used for the brain age pipeline. HC_test and MS_test were also segmented with icobrain, yielding the aforementioned set of features. The sole difference with HC_train is the additional availability of FLAIR images to perform lesion filling in the T1 image.

2. Linear regression. Along with chronological age, that is, the target variable to be predicted, the total set of features (z‐normalized) served as input for training a supervised machine learning model. Ordinary least squares regression was used, since it is amongst the most interpretable machine learning algorithms; the predicted brain age is simply the weighted sum of all features with their respective weight:

   $$\text{brain}\mathrm{age}=w_0+w_1{\text{feature}}_1+w_2{\text{feature}}_2+\dots +w_n{\text{feature}}_n$$

   with $w_0$ being the intercept or ‘bias’. The training phase consists of finding the weights that minimize the error between the prediction, that is, brain age, and a subject's true age. To ensure the comparability of weights, each feature was normalized as follows:

   $${\text{feature}}_{\text{normalized}}=\frac{\text{feature}-\text{mean}\left({\text{feature}}_{\mathrm{HC}\_\text{train}}\right)}{\mathrm{std}\left({\text{feature}}_{\mathrm{HC}\_\text{train}}\right)}$$

   This normalization process was used for every feature for both the training and testing phase.

3. Brain age correction. According to Le et al. [26], age‐predicting models are prone to ‘regression towards the mean’, a phenomenon that results in overestimation of the brain age of younger subjects and underestimation of the brain age of older subjects. There appears to be firm consensus throughout the literature that such bias should be corrected for, and several methods exist to do so [27]. The method described by Cole et al. [17] was used. First, ${\text{BrainAge}}_{\mathrm{raw}}$ on HC_train was estimated by adopting 10‐fold cross‐validation (CV). Second, a linear regression equation was fitted between the obtained raw brain ages and the respective chronological ages:

   $${\text{BrainAge}}_{\mathrm{raw}}={\beta }_0+{\beta }_1\text{ChronologicalAge}+\epsilon$$
   Here, ${\beta }_0$ and ${\beta }_1$ represent the intercept and slope of the regression line, respectively, whereas the error term $\epsilon$ represents the residuals between data points and the regression line. ${\beta }_0$ and ${\beta }_1$ serve to correct each brain age predicted by our model using

   $$\text{BrainAge}=\left({\text{BrainAge}}_{\mathrm{raw}}-{\beta }_0\right)/{\beta }_1$$

   They were first used to correct the raw brain age estimates of HC_train.

In summary, after segmentation of the MR images, 10‐fold CV on HC_train was first performed to obtain the correction weights, which additionally allows the mean absolute error (MAE) to be calculated on the HC_train dataset, providing an intuition in model performance on HC_train. Secondly, all available training data were used to train a final brain age model that was used for further analyses. Altogether, this is referred to as the training phase, which is represented visually in Figure 1a. Next, whether the learned weights generalize to other datasets as well was investigated (Figure 1b). Raw brain age on the HC_test and MS_test datasets was first calculated by calculating the weighted sum of the features (i.e., sex and brain volumes from icobrain) with their respective weights, which were then corrected by using the correction formula of preparatory step 3. In the remainder of this paper, ‘brain age’ consistently refers to the corrected brain age.

Finally, the latter variable was additionally used to calculate the brain‐predicted age difference (BPAD) [17]. It quantifies brain age overestimation by subtracting chronological age from brain age.

Statistical analyses

Statistical analyses and visualizations were performed in Python and R. Significance level alpha was set to 0.05 for all reported test results. Pearson correlation was used. Raincloud plots were generated with use of the PtitPrince package [28].

First, a Mann–Whitney U test was used to compare brain age, BPAD and chronological age distributions between MS_test and HC_test. To compare the BPAD of both test sets with 0, a one‐sample Wilcoxon signed rank test was used.

Second, the error of predicting age from brain images was calculated with MAE between true and predicted age for the healthy control datasets. Next, the Pearson correlation was used to establish the association between brain age and SDMT in the MS_test data. To assess whether it contains unique information beyond chronological age, two approaches were used. First, brain age and chronological age were considered together in a multivariate linear regression equation:

$$\text{SDMT}={\beta }_0+{\beta }_1\text{BrainAge}+{\beta }_2\text{ChronologicalAge}+\epsilon$$

Second, the relationship between BPAD and SDMT in the MS_test data was assessed using a Pearson correlation.

Predicting brain age from brain volumetry and sex using linear regression essentially represents a linear transformation that reduces the dimensionality of the feature space from 12 (brain volumetry + sex) to 1 (brain age). Another type of linear transformation that is commonly used to compress a set of variables is principal component analysis (PCA). PCA essentially ‘reorganizes’ the variables to a set of principal components that are uncorrelated and explains variance in a dataset in decreasing order; the first principal component (PC₁) explains the majority of this variance. To construct PC₁, a PCA was first fitted on the feature space of the HC_train dataset. Next, this was used to transform the feature space of the MS_test dataset by projecting along PC₁. The relationship between brain age and PC₁ in the MS_test data was assessed with a Pearson correlation.

RESULTS

The brain age pipeline

Linear regression between brain age, obtained with 10‐fold CV on HC_train (cf. Figure 1a), and chronological age yielded the following correction weights: ${\beta }_0=8.60$, ${\beta }_1=0.79$. In the same dataset, the MAE between corrected brain age and chronological age was 7.91 years. The result of the brain age correction is added to the supplementary material as Figure S2.

In a next step, a final brain age model was fitted by using all available HC_train data for training (cf. Figure 1a). The model's feature weights can be consulted in Table 2. To test its quality, it was applied to the HC_test set and MS_test set, represented in Figure 1b. The corrected brain age and BPAD values are summarized in Table 3 and visually displayed for HC_test and MS_test in the raincloud plots of Figure 2.

TABLE 2.

The final brain age model's characteristics

Feature	Weight	Standard Error	t	p
Intercept	41.8867	0.216	193.509	<0.001
Grey matter	−7.5859	1.021	−7.427	<0.001
White matter	−0.8746	0.269	−3.252	0.001
Lateral ventricles	2.2432	0.359	6.244	<0.001
Cortical grey matter—frontal lobe	−4.0462	0.628	−6.438	<0.001
Cortical grey matter—occipital lobe	0.4299	0.314	1.370	0.171
Cortical grey matter—temporal lobe	−1.0626	0.403	−2.638	0.008
Cortical grey matter—parietal lobe	−1.0037	0.424	−2.366	0.018
Hippocampus—left	0.2280	0.304	0.750	0.453
Hippocampus—right	1.4228	0.311	4.573	<0.001
Thalamus—left	−2.1227	0.526	−4.036	<0.001
Thalamus—right	−2.5859	0.511	−5.057	<0.001
Sex	−3.4668	0.229	−15.136	<0.001

TABLE 3.

Outputs from the brain age pipeline: corrected brain age and BPAD for the HC_train, HC_test and MS_test datasets

Dataset	HC_train	HC_test	MS_test
Source	Public	Brussels	Brussels	Greifswald	Total
N	1673	50	97	104	201
Brain age (mean ± SD)	41.9 ± 21.9†	46.1 ± 16.8	61.8 ± 16.6	62.6 ± 22.9	62.2 ± 20.1
BPAD (mean ± SD)	0 ± 10.0†	−1.9 ± 9.7	13.7 ± 14.7	19.5 ± 16.0	16.7 ± 15.6

Note: The dagger (†) indicates that these values were obtained by means of 10‐fold cross‐validation.

Abbreviation: BPAD, brain‐predicted age difference.

FIGURE 2.

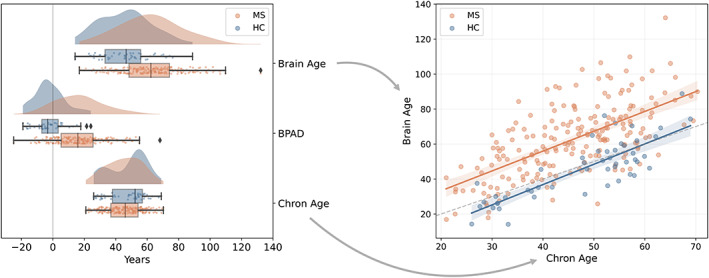
Group comparison between HC_test (blue) and MS_test (orange) for brain age, BPAD and chronological age. Left: The raincloud plots show the distribution of brain age, BPAD and chronological age for MS_test and HC_test. A reference line at x = 0 is included as visual aid. Right: The scatterplot shows the relationship between brain age and chronological age for MS_test and HC_test. The dotted line is added as reference, namely where brain age = chronological age [Color figure can be viewed at wileyonlinelibrary.com]

1. Evaluation on HC_test data. The model predicted brain age with an MAE of 7.85 years. BPAD was not significantly different from zero (T = 449, p = 0.069), indicating that, on average, brain age is similar to chronological age.

2. Evaluation on MS_test data. BPAD was significantly greater than zero (T = 1121, p < 0.001).

It is additionally noted that both brain age (U = 2708, p < 0.001) and BPAD (U = 1506, p < 0.001) were significantly higher in the MS_test data compared to HC_test. Chronological age was comparable between the two groups (U = 5721, p = 0.130).

The relation between brain age and cognitive performance

Brain age was significantly correlated with SDMT (Figure 3, r = −0.46, p < 0.001) and explained 20.85% of the variance in SDMT (R ²). Moreover, brain age explained unique variance in SDMT beyond chronological age, which is reflected by a significant correlation between BPAD and SDMT (Figure 4, left, r = −0.24, p < 0.001) and the significant weight (${\beta }_1$ = −0.25, p = 0.002) assigned to brain age when considering it in the multivariate regression equation $\text{SDMT}={\beta }_0+{\beta }_1\text{BrainAge}+{\beta }_2\text{ChronologicalAge}+\epsilon$ (Figure 4, right). Chronological age also contributed significantly to the model (${\beta }_2$ = −0.32, p < 0.001).

FIGURE 3.

Scatterplot between brain age and SDMT in the MS_test dataset. The textbox describes the Pearson r statistic, along with the p value [Color figure can be viewed at wileyonlinelibrary.com]

FIGURE 4.

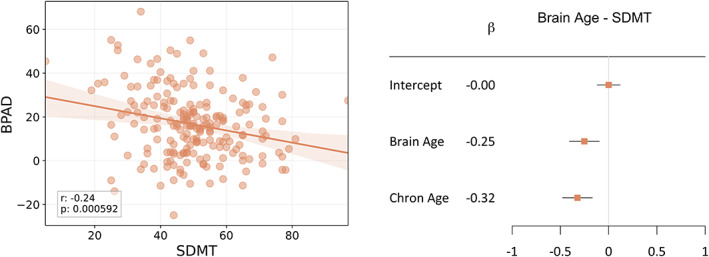
The relationship between brain age and SDMT, independent of chronological age. Left: Scatterplot between BPAD and SDMT in the MS_test dataset. The textbox describes the Pearson r statistic, along with the p value. Right: Forest plot visualizing the significance of the weights (β _n ) in the linear regression equation $\text{SDMT}={\beta }_0+{\beta }_1\text{BrainAge}+{\beta }_2\text{ChronologicalAge}+\epsilon$ in the MS_test dataset (note that variables were normalized with respect to mean and standard deviation before input in the regression equation). The maximum likelihood estimates of the weights (${\beta }_n$) are represented by the orange squares, along with a 95% confidence interval (horizontal bar). If the latter does not include 0, the contribution of that feature to the model is considered significant. Brain age and chronological age contributed significantly (p = 0.002 and p < 0.001 respectively) [Color figure can be viewed at wileyonlinelibrary.com]

The relation between brain age and brain volumetry

Figure 5 displays the relationship between PC₁ and brain age, revealing a strong linear relationship (r = 0.93, p < 0.001).

FIGURE 5.

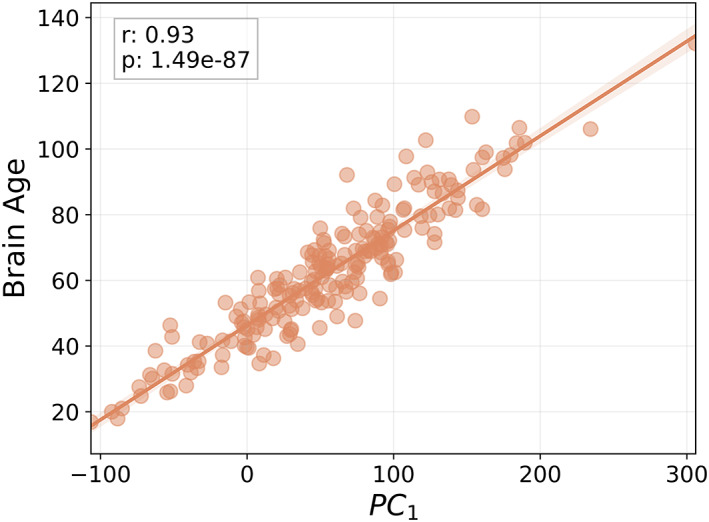
Scatterplot between the first principal component (PC₁) and brain age in the MS_test dataset. The textbox describes the Pearson r statistic, along with the p value [Color figure can be viewed at wileyonlinelibrary.com]

Table S3 shows the correlation of each brain volumetric feature with brain age. Whole brain volume, normalized for head size, was also included (r = −0.92, p < 0.001).

The relation between brain age and other clinical variables

Brain age was significantly correlated with both EDSS (r = 0.37, p < 0.001) and disease duration (r = 0.32, p < 0.001). BPAD was significantly correlated with EDSS (r = 0.17, p = 0.018) but not with disease duration (r = 0.04, p = 0.586). Figure S6 shows the effect of EDSS and disease duration, as well as age, on the relationship between brain age and SDMT.

DISCUSSION

This study aimed to investigate the potential of brain age, an intuitive metric of brain health, as a biomarker for cognitive dysfunction in MS. Our results suggest that brain age could be a promising candidate; it is significantly related to cognitive performance, independent of chronological age. Moreover, it was shown that brain age explained the majority of variance in brain volumetry by establishing a strong relationship with the PC₁ of our total set of features; both linear transformations appear to yield a similar metric of brain health.

Brain age and brain‐predicted age difference (BPAD)

In the past few years, most brain‐age‐related research in MS was dedicated to establishing clinical correlates of the BPAD [15, 16, 17]. Although BPAD might be regarded as a simplification of brain age, valuable information is in fact lost by subtracting two variables. Our results support this statement in two ways. First, BPAD showed a weaker correlation with cognitive performance than brain age. Second, brain age and chronological age both contributed unique information in explaining cognitive performance in MS. In terms of clinical significance, BPAD could be valuable for monitoring patients over time, for example to assess treatment effect. Since it takes into account the age at MRI assessment, a reduction of BPAD at follow‐up might indicate decreased disease activity, for example as a result of a certain treatment.

Brain age compared to existing biomarkers

Although brain age is a fair choice for decoding cognitive performance in MS, it is noted that its performance was comparable to whole brain volume, as shown by Golan et al. [29], reporting a correlation of r = 0.46 between whole brain volume and global cognitive functioning. This is consistent with findings of other studies with large sample sizes, reporting a higher prevalence of cognitive impairment in subjects with lower brain parenchymal fraction [30] and a correlation of r = 0.50 between whole brain fraction and processing speed [31]. Nonetheless, brain age has an important advantage in contrast to any biological correlate of cognition in MS: it is easy to grasp as ‘how old a brain looks’, which facilitates communication with persons with MS. Constructing an uncomplicated message with minimal jargon contributes to optimally transferring medical information to patients, in turn optimizing patient care [18]. The flipside of the same coin, however, might be that because patients can better imagine this metric of brain health it could be traumatic if not carefully communicated. The suitability of the metric as a communication tool will probably differ from patient to patient and should be carefully considered when aiming for a more personalized approach to medicine. Future research on patients' attitude towards brain age might shed new lights on patients' acceptance of brain age.

User trust

However, an important hurdle in the path of brain age models to clinical practice is nicely illustrated by a statement in Ribeiro et al.: ‘if the users do not trust a model or a prediction, they will not use it’ [32]. This issue should be addressed, in particular as efforts emerge to include brain age models in routine MRI examination [33]. First, to maximize trust of the MS clinician in our model, simple linear regression was used. The MS clinician has been familiarized with this method by decades of research adopting it for various purposes, for example studying the relation between MRI and cognitive performance in MS [34, 35]. The advantage of a linear model is that the impact of a change in a feature (in our case brain volumes and sex) is directly observable in the brain age: the change multiplied by the weight equals the number of years the brain will be estimated younger or older (the sign of the weight indicates whether the brain age will be estimated younger or older, whereas the magnitude of the weight indicates the number of years). Linear models are therefore both interpretable (obvious causal relationship between input and output) [36] and explainable (good understanding of the model's internal mechanisms) [36]. This contrasts with other studies on brain age in MS, mostly adopting models that are common in machine learning but not in clinical research, such as Gaussian processes regression [17] and extreme gradient boosting [16]. Secondly, trust in the prediction of our model, that is, predicted brain age, was enhanced by showing that brain age explains the majority of the variance in MRI‐derived volumetric features and sex, used to train our brain age model. This observation is logical in the light of what is known about the aging brain, shrinking as people get older [37].

Model performance and clinical implications

Our model achieved an MAE of 7.91 years on the HC_train dataset (10‐fold CV) and 7.85 years on an independent HC test set. This is relatively large compared to previously published models that adopted a more complex methodology compared to ours. For example, Cole et al. [17] achieved an MAE of 5.02 years on their training sample. However, as brain age is foremost a surrogate marker for clinical variables of interest, models should be assessed in terms of their clinical utility, rather than focusing solely on their age decoding capacity. The brain age model of Cole et al. [17] was therefore applied to our data, relying on Gaussian processes regression and being publicly available. A detailed description of the methodology and results of this post hoc analysis is available in the supplementary material. The model of Cole et al. [17] achieved an MAE of 5.52 on our HC_test sample. An F test was used to compare the variance of the BPAD distributions of the Cole model and our model, indicating that the Cole model was significantly more accurate in decoding age compared to our model (F = 2.23, p = 0.006). Interestingly, however, the correlations with SDMT of brain age (Figure S4, r = −0.50, p < 0.001) and BPAD (Figure S5, r = −0.21, p = 0.003) obtained with the model of Cole et al. [17] were similar to those of brain age (r = −0.46, p < 0.001) and BPAD (r = −0.24, p < 0.001) resulting from our model. Differences in correlation coefficients were not statistically significant (brain age, z = −1.43, p = 0.153; BPAD, z = 0.69, p = 0.492).

Hence, although the models differ with respect to performance in age decoding, the models are comparable in terms of clinical significance. As one should always strive to make models as simple as possible [38], our model is deemed to be more suitable for clinical practice.

Limitations

Our results imply that brain age has the potential to explain cognitive status in people with MS; brain age explained 20.85% (R ²) of the variance in SDMT. Yet, the cross‐sectional nature of the data limited us to investigate the potential of brain age to predict future cognitive decline. Furthermore, previous literature highlights the importance of paying careful attention when using data from different scanners for brain age research [39]. One way to address this issue is to maximize the variety of scanners used in the training set, which might prevent brain age models from becoming highly dependent on a specific type of scanner. This was the case for our HC_train dataset (cf. Table S1 for data sources), in which all three scanner types that were used in the test datasets were also represented (Philips Achieva, Philips Ingenia and Siemens Verio). Nonetheless, preprocessing of brain images already partly counteracts heterogeneity across scanners, as the icobrain software used to segment the MR images shows limited inter‐scanner variability [40, 41]. Therefore, this bias has been deemed to have been properly addressed.

Conclusive statement

In summary, the methodology of a linear brain age model can be interpreted by clinicians and its prediction by patients. Together with its potential to explain cognitive performance, predicted brain age could be a valuable clinical tool to analyse and communicate results from brain imaging data in MS.

AUTHOR CONTRIBUTIONS

Stijn Denissen: Conceptualization (equal); data curation (lead); formal analysis (lead); funding acquisition (equal); investigation (lead); methodology (lead); project administration (equal); resources (supporting); software (lead); validation (lead); visualization (lead); writing – original draft (lead); writing – review and editing (equal). Denis Alexander Engemann: Conceptualization (supporting); formal analysis (supporting); investigation (supporting); methodology (supporting); visualization (supporting); writing – original draft (supporting); writing – review and editing (supporting). Alexander De Cock: Writing – review and editing (supporting). Lars Costers: Data curation (supporting); resources (supporting); writing – review and editing (supporting). Johan Baijot: Data curation (supporting); resources (supporting); writing – review and editing (supporting). Jorne Laton: Data curation (supporting); resources (supporting); writing – review and editing (supporting). Iris‐Katharina Penner: Data curation (supporting); resources (supporting); writing – review and editing (supporting). Matthias Grothe: Data curation (supporting); resources (supporting); writing – review and editing (supporting). Michael Kirsch: Data curation (supporting); resources (supporting). Marie Beatrice D'hooghe: Writing – review and editing (supporting). Miguel D'Haeseleer: Writing – review and editing (supporting). Dominique Dive: Writing – review and editing (supporting). Johan De Mey: Data curation (supporting); funding acquisition (supporting); resources (supporting); supervision (supporting); writing – review and editing (supporting). Jeroen Van Schependom: Conceptualization (equal); data curation (equal); formal analysis (equal); funding acquisition (equal); investigation (equal); methodology (equal); project administration (supporting); resources (equal); supervision (equal); writing – original draft (equal); writing – review and editing (equal). Diana Maria Sima: Conceptualization (equal); data curation (equal); formal analysis (equal); funding acquisition (equal); investigation (equal); methodology (equal); project administration (equal); resources (equal); software (equal); supervision (lead); validation (equal); visualization (equal); writing – original draft (equal); writing – review and editing (equal). Guy Nagels: Conceptualization (equal); data curation (equal); formal analysis (equal); funding acquisition (equal); investigation (equal); methodology (equal); project administration (equal); resources (equal); software (equal); supervision (lead); validation (equal); visualization (equal); writing – original draft (equal); writing – review and editing (equal).

CONFLICT OF INTEREST

Stijn Denissen is an industrial PhD candidate in collaboration with icometrix. Diana Maria Sima and Lars Costers are employed at icometrix. Guy Nagels is on a 10% secondment from the UZ Brussel to icometrix as medical director and is a minority shareholder of icometrix.

Supporting information

 

Denissen S, Engemann DA, De Cock A, et al. Brain age as a surrogate marker for cognitive performance in multiple sclerosis. Eur J Neurol. 2022;29:3039‐3049. doi: 10.1111/ene.15473

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.