Abstract
The within-host evolutionary dynamics of tuberculosis (TB) remain unclear, and underlying biological characteristics render standard population genetic approaches based upon the Wright-Fisher model largely inappropriate. In addition, the compact genome combined with an absence of recombination is expected to result in strong purifying selection effects. Thus, it is imperative to establish a biologically relevant evolutionary framework incorporating these factors in order to enable an accurate study of this important human pathogen. Further, such a model is critical for inferring fundamental evolutionary parameters related to patient treatment, including mutation rates and the severity of infection bottlenecks. We here implement such a model and infer the underlying evolutionary parameters governing within-patient evolutionary dynamics. Results demonstrate that the progeny skew associated with the clonal nature of TB severely reduces genetic diversity and that the neglect of this parameter in previous studies has led to significant mis-inference of mutation rates. As such, our results suggest an underlying de novo mutation rate that is considerably faster than previously inferred, and a progeny distribution differing significantly from Wright-Fisher assumptions. This inference represents a more appropriate evolutionary null model, against which the periodic effects of positive selection, associated with drug-resistance for example, may be better assessed.
Keywords: Mutation rate, population bottleneck, population genetics, progeny-skew, tuberculosis, Wright-Fisher model
Tuberculosis (TB) is a public health threat worldwide (WHO 2018). Despite clear motivation for study, the observed within- and between-host evolutionary dynamics of Mycobacterium tuberculosis (M.TB) are not well understood, and results to date represent something of a paradox. On the one hand, drug resistance evolves rapidly (Fonseca et al. 2015; Eldholm et al. 2015); on the other, the genomic characteristics of M.TB do not appear conducive for such rapid adaptation, with inferred mutation rates being among the slowest of any human pathogen (Rocha et al. 2006; Ford et al. 2011; Ford et al. 2013; Colangeli et al. 2014; Payne et al. 2019; Menardo et al. 2019) and remarkably little genetic variation observed within or between hosts. Furthermore, purifying selection has been argued to play both a dominant as well as a weak role in shaping patterns of variation (Hershberg et al. 2008; Pepperell et al. 2013), and demographic estimates suggest a population history of TB that either matches or is uncorrelated with that of its human host (Comas et al. 2013; Bos et al. 2014; Brites and Gagneux 2015; Eldholm et al. 2016).
To obtain a more robust understanding of TB evolutionary dynamics, it is essential to first appreciate that between-population observations are simply an aggregation of within-population processes. As such, studying the population genetics of within-patient data is critical to understanding the genetic differences observed between patients as well as their treatment outcomes. Fortunately, recent advances in sequencing technologies have allowed for more abundant and higher quality within-patient data. These published datasets have revealed a few common features of M.TB, including low-levels of genome-wide variation. For instance, Trauner et al. (2017) deep-sequenced 12 patients across four-time points and observed fewer than 50 polymorphic sites per patient genome-wide. In addition, the observed site frequency spectrum (SFS) is generally characterized by an abundance of rare variants (i.e., it is strongly left-skewed). These patterns have partly led to the suggestion that purifying selection effects may be wide-spread in the M.TB genome (Brown et al. 2016; Phelan et al. 2016; Mortimer et al. 2018).
Additional evolutionary factors likely contribute to these genomic patterns as well. For example, population bottlenecks may reduce genetic variation and alter the shape of the SFS (see review Thornton et al. 2007). Previous M.TB studies have investigated these effects separately in both the deep-time view of the population bottleneck and subsequent growth experienced by the host human population (Hershberg et al. 2008; Liu et al. 2018), as well as the shallow-time view of the population bottleneck and subsequent growth characterizing each novel transmission event and treatment (e.g., Trauner et al. 2017). Additionally, in fitting the left-skewed SFS, Pepperell et al. (2013) found that such a demographic history combined with a mix of both deleterious and neutrally evolving sites produced the nearest fit to the observed SFS. Finally, given the lack of recombination in M.TB, related linkage effects (i.e., background selection; Charlesworth et al. 1993)) have similarly been discussed within these contexts (Pepperell et al. 2010; Copin et al. 2016).
While these studies have provided many important insights, there remains a relatively unexplored, although potentially highly significant, effect: clonality. Indeed, clonality and the related progeny distribution represents an important violation of commonly used evolutionary inference approaches based upon the Wright–Fisher (WF) model and the related Kingman coalescent (Eldon and Wakeley 2006; Dos Vultos et al. 2008; Huillet and Möhle 2011; Lapierre et al. 2016). Specifically, progeny distributions under the WF model are Poisson distributed with a small mean and variance. Therefore, when an individual produces many offspring, far in excess of simple replacement in the next generation, the assumption that only two lineages coalesce at a time is violated, resulting in multiple-merger coalescent (MMC) events (see reviews of Tellier and Lemaire 2014; Irwin et al. 2016).
While perhaps abstract at first blush, this violation has very important implications for the study of sequence variation and diversity. Namely, as M.TB has been found to exhibit strong progeny skew owing to obligate clonal reproduction (Baker et al. 2004; Dos Vultos et al. 2008), the null model against which the above studies are comparing becomes incorrect. For example, under a multiple-merger model, the effective population size (Ne) no longer scales linearly with census size (N) as it does under the Kingman coalescent (Huillet and Möhle 2011). As a result, genetic diversity is a nonlinear function of the underlying population size—a result of interest given the strongly constrained and similar levels of variation observed across TB patients, regardless of infection time or resistance status. Similarly, under these progeny-skew models, the SFS is skewed toward an excess of low-frequency variants, generating a negative Tajima’s D even under equilibrium neutrality (Eldon and Wakeley 2006; Birkner et al. 2013; Blath et al. 2016)—which appears of relevance to M.TB populations given the pervasively left-skewed SFS observed both within and between TB patients. Finally, the fixation probability of beneficial mutations under progeny skew may become much larger than under the WF model, owing to the increased probability of rapidly escaping stochastic loss (Der et al. 2011). This is fundamental to understanding the rapidly and independently evolving drug-resistance mutations in global TB populations—a result seemingly at odds with the previously inferred mutation rates (Sherman and Gagneux 2011; Colangeli et al. 2014; Duchêne et al. 2016). In sum, the general theoretical expectations owing to progeny skew alone appear to qualitatively match empirical observations from M.TB; observations that, to date, have been attributed to alternate processes.
Recent progress has been made in utilizing these models to disentangle and even co-estimate patterns of demography, progeny skew, and selection. While there exist a variety of potential MMC models (see review of Tellier and Lemaire 2014), the so-called Ψ-coalescent has been a major focus of this literature given the straight-forward biological interpretation. Namely, the parameter Ψ represents the proportion of the next generation arising from a single parent (e.g., Ψ = 0.05 implies that one individual contributes offspring that comprise 5% of the next generation). In addition to which, recent experimental measures are beginning to offer real-time insights into such progeny distributions (Vahey and Fletcher 2019). Three results are of particular importance here. First, Eldon et al. (2015) demonstrated that population growth may be distinguished from multiple-merger coalescent events owing to progeny-skew, given differing expectations in the SFS. Second, Matuszewski et al. (2018) derived analytical expectations for the SFS under a multiple merger coalescent model with changing population size and further demonstrated that these parameters can indeed be accurately inferred jointly within a likelihood framework. Finally, building upon the two above results as well as the approximate Bayesian statistical framework developed by Foll et al. (2014, 2015), Sackman et al. (2019) recently extended these results and demonstrated an ability to co-estimate progeny skew, effective population size, as well as persite selection coefficients from time-sampled polymorphism data.
Thus, a tremendous opportunity now exists to understand better the impact of mutation, genetic drift, and selection in dictating patterns of M.TB evolution and genomic variation under this more realistic coalescent model accounting for the underlying progeny distributions inherent to clonal reproduction. While the approximate Bayesian approach of Sackman et al. (2019) would appear ideal for this purpose, it is a time-sampled estimator reliant upon considerable levels of segregating variation in order to track changing allele frequencies (as is commonly observed in viral populations, for example). Thus, this approach is under-powered given the minimal levels of variation observed in M.TB. Further, as the underlying mutation rate itself is a question of great interest and importance in M.TB (Payne et al. 2019), it is desirable to additionally co-estimate this parameter rather than assume it to be known.
With this motivation, we developed a novel statistical approach utilizing the insights described above pertaining to infection dynamics and widespread purifying selection, while overlaying inference of underlying mutation rates and progeny distributions. Using this appropriate null model that accounts for these commonly occurring processes, we further assessed the ability to distinguish periodic processes, such as the infection-related bottleneck or selective sweeps associated with drug resistance. Owing to the major contributions of purifying selection and progeny skew in dictating patterns of diversity, and the resulting paucity of genomic variation, results suggest that these additional processes may be difficult to accurately quantify.
Materials and Methods
SIMULATIONS
We conducted forward-in-time simulations using the SLIM version 3 software package (Haller and Messer 2019). M.TB populations were modeled using a genome size of 441,153 kb, equivalent to a 10th portion of the true genome size, for computational efficiency. As M.TB is a compact, highly coding genome (Cole et al. 1998; Fleischmann et al. 2002), we assumed a distribution of fitness effects (DFE) characterized equally by deleterious (s = −0.01) and nearly neutral (s = −0.001) mutations. While a bi-modal DFE shape has been recurrently supported in directed mutagenesis studies in a variety of organisms (e.g., Bank et al. 2014), the relative density of the different DFE classes is unknown. Thus, we also assessed the impact of alternative DFE densities on the resulting inference—comparing a 60%/40% and 40%/60% split of deleterious and effectively neutral variants with the 50%/50% described above. More generally however, this consideration of both effectively neutral and deleterious mutations is essential, particularly given that the genome-wide effects of background selection are expected to be substantial given the lack of recombination in M.TB.
Mutation rate (μ) measured in vitro has been reported to be as slow as 2 × 10−10 (Ford et al. 2011). In contrast, higher estimates ranging from 1 × 10−9 to 9 × 10−6 (Ford et al. 2013) have been proposed; therefore, our study considered the full extent of this range. Furthermore, it is important to note that previous experiments have measured only the neutral mutation rate, not the total mutation rate. In other words, the large input of deleterious mutations—comprising a substantial component of the total mutation rate—has not been included in earlier estimates as these mutations are unlikely to be sampled as segregating variation or as fixed differences. However, as these mutations are important for shaping diversity via both purifying selection and background selection effects, and as our interest is in understanding the total rate at which all de novo mutations are input into the population, we considered the total rather than the neutral mutation rate. In order to infer this parameter within the context of an appropriate progeny-skew model, μ was drawn from a prior uniform distribution between 1 × 10−9 and 9 × 10−6 per site per generation.
Following an initial burn-in period of 10N generations, we considered a three-stage demographic model characterizing a single patient infection: moving forward in time, we describe (1) a neutral equilibrium population of size N, (2) an initial infection bottleneck leading to an instantaneous population reduction to size N2, and (3) a subsequent population size recovery to size N. In stage 1, we modeled a population of size N = 1000. In order to quantify the effects of underlying assumptions pertaining to population size, additional simulations and inference were performed at N = 25,000. During stage 2, the severity of the population bottleneck (β) was sampled from ~U[0.001, 0.1], where N2 = N*β–as the distribution of infection size in humans is unknown. However, it has been reported that in cattle TB (M. bovis) infection can be established by a single cell forming unit (Dean et al. 2005). During stage 2, the degree of progeny skew (or Ψ) was sampled from a prior distribution of ~U[0, 0.2]. A value of 0 corresponds to the standard WF model, whereas above 0.2 no sequence variation remains. Progeny skew was simulated following the procedure of Sackman et al. 2019. In brief, one individual is chosen from the primary population A and founds a separate subpopulation B, the single generation unidirectional migration rate from B to A is set to Ψ, and the chosen individual thus contributes NΨ offspring to the following generation of A. A series of mate choice callbacks in SLiM force the migration rate to be exact rather than stochastic (see supplementary materials of Sackman et al. 2019). Subpopulation B is removed, the next generation begins, and a new individual is randomly sampled for the following generation. As such, each generation is a combination of N(1 − Ψ) replacement events and a single sweepstakes event of magnitude NΨ. To emulate patient sampling at the onset of symptoms (approximately 3 months minimum; Behr et al. 2018), we allowed stage 2 to run for 90 generations, assuming a generation time of 24 h (Cole et al. 1998), and stage 3 to run for 910 generations before outputting genome alignments in ms format. Thus, the total generation time of our model was 11N.
Drawing from these prior distributions, 10,000 points (i.e., parameter combinations) were sampled. For each parameter combination, we conducted 1000 replicates in order to characterize both the mean and variance. Summary statistics were calculated in the R package PopGenome version 2.6.1 (Pfeifer et al. 2014).
DATA ANALYSIS AND JOINT POSTERIOR ESTIMATES
For comparison to patient data, we examined the distribution and mean of segregating sites in samples published by Trauner et al. (2017; see their ‘Additional file 2’; https://zenodo.org/record/322377#.XO2CAy2ZNBw). These samples were sequenced with an average depth of approximately 1247× and full genomic coverage. We primarily utilized these data to identify an upper- and lower-bound of observed within-patient variation, and to observe the frequency spectrum associated with these examples. Thus, we focused upon the first time-point (i.e., pretreatment) of patient 10, in whom was found the most segregating genome-wide variation (50 segregating sites). This patient sample had an average depth of ~1420×. For comparison, we also highlight the average number of observed polymorphic sites, corresponding to 20 segregating sites. Furthermore, given these low levels of variation, invariant genomes were also observed. In such cases there are naturally no SFS-based summary statistics, and so we utilized the expected fraction of invariant genomes to compare simulated and observed data (e.g., with very slow mutation rates and/or very high Ψ values, the expected fraction of invariant genomes far exceeds that observed in the empirical data). Further, given that patient data are subject to stringent filtering criteria (i.e., removing SNPs under a 2% frequency cutoff), it was necessary to filter the simulated data to allow a fair comparison. For the simulated replicates, variants with <2% frequency were filtered out before the calculation of summary statistics (Table S1)—although unfiltered values can also be found in the Supporting Information. Relevant scripts have been deposited on GitHub (https://github.com/AYMoralesArce/Within-host_Popgen_TB_project.git) and Dryad (https://doi.org/10.5061/dryad.1ns1rn8qq).
Results and Discussion
CONSIDERING LEVELS OF VARIATION
We report the first joint consideration of mutation rate, purifying selection, infection history, and progeny-skew in M.TB populations. A correlation of summary statistics (Fig. 1) demonstrates that while mutation rate (μ) increases the number of segregating sites as expected, progeny skew (Ψ) acts to reduce variation. Furthermore, as the Ψ-parameter is of relevance every generation (i.e., every reproduction event), the impact of this previously unconsidered progeny skew on levels of variation is in fact much stronger than the single bottleneck event associated with infection. Considering the full distribution of sampled μ values (Fig. S1), it is apparent that Ψ drastically reduces the average proportion of segregating sites genome-wide even for fast mutation rates, and that the probability of producing genomes devoid of any variation will naturally increase as μ decreases.
Figure 1.
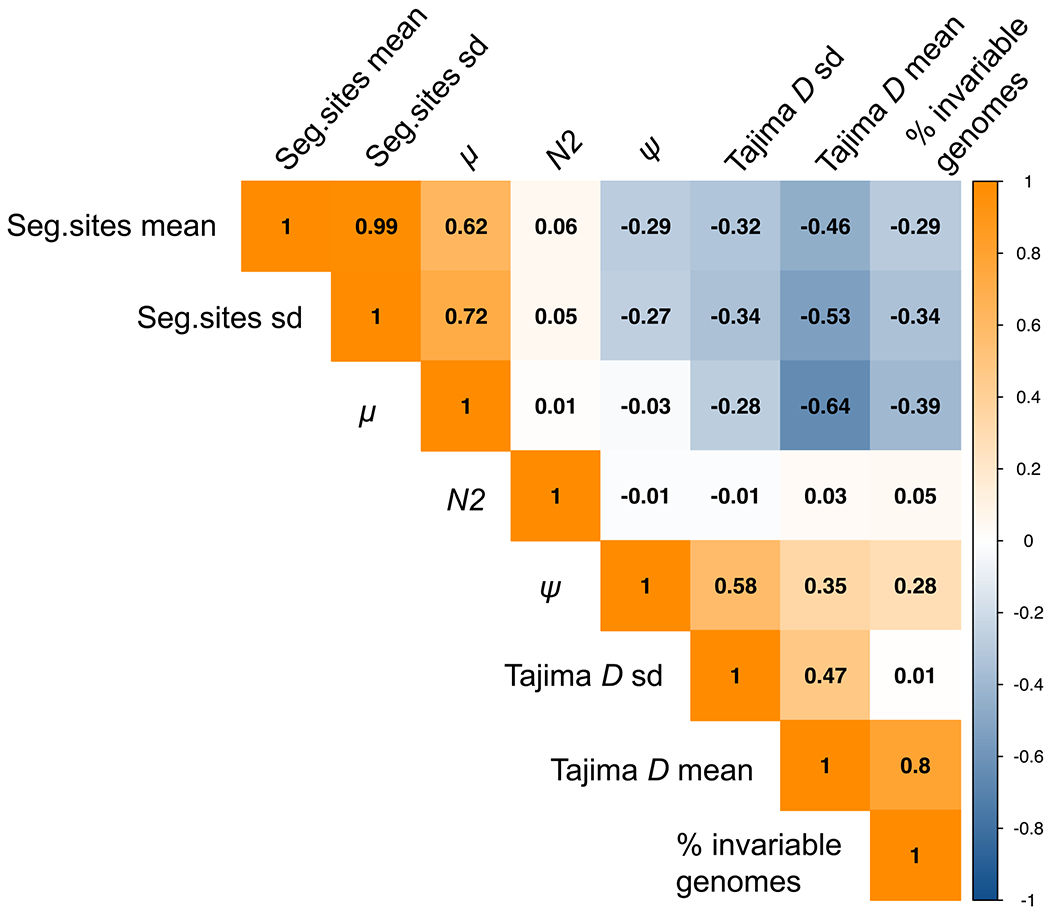
Correlation heatmap of parameters and summary statistics. Correlations are given between the parameters of interest (mutation rate (μ), progeny skew (Ψ), and bottleneck severity (N2)), and summary statistics (the mean and variance of the level of variation as measured by the number of segregating sites, and the mean and variance of the distribution of variation as measured by Tajima’s D). As shown, N2 values do not correlate with any of the summary statistics, as the effect of the single generation bottleneck is swamped by the per-generation reproductive skew. Further, as expected, μ positively correlates with the number of segregating sites, while Ψ acts to reduce variation and is thus negatively correlated. Finally, while μ would not be expected to strongly correlate with the shape of the SFS (here summarized by Tajima’s D) for neutral mutations, it does so here given that we explicitly account for the input of deleterious mutations (see Materials and Methods).
In order to consider a range of μ consistent with observed data—once pervasive purifying selection and progeny skew have been taken into account—two examples of patient data collected by Trauner et al. (2017) representing mean (20 segregating sites genome-wide) and high (50 segregating sites genome-wide) variation samples were plotted and compared to the simulated data. In order to compare simulated data with patient data, the same filtering steps must be applied. In this case, SNPs under 2% frequency were filtered in the empirical data, and thus, the simulated data were similarly filtered in order to be comparable (Fig. 2).
Figure 2.
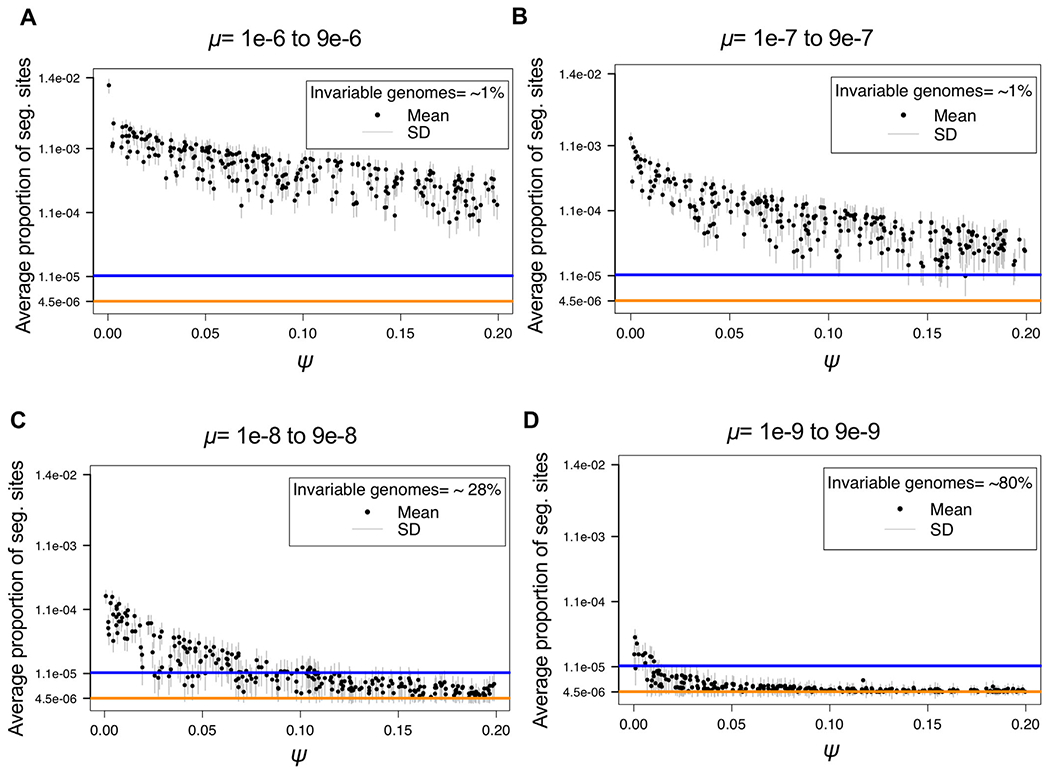
Log scale distribution of segregating sites above 2% frequency, as a function of mutation rate (μ) and progeny skew (Ψ). For each parameter combination (1,000 in total) of μ and Ψ drawn from the prior distributions, 1,000 replicates were simulated, with the mean given by the black dot and the standard deviation given by the gray bars. Each panel corresponds to a different order of magnitude of mutation rate range: (A) 1 × 10−6 to 9 × 10−6, (B) 1 × 10−7 to 9 × 10−7, (C) 1 × 10−8 to 9 × 10−8, and (D) 1 × 10−9 to 9 × 10−9. The colored lines correspond to two examples of the proportion of segregating sites observed genome-wide in empirical patient data: 20 segregating sites as a mean (orange), and 50 segregating sites from patient_10 (blue) (Trauner et al. 2017). As shown, the range of segregating sites for the fast mutation rates (panels A and B), result in expectations much larger than that observed in patient data, regardless of Ψ. Conversely, the slowest mutation rate (panel D), results in too little variation, except under WF conditions (i.e., Ψ near 0) that are known to be violated in this organism. Thus, rates on the order of 1 × 10−8 to 9 × 10−8 (panel C) appear to well explain the range of variation observed in patient data, and further imply values of Ψ ranging roughly from 0.05 to 0.1, consistent with values previously estimated for within-host virus data (Sackman et al. 2019).
As shown, fast mutation rates (μ on the order of 1 × 10−6 and 1 × 10−7) routinely produce expected numbers of segregating sites far above that observed in patients, regardless of other parameter values, while slow mutation rates (μ on the order of 1 × 10−9) generally result in too little variation to match observation—particularly considering the resulting expected fraction of invariant genomes. This result is of interest as M.TB mutation rates are generally believed to be exceedingly slow (Sherman and Gagneux 2011)—although importantly, this inference has largely neglected the important contribution of these additional evolutionary processes. Thus, once accounting for the diversity-reducing effects inherent to clonality, as well as the extent of purifying selection effects inherent to a compact, non-recombining genome, it is evident that the de novo mutation rate is likely faster than previously believed, with mutation rates on the order 1 × 10−8 well matching the range of observed data (Fig. 2). In addition, in order to consider the impact of underlying assumptions pertaining to population size, simulations were re-performed with a 25× larger population size. As shown in Fig. S2, owing to these diversity reducing effects, mutations rates on the order of 1 × 10−8 remain the best fit to observed levels of variation, with slower mutation rates still producing too little variation and too many invariable genomes to be consistent with patient data.
CONSIDERING DISTRIBUTIONS OF VARIATION
For the general range of μ identified above, the number of genome-wide segregating sites in simulated population data ranged from a minimum average of 2.1 to a maximum average of 78.7 SNPs (Table S1), depending on the combination of μ and Ψ drawn from the priors. Specifically, higher values of μ may be off-set by higher values of Ψ, resulting in a similar number of segregating sites for multiple parameter combinations. For example, for the mean observed patient diversity of 10 SNPs, simulation results demonstrate that μ = 8.13 × 10−08 and a Ψ = 0.06 would produce an average of 10.15 ± 4.64 SNPs, potentially suggesting a good fit to the data. However, μ = 3.1 × 10−08 and a Ψ = 0.02 can also generate similar results, yielding 10.40 ± 4.45 SNPs. More generally, this ridge in the posterior distributions (Fig. 3A) between these two parameters suggests that they will be difficult to estimate independently if only levels of variation are used.
Figure 3.
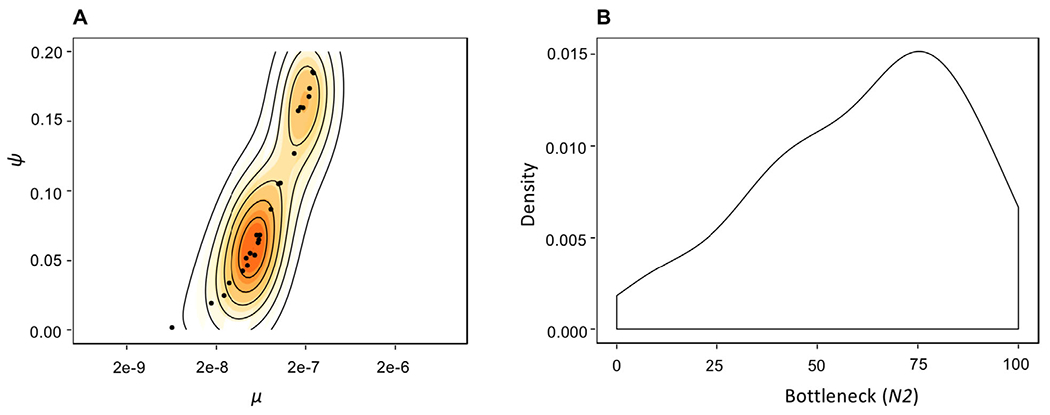
Posterior parameter estimates pertaining to patient data. (A) Joint posterior distribution for the parameters μ and Ψ. Solid contour lines specify the highest posterior density intervals. Owing to the diversity-increasing effect of μ and diversity-decreasing effect of Ψ, there exists a ridge in the joint posterior. Regardless, owing to differing expectations in the SFS along this ridge, inference suggests μ values within the 1 × 10−8 range in combination with Ψ < 0.10. (B) Posterior density for the severity of the infection bottleneck (N2). The X-axis gives the number of genomes at the time of infection reduced from 1000. While the posterior distribution is non-uniform, the observation that all tested values remain consistent with patient data strongly suggests that there is not sufficient information in the data to estimate this third parameter (i.e., size of the bottleneck, in addition to μ and Ψ).
Thus, while comparisons with general levels of variation are useful for identifying a range as in the above section, more information is needed to parse values further. Importantly, previous theoretical results (Eldon and Wakeley 2016; Matuszewski et al. 2018) have well described the effect of Ψ on the observed distribution of genetic variation (i.e., SFS). To utilize this information, a general summary of the SFS, Tajima’s D (1989), was calculated on the filtered simulated data. As shown (Fig. S3), the shape of the SFS, and thus the value of the D-statistic, is related to the value of Ψ. As the degree of progeny skew initially increases, D becomes increasingly negative, as previously described. However, as progeny distributions become highly skewed, levels of variation are sharply reduced, resulting in an apparent increase in D values (Fig. S3). Increasing D values could also be a result of the underlying filtering criteria, as after filtering simulations to match real data with segregating sites >2%, D values increased proportionally (Fig. S4). However, Tajima’s D is consistently negative in all mutation ranges, even after filtering.
PARAMETER INFERENCE FROM PATIENT SAMPLES
Thus, we next considered these results in light of published patient data. Recent publications have suggested that NGS technologies could facilitate personalized treatment in TB patients, allowing for improved outcomes (Copin et al. 2016; Cancino-Muñoz et al. 2019). To utilize such data, however, it is vital to understand the evolutionary dynamics shaping within-host M.TB diversity. As an illustrative example, we have re-examined the number of segregating sites in patient samples and estimated a mean ~10 segregating sites per sample (Trauner et al. 2017; Fig. S5). Using the results and expectations obtained above regarding the level and distribution of variation, the patient data appear best fit by simulated populations with μ values ranging from 7.3 × 10−9 to 3.8 × 10−7, with the strongest posterior density at μ ≈ 6e-8 and Ψ ≈ 0.06 (Fig. 3A). Furthermore, this inference appears robust to variation in the density of the DFE classes, an important consideration given that the precise nature of this underlying distribution is unknown (Fig. S6). Notably, even faster μ values could produce similar results, but only if Ψ proportions are in excess of 0.15 (Fig. 3A).
In addition, owing to the strong per-generation reductions associated with progeny skew, there remains no signal in the data to estimate the severity of the infection bottleneck accurately (Fig. 3B). Specifically, while there is an increase in density toward stronger bottleneck values, the posterior distribution is not notably distinct from the prior distribution ~U[0.001, 0.1] (Fig. 3B). Apart from the population size reduction associated with infection, these results have important implications for the ability to detect other parameters of clinical interest—namely, the presence of selective sweeps associated with beneficial mutations (e.g., potentially owing to drug-resistance). First, while there is strong statistical power to infer both μ and Ψ from patient data, there is little power to detect isolated events in the past (Fig. 3B). This result, although unexpected under standard WF assumptions, is intuitive given the non-WF progeny distributions related to clonality. Namely, the diversity reduction associated with a single bottleneck event multiple-generations in the past is not discernible from the per-generation diversity reduction related to clonal reproduction. Further, given that a selective sweep is, in fact, a type of population bottleneck (Barton 1998), this result also demonstrates that detecting selective sweeps associated with resistance mutations in this non-recombining organism, based on levels and patterns of genomic variation, will be exceedingly difficult. However, this observation reconciles the fact that levels of variation do not appear significantly different between resistant and non-resistant M.TB patient populations (Trauner et al. 2017)—that is, these additional evolutionary processes are shaping variation so strongly that the presence or absence of a resistance-associated selective sweep does not result in strongly differentiable expectations.
Finally, this difficulty raises the question of utilizing divergence-based inference determined from between-patient samples. While this is a topic of interest for future investigation, a number of major challenges exist for incorporating such data into this statistical framework. With regards to the model itself, the behavior of divergence-based statistics, such as Fst, can differ quite substantially from WF expectations. For example, the expectation of coalescent times within a subpopulation may become less than that between subpopulations, regardless of the timing or strength of gene flow (Eldon and Wakeley 2009). With regards to the empirical data, an inability to rely on molecular clock-based arguments in M.TB (Menardo et al. 2019), combined with commonly absent information related to re-infection status, renders a definition of the timescale of separation highly tenuous.
IMPLICATIONS FOR CHARACTERIZING THE HISTORY OF TB IN HUMANS
A topic of wide-spread interest in the literature pertains to the history of TB in the human host. This inference has primarily been made within a phylogenetic context, relying on the construction of a single consensus sequence per patient. While such a comparison of consensus sequences can be highly misleading when making evolutionary inference (see Renzette et al. 2017), these age estimates also inherently rely on an accurate knowledge of mutation rates in order to invoke the “clock-like” accumulation of neutral mutations as a proxy for time, as noted above (Menardo et al. 2019). As our results demonstrate that previous mutation rate estimates have likely been downwardly biased, it is of interest to consider what these revised mutation rates would imply for this evolutionary history. However, there are at least three difficulties in directly comparing population-level estimates with previous consensus-based phylogenetic inference. First, estimates are generally given per year, whereas the preferred evolutionary rate is per generation (as given here). There is support for one generation per day as a conversion (Cole et al. 1998), although further study is necessary to quantify the correct scaling factor. Second, when invoking a divergence-based clock, previous studies are measuring the neutral mutation rate, given that the rate of mutation is equivalent to the rate of divergence for neutral mutations only (Kimura 1968). However, we are here interested in the total mutation rate (that is, the rate at which neutral and non-neutral mutations arise per generation); therefore, our rate must be parsed into neutral and nonneutral components to enable appropriate comparison. Similar to the first point, additional research is necessary in order to better quantify the distribution of fitness effects in M.TB, as understanding the fraction of total mutations represented by neutral mutations is necessary for the conversion. Finally, we here consider the alleles segregating within a population for inference (i.e., within a patient), whereas previous studies often call a consensus sequence per patient (i.e., per population) and make inferences based on a collection of such consensus sequences. Such a summary of population-level variation into a single sequence is difficult to interpret, although what is evident is that a great majority of rare alleles will be neglected, and thus only a small subset of total variation (i.e., common alleles) will be considered (Renzette et al. 2017). As such, we propose that future evolutionary inference pertaining to TB would benefit tremendously from a full consideration of within-patient diversity, as we demonstrate here. In sum, any direct comparison with consensus-based phylogenetic age estimates would be overly speculative at this juncture.
Conclusions
TB patient infection dynamics have remained enigmatic. We here argue that much of the difficulty in interpreting patterns of variation and evolution has owed to an inappropriate underlying null model, relying on classical expectations developed for organisms with very different underlying biological properties. Fortunately, recent theoretical extensions in non-WF and alternative coalescent models, more appropriate for clonally reproducing organisms, have created an opportunity to revisit existing M.TB patient data. By accounting for the pervasive purifying selection effects associated with this non-recombining, highly coding genome, as well as the skewed progeny distributions inherent to clonal reproduction, we have provided improved insights into the evolutionary dynamics shaping within-host variation. Further, through a consideration of these diversity-reducing effects, results suggest an underlying de novo mutation rate that is considerably faster than previously inferred. This may reconcile the seemingly contradictory observations of both rapid resistance evolution, but extremely low levels of population variation. Namely, the population mutation rate may indeed be sufficiently fast to provide a steady input of beneficial mutations, explaining the rapid resistance evolution clinically observed. However, recurrent purifying selection and progeny skew act together to rapidly eliminate segregating variation from the population, reconciling the minimal levels of variation observed as well as the general homogeneity in levels and distributions of variation in both resistant and non-resistant patient samples alike. Furthermore, the role of these per-generation evolutionary forces in shaping patterns of variation is sufficiently strong that periodic events, including the infection-associated bottleneck and selective sweeps centered on drug-resistance mutations, will be challenging to detect and quantify on top of these more common processes. In general, this framework represents an approach for constructing appropriate evolutionary null models for the wide-array of organisms that are not well fit by WF progeny distribution assumptions—including a large variety of plants, viruses, and marine organisms.
Supplementary Material
Figure S1. Log scale distribution of segregating sites in unfiltered simulated populations as a function of mutation rate (μ) and progeny skew (Ψ).
Figure S2. Log scale distribution of segregating sites in filtered simulated populations of N = 25,000 as a function of mutation rate (μ) and progeny skew (Ψ).
Figure S3. The shape of the site frequency spectrum in unfiltered simulated populations, as summarized by Tajima’s D, as a function of mutation rate (μ) and progeny skew (Ψ).
Figure S4. The shape of the site frequency spectrum (SFS), as summarized by Tajima’s D, in simulated populations after filtering out segregating sites under 2% frequency, as a function of mutation rate (μ) and progeny skew (Ψ).
Figure S5. The distribution of segregating sites in real versus simulated datasets.
Figure S6. Log scale distribution of segregating sites in filtered simulated populations of mutation rates ranging from 1e-8 to 9e-8, for two differing proportions of DFE density.
Table S1. Simulation results.
ACKNOWLEDGMENTS
We thank Andrew Sackman for assistance with SLiM, as well as Susanne Pfeifer and members of the Jensen Lab for helpful feedback. We also thank Andrej Trauner for assistance with the patient data.
FUNDING INFORMATION
Arizona State University, Center for Evolution and Medicine
U.S. Department of Health and Human Services >
National Institutes of Health >
National Institute of General Medical Sciences
1R01GM135899
Footnotes
DATA ARCHIVING
All scripts used for simulation and analysis have been deposited on Dryad (https://doi.org/10.5061/dryad.1ns1rn8qq) and GitHub (https://github.com/AYMoralesArce/Within-host_Popgen_TB_project.git).
Supporting Information
Additional supporting information may be found online in the Supporting Information section at the end of the article.
LITERATURE CITED
- Baker L, Brown T, Maiden MC, and Drobniewski F. 2004. Silent nucleotide polymorphisms and a phylogeny for Mycobacterium tuberculosis. Emerg. Infect. Dis 10:1568–1577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bank C, Hietpas RT, Wong A, Bolon DNA, and Jensen JD. 2014. A Bayesian MCMC approach to assess the complete distribution of fitness effects of new mutations: uncovering the potential for adaptive walks in challenging environments. Genetics 196:841–852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton NH 1998. The effect of hitch-hiking on neutral genealogies. Genet. Res. Camb 72:123–133. [Google Scholar]
- Behr MA, Edelstein PH, and Ramakrishnan L. 2018. Revisiting the timetable of tuberculosis. BMJ 362:k2738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birkner M, Blath J, and Eldon B. 2013. Statistical properties of the site-frequency spectrum associated with ∧-coalescents. Genetics 195:1037–1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blath J, Cronjäger Christensen M, Eldon B, and Hammer M. 2016. The site-frequency spectrum associated with Ξ-coalescents. Theor. Popul. Biol 110:36–50. [DOI] [PubMed] [Google Scholar]
- Bos KI, Harkins KM, Herbig A, Coscolla M, Weber N, Comas I, Forrest SA, Bryant JM, Harris SR, Schuenemann VJ, et al. 2014. Pre-Columbian mycobacterial genomes reveal seals as a source of New World human tuberculosis. Nature 514:494–497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brites D, and Gagneux S. 2015. Co-evolution of Mycobacterium tuberculosis and Homo sapiens. Immunol. Rev 264:6–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown TS, Narechania A, Walker JR, Planet PJ, Bifani PJ, Kolokotronis S-O, Kreiswirth BN, and Mathema B. 2016. Genomic epidemiology of Lineage 4 Mycobacterium tuberculosis subpopulations in New York city and New Jersey, 1999–2009. BMC Genomics 17:947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cancino-Muñoz I, Moreno-Molina M, Furió V, Goig GA, Torres-Puente M, Chiner-Oms Á, Villamayor LM, Sanz F, Guna-Serrano MR, and Comas I. 2019. Cryptic resistance mutations associated with misdiagnoses of multidrug-resistant tuberculosis. J. Infect. Dis 220:316–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B, Morgan MT, and Charlesworth D. 1993. The effect of deleterious mutations on neutral molecular variation. Genetics 134:1289–1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colangeli R, Arcus VL, Cursons RT, Ruthe A, Karalus N, Coley K, Manning SD, Kim S, Marchiano E, and Alland D. 2014. Whole genome sequencing of Mycobacterium tuberculosis reveals slow growth and low mutation rates during latent infections in humans. PLoS One 9:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole ST, Brosch R, Parkhill J, Garnier T, Churcher C, Harris D, Gordon SV, Eiglmeier K, Gas S, Barry CE, et al. 1998. Deciphering the biology of Mycobacterium tuberculosis from the complete genome sequence. Nature 393:537–544. [DOI] [PubMed] [Google Scholar]
- Comas I, Coscolla M, Luo T, Borrell S, Holt KE, Kato-Maeda M, Parkhill J, Malla B, Berg S, Thwaites G, et al. 2013. Out-of-Africa migration and Neolithic coexpansion of Mycobacterium tuberculosis with modern humans. Nat. Genet 45:1176–1182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Copin R, Wang X, Louie E, Escuyer V, Coscolla M, Gagneux S, Palmer GH, and Ernst JD. 2016. Within host evolution selects for a dominant genotype of Mycobacterium tuberculosis while T cells increase pathogen genetic diversity. PLoS Pathog. 12:e1006111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dean GS, Rhodes SG, Coad M, Whelan AO, Cockle PJ, Clifford DJ, Hewinson RG, and Vordermeier HM. 2005. Minimum effective dose of Mycobacterium bovis in cattle. Infect Immunity 73:6467–6471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Der R, Epstein CL, and Plotkin JB. 2011. Generalized population models and the nature of genetic drift. Theor. Popul. Biol 80:80–99. [DOI] [PubMed] [Google Scholar]
- Dos Vultos T, Mestre O, Rauzier J, Golec M, Rastogi N, Rasolofo V, Tonjum T, Sola C, Matic I, and Gicquel B. 2008. Evolution and diversity of clonal bacteria: The paradigm of Mycobacterium tuberculosis. PLoS One 3:e1538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duchêne S, Holt KE, Weill FX, Le Hello S, Hawkey J, Edwards DJ, Fourment M, and Holmes EC. 2016. Genome-scale rates of evolutionary change in bacteria. Microb Genomics 2:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldon B, and Wakeley J. 2006. Coalescent processes when the distribution of offspring number among individuals is highly skewed. Genetics 172:2621–2633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- —.. 2009. Coalescent times and Fst under a skewed offspring distribution among individuals in a population. Genetics 181:615–629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldon B, Birkner M, Blath J, and Freund F. 2015. Can the site-frequency spectrum distinguish exponential population growth from multiple-merger coalescents? Genetics 199:841–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldholm V, Monteserin J, Rieux A, Lopez B, Sobkowiak B, Ritacco V, and Balloux F. 2015. Four decades of transmission of a multidrug-resistant Mycobacterium tuberculosis outbreak strain. Nat. Commun 6:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eldholm V, Pettersson JHO, Brynildsrud OB, Kitchen A, Rasmussen EM, Lillebaek T, RÃ̧nning JO, Crudu V, Mengshoel AT, Debech N, et al. 2016. Armed conflict and population displacement as drivers of the evolution and dispersal of Mycobacterium tuberculosis. Proc. Natl. Acad. Sci. U. S. A 113:13881–13886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleischmann RD, Alland D, Eisen JA, Carpenter L, White O, Peterson J, DeBoy R, Dodson R, Gwinn M, Haft D, et al. 2002. Whole-Genome comparison of Mycobacterium tuberculosis clinical and laboratory strains. J. Bacteriol 184:5479–5490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foll M, Poh YP, Renzette N, Ferrer-Admetlla A, Bank C, Shim H, Malaspinas A-S, Ewing G, Liu P, Wegmann D, et al. 2014. Influenza virus drug resistance: a time-sampled population genetics perspective. PLos Genet. 10:e1004185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foll M, Shim H, and Jensen JD. 2015. WFABC: A Wright-Fisher ABC-based approach for inferring effective population sizes and selection coefficients from time-sampled data. Mol. Ecol. Resour 15:87–98. [DOI] [PubMed] [Google Scholar]
- Fonseca JD, Knight GM, and McHugh TD. 2015. The complex evolution of antibiotic resistance in Mycobacterium tuberculosis. Int. J. Infect. Dis 32:94–100. [DOI] [PubMed] [Google Scholar]
- Ford CB, Lin PL, Chase M, Shah RR, Iartchouk O, Galagan J, Mohaideen N, Ioerger TR, Sacchettini JC, Lipsitch M, et al. 2011. Use of whole genome sequencing to estimate the mutation rate of Mycobacterium tuberculosis during latent infection. Nat. Genet 43:482–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ford CB, Shah RR, Kato-Maeda M, Gagneux S, Murray MB, Cohen T, Johnston JC, Gardy J, Lipsitch M, and Fortune SM. 2013. Mycobacterium tuberculosis mutation rate estimates from different lineages predict substantial differences in the emergence of drug-resistant tuberculosis. Nat. Genet 45:784–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haller BC, and Messer PW. 2019. SLiM 3: Forward genetic simulations beyond the Wright–Fisher model. Mol. Biol. Evol 36:632–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hershberg R, Lipatov M, Small PM, Sheffer H, Niemann S, Homolka S, Roach JC, Kremer K, Petrov DA, Feldman MW, et al. 2008. High functional diversity in Mycobacterium tuberculosis driven by genetic drift and human demography. PLoS Biol. 6:e311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huillet T, and Möhle M. 2011. Population genetics models with skewed fertilities: A forward and backward analysis. Stoch Model 27:521–554. [Google Scholar]
- Irwin KK, Laurent S, Matuszewski S, Vuilleumier S, Ormond L, Shim H, Bank C, and Jensen JD. 2016. On the importance of skewed offspring distributions and background selection in virus population genetics. Heredity 117:393–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M 1968. Evolutionary rate at the molecular level. Nature 217:624–626. [DOI] [PubMed] [Google Scholar]
- Lapierre M, Blin C, Lambert A, Achaz G, and Rocha EPC. 2016. The impact of selection, gene conversion, and biased sampling on the assessment of microbial demography. Mol. Biol. Evol 33:1711–1725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Q, Ma A, Wei L, Pang Y, Wu B, Luo T, Zhou Y, Zheng H-X, Jiang Q, Gan M, et al. 2018. China’s tuberculosis epidemic stems from historical expansion of four strains of Mycobacterium tuberculosis. Nat. Ecol. Evol 2:1982–1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matuszewski S, Hildebrandt ME, Achaz G, and Jensen JD. 2018. Coalescent processes with skewed offspring distributions and nonequilibrium demography. Genetics 208:323–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menardo F, Duchêne S, Brites D, and Gagneux S. 2019. The molecular clock of Mycobacterium tuberculosis. PLoS Pathog. 15:e1008067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mortimer TD, Weber AM, and Pepperell CS. 2018. Signatures of selection at drug resistance loci in Mycobacterium tuberculosis. mSystems 3:e00108–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne JL, Menardo F, Trauner A, Borrell S, Gygli SM, Loiseau C, Gagneux S, and Hall AR. 2019. Transition bias influences the evolution of antibiotic resistance in Mycobacterium tuberculosis. PLoS Biol. 17:e3000265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepperell CS, Hoeppner VH, Lipatov M, Wobeser W, Schoolnik GK, and Feldman MW. 2010. Bacterial genetic signatures of human social phenomena among M. tuberculosis from an aboriginal Canadian population. Mol. Biol. Evol 27:427–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepperell CS, Casto AM, Kitchen A, Granka JM, Cornejo OE, Holmes EC, Birren B, Galagan J, and Feldman MW. 2013. The role of selection in shaping diversity of natural M. tuberculosis populations. PLoS Pathog. 9:e1003543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeifer B, Wittelsbürger U, Ramos-Onsins SE, and Lercher MJ. 2014. PopGenome: An efficient swiss army knife for population genomic analyses in R. Mol. Biol. Evol 31:1929–1936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phelan J, Coll F, McNerney R, Ascher DB, Pires DEV, Furnham N, Coeck N, Hill-Cawthorne GA, Nair MB, Mallard K, et al. 2016. Mycobacterium tuberculosis whole genome sequencing and protein structure modelling provides insights into anti-tuberculosis drug resistance. BMC Med. 14:31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renzette N, Pfeifer SP, Matuszewski S, Kowalik TF, and Jensen JD. 2017. On the analysis of intrahost and interhost viral populations: human cytomegalovirus as a case study of pitfalls and expectations. J. Virol 91:e01976–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocha EPC, Maynard Smith J, Hurst LD, Holden MTG, Cooper JE, Smith NH, and Feil EJ. 2006. Comparisons of dN/dS are time dependent for closely related bacterial genomes. J. Theor. Biol 239:226–235. [DOI] [PubMed] [Google Scholar]
- Sackman AM, Harris RB, and Jensen JD. 2019. Inferring demography and selection in organisms characterized by skewed offspring distributions. Genetics 211:1019–1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherman DR, and Gagneux S. 2011. Estimating the mutation rate of Mycobacterium tuberculosis during infection. Nat. Genet 43:400–401. [DOI] [PubMed] [Google Scholar]
- Tajima F 1989. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123:585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tellier A, and Lemaire C. 2014. Coalescence 2.0: A multiple branching of recent theoretical developments and their applications. Mol. Ecol 23:2637–2652. [DOI] [PubMed] [Google Scholar]
- Thornton KR, Jensen JD, Becquet C, and Andolfatto P. 2007. Progress and prospects in mapping recent selection in the genome. Heredity 98:340–348. [DOI] [PubMed] [Google Scholar]
- Trauner A, Liu Q, Via LE, Liu X, Ruan X, Liang L, Shi H, Chen Y, Wang Z, Liang R, et al. 2017. The within-host population dynamics of Mycobacterium tuberculosis vary with treatment efficacy. Genome Biol. 18:71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vahey MD, and Fletcher DA. 2019. Low fidelity assembly of influenza a virus promotes escape from host cells. Cell 176:281–294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization (WHO). 2018. Global tuberculosis report 2018. World Health Organization, Geneva. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Log scale distribution of segregating sites in unfiltered simulated populations as a function of mutation rate (μ) and progeny skew (Ψ).
Figure S2. Log scale distribution of segregating sites in filtered simulated populations of N = 25,000 as a function of mutation rate (μ) and progeny skew (Ψ).
Figure S3. The shape of the site frequency spectrum in unfiltered simulated populations, as summarized by Tajima’s D, as a function of mutation rate (μ) and progeny skew (Ψ).
Figure S4. The shape of the site frequency spectrum (SFS), as summarized by Tajima’s D, in simulated populations after filtering out segregating sites under 2% frequency, as a function of mutation rate (μ) and progeny skew (Ψ).
Figure S5. The distribution of segregating sites in real versus simulated datasets.
Figure S6. Log scale distribution of segregating sites in filtered simulated populations of mutation rates ranging from 1e-8 to 9e-8, for two differing proportions of DFE density.
Table S1. Simulation results.


