Abstract
Neural responses to visual stimuli exhibit complex temporal dynamics, including subadditive temporal summation, response reduction with repeated or sustained stimuli (adaptation), and slower dynamics at low contrast. These phenomena are often studied independently. Here, we demonstrate these phenomena within the same experiment and model the underlying neural computations with a single computational model. We extracted time-varying responses from electrocorticographic recordings from patients presented with stimuli that varied in duration, interstimulus interval (ISI) and contrast. Aggregating data across patients from both sexes yielded 98 electrodes with robust visual responses, covering both earlier (V1–V3) and higher-order (V3a/b, LO, TO, IPS) retinotopic maps. In all regions, the temporal dynamics of neural responses exhibit several nonlinear features. Peak response amplitude saturates with high contrast and longer stimulus durations, the response to a second stimulus is suppressed for short ISIs and recovers for longer ISIs, and response latency decreases with increasing contrast. These features are accurately captured by a computational model composed of a small set of canonical neuronal operations, that is, linear filtering, rectification, exponentiation, and a delayed divisive normalization. We find that an increased normalization term captures both contrast- and adaptation-related response reductions, suggesting potentially shared underlying mechanisms. We additionally demonstrate both changes and invariance in temporal response dynamics between earlier and higher-order visual areas. Together, our results reveal the presence of a wide range of temporal and contrast-dependent neuronal dynamics in the human visual cortex and demonstrate that a simple model captures these dynamics at millisecond resolution.
SIGNIFICANCE STATEMENT Sensory inputs and neural responses change continuously over time. It is especially challenging to understand a system that has both dynamic inputs and outputs. Here, we use a computational modeling approach that specifies computations to convert a time-varying input stimulus to a neural response time course, and we use this to predict neural activity measured in the human visual cortex. We show that this computational model predicts a wide variety of complex neural response shapes, which we induced experimentally by manipulating the duration, repetition, and contrast of visual stimuli. By comparing data and model predictions, we uncover systematic properties of temporal dynamics of neural signals, allowing us to better understand how the brain processes dynamic sensory information.
Keywords: adaptation, broadband, contrast, ECOG, temporal dynamics, vision
Introduction
The manner in which neural responses change over short time scales, from milliseconds to seconds, is important for understanding cognitive, perceptual, and motor functions. Neural dynamics are critical for decision-making (Gold and Shadlen, 2007; Wang, 2012), motor planning (Churchland et al., 2012), and perception (Heeger, 2017), and they are important for achieving improved performance in artificial neural network models (Kubilius et al., 2019; Spoerer et al., 2020). Even for simple static stimuli, neural responses in sensory cortex exhibit interesting and complex temporal dynamics. For example, neural responses in visual cortex start to decrease when a static visual stimulus is prolonged in time (subadditive temporal summation), reduce to stimuli that are repeated (adaptation), and rise less rapidly for low contrast stimuli (phase delay).
Studies of temporal dynamics in visual cortex typically measure neural responses with a tailored set of stimuli designed to investigate one particular kind of temporal dynamics. For example, one study might show visual stimuli that vary in duration to investigate how neural activity sums over time (Tolhurst et al., 1980), whereas another study might show repeated stimuli to investigate neural response reductions because of adaptation (Motter, 2006), and yet another study might vary the level of stimulus contrast to study how input strength affects the rise and fall of neural responses over time (Albrecht et al., 2002). These phenomena are also often studied with different measurement techniques and different computational models.
Even when the same computational model is used across different stimulus manipulations, model parameters may be fit separately to different experiments (Zhou et al., 2019), leaving open the question of whether a single model, with a single set of parameters, can simultaneously account for the multiple phenomena. Here, we investigated multiple temporal dynamics in a single dataset by measuring neural responses to visual stimuli that varied systematically in three different ways—duration, repetition, and contrast. We measured electrocorticographic (ECoG) recordings of human visual cortex, which track neural responses at the millisecond scale with high spatial and temporal precision. From each electrode and for each stimulus, we extracted the time-varying broadband power (50–200 Hz). Using different stimulus manipulations in the same electrodes allows us to investigate links between phenomena and ask whether they can be explained by the same computational mechanism. For example, we demonstrate that reducing stimulus contrast and repeating a stimulus result in surprisingly similar changes in temporal dynamics of neural population responses and link these changes to specific computational model components.
By mapping the electrodes to a probabilistic retinotopic atlas within each participant and then aggregating measurements over multiple participants, we collected a large, comprehensive sample of neural responses from multiple visual areas in human visual cortex, covering earlier (V1–V3a/b) and higher-order (LO, TO, IPS) retinotopic maps. Testing the same stimuli in the same participants across multiple visual areas clarifies the qualitative similarities across areas as well as the quantitative differences. For example, our approach allows us to address discrepant claims about temporal window length in the visual hierarchy as there is some evidence both in support of (Hasson et al., 2008; Weiner et al., 2010; Honey et al., 2012) and against (Fritsche et al., 2020) the claim that temporal window length increases along the visual hierarchy.
The article is structured as follows. We first examine the different temporal dynamics resulting from each stimulus manipulation (changes in duration, repetition, and contrast) and their corresponding nonlinear effects in area V1. We show that these modulations are well captured by a delayed normalization model fit simultaneously to all stimulus types, and we perform a systematic comparison with reduced versions of the model, demonstrating the contribution of each individual canonical computation to its ability to fit the data. Finally, we investigate to what extent these temporal dynamics vary both across and within visual areas.
Materials and Methods
Subjects
Data were measured from 11 participants (six females) who were undergoing subdural electrode implantation for clinical purposes. Eight participants (five females) were included in the dataset after data preprocessing (see below). Data from nine participants were collected at New York University (NYU) Grossman School of Medicine, and two participants were tested at the University Medical Center Utrecht (UMCU) in The Netherlands. Written informed consent to participate in this study was given by all the patients. The study was approved by the NYU Grossman School of Medicine Institutional Review Board and the ethical committee of the UMCU, in accordance with the Declaration of Helsinki (2013). All participants were implanted with standard clinical subdural grid and/or strip electrodes. Several NYU participants were additionally implanted with standard clinical depth electrodes. For most participants, electrode implantation and location were guided solely by clinical requirements. Two NYU participants consented to the additional placement of a small, high-density grid (PMT), which provided denser sampling of underlying cortex. Detailed information about each participant and their implantation is provided in Table 1 and alongside the dataset provided on OpenNeuro (see below, Data Availability).
Table 1.
Overview of patient data included in this dataset
| Subject | Age | Sex | Site | Trials | Hemi | Implantation | Coverage | Visual no. | Matching areas | No. included |
|---|---|---|---|---|---|---|---|---|---|---|
| P01 | 30 | F | UMCU | 12 | L | Strip, depth | Lat-occ, lat-par, vent-temp | 9 | TO1, LO1, PHC2 | 0 |
| P02 | 18 | F | UMCU | 6 | R | Grid, strip | Med-occ, lat-occ, lat-temp, vent-temp | 24 | V1v, V1d, V2v, V3v, V3a, V3d, IPS0 | 9 |
| P03 | 27 | M | NYU | 12 | L | Grid, strip, depth | Lat-par, ant-temp, post-vent, frontal | 24 | V2d, V3d, V3a, V3b, TO1, IPS0-3, SPL1 | 4 |
| P04 | 28 | M | NYU | 10 | R | Grid, strip, depth | Lat-occ, ant-temp, frontal | 6 | V3d, V3a, TO1 | 2 |
| P05 | 31 | F | NYU | 12 | R | 2× grid, strip, depth | Lat-occ, lat-par, frontal, ant-temp | 40 | V2v, V3v, V3d, V3b, LO1, LO2, TO1, IPS2-3, hV4, PHC1 | 3 |
| P06 | 19 | F | NYU | 12 | L | Grid, strip, depth | Med-occ, lat-occ, lat-par, ant-temp, frontal | 26 | V1d, V2v, V3d, V3b, hV4, TO1, IPS0, PHC2 | 2 |
| P07 | 41 | F | NYU | 24 | L | Grid, strip, depth | Lat-occ, lat-par, med-occ, ant-temp, frontal | 17 | V1v, V1d, V2d, V3d, V3a, IPS0-3, FEF | 7 |
| P08 | 47 | M | NYU | 12 | R | Grid, strip, depth | Lat-par, ant-temp | 4 | LO2, TO1 | 0 |
| P09 | 25 | M | NYU | 24 | L, R | Bilateral grid, strip, depth | Lat-occ, lat-par | 8 | TO1, PHC2 | 0 |
| P10 | 23 | M | NYU | 36 | R | Grid, HD grid, strip, depth | Lat-occ, lat-par, post-vent | 123 | V2d, V3d, V3a, V3b, LO1, LO2, TO1, IPS0-2 | 45 |
| P11 | 19 | F | NYU | 36 | L | Grid, HD grid, strip, depth | Lat-occ, lat-par, post-vent | 100 | V3b, LO1, LO2, TO1, IPS2 | 26 |
Columns refer to the following: Subject, subject code in dataset. P, Patient. Age, age of patient at time of recording in years. Sex, patient sex (M, male; F, female). Site, hospital where recording took place (NYU, UMCU). Trials, Number of trials collected per stimulus condition. Hemi, implanted hemisphere (L, Left; R, right). Implantation, type of electrodes implanted. Grid, Standard clinical grid; strip, standard clinical strip; depth, depth electrodes; HD grid, high-density grid. Coverage, approximate overview of visual cortex covered (Lat, lateral; med, medial; vent, ventral; par, parietal; occ, occipital; temp, temporal; ant, anterior; post, posterior). Visual no., number of electrodes that had a match with either one of the retinotopic atlases used for initial electrode selection (see below, Materials and Methods). Matching areas, matched retinotopic maps according to the maximum probability atlas by Wang et al. (2015). This includes depth electrodes that were not analyzed in the current study. No. included, number of electrodes included in the final dataset, after rejection of depth electrodes, and epoch and electrode selection (see above, Materials and Methods). Note that for a few subjects, no electrodes survived the selection procedure. Although not all subjects contributed to the results reported in this article, we include all patients for whom data was collected and preprocessed in the overview, because alternative data pruning and electrode selection methods on the publicly available data may yield other inclusion results.
ECoG recordings
NYU
Stimuli were shown on a 15 inch MacBook Pro laptop. The laptop was placed 50 cm from the participant's eyes at chest level. Screen resolution was 1280 × 800 pixels (33 × 21 cm). Before the start of the experiment, the screen luminance was linearized using a lookup table based on spectrophotometer measurements (Cambridge Research Systems). Recordings were made using one of two amplifier types, NicoletOne amplifier (Natus Neurologics), bandpass filtered from 0.16 to 250 Hz and digitized at 512 Hz, and Neuroworks Quantum Amplifier (Natus Biomedical) recorded at 2048 Hz, bandpass filtered at 0.01–682.67 Hz, and then downsampled to 512 Hz. Stimulus onsets were recorded along with the ECoG data using an audio cable connecting the laptop and the ECoG amplifier. Behavioral responses were recorded using a Macintosh wired external numeric keypad that was placed in a comfortable position for the participant (usually on the lap) and connected to the laptop through a USB port. Participants self-initiated the start of the next run by pushing a designated response button on the number pad.
UMCU
Stimuli were shown on a NEC MultiSync E221N LCD monitor positioned 75 cm from the participant's eyes. Screen resolution was 1920 × 1080 pixels (48 × 27 cm). Stimulus onsets were recorded along with the ECoG data using a serial port that connected the laptop to the ECoG amplifier. As no spectrophotometer was available at UMCU, screen luminance was linearized by reverting the built-in gamma table of the display device. Data were recorded using a Micromed amplifier at 2048 Hz with a high-pass filter of 0.15 Hz and a low-pass filter of 500 Hz. Responses were recorded with a custom-made response pad.
Stimuli
The code mentioned in this article and all code used for generating the stimuli and for experimental stimulus presentation can be found at https://github.com/BAIRR01/BAIR_stimuli and https://github.com/BAIRR01/vistadisp.
Visual stimuli for the purpose of estimating changes in neural temporal dynamics were generated in MATLAB, release 2018b. Stimuli were shown within a circular aperture with a radius of 8.3° visual angle using Psychtoolbox-3 (https://psychtoolbox.org/) and were presented at a frame rate of 60 Hz. Custom code was developed to equalize visual stimulation across the two recording sites as much as possible; for example, all stimuli were constructed at high resolution (2000 × 2000 pixels) and subsequently downsampled in a site-specific manner so that the stimulus was displayed at the same visual angle at both recording sites (corresponding Matlab functions: stimMakeSpatiotemporalExperiment.m and bairExperimentSpecs.m). Stimuli consisted of grayscale bandpass noise patterns, which were created following procedures outlined in Kay et al. (2013a). Briefly, the pattern stimuli were created by low-pass filtering white noise, thresholding the result, performing edge detection, inverting the image polarity so that the edges are black, and applying a bandpass filter centered at three cycles per degree (createPatternStimulus.m). All stimuli were presented within a circular aperture; the remainder of the display was filled with neutral gray (Fig. 1A). The spatial pattern we used has been shown to effectively elicit responses in most retinotopic areas (Kay et al., 2013b; Zhou et al., 2018).
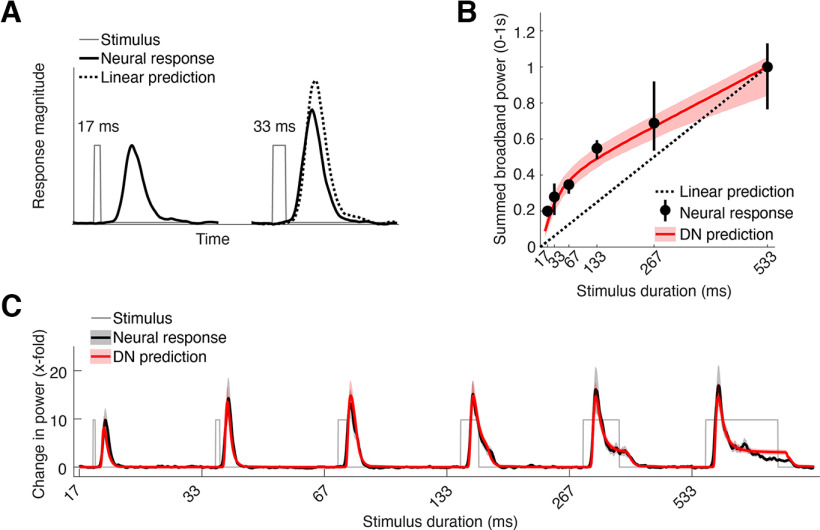
Figure 1.
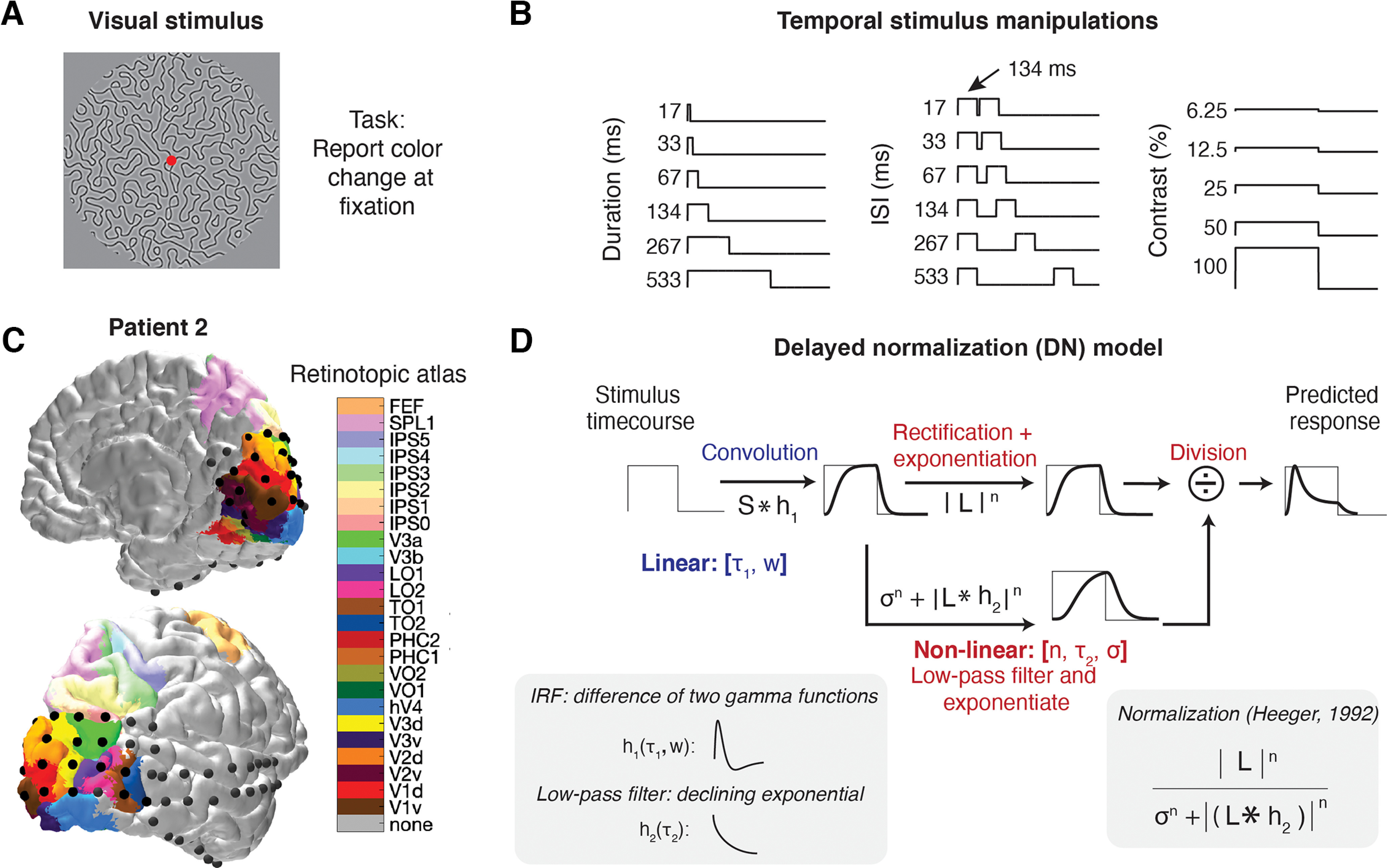
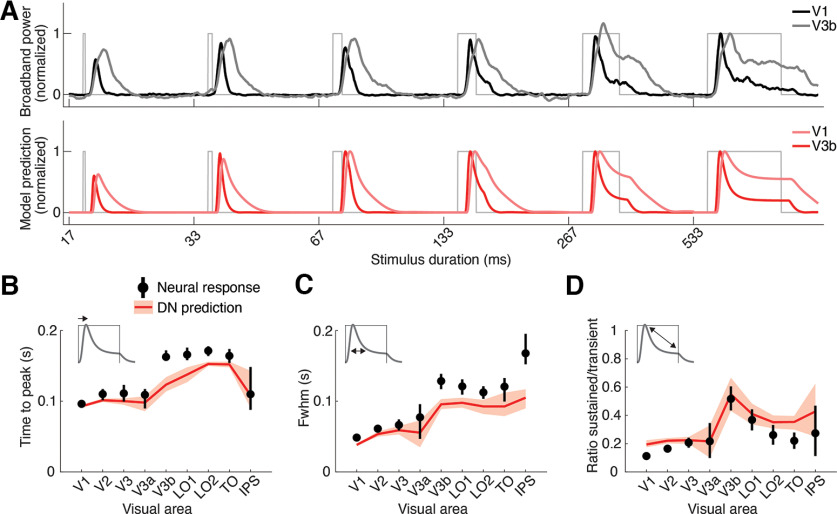
Experimental design, ECoG data, and delayed normalization model. A, Participants were shown large (16.6° diameter) grayscale pattern stimuli consisting of connected curved line segments. Unique individual stimuli were used for each stimulus condition. B, Stimulus time courses were varied in three different ways. For duration trials, a single full-contrast stimulus was presented for different durations ranging between 17 and 533 ms. For repetition trials, a full contrast stimulus was presented twice for 134 ms, with an ISI ranging between 17 and 533 ms. For contrast trials, a single stimulus was presented at a fixed duration (500 ms) with levels of contrast ranging between 6.25 and 100%. C, Electrode positions from an example participant overlaid on a pial surface reconstruction with predicted visual area locations. In this visualization, a surface node in the pial mesh was assigned a color if it had a nonzero probability of being on a visual region according to the full probability map from Wang et al. (2015). If the electrode had a nonzero probability of being in multiple regions, the region with the highest probability was assigned. A high-resolution figure containing each participant's electrode positions and retinotopic atlas projections is provided at OpenNeuro (https://openneuro.org/datasets/ds004194), and interactive 3D renderings for each individual participant can be generated using tde_mkFigure1_1.m at https://github.com/irisgroen/temporalECoG. D, Visual depiction of the DN model, first presented in Zhou et al. (2019). This linear-nonlinear gain model takes a stimulus time course as input and produces a predicted response time course as output by applying both linear and nonlinear computations. Inset (left), The initial linear part consists of convolution with an IRF parameterized as a difference of two gamma functions, with free parameters τ1 (time constant) and w (weight of negative to positive gamma). This is followed by a nonlinear part consisting of rectification, exponentiation with exponent n, and division by a semisaturation constant σ, plus a delayed copy of the input that is also rectified and exponentiated. The delay is implemented as a convolution of the linear response with an exponentially decaying function of time constant τ2 (lower left). Inset (right), This model form constitutes a temporal implementation of divisive normalization, as first proposed by Heeger (1992).
After generating independent pattern stimuli for each trial, stimuli were assigned to one of the following three different stimulus conditions (Fig. 1B): duration, ISI, or contrast (stimMakeSpatiotemporalExperiment.m). Duration and ISI trials were generated using the same parameters as in Zhou et al. (2018). For duration trials, a single pattern stimulus was shown at full contrast for one of six durations that ranged between 17 and 533 ms. For ISI trials, a single full-contrast pattern stimulus was shown for a fixed duration (134 ms) twice in a row, with one of six interstimulus intervals whose duration varied between 17 and 533 ms. Duration and ISIs were powers of two times the monitor dwell time (1/60 s). For contrast trials, contrast varied from 6.25% to 100% in five steps of powers of two. Contrast trials were shown at a fixed duration of 500 ms. Together, all trial types amounted to 17 stimulus conditions (six durations, six ISIs, and five contrasts). The stimulus durations, contrast, and interstimulus intervals were chosen to span a large dynamic range based on pilot data in V1–V3 in both fMRI and ECoG.
Experimental design and statistical analysis
Experimental procedure
Duration, repetition, and contrast conditions were divided across two runtypes, one containing the duration- and ISI-varying trials and one containing the contrast-varying trials, as well as an additional set of grating and density-varying stimuli that were not analyzed for the purpose of the current article. Trials were presented with an intertrial interval (ITI) that was randomly picked from a uniform distribution varying between 1.25 and 1.75 s. For each runtype, two unique stimulus sequences were created containing randomly ordered trials and ITIs. With the exception of participants P03 and P04 (who performed an earlier version of the experiment), all participants were presented with the same stimulus sequences. Each run contained 36 stimuli with three instances per stimulus condition and lasted ∼60 s. Screen flip times, as measured by Psychtoolbox, were saved during stimulus presentation and compared with the requested timings to ascertain that stimuli were presented with high temporal accuracy (maximum estimated accumulated timing error per run, <8 ms; maximum deviation of stimulus duration, <2 ms).
For all runtypes, participants were instructed to fixate on a cross located in the center of the screen and press a button every time the cross changed color (from green to red or red to green). Fixation cross color changes were created independently from the stimulus sequence and occurred at randomly chosen intervals ranging between 1 and 5 s. For each task, participants completed each unique run at least once. Runs were then repeated several times within the same experimental session or additional sessions recorded on different days. The amount of data collected for each patient is provided in Table 1. The experimenter stayed in the room during the experiment. Patients were encouraged to take short breaks between runs.
ECoG data analysis
Data preprocessing
Data were read into MATLAB, release 2020b, using the FieldTrip Toolbox (Oostenveld et al., 2011) and preprocessed with custom scripts available at https://github.com/WinawerLab/ECoG_utils. Raw data traces obtained in each recording session were visually inspected for spiking, drift, or other artifacts. Electrodes that showed large artifacts or showed epileptic activity were marked as bad and excluded from analysis. Data were then separated into individual runs and formatted to conform to the ieeg-BIDS (Brain Imaging Data Structure) format (Holdgraf et al., 2019). Data for each run were re-referenced to the common average across electrodes for that run, whereby a separate common average was calculated per electrode group (e.g., one for grid and one for strip electrodes; bidsEcogRereference.m). Next, a time-varying broadband estimate was computed for each run in the following way (bidsEcogBroadband.m). First, the voltage traces were bandpass filtered using a Butterworth filter (pass band ripples < 3 dB, stopband attenuation 60 dB) for 10-Hz-wide bands that ranged between 50 and 200 Hz. Bands that included frequencies that were expected to carry line noise and their harmonics were excluded (for NYU, bands 60, 120, and 180 Hz; for UMCU, 50, 100, and 150 Hz). The power envelope of each bandpass-filtered voltage time course was calculated as the square of the Hilbert transform of the time course. The resulting envelopes were then averaged across bands by taking the geometric mean (ecog_extractBroadband.m). Unlike the arithmetic mean, taking the geometric mean ensures that the resulting average is not biased toward the lower frequencies. The re-referenced voltage and broadband traces for each run were written to BIDS derivatives directories.
Electrode localization
Intracranial electrode arrays from NYU participants were localized based on preimplantation and postimplantation structural MRI images (Yang et al., 2012). Electrodes from UMCU participants were localized from the postoperative CT scan and coregistered to the preoperative MRI (Hermes et al., 2010). Electrode coordinates were computed in native T1 space and visualized onto pial surface reconstructions of the T1 scans generated using FreeSurfer (http://freesurfer.net). Visual maps of striate and extrastriate cortex were generated for each individual participant based on the preoperative anatomic MRI scan by aligning the surface topology with two atlases of retinotopic organization—an anatomically defined atlas (Benson et al., 2014; Benson and Winawer, 2018) and a probabilistically defined atlas derived from a retinotopic fMRI mapping dataset (Wang et al., 2015; Figure 1C). Using the alignment of the participant's cortical surface to the FreeSurfer fsaverage subject, atlas labels defined on the fsaverage were interpolated onto their cortical surface via nearest-neighbor interpolation.
Electrodes were then matched to both the anatomic and the probabilistic atlases using the following procedure (bidsEcogMatchElectrodesToAtlas.m). For each electrode, the distance to all the nodes in the FreeSurfer pial surface mesh were calculated, and the node with the smallest distance was determined to be the matching node. The atlas value for the matching node was then used to assign the electrode to one of the following visual areas in the anatomic atlas (hereafter referred to as the Benson atlas): V1, V2, V3, hV4, VO1, VO2, LO1, LO2, TO1, TO2, V3a, V3b, or none; and to assign it a probability of belonging to each of the following visual areas in the probabilistic atlas (hereafter referred to as the Wang atlas): V1v, V1d, V2v, V2d, V3v, V3d, hV4, VO1, VO2, PHC1, PHC2, TO2, TO1, LO2, LO1, V3b, V3a, IPS0, IPS1, IPS2, IPS3, IPS4, IPS5, SPL1, FEF, or none.
Data selection
The preprocessed data were analyzed for the purposes of this article using custom MATLAB code available at https://github.com/irisgroen/temporalECoG. First, a dataset was created by reading in the voltage and broadband traces of each run from each participant from the corresponding BIDS derivatives folders (tde_getData.m). Only electrodes that had a match with one of the visual areas from either the Benson atlas or the Wang atlas were selected for preprocessing. Only (high density) grid or strip electrodes were included (i.e., depth electrodes were excluded).
To combine the UMCU and NYU participants into a single dataset, the UMCU data were resampled at 512 Hz. Broadband and voltage traces from each run were subsequently segmented into individual epochs by extracting the neural time courses between [−0.1 and 1.2] seconds relative to stimulus onset. Visual inspection of the data indicated an obvious delay in response onset for the UMCU participants relative to the NYU participants. The cause of the delay could not be tracked down, but it was clearly artifactual. To correct the delay, UMCU data were aligned to the NYU data based on a cross-correlation of the average event-related potential across all stimulus conditions from V1 electrodes from three participants (1 UMCU, 2 NYU). The delay in stimulus presentation was estimated to be 72 ms (95% CI 63 to 85 ms by bootstrapping across a total of 18 electrode pairs), and stimulus onsets of all trials from the UMCU participants were shifted according to this average delay (s_determineOnsetShiftUMCUvsNYU.m)
Voltage epochs were baseline corrected by subtracting the average prestimulus amplitude within each trial. Broadband epochs were converted to percentage signal change by pointwise dividing and subtracting the average prestimulus baseline (average broadband power between −100 and 0 ms relative to stimulus onset) across all epochs within each run. We then performed two consecutive data trimming steps, (1) epoch selection and (2) electrode selection (tde_selectData.m).
Epoch selection was performed using both the voltage and broadband epochs. Epochs were automatically rejected according to the following criteria (ecog_selectEpochs.m): (1) a difference in voltage between consecutive samples larger than 200 mV anywhere in the epoch and (2) the maximum broadband amplitude in the epoch outside the time window [0.05, 0.85] relative to stimulus presentation exceeds the average of the maximum response across trials inside the stimulus presentation window by 3 SDs. Across participants, on average 2.5% of epochs were rejected (SD, 0.6%; minimum, 1.7%; maximum, 3.2%).
Electrode selection was performed based on the broadband epochs and the electrode locations. To be included in data analysis, electrodes had to meet one criterion (ecog_selectElectrodes.m), that is, an above-threshold correlation between two independent halves of the data (split-half reliability). To compute this measure for each electrode, all epochs for a given trial type were randomly assigned to one of two splits. Within each half, epochs of the same trial type were averaged and then concatenated across trial types, and the coefficient of determination (R2) was calculated between the two concatenated time series. Electrodes with a low split-half reliability (R2 < 0.22) were excluded.
For three participants, this electrode selection procedure resulted in all their electrodes being rejected from analysis. For the eight remaining participants, 70.5% of electrodes on average were rejected (SD, 14.5%; minimum, 50%; maximum, 92%; Table 1, subject-specific data).
Data summary
The data preprocessing, electrode localization, and data selection procedures outlined above resulted in a total of 98 electrodes with robust visual responses covering visual areas V1, V2, V3, V3a, V3b, hV4, LO1, LO2, TO1, TO2, IPS0–IPS4 (Table 2, overview of electrodes per area). The broadband epochs of selected electrodes were averaged across all trials within a stimulus condition, resulting in 17 response time courses per electrode, which constituted the data for computational model fitting.
Table 2.
Overview of electrodes and patients per visual area
| Visual area | Number of electrodes | Median number of electrodes per bootstrap | Contributing patients |
|---|---|---|---|
| V1 | 12 | 7 | Patients 2, 3, 6, 7, 10 |
| V2 | 37 | 12 | Patients 2, 3, 4, 5, 6, 7, 10 |
| V3 | 56 | 16 | Patients 2, 3, 4, 5, 6, 7, 10, 11 |
| V3a | 35 | 4 | Patients 3, 4, 7, 10, 11 |
| V3b | 50 | 17 | Patients 3, 4, 7, 10, 11 |
| LO1 | 73 | 19 | Patients 3, 4, 5, 7, 10, 11 |
| LO2 | 34 | 9 | Patients 3, 10, 11 |
| TO | 12 | 3 | Patients 3, 10, 11 |
| IPS | 23 | 4 | Patients 7, 10, 11 |
Columns refer to the following: Visual area, name of retinotopic map. Ventral and dorsal maps of early visual areas (V1–V3) were combined. Areas TO1 and TO2 were combined into a single area TO, and IPS0–IPS4 were combined into a single area IPS (see above, Materials and Methods). Number of electrodes, number of electrodes with nonzero overlap with each retinotopic area, according to the full probability retinotopic atlas by Wang et al. (2015). Note that the sum is larger than the total number of electrodes included in the dataset (n = 98) because electrodes can probabilistically map onto several areas. Median number of electrodes per bootstrap, for a given bootstrap, electrodes are sampled with replacement and probabilistically assigned to one visual area at a time. Note that the sum is smaller than the total number of electrodes included in the dataset because some electrodes had a nonzero probability of overlapping with hV4, which was excluded from this report (see Materials and Methods) but was still included in the area assignments. Contributing patients, patients who contributed electrodes for each visual area.
Probabilistic electrode assignment
When assigning individual electrodes to visual areas, we used a bootstrapping procedure that took into account the probability of each electrode overlapping with a visual retinotopic region. In this procedure, we repeatedly (for n bootstraps) assigned electrodes to visual areas in accordance with the probability distribution of the matched surface node of each electrode across areas determined by the Wang atlas (Wang et al., 2015), resulting in a distribution of bootstrapped electrodes for each visual area. From these distributions we then computed summary statistics (median or mean) and confidence intervals across neural responses or model predictions for each visual area. Before conducting the repeated assignments, we rescaled the probability values in the atlas to exclude the none probabilities, which ensured that each electrode would always get assigned to an area (e.g., if an electrode had 60% probability of belonging to V3b, 20% probability of belonging to V3a, and 20% probability of belonging to none, it would get assigned to V3b 75% of the time and to V3a 25% of the time). To guarantee robust estimates, we only report results from areas that had at least 10 electrodes with a nonzero probability of being positioned on that area. This resulted in the exclusion of area hV4. We additionally grouped TO1 and TO2 into a single area, TO and areas IPS0-4 into a single area IPS.
Computational modeling
Model fitting: temporal dynamics
We fit models of temporal dynamics to the 17 broadband time courses for each individual electrode (tde_fitModel.m). Each model takes stimulus time courses as input and predicts neural response time courses as output. For analyses focusing on describing different temporal phenomena in V1 (Figs. 2–4) and comparisons of model performance across different model forms or participants (see Figs. 7–10, 12), models were fit separately to individual electrodes, and parameters or metrics derived from these fits were then averaged within visual areas using the probabilistic assignment bootstrapping procedure described above. For analyses that characterized changes in temporal dynamics along the visual hierarchy (see Figs. 11, 13–14), we instead conducted repeated (n = 1000) fits to the average time courses across electrodes within an area, whereby for each fit the average time course per area was computed after performing the probabilistic assignment, yielding a slightly different average and thus different model fit each time. Although results and conclusions were not qualitatively different, we found that in higher visual areas, this averaging-then-fitting procedure yielded slightly more robust estimates compared with fitting individual electrodes and subsequently averaging them. For analyses illustrating similarities in contrast and adaptation time courses (see Figs. 5, 6), model predictions were generated after electrodes were first averaged probabilistically within V1.
Figure 2.
Subadditive temporal summation in neural responses in human V1. A, Compressive temporal summation in neural responses illustrated by two stimulus time courses (17 and 33 ms duration, gray thin lines) and corresponding ECoG broadband time courses (black thick lines). Doubling stimulation duration does not result in a doubling of the response, as predicted by a linear prediction, computed as the sum of the shortest duration response and a shifted and scaled copy of that response (dotted line). B, Sum of broadband response time courses between 0 and 1 s after stimulus onset for each stimulus duration (black) and the predicted response by the DN model (red), normalized to the response to the longest duration stimulus (533 ms). Compressive temporal summation is evident as the deviation of both data and model from the linear prediction extrapolated from the longest duration stimulus (dotted line). Data points indicate median across repeated samples of V1 electrodes (total n = 12; median n per bootstrap = 7; Table 2), taking into account their probability of overlap with a retinotopic atlas (see above, Materials and Methods). Error bars and shaded regions indicate 68% confidence intervals across 10,000 bootstraps of electrode assignments. C, Average ECoG broadband time courses in V1 (black) for all stimulus durations measured (17–533 ms), along with the average prediction by the DN model (red). Shaded regions indicate 68% confidence intervals across 1000 bootstraps of electrode assignments. This figure and all following figures can be reproduced with the code contained in the mkFigures folder in https://github.com/irisgroen/temporalECoG. This figure is produced with mkFigure2.m.
Figure 4.
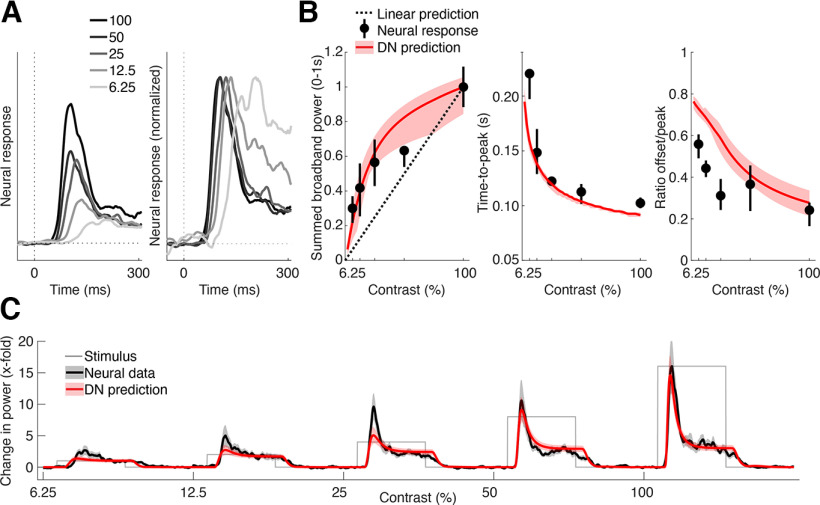
Contrast-dependent temporal dynamics of neuronal responses in human V1. A, Average ECoG broadband responses in V1 for different levels of contrast (6.25−100%), superimposed (left) and superimposed and peak normalized (right). Decreasing stimulus contrast results not only in a decrease in peak amplitude (left) but also a shift in peak latency and a decrease in the ratio of transient to sustained level of response (right). B, Summary statistics of contrast-dependent responses derived from individual electrodes (black dots) and DN model predictions (red line). Left, Contrast response functions, measured as summed broadband power between 0.05 and 1 s after stimulus onset. Middle, Time-to-peak. Right, Ratio of sustained response level (response magnitude at stimulus offset) to transient response level (maximum response level). Data points indicate median across probabilistically assigned V1 electrodes (total n = 12; median n per bootstrap = 7; Table 2, computed as in Figure 2B. C, Average ECoG broadband time courses in V1 (black) along with predictions by the DN model (red), computed as in Figure 2C. This figure is produced using tde_mkFigure4.m.
Figure 7.
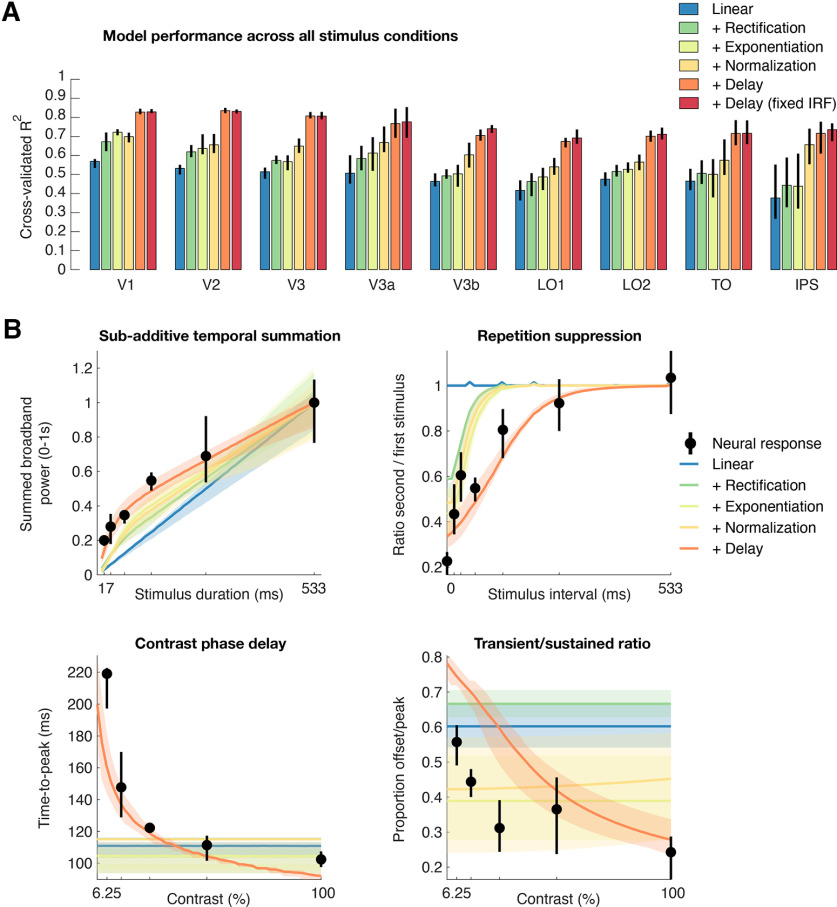
Delayed normalization explains multiple temporal dynamics in multiple visual areas. A, Average cross-validated explained variance (coefficient of determination) across all stimulus conditions in V1–IPS for the DN model along with deconstructed versions of the model from which each of the canonical nonlinear computations depicted in Figure 1D was removed in turn. Relative to a purely linear model (blue), adding nonlinear canonical operations of rectification, exponentiation, and delayed normalization each increase the model's ability to capture the variance in the dataset. Moreover, a full delayed normalized model with a constrained IRF (red) performs equally well as the more unconstrained IRF (2 additional free parameters, orange). B, Nonlinear temporal phenomena (subadditive temporal summation, repetition suppression, and contrast-related dynamics) in V1 as predicted by the deconstructed models. Bottom row, Delayed normalization is especially necessary to capture slowed response dynamics with low stimulus contrast. Error bars indicate 68% confidence intervals across 10,000 bootstraps of electrode assignments. This figure is produced by tde_mkFigure7.m.
Figure 10.
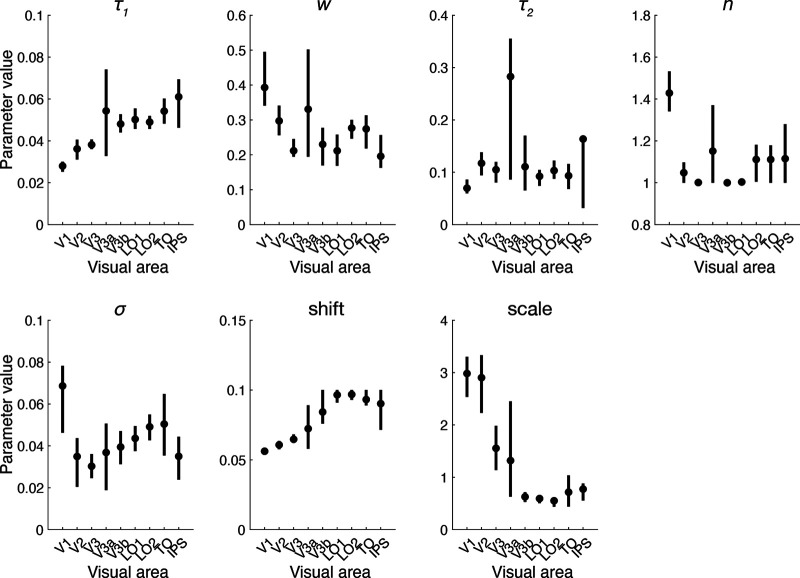
Fitted DN model parameters for all visual areas. The DN model has five model parameters that were fitted across all stimulus conditions: τ1 (time constant of the IRF), w (weight of the negative and positive IRFs), n (exponent), σ (semisaturation constant), and τ2 (time constant of the exponential decay), as well as two nuisance parameters, shift (delay in response onset relative to stimulus onset) and scale (gain of the response). Data points indicate median across probabilistically assigned electrodes. Error bars indicate 68% confidence intervals across 10,000 bootstraps of electrode assignments to visual areas. Initialization parameter values and bounds used during fitting can be found in JSON metadata files accompanying the code provided in the folder temporal_models in https://github.com/irisgroen/temporalECoG. This figure is produced using tde_mkFigure10.m.
Figure 12.
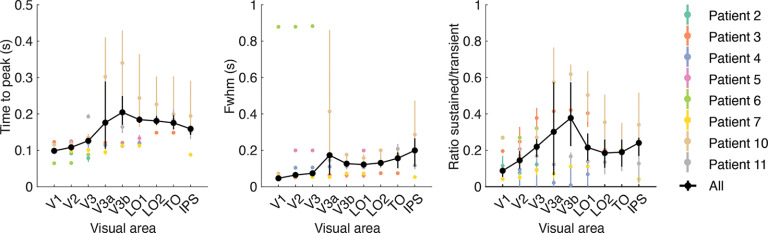
Temporal summation windows vary across individual participants. Time-to-peak, Full-width at half-maximum and sustained/transient ratio computed from the data but separately for each electrode and then grouped by visual area within each individual patient (colored data points) as well as across all patients (black data points and line). Note that the average here is not identical to the data shown in Figure 11B–D, where summary statistics were computed based on average time courses per area; here, they were calculated per individual electrode and then averaged. Data points indicate median across repeated samples of electrodes, taking into account the probability of overlap of each electrode with a retinotopic atlas (see above, Materials and Methods). Error bars and shaded regions indicate 68% confidence intervals across 1000 bootstraps of electrode assignments. Although individual electrode data are noisy, and there is substantial variety among individual patients, most patients show trends toward longer temporal summation windows for higher visual areas as evidenced by increase in time-to-peak, response width, and sustained to transient ratios. This figure is produced using tde_mkFigure12.m.
Figure 11.
Temporal summation window sizes increase in higher visual areas. A, Top, Average broadband ECoG responses for stimuli of increasing duration for an early (V1) and higher visual area (V3b). Table 2 shows the number of included electrodes per area. Bottom, DN model predictions for these same data. Compared with V1, responses in V3b rise more slowly and stay up longer, resulting in wider responses and higher sustained levels of response relative to the transient level. B–D, Three summary metrics derived from both the neural responses (black) and DN model predictions (red), separately for all visual areas in the dataset. Time-to-peak, computed from the neural response and model prediction to the longest duration stimulus (533 ms, B). Note that we use this duration as an example to compare across regions, and that the predicted time will be slightly different for other stimulus durations (with similar relative differences across regions). Full-width half-maximum, computed from the neural response and model prediction to the shortest duration stimulus (17 ms, C). Ratio of sustained (response level at stimulus offset) relative to the maximum response (peak), computed from the neural response and model prediction to the longest duration stimulus (D). Data points indicate means, and error bars indicate 68% confidence intervals across 1000 response averages and corresponding DN model fits using probabilistically assigned electrodes. This figure is produced using tde_mkFigure11.m.
Figure 13.
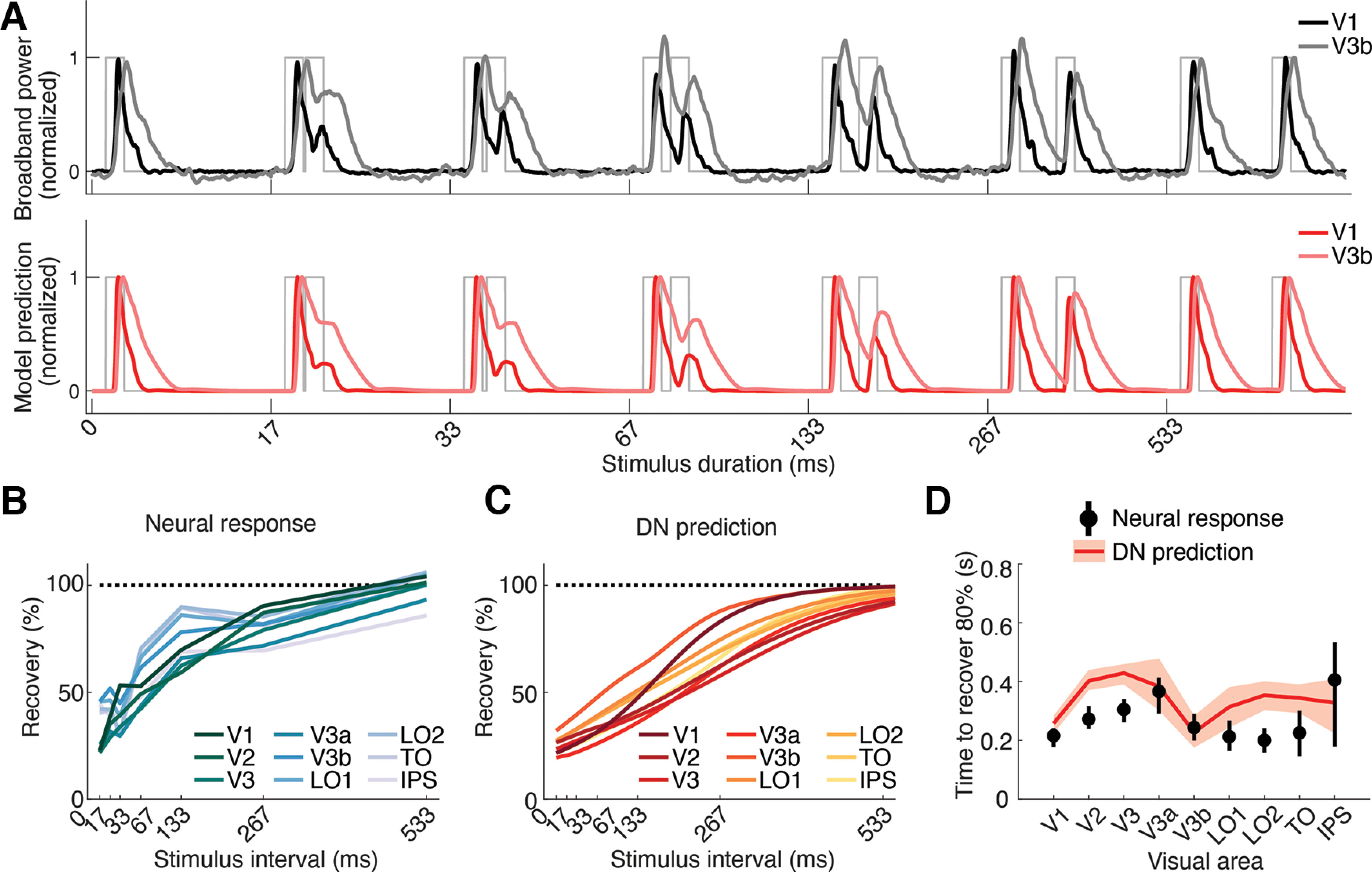
Temporal adaptation windows do not differ systematically between visual areas. A, Top, Average broadband ECoG responses to repeated stimuli with increasing ISI for an early (V1) and a higher visual area (V3b). Table 2 shows the number of included electrodes per area. Bottom, DN model predictions corresponding to these same data. Compared with V1, responses in V3b recover at a similar rate, with full recovery being achieved at the longest ISI measured (533 ms). B–D, Recovery from adaptation across visual areas. Although most higher visual areas show a somewhat slower recovery compared with V1 (e.g., V3a) some areas show a similar or faster recovery (e.g., V3b, LO1), and error bars are highly overlapping, suggesting no systematic change in recovery across the visual hierarchy. Measured recovery from adaptation across ISIs for V1-IPS (B, calculated the same way as in Fig. 3B). Predicted recovery from adaptation based on the DN model when simulating responses across a range of ISIs (C). Estimation of the ISI at which recovery is 80% of the response to the first stimulus, calculated for both neural data and DN model (D). Data points indicate means, and error bars indicate 68% confidence intervals across 1000 response averages; corresponding DN model fits using probabilistically assigned electrodes. This figure is produced using tde_mkFigure13.m.
Figure 14.
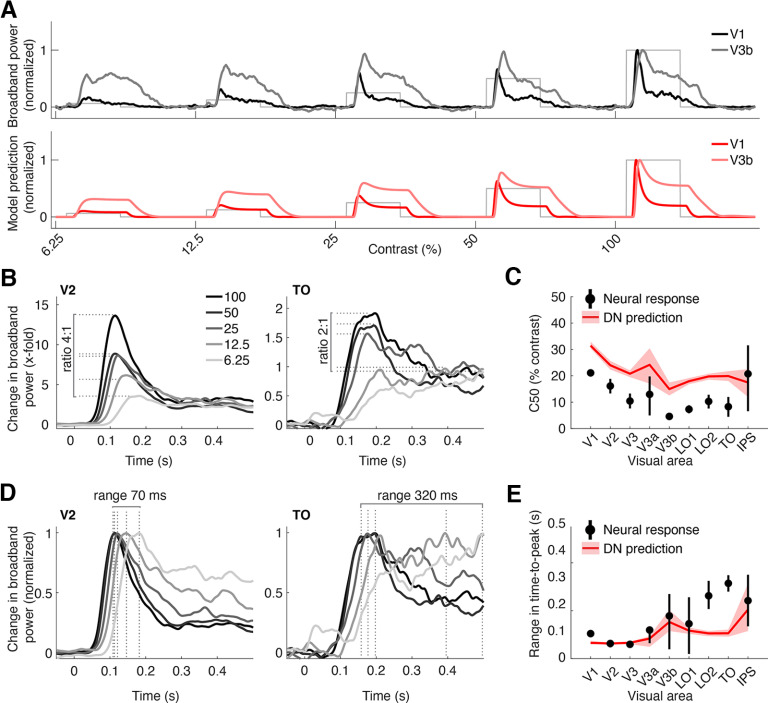
Opposite effects of contrast on response amplitude and timing across visual areas. A, Top, Average broadband ECoG responses to stimuli with increasing contrast for an early (V1) and a higher visual area (V3b). Table 2 shows the number of included electrodes per area. Bottom, DN model predictions corresponding to these same data. B, Average broadband ECoG responses to stimuli with different contrasts in early visual area V2 (left) and higher visual area TO (right), superimposed. Dashed lines indicate maximum amplitude in each condition. Time courses were slightly smoothed for illustrative purposes only. C, C50 for each visual area, computed both from the data and model predictions. D, Same data as in B, with each time course normalized to its peak, which illustrates differences in response rise. Dashed lines indicate time-to-peak in each condition. E, Range in time-to-peak across contrast for each visual area for both data and DN model predictions. Data points in C and E indicate means, and error bars indicate 68% confidence intervals for 1000 response averages of probabilistically assigned electrodes. This figure is produced using tde_mkFigure14.m.
Figure 5.
Comparison of contrast and repetition effects in ECoG data and DN model predictions. Top left, Average broadband time courses in V1 for the contrast-varying stimuli during the first 200 ms after stimulus onset. Darker lines indicate increasing contrast. Responses are stronger and rise faster with increasing contrast. Top right, Average broadband time course for the second stimulus in each repetition condition, after subtracting the response to the first stimulus (see above, Materials and Methods). Darker lines indicate increasing ISI. Responses are stronger and rise faster with longer ISIs. Bottom row, DN model predictions derived using parameters from fitting to the average time courses (top row) for contrast-varying stimuli (left) and repeated stimuli (right). This figure is produced using tde_mkFigure5.m.
Figure 6.
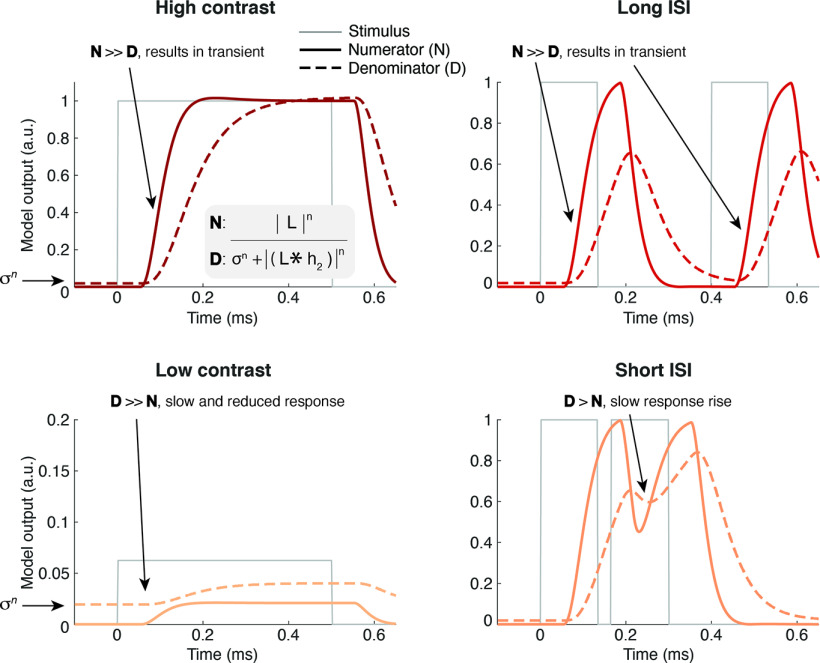
Illustration of how the DN model predicts similar effects of low-contrast and repetition. DN model numerator (solid lines) and denominator (dashed lines) for high contrast (top left), low contrast (bottom left), long ISI (top right), and short ISI (bottom right) for the model parameters fit to the average V1 response. (But note that no gain factor is applied, so the output units are relative to stimulus contrast.) With high contrast, the numerator quickly rises and thereby diminishes the influence of the denominator, which is slightly elevated at onset because of the semisaturation constant σn. With low contrast, the denominator term is bigger relative to the input drive, resulting in a slower, reduced response. For long ISIs, the denominator has sufficient time to decrease in between stimuli, but with shorter ISIs, the denominator is still increased because of delayed normalization from the first stimulus, leading to a reduced response to the second stimulus. In both cases, the response rises more slowly, and response magnitude is repressed because of a larger denominator term. This figure is produced using tde_mkFigure6.m.
Models were fit using Bayesian adaptive direct search (BADS; Acerbi and Ma, 2017). BADS alternates between a series of fast, local Bayesian optimization steps and a systematic, slower exploration of a mesh grid (https://github.com/lacerbi/bads provides code and a further explanation of the algorithm). Using BADS resulted in slightly more robust fits to the data compared with two built-in MATLAB alternatives, fmincon and lsqnonlin; however, results and conclusions did not change qualitatively when using these optimizers, and we implemented all three options in our fitting code (tde_fitModel.m). Model performance was evaluated using the cross-validated coefficient of determination (R2) computed via 17-fold leave-one-out cross-validation, whereby each of the stimulus conditions was once left out of the fitting procedure and then predicted based on the parameters estimated from the remaining 16 stimulus conditions. Model R2 was computed by averaging across the R2 values for the 17 left-out stimuli. Model parameter values and summary parameters (see below) were estimated based on fits to the full dataset.
Computational models of temporal dynamics
The delayed normalization (DN) model and its reduced versions (see below) are implemented as stand-alone functions in https://github.com/irisgroen/temporalECoG, folder temporal_models. Each model is paired with a JavaScript Object Notation (JSON) metadata file containing parameter descriptions, starting points, and upper and lower bounds that were used when fitting the model. As detailed below, models differ in the number and types of parameters fitted. In addition to the model-specific parameters, two nuisance parameters were fitted for all models, shift (delay in response onset relative to stimulus onset), and scale (gain of the response) to take into account differences between electrodes or visual areas in response onset latency and overall response magnitude (i.e., responses in V1 are much higher than in later visual areas). We tested the following models.
Delayed normalization model
Our main model of interest was the DN model (Fig. 1D), previously described in Zhou et al. (2019). The core idea of the model is that the stimulus drive is divisively normalized by delayed population activity (here, delayed via a low-pass filter). There is a long history of implementing models with a delay in the normalization pool (Heeger, 1992, 1993; Mikaelian and Simoncelli, 2001; Tsai et al., 2012; Sinz and Bethge, 2013). Zhou et al. (2019), their Fig. 7, contains a more elaborate discussion on the relation of the DN model with other implementations of delayed gain control mechanisms. Because prior model implementations were either conceptual, meaning not fit to data (Heeger, 1992) or fit to specific types of data (Zhou et al., 2019), it was necessary to implement a specific formulation that could be applied to a wide variety of ECoG data, as we have here. Zhou et al. (2019) demonstrated that the DN model was able to predict compressive temporal summation (in ECoG data to stimuli of a single duration), adaptation (in fMRI responses to stimuli of varying durations and interstimulus intervals), and contrast dynamics (in nonhuman primate multiunit activity recordings from V1). Here, we tested whether the same model could predict all three of these phenomena simultaneously in ECoG data. We largely reuse Zhou et al.'s (2019) implementation, which included a parameterized impulse response function, exponentiation of the driven activity, and an exponential decay filter applied to the normalization pool. The DN model is defined by a linear, nonlinear, and gain control structure and is described by the following set of equations.
First, a linear response (RL) is computed by convolving an input stimulus time course S of length t (dimensions 1 × t, with values ranging between 0 and 1) with an impulse response function (IRF) h1, consisting of a weighted difference of two gamma functions as follows:
| (1) |
in which t is time, w the weight on the second (negative) gamma function, and τ1 is a time constant determining the shape of the IRF. Symbols in parentheses are parameters. RL, S, and h1 are functions of time; we omit t for simplicity. Note that each individual gamma function here is a simplification of the gamma function provided in Boynton et al. (1996, their Eq. 3), whereby the phase delay of the IRF is fixed at value 2, as in Zhou et al. (2019). Moreover, as in Zhou et al. (2019), we assumed the peak timing of the second (negative) gamma function to be 1.5 times the first (positive) one, leaving only τ1 and w as the free parameters of the linear step. This version of the DN model (DN.m) was used for all analyses with the exception of the model reduction analysis (see Figs. 7, 8), where we compare this model to models with a more flexible IRF, which has two additional free parameters—one for the phase delay and one for the time constant of the negative gamma function (see next section).
Figure 8.
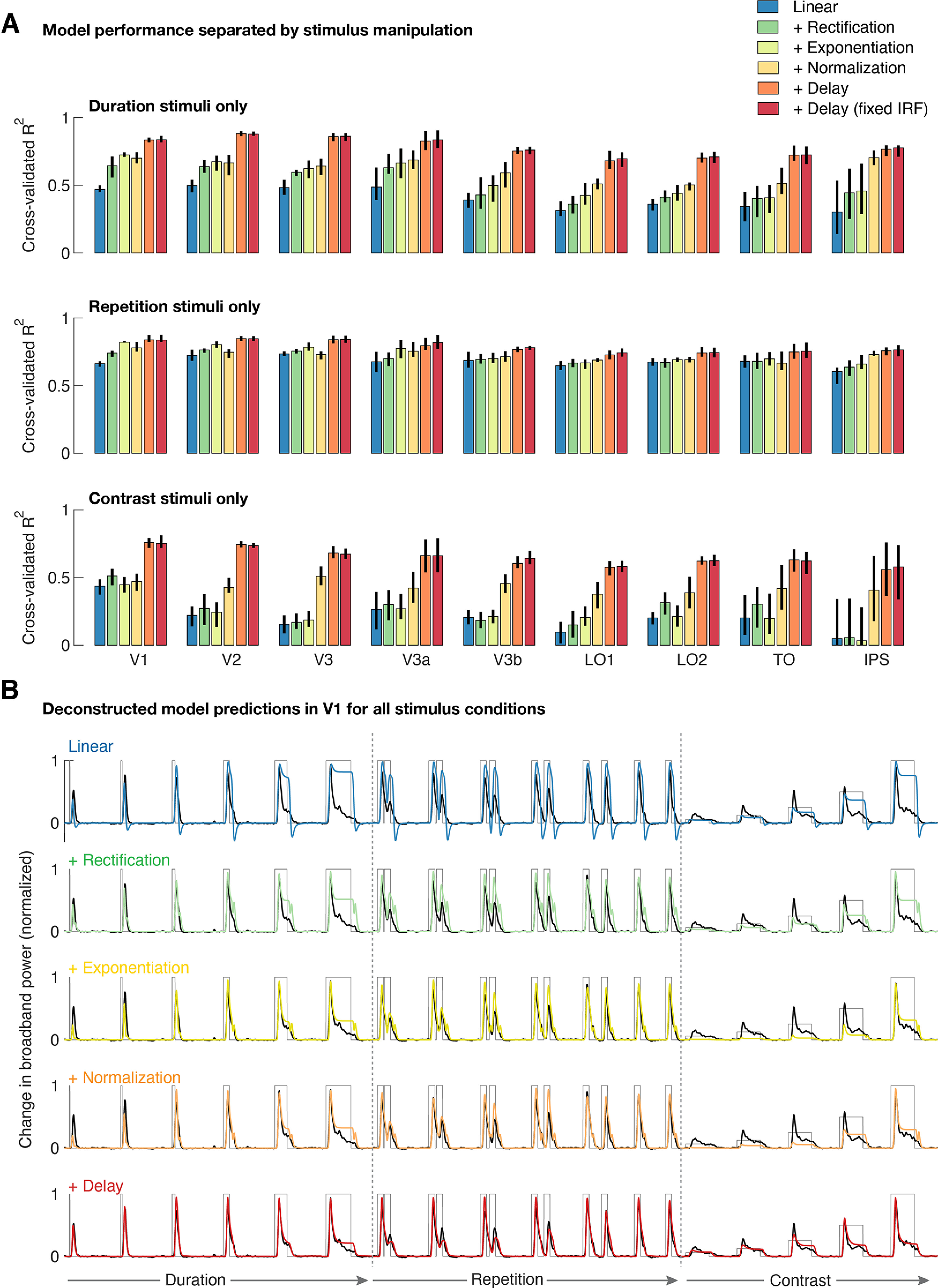
Delayed normalization is especially important for explaining contrast-related dynamics. A, Average cross-validated explained variance in V1–IPS for the DN model along with deconstructed versions of the model, separated by stimulus manipulation. Models were fit to all conditions simultaneously but are here evaluated separately for the duration, repetition, and contrast-varying stimuli. Error bars indicate 68% confidence intervals across 10,000 bootstraps of electrode assignments. B, V1 time courses with deconstructed DN model predictions from Figure 7 overlaid, for all stimuli. A linear model consisting of only a biphasic IRF fails to explain the neural responses across conditions. Adding canonical nonlinear computations, including instantaneous normalization, results in increased model performance in capturing the overall response shape, mostly for the duration and repetition conditions. Adding a temporal delay in normalization is especially critical for capturing changing temporal dynamics for contrast-varying stimuli (e.g., time-to-peak, sustained/transient ratio). Data and model predictions were averaged across electrodes using 1000 bootstraps of electrode assignments. This figure is reproduced using tde_mkFigure8.m.
The linear response (RL) is then converted into a nonlinear response, RLN, by applying a full-wave rectification and an exponentiation with exponent n (which is fitted), as follows:
| (2) |
The final step is divisive normalization of the nonlinear response RLN with a low-pass filtered version of RL that is also rectified and exponentiated to the same n. In addition, an exponentiated semisaturation constant σ is added to the denominator as follows:
| (3) |
The low-pass filtering here is achieved by means of convolution with an exponential decay function h2 with time constant τ2.
As noted in Figure 1D, Equation 3 has the form of canonical divisive normalization (Carandini and Heeger, 2011), in which a numerator (reflecting the rectified and exponentiated linear input) is divided by a denominator consisting of a normalization pool and a semisaturation constant, which each are also raised to the same exponent n as the numerator. Here, the normalization pool consists of a delayed version of the numerator, which means that the input drive is essentially normalized by a delayed version of itself. This yields an output time course that is characterized by a transient response rise followed by a decay to a sustained response level.
To summarize, for the main version of the DN model used throughout, the following five parameters were fitted in total: τ1 (time constant of the IRF), w (weight of the negative and positive IRFs), n (exponent), σ (semisaturation constant), and τ2 (time constant of the exponential decay). Model parameters and bounds were initialized using values used in Zhou et al. (2019).
Delayed normalization model, fully parameterized and deconstructed
In addition to the original model proposed by Zhou et al. (2019), we tested reduced versions of that same model in which nonlinear computations were consecutively added on top of the purely linear first step of the model. The motivation for including this model construction analysis was to investigate how much each step contributed to the overall predictive performance of the model. As explained above, we additionally adapted the model so that the IRF used for linear convolutions was less constrained, allowing the time constant of the negative gamma function and the phase delay of both gamma functions to be fitted in optimization so that it could capture as much variance in the data as possible with a maximally flexible IRF (total number of fitted parameters is four; τ1pos, τ1neg, phase delay r, and w; LINEAR.m). We then added full-wave rectification (LINEAR+RECTF.m; same parameters as LINEAR.m), exponentiation (LINEAR+RECTF+EXP.m; adding parameter n), normalization without delay (LINEAR+RECTF+EXP+NORM.m; adding parameter σ), and finally, normalization with delay (LINEAR+RECTF+EXP+NORM+DELAY.m; adding parameter τ2), which is equivalent to the DN model (DN.m), except that the IRF is less constrained. Model parameters and bounds were initialized using the same values as for the DN model and can be found in the JSON metadata of the fitting code in https://github.com/irisgroen/temporalECoG.
Summary metrics
To characterize the temporal dynamics of the broadband time courses, we computed several summary metrics on both data and model predictions (tde_computeDerivedParams.m).
Time-to-peak
We computed the time interval between stimulus onset and the maximum (peak) of the response time course (in seconds) based on responses or model predictions for the longest duration, full contrast stimulus (533 ms), which is the condition of maximal stimulation and thus the conditions where the response is overall expected to be greatest.
Full-width at half-maximum
The difference between the time point (relative to stimulus onset) at which the response has risen to half of the maximum and the time point at which the response has decayed again to the same half-way point (in seconds) was computed based on neural response or model prediction time courses to short duration stimuli (e.g., 17 ms), which have the least amount of sustained level activation and therefore the most symmetric response shapes.
Ratio sustained/transient
This is the response magnitude at the sustained level divided by the transient response magnitude (maximum/peak). For estimates of the sustained level, we took the response level at stimulus offset for the longest duration stimulus in the dataset (533 ms). To achieve robust estimates of the offset, data and model predictions were smoothed using a moving average filter with a span of 150 data samples (∼290 ms; tde_mkFigure4.m). The moving average is symmetric around each data point and, hence, does not systematically shift the timing of the peak.
Recovery from adaptation
This consists of the relative magnitude of response of the second stimulus relative to the first stimulus in the repeated stimuli conditions. The goal of this procedure is to estimate which part of the neural time course reflects the continuing activation to the first stimulus and which part reflects new neural activity elicited by the second stimulus. For each electrode, we compute an estimate of the response to the first stimulus by averaging together (1) the time course of an actual 134 ms stimulus presented in isolation (the fourth duration-varying condition), which includes all time points in entire epoch, and (2) each of the ISI-varying conditions but only including time points up to the onset of the second stimulus (tde_computeISIrecovery.m). The reason for additionally including these partial time courses instead of using the 134 ms duration stimulus only is that it gives us a more robust estimate of the response to the first stimulus (e.g., of the transient peak). Importantly, the estimated response to the first stimulus never includes data points after a second stimulus was presented. We then subtracted this average time course from each of the ISI-varying stimulus responses, yielding an estimate of the response of the second stimulus corrected for the response to the first stimulus. We then computed relative recovery by taking the maximum (peak) of the corrected second stimulus time courses and comparing it with the peak response of the average first stimulus estimate. Using the summed response across all time points in the time course for which a stimulus was present rather than the peak of the time course yielded qualitatively similar results.
C50
For both the neural data and the model predictions, percentage contrast for which response magnitude reaches 50% of the response to a 100% contrast stimulus was estimated by fitting a Naka-Rushton function (Naka and Rushton, 1966; Albrecht and Hamilton, 1982) to the maxima of the response time courses for each of the five contrast levels we measured. This equation takes the following form:
| (4) |
where C is the stimulus contrast level, Rmax is the maximum response amplitude, C50 the contrast at which the curve reaches half height, and exponent n controls the steepness of the sigmoid (fitNakaRushton.m). Taking the sum rather than the peak of the time course as the response per contrast level yielded qualitatively similar results.
Data availability
All code used for the purpose of this article can be found at the GitHub repositories mentioned above. The ieeg-BIDS-formatted data, derivatives, the processed dataset and model fits are available on OpenNeuro (https://openneuro.org/datasets/ds004194).
Results
We first examined how each of our three stimulus manipulations (duration, repetition, and contrast) affected the temporal dynamics of ECoG broadband time courses in area V1.
Neural responses in human V1 exhibit subadditive temporal summation
First, systematic variations of stimulus duration demonstrated the presence of subadditive temporal summation in neural responses in V1 (Fig. 2). When a stimulus doubles in duration, its resulting neural response is reduced relative to the linear prediction, that is, a sum of the responses to the shorter stimulus and a time-shifted copy of that response (Fig. 2A). This demonstrates that the additional visual exposure resulting from a longer presentation duration does not accumulate linearly. Comparison of summed neural responses across all stimulus durations indeed shows evidence of subadditive summation; throughout the 30-fold range measured in our experiment (17 ms to 533 ms), the obtained responses deviate systematically from the linear prediction, with responses to longer stimuli much smaller than the linear prediction extrapolated from the briefest stimulus (Fig. 2B).
The reason for this can be understood by looking at the average response time courses themselves (Fig. 2C). The largest response is the initial transient. For short duration stimuli, this is the only part of the response. At longer durations, there is also a lower-amplitude sustained response. Summed responses in Figure 2B reflect the combination of both the transient and sustained level activity; at longer durations, the lower-amplitude sustained component makes up an increasingly large fraction of the response.
We find that this temporal subadditivity in ECoG broadband responses is well captured by a delayed normalization model (Fig. 1D). The model accurately predicts the rapid increase in response at short durations and the slower increase at longer durations (Fig. 2B). Moreover the model time courses accurately fit both the transient and the sustained levels of neural response across different stimulus durations (Fig. 2C).
Neural responses in human in V1 exhibit response suppression because of adaptation
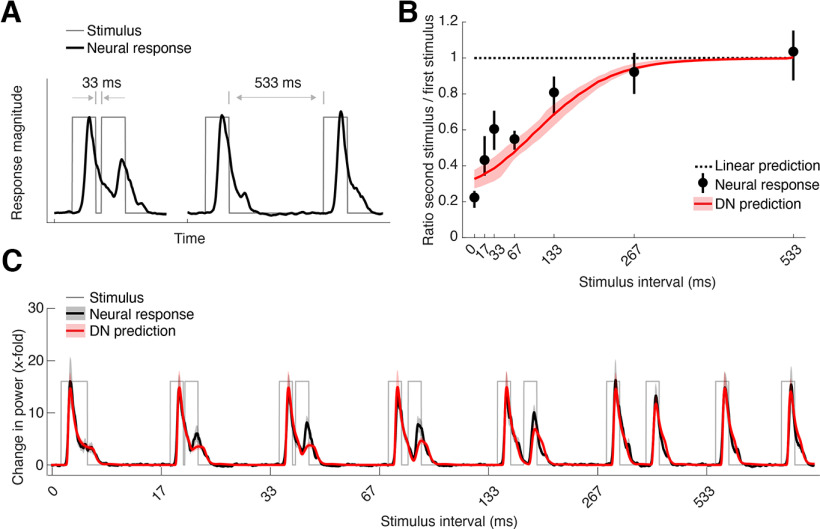
Second, repetitions of stimuli with different ISIs demonstrated the presence of adaptation in neural responses in V1 (Fig. 3). Adaptation is evident as a reduction in stimulus-evoked response because of the presence of a preceding stimulus and is most pronounced when the two stimuli are presented close together in time (Fig. 3A). Adaptation effects are nonlinear; although a linear model predicts no change in response magnitude because of preceding stimuli, the neural data reveal strong suppression for a stimulus that is presented in close temporal proximity to another stimulus, which gradually recovers as the ISI increases (Fig. 3B). These adaptation effects are clearly visible in the response time courses to the separate stimuli (Fig. 3C), where it can be seen that the response to the second stimulus achieves near-full recovery by the longest ISI tested (533 ms). Notably, these adaptation effects are well captured by the delayed normalization model, as indicated by the red lines in Figure 3B,C, although there are slight underpredictions for the response to the second stimulus at short ISIs.
Figure 3.
Adaptation of neuronal responses to stimulus repetition in human V1. A, Example of adaptation to a repeated stimulus, showing time courses for two stimuli of equal duration with a short (33 ms) and a long (533 ms) interstimulus interval (gray thin lines) and their corresponding ECoG broadband time courses (black thick lines). Short intervals lead to a strong suppression of the response to the second stimulus, and the response recovers with longer intervals. B, Recovery from adaptation for each condition, expressed as the difference in maximum response for the second stimulus compared with the maximum response of the first stimulus (black dots) along with the predicted recovery by the DN model (red line). Adaptation is evident from the deviation of both data and model from the linear prediction (dotted line). Data points indicate median across probabilistically assigned V1 electrodes (total n = 12; median n per bootstrap = 7; Table 2, computed as in Figure 2B. C, Average broadband time courses (black) in V1 for interstimulus intervals between 0 and 533 ms, along with predictions by the DN model (red), computed as in Figure 2C. This figure is produced using tde_mkFigure3.m.
Neural responses in human in V1 exhibit slower dynamics with reduced contrast
Third, we observed contrast-dependent temporal dynamics of neural responses in V1, despite the fact that the temporal structure of the stimulus time course itself did not differ across the contrast conditions (each stimulus was presented at a single duration of 500 ms). Increasing stimulus contrast resulted not only in an increase in peak response magnitude (Fig. 4A, left), but the response shape also changed in other ways independent of the peak magnitude, showing increased time-to-peak with lower contrast (phase delay) and a relatively less pronounced transient relative to the sustained level response (Fig. 4A, right). This result differs from the descriptive model in Albrecht et al. (2002) in which the effect of contrast is modeled as a shift and scale in the response shape.
We quantified these dynamics by computing three different summary statistics from the response time course of each electrode at each contrast level, which each again showed deviations from linearity (Fig. 4B). Summed responses over time give rise to a contrast response function that progressively increases for higher contrasts (Fig. 4B, left). Estimates of time-to-peak at each contrast level show that peak latency sharply decreases with increasing contrast (Fig. 4B, middle). A comparison of the sustained level response (at stimulus offset) compared with the transient level (peak response) shows that the difference between these two measures decreases as contrast decreases because of a less pronounced transient (Fig. 4B, right). All three effects are again also qualitatively captured by the DN model, resulting in highly accurate model predictions across all contrast levels (Fig. 4C). The model predictions are not perfect; they slightly underestimate the height of the transient part of the response for lower contrasts, resulting in elevated estimates of the sustained/transient response ratio (i.e., values closer to one; Fig. 4B). This slight model failure parallels the underprediction of the response to a second stimulus at short ISIs.
In sum, the V1 results show that there are several robust nonlinear temporal dynamics in ECoG responses in human V1 that are all consistent with a time-dependent normalization and thus well described by the DN model. We note that the model captures well-known nonlinear phenomena (e.g., contrast response function), as well as phenomena that are perhaps less well characterized in population responses in human visual cortex, such as temporal summation and short-latency visual adaptation.
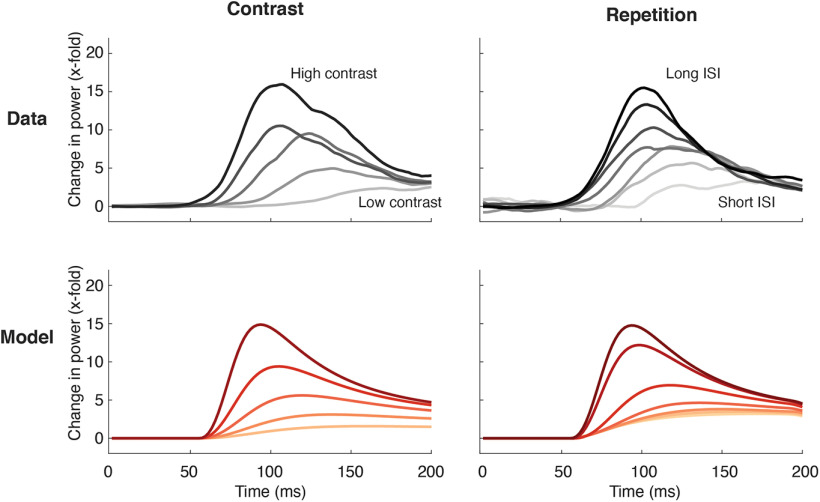
Contrast and repetition effects lead to similar response reductions in V1
An advantage of testing many stimuli in the same experiments is that we can directly compare the effects of different stimulus manipulations. We showed nonlinearities with respect to contrast manipulations (Fig. 4) and with respect to stimulus repetition (Fig. 3). Here, we ask how the two effects compare and how the DN model simultaneously accounts for them both.
First, zooming into the broadband time courses contrast responses (same data as in Fig. 4A) at the first 200 ms after stimulus onset clearly shows that lower stimulus contrast leads to more slowly rising responses, and to a change in response shape, with less distinction between transient and sustained responses (Fig. 5, top left). Interestingly, responses to repeated stimuli, after subtracting the influence of the first stimulus (see above, Materials and Methods) have remarkably similar shapes (Fig. 5, top right). The similarity of the effects of both contrast and repetition on the response dynamics is predicted by the DN model (Fig. 5, bottom row). Therefore, both the data and model suggest the possibility that V1 responds to a recently viewed stimulus similarly to a novel but low-contrast stimulus. One difference between model prediction and data are that in the predictions, the responses for all stimuli start rising at the same time (but at different rates), whereas in the data, the onset latency appears to be delayed for low contrast and short repetitions.
Inspecting the inner workings of the delayed normalization model helps understand why these responses look so similar and how the model accounts for the two effects simultaneously. In the model, the input drive is represented by the numerator, whereas the normalization pool is represented by the denominator (Fig. 1D). In Figure 6, these two components of the model are plotted separately for two different contrasts and two different ISIs. This shows that contrast and adaptation effects are both driven by differences in the normalization pool (denominator), but that for contrast, the effect can be attributed to the semisaturation constant (Fig. 1D, the left hand of the denominator), whereas for repetition, the effect can be attributed to the normalized input drive (i.e., the right hand of the denominator).
At high stimulus contrast, the semisaturation constant is negligible, and the numerator rises faster than the denominator, leading to a transient (Fig. 6, top left). At low contrast, the numerator never rises above the minimum possible value of the denominator, which is set by σn (Fig. 6, bottom left; see above, Materials and Methods). The main difference between the two contrast conditions, thus, is the driven response relative to σn. For repeated stimuli, the driven response is effectively the same regardless of ISI, and the denominator rises and decays similarly for both the first and second stimulus. However, when ISI is long (Figure 6, top right), the denominator has decayed more than when it is short (Figure 6, bottom right). Hence, for short ISIs, the ratio of numerator to denominator for the second stimulus is lower. The main difference between the two repetition conditions is thus the level of pre-existing normalization.
In summary, neural responses rise more slowly and are suppressed both when contrast is reduced and when stimuli are repeated with short intervals. According to the DN model, for contrast, this is because of a larger input drive (numerator) than background neural activity (σn), whereas for repetition, the reduction is because of an pre-existing delayed normalization (L*h2). Thus, the DN model is able to simultaneously predict the effects of both of these stimulus manipulations because it can achieve response reductions through either one of these terms.
Delayed normalization predicts temporal phenomena throughout visual hierarchy
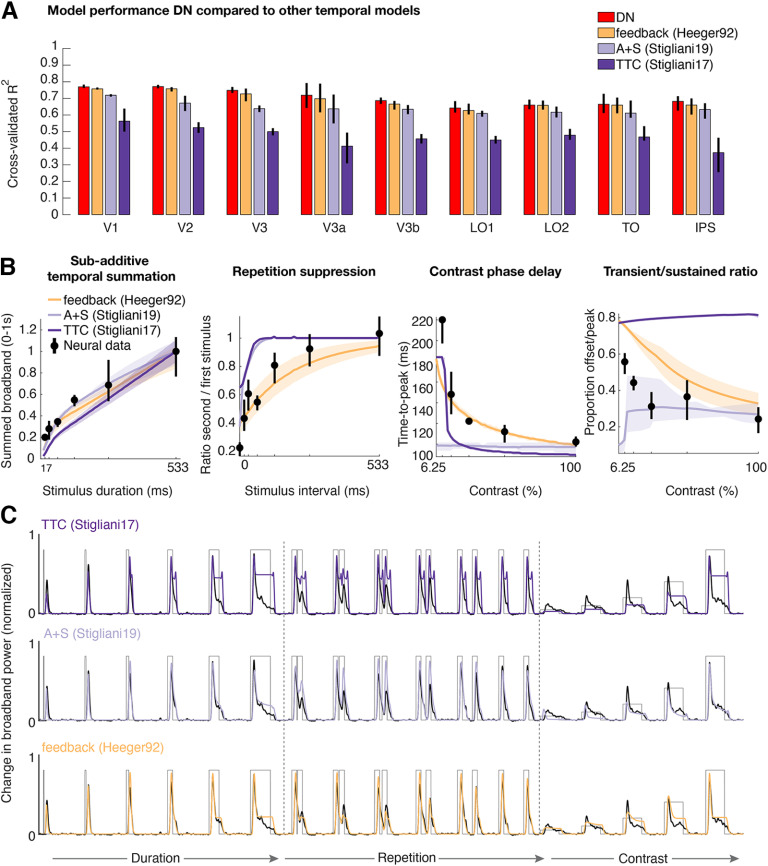
Next, we examined to what extent each of the canonical computations in the DN model contribute to its ability to predict neural responses for variations in duration, repetition, and contrast. To this end, we computed cross-validated explained variance for reduced versions of the model, starting with a linear model with fully parameterized IRFs (see above, Materials and Methods), after which each of the nonlinear operations in the DN model (rectification, exponentiation, normalization, normalization with delay; Figure 1D) were added in turn (Figure 7A). We find that delayed normalization is a key component in raising the prediction accuracy. Adding nonlinear operations to a purely linear model gradually increases the ability to explain responses in V1, and a clear gain in explanatory power is observed when adding the final step of delayed rather than instantaneous normalization.
Importantly, this pattern of results holds not only in V1 but in all retinotopic maps in which we had sufficient electrode coverage, including V2, V3, and higher-order lateral-occipital and parietal-occipital maps. Because accuracy is computed on left-out data (cross-validation), the result is not guaranteed simply because of adding more free parameters for each model. Indeed, there are some instances where adding parameters makes the fits less accurate (V1, +Exponentiation vs +Normalization).
In addition, Figure 7A shows that the version of the delayed normalization model with fully parameterized IRFs is on par with the more constrained DN model (in which the phase delay and time constants of the negative gamma function are fixed) as used in our analyses so far (see above, Materials and Methods), indicating that the data do not sufficiently constrain the detailed shape of the IRF and that the chosen IRF constraints are adequate for the current dataset.
The reduced explanatory power of the deconstructed models is coupled with a reduced ability to predict the different nonlinear temporal phenomena induced by our stimulus manipulations (temporal summation, repetition suppression, slower contrast dynamics; Figs. 2–4). Although compressive temporal summation and repetition suppression can to some extent be captured by reduced models that consist of canonical computations but lack the delayed normalization component (Figure 7B, top row), delayed normalization is critical to predict the slower dynamics associated with changes in stimulus contrast (Figure 7B, bottom row). In general, across visual regions, improvements in explained variance were most pronounced for the duration and contrast conditions, with reduced models performing relatively well when predicting responses to stimuli varying in repetition interval (Fig. 8A, cross-validated explained variance separated by condition and B for time course predictions for each deconstructed model across all stimulus conditions).
In addition to model reduction, we also compared the delayed normalization model to a few alternative models, in particular two-channel models proposed by (Stigliani et al., 2017, 2019), and an implementation of delayed divisive normalization via feedback (Heeger, 1992). Although the two-channel model from Stigliani et al. (2019) performs nearly on par with the DN model in terms of explained variance (Fig. 9A) and approximates temporal summation and adaptation effects to some degree, it fails to capture contrast-related dynamics (Fig. 9B,C). The feedback normalization model (Heeger, 1992) is very similar to the DN model it its ability to explain temporal phenomena. This suggests that delayed normalization can be implemented with multiple different underlying mechanistic models, either assuming feedback or not.
Figure 9.
Temporal models differ in their ability to predict multiple temporal dynamics. A, Cross-validated explained variance in V1–IPS for the DN model compared with a model implementing history-dependent normalization via feedback (Heeger, 1992) and two 2-channel (two-temporal channel; TTC, and adaption + sigmoid; A+S) models (Stigliani et al., 2017, 2019). B, Nonlinear temporal phenomena in V1 (same data as in Fig. 7B) as predicted by the alternative models. C, V1 time courses with alternative model predictions overlaid for all stimulus types. Two-temporal channel models can predict temporal summation and repetition suppression effects to some degree but fail to capture contrast-induced temporal dynamics. In contrast, the feedback model performs on par with the DN model. Model implementations and initialization parameters and bounds used during fitting can be found in the folder temporal_models in https://github.com/irisgroen/temporalECoG. This figure is produced using tde_mkFigure9.m.
Characterizing temporal dynamics throughout visual hierarchy using the DN model
Having established that the DN model predicts ECoG responses with high accuracy not only in V1 but in multiple visual regions, we next used it to investigate how temporal dynamics change along the visual hierarchy. Note that we use the term “visual hierarchy” as an approximation. By nearly any metric, V2 is a later area than V1, and V3 later than V2, and all the other areas later than V3. However, the hierarchical relationship among the areas beyond V3, if any, is uncertain.
A first hint of differences with visual hierarchy can be seen in the fitted DN model parameters shown separately for each visual area (Fig. 10). For example, the value of τ1 (time constant of the IRF) appears to increase in higher visual areas. However, we are cautious about comparing fitted parameters across areas directly because (1) although explained variance is still relatively high in higher areas, it is less than in early visual regions, which may imply poorer parameter estimates, and (2) the fitted parameters (to some degree) trade off against each other (Zhou et al., 2019, interpreting DN model parameters). Instead, we examine differences in temporal dynamics by computing various summary metrics (see above, Materials and Methods) from data and model time courses and comparing both model and data metrics across visual areas.
Temporal summation windows increase in higher visual areas
The responses to stimuli that vary in duration revealed a systematic change in temporal summation between visual areas (Fig. 11). Compared with V1, responses in, for example, V3b rise more slowly and stay elevated for a longer period of time, resulting in wider responses and higher sustained levels of response relative to the transient (Fig. 11A). We quantified these differences in response shapes across visual areas by computing three different summary metrics, which each capture a different aspect of the response dynamics, on both the data and DN model predictions (see above, Materials and Methods).
Relative to V1, all three measures increased in higher visual areas; the slower rise was reflected in increasing time-to-peak (Fig. 11B), the broadening of the transient was reflected in increasing full-width at half-maximum (Fig. 11C), and relatively higher sustained activity was reflected in a sustained/transient ratio that tended to become larger (Fig. 11D), although this latter summary metric was more variable across electrodes compared with the first two metrics. Overall, these summary metrics reflecting differences in temporal summation differ most between a group of earlier visual areas (V1–V3, V3a) and the later areas. These patterns were largely consistent when computed separately within individual participants (Fig. 12).
Temporal adaptation windows do not differ systematically between visual areas
In contrast to the pattern with temporal summation, adaptation to repeated stimuli showed less evidence of varying systematically across areas (Fig. 13). Although the response to the second stimulus in V3b is on average higher than that in V1 (Fig. 13A), this appears to result from the continued response to the first stimulus even after the second stimulus onset in V3b, rather than to less adaptation or a systematically different rate of recovery. In both areas, full recovery was achieved by the longest ISI measured (533 ms). Consistent with these observations, we did not observe a clear difference in the rate of recovery from adaptation across visual areas. To quantify this, we expressed the magnitude of the response to the second stimulus relative to the first stimulus separately for each ISI and visual area, yielding a measure of recovery from adaptation over time per area. Although areas V2, V3, and V3a recovered somewhat more slowly than V1 in both the data (Fig. 13B) and DN model predictions (Fig. 13C), area V3b did not. Indeed, when comparing the estimated ISI at which the response is nearly fully recovered (80%) for all areas shows that for both the data and the model, no systematic change in this measure is observed, with several higher-order visual regions having a similar recovery as V1 (Fig. 13D).
Opposite effects of contrast on response amplitude and latency across visual areas
In a third and final comparison of visual areas, we examined responses as a function of contrast (Fig. 14). Interestingly, we observed opposite effects of contrast on response amplitude and timing across visual areas. Amplitude differences between low- and high-contrast stimuli become smaller in higher visual areas (greater invariance to contrast), whereas time-to-peak differences tend to get larger (greater sensitivity to contrast).
The amplitude effects can be seen by comparing responses across different contrast conditions within a given area; compared with V1, responses in V3b are relatively enhanced for low-contrast stimuli (Fig. 14A). Similarly, compared with V2, responses in TO are relatively enhanced for low-contrast stimuli (Fig. 14B). We quantified this pattern by fitting a Naka-Rushton equation to the peak responses for both the data and the DN model predictions (see above, Materials and Methods). The C50 parameter is the contrast at which the response reaches half its maximum, with lower values indicating steeper rises in contrast response functions. This measure showed a downward trend along the visual hierarchy in both the data and the model predictions (Fig. 14C), indicating that less contrast is needed to elicit a robust response in higher compared with lower visual areas. Although the data and model predictions agree in showing decreasing C50 in higher areas, there is an overall offset between data and model, with the model predicting slightly higher C50 parameters overall. This matches our previous observation of small but systematic underpredictions of the transient response at low contrast noted in Figure 4C.
Differences in the time-to-peak between low- and high-contrast stimuli are more pronounced in the highest visual areas. This is illustrated in Figure 14D, which shows the same data as in Figure 14B but with each condition normalized to its peak (Fig. 4A, right, for same data in V1). Both V2 and TO show a greater and shallower slope at lower contrast (Fig. 14D). However, in area TO the range in latencies is larger compared with that of V2. To quantify these effects, we calculated the time-to-peak for each contrast (Fig. 14D, dashed vertical lines) and measured the range (difference between minimum and maximum value) across contrast levels in each area for both the data and the model (Fig. 14E). Although the range is relatively constant in early areas V1–V3, both data and model show an upward trend in the time-to-peak range across contrast conditions in the highest visual areas. This suggests that unlike response amplitude, response latency becomes more sensitive to contrast in higher visual areas.
Changes in temporal dynamics across visual areas
To summarize the comparisons across areas, we find that the temporal dynamics of neural responses differ across the visual areas we measured in several different ways. Most changes seem to reflect increasing invariance in higher visual areas, demonstrating, for example, less dramatic effects of changing stimulus duration on neural response shapes or less effect of changing contrast intensity on response amplitude, compared with lower visual areas. However, not all of our analyses were indicative of increased invariance along the visual hierarchy. In particular, recovery from adaptation remained fairly stable, suggesting that the rate of adaptation does not change systematically across areas or that our measurements were not sensitive enough to pick up differences in this response property. (We return to this below in Discussion). In addition, response latency becomes more sensitive to stimulus contrast in higher visual areas. Importantly, changes in response properties between low and higher visual areas were to a large extent recapitulated by the DN model, suggesting that the model captures temporal response dynamics not just in early visual regions but across visual cortex more broadly.
Discussion
We demonstrated several nonlinearities in the neural dynamics of visual cortex, for example, saturation as stimulus contrast and duration increase, suppression for repeated stimuli at short intervals, and slower onsets at low contrast. Although each of these has been demonstrated previously an important goal in systems neuroscience is to understand how apparently disparate phenomena might be linked (Wandell et al., 2015). Here, we showed that a delayed normalization model predicts these responses in multiple human retinotopic maps.
Fitting one model to many stimuli
This DN model was developed to account for similar temporal phenomena in separate, independent studies (Zhou et al., 2019). Although that work showed that a single model form could account for a wide variety of neural data, the various datasets were fit separately because they came from different experiments, measurement types, and species. Temporal dynamics and fitted parameters differed substantially across datasets; for example, the time to peak of single-unit macaque V1 data were tens of ms but more than 100 ms for human ECoG broadband. A key advance here is that for a given cortical site, a single instance of the DN model fit simultaneously to many stimulus types captures temporal dynamics arising from temporal summation, adaptation, and variation in contrast.
Parallels between responses to repeated and low-contrast stimuli
A surprising observation is that response time courses to a repeated stimulus at high contrast and a nonrepeated stimulus at low contrast are remarkably similar. The delayed normalization model accounts for this through the time-varying relationship between stimulus drive and normalization. At low contrast, the stimulus drive never gets large relative to the normalization, and for repeated stimuli, there is lingering normalization from the first stimulus.
The similarity in responses does not imply that the two stimulus dimensions are perfectly conflated in the brain. For example, monkeys can detect stimulus repetitions regardless of contrast, implying some contrast-independent stimulus memory (Mehrpour et al., 2020). Nonetheless, the parallels in ECoG responses raise the prospect that behavioral measures, for example, detection thresholds or response time, will show similar patterns for the two stimulus manipulations and might be explained by a single model. Such a model could clarify how stimulus contrast interacts with cognitive phenomena like the attentional blink (Raymond et al., 1992). A dynamic normalization model has recently been used to explain behavioral effects of temporal attention (Denison et al., 2021). Our findings suggest that a dynamic normalization model might also explain how effects of temporal attention interact with stimulus contrast.
Links among ECoG, fMRI, and single-unit electrophysiology
We quantified ECoG responses as the time-varying broadband envelope. Field potential results differ dramatically depending on the measure. For example, the broadband response, but not the steady-state evoked potential, shows subadditive spatial summation (Winawer et al., 2013). Narrowband gamma oscillations and broadband power elevations show different stimulus selectivity (Ray and Maunsell, 2011; Hermes et al., 2015, 2019). We studied the broadband response because it appears most strongly connected to other measures, including fMRI (Hermes et al., 2017), spiking (Miller et al., 2009; Ray and Maunsell, 2011), and behavior (Miller et al., 2014), thereby facilitating comparisons with those studies.
The temporal phenomena we report have been demonstrated with fMRI and single-unit physiology. However, these methods leave open some questions better addressed with ECoG. For example, fMRI visual responses show subadditive temporal summation (Boynton et al., 1996; Huettel and McCarthy, 2000; Birn et al., 2001; Mukamel et al., 2004; Zhou et al., 2018). These effects could reflect a mixture of nonlinear summation in the BOLD signal and neural activity. Here, we demonstrated temporal subadditivity in population responses in human ECoG, paralleling single-cell recordings (Tolhurst et al., 1980). Similarly, fMRI shows response suppression to repeated stimuli (Grill-Spector et al., 2006). However, responses to stimuli separated by short intervals cannot be measured independently with fMRI, whereas ECoG allows for separate estimations of the response time courses. Mirroring single-cell recordings (Motter, 2006), we find that adaptation is associated with both a reduction of response amplitude and slower rise time.
The ECoG measures also provide important data not easily obtained in animal studies. We made systematic comparisons of temporal dynamics across many visual areas, which is typically not feasible in microelectrode recordings.
Changes in temporal dynamics across visual areas
Several studies find that time scales of temporal processing become longer ascending the visual hierarchy (Hasson et al., 2008; Weiner et al., 2010; Honey et al., 2012; Mattar et al., 2016; Zhou et al., 2018), paralleling increases in spatial receptive fields (Maunsell and Newsome, 1987). In contrast, a recent fMRI study reported no differences in the recovery time of repetition suppression across visual areas (Fritsche et al., 2020). We replicated both patterns, suggesting there is not a single processing time scale per area. When temporal dynamics are characterized by the period over which responses sum, we find systematic increases in time scale from earlier to higher areas (Fig. 11). However, when characterized as recovery time from adaptation (Fig. 13), time scales were relatively constant, consistent with Fritsche et al. (2020). These patterns are not contradictory as both are also observed in the model fits, indicating that even a relatively simple model can result in complex behavior.
Another property that varies across visual areas is contrast sensitivity (Tootell et al., 1998; Avidan et al., 2002; Lu and Roe, 2007). As with temporal windows, the degree of contrast invariance depends on the quantification. Specifically, response amplitudes become more invariant in higher visual areas, but response latencies do not; if anything, higher areas show greater latency differences. Thus, some information about stimulus contrast remains in the neural responses of later areas. The fact that sensitivity to contrast remains in the response timing but not amplitude means that measurements that average across a trial (like fMRI or mean spike rates) will miss this feature.
Space and time
Some changes in dynamics across visual areas parallel findings in the spatial domain; for example, spatial receptive fields and temporal summation windows increase in higher areas. However, spatial and temporal properties are not perfectly separable. To make analyses tractable, we kept spatial stimulus properties (other than contrast) constant. Our stimuli effectively drive responses in multiple visual maps, especially V1–hV4 (Kay et al., 2013b; Zhou et al., 2018), but higher maps may respond better to more complex stimuli (Sayres and Grill-Spector, 2008; Arcaro et al., 2009; Silson et al., 2016). We recently found that ventral-temporal and lateral-occipital ECoG responses were several times larger for naturalistic images than for simple textures, with the amount of adaptation depending on the category preference of the electrode (faces, bodies, objects; Brands et al., 2021). A complete characterization of temporal dynamics thus also requires incorporating spatial stimulus properties (and vice versa). An important yet unachieved goal for the field is a space-time model that simultaneously accounts for spatial summation, stimulus selectivity, and temporal dynamics throughout visual cortex.
Model failures and limitations
Although the DN model captured many response variations, we also noted some small but systematic model failures. The model underpredicts the transient response at low contrasts and for short ISI repeats. The DN model produces response transients because of sluggish normalization, whereas other models account for transient and sustained responses with distinct temporal channels (Horiguchi et al., 2009; Stigliani et al., 2017, 2019). It is likely that neither type of model is complete. Although multiple-channel models do not explain slower dynamics at low contrast, incorporating multiple channels into the driven responses of a DN model might help ameliorate model failures at low contrast and short ISIs.
Our results are subject to several limitations. First, not all participants contributed data to all maps. When differences in response properties are expected to be small (say, V1 vs V2), variability across participants may be larger than the map differences (Fig. 12). Therefore, our comparisons focused primarily on coarse groupings, earlier (V1–V3) versus later maps. Second, we did not measure retinotopic maps in individual participants leading to some uncertainty in electrode assignments. For this reason, we developed a probabilistic resampling method to incorporate this uncertainty into our measures of variability. Third, we did not have electrodes with sufficiently reliable responses in ventral stream regions beyond V3. Those regions could exhibit different temporal dynamics than lateral-occipital and dorsal-parietal maps (Stigliani et al., 2019), which may or may not be well captured by the DN model. An important future direction is to measure temporal dynamics in neural population responses with more extensive sampling of ventral visual cortex.
The fact that the same model form accurately fits responses in several cortical areas does not imply that each area is computing the same thing. Rather, it implies that some aspects of the responses are captured by a common model form (although differing in parameters). There is in fact evidence that cortical areas with very different stimulus selectivity, V1 and MT, manifest a similar computational architecture, differing primarily in their inputs rather than computations (Heeger et al., 1996). Fitting a single model form (such as a spatial receptive field) with separate parameters to different locations in the visual pathways facilitates comparisons. More generally, our model of any area, say V1, is not a model of what that area computes but rather a model that summarizes the computations of the complete circuitry from eye to brain, including feedforward, lateral, and feedback pathways sampled at that location. Some of the delayed temporal normalization measured in the V1 responses may be inherited from earlier processing stages or arise from feedback from higher areas. This is the same logic used when, say, measuring the receptive field of a visual neuron in terms of visual field locations.
Finally, this dataset may serve as a useful benchmark for testing other models. As an example, we computed predictions for our data from a few previously published models (Heeger, 1992; Stigliani et al., 2017, 2019; Fig. 9). To facilitate model comparison, we make the data publicly available with open code that implements models modularly, allowing fitting multiple models to the same data using automated cross-validation and area comparison.
Footnotes
This work was supported by National Institute of Mental Health Grant R01MH111417.
The authors declare no competing financial interests.
References
- Acerbi L, Ma WJ (2017) Practical Bayesian optimization for model fitting with Bayesian adaptive direct search. Adv Neural Inf Process Syst 30:1834–1844. [Google Scholar]
- Albrecht DG, Hamilton DB (1982) Striate cortex of monkey and cat: contrast response function. J Neurophysiol 48:217–237. 10.1152/jn.1982.48.1.217 [DOI] [PubMed] [Google Scholar]
- Albrecht DG, Geisler WS, Frazor RA, Crane AM (2002) Visual cortex neurons of monkeys and cats: temporal dynamics of the contrast response function. J Neurophysiol 88:888–913. 10.1152/jn.2002.88.2.888 [DOI] [PubMed] [Google Scholar]
- Arcaro MJ, McMains SA, Singer BD, Kastner S (2009) Retinotopic organization of human ventral visual cortex. J Neurosci 29:10638–10652. 10.1523/JNEUROSCI.2807-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avidan G, Harel M, Hendler T, Ben-Bashat D, Zohary E, Malach R (2002) Contrast sensitivity in human visual areas and its relationship to object recognition. J Neurophysiol 87:3102–3116. 10.1152/jn.2002.87.6.3102 [DOI] [PubMed] [Google Scholar]
- Benson NC, Winawer J (2018) Bayesian analysis of retinotopic maps. Elife 7:e40224. 10.7554/eLife.40224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson NC, Butt OH, Brainard DH, Aguirre GK (2014) Correction of distortion in flattened representations of the cortical surface allows prediction of V1-V3 functional organization from anatomy. PLoS Comput Biol 10:e1003538. 10.1371/journal.pcbi.1003538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn RM, Saad ZS, Bandettini PA (2001) Spatial heterogeneity of the nonlinear dynamics in the FMRI BOLD response. Neuroimage 14:817–826. 10.1006/nimg.2001.0873 [DOI] [PubMed] [Google Scholar]
- Boynton GM, Engel SA, Glover GH, Heeger DJ (1996) Linear systems analysis of functional magnetic resonance imaging in human V1. J Neurosci 16:4207–4221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brands AM, Devore S, Devinsky O, Doyle WK, Flinker A, Winawer J, Groen A II (2021) Adaptation of neural responses to naturalistic visual categories in low- and high visual cortex. In: European Conference on Visual Perception. Available at https://doi.org/10.1177%2F03010066211059887.
- Carandini M, Heeger DJ (2011) Normalization as a canonical neural computation. Nat Rev Neurosci 13:51–62. 10.1038/nrn3136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchland MM, Cunningham JP, Kaufman MT, Foster JD, Nuyujukian P, Ryu SI, Shenoy KV (2012) Neural population dynamics during reaching. Nature 487:51–56. 10.1038/nature11129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Denison RN, Carrasco M, Heeger DJ (2021) A dynamic normalization model of temporal attention. Nat Hum Behav 5:1674–1685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fritsche M, Lawrence SJD, de Lange FP (2020) Temporal tuning of repetition suppression across the visual cortex. J Neurophysiol 123:224–233. 10.1152/jn.00582.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN (2007) The neural basis of decision making. Annu Rev Neurosci 30:535–574. 10.1146/annurev.neuro.29.051605.113038 [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Henson R, Martin A (2006) Repetition and the brain: neural models of stimulus-specific effects. Trends Cogn Sci 10:14–23. 10.1016/j.tics.2005.11.006 [DOI] [PubMed] [Google Scholar]
- Hasson U, Yang E, Vallines I, Heeger DJ, Rubin N (2008) A hierarchy of temporal receptive windows in human cortex. J Neurosci 28:2539–2550. 10.1523/JNEUROSCI.5487-07.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heeger DJ (1992) Normalization of cell responses in cat striate cortex. Vis Neurosci 9:181–197. 10.1017/s0952523800009640 [DOI] [PubMed] [Google Scholar]
- Heeger DJ (1993) Modeling simple-cell direction selectivity with normalized, half-squared, linear operators. J Neurophysiol 70:1885–1898. 10.1152/jn.1993.70.5.1885 [DOI] [PubMed] [Google Scholar]
- Heeger DJ (2017) Theory of cortical function. Proc Natl Acad Sci U S A 114:1773–1782. 10.1073/pnas.1619788114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heeger DJ, Simoncelli EP, Movshon JA (1996) Computational models of cortical visual processing. Proc Natl Acad Sci U S A 93:623–627. 10.1073/pnas.93.2.623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermes D, Miller KJ, Noordmans HJ, Vansteensel MJ, Ramsey NF (2010) Automated electrocorticographic electrode localization on individually rendered brain surfaces. J Neurosci Methods 185:293–298. 10.1016/j.jneumeth.2009.10.005 [DOI] [PubMed] [Google Scholar]
- Hermes D, Miller KJ, Wandell BA, Winawer J (2015) Stimulus dependence of gamma oscillations in human visual cortex. Cereb Cortex 25:2951–2959. 10.1093/cercor/bhu091 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermes D, Nguyen M, Winawer J (2017) Neuronal synchrony and the relation between the blood-oxygen-level dependent response and the local field potential. PLOS Biol 15:e2001461. 10.1371/journal.pbio.2001461 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hermes D, Petridou N, Kay KN, Winawer J (2019) An image-computable model for the stimulus selectivity of gamma oscillations. Elife 8:e47035. 10.7554/eLife.47035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holdgraf C, et al. (2019) iEEG-BIDS, extending the brain imaging data structure specification to human intracranial electrophysiology. Sci Data 6:102. 10.1038/s41597-019-0105-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey CJ, Thesen T, Donner TH, Silbert LJ, Carlson CE, Devinsky O, Doyle WK, Rubin N, Heeger DJ, Hasson U (2012) Slow cortical dynamics and the accumulation of information over long timescales. Neuron 76:423–434. 10.1016/j.neuron.2012.08.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horiguchi H, Nakadomari S, Misaki M, Wandell BA (2009) Two temporal channels in human V1 identified using fMRI. Neuroimage 47:273–280. 10.1016/j.neuroimage.2009.03.078 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huettel SA, McCarthy G (2000) Evidence for a refractory period in the hemodynamic response to visual stimuli as measured by MRI. Neuroimage 11:547–553. 10.1006/nimg.2000.0553 [DOI] [PubMed] [Google Scholar]
- Kay KN, Winawer J, Rokem A, Mezer A, Wandell BA (2013a) A two-stage cascade model of BOLD responses in human visual cortex. PLoS Comput Biol 9:e1003079. 10.1371/journal.pcbi.1003079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay KN, Winawer J, Mezer A, Wandell BA (2013b) Compressive spatial summation in human visual cortex. J Neurophysiol 110:481–494. 10.1152/jn.00105.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubilius J, Schrimpf M, Kar K, Hong H, Majaj NJ, Rajalingham R, Issa EB, Bashivan P, Prescott-Roy J, Schmidt K, Nayebi A, Bear D, Yamins DLK, DiCarlo JJ (2019) Brain-like object recognition with high-performing shallow recurrent ANNs. arXiv:1909.06161. 10.48550/arXiv.1909.06161 [DOI] [Google Scholar]
- Lu HD, Roe AW (2007) Optical imaging of contrast response in macaque monkey V1 and V2. Cereb Cortex 17:2675–2695. 10.1093/cercor/bhl177 [DOI] [PubMed] [Google Scholar]
- Mattar MG, Kahn DA, Thompson-Schill SL, Aguirre GK (2016) Varying timescales of stimulus integration unite neural adaptation and prototype formation. Curr Biol 26:1669–1676. 10.1016/j.cub.2016.04.065 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maunsell JHR, Newsome WT (1987) Visual processing in monkey extrastriate cortex. Annu Rev Neurosci 10:363–401. 10.1146/annurev.ne.10.030187.002051 [DOI] [PubMed] [Google Scholar]
- Mehrpour V, Meyer T, Simoncelli EPRust NC (2020) Pinpointing the neural signatures of single-exposure visual recognition memory. Proc Natl Acad Sci U S A 118:e2021660118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikaelian S, Simoncelli EP (2001) Modeling temporal response characteristics of V1 neurons with a dynamic normalization model. Neurocomputing 38-40:1461–1467. 10.1016/S0925-2312(01)00529-X [DOI] [Google Scholar]
- Miller KJ, Sorensen LB, Ojemann JG, den Nijs M (2009) Power-law scaling in the brain surface electric potential. PLoS Comput Biol 5:e1000609. 10.1371/journal.pcbi.1000609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KJ, Honey CJ, Hermes D, Rao RP, denNijs M, Ojemann JG (2014) Broadband changes in the cortical surface potential track activation of functionally diverse neuronal populations. Neuroimage 85:711–720. 10.1016/j.neuroimage.2013.08.070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Motter BC (2006) Modulation of transient and sustained response components of V4 neurons by temporal crowding in flashed stimulus sequences. J Neurosci 26:9683–9694. 10.1523/JNEUROSCI.5495-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukamel R, Harel M, Hendler T, Malach R (2004) Enhanced temporal non-linearities in human object-related occipito-temporal cortex. Cereb Cortex 14:575–585. 10.1093/cercor/bhh019 [DOI] [PubMed] [Google Scholar]
- Naka KI, Rushton WAH (1966) S-potentials from colour units in the retina of fish (Cyprinidae). J Physiol 185:536–555. 10.1113/jphysiol.1966.sp008001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oostenveld R, Fries P, Maris E, Schoffelen J-M (2011) FieldTrip: open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput Intell Neurosci 2011:156869–156869. 10.1155/2011/156869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ray S, Maunsell JHR (2011) Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLoS Biol 9:e1000610. 10.1371/journal.pbio.1000610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raymond J, Shapiro K, Arnell K (1992) Temporary suppression of visual processing in an RSVP task: an attentional blink? J Exp Psychol Hum Percept Perform 18:849–860. 10.1037/0096-1523.18.3.849 [DOI] [PubMed] [Google Scholar]
- Sayres R, Grill-Spector K (2008) Relating retinotopic and object-selective responses in human lateral occipital cortex. J Neurophysiol 100:249–267. 10.1152/jn.01383.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silson EH, Groen IIA, Kravitz DJ, Baker CI (2016) Evaluating the correspondence between face-, scene-, and object-selectivity and retinotopic organization within lateral occipitotemporal cortex. J Vis 16(6):14 1–21. 10.1167/16.6.14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinz F, Bethge M (2013) Temporal adaptation enhances efficient contrast gain control on natural images. PLoS Comput Biol 9:e1002889. 10.1371/journal.pcbi.1002889 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spoerer CJ, Kietzmann TC, Mehrer J, Charest I, Kriegeskorte N (2020) Recurrent neural networks can explain flexible trading of speed and accuracy in biological vision. PLOS Comput Biol 16:e1008215. 10.1371/journal.pcbi.1008215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stigliani A, Jeska B, Grill-Spector K (2017) Encoding model of temporal processing in human visual cortex. Proc Natl Acad Sci U S A 114:E11047–E11056. 10.1073/pnas.1704877114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stigliani A, Jeska B, Grill-Spector K (2019) Differential sustained and transient temporal processing across visual streams. PLOS Comput Biol 15:e1007011. 10.1371/journal.pcbi.1007011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolhurst DJ, Walker NS, Thompson ID, Dean AF (1980) Non-linearities of temporal summation in neurones in area 17 of the cat. Exp Brain Res 38:431–435. 10.1007/BF00237523 [DOI] [PubMed] [Google Scholar]
- Tootell RBH, Hadjikhani NK, Vanduffel W, Liu AK, Mendola JD, Sereno MI, Dale AM (1998) Functional analysis of primary visual cortex (V1) in humans. Proc Natl Acad Sci U S A 95:811–817. 10.1073/pnas.95.3.811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai JJ, Wade AR, Norcia AM (2012) Dynamics of normalization underlying masking in human visual cortex. J Neurosci 32:2783–2789. 10.1523/JNEUROSCI.4485-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wandell BA, Winawer J, Kay KN (2015) Computational modeling of responses in human visual cortex. In: Brain mapping (Toga AW, ed), pp 651–659. Academic. 10.1016/B978-0-12-397025-1.00347-X [DOI] [Google Scholar]
- Wang L, Mruczek REB, Arcaro MJ, Kastner S (2015) Probabilistic maps of visual topography in human cortex. Cereb Cortex 25:3911–3931. 10.1093/cercor/bhu277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X-J (2012) Neural dynamics and circuit mechanisms of decision-making. Curr Opin Neurobiol 22:1039–1046. 10.1016/j.conb.2012.08.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner KS, Sayres R, Vinberg J, Grill-Spector K (2010) fMRI-adaptation and category selectivity in human ventral temporal cortex: regional differences across time scales. J Neurophysiol 103:3349–3365. 10.1152/jn.01108.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winawer J, Kay KN, Foster BL, Rauschecker AM, Parvizi J, Wandell BA (2013) Asynchronous broadband signals are the principal source of the BOLD response in human visual cortex. Curr Biol 23:1145–1153. 10.1016/j.cub.2013.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang AI, Wang X, Doyle WK, Halgren E, Carlson C, Belcher TL, Cash SS, Devinsky O, Thesen T (2012) Localization of dense intracranial electrode arrays using magnetic resonance imaging. Neuroimage 63:157–165. 10.1016/j.neuroimage.2012.06.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J, Benson NC, Kay KN, Winawer J (2018) Compressive temporal summation in human visual cortex. J Neurosci 38:691–709. 10.1523/JNEUROSCI.1724-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J, Benson NC, Kay K, Winawer J (2019) Predicting neuronal dynamics with a delayed gain control model. PLOS Comput Biol 15:e1007484. 10.1371/journal.pcbi.1007484 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All code used for the purpose of this article can be found at the GitHub repositories mentioned above. The ieeg-BIDS-formatted data, derivatives, the processed dataset and model fits are available on OpenNeuro (https://openneuro.org/datasets/ds004194).