Elastic properties and shape of the Piezo dome underlying its mechanosensory function

Significance

Over the past two decades, structural biology has provided much insight into the shape of membrane proteins. Beyond shape, however, membrane protein function can also depend on the protein’s elastic properties. It has been difficult to characterize protein elastic properties in freestanding, unperturbed lipid bilayer membranes, which is the scenario most relevant for cell membranes. Here we show that, through a physical understanding of how proteins deform lipid bilayer membranes, it is possible to deduce elastic properties of membrane proteins solely from observations of membrane shape. On this basis, we provide the biophysical principles and mechanisms underlying the tension-dependent activation of the mechanosensitive ion channel Piezo, which mediates the sensation of touch and many other important biological processes.

Abstract

We show in the companion paper that the free membrane shape of lipid bilayer vesicles containing the mechanosensitive ion channel Piezo can be predicted, with no free parameters, from membrane elasticity theory together with measurements of the protein geometry and vesicle size [C. A. Haselwandter, Y. R. Guo, Z. Fu, R. MacKinnon, Proc. Natl. Acad. Sci. U.S.A., 10.1073/pnas.2208027119 (2022)]. Here we use these results to determine the force that the Piezo dome exerts on the free membrane and hence, that the free membrane exerts on the Piezo dome, for a range of vesicle sizes. From vesicle shape measurements alone, we thus obtain a force–distortion relationship for the Piezo dome, from which we deduce the Piezo dome’s intrinsic radius of curvature, $42\pm 12$ nm, and bending stiffness, $18\pm 2.1 k_{B}T$, in freestanding lipid bilayer membranes mimicking cell membranes. Applying these estimates to a spherical cap model of Piezo embedded in a lipid bilayer, we suggest that Piezo’s intrinsic curvature, surrounding membrane footprint, small stiffness, and large area are the key properties of Piezo that give rise to low-threshold, high-sensitivity mechanical gating.

Piezo 1 and 2 are called mechanosensitive ion channels because they conduct ions across the cell membrane when a mechanical force is applied to the cell (1). Thus, Piezo channels are somehow rigged to enable a mechanical force to open their pore. The ensuing ion conduction triggers subsequent processes inside the cell, culminating in a cell’s response to the mechanical force. This sequence of events, force on the membrane → ion conduction → cell response, is central to numerous biological processes (2, 3). Mediated by Piezo channels, these include, but are not limited to, volume regulation in red blood cells, the control of vascular blood pressure, and the sensation of touch (4, 5).

What physical properties endow Piezo channels with responsiveness to mechanical force? Their unique shape among ion channels has inspired one proposal, known as the membrane dome model (6). Piezo channels in their closed conformation are curved, in contrast to most other ion channels and membrane proteins that exhibit an approximately planar arrangement of transmembrane helices (7). Consequently, Piezo channels locally curve the membrane into a “Piezo dome” and surrounding “membrane footprint” (8). The membrane dome model posits that an open Piezo channel will be less curved, more like other membrane proteins (6, 8, 9), and it is known that Piezo can change its shape. Cryoelectron microscopy (cryo-EM) studies have shown that Piezo channels in lipid bilayer vesicles change their curvature depending on vesicle size (9, 10). High-speed atomic force microscopy (HS-AFM) has been used to flatten Piezo (9) and, by cryo-EM, nearly flat Piezo channels with a pore that appears to be somewhat widened compared to curved Piezo channels have been observed (11). If it is true that Piezo must reduce its curvature to open its pore, then increased lateral membrane tension will favor the open conformation by a work energy term $\gamma \mathrm{\Delta }{A}_{\text{proj}}$, where $\gamma$ is the lateral membrane tension and $\mathrm{\Delta }{A}_{\text{proj}}$ is the expansion of Piezo’s projected in-plane area due to its reduced curvature, which includes contributions arising from Piezo’s membrane footprint (6, 8). The membrane dome model is still unproven, but it rationalizes Piezo’s highly unusual curved shape.

Beyond shape alone, to understand Piezo’s responsiveness to mechanical force, we need to know how its shape changes when force is applied. To use an analogy: to describe a spring’s mechanical properties we need to know how its shape (that is, its length) depends on force; for a linear spring, for instance, the spring’s length is proportional to load, and this dependence is captured in the Hooke constant (spring stiffness). Structural biology lets us determine a molecule’s shape, but how can we do this while applying a force to a molecule? Furthermore, how do we apply a force while the molecule (in this case, a mechanosensitive ion channel) resides in an unsupported free membrane environment?

When a Piezo ion channel resides in a lipid bilayer vesicle, the curved lipid membrane surrounding the channel exerts a force on it. Different-sized vesicles exert different values of force, causing the channel to change its shape. In the companion paper, we developed a continuum elasticity theory of Piezo vesicle shape, and showed that this theory predicts Piezo vesicle shapes that are in quantitative agreement with those observed experimentally (10). In the present study, we build on this work to deduce Piezo’s force–shape relationship, which we then relate to Piezo’s mechanosensitive gating. In particular, we extract the force curve associated with the Piezo vesicles described in our companion paper (10), and apply it to understand how Piezo’s curvature, stiffness, and area give rise to its mechanosensory properties.

A point regarding notation: As in our companion paper (10), we refer with the term Piezo channel to the ion channel protein. Piezo dome refers to the functional unit consisting of the ion channel protein plus the lipid bilayer contained within the channel’s approximate perimeter, with the lipid membrane connecting smoothly across the Piezo dome boundary. We refer to the region of free membrane, or free lipid bilayer, outside the Piezo dome that is deformed by Piezo as Piezo’s membrane footprint. Piezo vesicle refers to a lipid bilayer vesicle containing Piezo.

Results

Shape of Piezo Vesicles.

Before deriving the force curve of the Piezo dome, we review some of the results of our companion paper (10) most pertinent to the present study. In our companion paper, we show how membrane elasticity theory can be used to predict the shape of the free membrane, outside the Piezo dome, in Piezo vesicles (10). Our starting point is thereby the Helfrich energy equation for the free membrane,

$$G_M=\frac{K_b}{2}{{\displaystyle \int }}^{}dA {\left(c_1+c_2\right)}^2,$$ [1]

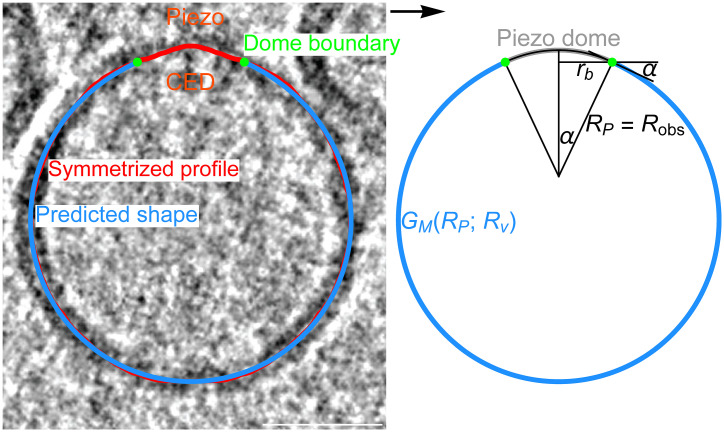
where the constant $K_b$ is the lipid bilayer bending modulus, $c_1$ and $c_2$ are the principal curvatures of the midmembrane surface, and the integral is carried out over the entire free membrane surface (12). We use $K_b= 20 k_{B}T$, which approximates the bending modulus of the lipid bilayers in our Piezo vesicles (13). Through Eq. 1, each possible free membrane shape gives an associated value of $G_M$. We determine the free membrane shape minimizing $G_M$ by solving the Hamilton equations associated with Eq. 1, subject to suitable constraints. One key constraint thereby specifies the size of Piezo vesicles. We find it convenient to define the vesicle size through the radius of a hypothetical sphere comprising the Piezo dome plus the free membrane, $R_v$ (10). Furthermore, Eq. 1 suggests that two key properties of the Piezo dome—the Piezo dome–free membrane contact angle, $\alpha$, and the projected in-plane radius of the Piezo dome, $r_b$—govern how Piezo affects the free membrane shape (Fig. 1). Comparing the free membrane shapes calculated from Eq. 1 for seven Piezo vesicles, ranging in size from $R_v\approx 12.1 \text{nm}$ to $R_v\approx 36.2 \text{nm}$, with the corresponding shapes obtained by tomographic reconstruction of cryo-EM images, we find that minimization of Eq. 1 successfully predicts the free membrane shape of Piezo vesicles, without any free parameters (Fig. 1) (10).

Fig. 1.

Predicting the shape of Piezo vesicles. Oriented Piezo vesicle image obtained by cryo-EM tomography (Left), associated symmetrized (measured) Piezo vesicle profile (red curve; Left), Piezo dome boundary obtained by integrating out a vesicle surface area equal to $A_P=450 {\text{nm}}^2$ starting at the vesicle north pole (green dots; Left and Right), and corresponding predicted free membrane profile (blue curves Left and Right). The predicted Piezo vesicle profile is obtained, with no free parameters, from the membrane elasticity theory of Piezo vesicle shape described in our companion paper (10), and minimizes the Helfrich energy equation, Eq. 1. The value of the minimized free membrane bending energy, $G_M\left(R_P;R_v\right)$ in Eq. 1, depends on the vesicle size, $R_v$, and on the radius of curvature at the Piezo dome boundary, $R_P$, with $R_{\text{obs}}$ denoting the values of $R_P$ associated with the predicted free membrane shapes in figure 4 of our companion paper (10). We obtain $R_{\text{obs}}$ from $R_{\text{obs}}=\frac{r_b}{\sin \alpha }$, where $r_b$ and $\alpha$ denote the in-plane Piezo dome radius and the Piezo dome contact angle associated with the predicted free membrane shapes in figure 4 of our companion paper (10), respectively. The vesicle shown here corresponds to vesicle 6 with $R_v\approx 35.0 \text{nm}$ in figure 4 of our companion paper (10). CED marks the Piezo C-terminal extracellular domain (CED). (Scale bar, 26 nm.)

The observed shape of the Piezo dome depends on the Piezo vesicle radius $R_v$, with the Piezo dome becoming less curved as $R_v$ is increased. In our companion paper, we show that if one models the Piezo dome as a spherical cap with fixed area $A_{\text{cap}}$, the measured changes in the shape of the Piezo dome are approximately captured by a single parameter, the Piezo dome radius of curvature $R_P=\frac{r_b}{\sin \alpha }$ (Fig. 1) (10). For a given value of $A_{\text{cap}}$, this model of the Piezo dome geometrically defines the Piezo dome properties affecting membrane shape deformations in Eq. 1, $\alpha$ and $r_b$, as a function of $R_P$ (14). For each measured Piezo vesicle, we choose here $A_{\text{cap}}$ so that we obtain the values of $\alpha$ and $r_b$ associated with the predicted free membrane shapes in figure 4 of our companion paper (10), and denote the corresponding value of $R_P$ by $R_{\text{obs}}$. To be clear, our approach for calculating the forces in Piezo vesicles does not rely on the spherical cap model of the Piezo dome. We employ here this model because it is simple and seems to capture, for the Piezo dome, the approximate relation between $\alpha$ and $r_b$.

The Force Curve.

As reviewed above, our companion paper demonstrates that minimization of the Helfrich energy equation, Eq. 1, successfully predicts the observed shapes of the free membrane in Piezo vesicles, over a range of vesicle radii $R_v$ (10). We denote this minimum energy by $G_M\left(R_P;R_v\right)$ to emphasize that distinct vesicle sizes $R_v$ yield, in general, a distinct dependence of $G_M$ on the Piezo dome radius of curvature $R_P$. We now analyze the balance of forces between the free membrane and the Piezo dome in Piezo vesicles. To demonstrate how this will work, we consider the following thought experiment.

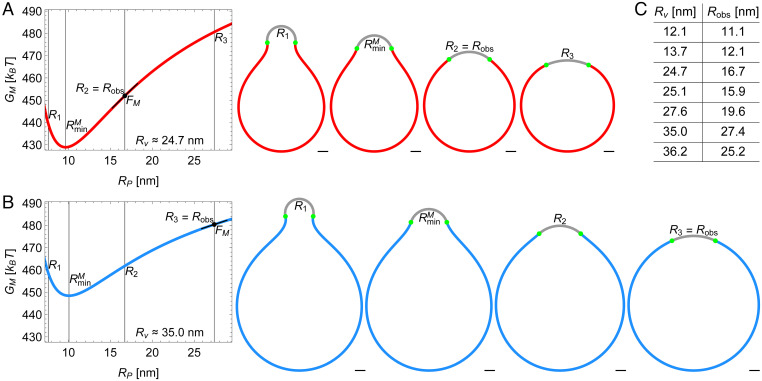
A hypothetical Piezo vesicle, with $R_v\approx 24.7 \text{nm}$, contains a Piezo dome that we model, as described above, as a spherical cap with fixed area $A_{\text{cap}}$ and variable radius of curvature $R_P$ (Fig. 2A). Now imagine that $R_P$ can be adjusted to any desired value; because $A_{\text{cap}}$ is fixed,* $R_P$ will specify $\alpha$ and $r_b$. For a given $R_P$, we calculate the free membrane shape by minimizing the Helfrich energy equation, Eq. 1, employing as input parameter values the values of $\alpha$ and $r_b$ obtained from $R_P$ along with the measured free membrane area. We then enter this shape into Eq. 1 to calculate the corresponding value of the free membrane energy, $G_M\left(R_P;R_v\right)$. Repeating this calculation for a range of $R_P$ values, we graph $G_M$ as a function of $R_P$, keeping $R_v$ fixed. This graph shows how the free membrane energy varies with $R_P$ for a given Piezo vesicle (Fig. 2A). We find that when Piezo has a radius of curvature $R_P=R_{\text{min}}^M\approx 9.67 \text{nm}$, the free membrane energy is least for the Piezo vesicle considered here. Some examples of the predicted free membrane shapes for specific values of $R_P$ are shown (Fig. 2A).

Fig. 2.

Energy landscape of Piezo vesicle shape. Stationary lipid membrane bending energy $G_M\left(R_P;R_v\right)$ as a function of Piezo dome radius of curvature $R_P$ for (A) the Piezo vesicle radius $R_v\approx 24.7 \text{nm}$ [vesicle 3 in figure 4 of our companion paper (10)] and (B) the Piezo vesicle radius $R_v\approx 35.0 \text{nm}$ [vesicle 6 in figure 4 of our companion paper (10)] together with selected vesicle cross-sections. These correspond to $R_P=R_1=7.6 \text{nm}$, $R_P=R_{\text{min}}^M\approx 9.67 \text{nm}$ in A and $R_P=R_{\text{min}}^M\approx 10.1 \text{nm}$ in B, $R_P=R_2\approx 16.7 \text{nm}$, and $R_P=R_3\approx 27.4 \text{nm}$. In A, $R_2$ is equal to the observed value of $R_P$, $R_2=R_{\text{obs}}$, while $R_3=R_{\text{obs}}$ in B. For each Piezo vesicle, we describe the Piezo dome geometry as a spherical cap with fixed cap area $A_{\text{cap}}$. The in-plane Piezo dome radius $r_b$ and the Piezo dome contact angle $\alpha$ associated with the predicted free membrane shapes in figure 4 of our companion paper (10) determine, for each Piezo vesicle, $A_{\text{cap}}$ via $A_{\text{cap}}=\frac{2\pi r_b^2}{1+\cos \alpha }$. (Scale bars, 5 nm.) (C) The table shows $R_{\text{obs}}$ vs. $R_v$ for the seven Piezo vesicles in figure 4 of our companion paper (10). The corresponding spherical cap areas $A_{\text{cap}}$ are approximately $471$, $414$, $421$, $471$, $428$, $444$, and $442 {\text{nm}}^2$ (from top to bottom).

The vesicle radius $R_v\approx 24.7 \text{nm}$ in the above thought experiment corresponds to the radius of measured Piezo vesicle 3 in figure 4 of our companion paper (10). Notably, Piezo vesicle 3, with an observed Piezo dome radius of curvature $R_P=R_{\text{obs}}\approx 16.7 \text{nm}$, does not look like the vesicle with least free membrane energy in the thought experiment, which would be associated with a Piezo dome radius of curvature $R_{\text{min}}^M\approx 9.67 \text{nm}$ (Fig. 2A). The discrepancy between the thought experiment and the measured Piezo vesicle is explicable because the thought experiment calculates only the free membrane contribution to the shape energy of a Piezo vesicle. In other words, if the Piezo dome did not contribute to the total energy of the Piezo vesicle, then it would adopt $R_P\approx 9.67 \text{nm}$ in a Piezo vesicle with $R_v\approx 24.7 \text{nm}$. However, the Piezo dome clearly does contribute to the total energy of a Piezo vesicle, expressed as $G_{\text{tot}}=G_M+G_P,$ where $G_P\left(R_P\right)$ is the Piezo dome contribution. The minimum energy shape (i.e., the shape corresponding to $R_P=R_{\text{obs}}$) then must occur when $\frac{\partial G_{\text{tot}}}{\partial R_P}=0.$ Here, the partial derivative notation reminds us that $G_{\text{tot}}$ is also a function of the Piezo vesicle radius $R_v$, which is held constant in the derivative with respect to $R_P$. From $G_{\text{tot}}=G_M+G_P$, we have $\frac{\partial G_{\text{tot}}}{\partial R_P}=\frac{\partial G_M}{\partial R_P}+\frac{\partial G_P}{\partial R_P}=0$ at $R_P=R_{\text{obs}}$ and therefore, $\frac{\partial G_P}{\partial R_P}=-\frac{\partial G_M}{\partial R_P}$ at $R_P=R_{\text{obs}}$. This last equation, rewritten as

$$\frac{\partial G_P}{\partial R_P}\equiv F_P=-\frac{\partial G_M}{\partial R_P}\equiv -F_M$$ [2]

at $R_P=R_{\text{obs}}$, expresses the equilibrium balance of forces between the Piezo dome and the free membrane in Piezo vesicles. In words, the slope of $G_M\left(R_P;R_v\right)$ with respect to $R_P$, evaluated at $R_P=R_{\text{obs}}$, equals the force exerted on the free membrane by the Piezo dome, $F_M$, and minus this slope is the force exerted on the Piezo dome by the free membrane, $F_P$. An intuitive understanding of this balance of forces can be grasped through inspection of the hypothetical vesicle shapes for $R_v\approx 24.7 \text{nm}$ (Fig. 2A). The free membrane tends toward its minimum energy shape associated with $R_P=R_{\text{min}}^M$, while the Piezo dome tends toward a larger $R_P$ (i.e., a flatter shape). A balance of forces is reached at an intermediate radius of curvature, when $R_P=R_{\text{obs}}$. Thus, the Piezo vesicle’s curved free membrane “squeezes” the Piezo dome, like compressing a spring, to be more curved than it would be in an asymptotically planar membrane. The force that the free membrane exerts on the Piezo dome in the measured Piezo vesicle 3 [i.e., minus the slope of $G_M\left(R_P;R_v\right)$ with respect to $R_P$ at $R_P=R_{\text{obs}}$] is given by $F_P\approx -3.6 \frac{k_{B}T}{\text{nm}}\approx -15 \text{pN}$. The minus sign here indicates that $F_P$ tends to decrease the value of $R_P$. From this analysis of the measured Piezo vesicle 3, we conclude that when the Piezo dome has a compressive force $F_P\approx -15 \text{pN}$ applied to it by the free vesicle membrane, it has a radius of curvature $R_P\approx 16.7 \text{nm}$.

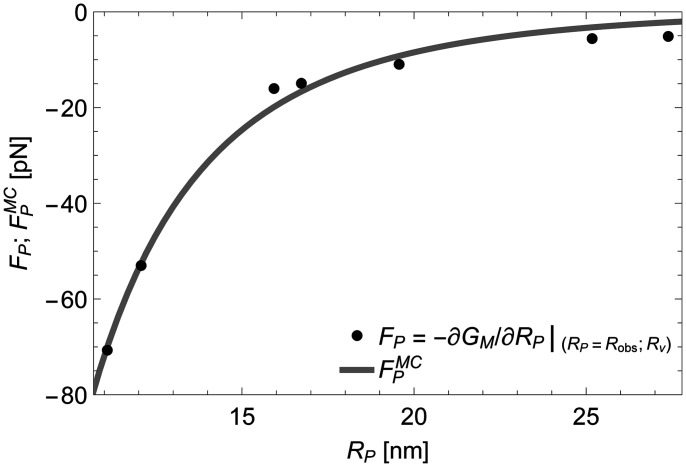
In Fig. 2B, we analyze in the same manner a larger vesicle with radius $R_v \approx 35.0 \text{nm}$, which corresponds to the measured Piezo vesicle 6 in figure 4 of our companion paper (10) and is also shown in Fig. 1. For this vesicle, the experimentally determined $R_{\text{obs}}\approx 27.4 \text{nm}$. From Eq. 2, the associated slope of $G_M\left(R_P;R_v\right)$ with respect to $R_P$ yields a force on the Piezo dome $F_P\approx -5.1 \text{pN}$. Again, the minus sign indicates a compressive force on the Piezo dome by the free vesicle membrane but, in this case, the force has a smaller magnitude. Application of Eq. 2 to all seven measured Piezo vesicles (Fig. 2C) yields a set of seven force–displacement values, $(R_P, F_P$), graphed in Fig. 3. The graph shows that highly curved vesicles (i.e., vesicles with small $R_v$) apply a large compressive force to curve the Piezo dome, and that larger vesicles exert a smaller force. Across the range of Piezo vesicle sizes considered here, the force on the Piezo dome varies from approximately $-71$ to $-5.1 \text{pN}$. In the limit of an infinitely large vesicle (i.e., in an asymptotically planar membrane without lateral tension), the surrounding membrane would exert no net elastic force on the Piezo dome. Thus, in a planar, tensionless membrane, the Piezo dome would adopt a shape that conforms to its intrinsic curvature, which we describe next.

Fig. 3.

Mechanics of the Piezo dome. Force exerted on the Piezo dome, $F_P$, for the observed Piezo dome radii of curvature, $R_P=R_{\text{obs}}$, obtained from (minus) the derivative of the stationary free membrane bending energy with respect to $R_P$, $F_P=-\frac{\partial G_M}{\partial R_P}$ in Eq. 2, at $R_P=R_{\text{obs}}$ for the measured Piezo vesicle radii $R_v$ in Fig. 2C. In mechanical equilibrium of the Piezo–membrane system, the restoring force generated internally by the Piezo dome is given by $-F_P$. The gray curve shows the force on the Piezo dome obtained by fitting the mean curvature force in Eq. 4, $F_P^{MC}\left(R_P\right)$, to the force–displacement values of the Piezo dome, $(R_P, F_P$), yielding $K_P=18\pm 2.1 k_{B}T$ and $R_0=42\pm 12 \text{nm}$ in Eqs. 3 and 4.

Relating Mechanics to Piezo Structure.

The force–displacement curve of a spring can be used to deduce key mechanical properties of the spring, such as its stiffness. Similarly, the force–displacement values of the Piezo dome, $(R_P, F_P$) in Fig. 3, can be used to deduce mechanical properties of the Piezo dome. To this end, it is instructive to consider, inspired by the Piezo dome shapes found in our companion paper, a highly simplified model of the energetics of the Piezo dome (10). In this model, we describe the Piezo dome as a spherical cap of fixed area $A_P=450 {\text{nm}}^2$. Furthermore, we adapt Eq. 1 to the Piezo dome itself, replacing the lipid bilayer bending modulus $K_b$ by the Piezo dome bending modulus $K_P$ and allowing for a preferred, intrinsic radius of curvature of the Piezo dome, $R_0$. We thus have the following mean curvature energy of the Piezo dome,

$$G_P^{MC}\left(R_P\right)=\frac{K_P}{2}{A}_P{\left(\frac{2}{R_P}-\frac{2}{R_0}\right)}^2,$$ [3]

where we have noted that the principal curvatures $c_1=c_2=\frac{1}{R_P}$ for a spherical cap with radius of curvature $R_P$. According to Eq. 3, the Piezo dome will adopt a radius of curvature $R_P=R_0$ if it is not perturbed by external forces. In other words, Eq. 3 implies that the Piezo dome’s minimum energy state occurs when $R_P=R_0$, in analogy to the natural length of a spring that can be compressed or stretched. Differentiation of Eq. 3 with respect to $R_P$ gives the mean curvature force,

$$F_P^{MC}\left(R_P\right)=\frac{4A_P K_P \left(R_P-R_0\right)}{R_P^3 R_0}.$$ [4]

The solid curve in Fig. 3 is a fit of $F_P^{MC}\left(R_P\right)$ to the force–displacement values of the Piezo dome, $(R_P, F_P)$. There are two fitting parameters in Eq. 4: $K_P$ ($=18\pm 2.1 k_{B}T$) and $R_0$ ($=42\pm 12 \text{nm}$). Note that the Piezo force curve data in Fig. 3 and, hence, the values of $K_P$ and $R_0$ depend on the lipid bilayer composition through, for instance, the bilayer bending modulus $K_b$ in Eq. 1 (13). Furthermore, to examine the dependence of $K_P$ and $R_0$ on the cap area $A_P,$ we obtain $K_P=17\pm 2.1 k_{B}T$ and $R_0=40\pm 11 \text{nm}$ for $A_P=410 {\text{nm}}^2$ and $K_P=18\pm 2.0 k_{B}T$ and $R_0=45\pm 13 \text{nm}$ for $A_P=490 {\text{nm}}^2$ (SI Appendix, Fig. S1). Clearly, the values of $K_P$ and $R_0$ depend only weakly on the value of $A_P$. This means that uncertainty in the location of the Piezo dome boundary will have little impact on the estimates of $K_P$ and $R_0$ for the Piezo dome.

While Eqs. 3 and 4 are seen to capture the basic trends in the Piezo force curve data in Fig. 3, we note several potential shortcomings of this model. First, while we provide evidence in our companion paper that the shape of the Piezo dome approximately conforms to a spherical cap geometry, the observed Piezo dome shapes do not, strictly speaking, show constant curvatures, as assumed in Eqs. 3 and 4 (10). Second, Eqs. 3 and 4 describe the Piezo dome as a homogeneous material, with constant $K_P$. Since the Piezo dome is composed of both a lipid bilayer and the Piezo protein, this assumption can only be correct in an approximate sense. Third, we focused in Eqs. 3 and 4 on contributions to the Piezo dome mechanics due to the mean curvature of the Piezo dome at the midmembrane surface and neglected any contributions due to the Gaussian curvature of the Piezo dome. The Gaussian curvature is expected to yield a contribution to the Piezo dome energy that depends on the detailed shape of the bilayer–protein boundary and is unlikely to show the simple dependence on $R_P$ assumed in Eq. 3 (15). Given the limited Piezo force curve data currently available, we focus here on the highly simplified model in Eqs. 3 and 4, which already provides a reasonably good fit with only two fitting parameters.

The force curve in Fig. 3 suggests that the Piezo dome has a radius of curvature $R_P\sim 40 \text{nm}$ in an asymptotically planar membrane without lateral tension, such as one might find on the surface of a mechanically unperturbed cell. The highly curved structures ($R_P\sim 10 \text{nm})$ of Piezo 1 and 2, determined in detergent micelles, indicate that Piezo proteins that are removed from the membrane are most stable in a conformation with high curvature. However, considering the space between Piezo’s extended protein arms, the area of a Piezo dome in a membrane comprises ∼75% lipid bilayer and 25% protein. As per Eq. 1, the energy cost to curve this bilayer away from a plane is considerable. It seems likely that the increased radius of curvature, from $R_P\sim 10 \text{nm}$ observed in isolated Piezo proteins to $R_P\sim 40 \text{nm}$ in a planar membrane, reflects an equilibrium balance of forces between the Piezo protein and the bilayer within the Piezo dome (SI Appendix, Fig. S2). Whatever the detailed molecular mechanisms involved, the force curve informs us that Piezo in planar cell membranes should be flatter in shape than the highly curved Piezo proteins in detergent micelles.

The bending modulus of the Piezo dome, $K_P=18\pm 2.1 k_{B}T$, is indistinguishable from the bending modulus of the pure lipid bilayer membrane used here, $K_b = 20 k_{B}T$. On the one hand, given that the Piezo dome’s area is $\sim 75\%$ lipid membrane, this might not seem surprising. On the other hand, we wonder how the Piezo protein avoids adding stiffness to the Piezo dome—after all, the Piezo protein is an integral part of the dome’s structure. How Piezo creates the membrane dome by introducing intrinsic curvature without increasing stiffness is unknown. However, the functional advantage afforded by these properties—intrinsic curvature without increased stiffness—can be understood when we consider their implications for sensing mechanical forces.

Relating Mechanics and Structure to Piezo Gating.

Now we consider the implications of $R_0\approx 42 \text{nm}$ and $K_P\approx 18 k_{B}T$ for the membrane dome model of mechanosensitive gating using a thought experiment. To start, we embed a Piezo dome with energy $G_P^{MC}\left(R_P\right)$ in Eq. 3 into an asymptotically planar free membrane that may be at a finite lateral tension $\gamma$. We refer to the Piezo dome plus its surrounding membrane as the Piezo–membrane system. The shape energy of the Piezo–membrane system is given by

$$G_{\text{sys}}\left(R_P\right)=\frac{K_P}{2}{A}_P{\left(\frac{2}{R_P}-\frac{2}{R_0}\right)}^2+\frac{K_b}{2}{{\displaystyle \int }}^{\text{}}dA {\left(c_1+c_2\right)}^2-\gamma \mathrm{\Delta }{A}_{\text{proj}}.$$ [5]

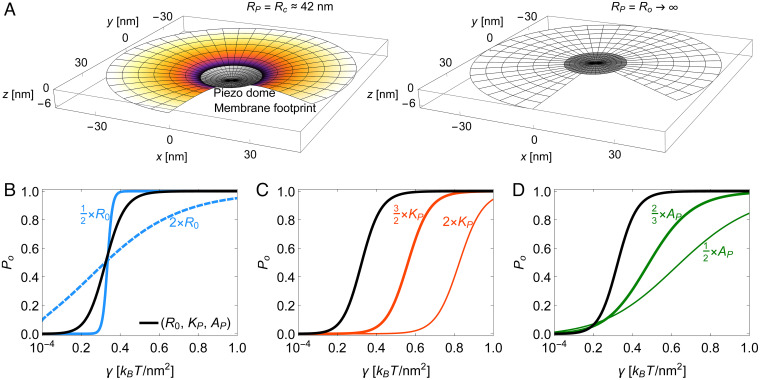
The first term in Eq. 5 is the Piezo dome mean curvature energy, Eq. 3. The second term is Eq. 1 for the free lipid bilayer membrane surrounding the Piezo dome. It captures, in analogy to the continuum elasticity theory describing the free membrane shape in Piezo vesicles, the membrane bending energy of Piezo’s membrane footprint (8, 10). The third term is a work energy term that becomes important when a lateral tension is applied to the system (16). $\mathrm{\Delta }{A}_{\text{proj}}<0$ refers here to the decrease in the projected (i.e., in-plane) area of the Piezo–membrane system due to the curved shape of the Piezo dome and its membrane footprint, relative to the completely flat system configuration. For a given $R_P$, we take Piezo’s membrane footprint to be in its minimum energy state obtained, similarly as for Piezo vesicles, by solving the corresponding Hamilton equations in an asymptotically flat, homogeneous bilayer membrane (SI Appendix, section S2) (8). As written, $G_{\text{sys}}\left(R_P\right)$ is thus the shape energy of the Piezo–membrane system relative to the energy of a completely flat configuration of the system (i.e., with the Piezo dome and free membrane in a plane, without curvature). When $\gamma =0$, the work energy term is equal to zero, and so is the bending energy of Piezo’s membrane footprint, with the membrane footprint assuming a catenoidal shape in which $c_1$ and $c_2$ at every point are equal in magnitude and opposite in sign (8). In this case, Piezo’s membrane footprint exerts no force on the Piezo dome, and $G_{\text{sys}}\left(R_P\right)$ attains its minimum at $R_P=R_0$. Thus, when $\gamma =0$, we have $G_{\text{sys}}=0$. Fig. 4 A, Left shows the shape of the Piezo–membrane system under nominal tension. The Piezo dome adopts its intrinsic radius of curvature, $R_P \approx 42 \text{nm}$, and the surrounding free membrane forms a curved membrane footprint that smoothly meets the edge of the Piezo dome.

Fig. 4.

Mechanics of Piezo activation. (A) Three-dimensional plots of the Piezo dome and its (partial) membrane footprint in the limit of an asymptotically planar membrane. We assume here that the closed state of Piezo approximately corresponds to the intrinsic Piezo dome radius of curvature $R_P=R_c\approx 42 \text{nm}$ (Left) and that the open state of Piezo approximately corresponds to a flat Piezo dome shape with radius of curvature $R_P=R_o\to \infty$ (Right). We calculated the shape of the membrane footprint by minimizing the shape energy of the Piezo–membrane system, $G_{\text{sys}}\left(R_P\right)$ in Eq. 5, at fixed $R_P$ with $A_P=450 {\text{nm}}^2$. In A, Left, we used a nominal lateral membrane tension $\gamma =0.01 \frac{k_{B}T}{{\text{nm}}^2}$. The membrane areas occupied by the Piezo dome as well as by the membrane footprint are identical in A, Left and Right. (B–D) Piezo gating curves, $P_o\left(\gamma \right)$ in Eq. 6, for the elastic properties of the Piezo dome estimated in Fig. 3, $R_0\approx 42 \text{nm}$ and $K_P\approx 18 k_{B}T$, with the Piezo dome area $A_P=450 {\text{nm}}^2$ (black curves) and with (B) a modified intrinsic Piezo dome radius of curvature $\frac{1}{2}{R}_0$ (blue solid curve) or $2R_0$ (blue dashed curve), (C) a modified Piezo dome bending rigidity $\frac{3}{2}{K}_P$ (thick red curve) or $2K_P$ (thin red curve), and (D) a modified Piezo dome area $\frac{2}{3}{A}_P$ (thick green curve) or $\frac{1}{2}{A}_P$ (thin green curve). For the predicted Piezo gating curve with $R_0\approx 42 \text{nm}$, $K_P\approx 18 k_{B}T$, and $A_P=450 {\text{nm}}^2$, Eq. 6 yields $P_o=\frac{1}{2}$ at the gating tension ${\gamma }_{1/2}\approx 0.33 \frac{k_{B}T}{{\text{nm}}^2}$ (black curves). In B, ${\gamma }_{1/2}\approx 0.34 \frac{k_{B}T}{{\text{nm}}^2}$ for $\frac{1}{2}{R}_0$ and ${\gamma }_{1/2}\approx 0.32\frac{k_{B}T}{{\text{nm}}^2}$ for $2R_0$. In C, ${\gamma }_{1/2}\approx 0.56 \frac{k_{B}T}{{\text{nm}}^2}$ for $\frac{3}{2}{K}_P$ and ${\gamma }_{1/2}\approx 0.83 \frac{k_{B}T}{{\text{nm}}^2}$ for $2K_P$. In D, ${\gamma }_{1/2}\approx 0.49 \frac{k_{B}T}{{\text{nm}}^2}$ for $\frac{2}{3}{A}_P$ and ${\gamma }_{1/2}\approx 0.65 \frac{k_{B}T}{{\text{nm}}^2}$ for $\frac{1}{2}{A}_P$.

When $\gamma >0$, a flattening of the Piezo dome tends to decrease the energetic cost of the work energy term in Eq. 5. At the same time, the energetic cost of curvature in the membrane footprint will also tend to flatten the Piezo dome. This is because, when $\gamma >0$, the membrane footprint deviates from its catenoidal shape and the associated energy contribution must be positive (i.e., unfavorable), but less so if the membrane flattens out, reducing its curvature (8). Thus, when $\gamma >0$, the second and third terms in Eq. 5 both favor a flatter, expanded configuration of the Piezo–membrane system, while the first term in Eq. 5 favors a shape of the Piezo dome with $R_P=R_0$. As a result, the second and third terms in Eq. 5 yield a force on the Piezo dome to flatten it away from $R_P=R_0$. This is how lateral membrane tension can alter the shape of the Piezo dome and its surrounding membrane (Fig. 4 A, Right).

As stated in the Introduction, we have proposed that the open conformation of Piezo is less curved. If we associate, for example, the closed Piezo channel with $R_P=R_0$ (Fig. 4 A, Left) and the open channel with $R_P\to \infty$ (Fig. 4 A, Right) (i.e., a flat conformation), then applying the Boltzmann distribution equation to these two configurations of the Piezo–membrane system, we have

$$\frac{P_o}{1-P_o}=e^{\frac{-\mathrm{\Delta }{G}_{\text{sys}}}{k_{B}T}},$$ [6]

where $P_o$ is the Piezo open probability and $\mathrm{\Delta }{G}_{\text{sys}}$ is the difference in the shape energy of the Piezo–membrane system, Eq. 5, between the open and closed states of the Piezo channel. The black curves (Figs. 4 B–D) show $P_o$ as a function of $\gamma$ according to Eqs. 5 and 6 for $A_P=450 {\text{nm}}^2$, $R_0\approx 42 \text{nm}$, and $K_P\approx 18 k_{B}T$. We predict, with no free parameters, $P_o=0.5$ at $\gamma \approx 0.33 \frac{k_{B}T}{{\text{nm}}^2}$, which is near published experimental values for the Piezo gating tension in cell membranes, with half activation around $\gamma \sim 0.4 \frac{k_{B}T}{{\text{nm}}^2}$ (17). The predicted and measured gating curves also show a comparable steepness.

Such a good correspondence between the predicted and measured tension–activation curves is surprising for several reasons. The assumption that the Piezo dome bending modulus, $K_P,$ for increasing the radius of curvature (i.e., flattening the dome) is the same as that for decreasing the radius of curvature, which we have measured, may be incorrect. Furthermore, Piezo is unlikely to be a two-state channel, and nonelastic (chemical) energy terms ought to contribute to the interaction between the Piezo protein and the lipid membrane, although it may be that these nonelastic energy terms do not change much between closed and opened conformations. With these assumptions understood, the elastic energy model of Piezo obtained here seems to approximate the functional behavior of the channel. More importantly, our motivation for this study is not to predict the activation curve, but to understand how the Piezo dome’s physical properties give rise to its mechanical force sensing ability. To this end, we systematically varied in our model Piezo’s intrinsic curvature, stiffness, and area to ask what effect these perturbations would have on its mechanosensing capability? The blue solid and dashed curves (Fig. 4B) show that Piezo’s steep, switch-like response to changes in membrane tension depends critically on the Piezo dome intrinsic radius of curvature, $R_0$. Without intrinsic curvature, in its closed, resting state, Piezo would not be mechanosensitive. The red curves (Fig. 4C) show that Piezo’s ability to respond mechanically in the low-tension regime relies on the bending modulus of the Piezo dome being small. By small, we mean comparable to that of the pure lipid bilayer. If the value of $K_P$ was doubled, for instance, then Piezo would not open until the membrane tension reached approximately one-third of the lytic tension of a lipid bilayer, which is about $2.5 \frac{k_{B}T}{{\text{nm}}^2}$ (13). Thus, intrinsic curvature of the Piezo dome with minimal stiffness appears to be an effective recipe for a switch-like conformational response in the low-tension regime.

The Piezo dome’s unusually large area is also important. The green curves (Fig. 4D) show that Piezo’s area influences both the steepness of its opening response and the tension range over which it opens. Thus, Piezo’s intrinsic curvature, membrane footprint, small bending modulus, and large area appear to be the key properties underlying Piezo’s ability to function as a highly responsive, tension-gated ion channel that operates in the low-tension regime.

Discussion

Our analysis of Piezo vesicles is analogous to the problem of two connected springs, one whose force–displacement relationship is known and the other, unknown. By measuring the displacement of the dual spring system at mechanical equilibrium, because the forces between the two springs must be equal in magnitude and opposite in sign, the force–displacement relationship of the unknown spring can be deduced, without perturbing the system. In the present study, the vesicle free membrane represents one spring and the Piezo dome, the other. To designate the free membrane as known, we must know its force–displacement relationship. Thus, we examined in the companion paper whether the Helfrich energy equation can predict the shape of the free membrane bounded by the edge of the Piezo dome (10). With no free parameters, we were able to accurately predict the shape of Piezo vesicles from the Helfrich energy equation. This justifies taking the Helfrich energy equation as a potential energy function for the free membrane, which means, through differentiation, we have the force. Thus, the free membrane serves as a known spring. Vesicles of different sizes permit the construction of a force–displacement relationship for the Piezo dome in unsupported, freestanding lipid membranes.

To connect the force–displacement relationship of the Piezo dome to channel gating, we model the Piezo dome as a spherical cap with intrinsic radius of curvature $R_0$, stiffness $K_P$, and (known) area $A_P$, whose deformation energy is governed by the dome’s mean curvature. Differentiation with respect to the Piezo dome radius of curvature, $R_P$, yields a force function, Eq. 4, that conforms to the Piezo force curve data and gives estimates for $R_0$ and $K_P$. We conclude that Piezo in an asymptotically planar, tensionless lipid bilayer membrane is curved, but less than in the detergent micelles used in cryo-EM studies. We also conclude that the Piezo dome exhibits low stiffness, comparable to that of the free lipid bilayer membrane.

The most interesting question in structural biology is not what does a molecule or collection of molecules look like, but why? Piezo is an extreme structural outlier among ion channels and membrane proteins in general. At its center, Piezo is a rather ordinary looking trimeric ion channel, but then each protomer extends radially a long, curved arm consisting of transmembrane helical units (6, 18, 19). Together, the three curved arms pucker the membrane to create a dome and surrounding membrane footprint that comprise a large area. The analysis we present argues that the structural features of large area and curvature are both important ingredients in the recipe for sensing lateral membrane tension. On top of these structural properties, the mechanical property of low stiffness is also important. To the question why regarding Piezo’s structure, we conclude that its large area, intrinsic curvature, and low stiffness are requirements for its ability to respond to membrane tension changes in the low-tension regime with high sensitivity. One could imagine in the evolution of its current form, that the Piezo channel began as an “ordinary” ion channel, which became modified through natural selection to have extended arms to recruit a large dome area and membrane footprint, with a shape to produce intrinsic curvature, and with mechanical properties to ensure low bending stiffness.

Piezo’s solution to sensing membrane tension by an ion channel is not the only one that emerged in life. The mechanosensitive K⁺ channels TWIK-related arachidonic acid activated potassium channel (TRAAK) and TWIK-related potassium channel (TREK) are small, wedge-shaped ion channels (20). Their shape probably produces a small membrane footprint, which would afford a $\gamma \mathrm{\Delta }{A}_{\text{proj}}$ work energy term in the gating transition, but these channels’ small area is suboptimal. TRAAK and TREK open with a very weak dependence on membrane tension compared to Piezo (21). In another example, the large conductance bacterial mechanosensitive channel, MscL, opens with a strong dependence on membrane tension, like Piezo (22). MscL mainly produces its mechanical work term, $\gamma \mathrm{\Delta }{A}_{\text{proj}}$, by direct in-plane expansion of a disk-like arrangement of transmembrane helices that surround the pore (23). However, there are two caveats. First, MscL functions as a pressure release valve in bacteria, opening a very wide pore in the face of osmotic shock. The large pore opening in MscL fulfills its role to release cytoplasmic content and to provide a strong tension dependence through a large magnitude of $\mathrm{\Delta }{A}_{\text{proj}}$, but such a large pore opening would be lethal to a eukaryotic cell. A eukaryotic cell must only open a narrow pore to mediate ion conduction, and thus, pore opening alone will not produce a large $\mathrm{\Delta }{A}_{\text{proj}}$. Second, MscL does not open until the membrane tension approaches lytic values (22). In other words, MscL does not open in the low-tension regime like Piezo. We would argue that the unique structure and elastic properties of Piezo reflect evolutionary adaptations to achieve strong tension-dependent gating in the low-tension regime for an ion channel that opens a narrow pore.

In a previous study, HS-AFM was used to analyze shape changes in Piezo as a function of force applied by the atomic force microscope (AFM) tip in imaging mode (9). Contrary to the present approach, the Piezo dome was thus perturbed by an external force applied from outside the membrane. The forces in that study were similar in magnitude to the forces estimated here, with both systems yielding estimates for the Piezo gating tension comparable with experimental values. The Piezo dome flattened and recoiled reversibly under the AFM tip; however, several observations and conclusions, especially regarding the Piezo dome geometry and force–displacement relationship, were different between the two studies. In the HS-AFM study, the low-force intrinsic radius of curvature of the Piezo dome was about 15 nm rather than 40 nm. This difference alone makes a direct comparison of the two force curves impossible. One reason for the difference, we suspect, is that the HS-AFM study was carried out in lipid bilayer membranes made from 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE) and 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1'-rac-glycerol) (POPG). These lipids, because of their shapes, may organize around the curved Piezo channel, permitting it to be more curved than in the 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC):1,2-dioleoyl-sn-glycero-3-phospho-L-serine (DOPS):cholesterol lipid bilayer membranes considered here (6, 10, 24). Another difference is that the membrane in the HS-AFM study was supported on a mica surface, whereas in the present study, the membrane is unsupported, more like a cell membrane, with Piezo’s response to forces depending on its membrane footprint. Perhaps a useful conclusion to be reached by comparing these studies is that different lipid compositions and membrane environments in cells have the potential to regulate Piezo’s structure and thus its function, by biasing the Piezo dome toward curved or flattened states.

A recent structural study on Piezo in lipid vesicles (11) requires comment here to avoid misinterpretation of our findings and to ensure that the principles of membrane elasticity theory are correctly conveyed. In ref. 11, the authors misuse the physical concepts force and, in particular, membrane tension, leading to an incorrect description of Piezo gating. They specify the closed-state radius of curvature of Piezo as 10 nm, the radius of curvature they observe in a spherical 10-nm-radius vesicle. They use this radius of curvature to compare the predictions of the membrane dome model for an asymptotically planar membrane (6, 9) to the measured Piezo gating tension in a patch of membrane (17)—a scenario that is fundamentally distinct from a 10-nm vesicle, with different forces acting on the Piezo dome and a different closed-state radius of curvature of Piezo. The authors of ref. 11 might have noticed in figure 1 of their paper that in larger vesicles, Piezo’s radius of curvature is greater than 10 nm, as was also shown previously (9), and they ought to have wondered what it would be in a planar membrane. The dependence of Piezo’s shape on vesicle size arises because Piezo’s structure and function are inextricably tied to the geometry of the membrane through bending elastic forces and emerge from Piezo–membrane interactions. This example raises the often-asked question in membrane protein structural biology: To what extent does the membrane (for example, compared to a detergent micelle) alter a membrane protein’s structure? For Piezo, the answer is, a great extent, and membrane elasticity theory permits us to understand why: because the responsiveness of Piezo’s structure to the membrane is deeply rooted in Piezo’s mechanism of sensing mechanical force.

In summary, Piezo in asymptotically planar lipid bilayer membranes is less curved than in detergent micelles, with a radius of curvature of about 40 nm at zero tension. However, low-threshold, sensitive mechanical gating properties are maintained nevertheless, owing to the creation of a membrane footprint surrounding Piezo. Realizing the biologically relevant shape and elastic properties of Piezo, which exploit the bending elastic properties of lipid bilayer membranes, is key to understanding its mechanosensory properties. The general concept of a dome model that utilizes $\gamma \mathrm{\Delta }{A}_{\text{proj}}$ for Piezo’s mechanosensitive gating was hypothesized based on a structure in detergent micelles (6), but a more accurate description required an understanding of Piezo’s interaction with lipid bilayer membranes (8). In this paper and the companion paper (10), we have quantified the bending elastic properties and shape of Piezo inside a freestanding lipid bilayer membrane. Collectively, these findings tie Piezo’s unusual form and mechanical properties to its mechanosensing ability.

Materials and Methods

For Figs. 1–3, we calculated the shape and elastic energy of the free membrane in Piezo vesicles as described in our companion paper (10). We calculated the shape and elastic energy of Piezo’s membrane footprint in asymptotically planar membranes in Fig. 4 based on the theory developed in ref. 8 using Mathematica (25). A summary of this theoretical approach can be found in SI Appendix, section S2.

Data, Materials, and Software Availability

The tomograms of Piezo vesicles are deposited in the EMDataBank [accession codes EMD-27569 (26) (vesicle 1), EMD-27571 (27) (vesicles 2 and 4), EMD-27568 (28) (vesicle 3), EMD-27567 (29) (vesicles 5 and 6), and EMD-27570 (30) (vesicle 7)]. All other data are included in the manuscript and/or SI Appendix.