Abstract
We report the retrieval of the Raman signal from coherent anti-Stokes Raman scattering (CARS) spectra using a convolutional neural network (CNN) model. Three different types of non-resonant backgrounds (NRBs) were explored to simulate the CARS spectra viz (1) product of two sigmoids following the original SpecNet model, (2) Single Sigmoid, and (3) fourth-order polynomial function. Later, 50 000 CARS spectra were separately synthesized using each NRB type to train the CNN model and, after training, we tested its performance on 300 simulated test spectra. The results have shown that imaginary part extraction capability is superior for the model trained with Polynomial NRB, and the extracted line shapes are in good agreement with the ground truth. Moreover, correlation analysis was carried out to compare the retrieved Raman signals to real ones, and a higher correlation coefficient was obtained for the model trained with the Polynomial NRB (on average, ∼0.95 for 300 test spectra), whereas it was ∼0.89 for the other NRBs. Finally, the predictive capability is evaluated on three complex experimental CARS spectra (DMPC, ADP, and yeast), where the Polynomial NRB model performance is found to stand out from the rest. This approach has a strong potential to simplify the analysis of complex CARS spectroscopy and can be helpful in real-time microscopy imaging applications.
Typical schematic of the CNN model architecture trained with CARS data generated from different non resonant backgrounds. The input is a CARS spectrum and the output is a Raman spectrum.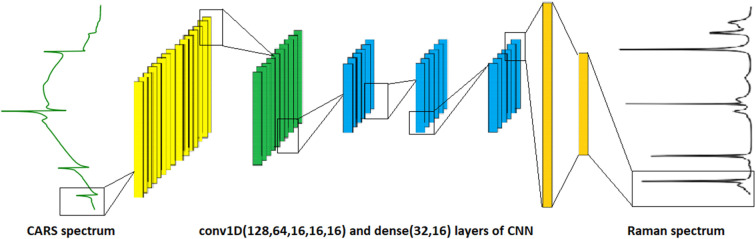
1. Introduction
Coherent anti-Stokes Raman scattering (CARS) is a nonlinear optical technique that provides the non-destructive, label-free fingerprint information of the molecule at high speeds.1,2 It is a four-wave mixing process where Stokes (1st) and pump (2nd) beams coherently excite the molecular vibrations, and a probe (3rd) beam scatters off the coherently excited vibrations. Finally, an anti-Stokes beam (4th) coherently generates with a frequency equal to the excited molecular vibration frequency plus the probe beam's frequency. In imaging application, it creates imaging structures by visualizing the vibrational contrast of the molecules, which require only fractions of a second for generating the micrograph of a specific vibrational mode. In contrast, it takes a few minutes to complete a hyperspectral image. These characteristics enabled it as a useful micro-imaging spectroscopic tool in various applications such as breast cancer tissue mapping,3in vivo imaging of biological cells,4 and understanding lipid biology,5etc.
Despite these advantages, CARS spectroscopy has one inherent major drawback, i.e., the presence of a strong non-resonant background (NRB) component in the measured CARS signal. It is observed due to the interactions involving highly detuned electronic energy levels and is considered as the origin of CARS spectral5–7 as well as spatial distortion (in imaging).8 The spectral/image contrast reduces further when the analyte concentration is relatively low as the NRB will be more dominant than the resonant CARS signal. Numerous optical-based approaches such as polarization CARS,9 frequency modulation CARS,10 single-Frequency CARS,11 pulse shaping CARS,12 and interferometric CARS13 have been demonstrated to reduce the NRB contribution to the CARS measurements. Among all polarization CARS, frequency modulation CARS are the most commonly used techniques where the first one inherently exploits different polarizations of the resonant and non-resonant contributions.9 In the second case, either the Stokes or pump beams are frequency-modulated such that their difference is modulated on and off the vibrational resonance.10
All these approaches have decreased the NRB contribution, albeit increased the complexity of experimental setup and cost. Also, each method has its own limitations. In conventional Raman measurements, the fluorescence acts as an additive background, but NRB co-generates with the resonant Raman components in the CARS technique. Hence, these alternative approaches not only reduced the NRB contribution but also minimized the Raman intensities in the measured CARS signal.14 Thus, NRB amplifies the CARS signal above the noise level, and without that, CARS does not show any benefit over conventional Raman spectroscopy.15 Meanwhile, this coherent contribution also introduces the distortions in the Raman line shapes that cannot be removed directly.
Nevertheless, the fixed “phase relationship” between the Raman and NRB components has been utilized to extract the Raman signal from the complex CARS spectra using computational methods such as the maximum entropy method (MEM)16 and the Kramers–Kronig (KK) relation.17 These studies were either performed by using the NRB of an appropriate surrogate material as a reference, such as coverslip-glass, water, and salt or assumed it as a known a priori.18 Albeit, these surrogate materials have also introduced errors in measured amplitude and phase, which were corrected using “scale-error correction” and “phase-error correction” methods.19 Further, other approaches were also reported in the literature to correct the experimental artefacts and line-shape distortions in CARS spectra, such as “factorized Kramers–Kronig and error correction”,20 and “wavelet prism decomposition analysis”.21
All the above mentioned approaches either require a “reference surrogate material” or the parameters need to be adjusted by the user to get optimum results. However, these complications can be circumvented by utilizing deep learning (DL) methods which have shown impact in various research fields.22 Deep neural networks (DNNs) have been employed in numerous applications such as natural language processing,23 weather forecasting,24 and computer vision,25etc. They have also been explored in various spectroscopic applications such as hyperspectral image analysis,26,27 vibrational spectroscopy,28 molecular excitation spectroscopy,29 and laser-induced breakdown spectroscopy.30–32
In recent times, these DL algorithms have also been deployed to solve the issue of NRB in CARS measurements.33–36 Houhou et al. have utilized the Long Short-Term Memory (LSTM) model to extract the Raman signal and compared their results with the KK & MEM computational techniques.33 Valensise et al. employed a convolutional neural network (CNN) model for retrieving the imaginary part of CARS spectra.34 They have named it as SpecNet. Wang et al. explored Very Deep Convolutional Autoencoders (VECTOR) for the NRB removal, and the performance is compared with SpecNet.35 In our recent work, we have also demonstrated that the training with semi-synthetic data in addition to the synthetic data improves the DL model performance.36 The SpecNet model performance was found to be poor when compared with our previous work36 and VECTOR model,35 where it could not able to extract the spectral lines with minimal intensities. More importantly, they have not evaluated the model accuracy quantitatively. It is also worth considering that no other paper reported to date has presented MSE error throughout the spectral range which inherently displays the efficacy of the trained model.
As aforesaid, the NRB plays a crucial role in CARS measurements. However, all the recent works on NRB removal using DL algorithms have assumed it as either constant or a product of two sigmoids to synthesize the CARS data. Thus, all investigations reported to date have trained their DL model only by considering the same type of NRB irrespective of their DL model architecture, and no other type is explored.34–36 Even the recent VECTOR model has shown that robust performance is merely achieved for the simulated datasets, whereas it is found to be sensitive when dealing with the actual experimental data. It is attributed to the fact that NRB used in that study is simply modelled as a product of the countervailing sigmoids and hinted that further improvements on NRB are required to handle complex CARS data. Also, we have visually noticed that the “Product of two Sigmoid NRB” output is mostly (7 out of 10 times) demonstrated as a Gaussian/bell-like shape, as shown in ESI Fig. 3(a)†. Hence, in this work, we have comprehensively studied three different types of NRBs to see their effect on the extraction of Raman signal. (1) Product of two sigmoids (it is SpecNet's NRB), (2) Single Sigmoid, and (3) Polynomial function.
For this investigation, we have considered all the spectral simulation parameters to be the same except for NRB to generate the CARS data. We have also adapted the same SpecNet model architecture and separately trained it with the CARS data generated from two different NRBs. Now onwards, these models are referred to as “One Sigmoid NRB/Sigmoid model” and “Polynomial NRB/Polynomial model” in the manuscript. In the case of “Product of two sigmoid NRB”, we have considered the original SpecNet model, which was already trained with the CARS data generated by using the product of two sigmoids as NRB. The SpecNet model weights are directly considered from the literature34 and compared their results with models trained with the other two NRB types. This comparative study has been done for the first time to the best of our knowledge and provides a giant leap towards the improvements in rapid extraction of Raman signal from CARS measurements.
2. Experimental details
The first part of this section provides an overview of the theoretical CARS spectral simulation procedure, and the second part presents the details of the CARS experimental setup.
2.1. Synthetic spectra generation
A CARS spectrum S(ω) can be synthesized as follows:
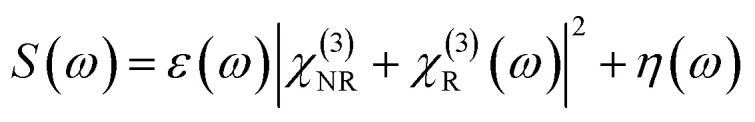 |
1 |
It is the combination of the non-resonant, resonant, and noise contributions. Here, χ(3)NR, χ(3)R corresponds to the non-resonant and resonant third-order susceptibilities, respectively. ε(ω) is a line-shape distortion error that arises from the experimental artefacts, and η(ω) represents the noise contribution. ω represents the frequency over a normalized scale [0, 1].
Further, χ(3)R can be defined as
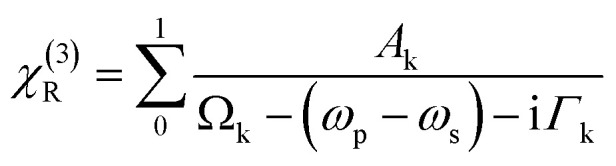 |
2 |
where, Ωkωs and ωp represent the resonance frequency of vibrational mode, Stokes and pump laser beam frequencies, respectively. Whereas Ak and Γk correspond to the spectral line's amplitude and width, respectively.
Fifteen spectral lines are considered as a maximum limit while simulating each synthetic spectra, and the minimum is set to be one line. The peak amplitudes are varied between 0.01 to 1, and the resonant frequencies are generated on a normalized scale, i.e., [0, 1]. The experimental CARS data can be acquired in the spectral range of ∼200–3200 cm−1. Thus, the spectral linewidth considered for simulating CARS data on the normalized scale [0.001, 0.008] corresponds to [2, 25.6 cm−1] in the wavenumber scale. Further, three different NRBs were simulated, as given in the following sections. All the synthetic spectra simulated with three different NRB types are generated in Python (TensorFlow 2.7.0) and the code is freely available37. The parameter ranges to generate synthetic NRB's were chosen to emulate the experimental NRB's as realistically as possible.
2.1.1. Product of two Sigmoid NRB
We have directly adapted this NRB and its parameters (s1, s2, c1, & c2) from the SpecNet paper published by Valensise et al.34 It was defined as a product of two sigmoid functions as follows:
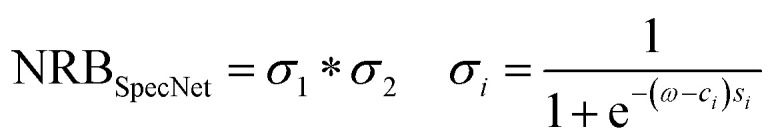 |
3 |
where σ1 and σ2 are two sigmoid functions, and the required parameters are randomly selected from of the following value ranges:s1 & s2 = [10, 5]; c1 = [0.2, 0.3]; c2 = [0.7, 0.3]
2.1.2. One Sigmoid NRB
Here, only one Sigmoid function but with different simulation parameters is considered for the generation:
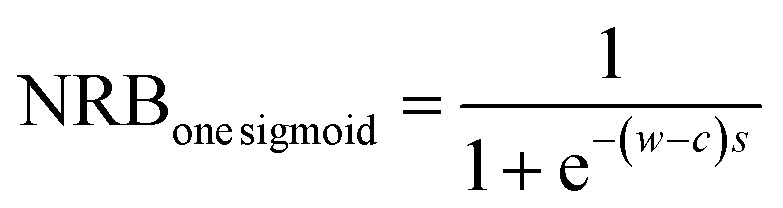 |
4 |
The parameters s and c are randomly selected from a range of values [−5, 5] and [−2, 2], respectively. A broad range of values (i.e., one order higher compared to SpecNet's range) were selected for s and c to simulate various NRBs.
2.1.3. Polynomial NRB
A Polynomial function is empirically considered to simulate NRB. In the case of “Product of two Sigmoid NRB”, four parameters are required to generate NRB (see eqn (3)). Hence, we have considered the fourth-order polynomial, which needs only one extra parameter (total five parameters [a–e] as given in eqn (5)) compared to SpecNet. A higher-order polynomial can also be explored; however, it requires more parameters and thus complicates the model training. Thus, we restricted to only to a 4th order polynomial function defined as follows:
| NRBPolynomial = aω4 + bω3 + cω2 + dω + e | 5 |
The Polynomial coefficients a, b, and d are randomly selected from the range of values [−10, 10], whereas it is [−1, 1] for c and e coefficients. The NRB is normalized between 0 and 1 and then added to χ(3)R data. Finally, uniformly distributed noise η(ω) is added to it for simulating the CARS spectra. In three models, all the spectral simulation parameters are the same except for NRB.
2.2. Details of the experimental CARS data
Multiplex CARS experimental details and its optical layout can be found here.38 A 10 ps laser pulse is utilized as a pump/probe beam which has a bandwidth of ∼1.5 cm−1 at 710 nm. An ∼80 fs laser pulse is considered as a Stokes beam, where the spectral range can be varied between ∼750 to 950 nm. This spectral range corresponds to 750–3500 cm−1 in the vibrational frequency scale. The Stokes pulse power is adjusted to 105 mW, whereas the pump/probe pulse is operated at 75 mW power. An achromatic lens (focal length ∼ 5 cm) has been deployed to focus these laser beams into a tandem cuvette. The Stokes and pump/probe beams exploited long pass and interference filters to block amplified spontaneous emission from lasers, respectively. The filtered CARS signal from the analyte is guided onto a spectrometer which has a resolution of ∼5 cm−1. All the CARS spectra were recorded with an acquisition time of ∼800 ms. Finally, The CARS spectrum is measured from three samples, namely ADP, DMPC, and Yeast. The first sample is an equimolar mixture of AMP, ADP, and ATP in water with a total concentration of 500 mM. DMPC is small unilamellar vesicles (SUV) suspension with a concentration of 75 mM. The third sample is a living budding yeast cell (a zygote of Saccharomyces cerevisiae) measured from the mitochondria of the yeast cell.39
3. Deep learning model
Artificial neural networks (ANNs) learn from the data by a non-linear mapping between the model input and output.40 The trained model can be utilized to perform inference, that is, make predictions about the output based on unseen input data. The learning is typically implemented in a supervised manner by using training data consisting of data samples and the desired output for each sample. It is achieved by the backpropagation algorithm where the error signal from the output passed towards the input by adjusting the model parameters, that is, the weights of computational units called neurons. In the case of complex modelling tasks, deep architectures containing a large number of interconnected layers of neurons are applied. Learning a huge number of parameters implies that an extensive training set is required. However, not all applications are such that a deep architecture is needed. Among the different ANN architectures, convolutional neural networks (CNN) have become an efficient solution for various machine learning-related problems such as time-series classification,41 image processing,42 and object detection.43
The CNN architecture consists mainly of convolutional and fully-connected layers together with pooling and flattening layers. The first part of a CNN includes a stack of convolution layers responsible for extracting the relevant features from the data and producing new data representations called “feature maps”. The main advantage of convolutional layers is that they function as filter banks where the parameters are learned, and the level of abstraction related to the data representation increases layer-by-layer. Another benefit is moderate invariance to spatial or spectral translation enabled by the fact that each neuron in the convolution layer is connected to a limited neighbourhood of neurons of the preceding layer and the weights are shared by the neurons. This is of particular interest for Raman spectroscopy applications where the spectral lines/peaks can be shifted within the spectrum. In the second part of the CNN architecture, fully-connected layers have no limitations concerning the connections from the preceding layer and their respective weights. They are used to learn the mapping from the feature representation to the desired output of a specific type and dimensionality.
The CNN architecture used here is directly adapted from the SpecNet model34 and used as-it-is without modifying its structure. Then the model is trained with CARS data generated with two different NRBS. i.e., ‘One Sigmoid NRB’ and ‘Polynomial NRB’. In the case of ‘Two sigmoid NRB’, the original SpecNet weights are used, and the results are compared. The architecture consists of five 1D convolution layers with 128, 64, 16, 16, and 16 neurons of dimensionality 32, 16, 8, 8, and 8, respectively. The schematic of the CNN model architecture is shown in ESI Fig. 2†. The convolutional part is followed by three fully connected layers of 32, 16, and 640 neurons. Rectified Linear Unit (ReLU) is used as the activation function, and mean squared error (MSE) is the loss function. Adam optimizer44 was used with a batch size of 256 samples. The code can be accessed from Git-Hub repository37.
4. Results and discussion
The following sections present the results of the three models. All the parameters used for creating the test set are the same as the train set. One hundred test spectra are generated for each NRB type which cumulatively accounts for 300 spectra for all the three NRB types. First, 100 spectra correspond to ‘Product of two Sigmoid NRB’, spectra 101–200 account for ‘One sigmoid NRB’, and spectra 201–300 correspond to ‘Polynomial NRB’. Finally, the Raman signal extraction efficiency of the models is tested on the 300 test spectra. These 300 test spectra can be found in ref. 37.
4.1. Retrieval of the imaginary part
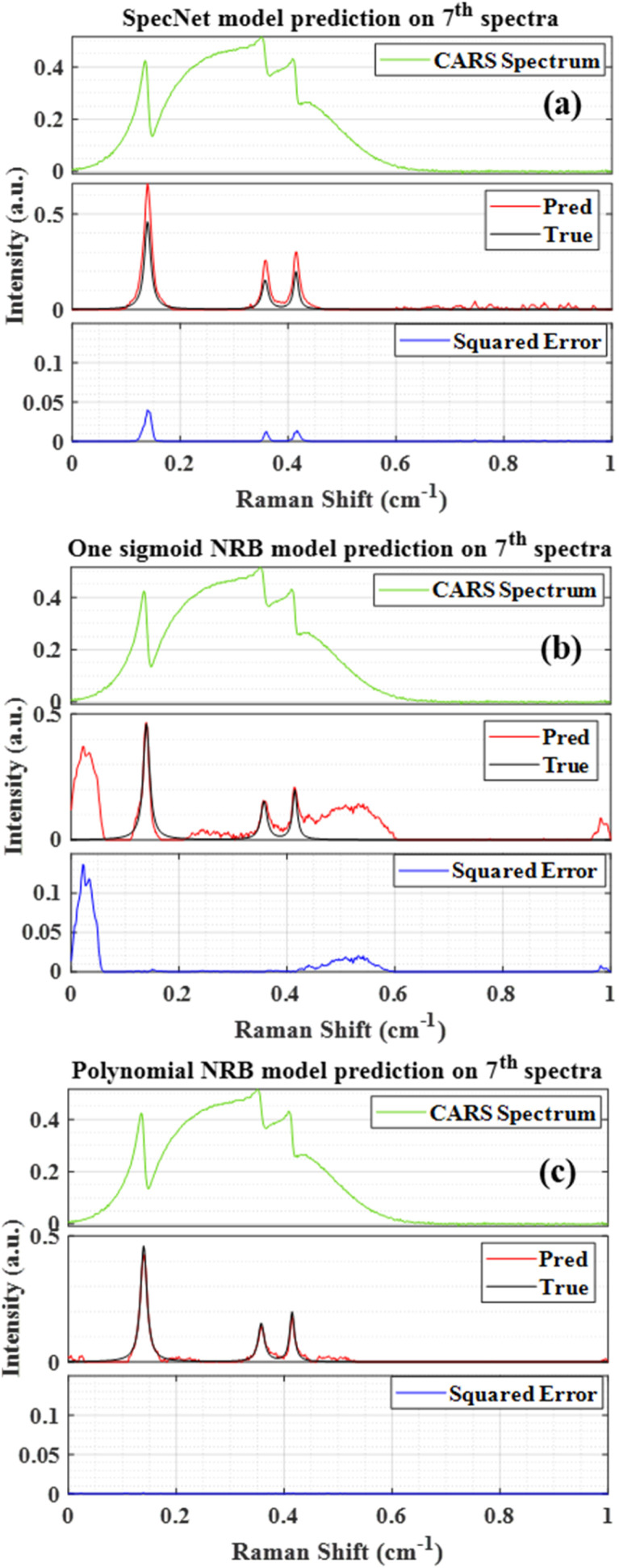
After training the three models, their predictive capability can be readily estimated by retrieving the imaginary part from unknown test spectra. As aforesaid, 300 standalone spectra were simulated for evaluation which were not used while training the models. Fig. 1(a–c) represents the results obtained from the SpecNet, Sigmoid, and Polynomial models, respectively. The frequency scale on the x-axis is normalized between 0 and 1. Thus the Raman shift can be considered as relative. Each plot in the figure has three subplots that visualize the CARS spectrum (top), true & predicted imaginary part (middle), and their squared difference (bottom), respectively. The squared error (SE) plot can provide quantitative information on a prediction error throughout the spectral range. This interpretation has paramount importance while comparing results obtained from the different models.
Fig. 1. Comparison of the results obtained from the three models. (a) SpecNet (2 Sigmoid NRB), (b) One Sigmoid NRB, and (C) Polynomial NRB. True & Pred represent the true and predicted imaginary parts.
Thus, this critical information can be utilized for validating the performance of each model. Fig. 1(a) presents the result of the 7th test spectra obtained from the SpecNet model (two Sigmoid NRB). We have arbitrarily chosen this spectrum from the total dataset to visually represent the efficacy of the trained models. The results of the other spectra are also discussed in the next section with the support of correlation analysis. As mentioned earlier, 1–100 test spectra were trained with two Sigmoid NRB. Hence the SpecNet predicted all the spectral lines, albeit their intensity has deviated from the actual one. On the other hand, some peaks with low intensity were also observed in the spectral region 0.6–1 cm−1 which were not present in the actual Raman signal.
Fig. 1(b) visualizes the Raman signal extracted from the Sigmoid model. It predicted all the spectral lines with correct intensities. However, some spurious spectral features with higher intestines were also observed at both ends of the spectra and mid of the spectral region. These spurious lines degraded performance compared with the SpecNet and Polynomial models. Fig. 1(c) illustrates the Raman signal retrieved from the Polynomial model on the same test spectra. Here, the extracted imaginary spectrum closely resembles the true spectrum, and it has not predicted any other spurious lines throughout the spectral range compared to the other models. Further, a qualitative assessment of each model can be made by considering the SE of a prominent spectral line. For this investigation, a spectral line at 0.14 cm−1 is considered which has a higher intensity among all the spectral features. Finally, it is noticed that the measured SE for SpecNet is 40 times higher compared to the Sigmoid & Polynomial models. It is also true for other spectral lines at 0.36 and 0.41 cm−1, where the deviance is higher by 70 and 40 times, respectively. However, the Sigmoid model has shown spurious lines at 0.02, 0.5, and 0.98 cm−1 which account for SE of 105, 103 and 102 times higher, respectively, compared to the other two models. Overall, the Polynomial model has well predicted the imaginary part than the other two models.
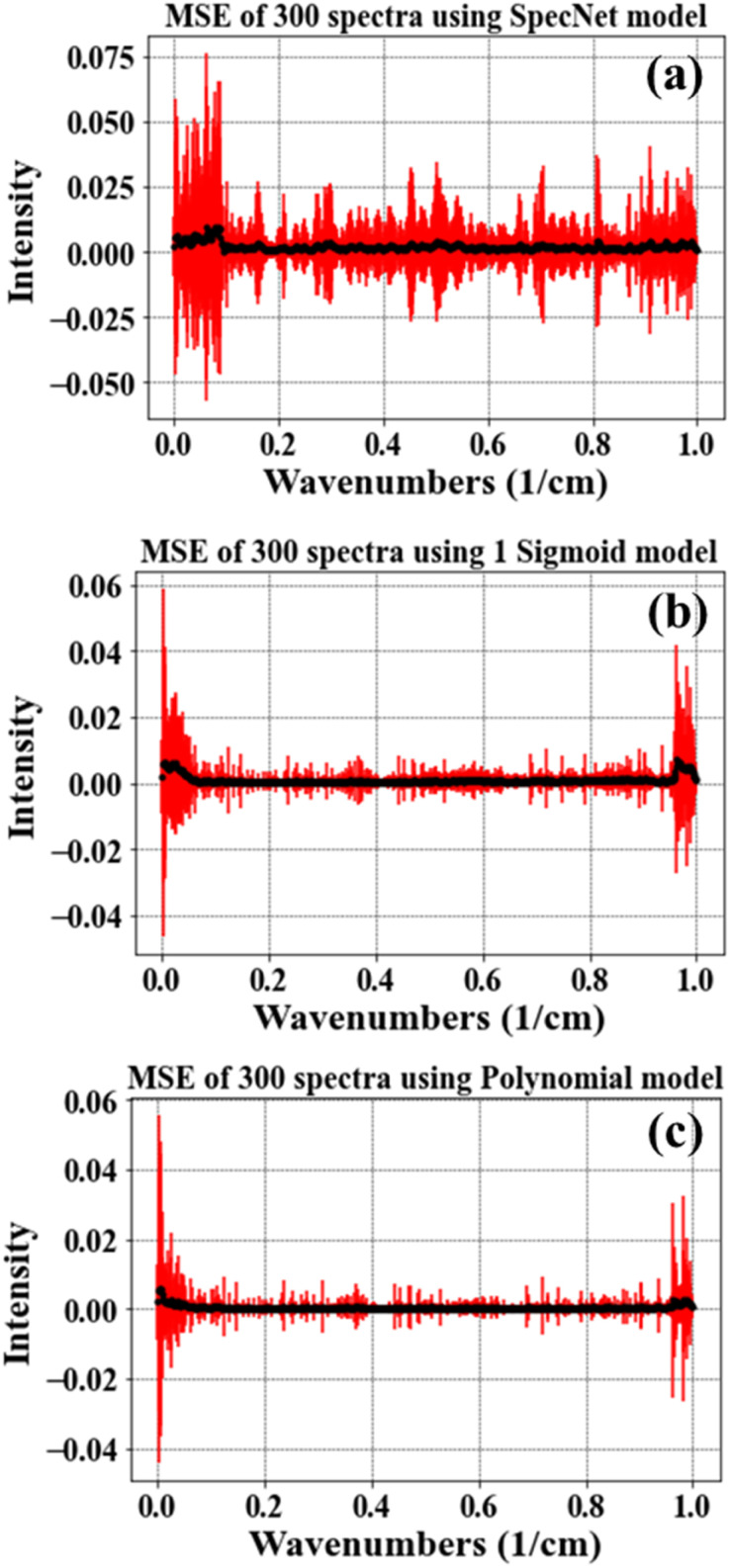
This SE plot visualization effectively presents the differences between the actual and measured Raman signals throughout the spectral range for a single spectrum. However, the illustration of the total 300 test spectra will be cumbersome. Hence their average or mean is estimated for each model and referred to as mean square error (MSE), as shown in Fig. 2(a–c). The black dot represents the mean value obtained from all the test spectra, and the red line corresponds to their standard deviation. Fig. 2(a–c) visually conveys the performance of the trained models. For easy understanding, the entire spectral range is divided as three parts 0–0.1, 0.1–0.9, and 0.9–1 cm−1. The mid-region (0.1–0.9 cm−1) itself accounts for 80% of total data points, and the remaining 20% falls in the first and last regions.
Fig. 2. (a–c) Represent the mean square error estimated for SpecNet, Sigmoid, and Polynomial NRB models, respectively. The black dots represent the mean value, whereas the red line corresponds to the standard deviation measured from the 300 test spectra.
As seen in Fig. 2, the MSE is higher in the first region (0–0.1 cm−1) compared to other regions irrespective of the trained model. Specifically, the deviation/error is maximum (∼0.075) for SpecNet and minimum (∼0.056) for the Polynomial model. Moreover, 50% of data points in this region have MSE > 0.04 for the SpecNet, but a significant difference is observed for the other two models, where only ∼5% of data points have MSE > 0.04. Also, a close inspection of the Sigmoid and Polynomial MSE plot revealed that the variation is slightly higher for most of the data points in the former case.
In the last region (0.9–1 cm−1), a maximum error (∼0.042) is noticed for the Sigmoid model, whereas it is a minimum (∼0.034) for the Polynomial model. However, it is also worth considering that the mean (black dots) is close to zero for the Polynomial model in these two regions. The mean is slightly higher in the other two models, reflecting the poor prediction at both ends of the spectrum. The measured MSE in the mid-region (0.1–0.9 cm−1) is similar for the Sigmoid and Polynomial models, where the error is less than 0.01 for all the data points. In the case of SpecNet, the error is almost twice that of other models for most of the data points. Also, the error is relatively higher (>0.03) for a few points compared to the other two models. In conclusion, the MSE plot visually demonstrated that the Polynomial model performance is optimum among the three models. The reason can be explained as follows. As mentioned earlier, the NRB generated from “Product of two Sigmoids” has mostly (7 out of 10 times) given a Gaussian like shape, as shown in ESI Fig. 3(a)†. This visualization suggests that the generated NRB is biased toward producing Gaussian like distribution instead of creating different NRB shapes for the generalization. However, in the case of the 4th order polynomial function, it generated various NRB line shape outputs, including Gaussian/bell-like structure. As seen from ESI Fig. 3(b),† only 2 out of 10 times it simulated Gaussian-like distribution. It is also noticed that the generated NRBs have different shapes, which are drastically different from each other and close to the NRB observed in the experimental CARS measurements. Thus, it serves as a better alternative to the Product of two Sigmoid NRB and can enhance the predictive ability of the deep learning models.
Further, correlation analysis is performed in the next section. It provides a unique quantity for each measurement/spectrum, i.e., a correlation coefficient is estimated for each test spectra for all three models. Therefore, it can be utilized as a performance metric while comparing the results of different models on a large number of spectra.
4.2. Correlation analysis
Correlation analysis is a statistical approach that measures the strength of the linear relationship between two different variables.45 Here, it computes the correlation between the true and predicted imaginary part of the CARS signal and numerically provides a percentage of their similarity. For this investigation, three different correlation methods (spectral matching algorithms)45 are employed, viz., (a) Pearson correlation coefficient (PCC), (b) Euclidean distance (ED), and (c) Cosine distance (CD). The first one is a correlation measurement, and the remaining two are distance metrics. The numerical value of PCC lies between [−1 & 1], where 1 represents the positive linear correlation, and −1 corresponds to the negative linear correlation.46 Further, zero represents no linear dependency between the two variables considered for the analysis. ED is the length of a line segment between the two variables/data points. CD measures the cosine angle between the true and predicted imaginary part of the CARS signal projected in a multi-dimensional space. In conclusion, for all the three methods (PCC, ED, & CD), 1 represents the best correlation, i.e., true and predicted spectrum are identical, whereas 0 corresponds to no similarity between these two measurements. The correlation analysis is performed on the 300 test spectra for the three models, and the results are presented in the following sections.
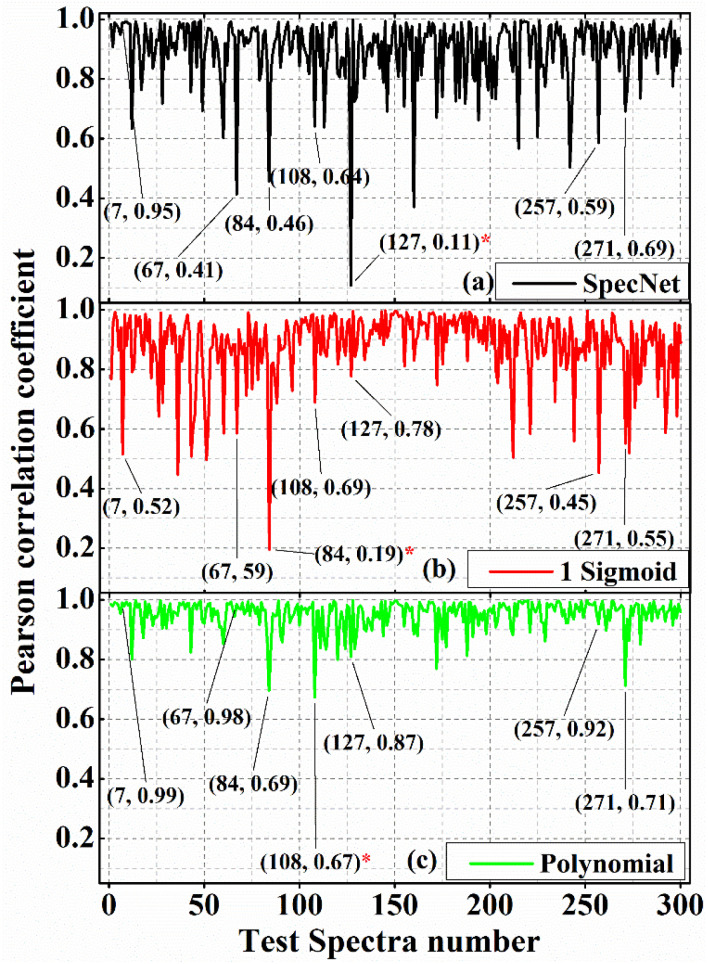
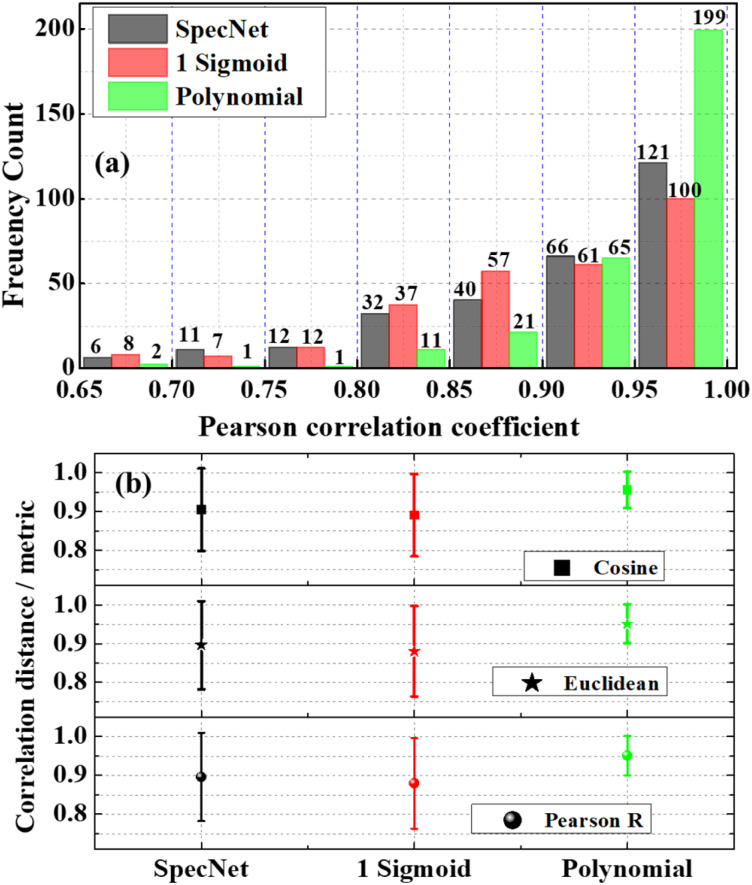
Fig. 3(a–c) illustrate the PCCs obtained from the 300 test spectra for SpecNet, Sigmoid, and Polynomial NRB models, respectively. The data points in parathesis represent the test spectrum number and their corresponding PCC value. It is evident from Fig. 3(c) that the PCC estimated for the Polynomial model has given higher coefficients for the 90% test spectra compared to the other models.
Fig. 3. Pearson correlation coefficient (PCC) obtained for the 300 test spectra for (a) Pearson correlation coefficient (PCC), (b) Euclidean distance (ED), and (c) Cosine distance (CD). The data points represent the test spectrum number and its PCC.
Only four spectra have given PCC less than 0.80, which corresponds to merely ∼1.3% of the total test data. The SpecNet and Sigmoid model's performances were found to be similar when comparing the PCC values. i.e., their PCCs difference is <0.05 for 151 spectra and it is <0.1 for 210 spectra (see Fig. 1 in ESI†). It is also noticed that the maximum PCC obtained is ∼0.99 for all the models. However, the minimum values have shown a significant difference when compared with the Polynomial model. The minimum value of PCC is ∼0.67 for the Polynomial model, whereas it is ∼0.19 and ∼0.11 for the Sigmoid and SpecNet models. For easy visualization, the test spectrum with a minimum PCC value in each model is marked with a red asterisk (*). For example, it is 127th spectra in SpecNet and 84 and 108th spectra in Sigmoid and Polynomial models, respectively. The Raman line shapes extracted from these three spectra using three models are presented in Fig. 4, which inherently visualizes their limitations in predicting the imaginary part. It also explores the route cause for achieving the lowest PCC value for each model.
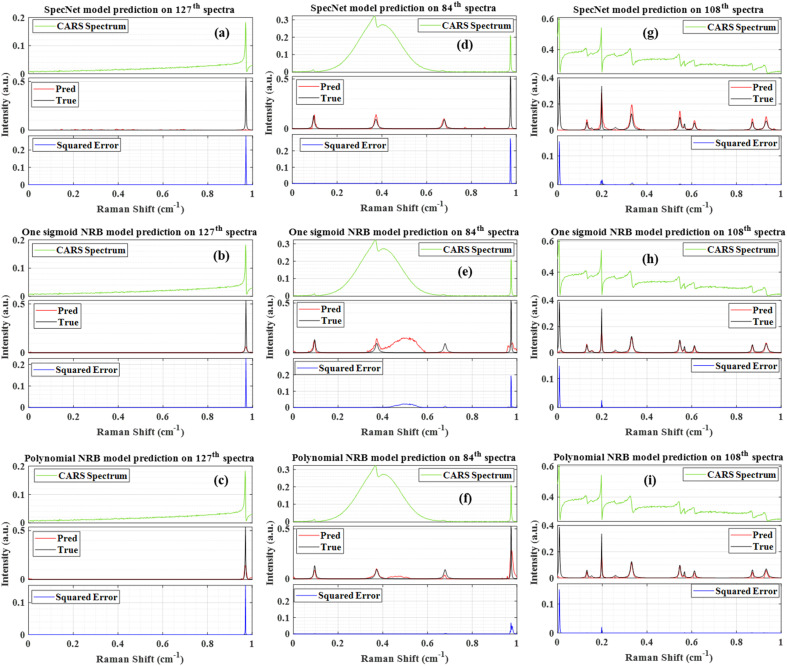
Fig. 4. Comparison of the results obtained from the three models. (a–c) Raman signal extracted from the 127th test spectra using SpecNet, Sigmoid and Polynomial models respectively, (d–f) results of 84th spectra, (g–i) results of the 108th spectra. Pred is the predicted Raman signal, and True represents the actual Raman signal. Squared error corresponds to their difference.
Fig. 4(a–c) represent the results obtained from the 127th test spectrum using SpecNet, Sigmoid, and Polynomial models, respectively. The input CARS spectrum has only one spectral feature in the entire spectral range. However, it is located near the right extrema, and SpecNet could not able to retrieve the Raman signal. A similar observation was noticed in our previous work.36 Further, this inefficient extraction of the Raman spectrum has given an SE of ∼0.29 at the peak centre and led to the lowest PCC in the entire test set, i.e., ∼0.11. The other two models have predicted the Raman line, albeit the extracted intensity is low compared to the actual one. Also, the estimated SE for the Sigmoid model is ∼2 times that of the Polynomial model. Fig. 4(d–f) illustrate the results of the 84th test spectrum obtained from the SpecNet, Sigmoid, and Polynomial models, respectively. The input CARS spectrum has one very broad peak in the region of 0.11–0.64 with centre at 0.37 cm−1 and one sharp line at 0.97 cm−1. It also consists of two faint spectral signatures at 0.09 and 0.67 cm−1. The SpecNet has predicted all the lines except for one line at 0.97 cm−1. Also, two fake lines with low intensities have appeared in the extracted Raman spectrum at 0.77 & 0.85 cm−1.
In the case of Sigmoid, all the lines were retrieved except for the spectral line at 0.77 cm−1. In addition, a large spurious signal is observed in the 0.4–0.6 cm−1 region. These limitations are reflected in PCC estimation, where its value is minimum (∼0.19) in the total test set for the Sigmoid model. Further, the Polynomial model has computed all the spectra lines. Nevertheless, the intensities of the two lines at 0.67 & 0.97 cm−1 do not agree with the true ones. Moreover, a spectral line shape with negligible intensity has appeared in the 0.4–0.6 cm−1 range. These observations also affected the PCC measurements, where the second-lowest coefficient (∼0.69) was achieved for this test spectrum for the Polynomial model.
Fig. 4(g–i) present the results of the 108th test spectrum obtained from the SpecNet, Sigmoid, and Polynomial models, respectively. The input CASRS spectrum has multiple spectral lines with different peak intensities. However, the first spectral line on the left extreme (at ∼0.006 cm−1) has only half part, i.e., the spectral line has started only with the trailing part instead of the rising part, as shown in Fig. 4(g–i). It happened due to considering a limited number of data points in the spectrum (640); otherwise, the total spectral line shape could be expected. It may also occur on the right side of the spectrum, as reported in our previous study.36 The three trained models have retrieved all the Raman lines except for the first line, which is attributed to considering merely half part of the spectral line. Similar observations were noticed in the previous studies where the DL model performance deteriorated when it encountered the spectral lines, with only having a rising or trailing part.36 This inherent limitation has led to a high SE of ∼0.15 and impacted the PCC measurements, where its value is minimum (∼0.67) for the Polynomial model. This could be a reason for the high MSE observed on either side of the extrema, as shown in Fig. 2(a–c).
In conclusion, Fig. 3 and 4 have visually demonstrated the imaginary part prediction capability of three models where the performance of the Polynomial model was found to be best. Numerically, it performed well on more than 90% of the total test data (i.e., it has a higher PCC value than the other models). It also revealed that its efficiency decreases (i.e., its correlation coefficient value) when it encounters the CARS spectrum with a very broad peak or spectral line located close to the edges or line shape with only having rising/trailing part.
Further, a histogram plot of the PCCs obtained for the 300 test spectra for the three models is shown in Fig. 5(a). It is an accurate method that graphically visualizes the numerical distribution of the PCC data. Here the frequency count represents the number of spectra that have PCC in a specified range. For example, six spectra have PCC between 0.65–0.7 for the SpecNet. The PCC values of the 97% test spectra lie in the region of 0.65–1 for all three models. Hence, the x-axis in Fig. 4(a) is started from 0.65 instead of zero. It ascertains a better visualization of the PCCs distribution. Also, it shows that ∼2/3 of total test data (199 test spectra) have more than a 0.95 correlation coefficient for the Polynomial model. It confirms that the predicted Raman signal from the CARS data is in better agreement with the true one. In contrast, only 121 and 100 spectra have PCC > 0.95 for the Specnet and Sigmoid models, respectively. Cumulatively 264, 165, and 187 spectra have PCCs of more than 0.9 for the Polynomial, Sigmoid, and SpecNet models, respectively.
Fig. 5. (a) Histogram plot of the PCC values of the three models. (b) Comparison of the different correlation metrics obtained from the three models. The symbol represents the mean value of the 300 test spectra, and the error bar corresponds to their standard deviation.
It is also noticed that the frequency count in most of the regions/bins is almost the same for the Sigmoid and SpecNet models. Moreover, it is observed that 29 & 27 spectra have PCC less than 0.8 for the SpecNet and Sigmoid models, respectively. Nevertheless, a significant difference is noticed for the Polynomial model, where only four spectra have PCC < 0.8. These findings demonstrate that the performance of the Polynomial model is superior in predicting the imaginary parts compared to the other models.
Further, Euclidean and Cosine distance methods have given results similar to the PCC approach. Hence their statistics are visualized in Fig. 5(b) instead of presenting individual metrics. The symbol in each model represents the mean value, and the error bar corresponds to the standard deviation measured from the 300 test spectra. It is envisioned from Fig. 5(b) that the correlation metrics have shown a similar trend irrespective of the model type. i.e., The average mean value is greater than ∼0.95 for the Polynomial model for all the metrics, whereas it is ∼0.89 & ∼0.9 for the Sigmoid and SpecNet models, respectively. It is also noticed that the error is minimum in the Polynomial model. In order to evaluate the preciseness of the correlation metric, its relative standard deviation (RSD) is calculated, which is found to be ∼5.1 for the Polynomial model. Whereas it is ∼12.4 & ∼12.8 for the SpecNet, and Sigmoid models, respectively.
To summarise, these metrics presented the predictive ability of the three models on the simulated test spectra. Results of the experimental CARS spectra are discussed in detail in the next section.
4.3. Prediction on experimental CARS spectra
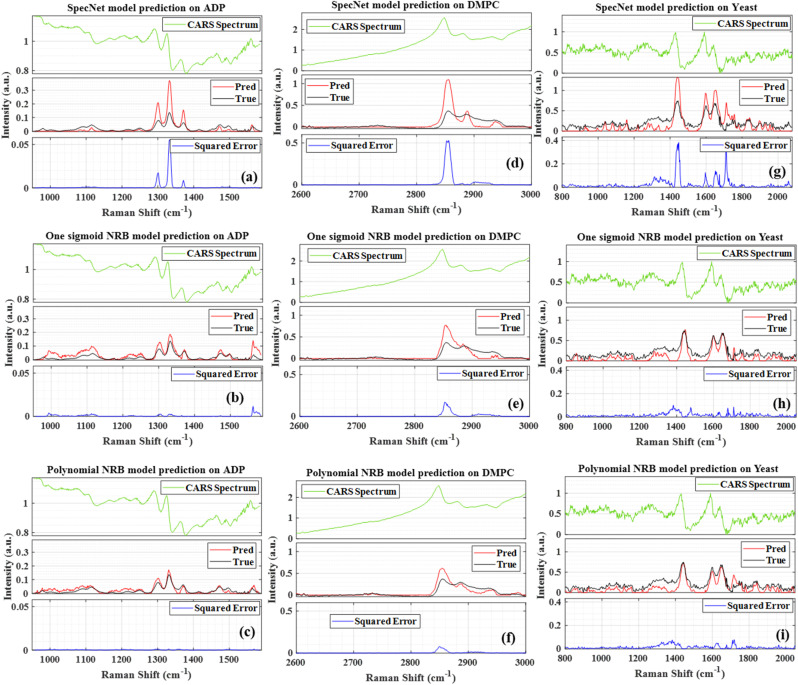
This section critically evaluates the trained model's efficiency by retrieving the vibrational spectrum from the experimentally recorded broadband CARS spectra. This investigation provides a complete overview of the model's performance when dealing with complex CARS data with different spectral backgrounds and vibrational features such as viz., ADP/AMP/ATP mixture, DMPC, and yeast samples. The experimental details of these samples are presented in Section 2.2. Fig. 6 illustrates the results of these test samples obtained from the three models. Further, each figure in Fig. 6 is a three-stacked plot where the first one is an input test CARS spectrum presented at the top with green color (see Fig. 6(a) for reference). The second plot in the middle visualizes the true and predicted imaginary parts with black and red colors, respectively. Here, ‘True’ and ‘Pred’ in the plot represent the imaginary part retrieved by the Maximum Entropy method and trained models, respectively. Further, the last plot at the bottom represents the squared error (blue line), i.e., the square of the difference between the true and predicted imaginary parts. In each sample, the y-axis scale is considered the same for all the models for better visualization.
Fig. 6. Results of the experimental CARS spectra. (a–c) The imaginary parts predicted by the SpecNet, Sigmoid and Polynomial models, respectively for the ADP/AMP/ATP. (d–f) For the DMPC, and (g–i) for the yeast.
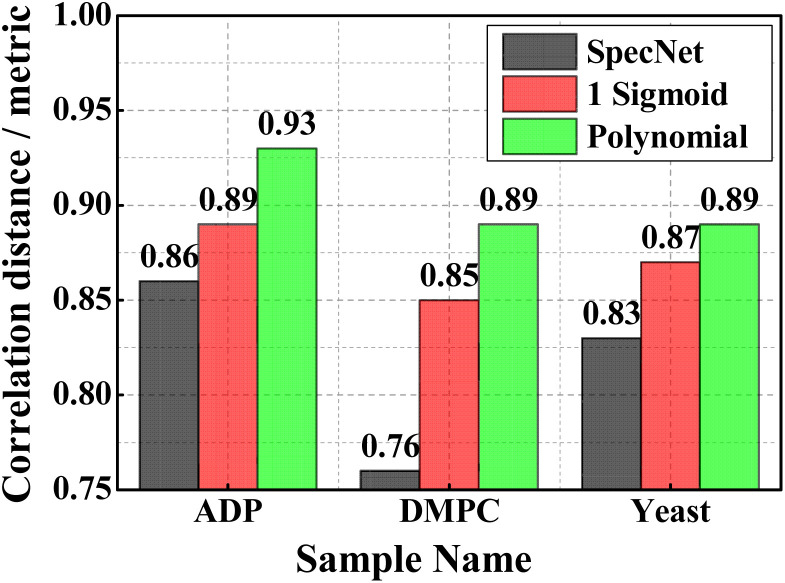
Fig. 6(a–c) represent the SpecNet, Sigmoid, and Polynomial models' prediction on the CARS spectrum of the ATP mixture, respectively. The adenine vibrations of the AMP/ADP/ATP molecules are the most prominent features and form the backbone of vibrations ranging from 1270 to 1400 cm−1. Among all, the strongest one is observed at ∼1330 cm−1 as shown in Fig. 6(a).47 All the models have extracted this vibrational mode, but the predicted intensities are not consistent with the actual intensities. The estimated SE is found to be minimum for the Polynomial model, i.e., ∼0.001 whereas it is three times higher in the case of the Sigmoid model and 50 times in SpecNet. Further, the phosphate vibrations in the spectral range of 950–1100 cm−1 can be utilized to identify different nucleotides.48 The symmetric stretching vibration of the triphosphate group of ATP has shown a strong vibrational resonance at ∼1123 cm−1. In this case also lowest SE is noticed for the Polynomial model, i.e., ∼10−5, and it is maximum for the Sigmoid ∼0.02. The SE for SpecNet is ∼10−4. The diphosphate broadened resonance at ∼1100 cm−1 is only found in Sigmoid and Polynomial models and absent in the SpecNet. The monophosphate resonance of AMP at 979 cm−1 was merely extracted by the Polynomial model and not observed in others. It is also noticed that the error is high on the right extreme for the Sigmoid model due to the significant deviation of the predicted intensity from the true one. Here also, we have estimated PCC for all the three models, and the results are presented in Fig. 7. It is evident from the correlation measurements that the performance of Polynomial is the best among all as it has the highest coefficient ∼0.93, followed by Sigmoid (∼0.89) and SpecNet (∼0.86).
Fig. 7. The PCCs estimated for the three experimental CARS spectra utilizing the three trained models.
Fig. 6(d–f) visualize the results of the DMPC sample obtained from the SpecNet, Sigmoid, and Polynomial models, respectively. It has a strong CH-stretch vibrational band between 2600 and 3000 cm−1. The vibrational band assignment of various resonant frequencies in the fingerprint CH-stretch region is well presented in the literature.49,50 It is also worth considering that this CARS spectral line shape and background are significantly affected by the broad vibrational response of water at the wings. The symmetric and antisymmetric stretching modes of methylene groups are assigned to the spectral lines at 2856 and 2892 cm−1, respectively.50 Further, the vibrational mode at 2946 cm−1 is attributed to the overtone of the methylene scissoring mode. All three models have retrieved these fingerprint lines. However, the extracted line strengths are not matching with the true intensities and lead to a high error in Sigmoid and SpecNet models. The measured SE at 2856 cm−1 is ∼0.51, ∼0.16, and ∼0.06 for SpecNet, Sigmoid and polynomial models, respectively. These errors are reflected in Pearson correlation measurements, where the PCCs of the three models are ∼0.76, ∼0.85, and ∼0.89, respectively. Also, a similar deviation is noticed for the three models for the spectral line at 2892 cm−1 as shown in Fig. 6(d–f). In the case of vibrational mode at 2946 cm−1, the performance of SpecNet and polynomial model is found to be similar, and the Sigmoid model has given an error by more than five times. Further, the predictions of the yeast sample using three models are presented in Fig. 6(g–i). The C–H bend of the aliphatic chain and amide band is noticed at 1440 cm−1 and 1654 cm−1, respectively. The C C bending mode of phenylalanine is observed at ∼1590 cm−1. The three models extracted all these spectral resonances nevertheless, predicted intensities have deviated for the SpecNet model. Also, a ringing structure has appeared in the 800–1200 cm−1 region, which is not present in the actual imaginary part. The SpecNet SE at 1440 cm−1 spectral line is more than 100 times compared to other models. The error in other peaks is also more than an order for the SpecNet. The estimated PCC also conveyed the same information where predictive capability is superior for the polynomial model than others.
Even though the polynomial NRB model performed well on the simulated and experimental data, it has shown minor shortcomings for a few synthetic spectra, such as low prediction intensities or the inability to find some peaks while extracting near the edges of the CARS spectrum. Also, the performance deteriorated when it encountered a partially simulated spectral line at the starting or ending point of the spectra, i.e., which has only a rising or trailing part instead of a complete line shape.
These limitations can be overcome by modifying spectral simulation parameters such as peak location, width, etc. in future work. It would also be interesting to explore various simulated data sets with different parameters, like the number of peaks, frequencies, amplitudes, noise, etc., to fit specific kinds of applications in different spectral regions.
Raman spectral line shapes are approximately known for applications like pharmaceutical analysis (distinct sharp peaks observed)51 and biomolecule cell mapping (broader peaks noticed).52 Hence, in future studies, NRB could be better approximated for these kinds of applications by considering the details of the excitation laser, such as spectral envelope and phase delay.35 Further, the order of the polynomial and range of the coefficients can be optimized in future work for better results. Also, experimentally recorded NRB can be utilized in synthesizing training data.
Moreover, the DL model hyper-parameters such as activation function, number of neurons, and number of layers can be modified to improve the performance.53 Also, fine-tuning or transferring learning mechanisms can be explored to circumvent these limitations, which positively impacts model performance. It is also interesting to explore Gaussian processes54 as an alternative model to extract Raman data from the CARS spectrum in future studies. In particular, it has successfully modelled 1D time series and spectral data and learned kernels having an extractable power spectral density.55 Further, non-stationary kernels achieved via input warping44 can also be useful for modelling the nonstationary behaviour of intensity as a function of Raman shift.
5. Conclusions
We have presented a comprehensive study by exploring different NRBs to efficiently extract Raman signals from the CARS spectra using the CNN model. This approach has an opportunity to retrieve the imaginary part without any user intervention. The input CARS data was simulated with three different non-resonant backgrounds (NRBs) types, i.e., (i) Product of two sigmoids, (ii) Single Sigmoid, and (iii) fourth-order polynomial function. All the spectral simulation parameters are considered the same except for the NRB. The CARS datasets were separately synthesized for each NRB type and then utilized to train the CNN model individually. Finally, the prediction efficiency of these three models was tested on 300 unknown test spectra. These studies have demonstrated that Polynomial NRB models' performance is superior to other models where the extracted line shapes are in better agreement with the true ones. Further, the correlation analysis has revealed that a higher correlation coefficient is achieved for the 90% of test data for the Polynomial NRB model. On average, it is found to be ∼0.95 for 300 test spectra, whereas it is only ∼0.89 for the other two models. Final measurements on three experimental CARS spectra (DMPC, ADP, and yeast) also confirmed that the predictive capability is best for the Polynomial NRB model compared to the other two. This investigation has shown potential improvement compared to the previous reports, where only one type of NRB is used to train the DL model irrespective of its architecture. Finally, the performance of the polynomial NRB model sets the baseline for this kind of research, and any future studies can be incrementally built on this work.
Author contributions
Rajendhar Junjuri (RJ), Lasse Lensu (LL), Erik M. Vartiainen (EMV) have conceived the idea of the experiment. Rajendhar Junjuri (RJ) has performed the analysis and prepared the initial draft. Ali Saghi (AS), partially contributed to the analysis part. Finally, the draft was revised by LL, EMV, and AS.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
This work is a part of the “Quantitative Chemically-Specific Imaging Infrastructure for Material and Life Sciences (qCSI)” project funded by the Academy of Finland (grant no. FIRI/327734). Also, we thank Michiel Müller and Hilde Rinia for providing the experimental measurements of the DMPC lipid sample and the AMP/ADP/ATP mixture, as well as, Masanari Okuno and Hideaki Kano for providing the experimental measurements of the yeast sample.
Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03983d
References
- Zumbusch A. Holtom G. R. Xie X. S. Phys. Rev. Lett. 1999;82:4142. [Google Scholar]
- Malard L. M. Lafeta L. Cunha R. S. Nadas R. Gadelha A. Cançado L. G. Jorio A. Phys. Chem. Chem. Phys. 2021;23:23428–23444. doi: 10.1039/d1cp03240b. [DOI] [PubMed] [Google Scholar]
- Petrov G. I. Arora R. V Yakovlev V. Analyst. 2021;146:1253–1259. doi: 10.1039/d0an01962c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popov K. I. Pegoraro A. F. Stolow A. Ramunno L. Opt. Lett. 2012;37:473–475. doi: 10.1364/OL.37.000473. [DOI] [PubMed] [Google Scholar]
- Evans C. L. Xie X. S. Annu. Rev. Anal. Chem. 2008;1:883–909. doi: 10.1146/annurev.anchem.1.031207.112754. [DOI] [PubMed] [Google Scholar]
- Konorov S. O. Blades M. W. Turner R. F. B. Opt. Express. 2011;19:25925–25934. doi: 10.1364/OE.19.025925. [DOI] [PubMed] [Google Scholar]
- Tolles W. M. Nibler J. W. McDonald J. R. Harvey A. B. Appl. Spectrosc. 1977;31:253–271. [Google Scholar]
- Popov K. I. Pegoraro A. F. Stolow A. Ramunno L. Opt. Express. 2011;19:5902–5911. doi: 10.1364/OE.19.005902. [DOI] [PubMed] [Google Scholar]
- Cheng J.-X. Book L. D. Xie X. S. Opt. Lett. 2001;26:1341–1343. doi: 10.1364/ol.26.001341. [DOI] [PubMed] [Google Scholar]
- Ganikhanov F. Evans C. L. Saar B. G. Xie X. S. Opt. Lett. 2006;31:1872–1874. doi: 10.1364/ol.31.001872. [DOI] [PubMed] [Google Scholar]
- Burkacky O. Zumbusch A. Brackmann C. Enejder A. Opt. Lett. 2006;31:3656–3658. doi: 10.1364/ol.31.003656. [DOI] [PubMed] [Google Scholar]
- Konorov S. O. Blades M. W. Turner R. F. B. Appl. Spectrosc. 2010;64:767–774. doi: 10.1366/000370210791666228. [DOI] [PubMed] [Google Scholar]
- Jurna M. Korterik J. P. Otto C. Herek J. L. Offerhaus H. L. Opt. Express. 2008;16:15863–15869. doi: 10.1364/oe.16.015863. [DOI] [PubMed] [Google Scholar]
- Müller M. Zumbusch A. ChemPhysChem. 2007;8:2156–2170. doi: 10.1002/cphc.200700202. [DOI] [PubMed] [Google Scholar]
- Cui M. Bachler B. R. Ogilvie J. P. Opt. Lett. 2009;34:773–775. doi: 10.1364/ol.34.000773. [DOI] [PubMed] [Google Scholar]
- Vartiainen E. M. J. Opt. Soc. Am. B. 1992;9:1209–1214. [Google Scholar]
- Liu Y. Lee Y. J. Cicerone M. T. Opt. Lett. 2009;34:1363–1365. doi: 10.1364/ol.34.001363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karuna A. Masia F. Borri P. Langbein W. J. Raman Spectrosc. 2016;47:1167–1173. doi: 10.1002/jrs.4876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camp Jr C. H. Lee Y. J. Cicerone M. T. J. Raman Spectrosc. 2016;47:408–415. doi: 10.1002/jrs.4824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camp Jr C. H. Bender J. S. Lee Y. J. Opt. Express. 2020;28:20422–20437. doi: 10.1364/OE.397606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kan Y. Lensu L. Hehl G. Volkmer A. Vartiainen E. M. Opt. Express. 2016;24:11905–11916. doi: 10.1364/OE.24.011905. [DOI] [PubMed] [Google Scholar]
- LeCun Y. Bengio Y. Hinton G. Nature. 2015;521:436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- Young T. Hazarika D. Poria S. Cambria E. IEEE Comput. Intell. Mag. 2018;13:55–75. [Google Scholar]
- Salman A. G., Kanigoro B. and Heryadi Y., in 2015 International Conference on Advanced Computer Science and Information Systems (ICACSIS), IEEE, 2015, pp. 281–285 [Google Scholar]
- Guo Y. Liu Y. Oerlemans A. Lao S. Wu S. Lew M. S. Neurocomputing. 2016;187:27–48. [Google Scholar]
- Lussier F. Thibault V. Charron B. Wallace G. Q. Masson J.-F. TrAC, Trends Anal. Chem. 2020;124:115796. [Google Scholar]
- Ozdemir A. Polat K. J. Inst. Electron. Comput. 2020;2:39–56. [Google Scholar]
- Junjuri R. Zhang C. Barman I. Gundawar M. K. Polym. Test. 2019;76:101–108. [Google Scholar]
- Ghosh K. Stuke A. Todorović M. Jørgensen P. B. Schmidt M. N. Vehtari A. Rinke P. Adv. Sci. 2019;6:1801367. doi: 10.1002/advs.201801367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Junjuri R. Gundawar M. K. Waste Manage. 2020;117:48–57. doi: 10.1016/j.wasman.2020.07.046. [DOI] [PubMed] [Google Scholar]
- Mal E. Junjuri R. Gundawar M. K. Khare A. Laser Part. Beams. 2020;38:14–24. [Google Scholar]
- Junjuri R. Nalam S. A. Manikanta E. Harsha S. S. Kiran P. P. Gundawar M. K. Opt. Express. 2021;29:10395. doi: 10.1364/OE.417842. [DOI] [PubMed] [Google Scholar]
- Houhou R. Barman P. Schmitt M. Meyer T. Popp J. Bocklitz T. Opt. Express. 2020;28:21002–21024. doi: 10.1364/OE.390413. [DOI] [PubMed] [Google Scholar]
- Valensise C. M. Giuseppi A. Vernuccio F. De la Cadena A. Cerullo G. Polli D. APL Photonics. 2020;5:61305. [Google Scholar]
- Wang Z. O’ Dwyer K. Muddiman R. Ward T. Camp C. H. Hennelly B. M. J. Raman Spectrosc. 2022;53:1081–1093. [Google Scholar]
- Junjuri R. Saghi A. Lensu L. Vartiainen E. M. Opt. Continuum. 2022;1:1324. [Google Scholar]
- Junjuri R., CARS data analysis with different NRB, https://github.com/Junjuri/LUT
- Müller M. Schins J. M. J. Phys. Chem. B. 2002;106:3715–3723. [Google Scholar]
- Okuno M. Kano H. Leproux P. Couderc V. Day J. P. R. Bonn M. Hamaguchi H. Angew. Chem., Int. Ed. Engl. 2010;122:6925–6929. doi: 10.1002/anie.201001560. [DOI] [PubMed] [Google Scholar]
- Krizhevsky A. Sutskever I. Hinton G. E. Commun. ACM. 2017;60:84–90. [Google Scholar]
- Zheng Y., Liu Q., Chen E., Ge Y. and Zhao J. L., in International Conference on web-age information management, Springer, 2014, pp. 298–310 [Google Scholar]
- Hijazi S., Kumar R. and Rowen C., Using Convolutional Neural Networks for Image Recognition, Cadence Des. Syst. Inc., San Jose, CA, USA, 2015, pp. 1–12 [Google Scholar]
- Kang K., Ouyang W., Li H. and Wang X., in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 817–825 [Google Scholar]
- Kingma D. P. and Ba J., 2014, arXiv:1412.6980, arXiv Prepr
- Tan X. Chen X. Song S. J. Raman Spectrosc. 2017;48:113–118. [Google Scholar]
- Schober P. Boer C. Schwarte L. A. Anesth. Analg. 2018;126:1763–1768. doi: 10.1213/ANE.0000000000002864. [DOI] [PubMed] [Google Scholar]
- Yue K. T. Martin C. L. Chen D. Nelson P. Sloan D. L. Callender R. Biochemistry. 1986;25:4941–4947. doi: 10.1021/bi00365a033. [DOI] [PubMed] [Google Scholar]
- Rimai L. Cole T. Parsons J. L. Hickmott Jr J. T. Carew E. B. Biophys. J. 1969;9:320–329. doi: 10.1016/S0006-3495(69)86389-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendelsohn R. Moore D. J. Chem. Phys. Lipids. 1998;96:141–157. doi: 10.1016/s0009-3084(98)00085-1. [DOI] [PubMed] [Google Scholar]
- Fasanella A. Cosentino K. Beneduci A. Chidichimo G. Cazzanelli E. Barberi R. C. Castriota M. Biochim. Biophys. Acta, Biomembr. 2018;1860:1253–1258. doi: 10.1016/j.bbamem.2018.02.021. [DOI] [PubMed] [Google Scholar]
- Vankeirsbilck T. Vercauteren A. Baeyens W. Van der Weken G. Verpoort F. Vergote G. Remon J. P. TrAC, Trends Anal. Chem. 2002;21:869–877. [Google Scholar]
- Talari A. C. S. Movasaghi Z. Rehman S. Rehman I. U. Appl. Spectrosc. Rev. 2015;50:46–111. [Google Scholar]
- Cowen-Rivers A. I. Lyu W. Tutunov R. Wang Z. Grosnit A. Griffiths R. R. Maraval A. M. Jianye H. Wang J. Peters J. J. Artif. Intell. Res. 2022;74:1269–1349. [Google Scholar]
- Rasmussen C. E. and Williams C. K. I., Gaussian Processes for Machine Learning, University Press Group Limited, 2006 [Google Scholar]
- Griffiths R.-R. Jiang J. Buisson D. J. K. Wilkins D. Gallo L. C. Ingram A. Grupe D. Kara E. Parker M. L. Alston W. Astrophys. J. 2021;914:144. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.