Electrophysiology

Abstract

Electrical signaling is a fast mode of communication for cells within an organism. We are concerned here with the formulation and analysis of mathematical models that are used to describe this important class of physiological processes. These models generally take the form of partial differential equations that are descendants of those introduced by Hodgkin and Huxley to describe the propagation of an action potential along the squid giant axon. We review that work here and then go on to describe more recent variations on the Hodgkin-Huxley theme, including the three-dimensional bidomain (and monodomain) equations for cardiac electrophysiology, multiscale models for the heart that take cellular structure into account near the action potential wavefront, and finally a more detailed reformulation of electrophysiology in terms of electrodiffusion.

1. Introduction to Neuronal Electrophysiology: The Hodgkin-Huxley Equations

Electrophysiology is concerned with the electrical activity of living cells. Every cell in the body has a resting electrical potential difference across its cell membrane, with the inside of the cell negative with respect to the outside. This rest potential is a byproduct of the cell’s need to pump ions continually in an effort to control the cell volume, which would otherwise increase without bound by osmosis until the cell would burst [54,87]. Specialized cells known as neurons have learned how to manipulate the electrical potential difference across the cell membrane in order to send electrical signals to other cells. All of human thought and action is made possible by this trick.

The mathematical framework for describing the electrical activity of neurons was introduced by Hodgkin and Huxley [35], who were concerned primarily with the wave of electrical activity that propagates along an axon, which is a long, thin, membrane-bound cylinder that typically carries signals away from the cell body of a neuron. Such signals are pulselike in character, and each pulse is called an action potential. The action potential has several remarkable characteristics that Hodgkin and Huxley sought to explain. First, the action potential has a fixed amplitude and waveform, and both are essentially independent of the stimulus, provided that the stimulus is strong enough to produce an action potential. Second, the action potential travels as a wave at a fixed speed, but despite the electrical nature of this wave, its speed is many orders of magnitude less than the speed of light. Third, there is no loss of amplitude as the wave propagates, even though it moves through a very lossy medium (essentially saltwater) and generates heat as it goes. Finally, if two action potentials traveling in opposite directions collide, they annihilate each other, a behavior which clearly distinguishes them from many other forms of wave propagation, both linear and nonlinear.

The equations proposed by Hodgkin and Huxley to describe the nerve action potential are as follows:

$$C_{\text{m}}\frac{\partial v}{\partial t}+\overline{g_{\text{Na}}}{m}^{3}h\left(v-E_{\text{Na}}\right)+\overline{g_{\text{K}}}{n}^4\left(v-E_{\text{K}}\right)+\overline{g_{\text{L}}}\left(v-E_{\text{L}}\right)=\frac{r}{2\rho }\frac{{\partial }^{2}v}{\partial x^2},$$ (1.1)

$${\tau }_m(v)\frac{\partial m}{\partial t}=m_{\infty }(v)-m,$$ (1.2)

$${\tau }_h(v)\frac{\partial h}{\partial t}=h_{\infty }(v)-h,$$ (1.3)

$${\tau }_n(v)\frac{\partial n}{\partial t}=n_{\infty }(v)-n.$$ (1.4)

In these equations, the unknown variables are v(x, t), m(x, t), h(x, t), and n(x, t). Here, x measures distance along the cylindrical axon, and t is the time. The voltage difference across the cell membrane (intracellular voltage minus extracellular voltage, with the extracellular space assumed isopotential and grounded) is denoted v(x, t). The gating variables, which are m(x, t), h(x, t), and n(x, t), take values in [0, 1]; their interpretation will be discussed more fully below.

The constants in equation (1.1) are the capacitance per unit area of membrane, C_m; the maximum possible Na⁺, K⁺, and “leakage” conductances per unit area, $\overline{g_{\text{Na}}}$, $\overline{g_K}$, and $\overline{g_{\text{L}}}$, respectively; the reversal potentials for the Na⁺, K⁺, and leakage channels, denoted E_Na, E_K, and E_L; the radius of the axon, r; and the electrical resistivity of the axoplasm, denoted ρ. The values of these constants for the squid giant axon, which is the preparation used by Hodgkin and Huxley in their classic studies, are given in Table 1.1.

Table 1.1.

Hodgkin-Huxley model parameters.

C m	1.0 μF/cm2
$\overline{g_{\text{Na}}}$	120 (μA/mV)/cm2
$\overline{g_{\text{K}}}$	36 (μA/mV)/cm2
$\overline{g_{\text{L}}}$	0.3 (μA/mV)/cm2
E Na	45 mV
E K	−82 mV
E L	−59 mV
r	0.0238 cm
ρ	0.0354 (mV/μA)cm

Besides the given constants, the Hodgkin-Huxley equations contain six functions of voltage that were determined by curve-fitting to experimental data, and which are regarded as known. These are the time constants τ_m(v), τ_h(v), and τ_n(v), as well as the steady-state values of m, h, and n at any given, fixed voltage, which are denoted m_∞(v), h_∞(v), and n_∞(v). These six functions, again for the squid giant axon, are recorded in Table 1.2, where they are expressed in terms of six other functions: α_m(v), β_m(v), α_h(v), β_h(v), α_n(v), and β_n(v). In each case s = m, h, or n, α_s(v) is the rate constant (probability per unit time) for opening a closed gate of type s, and β_s(v) is the rate constant for closing an open gate of type s. We emphasize that the specific functional forms used by Hodgkin and Huxley to fit their data to these measured rate constants have no known biophysical significance, but it is convenient to have the specific formulae they provided as a surrogate for the raw dataset. Extensions of this model that are more closely tied to the biophysics of ion channels are described in Section 3.2.

Table 1.2.

Hodgkin-Huxley gating functions.

For s = m,h,n:
$s_{\infty }(v)=\frac{{\alpha }_s(v)}{{\alpha }_s(v)+{\beta }_s(v)}$	${\tau }_s(v)=\frac{1}{{\alpha }_s(v)+{\beta }_s(v)}$
where
${\alpha }_m(v)=\frac{(v+45)/10}{1-\exp (-(v+45)/10)}$	βm(v) = 4exp(−(v + 70)/18)
αh(v) = 0.07 exp(−(v + 70)/20)	${\beta }_h(v)=\frac{1}{1+\exp (-(v+40)/10)}$
${\alpha }_n(v)=\frac{0.1(v+60)/10}{1-\exp (-(v+60)/10)}$	βn(v) = 0.125exp(−(v + 70)/18)
with υ in mV, and α and β in ms−1

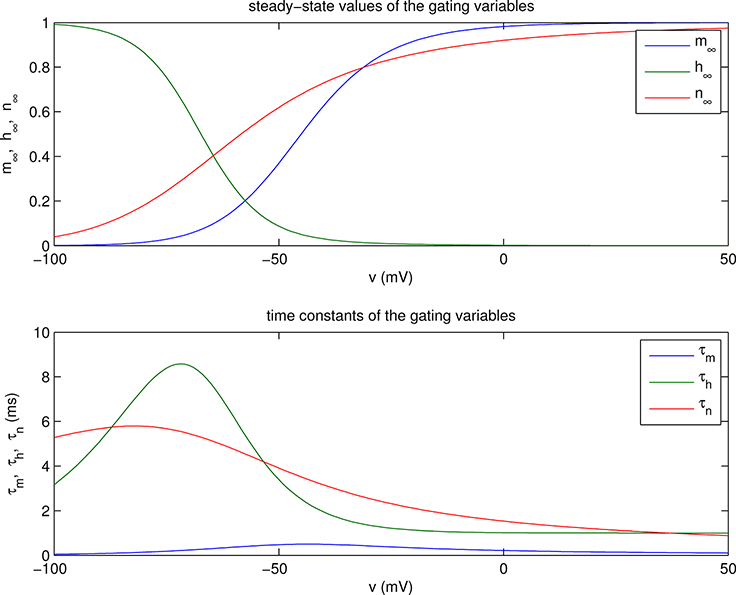
The functions m_∞(v), h_∞(v), and n_∞(v) are plotted in the upper panel of Figure 1.1, and τ_m(v), τ_h(v), and τ_n(v) are plotted in the lower panel. Important qualitative points to note are that m_∞(v), h_∞(v), and n_∞(v) each look like a smoothed version of a step function, and that m_∞(v) and n_∞(v) both increase monotonically from 0 at v = −∞ to 1 at v = +∞, whereas h_∞(v) has the opposite behavior, decreasing monotonically from 1 at v = −∞ to 0 at v = +∞. With regard to the time constants τ_m(v), τ_h(v), and τ_n(v), it should be noted that τ_h(v) and τ_n(v) are similar in magnitude to each other, and about an order of magnitude larger (i.e., slower) than τ_m(v).

Figure 1.1.

Steady-state values (top) and time constants (bottom) of the gating variables as functions of voltage. Note that m_∞ and n_∞ are increasing functions of voltage, whereas h_∞ is decreasing. Also, τ_m is an order of magnitude smaller than either τ_h or τ_n.

The Hodgkin-Huxley equations can be derived from electrical current conservation, together with certain assumptions about the transmembrane and axial currents. Let I_m(x, t) be the transmembrane current density (i.e., the transmembrane current per unit area of membrane), and let I_axial(x, t) be the axial current density (i.e., the axial current per unit cross-sectional area). Then the overall conservation of electrical current (including Maxwell’s displacement current) gives the continuity equation

$$\pi r^2\frac{\partial I_{\text{axial}}}{\partial x}+2\pi r{I}_{\text{m}}=0,$$ (1.5)

since πr² is the cross-sectional area of the axon, and 2πr is the membrane area per unit length of axon. Let us now assume that the axial current is given by the distributed version of Ohm’s law:

$$I_{\text{axial}}=-\frac{1}{\rho }\frac{\partial v}{\partial x}.$$ (1.6)

Substituting (1.6) into (1.5) and dividing by 2πr, we get equation (1.1) provided that we set

$$I_{\text{m}}=C_{\text{m}}\frac{\partial v}{\partial t}+\overline{g_{\text{Na}}}{m}^{3}h\left(v-E_{\text{Na}}\right)+\overline{g_{\text{K}}}{n}^4\left(v-E_{\text{K}}\right)+\overline{g_{\text{L}}}\left(v-E_{\text{L}}\right).$$ (1.7)

The rest of our discussion is therefore concerned with the interpretation of equation (1.7) as a formula for the transmembrane current per unit area of membrane.

Equation (1.7) states that the transmembrane current density is a sum of four terms: a capacitive current density and three ionic current densities. The capacitive term is a simple physical consequence of the nature of the membrane as a thin insulator (pierced, however, by conducting ionic channels) that separates two conductive media. As such, the membrane has a capacitance per unit area, denoted by C_m, which turns out to be approximately 1 μF=cm² for all lipid bilayer membranes. Of course, $C_{\text{m}}\frac{\partial v}{\partial t}$ is the standard formula for the current per unit area through such a capacitor. Each of the three ionic current densities is of the form g(v − E) where g is the conductance (reciprocal of resistance) per unit area, and E is the reversal potential (i.e., the voltage at which the current changes sign). This is the current-voltage relationship of a resistor in series with a battery. (Not all ionic channels have such a simple current-voltage relationship, but, following Hodgkin and Huxley, we assume it here.) The physical origin of the reversal potential is that ion concentrations are typically different on the two sides of the cell membrane, i.e., interior and exterior to the cell. In particular, Na⁺ concentrations are lower inside of cells than outside, whereas K⁺ concentrations are higher intracellularly than extracellularly. These concentration differences are brought about by the Na⁺-K⁺ exchange pump, a protein that spans the cell membrane and makes use of metabolic energy (in the form of adenosine triphosphate, or ATP) to pump Na⁺ ions out of the cell and K⁺ ions into the cell. The concentration differences thus established act as a reservoir of free energy that can be drawn upon to power the action potential.

The constants E_Na, E_K, and E_L in the Hodgkin-Huxley equations are nonzero because of these concentration differences. In particular,

$$E_{\text{Na}}=\frac{kT}{q}\ln \frac{{\left[{\text{Na}}^{+}\right]}_{\text{e}}}{{\left[{\text{Na}}^{+}\right]}_{\text{i}}}>0,$$ (1.8)

$$E_{\text{K}}=\frac{kT}{q}\ln \frac{{\left[{\text{K}}^{+}\right]}_{\text{e}}}{{\left[{\text{K}}^{+}\right]}_{\text{i}}}<0.$$ (1.9)

In these equations, k is Boltzmann’s constant, T is the absolute temperature, q is the elementary charge (i.e., the charge on a proton), [Na⁺]_i and [Na⁺]_e are the intracellular and extracellular Na⁺ concentrations, respectively, and [K⁺]_i and [K⁺]_e are the intracellular and extracellular K⁺ concentrations. It is worthwhile to know that kT/q is about 25 mV; this can be thought of as the natural unit of voltage in electrophysiology. Equations (1.8) and (1.9) are the Nernst equations, which can be derived from thermodynamics for the reversal potential of an ion channel that is perfectly selective for one species of ion. This is the case, to an excellent approximation, for the ion channels that carry the Na⁺ and K⁺ currents of the squid giant axon. In this situation of perfect ion selectivity, the reversal potential is also called the equilibrium potential. The leakage channel, by contrast, admits more than one species of ion, so its reversal potential is not an equilibrium potential and is not given by a Nernst equation. The reversal potential for the leakage channel depends on the ion concentrations of more than one ion species in a manner that cannot be determined by thermodynamics alone.

An important conceptual point (at least for large neurons) is that the ion concentrations, and hence the reversal potentials, do not change appreciably during an action potential, despite the ionic currents that flow across the cell membrane. In this respect a neuron is much like a flashlight that can be flashed many times before its batteries run down. In the case of a neuron, moreover, the batteries are rechargeable, and indeed are being continually recharged by the Na⁺-K⁺ exchange pump. For these reasons, the ion concentrations do not appear in the Hodgkin-Huxley equations as dynamical variables, and the quantities on which they depend, namely E_Na, E_K, and E_L, are treated as constants. There are, however, important exceptions to this principle, as we shall discuss in later sections of this paper.

Finally, we come to the most important and distinctive feature of the Hodgkin-Huxley equations, the gating variables m, h, and n. As mentioned above, ionic current flows through specialized channels. These are membrane-spanning proteins that surround an aqueous pore through which ions can flow. Besides being highly specific, such ion channels are often voltage-gated. This means that they undergo conformational changes that can be interpreted as the opening and closing of gates that regulate the flow of ions, and moreover, that the rate constants for the opening and closing of gates are functions of the voltage difference across the cell membrane.

We next give an interpretation of the Hodgkin-Huxley expressions for the Na⁺ and K⁺ currents that represents a possible scheme for the physical mechanism of ion channel gating. We now know that real ion channels do not work in exactly the way that Hodgkin and Huxley implicitly postulated, through their equations, even though their equations give a good fit to their data. What is remarkable, however, is how much of the Hodgkin-Huxley interpretation (explained in detail below) has survived, starting with the notion of ion channels themselves, which was itself a bold hypothesis at the time, and including the concept of discrete ion channel states, at least one of which represents the open channel, with voltage-dependent probabilities per unit time for transitions from one state to another.

To obtain the Hodgkin-Huxley expression for the K⁺ conductance, we make the assumption that each K⁺ channel has four identical gates that operate independently of each other, and that all four must be open for the channel to be open. Let n(x, t) be the probability that any particular one of these gates in a channel located near position x happens to be open at time t. Then n⁴(x, t) is the probability that any particular K⁺ channel near x happens to be open at time t. Thus, the expected K⁺ conductance per unit area at position x at time t is given by $g_{\text{K}}=\overline{g_{\text{K}}}{n}^4(x,t)$, where $\overline{g_K}$ is the maximum possible K⁺ conductance per unit area, i.e., the K⁺ conductance per unit area when all of the K⁺ channels are open.

The story for the Na⁺ channel is exactly the same, except that the four gates, although still independent, are no longer identical. In fact, there are three of one type (which might be called “m-gates”) and one of a different type (which might be called an “h-gate”). Now let m(x, t) be the probability that any particular m-gate in a Na⁺ channel near position x at time t is open, and let h(x, t) be the probability that any particular h-gate in a Na⁺ channel near x at time t is open; then the expected Na⁺ conductance per unit area at position x and time t is given by $g_{\text{Na}}=\overline{g_{\text{Na}}}{m}^3(x,t)h(x,t)$, where $\overline{g_{\text{Na}}}$ is the maximum possible Na⁺ conductance per unit area, i.e., the Na⁺ conductance per unit area when all of the Na⁺ channels are open.

As for the dynamics of the gating variables themselves, each of the gating variables of the Hodgkin-Huxley model obeys a first-order differential equation that describes the opening and closing of one particular kind of gate, with voltage-dependent opening and closing rates. Such an equation can always be put in the form that appears in (1.2)–(1.4).

2. Traveling Wave Solutions of a Simplified Hodgkin-Huxley System

Several ways of simplifying the Hodgkin-Huxley equations have been introduced by various authors in order to make it possible to see analytically that equations of this kind can have traveling wave solutions and to study the qualitative properties of such solutions. Here we combine ideas from the piecewise-linear approach of McKean [49] and Rinzel and Keller [75] with the singular perturbation method of Casten, Cohen, and Lagerstrom [6]. The particular combination described here (previously presented only in unpublished lecture notes [67]) has the virtue of allowing us to stay close to the original form of the Hodgkin-Huxley equations while still making it possible to obtain traveling wave solutions in a singular-perturbation limit almost completely analytically, with just one nonlinear equation in one unknown that has to be solved numerically for the action potential duration.

Our simplified Hodgkin-Huxley model is as follows:

$$\begin{gathered} ϵC_{\text{m}}\frac{\partial v}{\partial t}+\overline{g_{\text{Na}}}mh\left(v-E_{\text{Na}}\right) \\ +\overline{g_{\text{K}}}{n}^4\left(v-E_{\text{K}}\right)+\overline{g_{\text{L}}}\left(v-E_{\text{L}}\right)={ϵ}^2\frac{r}{2\rho }\frac{{\partial }^{2}v}{\partial x^2}, \end{gathered}$$ (2.1)

$$m=\{\begin{array}{ll}1,\hfill & v>v_{*},\hfill \\ 0,\hfill & v<v_{*},\hfill \end{array}$$ (2.2)

$${\tau }_h\frac{\partial h}{\partial t}=(1-m)-h,$$ (2.3)

$${\tau }_n\frac{\partial n}{\partial t}=m-n.$$ (2.4)

The changes that we have made in going from the original Hodgkin-Huxley system to the above model are as follows: First, we have introduced a dimensionless parameter ϵ in two places in equation (2.1). Later, we shall let ϵ → 0. If we have introduced this parameter ϵ in an artful way, then the solution obtained in the limit ϵ → 0 will be a good approximation to the solution with ϵ = 1. This method of sneaking a “small parameter” into an equation is surely more ad hoc and unmotivated than the more systematic approach of rewriting the equations in dimensionless form and looking for a small parameter to emerge naturally. The approach we follow here has one important advantage, however. It leaves all variables and parameters with their original physical meanings and their original physical values and units. This allows us to study an interesting limiting case without draining the life out of the equations by making everything dimensionless. The logic of what we are doing is that we are replacing the original system by a family of systems depending upon a parameter ϵ such that ϵ = 1 yields the original system, but the limit ϵ → 0 is one that we can analyze.

The remaining modifications all concern the gating variables. First, we have replaced the functions τ_m(v), τ_h(v), and τ_n(v) by constants, and, moreover, we have set τ_m(v) = 0 so that m = m_∞(v) instantaneously, with no lag. Next, we have replaced the smooth functions m_∞(v), h_∞(v), and n_∞(v) by step functions. In particular, we have set

$$n_{\infty }(v)=1-h_{\infty }(v)=m_{\infty }(v)=\{\begin{array}{ll}1,\hfill & v>v_{*},\hfill \\ 0,\hfill & v<v_{*}.\hfill \end{array}$$ (2.5)

This introduces an explicit threshold, denoted v_*, into our model. We assume that this threshold is related to the reversal potentials in the following way:

$$E_{\text{K}}<E_{\text{L}}<v_{*}<E_{\text{Na}}.$$ (2.6)

It is then easy to see by inspection that E_L is the rest potential of our simplified Hodgkin-Huxley system. The resting state is given by v = E_L, m = 0, h = 1, and n = 0.

Finally, since m is now equal to 0 or 1, we have, without actually making any further change, replaced m³ by m in the formula for the Na⁺ current density.

Note that equations (2.1)–(2.4) are now self-contained in the sense that there are no additional functions of voltage that need to be specified, as there were in the case of the original Hodgkin-Huxley equations.

We are now ready to construct a traveling wave solution of equations (2.1)–(2.4) in the limit ϵ → 0. The first step is to postulate a solution in the form of a traveling wave by setting

$$v=V\left(t+\frac{x}{\theta }\right)=V(T),$$ (2.7)

$$m=M\left(t+\frac{x}{\theta }\right)=M(T),$$ (2.8)

$$h=H\left(t+\frac{x}{\theta }\right)=H(T),$$ (2.9)

$$n=N\left(t+\frac{x}{\theta }\right)=N(T),$$ (2.10)

where θ is the unknown wave speed. The resulting ordinary differential equations are

$$\begin{gathered} ϵC_{\text{m}}{V}^{\prime }+\overline{g_{\text{Na}}}MH\left(V-E_{\text{Na}}\right) \\ +\overline{g_{\text{K}}}{N}^4\left(V-E_{\text{K}}\right)+\overline{g_{\text{L}}}\left(V-E_{\text{L}}\right)={ϵ}^2\frac{r}{2\rho {\theta }^2}{V}^{\prime \prime }, \end{gathered}$$ (2.11)

$$M=\{\begin{array}{ll}1,\hfill & V>v_{*},\hfill \\ 0,\hfill & V<v_{*},\hfill \end{array}$$ (2.12)

$${\tau }_h{H}^{\prime }=(1-M)-H,$$ (2.13)

$${\tau }_n{N}^{\prime }=M-N.$$ (2.14)

Here and in the following, ′ is used to indicate the derivative of any function of one variable with respect to its argument.

The next step is to specify the qualitative form of the traveling wave that we seek, namely an isolated pulse. That is to say, we look for a solution in which V(T) is above threshold during some bounded interval of values of T, and below threshold otherwise. Without loss of generality, we may assume that the above-threshold interval is of the form (0, T₁), in which the duration T₁ of the above-threshold interval is unknown. In that case, we can immediately write down formulae in terms of T₁ for M(T), H(T), and N(T), as follows:

$$M(T)=\{\begin{array}{ll}0,\hfill & T<0,\hfill \\ 1,\hfill & 0<T<T_1,\hfill \\ 0,\hfill & T_1<T,\hfill \end{array}$$ (2.15)

$$H(T)=\{\begin{array}{ll}1,\hfill & T<0,\hfill \\ \exp \left(-\frac{T}{{\tau }_h}\right),\hfill & 0<T<T_1,\hfill \\ 1-\left(1-\exp \left(-\frac{T}{{\tau }_h}\right)\right)\exp \left(-\frac{T-T_1}{{\tau }_h}\right),\hfill & T_1<T,\hfill \end{array}$$ (2.16)

$$N(T)=\{\begin{array}{ll}0,\hfill & T<0,\hfill \\ 1-\exp \left(-\frac{T}{{\tau }_n}\right),\hfill & 0<T<T_1,\hfill \\ \left(1-\exp \left(-\frac{T}{{\tau }_n}\right)\right)\exp \left(-\frac{T-T_1}{{\tau }_n}\right),\hfill & T_1<T.\hfill \end{array}$$ (2.17)

These functions are plotted in the lower panel of Figure 2.1. Of particular importance in the following are the values of H and N at T = 0 and at T = T₁. These are

$$H_0=H(0)=1,$$ (2.18)

$$N_0=N(0)=0,$$ (2.19)

$$H_1=H\left(T_1\right)=\exp \left(-\frac{T_1}{{\tau }_h}\right),$$ (2.20)

$$N_1=N\left(T_1\right)=1-\exp \left(-\frac{T_1}{{\tau }_n}\right).$$ (2.21)

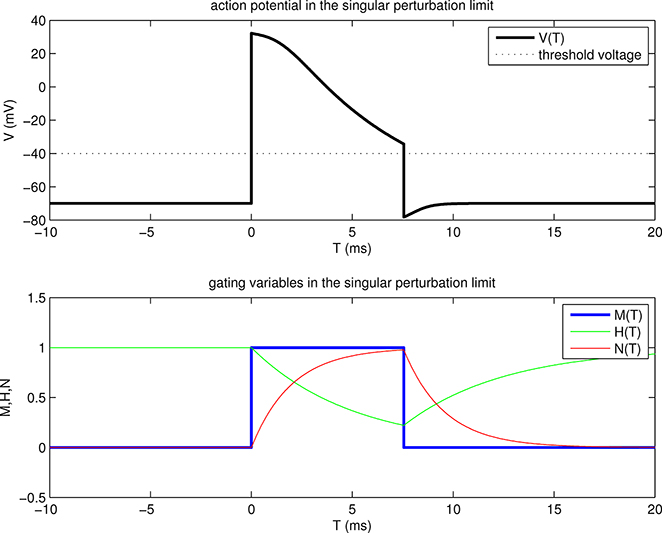
Figure 2.1.

Traveling wave solution of our model problem in the singular perturbation limit. The upper panel shows the transmembrane potential V as a function of T = t + x/θ, where θ is the wave speed, and where T = 0 defines the front of the wave, i.e., the trajectory x = −θt along which the voltage goes from below threshold to above threshold. The lower panel shows the gating variables M, H, N, also as functions of T. Parameters are the same as in Table 1.1 with the changes that $\overline{g_{\text{L}}}=15(\mu \text{A}/\text{mV})/{\text{cm}}^2$ and E_L = −70 mV, and the additional parameters that are not present (or not constant) in the original Hodgkin-Huxley equations: v_* = −40 mV, τ_h = 5 ms, and τ_n = 2 ms. The back of the wave occurs at about T = 7.5 ms. This time is denoted T₁ in the text, and the manner in which it is determined is illustrated in Fig. 2.2. At the front and also at the back of the wave, the voltage jumps through threshold. Physically, it is driven to do so by large axial currents arising from steep spatial voltage gradients in the neighborhood of the front and of the back.

Now we are ready to consider equation (2.11). If we simply let ϵ → 0 in equation (2.11) without any rescaling, we get an algebraic equation for what is known as the outer solution:

$$\overline{g_{\text{Na}}}MH\left(V-E_{\text{Na}}\right)+\overline{g_{\text{K}}}{N}^4\left(V-E_{\text{K}}\right)+\overline{g_{\text{L}}}\left(V-E_{\text{L}}\right)=0.$$ (2.22)

This is easily solved for V in terms of M, N, and H:

$$V=\frac{\overline{g_{\text{Na}}}MH{E}_{\text{Na}}+\overline{g_{\text{K}}}{N}^4{E}_{\text{K}}+\overline{g_{\text{L}}}{E}_{\text{L}}}{\overline{g_{\text{Na}}}MH+\overline{g_{\text{K}}}{N}^4+\overline{g_{\text{L}}}}.$$ (2.23)

Since M(T), H(T), and N(T) have already been determined, this defines a function V(T), which is plotted in the upper panel of Figure 2.1. Note that V(T) jumps through threshold at T = 0 and at T = T₁. These jumps are consequences of the jumps in M, since H and N are continuous functions of T.

At this stage our traveling wave solution is completely determined except for two important details. The wave speed θ and the duration T₁ of the above-threshold time interval are still unknown. In order to determine these quantities, we need to take a closer look at the structure of the solution in the neighborhood of T = 0 and also in the neighborhood of T = T₁. To do this, we need to rescale the T-variable before taking the limit ϵ → 0. Considering first the neighborhood of T = 0, which is called the front of the wave, we set

$$T=ϵS,$$ (2.24)

$$V(T)=V(ϵS)=U_0(S).$$ (2.25)

Equation (2.11) then becomes

$$C_{\text{m}}{U}_0^{\prime }+\overline{g_{\text{Na}}}MH\left(U_0-E_{\text{Na}}\right)+\overline{g_{\text{K}}}{N}^4\left(U_0-E_{\text{K}}\right)+\overline{g_{\text{L}}}\left(U_0-E_{\text{L}}\right)=\frac{r}{2\rho {\theta }^2}{U}_0^{\prime \prime }.$$ (2.26)

Notice that after this rescaling, the parameter ϵ no longer appears in our system except through the functions M, H, and N, which must now be evaluated at T = ϵS before letting ϵ → 0. Carrying out this program, we get

$$\underset{ϵ\to 0}{\lim }M(ϵS)=\{\begin{array}{ll}0,\hfill & S<0,\hfill \\ 1,\hfill & 0<S,\hfill \end{array}$$ (2.27)

$$\underset{ϵ\to 0}{\lim }H(ϵS)=H_0=1,$$ (2.28)

$$\underset{ϵ\to 0}{\lim }N(ϵS)=N_0=0.$$ (2.29)

Thus, to lowest order in ϵ, equation (2.26) simplifies as follows:

$$C_{\text{m}}{U}_0^{\prime }+g_0(S)\left(U_0-E_0(S)\right)=\frac{r}{2\rho {\theta }^2}{U}_0^{\prime \prime }$$ (2.30)

where g₀(S) and E₀(S) are each piecewise constant:

$$g_0(S)=\{\begin{array}{ll}{g}_0^{-}=\overline{g_{\text{L}}},\hfill & S<0,\hfill \\ g_0^{+}=\overline{g_{\text{L}}}+\overline{g_{\text{Na}}},\hfill & 0<S,\hfill \end{array}$$ (2.31)

$$E_0(S)=\{\begin{array}{ll}{E}_0^{-}=E_{\text{L}},\hfill & S<0,\hfill \\ E_0^{+}=\frac{\overline{g_{\text{L}}}{E}_{\text{L}}+\overline{g_{\text{Na}}}{E}_{\text{Na}}}{\overline{g_{\text{L}}}+\overline{g_{\text{Na}}}},\hfill & 0<S.\hfill \end{array}$$ (2.32)

Note that the superscripts ⁺ and ⁻ here refer to the above-threshold state and to the below-threshold state, respectively.

The unique solution to equation (2.30) with the property that

$$U_0(0)=v_{*}$$ (2.33)

and with U₀ bounded as S → ±∞ is as follows:

$$U_0(S)=\{\begin{array}{ll}{E}_0^{-}+\left(v_{*}-E_0^{-}\right)\exp \left({\lambda }_0^{-}S\right),\hfill & S<0,\hfill \\ E_0^{+}+\left(v_{*}-E_0^{+}\right)\exp \left({\lambda }_0^{+}S\right),\hfill & 0<S.\hfill \end{array}$$ (2.34)

Here ${\lambda }_0^{-}$ is the positive root of $P_0^{-}(\lambda )$ and ${\lambda }_0^{+}$ is the negative root of $P_0^{+}(\lambda )$, where

$$P_0^{\pm }(\lambda )=\frac{r}{2\rho C_{\text{m}}{\theta }^2}{\lambda }^2-\lambda -\frac{g_0^{\pm }}{C_{\text{m}}}.$$ (2.35)

Thus

$${\lambda }_0^{-}=\frac{\rho C_{\text{m}}{\theta }^2}{r}\left(1+\sqrt{1+\frac{2r{g}_0^{-}}{\rho C_{\text{m}}^2{\theta }^2}}\right),$$ (2.36)

$${\lambda }_0^{+}=\frac{\rho C_{\text{m}}{\theta }^2}{r}\left(1-\sqrt{1+\frac{2r{g}_0^{+}}{\rho C_{\text{m}}^2{\theta }^2}}\right).$$ (2.37)

A remarkable feature of our problem is that the matching conditions U₀(+∞) = V(0+) and U₀(−∞) = V(0−) are automatically satisfied, as the reader may easily verify, without having been imposed explicitly. Recall that only boundedness was imposed on U₀ as |S| → ∞; the equation for U₀ seems to know already what the limiting values of U₀ should be.

We have yet to impose the condition that $U_0^{\prime }(S)$ should be continuous at S = 0. This gives the equation

$${\lambda }_0^{-}\left(v_{*}-E_0^{-}\right)={\lambda }_0^{+}\left(v_{*}-E_0^{+}\right)$$ (2.38)

or

$$\frac{E_0^{+}-v_{*}}{v_{*}-E_0^{-}}=\frac{{\lambda }_0^{-}}{-{\lambda }_0^{+}}=\frac{\sqrt{1+\frac{2r{g}_0^{-}}{\rho C_{\text{m}}^2{\theta }^2}}+1}{\sqrt{1+\frac{2r{g}_0^{+}}{\rho C_{\text{m}}^2{\theta }^2}}-1}.$$ (2.39)

To simplify the notation, let

$${\alpha }_0=\frac{g_0^{-}}{g_0^{+}}=\frac{\overline{g_{\text{L}}}}{\overline{g_{\text{L}}}+\overline{g_{\text{Na}}}}\in (0,1),$$ (2.40)

$${\beta }_0=\frac{r{g}_0^{+}}{\rho C_{\text{m}}^2{\theta }^2}=\frac{r\left(\overline{g_{\text{L}}}+\overline{g_{\text{Na}}}\right)}{\rho C_{\text{m}}^2{\theta }^2}>0,$$ (2.41)

$${\gamma }_0=\frac{E_0^{+}-v_{*}}{v_{*}-E_0^{-}}=\frac{\frac{\overline{g_{\text{L}}}{E}_{\text{L}}+\overline{g_{\text{Na}}}{E}_{\text{Na}}}{\overline{g_{\text{L}}}+\overline{g_{\text{Na}}}}-v_{*}}{v_{*}-E_0^{-}}.$$ (2.42)

Then (2.39) becomes

$${\gamma }_0=\frac{\sqrt{1+2{\alpha }_0{\beta }_0}+1}{\sqrt{1+2{\beta }_0}-1}.$$ (2.43)

In this equation, α₀ and γ₀ are functions of the given parameters only, but β₀ contains the unknown wave speed θ. Thus, we can find the wave speed if we can solve equation (2.43) for β₀ as a function of α₀ and γ₀. As noted above, α₀ ∈ (0, 1), and we are interested only in β₀ > 0.

With α₀ ∈ (0, 1), it is straightforward to show that γ₀ as given by (2.43) is a strictly decreasing function of β₀ for β₀ > 0. As β₀ → 0, γ₀ → +∞, and as β₀ → +∞, ${\gamma }_0\to \sqrt{{\alpha }_0}$. It follows that (2.43) has a unique positive solution β₀ for each ${\gamma }_0>\sqrt{{\alpha }_0}$, and no positive solution for ${\gamma }_0\le \sqrt{{\alpha }_0}$.

Let us now proceed to find this solution explicitly (when it exists). A convenient way to do so is to reduce (2.43) to a pair of linear equations. Let

$$A=\sqrt{1+2{\alpha }_0{\beta }_0},$$ (2.44)

$$B=\sqrt{1+2{\beta }_0}.$$ (2.45)

Then (2.43) becomes

$${\gamma }_0=\frac{A+1}{B-1},$$ (2.46)

and we also have

$$\frac{A^2-1}{B^2-1}=\frac{2{\alpha }_0{\beta }_0}{2{\beta }_0}={\alpha }_0.$$ (2.47)

Now (2.47) can be written as

$$\left(\frac{A+1}{B-1}\right)\left(\frac{A-1}{B+1}\right)={\alpha }_0,$$ (2.48)

and this can be simplified with the help of (2.46) to read

$${\gamma }_0\frac{A-1}{B+1}={\alpha }_0.$$ (2.49)

Equations (2.46) and (2.49) can now be rearranged to yield a pair of linear equations in the unknowns A and B. The solution of this linear system is

$$A=\frac{{\alpha }_0+2{\alpha }_0{\gamma }_0+{\gamma }_0^2}{{\gamma }_0^2-{\alpha }_0},$$ (2.50)

$$B=\frac{{\alpha }_0+2{\gamma }_0+{\gamma }_0^2}{{\gamma }_0^2-{\alpha }_0}.$$ (2.51)

We can now solve for β₀ from either A or B (and of course we should get the same answer either way!). The result is

$${\beta }_0=2{\gamma }_0\frac{\left({\alpha }_0+{\gamma }_0\right)\left(1+{\gamma }_0\right)}{{\left({\gamma }_0^2-{\alpha }_0\right)}^2}.$$ (2.52)

It follows (see (2.41)) that

$$\theta =\pm \frac{{\gamma }_0^2-{\alpha }_0}{C_{\text{m}}}\sqrt{\frac{r\left(\overline{g_{\text{L}}}+\overline{g_{\text{Na}}}\right)}{2\rho {\gamma }_0\left({\alpha }_0+{\gamma }_0\right)\left(1+{\gamma }_0\right)}}$$ (2.53)

where α₀ and γ₀ are given by equations (2.40) and (2.42). The above formula for the wave speed is only valid when

$${\gamma }_0>\sqrt{{\alpha }_0}.$$ (2.54)

When this condition fails, there is no traveling wave of the type we are constructing here (at least not in the limit ϵ → 0).

Now that the wave speed is determined, there is only one unknown remaining: the duration T₁ of the time interval during which the voltage is above threshold. To find it, we resolve the rapid voltage change that occurs near T = T₁ by making the change of variables

$$T=T_1+ϵS,$$ (2.55)

$$V(T)=V\left(T_1+ϵS\right)=U_1(S).$$ (2.56)

Equation (2.11) then becomes

$$C_{\text{m}}{U}_1^{\prime }+\overline{g_{\text{Na}}}MH\left(U_1-E_{\text{Na}}\right)+\overline{g_{\text{K}}}{N}^4\left(U_1-E_{\text{K}}\right)+\overline{g_{\text{L}}}\left(U_1-E_{\text{L}}\right)=\frac{r}{2\rho {\theta }^2}{U}_1^{\prime \prime }.$$ (2.57)

As before, ϵ appears in this equation only through M, H, and N, but this time we have

$$\underset{ϵ\to 0}{\lim }M(ϵS)=\{\begin{array}{ll}1,\hfill & S<0,\hfill \\ 0,\hfill & 0<S,\hfill \end{array}$$ (2.58)

$$\underset{ϵ\to 0}{\lim }H(ϵS)=H_1=\exp \left(-\frac{T_1}{{\tau }_h}\right),$$ (2.59)

$$\underset{ϵ\to 0}{\lim }N(ϵS)=N_1=1-\exp \left(-\frac{T_1}{{\tau }_n}\right),$$ (2.60)

so that, to lowest order, (2.57) becomes

$$C_{\text{m}}{U}_1^{\prime }+g_1(S)\left(U_1-E_1(S)\right)=\frac{r}{2\rho {\theta }^2}{U}_1^{\prime \prime }$$ (2.61)

where g₁(S) and E₁(S) are piecewise constant:

$$g_1(S)=\{\begin{array}{ll}{g}_1^{+}=\overline{g_{\text{K}}}{N}_1^4+\overline{g_{\text{L}}}+\overline{g_{\text{Na}}}{H}_1,\hfill & S<0,\hfill \\ g_1^{-}=\overline{g_{\text{K}}}{N}_1^4+\overline{g_{\text{L}}},\hfill & S>0,\hfill \end{array}$$ (2.62)

$$E_1(S)=\{\begin{array}{ll}{E}_1^{+}=\frac{\overline{g_{\text{K}}}N{1}^4{E}_{\text{K}}+\overline{g_{\text{L}}}{E}_{\text{L}}+\overline{g_{\text{Na}}}{H}_1{E}_{\text{Na}}}{\overline{g_{\text{K}}}N{1}^4+\overline{g_{\text{L}}}+\overline{g_{\text{Na}}}{H}_1},\hfill & S<0,\hfill \\ E_1^{-}=\frac{\overline{g_{\text{K}}}N{1}^4{E}_{\text{K}}+\overline{g_{\text{L}}}{E}_{\text{L}}}{\overline{g_{\text{K}}}N{1}^4+\overline{g_{\text{L}}}},\hfill & S>0.\hfill \end{array}$$ (2.63)

As before, the superscripts ⁺ and ⁻ refer to the above-threshold state and to the below-threshold state, respectively. Here, however, the above-threshold state occurs during S < 0 and the below-threshold state during S > 0.

The solution to (2.61) that remains bounded as S → ±∞ and satisfies U₁(0) = v_* is

$$U_1(S)=\{\begin{array}{ll}{E}_1^{+}+(v_{*}-E_1^{+})\exp ({\lambda }_1^{+}S),\hfill & S<0,\hfill \\ E_1^{-}+(v_{*}-E_1^{-})\exp ({\lambda }_1^{-}S),\hfill & 0<S.\hfill \end{array}$$ (2.64)

Here ${\lambda }_1^{+}$ is the positive root of $P_1^{+}(\lambda )$, and ${\lambda }_1^{-}$ is the negative root of $P_1^{-}(\lambda )$, where

$$P_1^{\pm }(\lambda )=\frac{r}{2\rho C_{\text{m}}{\theta }^2}{\lambda }^2-\lambda -\frac{g_1^{\pm }}{C_{\text{m}}}.$$ (2.65)

Thus,

$${\lambda }_1^{+}=\frac{\rho C_{\text{m}}{\theta }^2}{r}\left(1+\sqrt{1+\frac{2r{g}_1^{+}}{\rho C_{\text{m}}^2{\theta }^2}}\right),$$ (2.66)

$${\lambda }_1^{-}=\frac{\rho C_{\text{m}}{\theta }^2}{r}\left(1-\sqrt{1+\frac{2r{g}_1^{-}}{\rho C_{\text{m}}^2{\theta }^2}}\right).$$ (2.67)

We still need to impose the boundary condition that $U_1^{\prime }(S)$ is continuous at S = 0. This gives

$${\lambda }_1^{+}\left(v_{*}-E_1^{+}\right)={\lambda }_1^{-}\left(v_{*}-E_1^{-}\right)$$ (2.68)

or

$$\frac{E_1^{+}-v_{*}}{v_{*}-E_1^{-}}=\frac{-{\lambda }_1^{-}}{{\lambda }_1^{+}}=\frac{\sqrt{1+\frac{2r{g}_1^{-}}{\rho C_{\text{m}}^2{\theta }^2}}-1}{\sqrt{1+\frac{2r{g}_1^{+}}{\rho C_{\text{m}}^2{\theta }^2}}+1}.$$ (2.69)

Recall that the wave speed θ is already known. Therefore, the only unknown in equation (2.69) is T₁, which appears indirectly through $E_1^{+}$, $E_1^{-}$, $g_1^{+}$, and $g_1^{-}$, which in turn depend on H₁ and N₁, which are functions of T₁. Let

$${\gamma }_1\left(T_1\right)=\frac{E_1^{+}\left(T_1\right)-v_{*}}{v_{*}-E_1^{-}\left(T_1\right)},$$ (2.70)

$${\omega }_1\left(T_1\right)=\frac{\sqrt{1+2a{g}_1^{-}\left(T_1\right)}-1}{\sqrt{1+2a{g}_1^{+}\left(T_1\right)}+1},$$ (2.71)

where

$$a=\frac{r}{\rho C_{\text{m}}^2{\theta }^2}.$$ (2.72)

Then equation (2.69) reduces to

$${\gamma }_1\left(T_1\right)={\omega }_1\left(T_1\right).$$ (2.73)

We propose to show that this equation has a unique positive solution. To do so, we study the properties of the functions γ₁ and ω₁.

Since H₁(0) = 1 and N₁(0) = 0, we see immediately that

$${\gamma }_1(0)={\gamma }_0.$$ (2.74)

Now recall that E_K < E_L < v_* < E_Na, and also that H₁(T₁) is a decreasing function with the property that H₁(T₁) → 0 as T₁ → ∞, whereas N₁(T₁) is an increasing function with the property that N₁(T₁) → 1 as T₁ → ∞. Moreover, $E_1^{+}\left(T_1\right)$ is a weighted average of E_K, E_L, and E_Na, with weights $\overline{g_K}{\left(N_1\left(T_1\right)\right)}^4$, $\overline{g_{\text{L}}}$, and $\overline{g_{\text{Na}}}{H}_1\left(T_1\right)$, respectively, whereas $E_1^{-}$ is a weighted average only of E_K and E_L with weights $\overline{g_K}{\left(N_1\left(T_1\right)\right)}^4$ and $\overline{g_{\text{L}}}$, respectively. It follows from these facts that $E_1^{+}$ and $E_1^{-}$ are both decreasing functions of T₁, and therefore that γ₁ is also a decreasing function of T₁. In fact, it follows further that there is some finite positive value of T₁, which we shall call T_*, such that $E_1^{+}\left(T_{*}\right)=v_{*}$, which implies that γ₁(T_*) = 0. Thus, in summary, γ₁(T₁) is a decreasing function with γ₁(0) = γ₀ and γ₁(T_*) = 0.

We now turn to the study of ω₁(T₁). First, we note that

$${\omega }_1(0)=\frac{\sqrt{1+2a{g}_1^{-}(0)}-1}{\sqrt{1+2a{g}_1^{+}(0)}+1}<\frac{\sqrt{1+2a{g}_1^{-}(0)}+1}{\sqrt{1+2a{g}_1^{+}(0)}-1}={\gamma }_0={\gamma }_1(0).$$ (2.75)

Next, we consider the sign of the derivative of ω₁(T₁). Let

$$N\left(T_1\right)=\sqrt{1+2a{g}_1^{-}\left(T_1\right)}-1,$$ (2.76)

$$D\left(T_1\right)=\sqrt{1+2a{g}_1^{+}\left(T_1\right)}+1,$$ (2.77)

so that

$${\omega }_1\left(T_1\right)=\frac{N\left(T_1\right)}{D\left(T_1\right)}.$$ (2.78)

Then

$$N^{\prime }\left(T_1\right)=\frac{a{\left(g_1^{-}\right)}^{\prime }\left(T_1\right)}{\sqrt{1+2a{g}_1^{-}\left(T_1\right)}},$$ (2.79)

$$D^{\prime }\left(T_1\right)=\frac{a{\left(g_1^{+}\right)}^{\prime }\left(T_1\right)}{\sqrt{1+2a{g}_1^{+}\left(T_1\right)}},$$ (2.80)

and the sign of ${\omega }_1^{\prime }\left(T_1\right)$ is the same as the sign of the expression

$$\begin{gathered} D\left(T_1\right)N^{\prime }\left(T_1\right)-N\left(T_1\right)D^{\prime }\left(T_1\right) \\ =a{\left(g_1^{-}\right)}^{\prime }\left(T_1\right)\frac{\sqrt{1+2a{g}_1^{+}\left(T_1\right)}+1}{\sqrt{1+2a{g}_1^{-}\left(T_1\right)}} \\ -a{\left(g_1^{+}\right)}^{\prime }\left(T_1\right)\frac{\sqrt{1+2a{g}_1^{-}\left(T_1\right)}-1}{\sqrt{1+2a{g}_1^{+}\left(T_1\right)}}. \end{gathered}$$ (2.81)

Recall that

$$g_1^{-}\left(T_1\right)=\overline{g_{\text{K}}}{\left(N_1(T)\right)}^4+\overline{g_{\text{L}}},$$ (2.82)

$$g_1^{+}\left(T_1\right)=\overline{g_{\text{K}}}{\left(N_1(T)\right)}^4+\overline{g_{\text{L}}}+\overline{g_{\text{Na}}}{H}_1\left(T_1\right),$$ (2.83)

and that H₁ is a decreasing function of T₁, whereas N₁ is increasing. Also, all of the quantities appearing in (2.82)–(2.83) are positive. It follows that

$$g_1^{-}\left(T_1\right)<g_1^{+}\left(T_1\right),$$ (2.84)

$${\left(g_1^{-}\right)}^{\prime }\left(T_1\right)>{\left(g_1^{+}\right)}^{\prime }\left(T_1\right).$$ (2.85)

Given these facts, it is clear that the right-hand side of (2.81) is positive: If ${\left(g_1^{+}\right)}^{\prime }\le 0$, then the first term is positive and the second is nonnegative, so the whole expression is obviously positive. If ${\left(g_1^{+}\right)}^{\prime }>0$, then the first term dominates the second one because of (2.84) and (2.85).

In summary, we have shown that ω₁(0) < γ₁(0) and that ω₁(T₁) is an increasing function of T₁. It follows from this and the properties of γ₁(T₁) derived above that the equation γ₁(T₁) = ω₁(T₁) has a unique positive solution, and that this solution lies in the interval (0, T_*); see Figure 2.2. Although we do not have an explicit formula for T₁, it is a simple matter to evaluate T₁ numerically. This completes the construction of a traveling wave solution of our simplified Hodgkin-Huxley equations (2.1)–(2.4) in the limit ϵ → 0.

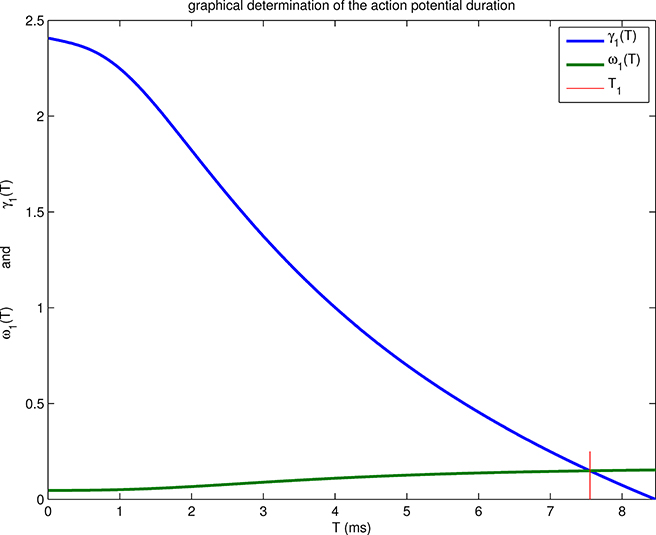
Figure 2.2.

Graphical determination of the time T₁ that defines the back of the wave, and hence the action potential duration. The value of T₁ (red vertical line) is such that γ₁(T₁) = ω₁(T₁). Note that T₁ < T_*, where T_* is defined by γ₁(T_*) = 0. This means that the action potential repolarizes before the voltage of the excited state reaches threshold; see Figure 2.1.

Some important qualitative properties of the traveling wave constructed above are as follows. These properties are literally true in the limit ϵ → 0, and approximately true for sufficiently small ϵ.

First, the wave has a well-defined front and back, designated in the foregoing by T = 0 and T = T₁, respectively. At the front, the voltage jumps up through the threshold value as the Na⁺ current turns on; at the back it jumps down through the threshold value as the Na⁺ current turns off. Thus, in particular, the action potential has a shorter duration than one would expect based on the idea that the slow evolution of the h and n variables has to bring the voltage all the way back down to threshold before the Na⁺ current can turn off. That reasoning would predict an action potential duration of T_*, but in fact T₁ < T_*; see Figure 2.2. The physical reason for this effect is that axial currents, which are large in the neighborhood of the front and back of the wave, bring about the rapid changes in voltage that are seen at the front and at the back.

Another interesting phenomenon is that the wave speed is determined by conditions at the front, whereas the action potential duration is determined by conditions at the back. In the case we have considered here, the action potential travels into an axon at rest, so that H₀ = 1 and N₀ = 0. More generally (see, for example, the discussion of periodic traveling waves below), the wave speed may differ from the value found above if the values of H and N at the front are different from their resting values.

It is of particular interest to see how the different parameters of the problem come together to determine the wave speed, which is given explicitly for our model by equation (2.53), together with the definitions (2.40) and (2.42). First, the wave speed involves the dimensional quantity

$$\sqrt{\frac{r\left(\overline{g_{\text{L}}}+\overline{g_{\text{Na}}}\right)}{2\rho C_{\text{m}}^2}},$$ (2.86)

which has units of velocity, since r/(2ρC_m) is the effective diffusion coefficient in the Hodgkin-Huxley equations and therefore has units of length²/time, whereas $\left(\overline{g_{\text{L}}}+\overline{g_{\text{Na}}}\right)/C_{\text{m}}$ has units of 1/time.

Notice, however, that the wave speed also depends on the dimensionless quantities γ₀ and α₀, which have the following interpretations. The parameter α₀ is the ratio of the below-threshold membrane conductance to the above-threshold membrane conductance at the front of the wave. In practice, α₀ is a small parameter, since $\overline{g_{\text{Na}}}\gg \overline{g_{\text{L}}}$. To describe the parameter γ₀, we note that there are three relevant voltages at the front. These are the voltage immediately before the arrival of the front, denoted $E_0^{-}$, the threshold voltage, denoted v_*, and the voltage immediately after the front has passed, which is denoted $E_0^{+}$. In the case we have considered here, $E_0^{-}$ is equal to the rest potential (which is E_L in our model), and $E_0^{+}$ is approximately equal to E_Na. The parameter γ₀ is the ratio $\left(E_0^{+}-v_{*}\right)/\left(v_{*}-E_0^{-}\right)$. The wave speed is an increasing function of γ₀; in fact, it is proportional to $\sqrt{{\gamma }_0}$ when γ₀ is large, which is in fact the case. When γ₀ becomes less than $\sqrt{{\alpha }_0}$, propagation fails.

An interesting exercise, which we leave for the enjoyment of the reader, is to generalize the results of this section to the case of a periodic traveling wave, in which an above-threshold interval of duration T₁ alternates with a below-threshold interval of duration T₂, so that the period of the wave is T₁+T₂. As a first step, it is straightforward to solve for periodic H(T) and N(T) and, in particular, to find the values of (H₀, N₀) and (H₁, N₁) that apply at the front and at the back of the wave, respectively, as functions of T₁ and T₂. The slope-matching conditions at the front and at the back of the wave then give two nonlinear equations that relate the three unknowns (θ, T₁, T₂). We thus expect a one-parameter family of solutions, and it is convenient to choose this one parameter to be the wave speed θ. By solving numerically for T₁ and T₂ as functions of θ and then adding the results, one can compute the period of the wave as a function of the wave speed. This is the inverse of the dispersion relation, which is the wave speed as a function of the period. The dispersion relation is an important property of any Hodgkin-Huxley-like system, since it sets limits on the fidelity of neuronal communication [51], and also since it can be used as the foundation of an approximation scheme [18, 51, 76] for the solution of more general initial/boundary value problems.

In the case of periodic traveling waves, it is also of interest to consider the situation in which the threshold is below the rest potential, contrary to what we have assumed up to now. This leads to spontaneous oscillation, also known as automaticity or pacemaker activity, which is particularly important in the heart but which also occurs in the nervous system. In the context of periodic traveling waves, such pacemaker activity manifests itself through the existence of traveling waves of arbitrarily high wave speed. The limit of infinite wave speed corresponds to synchronized activity, in which all variables are independent of x. The case of large but finite wave speed arises when the system is driven at a higher frequency (shorter period) than the one at which it would spontaneously oscillate. Such a wave can be thought of as a wave of entrainment—its speed is larger when there is a better match between the driving frequency and the natural frequency of the system, becoming infinite when the two frequencies coincide.

In summary, there are two distinct cases of the the foregoing exercise for the reader, depending on whether the rest potential is below or above threshold. In the former case, the period can be arbitrarily large, and the wave speed is bounded from above. In the latter case, there is pacemaker activity, with a upper bound on the period and no upper bound on the wave speed.

3. Introduction to Cardiac Electrophysiology: Cardiac Myocytes

In humans and other mammals, and also in birds (and crocodiles!), the heart is a four-chambered organ. The left side of the heart pumps oxygenated blood from the lungs to all of the tissues of the body, and the right side of the heart pumps deoxygenated blood back to the lungs, where the blood is reoxygenated. Each side of the heart has two chambers, an atrium and a ventricle, with the atrium acting as a primer pump for the more powerful ventricle. In a normal heart beat, first the atria contract; then, after a brief delay, the ventricles contract. These contractions are coordinated by cardiac action potentials that are three-dimensional waves which are similar to the essentially one-dimensional action potential waves that propagate along nerve axons. Each cardiac action potential wave originates from the sinoatrial node, which is a collection of pacemaker cells with oscillatory transmembrane voltages that is located in the right atrium and spontaneously generates propagating action potential waves at regular intervals. Because the atria are electrically coupled, the action potential wavefront that emanates from the cardiac pacemaker is able to spread through the right atrium and to the left atrium. The atria and ventricles are electrically insulated from each other except at the atrioventricular node, which is a specialized structure where the atrial waves collect. Following a delay at the atrioventricular node, the electrical impulse is transmitted to the ventricles by a specialized system of fast-conducting fibers, including the bundle of His and the Purkinje fibers.¹ The electrical impulse is delivered to the working ventricular myocardium at Purkinje-muscle junctions located along the endocardial (inner) surface of the heart.² The action potential wavefront then propagates transmurally to the epicardial (outer) surface of the heart.

By volume, cardiac muscle is primarily composed of myocytes, which are electrically excitable contractile cells. Cardiomyocytes are roughly cylindrical, with a length of approximately 100 μm and a radius of approximately 10 μm. At the cell scale, myocyte models may be formulated by requiring that the capacitive current $C_{\text{m}}\frac{dv}{dt}$ balances the total transmembrane ionic current I_ion(v, w) and any applied stimulus current I_s(t),

$$C_{\text{m}}\frac{dv}{dt}=-I_{\text{ion}}(v,w)+I_s(t),$$ (3.1)

in which w is a collection of variables that includes both state variables for the transmembrane ion channels and also dynamic ion concentrations. The dynamics of the state variables w are determined by a system of nonlinear ordinary differential equations,

$$\frac{dw}{dt}=f(v,w).$$ (3.2)

The forms of the functions I_ion(v, w) and f(v, w) are different for models of different types of myocytes (e.g., atrial or ventricular) and for different species. In the Hodgkin-Huxley neuronal model that is the subject of Sections 1 and 2,

$$I_{\text{ion}}=\overline{g_{\text{Na}}}{m}^{3}h\left(v-E_{\text{Na}}\right)+\overline{g_{\text{K}}}{n}^4\left(v-E_{\text{K}}\right)+\overline{g_{\text{L}}}\left(v-E_{\text{L}}\right),$$ (3.3)

w = (m, h, n), and f(v, w) is given by equations (1.2)–(1.4). Modern cardiac cell models like those outlined in Section 3.1 include significantly more membrane state variables.

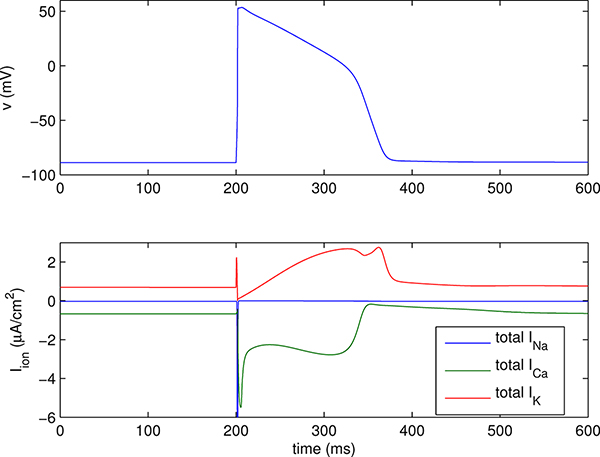
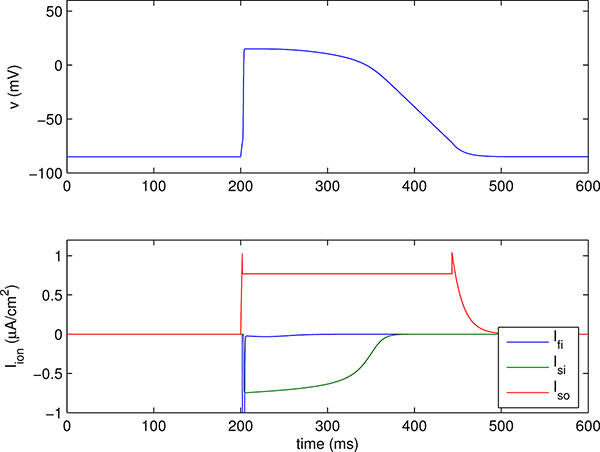
The cardiac action potential is similar to that of neurons, but cardiac cells generally exhibit a prolonged period of depolarization, the plateau of the action potential, which lasts for hundreds of milliseconds. The cardiac action potential proceeds as follows: Depolarization of the cell membrane opens voltage-gated sodium channels, drawing inward current and further depolarizing the cell membrane.³ The large depolarization induced by the inward sodium current activates calcium channels, which open more slowly than the Na⁺ channels and which draw additional current into the cell. Potassium channels, which also activate more slowly than sodium channels, generate outward K⁺ currents that balance the inward Ca²⁺ currents during the plateau of the action potential and are ultimately responsible for returning the cell to its resting potential. An action potential generated by a detailed model of the guinea pig ventricular myocyte [19] is shown in Figure 3.1, and an action potential generated by a reduced model of a guinea pig ventricular myocyte [21] is shown in Figure 3.3. Both figures demonstrate these major features of the cardiac action potential.

Figure 3.1.

Action potential generated by a version of the Luo-Rudy ventricular cell model [19]. The upper panel shows the transmembrane voltage, and lower panel shows the transmembrane ionic currents. The plotted current is the total for each ion species; the different currents of the model carried by any one ion species have been lumped together here to avoid making the plot too complicated. Note that the (negative) peak of the Na⁺ current is about −500 μA/cm², which is much too large in magnitude to appear on the scale of the plot.

Figure 3.3.

Action potential generated by a version of the Fenton-Karma ventricular cell model [21] using parameters that have been fit to the Luo-Rudy I model [45]. The upper panel shows the transmembrane voltage, and lower panel shows the transmembrane currents, which are I_fi = fast inward (Na⁺-like) current, I_si = slow inward (Ca²⁺-like) current, and I_so = slow outward (K⁺-like) current. The fast inward current has a (negative) peak of about −85 μA/cm², which is much too large in magnitude to appear on the scale of this plot.

Cardiac contraction is triggered by the presence of free calcium ions in the cytosol, and when the cell is at rest, it sequesters Ca²⁺ in the sarcoplasmic reticulum. Intracellular calcium buffers (i.e., proteins that bind to free calcium ions) also act to maintain low levels of cytosolic calcium when the cell is at rest. Contraction is initiated by the calcium influx during the action potential; however, the transmembrane calcium currents do not provide sufficient calcium to produce in maximal contraction. Instead, the transmembrane Ca²⁺ currents trigger the myocyte to release its intracellular stores of free calcium ions maintained within the sarcoplasmic reticulum, a process known as calcium-induced calcium release (CICR). Thus, modeling excitation-contraction coupling requires descriptions of not just the transmembrane calcium channels but also the calcium dynamics within the cell.

A feature of many types of ion channels is that they may be activated (i.e., open), deactivated (i.e., closed, but able to reactivate), or inactivated (i.e., closed, but temporarily unable to reactivate). Deactivation and inactivation are distinct states that correspond to different channel conformations. Specifically, when a voltage-gated channel is closed but not inactivated, it may be activated by a sufficiently large perturbation to the membrane potential. By contrast, an inactivated channel is unable to be activated until the channel recovers from inactivation. In particular, once inactivated, a large current stimulus or change in transmembrane voltage will not cause the inactivated channel to reopen. A typical mode of voltage-dependent inactivation is for channels to transition from activated to inactivated states, with recovery from inactivated to deactivated states requiring repolarization of the cell membrane. This mode of inactivation and recovery from inactivation is seen in Na⁺ channels. Thus, after opening during the action potential upstroke, the sodium channels inactivate and become unavailable to reactivate until after the completion of the action potential. Because large inward sodium currents are responsible for the fast action potential upstroke, inactivation of the sodium channels helps to protect the heart from propagating premature or ectopic beats that can lead to the formation of fatal arrhythmias. K⁺ channels also show voltage-dependent inactivation, and Ca²⁺ channels display calcium-dependent inactivation. For further details, see the monograph of Bers [4].

3.1. Detailed Models of Single-Cell Cardiac Electrophysiology

Much of the work to characterize mathematically the electrophysiology of cardiac myocytes has been carried out by physiologists who have sought to develop increasingly complete quantitative descriptions of the transmembrane ion channels, pumps, and exchangers present in cardiomyocytes, as well as the intracellular ion dynamics, especially intracellular calcium dynamics. This approach has resulted in biophysically detailed models of high complexity that rely heavily on numerical analysis and computer simulation.

The same mathematical formalisms introduced to describe neurons can also be used to describe the dynamics of cardiac cells. Indeed, the first mathematical model in cardiac electrophysiology based on experimental data was due to Noble [61], who adapted and extended the Hodgkin-Huxley model (1.1)–(1.4) to fit data from cardiac Purkinje cells. McAllister, Noble, and Tsien extended the original Noble model to include a more complete description of the transmembrane ion currents and developed the first cardiac model to include a description of the transmembrane calcium channels [48]. DiFrancesco and Noble further extended this model and produced the first cardiac model to include a description of intracellular calcium dynamics [13]. The first mathematical model of the ventricular action potential was introduced by Beeler and Reuter [3]. During this time, mathematical models were also introduced for atrial cells [14] and the sinoatrial node [62].

In 1991, Luo and Rudy published an updated version of the Beeler-Reuter model [45]. This initial version of the Luo-Rudy model was among the first cardiac models to incorporate voltage-clamp recordings obtained from isolated myocytes and was arguably the most influential of the early models to incorporate such data. In 1994, Luo and Rudy published an updated version of their model that was the first ventricular model to account for intracellular ion dynamics [46, 47]. This Luo-Rudy dynamic model became the prototype of modern, biophysically detailed cellular models. Such models include experimentally based descriptions of all of the major transmembrane ion transporters and intracellular compartments that influence the action potential, and over the more than twenty years following the publication of the original Luo-Rudy model, there has been tremendous growth in the number of species and cell types for which detailed, experimentally based cellular models are available. Models that were at least partially based on human data began to appear in the research literature in the late 1990s [12, 36, 63, 85, 86]. The most recent human cardiac models are those of Bers and coworkers [25, 26] and of Rudy and coworkers [64].

3.2. Beyond the Hodgkin-Huxley Model of Ion Channel Gating

From the first cardiac models of Noble until the late 1990s, models of cardiac electrophysiology generally continued to employ the Hodgkin-Huxley formalism to describe the voltage-dependent gating of transmembrane ion channels. This formalism was developed before experimental data were available on ion channel structure, and such models generally do not reflect the actual biophysics of individual channels. Hodgkin-Huxley-type models are therefore primarily phenomenological and cannot be readily modified to account for experimental data on structural differences between wild-type and mutant channels. Ion channel models based on a more general Markov chain description can better reflect the structure of individual channels. The first detailed cardiac cell models to incorporate such Markovian ion channel models were due to Clancy and Rudy [8, 10], who developed new models of the wild-type sodium channel as well as sodium channel mutants implicated in conduction abnormalities that result in an increased susceptibility to the development of fatal arrhythmias.

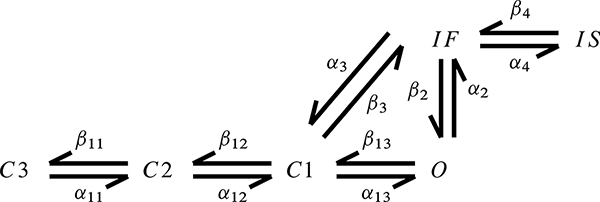
In the original Markovian wild-type Na⁺ channel model of Clancy and Rudy [8], each Na⁺ channel may be in one of several different states, including three closed states (C1, C2, and C3); a fast-inactivated state (IF); a slow-inactivated state (IS); and an open state (O), which is the only state in which the channel is able to conduct transmembrane current.⁴ The state variables of the model are the fractions of channels that are in a particular state, and the dynamics of these state variables are governed by a first-order system of ODE,

$$\begin{gathered} \frac{dC1}{dt}={\alpha }_{12}(v)C2+{\beta }_{13}(v)O+{\alpha }_3(v)IF \\ -\left({\alpha }_{13}(v)+{\beta }_{12}(v)+{\beta }_3(v)\right)C1, \end{gathered}$$ (3.4)

$$\frac{dC2}{dt}={\alpha }_{11}(v)C3+{\beta }_{12}(v)C1-\left({\alpha }_{12}(v)+{\beta }_{11}(v)\right)C2,$$ (3.5)

$$\frac{dC3}{dt}={\beta }_{11}(v)C2-{\alpha }_{11}(v)C3,$$ (3.6)

$$\frac{dIF}{dt}={\alpha }_2(v)O+{\beta }_3(v)C1+{\beta }_4(v)IS-\left({\alpha }_3(v)+{\alpha }_4(v)+{\beta }_2(v)\right)IF,$$ (3.7)

$$\frac{dIS}{dt}={\alpha }_4(v)IF-{\beta }_4(v)IS,$$ (3.8)

$$\frac{dO}{dt}={\alpha }_{13}(v)C1+{\beta }_2(v)IF-\left({\alpha }_2(v)+{\beta }_{13}(v)\right)O,$$ (3.9)

with [8]

$${\alpha }_{11}(v)=3.802/(0.1027\exp (-v/17)+0.20\exp (v/150)),$$ (3.10)

$${\alpha }_{12}(v)=3.802/(0.1027\exp (-v/15)+0.23\exp (-v/150)),$$ (3.11)

$${\alpha }_{13}(v)=3.802/(0.1027\exp (-v/12)+0.25\exp (-v/150)),$$ (3.12)

$${\beta }_{11}(v)=0.1917\exp (-v/20.3),$$ (3.13)

$${\beta }_{12}(v)=0.20\exp (-(v-5)/20.3),$$ (3.14)

$${\beta }_{13}(v)=0.22\exp (-(v-10)/20.3),$$ (3.15)

$${\alpha }_2(v)=9.178\exp (v/29.68),$$ (3.16)

$${\beta }_2(v)=\left({\alpha }_{13}(v){\alpha }_2(v){\alpha }_3(v)\right)/\left({\beta }_{13}(v){\beta }_3(v)\right),$$ (3.17)

$${\alpha }_3(v)=3.7933\text{e-}9\exp (-v/5.2),$$ (3.18)

$${\beta }_3(v)=8.4\text{e-}3+2.0\text{e-}5v,$$ (3.19)

$${\alpha }_4(v)={\alpha }_2(v)/100,$$ (3.20)

$${\beta }_4(v)={\alpha }_3(v).$$ (3.21)

Here the state occupancy variables are nondimensional and lie within the interval [0,1], the transmembrane voltage is in mV, and the state transition rates are in units of 1/ms. The macroscopic sodium current density is given by

$$I_{\text{Na}}=\overline{g_{\text{Na}}}O\left(v-E_{\text{Na}}\right),$$ (3.22)

which is similar to the corresponding expression in the Hodgkin-Huxley model (1.1), but with $g_{\text{Na}}=\overline{g_{\text{Na}}}O$ instead of $g_{\text{Na}}=\overline{g_{\text{Na}}}{m}^{3}h$. This model is summarized by the state-transition diagram shown in Figure 3.2. The mutant Na⁺ channel model of Clancy and Rudy was similar, but it also included a second set of open and closed states that lack inactivation and therefore generate a persistent inward sodium current. Persistent inward currents act to prolong the action potential duration, which is a hallmark of electrophysiological disorders such as long QT syndrome. Subsequent Markovian models were introduced by Rudy and coworkers for the rapid-activating [9] and slow-activating [81] components of the delayed rectifier K⁺ current, and of the L-type Ca²⁺ channel [19]. (Notice that the version of the Luo-Rudy model [19] shown in Figure 3.1 incorporates this Markovian L-type Ca²⁺ channel model.) Markov chain models of ion channels have also been developed and adopted by others, and represent the present state of the art in macroscopic ion channel modeling.

Figure 3.2.

State transition diagram for the wild-type Na⁺ channel model of Clancy and Rudy (adapted from Clancy and Rudy [8]).

Although the Markovian approach allows for a clearer relationship between the ion channel model and the underlying biophysics, in practice, many of these models have a somewhat limited connection to the actual structure of the channel. A notable exception is the work of Rudy and coworkers [80], who developed a Markovian model of the slow-activating delayed rectifier K⁺ current I_Ks, in which the transition rates are determined from detailed molecular dynamics and continuum electrostatic simulations of wild-type and mutant channels. By spanning length scales from the molecular to the cellular, and by offering a more direct means to understand the effects of molecular structure on cellular activity, this work could represent the next stage in the evolution of cellular cardiac electrophysiology models.

3.3. Reduced Models of Single-Cell Cardiac Electrophysiology

A major limitation of detailed models of single-cell cardiac electrophysiology is their complexity. This complexity makes simulations that use these detailed models computationally expensive. It also precludes, or at least greatly complicates, detailed mathematical analyses of the model equations like that performed in Section 2 for a reduced version of the Hodgkin-Huxley model. Reduced cellular models of cardiac electrophysiology have also been developed. These include the FitzHugh-Nagumo model [22,23,59], which was originally introduced as a simplification of the Hodgkin-Huxley neuronal model but was subsequently adapted for use as a model of the cardiac action potential, e.g., by Rogers and McCulloch [77] and by Aliev and Panfilov [2]; the Fenton-Karma model [21]; and the Mitchell-Schaeffer model [52], which is a reduction of the Fenton-Karma model.

Of these simplified models, the formulation that most closely reflects the underlying biophysics is the Fenton-Karma model [21]. It describes the total transmembrane ionic current I_ion as

$$I_{\text{ion}}(v,w)=I_{\text{fi}}(v,w)+I_{so}(v,w)+I_{\text{si}}(v,w),$$ (3.23)

in which I_fi is a fast inward current analogous to the Na⁺ current, I_so is a slow outward current analogous to the K⁺ current, I_si is a slow inward current analogous to the Ca²⁺ current, and w = (h, d) are gating variables. The currents and the dynamics of the gating variables can be concisely stated in terms of a nondimensionalized membrane voltage u = (v − v_o)/(E_fi − v_o), in which v_o is the resting membrane potential in mV and E_fi is the Nernst potential of the fast inward current. The currents are defined in terms of the functions

$$J_{\text{fi}}=\{\begin{array}{ll}-\frac{h}{{\tau }_{\text{d}}}(1-u)\left(u-u_{\text{c}}\right)\hfill & \text{if}u\ge u_{\text{c}},\hfill \\ 0\hfill & \text{otherwise,}\hfill \end{array}$$ (3.24)

$$J_{so}=\{\begin{array}{ll}\frac{1}{{\tau }_{\text{r}}}\hfill & \text{if}u\ge u_{\text{c}},\hfill \\ \frac{u}{{\tau }_0}\hfill & \text{otherwise,}\hfill \end{array}$$ (3.25)

$$J_{\text{si}}=-\frac{d}{2{\tau }_{\text{si}}}\left(1+\tanh \left(k\left(u-u_{\text{c}}^{\text{si}}\right)\right)\right).$$ (3.26)

The dimensional forms of the currents are given by I_fi = C_m(E_fi − v_o)J_fi, I_so = C_m(E_fi − v_o)J_so, and I_si = C_m(E_fi − v_o)J_si. The gating variables are governed by the piecewise-linear dynamics

$$\frac{dh}{dt}=\{\begin{array}{ll}-\frac{h}{{\tau }_h^{+}}\hfill & \text{if}u\ge u_{\text{c}},\hfill \\ \frac{1-h}{{\tau }_{h1}^{-}}\hfill & \text{if}{u}_{\text{c}}>u\ge u_h,\hfill \\ \frac{1-h}{{\tau }_{h2}^{-}}\hfill & \text{otherwise,}\hfill \end{array}$$ (3.27)

$$\frac{dd}{dt}=\{\begin{array}{ll}-\frac{d}{{\tau }_d^{+}}\hfill & \text{if}u\ge u_{\text{c}},\hfill \\ \frac{1-d}{{\tau }_d^{-}}\hfill & \text{otherwise}.\hfill \end{array}$$ (3.28)

Notice that the nondimensional voltage u_c is a threshold potential. Once u ≥ u_c, the fast inward current activates instantaneously, with no lag, and then rapidly but smoothly inactivates. The slow outward current also instantaneously achieves maximal activation when u > u_c but only inactivates once the membrane potential decreases below the fixed threshold value. Unlike the fast inward and slow outward currents, the slow inward current smoothly activates in response to the depolarization of the cell membrane before smoothly inactivating. Because the inward currents both inactivate following activation, whereas the outward current remains maximally activated so long as the cell is above threshold, the outward current ultimately acts to return the membrane voltage to its resting value. An action potential generated by a fit of the Fenton-Karma model to the 1991 version of the Luo-Rudy ventricular model [45] is shown in Figure 3.3. The parameter values used in this simulation are reported in Table 3.1. Other parameterizations of the model are provided by Fenton and Karma [20, 21].⁵

Table 3.1.

Fenton-Karma model parametrization of the Luo-Rudy I ventricular model.

C m	1 μF/cm2
${\overline{g}}_{\text{fi}}$	5.8 mS/cm2
τ d	$C_{\text{m}}/{\overline{g}}_{\text{fi}}=0.17\text{ms}$
τ r	130 ms
τ si	127 ms
τ o	12.5 ms
${\tau }_h^{+}$	10 ms
${\tau }_{h1}^{-}$	18.2 ms
${\tau }_{h2}^{-}$	18.2 ms
${\tau }_d^{+}$	1020 ms
${\tau }_d^{-}$	80 ms
u c	0.13 (dimensionless)
uh	0.13 (dimensionless)
$u_{\text{c}}^{\text{si}}$	0.85 (dimensionless)

The formulation and dynamics of this model are similar to those of the simplified Hodgkin-Huxley model (2.1)–(2.4). Both models feature a fast inward (Na⁺-like) current that is activated only when the transmembrane voltage exceeds a fixed threshold and which rapidly inactivates following activation. The dynamics of the h gate, which drives the inactivation of the fast inward current, are similar in both models, although in the Fenton-Karma model, τ_h is a function of v, whereas the reduced Hodgkin-Huxley model uses a fixed value for τ_h. The dynamics of the slow outward (K⁺-like) currents are somewhat different in the two models. In the Fenton-Karma model, the conductance of the slow outward current is set to a constant value whenever v is above threshold, and the dynamics of this current are not governed by any gating variables. In the reduced Hodgkin-Huxley model, the slow outward current has a gating variable n that smoothly tracks the m gating variable. Because m is a step function, achieving the value 1 whenever v is above threshold, n acts like a smoothed step function, and the outward current activates rapidly but continuously as a function of v. Finally, the Fenton-Karma model includes a slow inward (Ca²⁺-like) current with nontrivial dynamics, whereas the reduced Hodgkin-Huxley model includes only a linear “leakage” current that is meant to account for the effects of various transmembrane currents, including calcium and chloride currents.

4. Electrical Impulse Propagation in Cardiac Tissue

In a healthy heart, the left and right atria contract nearly synchronously, as do the left and right ventricles. Abnormal timing of the contractions of the heart can impair pumping efficacy, thereby reducing cardiac output and possibly leading to or complicating heart failure. Cardiac conduction system disorders such as bundle branch block can result in an abnormal time difference between the activation of the left and right ventricles. A treatment for this condition is cardiac resynchronization therapy, in which an implanted biventricular pacemaker reestablishes the synchronous contraction of the left and right sides of the heart [1, 42]. Pump function can also be impaired by arrhythmic activation of the heart muscle. A tachyarrhythmia, such as atrial or ventricular tachycardia, is a rapid, uncontrolled beating of the heart. Stable tachyarrhythmias are generally not themselves fatal, although they can induce circulating blood clots that may lead to stroke or pulmonary embolism. Unstable tachyarrhythmias, however, can devolve into fibrillation, an electrophysiological analogue of turbulence, in which multiple reentrant activation waves produce completely uncoordinated and therefore ineffective contractions of the cardiac muscle. The most dangerous cardiac arrhythmia is ventricular fibrillation, which rapidly leads to death unless halted. A common approach to defibrillation is to apply a large external electric shock that is meant to extinguish the reentrant waves and allow the heart a chance to reestablish normal activation [39]. Patients with a high susceptibility to ventricular fibrillation may be fitted with an implanted cardioverter-defibrillator [58]. When this device detects the presence of a potentially fatal arrhythmia, it automatically administers a defibrillatory shock. Equations describing cardiac impulse propagation are needed to model conditions such as cardiac arrhythmias and to model electrophysiological interventions such as cardiac resynchronization therapy, and such models increasingly inform clinical decision making.

In cardiac muscle, the intracellular spaces of neighboring myocytes are electrically coupled via gap junction channels, which are low-resistance connections that allow for the direct transfer of ions between pairs of cells. Cardiac muscle is therefore frequently referred to as a syncytium or as syncytial tissue. Depolarization of a myocyte is able to initiate intercellular currents that are transmitted via gap junctional connections. Thus, although the dynamics of the cardiac action potential are driven at the level of an individual cell by voltage-gated transmembrane currents, the spatial spread of excitation throughout the tissue is driven by the essentially passive flow of intracellular, intercellular, and extracellular currents. Cardiac conduction can therefore be described as a reaction-diffusion process.

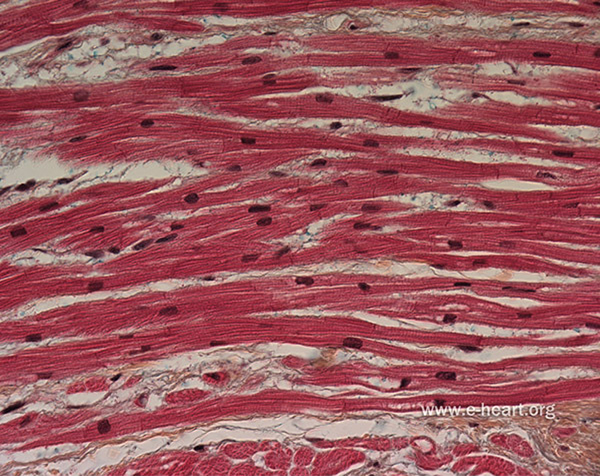
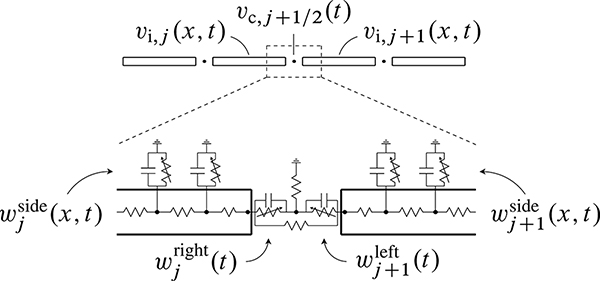
Gap junctions are preferentially localized to structures called intercalated discs, which are located at the ends of the myocytes, where the membranes of neighboring cells are in close proximity. Individual myocytes are organized into muscle fibers, and the myocytes are aligned with the macroscopic fiber direction. Because of the preferential localization of gap junctions to the ends of the cells and the effects of cellular geometry, macroscopic conduction is highly anisotropic, and action potential waves travel more rapidly along fibers than in the cross-fiber directions. The cellular architecture of cardiac muscle is shown in Figure 4.1.

Figure 4.1.

By volume, cardiac muscle is primarily composed of cardiomyocytes, which are electrically active contractile cells. Myocytes are arranged into fibers and are electrically coupled via gap junction channels, which are preferentially localized to structures called intercalated discs located at the ends of the myocytes. Macroscopic conduction is highly anisotropic, and action potential waves travel more rapidly along fibers than in the cross-fiber directions. See also Figure 4.5, which describes the microscale geometry and equivalent circuit of a model of a linear strand of myocytes. Figure adapted with permission from www.e-heart.org.

Mathematical models that describe excitation propagation in cardiac tissue must account for these cellular and subcellular features; however, the computational costs associated with fully microscale models that include detailed representations of the tissue microstructure are high, and three-dimensional versions of such models have only been used to simulate excitation propagation for relatively small regions comprised of tens to hundreds of cells. In particular, the computational demands of fully microscale models presently preclude their use in simulating tissue- or organ-scale propagation.

Macroscale models of cardiac conduction, in which the cellular microstructure is averaged away to yield a homogenized description of impulse propagation, were introduced in part to yield equations that are less computationally demanding than fully microscale models. This approach has been extremely successful, and at present, most tissue- and organ-scale simulations of cardiac electrical dynamics use such models. However, because the spatial extent of the upstroke of the normal action potential wavefront is typically only a few hundreds of microns, accurate numerical simulations of the macroscale equations require spatial discretizations that use relatively fine macroscopic grids with nearly cell-scale resolutions. Moreover, in pathological conditions in which conduction is slowed, the action potential upstroke may have a spatial extent of only one or two cell lengths. In such cases, the continuum macroscale equations are unable to capture the dynamics of the underlying microscale model because the key assumptions underlying the derivation of the homogenized equations, namely that the voltage and membrane state variables vary slowly at the length scale of cells, are strongly violated. Standard macroscale models also cannot account for certain aspects of the microstructure of cardiac tissue, such as the difference between the extracellular potential along the sides of cells and the extracellular potential at the ends of cells, or the differences in the subcellular localization of different types of transmembrane ion channels.

Multiscale models offer an alternative to fully microscale models that is suitable for tissue- and organ-scale simulations of cardiac dynamics. In this approach, detailed descriptions of the microstructure are deployed only in critical tissue subregions, and macroscale equations are used in the remainder of the tissue domain. We discuss one possible multiscale approach below. Before doing so, however, we first describe much more commonly used macroscale approaches to modeling cardiac conduction.

4.1. Macroscale Models of Cardiac Impulse Propagation

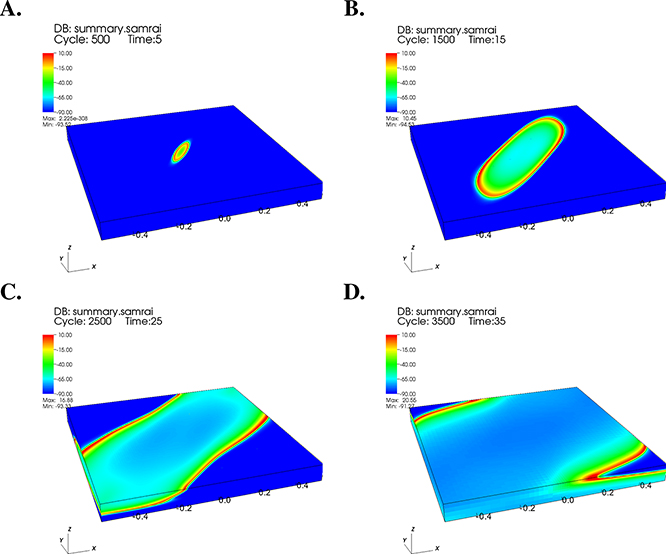
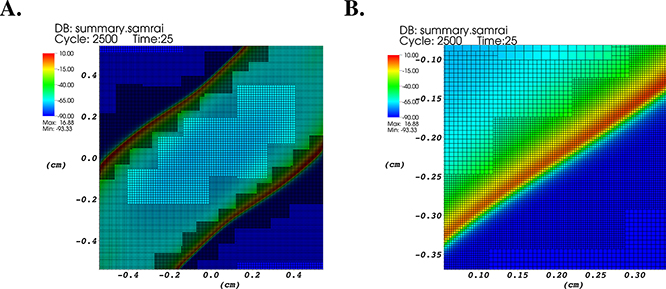
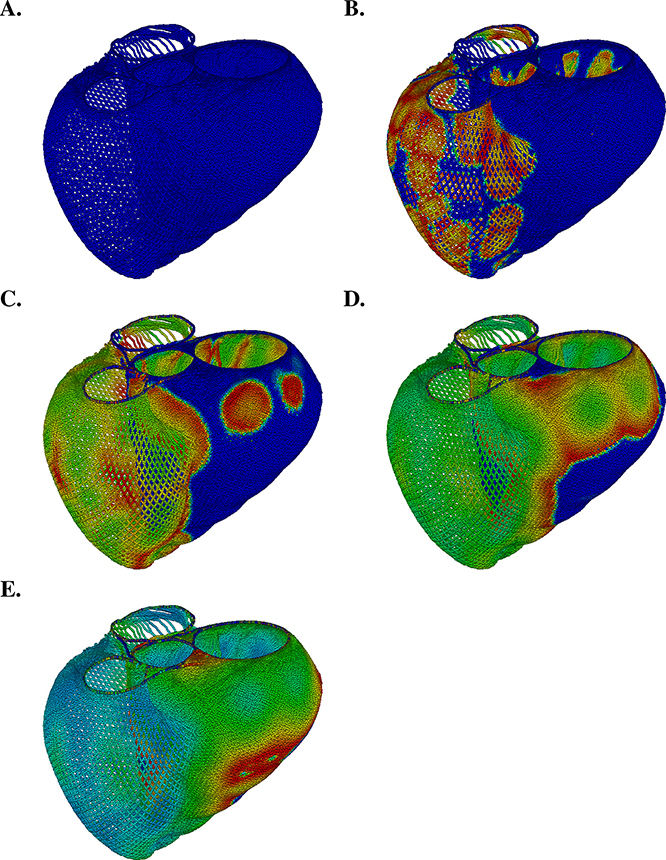
Most large-scale models of cardiac impulse propagation use either the bidomain model or the closely related monodomain model. Both are macroscopic descriptions of cardiac impulse propagation that are extensions of the one-dimensional cable model of Hodgkin and Huxley to three-dimensional tissues. An early description of the monodomain model appears in the 1975 monograph of Jack, Noble, and Tsien [37], and the bidomain model of cardiac tissue was introduced in 1978 by Tung in his Ph.D. thesis [88] and by Miller and Geselowitz [24, 50]. Related work on formulating bidomain-type models was also carried out by Eisenberg and coworkers [17] and by Peskoff [69, 70]. We focus here primarily on the bidomain model, which provides a more complete description of the underlying biophysics. In particular, the bidomain model is able to account for the strong difference in tissue anisotropy in the intracellular and extracellular spaces. In addition, the bidomain model allows for extracellular current sources, as required to model interventions such as defibrillation or devices such as pacemakers. As described below, the equations of the monodomain model can be obtained directly from the bidomain equations. Sample results from two types of bidomain calculations are shown in Figures 4.2, 4.3, and 4.4.

Figure 4.2.

Results from a computer simulation of cardiac excitation propagation using a bidomain model of a three-dimensional (1 cm × 1 cm × 1 mm) region of murine (mouse) ventricular myocardium. To account for transmural fiber rotation in the model, the direction of strongest conductivity rotates from endocardium to epicardium by 120°. The transmembrane voltage difference (mV) is plotted along the surface of a three-dimensional tissue region at (A) 5 ms, (B) 15 ms, (C) 25 ms, and (D) 35 ms following a current stimulus.

Figure 4.3.

Results from a computer simulation of cardiac excitation propagation using a bidomain model of a three-dimensional (1 cm × 1 cm × 1 mm) region of murine ventricular myocardium. A. Similar to Figure 4.2C, but here viewed from above and showing the adaptively refined computational grid. B. Similar to A, but magnified to show the grid in the vicinity of the action potential wavefront. Ultrafine (cell-level) spatial resolution is deployed in a localized fashion near the action potential wavefront.

Figure 4.4.

Immersed boundary model of cardiac electrophysiology in an idealized model of the ventricles. In this simulation, we use a novel formulation [27] of the bidomain equations that is based on the mathematical structure of the immersed boundary method [68] to model electrical impulse propagation in cardiac muscle. Transmembrane potential difference is plotted on the surface of the model heart (blue = −80 mV; red = +20 mV).

The bidomain model [33] conceptually partitions the myocardium into continuous (i.e., connected) intracellular and extracellular compartments that are electrically coupled via a continuous membrane. The intracellular spaces of neighboring myocytes are connected via gap junction channels, and it is natural to regard the interiors of the gap junctions themselves as part of the intracellular space. This makes the intracellular space of the whole myocardium into a single connected set. Similarly, it is natural to regard the protein walls (or “sleeves”) of the gap junctions as extensions of the cell membrane, since these walls separate the intracellular milieu from the extracellular, and this connects the membranes of the different myocytes into one large continuous “membrane” for the myocardium as a whole.

The standard bidomain model does not, however, make any attempt to resolve the microstructure described in the previous paragraph. Instead, it employs the conceptual framework of homogenization (see further discussion, with references, at the end of this section), which is intuitively described as follows: Let v_i(x, t) and v_e(x, t) be smooth functions of space and time which are defined for all x in the myocardium, without regard to whether x is an interior, exterior, or membrane point. In the following, we denote the region of space occupied by the myocardium by $\Omega \subset {ℝ}^3$. The function v_i(x, t) gives the local average of the intracellular voltage in the neighborhood of the point x at time t. By local average of the intracellular voltage in the neighborhood of x, we mean the integral over the intersection of some control volume containing x with the intracellular space divided by the volume of that intersection. The control volume needs to be large in comparison to the scale of the cellular structure of the myocardium, but small in comparison to any spatial scale that may be of interest (e.g., the thickness of the action potential wavefront). The existence of such an intermediate size for the control volume is a condition for the validity of homogenization. (Indeed, as we have already mentioned and discuss further later in this section, this condition is only moderately well satisfied, if at all.) The extracellular voltage v_e(x, t) is defined in exactly the same way as v_i but with the word extracellular substituted for intracellular.

We emphasize that, in the above definitions, it does not matter whether the point x itself is an intracellular point, an extracellular point, or a point of the membrane. What matters is that the control volume, which is large in comparison to the microstructure, is intersected with the intracellular space in the definition of v_i and with the extracellular space in the definition of v_e. Also, because the control volume is large in comparison to the scale of the microstructure, the functions v_i(x, t) and v_e(x, t) vary very little over distances that are comparable to the scale of the microstructure.

Besides voltages, we must also consider the intracellular and extracellular current densities, j_i(x, t) and j_e(x, t). These are vector fields, defined on Ω and slowly varying on the scale of the microstructure, and defined so that, for any smooth surface S with a scale that is large in comparison to the microstructure,

$$\underset{S}{\int }{\mathbf{j}}_{\text{i}}(\mathbf{x},t)\cdot \mathbf{n}(\mathbf{x})da={\int }_{S_{\text{i}}}{\mathbf{j}}_{\text{micro}}(\mathbf{x},t)\cdot \mathbf{n}(\mathbf{x})da,$$ (4.1)

$$\underset{S}{\int }{\mathbf{j}}_{\mathbf{e}}(\mathbf{x},t)\cdot \mathbf{n}(\mathbf{x})da=\underset{S_{\text{e}}}{\int }{\mathbf{j}}_{\text{micro}}(\mathbf{x},t)\cdot \mathbf{n}(\mathbf{x})da.$$ (4.2)

Here n(x) is the unit normal to S and da is the area element on S. On the right-hand sides of these equations, j_micro is the microscopic current density, S_i is the intersection of the surface S with the intracellular space, and S_e is the intersection of the surface S with the extracellular space. Like v_i and v_e, j_i and j_e are defined for all x, regardless of whether x belongs to the intracellular space, the extracellular space, or the membrane. Note that j_i is intracellular current per unit area and not intracellular current per unit intracellular area. Similarly, j_e is extracellular current per unit area, without any distinction between intracellular and extracellular area.

We assume that the relationship between intracellular voltage and intracellular current density can be described by a conductivity tensor (that is, by a symmetric, positive definite, 3 × 3 matrix at every x) denoted σ_i(x), and likewise that the relationship between extracellular voltage and extracellular current density can be described by a conductivity tensor denoted σ_e(x), so that

$${\mathbf{j}}_{\text{i}}=-{\sigma }_{\text{i}}\nabla v_i,$$ (4.3)

$${\mathbf{j}}_{\text{e}}=-{\sigma }_{\text{e}}\nabla v_e.$$ (4.4)

The conductivity tensors σ_i and σ_e account for the effects of local muscle fiber orientation (and perhaps also for the local distribution of muscle fiber orientations, as discussed below) on conduction. Because the influence of fiber orientation on conduction is stronger intracellularly than extracellularly, these conductivity tensors are generally different, and, moreover, there is no simple scaling that relates them (i.e., there is generally no scalar λ such that σ_e = λσ_i, even though the principal axes of σ_i and σ_e will generally be aligned).

The intracellular and extracellular currents are coupled by transmembrane current, which is driven by transmembrane voltage. We evaluate the transmembrane voltage v in the following simple way:

$$v(\mathbf{x},t)=v_{\text{i}}(\mathbf{x},t)-v_{\text{e}}(\mathbf{x},t),$$ (4.5)

so that v, like v_i and v_e, is defined throughout the myocardium.

By identifying v as defined by (4.5) with the transmembrane voltage difference, it is clear that we are making an approximation. Recall that v_i and v_e are locally averaged, so v is locally averaged as well. Since the response of the membrane current to v is generally nonlinear, either directly or through gating variables (see next paragraph), it is clear that computing transmembrane current from an averaged transmembrane voltage is not the same thing as computing the transmembrane current from local transmembrane voltage and then averaging the result. Nevertheless, because the local transmembrane voltage is not readily available in the bidomain model, we shall proceed without worrying about this!

The transmembrane current also depends on additional state variables, like the gating variables m, h, n of the original Hodgkin-Huxley equations, the state variables of the Markovian Na⁺ channel model of Clancy and Rudy, and possibly dynamic ion concentrations. These will be collectively denoted w(x, t). The variables denoted by w satisfy spatially decoupled differential equations of the form

$$\frac{\partial w}{\partial t}=f(v,w).$$ (4.6)

Since this equation, together with suitable initial conditions that will be stated below, defines w(x, t), we see that w inherits from v the property of being defined throughout Ω, i.e., throughout the myocardium.

Finally, with v and w defined, the transmembrane current is given by

$$I_{\text{m}}(\mathbf{x},t)=C_{\text{m}}\frac{\partial v}{\partial t}+I_{\text{ion}}(v,w),$$ (4.7)

in which C_m is the membrane capacitance per unit area, and I_ion(v, w) is the ionic transmembrane current per unit area, so that I_m is the total transmembrane current per unit area of membrane.

We can convert current/area to current/volume by making use of a geometrical parameter β, which is the area of membrane per unit volume of tissue. Note that 1/β has units of length and defines the length scale of the microstructure. The quantity βI_m is the transmembrane current per unit volume of tissue. Because of the sign convention that outward transmembrane current is positive, the term βI_m will appear as a source in the equation of the extracellular current density and as a sink in the equation of the intracellular current density. Another possible source in either compartment is an externally applied stimulus current per unit volume of tissue, which we denote by I_s,i(x, t) in the intracellular compartment and by I_s,e(x, t) in the extracellular compartment. Thus, using the notation ${\mathcal{L}}_k=\nabla \cdot {\sigma }_k\nabla$ for k = i or e, we have the following equations of current conservation:

$$\nabla \cdot {\mathbf{j}}_{\text{i}}=-{\mathcal{L}}_{\text{i}}{v}_{\text{i}}=-\beta I_{\text{m}}+I_{\text{s},\text{i}},$$ (4.8)

$$\nabla \cdot {\mathbf{j}}_{\text{e}}=-{\mathcal{L}}_{\text{e}}{v}_{\text{e}}=+\beta I_{\text{m}}+I_{\text{s},\text{e}}.$$ (4.9)

Adding equations (4.8) and (4.9), it is clear that in the bidomain model, current conservation takes the form of an elliptic constraint on v_i and v_e, namely,

$$\nabla \cdot {\mathbf{j}}_{\text{i}}+\nabla \cdot {\mathbf{j}}_{\text{e}}=-\left({\mathcal{L}}_{\text{i}}{v}_{\text{i}}+{\mathcal{L}}_{\text{e}}{v}_{\text{e}}\right)=I_{\text{s},\text{i}}+I_{\text{s},\text{e}}.$$ (4.10)

Although it is not essential to do so, we assume for simplicity that I_s,i = −I_s,e, so that

$${\mathcal{L}}_{\text{i}}{v}_{\text{i}}+{\mathcal{L}}_{\text{e}}{v}_{\text{e}}=0,$$ (4.11)

and we use the simpler notation I_s for I_s,i and −I_s for I_s,e. Assuming that the current stimuli are of this form makes it especially easy to model the application of localized current stimulations such as those provided by a pair of colocated microelectrodes, one injecting current intracellularly and the other removing that same current extracellularly.

The bidomain equations can now be summarized:

$${\mathcal{L}}_{\text{i}}{v}_{\text{i}}=+\beta \left(C_{\text{m}}\frac{\partial v}{\partial t}+I_{\text{ion}}(v,w)\right)-I_{\text{s}},$$ (4.12)

$${\mathcal{L}}_{\text{e}}{v}_{\text{e}}=-\beta \left(C_{\text{m}}\frac{\partial v}{\partial t}+I_{\text{ion}}(v,w)\right)+I_{\text{s}},$$ (4.13)

$$v=v_{\text{i}}-v_{\text{e}},$$ (4.14)

$$\frac{\partial w}{\partial t}=f(v,w).$$ (4.15)

Suitable boundary conditions for the bidomain equations may be specified in the following way. For simplicity, we assume that no current passes through the boundary ∂Ω of the tissue volume Ω in either compartment, so that for x ∈ ∂Ω,

$${\mathbf{j}}_{\text{i}}\cdot \mathbf{n}=\left(-{\sigma }_{\text{i}}\nabla v_{\text{i}}\right)\cdot \mathbf{n}=0,$$ (4.16)

$${\mathbf{j}}_{\text{e}}\cdot \mathbf{n}=\left(-{\sigma }_{\text{e}}\nabla v_{\text{e}}\right)\cdot \mathbf{n}=0,$$ (4.17)

in which n is the exterior unit normal to ∂Ω.

With these boundary conditions, v_i and v_e can only be determined up to an arbitrary, spatially uniform function of time. That is to say, if v_i and v_e are solutions of the bidomain equations, then so are

$${\widehat{v}}_{\text{i}}(\mathbf{x},t)=v_{\text{i}}(\mathbf{x},t)+\psi (t),$$ (4.18)

$${\widehat{v}}_{\text{e}}(\mathbf{x},t)=v_{\text{e}}(\mathbf{x},t)+\psi (t),$$ (4.19)

in which ψ depends only on t and not on x. We can obtain unique values for v_i and v_e by requiring v_e to satisfy⁶

$$\underset{\Omega }{\int }{v}_{\text{e}}d\mathbf{x}=0.$$ (4.20)

Notice that the arbitrariness of the intracellular and extracellular voltages does not complicate the use of the bidomain model in interpreting experimental voltage recordings since such recordings always take the form of a difference of voltages recorded at two spatial locations. Because ψ(t) is spatially uniform, its value does not affect the numerical value of such voltage differences.

A confusing feature of the bidomain equations is that the state of the system may appear to be (v_i, v_e, w), but the equations (4.12)–(4.15) do not give a recipe for ∂v_i/∂t and ∂v_e/∂t in terms of (v_i, v_e, w). Instead, they only define ∂(v_i − v_e)/∂t. Worse, they give two recipes for ∂(v_i − v_e)/∂t, and it is not obvious that these are consistent (and indeed they are not if v_i and v_e are chosen arbitrarily; see (4.11)). In fact, the state of the system described by the bidomain equations is given by (v, w), so that good initial data⁷ for these equations are v(x, 0) and w(x, 0), with no initial condition on v_i or v_e.

We illustrate this general fact by proving uniqueness with these initial conditions in a special case. Suppose that we replace I_ion(v, w) by

$$I_{\text{ion}}(v,\mathbf{x})=g(\mathbf{x})v,$$ (4.21)

in which g is some given function with g(x) > 0 for all x ∈ Ω. Note that there are no dynamical gating variables in this special case, but there are, in effect, “frozen” gating variables, since we allow the membrane conductance to depend on position. With the above form for I_ion the bidomain equations become linear and read as follows:

$${\mathcal{L}}_{\text{i}}{v}_{\text{i}}=+\beta \left(C_{\text{m}}\frac{\partial v}{\partial t}+gv\right)-I_{\text{s}},$$ (4.22)

$${\mathcal{L}}_{\text{e}}{v}_{\text{e}}=-\beta \left(C_{\text{m}}\frac{\partial v}{\partial t}+gv\right)+I_{\text{s}},$$ (4.23)

$$v=v_{\text{i}}-v_{\text{e}},$$ (4.24)

with the same boundary conditions (4.16)–(4.17) as before. We specify initial data for the above system of equations as

$$v(\mathbf{x},0)=v_0(\mathbf{x}),$$ (4.25)

with no initial condition on v_i or v_e separately. The stimulus current I_s(x, t) is taken to be a given function of position and time.

We claim that the solution to equations (4.22)–(4.24) with boundary conditions (4.16)–(4.17) and initial condition (4.25) is uniquely determined in the sense that v, ∇v_i, and ∇v_e are uniquely determined. As discussed above, this means that v_i and v_e are determined only up to one arbitrary function of time (not two separate functions of time, since v_i−v_e = v is uniquely determined). This arbitrary function of time has no physical consequences and can in any case be fixed by imposing the condition (4.20).

To prove this uniqueness result, we first derive an energy identity for the bidomain equations in the above special case. To do so, we multiply both sides of equation (4.22) by v_i, both sides of equation (4.23) by v_e, add the results, and integrate over Ω. Note on the right-hand side that the multiplying factors v_i and v_e conveniently combine to give v when the equations are added together. The result is

$$\begin{gathered} \underset{\Omega }{\int }\left(v_{\text{i}}{\mathcal{L}}_{\text{i}}{v}_{\text{i}}+v_{\text{e}}{\mathcal{L}}_{\text{e}}{v}_{\text{e}}\right)d\mathbf{x}=\underset{\Omega }{\int }v\left(\beta \left(C_{\text{m}}\frac{\partial v}{\partial t}+gv\right)-I_{\text{s}}\right)d\mathbf{x} \\ =\frac{d}{dt}\underset{\Omega }{\int }\beta \frac{1}{2}{C}_{\text{m}}{v}^{2}d\mathbf{x}+\underset{\Omega }{\int }\left(\beta g{v}^2-v{I}_{\text{s}}\right)d\mathbf{x}. \end{gathered}$$ (4.26)

On the left-hand side, we can integrate by parts and make use of the boundary conditions to eliminate the boundary terms. The result, slightly rearranged, is as follows:

$$\begin{gathered} \frac{d}{dt}\underset{\Omega }{\int }\beta \frac{1}{2}{C}_{\text{m}}{v}^{2}d\mathbf{x}= \\ \underset{\Omega }{\int }v{I}_{\text{s}}d\mathbf{x}-\underset{\Omega }{\int }\left(\beta g{v}^2+\nabla v_{\text{i}}\cdot {\sigma }_{\text{i}}\nabla v_{\text{i}}+\nabla v_{\text{e}}\cdot {\sigma }_{\text{e}}\nabla v_{\text{e}}\right)d\mathbf{x}. \end{gathered}$$ (4.27)

On the left-hand side of (4.27) we have the rate of change of the energy stored in the membrane capacitance (recall that β is the membrane area per unit volume of tissue, and C_m is the capacitance per unit area of membrane). On the right-hand side, the first term is the power applied by the stimulus, and the second term is minus the rate of Joule heating produced by transmembrane currents, intracellular currents, and extracellular currents. Note that the rate of Joule heating is nonnegative, since σ_i and σ_e are symmetric positive-definite matrices at each x.

Let $(v^{(1)},v_{\text{i}}^{(1)},v_{\text{e}}^{(1)})$ and $(v^{(2)},v_{\text{i}}^{(2)},v_{\text{e}}^{(2)})$ be two solutions to (4.22)–(4.24) with boundary conditions (4.16)–(4.17), with the same initial condition (4.25), and with the same stimulus current I_s. Let u = v⁽¹⁾ – v⁽²⁾, $u_{\text{i}}=v_{\text{i}}^{(1)}-v_{\text{i}}^{(2)}$, and $u_{\text{e}}=v_{\text{e}}^{(1)}-v_{\text{e}}^{(2)}$. Then u, u_i, and u_e satisfy the same equations and boundary conditions but with the initial condition u(x, 0) = 0 and with I_s = 0. It follows that

$$\frac{d}{dt}\underset{\Omega }{\int }\beta \frac{1}{2}{C}_{\text{m}}{u}^{2}d\mathbf{x}=-\underset{\Omega }{\int }\left(\beta g{u}^2+\nabla u_{\text{i}}\cdot {\sigma }_{\text{i}}\nabla u_{\text{i}}+\nabla u_{\text{e}}\cdot {\sigma }_{\text{e}}\nabla u_{\text{e}}\right)d\mathbf{x}\le 0.$$ (4.28)

Thus, since u(x, 0) = 0, we have u(x, t) = 0 for all t > 0. This proves the uniqueness of v. With u = 0, equation (4.28) also shows that ∇u_i = ∇u_e = 0, which implies that v_i and v_e are uniquely determined up to an arbitrary function of time only, as claimed above.

Next, we describe a practical time discretization of the bidomain equations. Let vⁿ(x) = v(x, nΔt), and similarly for all other variables. Consider the scheme

$${\mathcal{L}}_{\text{i}}{v}_{\text{i}}^{n+1}=+\beta \left(C_{\text{m}}\frac{v^{n+1}-v^n}{\mathrm{\Delta }t}+I_{\text{ion}}\left(v^n,w^n\right)\right)-I_{\text{s}}^n,$$ (4.29)

$${\mathcal{L}}_{\text{e}}{v}_{\text{e}}^{n+1}=-\beta \left(C_{\text{m}}\frac{v^{n+1}-v^n}{\mathrm{\Delta }t}+I_{\text{ion}}\left(v^n,w^n\right)\right)+I_{\text{s}}^n,$$ (4.30)

$$v^{n+1}=v_{\text{i}}^{n+1}-v_{\text{e}}^{n+1},$$ (4.31)

$$\frac{w^{n+1}-w^n}{\mathrm{\Delta }t}=f\left(v^n,w^n\right).$$ (4.32)

Note that this scheme is a hybrid of the forward- and backward-Euler time discretizations. In particular, the backward (or implicit) part of the scheme is that (4.29)–(4.31) is a system of equations that needs to be solved for the unknowns $(v^{n+1},v_{\text{i}}^{n+1},v_{\text{e}}^{n+1})$, subject to the boundary conditions

$$\left({\sigma }_{\text{i}}\nabla v_{\text{i}}^{n+1}\right)\cdot \mathbf{n}=0,$$ (4.33)

$$\left({\sigma }_{\text{e}}\nabla v_{\text{e}}^{n+1}\right)\cdot \mathbf{n}=0,$$ (4.34)

and also subject to the constant-determining condition

$$\underset{\Omega }{\int }{v}_{\text{e}}^{n+1}d\mathbf{x}=0.$$ (4.35)

We claim that vⁿ⁺¹, $v_{\text{i}}^{n+1}$, and $v_{\text{e}}^{n+1}$ are uniquely determined by the above equations (with all quantities at time level n regarded as given data). The proof is very similar to the previous uniqueness proof, so we omit the details.

In practice, when using the above scheme, we eliminate v_i and work with the variables v and v_e. This gives the system

$$\left(\begin{array}{cc}\left(\frac{\beta C_{\text{m}}}{\mathrm{\Delta }t}\right)-{\mathcal{L}}_{\text{i}}& -{\mathcal{L}}_{\text{i}}\\ -{\mathcal{L}}_{\text{i}}& -\left({\mathcal{L}}_{\text{i}}+{\mathcal{L}}_{\text{e}}\right)\end{array}\right)\left(\begin{array}{c}{v}^{n+1}\\ v_{\text{e}}^{n+1}\end{array}\right)=\left(\begin{array}{c}\left(\frac{\beta C_{\text{m}}}{\mathrm{\Delta }t}\right)u^n\\ 0\end{array}\right),$$ (4.36)

where uⁿ (not the same u as in the discussion of uniqueness above) is defined by

$$u^n=v^n+\frac{\mathrm{\Delta }t}{C_{\text{m}}}\left(-I_{\text{ion}}\left(v^n,w^n\right)+\frac{I_{\text{s}}^n}{\beta }\right).$$ (4.37)

As before, we have the constant-fixing condition (4.35) and also the boundary conditions (4.33)–(4.34), except that (4.33) must here be rewritten in terms of v and v_e. This gives

$$\left({\sigma }_{\text{i}}\nabla v_{\text{e}}^{n+1}\right)\cdot \mathbf{n}+\left({\sigma }_{\text{i}}\nabla v^{n+1}\right)\cdot \mathbf{n}=0.$$ (4.38)

As in the earlier work of Pennacchio and Simoncini [66], we solve (4.36) iteratively using multigrid-preconditioned Krylov subspace methods such as GMRES [79].

The monodomain model is similar to the bidomain model except that the monodomain model does not separately account for the intracellular and extracellular currents, but instead describes the state of the tissue in terms of only the transmembrane voltage v and the spatially distributed gating variables w. One way to obtain the monodomain model from the bidomain model is to assume that the extracellular compartment is well approximated as being isopotential. This will occur, for instance, if the extracellular conductivity is very large. In the limiting case of infinite extracellular conductivity, v_e = 0, v = v_i, and (4.12)–(4.15) reduce to

$${\mathcal{L}}_{\text{i}}v=\beta \left(C_{\text{m}}\frac{\partial v}{\partial t}+I_{\text{ion}}(v,w)\right)-I_{\text{s}},$$ (4.39)

$$\frac{\partial w}{\partial t}=f(v,w).$$ (4.40)

Similar equations can also be obtained without the assumption of large extracellular conductivity if we assume instead that there exists a scalar value λ, independent of x, such that σ_e(x) = λσ_i(x). In this case,

$${\mathcal{L}}_{\text{e}}=\lambda {\mathcal{L}}_{\text{i}},$$ (4.41)

and we can look for a solution to (4.12)–(4.15) in which

$$v_{\text{i}}=\frac{\lambda v}{1+\lambda },$$ (4.42)

$$v_{\text{e}}=\frac{-v}{1+\lambda }.$$ (4.43)

Equations (4.12)–(4.15) then reduce to

$$\frac{\lambda }{1+\lambda }{\mathcal{L}}_{\text{i}}v=\beta \left(C_{\text{m}}\frac{\partial v}{\partial t}+I_{\text{ion}}(v,w)\right)-I_{\text{s}},$$ (4.44)

$$\frac{\partial w}{\partial t}=f(v,w).$$ (4.45)

In the limit λ → ∞, the extracellular conductivity becomes infinite and these two monodomain formulations become identical.

The requirement that v_i and v_e satisfy equation (4.10) makes the numerical solution of the bidomain equations significantly more computationally intensive than the solution of the monodomain equations. The monodomain model is also conceptually simpler than the bidomain model, and in many cases of interest it gives reasonable results. For these reasons, the monodomain model remains popular, despite the greater realism of the bidomain model. It is therefore of interest to consider how to construct a monodomain model that best approximates some particular bidomain model. Of course, “best approximates” can be defined in many ways. One possibility that we think would be reasonable (although to the best of our knowledge it has not yet been tried) is to find the number λ that minimizes

$$\underset{\Omega }{\int }{\Vert {\sigma }_{\text{e}}(\mathbf{x})-\lambda {\sigma }_{\text{i}}(\mathbf{x})\Vert }^{2}d\mathbf{x},$$ (4.46)

in which, for any 3 × 3 symmetric matrix A, we define its norm by

$$\Vert A\Vert =\sqrt{\mathrm{trace}\left(A^2\right)}.$$ (4.47)

It is then easy to see that the optimal λ is given by

$$\lambda =\frac{{\int }_{\Omega }\mathrm{trace}\left({\sigma }_{\text{i}}{\sigma }_{\text{e}}\right)d\mathbf{x}}{{\int }_{\Omega }\mathrm{trace}\left({\sigma }_{\text{i}}^2\right)d\mathbf{x}}.$$ (4.48)

With λ known, we replace σ_e by λσ_i (thereby changing the model, but by an amount that we hope is small), and after that we can work with the equivalent monodomain formulation, as given by equations (4.44)–(4.45).

Note that the above procedure is asymmetrical, in that it leaves σ_i alone, while tinkering only with σ_e. This reflects the intuition that the intracellular conductivity has a more profound influence on cardiac conduction than the extracellular conductivity, but it might be possible to achieve a better monodomain approximation to the bidomain model by allowing both the intracellular and the extracellular conductivities to change.

It should be a source of concern, however, that the derivation of the monodomain model from the bidomain model requires unrealistic assumptions. In reality, the extracellular conductivity is not so large that the extracellular space is approximately isopotential, nor does there exist some constant λ such that σ_e(x) ≈ λσ_i(x). In fact, concerning the latter issue, the intracellular space is much more anisotropic than the extracellular space. The ratio of maximum to minimum conductivity is about 10 : 1 intracellularly, but only about 2 : 1 extracellularly. This implies that σ_e is very far from being a scalar multiple of σ_i. One case in which it is clearly not suitable to employ the monodomain model is in simulations of defibrillation. This is because the defibrillatory shock appears as a current stimulus or boundary condition in the extracellular compartment, thereby requiring the use of the bidomain model [38, 39].

Although we have given an informal derivation of the bidomain equations here, it is important to note that these equations can also be derived more formally by the methods of homogenization [31,39,60,65,74]. The starting point for such a derivation is a detailed microscopic cardiac tissue model. Homogenization can also be used to obtain numerical values for the intracellular and extracellular conductivity tensors from experimentally measurable quantities such as cellular dimension and distributions of gap junction coupling strengths. The first derivation of the bidomain equations via homogenization was due to Neu and Krassowska [60], who used a PDE-based description of the microstructure in their derivation. To obtain numerical values for the macroscopic parameters of the bidomain model, however, Neu and Krassowska used a simplified resistor network-based microscale model. To our knowledge, the first work to use the tools of homogenization theory to compute macroscopic bidomain parameters was that of Hand, Griffith, and Peskin [31], who described myocytes as rectangular prisms and gap junctions as flux boundary conditions imposed at the ends and the sides of the cells. This approach allows for the parameters of the bidomain model to be obtained directly from measurable microscale properties. The numerical values obtained in this manner were found to be in good agreement with similar values obtained from simulations of a detailed, physiologically realistic cardiac microstructure [84].

An open problem related to the determination of the macroscopic model parameters from microscale data, regardless of approach, is that the resulting macroscopic conductivities are too small in the sense that when these parameter values are used in bidomain simulations, the speed of propagation is unphysiologically slow. This effect is strongest in the transverse (cross-fiber) directions. The cause of this discrepancy is presently unknown. One possibility is that the underlying microscale models generally assume parallel arrays of cardiomyocytes, whereas in reality, although myocytes are roughly aligned with a predominant fiber direction, myocytes can branch and are not perfectly aligned with the macroscopic fiber direction. Incorporating some dispersion in the local myocyte orientation may provide enough additional transverse coupling at the macroscale to yield significantly more realistic propagation velocities.

4.2. Multiscale Models of Cardiac Impulse Propagation

As discussed earlier in this section, macroscale models of cardiac impulse propagation are widely used, but they also present challenges. For instance, because the spatial extent of the upstroke of the normal action potential wavefront is typically only a few hundreds of microns, accurate numerical simulations of the macroscale equations require spatial discretizations that use relatively fine macroscopic grids with nearly cell-scale resolutions. In addition, in pathological situations that lead to propagation slowing, the voltage and membrane state variables may no longer vary slowly at the cellular-length scale of the microstructure, and in such cases, the macroscale equations cannot describe the dynamics of the underlying microscale system.

Standard macroscale models like the bidomain model also cannot account for certain aspects of the microscopic anatomy and physiology of the cardiac tissue. An example is the difference between the extracellular potential along the sides of cells and the extracellular potential at the ends of cells. Specifically, because neighboring cardiomyocytes are separated at their ends by extremely narrow cleft spaces, and because inward sodium channels are preferentially located on the cleft-facing membranes, the voltage in the cleft space is not equal to the bulk extracellular potential throughout the entire action potential, and the differences between the bulk and cleft potentials are most pronounced during the action potential upstroke. In fact, the effects of such cleft potentials offer one explanation for the experimental observations of Fishman and coworkers [28], who demonstrated that the ventricular tissue of mice with a tissue-specific knockout of the gene that expresses the major ventricular gap junction protein still exhibits conduction, although at dramatically reduced propagation speeds. A possible route by which action potential propagation occurs in the absence of gap junctions is known as ephaptic conduction or as the electric field mechanism [11, 55, 71, 73, 82]. Standard macroscale models also cannot account for physiological differences in the subcellular localization of certain types of transmembrane ion channels, although it is possible to derive homogenized equations that include such features [32].

The mechanism of ephaptic conduction can be described most simply by considering two neighboring cells within a tissue that are coupled end-to-end. Suppose that the action potential wave first reaches the “prejunctional” cell, depolarizing the cell membrane and activating the Na⁺ channels of that cell. The Na⁺ channels located along the intercalated disc will draw inward current through the cleft and thereby reduce the cleft potential and increase⁸ the transmembrane voltage along the cleft-facing membrane of the “postjunctional” cell. If this depolarization is sufficient to activate the Na⁺ channels of the postjunctional cell, then the action potential is able to continue to propagate even without the benefit of gap-junctional currents. Although this ephaptic conduction mechanism does not strictly require the presence of narrow cleft spaces and, in principle, could be mediated by the bulk extracellular space, in physiological parameter regimes, ephaptic coupling appears to be an effective mechanism of propagation only for extremely narrow domains like those observed at the intercalated discs.

A microscale model of cardiac conduction that includes this electric field mechanism was described by Kucera, Rohr, and Rudy [41], and Hand and Peskin [32] subsequently developed a homogenized version of this microscale model. The macroscale equations of the homogenized model successfully capture the dynamics of the microscale model for tissues with high levels of gap-junctional coupling, but they yield inaccurate results at low levels of gap-junctional coupling, and they do not predict propagation in the complete absence of gap junctions. Thus, the macroscale model yields accurate results in cases in which the action potential waveform is relatively smooth at the length scale of cells, but it produces inaccurate results in conditions that yield very slow conduction.

To address the shortcomings of the macroscale model of Hand and Peskin, Hand and Griffith [29] developed an adaptive multiscale model in which the microscale equations of Kucera et al. [41] are used in only a fully resolved tissue subregion, whereas the macroscale equations of Hand and Peskin [32], or a simplification of those equations, are used in the remainder of the tissue. Specifically, the microscale equations are used only in the vicinity of action potential upstrokes, where the large inward Na⁺ currents along the cleft-facing membranes result in large negative cleft potentials.

This model has been shown to produce results that are essentially identical to those of the fully microscale model [29], and it has been demonstrated to be remarkably insensitive to the macroscale grid used to discretize the equations in the “unresolved” tissue subregions [30]. In addition, this multiscale model is able to yield propagation even under the complete ablation of gap-junctional coupling, despite the fact that the macroscale model is not able to generate such dynamics [30]. Important extensions of this work that have not yet been attempted include developing a three-dimensional version of the model. Because the models described above all assume that the bulk extracellular space is isopotential, another possible extension of the model would be to allow for spatial variations in bulk extracellular voltage. Work to develop a microscale model that is similar to the bidomain model has been carried out by Lin and Keener [44].

Microscale Model

The microscale model describes the dynamics of a linear strand of myocytes. Each myocyte is idealized as a cylindrical cell of length ℓ and radius r. A cable model similar to the Hodgkin-Huxley axonal model is used to describe the dynamics of each cell. Neighboring cells in the strand are directly coupled via gap junctions that are modeled as linear resistors. Neighboring cells are also indirectly coupled via a shared cleft space of the intercalated disc, which is modeled as isopotential and is resistively coupled to the grounded extracellular space. A schematic diagram of the microscale model is shown in Figure 4.5.

Figure 4.5.

The microscale geometry and equivalent circuit of a model of a linear strand of cardiomyocytes. Adjacent cells are coupled by gap junctions that are modeled as linear resistors and by a shared cleft space that is resistively coupled to the bulk extracellular space. In this model, the bulk extracellular space is treated as isopotential. Figure adapted from Hand and Griffith [29].

Let v_i,j (x, t) be the intracellular potential in cell j, with x ∈ (0, ℓ], and let v_c,j+1/2(t) be the cleft potential in the intercalated disk to the right of cell j. Let $w_j^{\text{side}}(x,t)$ be the collection of membrane state variables along the sides of cell j, and let $w_j^{\text{left}}(t)$ and $w_j^{\text{right}}(t)$ be the membrane state variables along the left and right ends of cell j, respectively. Because we assume that the extracellular space is grounded, the transmembrane voltage difference along the sides of the cell j is $v_j^{\text{side}}(x,t)=v_{\text{i},j}(x,t)$. At the left end of the cell, the transmembrane voltage is the difference between the intracellular voltage and the cleft voltage, i.e., $v_j^{\text{left}}(t)=v_{\text{i},j}(0,t)-v_{\text{c},j-1/2}(t)$, and at the right side of the cell, the transmembrane voltage is $v_j^{\text{right}}(t)=v_{\text{i},j}(\ell ,t)-v_{\text{c},j+1/2}(t)$. For convenience, we also define $v_{\text{i},j}^{\text{left}}(t)=v_{\text{i},j}(0,t)$ and $v_{\text{i},j}^{\text{right}}(t)=v_{\text{i},j}(\ell ,t)$. The transmembrane ionic currents along the sides and left and right ends of cell j are $I_{\text{ion,}j}^{\text{side}}(x,t)=I_{\text{ion}}^{\text{side}}(v_j^{\text{side}}(x,t),w_j^{\text{side}}(x,t))$, $I_{\text{ion},j}^{\text{left}}(t)=I_{\text{ion}}^{\text{end}}(v_j^{\text{left}}(t),w_j^{\text{left}}(t))$ and $I_{\text{ion,}j}^{\text{right}}(t)=I_{\text{ion}}^{\text{end}}(v_j^{\text{right}}(t),w_j^{\text{right}}(t))$, respectively.⁹ The governing equations of the microscale system are

$$\frac{A}{S}{\sigma }_{\text{cyt}}\frac{{\partial }^2{v}_{\text{i},j}}{\partial x^2}=C_{\text{m}}\frac{\partial v_j^{\text{side}}}{\partial t}+I_{\text{ion,},j}^{\text{side}},$$ (4.49)

$$+{{\sigma }_{\text{cyt}}\frac{\partial v_{\text{i},j}}{\partial x}|}_{x=0}=C_{\text{m}}\frac{\partial v_j^{\text{left}}}{\partial t}+I_{\text{ion},j}^{\text{left}}+g_{\text{GJ}}(v_{\text{i},j}^{\text{left}}-v_{\text{i},j-1}^{\text{right}}),$$ (4.50)

$$-{{\sigma }_{\text{cyt}}\frac{\partial v_{\text{i},j}}{\partial x}|}_{x=\ell }=C_{\text{m}}\frac{\partial v_j^{\text{right}}}{\partial t}+I_{\text{ion},j}^{\text{right}}+g_{\text{GJ}}(v_{\text{i},j}^{\text{right}}-v_{\text{i},j+1}^{\text{left}}),$$ (4.51)

$$v_{\text{c},j+1/2}=R_{\text{c}}A{\sigma }_{\text{cyt}}\left({\frac{\partial v_{\text{i},j+1}}{\partial x}|}_{x=0}-{\frac{\partial v_{\text{i},j}}{\partial x}|}_{x=\ell }\right),$$ (4.52)

$$\frac{\partial w_j^{\text{side}}}{\partial t}=f(v_j^{\text{side}},w_j^{\text{side}}),$$ (4.53)

$$\frac{\partial w_j^{\text{left}}}{\partial t}=f(v_j^{\text{left}},w_j^{\text{left}}),$$ (4.54)

$$\frac{\partial w_j^{\text{right}}}{\partial t}=f(v_j^{\text{right}},w_j^{\text{right}}),$$ (4.55)

in which A = πr² is the cross-sectional area of a cell, S = 2πr is the perimeter of a cross section, σ_cyt is the cytosolic conductivity, g_GJ is the gap-junctional conductance per unit area of membrane, C_m is the membrane capacitance per unit area of membrane, and R_c is the cleft-to-ground resistance. A version of the model that does not include ephaptic coupling is obtained by setting R_c = 0, and in this limiting case, the bulk and cleft extracellular potentials are equal, so that v_c,j+1/2 = 0.

Macroscale Model

A homogenized version of the microscale model is defined in terms of the macroscopic intracellular voltage v_i(x) and cleft potential v_c(x) along with macroscopic membrane state variables defined along the sides and ends of the cells, respectively w^side(x) and w^end(x). Because the extracellular space is assumed isopotential, the macroscopic transmembrane voltage difference along the sides of the cells is v^side(x, t) = v_i(x, t). The transmembrane voltage at the ends of the cells is v^end(x, t) = v_i(x, t) − v_c(x, t). The transmembrane ionic current along the sides of the cells is $I_{\text{ion}}^{\text{side}}=I_{\text{ion}}^{\text{side}}\left(v^{\text{side}}(x,t),w^{\text{side}}(x,t)\right)$, and the transmembrane current along the ends of the cells is $I_{\text{ion}}^{\text{end}}=I_{\text{ion}}^{\text{end}}\left(v^{\text{end}}(x,t),w^{\text{end}}(x,t)\right)$. The governing equations for the macroscale model are

$$\frac{A}{S}\sigma \frac{{\partial }^2{v}_{\text{i}}}{\partial x^2}=C_{\text{m}}\frac{\partial v^{\text{side}}}{\partial t}+I_{\text{ion}}^{\text{side}}+\frac{1}{S\ell R_{\text{c}}}{v}_{\text{c}},$$ (4.56)

$$\frac{1}{2A{R}_{\text{c}}}{v}_{\text{c}}=C_{\text{m}}\frac{\partial v^{\text{end}}}{\partial t}+I_{\text{ion}}^{\text{end}},$$ (4.57)

$$\frac{\partial w^{\text{side}}}{\partial t}=f\left(v^{\text{side}},w^{\text{side}}\right),$$ (4.58)

$$\frac{\partial w^{\text{end}}}{\partial t}=f\left(v^{\text{end}},w^{\text{end}}\right),$$ (4.59)

in which κ = ℓg_GJ/σ_cyt is the ratio of gap-junctional and cytosolic conductances and $\sigma =\left(\frac{\kappa }{1+\kappa }\right){\sigma }_{\text{cyt}}$.

In simulations using this model, the cleft potential v_c is found to be significantly different from 0 only near action potential wavefronts, where the inward sodium current is activated. In the multiscale model, such locations within the tissue are precisely where we deploy the localized microscale model. Consequently, in the regions of the tissue where we employ the macroscale equations in the multiscale model, the full macroscale equations are extremely well approximated by treating the cleft space at the intercalated discs as grounded, which corresponds to limit R_c → 0. In this limit, v_c(x, t) = 0, and it becomes impossible to distinguish between the sides and ends of cells. Consequently, v(x, t) = v_i(x, t) is the voltage difference across the cell membrane and w(x) are the membrane state variables along both the sides and ends of cells. In addition, $I_{\text{ion}}^{\text{side}}=I_{\text{ion}}^{\text{end}}=I_{\text{ion}}(v(x,t),w(x,t))$. With these simplifications, equations (4.56)–(4.59) become

$$\frac{\ell A}{S\ell +2A}\sigma \frac{{\partial }^2{v}_{\text{i}}}{\partial x^2}=C_{\text{m}}\frac{\partial v}{\partial t}+I_{\text{ion}},$$ (4.60)

$$\frac{\partial w}{\partial t}=f(v,w).$$ (4.61)

Multiscale Model

The macroscale model equations are derived via a homogenization procedure that assumes that spatial variations in the voltages and membrane state variables vary slowly over the cellular length scale. This assumption generally holds away from action potential wavefronts, but it may be violated near action potential wavefronts. The multiscale model therefore deploys the microscale equations (4.49)–(4.55) in a localized fashion near action potential wavefronts. The simplified macroscale equations (4.60)–(4.61) are employed in the remainder of the tissue, where the macroscale model yields an excellent approximation to the dynamics of the underlying microscale model. Figure 4.6 provides a schematic depiction of the microscale domain, a particular multiscale representation of that domain, and a possible discretization of that multiscale representation.

Figure 4.6.

A. Schematic depiction of a detailed model of a linear strand of myocytes. B. Particular multiscale representation of the tissue domain shown in panel A. Here, dark lines indicate the “unresolved” region, where the macroscale equations are employed, and the thin broken lines indicate the “resolved” region, where the microscale equations are employed. C. Possible discretization of the multiscale representation shown in panel B. In the discretization depicted in this panel, the coarse macroscopic grid spacing Δx_macro is on the order of two cell lengths, whereas the fine microscopic grid spacing Δx_micro uses five grid points per cardiac cell. Figure from Hand and Griffith [29].

The microscale and macroscale equations can be coupled by requiring current and voltage to be continuous at interfaces in model resolution. The relevant currents can be either gap-junctional or intracellular currents. Here we present the case in which the macro- and microdomains are coupled via gap-junctional current. Let x* be an interface in model resolution, and assume that the unresolved region is to the left of x*, and that the resolved region is to the right. Let j* be the index of the myocyte immediately to the right of x*. In this case, equations (4.49)–(4.55) and (4.60)–(4.61) are supplemented by the boundary conditions:

$$-{\sigma \frac{\partial v_{\text{i}}}{\partial x}|}_{x=x^{*}}=g_{\text{GJ}}\left({v_{\text{i}}|}_{x=x^{*}}-{v_{\text{i},j^{*}}|}_{x=0}\right),$$ (4.62)

$${{\sigma }_{\text{cyt}}\frac{\partial v_{\text{i},j^{*}}}{\partial x}|}_{x=0}=C_{\text{m}}\frac{\partial v_{j^{*}}^{\text{left}}}{\partial t}+I_{\text{ion},j}^{\text{left}}+g_{\text{GJ}}\left({v_{\text{i},j^{*}}|}_{x=0}-{v_{\text{i}}|}_{x=x^{*}}\right).$$ (4.63)

Analogous coupling conditions would apply at other interfaces in model resolution. The conditions for the case that continuity of intracellular current is used to couple the microscale and macroscale equations are similar [30].

Comparisons of simulation results for the microscale, macroscale, and multiscale models are shown in Figures 4.7 and 4.8 for the nonephaptic version of the model, in which R_c = 0, and in Figures 4.9 and 4.10 for the ephaptic version of the model. In all cases, the macroscale model is shown to fail to reproduce the dynamics of the underlying microscale model for certain numerical or physical parameters. For instance, even without accounting for ephaptic conduction (i.e., with R_c = 0), the macroscale model is shown to be extremely sensitive to numerical discretization in the slow-conducting regime, as seen in Figures 4.7 and 4.8. By contrast, the multiscale model exactly reproduces the dynamics, including both the wave speed and the shape of the action potential wave, of the underlying microscale model. In addition, although not shown here, it does so in a manner that is robust to the numerical grid used to discretize the macroscale part of the domain [30].

Figure 4.7.

Conduction speed along different models of a linear strand of myocytes without ephaptic coupling (R_c = 0) as a function of the gap-junctional coupling strength g_GJ. The multiscale model reproduces the dynamics of the underlying microscale model across the entire range of values of g_GJ surveyed. In particular, notice that the multiscale model captures the level of gap-junctional coupling that yields propagation failure in the microscale model. By contrast, the macroscale model predicts substantially different values of g_GJ that lead to propagation failure for different numerical grid spacings. In particular, coarse macroscale grid spacings yield a model that predicts propagation failure at substantially higher levels of gap-junctional coupling than the micro- and multiscale models, and fine macroscopic grid spacings yield propagation success for substantially smaller values of g_GJ. It is interesting to note that if the macroscopic grid spacing is equal to the cell size (100 μm), then the macroscopic model is in perfect agreement with the micro- and multiscale models. Figure from Hand and Griffith [29].

Figure 4.8.

Action potential wavefront along different models of a linear strand of myocytes without ephaptic coupling (R_c = 0) at a gap-junctional coupling strength that is 1% of normal. The waveform predicted by the multiscale model is in excellent agreement with the microscale model, whereas the macroscale model with a coarse macroscopic grid spacing yields artificially slow action potential wavefronts, and this model with a fine macroscopic grid yields artificially fast action potentials. As seen in Figure 4.7, the macroscopic model results agree with those of the micro- and multiscale models if the macroscopic grid spacing is equal to the cell size (100 μm). Figure from Hand and Griffith [29].

Figure 4.9.

Conduction speed along different models of a linear strand of myocytes with ephaptic coupling as a function of the cleft-to-ground resistance R_c. In these simulations, gap-junctional coupling strength is 1% of normal. As in the non-ephaptic case, the micro- and multiscale models are in excellent agreement. Unlike the non-ephaptic case, however, here the macroscale model yields neither qualitative nor quantitative agreement for any macroscopic grid spacing over the range of values of R_c surveyed, except for high levels of R_c where all models yield propagation failure. In particular, the macroscale model does not reproduce the non-monotonic relationship between R_c and conduction speed observed with the micro- and multiscale models. Figure from Hand and Griffith [29].

Figure 4.10.

Action potential wavefront (top panel) and cleft potential (bottom panel) along different models of a linear strand of myocytes with ephaptic coupling as a function of the cleft-to-ground resistance R_c. In these simulations, gap-junctional coupling strength is 1% of normal. Again, excellent agreement is observed between the microscale and multiscale models. As shown in Figure 4.9, the macroscale model does not agree with the micro- or multiscale models for any macroscopic grid spacing considered. Notice that the multiscale model computes the cleft potential only within the fully resolved tissue subdomain. Figure from Hand and Griffith [29].

The difference between the macroscale and multiscale models is more pronounced in cases that include both conduction slowing and ephaptic conduction (i.e., in slow-conducting regimes with R_c ≠ 0). In these parameter regimes, the macroscale model is fundamentally unable to reproduce the dynamics of the microscale model, independent of the macroscale grid spacing. Again, the multiscale model exactly reproduces the wave shapes generated by the microscale model. Moreover, the multiscale model also captures the wave speeds of the multiscale model, including the nonlinear relationship between cleft width and conduction velocity, i.e., the so-called ephaptic effect.

Because nearly cell-scale resolution appears to be required when solving the macroscale equations even in fast-conducting regimes, we expect that the additional robustness of adaptive multiscale models will ultimately outweigh their modest increase in model complexity and will lead to the adoption of these or similar approaches in large-scale models of cardiac dynamics.

5. Electrodiffusion

In this section, we describe a framework for electrophysiological modeling that is based on the electrodiffusion of ions [78]. The difference between electrodiffusion and ordinary diffusion is that in electrodiffusion the diffusing particles do not move independently. Instead, they interact through the electric field which they themselves create.

An important complication in electrodiffusion is the phenomenon of electroneutrality with space charge layers near membranes. This is a consequence of a small parameter: the ratio of the Debye length (which roughly measures the range of the influence of one ion on another through an ionic solution) to any of the typical dimensions of the region of interest, which in our case would be a collection of biological cells. This small parameter makes it impractical to solve the equations of electrodiffusion directly, except possibly for very small systems [43].

This section is an expository introduction to the mathematical formulation of the electroneutral limit of the electrodiffusion equations, following closely the papers of Mori et al. [53, 55–57]. In this formulation, there is a subtle issue of well-posedness of the electroneutral limit, which we resolve here in a new and physically intuitive way.

Our framework is fundamentally three-dimensional. Unlike in the formulation of the bidomain equations, we do not homogenize, but instead model the microstructure of the cardiac or neural tissue as it actually exists. That is, we think of the tissue of interest as a region of three-dimensional space partitioned by membranes, on which we apply internal boundary conditions that reflect the properties of the ion channels that reside in these membranes. This framework therefore provides a significantly more detailed microscale model than that considered in the previous section.

5.1. The Equations of Electrodiffusion

Away from the membranes, we have the drift-diffusion equations, also known as the Poisson-Nernst-Planck system [7] or, in the semiconductor literature, as the van Roosbroeck equations [89]:

$$\frac{\partial c_i}{\partial t}+\nabla \cdot {\mathbf{f}}_i=0,$$ (5.1)

$${\mathbf{f}}_i=-D_i\left(\nabla c_i+\frac{q{z}_i}{k_{\text{B}}T}(\nabla \varphi )c_i\right),$$ (5.2)

$$-\mathrm{\Delta }\varphi =\frac{1}{{ϵ}_{\text{W}}}\left(\sum _{i=1}^{n}q{z}_i{c}_i+{\rho }_0(\mathbf{x})\right).$$ (5.3)

Here c_i (x, t) is the concentration and f_i (x, t) is the flux of the i^th species of ion, and ϕ(x, t) is the electrostatic potential. These are the 4n+1 unknown functions (since each of the f_i has three components) of our problem, where n is the number of ion species that we are considering. The given constants are the diffusion coefficient D_i and the charge number z_i of the i^th species of ion; the elementary charge q, which is the absolute value of the charge on an electron; Boltzmann’s constant k_B; the absolute temperature T; and the dielectric constant of water ϵ_w. The given function ρ₀(x) represents the density of any immobile background charge that may be present.

Equation (5.1) is simply the conservation law for the i^th species of ion. Equation (5.2) resolves the flux of the i^th species into two terms. The first term −D_i∇c_i is the diffusion term and expresses Fick’s law that the flux is proportional to minus the concentration gradient. The second term,

$$-\frac{D_i}{k_{\text{B}}T}q{z}_i(\nabla \varphi )c_i,$$ (5.4)

is the drift term, which is explained as follows: First, −∇ϕ is the electric field, and qz_i is the charge on each ion of the i^th species, so −qz_i (∇ϕ) is the force of the electric field on each individual ion of the i^th species. In a condensed medium, such as an aqueous solution, this force results in a drift velocity that is proportional to the force. The constant of proportionality is related (as shown by Einstein [16]) to the diffusion coefficient and in fact is given explicitly by D_i/(k_BT). Thus, the drift velocity of the i^th species of ion is

$$-\frac{D_i}{k_{\text{B}}T}q{z}_i(\nabla \varphi ).$$ (5.5)

Finally, this drift velocity is multiplied by the concentration c_i to get the contribution of drift to the flux as given by (5.4).

Equation (5.3) is simply the Maxwell equation ∇ · E = ρ/ϵ with an electric field E of the form −∇ϕ so that ∇ · E = −Δϕ, a dielectric constant ϵ equal to that of water ϵ_w, and a total charge density ρ that includes a contribution from each species of ion and also from any background charge that may be present.

Note that the above formulation completely neglects the effects of magnetic fields. In particular, the force on an ion is assumed to come from the electric field alone, and the electric field itself is assumed to be curl-free, which can only be true to the extent that there are no time-dependent magnetic fields in the region of interest.

(5.2). The Electroneutral Limit

Equations (5.1)–(5.3) can be made dimensionless in the following way. Let ℓ* be a typical length, t* a typical time, and c* a typical concentration. Also let

$${\varphi }^{*}=\frac{k_{\text{B}}T}{q}.$$ (5.6)

Then introduce the following dimensionless variables, constants, and operators, denoted by a bar above the usual symbol, and defined as follows:

$$\mathbf{x}={\ell }^{*}\overline{\mathbf{x}},$$ (5.7)

$$t=t^{*}\overline{t},$$ (5.8)

$$c_i=c^{*}{\overline{c}}_i,$$ (5.9)

$${\mathbf{f}}_i=\frac{c^{*}{\ell }^{*}}{t^{*}}{\overline{\mathbf{f}}}_i,$$ (5.10)

$$\varphi ={\varphi }^{*}\overline{\varphi }=\frac{k_{\text{B}}T}{q}\overline{\varphi },$$ (5.11)

$$D_i=\frac{{\left({\ell }^{*}\right)}^2}{t^{*}}{\overline{D}}_i,$$ (5.12)

$$\nabla =\frac{1}{{\ell }^{*}}\overline{\nabla },$$ (5.13)

$$\mathrm{\Delta }=\frac{1}{{\left({\mathcal{l}}^{*}\right)}^2}\overline{\mathrm{\Delta }},$$ (5.14)

$${\rho }_0=q{c}^{*}{\overline{\rho }}_0.$$ (5.15)

Equations (5.1)–(5.3) then become

$$\frac{\partial {\overline{c}}_i}{\partial \overline{t}}+\nabla \cdot {\overline{\mathbf{f}}}_i=0,$$ (5.16)

$${\overline{\mathbf{f}}}_i=-{\overline{D}}_i\left(\overline{\nabla }{\overline{c}}_i+z_i(\overline{\nabla }\overline{\varphi }){\overline{c}}_i\right),$$ (5.17)

$$-{\beta }^2\overline{\mathrm{\Delta }}\overline{\varphi }=\sum _{i=1}^n{z}_i{\overline{c}}_i+{\overline{\rho }}_0(\overline{x}),$$ (5.18)

in which

$$-{\beta }^2=\frac{k_{\text{B}}T{ϵ}_{\text{w}}}{{\left({\ell }^{*}\right)}^2{q}^2{c}^{*}}$$ (5.19)

so that

$$\beta =\frac{{\ell }_{\text{D}}}{{\ell }^{*}}$$ (5.20)

in which

$${\ell }_{\text{D}}=\sqrt{\frac{k_{\text{B}}T{ϵ}_{\text{W}}}{q^2{c}^{*}}}$$ (5.21)

is called the Debye length. The significance of the Debye length will become clear later, when we study the structure of the space charge layers that arise near membranes.

Typical values of the quantities that appear in the formula for ℓ_D are ϵ_w = 80 × 8.85 × 10⁻¹² C/(V m), k_BT/q = 0.025 V, q = 1.6 × 10⁻¹⁹ C, and c* = 0.12 M = 7.22 × 10²⁵/m³, with the result that ℓ_D = 1.2 × 10⁻⁹ m. This is actually 8 times smaller than the thickness of the cell membrane, so it is certainly very small in comparison to any cellular dimension ℓ* that may be of interest. The diameter of a red blood cell, for example, is about 10⁻⁵ m.

It follows from these quantitative considerations that β = ℓ_D/ℓ* is a small parameter of our problem. If we let β → 0 without any rescaling in (5.18), we get

$$\sum _{i=1}^n{z}_i{\overline{c}}_i+{\overline{\rho }}_0(\overline{\mathbf{x}})=0,$$ (5.22)

which is a statement of electroneutrality.

An important remark (that should be obvious) is that we cannot now substitute (5.22) back into (5.18) and conclude that $\overline{\mathrm{\Delta }}\overline{\varphi }=0$. Since (5.22) holds only to the extent that β is small, the correct conclusion is that $\overline{\mathrm{\Delta }}\overline{\varphi }$ cannot be determined from equation (5.18) in the limit β → 0. We shall now show, however, that a different elliptic equation for $\overline{\varphi }$ that holds in the limit β → 0 can indeed be derived from equations (5.16)–(5.17) by making use of equation (5.22). To do so, we proceed as follows:

In equations (5.16) and (5.17), multiply both sides of each equation by z_i and then sum over i. The resulting equations can be combined to yield the equation of charge conservation in the form

$$\frac{\partial \overline{\rho }}{\partial \overline{t}}+\overline{\nabla }\cdot \overline{\mathbf{J}}=0$$ (5.23)

where

$$\overline{\rho }(\overline{\mathbf{x}},\overline{t})=\sum _{i=1}^n{z}_i{\overline{c}}_i(\overline{\mathbf{x}},\overline{t})+{\overline{\rho }}_0(\overline{\mathbf{x}}),$$ (5.24)

$$\begin{gathered} \overline{\mathbf{J}}(\overline{\mathbf{x}},\overline{t})=\sum _{i=1}^n{z}_i{\overline{\mathbf{f}}}_i(\overline{\mathbf{x}},\overline{t}), \\ =-\sum _{i=1}^n{z}_i{\overline{D}}_i\left(\overline{\nabla }{\overline{c}}_i+(\overline{\nabla }\overline{\varphi }){\overline{c}}_i\right) \\ =-\overline{\nabla }\left(\sum _{i=1}^n{z}_i{\overline{D}}_i{\overline{c}}_i\right)-\left(\sum _{i=1}^n{\overline{D}}_i{z}_i^2{\overline{c}}_i\right)\overline{\nabla }\overline{\varphi }. \end{gathered}$$ (5.25)

Here $\overline{\rho }(\overline{\mathbf{x}},\overline{t})$ is the (dimensionless) net charge density. (Note that equation (5.23) is correct with or without the inclusion of the term ${\rho }_0(\overline{\mathbf{x}})$ in the definition of $\overline{\rho }(\overline{\mathbf{x}},\overline{t})$, since ${\overline{\rho }}_0(\overline{\mathbf{x}})$ is independent of $\overline{t}$.) Equation (5.25) gives the total dimensionless current density $\overline{\mathbf{J}}$, including drift and diffusion of all mobile ions.

In the electroneutral limit, β → 0, we have $\overline{\rho }=0$ and therefore $\overline{\nabla }\cdot \overline{\mathbf{J}}=0$. This gives the promised elliptic equation for $\overline{\varphi }$:

$$-\overline{\nabla }\cdot \left(\left(\sum _{i=1}^n{\overline{D}}_i{z}_i^2{\overline{c}}_i\right)\overline{\nabla }\overline{\varphi }\right)=\overline{\mathrm{\Delta }}\left(\sum _{i=1}^n{z}_i{\overline{D}}_i{\overline{c}}_i\right).$$ (5.26)

In the original (dimensional) variables, (5.26) reads:

$$-\nabla \cdot \left(\left(\sum _{i=1}^n{D}_i\frac{{\left(q{z}_i\right)}^2{c}_i}{k_{\text{B}}T}\right)\nabla \varphi \right)=\mathrm{\Delta }\left(\sum _{i=1}^{n}q{z}_i{D}_i{c}_i\right).$$ (5.27)

This is the equation that ϕ must satisfy in order to maintain electroneutrality. Even though, as mentioned above, Δϕ is in general nonzero in the electroneutral limit, equation (5.27) does reduce to Δϕ = 0 in the special case that all of the ion concentrations are spatially uniform.

Within a Debye length of a membrane surface, electroneutrality is substantially violated, and a space charge layer forms. One can analyze this phenomenon by rescaling the distance variable normal to the membrane before taking the limit β → 0. To simplify the presentation of this analysis, we consider only the special case in which the membrane lies in the plane x = 0 and in which all quantities are independent of y and z. The results we derive in this way actually hold more generally, as we discuss briefly later. In this special case, equations (5.16)–(5.18) reduce to

$$\frac{\partial {\overline{c}}_i}{\partial \overline{t}}+\frac{\partial {\overline{f}}_i}{\partial \overline{x}}=0,$$ (5.28)

$${\overline{f}}_i=-{\overline{D}}_i\left(\frac{\partial {\overline{c}}_i}{\partial \overline{x}}+z_i\frac{\partial \overline{\varphi }}{\partial \overline{x}}{\overline{c}}_i\right),$$ (5.29)

$$-{\beta }^2\frac{{\partial }^2\overline{\varphi }}{\partial {\overline{x}}^2}=\sum _{i=1}^n{z}_i{\overline{c}}_i+{\overline{\rho }}_0(\overline{x}),$$ (5.30)

in which $\overline{x}$ and ${\overline{f}}_i$ are now scalars, since our analysis is one-dimensional.

Now make the change of variables

$$\overline{x}=\beta \overline{\overline{x}},$$ (5.31)

$$\overline{t}=\beta \overline{\overline{t}},$$ (5.32)

$${\overline{\overline{c}}}_i(\overline{\overline{x}},\overline{\overline{t}})={\overline{c}}_i(\beta \overline{\overline{x}},\beta \overline{\overline{t}}),$$ (5.33)

$${\overline{\overline{f}}}_i(\overline{\overline{x}},\overline{\overline{t}})={\overline{f}}_i(\beta \overline{\overline{x}},\beta \overline{\overline{t}}),$$ (5.34)

$$\overline{\overline{\varphi }}(\overline{\overline{x}},\overline{\overline{t}})=\overline{\varphi }(\beta \overline{\overline{x}},\beta \overline{\overline{t}}),$$ (5.35)

so that our equations become

$$\frac{\partial {\overline{\overline{c}}}_i}{\partial \overline{\overline{t}}}+\frac{\partial {\overline{\overline{f}}}_i}{\partial \overline{\overline{x}}}=0,$$ (5.36)

$$\beta {\overline{\overline{f}}}_i=-{\overline{D}}_i\left(\frac{\partial {\overline{\overline{c}}}_i}{\partial \overline{\overline{x}}}+z_i\frac{\partial \overline{\overline{\varphi }}}{\partial \overline{\overline{x}}}{\overline{\overline{c}}}_i\right),$$ (5.37)

$$-\frac{{\partial }^2\overline{\overline{\varphi }}}{\partial {\overline{\overline{x}}}^2}=\sum _{i=1}^n{z}_i{\overline{\overline{c}}}_i+{\overline{\rho }}_0(\beta \overline{\overline{x}}).$$ (5.38)

Now letting β → 0, equations (5.37)–(5.38) become

$$0=\frac{\partial {\overline{\overline{c}}}_i}{\partial \overline{\overline{x}}}+z_i\frac{\partial \overline{\overline{\varphi }}}{\partial \overline{\overline{x}}}{\overline{\overline{c}}}_i,$$ (5.39)

$$-\frac{{\partial }^2\overline{\overline{\varphi }}}{\partial {\overline{\overline{x}}}^2}=\sum _{i=1}^n{z}_i{\overline{\overline{c}}}_i+{\overline{\rho }}_0(0).$$ (5.40)

Note that (5.39) is the same equation that would hold in the absence of any fluxes, that is, at thermodynamic equilibrium. Thus, to lowest order in β, the ionic concentrations near the membrane adjust themselves to the electrostatic potential as if they were at equilibrium, even in the presence of nonzero fluxes.

Equations (5.39)–(5.40) are the one-dimensional Poisson-Boltzmann equations for the structure of the space charge layer. Even though we derived these equations in a very special case (membrane in the plane x = 0 and all quantities independent of y and z), they are correct to lowest order in β even when these assumptions are violated, with the reinterpretation that x measures distance normal to the membrane provided that the principal curvatures of the membrane are O(1), and that the derivatives of all quantities in directions parallel to the membrane (i.e., with x constant) are also O(1).

In the original dimensional variables, equations (5.39)–(5.40) read as follows:

$$0=\frac{\partial c_i}{\partial x}+\frac{q{z}_i{c}_i}{k_{\text{B}}T}\frac{\partial \varphi }{\partial x},$$ (5.41)

$$-\frac{{\partial }^2\varphi }{\partial x^2}=\frac{1}{{ϵ}_{\text{w}}}\left(\sum _{i=1}^{n}q{z}_i{c}_i+{\rho }_0\right).$$ (5.42)

Here x measures distance normal to the cell membrane, with x = 0 at the face of the membrane and x = ∞ in the bulk solution. Note that ρ₀ in (5.42) is independent of x.

Equation (5.41) is easily solved for c_i(x) in terms of ϕ(x):

$$c_i(x)=c_i^{\infty }\exp \left(-\frac{q{z}_i(\varphi (x)-\varphi (\infty ))}{k_{\text{B}}T}\right)$$ (5.43)

in which $c_i^{\infty }$ denotes the concentration of the i^th species of ion at x = ∞. As usual in lowest-order boundary layer theory, this is set equal to the value of c_i in the bulk solution at the membrane itself, or to put it more physically, by the value of c_i just outside the space charge layer. (Note that the thickness of the space charge layer approaches 0 in the limit under consideration here.) The quantities $c_i^{\infty }$ satisfy electroneutrality:

$$\sum _{i=1}^{n}q{z}_i{c}_i^{\infty }+{\rho }_0=0.$$ (5.44)

If

$$\left|\frac{q{z}_i(\varphi (x)-\varphi (\infty ))}{k_{\text{B}}T}\right|\ll 1,$$ (5.45)

which we now assume, then (5.43) can be approximated by

$$c_i(x)=c_i^{\infty }\left(1-\frac{q{z}_i(\varphi (x)-\varphi (\infty ))}{k_{\text{B}}T}\right).$$ (5.46)

Substituting (5.46) into (5.45) and making use of (5.44) gives

$$-\frac{{\partial }^2\varphi }{\partial x^2}=\frac{1}{{ϵ}_{\text{W}}}\sum _{i=1}^n-\frac{{\left(q{z}_i\right)}^2{c}_i^{\infty }}{k_{\text{B}}T}(\varphi (x)-\varphi (\infty ))$$ (5.47)

or

$$\frac{{\partial }^2\varphi }{\partial x^2}=\frac{1}{{\ell }_{\text{D}}^2}(\varphi (x)-\varphi (\infty ))$$ (5.48)

where ℓ_D is given by

$${\ell }_{\text{D}}=\sqrt{\frac{k_{\text{B}}T{ϵ}_w}{{\sum }_{i=1}^n{\left(q{z}_i\right)}^2{c}_i^{\infty }}}.$$ (5.49)

Comparison of this with (5.21) gives an explicit formula for the “typical concentration” c*, namely

$$c^{*}=\sum _{i=1}^n{z}_i^2{c}_i^{\infty }.$$ (5.50)

Note that in this formula for c*, the bulk concentration of each ion species is weighted by the square of its charge number.

The solutions of (5.48) that are bounded as x → ∞ are of the form

$$\varphi (x)-\varphi (\infty )=(\varphi (0)-\varphi (\infty ))\exp \left(-\frac{x}{{\ell }_{\text{D}}}\right).$$ (5.51)

The determination of ϕ(0) will be discussed below. Substituting (5.51) into (5.46), we get a formula for the profile of the i^th species of ion within the space charge layer:

$$c_i(x)=c_i^{\infty }\left(1-\frac{q{z}_i(\varphi (0)-\varphi (\infty ))}{k_{\text{B}}T}\exp \left(-\frac{x}{{\ell }_{\text{D}}}\right)\right).$$ (5.52)

The significance of the Debye length ℓ_D as a space constant for the decay of disturbances is now clear.

The charge density within the space charge layer is given by

$$\begin{gathered} \rho (x)=\sum _{i=1}^{n}q{z}_i{c}_i(x)+{\rho }_0 \\ =-\frac{\varphi (0)-\varphi (\infty )}{k_{\text{B}}T}\sum _{i=1}^n{\left(q{z}_i\right)}^2{c}_i^{\infty }\exp \left(-\frac{x}{{\ell }_{\text{D}}}\right). \end{gathered}$$ (5.53)

Here, we have made use of the electroneutrality of the bulk solution to eliminate the terms ${\sum }_{i=1}^{n}q{z}_i{c}_i^{\infty }+{\rho }_0$.

The total charge per unit area in the space charge layer, denoted σ, can now be found as follows:

$$\begin{gathered} \sigma ={\int }_0^{\infty }\rho (x)dx \\ =-\frac{\varphi (0)-\varphi (\infty )}{k_{\text{B}}T}\left(\sum _{i=1}^n{\left(q{z}_i\right)}^2{c}_i^{\infty }\right){\ell }_{\text{D}}, \end{gathered}$$ (5.54)

and this result can be simplified by making use of equation (5.49) to obtain

$$\sigma =-(\varphi (0)-\varphi (\infty ))\frac{{ϵ}_w}{{\ell }_{\text{D}}}.$$ (5.55)

To find ϕ(0), we have to consider the membrane itself, as well as the space charge layer on the other side of the membrane, and also the composition of the bulk solution with which that space charge layer makes contact. Accordingly, we expand our point of view to encompass the domain (−∞, ∞), and we assume that the subdomain (−d_m, 0) is occupied by membrane, which we model as an insulator, with dielectric constant ϵ_m. We use the symbol “+” to denote quantities defined on the side of the membrane where x is positive, and “−” to denote the side of the membrane where x is negative. Thus (5.55) becomes

$${\sigma }^{+}=-(\varphi (0)-\varphi (\infty ))\frac{{ϵ}_w}{{\ell }_{\text{D}}^{+}},$$ (5.56)

and we similarly have

$${\sigma }^{-}=+\left(\varphi \left(-d_{\text{m}}\right)-\varphi (-\infty )\right)\frac{{ϵ}_{\text{w}}}{{\ell }_{\text{D}}^{-}}.$$ (5.57)

Within the membrane itself, the electric field is constant, and is given by

$$E_{\text{m}}=\frac{\varphi \left(-d_{\text{m}}\right)-\varphi (0)}{d_{\text{m}}}.$$ (5.58)

Immediately adjacent to the membrane on its “+” face we have, from equation (5.51),

$$E\left(0^{+}\right)=-\frac{\partial \varphi }{\partial x}\left(0^{+}\right)=\frac{\varphi (0)-\varphi (\infty )}{{\ell }_{\text{D}}^{+}}$$ (5.59)

and similarly, on the “−” face of the membrane

$$E\left(d_{\text{m}}^{-}\right)=-\frac{\varphi \left(-d_{\text{m}}\right)-\varphi (-\infty )}{{\ell }_{\text{D}}^{-}}.$$ (5.60)

The reason for the minus sign in (5.60) is that the electric field is considered positive if it points in the direction of increasing x, which is out of the membrane at x = 0 but into the membrane at x = −d_m.

We now invoke the boundary condition from electrostatics of material media that ϵE is continuous across each face of the membrane. This gives the pair of equations

$${ϵ}_{\text{w}}E\left(d_{\text{m}}^{-}\right)={ϵ}_{\text{m}}{E}_{\text{m}}={ϵ}_{\text{w}}E\left(0^{+}\right)$$ (5.61)

or

$$\frac{{ϵ}_{\text{w}}}{{\ell }_{\text{D}}^{-}}\left(\varphi (-\infty )-\varphi \left(-d_{\text{m}}\right)\right)=\frac{{ϵ}_{\text{m}}}{d_{\text{m}}}\left(\varphi \left(-d_{\text{m}}\right)-\varphi (0)\right)=\frac{{ϵ}_{\text{w}}}{{\ell }_{\text{D}}^{+}}(\varphi (0)-\varphi (\infty )).$$ (5.62)

We can think of (5.62) as a pair of linear equations in the two unknowns ϕ(−∞) − ϕ(−d_m) and ϕ(0) − ϕ(∞). The solution to this pair of linear equations is

$$\varphi (-\infty )-\varphi \left(-d_{\text{m}}\right)=\frac{\left({\ell }_{\text{D}}^{-}/{ϵ}_{\text{w}}\right)(\varphi (-\infty )-\varphi (\infty ))}{{\ell }_{\text{D}}^{-}/{ϵ}_{\text{w}}+d_{\text{m}}/{ϵ}_{\text{m}}+{\ell }_{\text{D}}^{+}/{ϵ}_{\text{w}}},$$ (5.63)

$$\varphi (0)-\varphi (\infty )=\frac{\left({\ell }_{\text{D}}^{+}/{ϵ}_{\text{w}}\right)(\varphi (-\infty )-\varphi (\infty ))}{{\ell }_{\text{D}}^{-}/{ϵ}_{\text{w}}+d_{\text{m}}/{ϵ}_{\text{m}}+{\ell }_{\text{D}}^{+}/{ϵ}_{\text{w}}}.$$ (5.64)

Now substituting (5.64) into (5.56) and (5.63) into (5.57), we see that

$$-{\sigma }^{-}={\sigma }^{+}=C_{\text{m}}(\varphi (-\infty )-\varphi (\infty )),$$ (5.65)

in which ϕ(−∞) − ϕ(∞) is the potential difference across the complex formed by the membrane together with its space charge layers, and in which the effective membrane capacitance per unit area, denoted C_m, is therefore given by

$$\frac{1}{C_{\text{m}}}=\frac{{\ell }_{\text{D}}^{-}}{{ϵ}_{\text{w}}}+\frac{d_{\text{m}}}{{ϵ}_{\text{m}}}+\frac{{\ell }_{\text{D}}^{+}}{{ϵ}_{\text{w}}}.$$ (5.66)

Note that the value of C_m as given by (5.66) is precisely the capacitance per unit area of a three-layer structure made up of a slab of material with dielectric constant ϵ_w and thickness ${\ell }_{\text{D}}^{-}$, another slab with dielectric constant ϵ_m and thickness d_m, and finally a third slab with dielectric constant ϵ_w and thickness ${\ell }_{\text{D}}^{+}$. Because ${\ell }_{\text{D}}^{-}$ and ${\ell }_{\text{D}}^{+}$ are considerably smaller than d_m, and also because ϵ_w/ϵ_m is about 40, the term d_m/ϵ_m dominates the right-hand side of (5.66), and the effective membrane capacitance is only slightly smaller than the capacitance of the bare membrane. For precisely these same reasons, the effective membrane capacitance is insensitive to the ionic concentrations on the two sides of the membrane (which appear in (5.66) through ${\ell }_{\text{D}}^{\pm }$). For practical purposes, then, C_m is a constant. This constant happens to be approximately equal to 1 μF/cm² for all biological cell membranes.

To formulate boundary conditions for the electroneutral equations that hold outside of the space charge layers, we need to consider not only the total amount of charge that is stored in the space charge layers but also the amount of each ion that is stored there. The key to this is equation (5.52), which describes the concentration profile of each ion.

From (5.52), with the help of (5.55) and (5.49), we derive

$$\begin{gathered} {\int }_0^{\infty }\left(c_i(x)-c_i^{\infty }\right)dx=-\frac{q{z}_i{c}_i^{\infty }}{k_{\text{B}}T}{\ell }_{\text{D}}(\varphi (0)-\varphi (\infty )) \\ =q{z}_i{c}_i^{\infty }{\ell }_{\text{D}}^2{k}_{\text{B}}T{ϵ}_w \\ =\frac{q{z}_i{c}_i^{\infty }}{{\sum }_{j=1}^n{\left(q{z}_j\right)}^2{c}_j^{\infty }}\sigma . \end{gathered}$$ (5.67)

Multiplying both sides of the foregoing equation by qz_i, we get

$${\sigma }_i={\theta }_i\sigma$$ (5.68)

in which

$${\sigma }_i=q{z}_i{\int }_0^{\infty }\left(c_i(x)-c_i^{\infty }\right)dx,$$ (5.69)

$${\theta }_i=\frac{z_i^2{c}_i^{\infty }}{{\sum }_{j=1}^n{z}_j^2{c}_j^{\infty }}.$$ (5.70)

Equations (5.67)–(5.70) show that the contribution σ_i of the i^th species of ion to the surface charge density σ of a space charge layer is proportional to the nearby bulk concentration $c_i^{\infty }$ of that ion species weighted by the square of its charge number z_i. Thus, positive and negative ions both make contributions of the same sign to any particular space charge layer, that sign being the same as that of the total space charge density σ. The reason for this somewhat surprising fact is that a space charge layer with σ > 0, for example, contains an excess of each positive ion (in comparison to its bulk concentration) and a deficit of each negative ion, both of which contribute positively to the overall positive charge of the layer, and similarly (with positive and negative interchanged) for a space charge layer with σ < 0.

5.3. An Issue of Ill-Posedness and Its Resolution

The reason that we can subtract $c_i^{\infty }$ in the definition of σ_i, equation (5.69), is that the bulk solution is electrically neutral; see equation (5.44). Thus, in the computation of excess charge, we can safely ignore the contributions of the bulk ion concentrations and consider only the deviations $c_i(x)-c_i^{\infty }$. This is no longer true when we consider the amount of each species of ion in the space charge layer. Here the bulk ion concentration makes a contribution, which unfortunately is infinite if we calculate it as ${\int }_0^{\infty }{c}_i^{\infty }dx$.

We circumvent the above difficulty by making the following definition of the surface concentration of the i^th species of ion in the space charge layer:

$$b_i=c_i^{\infty }{\ell }_0+\frac{{\sigma }_i}{q{z}_i}.$$ (5.71)

This definition includes all of the ions that account for the excess charge, σ_i, as defined above in equation (5.69), and also, in addition to those, the number of ions of species i per unit area that would occupy a layer of thickness ℓ₀ at concentration $c_i^{\infty }$.

The constant ℓ₀ is chosen to be greater than any of the Debye lengths that occur in our problem, and yet smaller than any of the lengths that we want to resolve. The existence of such an ℓ₀ is required for the validity of the electroneutral limit. If we want to resolve distances on the scale of the Debye length, then we should be using the original Poisson-Nernst-Planck system, equations (5.1)–(5.3), instead of the electroneutral model. A suitable choice of ℓ₀ for cellular physiology would be 10 nm, which is approximately equal to the membrane thickness, and about 8 times greater than a typical Debye length. Of course, one should check that the results of any computation are insensitive to ℓ₀ within the range defined by the above criteria.

Omission of the term $c_i^{\infty }{\ell }_0$ in the above definition leads to an ill-posed formulation of the boundary value problem for the electroneutral limit [53]. The reason for this is that σ_i, having the same sign as σ, always has opposite signs on the two sides of any membrane. On one side or the other, then, the sign of σ_i differs from that of z_i. On that side of the membrane σ_i/(qz_i) < 0, and this means that an increase in the bulk concentration $c_i^{\infty }$ on that side of the membrane leads to a decrease in σ_i/(qz_i), that is, to a decrease in the amount of the i^th species of ion that is stored in the space charge layer. This requires a flux out of the space charge layer and into the bulk, and the effect of this flux is to reinforce the increase in bulk concentration. This positive feedback mechanism is the root of the ill-posedness.

Inclusion of the term $c_i^{\infty }{\ell }_0$ in (5.71) overcomes this difficulty. In the situation we are considering here, in which (5.45) holds and the linearized space charge layer equations are therefore valid, the term $c_i^{\infty }{\ell }_0$ is always greater in magnitude than σ_i/(qz_i), with the result that an increase in the bulk concentration of any ion on either side of the membrane leads to an increase in the amount of that ion in the adjacent space charge layer. For analysis that supports this qualitative discussion, see Stinchcombe, Mori, and Peskin [83]. An alternative but somewhat less intuitive way of making the electroneutral model well-posed has been described by Mori [53].

A further remark of importance in relation to equation (5.71) is that the term $c_i^{\infty }{\ell }_0$ is automatically included in a seamless way when a finite-volume scheme is used to discretize the equations of the electroneutral limit, as has been done by Mori and Peskin [57]. To explain this, we consider a computational cell of volume V with part of the surface of this cell being along a membrane and having area A. (The rest of the surface of the computational cell is simply adjacent to other computational cells, with no physical barrier, and hence no space charge layer along these nonmembrane boundaries.) Now let X_i be the number of ions of type i within the computational cell, including both those in the bulk solution and also those in the space charge layer adjacent to the membrane. Then

$$\begin{gathered} X_i=A{b}_i+\left(V-{\ell }_{0}A\right)c_i^{\infty } \\ =A{c}_i^{\infty }{\ell }_0+\frac{A{\sigma }_i}{q{z}_i}+V{c}_i^{\infty }-A{c}_i^{\infty }{\ell }_0 \\ =\frac{A{\sigma }_i}{q{z}_i}+V{c}_i^{\infty }. \end{gathered}$$ (5.72)

Here we have assigned a volume ℓ₀A to the space charge layer, and a volume V − ℓ₀A to the bulk solution within the computational cell. This may seem somewhat arbitrary, but the arbitrariness disappears in the end because of the cancellation of the terms involving ℓ₀. If the computational cell is large enough to contain the space charge layer (when we think of the space charge layer as having thickness ℓ₀), then the term $V{c}_i^{\infty }$ dominates the right-hand side of (5.72), and there is no dependence at all of the discretized equations on the parameter ℓ₀.

5.4. Internal Boundary Conditions in the Electroneutral Limit

We are now ready to state the internal boundary conditions that hold across membranes in the electroneutral limit. Consider in particular a membrane that separates region k from region l. We use superscripts to denote the boundary values within the bulk solution, i.e., just outside the space charge layers. Thus ϕ^k is the potential on side k, and ϕ^l is the potential on side l of the membrane, and similarly for $c_i^k$ and $c_i^l$. We use bulk values rather than values at the surface of the bare membrane because the bulk values are measurable, and the transmembrane fluxes are empirically determined functions of these measurable quantities. We use the following notation for these transmembrane fluxes. Let

$$f_i^{kl}\left({\varphi }^k-{\varphi }^l,c^k,c^l,w^{kl},w^{lk},\mathbf{x}\right)$$ (5.73)

be the flux (number of ions per unit area per unit time) across membrane (k, l), in the vicinity of the point x on this membrane, with flux in the direction k → l considered positive. Note that we allow the flux of the i^th species of ion to depend on the entire vector of solute concentrations on the two sides of the membrane, c^k and c^l. This allows for cotransport or antitransport of ions, and also for ion-gated or neurotransmitter-gated channels (the neurotransmitter being included as one of the species whose concentrations are contained in the vector c). For further discussion of the transmembrane fluxes, including discussion of the gating variables w (and why we need two sets of those gating variables, one for kl and one for lk); see Section 5.5,

The conservation of the i^th species of ion requires that, on face k of the membrane kl, at location x,

$$\frac{\partial b_i^k}{\partial t}={\mathbf{f}}_i^k(\mathbf{x},t)\cdot {\mathbf{n}}^{kl}(\mathbf{x})-f_i^{kl}\left({\varphi }^k-{\varphi }^l,c^k,c^l,w^{kl},w^{lk},\mathbf{x}\right)$$ (5.74)

with (see equation (5.71))

$$b_i(\mathbf{x},t)=c_i^k(\mathbf{x},t){\ell }_0+\frac{{\sigma }_i^k(\mathbf{x},t)}{q{z}_i}.$$ (5.75)

The notation here is that $c_i^k(\mathbf{x},t)$ denotes the concentration of the i^th species of ion in the bulk solution, just outside the space charge layer, on side k of the membrane, near membrane location x at time t. In equation (5.74), n^kl (x) is the unit normal to the membrane at location x pointing from side k to side l of the membrane, and ${\mathbf{f}}_i^k$ is given by equation (5.2) with the remark that the quantities that appear on the right-hand side of (5.2) are to be evaluated in the bulk solution, just outside the space charge layer, on side k of the membrane, near membrane point x. Finally, $f_i^{kl}$ is the transmembrane flux defined above and further discussed in the appendix.

We can derive an electrical boundary condition from equations (5.74)–(5.75) by multiplying both sides of each of these equations by qz_i, summing over i, and then adding ${\rho }_0^k{\ell }_0$. With these manipulations, equation (5.75) gives

$$\sum _{i=1}^{n}q{z}_i{b}_i^k(\mathbf{x},t)+{\rho }_0^k{\ell }_0=\sum _{i=1}^n{\sigma }_i^k(\mathbf{x},t)={\sigma }^k(\mathbf{x},t),$$ (5.76)

in which we have made use of the electroneutrality of the bulk solution, which tells us that ${\sum }_{i=1}^{n}q{z}_i{c}_i^k+{\rho }_0^k=0$. With the help of (5.76), since ${\rho }_0^k$ and ℓ₀ are independent of time, we see that (5.74) implies

$$\frac{\partial {\sigma }^k}{\partial t}={\mathbf{J}}^k(\mathbf{x},t)\cdot {\mathbf{n}}^{kl}-J^{kl}\left({\varphi }^k-{\varphi }^l,c^k,c^l,w^{kl},w^{lk},\mathbf{x}\right),$$ (5.77)

in which

$${\mathbf{J}}^k(\mathbf{x},t)=\sum _{i=1}^{n}q{z}_i{\mathbf{f}}_i^k(\mathbf{x},t)$$ (5.78)

and

$$J^{kl}\left({\varphi }^k-{\varphi }^l,c^k,c^l,w^{kl},w^{lk},\mathbf{x}\right)=q{z}_i{f}_i^{kl}\left({\varphi }^k-{\varphi }^l,c^k,c^l,w^{kl},w^{lk},\mathbf{x}\right).$$ (5.79)

Thus, J^k(x, t) is the current density in the bulk solution, just outside the space charge layer, on side k of the membrane, near the membrane point x at time t, and J^kl(x, t) is the current density through the membrane itself at location x at time t.

Now (5.77) becomes an evolution equation for the voltage difference across the membrane when we recall that σ^k = C_m(ϕ^k − ϕ^l). If we introduce the notation

$${\varphi }^{kl}={\varphi }^k-{\varphi }^l$$ (5.80)

and recall the approximation that the membrane capacitance per unit area, C_m, is constant, then

$$\begin{gathered} C_{\text{m}}\frac{\partial {\varphi }^{kl}}{\partial t}(\mathbf{x},t)={\mathbf{J}}^k(\mathbf{x},t)\cdot {\mathbf{n}}^{kl}(\mathbf{x})-J^{kl}({\varphi }^{kl}(\mathbf{x},t),c^k(\mathbf{x},t),c^l(\mathbf{x},t), \\ {w}^{kl}(\mathbf{x},t),w^{lk}(\mathbf{x},t),\mathbf{x}). \end{gathered}$$ (5.81)

Returning now to equation (5.75) and recalling equation (5.64), we see that the amount of the i^th species of ion per unit area in the space charge layer on face k of the membrane is given by

$$b_i^k(\mathbf{x},t)=c_i^k(\mathbf{x},t){\ell }_0+\frac{z_i^2{c}_i^k(\mathbf{x},t)}{{\sum }_{j=1}^n{z}_j^2{c}_j(\mathbf{x},t)}\frac{C_{\text{m}}{\varphi }^{kl}}{q{z}_i}.$$ (5.82)

Note that equation (5.82) gives the ionic content of the space charge layer in terms of nearby bulk quantities only.

We can now summarize the electroneutral model. The state variables of the model are the bulk concentrations c_i, the transmembrane potential differences ϕ^kl, and the gating variables w^kl. The model will be fully specified when we say how to determine the rate of change of the state variables in terms of the values of the state variables at any given time.

The evolution equation for the gating variables is given in the Appendix; see equations (5.88)–(5.89). The evolution equations for the concentrations c_i and for the transmembrane potential differences ϕ^kl both involve the potential field ϕ(x, t), so we discuss now how this field is determined from the state variables at any given time. This is done by solving the elliptic equation (5.27), which we rewrite here in the following way:

$$\nabla \cdot (A(\mathbf{x},t)\nabla \varphi +\nabla B(\mathbf{x},t))=0,$$ (5.83)

in which

$$A(\mathbf{x},t)=\sum _{i=1}^n{D}_i\frac{{\left(q{z}_i\right)}^2{c}_i(\mathbf{x},t)}{k_{\text{B}}T}>0,$$ (5.84)

$$B(\mathbf{x},t)=\sum _{i=1}^{n}q{z}_i{D}_i{c}_i(\mathbf{x},t).$$ (5.85)

Note that A(x, t) and B(x, t) are determined by the c_i(x, t). Thus, they are known functions of x at a given time t if the state of the system (as defined above) is known at that time.

The boundary conditions for equation (5.83) are that the jump in ϕ is known across each membrane (since ϕ^kl is part of the specification of the state of the system), and also that

$${\mathbf{n}}^{kl}\cdot \left({(A(\mathbf{x},t)\nabla \varphi +\nabla B(\mathbf{x},t))}^k-{(A(\mathbf{x},t)\nabla \varphi +\nabla B(\mathbf{x},t))}^l\right)=0.$$ (5.86)

Equation (5.86) asserts that the normal component of the bulk current density is the same on the two sides of any membrane at any membrane location. This follows from conservation of charge, since we have seen above that in the electroneutral limit the space charge layers on the two sides of the membrane have surface charge densities that are equal in magnitude but opposite in sign. Thus there is no net charge stored on any membrane, so the current density onto one face has to equal the current density off of the other one. A more formal way to derive (5.86) is to start from equation (5.81), interchange k and l, and add the result to equation (5.81), taking into account such symmetries as ϕ^kl = −ϕ^lk. The result of these manipulations is n^kl · (J^k − J^l) = 0, which is equivalent to (5.86).

In summary, at any given time t, ϕ(·, t) is determined by solving (5.83) subject to the given values of ϕ^kl and also subject to the jump condition (5.86) at each internal membrane.

With ϕ known at a given time, ∂c_i/∂t is determined by equations (5.1)–(5.2). These equations need boundary conditions, however, which we obtain from equations (5.74)–(5.75) and write as follows:

$$\begin{gathered} {\mathbf{f}}_i^k\cdot {\mathbf{n}}^{kl}=f_i^{kl}\left({\varphi }^{kl},c^k,c^l,w^{kl},w^{lk},\mathbf{x}\right)+\frac{\partial }{\partial t}\left(c_i^k{\ell }_0+\frac{{\sigma }_i^k}{q{z}_i}\right) \\ =f_i^{kl}\left({\varphi }^{kl},c^k,c^l,w^{kl},w^{lk},\mathbf{x}\right)+\frac{\partial }{\partial t}\left(c_i^k{\ell }_0+\frac{z_i^2{c}_i^k}{{\sum }_{j=1}^n{z}_j^2{c}_j^k}\frac{C_{\text{m}}{\varphi }^{kl}}{q{z}_i}\right). \end{gathered}$$ (5.87)

As discussed above (see equation (5.72) and the surrounding text), the term involving ℓ₀ is needed to make the electroneutral model well-posed, but the parameter ℓ₀ actually cancels out and disappears in a finite-volume discretization of the electroneutral model provided that the computational elements are not too small.

For an application of the electroneutral model of electrodiffusion to cardiac conduction with reduced gap junctional connectivity, see the work of Mori, Fishman, and Peskin [55]. Note in particular that this investigation considers not only voltage changes in the narrow cleft between the ends of cardiac myocytes, but also the concentration changes that may occur there as a result of transmembrane currents, which can cause significant concentration changes when such currents flow into or out of a restricted (in this case, extracellular) space. In this work, the geometry of the cleft was very much simplified, and it would be interesting to see how the results would change if more realistic microscopic anatomy were used. More generally, it would be of great interest to study the influence on electrophysiology of the detailed architecture of electrically active cells, including the spatial arrangement of their organelles.

We expect that future investigations involving the electroneutral model will similarly focus on subcellular phenomena in which ion transport is important and in which the microscopic anatomy provides enough resistance to current flow that significant voltage differences can occur without crossing a membrane, or provides partially restricted spaces in which significant ion concentration changes can build up over time as a result of electrical activity. Considering the intricate extracellular and intracellular microanatomy of real tissues, we believe that the scope for such investigations is vast.

5.5. Transmembrane Fluxes

In this subsection, we discuss in more detail the functions $f_i^{kl}$ that describe the transmembrane flux of the i^th species of ion. The arguments w^kl and w^lk of $f_i^{kl}$ are vectors of all possible gating variables (like m, h, and n in the Hodgkin-Huxley equations for the squid giant axon). We need two sets of gating variables because ion channels are typically asymmetrical, so the dependence of any particular gating variable on membrane potential will depend on which way the ion channel to which it refers is “installed” in the membrane. The components of the vectors w^kl and w^lk obey differential equations of the following form:

$$\frac{\partial w_j^{kl}}{\partial t}={\alpha }_j\left({\varphi }^k-{\varphi }^l\right)\left(1-w_j^{kl}\right)-{\beta }_j\left({\varphi }^k-{\varphi }^l\right)w_j^{kl},$$ (5.88)

$$\frac{\partial w_j^{lk}}{\partial t}={\alpha }_j\left({\varphi }^l-{\varphi }^k\right)\left(1-w_j^{lk}\right)-{\beta }_j\left({\varphi }^l-{\varphi }^k\right)w_j^{lk},$$ (5.89)

in which (5.89) is obtained from (5.88) merely by interchanging the indices k and l. Here the index j runs over all of the different types of gates that may be present in the system, whether or not the ion channels containing those gates happen to be present within the membrane kl. Note that there is no simple correspondence between the ion type i and the gate type j. First, a specific ion channel may contain more than one type of gate (an example being the m and h gates of the Hodgkin-Huxley Na⁺ channel). Also, a given ion channel may not be completely specific; that is, it may be used by more than one type of ion. Finally, a given ion type may flow through more than one type of channel and therefore be influenced by several different gating variables. Our formalism allows for all of these possibilities.

Note that the functions α_j and β_j, which give the opening and closing rates for a gate of type j as a function of the transmembrane potential difference, do not depend on the indices k, l or on the specific spatial location x on the membrane. This is because we assume that the response of a gate of a given type to transmembrane voltage is the same regardless of where the channel containing that gate may happen to be located. As mentioned above, however, the response to membrane voltage does depend on the orientation of the channel within the membrane.

Thus, in the equation for $\partial w_j^{kl}/\partial t$, the functions α_j and β_j are evaluated at ϕ^k −ϕ^l, whereas in the equation for $\partial w_j^{lk}/\partial t$, they are evaluated at ϕ^l −ϕ^k. Since the functions α_j and β_j typically have no particular symmetry with respect to a change of sign of their argument, this means that there is no simple relationship between the values of $w_j^{kl}$ and $w_j^{lk}$ at any given time, which is why we need to keep track of both of them, since, at the level of a general formalism such as the one we are constructing here, we do not know which way a particular channel type will be oriented in a particular membrane.

The functions $f_i^{kl}$ have the following important antisymmetry:

$$f_i^{kl}\left({\varphi }^k-{\varphi }^l,c^k,c^l,w^{kl},w^{lk},\mathbf{x}\right)=-f_i^{lk}\left({\varphi }^l-{\varphi }^k,c^l,c^k,w^{lk},w^{kl},\mathbf{x}\right).$$ (5.90)

This is because $f_i^{kl}$ on the left-hand side of (5.90) is the transmembrane flux of the i^th ion species with the direction k → l considered positive, whereas $f_i^{lk}$ on the right-hand side is the same flux but with the direction l → k considered positive. The interchange of k and l in the argument lists on the two sides of the equation is so that both will refer to the same physical situation viewed, so to speak, from opposite sides of the membrane.

Note that equation (5.90) does not imply that membrane channels are symmetrical. To illustrate this, we consider the following simple example. Suppose $f_i^{kl}$ depends only on ϕ^k − ϕ^l and is given by

$$f_i^{kl}\left({\varphi }^k-{\varphi }^l\right)=f_0\left(\exp \left(\frac{q\left({\varphi }^k-{\varphi }^l\right)}{k_{\text{B}}T}\right)-1\right)$$ (5.91)

which describes a physical rectifier. Then, according to (5.90),

$$\begin{gathered} f_i^{lk}\left({\varphi }^l-{\varphi }^k\right)=-f_i^{kl}\left({\varphi }^k-{\varphi }^l\right) \\ =-f_0\left(\exp \left(\frac{q\left({\varphi }^k-{\varphi }^l\right)}{k_{\text{B}}T}\right)-1\right) \\ =f_0\left(1-\exp \left(-\frac{q\left({\varphi }^l-{\varphi }^k\right)}{k_{\text{B}}T}\right)\right). \end{gathered}$$ (5.92)

Thus $f_i^{lk}$ is not at all the same function as $f_i^{kl}$.

It is possible, however, for a membrane channel to be fundamentally symmetrical and for asymmetry in its behavior to be a consequence of asymmetrical conditions on the two sides of the membrane. Consider, for example, the ion flux through a “constant-field” channel, as given by the Goldman-Hodgkin-Katz formula [34]:

$$f_i^{kl}\left({\varphi }^k-{\varphi }^l,c^k,c^l\right)=\frac{D}{L}\left(\frac{q\left({\varphi }^k-{\varphi }^l\right)}{k_{\text{B}}T}\right)\frac{c^k\exp \left(q\left({\varphi }^k-{\varphi }^l\right)/k_{\text{B}}T\right)-c^l}{\exp \left(q\left({\varphi }^k-{\varphi }^l\right)/k_{\text{B}}T\right)-1}.$$ (5.93)

We leave it as an exercise for the reader to show that in this case the combination of (5.93) and (5.90) implies that

$$f_i^{lk}\left({\varphi }^l-{\varphi }^k,c^l,c^k\right)=f_i^{kl}\left({\varphi }^l-{\varphi }^k,c^l,c^k\right).$$ (5.94)

In contrast to (5.90), we here have the same sign on both sides of the equation, and the indices k and l are only interchanged in the labels of the two functions, not in their argument lists. Thus, equation (5.94) asserts that $f_i^{kl}$ and $f_i^{lk}$ are the same function, which means that the membrane channel they describe is symmetrical.

Although the formalism described here for the transmembrane fluxes is very general, it is not by any means completely general, and would no doubt need further elaboration in particular applications. We have assumed, for example, that the different types of gates behave independently of each other, with each gate having only two states. In reality, as discussed above, channel gating may in some cases be described more completely by Markov chains with multiple states. Another limitation of the present formalism is that any influence of a concentration on a transmembrane flux is assumed to be instantaneous. In reality, the binding of ligands to channels, and the subsequent opening and closing of gates, may proceed by finite-rate kinetics. Also, the numbers of channels of any particular type may change as a result of altered gene expression, or other regulatory mechanisms, in response to signals that a cell may receive, or as a result of the cell’s own pattern of activity. Although such effects require more complicated expressions for $f_i^{kl}$, they do not fundamentally alter the role that $f_i^{kl}$ plays in the rest of our formulation.

6. Conclusions

The spatial dimension in electrophysiology is important. This was evident already in the pioneering work of Hodgkin and Huxley, whose great triumph, once they had developed the ordinary differential equations describing the transmembrane current, was to embed these ODEs in a system of partial differential equations, and to show that this system has traveling wave solutions with a propagation speed that agrees well with the experimental propagation speed of an action potential along the squid giant axon. Although not covered in this review, the sometimes linear and sometimes nonlinear but generally dissipative wave propagation that occurs in the elaborate dendritic trees of neurons [72] is, if anything, even more important for neuronal information processing than the highly stereotyped propagation of the action potential that occurs in axons. Broadly speaking, axons report the results of subtle computations that occur in dendrites [40].

Neglect of the spatial dimension in cardiac electrophysiology is dangerous. Cardiac ectopy—the spontaneous formation of an action potential outside of the pace-making regions of the heart—is a risk factor for developing potentially fatal arrhythmias. Ectopic beats can be triggered by delayed afterdepolarizations (DADs) or early afterdepolarizations (EADs). In either case, the sodium current reactivates prematurely, drawing inward current that can cause propagating action potential waves. The Cardiac Arrhythmia Suppression Trial (CAST) was a multicenter, placebo-controlled clinical trial of antiarrhythmic medications intended to suppress such premature depolarizations by sodium-channel-blocking drugs that act to reduce the strength of the sodium current and thereby reduce or eliminate premature contractions. Patient enrollment was planned for June 1987–June 1990; however, the trial was halted in 1989: patients receiving the drug were found to be approximately three times as likely to suffer from sudden cardiac death than those receiving placebo [5, 15]. Because the drugs were sodium channel blockers, they acted not only to suppress ectopic beats, but also to lower cardiac conduction velocity. One presumably unintended consequence of such drugs is that they increase the effective electrical size of the chambers, thereby facilitating the formation of reentrant waves that otherwise could not have formed. Thus, a class of drugs that looked promising from an ODE point of view actually proved harmful, and the mechanism by which they caused harm could only be understood by thinking about cardiac electrical activity as occurring in space as well as time, and therefore as described by a system of PDEs.

Besides being three-dimensional (or four-dimensional if time is included in the dimension count), cardiac electrophysiology has an important multiscale aspect. This is because the length of an individual cardiac myocyte is not that much smaller than the width of the action potential wavefront, especially in pathological conditions that slow wave propagation. This suggests that continuum models might give incorrect results, and indeed we have seen examples in which they do. An extremely expensive way to overcome this difficulty is to abandon macroscale continuum modeling and to resolve every cell of the myocardium, each as its own microcontinuum. We have seen, however, in a one-dimensional model problem, that this expense can be avoided, without loss of accuracy, by a multiscale method that resolves individual cells near the action potential wavefront only and employs a macroscale continuum model elsewhere. The three-dimensional implementation of this multiscale method remains a challenge for the future.

Electrophysiology fundamentally involves the three-dimensional electrodiffusion of ions within a space partitioned by membranes, where internal boundary conditions must be applied. These boundary conditions describe the transport of ions by channels, exchangers, and pumps, and involve equations like those first written down by Hodgkin and Huxley, suitably generalized and modified to take into account more recent knowledge about the different transport mechanisms [34]. Electrodiffusion has a characteristic length scale, known as the Debye length, which is substantially less than the thickness of the cell membrane, and therefore much smaller than typical cellular or even than typical subcellular dimensions. Because of these size relationships, the electroneutral limit of the electrodiffusion equations is highly relevant in electrophysiology. This limit involves electroneutrality away from membranes, and space charge layers of equal magnitude but opposite sign on the opposite membrane faces. We have given an expository account of the electroneutral limit of the electrodiffusion equations in the hope that this will prove useful as a framework for future electrophysiological investigations. One strength of this approach is that it makes it possible to take the intricate intracellular and extracellular microanatomy and microphysiology (i.e., the detailed spatial distribution of transport mechanisms along membranes) of electrically active tissue as a starting point for the construction of a realistic computer model. Another strength is that the electroneutral limit of the electrodiffusion equations allows for the study of ion concentration changes, which may be highly localized, and that are subject to the constraint of electroneutrality, which couples together the dynamics of different species of ions. Models constructed in this way will be far more detailed than those in current use and may reveal hitherto unsuspected ways in which cellular and subcellular spatial structure is important in the function of electrically active cells.