Abstract
Molecular dynamics (MD) computer simulations are used routinely to compute atomistic trajectories of complex systems. Systems are simulated in various ensembles, depending on the experimental conditions one aims to mimic. While constant energy, temperature, volume, and pressure are rather straightforward to model, pH, which is an equally important parameter in experiments, is more difficult to account for in simulations. Although a constant pH algorithm based on the λ-dynamics approach by Brooks and co-workers [Kong, X.; Brooks III, C. L. J. Chem. Phys.1996, 105, 2414–2423] was implemented in a fork of the GROMACS molecular dynamics program, uptake has been rather limited, presumably due to the poor scaling of that code with respect to the number of titratable sites. To overcome this limitation, we implemented an alternative scheme for interpolating the Hamiltonians of the protonation states that makes the constant pH molecular dynamics simulations almost as fast as a normal MD simulation with GROMACS. In addition, we implemented a simpler scheme, called multisite representation, for modeling side chains with multiple titratable sites, such as imidazole rings. This scheme, which is based on constraining the sum of the λ-coordinates, not only reduces the complexity associated with parametrizing the intramolecular interactions between the sites but also is easily extendable to other molecules with multiple titratable sites. With the combination of a more efficient interpolation scheme and multisite representation of titratable groups, we anticipate a rapid uptake of constant pH molecular dynamics simulations within the GROMACS user community.
Introduction
Since their introduction more than four decades ago, molecular dynamics (MD) computer simulations have come of age.1 Thanks to improvements in computer hardware, algorithmic developments, as well as increased accuracy of force fields, MD simulation has evolved into a predictive technique that can complement experiments by providing atomistic insights into the dynamics of complex systems.1,2 While many experimental conditions can be modeled with good accuracy, the aqueous proton concentration, or pH, is typically accounted for indirectly by constraining the protonation states of titratable residues to their, presumed, most probable form at the start of the simulation. Because the electrostatic interactions depend critically on the protonation state of the residues, the pH affects the conformational ensemble. Conversely, because the conformation can influence the proton affinity of the residues, or pKa, a direct correlation exists between pH and conformational dynamics, which cannot be captured if the protonation state is kept fixed in the simulation.3
To overcome this limitation in classical MD simulations and include the effect of pH on the conformational sampling directly, several solutions have been proposed in the last decades4,5 and used to investigate pH-dependent protein–protein6 and protein-RNA interactions,7 drug binding,8,9 and structural changes.10,11 These solutions can be roughly divided into a category that relies on discrete changes in protonation states12−19 and a second category in which a protonation state can change continuously.20−33 More recently, a third category that relies on the transfer of proton-like particles between titratable sites, including protein residues and solvent molecules, was proposed for the Martini force field.34
In the discrete constant pH approaches, the protonation state of a residue can change at regular intervals of the simulation according to a Metropolis Monte Carlo criterion.16,17,28,35,36 To avoid a low acceptance rate due to unfavorable solvent configurations, the Monte Carlo step is performed based on free energies calculated using the approximation of either an implicit solvent representation,13,15 or a short all-atom thermodynamic integration.14,37
Most continuous approaches for MD at constant pH are based on the λ-dynamics technique developed by Brooks and co-workers.38 A one-dimensional λ-coordinate with fictitious mass mλ is introduced for each titratable site, and the equations of motion for these additional degrees of freedom are integrated along with the Cartesian positions of the atoms.21 The λ-coordinate defines the protonation state of the residue: at λ = 0 the residue is protonated and interacts with the rest of the system as such, while at λ = 1 it is deprotonated. The energy function that acts on the λ-coordinates depends on (i) the intrinsic proton affinity (reference pKa) of the titratable site in water, (ii) the interactions with the environment, which are mostly electrostatic,39 and (iii) the pH of the solvent, which is set by the user. In addition, potentials are introduced to bias sampling toward the physical states at λ = 0 and λ = 1. Protons are not transferred directly between the titratable residues and the solvent molecules but rather exchanged with an external proton bath. Because the chemical potential of this bath is determined by the proton concentration (pH) of the aqueous solution, constant pH MD (CpHMD) simulations based on λ-dynamics are performed in a grand canonical ensemble for the proton degrees of freedom.
While λ-dynamics-based constant pH approaches were originally developed for implicit solvent simulations,21 they have since then been adapted for explicit solvent simulations as well.18,23−26,28,30 The key computational challenge for explicit solvent implementations is the long-range electrostatic interaction, for which multiple solutions have been suggested, including a shifted cutoff scheme,26 a hybrid scheme combining the particle mesh Ewald (PME) treatment for the Cartesian coordinates with the generalized Born model for the λ-particles,24,40 and a fully consistent PME treatment for both λ and Cartesian degrees of freedom.23,30
In addition to accurate modeling of the long-range electrostatic interactions, also sampling can pose a serious challenge to simulations at constant pH. While the choice for the PME method in the original implementation of λ-dynamics in the fork of GROMACS 3.3 release23 was motivated by its accurate description of long-range electrostatics, the linear increase of the computational effort with the number of titratable sites limited the sampling efficiency, which meant that systems with many titratable sites could not be studied in practice.
To remove this bottleneck and enable constant pH MD with GROMACS at a modest additional cost compared to a standard simulation, we switch to an alternative scheme for computing the long-range electrostatic interactions of the λ-particles under periodic boundary conditions. The alternative scheme is based on a linear interpolation of partial charges21 rather than the potential energy functions as in the original implementation of constant pH MD in a GROMACS fork.23
Although the previous implementation of constant pH in a GROMACS fork was documented and shared with the community as an open-source program, there has been some misunderstanding about how electrostatic interactions were computed for λ-particles.24,25,30 To resolve this controversy, we first explain in detail how the electrostatic interactions were calculated in the previous GROMACS implementation of constant pH MD. We next contrast this linear interpolation between the potential energy functions of the protonated and deprotonated states of a residue on the one hand to the interpolation between the partial charges of both states on the other hand21 and show why the latter is computationally much more efficient. We then demonstrate the superior performance of the charge-interpolation scheme by running a series of constant pH MD simulations of amino acids and proteins. To emphasize that the new constant pH implementation in GROMACS is not restricted to a specific force field (or the resolution of a force field model) nor to a specific algorithm for evaluating electrostatic interactions, we also show the results of constant pH MD simulations with the Martini coarse-grained force field,41 in combination with a shifted cutoff electrostatics model. Because of GROMACS’ large user community, we expect our work to increase the popularity of constant pH MD simulations.
Theory
Before discussing the differences between linear interpolating of the potential energy functions on the one hand,23 and of partial charges on the other hand,21 for computing the potential energy landscape of the titration coordinates, we briefly review the λ-dynamics approach38 that forms the basis for the constant pH molecular dynamics algorithm in GROMACS.23
λ-Dynamics-Based Constant pH MD Simulations
A titratable site i can exist in a protonated or deprotonated state. The protonation state affects the interactions between the site and the rest of the system. In constant pH MD simulations based on λ-dynamics,38 an additional coordinate λi is introduced for each site i, and the potential energy function of the total system is continuously interpolated between the two protonation states along this coordinate, i.e., V(λi) .21 A fictitious mass mλ is assigned to each λi-coordinate, and the coordinates evolve along with the Cartesian degrees of freedom of all atoms in the system, based on Newton’s equations of motion. Thus, the total Hamiltonian of the system is
| 1 |
where R is the vector of the Cartesian coordinates rj of all Natoms atoms with mass mj and λ is the vector of the λi coordinates of all Nsites titratable sites.
λ-Dependent Potential Energy Function
In addition to the interpolation between the potentials of the protonated VA(R) and deprotonated states VB(R), three more λ-dependent terms are included in the potential energy function of the total system V(R, λ), as illustrated in Figure 1: (i) a correction potential ViMM(λi) to compensate for missing quantum mechanical contributions to proton affinities (Figure 1B); (ii) a biasing potential Vi(λi) that enhances sampling of the physical end states at λi = 0 and λi = 1 (Figure 1C); and (iii) a pH-dependent term VpH(λi) to model the chemical potential of protons in water (Figure 1D).
Figure 1.
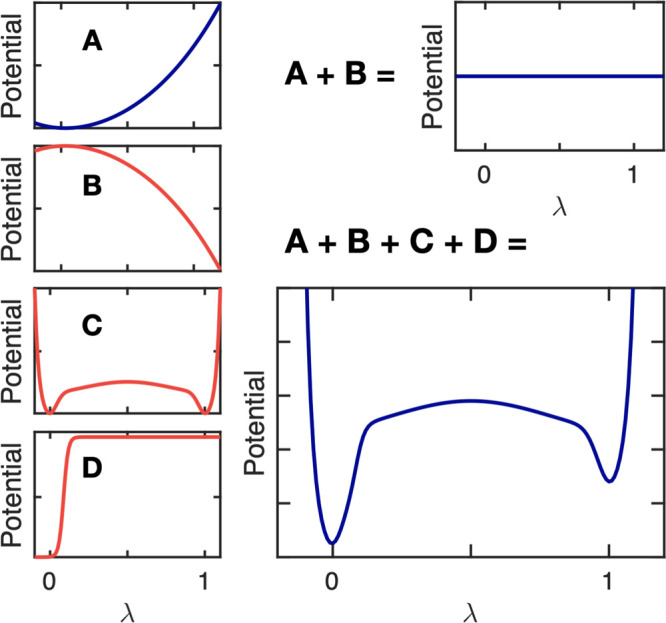
Illustration of the additional λ-dependent potential energy terms (B–D). Panel A shows the protonation free energy of a titratable residue in its reference state obtained at the force field level, ΔGiMM(λi) . To compensate for the shortcomings of the force field and obtain a zero free energy difference between the two protonation states (A + B), we add the correction potential, Vi(λ), shown in panel B. A biasing potential, Vibias(λ),42 is introduced to avoid sampling of nonphysical states (panel C). To model the proton chemical potential (pH), we add a pH-dependent term, VpH(λi) (panel D). For a titratable residue at pH ≠ pKa, the total λ-dependent potential, including the interpolated force field functions and the three additional terms, is illustrated in panel (A + B + C + D).
The purpose of adding the correction term ViMM(λi) (Figure 1B) is to make the interpolated potential function flat if the titratable site i is in its reference state, for which the proton affinity is known experimentally, at pH = pKa,i. This potential is determined by evaluating the deprotonation free energy of the single residue in water (reference state) at the force field level by thermodynamic integration along the λ-coordinate (Figure 1A):
| 2 |
To prevent sampling of the nonphysical states between λi = 0 and λi = 1 on this flat potential energy surface while still enabling sufficient transitions between the physical end-states to sample both protonation states with the correct thermodynamic weight, we introduce the biasing potential Vibias(λi) suggested by Donnini et al.42 (Figure 1C).
The pH-dependent term VpH(λi) (Figure 1D) is a correction that includes the effect of the solution pH on the free energy difference between the protonated and deprotonated states, such that this difference is
| 3 |
where we use the experimentally determined pKa,i value of residue i in its reference state. Although various forms for this potential have been suggested,29,42,43 we propose a smooth step-function-based potential:
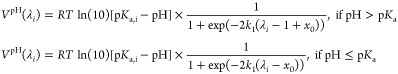 |
4 |
where k1 and x0 define the steepness and kink position of the step function. In this form, illustrated in Figure 1D, the pH-dependent potential also aids in preventing the sampling of nonphysical states, i.e., 0.1 < λ < 0.9.
Linear Interpolation of Potential Energy Functions
In the previous implementation of constant pH MD in a GROMACS fork, the smooth interpolation of the force field potential energy function between the protonated and deprotonated states was achieved by linearly interpolating the force field potentials of these states.23 Thus, for a single titratable site, the λ-dependent potential is given by
| 5 |
with VMM(R, λ), Vbias(λ), and VpH(λ) the correction, biasing, and pH-dependent potentials, respectively, that were briefly discussed above, and with short-hand notations for
The gradient required for updating λ according to Newton’s equations of motion is
| 6 |
Thus, the evaluation of the force on the λ-particle requires that the potential energy, including the long-range electrostatic interactions, is computed twice: once for λ = 0 (i.e., VA) and once more for λ = 1 (i.e., VB). If the Particle-Mesh-Ewald (PME) method is used to compute those long-range electrostatic interactions,44,45 separate PME grid builds are needed because the charge distributions are not identical in states A and B.
For systems with many titratable sites, multiple λ-groups are introduced. Because the analytical expressions for the correction, biasing, and pH-dependent terms in eq 5 are additive, we no longer consider them explicitly in what follows and focus exclusively on the interpolation of the force field potential energies between the multiple protonation states of the system. For N λ-coordinates, there are 2N such states and the interpolation generalizes to20
| 7 |
Here, we represent the N λi-coordinates as an N-dimensional vector λ. The 2N possible protonation states of the system are represented by the N-dimensional vector l with elements li equal to 0 or 1 that indicate whether a site i is protonated (λi = 0) or deprotonated (λi = 1). The sum runs over all 2N possible combinations of li = 0 and li = 1. The gradient required for updating λi is obtained by deriving the interpolated potential, V(R, λ), with respect to λi:
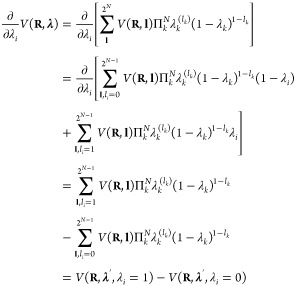 |
8 |
where the ′ indicates that λi is omitted from vector λ. Note that, as we focus only on the interpolated potentials, the biasing, correction, and pH-dependent terms are left out.
In general, the number of terms in the potential (eq 7) increases exponentially with the number of titratable sites. However, for pairwise interactions involving titratable sites whose nonbonded force field parameters do not depend on the protonation state of the other sites (chemically uncoupled sites), the number of terms required to evaluate the interpolated potential scales linearly. For systems with such “chemically”, or “topologically” uncoupled sites, the interpolated potential contains four types of interactions
| 9 |
For pairwise electrostatic interactions, the terms on the right-hand side are defined as
-
1.Interactions between atoms that are not part of any λ-group, and hence independent of the λi’s:
where the sums run over all nrest atoms that are not part of a λ-group.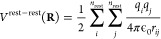
10 -
2.Interpolated interactions between atoms of each λ-group with atoms that are not part of any λ-group:
where the first sum runs over all titratable sites, the second one runs over all nk atoms of the k th λ-group, and the final sum runs over all atoms that are not part of any λ group.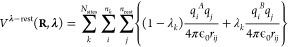
11 -
3.Interpolated interactions between atoms belonging to two different λ-groups:
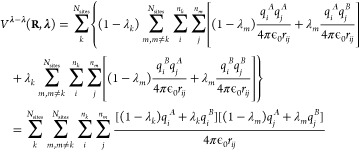
12 -
4.Interpolated interactions within each of the λ-groups:
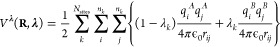
13
From eq 8, the gradient with respect to λk is
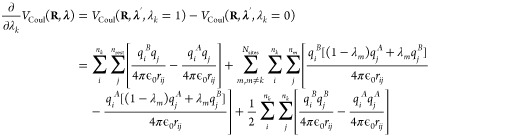 |
14 |
Thus, the evaluation of the Coulomb contribution to the gradient for each λk-group requires two electrostatic computations, with the interpolated partial charges of the other λm sites (i.e., qj(λm) = (1 – λm)qjA + λmqj):
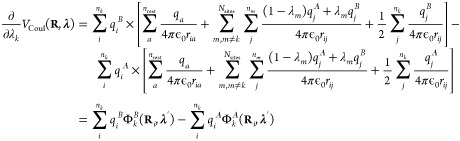 |
15 |
Here, we introduced the electrostatic potential ΦkA(Ri, λ′) of the system with partial charges of λ-group k in the protonated state (qi) and interpolated charges for all other λ-groups. As before, λ′ is the vector with all λm’s except λk. Likewise, electrostatic potential ΦkB(Ri, λ′) is evaluated with the partial charges of λ-group k in the deprotonated state (qi) and the same interpolated charges for all other λ-groups. Thus, 2Nsites computations are needed to evaluate the gradients for all titratable sites. The same arguments apply to pairwise Lennard-Jones interactions, but because the contribution of Lennard-Jones interaction to pKa shift is minor, we neglected them in this work (see Supporting Information).
Linear Interpolation of Partial Charges
While the linear scaling of the gradients for the pairwise potentials in eq 15 in principle is a great improvement over the formal exponential scaling in eq 8, the requirement of performing 2Nsites calculations per MD step still poses a computational bottleneck, in particular for larger systems. To overcome this bottleneck for electrostatic interactions, we follow the suggestion by Brooks and co-workers to interpolate charges rather than interaction functions.21 When interpolating the partial charges between the protonation states of Nsites chemically uncoupled titratable sites, the λ-dependent Coulomb energy becomes
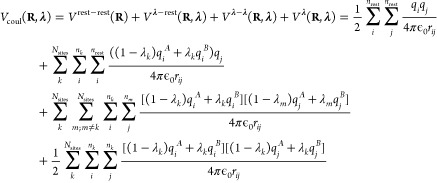 |
16 |
The gradient of the potential energy with respect to λk is
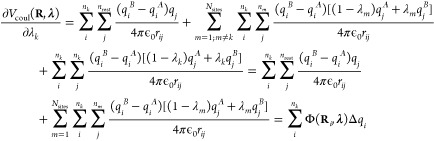 |
17 |
where Φ(Ri, λ) is the electrostatic potential at the position of atom i due to the charge distribution of all other atoms in the system, including the atoms of all titratable sites, for which the partial charges are interpolated:
and Δqi is the difference between the atomic charges of titratable residue i in the protonated (A) and deprotonated (B) states:
In contrast to when potential energy functions are interpolated, the same electrostatic potential is used to evaluate the electrostatic forces on both the atoms and the λ-particles. Therefore, a single electrostatic calculation per time step suffices. If the electrostatic interactions are modeled with the smooth Particle Mesh Ewald method,44,45 the short-range real-space interactions and long-range reciprocal-space interactions are computed separately. For the pairwise short-range interactions in real space, an additional calculation for each interacting pair and a subsequent accumulation of the potential at each atom is needed. Whereas this calculation comes at no extra computational cost if the standard pair interaction kernels are used, the accumulation leads to a measurable computational overhead, as we will show later. For the mesh part of the PME calculation, a gathering of potentials from the grid is required for charges in λ-groups only, but this also comes at a negligible computational overhead. Because the extra effort required to compute the gradients on the λ-particles is rather small, a constant pH MD implementation based on charge interpolation is computationally not much more expensive than a normal MD simulation, which is a major improvement with respect to the previous CpHMD implementation in GROMACS.23
Multisite Representation of Chemically Coupled Titratable Sites
If titratable sites are “chemically” or “topologically” coupled, the force field parameters of one site depend on the value of the λ-coordinate of the other site, and vice versa. For example, histidine can exist in three protonation states, as shown in Figure 2. In most force fields, the partial charges of all atoms in the His side chain, including the two sites, depend on the protonation state. Hence, if the Nδ site changes protonation, the electrostatic interactions of the Nϵ site are also affected.
Figure 2.
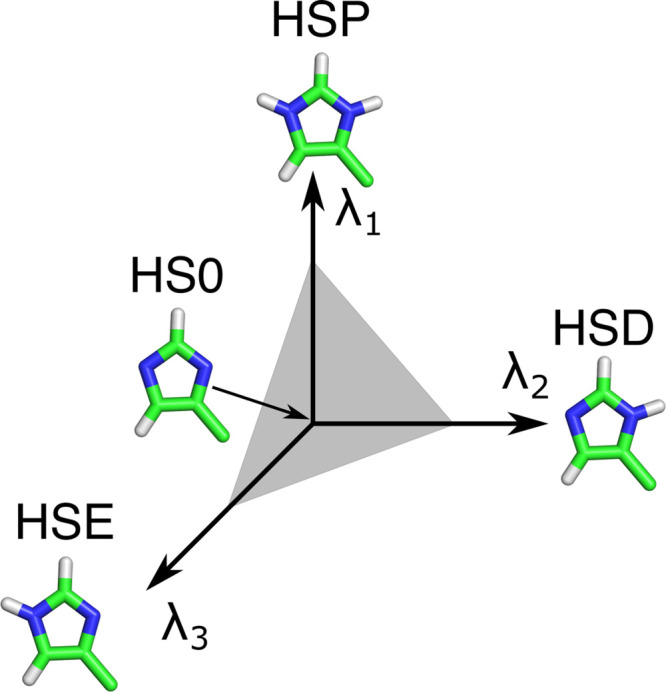
Multisite representation illustrated for a histidine side chain. Each possible protonation state is represented by its own λ-coordinate. HSP refers to doubly protonated histidine, HSD, and HSE to histidine singly protonated at the Nδ or Nϵ, respectively. HS0 is a common, nonphysical state of the residue. To restrict the sampling to the plane connecting the physical states, a constraint λ1 + λ2 + λ3 = 1 is applied (gray plane). A biasing potential is also applied to enhance sampling at the end states, where one of the λ-coordinates is close to one, while the other coordinates are close to zero.
To model the chemically coupled sites in the histidine side chain, Khandogin and Brooks introduced two λ-coordinates:22 one that interpolates between the double and single protonated forms and a second coordinate switching between protonation at the Nδ and the Nϵ atoms. Donnini et al. introduced separate λ-coordinates for Nδ and Nϵ.23 In both solutions, the coupling between the coordinates is achieved with a two-dimensional correction potential.
Because extending the dimensionality beyond two coordinates is difficult from both the implementation and parametrization perspective, Brooks and co-workers introduced a multisite representation,46,47 where a separate λi,k-coordinate is assigned to each physical state k of a titratable group i. For a residue with multiple “chemically”-coupled titratable sites, each λi,k-coordinate has the same state at λi,k = 0, while at λi,k = 1, the group is in one of the ni possible protonation states (i.e., state k) of residue i. The state at λi,k = 0 is the same for all λi,k-coordinates in residue i but does not correspond to a physical protonation state of the residue and neither do states for which the sum of the λi,k-s is not equal to 1 (Figure 2). To restrict sampling to the (hyper-)plane connecting the physical states, the sum of the λi,k values is constrained (∑kλi,k = 1). Since the λ-dynamics implementation in a fork of GROMACS relies on linear λ-coordinates, rather than on auxiliary circular coordinates that would fulfill the constraints by construction,46,48 we apply a constraint on the sum of λi,k-coordinates. To efficiently apply this constraint, we use an analytical expression to solve a generalized version of the charge constraint introduced by Donnini et al.42 (see the Appendix). While an atom can be part of multiple λi,k-coordinates in residue i, each affecting its charge, we show in the Supporting Information that the expression for the contribution of this atom to the total Coulomb energy is identical to that of an uncoupled site (eq 17).
In the multisite representation, each λ-coordinate is independent of the others and thus evolves on a one-dimensional potential (eq 4), similar to that of “chemically” uncoupled sites. However, in contrast to the uncoupled sites, the correction potential VMM is multidimensional as its value depends on all λi,k-coordinates representing each of the possible protonation states of residue i. These potentials are obtained through a least-squares fit of a multidimensional polynomial to the ensemble-averaged gradients of the potentials with respect to λi,k evaluated on the (ni – 1)-dimensional grid of the ni coupled λ-coordinates, i.e., ⟨∂ V/∂λi,k⟩λ1...λni. The fitting procedure is explained in detail in the Supporting Information.
The multisite representation can be applied to residues with any number of titratable sites, including residues with only a single titratable site. In the latter case, two λ-coordinates, corresponding to the protonated state (λi,1 = 1, λi,2 = 0) and deprotonated state (λi,1 = 0, λi,2 = 1), are introduced with a constraint on their sum (λi,1 + λi,2 = 1).
Methods
We have implemented the algorithms for CpHMD with charge interpolation in a fork of GROMACS software package (2021 release).49 The code and manuals are available for free at https://gitlab.com/gromacs-constantph/constantph. Here we verify the validity of our implementation for reproducing pKa values of peptides and proteins. To demonstrate that the linear interpolation of charges (eq 17) scales better with the number of titratable sites in the system than the linear interpolation of interaction functions (eq 15), we compared the scaling between our new implementation, which is based on linear charge interpolation on the one hand, and a previous implementation in a fork of the GROMACS 3.3 release, which is based on linear interpolation of the force field potentials on the other hand.23 To estimate the additional computational effort required for performing CpHMD with the new implementation, we also compared the performance of a CpHMD simulation to that of a normal MD simulations on both CPUs and GPUs.
Simulated Systems
To test the implementation, we performed constant pH MD simulations of the following systems: (1) glutamic acid (Glu), (2) aspartic acid (Asp), (3) histidine (His), (4) Cardiotoxin V (PDB ID: 1CVO(50)), (5) hen egg white lyzozyme (HEWL, PDB ID: 2LZT(51)), (6) the GLIC pentameric ligand-gated ion channel (PDB ID: 4HFI(52)), and (7) turkey ovomucoid inhibitor (PDB ID: 2GKR(53)).
In systems 1–6, the interactions were modeled with the CHARMM3654 all-atom (AA) force field, with some modifications in the torsion parameters to accelerate the convergence. These modifications are presented and validated in an accompanying paper, in which we report the application of our constant pH implementation to lysine, C-, and N-termini.55 Systems 1–5 were also simulated with the Martini 2.0 coarse grained (CG) force field.41 The martinize.py script was used to automatically generate the CG representation of these systems.56 System 7 was simulated to compare the efficiency of interpolating charges and potentials. The interactions in this system were modeled with the OPLS force field57 because the GROMACS 3.3 release, on which the linear interpolation of potentials implementation was based, does not support the CMAP correction that is needed for the CHARMM36 force field.58
The amino acids Glu, Asp, and His were modeled as tripeptides Ala-X-Ala with acetylated N-terminus (ACE) and N-methylamidated C-terminus (CT3). The proteins were simulated with charged termini. The tripeptides were placed in a periodic rectangular box of dimensions 5 × 5 × 5 nm3 with approximately 4000 CHARMM TIP3P59,60 water molecules in the AA simulations and 950 polarizable water particles in the CG simulations.61 The water-soluble protein cardiotoxin V was placed in a periodic rectangular box of 7.9 × 7.9 × 7.9 nm3 and filled with 16500 CHARMM TIP3P water molecules in the AA simulations. In the CG simulations, the protein was placed inside a periodic rectangular box of 5.7 × 5.7 × 5.7 nm3 and filled with 1800 polarizable water particles. The larger water-soluble protein HEWL was placed in a periodic rectangular box of 8.9 × 8.9 × 8.9 nm3 and filled with 23000 CHARMM TIP3P water molecules in the AA simulations and 5400 polarizable water particles in the CG simulations. Na+ and Cl– ions were added to all systems at 0.15 M concentration to neutralize the protein systems. The turkey ovomucoid inhibitor protein was placed in a box of 4.9 × 4.9 × 4.9 nm3 with 3086 SPC62 water molecules. The GLIC protein was embedded into a bilayer membrane containing 498 phosphatidylcholine (POPC) lipids, placed in a box of 14.0 × 14.0 × 15.9 nm3, and filled with 66494 CHARMM TIP3P waters, 58 Na+, and 123 Cl– ions. The system contained 292135 atoms in total. The simulation of this system was performed with the GROMACS 2021.4 release as reference. The GLIC benchmarks were run with default settings on an Intel i9–7920X 12-core CPU and an Nvidia RTX 2080 Ti GPU. All input configurations are provided as the Supporting Information.
In the AA simulations, Coulomb interactions were modeled with the smooth PME method with a real-space cutoff of 1.2 nm and a grid spacing of 0.14 nm,44,45 while Lennard-Jones interactions were smoothly switched to zero in a range from 1.0 to 1.2 nm. In the CG simulations, Coulomb interactions were modeled by a Reaction Field potential with a 1.1 nm cutoff, ϵr = 2.5, and ϵRF = ∞, while Lennard-Jones interactions were truncated at 1.1 nm.63 To keep the temperature constant at 300 K, we used the v-rescale thermostat64 with time constants of 0.5 and 1.0 ps–1 for AA and CG simulations, respectively. The pressure was kept constant at 1 bar with the Parrinello–Rahman barostat65 with relaxation times of 2.0 and 12.0 ps for AA and CG simulations, respectively. A leapfrog integrator was used with an integration step of 2 and 20 fs for AA and CG simulations, respectively. In the AA simulations, the LINCS algorithm66 was used to constrain h-bond lengths of the solutes, while the SETTLE67 algorithm was used to constrain internal degrees of freedom of the water molecules. Prior to the constant pH MD simulations, the potential energy of each system was minimized using the steepest descent method, followed by 1 ns of equilibration.
Constant pH MD Simulation Setups
In the atomistic simulations, the multisite representation was used to model the protonation states of titratable residues. Two λ-coordinates were introduced to model the two forms of the carboxylic acid side chain in Asp and Glu, while three coordinates were used to describe the three protonation states of the imidazole side chain in His. In the CG simulations, the single-site representation was used, in which the A and B states represent the protonated and deprotonated states of the titratable beads. Because, in contrast to AA force fields, there is no distinction between the two neutral forms of the His side chain in the Martini force field, the single-site description for HIS suffices in the CG simulations. In both atomistic and coarse-grained simulations, the transformations between the different protonation states were achieved by changing the charges of the ionizable groups. The Lennard-Jones and bonded terms (bonds, angles, and torsions) were kept in the protonated and deprotonated states in AA and CG simulations, respectively. We show in Figure S3 that the contribution of these terms is sufficiently small to be neglected without significant error. We note, however, that these terms can be made λ-dependent as well, but this is beyond the scope of the current work since the efforts to implement this are high.
The mass of the λ-particles was set to 5 atomic units, and their temperature was maintained at 300 K by using a separate v-rescale thermostat for the λ-coordinates with a time constant of 2.0 ps–1. For all λ-coordinates the biasing potential Vibias(λi) was defined by equation S1 in the Supporting Information. The barrier height of the double-well potential was set to 5.0 and 7.5 kJ/mol for AA and CG simulations, respectively. The parameters for the double-well potential and the pH-dependent potential (eq 4) are provided in Table S1.
For the tripeptides, we calculated five independent CpHMD trajectories of 20 ns each at 13 pH values, ranging from 1.0 to 7.0 for the peptides with Glu and Asp, and from 4.0 to 10.0 for the peptides with His. For the cardiotoxin V protein (three Asp and one His titratable residues), we performed five independent CpHMD simulations of 50 ns at 15 pH values between 1.0 to 8.0. For the HEWL protein (seven Asp, two Glu, and one His titratable residues), we performed five independent CpHMD simulations of 75 ns at 21 pH values between −1.0 to 9.0. The values of the λ-coordinates were written to the output file with a frequency of 1 ps–1.
Reference States and Force Field Correction Potentials
The constant pH simulations of the aforementioned systems require reference states for Asp, Glu, and His, in which the proton affinity (pKa) is known from the experiment. The measured and calculated (force field) deprotonation free energies of these reference states were used to include the effect of the pH bath, VpH(λ), as well as the effects of the breaking and forming of chemical bonds in the simulation, i.e., VMM in eq 2. The measured reference pKa values used in this work are included in Table 1. Note that the experimental values were obtained for pentapeptides, while tripeptides were used for computing VMM. This however did not affect the results, as shown in Figure S2.
Table 1. pKa Values Obtained from Titration Simulationsa.
| tripeptide
simulations69,70 |
|||
|---|---|---|---|
| pKa values |
|||
| amino acid | CHARMM36 | MARTINI | exp. |
| Asp | 3.61 ± 0.03 | 3.69 ± 0.02 | 3.65 |
| Glu | 4.26 ± 0.04 | 4.30 ± 0.03 | 4.25 |
| His macroscopic | 6.34 ± 0.08 | 6.40 ± 0.03 | 6.42 |
| His HSD | 6.56 ± 0.06 | 6.53 | |
| His HSE | 6.90 ± 0.05 | 6.94 | |
| simulation
of cardiotoxin V71,72 |
|||
|---|---|---|---|
| pKa values |
|||
| amino acid | CHARMM36 | MARTINI | exp. |
| His-4 | 5.14 ± 0.16 | 4.54 ± 0.09 | 5.5 |
| Glu-17 | 4.08 ± 0.08 | 4.36 ± 0.04 | 4 |
| Asp-42 | 4.02 ± 0.10 | 4.30 ± 0.05 | 3.2 |
| Asp-59 | 2.41 ± 0.07 | 1.45 ± 0.03 | <2 |
| r = 0.96 | r = 0.80 | ||
| MSE = 0.24 | MSE = 0.64 | ||
| RMSE = 0.49 | RMSE = 0.80 | ||
| simulation
of HEWL73 |
|||
|---|---|---|---|
| pKa values |
|||
| amino acid | CHARMM36 | MARTINI | exp. |
| Glu-7 | 2.82 ± 0.07 | 4.86 ± 0.05 | 2.6 |
| His-15 | 4.84 ± 0.05 | 5.42 ± 0.05 | 5.5 |
| Asp-18 | 3.35 ± 0.05 | 3.31 ± 0.03 | 2.8 |
| Glu-35 | 7.64 ± 0.13 | 6.36 ± 0.05 | 6.1 |
| Asp-48 | 0.99 ± 0.07 | 3.36 ± 0.05 | 1.4 |
| Asp-52 | 5.69 ± 0.12 | 7.18 ± 0.10 | 3.6 |
| Asp-66 | 1.70 ± 0.10 | 5.22 ± 0.05 | 1.2 |
| Asp-87 | 1.73 ± 0.03 | 3.47 ± 0.05 | 2.2 |
| Asp-101 | 5.43 ± 0.11 | 4.20 ± 0.06 | 4.5 |
| Asp-119 | 2.77 ± 0.05 | 3.80 ± 0.05 | 3.5 |
| r = 0.90 | r = 0.49 | ||
| MSE = 0.96 | MSE = 4.01 | ||
| RMSE = 0.98 | RMSE = 2.00 | ||
The reference pKa values for tripeptides are given in the last column that contain the experimental pKa values. The values for Asp and Glu are taken from ref (69), while the microscopic and macroscopic pKa values for His are taken from ref (70). Experimental pKa values for cardiotoxin V are from refs (71 and 72) and for HEWL from ref (73). For both proteins Pearson correlation (r), MSE and RMSE errors are provided.
Thermodynamic integration was used to compute the reference free energies as follows: the partial charges in tripeptide systems representing the reference states of Glu, Asp, and His were linearly interpolated between λ = −0.1 and λ = 1.1 with a step of 0.05 under the constraint λ1 + λ2 = 1 for Glu and Asp, while for His, the constraint was λ1 + λ2 + λ3 = 1. For each set of λ values, called a grid point, a 10 ns MD simulation was performed. The ∂V/∂λi values were saved every ps, which is approximately equal to the autocorrelation times for the λ-coordinates. The total charge of the system was kept neutral by simultaneously changing the charge of a single buffer particle, as discussed below. The ∂V/∂λi values were averaged over the last 9 ns of the trajectories. To obtain an analytical expression for VMM, a fifth-order polynomial was fitted to these averages for Asp and Glu, while an eighth-order polynomial was fitted for His, taking into account possible linear dependencies of the coefficients (see the Supporting Information). Fitting errors were below 0.5 kJ/mol for Asp and Glu and below 1 kJ/mol for His, which are of similar magnitude as the statistical accuracy of the derivatives.
Buffer Particles
Dynamically changing partial charges can affect the total charge of the simulation unit cell, which can lead to artifacts, as documented for instance in Hub et al. for Ewald-based methods.68 To avoid such artifacts, it is essential to keep the total charge of the unit cell constant. Two approaches have been proposed: (i) direct coupling between each titratable residue and a water,27 or ion,25 and (ii) titratable buffers that collectively compensate for changes in charge of all titratable residues.42
Here, we follow the latter approach, but with several improvements for all-atom simulations. First, to avoid restraints, which were needed to minimize interactions between the buffers and the titrable sites in previous work,42 we introduced buffer particles with both small LJ radius and small partial charges of maximal |0.5|e, such that they do not disturb the hydrogen bond network, nor interact too strongly with the titratable sites or other buffers. Second, to also prevent strong interactions with hydrophobic regions in the system, the C(6) dispersion parameter with anything other than water was set to zero, including the other buffers. The latter also avoids the clustering of buffers during the simulation. Thus, the buffer particles have an σ of 0.25 nm and an ϵ of 4 kJ/mol. Further details on buffer parametrization are provided in the accompanying paper.55 In coarse-grained simulations, standard Na+ ions were used as buffer particles.
As in Donnini et al.,42 the buffers were collectively coupled to the titratable sites in the system via a charge constraint. The charges of all buffers were thus simultaneously interpolated between −0.5e and 0.5e, keeping the simulation box neutral. For all peptide simulations, 10 such buffers were introduced into the system, while 20 and 50 buffers were added to the simulation boxes with cardiotoxin V and HEWL proteins (systems 4–5), respectively, in both AA and CG models. 185 buffer particles were used in GLIC simulations.
Analysis of the Constant pH Trajectories
To estimate the pKa values of titratable groups from multiple simulations at various pH values, we computed the average fraction of deprotonated frames (Sdeprot) over all replicas. For a group with a single titratable site, this average was obtained as
| 18 |
where Nprot and Ndeprot are the total number of frames in which the site is protonated and deprotonated, respectively. For titratable sites modeled in the single-site representation, we considered it protonated if λ is below 0.2 and deprotonated if λ is above 0.8. For sites that are described with the multisite description, we considered a state protonated if the λ associated with the protonated form of the residue is above 0.8 and deprotonated if the λ associated with the deprotonated form of the residue is above 0.8.
To estimate the macroscopic pKa values of histidine, which contains two titratable sites Nϵ and Nδ, we calculated for each pH value the average fraction of frames in which the residue is deprotonated at either of the two sites:
| 19 |
where Nλp, Nλϵ, and Nλδ are the numbers of frames in which λp > 0.8, λϵ > 0.8, and λδ > 0.8 (Figure 2). To estimate the microscopic pKa values for the two sites of His, we calculated for each site the average fraction of frames in which that site was deprotonated:
| 20 |
Errors were estimated from the standard error of the mean for the different replicas.
The averaged fractions at each pH value were fitted to the Henderson–Hasselbalch equation:
| 21 |
which yielded the pKa values as fitting parameters. The error in the pKa was estimated from the 95% confidence interval for the nonlinear least-squares fit to the average (Sdeprot) values.
Results and Discussion
Here we discuss the results obtained with our new implementation of constant pH into the fork of the GROMACS 2021 release.49 While here our focus is on the validity and performance of the constant pH MD implementation, the convergence of the conformational and λ degrees of freedom are investigated systematically in the accompanying paper.55
Titration of Single Amino Acids
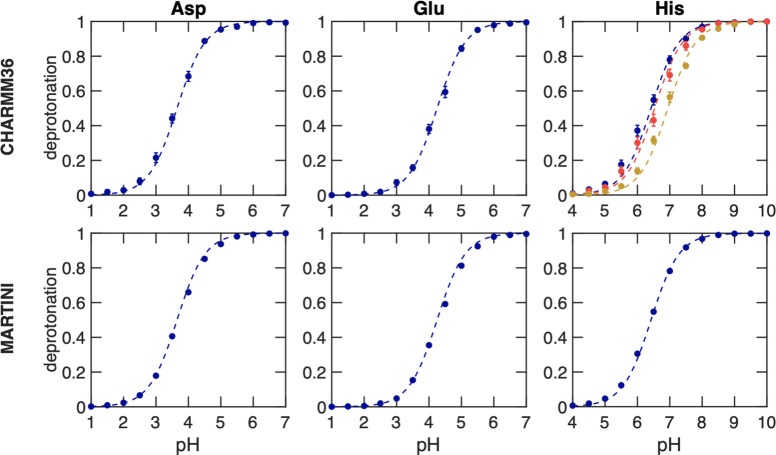
In Figure 3, we show the titration curves for AlaAspAla, AlaGluAla, and AlaHisAla tripeptides, obtained from simulations with the modified all-atom CHARMM3655 and coarse-grained Martini 2.0 force fields.41 Fitting the deprotonated fractions as a function of pH value to the Henderson–Hasselbalch equation (dashed lines in Figure 3) yields pKa values for the tripeptides that are within 0.1 pKa units from the reference values. Comparing the titration curves obtained with the Martini 2.0 force field in our implementation to those computed with the constant pH approach developed explicitly for this coarse-grained model,34 our results suggest a much better agreement with the experiment than the latter. We attribute this difference to the more sophisticated explicit treatment of proton-like particles in the Martini constant pH approach. The rather good agreement between the titration curves obtained for both force fields on the one hand and the experiment on the other hand suggests that our implementation has little to no dependency on the force field, in line with the GROMACS philosophy of supporting a wide range of popular force fields.
Figure 3.
Titrations of tripeptide amino acids (Glu, Asp, and His) in water. The top and bottom rows show titrations performed with the modified AA CHARMM3655 and CG Martini41 force fields, respectively. In all simulations, neutrality was maintained by including ten buffer particles in combination with the charge constraint. Dots show the fraction of frames in which the residue is deprotonated, and the dashed lines represent the fits to the Henderson–Hasselbalch equation. For His, the blue color represents the macroscopic pKa, while yellow and red represent the microscopic pKa values for HSD (proton on Nδ) and HSE (proton on Nϵ), respectively. In the Martini 2.0 model, HSD and HSE are indistinguishable and hence only the macroscopic titration curve is shown. Errors of Sdeprot were estimated from the standard error of the mean for the different replicas. From the fits, the pKa values were estimated and listed in Table 1.
Titration of Proteins
The titration curves of cardiotoxin V and HEWL proteins are shown in Figures 4 and 5, respectively. The pKa values obtained from fitting the Henderson–Hasselbalch equation to the degree of deprotonation in the all-atom simulations of both proteins with the CHARMM36 force field, listed in Table 1, are in good agreement with previous constant pH MD simulations30,74 and in reasonable agreement with experimental estimates from NMR spectroscopy [Pearson correlation coefficient (r) 0.96 and 0.9, RMSE 0.49 and 0.98 for cardiotoxin V and HEWL, respectively].71−73 The pKa values and Sdeprot are converged in 50 ns, as discussed in the Supporting Information section 5 (Figures S6–S9). Analysis of the RMS deviation of the backbone and of the RMS fluctuation of the residues, plotted in Figures S10–S13, suggest no major influence of the pH on the structural stability of these proteins. The titration correlates with solvent exposure, which contributes to the stabilization of the charged protonation state (see Supporting Information section 7) (Figures S14–S16). The trends in the pKa shifts are well reproduced, including the downshift of Asp-59 in cardiotoxin V, and, with the exception of Glu-35 and Asp-52 in HEWL, the deviations are below 1 pKa unit. We note that also in previous constant pH simulations with the CHARMM force field,22,30 similar deviations were found for these two residues (see Figure S5). This suggests that the origin of the discrepancy might lie beyond the implementation, and could be due to either a lack of sampling or systematic shortcomings in the force field, as was discussed in Huang et al.30 For detailed insights into the structural origins of these pKa shifts, we refer the reader to the paper of Swails and Roitberg.19
Figure 4.
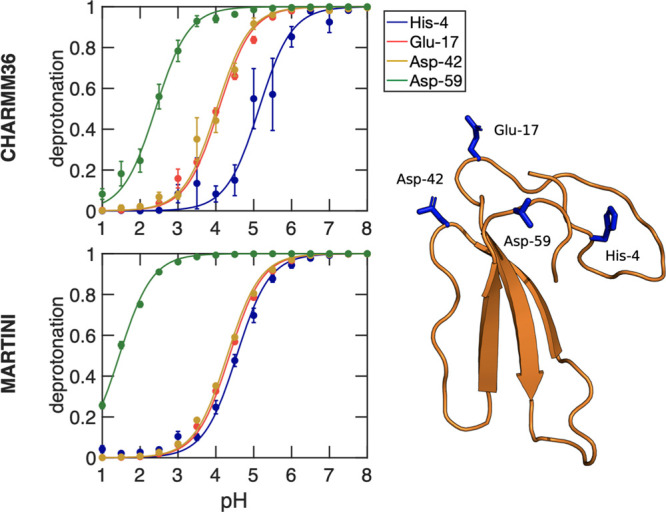
Titration curves of the cardiotoxin V protein obtained from constant pH MD simulations with the CHARMM36 (top) and Martini 2.0 force fields (bottom). For each of the four titratable residues in this protein, the dots show the fraction of frames in which the residue is deprotonated. Errors of Sdeprot were estimated from the standard error of the mean for the different replicas. The lines show the best fits to the Henderson–Hasselbalch equation. The pKa values for each titratable residue were estimated from these fits and listed in Table 1. The right panel shows the protein structure with the four titratable residues highlighted in stick representation.
Figure 5.
Titration curves of the HEWL protein obtained from constant pH MD simulations with the CHARMM36 (top) and Martini 2.0 force fields (bottom). For each of the ten titratable residues, the dots show the fraction of frames in which that residue is deprotonated. Errors of Sdeprot were estimated from the standard error of the mean for the different replicas. The lines show the best fit to the Henderson-Hasselbach equation. The pKa values for each titratable residue were estimated from these fits and listed in Table 1. The right panel shows the protein structure with the ten titratable residues highlighted in stick representation.
The pKa values estimated from the Martini 2.0 force field simulations of these proteins do not agree as well with the experiment as those derived from the all-atom simulations (Pearson correlation coefficient (r) 0.8 and 0.49; RMSE 0.8 and 2.0 for cardiotoxin V and HEWL, respectively). We speculate that the larger deviation of the pKa’s in the coarse-grained constant pH simulations could be due to the lower accuracy of the electrostatic interactions. Although we still consider the results obtained with the Martini simulations reasonable, in particular for the peptides, the discrepancies for the titratable residues in proteins suggest that additional parametrization efforts may be required to systematically improve the force field for constant pH MD simulations based on λ-dynamics. Such improvements would be particularly worthwhile considering coarse grained simulations pave the way to perform MD simulations of complete organelles,75 in which many processes have a strong pH dependence.
Efficiency of the Implementation
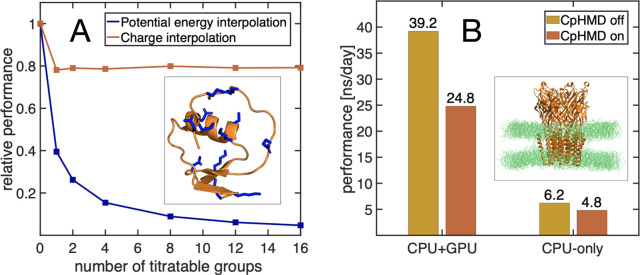
To demonstrate that linear interpolation of charges is computationally more efficient than the linear interpolation of the potential energy functions for systems with many titratable sites, we investigated how the computational cost of a simulation scales with the number of titratable sites in the system for both approaches. Because we have implemented the interpolation of the charges rather than potential energy functions into the fork of GROMACS 2021 release, whereas the potential energy function interpolation was implemented in a fork of GROMACS 3.3 release, we compare the relative performances of both codes for an increasing number of titratable sites in the system. We define the relative performance as the ratio between the average number of integration steps per time unit for a simulation with constant pH on the one hand and the average number of integration steps per time unit for a normal simulation without constant pH on the other hand.
Figure 6A shows that the relative performance of constant pH simulations with charge interpolation does not decrease when the number of titratable sites included in the simulation increases. Most of the 30–40% drop in performance compared to a normal MD simulation with the same version of GROMACS is caused by the additional calculations and reductions in the nonbonded pair-interaction kernels that are required to obtain the real-space part of the electrostatic potential (Φ(Ri, λ) in eq 17).
Figure 6.
(A) Relative performance of interpolating potentials in a previous implementation of CpHMD into a fork of GROMACS 3.3 release (blue) and of charge interpolation in our new implementation (red) as a function of the number of titratable sites. The simulations were performed for the turkey ovomucoid inhibitor protein (PDB ID: 2GKR(53)), shown in the inset, where the titratable sites are highlighted in stick representation. (B) Comparison of the performance between CPU-only and CPU+GPU implementations for the ligand-gated ion channel GLIC (PDB ID: 4HFI(52)) with 185 titratable sites. In total, the GLIC system contained 292135 atoms.
In contrast, the relative performance of constant pH simulations based on the linear interpolation of potential energy functions decreases with the number of titratable sites in the system. This comparison thus demonstrates that by replacing linear interpolation of potentials with linear interpolation of partial charges, we have overcome the major bottleneck in the earlier constant pH implementation in the fork of GROMACS 3.3 release and paved the way toward simulations of large biomolecular systems at constant pH.
An example of such a large system is the proton-gated ion channel GLIC, a membrane protein with 185 titratable residues. Figure 6B shows the performance of the new implementation for this large system when running the simulation on CPU and on a combination of CPU and GPU. While the computational overhead is somewhat larger when using a GPU in addition to a CPU, the overall performance still improves significantly when adding a GPU. We have also implemented a parallel version using MPI. For the GLIC system, the code scales up to 256 cores, on the Mahti supercomputer at CSC, with a performance of 42 ns/day, compared with 61 ns/day without constant pH.
Conclusions
We have presented and validated a new implementation of λ-dynamics based constant pH molecular dynamics in the GROMACS software. Our implementation combines several developments in this field into a single MD program, including the multisite representation of titratable groups,46 charge interpolation,21 Particle Mesh Ewald electrostatics,30 and charge constraints.42 Test calculations on amino acids and proteins suggest that the new implementation is efficient, accurate, and agnostic to force fields. Combined with user-friendly parametrization protocols, presented in the accompanying paper,55 we expect that this implementation will pave the way toward routinely including the effect of pH in biomolecular MD simulations.76
Acknowledgments
This research was supported by the Swedish Research Council (Grant 2019-04477), Academy of Finland (Grants 311031 and 332743), and the BioExcel CoE (Grant H2020-INFRAEDI-02-2018-823830). The simulations were performed on resources provided by the CSC — IT Center for Science, Finland, and the Swedish National Infrastructure for Computing (SNIC 2021/1-38). We also thank Erik Lindahl, Helmut Grubmüller, Dmitry Morozov, Serena Donnini, and Plamen Dobrev for their support during the project.
Appendix: Constraint Algorithm
We use constraints to restrict sampling to the correct protonation states in the multisite representation as well as to maintain a neutral charge of the simulation box. Both multisite and charge constraints keep the linear combination of a subset of λ-coordinates constant and are applied simultaneously. Thus, there are Nc constraint equations
| 22 |
for k ≤ Nc. Here, λ is the vector of all λi-coordinates, and Ck is the value of constraint k, which can be zero. If σk(λ) is a multisite constraint, αik = 1 for λi-coordinates that represent one of the protonation states of a residue, while αi = 0 for all other λi-coordinates. If σk(λ) is a constraint for keeping the overall charge constant, αik = ∑jqj,iB – qj,i, with Natomsi the number of atoms whose charges change as a function of λi.
During a leapfrog integration step, all λi-coordinates are first propagated without constraints to their unconstrained new values λiu, which do not fulfill the constraints in eq 22. To obtain the constrained λi values, we first connect the constrained and unconstrained λi values using the definition of σk(λ):
| 23 |
Because
the unconstrained and constrained
λi-coordinates are also connected
by the constraint forces 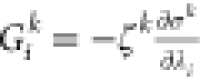 , we
have in addition that
, we
have in addition that
| 24 |
where ζk is the Lagrange multiplier for constraint k, mi the fictitious mass of λi, and Δt the integration time step. Substituting eq 24 in 23 yields
| 25 |
which after rearranging can be expressed as
| 26 |
The last expression can be rewritten in matrix form
| 27 |
where ζ = (ζ1,···,ζNc)T and
| 28 |
Because the αik coefficients remain the same, matrix A is computed once at the start of the simulation. At each step, the elements Δσk are evaluated as the difference between the σk(λu) and σk(λc) = Ck:
| 29 |
The Lagrange multipliers ζk are then obtained from eq 27 and used to correct the unconstrained λi values (eq 24).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c00516.
The input files and parameters used for MD simulations in the presented work (ZIP)
A Mathematica notebook with instructions and routines to fit VMM (ZIP)
Description of λ-potentials, the effect of neglecting the interpolation of Lennard-Jones interactions, titration results for Asp and Glu within the single-site representation, a comparison of pKa values for HEWL obtained with various λ-dynamics-based constant pH methods, demonstration that charge interpolation requires a single evaluation of the electrostatic potential for both single- and multisite representations (PDF)
Author Contributions
N.A. and P.B. contributed equally.
The authors declare no competing financial interest.
Notes
The fork of GROMACS 2021 with constant pH implemented as described here, is available for download free of charge from https://gitlab.com/gromacs-constantph/constantph. In addition to the source code, also instructions on how to set up and perform MD simulations are available
Supplementary Material
References
- Hollingsworth S. A.; Dror R. O. Molecular Dynamics Simulation for All. Neuron 2018, 99, 1129–1143. 10.1016/j.neuron.2018.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groenhof G.; Modi V.; Morozov D. Observe while it happens: catching photoactive proteins in the act with non-adiabatic molecular dynamics simulations. Curr. Opin. Struct. Biol. 2020, 61, 106–112. 10.1016/j.sbi.2019.12.013. [DOI] [PubMed] [Google Scholar]
- Warshel A.; Sussman F.; King G. Free energy of charges in solvated proteins: microscopic calculations using a reversible charging process. Biochemistry 1986, 25, 8368–8372. 10.1021/bi00374a006. [DOI] [PubMed] [Google Scholar]
- Alexov E.; Mehler E. L.; Baker N.; Baptista A. M.; Huang Y.; Milletti F.; Erik Nielsen J.; Farrell D.; Carstensen T.; Olsson M. H. M.; Shen J. K.; Warwicker J.; Williams S.; Word J. M. Progress in the prediction of pKa values in proteins. Proteins: Struct., Funct., Bioinf. 2011, 79, 3260–3275. 10.1002/prot.23189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W.; Morrow B. H.; Shi C.; Shen J. K. Recent development and application of constant pH molecular dynamics. Mol. Simul. 2014, 40, 830–838. 10.1080/08927022.2014.907492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng X.; Mukhopadhyay S.; Brooks C. L. III Residue-level resolution of alphavirus envelope protein interactions in pH-dependent fusion. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 2034–2039. 10.1073/pnas.1414190112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Law S. M.; Zhang B. W.; Brooks C. L. III pH-sensitive residues in the p19 RNA silencing suppressor protein from carnation Italian ringspot virus affect siRNA binding stability. Protein Sci. 2013, 22, 595–604. 10.1002/pro.2243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis C. R.; Shen J. pH-dependent population shift regulates BACE1 activity and inhibition. J. Am. Chem. Soc. 2015, 137, 9543–9546. 10.1021/jacs.5b05891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim M. O.; Blachly P. G.; McCammon J. A. Conformational dynamics and binding free energies of inhibitors of BACE-1: from the perspective of protonation equilibria. PLoS computational biology 2015, 11, e1004341. 10.1371/journal.pcbi.1004341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarkar A.; Gupta P. L.; Roitberg A. E. pH-dependent conformational changes due to ionizable residues in a hydrophobic protein interior: The study of L25K and L125K variants of SNase. J. Phys. Chem. B 2019, 123, 5742–5754. 10.1021/acs.jpcb.9b03816. [DOI] [PubMed] [Google Scholar]
- Sarkar A.; Roitberg A. E. PH-Dependent Conformational Changes Lead to a Highly Shifted p K a for a Buried Glutamic Acid Mutant of SNase. J. Phys. Chem. B 2020, 124, 11072–11080. 10.1021/acs.jpcb.0c07136. [DOI] [PubMed] [Google Scholar]
- Baptista A. M.; Martel P. J.; Petersen S. B. Simulation of protein conformational freedom as a function of pH: constant-pH molecular dynamics using implicit titration. Proteins: Struct., Funct., Bioinf. 1997, 27, 523–544. . [DOI] [PubMed] [Google Scholar]
- Baptista A. M.; Teixeira V. H.; Soares C. M. Constant-pH molecular dynamics using stochastic titration. J. Chem. Phys. 2002, 117, 4184–4200. 10.1063/1.1497164. [DOI] [Google Scholar]
- Bürgi R.; Kollman P. A.; van Gunsteren W. F. Simulating proteins at constant pH: An approach combining molecular dynamics and Monte Carlo simulation. Proteins: Struct., Funct., Bioinf. 2002, 47, 469–480. 10.1002/prot.10046. [DOI] [PubMed] [Google Scholar]
- Mongan J.; Case D. A.; McCammon J. A. Constant pH molecular dynamics in generalized Born implicit solvent. J. Comput. Chem. 2004, 25, 2038–2048. 10.1002/jcc.20139. [DOI] [PubMed] [Google Scholar]
- Meng Y.; Roitberg A. E. Constant pH Replica Exchange Molecular Dynamics in Biomolecules Using a Discrete Protonation Model. J. Chem. Theory Comput. 2010, 6, 1401–1412. 10.1021/ct900676b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itoh S. G.; Damjanovic A.; Brooks B. R. pH replica-exchange method based on discrete protonation states. Proteins: Struct., Funct., Bioinf. 2011, 79, 3420–3436. 10.1002/prot.23176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swails J. M.; York D. M.; Roitberg A. E. Constant pH Replica Exchange Molecular Dynamics in Explicit Solvent Using Discrete Protonation States: Implementation, Testing, and Validation. J. Chem. Theory Comput. 2014, 10, 1341–1352. 10.1021/ct401042b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swails J. M.; Roitberg A. E. Enhancing conformation and protonation state sampling of hen egg white lysozyme using pH replica exchange molecular dynamics. J. Chem. Theory Comput. 2012, 8, 4393–4404. 10.1021/ct300512h. [DOI] [PubMed] [Google Scholar]
- Börjesson U.; Hünenberger P. H. Explicit-solvent molecular dynamics simulation at constant pH: Methodology and application to small amines. J. Chem. Phys. 2001, 114, 9706–9719. 10.1063/1.1370959. [DOI] [Google Scholar]
- Lee M. S.; Salsbury F. R. Jr.; Brooks C. L. III Constant-pH molecular dynamics using continuous titration coordinates. Proteins: Struct., Funct., Bioinf. 2004, 56, 738–752. 10.1002/prot.20128. [DOI] [PubMed] [Google Scholar]
- Khandogin J.; Brooks C. L. Constant pH Molecular Dynamics with proton tautomerism. Biophys. J. 2005, 89, 141–157. 10.1529/biophysj.105.061341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donnini S.; Tegeler F.; Groenhof G.; Grubmüller H. Constant pH molecular dynamics in explicit solvent with λ-dynamics. J. Chem. Theory Comput. 2011, 7, 1962–1978. 10.1021/ct200061r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace J. A.; Shen J. K. Continuous Constant pH Molecular Dynamics in Explicit Solvent with pH-Based Replica Exchange. J. Chem. Theory Comput. 2011, 7, 2617–2629. 10.1021/ct200146j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace J. A.; Shen J. K. Charge-leveling and proper treatment of long-range electrostatics in all-atom molecular dynamics at constant pH. J. Chem. Phys. 2012, 137, 184105. 10.1063/1.4766352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goh G. B.; Knight J. L.; Brooks C. L. Constant pH Molecular Dynamics Simulations of Nucleic Acids in Explicit Solvent. J. Chem. Theory Comput. 2012, 8, 36–46. 10.1021/ct2006314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W.; Wallace J. A.; Yue Z.; Shen J. K. Introducing Titratable Water to All-Atom Molecular Dynamics at Constant pH. Biophys. J. 2013, 105, L15–L17. 10.1016/j.bpj.2013.06.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J.; Miller B. T.; Damjanovic A.; Brooks B. R. Constant pH Molecular Dynamics in Explicit Solvent with Enveloping Distribution Sampling and Hamiltonian Exchange. J. Chem. Theory Comput. 2014, 10, 2738–2750. 10.1021/ct500175m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobrev P.; Donnini S.; Groenhof G.; Grubmüller H. Accurate Three States Model for Amino Acids with Two Chemically Coupled Titrating Sites in Explicit Solvent Atomistic Constant pH Simulations and p K a Calculations. J. Chem. Theory Comput. 2017, 13, 147–160. 10.1021/acs.jctc.6b00807. [DOI] [PubMed] [Google Scholar]
- Huang Y.; Chen W.; Wallace J. A.; Shen J. All-atom continuous constant pH molecular dynamics with particle mesh Ewald and titratable water. J. Chem. Theory Comput. 2016, 12, 5411–5421. 10.1021/acs.jctc.6b00552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y.; Harris R. C.; Shen J. Generalized Born based continuous constant pH molecular dynamics in Amber: Implementation, benchmarking and analysis. J. Chem. Inf. Model. 2018, 58, 1372–1383. 10.1021/acs.jcim.8b00227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris R. C.; Shen J. GPU-accelerated implementation of continuous constant pH molecular dynamics in amber: pKa predictions with single-pH simulations. J. Chem. Inf. Model. 2019, 59, 4821–4832. 10.1021/acs.jcim.9b00754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris R. C.; Liu R.; Shen J. Predicting reactive cysteines with implicit-solvent-based continuous constant pH molecular dynamics in amber. J. Chem. Theory Comput. 2020, 16, 3689–3698. 10.1021/acs.jctc.0c00258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grünewald F.; Souza P. C.; Abdizadeh H.; Barnoud J.; de Vries A. H.; Marrink S. J. Titratable Martini model for constant pH simulations. J. Chem. Phys. 2020, 153, 024118. 10.1063/5.0014258. [DOI] [PubMed] [Google Scholar]
- Mongan J.; Case D. A. Biomolecular simulations at constant pH. Curr. Opin. Struct. Biol. 2005, 15, 157–163. 10.1016/j.sbi.2005.02.002. [DOI] [PubMed] [Google Scholar]
- Damjanovic A.; Miller B. T.; Okur A.; Brooks B. R. Reservoir pH replica exchange. J. Chem. Phys. 2018, 149, 072321. 10.1063/1.5027413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y.; Roux B. Constant-pH Hybrid Nonequilibrium Molecular Dynamics - Monte Carlo Simulation Method. J. Chem. Theory Comput. 2015, 11, 3919–3931. 10.1021/acs.jctc.5b00261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong X.; Brooks C. L. III λ-dynamics: A new approach to free energy calculations. J. Chem. Phys. 1996, 105, 2414–2423. 10.1063/1.472109. [DOI] [Google Scholar]
- Simonson T.; Carlsson J.; Case D. A. Proton binding to proteins: p K a calculations with explicit and implicit solvent models. J. Am. Chem. Soc. 2004, 126, 4167–4180. 10.1021/ja039788m. [DOI] [PubMed] [Google Scholar]
- Chen W.; Shen J. K. Effects of System Net Charge and Electrostic Truncation on All-Atom Constant pH Molecular Dynamics. J. Comput. Chem. 2014, 35, 1986–1996. 10.1002/jcc.23713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; De Vries A. H. The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- Donnini S.; Ullmann R. T.; Groenhof G.; Grubmüller H. Charge-neutral constant pH molecular dynamics simulations using a parsimonious proton buffer. J. Chem. Theory Comput. 2016, 12, 1040–1051. 10.1021/acs.jctc.5b01160. [DOI] [PubMed] [Google Scholar]
- Dobrev P.; Vemulapalli S. P. B.; Nath N.; Griesinger C.; Grubmüller H. Probing the accuracy of explicit solvent constant pH molecular dynamics simulations for peptides. J. Chem. Theory Comput. 2020, 16, 2561–2569. 10.1021/acs.jctc.9b01232. [DOI] [PubMed] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle mesh Ewald: An Nlog(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Knight J. L.; Brooks C. L. III Multisite λ dynamics for simulated structure-activity relationship studies. J. Chem. Theory Comput. 2011, 7, 2728–2739. 10.1021/ct200444f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goh G. B.; Hulbert B. S.; Zhou H.; Brooks C. L. III Constant pH molecular dynamics of proteins in explicit solvent with proton tautomerism. Proteins: Struct., Funct., Bioinf. 2014, 82, 1319–1331. 10.1002/prot.24499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight J. L.; Brooks C. L. III Applying efficient implicit nongeometric constraints in alchemical free energy simulations. Journal of computational chemistry 2011, 32, 3423–3432. 10.1002/jcc.21921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Singhal A. K.; Chien K. Y.; Wu W. G.; Rule G. S. Solution structure of cardiotoxin V from Naja naja atra. Biochemistry 1993, 32, 8036–8044. 10.1021/bi00082a026. [DOI] [PubMed] [Google Scholar]
- Ramanadham M.; Sieker L.; Jensen L. Refinement of triclinic lysozyme: II. The method of stereochemically restrained least squares. Acta Crystallographica Section B: Structural Science 1990, 46, 63–69. 10.1107/S0108768189009195. [DOI] [PubMed] [Google Scholar]
- Sauguet L.; Poitevin F.; Murail S.; Van Renterghem C.; Moraga-Cid G.; Malherbe L.; Thompson A. W.; Koehl P.; Corringer P.-J.; Baaden M.; Delarue M. Structural basis for ion permeation mechanism in pentameric ligand-gated ion channels. EMBO journal 2013, 32, 728–741. 10.1038/emboj.2013.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee T.-W.; Qasim M. Jr; Laskowski M. Jr; James M. N. Structural insights into the non-additivity effects in the sequence-to-reactivity algorithm for serine peptidases and their inhibitors. Journal of molecular biology 2007, 367, 527–546. 10.1016/j.jmb.2007.01.008. [DOI] [PubMed] [Google Scholar]
- Huang J.; MacKerell A. D. Jr CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. Journal of computational chemistry 2013, 34, 2135–2145. 10.1002/jcc.23354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buslaev P.; Aho N.; Jansen A.; Bauer P.; Hess B.; Groenhof G.. Best practices in constant pH MD simulations: accuracy and precision. J. Chem. Theory Comput. 2022, 10.1021/acs.jctc.2c00517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martini-website, General purpose coarse-grained force field. http://cgmartini.nl/index.php/tools2/proteins-and-bilayers/204-martinize (accessed October 01, 2021).
- Kaminski G. A.; Friesner R. A.; Tirado-Rives J.; Jorgensen W. L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B 2001, 105, 6474–6487. 10.1021/jp003919d. [DOI] [Google Scholar]
- Buck M.; Bouguet-Bonnet S.; Pastor R. W.; MacKerell A. D. Jr Importance of the CMAP correction to the CHARMM22 protein force field: dynamics of hen lysozyme. Biophysical journal 2006, 90, L36–L38. 10.1529/biophysj.105.078154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durell S. R.; Brooks B. R.; Ben-Naim A. Solvent-induced forces between two hydrophilic groups. J. Phys. Chem. 1994, 98, 2198–2202. 10.1021/j100059a038. [DOI] [Google Scholar]
- Neria E.; Fischer S.; Karplus M. Simulation of activation free energies in molecular systems. J. Chem. Phys. 1996, 105, 1902–1921. 10.1063/1.472061. [DOI] [Google Scholar]
- Yesylevskyy S. O.; Schäfer L. V.; Sengupta D.; Marrink S. J. Polarizable water model for the coarse-grained MARTINI force field. PLoS computational biology 2010, 6, e1000810. 10.1371/journal.pcbi.1000810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berendsen H. J.; Postma J. P.; van Gunsteren W. F.; Hermans J.. Intermolecular forces; Springer, 1981; pp 331–342. [Google Scholar]
- De Jong D. H.; Baoukina S.; Ingólfsson H. I.; Marrink S. J. Martini straight: Boosting performance using a shorter cutoff and GPUs. Comput. Phys. Commun. 2016, 199, 1–7. 10.1016/j.cpc.2015.09.014. [DOI] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J.; Fraaije J. G. LINCS: a linear constraint solver for molecular simulations. Journal of computational chemistry 1997, 18, 1463–1472. . [DOI] [Google Scholar]
- Miyamoto S.; Kollman P. A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. Journal of computational chemistry 1992, 13, 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
- Hub J. S.; de Groot B. L.; Grubmüller H.; Groenhof G. Quantifying artifacts in Ewald simulations of inhomogeneous systems with a net charge. J. Chem. Theory Comput. 2014, 10, 381–390. 10.1021/ct400626b. [DOI] [PubMed] [Google Scholar]
- Thurlkill R. L.; Grimsley G. R.; Scholtz J. M.; Pace C. N. pK values of the ionizable groups of proteins. Protein science 2006, 15, 1214–1218. 10.1110/ps.051840806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanokura M. 1H-NMR study on the tautomerism of the imidazole ring of histidine residues: I. Microscopic pK values and molar ratios of tautomers in histidine-containing peptides. Biochimica et Biophysica Acta (BBA)-Protein Structure and Molecular Enzymology 1983, 742, 576–585. 10.1016/0167-4838(83)90276-5. [DOI] [PubMed] [Google Scholar]
- Chiang C.-M.; Chien K.-Y.; Lin H.-j.; Lin J.-F.; Yeh H.-C.; Ho P.-l.; Wu W.-g. Conformational change and inactivation of membrane phospholipid-related activity of cardiotoxin V from Taiwan cobra venom at acidic pH. Biochemistry 1996, 35, 9167–9176. 10.1021/bi952823k. [DOI] [PubMed] [Google Scholar]
- Chiang C.-M.; Chang S.-L.; Lin H.-j.; Wu W.-g. The role of acidic amino acid residues in the structural stability of snake cardiotoxins. Biochemistry 1996, 35, 9177–9186. 10.1021/bi960077t. [DOI] [PubMed] [Google Scholar]
- Webb H.; Tynan-Connolly B. M.; Lee G. M.; Farrell D.; O’Meara F.; Søndergaard C. R.; Teilum K.; Hewage C.; McIntosh L. P.; Nielsen J. E. Remeasuring HEWL pKa values by NMR spectroscopy: Methods, analysis, accuracy, and implications for theoretical pKa calculations. Proteins: Struct., Funct., Bioinf. 2011, 79, 685–702. 10.1002/prot.22886. [DOI] [PubMed] [Google Scholar]
- Lee J.; Miller B. T.; Damjanovic A.; Brooks B. R. Enhancing constant-pH simulation in explicit solvent with a two-dimensional replica exchange method. J. Chem. Theory Comput. 2015, 11, 2560–2574. 10.1021/ct501101f. [DOI] [PubMed] [Google Scholar]
- Pezeshkian W.; König M.; Wassenaar T. A.; Marrink S. J. Backmapping triangulated surfaces to coarse-grained membrane models. Nat. Commun. 2020, 11, 2296. 10.1038/s41467-020-16094-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfram Research, Inc. Mathematica, Version 11.3. Champaign: IL, 2018.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.