In vivo extracellular recordings of thalamic and cortical visual responses reveal V1 connectivity rules

Significance

The relation between structure and function is particularly fascinating in neural networks. Direct connectivity measurements in the mouse primary visual cortex show large variability across experimental reports. Can various synaptic connectivity matrices lead to similar firing patterns recorded in the cortex? Vice versa, can observations of firing rate activity constrain possible synaptic wiring patterns? We show that model-based connectivity inference from activity recorded in the thalamus and primary visual cortex reveals hidden ascending order in the strengths of otherwise diverse experimentally reported cortical connections. Thus, diverse cortical connectivity patterns contain mutual motifs that support canonical neural computations observed across cortices and experiments.

Abstract

The brain’s connectome provides the scaffold for canonical neural computations. However, a comparison of connectivity studies in the mouse primary visual cortex (V1) reveals that the average number and strength of connections between specific neuron types can vary. Can variability in V1 connectivity measurements coexist with canonical neural computations? We developed a theory-driven approach to deduce V1 network connectivity from visual responses in mouse V1 and visual thalamus (dLGN). Our method revealed that the same recorded visual responses were captured by multiple connectivity configurations. Remarkably, the magnitude and selectivity of connectivity weights followed a specific order across most of the inferred connectivity configurations. We argue that this order stems from the specific shapes of the recorded contrast response functions and contrast invariance of orientation tuning. Remarkably, despite variability across connectivity studies, connectivity weights computed from individual published connectivity reports followed the order we identified with our method, suggesting that the relations between the weights, rather than their magnitudes, represent a connectivity motif supporting canonical V1 computations.

Ten years ago, connectomics (1, 2) was declared as a future milestone achievement in circuit neuroscience. Since then, a series of connectivity studies in mouse primary visual cortex (V1) substantially advanced our knowledge of the V1 circuit connectome (3–9). However, these studies have also revealed that connection probability and connection strength between any two selected cell types in V1 can vary by up to one order of magnitude across experiments. Such variability in connectivity measurements represents a puzzle for explaining canonical cortical computations ubiquitously observed in functional recordings. For example, the paradoxical response, i.e., the decrease of inhibitory activity following stimulation of the inhibitory population, is present across cortices and experiments (10–12). The presence of such paradoxical decrease across activity recordings suggests that the connectivity patterns of the underlying network may contain motifs supporting this canonical computation. Indeed, theoretical analysis of network models shows that the paradoxical response is only possible for a sufficiently strong connection between excitatory neurons in the underlying network (10, 11). In this sense, a canonical activity feature—paradoxical response—constrains the connectivity of the underlying network. Motivated by this observation, we argue that studying connectivity rules in a theoretical network model starting from canonical computations, such as inhibitory stabilization, offers a promising perspective that may help uncover ubiquitous connectivity motifs within the diverse experimental connectivity measurements.

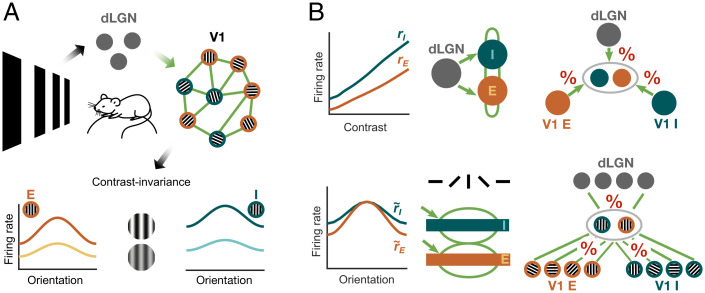
Previous experimental work reported two further canonical computations present across activity recordings in V1: normalization and contrast invariance. Normalization (13) manifests itself in the specific S-shaped profiles of V1 contrast responses. The canonical computation of contrast invariance observed in the activity of orientation-selective V1 cells is characterized by the uniform width of orientation responses preserved across different levels of contrast (14–17). Since normalization and contrast invariance are activity features observed across experiments, we hypothesize that their existence and, in particular, the specific shapes of the corresponding contrast and orientation responses might rely on specific connectivity motifs of the underlying V1 circuit. To understand which connectivity motifs underlie the specific shapes of the recorded contrast and orientation responses, we use the stabilized supralinear network model (SSN) to infer V1 connectivity from activity recordings because this model can account for canonical computations of normalization (18), contrast invariance (19, 20), and inhibitory stabilization (21). Notably, the SSN is one of the few nonlinear population network models for which the mathematical description of possible firing steady-state configurations is available (22), granting a unique opportunity to compare possible activity regimes to observed ones.

We show that combining in vivo extracellular recordings of visual responses in mouse dLGN and V1 with the SSN allows determining diverse sets of V1 connectivity weights leading to the recorded visual responses. Specifically, we find that connectivity weights of different magnitudes can support the same recorded responses, suggesting that variability in connectivity measurements need not contradict the presence of canonical cortical computations. Although each weight shows variability across the inferred connectivity sets, the connectivity weights within individual sets followed a specific order in their magnitudes. For example, the excitatory-to-inhibitory weight was the strongest cortical connection, while the thalamic input weight targeting the excitatory population was the weakest. Remarkably, although experimental connectivity estimates often show large variability across studies (3–7), we found that the magnitudes of connectivity weights within individual experimental connectivity reports follow the same order as we found in our inferred connectivity weights. Using the SSN model, we show how the discovered relationships between the cortical connectivity weights directly relate to specific features of the recorded visual responses. Here, the specific shapes of the recorded nonlinear cortical and thalamic contrast responses and inhibition stabilized network (ISN) condition combined with the SSN model are of particular relevance. Finally, we reveal that the sharper orientation tuning of excitatory cortical neurons compared to inhibitory neurons combined with contrast invariance implies a specific order in the widths of V1 connectivity and thalamic input profiles, explaining why almost untuned thalamic inputs lead to sharper orientation tuning of cortical populations. Overall, our theory-driven approach of determining network connectivity solely based on the recorded in vivo activity allowed us to dissect a series of V1 connectivity motifs underlying canonical V1 computations.

Results

To explore the currently available knowledge about the connectivity of local circuits in mouse V1, we first performed a survey of the literature (SI Appendix, Table S1). Focusing on connection probability and connection strength obtained from multipatch clamp recordings across layers in mouse V1, we found that both connectivity measures showed large variability across experimental reports (SI Appendix, Table S1). For example, we found the connection probability between excitatory neurons in layer 2/3 to vary by a factor of 10, from 2 to 19% (4–6). The probability of a connection from excitatory to parvalbumin-positive (PV+) neurons ranged between 15% (4) and 89% (6), while the value of the average amplitude of the postsynaptic potential (PSP) for this connection varied by more than a factor of 5 (4, 8). Given the large variability across experimental measurements of connection probability and strength, we found that the connectivity weights between neuronal populations, estimated as connection probabilities combined with the corresponding response amplitudes (computation in SI Appendix, Table S1), could vary by up to an order of magnitude. In particular, connectivity weights within the V1 excitatory population (J_EE) or from the excitatory to the inhibitory (PV+) population (J_IE) have the largest variability in layer 2/3 (SI Appendix, Table S1), varying by a factor of 10 across studies.

Faced with this variability, we wondered how to reconcile it with canonical responses found widely across experimental studies. Seminal computational work has shown that variability across some parameters of a circuit model can lead to fundamentally different activity regimes, for example, transitioning from healthy to pathological, while other model parameters can vary by orders of magnitude and still result in stable and similar network activity (23). The latter computational stability can emerge when certain parameter relations (e.g., a ratio of two parameters in the simplest case) remain unchanged, while individual parameters vary, creating a complex map of configurations consistent with specific activity regimes. Assuming that canonical V1 activity features in response to visual stimuli can be used to infer connectivity in a framework of a powerful network model, we suggest an alternative approach for investigating connectivity between neuronal populations in mouse V1. We used the SSN (18, 24) to infer the V1 recurrent and feedforward connectivity weights from the recordings of dLGN and V1 responses (Fig. 1A, Top) (25). Hereby, we exploited contrast invariance (14–17, 19, 20), i.e., the finding that orientation tuning curves preserve their width across different levels of contrast (Fig. 1A, Bottom). Contrast invariance, which we confirmed in our data, allowed us to split the response into contrast and orientation components and develop a two-step inference procedure. In the first step of our connectivity inference, we concentrated on the recorded contrast responses (Fig. 1B, Top Left), which allowed us to fit the SSN model consisting of one excitatory (E) and one inhibitory (I) population that receive input from dLGN (Fig. 1B, Top Middle). Specifically, we determined the dLGN input weights and the recurrent V1 connectivity weights between the E and I populations that best matched the recorded activity (Fig. 1B, Top Right). In the second step, we could expand our inference to the orientation components of the cortical responses (Fig. 1B, Bottom Left) within an extended SSN model that took into account the orientation tuning of the cortical populations (Fig. 1B, Bottom Middle). Here we determined the relative amount of orientation-specific input from each presynaptic source (Fig. 1B, Bottom Right).

Fig. 1.

Inference of thalamic input and V1 recurrent connectivity weights using in vivo extracellular recordings from mouse dLGN and V1 and a network model. (A) (Top) Neurons in area V1 integrate inputs from dLGN and V1 excitatory (E) and inhibitory (I) neurons. The dLGN input, together with the strengths of connections between neurons (green), determines the response of the V1 network. (Bottom) Contrast invariance of E and I V1 neurons means that the width of orientation responses is invariant with respect to contrast. (B) Contrast invariance in V1 allows contrast responses (Top Left) and orientation tuning (Bottom Left) to be treated separately. Due to contrast invariance, the two-population SSN model used for the contrast response analysis (Top Middle) can be embedded in the extended SSN model, which reproduces V1 responses as a function of stimulus contrast and orientation (Bottom Middle). The shape of the contrast responses determines the connectivity weights to the E and I V1 populations arising from dLGN inputs, and recurrent V1 E and V1 I connections (Top Right). The orientation component of the response contains information about the relative amounts of orientation-specific inputs to a population with a particular orientation preference (Bottom Right).

In Vivo Recordings of Mouse V1 Confirm Contrast Invariance of Orientation Tuning.

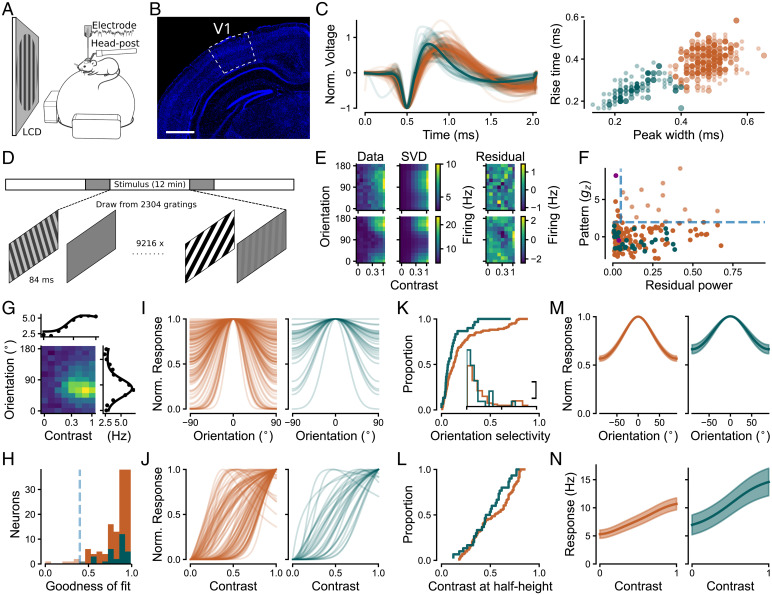
To obtain neuronal responses for the inference of connectivity, we performed extracellular recordings in awake, head-fixed mice (Fig. 2A). We measured visual responses across all layers of V1 (Fig. 2B), with the majority of recorded neurons being located in granular and infragranular layers (see SI Appendix for quantification). To obtain stimulus selectivities separately for the E and I V1 populations, we classified individual neurons (n = 242), based on the extracellular spike wave shape, as putative excitatory (broad-spiking; orange) and putative inhibitory (narrow-spiking; teal) (Fig. 2C). Narrow spike wave shapes are indicative of parvalbumin-positive (PV+) inhibitory interneurons (30–32), which preferentially inhibit one another and pyramidal cells (33, 34) and thus resemble the SSN I population. We confirmed with optotagging of a few neurons (SI Appendix) that PV+ V1 neurons indeed fell into the cluster of narrow-spiking units, as expected from previous studies (34).

Fig. 2.

Population tuning curves for excitatory and inhibitory neurons in V1 are contrast-invariant. (A) Schematic of the setup for extracellular silicon probe recordings in V1. (B) Histology of example V1 recording site. Blue indicates DAPI, and white outline indicates V1, labeled according to ref. 26. Bregma, –2.7 mm. (Scale bar, 1 mm.) (C) Classification of single units based on extracellular wave shape into putative excitatory (broad-spiking, E; orange) and inhibitory (narrow-spiking, I; teal) neurons. (Left) Normalized extracellular wave shapes. (Right) Clustering based on wave shape parameters. Large dots indicate neurons recorded in sessions relevant to the current study, i.e., sessions containing the flashed grating stimulus, $(N=204 \text{E}+38 \text{I})$; small dots indicate V1 neurons recorded in other sessions, used to improve N for clustering. (D) Flashed gratings stimulus paradigm consisting of three stimulus intervals containing a random sequence of gratings (white bars), with interleaved blank periods (gray bars). In some sessions, the blank periods were used for photoactivation of ChR2 expressed in V1 PV+ inhibitory interneurons. (E) Responses of two V1 example neurons to combinations of orientation and contrast (Left), first SVD component (Middle), and SVD residual (Right). Spatial patterns in the residual, such as those that are evident for the lower example neuron, reveal violations of contrast invariance. (F) Violations of contrast invariance were assessed by the power of the SVD residual (> 5%) and significance of spatial autocorrelation ($g_z>1.96$). Light dots indicate contrast-dependent neurons (14/144 E, 0/30 I neurons). Solid dots indicate contrast-invariant neurons, considered for further analysis (130 E, 30 I neurons). Purple indicates example neurons from E. (G) Two-dimensional tuning fit consisting of a product of a hyperbolic ratio function and a wrapped Gaussian (27) for an example V1 neuron. (H) Distribution of fit quality across neurons. Dashed line indicates fit quality threshold (0.4). Solid bars indicate neurons considered for further analysis (125/130 E, 30/30 I neurons). (I) Normalized orientation tuning component for E (Left) and I (Right) neurons. (K) Cumulative distribution of orientation selectivity (OSI; 28, 29). (Inset) Density histogram of orientation selectivity. The x axis is the same as the cumulative distribution; y scale bar represents two neurons per bin of OSI. (J and L) Same as I and K but for normalized contrast response component and cumulative distribution of contrast sensitivity (contrast at which the contrast response function reaches half height). (M and N) Pooled population responses from V1 (mean ± SEM). In C, F, and H–N, orange indicates putative excitatory neurons, and teal indicates putative inhibitory neurons.

During our recordings, we presented briefly flashed (84 ms), static gratings of different orientations and contrasts (Fig. 2D). To determine two-dimensional (2D) contrast and orientation response profiles (Fig. 2E), we performed subspace reverse correlation analysis (36) (SI Appendix, Fig. S1A). For the subsequent analyses, we concentrated on visually responsive neurons (SI Appendix; 181/242 neurons) and determined each neuron’s optimal response time (SI Appendix, Fig. S1B). Since transmission of visual information to V1 requires time, we only considered visually responsive neurons with optimal response times greater than 25 ms (174/242; SI Appendix, Fig. S1B).

We first asked whether responses of individual V1 neurons are contrast-invariant. To this end, we applied a singular value decomposition (SVD) to split response profiles into their largest contrast-invariant component and a residual component (37) (Fig. 2E). Since violations of contrast invariance would be visible as nonrandom spatial patterns in the residual, we used spatial autocorrelation analysis (38) to statistically assess the presence of spatial structure in the residuals (z-scored Gamma index, g_z). Additionally, we computed the power of the residual within the SVD as a measure of the strength of the remaining responses not captured by the separable component (SI Appendix). Similar to the example neuron in Fig. 2E, Top ($g_z=-0.48$, power of residual = 4%), most neurons’ residual lacked spatial structure and constituted only a minor part of the response profile. For other neurons, such as the example neuron in Fig. 2E, Bottom, the SVD residual indeed contained spatial structure ($g_z=8.21$), but its power was negligible (residual power = 2%). Across the population of recorded responses, we thus classified neurons as contrast-invariant if their residual SVD component’s power was small (< 5%) or if the residual did not contain a significant spatial pattern ($g_z<1.96$; Fig. 2F). Consistent with previous studies (14–17), we classified the vast majority of V1 neurons as contrast-invariant (91%, 160/174). The observed violations of contrast invariance were restricted to excitatory neurons (E, 14/144; I, 0/30), but the low number of inhibitory neurons leaves open the possibility that the proportion of contrast invariance in the two populations was similar (Fisher–Yates test, p = 0.13).

Next, we investigated the orientation tuning and contrast response curves of the contrast-invariant neurons (160 neurons). We fitted individual response profiles with a separable 2D tuning model constructed from a hyperbolic ratio function (39) for contrast responses and a wrapped Gaussian (27) for orientation tuning (Fig. 2G). The separable tuning model described the responses of the majority of neurons well (mean $R^2=0.81$ for both excitatory and inhibitory neurons; Fig. 2H), further strengthening our assertion of contrast invariance. Among the well-fit neurons ($R^2>0.4$) used for further analysis (125/130 E, 30/30 I), we concentrated on those neurons with rising contrast response functions (101 E, 30 I).

To characterize selectivity for orientation and contrast, we next analyzed the individual, normalized tuning components of the fitted 2D tuning model (Fig. 2 I–L; normalization by division by maximal response). Focusing first on orientation tuning (Fig. 2I), visual inspection suggested—in the face of a broad range of tuning for both populations—that the inhibitory population had few neurons of narrow tuning. To quantify differences in tuning strength, we computed an orientation selectivity index (OSI) (28, 29) (Fig. 2K). Consistent with previous studies (6, 40–43), we found that excitatory neurons had overall stronger orientation selectivity than inhibitory neurons (E, 0.21 ±0.02; I, 0.13 ±0.03, mean ± SEM; two-tailed Welch’s t test: t = 2.28, p = 0.03). Note that the overall weak orientation selectivity compared to previous results, also in the E population (17), might be at least partially related to our sampling from mostly the infragranular layers (17) and our visual stimulation paradigm with short stimulus duration. We then investigated the normalized contrast response component of the fitted 2D tuning functions (Fig. 2J) and found a broad range of contrast sensitivity. Inspecting the contrast at half-height of the normalized responses (Fig. 2L), we did not find a significant difference between excitatory and inhibitory neurons (E, 0.54 ±0.02; I, 0.49 ±0.02, mean contrast at half-height ± SEM; two-tailed Welch’s t test, $t=1.07,p=0.29$).

Finally, to test whether the average population response was also contrast-invariant, we pooled across individual contrast-invariant neurons by averaging their tuning curves, after aligning them to their preferred orientations. This is important because an average of contrast-invariant neurons does not guarantee contrast invariance of the population (44–46). Analogous to the procedure for the individual neurons, we applied SVD to the population average and studied the spatial autocorrelation of the residual in order to test for contrast invariance. This analysis revealed that the first SVD component accounted for 99.9% of the variance, albeit with a significant spatial pattern in the residual (SI Appendix, Fig. S3A). Due to the small strength of the residual ($<0.1\%$), we conclude that the pooled population response was also contrast-invariant, complementing the invariance of the individual neurons.

To allow connectivity inference in the SSN model (Fig. 1), another key ingredient besides the V1 E and I population responses is the input to the cortical network. Instead of assuming the thalamic input to be linear or retrieving average values from the literature, we used the same stimulus and analysis framework to obtain the dLGN population response for contrast (72 neurons; SI Appendix, Fig. S4). We found its shape to be sigmoidal, with firing rates lying in between those for V1 E and I neurons (SI Appendix, Fig. S4, and Fig. 3A). Taken together, our in vivo extracellular measurements of dLGN and V1 E and I population responses provided contrast-invariant response profiles which we next used for connectivity inference in the SSN model.

Fig. 3.

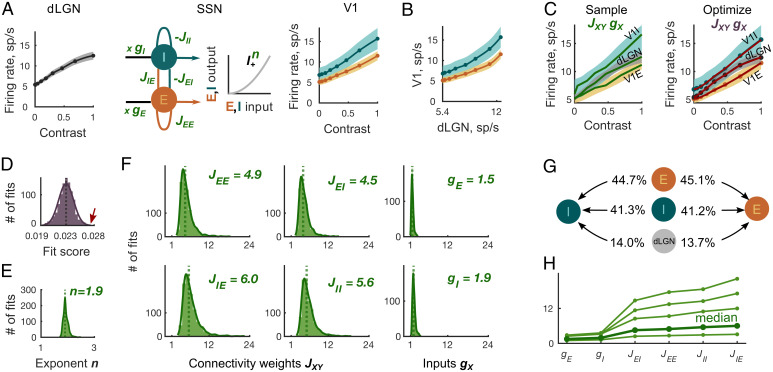
Inference of cortical and thalamic input weights from contrast responses using the SSN model. (A) The cortical network transforms the dLGN population contrast response (Left) to the contrast responses of E and I V1 populations (Right). The SSN model (Middle) represents the cortical network. The weights J_XY > 0 denote the strength of the recurrent connections from cortical population Y to X, and $g_X>0$ denotes the strength of the thalamic input to cortical population X. The transfer function relating input to output of the cortical E and I populations is $I_{+}^n={(\max \{I,0\})}^n$. Shaded areas represent ± SEM of the recorded responses. (B) Supralinear thalamocortical mapping of contrast responses excludes the exponent n = 1 in the SSN model. (C) (Left) Randomly generated sample curves (green lines) within ± SEM of the dLGN and V1 contrast responses (shaded areas) were substituted into the SSN model to yield the initial parameters J_XY and g_X for the fixed exponents n. (Right) Subsequently, the SSN parameters J_XY, g_X, and n were optimized to minimize the distance between the fit (red) and the mean of the recorded responses (orange, gray, and teal). (D) The distribution of fit scores of the final 10³ fits has a mean of $2\times {10}^{-2}$. The arrow (red) points to the largest score value used to produce the example fit in C (red). (E) The distribution of the optimized power law exponents n corresponding to the final 10³ fits has a median of n = 1.9. (F) The distributions of the optimized connectivity weights J_XY are broader than that of input weights g_X. The location of vertical dotted lines corresponds to the J_XY and g_X medians presented in the plot’s upper right corners. (G) The average ratios of connectivity weights from three input sources (local E, local I, and external dLGN) to E cortical population are similar to those to the I population. (H) In 99% of the inferred connectivity parameter sets, the recurrent and input connectivity weights, ordered according to the x axis labels, build an increasing sequence. Thin green lines indicate four representative examples of fits; bold green line indicates median of parameter distributions.

Contrast Responses Reveal Consistent Relations between Connectivity and Input Weights.

Having confirmed contrast invariance of orientation tuning in our in vivo recordings, we first focused on the contrast components of the dLGN and V1 responses to infer feedforward and recurrent connectivity weights. The SSN model (Fig. 3A, Middle) represented the V1 network and translated the thalamic contrast response (Fig. 3A, Left) into contrast responses of the E and I cortical populations (Fig. 3A, Right). The constants J_XY > 0 corresponded to the connectivity weights from the cortical population Y to X with $Y,X\in \{E,I\}$, and the constants $g_X>0$ represented the thalamic input weights to the cortical populations X (Fig. 3A, Middle). The power law transfer function $I_{+}^n={(\max \{I,0\})}^n$ with exponent n (Fig. 3A, Middle) described the nonlinear relationship between the input and output spike rate of a V1 neuron (see figure 5 J and K in ref. 47). Our goal was to determine J_XY, g_X, and n, for which the SSN model reproduced the average recorded thalamic and cortical contrast responses. Specifically, for each recorded contrast C, we required that the stable steady states r_E and r_I and the input $T_{\text{dLGN}}$ of the SSN model equations

$$\begin{array}{l}{r}_X{(C)}^{\frac{1}{n}}=J_{XE}·r_E(C)-J_{XI}·r_I(C)\\ \hspace{1em}+g_X·T_{\text{dLGN}}(C),\hspace{1em}X\in \{E,I\}\end{array}$$ [1]

approximated the mean recorded contrast responses of the V1 and dLGN populations, relative to the spontaneous activity at 0% contrast (Fig. 3A and SI Appendix, Eq.S3). To provide an unbiased comparison with the direct, experimental measurements of connectivity, we computed the J_XY and g_X without prior assumptions about their possible range and without the hyperbolic ratio fit used for Fig. 2. Our only experimentally motivated parameter constraint was the assumption that the power law exponent n ranged between 1 and 5 (48, 49). Notably, plotting the V1 population contrast responses as a function of dLGN contrast response (Fig. 3B), we found a supralinear relationship, which ruled out the possibility that the transfer function was linear (n = 1).

Fig. 5.

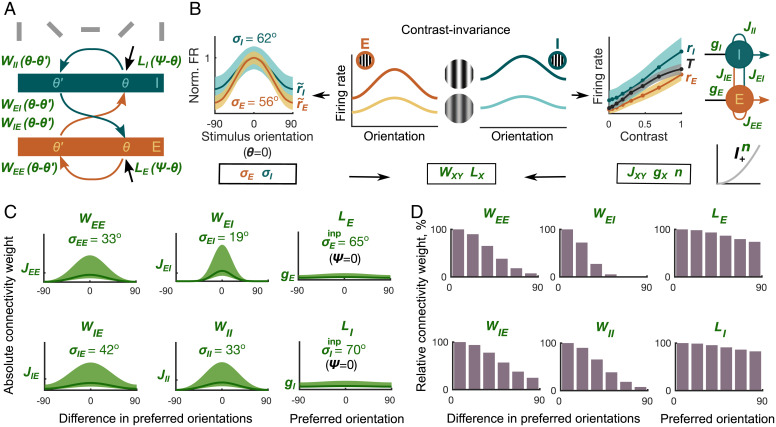
Inferring orientation dependence of recurrent and feedforward connectivity. (A) The connectivity profile $W_{XY}(\theta -\theta \prime )$ describes the connection strength from a population Y to X with a difference in their preferred orientations of $|\theta -\theta \prime |$. The input profile $L_X(\psi -\theta )$ represents the thalamic input to a population with the preferred orientation θ. (B) The width of the normalized orientation tuning curve ${\tilde{r}}_E$ is smaller than ${\tilde{r}}_I$, wrapped Gaussian fit ${\sigma }_E={56}^{°}\pm 2^{°},\hspace{0.17em}{\sigma }_I={62}^{°}\pm 3^{°}$ mean ± SEM (Left). The orientation-dependent connectivity (W_XY) and input connectivity profiles (L_X) are determined using the widths of the recorded orientation tuning curves σ_E and σ_I and the connectivity weights J_XY, g_X, n derived from the contrast responses in Fig. 3. (C) The connectivity profiles W_XY (Left and Middle) can be calculated using σ_X, J_XY, and n. The input profiles L_X (Right) depend on σ_X, g_X, and n. Line indicates connectivity and input profiles for median J_XY, g_X, and n. Shaded area indicates distributions of connectivity and input profiles corresponding to J_XY, g_X, and n distributions in Fig. 3 E and F. (D) Normalized connection strengths between populations with different preferred orientations. The orientations are binned in ${15}^{°}$ steps to aid comparison with experimental findings.

Since direct connectivity measurements often show large variability across studies (SI Appendix, Table S1), we wanted to understand if the V1 network model can reproduce the same recorded contrast response (Fig. 3A, Left and Right) with connectivity weights of different magnitudes and, if yes, how different these connectivity weights could be. Intuitively, if one increases the excitatory weight J_XE to a population, it is necessary to compensate it with a proportional increase in the inhibitory weight J_XI in order to keep the overall firing rates the same. Therefore, we expect J_XE and J_XI that are consistent with the experimentally recorded firing rates to be variable, yet correlated. Thus, to infer distributions of connectivity weights that are consistent with the recorded firing rates, we first generated diverse initial sets of the SSN connectivity parameters J_XY and g_X. In the next step, we optimized these initial SSN parameters to ensure that the SSN steady states and input (r_E, r_I, and $T_{\text{dLGN}}$) closely approximated the average recorded cortical and thalamic contrast responses.

To obtain initial sets of the SSN parameters J_XY, g_X, and n, we generated triplets of sample thalamic and cortical contrast responses $T_{\text{dLGN}}$, r_E, and r_I as random monotonically increasing functions of the contrast C within the ± SEM areas of the measured contrast responses (Fig. 3C, Left). For each such triplet, we kept n constant in the range between 1.1 and 5 and computed the initial six weights J_XY, g_X as a solution of the overdetermined linear system in Eq. 1. We kept the resulting initial weights J_XY, g_X for the optimization procedure if they were positive, and led to a stable steady state of the SSN model (SI Appendix, Eqs. S4–S7). In the next step, we minimized a score function (SI Appendix, Eq. S8) to obtain the optimized weights which accurately reproduced the mean contrast responses (Fig. 3C, Right). The resulting optimal weights yielded excellent fits with low scores (SI Appendix, Eq. S8, and Fig. 3D; to illustrate the accuracy of these fits we show the worst resulting fit in Fig. 3C, Right). Considering the resulting optimal fits, we found that, in line with previous experimental and theoretical evidence (19, 20, 48, 49), the distribution of the power law exponents n peaked at n = 1.9 (Fig. 3E).

Next, we highlight four characteristic features of the resulting connectivity distributions. First, the recorded thalamic and cortical responses were supported by connectivity weights of diverse magnitudes (Fig. 3F), showing that variability in connectivity strengths across experiments does not necessarily contradict the existence of canonical cortical computations. Specifically, we found that the distributions of the inferred thalamic input weights g_E and g_I were largely limited to the range 1 to 5, while distributions of recurrent connectivity weights J_XY were broader and spanned almost a fivefold range, with values from 1 to 24 (Fig. 3F). Second, since it has previously been demonstrated that mouse E and PV+ V1 neurons respond paradoxically to excitation of the PV+ population (12), we asked if the resulting circuit was an ISN (10, 11). We found that all inferred connectivity weights were consistent with the ISN regime (SI Appendix, Eq. S11) (10, 12, 21, 50), starting from the smallest contrast value of 4% recorded in our experiments (SI Appendix, Fig. S5C). Third, the connectivity weights to the I population were stronger than the weights to the E population in all inferred sets of parameters (Fig. 3F, Top, weights to E; Fig. 3F, Bottom, weights to I). However, the relative contributions of the weights from all three input sources (E, I, and dLGN) targeting the E population were remarkably similar to the relative contributions of the weights targeting the I population (Fig. 3G). Finally, even though J_XY and g_X were broadly distributed, the connectivity weights in 98.5% of the 10³ final parameter sets represented an ascending sequence following the order $g_E<g_I<J_{EI}<J_{EE}<J_{II}<J_{IE}$ (Fig. 3H).

Having discovered this strikingly consistent order within the inferred connectivity weights, we next focused on those pairs of connectivity weights for which connection probabilities and amplitudes have been previously reported within experimental studies (Fig. 4). First, we addressed the relationship between the thalamic input weights g_I and g_E. Recently, an extensive in vitro study (51) reported connection probabilities and response amplitudes of thalamocortical connections across V1 layers and cell types. Specifically, Ji et al. (51) demonstrated that the thalamic projections to V1 E neurons had either similar (L2/3 and L6) or slightly lower (L4 and L5) connection probabilities than thalamic projections to PV+ V1 neurons; the response amplitudes, however, were substantially lower in V1 E cells than in PV+ neurons in all V1 layers (see also ref. 52 for L4). Connection probabilities combined with corresponding response amplitudes estimate the connectivity weight between cortical populations. Thus, the data in ref. 51 suggest that the connectivity strength of thalamocortical projections to E neurons is lower than to PV+ V1 neurons. Consistent with this report, our inferred input weights to E cortical neurons were lower (median $g_E=1.5$) than the thalamic input weights to the I neurons (median $g_I=1.9$) across all inferred parameter sets (Fig. 4A).

Fig. 4.

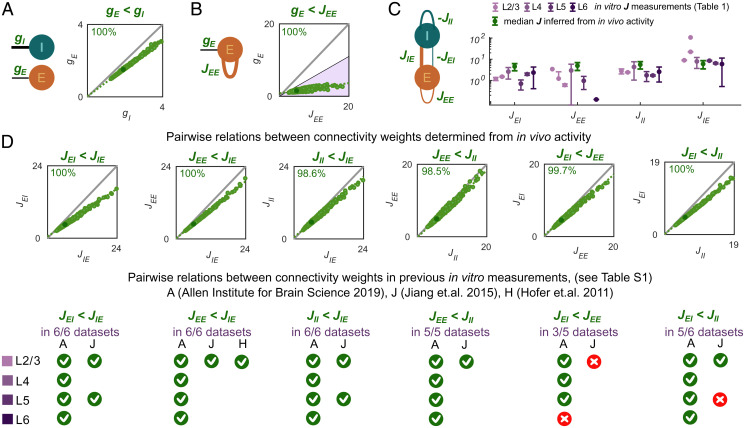
Comparison of the cortical and thalamic input weights inferred from the contrast responses and computed based on the direct experimental connectivity measurements. (A) The thalamic input weights to E cortical population were lower than the I-weights in 100% of the inferred connectivity parameter sets. (B) For cortical E neurons, the weight g_E of the dLGN input was lower than the recurrent cortical weight J_EE in 100% of the inferred connectivity parameter sets. The colored area (purple) comprises relations between J_EE and g_E for which thalamic contribution of excitatory input entering the E cortical population would be smaller than the experimentally determined upper bound of $36\pm 2\%$ (53, 54). (C) The connectivity weights between V1 populations computed from previously published in vitro measurements have largely the same increasing order as the connectivity parameters obtained from our SSN-based inference procedure based on in vivo activity. (D) Most of the pairwise relations between connectivity weights (Fig. 3H) inferred from in vivo activity were consistent with relations computed from previous in vitro measurements (SI Appendix, Table S1).

We next examined the relation between the thalamic feedforward weight g_E and recurrent cortical weight J_EE. Specifically, we related our findings to the experimental results by Lien and Scanziani (53), who performed in vivo recordings of excitatory postsynaptic currents in V1 L4 pyramidal cells and found that thalamic excitation, isolated by optogenetic silencing of V1, was $36\pm 2\%$ of the total pyramidal cell excitation. To understand whether our inferred connectivity was compatible with the lower thalamic contribution to overall V1 excitation reported by Lien and Scanziani (53), we computed thalamic and cortical excitatory contributions to the E cortical population as the product of our recorded cortical and thalamic firing rates with the inferred connectivity weights J_EE and g_E (SI Appendix). Consistent with this observation, the relationship $g_E<J_{EE}$ held across 100% of our inferred sets of connectivity weights (Fig. 4B), suggesting the predominant role of recurrent cortical connections over the thalamic input weights.

We now turned to the cortical circuit and compared the inferred recurrent connectivity weights J_XY with reports from in vitro whole-cell patch-clamp recordings of pyramidal cells and PV+ neurons (SI Appendix, Table S1). For each experimental source, we computed the connectivity weights J_XY (gray cells in SI Appendix, Table S1) as a product of the measured connection probability, the measured strength of the PSP (white cells in SI Appendix, Table S1), and the percentage of neurons in the source population Y of the connection XY. Since our network represents the circuit motif between V1 pyramidal cells and PV+ inhibitory neurons, we made the following assumptions to determine the percentage of neurons in the source population: we set the fraction of excitatory neurons to be 80% of all V1 neurons (55) and the fraction of PV+ neurons to 50% of the inhibitory V1 population in layers 2/3 to 6 (56) (SI Appendix). This resulted in 89% of neurons in the E SSN population and 11% of neurons in the I SSN population (SI Appendix). Visual inspection of the computed connectivity weights in the experimental reports (SI Appendix, Table S1) suggested a similar ascending order to that observed in our inferred connectivity sets (Fig. 4C and SI Appendix, Fig. S5B; for each column in SI Appendix, Table S1, consider the estimated J_XY values in subsequent rows highlighted in gray). Since connectivity weights computed from experimental measurements (SI Appendix, Table S1) sometimes showed large variability across experimental studies, we decided to next analyze the relationship between the weights J_XY within individual studies (4, 6, 8) that contained information on at least one pair of connectivity weights J_XY.

To understand how often the relationship in a pair of the connectivity weights J_XY inferred from our activity recordings coincided with the relationship between connectivity weights determined based on the experimental reports (4, 6, 8) (SI Appendix, Table S1), we systematically analyzed each of six possible pairs built from four connectivity weights J_XY. Remarkably, all measured relations, in which the experimental results among themselves were consistent across all available sources and V1 layers, corresponded to those inferred by our model (J_EI < J_IE, J_EE < J_IE, J_II < J_IE, and J_EE < J_II) (SI Appendix, Table S1, and Fig. 4D, Bottom). Specifically, J_IE was always the strongest connectivity weight, and J_II exceeded J_EE in all cortical layers and in our inferred connectivity sets (SI Appendix, Table S1, and Fig. 4D). The remaining two pairwise relations found in our inferred connectivity sets (J_EI < J_EE and J_EI < J_II) held true for the majority of cortical layers and experimental sources. Specifically, we found three exceptions from the above rules: the relation J_EI < J_EE did not hold in L6, and two available experimental reports for the relation $(J_{EE},J_{EI})$ in L2/3 and $(J_{II},J_{EI})$ in L5 did not lead to consistent conclusions (Fig. 4D, Bottom).

Is it possible to specify which features of the recorded contrast response trajectories lead to the discovered ascending order in the connectivity weights $g_E<g_I<J_{EI}<J_{EE}<J_{II}<J_{IE}$? We used the SSN model equations to analyze the impact of the contrast response shapes and magnitudes on the relations between the connectivity weights. First, we could show that the relation g_E < g_I between the input weights g_E and g_I follows from the SSN equations whenever the relative increase of the I firing rate r_I for low contrasts overtakes the E firing rate r_E increase (SI Appendix, Fig. S6A). The supralinear power law transfer function makes the feedforward thalamic contrast response dominate the recurrent cortical input for low contrasts (24), and the higher input weight g_I ensures that the I firing rate exceeds the E firing rate, as observed in our recorded contrast response functions (SI Appendix). Second, we found that the relation $g_E<J_{EI}$ follows directly from the fact that the cortical network operates as an ISN and because there exists an interval of contrasts where the thalamic contrast response grows faster than the contrast response of the I cortical population (SI Appendix, Fig. S6B). Notably, while the connectivity weights inferred using the nonlinear thalamic response fulfilled the ISN condition automatically (SI Appendix, Fig. S5), none of the connectivity weights inferred assuming a linear thalamic input satisfied the ISN condition for low and intermediate contrasts. Additionally, reflecting the lack of the ISN condition, inference led to thalamic input weights g_E that exceeded the cortical connectivity weights J_EI (SI Appendix, Fig. S7). Finally, we found that the specific shapes of the contrast response functions imply the relations $g_E<J_{EE}$, J_EI < J_EE, $g_I<J_{IE}$, and J_II < J_IE. In particular, these relations hold if for some contrast values, the dLGN contrast response lies above the linear contrast response—the line connecting zero and 100% contrast values—while the recorded cortical contrast responses are located below the linear responses (SI Appendix, Fig. S6C). Notably, as we tested our inference method with the recorded cortical responses and artificial linear thalamic inputs, both thalamic feedforward input weights g_E and g_I exceeded recurrent cortical excitation weights J_EE and J_IE (SI Appendix, Fig. S7). Using this observation and the SSN model, we have shown that the specific concave shape of the thalamic response impacts the relationship between the recurrent connectivity weights of the cortical network (SI Appendix).

Taken together, with minimal prior assumptions and solely based on the recorded in vivo extracellular data, our SSN-based inference method found a consistent ascending order between the inferred cortical and input connectivity weights $g_E<g_I<J_{EI}<J_{EE}<J_{II}<J_{IE}$. Remarkably, despite substantial variability in the absolute values of connectivity measurements in previous in vitro connectomics estimates (white rows in SI Appendix, Table S1), the inferred pairwise relations between connectivity weights (J_EI < J_IE, J_EE < J_IE, J_II < J_IE, and J_EE < J_II, $g_E<J_{EE}$, g_E < g_I) were preserved across experimental sources and cortical layers and matched the relations identified through our inference method. Finally, we used the SSN model to analyze which features of the recorded contrast responses underlie the relations between the thalamic input weights g_E < g_I and the relations $g_E<J_{EE}$, J_EI < J_EE, $g_I<J_{IE}$, and J_II < J_IE between the cortical connectivity and input weights. Additionally, we discovered that the relation $g_E<J_{EI}$ is a consequence of the ISN condition.

Determining Connectivity and Input Profiles from Contrast and Orientation Responses.

Since it is known that V1 neurons form fine-scale subnetworks according to orientation preference and general response similarity (5–7, 57–59), our next goal was to infer orientation-dependent connectivity patterns in a network of orientation-selective cortical neurons. To reproduce the recorded dLGN contrast responses and V1 responses to orientations and contrasts (Fig. 5A and B), we assumed that the cortical firing rates are the steady states R_E and R_I of the SSN model

$$\begin{array}{l}{R}_X(\psi -\theta ,C)=({\displaystyle \underset{-\pi /2}{\overset{\pi /2}{\int }}(}{W}_{XE}(\theta -\theta \prime )R_E(\psi -\theta \prime ,C)\\ -W_{XI}(\theta -\theta \prime )R_I(\psi -\theta \prime ,C))d\theta \prime \\ \hspace{1em}+T_{\text{dLGN}}(C)L_X(\psi -\theta ){)}_{+}^n.\end{array}$$ [2]

Here C represents the stimulus contrast, n is the exponent of the transfer function, θ is the preferred orientation of a cortical population X, $X\in \{E,I\}$, and $R_X(\psi -\theta ,C)$ represents the firing rate of the population X with the preferred orientation θ in response to a grating stimulus having orientation ψ. The connectivity profiles $W_{XY}(\theta -\theta \prime )$ correspond to the strength of connections from population Y to population X that differ in their preferred orientations by $|\theta -\theta \prime |$. The X population with the preferred orientation θ receives the thalamic input $T_{\text{dLGN}}(C)L_X(\psi -\theta )$, and the function L_X describes orientation dependence.

Next, we used our experimental observation of contrast invariance to constrain the recurrent and input connectivity profiles W_XY and L_X in Eq. 2. Contrast invariance means that for a fixed grating orientation, the response can be represented as a product of contrast and orientation components, namely, the firing rates R_E and R_I follow the relations (19, 20)

$$\begin{array}{l}{R}_E(\psi -\theta ,C)=r_E(C){\tilde{r}}_E(\psi -\theta ),\\ R_I(\psi -\theta ,C)=r_I(C){\tilde{r}}_I(\psi -\theta ).\end{array}$$ [3]

Here r_E and r_I are the contrast response functions studied in the previous section, and ${\tilde{r}}_E$ and ${\tilde{r}}_I$ are the peak-aligned and normalized orientation tuning curves (Fig. 5B, Left). The property of contrast invariance is computationally advantageous because it allowed us to reduce the 2D product of its 1D contrast and orientation components and study each component independently. We found that contrast responses r_X, $T_{\text{dLGN}}$ (Fig. 5B, Right), and orientation tuning curves ${\tilde{r}}_X$ (Fig. 5B, Left) provide direct access to the connectivity W_XY and input tuning profiles L_X as expressed by the following relations:

$$\begin{array}{l}{\displaystyle {\int }_{-\pi /2}^{\pi /2}{W}_{XY}}(\theta -\theta \prime ){\tilde{r}}_Y(\psi -\theta \prime )d\theta \prime \text{}=\text{}{J}_{XY}{({\tilde{r}}_X(\psi -\theta ))}^{1/n},\\ \hspace{1em}{L}_X(\psi -\theta )=g_X{({\tilde{r}}_X(\psi -\theta ))}^{1/n},\hspace{1em}X,Y\in \{E,I\},\end{array}$$ [4]

where the connectivity and input weights J_XY and g_X correspond to the cortical and thalamic contrast response functions studied in the previous section (for full derivation, see SI Appendix, Eqs. S18–S27). Relations in Eq. 4 generalize the result in Persi et al. (60), which showed that the wrapped Gaussian approximation makes it possible to relate orientation tuning curves and connectivity profiles.

In order to understand how our inferred connectivity between populations depends on the similarity of their orientation preference, we next determined the widths of the recurrent connectivity profiles W_XY (Fig. 5C, Left and Middle) and the input profiles L_X (Fig. 5C, Right and SI Appendix, Eqs. S29 and S31). Interestingly, inspecting equations in SI Appendix, Eqs. S29 and S31, we realized that the recorded contrast responses corresponding to J_XY and g_X mostly determine the amplitudes of the connectivity and input profiles and represent connectivity strength between populations with similar preferred orientations (Fig. 5C). In contrast, the widths of orientation tuning curves σ_X together with the power law exponent n characterizing the neuronal transfer properties determine the widths of connectivity profiles. The relative widths of connectivity and input profiles are best visible after normalizing their amplitudes (Fig. 5D). We found that the widths of connectivity profiles in each parameter set followed the order ${\sigma }_{EI}<{\sigma }_{EE}\approx {\sigma }_{II}<{\sigma }_{IE}$. This order of connectivity profiles’ widths resembled the ascending order of connectivity weights $J_{EI}<J_{EE}<J_{II}<J_{IE}$ discussed in the previous section.

How do our inferred connectivity profiles W_XY and tuning properties of the thalamic inputs L_X relate to previous experimental results? We first compared the width of the inferred thalamic input profiles L_X with the width of V1 orientation tuning curves (Fig. 5B, Left), a relation addressed in prior experimental reports (e.g., refs. 53, 61–64). We found that the widths of the inferred orientation-specific thalamic inputs to cortical neurons (mean ${\sigma }_E^{\text{inp}}={65}^{°},\hspace{0.17em}{\sigma }_I^{\text{inp}}={70}^{°}$) have a broader tuning than the average V1 orientation tuning curves themselves (mean ${\sigma }_E={56}^{°},\hspace{0.17em}{\sigma }_I={62}^{°}$). This is consistent with a wide range of experimental studies across cortical layers, showing broader dLGN input than V1 orientation tuning curves (53, 61–64).

We also compared our derived cortical connectivity profiles W_XY with previous direct connectivity measurements. To the best of our knowledge, information on how connection probability and the relative connection strength of I-to-E, and I-to-I projections depend on the difference in the populations’ preferred orientations does not seem to be available (but see ref. 57). Hence, for our comparison of inferred and experimentally measured orientation-dependent profiles, we concentrated on the direct measurements currently available for E-to-E and E-to-PV+ connections in L2/3 (5, 6). The orientation dependence of our inferred connectivity profiles (mean ${\sigma }_{EE}={33}^{°},\hspace{0.17em}{\sigma }_{IE}={42}^{°}$; Eq. 4 and SI Appendix, Eq. S31) is consistent with direct experimental measurements of connection probability (5, 6), demonstrating that the connectivity profile between pairs of E neurons was sharper than the E-to-I connectivity profile.

In summary, we found that the widths of the connectivity profiles we derived from in vivo extracellular activity followed the order ${\sigma }_{EI}<{\sigma }_{EE}\approx {\sigma }_{II}<{\sigma }_{IE}$, resembling the order of the connectivity weights $J_{EI}<J_{EE}<J_{II}<J_{IE}$. Consistent with experimental reports across cortical layers, we found that both E and I input profiles L_X were broader than the average cortical orientation tuning curves. For future experiments, our results predict that W_EI is the narrowest and W_IE is the broadest profile of all four projections. We derived this relation from two observations: 1) that the width of the I orientation profile σ_I exceeds that of the E population σ_E and 2) that the width ${\sigma }_E^{\text{inp}}$ of the E input profile L_E exceeds the width of orientation tuning curve σ_I (SI Appendix).

Discussion

Here we combined in vivo extracellular dLGN and V1 responses with the stabilized supralinear network (SSN) model to infer feedforward and recurrent connectivity weights of mouse primary visual cortex and their orientation-dependent connectivity profiles. In a two-step inference procedure based on the separation of contrast and orientation tuning of V1 responses, we identified consistent relationships between the input and recurrent cortical connectivity weights, g_E < g_I, $g_E<J_{EE}$, and $J_{EI}<J_{EE}<J_{II}<J_{IE}$. We were also able to extract these relations from experimental functional connectomics results showing variability across studies. Our results demonstrate that connectivity weights of diverse magnitudes can support the same recorded thalamic and cortical responses. However, the specific shapes of the recorded responses rely on ubiquitous connectivity motifs present across otherwise diverse connectivity measurements. These results provide evidence that key computations of visual processing are imprinted into the underlying connectivity and can be discovered via a circuit model.

Inferred Connectivity Reveals Principles Consistent with Previous Functional Connectomics Estimates.

Cell type–specific connectivity in mouse V1 has been measured by a number of functional connectomics studies (4, 6, 8). These studies reported amplitudes of PSPs and connection probabilities which can differ by an order of magnitude across experiments (SI Appendix, Table S1). Specifically, considering relations between pairs of connectivity weights—a procedure similar to methods applied to single slices or individual neurons to remove experimental variability (e.g., refs. 51, 65, 66)—revealed that the relative magnitude of the recurrent weights followed the order $J_{EI}<J_{EE}<J_{II}<J_{IE}$ across the majority of experimental studies and across the different cortical layers. Intriguingly, this order was also contained in the connectivity we derived from our in vivo data. Our further theoretical analysis of the recorded cortical and thalamic contrast responses suggests that the specific response shapes rely on the order we identified using our inference procedure. We note that a specific rank structure of the connectivity weights between the neuronal populations requires combining PSP amplitudes with the connection probability. In contrast to the connectivity weights between the neuronal populations, the PSP amplitudes between individual cell types alone do not seem to follow a specific rank structure.

Our results support several experimental and theoretical findings related to the computational regime of the cortex. First, the strong E-to-I connection has been linked in a previous computational study to image discriminability (67). Second, we found that 100% of the inferred feedforward and recurrent connectivity weights were consistent with the inhibition stabilized regime (12, 50). This regime has been associated with the paradoxical firing rate reduction in response to increased excitation of the I population and a fast, flexible stabilization mechanism that balances otherwise unstable networks (11, 50). Such a paradoxical response of cortical populations seems to be present in both superficial and deep layers of mouse V1 (12). Interestingly, although previous studies hypothesized that a strong connectivity weight J_EE might be a requirement for inhibitory stabilization (11, 50, 67), the ISN regime arises in our network even though the connectivity weights J_EE and J_EI were the smallest entries in the connectivity matrix (Fig. 3). Last, our inference method exploited the property of contrast invariance (19, 20), which we confirmed at the level of single neurons as well as cortical excitatory and inhibitory populations. This indicates that contrast invariance and inhibitory stabilization can be supported jointly by a connectivity pattern consistent with recorded cortical and thalamic activity.

Furthermore, we determined the widths of the orientation-dependent connectivity profiles showing that they follow the order ${\sigma }_{EI}<{\sigma }_{EE}\approx {\sigma }_{II}<{\sigma }_{IE}$. Specifically, we have shown that this ascending order of the connectivity profiles’ widths is a direct consequence of the property of contrast invariance, combined with the observation that the recorded inhibitory orientation tuning curve is broader than its excitatory counterpart. In line with our inferred relation ${\sigma }_{EI}<{\sigma }_{EE}$, direct measurements of orientation-dependent connectivity profiles report that the E-to-E connection is sharper than that of E-to-PV+ in V1 L2/3 (5, 6). However, both profiles W_EE and W_IE which we inferred from our in vivo recorded data were sharper than respective profiles reported in the direct connectivity measurements (5, 6). Investigating our network model and its implications, we found that broader profiles W_EE and W_IE correlate with narrower orientation tuning in the excitatory population. Interestingly, V1 L2/3 pyramidal neurons targeted in the previous connectivity measurements (5, 6) are known to display sharper orientation tuning (e.g., refs. 17, 63) compared to lower layers, which dominate in our experimental data. Thus, the overall broader orientation tuning curves in deeper cortical layers might cause the sharper tuning of connectivity profiles W_EE and W_IE we find based on our recorded data.

Previous work reported that E cortical neurons receive primarily untuned input from their local inhibitory afferents (68). We emphasize that our highly selective W_EI represents the connectivity profile and not the recurrent input current profile measured in these experiments. Indeed, our theory predicts that the input arriving at E cortical population from their local I afferents is a convolution of the functions W_EI with the I orientation tuning curve (SI Appendix). Consequently, we show that the resulting width of the recurrent input profiles from each of the local afferents is equal to the widths of the corresponding external thalamic input profiles, which we found to be almost flat. Additionally, although direct measurements of the highly selective connectivity profile W_EI do not seem to be available at present, the overall similarity of neuronal feature selectivity found for this connection in Znamenskiy et al. (57) can serve as a predictor of connectivity in mouse V1 L2/3.

We not only studied the recurrent connections in cortex but also considered simultaneously the thalamic input strengths and their profiles. Recurrent connections and feedforward input weights are rarely measured at the same time (53, 54, 63, 68); therefore, it is often difficult to study their relative strength. Consistent with previous experimental results, we found cortical connections to be stronger than the thalamic input weights, indicating that only a fraction of the excitation in cortex is due to the thalamic connections (53, 54, 63). Our findings are also in line with direct comparisons of orientation selectivity of dLGN spiking output, V1 membrane potential, and V1 spiking activity (61), where dLGN spiking output was found to be more strongly orientation-tuned than the average V1 membrane potential. This would predict that orientation-tuned information from thalamus is either mixed when converging on V1 neurons or preserved only for specific projections, such as shown for the relay of direction selectivity from retinal ganglion cells via the shell of dLGN to upper layers in V1 (70). In general, the tuning of thalamocortical afferents and their interplay with intracortical connections in the emergence of orientation selectivity have been under intense discussion. Our model results provide evidence that if thalamic afferents, cortical inputs, membrane transfer functions, and stimulus responses are considered together, orientation tuning can be generated with a combination of weaker, broadly tuned thalamic input and strong, sharply tuned cortical connections (53, 54, 63).

Theory-Based Inference of Connectivity from In Vivo Responses Complements Existing In Vitro Approaches.

Inferring network connectivity using a theory-driven network model and in vivo responses complements existing in vitro approaches based on paired whole-cell recordings (3–9, 34), photostimulation (71), or glutamate uncaging (72), gold standard methods for assessing circuit-level connectivity. One strength of our method is that it is based on functional measurements in the intact, living brain, which has the potential to overcome limitations imposed by the unavoidable truncation of axodendritic branches in slices, where connectivity measurements constitute a lower bound. In addition, since our in vivo activity recordings are obtained under thalamocortical operating regimes established by local and long-range activity, they reflect, for instance, neuromodulatory input (73, 74), specific short-term synaptic dynamics (75), and background synaptic activity, rarely present under in vitro conditions (76). Finally, our inference method rests on stimulus-driven responses of neuronal populations and can thus yield estimates of connectivity in the context of functional response properties. This is important because fine-scale specificity of connectivity with respect to visual tuning similarity is a prominent motif in primary visual cortex (5–7, 59) but typically requires technically challenging experiments involving a reidentification of neurons in vitro after their visual response properties were first characterized in vivo (5–7, 57, 59, 77–79). Such mapping is currently only performed by a few laboratories worldwide, which have the appropriate technical resources and broad methodological expertise.

Our model-based connectivity inference connects a mathematically interpretable, generative model of brain activity with the underlying circuit. In contrast to direct connectivity reconstruction (3, 80, 81) or inference approaches using large spiking networks (82–84), which focus on detailed neuron-to-neuron connectivity, we are able to deduce cortical firing regimes and possible network states directly from the inferred weight matrix. Since the inferred connectivity is connected to a generative model, it can additionally be used to generate predictions about network activity that can be tested experimentally. Other groups have recently made complementary progress in inferring connectivity from constrained models, focusing on spatial integration and behavioral state (85), inhibitory cell types (86), or response perturbations (87), showing that model-based connectivity inference can be used flexibly to elucidate multiple aspects of cortical information processing. Yet, our approach is unique in that it succeeds in inferring remarkably accurate cortical connectivity features directly and exclusively from dLGN and V1 response data, without imposing connectivity constraints taken from the literature.

Future Directions.

Our results can be extended in several directions. Conceptual advances on the experimental side demonstrate that not only orientation preference but general similarity in stimulus selectivity can influence V1 connectivity (7, 57). Future modeling efforts could thus expand the computational framework we present here to other aspects of feature selectivity, such as receptive field location, spatial and temporal frequency preferences, and similarity of responses to temporally varying stimuli. More substantially, while V1 neurons can be broadly classified into excitatory and inhibitory types, there are many known subtypes for both excitatory and in particular inhibitory V1 neurons (4, 34, 88–94). Future work, both on the recording and modeling front, could therefore consider more neuronal subtypes in relation to specific computations. For instance, interneuron-specific two-photon calcium imaging (85–87) or optogenetic perturbations (12, 87) would have the potential to inform multidimensional circuit models including multiple cell types. In this context, it might also be interesting to further explore the role of SbC neurons, which we found to constitute a substantial fraction of dLGN and V1 neurons. Here multipopulation SSNs might help elucidate their so-far relatively unexplored function (17, 95–97). Future work could also consider cortical layers separately, providing insights into the pronounced differences in connectivity and potentially operating regime observed experimentally (11, 98, 99). For instance, L2/3 is well known for its long-range connectivity between similarly tuned pyramidal cells (5, 58), strong lateral inhibition, and the sparsity of responses (41, 98), while L5 coding is considered dense, with higher firing rates and broader stimulus selectivity (98, 100).

With respect to theoretical insights, an important next step would be establishing ubiquitous connectivity statistics in the alternative modeling frameworks (101) taking into account additional or complementary circuit mechanisms. This step would require mathematical theories to bridge these models with the SSN-type circuits and direct connectivity measurements. Besides, we have so far restricted our analyses on the steady state, but responses to contrast and orientation are well known to exhibit interesting and relevant dynamics, such as phase advance (16) and time-dependent sharpening of tuning (102). In the future, it will be important to extend our approach to understand whether and to which degree the dynamic changes in the population responses are accompanied by changes in the underlying functional connectivity.

Finally, future studies could investigate how recurrent V1 and thalamic input connectivity change as a function of behavioral state of the animal. Indeed, previous work has suggested that effective connectivity might change with locomotion and stimulus context (85, 103). Exploiting in vivo recordings, which can encompass the full spectrum of behavioral state-related neuronal modulations, and our model-based inference framework to study circuit connectivity promises to generate novel insights into the potentially highly dynamic relationship between connectivity and computations.

Data, Materials, and Software Availability

Data and computer code underlying this manuscript can be found at G-Node (https://doi.gin.g-node.org/10.12751/g-node.qwc7y5) (25). All other study data are included in the article and/or SI Appendix.