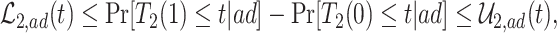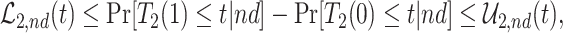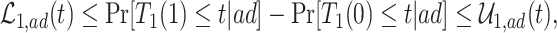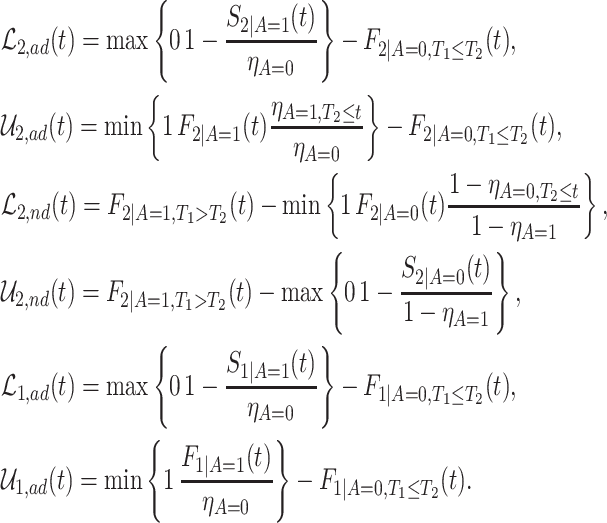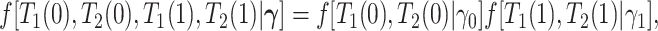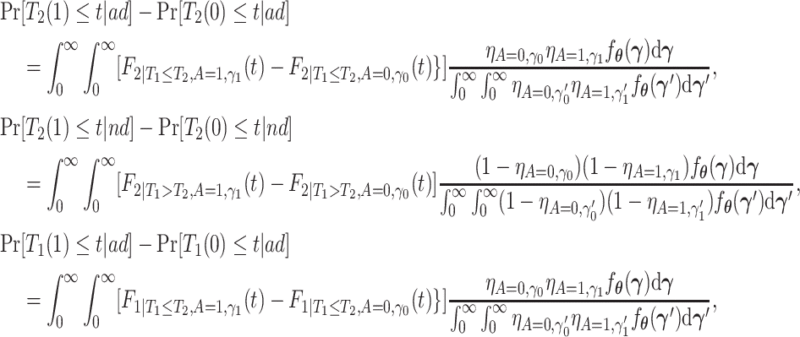Summary
The causal effects of Apolipoprotein E 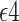 allele (APOE) on late-onset Alzheimer’s disease (AD) and death are complicated to define because AD may occur under one intervention but not under the other, and because AD occurrence may affect age of death. In this article, this dual outcome scenario is studied using the semi-competing risks framework for time-to-event data. Two event times are of interest: a nonterminal event time (age at AD diagnosis), and a terminal event time (age at death). AD diagnosis time is observed only if it precedes death, which may occur before or after AD. We propose new estimands for capturing the causal effect of APOE on AD and death. Our proposal is based on a stratification of the population with respect to the order of the two events. We present a novel assumption utilizing the time-to-event nature of the data, which is more flexible than the often-invoked monotonicity assumption. We derive results on partial identifiability, suggest a sensitivity analysis approach, and give conditions under which full identification is possible. Finally, we present and implement nonparametric and semiparametric estimation methods under right-censored semi-competing risks data for studying the complex effect of APOE on AD and death.
allele (APOE) on late-onset Alzheimer’s disease (AD) and death are complicated to define because AD may occur under one intervention but not under the other, and because AD occurrence may affect age of death. In this article, this dual outcome scenario is studied using the semi-competing risks framework for time-to-event data. Two event times are of interest: a nonterminal event time (age at AD diagnosis), and a terminal event time (age at death). AD diagnosis time is observed only if it precedes death, which may occur before or after AD. We propose new estimands for capturing the causal effect of APOE on AD and death. Our proposal is based on a stratification of the population with respect to the order of the two events. We present a novel assumption utilizing the time-to-event nature of the data, which is more flexible than the often-invoked monotonicity assumption. We derive results on partial identifiability, suggest a sensitivity analysis approach, and give conditions under which full identification is possible. Finally, we present and implement nonparametric and semiparametric estimation methods under right-censored semi-competing risks data for studying the complex effect of APOE on AD and death.
Keywords: Alzheimer’s disease, Bounds, Frailty model, Illness-death model, Principal stratification
1. Introduction
Having at least one Apolipoprotein E 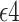 allele (APOE) has been associated with a substantial increase in risk of late-onset Alzheimer’s disease (AD) (Alzheimer’s Association, 2019). With the development of clustered regularly interspaced short palindromic repeats (CRISPR) for possible gene editing, researchers have begun contemplating gene editing on APOE as a preventive intervention against AD (Safieh and others, 2019). However, the standard average causal effect on AD is ill-defined because some study participants die without an AD diagnosis, and it is unknown whether APOE has a causal effect on survival (Corder and others, 1993; Dal Forno and others, 2002). When considering the impact of intervening on APOE, a holistic approach focusing on effects on both AD and death is desirable to help public health officials to weigh potential benefits and risks and to conclude whether gene editing of APOE is a viable intervention.
allele (APOE) has been associated with a substantial increase in risk of late-onset Alzheimer’s disease (AD) (Alzheimer’s Association, 2019). With the development of clustered regularly interspaced short palindromic repeats (CRISPR) for possible gene editing, researchers have begun contemplating gene editing on APOE as a preventive intervention against AD (Safieh and others, 2019). However, the standard average causal effect on AD is ill-defined because some study participants die without an AD diagnosis, and it is unknown whether APOE has a causal effect on survival (Corder and others, 1993; Dal Forno and others, 2002). When considering the impact of intervening on APOE, a holistic approach focusing on effects on both AD and death is desirable to help public health officials to weigh potential benefits and risks and to conclude whether gene editing of APOE is a viable intervention.
The semi-competing risks (SCR) framework have been used as a basis for studying AD and death jointly (Varadhan and others, 2014; Lee and others, 2017; Nevo and others, 2021a). More generally, SCR data arise when times to two events of interest are studied, nonterminal (e.g., disease diagnosis) and terminal (e.g., death) events. The nonterminal event is observed only if it precedes the terminal event, which may occur before or after the nonterminal event.
The illness-death model is often used for studying SCR data. It focuses on transition times between three different states: An initial state (state “0,” healthy), a diseased state (“1,” AD), and an absorbing state (“2,” death). Possible transitions are 0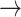 1, 0
1, 0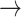 2, and 1
2, and 1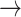 2. Various time-to-event models have been suggested to analyze SCR data in this framework. Typically, inter-personal dependence between illness and death times is modeled via a random effect, known as frailty (Xu and others, 2010; Lee and others, 2017; Gorfine and others, 2021).
2. Various time-to-event models have been suggested to analyze SCR data in this framework. Typically, inter-personal dependence between illness and death times is modeled via a random effect, known as frailty (Xu and others, 2010; Lee and others, 2017; Gorfine and others, 2021).
In the causal inference paradigm, the related “truncation by death” problem has been studied (Zhang and Rubin, 2003; Long and Hudgens, 2013; Tchetgen Tchetgen, 2014; Ding and Lu, 2017; Zehavi and Nevo, 2021). This problem arises when researchers aspire to compare outcomes between the treated and untreated groups at a fixed time point after the treatment was assigned, but some study participants may die prior to outcome collection, hence the average causal effect is not well-defined. Using principal stratification (Frangakis and Rubin, 2002), the survivor average causal effect (SACE) is the causal effect within the stratum of people who would have survived under both treatment values. A similar problem arises in vaccination studies, as vaccine effects on post-infection outcomes are well-defined only among those who would have been infected with or without vaccinating (Shepherd and others, 2007). The SACE is nonparametrically unidentifiable, unless strong assumptions are made. Therefore, researchers have developed bounds (Zhang and Rubin, 2003; Long and Hudgens, 2013) and sensitivity analyses (Shepherd and others, 2007). However, none of these papers apply to SCR data, where the time-to-event nature of both AD diagnosis and death must be addressed.
Robins (1995) utilized additional assumptions to show the average causal effect (not SACE) is identifiable when censoring time is always observed, and without distinguishing between censoring due to death or other reasons. More recently, two papers have considered causal questions for SCR data (Comment and others, 2019; Xu and others, 2020). These papers suggested Bayesian methods to estimate the time-varying SACE (TV-SACE) and restricted mean SACE (RM-SACE). These papers provide major improvement towards causal reasoning for SCR data. One of the works rely on parametric frailty-based illness-death models (Comment and others, 2019), while the other coupled a parametric sensitivity copula-based analysis with a nonparametric Bayesian method under an additional identifying assumption (Xu and others, 2020). Questions of nonparametric partial identifiability under weaker assumptions, or sensitivity analyses without the copula model, as well as frequentist estimation were all not addressed.
In this article, we define new causal estimands for capturing the causal effect of APOE on AD and death times within the SCR framework. The general idea resembles principal stratification in that we propose to stratify the population according to their potential outcomes. In Section 2, we propose new causal estimands for SCR data, that focus on effects defined within a fixed, not time-varying, population. As with principal stratification, membership status of this subpopulation is unobserved. In Section 3, we present novel causal assumptions under the SCR data structure that are motivated by the study of APOE and AD. Our new assumption termed order preservation is more flexible than the traditionally used monotonicity assumption (Zhang and Rubin, 2003). Section 3 also provides partial identifiability results for the proposed estimands under the new assumptions and full identifiability results under a bivariate frailty semiparametric illness-death model. In Section 4, we propose kernel-based nonparametric methods and a sensitivity analysis built upon a semiparametric illness-death frailty model. A fully reproducible simulation study is described in Section 5, before turning to the study of APOE effects on AD and death, in length, in Section 6. Concluding remarks are given in Section 7. The R package  implements all the developed methodologies and is available from https://github.com/daniel258/CausalSemiComp and the reproducibility materials are available from https://github.com/daniel258/CausalSemiCompReproduce.
implements all the developed methodologies and is available from https://github.com/daniel258/CausalSemiComp and the reproducibility materials are available from https://github.com/daniel258/CausalSemiCompReproduce.
2. Notation and causal estimands
Let 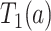 and
and 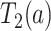 be the times to AD diagnosis and death, respectively, had we set APOE level to
be the times to AD diagnosis and death, respectively, had we set APOE level to 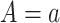 , with
, with 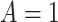 indicating having at least one APOE
indicating having at least one APOE 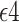 allele, and
allele, and 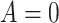 indicating no APOE
indicating no APOE 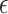 4 alleles. Let
4 alleles. Let 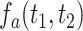 be the joint density function of
be the joint density function of 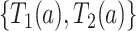 on
on 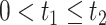 for
for 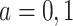 . Because death may occur before AD diagnosis,
. Because death may occur before AD diagnosis, 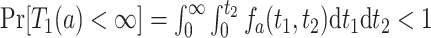 . The event
. The event 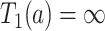 or, stated differently,
or, stated differently, 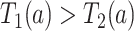 corresponds to not having AD under
corresponds to not having AD under 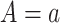 . We defer assumptions on the joint distribution of
. We defer assumptions on the joint distribution of 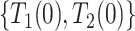 and
and 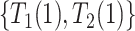 for later; these two pairs could never be observed simultaneously.
for later; these two pairs could never be observed simultaneously.
Consider the average causal effect of APOE on the survival time 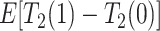 . Because APOE affects AD incidence (Alzheimer’s Association, 2019), and because AD patients are likely to die earlier compared to the scenario they did not have AD (Tom and others, 2015), we would expect
. Because APOE affects AD incidence (Alzheimer’s Association, 2019), and because AD patients are likely to die earlier compared to the scenario they did not have AD (Tom and others, 2015), we would expect  , even if APOE does not carry an effect on age at death other than the effect resulting from earlier AD onset. Additionally, when focus is on AD,
, even if APOE does not carry an effect on age at death other than the effect resulting from earlier AD onset. Additionally, when focus is on AD, 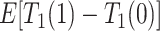 is ill-defined, because
is ill-defined, because 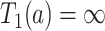 for some study units for either or both
for some study units for either or both 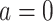 and
and 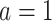 .
.
Therefore, causal inference for SCR data is entangled. Principal stratification effects suggested to address this challenge are defined within a strata of the population created by the potential values of a postrandomization variable, which is not the object of inquiry (Frangakis and Rubin, 2002). For SCR data, principal stratification approaches can be divided into two types: time-fixed and time-varying estimands. The time-fixed approach focuses on a single time point 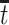 , say age 80, and defines the binary potential outcomes
, say age 80, and defines the binary potential outcomes 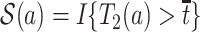 and
and 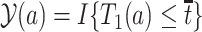 as the survival status and AD status at time
as the survival status and AD status at time 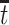 under APOE level
under APOE level 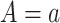 . The SACE
. The SACE 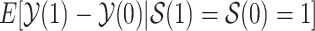 compares the population-level risk of AD by age
compares the population-level risk of AD by age 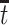 with and without APOE only among those who would have survived until age
with and without APOE only among those who would have survived until age 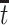 under both APOE statuses. Typically, strong assumptions are needed for identifying the SACE. One commonly made assumption is the monotonicity assumption
under both APOE statuses. Typically, strong assumptions are needed for identifying the SACE. One commonly made assumption is the monotonicity assumption 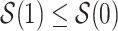 (Zhang and Rubin, 2003; Ding and Lu, 2017; Zehavi and Nevo, 2021). That is, those surviving beyond time
(Zhang and Rubin, 2003; Ding and Lu, 2017; Zehavi and Nevo, 2021). That is, those surviving beyond time 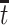 and have APOE would also survive beyond
and have APOE would also survive beyond 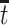 had they did not have APOE. A more recent approach (Comment and others, 2019; Xu and others, 2020) focuses on the TV-SACE causal effect
had they did not have APOE. A more recent approach (Comment and others, 2019; Xu and others, 2020) focuses on the TV-SACE causal effect 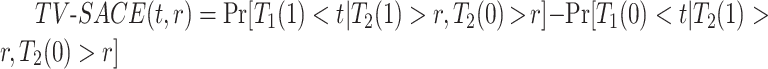 for
for 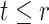 . The
. The 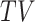 -
- has two major advantages over the standard SACE: at each survival age
has two major advantages over the standard SACE: at each survival age 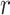 it compares nonterminal event rates in multiple time points, and it respects that the population of always-survivors depends on the chosen time
it compares nonterminal event rates in multiple time points, and it respects that the population of always-survivors depends on the chosen time 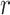 . Of note is that because the population changes with time, a change in
. Of note is that because the population changes with time, a change in 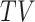 -
-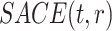 as a function of
as a function of 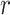 may reflect a change in the population or a change in the efficacy of the intervention.
may reflect a change in the population or a change in the efficacy of the intervention.
2.1. Population stratification and alternative estimands
We propose alternative estimands, based on a single partition of the population. Unlike the partitions defining the SACE and TV-SACE, this single partition is not defined with respect to a specific (possibly varying) time point. Instead, we divide the population into four strata according to their AD and death “order.” Because our partition involves the dual outcomes, we term it population stratification. Define the following four subpopulations with respect to the order of 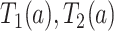 for
for 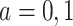 . The “always-diseased” (
. The “always-diseased” (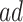 ) will be diagnosed with AD at some point of their life, regardless of their APOE status (
) will be diagnosed with AD at some point of their life, regardless of their APOE status (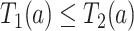 for
for 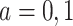 ); the “never-diseased” (
); the “never-diseased” (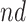 ) will die without having AD first, regardless of their APOE status (
) will die without having AD first, regardless of their APOE status (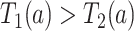 for
for 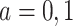 ); the “harmed’’ (
); the “harmed’’ (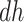 ) would be diagnosed with AD prior to death only had they had APOE (
) would be diagnosed with AD prior to death only had they had APOE (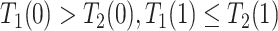 ); and the “protected” (
); and the “protected” (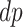 ) would be diagnosed with the disease only without APOE (
) would be diagnosed with the disease only without APOE ( ). Let
). Let 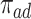 ,
, 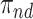 ,
, 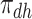 and
and 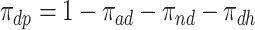 be the respective subpopulation proportions; see also Table 1.
be the respective subpopulation proportions; see also Table 1.
Table 1.
Population stratification for semi-competing risks data
| Name | Stratum definition | Stratum proportion |
|---|---|---|
| Always-diseased (ad) |
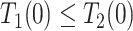 &
& 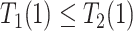
|
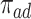
|
| Never-diseased (nd) |
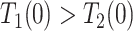 &
& 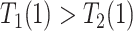
|
|
| Disease-harmed (dh) |
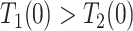 &
& 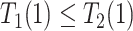
|
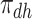
|
| Disease-protected (dp) |
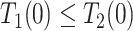 &
& 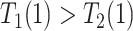
|
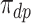
|
Consider the stratum-specific causal estimands 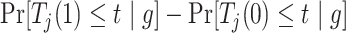 for
for 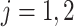 and
and 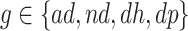 . Of note is that
. Of note is that 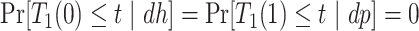 . Furthermore, the contrast
. Furthermore, the contrast 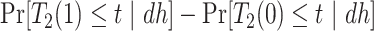 is hard to interpret because under APOE, all
is hard to interpret because under APOE, all 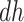 would have AD before their death, but none of them would have AD before death under no APOE. A similar concern arise for the
would have AD before their death, but none of them would have AD before death under no APOE. A similar concern arise for the  stratum. While
stratum. While  is the additional proportion of AD patients in the population had the entire population had APOE versus had none of the population had APOE, this quantity should be interpreted with care. The
is the additional proportion of AD patients in the population had the entire population had APOE versus had none of the population had APOE, this quantity should be interpreted with care. The 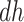 stratum may include people for whom APOE induces early AD onset without affecting age of death and people for whom APOE prolongs survival long enough to be diagnosed with AD. Therefore, we henceforth focus on the following effects defined in the
stratum may include people for whom APOE induces early AD onset without affecting age of death and people for whom APOE prolongs survival long enough to be diagnosed with AD. Therefore, we henceforth focus on the following effects defined in the 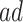 and
and 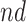 strata
strata
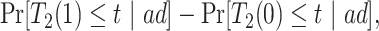 |
(2.1) |
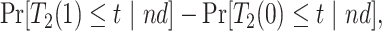 |
(2.2) |
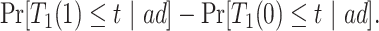 |
(2.3) |
Causal effects that better summarize the impact of  could be based on the restricted mean survival time (RMST). For a given time point
could be based on the restricted mean survival time (RMST). For a given time point  , let
, let  , and define
, and define
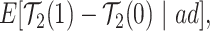 |
(2.4) |
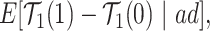 |
(2.5) |
 |
(2.6) |
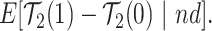 |
(2.7) |
Each of the estimands characterizes a different causal effect of 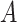 on the outcomes within the
on the outcomes within the  or
or 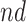 stratum. Effect (2.4) is the mean (possibly negative) gain in life expectancy caused by APOE, (2.5) is the effect of APOE on AD diagnosis age, and (2.6), which is obtained by subtracting (2.5) from (2.4), is the effect on the residual lifetime with AD. If, for example, the latter equals zero, it means the same life expectancy with AD is expected for those with and without APOE within the
stratum. Effect (2.4) is the mean (possibly negative) gain in life expectancy caused by APOE, (2.5) is the effect of APOE on AD diagnosis age, and (2.6), which is obtained by subtracting (2.5) from (2.4), is the effect on the residual lifetime with AD. If, for example, the latter equals zero, it means the same life expectancy with AD is expected for those with and without APOE within the 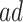 stratum. Effect (2.7) is also of great interest, as it is the effect of APOE on life expectancy among the
stratum. Effect (2.7) is also of great interest, as it is the effect of APOE on life expectancy among the 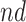 population, thus it captures another form of APOE effect on survival. Other summary measures (e.g., median time-to-events) can also be used to define causal effects.
population, thus it captures another form of APOE effect on survival. Other summary measures (e.g., median time-to-events) can also be used to define causal effects.
2.2. Utility of proposed estimands and comparison to existing approaches
Had we ignored follow-up after AD diagnosis, we would have a classical competing risks setup with the events AD diagnosis and AD-free death. Recently, there have been major advancements towards causal inference in the presence of competing events (Young and others, 2020; Stensrud and others, 2020; Nevo and others, 2021b). The total effect (Young and others, 2020) contrasts the proportion of AD patients by age  under APOE and no APOE for the entire population. A total effect can be also defined for the APOE effect on survival. The total effects are useful to answer a multitude of research questions, but one should be aware that interpretation can be complicated. For example, it may seems as if APOE protects against AD-free death, simply because it induces earlier onset of AD. The direct effect (Young and others, 2020) of APOE on AD contrasts the counterfactual AD risk with and without APOE had we eliminated the competing event for the entire population. To our knowledge, such intervention is not available for either AD or death. Stensrud and others (2020) proposed alternative casual estimands for competing-risks data, based on conceptual separation of the treatment into components such that each component affects a different competing event. The SCR framework has been increasingly used for aging research; see Varadhan and others (2014) for review and comparisons with competing risks. Unlike competing risks, the SCR viewpoint additionally considers follow-up after the occurrence of the nonterminal event. Therefore, the SCR framework presents an opportunity to study the dual outcomes of interest holistically, while considering simultaneously benefits and risks with respect to both events. As we demonstrate below, the proposed estimands can be used, for example, for studying the effect of APOE on AD age-of-onset among those who would have AD regardless of APOE status, or the effect of APOE on survival, separately for those would and would not have AD regardless of APOE status. The latter effect cannot be studied if follow-up after AD is ignored. In addition, SCR data provide partial information about the dependence of the two event times (conditionally on
under APOE and no APOE for the entire population. A total effect can be also defined for the APOE effect on survival. The total effects are useful to answer a multitude of research questions, but one should be aware that interpretation can be complicated. For example, it may seems as if APOE protects against AD-free death, simply because it induces earlier onset of AD. The direct effect (Young and others, 2020) of APOE on AD contrasts the counterfactual AD risk with and without APOE had we eliminated the competing event for the entire population. To our knowledge, such intervention is not available for either AD or death. Stensrud and others (2020) proposed alternative casual estimands for competing-risks data, based on conceptual separation of the treatment into components such that each component affects a different competing event. The SCR framework has been increasingly used for aging research; see Varadhan and others (2014) for review and comparisons with competing risks. Unlike competing risks, the SCR viewpoint additionally considers follow-up after the occurrence of the nonterminal event. Therefore, the SCR framework presents an opportunity to study the dual outcomes of interest holistically, while considering simultaneously benefits and risks with respect to both events. As we demonstrate below, the proposed estimands can be used, for example, for studying the effect of APOE on AD age-of-onset among those who would have AD regardless of APOE status, or the effect of APOE on survival, separately for those would and would not have AD regardless of APOE status. The latter effect cannot be studied if follow-up after AD is ignored. In addition, SCR data provide partial information about the dependence of the two event times (conditionally on  ), which is unidentifiable from competing-risks data, a fact often leveraged in models for SCR data.
), which is unidentifiable from competing-risks data, a fact often leveraged in models for SCR data.
A second approach views AD diagnosis as a time-varying and possibly death-truncated mediator of the effect of APOE on survival. Interventional direct and indirect effects are more appealing for such a task, as the assumption of no common causes of AD and death affected by APOE seems too strong; see Lin and others (2017). The mediation approach is desirable when the question of interest is the extent to which AD mediates the effect of APOE on survival. In this work, we make no direct attempt to answer such questions. Our approach does not specify the role of AD as a mediator. For example, APOE may affect cognitive decline underpinning AD, and this cognitive decline may affect death not only through earlier AD onset. Therefore, it is possible that AD is a proxy of an unmeasured mediator in addition to its possible, though not necessary, own mediating role.
Nevertheless, a connection of the proposed estimands to the mediation literature can be made. Let 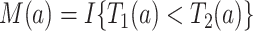 . One may argue that estimands (2.4) and (2.7) resemble principal stratum direct effects (PSDEs) under
. One may argue that estimands (2.4) and (2.7) resemble principal stratum direct effects (PSDEs) under 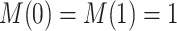 and
and 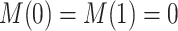 , respectively. As highlighted by VanderWeele (2011), PSDEs are generally interpretable as direct effects. In our motivating example, one may consider (2.4) as the effect of APOE on survival which is not mediated by the occurrence of AD.
, respectively. As highlighted by VanderWeele (2011), PSDEs are generally interpretable as direct effects. In our motivating example, one may consider (2.4) as the effect of APOE on survival which is not mediated by the occurrence of AD.
From a public health policy point of view, the decision whether CRISPR should be used to eliminate APOE must consider the population effect on the dual outcomes of AD and death. Our proposed estimands offer a number of information pieces needed when considering the population health and economic value of such intervention. In Section 6, we estimate 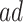 proportion to be 35% and the median gain in AD-free years by age 100 (analog of estimand (2.5)) to be 2.01 years (95% CI 1.92–2.09). This means that eliminating APOE would delay in at least 2 years AD diagnosis for at least half of those who would have AD under any APOE status. To complement this quantity, (2.4) is the gain in survival in the same population; the median gain is estimated to be 3.00 years (95% CI 2.93–3.07), meaning that eliminating APOE extends life for at least half of those within the
proportion to be 35% and the median gain in AD-free years by age 100 (analog of estimand (2.5)) to be 2.01 years (95% CI 1.92–2.09). This means that eliminating APOE would delay in at least 2 years AD diagnosis for at least half of those who would have AD under any APOE status. To complement this quantity, (2.4) is the gain in survival in the same population; the median gain is estimated to be 3.00 years (95% CI 2.93–3.07), meaning that eliminating APOE extends life for at least half of those within the 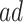 strata by at least 3 years. The APOE intervention effect is not limited to the
strata by at least 3 years. The APOE intervention effect is not limited to the 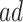 strata. In Section 6, we estimate the
strata. In Section 6, we estimate the  proportion to be 53%, and the median gain in survival by age 100 to be 1.99 years (95% CI 1.90–2.08). Considered collectively, the results provide initial evidence for desirable effects of eliminating APOE on both AD and survival in the population. A careful inspection will help regulators and public health officials to weigh the consequences of APOE intervention at scale. The TV-SACE and RM-SACE do not provide the above-described information, but they can complement it by providing insight into heterogeneity of the effect across time.
proportion to be 53%, and the median gain in survival by age 100 to be 1.99 years (95% CI 1.90–2.08). Considered collectively, the results provide initial evidence for desirable effects of eliminating APOE on both AD and survival in the population. A careful inspection will help regulators and public health officials to weigh the consequences of APOE intervention at scale. The TV-SACE and RM-SACE do not provide the above-described information, but they can complement it by providing insight into heterogeneity of the effect across time.
3. Identifiability
The focus of this section is on assumptions and identifiability. Methods for estimation and inference under right censoring are developed in Section 4. Let 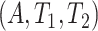 be the actual APOE and event times. Throughout this article, we assume no interference between individuals and the following two standard assumptions.
be the actual APOE and event times. Throughout this article, we assume no interference between individuals and the following two standard assumptions.
Assumption 1
Consistency.
and
.
Assumption 2
Weak Ignorability,
for
.
In many observational studies that lack randomization, a conditional version of Assumption 2, conditionally on covariates, is more plausible; see also Section 3.4.
3.1. Bounds
Because principal stratum effects are not identified from the data unless additional assumptions are leveraged, researchers often develop bounds (Zhang and Rubin, 2003; Long and Hudgens, 2013). Here, we present various bounds for the causal effects based on the identifiable distribution of 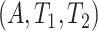 , constructed differently depending on the assumptions a researcher is willing to make. First, we present a new assumption, tailored for SCR data.
, constructed differently depending on the assumptions a researcher is willing to make. First, we present a new assumption, tailored for SCR data.
Assumption 3
Order preservation. If
, then
.
Under Assumption 3, anyone who would have been diagnosed with AD without having APOE, would also have AD had they had APOE, but not necessarily at the same age. It is consistent with the overwhelming evidence that APOE significantly increases the risk of AD (Alzheimer’s Association, 2019). Assumption 3 is more flexible than the often-invoked monotonicity assumption, in that it acknowledges the realistic scenario that 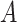 may impact survival time for either direction. Specifically, it allows that
may impact survival time for either direction. Specifically, it allows that 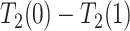 and
and 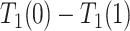 are of different signs at the unit level. To see this, observe that
are of different signs at the unit level. To see this, observe that 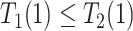 implies
implies 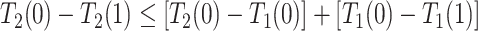 . Figure 1 presents potential AD and death times for seven hypothetical units, differing at the timing and order of the potential event times. The figure depicts examples of units existing under both assumptions, and units that their existence violates one of the assumptions (or both). Of note is that for a unit with no AD under either APOE status, Assumption 3 holds, while monotonicity would not hold if APOE prolongs the lifetime of that unit. Finally, Assumption 3 implies that the
. Figure 1 presents potential AD and death times for seven hypothetical units, differing at the timing and order of the potential event times. The figure depicts examples of units existing under both assumptions, and units that their existence violates one of the assumptions (or both). Of note is that for a unit with no AD under either APOE status, Assumption 3 holds, while monotonicity would not hold if APOE prolongs the lifetime of that unit. Finally, Assumption 3 implies that the 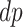 stratum is empty, that is,
stratum is empty, that is, 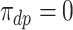 .
.
Fig. 1.
Illustration of Assumption 3 and its distinction compared to the monotonicity assumption using seven hypothetical units. Units  and
and  are allowed under both assumptions, Assumption 3 and monotonicity. For unit
are allowed under both assumptions, Assumption 3 and monotonicity. For unit 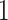 , APOE expedites both AD and death, but in a way that AD remains before death. For unit 2, APOE impedes AD but expedites death. Nevertheless, unit 2 would live long enough under APOE for AD to occur. Similar protective effect occurs for unit
, APOE expedites both AD and death, but in a way that AD remains before death. For unit 2, APOE impedes AD but expedites death. Nevertheless, unit 2 would live long enough under APOE for AD to occur. Similar protective effect occurs for unit  , however, this unit violates monotonicity at time
, however, this unit violates monotonicity at time 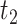 (as an example). Unit
(as an example). Unit 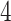 also violates monotonicity (at
also violates monotonicity (at 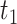 and
and 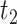 ) but not Assumption 3. Unit
) but not Assumption 3. Unit 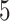 does not suffer from AD under any APOE value, hence it is allowed by Assumption 3 but it does violate monotonicity (at
does not suffer from AD under any APOE value, hence it is allowed by Assumption 3 but it does violate monotonicity (at 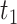 and
and 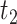 ) as AD carries a protective effect against death. Unit
) as AD carries a protective effect against death. Unit 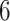 violates Assumption 3 but not monotonicity. Arguably, for this unit the APOE effect on death is so strong the unit would have died under APOE before getting the chance to have AD. Finally, unit
violates Assumption 3 but not monotonicity. Arguably, for this unit the APOE effect on death is so strong the unit would have died under APOE before getting the chance to have AD. Finally, unit 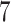 violates both assumptions.
violates both assumptions.
As is typically the case in truncation-by-death problems, even under Assumptions 1–3, none of the causal effects (2.1)–(2.7) are nonparametrically identifiable. These effects are however partially identifiable, in the sense that the data, coupled with the assumptions, provide bounds on these effects. For any event 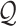 , let
, let 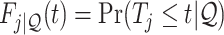 ,
, 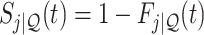 and
and 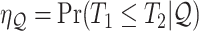 . Under Assumptions 1–3,
. Under Assumptions 1–3, 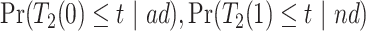 and
and 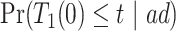 are identified, while
are identified, while 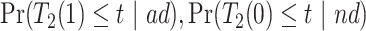 and
and 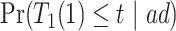 are only partially identified. The following proposition establishes partial identifiability under Assumptions 1–3.
are only partially identified. The following proposition establishes partial identifiability under Assumptions 1–3.
Proposition 1
Under Assumptions 1–3, effects (2.1)–(2.3) are partially identified by
(3.8)
(3.9)
(3.10) where
(3.11)
The proof is given in Section A.1 of the Supplementary material available at Biostatistics online. Under Assumptions 1–3, the strata proportions are identified by  ,
,  ,
, 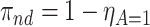 . RMST effects (2.5)–(2.7) are (partially) identified by recalling that for any nonnegative random variable
. RMST effects (2.5)–(2.7) are (partially) identified by recalling that for any nonnegative random variable 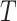 and any fixed time
and any fixed time 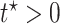 , we have
, we have 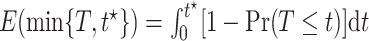 . Had we had unlimited uncensored data, we could have calculated the bounds using
. Had we had unlimited uncensored data, we could have calculated the bounds using 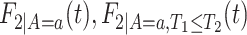 ,
, 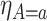 and
and 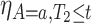 . As for
. As for 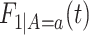 , we could have used
, we could have used 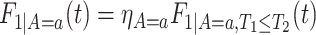 .
.
Generally, bounds derived under additional assumptions might be narrower (Zhang and Rubin, 2003; Long and Hudgens, 2013). Of course, these assumptions need to be plausible in the scientific problem at hand for the bounds to be valid. One particular bound that may not be informative enough is 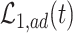 . As
. As 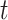 increases, the second term
increases, the second term  get closer to one while the first term is not, because
get closer to one while the first term is not, because 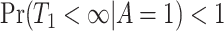 . As a remedy for this problem, consider the following assumption and proposition providing a more informative lower bound for (2.3).
. As a remedy for this problem, consider the following assumption and proposition providing a more informative lower bound for (2.3).
Assumption 4
For a given
,
.
This assumption resembles the ranked average score assumption (Zhang and Rubin, 2003), but tailored for time-to-event data. Assumption 4 reflects researcher belief that the 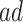 are generally more frail (with respect to AD), and hence are expected to be diagnosed at earlier ages than those in the
are generally more frail (with respect to AD), and hence are expected to be diagnosed at earlier ages than those in the 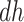 stratum. For example, if those in the
stratum. For example, if those in the 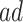 stratum are more likely than those at the
stratum are more likely than those at the 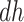 stratum to have other AD risk factors. In practice, Assumption 4 can hold for some, all, or none of the values of
stratum to have other AD risk factors. In practice, Assumption 4 can hold for some, all, or none of the values of 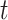 .
.
Proposition 2
Under Assumptions 1–3, for any
for which Assumption 4 holds,
is partially identified by
, where
and
is given in Proposition 1.
The proof is given in Section A.2 of the Supplementary material available at Biostatistics online. In some studies, the obtained bounds, with or without additional assumptions, might be too wide to have practical utility. Therefore, following Long and Hudgens (2013), we develop narrower bounds utilizing a preintervention discrete covariate 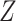 . In our study,
. In our study, 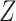 can be, for example, gender. An adjusted version of Proposition 1 can be obtained under the following assumption.
can be, for example, gender. An adjusted version of Proposition 1 can be obtained under the following assumption.
Assumption 5
for
.
For example, we show in Section A.3 of the Supplementary material available at Biostatistics online that under Assumptions 1, 3, and 5, adjusted bounds for (2.1) are given by 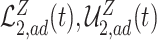 , where
, where
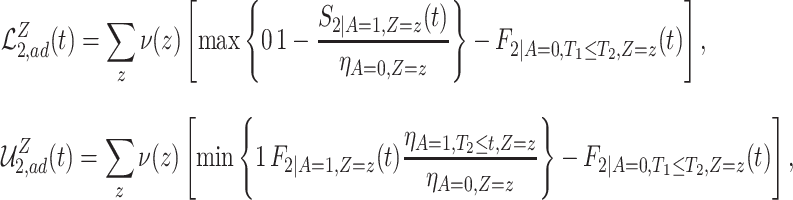 |
(3.12) |
and 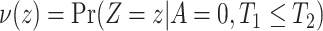 . Similarly, adjusted bounds
. Similarly, adjusted bounds 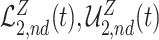 and
and 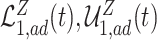 can be constructed. Furthermore, the following proposition establishes that the adjusted bounds are always within the unadjusted bounds.
can be constructed. Furthermore, the following proposition establishes that the adjusted bounds are always within the unadjusted bounds.
Proposition 3
Under Assumptions 1, 3 and 5,
and
.
The proof is given in Section A.4 of the Supplementary material available at Biostatistics online. Proposition 3 is the analog of Proposition 1 in Long and Hudgens (2013), who developed bounds for binary outcomes. Of note is that due to finite-sample variation, Proposition 3 may not hold empirically. Therefore, as suggested by Long and Hudgens (2013), the bounds 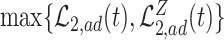 and
and 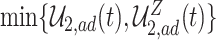 can be used.
can be used.
Figure 2 illustrates the various bounds under three different scenarios. The data-generating mechanism (DGM) and the resulting per-stratum cumulative distribution functions are described in Section D.1 of the Supplementary material available at Biostatistics online. Under Scenario (I) (top row), Assumptions 3 and 4 hold, and 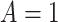 shorten the
shorten the 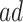 time-to-disease and time-to-death, and
time-to-disease and time-to-death, and 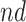 die faster under
die faster under 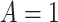 . The bounds
. The bounds 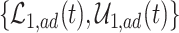 ,
, 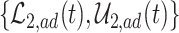 , and
, and 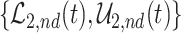 (in pink shade) are quite wide in this scenario. The bound
(in pink shade) are quite wide in this scenario. The bound 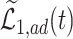 (dashed green line) is far more informative, being only slightly lower than the true difference (black solid curve). The adjusted bounds (blue dotted lines) were narrower than the unadjusted bounds, most notably for
(dashed green line) is far more informative, being only slightly lower than the true difference (black solid curve). The adjusted bounds (blue dotted lines) were narrower than the unadjusted bounds, most notably for 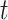 values for which the unadjusted bounds are very wide. For the causal effect on time-to-disease within the
values for which the unadjusted bounds are very wide. For the causal effect on time-to-disease within the 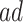 (top left corner) the narrower bound is obtained as
(top left corner) the narrower bound is obtained as 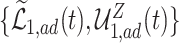 . The bounds for time-to-death among the
. The bounds for time-to-death among the 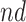 are quite wide. This is likely because there is least information on this group from the observed data, as the true stratum probabilities were
are quite wide. This is likely because there is least information on this group from the observed data, as the true stratum probabilities were 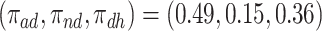 .
.
Fig. 2.
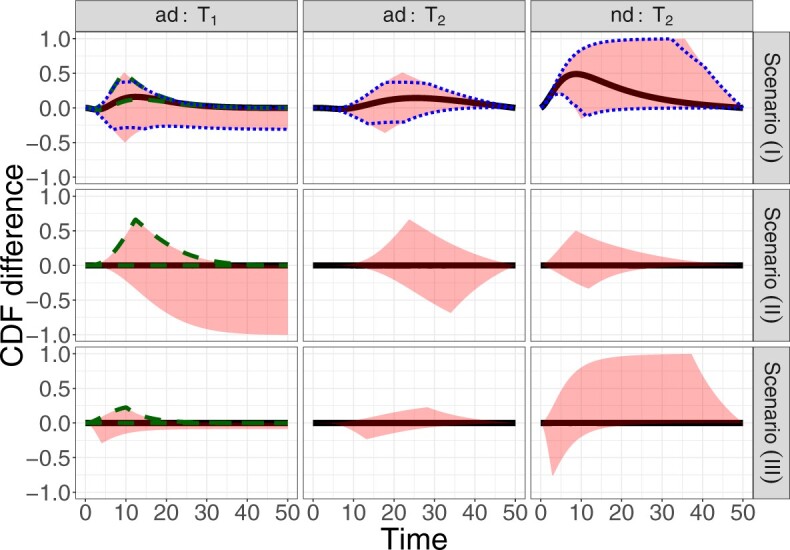
True causal effects (2.1)–(2.3) and different bounds under three simulated scenarios. The bounds derived in Proposition 1, 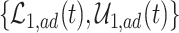 ,
, 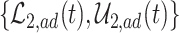 , and
, and 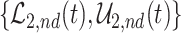 , are in pink shade. The blue dotted lines are the adjusted bounds
, are in pink shade. The blue dotted lines are the adjusted bounds 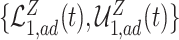 ,
, 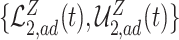 , and
, and 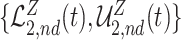 . The green dashed lines are the bounds
. The green dashed lines are the bounds 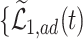 ,
, 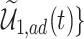 .
.
For further illustration of the latter point, consider the two bottom rows of Figure 2, both under null effects. In Scenario (II), the 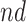 stratum comprised most of the population,
stratum comprised most of the population,  , and the bounds were quite narrow for the within
, and the bounds were quite narrow for the within 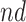 effect (2.2), and less informative for the
effect (2.2), and less informative for the 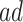 . In Scenario (III),
. In Scenario (III), 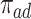 was substantial,
was substantial, 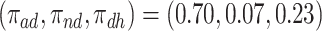 , and the bounds were quite narrow only for causal effects within the
, and the bounds were quite narrow only for causal effects within the 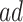 . In conclusion, if one of the proportions
. In conclusion, if one of the proportions 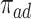 or
or 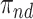 is large enough, the bounds can be useful, and a covariate
is large enough, the bounds can be useful, and a covariate 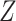 may help to create narrower bounds. Under Assumption 4, the lower bound
may help to create narrower bounds. Under Assumption 4, the lower bound 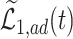 is quite informative.
is quite informative.
3.2. Identification by frailty assumptions
We turn to present stronger assumptions under which effects (2.1)–(2.3) are identified from the data. The proposed overarching strategy formulates two illness-death models and tying them together via a bivariate frailty random variable  . For
. For  , let
, let
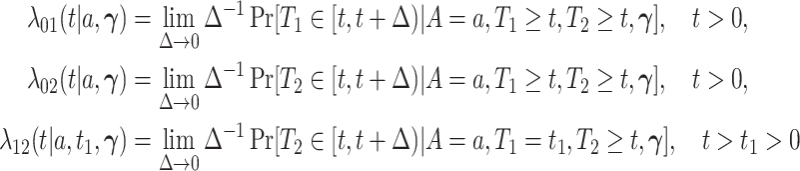 |
be the three cause-specific hazard functions under the SCR setting (Xu and others, 2010), associated with the transitions 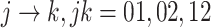 (0: healthy, 1: AD, 2: death); see Figure C.1 of the Supplementary material available at Biostatistics online for illustration. The strategy of how to model the distribution of
(0: healthy, 1: AD, 2: death); see Figure C.1 of the Supplementary material available at Biostatistics online for illustration. The strategy of how to model the distribution of  dictates two forms of dependence, cross-world and within-world. A frailty-based approach with parametric assumptions on the hazard functions, coupled with Bayesian estimation was considered by Comment and others (2019). The authors assumed
dictates two forms of dependence, cross-world and within-world. A frailty-based approach with parametric assumptions on the hazard functions, coupled with Bayesian estimation was considered by Comment and others (2019). The authors assumed  leading to identifiability of the causal effects. That
leading to identifiability of the causal effects. That 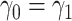 implies the same dependence between AD and death times in both worlds. However, it would generally not hold unless all effect modifiers can be measured and correctly accounted for. We extend this approach by incorporating a sensitivity parameter
implies the same dependence between AD and death times in both worlds. However, it would generally not hold unless all effect modifiers can be measured and correctly accounted for. We extend this approach by incorporating a sensitivity parameter 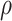 that encapsulates the cross-world, and unidentifiable, dependence.
that encapsulates the cross-world, and unidentifiable, dependence.
Assumption 6
There exists a bivariate random variable
such that
- (i)
for
.
- (ii)
Given, the joint distribution of the potential event times can be factored as follows
where
(3.13) denotes a density function of a possibly multivariate random variable.
- (iii)
The frailty variable operates multiplicatively on the hazard function
for
and
for
, for some
functions.
- (iv)
The probability density function of
,
, is known up to a finite dimensional parameter
that is identifiable from the observed data distribution.
Part (i) of Assumption 6 adapts Assumption 2 for the frailty. Part (ii) implies a cross-world independence conditionally on the unobserved 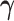 . That is, the inclusion of the frailty represents a model for the collection of unobserved covariates governing the cross-world dependence. This model induces marginal (with respect to
. That is, the inclusion of the frailty represents a model for the collection of unobserved covariates governing the cross-world dependence. This model induces marginal (with respect to 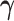 ) complex dependence and conditional independence between
) complex dependence and conditional independence between 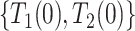 and
and 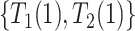 . Parts (iii) and (iv) guarantee identification of the observed data distribution. As with any parametric model, one cannot expect the model to hold exactly. Nevertheless, it is well-known that usually misspecification of the frailty distribution leads to only small bias in the estimated cumulative incidence function (of the observed data distribution), integrated over the frailty distribution; see Gorfine and others (2021) and references therein.
. Parts (iii) and (iv) guarantee identification of the observed data distribution. As with any parametric model, one cannot expect the model to hold exactly. Nevertheless, it is well-known that usually misspecification of the frailty distribution leads to only small bias in the estimated cumulative incidence function (of the observed data distribution), integrated over the frailty distribution; see Gorfine and others (2021) and references therein.
While other specifications are possible, we assume that 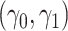 are correlated Gamma variables, with mean one, variances
are correlated Gamma variables, with mean one, variances 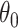 and
and 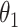 , and correlation
, and correlation 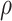 . The frailty variances
. The frailty variances 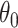 and
and 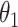 are identifiable from the data, while
are identifiable from the data, while 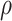 is unidentifiable and is supplied by the researcher. Taking
is unidentifiable and is supplied by the researcher. Taking 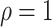 is analogous to the approach of Comment and others (2019), and results in point identification. The following proposition provides identification as a function of
is analogous to the approach of Comment and others (2019), and results in point identification. The following proposition provides identification as a function of 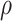 , thus allowing a more flexible consideration of the unidentifiable cross-world dependence.
, thus allowing a more flexible consideration of the unidentifiable cross-world dependence.
Proposition 4
Under Assumptions 1 and 6, the causal effects (2.1)–(2.3) are identified by
where for any event
,
,
.
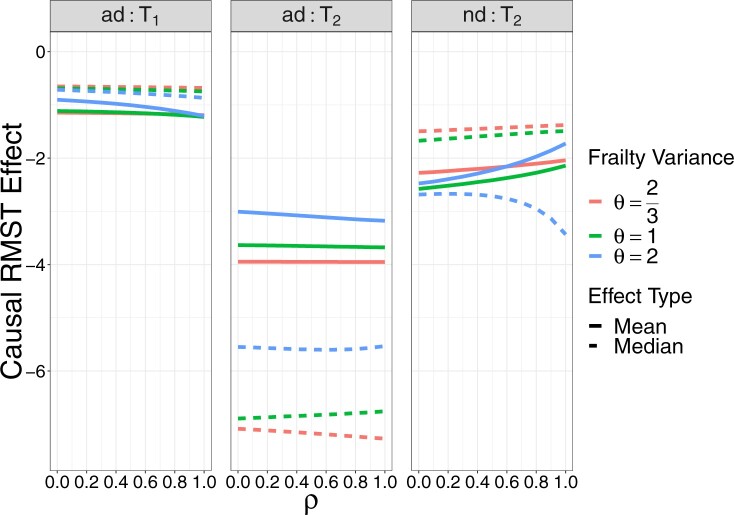
The proof is given in Section A.5 of the Supplementary material available at Biostatistics online. RMST-like estimands (2.4)–(2.7) are identified by suitable integration over 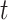 . Figure 3 illustrates the RMST effects (2.4), (2.5), and (2.7) under the DGM described in Section 4 and Section D.1 of the Supplementary material available at Biostatistics online, with equal variances
. Figure 3 illustrates the RMST effects (2.4), (2.5), and (2.7) under the DGM described in Section 4 and Section D.1 of the Supplementary material available at Biostatistics online, with equal variances 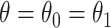 and as a function of
and as a function of 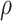 . Stratum proportions varied between 41–45% for
. Stratum proportions varied between 41–45% for 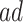 stratum and 8–12% for the
stratum and 8–12% for the 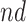 stratum. The causal RMST effects, calculated at
stratum. The causal RMST effects, calculated at 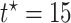 , were sensitive to
, were sensitive to 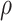 when the stratum proportion was very small and the frailty variance was large and were otherwise quite robust to
when the stratum proportion was very small and the frailty variance was large and were otherwise quite robust to 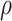 .
.
Fig. 3.
Causal restricted mean and median survival time effects at 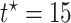 as a function of the frailty variance
as a function of the frailty variance 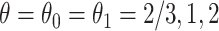 , (corresponding to Kendall’s
, (corresponding to Kendall’s 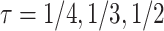 ) as a function of the correlation between the frailty variables
) as a function of the correlation between the frailty variables 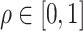 .
.
3.3. Right censoring
Time-to-event outcome data are often not fully observed for all individuals due to right censoring. Two issues arise when considering right censoring. The first is identification of the causal estimand, considered in this section, and the second is how to estimate the different quantities and provide inference, which is embedded in the nonparametric and semiparametric methods presented in Section 4. Let 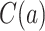 be the right-censoring time under
be the right-censoring time under 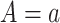 . Assumption 2 is adjusted for the case of censoring by assuming
. Assumption 2 is adjusted for the case of censoring by assuming 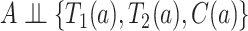 for
for 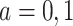 . We also assume within-world independent censoring, namely that
. We also assume within-world independent censoring, namely that 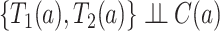 for
for 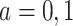 . In our study, this assumption asserts that, under each APOE value, the two event times and censoring time are independent. We also assume that
. In our study, this assumption asserts that, under each APOE value, the two event times and censoring time are independent. We also assume that 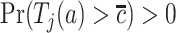 for
for 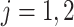 with
with 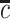 being the end of follow-up time. Combining the weak ignorability and within-world independent-censoring assumptions together, and by Assumption 1, we get the standard independent censoring assumption for SCR data
being the end of follow-up time. Combining the weak ignorability and within-world independent-censoring assumptions together, and by Assumption 1, we get the standard independent censoring assumption for SCR data 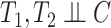 , with
, with 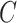 being the censoring time under
being the censoring time under 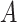 .
.
3.4. Covariates inclusion
Often the ignorability and independent censoring assumptions are more plausible when made conditionally on covariates 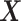 . Assumption 6 is also more plausible when made conditionally on covariates. For simplicity, we use the same vector
. Assumption 6 is also more plausible when made conditionally on covariates. For simplicity, we use the same vector 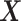 for all assumptions to hold. In Section A.6 of the Supplementary material available at Biostatistics online, we adapt Propositions 1 and 4 to include covariates. An additional reason to include covariates is to improve estimators’ efficiency. In our study (Section 6), we use gender and race as covariates. Note that the role of
for all assumptions to hold. In Section A.6 of the Supplementary material available at Biostatistics online, we adapt Propositions 1 and 4 to include covariates. An additional reason to include covariates is to improve estimators’ efficiency. In our study (Section 6), we use gender and race as covariates. Note that the role of 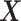 is different from the role of the covariate
is different from the role of the covariate 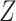 we utilized in Section 3.1.
we utilized in Section 3.1.
While a variety of statistical models have been used for SCR data, how to elucidate information on causal effects is typically overlooked and, in practice, focus is often on specific regression coefficients. Therefore, our work enables translation of existing model results into knowledge on causal effects. With this is mind, we focus on frequentist estimation of causal effects (2.4)–(2.7) under semiparametric frailty models that align with Assumption 6.
4. Estimation and inference
We now turn to estimation and inference from right-censored SCR data. We first propose nonparametric estimators, before considering semiparametric models. For the nonparametric estimators, the quantities of interest are the building blocks of the bounds, namely 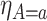 ,
, 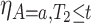 ,
, 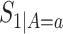 ,
, 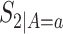 ,
, 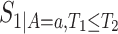 ,
, 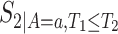 , and
, and 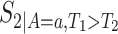 (for
(for 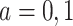 ). For the semiparametric estimation, we focus on a frailty-based proportional-hazard model that allows estimation of causal effects utilizing Proposition 4.
). For the semiparametric estimation, we focus on a frailty-based proportional-hazard model that allows estimation of causal effects utilizing Proposition 4.
For each participant 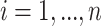 denote by
denote by 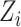 a covariate that is used for obtaining sharper bounds (when available), by
a covariate that is used for obtaining sharper bounds (when available), by 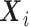 a vector of baseline covariates (when available), by
a vector of baseline covariates (when available), by 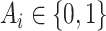 , the APOE value, and by
, the APOE value, and by 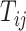 the AD (
the AD (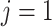 ) and death (
) and death (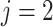 ) times. Let also
) times. Let also 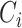 be the censoring time. The data for each unit are
be the censoring time. The data for each unit are 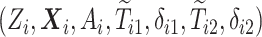 where
where 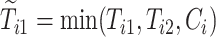 and
and 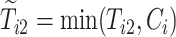 are the observed times, and
are the observed times, and 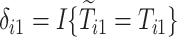 and
and 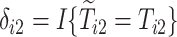 are the indicators of AD and death, respectively. Finally,
are the indicators of AD and death, respectively. Finally, 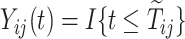 are the at-risk processes.
are the at-risk processes.
4.1. Nonparametric estimation
We suggest to estimate 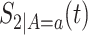 by the Kaplan–Meier (KM) estimator. Regarding
by the Kaplan–Meier (KM) estimator. Regarding 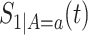 ,
,
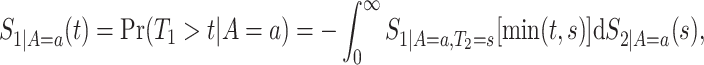 |
(4.14) |
because for 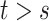 ,
, 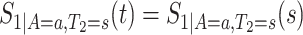 , that is, among those who die at time
, that is, among those who die at time 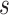 , no new disease cases are possible later than
, no new disease cases are possible later than 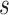 . The function
. The function 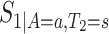 is well-defined, and thus can be estimated nonparametrically.
is well-defined, and thus can be estimated nonparametrically.
We propose to estimate 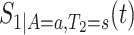 by a kernel-smoothed KM estimator (Beran, 1981) within the
by a kernel-smoothed KM estimator (Beran, 1981) within the 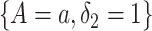 group. Let
group. Let 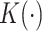 be a kernel function (
be a kernel function (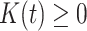 ,
, 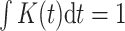 ), and let
), and let 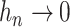 be a sequence of bandwidths. In practice, one might consider a separate bandwidth for each level of
be a sequence of bandwidths. In practice, one might consider a separate bandwidth for each level of  . For simplicity of presentation, we assume
. For simplicity of presentation, we assume 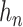 is the same for both
is the same for both 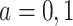 . Let
. Let 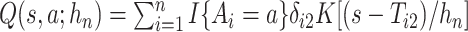 , and
, and 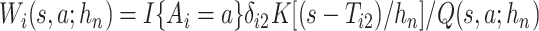 . The kernel-smoothed KM estimator for
. The kernel-smoothed KM estimator for 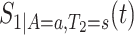 is then defined by
is then defined by
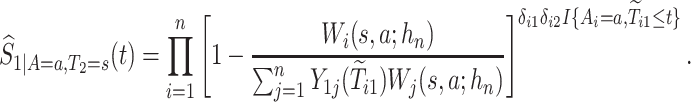 |
(4.15) |
We propose to estimate 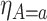 in similar fashion utilizing that
in similar fashion utilizing that
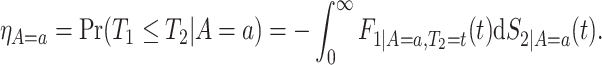 |
(4.16) |
In Section C.1 of the Supplementary material available at Biostatistics online, we give similar explicit formulas for 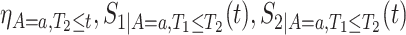 , and
, and 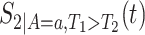 . Covariate-adjusted bounds (3.12) are estimated at each level of
. Covariate-adjusted bounds (3.12) are estimated at each level of 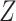 and averaged by
and averaged by  . A sketch of the proof for the asymptotic properties of the proposed estimators using existing results for the KM estimator and kernel-smoothed KM estimator is provided in Section C.2 of the Supplementary material available at Biostatistics online; see also Akritas and Van Keilegom (2003).
. A sketch of the proof for the asymptotic properties of the proposed estimators using existing results for the KM estimator and kernel-smoothed KM estimator is provided in Section C.2 of the Supplementary material available at Biostatistics online; see also Akritas and Van Keilegom (2003).
4.2. Semiparametric frailty models
Under Assumption 6, we propose to use the following proportional hazard specification
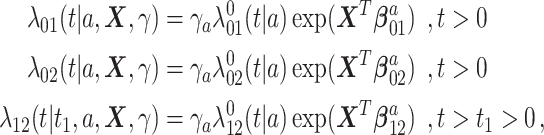 |
(4.17) |
where 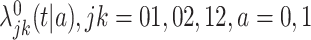 are unspecified baseline hazard functions. Define also the cumulative baseline hazard functions,
are unspecified baseline hazard functions. Define also the cumulative baseline hazard functions, 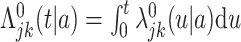 , and let
, and let 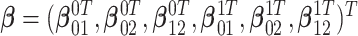 , and
, and 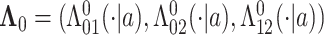 for
for 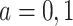 . Finally, let
. Finally, let 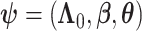 be the collection of parameters to be estimated from the data. For prospectively collected data with all participants being AD-free at study starting time, the likelihood function is proportional to
be the collection of parameters to be estimated from the data. For prospectively collected data with all participants being AD-free at study starting time, the likelihood function is proportional to
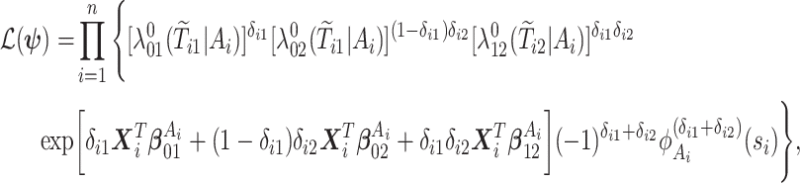 |
(4.18) |
where 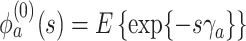 ,
, 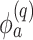 is the
is the 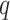 th derivative of
th derivative of 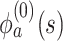 with respect to
with respect to 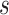 ,
, 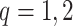 , and
, and 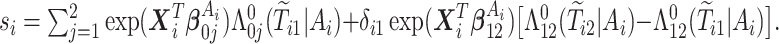 The likelihood derivation follows from SM3 of Gorfine and others (2021). In Section C.3 of the Supplementary material available at Biostatistics online, we present an EM algorithm for maximizing (4.18). The estimation phase ignores the unidentifiable component
The likelihood derivation follows from SM3 of Gorfine and others (2021). In Section C.3 of the Supplementary material available at Biostatistics online, we present an EM algorithm for maximizing (4.18). The estimation phase ignores the unidentifiable component 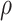 . Assumptions on the joint distribution of
. Assumptions on the joint distribution of 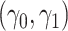 are used to map the estimator
are used to map the estimator 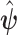 into estimates of causal effects. Upon estimating
into estimates of causal effects. Upon estimating 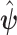 , the quantities in the identifying formulas from Proposition 4 can be calculated by numerical integration or Monte Carlo simulations, as we do in Section 5.
, the quantities in the identifying formulas from Proposition 4 can be calculated by numerical integration or Monte Carlo simulations, as we do in Section 5.
5. Simulations
To assess the finite-sample properties of the proposed estimators, we conducted simulations under various scenarios with 1,000 simulation iterations per scenario. Sample size was 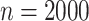 and different censoring rates were considered. The DGM initially followed (4.17) with Weibull baseline hazards, two covariates, and Gamma frailty as described in Section 3.2 with
and different censoring rates were considered. The DGM initially followed (4.17) with Weibull baseline hazards, two covariates, and Gamma frailty as described in Section 3.2 with 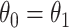 for simplicity. Treatment was randomized with
for simplicity. Treatment was randomized with 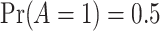 and observed event times (pre censoring) were created by Assumption 1. Details on the different DGMs, analyses and comprehensive results are presented in Section D of the Supplementary material available at Biostatistics online and described briefly here.
and observed event times (pre censoring) were created by Assumption 1. Details on the different DGMs, analyses and comprehensive results are presented in Section D of the Supplementary material available at Biostatistics online and described briefly here.
For the nonparametric estimation, we considered the scenarios previously used in Figure 2. Assumption 3 was imposed by re-simulating those initially at the 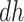 stratum. For the smoothed KM estimator, default choices of the R package
stratum. For the smoothed KM estimator, default choices of the R package  were used (Gerds, 2019). Standard errors were estimated by bootstrap (sampling at the unit level) with 100 repetitions. For all parameters considered, bias was negligible, standard errors were well estimated and 95% Wald-type confidence intervals had satisfactory empirical coverage rate.
were used (Gerds, 2019). Standard errors were estimated by bootstrap (sampling at the unit level) with 100 repetitions. For all parameters considered, bias was negligible, standard errors were well estimated and 95% Wald-type confidence intervals had satisfactory empirical coverage rate.
For the semiparametric estimation, data was generated under model (4.17) and was not restricted to follow Assumption 3. Gamma frailties were simulated with 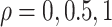 and equal variances
and equal variances 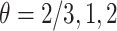 , corresponding to Kendall’s
, corresponding to Kendall’s 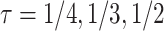 between
between 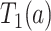 and
and 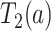 . For each simulated dataset, we fitted two illness-death frailty models for
. For each simulated dataset, we fitted two illness-death frailty models for 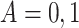 using the EM algorithm (Section C.3 of the Supplementary material available at Biostatistics online). Frailty variances were estimated separately and then combined (Section D.2.2 of the Supplementary material available at Biostatistics online). RMST causal effects were estimated by a Monte Carlo integration using the estimated baseline hazards
using the EM algorithm (Section C.3 of the Supplementary material available at Biostatistics online). Frailty variances were estimated separately and then combined (Section D.2.2 of the Supplementary material available at Biostatistics online). RMST causal effects were estimated by a Monte Carlo integration using the estimated baseline hazards 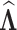 , coefficients
, coefficients 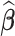 and
and 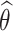 (Section D.2 of the Supplementary material available at Biostatistics online). Standard errors were estimated using bootstrap with 100 repetitions. Generally, the empirical bias of the estimated mean and median RMST effects was relatively negligible, standard errors were well estimated, and coverage provabilities were satisfactory. The regression coefficients, baseline hazard functions, and frailty variance were all also well estimated (Section D.3 of the Supplementary material available at Biostatistics online).
(Section D.2 of the Supplementary material available at Biostatistics online). Standard errors were estimated using bootstrap with 100 repetitions. Generally, the empirical bias of the estimated mean and median RMST effects was relatively negligible, standard errors were well estimated, and coverage provabilities were satisfactory. The regression coefficients, baseline hazard functions, and frailty variance were all also well estimated (Section D.3 of the Supplementary material available at Biostatistics online).
6. Data analysis
The Adult Changes in Thought (ACT) Study is a prospective cohort study focused on dementia in the elderly. Starting from 1994, AD-free participants of age 65 and older from the Seattle metropolitan area have been recruited (Kukull and others, 2002). Our analyses include the binary variables gender and race (white/nonwhite). Other available covariates (e.g., years of education) were not used as they are determined post-intervention. Out of 4453 participants, 1783 (40%) were censored prior to any event, 211 (5%) were diagnosed with AD and then censored, 1635 (37%) died without an AD diagnosis, and 824 (19%) were diagnosed with AD and died during follow-up. APOE was present for 1073 (24%) study participants. Because APOE is inherited and independent of other inherited traits, the ignorability assumptions seem plausible in this study.
Figure 4 presents the estimated bounds for causal effects (2.1)–(2.3) under Assumption 3 (pink shade), utilizing gender as an additional covariate (blue), and under the additional Assumption 4 (green, for (2.3) only). Assumptions 3 and 4 seem reasonably plausible in this application, because APOE is a well-known strong predictor of AD. The 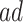 proportion
proportion 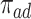 was estimated to be 35% (95% CI 32%–37%). The bounds
was estimated to be 35% (95% CI 32%–37%). The bounds 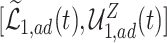 (bottom green and top blue) demonstrate that APOE induces earlier AD onset within the
(bottom green and top blue) demonstrate that APOE induces earlier AD onset within the 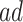 stratum. The bounds do not allow for definite conclusions regarding the effect of APOE on death, and the inclusion of the variable gender had only minor effect. Focusing on the
stratum. The bounds do not allow for definite conclusions regarding the effect of APOE on death, and the inclusion of the variable gender had only minor effect. Focusing on the 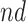 stratum, its proportion was estimated to be 53% (95% CI 49%–58%), meaning the two stratum of interest together comprise the vast majority of the population. Whether APOE had a positive or negative effect on survival in the
stratum, its proportion was estimated to be 53% (95% CI 49%–58%), meaning the two stratum of interest together comprise the vast majority of the population. Whether APOE had a positive or negative effect on survival in the 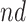 is unclear, although the lower bound was larger than zero for early ages. The
is unclear, although the lower bound was larger than zero for early ages. The 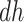 stratum proportion was estimated to be 12% (95% CI 7%–17%), meaning that had the entire population had APOE, we would have expect a 12% increase of in the proportion of people with AD diagnosis sometime in their lifetime, compared to the scenario that none of the population had APOE.
stratum proportion was estimated to be 12% (95% CI 7%–17%), meaning that had the entire population had APOE, we would have expect a 12% increase of in the proportion of people with AD diagnosis sometime in their lifetime, compared to the scenario that none of the population had APOE.
Fig. 4.

Bounds for principal effects of APOE on AD and death based on the ACT data. In pink shade the simple bounds, in blue bounds adjusted for gender, and in green bounds based on Assumption 4.
In the semiparametric analysis under Assumption 6, two illness-death models (4.17) were fitted using the EM algorithm, and included gender and race as covariates 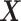 (SM Table E.15 presents the estimated coefficients). Because participants in the ACT were recruited in varying ages, data were left truncated. We followed the approximation of Nielsen and others (1992), by replacing all risk indicators
(SM Table E.15 presents the estimated coefficients). Because participants in the ACT were recruited in varying ages, data were left truncated. We followed the approximation of Nielsen and others (1992), by replacing all risk indicators 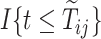 with
with 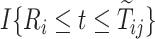 , where
, where 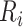 is the age at recruitment. The estimated frailty variance was
is the age at recruitment. The estimated frailty variance was 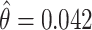 (SE:
(SE: 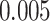 ), corresponding to Kendall’s
), corresponding to Kendall’s 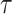 of 0.02. Turning to causal effects (Table 2), significant long-term negative effects of APOE on AD onset within the
of 0.02. Turning to causal effects (Table 2), significant long-term negative effects of APOE on AD onset within the 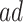 stratum were estimated; those with APOE are expected to receive an AD diagnosis approximately 2 years earlier. Additionally, death at earlier age was expected in both strata under APOE. For
stratum were estimated; those with APOE are expected to receive an AD diagnosis approximately 2 years earlier. Additionally, death at earlier age was expected in both strata under APOE. For  (age 80), effects were zero for the
(age 80), effects were zero for the 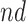 stratum and negative though small for the
stratum and negative though small for the 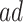 . For
. For 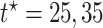 (ages 90,100), effects were negative in both strata, but stronger for the
(ages 90,100), effects were negative in both strata, but stronger for the 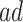 . The estimated effects did not change substantially as a function of
. The estimated effects did not change substantially as a function of 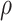 .
.
Table 2.
Estimated RMST causal effects of APOE on AD and death times within the 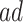 and
and 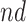 strata. Effects presented are mean (ATE) and median (MTE) differences. Results presented for
strata. Effects presented are mean (ATE) and median (MTE) differences. Results presented for 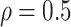 . The empirical distribution of gender and race in the data was used for calculating RMST effects
. The empirical distribution of gender and race in the data was used for calculating RMST effects
| AD | Death | ||||
|---|---|---|---|---|---|
| Stratum |
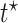
|
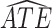 (95% CI)
(95% CI) |
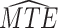 (95% CI)
(95% CI) |
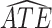 (95% CI)
(95% CI) |
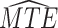 (95% CI)
(95% CI) |
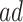
|
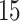
|
 0.04 (
0.04 ( 0.12 to 0.04) 0.12 to 0.04) |
0.00 ( 0.07 to 0.07) 0.07 to 0.07) |
 0.61 (
0.61 ( 0.7 to 0.7 to  0.52) 0.52) |
 1.00 (
1.00 ( 1.09 to 1.09 to  0.91) 0.91) |
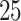
|
 1.28 (
1.28 ( 1.35 to 1.35 to  1.20) 1.20) |
 2.00 (
2.00 ( 2.07 to 2.07 to  1.92) 1.92) |
 2.52 (
2.52 ( 2.61 to 2.61 to  2.43) 2.43) |
 3.00 (
3.00 ( 3.08 to 3.08 to  2.92) 2.92) |
|
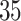
|
 1.82 (
1.82 ( 1.89 to 1.89 to  1.74) 1.74) |
 2.01 (
2.01 ( 2.09 to 2.09 to  1.92) 1.92) |
 2.42 (
2.42 ( 2.5 to 2.5 to  2.35) 2.35) |
 3.00 (
3.00 ( 3.07 to 3.07 to  2.93) 2.93) |
|
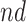
|
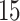
|
 0.13 (
0.13 ( 0.22 to 0.22 to  0.05) 0.05) |
0.00 ( 0.08 to 0.08) 0.08 to 0.08) |
||

|
 0.56 (
0.56 ( 0.65 to 0.65 to  0.48) 0.48) |
 1.00 (
1.00 ( 1.08 to 1.08 to  0.92) 0.92) |
|||
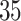
|
 1.75 (
1.75 ( 1.84 to 1.84 to  1.67) 1.67) |
 1.99 (
1.99 ( 2.08 to 2.08 to  1.90) 1.90) |
|||
To summarize the findings, APOE was found to expedite AD development within the 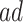 stratum. APOE was shown to have harmful effect on long-term age at death in both strata only under Assumption 6 and the semiparametric modeling.
stratum. APOE was shown to have harmful effect on long-term age at death in both strata only under Assumption 6 and the semiparametric modeling.
7. Discussion
It has been increasingly acknowledged that considering dual outcomes may provide unique information about the scientific problem in hand, especially in the presence of death as a competing event. While the SCR framework allows for consideration of dual outcomes, questions of causality under this framework were only recently began to be studied. To study causal effects of APOE on AD and death, we proposed new estimands built upon a population stratification approach.
Population stratification may suffer from similar disadvantages to principal stratification - that one cannot know the stratum a unit belongs to at baseline, and that the 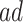 and
and 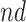 strata may be small or irregular subsets of the population. When the
strata may be small or irregular subsets of the population. When the 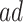 and/or the
and/or the 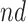 strata comprise small part of the population, the TV-SACE and TV-RMST can be more informative. The TV-SACE and RM- SACE are also attractive when heterogeneity in treatment effect across time is of interest. When the goal is to assess the extent to which an intervention effect is mediated through a disease, a mediation approach should be preferred. Finally, when interest lies in the disease event only, causal estimands from the competing events literature might be more appealing.
strata comprise small part of the population, the TV-SACE and TV-RMST can be more informative. The TV-SACE and RM- SACE are also attractive when heterogeneity in treatment effect across time is of interest. When the goal is to assess the extent to which an intervention effect is mediated through a disease, a mediation approach should be preferred. Finally, when interest lies in the disease event only, causal estimands from the competing events literature might be more appealing.
We presented two overarching strategies towards studying the proposed causal estimands. The large-sample bounds we developed are built upon a set of assumptions a researcher is willing to make explicitly on the relation between potential outcomes under two different interventions. The frailty-based approach models cross-world dependence via semiparametric assumptions and carries out a sensitivity analysis as a function of the sensitivity parameter. One disadvantage of the latter is that the exact restrictions imposed on the potential outcomes beyond the conditional independence are implicit. Our sensitivity analysis strategy resembles the approach of Xu and others (2020) in that a correlation parameter for the cross-world dependence is introduced together with a distribution assumption. We used a frailty approach, while Xu and others (2020) assumed a Gaussian copula model for the joint distribution function of 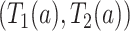 conditionally on
conditionally on 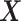 . Xu and others (2020) then considered a flexible Bayesian regression model.
. Xu and others (2020) then considered a flexible Bayesian regression model.
Supplementary Material
Acknowledgments
The authors thank two anonymous reviewers and the Associate Editor for helpful comments that improved the article.
Conflict of Interest: None declared.
Contributor Information
Daniel Nevo, Department of Statistics and Operations Research, Tel Aviv University, Tel Aviv, Israel.
Malka Gorfine, Department of Statistics and Operations Research, Tel Aviv University, Tel Aviv, Israel.
8. Software
Our R package  (Version 1.0.0) implements the proposed methodology and is available from https://github.com/daniel258/CausalSemiComp.
(Version 1.0.0) implements the proposed methodology and is available from https://github.com/daniel258/CausalSemiComp.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
The ACT study was funded by the National Institute on Aging (U01 AG006781). The authors gratefully acknowledge the Adults Changes in Thought Study team for sharing the data for the motivating example. The authors gratefully acknowledge support from the Israel Science Foundation (DN: ISF 827/21; MG: ISF 1067/17) and the U.S.-Israel Binational Science Foundation (MG: BSF 2016126).
References
- Akritas, M. G. and Van Keilegom, I. (2003). Estimation of bivariate and marginal distributions with censored data. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 65, 457–471. [Google Scholar]
- Alzheimer’s Association. (2019). 2019 Alzheimer’s disease facts and figures. Alzheimer’s & Dementia 15, 321 – 387. [Google Scholar]
- Beran, R. (1981). Nonparametric regression with randomly censored survival data. Technical Report, Department of Statistics, University of California. California, Berkeley. [Google Scholar]
- Comment, L., Mealli, F., Haneuse, S. and Zigler, C. (2019). Survivor average causal effects for continuous time: a principal stratification approach to causal inference with semi-competing risks. arXiv preprint arXiv:1902.09304. [Google Scholar]
- Corder, E., Saunders, A., Strittmatter, W., Schmechel, D., Gaskell, P., Small, G, Roses, A., Haines, J. and Pericak-Vance, M. (1993). Gene dose of Apolipoprotein E type 4 allele and the risk of Alzheimer’s disease in late onset families. Science 261, 921–923. [DOI] [PubMed] [Google Scholar]
- Dal Forno, G., Carson, K. A., Brookmeyer, R., Troncoso, J., Kawas, C. H. and Brandt, J. (2002). APOE genotype and survival in men and women with Alzheimer’s disease. Neurology 58, 1045–1050. [DOI] [PubMed] [Google Scholar]
- Ding, P. and Lu, J. (2017). Principal stratification analysis using principal scores. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 79, 757–777. [Google Scholar]
- Frangakis, C. E. and Rubin, D. B. (2002). Principal stratification in causal inference. Biometrics 58, 21–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerds, T. A. (2019). prodlim: Product-Limit Estimation for Censored Event History Analysis. R package version 2019.11.13. [Google Scholar]
- Gorfine, M., Keret, N., Ben Arie, A., Zucker, D. and Hsu, L. (2021). Marginalized frailty-based illness-death model: application to the UK-Biobank survival data. Journal of the American Statistical Association 116, 1155–1167. DOI 10.1080/01621459.2020.1831922. [DOI] [Google Scholar]
- Kukull, W. A., Higdon, R., Bowen, J. D., McCormick, W. C., Teri, L., Schellenberg, G. D., van Belle, G., Jolley, L. and Larson, E. B. (2002). Dementia and Alzheimer disease incidence: a prospective cohort study. Arch of Neurology 59, 1737–1746. [DOI] [PubMed] [Google Scholar]
- Lee, K-H, Rondeau, V. and Haneuse, S. (2017). Accelerated failure time models for semi-competing risks data in the presence of complex censoring. Biometrics 73, 1401–1412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, S-H, Young, J. G., Logan, R. and VanderWeele, T. J. (2017). Mediation analysis for a survival outcome with time-varying exposures, mediators, and confounders. Statistics in medicine 36, 4153–4166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long, D. M. and Hudgens, M. G. (2013). Sharpening bounds on principal effects with covariates. Biometrics 69, 812–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevo, D., Blacker, D., Larson, E. B. and Haneuse, S. (2021a). Modeling semi-competing risks data as a longitudinal bivariate process. Biometrics, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevo, D., Ogino, S. and Wang, M. (2021b). Reflection on modern methods: causal inference considerations for heterogeneous disease etiology. International Journal of Epidemiology 50, 1030–1037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen, G. G., Gill, R. D., Andersen, P. K. and Sørensen, T. I. A. (1992). A counting process approach to maximum likelihood estimation in frailty models. Scandinavian Journal of Statistics 19, 25–43. [Google Scholar]
- Robins, J. M. (1995). An analytic method for randomized trials with informative censoring: part 1. Lifetime Data Analysis 1, 241–254. [DOI] [PubMed] [Google Scholar]
- Safieh, M., Korczyn, A. D. and Michaelson, D. M. (2019). ApoE4: an emerging therapeutic target for Alzheimer’s disease. BMC Medicine 17, 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepherd, B.E., Gilbert, P.B. and Lumley, T. (2007). Sensitivity analyses comparing time-to-event outcomes existing only in a subset selected postrandomization. Journal of the American Statistical Association 102, 573–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stensrud, M. J., Young, J. G., Didelez, V., Robins, J. M. and Hernán, M. A. (2020). Separable effects for causal inference in the presence of competing events. Journal of the American Statistical Association, 1–9. [Google Scholar]
- Tchetgen Tchetgen, E. J. (2014). Identification and estimation of survivor average causal effects. Statistics in Medicine 33, 3601–3628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tom, S. E., Hubbard, R. A., Crane, P. K., Haneuse, S. J., Bowen, J., McCormick, W. C., McCurry, S. and Larson, E. B. (2015). Characterization of dementia and Alzheimer’s disease in an older population: updated incidence and life expectancy with and without dementia. American Journal of Public Health 105, 408–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanderWeele, T. J. (2011). Principal stratification–uses and limitations. The International Journal of Biostatistics 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varadhan, R., Xue, Q-L. and Bandeen-Roche, K. (2014). semi-competing risks in aging research: methods, issues and needs. Lifetime Data Analysis 20, 538–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu, J., Kalbfleisch, J. D. and Tai, B. (2010). Statistical analysis of illness–death processes and semi-competing risks data. Biometrics 66, 716–725. [DOI] [PubMed] [Google Scholar]
- Xu, Y., Scharfstein, D., Müller, P. and Daniels, M. (2020). A Bayesian nonparametric approach for evaluating the causal effect of treatment in randomized trials with semi-competing risks. Biostatistics, kxaa008. 10.1093/biostatistics/kxaa008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young, J. G., Stensrud, M. J., Tchetgen Tchetgen, E. J. and Hernán, M. A. (2020). A causal framework for classical statistical estimands in failure-time settings with competing events. Statistics in Medicine 39, 1199–1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zehavi, T. and Nevo, D. (2021). A matching framework for truncation by death problems. arXiv preprint arXiv:2110.10186. [Google Scholar]
- Zhang, J. L. and Rubin, D. B. (2003). Estimation of causal effects via principal stratification when some outcomes are truncated by “death”. Journal of Educational and Behavioral Statistics 28, 353–368. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.