Number of necessary training examples for Neural Networks with different number of trainable parameters

Abstract

In this work, the network complexity should be reduced with a concomitant reduction in the number of necessary training examples. The focus thus was on the dependence of proper evaluation metrics on the number of adjustable parameters of the considered deep neural network. The used data set encompassed Hematoxylin and Eosin (H&E) colored cell images provided by various clinics. We used a deep convolutional neural network to get the relation between a model’s complexity, its concomitant set of parameters, and the size of the training sample necessary to achieve a certain classification accuracy. The complexity of the deep neural networks was reduced by pruning a certain amount of filters in the network. As expected, the unpruned neural network showed best performance. The network with the highest number of trainable parameter achieved, within the estimated standard error of the optimized cross-entropy loss, best results up to 30% pruning. Strongly pruned networks are highly viable and the classification accuracy declines quickly with decreasing number of training patterns. However, up to a pruning ratio of 40%, we found a comparable performance of pruned and unpruned deep convolutional neural networks (DCNN) and densely connected convolutional networks (DCCN).

Introduction

Modern deep convolutional neural networks (DCNN) can easily encompass millions of parameters, quite a number of them being redundant or close to zero in magnitude. As such, highly complex network architectures put a heavy load to the necessary hardware as well as to computation time and require a large training sample. Especially in the medical area, data samples are often small lacking sufficient data to train complex networks, thus incurring the risk of overfitting. Moreover, it is difficult to know how many training examples are necessary for a neural network with a given number of parameters. Hence, efforts have increased recently to reduce network complexity. One way to do so is network pruning, whereby one tries to simplify the network architecture without impairing network performance. Removing weak or redundant weights speeds up learning and occasionally also improves prediction accuracy. Anyway, pruning first tries to identify the most promising network units (neurons, channels, filters) to be removed. Afterwards, the pruned network model needs further training and fine-tuning to recover the base model’s prediction performance.¹³ In practice, analytical proxies like the number of adjustable parameters or floating point operations (FLOPs) are commonly used to quantify pruning efficacy. Such DCNNs with reduced network complexity have several advantages to offer: Concerning server computations, less complex models reduce bandwidth usage, power consumption, and operational costs, while computations on embedded systems or edge devices guaranty privacy, low latency, and better customization.³⁷

Work related to pruning

When considering network pruning, often heuristics are employed to identify candidate units to be removed. Generally, either data-agnostic saliency criteria are computed or data-aware techniques are considered. The former group is, for example, represented by methods considering the Hessian matrix to identify weights to be removed without harming the prediction accuracy.¹⁵ As such techniques encompass heavy computations, alternatively weights may be grouped according to some similarity measures and each group is then replaced by its prototype weight.⁵⁰ If weight values, i.e. their L₂-norms, represent a saliency criterion, pruning them iteratively provides another simple alternative.¹³ The grain of salt with such techniques is the sparse matrices they create, which don’t help speeding up inference. These drawbacks can be leveraged by applying structural pruning methods.³⁰ The latter commonly deploy L₁-norm Lasso constraints and consider channel- or filter-based pruning approaches.^31,33 More generally, a Group Lasso approach⁵⁸ to pruning dealt with variable selection problems at the group level. Smoothing functions were introduced to alleviate problems arising with gradient computations at the origin. Enforcing sparsity even further, the L₁-norm constraint has been replaced in some studies by a L_1/2-norm regularization. The latter penalty yielded better sparsity than the L₁-norm regularization at similar computational costs. Chang et al.⁴ proposed a network pruning method based on the L_1/2 penalty, which reduced incorrect pruning by increasing the sparsity of the pre-trained models. Also in Wang et al,⁶⁰ the L_1/2-norm constraints have been considered at the channel level, while channel importance has been evaluated by a genetic algorithm. Structured sparsity also often needs some control based on attention mechanisms as pointed out in Torfi et al,⁵⁴ whose work is an extension of the work of Wen et al.⁶¹ Similarly, the work of Lin et al³⁵ considered regularized structured filter pruning by incorporating 2 different regularizers into the objective function to fully coordinate global outputs and local filter pruning operations. Also a novel regularization-based pruning method, named IncReg, was proposed by Wang et al,⁵⁷ which incrementally assigns different regularization factors to different weights based on their relative importance. Further pruning methods on the filter pruning level considered the scaling factor of batch normalization layers as salient feature⁶⁵ or removed filters close to their geometric median.¹⁶ Recently structured Dirichlet filter pruning has been proposed by Adamczewski and Park.¹ The authors assigned Dirichlet distributions over every channel’s convolutional layers and estimated by variational inference the parameters of the distribution. The latter allowed them to identify irrelevant filters of the architecture. As a by-product, the method provided interpretable features. Filter pruning methods also have close connections to low rank network matrix decomposition techniques.³⁴,⁵ Swaminathan et al⁵² proposed a sparse low rank weight matrix decomposition, while considering the significance of both input and output nodes of a layer. Recent work by Yeom et al⁶³ also explored connections between pruning and matrix decomposition methods by developing a new energy-aware pruning technique. The preserved energy corresponded to the summed singular values of the filter decomposition and filters were pruned on the basis of their energy content. Concerning data-driven pruning methods on the weight level, the average percentage of zeros of nodes¹⁹ served as saliency criterion for weight importance and network trimming. Structured pruning at the channel level was considered by He et al¹⁷ by minimizing the reconstruction error for input data. Also the entropy of channel activation was considered a suitable saliency measure for channel removal³⁸ as well as cross entropy.³ Concerning loss functions, their derivatives can serve as cost measures for feature dropping and were deployed by Molchanov et al⁴¹ to prune network structures based on grouped feature map activation. Similarly, the magnitude of gradients has also been considered a proper saliency measure for network pruning.¹¹

Work related to cell segmentation

A seminal recent review of deep learning methods for cellular image analysis is provided by Moen et al⁴⁰ highlighting to biologists the use of deep learning techniques for biological image understanding. If image classification is intended, biological images often lack appropriate annotation with class labels, hence transfer learning deems most suitable here.^44,64 Transfer learning resorts to an image classifier that has been trained on a generally huge image data set, such as ImageNet, and only re-trains the final fully connected layer with an often small image data set of interest.^10,64

Changes in cell morphology may not always be captured by a labeled training data set. Here, deep learning can be used to extract feature vectors rather than labels. These features can then be clustered according to some similarity measure and appropriately classified.^24,44,49 Image classification can also be employed to identify cell states. A recent study trained a classifier with images labeled with a fluorescence marker for cell differentiation. The trained classifier was then employed to identify differentiated cells directly from corresponding bright field images.^48,49 Yet another study applied a deep learning classifier to fluorescence images to determine characteristic spatial patterns in the images which indicated protein localization in large data sets from yeast^27,28,43 and humans.⁵¹

Another large field of image analysis, where deep learning techniques can be employed favorably, is image segmentation. Classical segmentation methods often rely on simple thresholding,²³ but with moderate success only. Modern segmentation techniques come in 2 flavors: semantic segmentation and instance-based segmentation. The former partitions a cell image into semantically meaningful parts, like cytoplasm, nucleus, cytoskeleton etc. and labels all pixels belonging to the latter appropriately. Instance-based segmentation, instead, focuses on every instance of a class in any given cell image. Early examples of the latter approaches are given by the software packages U-Net^9,47 and DeepCell.⁵⁶ They consider instance-based segmentation as a pixel-level classification task. The trained image classifier then generates predictions about class membership pixel-wise thereby grouping pixels into categories like cell interior, cell edges, and background, for instance. A rather more classical segmentation technique is watershedding, whereby deep learning has recently been employed to learn a distance measure. This allows to build a mask encompassing those pixels which have at least a minimal distance from the background of the image.^2,7 A recent application to segment single cells in images performed surprisingly well.⁵⁹ Other approaches to image segmentation are based on object detection techniques, whereby the bounding box of every object is identified. Deep learning algorithms like Faster R-CNN⁴⁶ and Retinanet³⁶ combine bounding box detection with a suppression of non-maximal pixels to avoid redundant bounding box predictions.^18,21,22,55 A rather different approach to image segmentation considers the segmentation problem as a vector embedding problem.^6,45 Thereby, all pixels belonging to an object are assigned by a discriminative loss function to the same vector, while pixels of different objects belong to different vectors. All objects are finally identified through clustering techniques applied on the embedding space.^14,39,66 Recently, most of these techniques have been generalized to be applicable to 3D data sets.^12,64,53 These deep learning-based image segmentation techniques are applicable in many fields of science. They help to automatize common computer vision workflows and render possible segmentation tasks that previously deemed impossible. For example, a precise quantification of localization-based live-cell reporters became possible by way of an accurate identification of the cytoplasm in mammalian cells.^42,56 A recent study explored this image segmentation method to investigate the mechanisms of cell size control during the fission of yeast cells.⁸ Another exciting application concerns the use of instance-based segmentation in pathology images.^25,26,29,39 There interactions between tumor cells and immune cells were investigated employing spatial proteomics methods in a formalin-fixed and paraffin-embedded substrate.²⁶

In this work, filter pruning methods are deployed to reduce network complexity and the question of the number of necessary training examples for various numbers of trainable parameters is investigated, using the example of a cell segmentation network.

Method

In this section, the used data set is described and its preprocessing is explained. Moreover, we sketch the state-of-the-art neural network applied, and provide an overview of the number of trainable parameters.

Data set

In this work, part of the data set provided by Kumar et al²⁹ - henceforth called the Kumar data set for simplicity - was used. It encompassed Hematoxylin and Eosin stain (H & E) cell images provided by various clinics (for an example see Fig. 1). Table 1 collects all information about the various images employed in this study.

Fig. 1.

Cell image of size $\mathsf{250}\times \mathsf{250}$ pixels with corresponding segmentation.⁶²

Table 1.

A list of images used for pre-training, training, and testing.

Patient ID TCGA-	Organ	Disease type	Usage
A7 − A13E − 01Z − $\mathsf{00}-$DX1	Breast	Breast invasive carcinoma	Pre-training
A7 − A13F − 01Z − $\mathsf{00}-$DX1	Breast	Breast invasive carcinoma	Pre-training
AR − A1AK − 01Z − $\mathsf{00}-$DX1	Breast	Breast invasive carcinoma	Training
E2 − A1B5 − 01Z − $\mathsf{00}-$DX1	Breast	Breast invasive carcinoma	Testing
HE − $\mathsf{7128}-\mathsf{01}$Z − $\mathsf{00}-$DX1	Kidney	Kidney renal papillary cell carcinoma	Training
B0 − $\mathsf{5711}-\mathsf{01}$Z − $\mathsf{00}-$DX1	Kidney	Kidney renal clear cell carcinoma	Testing
38 − $\mathsf{6178}-\mathsf{01}$Z − $\mathsf{00}-$DX1	Liver	Lung adenocarcinoma	Training
21 − $\mathsf{5784}-\mathsf{01}$Z − $\mathsf{00}-$DX1	Liver	Lung squamous cell carcinoma	Testing
G9 − $\mathsf{6336}-\mathsf{01}$Z − $\mathsf{00}-$DX1	Prostate	Prostate adenocarcinoma	Training
CH − $\mathsf{5767}-\mathsf{01}$Z − $\mathsf{00}-$DX1	Prostate	Prostate adenocarcinoma	Testing
DK − A2I6 − 01A − $\mathsf{01}-$TS1	Bladder	Bladder urothelial carcinoma	Training
G2 − A2EK − 01A − $\mathsf{02}-$TSB	Bladder	Bladder urothelial carcinoma	Testing
AY − A8Y K − 01A − $\mathsf{01}-$TS1	Colon	Colon adenocarcinoma	Training
NH − A8F7 − 01A − $\mathsf{01}-$TS1	Colon	Colon adenocarcinoma	Testing
KB − A93J − 01A − $\mathsf{01}-$TS1	Stomach	Stomach adenocarcinoma	Training
RD − A8N9 − 01A − $\mathsf{01}-$TS1	Stomach	Stomach adenocarcinoma	Testing

The Kumar data set consisted of an equal number of images for every tissue class. Only part of the data was used in this study, thereby assuring a balanced data set such that each tissue class was represented by one image for training and another image for testing. While selecting them, care was taken that the images came from different clinics and, if possible, represented different tumor types. This selection should render the classification task as hard as possible. Furthermore, the trained networks should be suitable for transfer learning on cell images of other clinics. All images were subdivided into overlapping image patches of size ( $51\times 51=2601$ pixels). In total, the data set encompassed 14 654 944 such image patches. However, only N_tr = 915 934 overlapping image patches were taken of every input image and constituted the size of the training sample for an unpruned DCNN. Furthermore, the number N_tr of training samples was chosen to match the number ${\mathsf{N}}_{\mathsf{p}}=\mathsf{915}$ 934 of adjustable parameters of our deep convolutional neural network (DCNN). The pixels of every image were classified as belonging either to class cell or class background, whereby the goal of the classification effort was to properly classify the center pixel of every image patch. During the training process, the total number N_tr of image patches were separated into 70% training examples and 30% validation examples using a cross-validation method. Also from every tissue, class 1 image was kept out of bag for testing and estimating standard errors. Thus, the out of bag test set consisted of 7 images, each for every tissue class, from which a corresponding number of patches was drawn for testing.

Neural network architecture

To optimize the number of training examples needed by the given neural network architecture, a deep convolutional neural network (DCNN) in analogy with Xing et al⁶² and a densely connected convolutional network (DCCN)²⁰ were employed. The architecture of the networks is illustrated in Fig. 2 and Fig. 3 and the trainable parameters are given in Table 2. The DCNN network consisted of 3 convolutional layers, 3 max-pooling layers, 2 fully connected layers, and 1 softmax output layer. The input array encompassed $\mathsf{51}\times \mathsf{51}$ × 3 pixels, which corresponded to a 3-channel RGB image patch of the cell images. The output layer implemented a softmax activation function. The DCCN network consisted of 4 convolutional layers, 1 max-pooling, and 3 average-pooling layers, 3 dense blocks, 1 fully connected layer, and 1 sigmoid output layer. The input array size was the same as for the DCNN. Because of the binary classification at the output, a cross-entropy loss function L_ce was implemented to guide the training of both the DCNN and the DCCN.

Fig. 2.

Architecture of the DCNN for cell segmentation similar to Xing et al.⁶²

Fig. 3.

Architecture of the DCCN for cell segmentation similar to Huang et al.²⁰

Table 2.

Number of trainable parameters in each layer of the 2 neural network architectures.

DCNN		DCCN
Layer	Parameters	Layer	Parameters
conv 1	1225	conv 1	9536
conv 2	31 300	DenseBlock	335 040
conv 3	144 080	conv 2	33 280
FC 1	738 104	DenseBlock	1 047 552
FC 2	2050	conv 3	132 096
		DenseBlock	2 709 888
		conv 4	526 336
		FC	1026
Total number	916 759	Total number	4 794 754

Experiments

The central question we were focusing on, was about the relation between a model’s complexity, its concomitant set of parameters, and the size of the training sample necessary to achieve a satisfactory classification accuracy. Thus, the study explored possibilities to reduce network complexity resulting in a reduced number of needed training examples. For this task, we chose a neural network with several million parameters and another with less than 1 million parameters. The selected network architectures perfectly suited this purpose, as we only wanted to achieve a classification of the central pixel of every image patch.

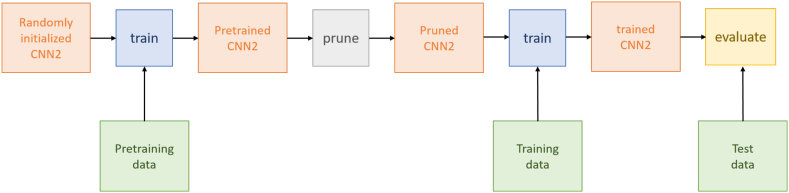
In Fig. 4, the training and evaluation process is illustrated. First, the DCNN and DCCN were implemented and randomly initialized. The networks were then pre-trained for 10 epochs employing the breast data set indicated in Table 1 of the previous section. The data set, used for pre-training, consisted of only 2 breast carcinoma cell images recorded in a clinic. These images were partitioned into 1 831 868 image patches. This set of image patches was used to train the set of ${\mathsf{N}}_{\mathsf{p}}=\mathsf{915}$ 934 adjustable parameters of our network models and provided us with a pre-trained neural network that served as the basis for all further experiments. To reduce network complexity, the pre-trained neural networks were pruned by applying different pruning ratios, starting with 0% pruning and increasing to 90% pruning in steps of 10%. Thereby, pruning was done by adopting the structured L₁ pruning method implemented by PyTorch.

Fig. 4.

Principal training and evaluation process.

This method is based on Li et al³² and uses the L₁ norm of filters as an indicator of the importance of the filter. It is assumed that if the L₁ norm of a filter is small, the importance of the filter is also low. This norm is calculated for all filters of a conv layer and then 30% of the least important filters are eliminated. This procedure is carried out one after the other for each conv layer.

All layers of the pruned networks were then further trained for 30 epochs employing various numbers of training examples N_tr(r). The latter have been computed by taking the following multiples r of the number N_p of trainable parameters of the pruned DCNN architecture:

$$\begin{array}{c}{N}_{\mathit{tr}}\left(r\right)=r·N_p,\\ \mathit{where}r=2,1,0.5,0.1,0.05,0.01,0.005,0.001\end{array}$$ (1)

For the DCCN computations were performed using only r values between 0.5 and 0.001, because of the demanding compute time and the missing number of training samples. Note that this resulted in different numbers of training examples depending on the chosen pruning ratios. Additionally, all pruned neural networks were trained for further comparability with identical training sample sizes as given in Table 3. The latter have been deduced from the number N_p of parameters of the unpruned DCNN or DCCN, respectively.

Table 3.

Reduction factor r and corresponding number of training patterns N_tr(r). The number of training samples with the label cell N_cell and the one with the label no cell N_nocell are also given. Remember that the number of adjustable parameters of the unpruned DCNN amounted to ${\mathsf{N}}_{\mathsf{p}}=\mathsf{915}$ 934 and for the DCCN amounted to ${\mathsf{N}}_{\mathsf{p}}=\mathsf{4}$ 794 754.

DCNN
r	0.001	0.005	0.01	0.05	0.1	0.5	1	2
Ntr(r)	916	4580	9159	45 797	91 593	457 967	915 934	1 831 868
Ncell	675	3404	6816	34 404	68 827	344 373	688 780	1 376 401
Nnocell	241	1176	2343	11 393	22 766	113 594	227 154	455 467

DCCN
r	0.001	0.005	0.01	0.05	0.1	0.5
Ntr(r)	4795	23 974	47 948	239 738	479 475	2 397 377
Ncell	3622	18 045	36 047	180 505	360 383	1 800 694
Nnocell	1173	5929	11 901	59 233	119 092	596 683

After the training process, every trained network was applied to segment the test data sample. When increasing N_tr, every larger training data set contained the smaller training data set used before. Also care was taken to ensure balanced training data sets with a roughly equal number of pixels per class (cell, non-cell) in each set $\mathcal{X}$. To ensure that the data sets $\mathcal{X}$ are representative, the distributions of the mutual information between all images of a data set were chosen to be similar.

Despite facing a 2-class classification problem here, we formulate the optimization problem for K classes. Hence, training was guided by a softmax cross-entropy loss function

$$\mathcal{L}\left({\mathbf{y}}_i,{\widehat{\mathbf{y}}}_i\right)=-\frac{1}{N}\sum _k\sum _n\left[y_{\mathit{in}}^{\left(k\right)}{\widehat{y}}_{\mathit{in}}^{\left(k\right)}+y_{\mathit{in}}^{\left(k\right)}ln\left(\sum _{k\prime }exp\left({\widehat{y}}_{\mathit{in}}^{\left(k\prime \right)}\right)\right)\right]$$ (2)

where N denotes the number of pixels in input patch x_i. Furthermore, y_in ∈ {0.1}^K denotes a 1-hot encoded ground-truth vector and ${\widehat{\mathbf{y}}}_{\mathit{in}}\in {\mathrm{ℝ}}^K$ represents a vector of class membership probabilities.

Evaluation metrics play an important role in assessing the outcomes of segmentation models. Hence, prediction quality was assessed deploying the following performance metrics: Dice Sørensen coefficient DSC, accuracy acc, sensitivity Se, and recall Rec, specificity Sp, and precision Pre.

In order to analyze the robustness of the training process, the unpruned DCNN was trained 7-fold with different random seed numbers and $N_p=91539$  training examples, corresponding to a reduction factor r = 0.1. Finally, all test images were segmented with the trained networks. The standard deviation over these predictions was taken as a measure of the inaccuracy of the predictions for all investigated network configurations, which could not be fully exploited due to an insufficient computing capacity.

Results

Test of reproducibility

As mentioned in the last section, in order to be able to distinguish networks with different pruning configurations, hence different numbers of trainable parameters, the reproducibility of the network architecture was examined first. In 7 different training runs of an unpruned network with N_tr(r = 1.0) = 915 934 training examples, each initialized with a different random seed, the predictions of the pixel class memberships achieved with a DCNN model a standard error for the accuracy of s_acc = 1.7 · 10⁻³ and for the cross entropy of s_ce = 4.3 · 10⁻³, respectively. These numbers were rounded to s_acc = 2 · 10⁻³ and s_ce = 4 · 10⁻³ for convenience. For the DCCN model corresponding standard errors read s_acc = 2.8 · 10 − 3 and s_ce = 1.3 · 10⁻³, respectively, which were rounded to s_acc = 3 · 10⁻³ and s_ce = 1 · 10⁻³ for the sake of an easy comparison. These figures of merit were considered valid for all network configurations investigated in this study, as already explained above.

Varying the number of training examples

Next the unpruned DCNN was trained with various numbers of training examples. The latter were determined, given the pruning ratio δ, as N_tr(r,δ) = N_tr(r)(1 - δ). Up to a pruning ratio δ of 50% ≡ δ = 0.5 and N_tr ≥ N_p, the accuracy remained practically constant with a maximal test accuracy of acc = $\mathsf{0.932}\pm \mathsf{0.002}$, and a minimal cross-entropy loss of L_ce ≡ H(p,q) = $\mathsf{0.181}\pm \mathsf{0.003}$ was achieved. Note that 99% of the maximal test accuracy could already be obtained with only 9159 training patterns, corresponding to r = 0.01 (see Table 4).

Table 4.

Cross-entropy loss L_ce ≡ H(p,q), Segmentation accuracy acc, Sensitivity, Specificity, and Dice coefficient for different trained network configurations. Number of training examples: N_tr, related cross-entropy loss: L_ce, test accuracy: acc. The best result per row, i.e. per reduction factor r, is highlighted as bold. Note that s_ce = 1 · 10⁻³ and s_acc = 3 ⋅ 10⁻³ are considered to hold for all DCNN network configurations.

r	Ntr	Sensitivity	Specificity	DiceCo	acc	Lce	Ntr	Sensitivity	Specificity	DiceCo	acc	Lce
	0% pruning						10% pruning
2	1 831 868	0.835	0.952	0.802	0.933	0.176	1 648 681	0.834	0.953	0.803	0.934	0.178
1	915 934	0.828	0.953	0.801	0.932	0.180	824 341	0.810	0.953	0.790	0.930	0.181
0.5	457 967	0.828	0.952	0.799	0.931	0.180	412 170	0.820	0.950	0.790	0.929	0.184
0.1	91 593	0.828	0.946	0.788	0.927	0.197	82 434	0.829	0.944	0.783	0.926	0.190
0.05	45 797	0.827	0.945	0.785	0.924	0.204	41 217	0.811	0.946	0.776	0.923	0.210
0.01	9159	0.789	0.946	0.768	0.921	0.220	8243	0.802	0.930	0.747	0.910	0.237
0.005	4580	0.744	0.949	0.743	0.915	0.241	4122	0.779	0.945	0.758	0.917	0.239
0.001	916	0.684	0.936	0.674	0.899	0.306	824	0.619	0.944	0.630	0.898	0.343
	20% pruning						30% pruning
2	1 465 494	0.815	0.956	0.798	0.933	0.177	1 282 308	0.789	0.960	0.791	0.933	0.181
1	732 747	0.834	0.950	0.797	0.930	0.182	641 154	0.859	0.942	0.798	0.929	0.177
0.5	366 374	0.817	0.951	0.792	0.929	0.183	320 577	0.819	0.950	0.789	0.928	0.189
0.1	73 275	0.809	0.947	0.776	0.924	0.201	64 115	0.809	0.945	0.775	0.923	0.207
0.05	36 637	0.827	0.941	0.777	0.921	0.204	32 058	0.800	0.944	0.767	0.921	0.205
0.01	7327	0.825	0.930	0.765	0.915	0.231	6411	0.798	0.931	0.750	0.912	0.231
0.005	3664	0.715	0.951	0.730	0.913	0.238	3206	0.769	0.937	0.746	0.912	0.242
0.001	733	0.596	0.946	0.613	0.898	0.327	641	0.606	0.941	0.606	0.896	0.373
	40% pruning						50% pruning
2	1 099 121	0.742	0.933	0.709	0.932	0.181	915 934	0.718	0.935	0.695	0.930	0.181
1	549 560	0.723	0.936	0.702	0.931	0.181	457 967	0.727	0.933	0.699	0.930	0.184
0.5	274 780	0.719	0.934	0.697	0.927	0.185	228 984	0.709	0.936	0.692	0.928	0.191
0.1	54 956	0.712	0.931	0.687	0.924	0.206	45 797	0.698	0.930	0.676	0.921	0.213
0.05	27 478	0.727	0.922	0.684	0.920	0.212	22 899	0.716	0.927	0.681	0.920	0.228
0.01	5496	0.661	0.929	0.653	0.914	0.237	4580	0.702	0.930	0.679	0.919	0.232
0.005	2748	0.674	0.930	0.663	0.915	0.237	2290	0.671	0.931	0.664	0.916	0.246
0.001	550	0.540	0.938	0.559	0.901	0.323	458	0.534	0.909	0.501	0.880	0.344
	60% pruning						70% pruning
2	732 747	0.826	0.946	0.783	0.927	0.186	549 560	0.816	0.953	0.791	0.930	0.181
1	366 374	0.797	0.954	0.783	0.928	0.187	274 780	0.813	0.951	0.787	0.929	0.191
0.5	183 187	0.800	0.952	0.783	0.927	0.195	137 390	0.808	0.950	0.784	0.928	0.199
0.1	36 637	0.805	0.944	0.770	0.920	0.218	27 478	0.771	0.951	0.764	0.921	0.227
0.05	18 319	0.783	0.948	0.764	0.919	0.224	13 739	0.765	0.948	0.755	0.919	0.236
0.01	3664	0.676	0.950	0.700	0.907	0.274	2748	0.441	0.975	0.525	0.887	0.301
0.005	1832	0.476	0.968	0.539	0.892	0.359	1374	0.486	0.972	0.576	0.889	0.339
0.001	366	0.443	0.923	0.441	0.863	0.390	275	0.146	0.973	0.201	0.836	0.481
	80% pruning						90% pruning
2	366 374	0.791	0.956	0.783	0.929	0.193	183 187	0.816	0.941	0.774	0.921	0.232
1	183 187	0.812	0.947	0.782	0.926	0.202	91 593	0.801	0.945	0.771	0.922	0.226
0.5	91 593	0.792	0.948	0.771	0.923	0.217	45 797	0.678	0.951	0.704	0.911	0.243
0.1	18 319	0.618	0.958	0.654	0.908	0.242	9159	0.653	0.950	0.685	0.905	0.266
0.05	9159	0.523	0.970	0.585	0.901	0.296	4580	0.513	0.962	0.576	0.893	0.308
0.01	1832	0.428	0.974	0.498	0.887	0.336	916	0.000	1.000	0.000	0.818	0.476
0.005	916	0.000	1.000	0.000	0.818	0.497	458	0.000	1.000	0.000	0.818	0.471
0.001	183	0.097	0.968	0.129	0.809	0.521	92	0.000	1.000	0.000	0.818	0.465

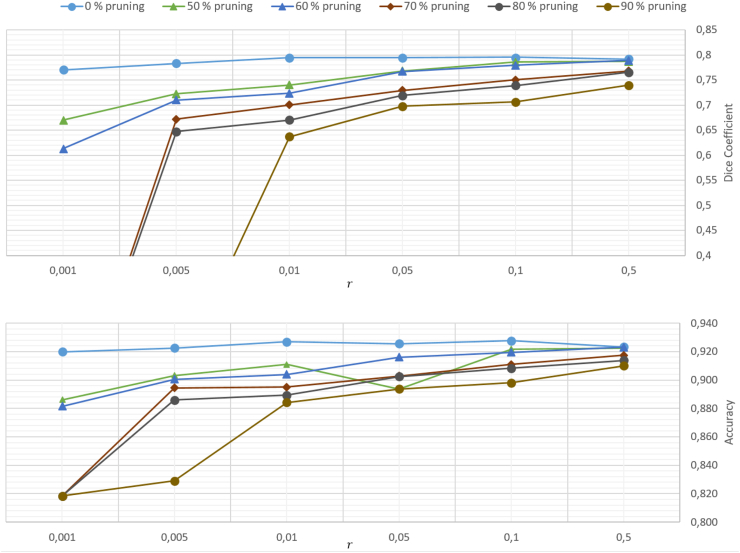
First, Fig. 5 illustrates the dependence of the test accuracies, achieved with the various DCNN pruning configurations, on the number of training examples. Corresponding result in case of the more complex DCCN are shown in Fig. 6. All networks were trained for best image segmentation by minimizing the cross-entropy loss. During training, the number of necessary training examples was varied for a given set of adjustable parameters as determined by the pruning ratio. The former was determined by the chosen network architecture via r · N_p, with r denoting a factor multiplying the number N_p of trainable parameters. The most complex unpruned network, either DCNN or DCCN, yielded best results among all training runs. It is remarkable to see that even a reduction of the number of training samples by a factor r = 0.001 leads to a rather modest decrease of the accuracy by roughly 5% only for both network architectures. A similar observation holds for the Dice coefficient, which decreased by 6% and 1%, respectively. With increased network pruning, however, both accuracy and Dice coefficient degrade substantially for strongly reduced training sample sizes r < 0.1. With δ = 0.9, for example, we observed a decrease of the accuracy by 11% and 9%, respectively while Dice coefficients decreased to zero for both networks. This is amazing as a reduced network complexity results in a smaller number of adjustable model parameters. Obviously, a too strong reduction of the training sample size results in a worsening of the learning ability of the resulting network. Considering the cross-entropy loss, i.e. the objective that was optimized during training, it steadily increases with decreasing reduction factor r. For the unpruned networks, cross entropy increased by 70% in case of a DCNN but only by 4% in case of a DCCN. However, the increase is especially strong for less complex networks at pruning ratios larger than 50%, where L_ce more than doubles in case of the DCNN, while the increase is only 22% in case of the DCCN.

Fig. 5.

Dice coefficient and test accuracy for the DCNN with different pruning ratios. The network configurations were trained with different data sample sizes, scaled by the factor r.

Fig. 6.

Dice coefficient and test accuracy for the DCCN with different pruning ratios. The network configurations were trained with different data sample sizes, scaled by the factor r.

Reducing network complexity by pruning

Next, the dependence of the performance metrics on network complexity was studied. With large training sample sizes, i.e. r = 1 and r = 2, respectively, in case of the DCNN network and r = 0.5 in case of the DCCN network, classification accuracy remained practically unaffected. This was expected as there the largest numbers of training examples were used. The same held true for the Dice coefficient, with the exception of 40% and 50% pruning ratios in case of the DCNN network, which unexpectedly showed a sudden drop for all numbers of training examples. Lacking any reasonable explanation, we consider the results for these 2 pruning ratios as outliers. Remarkably, up to a pruning ratio of 50% prediction accuracy remained rather high, amounting to a drop of a mere 0.2%. This is not the case for the corresponding Dice coefficient, which for the DCNN network decreased by almost 13% over the same range of network pruning (compare Table 4 but remember that the 50% values were considered outlier). More realistic might be the drop seen over the entire pruning range δ = 0 → 0.9, where the corresponding figures read 1% for the accuracy and 4% for the Dice coefficient. Remarkably, for the more complex DCCN network the corresponding decrease at r = 0.5 amounted to 1%, roughly for δ = 0 → 0.5 while it was seen to be 7% for δ = 0 → 0.9 (compare Table 5). The corresponding figures for the accuracy read 0.6% and 3%, respectively. For even larger pruning ratios, i.e. r = 0.001, both metrics degraded rapidly with decreasing training sample size and decreasing network complexity for both network architectures. Thus, the accuracy dropped by 9% for δ = 0 → 0.9 and 2% for δ = 0 → 0.5 in case of the DCNN network. For the DCCN architecture, the corresponding accuracies dropped by 11% for δ = 0 → 0.9 and 4% for δ = 0 → 0.5. This degradation was, however, especially visible for the Dice coefficient, which reduced to zero for δ = 0 → 0.9 for both architectures and yielded 25% for δ = 0 → 0.5 in case of DCNN and 13% under the same conditions in case of DCCN. Considering the cross-entropy loss, it again stood almost constant up to a pruning ratio of 50% before starting to increase with further decreasing network complexity. For instance, at r = 1 cross entropy increased in case of a DCNN by a mere 2% for δ = 0 → 0.5 but by 26% for δ = 0 → 0.9. At high reduction factors r = 0.001, the corresponding values were 12% and 52%, respectively. In case of more complex DCCN networks, we observed an increase by 3% for δ = 0 → 0.9 and by 0.3% for δ = 0 → 0.5 and r = 0.5. Again, for very parsimonious networks (r = 0.001) we, instead, observed an increase in L_CE by 39% for δ = 0 → 0.9 and by 8% for δ = 0 → 0.5. The results for the cross-entropy loss L_ce and the test accuracy acc for different network configurations are summarized in Table 4 and Table 5.

Table 5.

Cross-entropy loss L_ce ≡ H(p,q), Segmentation accuracy acc, Sensitivity, Specificity, and Dice coefficient for different trained network configurations. Number of training examples: N_tr, related cross-entropy loss: L_ce, test accuracy: acc. The best result per row, i.e. per reduction factor r, is highlighted as bold. Note that s_ce = 1 · 10⁻³ and s_acc = 3 · 10⁻³ are considered to hold for all DCCN network configurations.

r	Ntr	Sensitivity	Specificity	DiceCo	acc	Lce	Ntr	Sensitivity	Specificity	DiceCo	acc	Lce
	0% pruning						50% pruning
0.5	2 397 377	0.846	0.940	0.792	0.923	0.384	1 198 689	0.838	0.941	0.787	0.922	0.385
0.1	479 475	0.823	0.952	0.796	0.928	0.382	239 738	0.829	0.943	0.786	0.922	0.386
0.05	239 738	0.838	0.944	0.795	0.926	0.384	119 869	0.823	0.935	0.768	0.894	0.419
0.01	47 948	0.818	0.949	0.795	0.927	0.386	23 974	0.754	0.942	0.740	0.911	0.399
0.005	23 974	0.803	0.947	0.783	0.923	0.387	11 987	0.746	0.935	0.723	0.903	0.408
0.001	4795	0.771	0.951	0.770	0.920	0.396	2397	0.670	0.935	0.669	0.886	0.428
	60% pruning						70% pruning
0.5	958 951	0.835	0.944	0.789	0.923	0.386	719 213	0.817	0.940	0.768	0.917	0.391
0.1	191 790	0.816	0.944	0.779	0.920	0.390	143 843	0.799	0.936	0.750	0.911	0.395
0.05	95 895	0.807	0.940	0.767	0.916	0.392	71 921	0.773	0.932	0.729	0.903	0.402
0.01	19 179	0.733	0.941	0.724	0.904	0.408	14 384	0.728	0.926	0.700	0.895	0.413
0.005	9590	0.715	0.940	0.710	0.900	0.415	7192	0.647	0.942	0.672	0.854	0.421
0.001	1918	0.595	0.939	0.613	0.882	0.435	1438	0.000	1.000	0.000	0.818	0.500
	80% pruning						90% pruning
0.5	479 475	0.834	0.932	0.765	0.914	0.392	239 738	0.772	0.937	0.739	0.910	0.396
0.1	95 895	0.770	0.936	0.739	0.908	0.401	47 948	0.745	0.924	0.706	0.898	0.411
0.05	47 948	0.749	0.931	0.719	0.902	0.409	23 974	0.737	0.922	0.698	0.894	0.419
0.01	9590	0.686	0.927	0.670	0.889	0.424	4795	0.625	0.932	0.637	0.884	0.434
0.005	4795	0.651	0.928	0.647	0.886	0.428	2397	0.098	0.991	0.154	0.829	0.470
0.001	959	0.000	1.000	0.000	0.818	0.500	479	0.000	1.000	0.000	0.818	0.500

Network training with fixed training set size

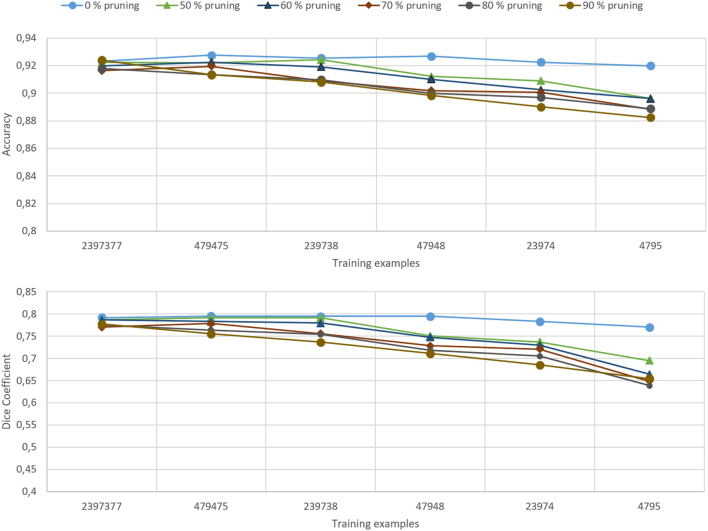
In order to be able to directly compare the performance of pruned neural networks, the different network configurations were trained once again for both network architectures with identical numbers of training examples. All results are collected in Table 6 and Table 7, respectively. Note that here the number N_tr of training examples corresponds to a fraction r deduced from the number of adjustable parameters N_p of the original, unpruned network. The number of predicted cells for different pruning ratios δ and number of training examples N_tr is illustrated in case of the DCNN architecture in Fig. 7 (See Fig. 8).

Table 6.

Cross-entropy loss L_ce ± 10⁻³ and statistical metrics (Sensitivity, Specificity, acc ± 10^-3) for the segmentation prediction of different network configurations are presented. Note that here the number of training examples is the same for all tested pruning ratios. Again remember that the number of adjustable parameters of the unpruned DCNN amounted to ${\mathsf{N}}_{\mathsf{p}}=\mathsf{91}$6 959. The rows marked yellow present results obtained with networks where the condition N_tr ≥ N_p held.

Ntr	Sensitivity	Specificity	DiceCo	acc	Lce	Sensitivity	Specificity	DiceCo	acc	Lce
	0% Pruning,$N_p=915934$					10% Pruning,$N_p=824341$
1 831 868	0.835	0.952	0.802	0.933	0.176	0.828	0.955	0.804	0.934	0.178
915 934	0.828	0.953	0.801	0.932	0.180	0.821	0.951	0.792	0.930	0.180
457 967	0.828	0.952	0.799	0.931	0.180	0.824	0.950	0.792	0.930	0.180
91 593	0.828	0.946	0.788	0.927	0.197	0.803	0.951	0.780	0.926	0.193
45 797	0.827	0.945	0.785	0.924	0.204	0.800	0.947	0.773	0.923	0.211
9159	0.789	0.946	0.768	0.921	0.220	0.791	0.933	0.739	0.909	0.252
4580	0.744	0.949	0.743	0.915	0.241	0.752	0.950	0.753	0.918	0.234
916	0.684	0.936	0.674	0.899	0.306	0.743	0.927	0.704	0.898	0.305
	20% Pruning, $N_p=732747$					30% Pruning, $N_p=641154$
1 831 868	0.811	0.954	0.790	0.931	0.178	0.829	0.951	0.796	0.931	0.179
915 934	0.827	0.950	0.792	0.930	0.179	0.822	0.952	0.797	0.932	0.178
457 967	0.813	0.952	0.789	0.930	0.182	0.822	0.952	0.792	0.931	0.182
91 593	0.822	0.949	0.789	0.926	0.199	0.818	0.947	0.782	0.925	0.198
45 797	0.801	0.947	0.772	0.922	0.206	0.821	0.944	0.777	0.923	0.208
9159	0.795	0.938	0.756	0.916	0.224	0.774	0.946	0.757	0.918	0.226
4580	0.741	0.950	0.745	0.917	0.234	0.758	0.940	0.739	0.912	0.252
916	0.634	0.958	0.676	0.908	0.280	0.731	0.924	0.699	0.896	0.303
	40% Pruning,$N_p=549560$					50% Pruning,$N_p=457967$
1 831 868	0.825	0.949	0.789	0.929	0.179	0.807	0.954	0.790	0.931	0.180
915 934	0.838	0.947	0.793	0.929	0.176	0.817	0.951	0.789	0.929	0.177
457 967	0.817	0.952	0.791	0.931	0.185	0.816	0.952	0.790	0.930	0.185
91 593	0.819	0.947	0.783	0.925	0.203	0.790	0.953	0.776	0.926	0.205
45 797	0.834	0.940	0.778	0.923	0.209	0.784	0.949	0.765	0.922	0.210
9159	0.774	0.949	0.761	0.921	0.222	0.789	0.939	0.755	0.915	0.237
4580	0.791	0.930	0.742	0.909	0.249	0.748	0.954	0.757	0.921	0.228
916	0.660	0.940	0.667	0.899	0.321	0.611	0.944	0.634	0.896	0.309
	60% Pruning,$N_p=366374$					70% Pruning,$N_p=274780$
1 831 868	0.853	0.946	0.800	0.930	0.184	0.816	0.950	0.787	0.928	0.187
915 934	0.826	0.948	0.790	0.929	0.179	0.835	0.934	0.772	0.920	0.204
457 967	0.825	0.950	0.791	0.929	0.190	0.838	0.947	0.795	0.930	0.193
91 593	0.822	0.944	0.778	0.923	0.214	0.827	0.946	0.788	0.927	0.215
45 797	0.783	0.949	0.766	0.922	0.215	0.801	0.947	0.773	0.923	0.224
9159	0.771	0.942	0.750	0.915	0.237	0.654	0.957	0.687	0.910	0.258
4580	0.750	0.945	0.746	0.915	0.242	0.682	0.951	0.704	0.907	0.269
916	0.401	0.968	0.461	0.881	0.377	0.008	1.000	0.015	0.820	0.455
	80% Pruning,$N_p=183187$					90% Pruning,$N_p=91593$
1 831 868	0.838	0.949	0.799	0.930	0.181	0.839	0.939	0.780	0.923	0.207
915 934	0.833	0.950	0.796	0.930	0.191	0.831	0.942	0.780	0.923	0.218
457 967	0.827	0.947	0.789	0.928	0.199	0.831	0.942	0.780	0.923	0.224
91 593	0.784	0.951	0.770	0.925	0.210	0.831	0.937	0.775	0.920	0.231
45 797	0.727	0.955	0.741	0.920	0.227	0.795	0.941	0.761	0.918	0.239
9159	0.557	0.961	0.601	0.901	0.293	0.620	0.933	0.639	0.888	0.325
4580	0.563	0.955	0.602	0.899	0.270	0.573	0.952	0.627	0.894	0.305
916	0.000	1.000	0.000	0.818	0.492	0.000	1.000	0.000	0.818	0.482

Table 7.

Cross-entropy loss L_ce ± 10⁻³ and statistical metrics (Sensitivity, Specificity, acc ± 10^-3) for the segmentation prediction of different network configurations are presented. Note that here the number of training examples is the same for all tested pruning ratios. Again remember that the number of adjustable parameters of the unpruned DCCN amounted to ${\mathsf{N}}_{\mathsf{p}}=\mathsf{4}$ 794 754. The rows marked yellow present results obtained with networks where the condition N_tr ≥ N_p held.

Ntr	Sensitivity	Specificity	DiceCo	acc	Lce	Sensitivity	Specificity	DiceCo	acc	Lce
	0% Pruning,${\mathsf{N}}_{\mathsf{p}}\mathsf{=}\mathsf{915}$ 934					50% Pruning,${\mathsf{N}}_{\mathsf{p}}\mathsf{=}\mathsf{824}$ 341
2 397 377	0.846	0.940	0.792	0.923	0.384	0.838	0.941	0.787	0.922	0.385
479 475	0.823	0.951	0.796	0.928	0.382	0.848	0.939	0.791	0.922	0.386
239 738	0.838	0.944	0.795	0.926	0.384	0.827	0.946	0.791	0.924	0.385
47 948	0.818	0.949	0.795	0.927	0.386	0.772	0.941	0.750	0.912	0.394
23 974	0.803	0.947	0.783	0.923	0.387	0.756	0.940	0.737	0.909	0.400
4795	0.771	0.951	0.770	0.920	0.396	0.712	0.935	0.695	0.896	0.417
	60% Pruning, ${\mathsf{N}}_{\mathsf{p}}=\mathsf{366}$ 374					70% Pruning, ${\mathsf{N}}_{\mathsf{p}}=\mathsf{274}$ 780
2 397 377	0.859	0.934	0.787	0.920	0.389	0.836	0.935	0.771	0.916	0.389
479 475	0.814	0.946	0.783	0.923	0.387	0.833	0.938	0.779	0.920	0.390
239 738	0.824	0.941	0.780	0.919	0.389	0.838	0.838	0.756	0.909	0.394
47 948	0.785	0.937	0.747	0.910	0.401	0.774	0.774	0.729	0.902	0.405
23 974	0.775	0.930	0.729	0.902	0.408	0.757	0.757	0.721	0.901	0.409
4795	0.638	0.948	0.665	0.896	0.421	0.625	0.625	0.649	0.888	0.426
	80% Pruning,${\mathsf{N}}_{\mathsf{p}}\mathsf{=}\mathsf{183}$ 187					90% Pruning,${\mathsf{N}}_{\mathsf{p}}\mathsf{=}\mathsf{91}$ 593
2 397 377	0.843	0.935	0.775	0.918	0.387	0.805	0.948	0.777	0.924	0.386
479 475	0.828	0.933	0.764	0.914	0.392	0.801	0.937	0.755	0.913	0.391
239 738	0.824	0.927	0.754	0.910	0.397	0.774	0.936	0.737	0.908	0.396
47 948	0.762	0.925	0.718	0.900	0.411	0.758	0.923	0.711	0.898	0.410
23 974	0.738	0.925	0.705	0.897	0.416	0.723	0.920	0.686	0.890	0.421
4795	0.622	0.938	0.639	0.889	0.426	0.675	0.921	0.654	0.882	0.432

Fig. 7.

Test accuracy and Dice coefficient for neural network configurations resulting from different pruning ratios. Each configuration was trained with an identical but variable number of training examples.

Fig. 8.

Test accuracy and Dice coefficient for neural network DCCN configurations resulting from different pruning ratios. Each configuration was trained with an identical but variable number of training examples.

Let us first consider the simpler DCNN architecture. The results showed that up to a pruning ratio of 50%, both accuracy and Dice coefficient remained rather insensitive to the actual network complexity at the maximal number of training samples N_tr = max. While the accuracy remained constant in this range, the observed reduction of the Dice coefficient amounted to 1.5%. Only for pruning ratios above 50%, both metrics declined more strongly, with the Dice coefficient responding earlier and stronger. Thus, we observed a decrease of the Dice coefficient by 3%, while the accuracy dropped by only 1% for δ = 0 → 0.9 at N_tr = max. In case of the minimal number of training samples N_tr = min, the Dice coefficient dropped to zero at δ = 0.9, however, while the accuracy was reduced by 9%. For less strongly pruned networks, i.e. δ = 0 → 0.5, the Dice coefficient dropped by 6% while the accuracy remained constant. In general, the higher the number of training examples, the higher the prediction accuracy. However, the higher the pruning rate, the lower the accuracy.

For the more complex DCCN architecture, the following observations could be made: Considering first the situation, where the number of training samples was maximal (N_tr = max) and the network pruning also reached its larges value (δ = 0.9), the Dice coefficient dropped by 5% while the accuracy only decreased by 2% and the cross-entropy objective raised by 2% as well. If, instead, the number of training samples was minimal (N_tr = min), the corresponding changes were ΔDC(N_tr^min, δ = 0.9) = 15 % , Δacc(N_tr^min, δ = 0.9) = 4 % , ΔL_CE(N_tr^min, δ = 0.9) = 9%. In case of less strongly pruned DCCN networks and a maximal number of training samples we got ΔDC(N_tr^max, δ = 0.5) = 0.6 % , Δacc(N_tr^max, δ = 0.5) = 1 % , ΔL_CE(N_tr^max, δ = 0.5) = 1%. If, however, the number of training patterns was minimal, the corresponding numbers read ΔDC(N_tr^min, δ = 0.5) = 10 % , Δacc(N_tr^min, δ = 0.5) = 3 % , ΔL_CE(N_tr^min, δ = 0.5) = 5%. Hence, given a maximal number of training samples, strong network pruning had only a minor effect on the performance metrics, which was even less pronounced in case of less strongly pruned networks. There all changes did not exceed 1%. But the effects were much stronger, if the number of training patterns was minimal. In Fig. 9, the predictions of different networks are illustrated. The x-axis corresponds to the number of training samples and the y-axis to the pruning ratio. The test accuracy for all neural network configurations are summarized in Fig. 10.

Fig. 9.

Qualitative illustration of the predictions of different network configurations in dependence on the number of training examples and pruning ratios.

Fig. 10.

Color-coded test accuracy acc for neural network configurations resulting from different pruning rates and concomitant number of training data sample points. The accuracy is color coded according to the color bar on the right.

Analysis of computational parameters

The pruning of networks lead to a decrease in average inference time 〈t_inf(δ)〉 and to a decrease in disk space V _DS(see Table 8). This was verified by predicting 100 samples and taking the average of the single inference time values. For pruning ratios δ = 0.5,0.9, inference times were reduced to t_inf(δ = 0.5) ≈ 0.5t_inf(delta = 0) and t_inf(0.9) ≈ 0.24t_inf(0), respectively for both network architectures. Similarly disk space could be reduced in case of a DCNN architecture to 46 % and 9 % and for a DCCN architecture to 24% and 2%, for pruning ratios of δ = 0.5 and δ = 0.9. The experiments were performed on a GPU (GeForce GTX 1070 with total memory of 31.25 GB and 8GB RAM).

Table 8.

Compute time and disk space for different pruning ratios δ.

δ	0	0.10	0.20	0.30	0.40	0.50	0.60	0.70	0.80	0.90
VDS in KB (DCNN)	3586	3172	2822	2376	1996	1634	1282	947	623	315
VDS in KB (DCCN)	19 147	15 766	12 602	9805	7356	5058	3423	2079	1096	467
〈tinf〉 in ms (DCNN)	7.6	6.1	5.4	5.9	5.2	3.9	3.3	2.8	2.2	1.8
〈tinf〉 in ms (DCCN)	47.6	43.1	40.6	35.2	31.9	22.3	18.5	16.3	11.1	9.8

Discussion

The main goal of this work was to reduce network complexity with a concomitant reduction in the number of necessary training examples. Network optimization was driven by cross-entropy minimization, yielding a standard error as small as s_ce = 3 ⋅ 10⁻³ in case of a DCNN architecture and s_ce = 1 ⋅ 10⁻³ in case of the more complex DCCN architecture. Network predictions were evaluated employing standard statistical metrics like prediction accuracy on a test set, true-positive rate and true-negative rate. The focus thus was on the dependence of proper evaluation metrics on the number of adjustable parameters of the considered deep neural network. First, given a DCNN architecture with its concomitant number of adjustable parameters, the variance of the prediction accuracy was analyzed. With a standard error for the accuracy of s_acc = 9 ⋅ 10⁻⁴, the uncertainty of the results is comparatively low. Next, the number of trainable parameters of the DCNN architecture was reduced by pruning a certain amount of weights in the network. For these parsimonious networks with reduced complexity of the weight connectivity, the training sample size was reduced by scaling down the number of training examples by a factor r, which multiplies the number of adjustable parameters of the considered DCNN. Again performance was evaluated by estimating both the standard error of the accuracy s_acc and of the cross entropy s_ce.

The predictions of different DCNN network configurations are illustrated in Fig. 9. As expected, the unpruned DCNN neural network showed best performance. This network with the highest complexity, hence the largest number of training examples N_tr, corresponding to r = 1, achieved, within the estimated standard error of the optimized cross-entropy loss, best results, which roughly persisted up to 40% pruning. Despite the rather small standard error s_acc, it appears that this observation holds across all reduction factors r, i.e. across a rather large range of training sample sizes N_tr. Remarkably, even with a pruning rate of 90%, δ = 0.9, the achieved test accuracy amounted to 98% of the accuracy of the unpruned network. Even more astonishing, if for this network the number of training examples is reduced by a factor of r = 0.01 to N_tr = 9159, the trained network (acc = 0.905) still reached 98% of the maximum achievable accuracy (acc = 0.922). Again, this accuracy was achieved on the independent test set, hence overfitting was not an issue here despite the fact that this network had 10 times more adjustable parameters than training examples.

But with further decreasing numbers of training examples, corresponding to reduction factors lower than r < 0.01, no good results could be achieved for any network configuration and number of training examples. Taken the other way round, a remarkably high accuracy remained even when the training sample size was reduced by a factor of 100, corresponding to r = 0.01 for networks with pruning ratios δ ≤ 0.5. Only then prediction accuracy degraded rapidly, especially for pruning ratios δ ≥ 0.5. The same was true for the other metric, the Dice coefficient (DC) and was also reflected in an increasing minimal cross-entropy (ce) loss. The additional metrics sensitivity (se) and specificity (sp) provided an even more detailed picture. Sensitivity measured how many of the pixels belonging to class cell were correctly predicted, while specificity measured the percentage of correctly assigned background pixels. Remarkably, the specificity or true-negative rate (TNR) was rather high and remained so across all pruning rates. On the contrary, the sensitivity or true-positive rate (TPR) was smaller and decreased further with increasing pruning rate. Furthermore, sensitivity showed a much stronger dependence on the number of training examples and decreased considerably with decreasing N_tr. Note that a high sensitivity indicates that a large number of all pixels belonging to a specific class was classified correctly. Also a high specificity indicates that a large number of pixels not belonging to a specific class were correctly classified accordingly. Fig. 10 provides a qualitative illustration of the accuracy when the number of adjustable parameters and/or the number of training examples changed. As long as the number of model parameters matched the number of training examples, accuracy was generally very high (acc > 90%). But even in case of an insufficient number of training examples, the test accuracy remained amazingly high. As this concerns the previously unseen test data set, overfitting can be safely excluded.

Considering networks of various complexities, i.e. different pruning ratios δ, the latter were also trained by a fixed but variable number of training examples. The latter was deduced from the number of adjustable parameters of the unpruned network by applying the reduction factor r. If considered as a function of the number of training examples, a common observation is that as along as N_p ≤ N_tr holds, all metrics evaluated remained largely insensitive to N_tr (These values are marked with a yellow background in Table 6). But if N_tr < N_p is met, then some metrics like the sensitivity or the cross-entropy quickly degraded strongly with decreasing N_tr for all network configurations considered, while others like the specificity, Dice coefficient or the accuracy remained still pretty insensitive to the number of stimuli. Remember that the specificity represented the proportion of the non-cell pixels, and the sensitivity the proportion of cell pixels, that were correctly classified. The following Table 9 provides a comprehensive summary to the detailed results presented in Table 6.

Table 9.

Comprehensive summary of the results obtained with fixed numbers of training examples and a DCNN architecture.

δ	0		0.5	0.9
r	0.001	0.01	0.01	0.01
SE	82%	95%	93%	0%
SP	98%	99%	100%	100%
ACC	96%	99%	99%	89%
DSC	84%	96%	96%	0%
CE	174%	125%	127%	233%

For example, given a pruning ratio δ = 0.9, corresponding to the least complex network architecture, and a number N_tr = 0.5N_p of stimuli, the specificity (SP) was unchanged, the Dice coefficient (DSC) still achieved 97.6% and the accuracy (ACC) amounted to 99.5% of the values prevailing at N_tr > N_p. At the same time, the sensitivity (SE) declined to 95% and the cross entropy (CE) increased to 115.5%. Even worse, at N_tr = 0.01N_p we observed an unchanged specificity, an accuracy that still reached 88.6% of its original value, while sensitivity and Dice coefficient vanished and the cross entropy raised to 233% of its starting value. To the contrary, in case of the most complex, unpruned DCNN network, when reducing the number of stimuli by a factor of 10³, we rather observed a sensitivity that reached only 82% of its starting value, a specificity of still 98% of its value, when N_tr was abundant, an accuracy of 96% of its best value, a Dice coefficient of only 84% of its starting value and a cross-entropy objective, which raised to 174% of its value with an abundant number of training examples. For an intermediate complexity with a pruning ratio of 50%, we observed an unchanged specificity, a slightly reduced sensitivity ($\mathsf{Se}=\mathsf{92.7}$%), a hardly reduced accuracy acc = 99%, a still respectable Dice coefficient of $\mathsf{DSC}=\mathsf{95.8}$% but an already considerably increased cross entropy $\mathsf{CE}=\mathsf{126.7}$%. Still these metrics indicate that even with a considerably reduced network complexity and a rather small number of stimuli a good classification performance can be achieved.

A similar picture results in case of the more complex DCCN architecture as can be seen from Table 10, where percentage changes of all metrics are presented. The changes relate to a decrease of the number of training samples from N_tr^max to N_tr^min with all other variables kept constant. While the metrics accuracy ACC and specificity SP remain largely unchanged by a variation of the number of training samples, irrespective of the state of network pruning, sensitivity SE, Dice - Sørensen coeficient DSC and cross-entropy loss CE respond much more strongly. The changes even increase in case of parsimonious networks with a maximal pruning applied to the network weights.

Table 10.

Comprehensive summary of the percentage changes of the performance metrics obtained with fixed numbers of training examples and a DCCN architecture.

δ	0	0.5	0.9
SE	6%	16%	16%
SP	0%	0.4%	2%
ACC	1%	3%	3.4%
DSC	3%	12%	13%
CE	3.6%	8%	10%

In Table 8, the inference time for the DCNN and DCCN for different pruning rates are summarized. Increasing pruning rates could decrease the inference time and the disk space. For the DCNN the inference time was reduced by 77% between no and 90% pruning, for the DCCN the reduction was 79%. Also the disc space could be reduced by 92% for the DCNN and by 98% for the DCCN.

Conclusion

This study focused on the question, how the number of training examples controlled the performance of a DCNN of given complexity, i.e. number of adjustable parameters. This is especially relevant in many biomedical problem settings, where the number of training stimuli is limited compared with the number of degrees of freedom of the deep neural network used to analyze the data. Network complexity was reduced by weight pruning, and the number of training examples N_tr was deduced from the number of degrees of freedom N_p of these pruned networks. Two different scenarios where explored: First N_tr(δ) was deduced from N_p(δ) of the pruned DCNN by a reduction factor $\mathsf{0.001}\le$ r ≤ 1. Here, δ denoted the pruning ratio. Second N_tr was estimated from N_p of the unpruned DCNN by the same reduction factors. While in the first scenario N_p ≥ N_tr, we always considered an oversized network configuration, in the second scenario for a certain range of pruning ratios δ the condition N_p(δ) ≤ N_tr held, while for larger δ the condition changed to N_p(δ) ≥ N_tr. Network performance was evaluated with a set of statistical metrics which showed that up to δ ≤ 0.5, classification performance was hardly hampered, while for larger pruning ratios some statistical metrics degraded noticeably. The conclusion is that N_tr ≥ N_p is not a necessary condition and that oversized networks often achieve an equally good classification performance. Finally, remember that at a pruning ratio δ = 0.5, where all evaluation metrics still achieved respectable values, average inference time was halved and the used disk space shrank to half of its size needed for the unpruned network. This may be of concern, if such evaluations have to be performed on edge devices.

Conflict of interest

None.