Remembering the pattern: A longitudinal case study on statistical learning in spatial navigation and memory consolidation

Abstract

Distinct brain systems are thought to support statistical learning over different timescales. Regularities encountered during online perceptual experience can be acquired rapidly by the hippocampus. Further processing during offline consolidation can establish these regularities gradually in cortical regions, including the medial prefrontal cortex (mPFC). These mechanisms of statistical learning may be critical during spatial navigation, for which knowledge of the structure of an environment can facilitate future behavior. Rapid acquisition and prolonged retention of regularities have been investigated in isolation, but how they interact in the context of spatial navigation is unknown. We had the rare opportunity to study the brain systems underlying both rapid and gradual timescales of statistical learning using intracranial electroencephalography (iEEG) longitudinally in the same patient over a period of three weeks. As hypothesized, spatial patterns were represented in the hippocampus but not mPFC for up to one week after statistical learning and then represented in the mPFC but not hippocampus two and three weeks after statistical learning. Taken together, these findings suggest that the hippocampus may contribute to the initial extraction of regularities prior to cortical consolidation.

1. Introduction

When you move to a new city, even on your first walk around town, you begin mapping out the streets and landmarks in your head, allowing you to subsequently find your way home that day. This knowledge grows over time through continued experience, such that it can help you find particular places on future excursions that you have never visited before. This ability to immediately represent the structure of one’s surroundings and to retain and refine this knowledge over time reflects two different timescales of statistical learning, or extraction of regularities from the environment.

On rapid timescales of minutes to hours, statistical learning occurs robustly across modalities (Sherman, Graves, & Turk-Browne, 2020), from auditory sequences of tones (Saffran, Johnson, Aslin, & Newport, 1999) to visual series of shapes (Turk-Browne, Jungé, & Scholl, 2005) to haptic properties (Lengyel et al., 2019), and within multiple domains, from abstract categories (Brady & Oliva, 2008) to music (Leung & Dean, 2018) to faces (Dotsch, Hassin, & Todorov, 2017). It supports parsing of streams of speech into words (Karuza et al., 2013; McNealy, Mazziotta, & Dapretto, 2006), as well as learning of motor sequences (Janacsek et al., 2020) and reward contingencies (Goldfarb, Chun, & Phelps, 2016). In the brain, this process relies at least in part on the hippocampus (Schapiro & Turk-Browne, 2015), which computational models have shown contains the necessary architecture for rapid, online learning of regularities from the environment (Schapiro, Turk-Browne, Botvinick, & Norman, 2017).

On more gradual timescales of days to weeks, or even years, cortical consolidation of encoded experiences shapes our semantic knowledge, supporting the emergence of spatial, contextual, and conceptual schemas (Gilboa & Marlatte, 2017). The formation of schemas is supported by the medial prefrontal cortex (mPFC), which represents overlapping features of previously encoded stimuli in humans (Tompary & Davachi, 2017) and spatial locations in rodents (Richards et al., 2014). For example, this latter study established a causal link between rodent mPFC and pattern consolidation by having rats learn locations in a Morris Water Maze that were drawn from an underlying, hidden distribution. After learning the individual locations, the mPFC of rats in the experimental group was disabled via a pharmacological manipulation, whereas the mPFC of rats in the control group was left intact. During a test phase 30 days later, the rats were placed back in the water maze to measure whether they had extracted the distribution through consolidation of individual locations. Rats with an intact mPFC searched according to the distribution, indicating statistical learning, but those with an impaired mPFC did not. This finding suggested a critical role for mPFC in consolidation and prolonged retention of spatial regularities.

It remains unclear how the multiple timescales of statistical learning relate to spatial navigation in humans. For example, whereas it takes a month for rodents to extract spatial patterns during navigation, humans can do so immediately during online behavior (Graves, Antony, & Turk-Browne, 2020). Participants in this study performed a virtual analogue of the Morris Water Maze, finding hidden locations in an arena that were drawn from a Gaussian distribution. Over the course of a few minutes of learning, navigation behavior switched from a bias toward previously learned individual locations to a bias toward the mean of the distribution of locations. Despite being acquired rapidly, the fate of this acquired representation over time is unknown. Moreover, whereas we hypothesize that the hippocampus may support rapid extraction, followed by more prolonged retention in mPFC, such time-dependent changes in the brain systems involved in human navigation have not been tested previously.

In the current study, we tracked the cognitive and neural trajectory of learned spatial patterns during navigation via intracranial electroencephalography (iEEG). We had the rare opportunity to repeatedly test a single patient, who was in the hospital for clinical seizure monitoring substantially longer than an average study (6 weeks vs. 1–1.5 weeks typically). The patient performed a screen-based virtual maze task (Graves et al., 2020) where hidden target locations were drawn from a Gaussian distribution. She learned two distributions of locations on two separate days of encoding, after which the extent of her distribution extraction was tested at multiple intervals. We predicted that the hippocampus would represent the underlying distribution initially after learning, but that this pattern would come to be represented in mPFC over time.

2. Materials and Methods

2.1. Participant

We tested one patient (female, age 26, right-handed) admitted to Yale New Haven Hospital for iEEG seizure monitoring. She had a history of epilepsy and attention deficit hyperactivity disorder (ADHD) starting at age 10, as well as recurring depression starting when she was a teenager. Her medications included oxcarbazepine and intronasal midazolam for epilepsy, as well as occasional Adderall for ADHD. A structural MRI in 2017 revealed normal hippocampal volume. Neuropsychological test scores were high overall (Full Scale Intelligence Quotient (FSIQ)=131, Verbal Comprehension Index (VCI)=141, Perceptual Reasoning Index (PRI)=123) and non-indicative of any seizure lateralization or localization. Pre-implant video and EEG monitoring suggested seizures were likely arising from the left posterior lateral temporal region.

The patient was implanted with subdural electrodes on the cortical surface over the left hemisphere, as well as multiple depth electrodes implanted in subcortical structures including the left hippocampus (Fig. 1). Decisions on electrode placement were determined solely by the clinical care team to optimize localization of seizure foci. The patient completed three sessions of a virtual Morris Water Maze task, referred to hereafter as Day 1, Day 8, and Day 21. The research protocol was approved by the Yale University Institutional Review Board.

Fig. 1.

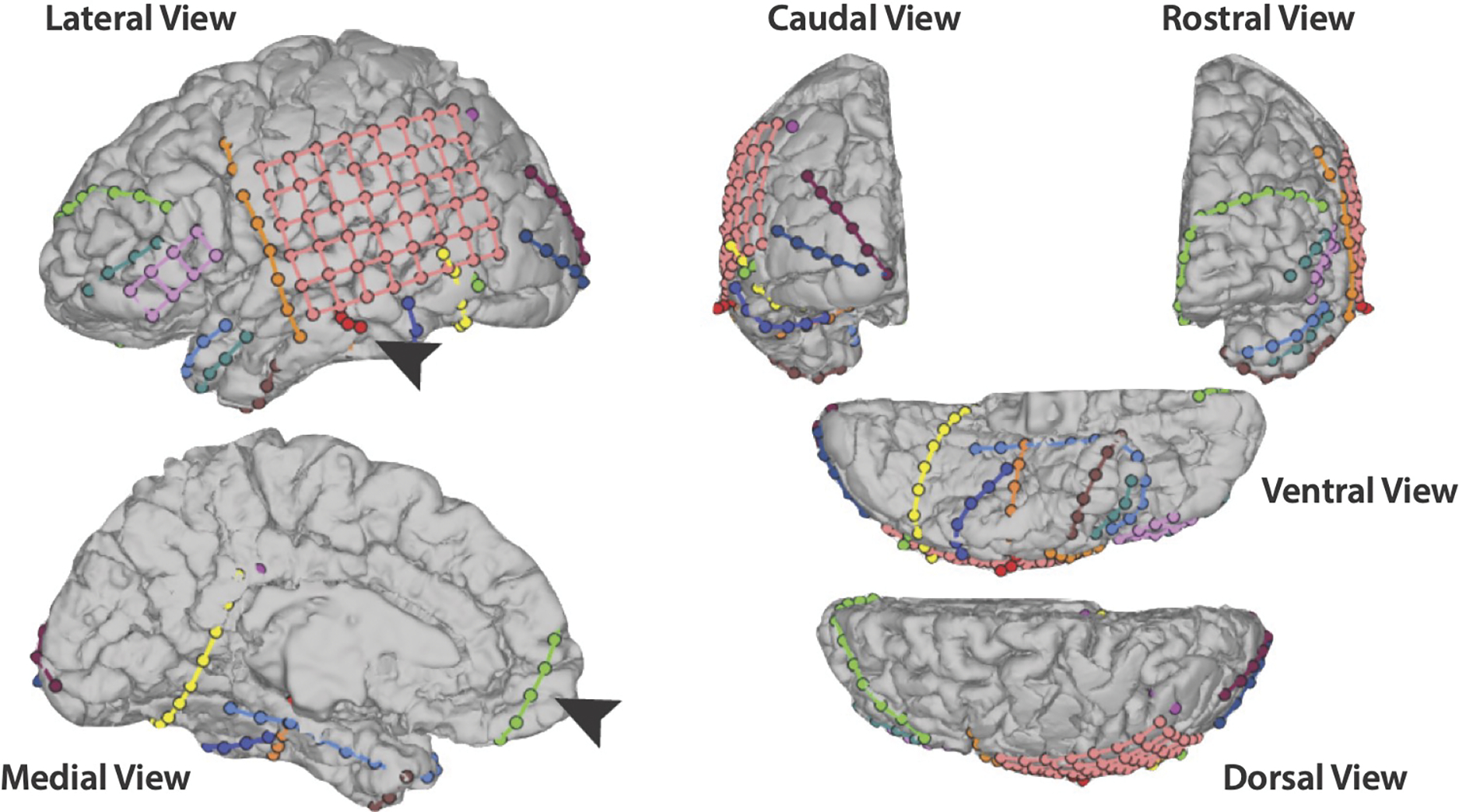
Reconstruction of the patient’s electrode coverage. All views are of the left hemisphere, where all of the electrodes were placed. Arrows are pointing to a (red) depth electrode containing left hippocampal contacts at the tip and to a (green) electrode strip covering left mPFC.

2.2. Experimental Design

The virtual environment was designed as a circular arena and constructed in Blender (www.blender.org). The environment was rendered in Matlab (Mathworks, Natick, MA, USA), and Psychtoolbox (Brainard, 1997) was used to display task instructions. The arena was designed graphically with an island beach theme. The circular floor (radius=7.85 arbitrary units, AU) was covered by an image of sand. Mountains appeared on the north end and palm trees on the south end; similar to the classic water maze task, these landmarks served as directional headings. Each “platform” was a shell in the first session and a crab in the second session. Following Richards et al. (2014), the locations of the shells were drawn from a normal distribution of distances d from center (μ=3.4 AU, σ=0.9067 AU) and a circular normal distribution of angles θ between the platform and the eastern cardinal direction (μ=0.2618 radians, κ=8). The locations of the crabs were generated by taking the shell distribution and rotating it 160 degrees counterclockwise around the arena. We chose 160 degrees instead of a full 180 degree rotation to prevent the use of symmetry-based heuristics.

2.3. Procedure

On Day 1, the patient was trained on the shell distribution. She was instructed that she was on an island, searching for a total of 20 seashells buried below the sand. She could only find one shell at a time and had to walk around the beach until she found it. The patient used the I key to walk forward, the J and L keys to turn left and right, respectively, and the M key to walk backward. The participant moved at a constant speed of .06 arbitrary units per second, with a camera height of .85 units. At the beginning of the search for each new shell, the patient’s location was initialized to the center of the arena, always facing a new random direction. Navigation was initiated by the patient following a minimum of 4 seconds in which the ground was green and the I/M keys were locked only allowing the patient to rotate in place left or right. The ground then turned to sand, cuing the patient that she could now start moving forward and backward. There was no time limit, and thus the searches varied in length. The patient successfully located a shell when she walked within a 1 1/3-unit radius of the platform location of that shell. When this occurred, further navigation was locked, and the walls turned green to reveal the outline of a shell. The screen then went black, and the patient was told how many new shells remained to be found before beginning to search for the next shell.

On Day 8, the patient was first trained on a now 160 degree-rotated distribution, this time looking for crabs. This second distribution was introduced to provide another set of lags between encoding and test, over which we could examine time-dependent changes in hippocampal and mPFC representations. The crab encoding on Day 8 was nearly identical to the shell encoding on Day 1, with the only difference being that the patient was now looking for crabs instead of shells and the distribution was centered in a new part of the arena. After finding all of the crabs, the patient then completed a test phase following a brief delay for instructions. During the test phase, the patient was instructed that she was back on the island and that she would alternate between finding more shells and crabs. She received a cue on each trial indicating which object was the target. The test phase differed critically from encoding in that search was limited to 16 seconds and no feedback was given until the end of the time. This resulted in the patient searching an empty arena based on what was learned during encoding. The patient completed four alternating trials of searching for shells and searching for crabs. The Day 8 shell test evaluates a lag of 7 days, whereas the Day 8 crab test evaluates an immediate lag of 0 days.

On Day 21, the patient completed six more alternating tests of searching for shells and crabs in the empty arena (Fig. 2). The Day 21 shell test evaluates a lag of 20 days, whereas the crab test evaluates a lag of 13 days. Thus, across distributions we tested for the representation of spatial patterns 0, 7, 13, and 20 days after encoding.

Fig. 2.

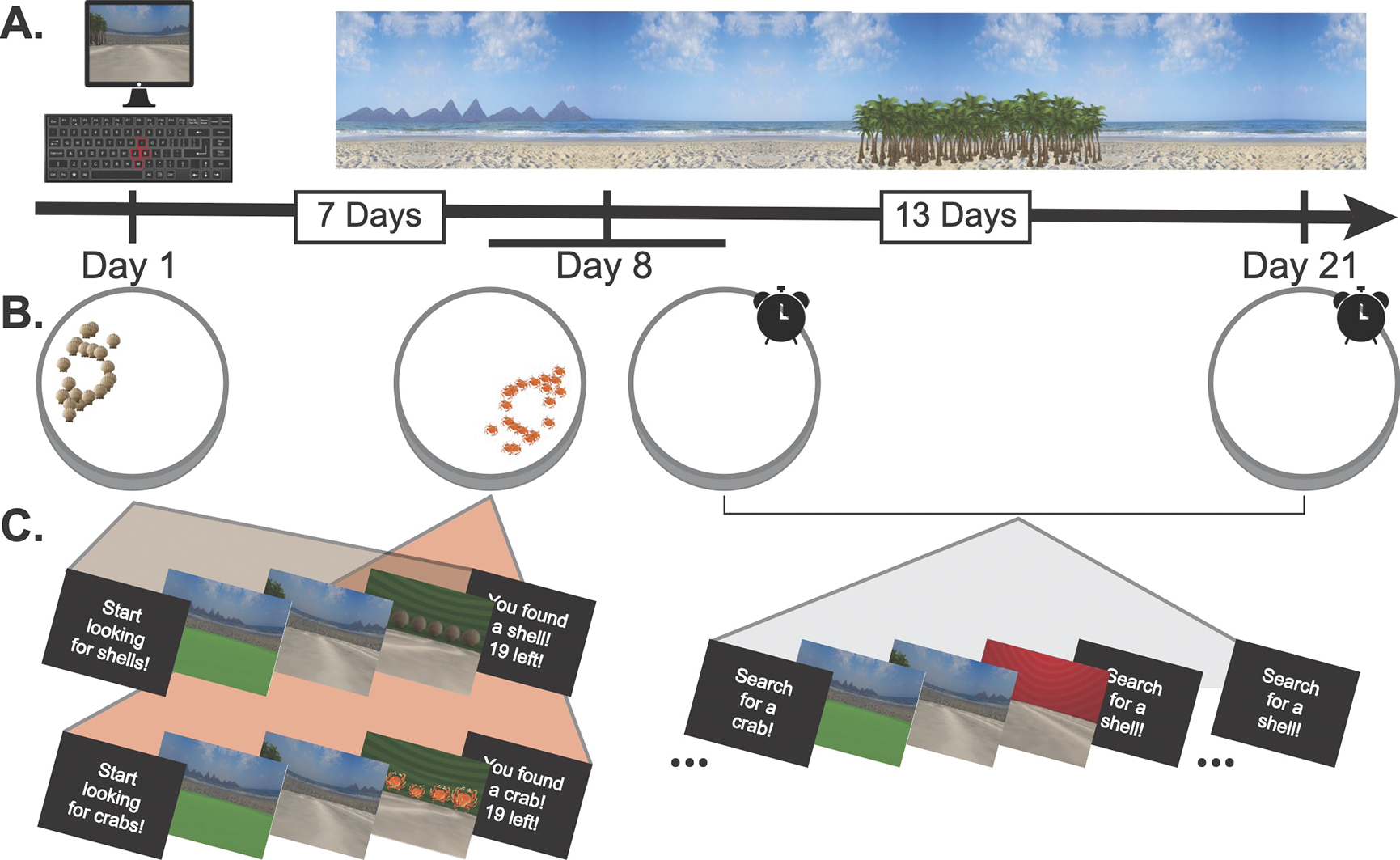
The patient’s testing schedule. A) The experiment was conducted in a virtual beach environment. B) On Day 1, the patient found a distribution of shells (brown icons). On Day 8, she found a distribution of crabs (orange icons), and then performed the first test phase, where she alternated searching for shells (7-day lag) and crabs (0-day lag) in an empty arena. She completed another alternating test phase on Day 21 for shells (20-day lag) and crabs (13-day lag). C) Each trial of encoding and test consisted of a cue, a pre-navigation period where forward motion was locked, a navigation period, and a post-navigation period.

2.4. Intracranial Recordings

Intracranial EEG (iEEG) was recorded in Natus Neuroworks 8.5.1 using a Natus Quantum amplifier, sampled at 4,096 Hz. Signals were referenced to an inverted (facing away from brain) left parieto-temporal strip electrode. The implanted electrodes contained a total of 174 contacts (no microwires). See Table 1 for a complete breakdown of electrode type and location. Neural data were synchronized to behavior via a custom-configured LabJack U3-LV USB Data Acquisition device that converted analogue MATLAB commands from the research computer to 8-bit “triggers” inserted into an open channel. In post-processing, to reduce electrical line noise, a notch filter was applied between 55–65 Hz. Data corresponding to each trial were segmented into fixation, pre-navigation, navigation, and post-navigation epochs, and downsampled to 256 Hz. To eliminate events containing epileptiform activity, epochs were removed from analysis if kurtosis of the voltage trace within epoch exceeded a threshold of 5 (van Vugt, Schulze-Bonhage, Litt, Brandt, & Kahana, 2010). This resulted in an exclusion 2.8% of experimental events. Data from the pre-navigation and navigation epochs were used for analysis. Our analyses included recordings from three hippocampal contacts and three mPFC contacts.

Table 1.

Patient’s electrode placement. All electrodes were implanted in the left hemisphere.

Electrode Placement
Region	Type	Count
Hippocampus	Depth	12
Medial Occipital/Cortical Dysplasia	Depth	12
Posterior Cingulate	Depth	12
Frontal Temporal Parietal Occipital	Grid	48 (8×6)
Inferior Frontal	Grid	8 (2×4)
Frontal Pole	Strip	12
Anterior Medial Temporal	Strip	12
Anterior Lateral Temporal Pole	Strip	6
Middle Temporal Pole	Strip	6
Anterior Lateral Frontal Temporal	Strip	8
Posterior Temporal	Strip	6
Posterior Temporal Occipital	Strip	12
Inferior Occipital Pole	Strip	6
Superior Occipital Pole	Strip	6
Inverted Superior Frontal (Ground)	Strip	4
Inverted Lateral Temporal Pole (Reference)	Strip	4

2.5. Electrode Localization

Electrodes were localized with BioImage Suite (http://www.bioimagesuite.org) and Matlab. The patient’s skull-stripped T1 weighted structural brain MRI was registered to an MNI T1 average structural MRI via nonlinear registration. The resulting transformation file was used to transform the patient’s electrode locations into standard space. Hippocampus and mPFC regions of interest (ROIs) were constructed from the Automated Anatomical Labeling (AAL) map in MNI space (Tzourio-Mazoyer et al., 2002) and used to determine which electrodes fell within each ROI.

We further localized the hippocampal contacts by performing manual hippocampal subfield segmentation via a previously published method (Sherman & Turk-Browne, 2020). We determined that the three contacts were located across the left dentate gyrus, CA2/3, and CA1 in the hippocampal body (Fig. 3).

Fig. 3.

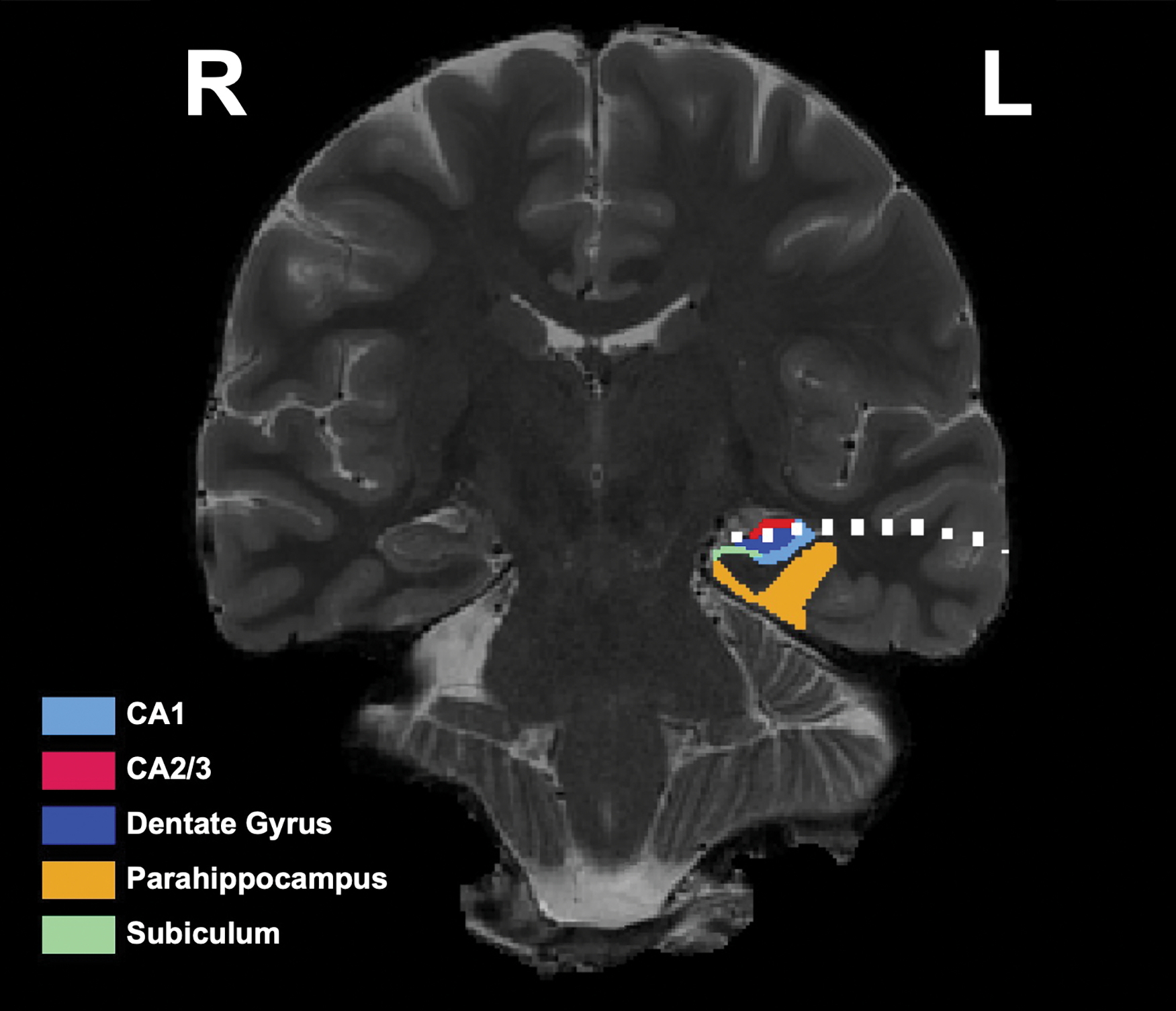
High-resolution T2 with segmented hippocampal subfields. The contacts from the hippocampal depth are depicted in white. Contacts are located in CA2/3 (red), CA4/Dentate Gyrus (dark blue), and CA1 (light blue) of the left hippocampal body

2.6. Behavioral Analyses

Raw behavioral data consisted of X and Y coordinates output every 40 ms of navigation, and all behavioral analyses were performed on this data. First, we sought to confirm that by learning each hidden location during encoding, the patient was also learning the underlying distribution. We predicted that acquisition of the spatial distribution would result in subsequent navigation that was biased towards the distribution’s central tendency.

We first probed for evidence of pattern extraction during the encoding phases. In our previous work (Graves et al., 2020), we confirmed on the group level that participants were navigating based on a representation of the distribution mean, and not simply the most recently learned location, by running two agent-based computer simulations: one with “memory” only for the underlying distribution mean, and one with memory for only the previous individual locations. We quantified the amount of mean-based and location-based navigation during the first and second halves of the experiment for each model and assessed how well the simulated behavior matched the (human) group behavior. We found that both models fit equally well in the first half of the experiment, but by the second half, the mean model fit significantly better, suggesting that participants’ behavior arose specifically from a representation of the underlying pattern and not accidental or proximal passage of the mean during search for individual locations. We additionally confirmed that the most recently learned location was the most salient episodic spatial representation by showing greater navigation to this relative to other potentially salient single locations from the distribution (the first learned, a randomly drawn location, etc). With one participant in the current study, behavior during encoding of each distribution was quite noisy, but we nonetheless aimed to quantify pattern acquisition during the encoding phase via a similar set of analyses comparing bias to the mean with bias to other potentially salient location representations.

For this analysis, we used the behavioral data from trial 3 onward, as there was no prior experience on trial 1 and no opportunity to integrate across multiple previous experiences on trial 2. For each subsequent trial, we computed the change in distance to the distribution mean from the patient’s starting location (the center of the maze) to her location 3 seconds later. We chose this time window because it was the duration of the shortest encoding trial, and in hopes of indexing the patient’s most salient spatial representation, which should guide her initial search trajectory. If the patient was learning the underlying distribution, her early search behavior should reflect a bias towards the mean, and she should therefore be closer to the mean after the first 3 seconds. We computed this change in distance measure for each trial and then binned the trial-wise measures by first and second half of the task, to increase statistical power. We then ran a linear regression and follow-up pairwise tests to determine changes in mean bias from earlier to later encoding and across Day 1 and Day 8 of encoding. Lastly, as control analyses, we computed the change in distance not to the distribution mean, but to the first, second, most recently learned, and a randomly drawn shell and crab location to confirm that any bias was mean-specific and not a bias to other potentially salient individual locations (Graves et al., 2020).

We then analyzed the extent to which learning the underlying distribution biased search behavior during the test phases by measuring whether the patient’s search path brought them closer to the location of each distribution’s mean than what would be expected by chance (Graves et al., 2020). To this end, we calculated the patient’s average proximity to the distribution mean during search across all test trials, separately for each distribution and testing day. We then generated a null distribution of proximity measures by rotating the spatial distribution locations a random angle between 5 and 355 degrees away from the learned distribution 1,000 times. Per rotation, we calculated the average proximity to the dummy rotated mean. An empirical p-value was calculated as the proportion of rotated proximity measures that were closer to the mean than the true proximity. We repeated this analysis for the distribution randomly rotated within plus and minus 90 degrees of the true distribution, and plus and minus 45 degrees, to compare search behavior to more conservative null distributions and confirm that the patient didn’t simply search uniformly in the half or quarter of the arena that contained found locations. The objective of this analysis was to quantify the specificity of the patient’s distribution memory.

In order to disentangle whether any mean-proximal navigation was due to learning of the underlying distribution or merely memory for learned episodes of individual locations, we repeated this null-distribution-based analysis for each learned location from the distributions. We then correlated the first-level p-values per location, which served as measures of the reliability of navigation to each individual location, with two variables: the trial number on which that location was encountered during encoding, and the proximity of that location to the distribution mean. Based on our past work, we predicted that if the patient was navigating merely based on memory of the previously encoded locations, she would navigate to them roughly in order of recency (Graves et al., 2020). Thus, her navigation near individual locations would negatively correlate with trial number. If the patient was representing the underlying distribution and therefore biased towards the mean, her trajectory would be incidentally most proximal to the locations nearest to the mean, regardless of when they were experienced during encoding. Thus, her navigation near individual locations would positively correlate with the proximity of those locations to the mean.

2.7. Time-Frequency Decomposition

To model power over time, we applied a continuous Morlet wavelet transform (wave number 5) in a moving window and at 50 logarithmically spaced frequencies between 1 and 120 Hz for each epoch in the encoding and test sessions, using a procedure similar to published methods (e.g. Miller et al., 2018). A 5-second buffer was added to both ends of all power calculations to account for edge effects, and subsequently was discarded. We then estimated the background power spectrum via a linear regression fit to the power spectrum in log-log coordinates, and subtracted the subsequent 1/f from our data. Lastly, the data were z-scored per frequency band, electrode, and session. These data were used in a subsequent inverted encoding model (IEM). We note that the frequency decomposition was performed over a larger set of frequencies in service of other analyses not included in this manuscript. Including this broader range of frequencies did not impact the results for the narrower bands of focus here.

2.8. Inverted Encoding Model

Spatial representations during test were assessed via a 2-D IEM method (Sprague & Serences, 2013). Briefly, this method enables reconstruction of a spatial representation from neural data that is modeled as a sum of the weighted activations of a set of information channels. The information channels in this study were initialized as 100 2-D Gaussians distributed throughout the surface of the beach arena, representing hypothesized place-coding activity (Fig. 4). We selected this number of initial channels simply to tile the space. Ultimately, only channels that were significantly responsive (as described below) were retained in the model.

Fig. 4.

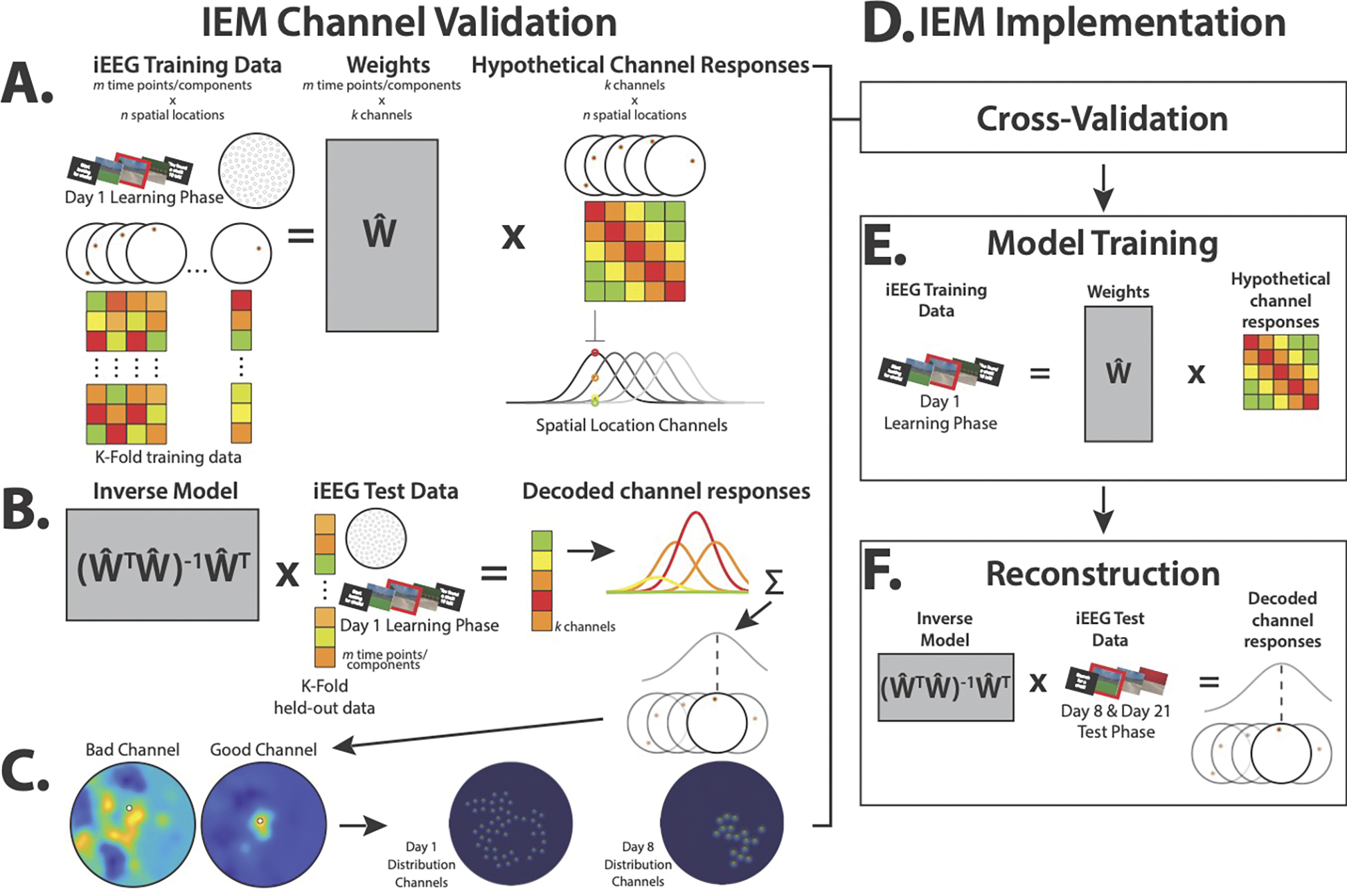
Model channel validation and implementation. Models were optimized via a channel validation step prior to implementation on the test phases of the task on Day 8 and Day 21. A.) Model architecture assumes the neural response at a given spatial location (illustrated by the color matrices below each schematic location in the water maze) is the sum of weighted hypothetical channel responses, where the channels are Gaussians that span the maze. To determine which channels contributed significantly to reconstruction, per encoding Day (1 or 8), a subset of data from within each channel radius was iteratively held out, and the model was trained on remaining data. B) The inverse model was tested on the subset, producing a sum of channel responses, the peak of which was the reconstructed location within the maze. C.) Good channels, for which this summed activity was significantly proximal to the channel’s location in the environment, were left in the model, resulting in 46 good channels for Day 1 and 17 good channels for Day 8. D) Channel validation was the first step of model implementation, resulting in separate optimized models for Day 1 and 8. E) Optimized models were then trained on all encoding data from their respective encoding days. F) The inverse optimized, trained models were then applied to the pre-navigation periods on test Days 8 and 21 to reconstruct the patient’s spatial representations at test.

Because the patient did not explore the entirety of the arena when learning either distribution, and therefore would not have provided neural data to train all of the channels, we conducted a channel validation step that allowed us to select for our final model only the channels for which there was enough data and that subsequently showed significant place-coding activity. This step only used data from the encoding phases. The resultant models were then used to reconstruct representations from unseen test phase data.

In separate models for each encoding day’s distribution, channel validation consisted of holding out a subset of hippocampal activity from when the patient was standing within each channel’s radius, training the model, and then testing it on the held-out data. A channel for which peak reconstructed activity (i.e., the magnitude of the reconstructed response above the 99^th percentile) was more proximal to the tested channel than all other channels was considered a “good” channel (Fig. 4C).

We conducted separate channel validations using time-frequency decomposed power from the 1–3 Hz band (delta, which some have termed “low theta”) and the 3–10 Hz band (theta/low alpha, which some have termed “high theta”) as model training data. Previous work in human virtual navigation has implicated hippocampal oscillations at around 3 Hz (Goyal et al., 2020; Watrous et al., 2013) and 8 Hz (Miller et al., 2018) in spatial navigation and spatial memory encoding. We thus sought to determine which band would yield greater place coding activity and recover a greater number of channels. We conducted a principal components analysis (PCA) over the frequencies by hippocampal electrodes for each band (12 frequencies between 1–3 Hz, 12 frequencies between 3–10 Hz) in order to better compute the aggregate response within-region while controlling for potential signal redundancy across neighboring contacts. We then iteratively repeated the channel validation on each number of components. We additionally iterated through a range of stimulus and receptive field size parameters, which determine the shape of the Gaussians (Sprague & Serences, 2013). The epochs during Day 1 and Day 8 encoding were subdivided into windows of length 125 ms (optimized via iteration) from which features were estimated for training the model. These encoding epochs varied in length meaning that a variable number of windows were extracted per epoch. The test trials, however, had a fixed length, and thus the same number of windows were extracted from each test trial. The maximum number of recovered channels and their associated stimulus size, frequency band, and number of PCA components per distribution across all iterations served as our basis set for reconstructing the spatial representations from the test phase of the experiment. Critically, these model optimizations were performed entirely within the encoding phase data; test phase data were held out of all of these steps to avoid double-dipping. Because our objective at test was to reconstruct not individual place representations, but an aggregate distribution representation, we increased the receptive field size for each distribution’s set of channels. This allowed us to generate smooth reconstructions via a similar manual parameter selection procedure as has been shown previously (Sprague & Serences, 2013).

Our main analyses build from this method of parameter and channel selection, in which we iterated through multiple receptive field sizes to determine which channels showed significant decoding of their individual locations, irrespective of Gaussian width. We found the largest number of good channels with small receptive fields, but for reconstructing representations during the test phase of the experiment this resulted in sparse, patchy reconstructions. Because of this, we increased the receptive field size for this analysis step to produce smoother reconstructions, as has been done in previous implementations(Sprague & Serences, 2013). However, if we simply threshold channel inclusion by amount of data available per channel, manually set all parameters (skipping the channel validation step), and then reconstruct from test, the results are qualitatively the same (Supplemental Fig. 1).

To examine representations at test, we built separate models on encoding data from the shell and crab distributions. For each test trial, we applied the model for the corresponding cued distribution to reconstruct place activity. We used test data from the first four pre-navigation seconds of each trial when the patient was confined to the origin of the arena, for two reasons. First, we predicted that, during this period, the patient would be most saliently representing what she had learned during encoding in planning her search. Second, data from the pre-navigation period, as opposed to the period when she was actively navigating, would not be confounded with her current position. We combined reconstructions over all trials from a given distribution and test session, yielding a reconstruction for each lag and brain region.

We then assessed whether the peak reconstructed activity was significantly proximal to the distribution mean to quantify neural evidence of statistical learning of the distribution. We first determined the most active channel and then calculated the distance from that channel to the distribution mean. We then shuffled the assignment of reconstructed activity to channel, determined the most active channel contributing to the shuffled reconstruction, and calculated its proximity to the mean. We repeated this measure 1,000 times, and computed and empirical p-value as the proportion of true distances to the distribution mean that were smaller than the shuffled distances.

2.9. Reconstructions and Test Behavior

Lastly, we sought to relate the reconstructed place representations in hippocampus and mPFC to the patient’s behavior during test. To do this, we analyzed whether the patient’s behavioral trajectory during test trials was closer to the neural reconstruction than would be expected by chance. To assess chance, we performed a similar null distribution procedure as was described in section 2.6, in which the behavioral trajectory was compared to the neural reconstruction rotated at a random angle plus or minus 180 degrees (360 degrees total), 90 degrees (180 degrees total), or 45 degrees (90 degrees total) of the true location.

3. Results

3.1. Behavior

On average, the patient took 33.63 s (42.43 s SD) to find shells on the first day of encoding (Day 1) and 8.47 s (6.39 s SD) to find crabs on the second day of encoding (Day 8). Linear regression did not reveal a significant decrease in search times from the first to second half of trials within day (β=−0.27, t=−0.71, p=0.482), but the average time was significantly different between the two days (β=−0.90, t=−2.37, p=0.023), with a Wilcoxon signed-rank test revealing faster average times on Day 8 (Z=−2.64, p=0.008, r=0.88, 95% CI=[4.14, 36.04]).

First, we probed for evidence of pattern extraction during encoding of the two distributions. We observed increased navigation to the distribution mean over the course of encoding of the second distribution on Day 8. Linear regression revealed a significant interaction between encoding day and first/second half of encoding, where navigation was significantly more proximal to the distribution mean during the second half of encoding on Day 8 (β=0.61, t=2.05, p=0.049). A Wilcoxon signed-rank test of change in mean proximity from the first to second half of the Day 8 encoding phase revealed a significant increase (Z=−2.31, p=0.021, r=0.77, 95% CI=[−1.17, −0.17]). the same test for encoding of the first distribution on Day 1 was not reliable (Z=−0.11, p=0.910, r=0.04, 95% CI=[−0.41, 0.52]). Control analyses testing increased navigation to the first learned location, second learned location, most recently learned location, and a randomly drawn location yielded no significant changes from the first to second halves of the task on either day (ps>0.1). These findings demonstrate that the mean of the second distribution was gradually extracted, and that this increased mean proximity was not an incidental consequence of relying on certain salient individual locations (Fig. 5). Of note, linear regression revealed no significant difference in overall mean proximity on Day 8 vs. Day 1 of encoding (β=−0.34, t=−1.59, p=0.120), nor was there a difference in bias to other potentially salient locations (first learned location, second learned location, most recently learned location, and a randomly drawn location; ps>0.05).

Fig. 5.

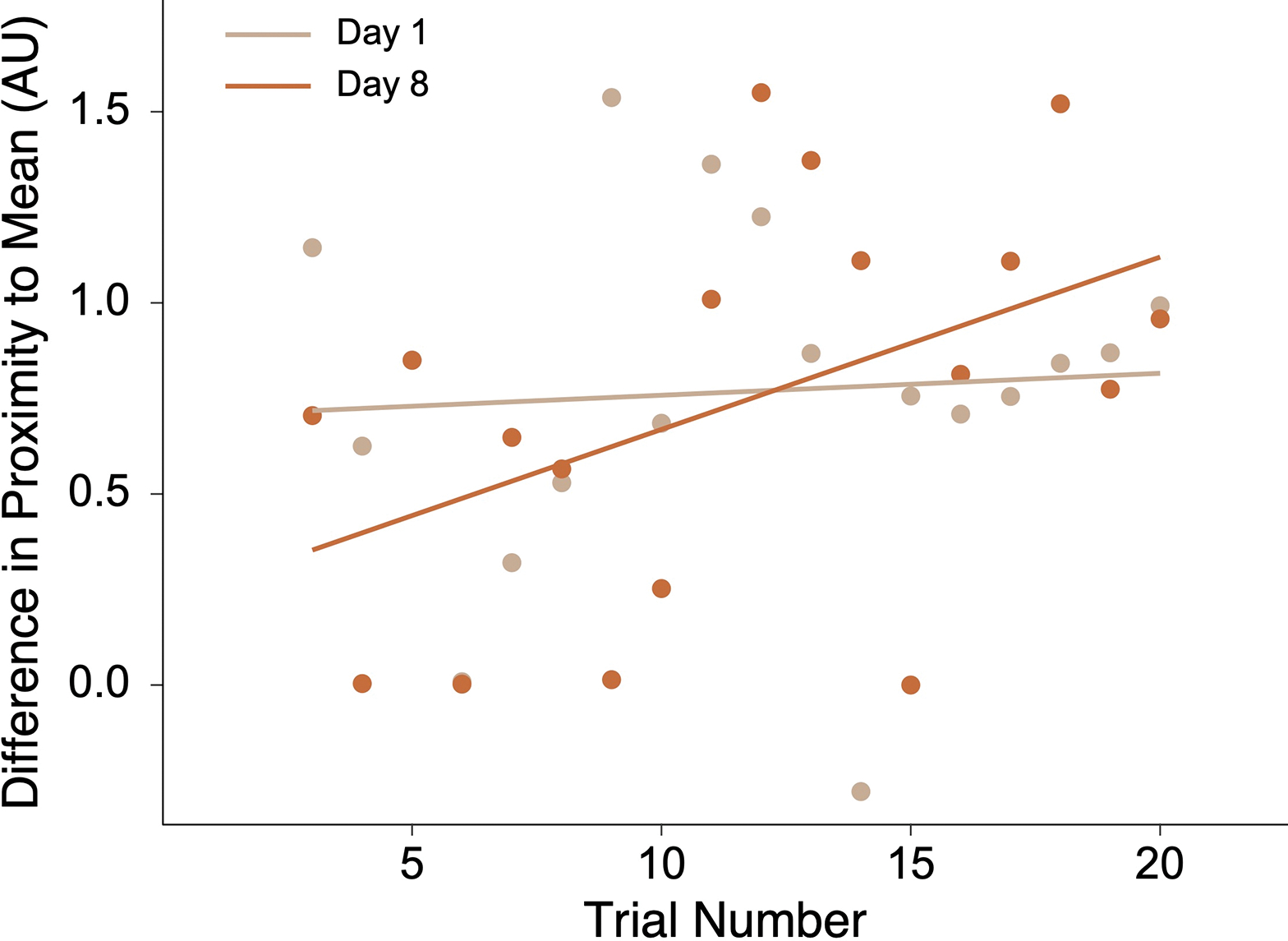
The participant’s change in proximity to the distribution mean after the first 3 seconds of each trial during the encoding phases on Day 1 and Day 8. On the x-axis are trial numbers from the encoding phase of each distribution (for our analyses, we collapsed across first and second task halves). On the y-axis, differences in distance were measured in arbitrary units. Each point is a measure from an individual trial.

Next, we examined representations during the test phases. The findings below are ordered by latency between encoding and test: 0-day lag = crab distribution on Day 8; 7-day lag = shell distribution on Day 8; 13-day lag = crab distribution on Day 21; and 20-day lag = shell distribution on Day 21 (Fig. 6).

Fig. 6.

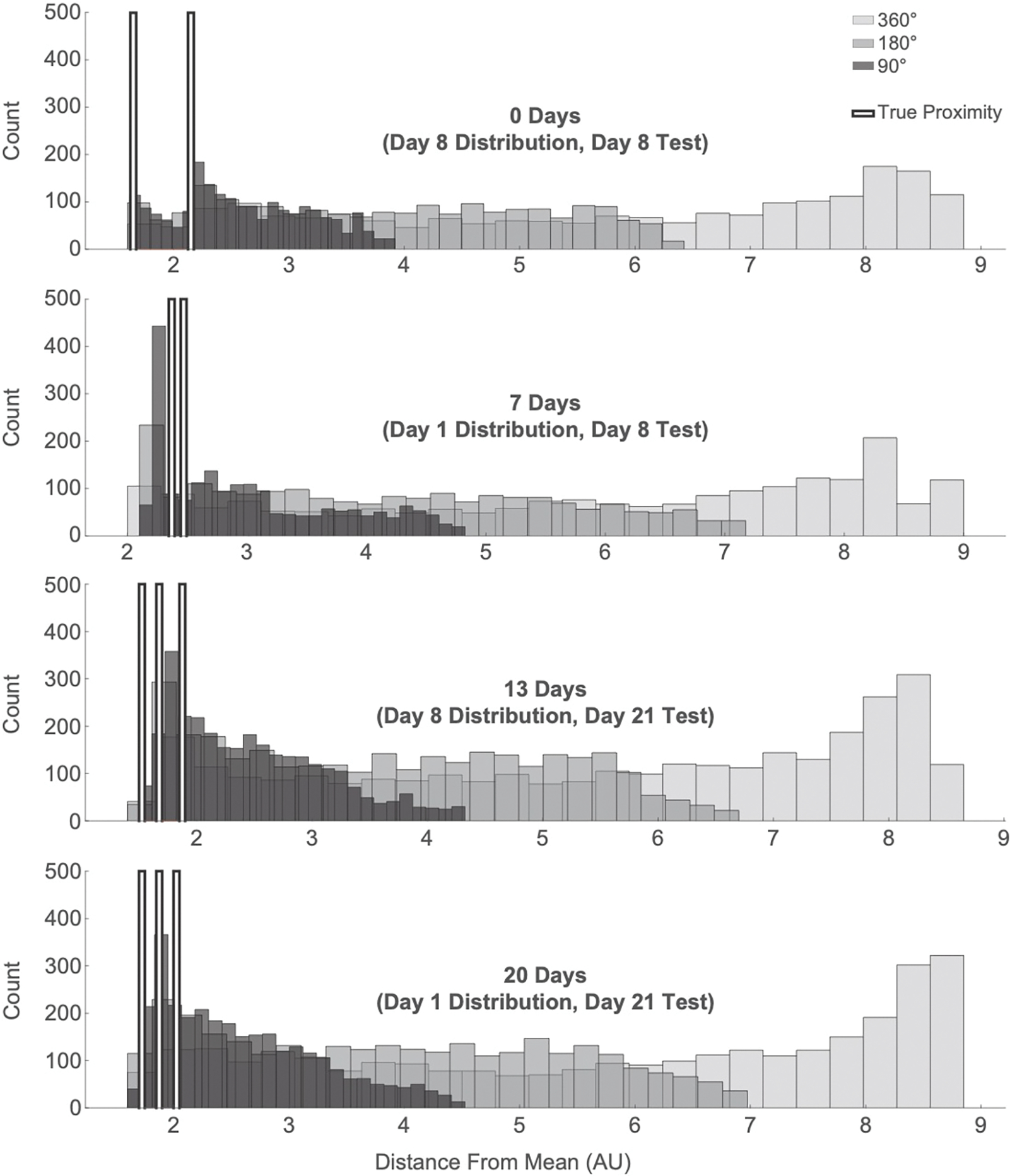
The participant’s proximity to the distribution mean during the test phase was compared to increasingly conservative null distributions. Each row is an encoding/test latency, from shortest latency (0-day) and to longest latency (20-day). Within each plot, the light gray histograms are the 360° rotated null proximities, the medium gray are the 180° rotated null proximities, the dark gray are the 90° rotated null proximities, and the white bars mark the true average proximities, per trial (2 trials on Day 8 Test, 3 on Day 21 Test) of the patient’s trajectories to the distribution mean.

At the shortest lag (0-day), null distributions revealed above chance navigation to the mean for all ranges of rotation (360°: p_rot=0.001; 180°: p_rot=0.002; 90°: p_rot=0.005). We then related this finding by the patient’s navigation to individual crab locations. Null distributions at all ranges of rotation revealed a significant positive correlation between the patient’s navigation to a specific crab location and that location’s proximity to the distribution mean (360°: r=0.77, p<0.001; 180°: r=0.77, p<0.001; 90°: r=0.76, p<0.001). None of the correlations between navigation to locations and the trial numbers of those locations from the encoding phase reached significance (360°: r=−0.10, p=0.672; 180°: r=−0.10, p=0.682; 90°: r=−0.17, p=0.469). More broadly, these findings suggest that the patient’s proximity to specific crab locations during search at test were a function of her navigation towards the mean, and not towards the locations she had learned most recently.

Navigation at the second shortest lag (7-day) was marginally more biased than a 360°rotated null (p_rot=0.076), but not significantly different from the 180°rotated null (p_rot=0.144) or 90°rotated null (p_rot=0.301). We found no correlation between navigation to individual shell locations and either proximity of the shell to the distribution mean (360°: r=0.24, p=0.302; 180°: r=0.23, p=0.337; 90°: r=0.23, p=0.321) or trial number (360°: r=−0.11, p=0.640; 180°: r=−0.10, p=0.668; 90°: r=−0.02, p=0.918). Despite weak evidence that the patient was representing the mean, it’s not clear the extent to which that representation versus individual shell representations guided her search.

At the second-longest lag (13-day), test behavior revealed navigation to the mean as compared to the 360°(p_rot=0.023) and 180°(p_rot=0.044) null distributions, although only marginal in comparison to the 90°null (p_rot=0.092). There was a significant correlation between the patient’s navigation to a specific crab location and that location’s proximity to the distribution mean (360°: r=0.74, p<0.001; 180°: r=0.62, p=0.004; 90°: r=0.68, p<0.001). We found no significant correlations between trial number and the patient’s navigation to specific crab locations (360°: r=−0.06, p=0.813; 180°: r=−0.07, p=0.777; 90°: r=−0.07, p=0.772). As with the 0-day lag, this suggests that the patient navigated based on a representation of the mean rather than the most recent location.

At the longest lag (20-day), navigation to the distribution mean was significantly greater than the 360° null distribution (p_rot=0.029), marginally greater than the 180°null (p_rot=0.074), and not significantly different from the 90° null (p_rot=0.138). We found a significant positive correlation between the patient’s navigation to a shell location and the proximity of that location to the distribution mean for the null 360° (r=0.51, p=0.022) and 180° (r=0.49, p=0.027). This effect was marginal at the 90° null distribution (r=0.38, p=0.096), and we did not find any correlation with trial number (360°: r=−0.25, p=0.285; 180°: r=−0.20, p=0.398; 90°: r=−0.21, p=0.371). These findings mirror the 0-day and 13-day lag in showing navigation to the mean but not to the most recent individual location.

3.2. Reconstructed Location Representations

We then sought to reconstruct spatial representations during the first four seconds of the pre-navigation period, when the participant was preparing to initiate their search.

For the shell distribution, 46 information channels (out of 100) showed significant hippocampal place-coding activity. For the crab distribution, 17 information channels showed significant place-coding activity. We attribute the greater number of validated shell vs. crab channels to the patient exploring more of the arena on the first day of encoding, as she was gaining familiarity with the task and learning the first distribution. The participant physically covered more ground when learning the first distribution. Because data per channel is generated by crossing through that channel’s radius, this resulted in a larger spread of channels with sufficient data for successful place reconstruction than was generated during encoding on Day 8 (Fig. 7)

Fig. 7.

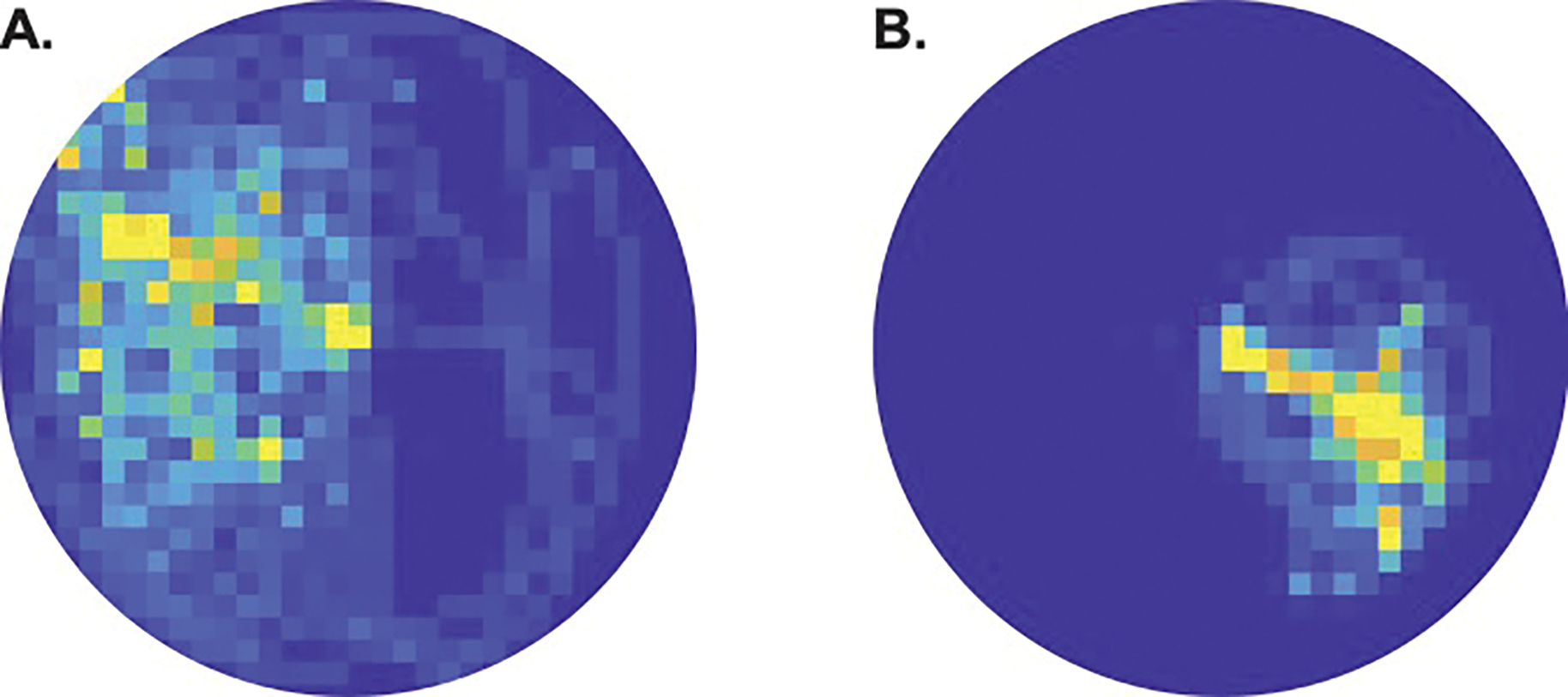
Heatmaps showing the density of the patient’s navigation during the encoding phases of the task. A) The patient explored more of the environment when encoding the shell distribution on Day 1 than when encoding the B) crab distribution on Day 8.

We investigated representational change from the shortest to the longest latency between encoding and test. Hippocampal activity patterns allowed us to reconstruct the distribution mean at the shortest lag (0-day: p_rot=0.049) and second shortest lag (7-day: p_rot=0.015). However, mPFC activity patterns did not contain information about the distribution mean at either of these lags (0-day: p_rot=1; 7-day, p_rot=0.333).

As hypothesized, we found the inverse at a longer latency. mPFC activity patterns allowed us to reconstruct the distribution mean at the second longest lag (13-day: p_rot=0.009) and longest lag (20-day: p_rot=0.048). However, hippocampal activity patterns did not contain information about the distribution mean at either of these lags (13-day: p_rot=0.421; 20-day: p_rot=0.539). These results indicate a double dissociation between the hippocampus and mPFC in the representation of spatial regularities as a function of time (Fig. 8).

Fig. 8.

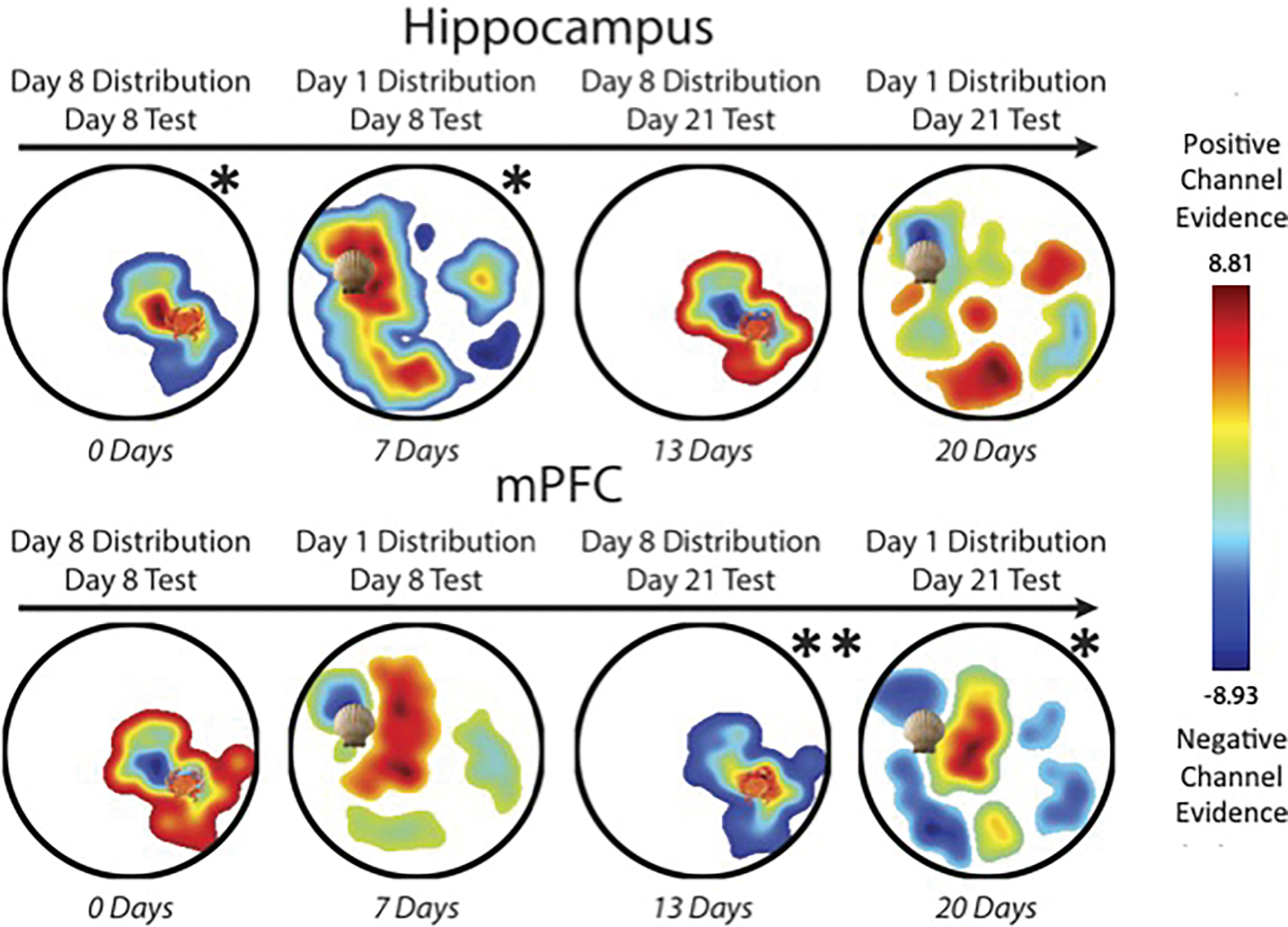
Place representations reconstructed from the first four seconds of pre-navigation test data, plotted left-to-right as a function of lag between encoding and test. Each image is thresholded to exclude reconstruction from locations with no active channel. Colors are scaled from negative to positive channel evidence, where cooler colors indicate negative channel evidence and warmer colors indicate positive channel evidence. The colorbar to the right indicates the z-scored range. Shell and crab icons mark the mean location from each distribution. Top row: At encoding/test lags of 0 and 7 days, hippocampal reconstructions were significantly proximal to the mean, but at lags of 13 and 20 days, they were no longer significant. Bottom row: At lags of 0 to 7 days, mPFC reconstructed representations were not significantly proximal to the distribution mean. Significantly mean-proximal mPFC reconstructions emerged at the later lags of 13 and 20 days.

3.3. Linking Reconstruction to Behavior

Finally, we aimed to relate brain to behavior by comparing the proximity of the patient’s behavioral search trajectory at test to the reconstructed neural place representation. At the shortest lag of 0 days, the patient’s trajectory was significantly proximal to the hippocampal reconstruction compared to all rotated nulls (360°: p_rot=0.010, 180°: p_rot=0.013, 90°: p_rot=0.024), but not the mPFC reconstruction (360°: p_rot=1, 180°: p_rot=1, 90°: p_rot=1). At the lag of 7 days, the trajectory was not significantly proximal to either reconstruction (hippocampus, 360°: p_rot=0.155, 180°: p_rot=0.381, 90°: p_rot=0.482; mPFC, 360°: p_rot=0.570, 180°: p_rot=0.507, 90°: p_rot=0.485). At the lag of 13 days, the trajectory was not significantly proximal to the hippocampal reconstruction (360°: p_rot=0.110, 180°: p_rot=0.256, 90°: p_rot=0.481), but was significantly proximal to the mPFC reconstruction compared to the coarser 360°(p_rot=0.019) and 180°(p_rot=0.040) null distributions; the effect was marginal at the 90°null (p_rot=0.086). At the longest lag of 20 days, the trajectory was not significantly proximal to either reconstruction (hippocampus, 360°: p_rot=0.679, 180°: p_rot=0.506, 90°: p_rot=0.488; mPFC, 360°: p_rot=0.218, 180°: p_rot=0.438, 90°: p_rot=0.482). Thus, consistent with the overall transition of mean representations from the hippocampus to mPFC over time, neural reconstructions in the hippocampus were associated with navigation behavior at the shortest lag (0-day) and in the mPFC were associated with navigation behavior at the second longest lag (13-day). Whether the intermediate lag (7-day) was a transition between the two and whether neural reconstructions at the longest lag (20-day) were no longer behaviorally relevant cannot be determined from these null results, but warrants further study.

4. Discussion

We found evidence of statistical learning on two timescales by reconstructing place information from neural activity in the human brain. The learned spatial distributions switched from being represented only in the hippocampus at shorter latencies to being represented only in the mPFC at longer latencies. The data suggest that the hippocampus preferentially represents spatial locations initially, while the mPFC preferentially represents the locations after a delay.

We argue that the spatial locations being represented, which subsequently biased navigation, were the means of each encoded distribution. An alternative interpretation is that the patient merely represented individual locations from each distribution, rather than the means, and navigated to them at test. In this case, the patient’s behavior at test reflected incidental crossings through the means on the way to these locations, which by definition were clustered nearby. These crossings may have then been reconstructed from the neural data, giving a false semblance of a mean representation in the brain.

Further research will be needed to definitively adjudicate between the mean vs. individual location accounts. Nevertheless, some of our findings are consistent with the mean location account and inconsistent with the idea that knowledge of individual locations is sufficient, including evidence of pattern extraction during encoding of new locations and search behavior at test biased towards the mean as opposed to individual learned locations. Moreover, the mean location interpretation is consistent with past modeling and fMRI work that has implicated the hippocampus in rapid, within-session statistical learning (Schapiro et al., 2017; Sherman & Turk-Browne, 2020). Combined with its role in spatial navigation (Ekstrom et al., 2003; Leutgeb, Leutgeb, Treves, Moser, & Moser, 2004; Miller et al., 2018), the hippocampus is well-positioned to extract spatial regularities during navigation.

Whether the hippocampus is necessary for extracting the mean location and for the emergence of neural representations of the mean in the hippocampus over the short term and in mPFC longer term requires different types of studies. A causal role of the hippocampus could be tested by delivering electrical stimulation to the hippocampus during the encoding or test of a distribution. Moreover, patients with hippocampal lesions could be used to test for the necessity of the hippocampus in behavioral mean navigation (cf. Covington, Brown-Schmidt, & Duff, 2018; Schapiro, Gregory, Landau, McCloskey, & Turk-Browne, 2014) and delayed neural representations of the mean in mPFC (this damage would prevent study of hippocampal representations). Such studies would help close the remaining theoretical gaps that this study cannot address.

Our findings are partially consistent with a previous study on the role of consolidation in accentuating stimulus overlap, which found that abstracted representations come online in mPFC only following a period of consolidation (Tompary & Davachi, 2017). However, that study additionally found parallel abstracted representations in the hippocampus after consolidation. The difference in length of consolidation may partly explain this discrepancy, with their study testing after one week of consolidation compared to our two and three week intervals. This additional time may have allowed for further transformation and weakening of the hippocampal representation. Given that the shell distribution was still represented in the hippocampus (but not mPFC) after one week, it may be that these two studies, with different tasks and stimuli, index different points along a trajectory of memory transformation. The endpoint of this trajectory in our study aligns well with previous rodent work showing cortically dependent spatial pattern representations emerging after 30 days of consolidation (Richards et al., 2014).

Importantly, however, other studies have suggested that cortical representations arise on much faster timescales — days (Tse et al., 2011; Van Kesteren, Brown, & Wagner, 2018) or even hours (Varga & Manns, 2021). We did not see such rapid effects in our study, and had we limited testing to these timepoints we would not have implicated mPFC. The discordance between these and our findings may be attributable to task differences, including the nature of the knowledge being formed. Further work investigating the timescale of systems-level representational change across domains is needed to clarify the timeline of cortical consolidation, especially for patterned knowledge of spatial environments as studied here.

In our design, we constructed the Day 8 distribution by rotating the Day 1 distribution 160 degrees around the arena. Our goal was to convey clearly that the distributions were distinct by placing them in different parts in the arena with different landmarks, while also attempting to equate them in terms of task difficulty and learning by preserving the relative distances between items within each distribution. Although we still ended up with performance differences (faster overall search times and increasing mean proximity during Day 8 but not Day 1 encoding), the intention was to be able to pool the data from both distributions to look at consolidation across four time lags. One downside of this approach, however, is that retaining the same relative distribution on Day 8 may have allowed the patient to carry over knowledge from the Day 1 distribution. However, note that the patient did not seem to begin Day 8 with increased navigation to the mean (see early Day 8 trials in Figure 5) or show greater overall navigation to other salient locations that carryover would allow. Moreover, the performance differences that were observed between days could have unrelated explanations. The overall faster search times on Day 8 could result from session-wise practice effects or uncontrolled differences in the state of the patient (e.g., motivation, arousal, pain, etc.). The lack of an increase in mean navigation on Day 1 might be a false negative, given the reliance on a split half of a small number of trials and the presence in the first half of possibly spurious trials proximal to the mean. Alternatively, this null effect might indicate that statistical learning was weaker on Day 1. For example, the familiarity of the arena on Day 8 may have served as a schema that facilitated spatial memory (Tse et al., 2007).

In our analyses, we chose to validate the model channels using hippocampal data because it was critical for our interpretation that the models first show significant evidence of hippocampal place-code like activity when the patient was virtually ambulating during encoding. While this could theoretically bias the models to perform poorly when reconstructing from mPFC, we believe our main findings argue against this — instead of overall dominance of hippocampal reconstructions, we see a hypothesized time-dependent transition between regions.

Interestingly, this patient showed evidence of significantly mean-proximal navigation at the 13-day lag, but not the 7-day lag. We attribute this to the patient’s overall better acquisition of the distribution tested at that lag, i.e., the Day 8 crab distribution compared to the Day 1 shell distribution.

Our findings also serve to extend previous discoveries of ensemble-level spatial coding in the human brain. Single-unit recordings have identified sparse distributions of place cells (Ekstrom et al., 2003), and at the level of regional activity, multiple fMRI studies have revealed increasing hippocampal pattern similarity as a function of spatial distance between locations (Deuker, Bellmund, Schröder, & Doeller, 2016; Morgan, MacEvoy, Aguirre, & Epstein, 2011). Here, using inverted encoding models, we demonstrate more explicitly, and from fewer recordings, evidence of hippocampal place coding at the level of ensemble local field potentials. This result illustrates the high degree of information that can be derived from neural oscillations in a handful of macro electrodes, and provides a promising avenue for future navigation studies with iEEG.

This unique patient allowed us to track acquisition of spatial patterns across multiple timescales. An obvious limitation of the current study is the sample size of one. As a case study, our results should be interpreted with caution for their generalizability. However, this study provides initial support for the notion that consolidation operates over not only episodic memories, but extracted navigational patterns acquired online during learning. We additionally extend previous findings of the link between statistical learning and pattern similarity (Schapiro, Kustner, & Turk-Browne, 2012), arguing for an analogous process during human virtual navigation. Although it is unlikely that such a rare data collection opportunity will arise in a larger cohort of epilepsy patients, future noninvasive neuroimaging work could seek to verify the timeline discovered here. Our investigation provides another step in understanding the relationship between the hippocampus and mPFC in representing underlying structure in the world.

Highlights.

• Case study of an epilepsy patient tested longitudinally over three weeks.

• We tracked time-dependent changes in neural representations of spatial patterns.

• Representations reconstructed from hippocampal activity reflected patterns learned within a week.

• Representations reconstructed from activity in the mPFC reflected patterns learned 2–3 weeks ago.