Abstract
To disentangle the information contained in transition-metal K-edge X-ray magnetic circular dichroism (XMCD), two series of Prussian blue analogs (PBAs) were investigated as model compounds. The number of 3d electrons and the magnetic orbitals have been varied on both sites of the bimetallic cyanide polymer by combining with the hexacyanoferrate or the hexacyanochromate entities’ various divalent metal ions A2+ (Mn2+, Fe2+, Co2+, Ni2+, and Cu2+). These PBA were studied by Fe and Cr X-ray absorption spectroscopy and XMCD. The results, compared to those obtained at the A K-edges in a previous work, show that transition-metal K-edge XMCD is very sensitive to orbital symmetry and can therefore give valuable information on the local structure of the magnetic centers. Expressions of the intensity of the main 1s → 4p contribution to the signal are proposed for all K-edges and all compounds. The results pave the way toward a new tool for molecular materials able to give access to valuable information on the local orientation of the magnetic moments or to better understand the role of 4p orbitals involved in their magnetic properties.
1. Introduction
Improvement and discovery of new magnetic properties are major challenges to enable novel technological applications in several fields. In this context, a strong interest has grown for techniques able to probe at a local scale the magnetic properties of matter such as X-ray magnetic circular dichroism (XMCD). XMCD, derived from X-ray absorption spectroscopy,1 has indeed the great advantage to present both a chemical and an orbital selectivity. This technique has rapidly become over the past few decades of major importance for several scientific communities, especially physics, chemistry, or biochemistry.2−4 Nevertheless, if the element selectivity has been largely explored, the full exploitation of orbital selectivity has been impeded by the lack of satisfactory interpretation of the XMCD signal at some metal edges. Thus, in the case of first-row transition metals (TMs), which are of first importance in the fields of magnetometry and magnetic materials, XMCD at the L2,3 edges has become a reference technique. Due to the sum rules,5−7 quantitative information about the spin and orbital momenta can be extracted from the XMCD signals and crystal field multiplet calculations8 well reproduce the signals. On the contrary, the interpretation of TM K-edges XMCD signals is still widely debated, despite the first spin-dependent absorption in the X-ray range was observed at the K-edge of iron.9 And yet this technique offers many advantages, among them (i) compatibility with demanding sample environments, which made it the preferred technique to probe magnetism under pressure,10−15 and (ii) bulk sensitivity without limitation to surface species. However, a clear interpretation of these signals is still missing, in spite of the many efforts devoted to apply the sum rule at the K-edges6,16,17 and to understand and reproduce the signals, especially by using different calculation approaches.17−25
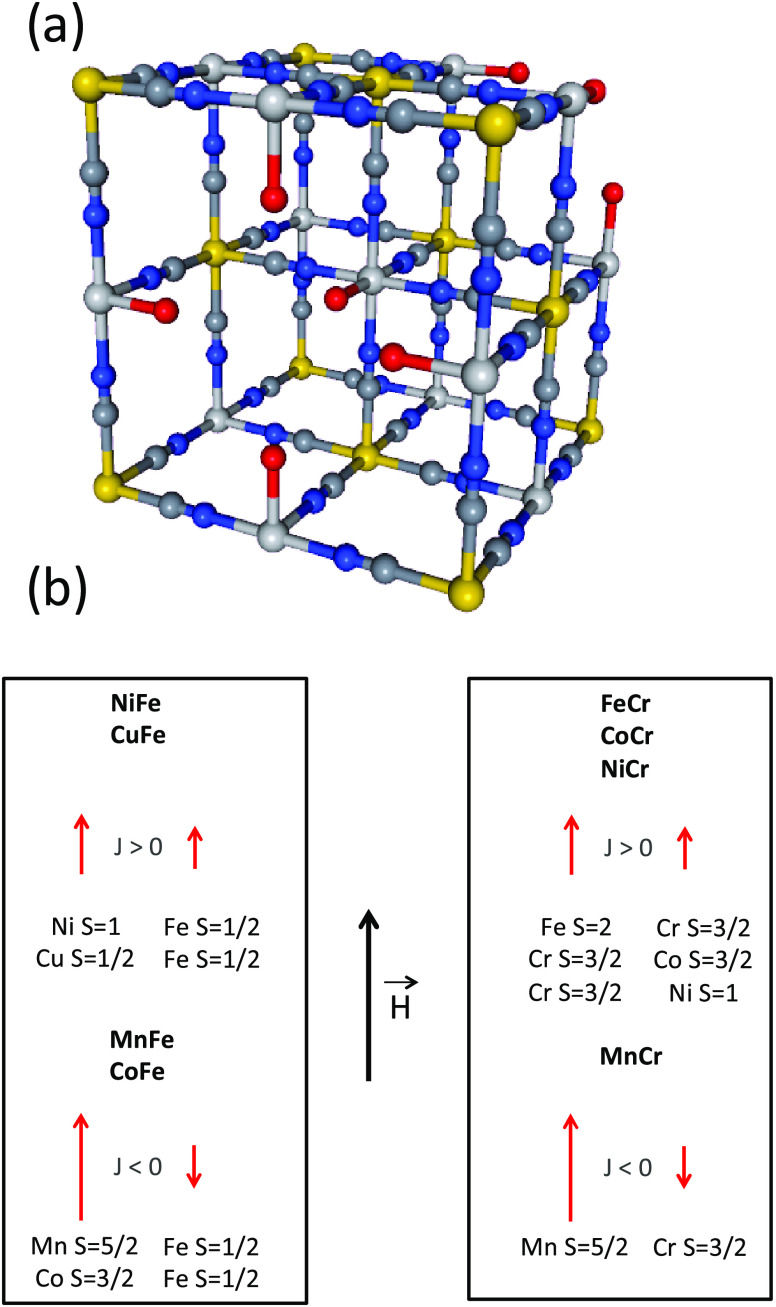
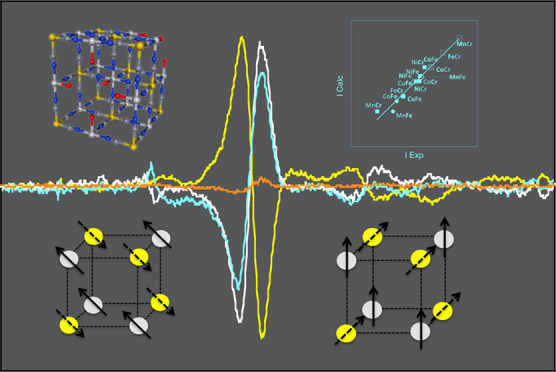
So, we are engaged in the development and implementation of an original experimental approach,12,26−28 so that the processes at the origin of these TM K-edges XMCD signals can be disentangled. Most of the works on TM K-edges in the literature deal with the investigation of metal oxides and especially metals, metal alloys, and intermetallics,29−31 the electronic properties of which are well described in terms of the band structure. Works dealing with molecular compounds, in which the electrons are localized and the electronic properties are well described in terms of molecular orbitals, are scarcer.32−34 And yet, molecular orbital approaches have proved fruitful to describe and anticipate some electronic properties of molecular compounds. Our work belongs within this kind of less developed approach and invites us to take a fresh look at this long-standing issue. Our strategy, presented in a previous work,28 uses the versatile chemistry of a family of isostructural coordination compounds, the Prussian blue analogs (PBAs). Briefly, PBAs with the chemical formula Ap[B(CN)6]q·xH2O, where A and B mostly are first-row TM ions, form a large family of compounds exhibiting the well-known face-centered cubic structure.35−37Figure 1a presents one unit cell of PBA. The charges of the [B(CN)6]p– entities and of the Aq+ ions are generally different so that the electroneutrality of the solid is ensured by [B(CN)6]p– vacancies. A large variety of A and B TM ions can thus be combined in isostructural compounds, allowing for the independent variation of the magnetic orbitals on both A and B sites and consequently for the analysis of their effect on the XMCD signal at both TM K-edges. Nevertheless, it has to be noticed that PBAs are usually obtained in powder form and crystals having a size big enough to be analyzed by single-crystal diffraction are scarce.36,38,39 Given this lack of big enough crystals and the intrinsic structural disorder of the compounds due to the presence of vacancies and water molecules as well as possible distortions of the B–CN–A linkages, the crystallographic position of all atoms (with the exception of the TM ions) is generally not exactly known. These structural features make also tricky the implementation of theoretical calculations or the use of some techniques such as neutron diffraction for instance. Regarding the TM sites, the two A and B sites are different from a chemical and a structural point of view. In the alkali cation-free PBAs made of A2+ and B3+ cations, the A cation is linked to an average of four cyanide ligands linked by the N side and two water molecules. The ratio of −NC and OH2 ligands in the coordination sphere of the A2+ cation can also vary from one A2+ cation to another depending on the distribution of the B(CN)6 vacancies. Thus, the symmetry at the A site departs from the centro-symmetric octahedral one. The cation at the B site is six-fold coordinated, linked to the C side of six same cyanide ligands. The B–CN covalent bonds are linear and the cyanide exerts a strong ligand field. The hexacyanometallate entities are thus stable, rigid, and usually assumed to have a perfect Oh symmetry.40,41
Figure 1.
(a) Scheme of the unit cell of a Prussian blue analog with the chemical formula A4[B(CN)6]2.7·xH2O. Yellow circles stand for the B3+ ion (Cr3+ or Fe3+), light gray circles for the A2+ ions (Mn2+, Fe2+, Co2+, Ni2+, Cu2+), dark gray circles for the carbon atoms, blue circles for the nitrogen atoms, and red circles for the oxygen atoms. The zeolitic water molecules are omitted for clarity. (b) Spin quantum number and expected orientation of the magnetic moments carried by the A2+ and B3+ (Cr3+, Fe3+) TM ions in an external magnetic field for the AFe (left) and ACr (right) series.
In our previous work mentioned above,28 we focused on the XMCD signal at the A K-edges of two series of PBAs of the chemical formula A4II[FeIII(CN)6]3·nH2O (A2+ = Mn2+, Co2+, Ni2+, Cu2+) and A4II[CrIII(CN)6]3·nH2O (A2+ = Mn2+, Fe2+, Co2+, Ni2+); in the following, we call AFe and ACr these two series of model PBAs. The characterization of their chemical composition and structure as well as of their macroscopic magnetic properties are presented in reference (28). The magnetic information needed for the present study can be summed up as follows. In the AFe series, NiFe and CuFe are ferromagnetic with a magnetic ordering temperature of 22 and 19 K, respectively, while MnFe and CoFe are ferrimagnetic below 12 and 14 K, respectively. In the ACr series, FeCr, CoCr, and NiCr are ferromagnetic with a magnetic ordering temperature of 16, 25, and 65 K, respectively, while MnCr is ferrimagnetic below 64 K. The spin quantum number (S) and the expected direction of the magnetic moment carried by each A2+ and B3+ TM ion of the coordination polymer in an external magnetic field are given in Figure 1b.28 We showed in reference (28) that the 1s → 4p contribution to the A K-edge XMCD signal can be related to the magnetic behavior of the probed A2+ ion: the shape of the signal to the filling of the 3d orbitals, the sign of the XMCD signal to the direction of the magnetic moment with respect to the applied magnetic field, and the intensity of the signal and the area under the curve to the total spin number SA and the Curie constant CA of the absorber atom, respectively.
In this work, we focus on the XMCD signal at the K-edges of the B site of the coordination polymer. The CrIII(CN)6 and FeIII(CN)6 entities have nondegenerate 4A2g and degenerate 2T2g electronic ground states, respectively. Like at the A K-edge, the contributions to the XMCD signals are compared to the XANES spectra to assign the different contributions and then extract qualitative and quantitative data from the variation of the XMCD signals along the series of compounds. We can thus compare the characteristics of the XMCD signals at the A and B K-edges and particularly the intensity of the XMCD signal to get a better insight into the information contained in these signals. The new data obtained at the Cr and Fe K-edges allow us (i) to clearly evidence different local magnetic behaviors of the A and B sites of the coordination polymer and (ii) to go deeper in the interpretation of the intensity of the XMCD signal. In return, this information combined with macroscopic magnetometry measurements and local X-ray absorption data can be used to get new insight into the macroscopic magnetic properties of the compounds.
2. Experimental Section
The syntheses and macroscopic characterizations of the four A4[Fe(CN)6]2.7 (AFe series) and four A4[Cr(CN)6]2.7 (ACr series) PBAs are presented in reference (28).
TM K-edge XAS
Cr (5989 eV) and Fe (7112 eV) K-edge X-ray absorption spectra were recorded for, respectively, the ACr and AFe series on the SAMBA beamline42 at SOLEIL synchrotron (Gif sur Yvette, France). Room-temperature spectra were recorded up to 500–1000 eV above the edge (depending on the PBA) on pellets in the transmission mode, using the continuous mode of the Si(220) monochromator. No radiation damage occurred. We used the ATHENA software43 to perform the energy calibration and conventionally normalize the spectra.
TM K-edge XMCD
Cr and Fe K-edges X-ray absorption near-edge structure (XANES) spectra and XMCD signals were recorded in the transmission mode using the dispersive setup of the ODE44 beamline at SOLEIL synchrotron (Gif sur Yvette, France). Detailed information is given about the measurements and normalization procedure in ref (27), so only the main ones are reminded here. The circular polarization rate is the same for all of the edges. The Si(311) polychromator was chosen to reach the highest possible resolution in the white line region of the spectra. Then, it is critical (i) to be well below the Curie temperature of the eight investigated PBAs and (ii) to avoid any artifact in the intensity related to a change in the temperature, so we were careful to perform the measurements at 4 K. The largest external magnetic field (1.3 T) that can be reached when the cryostat is used was applied alternatively parallel and antiparallel to the direction of the photon beam. For the AFe series, the samples were placed in a diamond anvil cell (DAC) (with no pressure-transmitting medium), which ensures an optimized homogeneity of the sample. In the case of the ACr series, an experimental challenge was to minimize the absorption of the beam while retaining a brilliant enough flux to be able to perform the measurements; this was achieved by replacing the diamonds of the DAC with a Plexiglas strip. No radiation damage occurred due to attenuators of appropriate thickness. A metallic foil was recorded at both edges for energy calibration. We normalized the XANES spectra and XMCD signals using the procedure described in ref (27).
3. Results
3.1. Cr K-edge XMCD Signals
Figure 2a shows the normalized XMCD signals at the Cr K-edge of MnCr, FeCr, CoCr, and NiCr. The different contributions were clearly assigned due to the comparison of the XMCD signals with the corresponding XANES spectra (S1), which are very similar from one compound to another along the ACr series. This reflects a very similar electronic structure of the Cr3+ ion and a very similar local structure around the absorber atom along the series. One can notice the intense multiple scattering contribution just above the absorption edge characteristic of the linear Cr–CN linkages. The XMCD signals are compared to the XANES spectrum of CoCr in Figure 2b.
Figure 2.
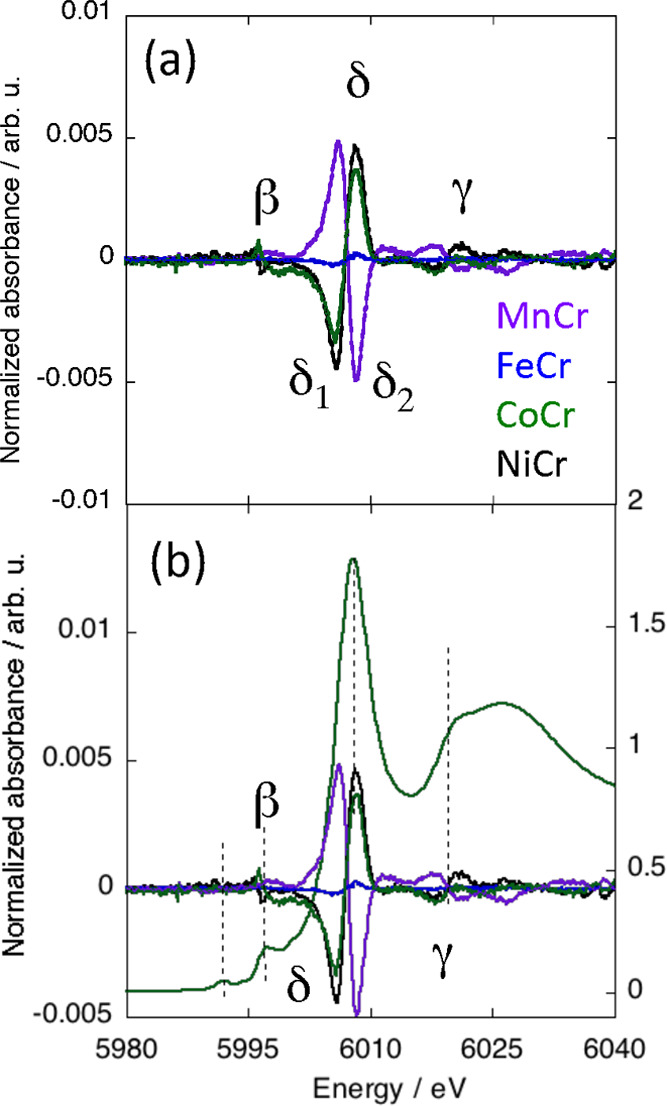
(a) Normalized Cr K-edge XMCD signals of MnCr, FeCr, CoCr, and NiCr. (b) Comparison of these signals to the Cr K-edge XANES spectrum of CoCr over the 5980–6040 eV energy range.
The XMCD signal is different from one compound to another along the series, whereas the Cr K-edge XANES spectra are almost exactly the same (S1). The differences among the XMCD signals therefore arise from different magnetic environments of the Cr ion. Nevertheless, even though the contributions exhibit variable signs and intensities, the XMCD signals all exhibit the same shape with the same number of contributions located at the same energies: one main contribution (δ) and two other contributions with significantly smaller intensity (β and γ). The γ contribution will not be discussed here.
The main contribution to the XMCD signal (δ) is at the energy of the XANES white line and can therefore be assigned to the electric dipole-allowed 1s → 4p transitions. We already discussed the shape of this main δ contribution to the XMCD signal in reference (28). The derivative shape of the signal is associated with the same spin quantum number for all electrons in the 3d orbitals, which is the case for the (t2g)3(eg)0 electronic configuration of the Cr3+ ion.
The β contribution to the XMCD signal is located at the same energy as the main structure in the rising edge of the XANES spectra. This structure is assigned to the 1s → t1u CNπ* transitions, having the same symmetry as the 4p orbitals in the Oh symmetry. K-edge XMCD gaining intensity from the 1s → 4p transition, a contribution to the XMCD signal at this energy, is therefore expected.
Over the pre-edge energy range (below 5995 eV), no contribution to the XMCD signal is detectable (Figure 2b). Over this energy range, the Cr K-edge XANES spectra exhibit two peaks (S1) assignable to the electric quadrupole 1s → 3d transitions. This indicates that XMCD at the TM K-edges does not gain intensity from such electric quadrupole transitions in the centro-symmetric environment, for which no contribution from the electric dipole-allowed 1s → 4p transitions is expected over this energy range.
3.2. Fe K-edge XMCD Signals
Figure 3a shows the normalized XMCD signals at the Fe K-edge of MnFe, CoFe, NiFe, and CuFe. The different contributions were clearly assigned due to the comparison of the XMCD signals with the corresponding XANES spectra (S2). All XANES spectra are almost exactly the same, showing that, like at the Cr K-edge, the electronic structure and the local structure around the Fe3+ ions are very close from one compound to the other. These spectra are characteristic of the Fe(CN)6 entity.45−49 As at the Cr K-edge, the intense multiple scattering contribution above the edge is characteristic of the linear Fe–CN linkages. We can observe that the profile of the Fe K-edge spectra along the AFe series is very close to that of the Cr K-edge spectra along the ACr series, showing that the local structure around the absorber atom and therefore the local structures of both Fe(CN)6 and Cr(CN)6 entities are very close in both series. The XMCD signals are compared to the XANES spectrum of CoFe in Figure 3b.
Figure 3.
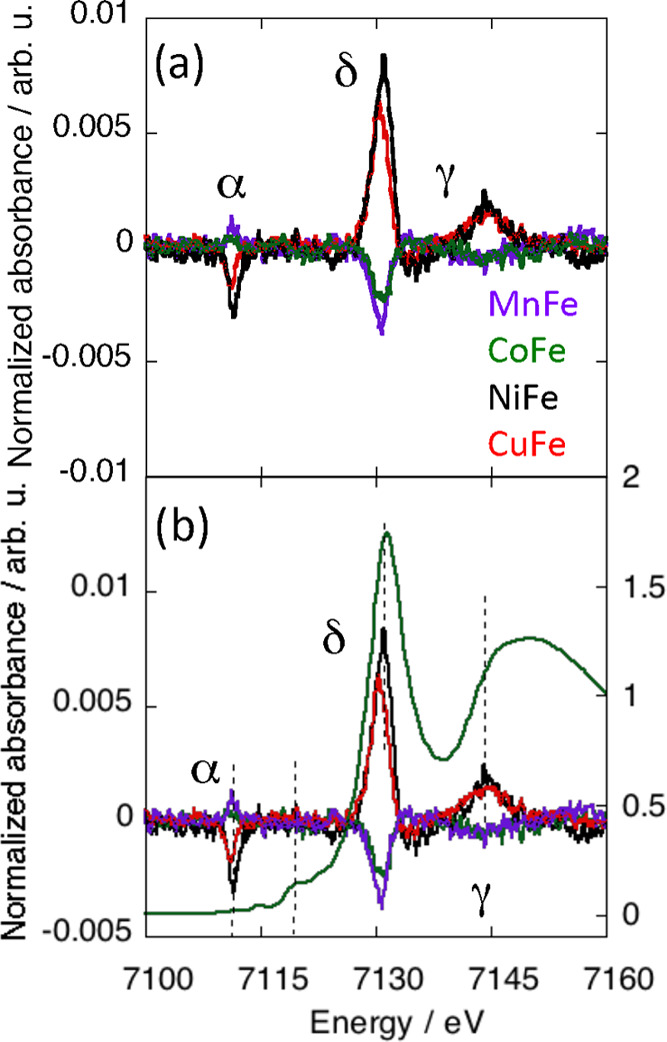
(a) Normalized Fe K-edge XMCD signals of MnFe, CoFe, NiFe, and CuFe. (b) Comparison of these signals to the Fe K-edge XANES spectrum of CoFe over the 7100–7170 eV energy range.
As at the Cr K-edge, the XMCD signal is different from one compound to the other along the series, whereas the Fe K-edge XANES spectra are almost exactly the same (S2). One can again conclude that the differences among the XMCD signals arise from different magnetic environments of the Fe3+ ion. All Fe K-edge signals exhibit the same contributions: one main (δ) and two smaller ones (α and γ). These contributions have the same shape, only their sign and intensity vary. The γ contribution will not be discussed here.
As at the Cr K-edge, the main contribution to the XMCD signal (δ) is at the energy of the XANES white line and can be assigned to the electric dipole-allowed 1s → 4p transitions. The shape of the contribution with one dominant lobe is in line with the presence of one electron pair in the t2g orbitals of the Fe3+ low spin ion.28
Surprisingly, the low-energy contribution to the XMCD signal (α peak) is located over the pre-edge energy range of the XANES spectra (below 7115 eV). At the Fe K-edge, the XANES spectra of the AFe series (S2) exhibit two weak pre-edge peaks located at 7112 and 7115 eV (peaks α1 and α2 on S2), which can be assigned to 1s → 3d transitions.45−49 The α XMCD peak is situated at the same energy as the α1 peak on the XANES spectrum, whereas XMCD gains no intensity at the energy corresponding to the α2 peak of the XANES spectra. It is noticeable that the intensity of the α XMCD peak varies as one of the main δ peaks, as confirmed by the plot of the intensity of the α peak as a function of that of the δ peak (S3). The observed linear variation shows that the α XMCD peak gains intensity from the 1s → 4p transition, which reflects some 3d-4p orbital mixing that can be assigned to a slight departure of the Fe(CN)6 entities from the pure Oh centro-symmetric geometry. The linear variation between the intensities of the α and δ XMCD peaks also indicates that the structural distortion is the same for all Fe(CN)6 entities of the AFe series and is therefore inherent to the Fe(CN)6 entity and independent of the nature of the other ion on the A site. A configuration mixing in the ground configuration of the Fe(CN)6 entity in the pure Oh symmetry can be ruled out due to the important energy gap between the ground and excited states in the strong ligand field exerted by the cyanide ions linked by the C side, as it is also the case for the Cr(CN)6 entity.
At last, the XMCD signal at the Fe K-edge gains no intensity over the energy range corresponding to the rising edge of the XANES spectra. This observation, which is again not expected for a pure centro-symmetric Oh geometry, is probably associated with the slight structural distortion of the Fe(CN)6 entities clearly highlighted by the presence and the behavior of the α XMCD peak.
3.3. Pre-edge Contribution to the XMCD Signals
Over the pre-edge energy range, the XMCD signals at the Cr and Fe K-edges of the ACr and AFe series are very different (Figures 2 and 3). They are also different from the XMCD signals at the A K-edge of both series presented in ref (28) and reminded in S4. Nevertheless, for all compounds and all edges, when XMCD gains intensity over this energy range, the contribution always has an opposite sign but the same shape as the main contribution. Its intensity is also linked to that of the main contribution, indicating that over this energy range, XMCD gains intensity from the 1s → 4p transitions. The absolute value of the intensity of the pre-edge contributions and its relative intensity with regard to the main contribution (in %) are gathered in Table S1.
For both the ACr and AFe series, the A K-edges XANES spectra and XMCD signals are presented in ref (28) and are reminded here in S4. The XANES spectra of all compounds exhibit one single pre-edge peak with variable broadness and intensity, assigned to the 1s → 3d transitions.28 At all A K-edges, XMCD gains intensity at the energy of the XANES pre-edge peak, whatever the population of the 3d orbitals (from d5 to d8). From a molecular point of view, the coordination sphere of the A2+ ion is mainly made of four −NC and two −OH2 ligands. For this chemical composition, the cis-configuration with two adjacent water molecules, belonging to the C2v point group, is expected to be the main species. Nevertheless, given the random distribution of B(CN)6 vacancies in the coordination polymer, the trans- configuration of the A(NC)4(OH2)2 coordination polyhedron can also be found, as well as coordination polyhedra with chemical composition A(NC)5(OH2)1 and A(NC)3(OH2)3. From a solid-state point of view, the symmetry of the A site is therefore very low and can rather be considered to belong to the C1 point group with generalized- or multiple-pathway 3d-4p orbital mixing, explaining the XMCD contribution over the pre-edge energy range of the XANES spectra.
In the ACr series, the absence of contribution to the XMCD signal over the pre-edge energy range at the Cr K-edge can be assigned, as mentioned above, to the centro-symmetric Oh geometry of the Cr(CN)6 entities in the coordination polymer. Without 3d-4p orbital mixing associated with a contribution of the electric dipole-allowed 1s → 4p transitions over this energy range, XMCD gains no intensity from the electric quadrupole 1s → 3d transitions, whatever the population of the 3d orbitals.
In the AFe series, the Fe K-edge XMCD contribution at the energy of the α1 XANES peak reveals some 3d-4p orbital mixing and the departure of the Fe(CN)6 entities from the pure Oh centro-symmetric geometry. Nevertheless, the lack of XMCD contribution at the energy of the α2 XANES peak also indicates that 3d-4p orbital mixing associated with the symmetry lowering is restricted to one or few 3d orbitals involved in the transitions originating in the α1 XANES peak. The fact that the same α peak appears on all Fe K-edge XMCD signals of the AFe series and that its intensity varies as that of the main contribution shows that the Fe(CN)6 entities undergo the same slight structural distortion in all compounds of the AFe series, independently of the associated A2+ ion. Such a structural distortion specific to the Fe(CN)6 entity is not surprising and can be related to the degenerate electronic 2T2g state of the FeIII(CN)6 entity likely to undergo a spontaneous Jahn–Teller distortion,50,51 which is not expected for the nondegenerate 4A2g ground state of the CrIII(CN)6 moiety. Thus, a DFT-based study on the Jahn–Teller effect in 3d hexacyanometalates with orbitally degenerate ground states52 predicts a compressed trigonal geometry for the FeIII(CN)6 entity, with a D3d point group as the highest possible symmetry. This is in agreement with the room-temperature crystal structures of K3[Fe(CN)6] in its monoclinic and orthorhombic forms, showing a trigonal geometry of the hexacyanometalate unit with the C3 axis approximately parallel to the crystallographic axis (a), superimposed by an additional orthorhombic distortion.53 Such a distortion can explain our observation. In our case, the symmetry is obviously noncentrosymmetric, i.e., lower than D3d.
In summary, the TM K-edge XMCD signal is very sensitive to slight structural distortions, hardly detectable on the XANES spectra. The observed pre-edge contributions are in line with (i) a low symmetry of the A site surrounded by randomly distributed M(CN)6 vacancies in the two ACr and AFe series, (ii) a pure centro-symmetric Oh geometry for the nondegenerate 4A2g ground state of the CrIII(CN)6 entities in the ACr series, and (iii) a slight departure from the centro-symmetric Oh geometry in the degenerate electronic 2T2g state of the FeIII(CN)6 moieties in the AFe series, which can be assigned to a Jahn–Teller effect.
3.4. Main δ Contribution to the XMCD Signal
Sign of the Signal
The sign of the high-energy lobe of the main δ contribution to the XMCD signal of molecular compounds is assigned in the literature to the direction of the magnetic moment carried by the absorber atom with regard to that of the applied magnetic field.28,54 This can be verified here too. The magnetic moments borne by the A2+ ions point in the same direction as the applied magnetic field for all compounds (Figure 1b). We choose as a convention to define the positive sign of the high-energy lobe of the XMCD signal when the magnetic moment of the absorbing atom points in the same direction as the external magnetic field. The A K-edge XMCD signals of all compounds of both AFe and ACr series are thus all positive (S4, Figure 1b).28 At the B K-edges of the two AB series, the XMCD signals also have the expected sign with respect to this convention. In the ferromagnetic NiFe, CuFe, FeCr, CoCr, and NiCr compounds, the XMCD signals are positive (Figures 2 and 3), in agreement with a magnetic moment carried by the Fe3+(Cr3+) ions pointing, as that of the A2+ ion, in the same direction as the applied magnetic field (Figure 1b). In contrast, the XMCD signal is negative in the ferrimagnetic MnFe, CoFe, and MnCr compounds (Figures 2 and 3), in agreement with a magnetic moment carried by the Fe3+(Cr3+) ions pointing in the opposite direction as that of both the A2+ ion and applied magnetic field (Figure 1b).28
Peak Area under the Curve
We showed at the A K-edge of both ACr and AFe series that the absolute intensity and the integrated intensity, i.e., the peak area under the curve, of the XMCD signal can bring information: the intensity of the signal and the peak area under the curve are linear functions of the total spin quantum number and of the Curie constant of the A2+ ion, respectively.28 However, at the Fe K-edge, the peak area under the curve for the main δ peak is a linear function of its intensity with a slope of 3 (S5). At the Cr K-edge, the peak areas under each lobe of the curve of the XMCD signal, as well as the difference between the peak areas under the two lobes, are, respectively, linear functions of the intensity of each lobe and of the difference between their intensities, with a slope of 1.95 (S6). As the peak areas under curves and the intensities are proportional, only the intensity of the main peak at the Fe K-edge and the difference between the intensities of the two lobes at the Cr K-edge are considered in the following; they are called IFe and ICr, respectively. Work is in progress to understand this different behavior of the main contribution to the XMCD signal between the two A and B sites of the coordination polymers. The differences between the intensities of the two lobes at the Cr K-edge have been considered because we showed that, at the Mn K-edge of MnCr, this value follows the same trend as the intensity of the main lobe when the XMCD main contribution exhibits one predominant lobe.28
Expression of the Intensity
In both the ACr and AFe series, the intensity of the main peak as defined above (ICr and IFe) depends on the nature of the magnetic neighbor of the absorber ion. No variation trend of the maximum intensity with any magnetic parameters such as the magnetization value at 1.3 T and 4 K, SA the total spin quantum number of the A2+ ion..., emerges at first glance. Nevertheless, we showed in our previous work on the A K-edges28 that the intensity of the main contribution to the A K-edges XMCD signal is the sum of a constant term and an SA-dependent term. So, we also tried to add or subtract a constant term to the XMCD intensity at the Fe and Cr K-edges, and we plotted the result as well as its absolute value as a function of SA.
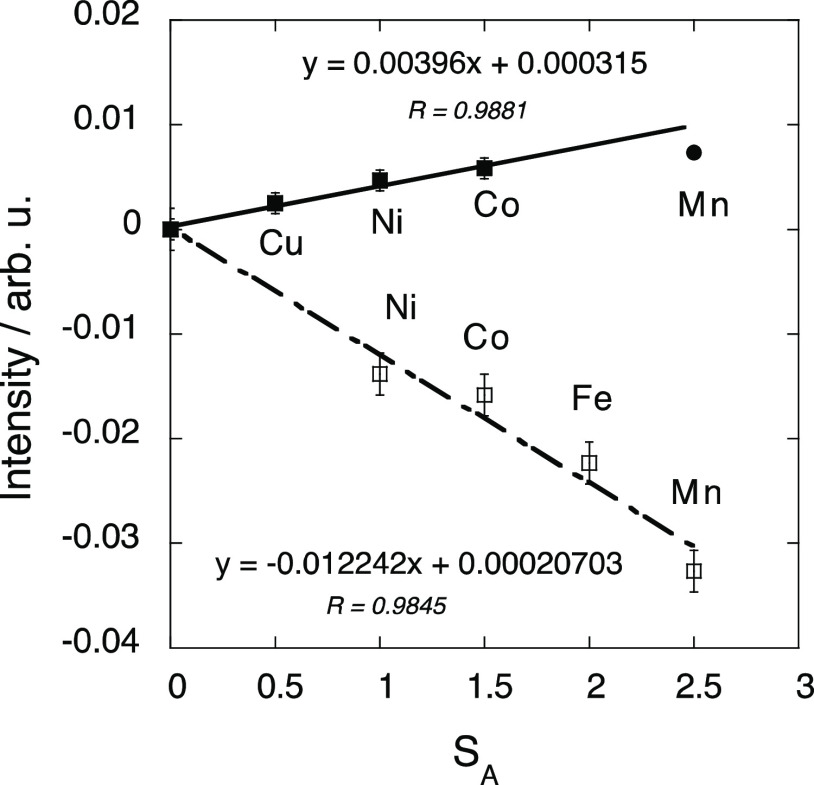
At the Fe K-edge of the AFe compounds, we found, after trials and errors, a linear trend when plotting as a function of SA the absolute value of the difference between IFe and 0.0036; this plot is presented in Figure 4. The point corresponding to MnFe slightly deviates from the trend. As this compound exhibits a peculiar behavior in its magnetic properties and at the Mn K-edge,28 it has not been taken into account in the first step. It is striking that within the error bar (±0.001), (i) the correlation line passes through the origin and (ii) the value of the slope (0.004) is very close to the value subtracted from the XMCD intensity (0.0036). The XMCD intensity at the Fe K-edge can hence be expressed as
| 1 |
where the sign +(−) depends on the F(AF) exchange interaction between the magnetic moments carried by the A2+ and Fe3+ ions (Figure 1b).
Figure 4.
Absolute value of the difference between the intensity of the main XMCD signal at the Fe K-edge and 0.0036 versus the total spin quantum number SA of the A2+ ion for MnFe (black circle), CoFe, NiFe, and CuFe (black square). Difference between the intensity of the main XMCD signal at the Cr K-edge and 0.023 versus the total spin quantum number SA of the A2+ ion for MnCr, FeCr, CoCr, and NiCr (white square).
The same treatment was performed for the signal intensity (ICr) at the Cr K-edge (ICr is the difference between the intensity of the two lobes). After trials and errors, we found a linear trend when plotting as a function of SA the difference between ICr and 0.023; this plot is presented in Figure 4. As at the Fe K-edge, it is striking that, within the error bar (±0.002), (i) the correlation line passes through the origin and (ii) the value of the slope (−0.012) is very close to half the value subtracted to the XMCD maximum intensity (−0.023). The XMCD intensity at the Cr K-edge can hence be expressed as
| 2 |
These expressions (eqs 1 and 2) have to be compared to the ones obtained at the A K-edges for CoFe, NiFe, CuFe, MnCr, FeCr, CoCr, NiCr (eq 3), and MnFe (eq 4) in ref (28) and recalled below
| 3 |
| 4 |
Within the error bar, the proportional coefficients are the same in eqs 1 and 4 on the one hand and in eqs 2 and 3 on the other hand. If we define this proportional coefficient in eq 3 as Pexp (Phν in ref (28)), eqs 1–4 can be rewritten as follows
| 5 |
| 6 |
| 7 |
| 8 |
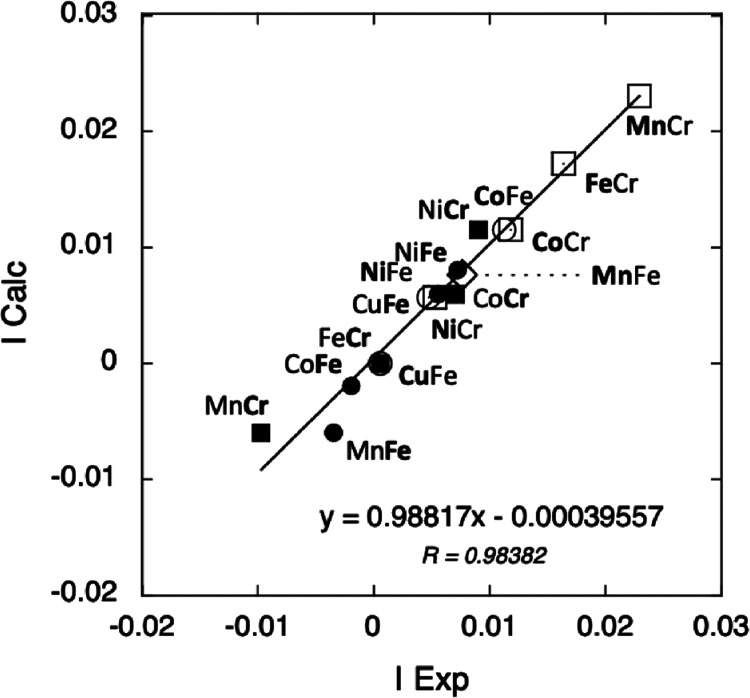
For all compounds at both A and B K-edges, the calculated intensity using eqs 5–8 with Pexp = 0.012 is plotted as a function of the experimental intensity in Figure 5.
Figure 5.
Calculated intensity of the XMCD signal as a function of the experimental intensity at the A K-edge of CoFe, NiFe, and CuFe (white circle), MnFe (white diamond), and of the ACr series (white square), at the Fe K-edge of the AFe series (black circle), and at the Cr K-edges of the ACr series (black square).
The linear variation with a correlation coefficient close to 1 shows that eqs 5–8 very well reproduce the intensity of the XMCD signal for all compounds. It is also satisfying to see that the four equations are made of comparable terms. They will be further discussed later.
4. Discussion
The knowledge of the information contained in the TM K-edge XMCD signals is essential to make the technique become a widely used tool for the study of molecular magnetic materials. The establishment of the expressions of the intensity of the main contribution to the XMCD signal is the first promising step. In the first part of the discussion, we will try to go a bit further in our understanding of these expressions. In the second part, we will try to use the data extracted from the technique to better understand the magnetic properties of the model compounds.
4.1. Intensity of the Main δ Contribution to the XMCD Signal
A magnetic dichroic signal appears at the K-edge of TM in the presence of spin–orbit coupling in the 4p orbitals in the excited state. Information on the magnetic properties then derives from exchange interactions between the photoelectron in the 4p orbital and the 3d unpaired electrons.
Equations 5–8 are a product of three terms: the first one depending on SA, the total spin quantum number of the A2+ ion, the second one taking the value of 1 or 1/3 depending on the sample and on the K-edge and called Ω in the following, and the third one is the Pexp coefficient. These three terms are further discussed in the following:
Pexp coefficient
The Pexp coefficient depends neither on the sample nor on the K-edge. It must therefore depend on experimental parameters, such as the temperature, the magnetic field, and the rate of circular polarization of light, as suggested in this study and our previous works.27,28 We indeed showed in ref (27) that, for a given position of the slits used to select the circular polarization of the X-ray beam, the rate of circular polarization does not change over the energy range for our experiments. So, this parameter is the same for all measurements. As the intensity of the XMCD signal strongly depends on the magnetic field and even more on the temperature (even below the magnetic ordering temperature of the compounds),27 it was therefore of prime importance to have fixed them at exactly the same values for the whole study, an experimental constraint we strictly respected.
SA-Dependent Term
The SA-dependent term (eqs 5–8) has the form of a sum or a difference between SA and a constant. At the A K-edge, this term is thus composed of the total spin quantum number of the absorber atom (SA) and the 1/2 value, which we proposed to assign to the spin of the photoelectron.28eqs 5 and 6 can be reformulated to make appear the total spin quantum number of the absorber atom (SFe = 1/2 and SCr = 3/2), which also induces the presence of the 1/2 value
| 9 |
| 10 |
This shows that the constant term that was added or subtracted to the experimental intensity of the XMCD signal to get eqs 1 and 2 and then eqs 5 and 6 is directly linked to the spin of the absorbing atom and the 1/2 value and has therefore a physical meaning. Thus, the SA-dependent terms in eqs 7–9 all contain the spin of the absorbing atom (SA in IA in eq 7, SMn in IMnFe in eq 8, SFe in IFe in eq 9, and SCr in ICr in eq 10). In addition to the spin of the absorbing atom, the SA-dependent term can contain the spin of the other TM ion (SA in eqs 9 and 10). At last, the SA-dependent terms always contain the 1/2 value in addition to the other spin value(s). It is therefore appealing to assign this value of 1/2 to a spin value, which would be the same for all K-edges and which we propose to assign to the spin of the photoelectron. Nevertheless, this assignment remains to be demonstrated.
In what follows, we concentrate on better understanding the origin of the elements of this SA-dependent term.
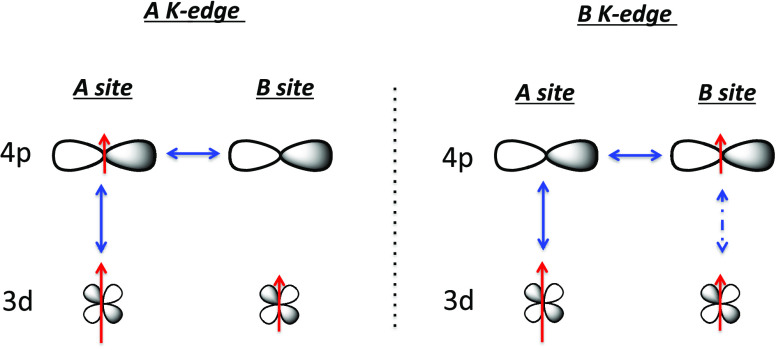
Intrasite Spin Polarization
At all K-edges of the TM ions, the spin-dependent term contains the total spin of the absorber ion (SA in eqs 7 and 8, SFe in eq 9, and SCr in eq 10), indicating that the 4p orbitals of the absorber atom are always spin-polarized by the unpaired electrons in the 3d orbitals in the same atom through intra-atomic 3dA-4pA or 3dB-4pB interactions. One can notice that the sign in front of the spin of the absorber atom is always positive and does not depend on the direction of the magnetic moment with regard to that of the applied magnetic field, although the overall sign of the signal directly depends on it.
Intersite Spin Polarization
The presence of SA in the expression of the intensity of the signal at the Fe and Cr K-edges (eqs 9 and 10) shows that the 4pB orbitals are also spin-polarized by the 3dA electrons of the A site for the two AFe and ACr series. A direct interaction between electrons in 4pB and 3dA orbitals is expected to be very small, too small to be involved in such a polarization process. Besides, if such interactions would be involved, an intersite spin polarization by the 3d electrons would be expected for both A and B sites, which is not the case. Therefore, the interaction between the photoelectron in the 4pB orbitals and the 3dA electrons goes through either (i) the 4pB-4pA-3dA three-orbital pathway or (ii) the 4pB-3dB-3dA one. This 4pB-3dB-3dA pathway can be excluded as such a pathway implies that IA should also contain a contribution from the B3+ ion through the 4pA-3dA-3dB pathway, which is not the case. Therefore, the interaction originating in the SA term in eqs 9 and 10 goes through the empty 4pA orbitals, i.e., intra-atomic 3dA-4pA mixing on the A site with low symmetry and interatomic 4pA-4pB orbital mixing between both sites. This suggests that spin polarization propagates through many-orbital mixing also involving empty 4p orbitals (4pA). The delocalized 4pA and 4pB orbitals of the A2+ and B3+ ions, having relatively close energy levels as well as the same symmetry and strong overlapping along one axis out of three, significantly mix along this axis. Thus, the presence of a SA term in eqs 9 and 10 can be explained by the combination of 3dA-4pA intrasite and 4pA-4pB intersite orbital mixing. Without overlap or without enough overlap pathways between the 3dB and 4pB orbitals, the 4pA orbitals are not spin-polarized by the 3dB unpaired electrons, so that eqs 7 and 8 do not contain any SB term.
The proposed explanation for intersite spin polarization can thus be summarized as follows and schematized in Figure 6.
Figure 6.
Scheme illustrating the proposed explanation for intersite spin polarization.
Spin polarization propagates through orbital mixing (monoelectronic overlap integral) schematized by plain arrows in Figure 6. These orbitals are 3dA-4pA on the A site and 4pA-4pB intersite. Thus, at the B K-edge, the probed 4pB orbitals are spin-polarized both by the 3dA electrons through 3dA-4pA-4pB orbital mixing and by the 3dB electron(s) through bielectronic exchange interaction (schematized by dotted arrows in Figure 6). The expression of the intensity of the XMCD main contribution hence contains both SA and SB. This latter interaction (between 4pB and 3dB) implies the presence of electrons on both 3dB and 4pB orbitals, which means that this interaction is switched on at the B K-edge probing the 4pB orbital, but switched off at the A K-edge, for which the 4pB orbitals are empty. Thus, at the A K-edge, the 3dB-4pB interaction pathway is switched off and the expression of the intensity of the XMCD main contribution only contains SA.
The sign in front of the SA term in eqs 9 and 10 remains intriguing. In the expression of the intensity of the signal at the Fe K-edge, it seems to be linked to the relative orientation of the magnetic moment on the A and B sites (i.e., to the nature of the exchange interaction between both sites), whereas in the expression of the intensity of the signal at the Cr K-edge, it is always negative whatever the relative orientation of the magnetic moments on the A and B sites. This difference is probably once again related to the different electronic and local structures of both Cr(CN)6 and Fe(CN)6 entities. Work is in progress to better understand the origin of this sign.
Conclusions
It appears from the discussion on the SA-dependent term in the intensity of the main contribution to the XMCD signal that:
-
(i)
the 4pi orbitals of the absorber atom are always spin-polarized by the unpaired electrons on the 3di orbitals on the same site and the sign in front of the associated term Si is always positive,
-
(ii)
the 4pi orbitals of the absorber atom can be spin-polarized by the 3dj unpaired electrons on the neighboring site through a combination of intrasite and intersite orbital mixing, and the sign in front of the corresponding term remains to be understood.
It is remarkable that empty 4p orbitals can propagate exchange interactions between intersite 3d and 4p orbitals. One can thus foresee that they could even do so between 3d orbitals when the sites of the magnetic centers are non-centro-symmetric. This suggests that empty 4p orbitals could play a noninnocent role in the magnetic properties of molecular materials.
The Ω coefficient
The Ω coefficient takes the values of 1 or 1/3 for all samples and all K-edges (eqs 7–10). With doubt about neither the magnetic moment borne by the ions nor the measurement conditions, we proposed in our previous work focused on the A K-edges28 to assign these different values (1 and 1/3) to different orientations of the magnetic moment borne by the absorber atom with regard to the ⟨100⟩ crystallographic axes, which are also the axes of the probed 4p orbitals. The same assignment for Ω can be proposed at the Cr and Fe K-edges. The local environments around the Cr3+ and the Fe3+ ions are different, octahedral in the former and slightly departing from centro-symmetric Oh in the latter. This difference can generate different magnetocrystalline anisotropy for the two sublattices with possible different easy axes of magnetization. Thus, in the Oh Cr(CN)6 units, an alignment of the magnetic moment along the ⟨100⟩ crystallographic axes through spin–orbit coupling can be anticipated. In contrast, in the distorted Fe(CN)6 units, assuming a trigonal distortion like in the K3[Fe(CN)6] crystals mentioned above,52 an alignment of the magnetic moments along the ⟨111⟩ directions, which are also the C3 axes of the distorted coordination polyhedra, can be foreseen like in K3[Fe(CN)6].52 Such an assignment is supported by the fact that the 1 and 1/3 values correspond to the value of cos2(θ), where θ is the angle between the proposed direction for the magnetic moments and the axes of the probed 4p orbitals. A scheme of the proposed orientations for all of the magnetic moments along the ACr and AFe series is shown in Figure 7. With the same Ω value in the expression of the intensity of the XMCD signal at the Mn K-edge of MnFe and the intensity of the XMCD at the Fe K-edge in the AFe series, the same orientation of the magnetic moment carried by the Mn2+ ion in MnFe as that borne by the Fe+3 ions along the AFe series is proposed. The direction of the magnetic moments was deduced from the nature of the exchange interaction between both TM obtained from the sign of the Weiss temperature in the Curie–Weiss law and the magnetization value under a high magnetic field.28
Figure 7.
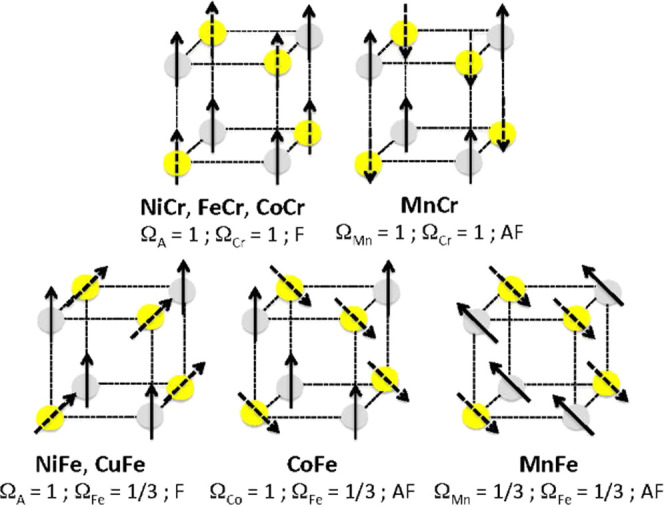
Scheme of the proposed orientations of the magnetic moments for an octant of the structure. The magnetic moments carried by the A (gray) and B (yellow) sites are represented by a plain and a dotted arrow, respectively.
4.2. Complementarity of Macroscopic SQUID and Local TM K-edge XAS and XMCD Data Toward a Better Understanding of the Magnetic Properties of PBAs
The investigation of the macroscopic magnetic properties of the ACr and AFe series of PBAs is presented in reference (28). The magnetic ordering temperatures were determined from the derivative of the FC magnetization curves. The Curie constant and the Weiss temperature were determined from the temperature dependence of the inverse of the molar magnetic susceptibility.28 The magnetic ordering temperature and the sign of the Weiss temperature have already been well explained by an orbital approach,55 and the Curie constant can be related to the total spin of the ions with possible orbital contribution depending on the ground state.28 If these magnetic data are well understood,55 questions remain on the magnetic field dependence of the magnetization curves below the magnetic ordering temperature. These curves recorded at 4 K, temperatures at which the XMCD measurements were performed, are shown in S7, and the main magnetic parameters deduced from these curves (magnetization at 1.3 T (temperature of the XMCD measurements), magnetization at 4 T (highest magnetic field reached by the magnetometer used for the magnetic measurements), calculated saturation magnetization, and coercive field) are gathered in Table 1. Assuming that the Ω values (1 or 1/3) characterize the local orientation of the magnetic moments as proposed above, one can propose a further interpretation of these curves.
Table 1. Calculated Saturation Magnetization (Msat), Experimental Magnetization at 4 T (M(4 K)) and 1.3 T (M(1.3 T)), and Coercive Field (HC) for Both AFe and ACr Series of Compounds.
| Msat calc NμB | M (4 T) NμB | M (1.3 T) NμB | Hc 10–4 T | |
|---|---|---|---|---|
| MnFe | 17.3 | 14.1 (81%) | 9.1 (53%) | 246 |
| CoFe | 9.3 | 8.3 (89%) | 6.2 (67%) | 1240 |
| NiFe | 10.7 | 10.1 (94%) | 8.5 (79%) | 2000 |
| CuFe | 6.7 | 6.3 (94%) | 5.3 (79%) | 2250 |
| MnCr | 11.9 | 11.7 (100%) | 11.7 (100%) | 10 |
| FeCr | 24.1 | 18.4 (76%) | 16 (66%) | 175 |
| CoCr | 20.1 | 17.1 (85%) | 16.3 (81%) | 550 |
| NiCr | 16.1 | 16 (100%) | 16 (100%) | 67 |
Magnetization Value at 1.3 T
It is striking to note that the macroscopic magnetization value measured by SQUID magnetometry at the magnetic field applied for the XMCD measurements (1.3 T) does not reach the saturation magnetization for most of the compounds (Table 1, S7), with various gaps between the magnetization at 1.3 T and the saturation magnetization (departure from the saturation magnetization by 53–100% along the series of compounds). Our experimental results clearly show that the intensity of the TM K-edge XMCD signal does not depend on these deviations (such deviations are too big to be included in the experimental error). If this were the case, the experimental intensity of the XMCD signal would not be proportional to the spin of the absorbing atom with the same proportional coefficient (1 × Pexp or (1/3) × Pexp) for all compounds and all edges, which is nevertheless experimentally observed. This means that at least for our molecular materials, the intensities of the TM K-edge XMCD signal and SQUID magnetometry data do not give access to the same component of the magnetic moment.
Regarding the macroscopic magnetization measured by SQUID magnetometry at 1.3 T, the projection of the magnetic moment of the compound onto the applied magnetic field direction is measured. The compounds can be classified into two groups (S7, Table 1). All of the compounds of the AFe series, CoCr and FeCr, do not reach saturation even at 4 T. In contrast, the saturation magnetization of the compounds MnCr and NiCr is reached at a magnetic field as low as 0.2 T. One can notice that the compounds of the first group all contain at least one TM ion with a first-order orbital momentum (the low spin Fe3+ ion (2T2g ground state) in the AFe series, the Co2+ ion (4T1g ground state) in CoCr, and the Fe2+ ion (5T2g ground state) in FeCr), whereas in the compounds of the second group (MnCr and NiCr) neither TM ion has a first-order orbital momentum. The different macroscopic magnetic behavior of the compounds belonging to the two groups can be explained by the fact that the magnetic anisotropy is often much more important for ions, for which the ground state has a first-order orbital momentum. In cubic systems such as the PBAs, the easy magnetization axes are generally oriented along the ⟨100⟩ or the ⟨111⟩ axes. The cubic structure of PBA is made of octahedral coordination complexes having the metal–ligand axes aligned along the ⟨100⟩ directions, these directions can a priori be expected to be the easy magnetization axes. Below the magnetic ordering temperature, the magnetic moments carried by the TM ions are aligned in these directions. Without an applied magnetic field, the three directions are equally populated, so that the average magnetization is equal to zero. Applying an increasing magnetic field progressively aligns the magnetic moments along the direction the closest to that of the applied magnetic field. The magnetic field needed to align the magnetic moments along the magnetic field direction increases with the magneto-crystalline anisotropy energy. As the magneto-crystalline anisotropy energy is higher for compounds containing ions, for which the ground state has a first-order orbital momentum, the magnetic field needed to reach the saturation magnetization is therefore significantly higher. This can explain why saturation magnetization is not reached in FeCr, CoCr, MnFe, CoFe, NiFe, and CuFe, whereas it is reached at a magnetic field as low as 0.2 T in MnCr and NiCr.
The intensity of the TM K-edge XMCD signal does not depend on the gap between the macroscopic magnetization at 1.3 T measured by SQUID magnetometry and the saturation magnetization, meaning that it does not depend on the distribution of the orientations of the magnetic moments in the three ⟨100⟩ (or ⟨111⟩) directions (easy magnetization axes). This means that the intensity of the TM K-edge XMCD signal rather depends on the projection of the magnetic moments on the axes of the probed 4p orbitals. In the PBA cubic structure, the three axes of the 4p orbitals are equivalent, so that the contribution of the magnetic moments aligned in any equivalent direction with regard to these axes is the same, which can explain why the intensity of the TM K-edge XMCD signal does not depend on the gap between the macroscopic magnetization at 1.3 T measured by SQUID magnetometry and the saturation magnetization.
Coercive Field
If we now consider the coercive field values, the samples can be divided into three groups (Table 1). In the first group composed of MnCr and NiCr, the coercive field values do not exceed some tens Oe (10 Oe for MnFe and 67 Oe for NiCr). In the second group composed of MnFe, FeCr, and CoCr, their values do not exceed some hundreds Oe (246 Oe for MnFe, 175 Oe for FeCr and 550 Oe for CoCr). And, in the third group composed of CoFe, NiFe, and CuFe, their values exceed 1000 Oe (1240 Oe for CoFe, 2000 Oe for NiFe and 2250 Oe for CuFe).
The coercive field is expected to increase with magneto-crystalline anisotropy energy. It is thus unsurprising to find in the first group MnCr and NiCr, which do not contain ions for which the ground state has a first-order orbital momentum in the Oh symmetry: Cr3+ (4A2g ground state), Mn2+ (6A1g ground state), and Ni2+ (3A2g ground state). A magnetic field as low as a few tens of Oe is enough to make the magnetic moments flip along the direction of the applied magnetic field. It is also not surprising that the easy magnetization axes are in the ⟨100⟩ directions of the cubic lattice as mentioned above (Ω = 1 in eqs 7 and 10).
In the compounds of the second group (MnFe, FeCr and CoCr), one out of the two sites is occupied by an ion for which the ground state has a first-order orbital momentum and for which higher magneto-crystalline anisotropy energy is expected (Fe3+ in MnFe, Fe2+ in FeCr and Co2+ in CoCr). This can explain the higher coercive field value. In FeCr and CoCr, it is not surprising that the easy magnetization axes are the ⟨100⟩ directions in the two sublattices (Ω = 1 in eqs 7 and 10). In contrast, in the case of MnFe, the Fe3+ ions in distorted octahedral geometry have the highest magneto-crystalline anisotropy energy with magnetic moments oriented along the ⟨111⟩ directions as proposed above (Ω = 1/3 in eq 9). The same Ω value of 1/3 in eq 8 indicates that the magnetic moments carried by the Mn2+ ions are oriented along the same ⟨111⟩ directions. This also indicates that the orientation of the magnetic moments carried by the Mn2+ ion sublattice is dictated by that of the Fe3+ion sublattice, suggesting that the exchange interaction between both Fe3+ and Mn2+ ions is stronger than the magneto-crystalline anisotropy on the Mn2+ ion. This can also explain the specific behavior of MnFe, for which the magnetization value departs the most from saturation in both the AFe and ACr series.
Finally, in the compounds of the third group (CoFe, NiFe and CuFe), both sites are occupied by ions having different Ω values (1 at the A site and 1/3 at the Fe site, eqs 7 and 9) and therefore different orientations of the magnetic moments. This would mean that the easy magnetization axes are different on both sites and the magneto-crystalline anisotropy energy is high on both sites (higher than the exchange interaction energy). As discussed above, the magneto-crystalline anisotropy energy of the Fe3+ ions is high and, due to the peculiar distortion of the coordination polyhedron, their magnetic moments are oriented along the ⟨111⟩ directions. The easy magnetization axes of the A2+ ions (six-fold coordinated ions with metal-to-ligand axes oriented along the ⟨100⟩ directions) are the ⟨100⟩ directions. The Co2+ ion in CoFe has a first-order orbital momentum so that the magnetic anisotropy energy can indeed be expected to be important, higher than the exchange interaction energy (which is not the case for MnFe). Contrary to the Co2+ ion, the Cu2+ and Ni2+ ions have no first-order orbital momentum. In the case of the Cu2+ ion, a significant magnetic anisotropy can arise from a slight axial distortion due to the Jahn–Teller effect.56 Such a distortion is hardly detectable in the alkali cation-free CuFe PBA. Indeed, the Cu2+ being neighbored by an average of two randomly distributed Fe(CN)6 vacancies acting as strain relaxation points in the lattice, the elongated axes develop in all ⟨100⟩ directions, while keeping a cubic structure. The Jahn–Teller effect exhibited by the Cu2+ ions can nevertheless be revealed in CuFe PBAs containing enough alkali cations, for which a collective distortion is clearly detectable on the powder X-ray diffraction pattern (S8). The case of the Ni2+ ion is again different. Associated with Cr(CN)6 entities in the PBA structure, the macroscopic magnetic behavior is in line with a low magneto-crystalline anisotropy energy of the Ni2+ complexes (see above). One possible explanation for the different behavior of the Ni2+ ion in NiFe can be found in the comparison of the XANES spectra at the Ni K-edge of NiFe and NiCr. If the overall spectra show that the electronic structure and the local structure of the Ni2+ ions are very close in both compounds in agreement with the location in the same octahedral site of the PBA cubic structure, the pre-edge regions of the spectra are clearly different (S9). These differences reveal slightly different geometries of the Ni2+ coordination polyhedra in both compounds with an expected impact on the magnetic behavior of the Ni2+ sublattice and its magnetic anisotropy. Work is in progress to better characterize the local structure difference around the Ni2+ ion and to better understand the different magnetic behavior of this ion in both compounds.
5. Conclusions
This study shows, like our previous work at the A K-edges of the same series of compounds,28 that the Prussian blue analog family is particularly well suited to gain insight into XMCD at the transition-metal K-edges in molecular compounds. And in turn, XMCD at the transition-metal K-edges can provide valuable and original information on the electronic and local structure as well as on the magnetic properties of those compounds.
TM K-edge XMCD gains intensity from the dipole-allowed 1s → 4p transitions. Therefore, this technique is particularly well suited to evidence orbital mixing with 4p orbitals. In the pre-edge region, XMCD gains intensity for non-centro-symmetric sites and it is proving to be very sensitive to slight structural distortions.
An expression for the intensity of the main contribution of the TM K-edge XMCD signal has been proposed for all K-edges of the TM ions of all compounds of both series. The intensity is a product of three components. The first component depends on experimental parameters (temperature, magnetic field, rate of circular polarization of light). It is constant in our case since the measurement conditions have been strictly kept the same all along the experiments. The second component is assigned to the local orientation of the magnetic moment carried by the absorber atom.
The third component is a function of spin quantum numbers. In all cases, the intensity of the XMCD signal depends on the total spin of the absorber atom (Si). The intensity of TM K-edge XMCD can also contain an intersite contribution reflecting the spin polarization of the probed 4p orbitals by the spin of the other sublattice. This spin polarization originates from three-orbital interactions going through intrasite 3d-4p and intersite 4p-4p orbital mixing. The existence of such magnetic interaction spreading through empty 4p orbitals suggests that 4p orbitals could play a significant role in the magnetic properties of molecular materials made of 3d magnetic centers and that TM K-edge XMCD is a particularly appropriate technique to tackle such a question.
The whole study shows that the expressions of the intensity of the TM K-edge XMCD signals are very different at the A and B sites of the coordination polymers and that these differences are related to the different local symmetry of the sites. It also shows that TM K-edge XMCD can provide new local magnetic information, which, combined with magnetic macroscopic data and local structure data, can provide a new tool, which should be able to tackle tricky magnetic anisotropy issues or to better understand the role of the 4p orbitals in the magnetic properties of TM ions.
To our knowledge, this is the first time that a systematic study of molecular compounds allows for establishing relationships between experimental TM K-edge XMCD signals and some magnetic parameters of the compounds. In this context, the proposition of expressions that fairly reproduce the intensity of the XMCD signals at the two TM K-edges of eight PBAs opens new perspectives toward a better understanding of such signals, toward the possible extension of such an approach to the study of other molecular compounds, and as a consequence toward an increased use and general understanding of the technique. We also hope that this work could be the starting point for further experimental systematic work to better understand TM K-edge XMCD for molecular compounds. Neutron diffraction57,58 on model compounds or the investigation of molecular compounds with well-known easy axes of magnetization could for instance provide complementary information on the orientation of the local magnetic moments. All of these experimental data could also be confronted with theoretical studies.
Acknowledgments
The authors thank E. Fonda, G. Landrot, and A. Zitolo (SAMBA beamline, SOLEIL, France) for help during the XAS experiments. The authors also acknowledge SOLEIL for the provision of a synchrotron radiation facility on the ODE beamline through proposals 20180264 and 20181406 and on the SAMBA beamline through proposals 20180264 and 20200652.
Glossary
Abbreviations Used
- PBA
Prussian blue analog
- XANES
X-ray absorption near-edge structure
- XAS
X-ray absorption spectroscopy
- MT
transition metal
- ZFC
zero field cooled
- FC
field cooled
- XMCD
X-ray magnetic circular dichroism
- DAC
diamond anvil cell
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c04049.
S1 Cr K-edge XANES spectra; S2 Fe K-edge XANES spectra; S3 Intensities of the XMCD α and γ peaks as a function of the intensity of the δ peak; S4 XMCD signal compared to the XANES spectrum at the A K-edge; S5 and S6 Area under the curve versus intensity for the main δ peak of the XMCD signal; S7 Magnetic field dependence of the magnetization at 4 K; S8 Powder X-ray diffraction of CuFe PBAs containing an increasing amount of Cs+ cations inserted in interstitial sites; S9 XANES spectra of NiFe and NiCr (PDF)
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. All of the authors contributed equally.
Financial support was provided for the whole TM K-edge XMCD project and the Ph.D. grant of A.N.D. by ANR MAgDiDi (ANR-17-CE29-0011), Paris-Saclay University, and the CNRS. This research was carried also out with the support of the synchrotron SOLEIL.
The authors declare no competing financial interest.
Author Status
⊥ The authors are sad to specify that their colleague, co-author, and friend, François Baudelet, passed on January 28, 2022.
Supplementary Material
References
- de Groot F. M. F. High-Resolution X-ray Emission and X-ray Absorption Spectroscopy. Chem. Rev. 2001, 101, 1779. 10.1021/cr9900681. [DOI] [PubMed] [Google Scholar]
- van der Laan G.; Figueroa A. I. X-ray magnetic circular dichroism—A versatile tool to study magnetism. Coord. Chem. Rev. 2014, 277–278, 95. 10.1016/j.ccr.2014.03.018. [DOI] [Google Scholar]
- de Groot F.M.F. X-ray absorption and dichroism of transition metals and their compounds. J. Electron Spectros. Relat. Phenom. 1994, 67, 529. 10.1016/0368-2048(93)02041-J. [DOI] [Google Scholar]
- Rogalev A.; Wilhelm F. Magnetic circular dichroism in the hard X-ray range. Phys. Met. Metallogr. 2015, 116, 1285. 10.1134/S0031918X15130013. [DOI] [Google Scholar]
- Thole B. T.; Carra P.; Sette F.; van der Laan G. X-ray circular dichroism as a probe of orbital magnetization. Phys. Rev. Lett. 1992, 68, 1943. 10.1103/PhysRevLett.68.1943. [DOI] [PubMed] [Google Scholar]
- Carra P.; Thole B. T.; Altarelli M.; Wang X. X-ray circular dichroism and local magnetic fields. Phys. Rev. Lett. 1993, 70, 694. 10.1103/PhysRevLett.70.694. [DOI] [PubMed] [Google Scholar]
- Chen C. T.; Idzerda Y. U.; Lin H.-J.; Smith N. V.; Meigs G.; Chaban E.; Ho G. H.; Pellegrin E.; Sette F. Experimental Confirmation of the X-Ray Magnetic Circular Dichroism Sum Rules for Iron and Cobalt. Phys. Rev. Lett. 1995, 75, 152. 10.1103/PhysRevLett.75.152. [DOI] [PubMed] [Google Scholar]
- Moroni R.; Cartier dit Moulin C.; Champion G.; Arrio M.-A.; Sainctavit Ph.; Verdaguer M.; Gatteschi D. X-ray magnetic circular dichroism investigation of magnetic contributions from Mn(III) and Mn(IV) ions in Mn12-ac. Phys. Rev. B 2003, 68, 064407 10.1103/PhysRevB.68.064407. [DOI] [Google Scholar]
- Schütz G.; Wagner W.; Wilhelm W.; Kienle P.; Zeller R.; Frahm R.; Materlik G. Absorption of circularly polarized x rays in iron. Phys. Rev. Lett. 1987, 58, 737. 10.1103/PhysRevLett.58.737. [DOI] [PubMed] [Google Scholar]
- Torchio R.; Mathon O.; Pascarelli S. XAS and XMCD spectroscopies to study matter at high pressure: Probing the correlation between structure and magnetism in the 3d metals. Coord. Chem. Rev. 2014, 277–278, 80. 10.1016/j.ccr.2014.02.024. [DOI] [Google Scholar]
- Baudelet F.; Pascarelli S.; Mathon O.; Itié J.-P.; Polian A.; d’Astuto M.; Chervin J.-C. X-ray absorption spectroscopy and x-ray magnetic circular dichroism simultaneous measurements under high pressure: the iron bcc–hcp transition case. J. Phys.: Condens. Matter 2005, 17, S957. 10.1088/0953-8984/17/11/028. [DOI] [Google Scholar]
- Cafun J.-D.; Lejeune J.; Itié J.-P.; Baudelet F.; Bleuzen A. XMCD at the Transition Metal K-Edges as a Probe of Small Pressure-Induced Structural Distortions in Prussian Blue Analogues. J. Phys. Chem. C 2013, 117, 19645. 10.1021/jp403337w. [DOI] [Google Scholar]
- Ishimatsu N.; Shichijo T.; Matsushima Y.; Maruyama H.; Matsuura Y.; Tsumuraya T.; Shishidou T.; Oguchi T.; Kawamura N.; Mizumaki M.; Matsuoka T.; Takemura K. Hydrogen-induced modification of the electronic structure and magnetic states in Fe, Co, and Ni monohydrides. Phys. Rev. B 2012, 86, 104430 10.1103/PhysRevB.86.104430. [DOI] [Google Scholar]
- Torchio R.; Kvashnin Y. O.; Pascarelli S.; Mathon O.; Marini C.; Genovese L.; Bruno P.; Garbarino G.; Dewaele A.; Occelli F.; Loubeyre P. X-Ray Magnetic Circular Dichroism Measurements in Ni up to 200 GPa: Resistant Ferromagnetism. Phys. Rev. Lett 2011, 107, 237202 10.1103/PhysRevLett.107.237202. [DOI] [PubMed] [Google Scholar]
- Torchio R.; Monza A.; Baudelet F.; Pascarelli S.; Mathon O.; Pugh E.; Antonangeli D.; Itié J.-P. Pressure-induced collapse of ferromagnetism in cobalt up to 120 GPa as seen via x-ray magnetic circular dichroism. Phys. Rev. B 2011, 84, 060403 10.1103/PhysRevB.84.060403. [DOI] [Google Scholar]
- Igarashi J. I.; Hirai K. Orbital moment and magnetic circular dichroism at the K edge in ferromagnetic cobalt. Phys. Rev. B 1996, 53, 6442. 10.1103/PhysRevB.53.6442. [DOI] [PubMed] [Google Scholar]
- Bouldi N.; Vollmers N. J.; Delpy-Laplanche C. G.; Joly Y.; Juhin A.; Sainctavit Ph.; Brouder Ch.; Calandra M.; Paulatto L.; Mauri F.; Gerstmann U. X-ray magnetic and natural circular dichroism from first principles: Calculation of K- and L1-edge spectra. Phys. Rev. B 2017, 96, 085123 10.1103/PhysRevB.96.085123. [DOI] [Google Scholar]
- Ebert H. Influence of the orbital polarization on the magnetic X-ray dichroism of transition metals. Solid State Commun. 1996, 100, 677. 10.1016/0038-1098(96)00592-3. [DOI] [Google Scholar]
- Stähler S.; Schütz G.; Ebert H. Magnetic K-edge absorption in 3d elements and its relation to local magnetic structure. Phys. Rev. B 1993, 47, 818. 10.1103/PhysRevB.47.818. [DOI] [PubMed] [Google Scholar]
- Gotsis H. J.; Strange P. A first-principles theory of X-ray Faraday effects. J. Phys.: Condens. Matter 1994, 6, 1409. 10.1088/0953-8984/6/7/012. [DOI] [Google Scholar]
- Guo G. Y. What does the K-edge x-ray magnetic circular dichroism spectrum tell us?. J. Phys.: Condens. Matter 1996, 8, L747. 10.1088/0953-8984/8/49/005. [DOI] [Google Scholar]
- Brouder Ch.; Hikam M. Multiple-scattering theory of magnetic x-ray circular dichroism. Phys. Rev. B 1991, 43, 3809. 10.1103/PhysRevB.43.3809. [DOI] [PubMed] [Google Scholar]
- Brouder Ch.; Alouani M.; Bennemann K. H. Multiple-scattering theory of x-ray magnetic circular dichroism: Implementation and results for the iron K edge. Phys. Rev. B 1996, 54, 7334. 10.1103/PhysRevB.54.7334. [DOI] [PubMed] [Google Scholar]
- Natoli C. R.; Benfatto M.; Doniach S. Use of general potentials in multiple-scattering theory. Phys. Rev. A 1986, 34, 4682. 10.1103/PhysRevA.34.4682. [DOI] [PubMed] [Google Scholar]
- Joly Y.; Bunau O.; Lorenzo J. E.; Galéra R. M.; Grenier S.; Thompson B. Self-consistency, spin-orbit and other advances in the FDMNES code to simulate XANES and RXD experiments. J. Phys.: Conf. Ser. 2009, 190, 012007 10.1088/1742-6596/190/1/012007. [DOI] [Google Scholar]
- Bordage A.; Nataf L.; Baudelet F.; Bleuzen A. Investigation of Prussian Blue Analogs by XMCD at the K-edge of transition metals. J. Phys.: Conf. Ser. 2016, 712, 012109 10.1088/1742-6596/712/1/012109. [DOI] [Google Scholar]
- N’Diaye A.; N’Diaye A.; Bordage A.; Nataf L.; Baudelet F.; Moreno T.; Bleuzen A. A cookbook for the investigation of coordination polymers by transition metal K-edge XMCD. J. Synchrotron Radiat. 2021, 28, 1127. 10.1107/S1600577521004884. [DOI] [PubMed] [Google Scholar]
- N’Diaye A.; Bordage A.; Nataf L.; Baudelet F.; Rivière E.; Bleuzen A. Towards quantitative magnetic information from transition metal K-edge XMCD of Prussian Blue analogs. Inorg. Chem. 2022, 61, 6326. 10.1021/acs.inorgchem.2c00637. [DOI] [PubMed] [Google Scholar]
- Rueff J. P.; Galéra R. M.; Giorgetti Ch.; Dartyge E.; Brouder Ch.; Alouani M. Rare-earth contributions to the x-ray magnetic circular dichroism at the Co K edge in rare-earth–cobalt compounds investigated by multiple-scattering calculations. Phys. Rev. B 1998, 58, 12271. 10.1103/PhysRevB.58.12271. [DOI] [Google Scholar]
- Herrero-Albillos J.; Bartolomé F.; Garcia L. M.; Cerbuna P.; Casanova F.; Labarta A.; Batlle X. Reply to “Comment on ‘Nature and entropy content of the ordering transitions in RCo2’’’. Phys. Rev. B 2007, 75, 187402 10.1103/PhysRevB.75.187402. [DOI] [Google Scholar]
- Laguna-Marco M. A.; Piquer C.; Chaboy J. X-ray magnetic circular dichroic spectrum at the K edge of the transition metal in R-T intermetallics and its relationship with the magnetism of the rare earth. Phys. Rev. B 2009, 80, 144419 10.1103/PhysRevB.80.144419. [DOI] [Google Scholar]
- Verdaguer M.; Mallah T.; Hélary C.; L’Hermite F.; Sainctavit P.; Arrio M. A.; Babel D.; Baudelet F.; Dartyge E.; Fontaine A. K edge X-ray magnetic circular dichroism in molecule-based magnets. Physica B 1995, 208–209, 765. 10.1016/0921-4526(94)00803-4. [DOI] [Google Scholar]
- Train C.; Baudelet F.; Cartier dit Moulin C. Remnant X-ray Magnetic Circular Dichroism Investigation of the Local Magnetic Contributions to the Magnetization of a Coercive Bimetallic Molecule-Based Magnet. J. Phys. Chem. B 2004, 108, 12413. 10.1021/jp049522h. [DOI] [Google Scholar]
- Bartolomé J.; Bartolomé F.; Figueroa A. I.; Bunau O.; Schuller I. K.; Gredig T.; Wilhelm F.; Rogalev A.; Krüger P.; Natoli C. R. Quadrupolar XMCD at the Fe K-edge in Fe phthalocyanine film on Au: Insight into the magnetic ground state. Phys. Rev. B 2015, 91, 220401 10.1103/PhysRevB.91.220401. [DOI] [Google Scholar]
- Lüdi A.; Güdel H. U.. Structural chemistry of polynuclear transition metal cyanides. In Structure and Bonding; Springer-Verlag: Berlin, 1973; Vol. 14, p 1. [Google Scholar]
- Buser H. J.; Ludi A.; Petter W.; Schwarzenbach D. The crystal structure of Prussian Blue: Fe4[Fe(CN)6]3·xH2O. Inorg. Chem. 1977, 16, 2704. 10.1021/ic50177a008. [DOI] [Google Scholar]
- Simonov A.; De Baerdemaeker T.; Boström H. L. B.; Ríos Gómez M. L.; Gray H. J.; Chernyshov D.; Bosak A.; Bürgi H.-B.; Goodwin A. L. Hidden diversity of vacancy networks in Prussian blue analogues. Nature 2020, 578, 256. 10.1038/s41586-020-1980-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tokoro H.; Shiro M.; Hashimoto K.; Ohkoshi S.-I. Single crystal of a Prussian Blue Analog based on Rubidium Manganese Hexacyanoferate. Z. Anorg. Allg. Chem. 2007, 633, 1134. 10.1002/zaac.200700129. [DOI] [Google Scholar]
- Vertelman E. J. M.; Lummen T. T. A.; Meetsma A.; Bouwkamp M. W.; Molnar G.; van Loosdrecht P. H. M.; van Koningsbruggen P. J. Light- and Temperature-Induced Electron Transfer in Single Crystals of RbMn[Fe(CN)6]·H2O. Chem. Mater. 2008, 20, 1236. 10.1021/cm7032965. [DOI] [Google Scholar]
- Haser R.; De Broin C. E.; Pierrot M. Etude Structurale de la Série des Hexacyanoferates(II,III) d’Hydrogène:H3+x[FeIIFe1-xIII(CN)6]•yH2O I. Structures Cristallines des Phases Hexagonales H, H3FeIII(CN)6 et H3CoIII(CN)6, par Diffraction des Rayons X et des Netrons. Acta Cryst. 1972, B28, 2530. 10.1107/S0567740872006429. [DOI] [Google Scholar]
- Gravereau P.; Garnier E. Structure de la Phase Cubique de l’Hexacyanoferrate(III) de zinc: Zn3[Fe(CN)6]2•nH2O. Acta Cryst. 1984, C40, 1306. 10.1107/S0108270184007757. [DOI] [Google Scholar]
- Briois V.; Fonda E.; Belin S.; Barthe L.; La Fontaine C.; Langlois F.; Ribens M.; Villain F. SAMBA: The 4–40 keV X-ray absorption spectroscopy beamline at SOLEIL. UVX 2010 EDP Sciences 2011, 41. [Google Scholar]
- Ravel B.; Newville M. ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 2005, 12, 537. 10.1107/S0909049505012719. [DOI] [PubMed] [Google Scholar]
- Baudelet F.; Kong Q.; Nataf L.; Cafun J.-D.; Congedutti A.; Monza A.; Chagnot S.; Itié J.-P. ODE: a new beam line for high-pressure XAS and XMCD studies at SOLEIL. High Pressure Research 2011, 31, 136. 10.1080/08957959.2010.532794. [DOI] [Google Scholar]
- Bianconi A.; Dell’Ariccia M.; Durham P. J.; Pendry J. B. Multiple-scattering resonances and structural effects in the x-ray-absorption near-edge spectra of Fe II and Fe III hexacyanide complexes. Phys. Rev. B 1982, 26, 6502. 10.1103/PhysRevB.26.6502. [DOI] [Google Scholar]
- Yokoyama T.; Ohta T.; Sato O.; Hashimoto K. Characterization of magnetic CoFe cyanides by x-ray-absorption fine-structure spectroscopy. Phys. Rev. B 1998, 58, 8257. 10.1103/PhysRevB.58.8257. [DOI] [Google Scholar]
- Hocking R. K.; Wasinger E. C.; de Groot F. M. F.; Hodgson K. O.; Hedman B.; Solomon E. I.; Fe L-Edge XAS. Studies of K4[Fe(CN)6] and K3[Fe(CN)6]: A Direct Probe of Back-Bonding. J. Am. Chem. Soc. 2006, 128, 10442. 10.1021/ja061802i. [DOI] [PubMed] [Google Scholar]
- Bleuzen A.; Lomenech C.; Escax V.; Villain F.; Cartier dit Moulin C.; Varret F.; Verdaguer M. Photo-Induced Ferrimagnetic systems in Prussian Blue Analogs CxICo4[Fe(CN)6]y (CI=alkali cation). 1. Conditions to observe the phenomenon. J. Am. Chem. Soc. 2000, 122, 6648. 10.1021/ja000348u. [DOI] [Google Scholar]
- Escax V.; Bleuzen A.; Cartier dit Moulin C.; Villain F.; Goujon A.; Varret F.; Verdaguer M. Photo-Induced Ferrimagnetic systems in Prussian Blue Analogs CxICo4[Fe(CN)6]y (CI=alkali cation). 3. Why and How the Efficiency of the Photoinduced Process depends on a Compromise between Co-Fe Diamagnetic Pairs and [Fe(CN)6] Vacancies. J. Am. Chem. Soc. 2001, 123, 12536. 10.1021/ja011296r. [DOI] [PubMed] [Google Scholar]
- Jahn H. A.; Teller E. Stability of polyatomic molecules in degenerate electronic states - I—Orbital degeneracy. Proc. R. Soc. London A 1937, 161, 220. 10.1098/rspa.1937.0142. [DOI] [Google Scholar]
- Bersuker I. B. Jahn-Teller and Pseudo-Jahn-Teller Effects: From Particular Features to General Tools in Exploring Molecular and Solid State Properties. Chem. Rev. 2021, 121, 1463. 10.1021/acs.chemrev.0c00718. [DOI] [PubMed] [Google Scholar]
- Atanasov M.; Comba P.; Daul C. A.; Hauser A. DFT-Based Studies on the Jahn-Teller Effect in 3d Hexacyanometalates with Orbitally Degenerate Ground States. J. Phys. Chem. A 2007, 111, 9145. 10.1021/jp0731912. [DOI] [PubMed] [Google Scholar]
- Figgis B. N.; Skelton B. W.; White A. H. Crystal structures of the simple monoclinic and orthorhombic polytypes of tripotassium hexacyanoferrate(III). Aust. J. Chem. 1978, 31, 1195. 10.1071/CH9781195. [DOI] [Google Scholar]
- Dujardin E.; Ferlay S.; Phan X.; Desplanches C.; Cartier dit Moulin C.; Sainctavit Ph.; Baudelet F.; Dartyge E.; Veillet P.; Verdaguer P. Synthesis and Magnetization of New Room-Temperature Molecule-Based Magnets: Effect of Stoichiometry on Local Magnetic Structure by X-ray Magnetic Circular Dichroism. J. Am. Chem. Soc. 1998, 120, 11347. 10.1021/ja974076f. [DOI] [Google Scholar]
- Verdaguer M.; Bleuzen A.; Marvaud V.; Vaissermann J.; Seuleiman M.; Desplanches C.; Scuiller A.; Train C.; Garde R.; Gelly G.; Lomenech C.; Rosenman I.; Veillet P.; Cartier C.; Villain F. Molecules to build solids: High TC Molecule-based magnets by design and recent revival of cyano complexes chemistry. Coord. Chem. Rev. 1999, 190–192, 1023. 10.1016/S0010-8545(99)00156-3. [DOI] [Google Scholar]
- Matsuda T.; Kimb J.; Moritomo Y. Control of the alkali cation alignment in Prussian blue framework. Dalton Trans. 2012, 41, 7620. 10.1039/c2dt12296k. [DOI] [PubMed] [Google Scholar]
- Kumar A.; Yusuf S. M.; Keller L.; Yakhmi J. V. Microscopic Understanding of Negative Magnetization in Cu, Mn, and Fe Based Prussian Blue Analogues. Phys. Rev. Lett. 2008, 101, 207206 10.1103/PhysRevLett.101.207206. [DOI] [PubMed] [Google Scholar]
- Pajerowski D. M.; Conklin S. E.; Leao J.; Harriger L. W.; Phelan D. High-pressure neutron scattering of the magnetoelastic Ni-Cr Prussian blue analog. Phys. Rev. B 2015, 91, 094104 10.1103/PhysRevB.91.094104. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.