The resurgence risk of COVID-19 in China in the presence of immunity waning and ADE: A mathematical modelling study

Abstract

The mass vaccination program has been actively promoted since the end of 2020. However, waning immunity, antibody-dependent enhancement (ADE), and increased transmissibility of variants make the herd immunity untenable and the implementation of dynamic zero-COVID policy challenging in China. To explore how long the vaccination program can prevent China at low resurgence risk, and how these factors affect the long-term trajectory of the COVID-19 epidemics, we developed a dynamic transmission model of COVID-19 incorporating vaccination and waning immunity, calibrated using the data of accumulative vaccine doses administered and the COVID-19 epidemic in 2020 in mainland China. The prediction suggests that the vaccination coverage with at least one dose reach 95.87%, and two doses reach 77.92% on 31 August 2021. However, despite the mass vaccination, randomly introducing infected cases in the post-vaccination period causes large outbreaks quickly with waning immunity, particularly for SARS-CoV-2 variants with higher transmissibility. The results showed that with the current vaccination program and 50% of the population wearing masks, mainland China can be protected at low resurgence risk until 8 January 2023. However, ADE and higher transmissibility for variants would significantly shorten the low-risk period by over 1 year. Furthermore, intermittent outbreaks can occur while the peak values of the subsequent outbreaks decrease, indicating that subsequent outbreaks boosted immunity in the population level, further indicating that follow-up vaccination programs can help mitigate or avoid the possible outbreaks. The findings revealed that the integrated effects of multiple factors: waning immunity, ADE, relaxed interventions, and higher variant transmissibility, make controlling COVID-19 challenging. We should prepare for a long struggle with COVID-19, and not entirely rely on the COVID-19 vaccine.

1. Introduction

Vaccination against COVID-19 is an important measure for breaking the transmission chain of SARS-CoV-2. Several SARS-CoV-2 vaccines have been developed and approved by the World Health Organization (WHO) since the end of 2020 [1]. In mainland China, the two-dose vaccination program has been actively and widely promoted by injecting inactivated vaccines. Vaccination of high-risk populations was initiated on 15 December 2020, and over 1.82 billion COVID-19 vaccination doses had been administered by 13 August 2021 [2]. The mass vaccination strategy may end the COVID-19 pandemic based on real epidemic data [3]. However, emerging evidence indicates that vaccination does not help eradicate the SARS-CoV-2 spread. On the one hand, waning immunity and limited vaccine efficacy result in a large number of vaccinated population still being susceptible to SARS-CoV-2, particularly regarding SARS-CoV-2 variants [4], [5], [6]. On the other hand, antibody-dependent enhancement (ADE) in SARS-CoV-2 infection has been reported recently [7].

ADE is the phenomenon in which pre-existing antibodies enhance the infectivity of secondary virus infection, and facilitate its transmission. ADE is well documented between different dengue serotypes [8], [9], [10] and Zika virus [11], [12], [13], and infection by other coronaviruses, including MERS [14] and SARS [15]. In a recent research, Liu et al. revealed that COVID-19 patients could not only produce antibodies against the RBD of the spike protein to block SARS-CoV-2 infection, but also produce anti-spike antibodies that enhance ACE2 binding, consequently enhancing the infectivity of SARS-CoV-2 [7]. This supports the existence of ADE in SARS-CoV-2 infections. In [16], the author concluded two possible ways to induce ADE by COVID-19 vaccines. Lots of mathematical models have been developed to discuss the impact of ADE on the transmission dynamics and viral dynamics of various dengue serotypes [17], [18], [19] or between dengue and Zika [20], [21], [22]. During the early stages of COVID-19 vaccine development, several researchers pointed out that ADE can be a potential safety issue [23], [24]. However, it remains unclear and challenging how the ADE effect in SARS-CoV-2 infection affects the COVID-19 pandemic trajectory despite using the COVID-19 vaccines.

Moreover, Choe et al. conducted a clinical study to measure the changes of neutralizing antibodies in symptomatic and asymptomatic SARS-CoV-2 infection and observed that the geometric mean titre of neutralizing antibodies declined from 219.4 at two months to 143.7 at five months after infection [5]. Similarly, in [6], based on a longitudinal study of 517 COVID-19 patients, the authors observed different levels of immunity waning after symptoms onset. Immunity waning makes the prospect of achieving herd immunity increasingly remote, that is, the prominence of herd immunity being touted as a solution to the pandemic might be about to change [25]. Therefore, it is urgent to evaluate the impact of immunity waning on the trends of COVID-19 epidemics, and it is essential to re-design optimal control interventions to combat it long-term. This remains challenging.

Hence, immunity waning and ADE make the long-term trajectory of COVID-19 epidemics full of uncertainty. This study aimed to develop a mathematical model describing the transmission process of COVID-19 and the two-dose vaccination program incorporating waning of immunity and ADE, to investigate the effects of them. We used the COVID-19 epidemic data between 23 January and 8 April 2020 and cumulative vaccine doses administered in mainland China to inform model parameters and conducted a sensitivity analysis to evaluate how long the program can protect China in a low risk of resurgence and how ADE will affect the transmission dynamics of the COVID-19 epidemic. The findings of this study will provide important information for policymakers on the critical time of implementing strict control measures and when a catch-up vaccination program should be launched.

2. Methods

2.1. Model overview

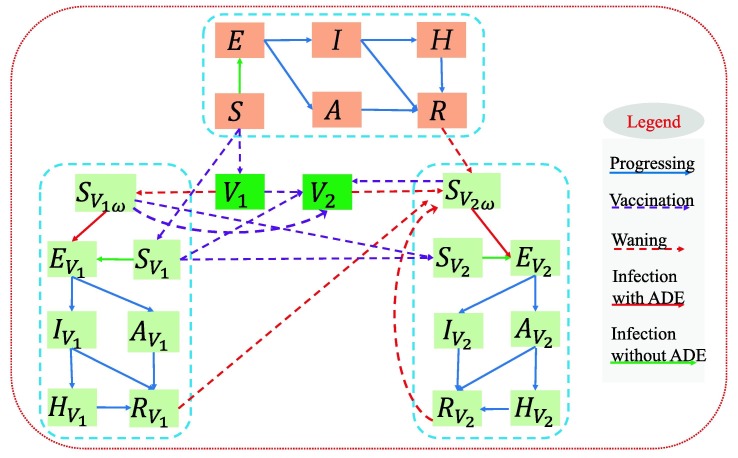
We developed a dynamic model of COVID-19 infection and transmission incorporating with the vaccination program and immunity waning in mainland China. The flow diagram was shown in Fig. 1 . The modelling framework was based on the SEIAHR model [26], [27]. $S,E,I,A,H$ and R denoted the number of susceptible, exposed, symptomatic infected, asymptomatic infected, hospitalized and recovered individuals respectively. The population was further divided into three categories according to their vaccination states: not vaccinated, vaccinated by one-dose (with subscript $V_1$), and vaccinated by two-doses (with subscript $V_2$). We assumed that individuals gained immunity after infection or from vaccination. Furthermore, our model explicitly accounted for the progressive waning of immunity over time, by assuming an average protection period $\frac{1}{{\omega }_i}$ ($i=R,R_{V_1},R_{V_2},V_1,V_2$). The modelling method has been commonly used to describe the waning of immunity in the population [28], [29], [30]. Note that the term $-{\omega }_{i}i$ transferred from i ($i=R,R_{V_1},R_{V_2},V_1,V_2$) to $S_{V_{1\omega }}$ or $S_{V_{2\omega }}$ in the model represented the decreasing rate of the completely protected population through immunity waning, from which we can obtain that the completely protected population would decrease with exponential trend, reflecting the continuous antibody declining in individual-level [31] in the manner of continuous population-level immunity declining. Then given the possibility of the existence of ADE [7], we assumed that the susceptibility of the individuals lost immunity ($S_{V_{1\omega }}$ and $S_{V_{2\omega }}$) was higher than those had not been infected or vaccinated before. $\kappa$ was the modification factor for susceptibility. Detailed assumptions and the corresponding model equations were shown in the Supplementary Information (SI).

Fig. 1.

Schematic diagram illustrating the COVID-19 transmission incorporated with the vaccination program and immunity waning.

2.2. Data

We obtained data on the COVID-19 epidemic, and the mass vaccination program in mainland China from the National Health Commission of the People’s Republic of China [2] and Our World in Data [32], which included the number of daily confirmed cases and deaths between 23 January 2020 and 8 April 2020, the cumulative vaccine doses administered, and the daily vaccine doses administered between 15 December 2020 and 29 June 2021, as shown in Fig. S1 in SI.

2.3. Model calibration and parameter settings

The model can be reduced to a transmission dynamic model without vaccination (model (S3) in SI) and a vaccination dynamic model without transmission (model (S6) in SI). These models were calibrated using the least square method (LS) to fit the epidemic and vaccination data. When performing the following simulations, we set the diagnosis rate as the estimated maximum rate (${\delta }_I={\delta }_{I_1}$) due to the highly improved testing capacity in China. The baseline protection rates of the first and second dose vaccines were $p_1=0.3,p_2=0.9$, respectively [33], [34], [35]. Suppose the immunity produced by infection or vaccination lasts 1 year on average, then the immunity waning rate were ${\omega }_R={\omega }_{V_1}={\omega }_{V_1}={\omega }_{R_{V_1}}={\omega }_{R_{V_2}}=\omega =1/365$ per day. Note that using face masks is a useful self-protective method to prevent COVID-19 infection. Based on a recent meta-analysis[36], we assumed that the baseline proportion of face mask use is about $50\%$ in the post-pandemic era, the effectiveness of face mask in preventing COVID-19 infection or infecting others is 80%. Thus, the baseline transmission rate with a normalized control intervention of wearing masks would be $(1-50\%\times 80\%){\beta }_0=60\%{\beta }_0$. Given the enhanced intervention, the transmission rate can decrease further. Considering the higher transmissibility of SARS-CoV-2 variants, the transmission rate can be higher than the baseline value ${\beta }_0$. Consequently, when performing the sensitivity analysis, we chose a transmission rate varying from $0.4{\beta }_0$ to $1.5{\beta }_0$. In the absence of real data, we chose a range of $[1,3]$ as the modification factor of ADE ($\kappa$) from the studies on the ADE in dengue infections [17], [18], [19], [37], [38].

3. Main results

3.1. Estimation results

The estimated parameters related to the transmission dynamics and the vaccination dynamics were listed in Table S1 in SI. The results revealed that the population vaccinated with at least one dose of the vaccine reached 56.4% (95% CI [55.38%, 57.08%]) whereas the population vaccinated with two doses reached 32.02% (95%CI [31.93%, 32.06%]) on 29 June 2021 (the last data collection date). A further prediction revealed that the population vaccinated with at least one dose would reach 95.87% (95%CI [91.12%,98.16%]) and the population fully vaccinated would reach 77.92% (95% CI[73.33%,79.33%]) on 31 August 2021. Therefore, the vaccination coverage in China would be very high by 31 August 2021. Hence, we assume that the routine vaccination program would be stopped by 31 August 2021 and only individuals who have been administered the first dose should complete the second dose after that. Unless otherwise stated, the considered simulation period is at the end of 2022.

3.2. Resurgence risk evaluation

Based on the above estimation results, through numerical simulations, we focused on discussing the impact of immunity waning and ADE effects on the transmission dynamics of COVID-19, and evaluating the resurgence risk of COVID-19 in China. The strictly implemented dynamic zero-COVID policy in China has prevented large outbreaks. No community cases occurred in China except for local outbreaks caused by imported cases. Therefore, we analyzed whether there could be large outbreak by randomly introducing several infected cases into the community, only with mass vaccination or vaccination plus a normalized control intervention by wearing masks.

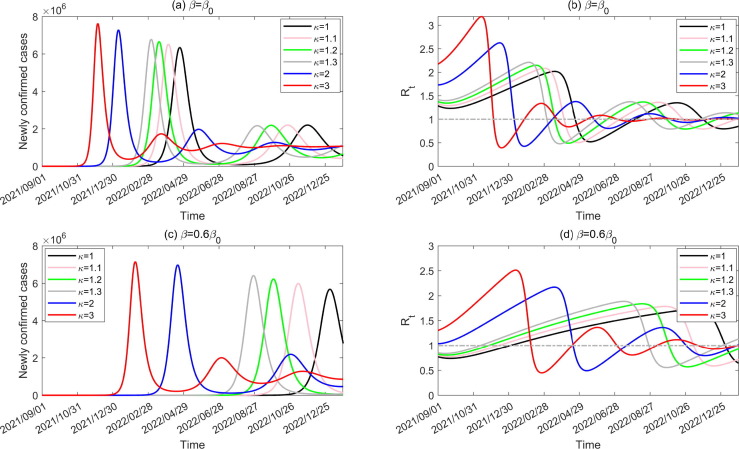
Assuming that 10 infected cases are introduced into the community on 1 September 2021, Fig. 2 shows the number of newly confirmed cases and the effective reproduction number $R_t$ during the transmission process, with different transmission rate and various ADE degree. It follows from Fig. 2, Fig. 2(c) that, even without ADE ($\kappa =1$), introducing infected cases would cause large outbreaks (black curves) as immunity wanes. Worse still, ADE would facilitate the outbreak by bringing the peak time forward and increasing the peak value. Higher ADE results in an earlier peak time and larger peak value. Normalized intervention ($\beta =0.6{\beta }_0$) can help delay the outbreak and reduce the peak value. We observed that there are several subsequent epidemic waves with decreasing peak values. Furthermore, ADE and a higher transmissibility can increase the outbreak frequency. Correspondingly, the effective reproduction number fluctuates around the threshold of unit, as shown in Fig. 2, Fig. 2(d).

Fig. 2.

Impact of ADE and normalized interventions on the number of newly confirmed cases and effective reproduction number during the transmission period when 10 infected cases are introduced on 1 September 2021.

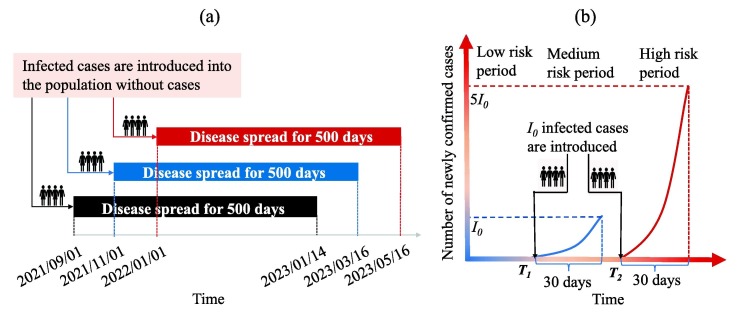
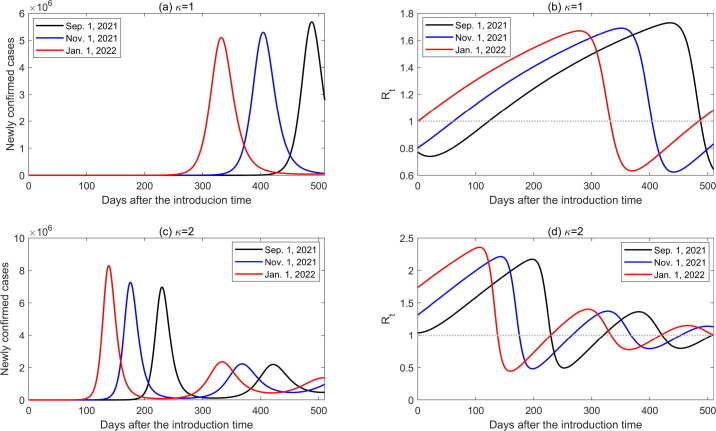
In Fig. 2, the infected cases are assumed to be introduced on 1 September 2021, then the impact of the time when infected cases are introduced (which we call introduction time) on the transmission dynamics of COVID-19 in China, was explored in the following. Assuming that 10 infected cases are introduced into the community on 1 September 2021, 1 November 2021 and 1 January 2022, respectively, the transmission dynamics of COVID-19 were simulated during the following 500 days (Fig. 3 (a)). The time-varying number of newly confirmed cases and the effective reproduction number $R_t$ with a normalized control intervention ($\beta =0.6{\beta }_0$) are shown in Fig. 4 by setting the introduction time as the initial transmission time. From Fig. 4, Fig. 4(c), we can see that later introduction time correlates a shorter time that the outbreak takes to the peak. This is because the reproduction number at the initial stage for the introduction time of 1 January 2022 is higher than those for the introduction time of 1 November and 1 Sep September 2021, as shown in Fig. 4, Fig. 4(d). We observed an interesting phenomenon: when $\kappa =1$, an earlier introduction time causes larger outbreak, whereas when $\kappa =2$, a later introduction time causes a larger outbreak. This means that the peak value of the outbreak is non-monotonous as regards the introduction time, and is dependent on the ADE effect. Without ADE ($\kappa =1$), a higher transmission risk (greater effective reproduction number initially) leads to a smaller outbreak (Fig. 4, Fig. 4(b)). However, with ADE ($\kappa =2$), the expedited growth rate of infection (enlarged effective reproduction number initially) facilitates the immunity level obtained by infection in the population, which wanes and produces susceptible population with higher susceptibility with ADE. Consequently, a higher peak value was observed (Fig. 4, Fig. 4(d)). Therefore, the introduction time significantly impacts the transmission dynamics of COVID-19 with immunity waning and ADE.

Fig. 3.

Schematic diagram illustrating (a) the different introduction times and the simulation period, (b) the critical introduction time $T_1$ and $T_2$ separating the low-risk, medium-risk, and high-risk periods.

Fig. 4.

Impact of the ADE and different introduction time on the number of newly confirmed cases and the effective reproduction number by setting the introduction time as the initial transmission time. Introduction times are assumed to be 1 September 2021, 1 November 2021, and 1 January 2022, respectively.

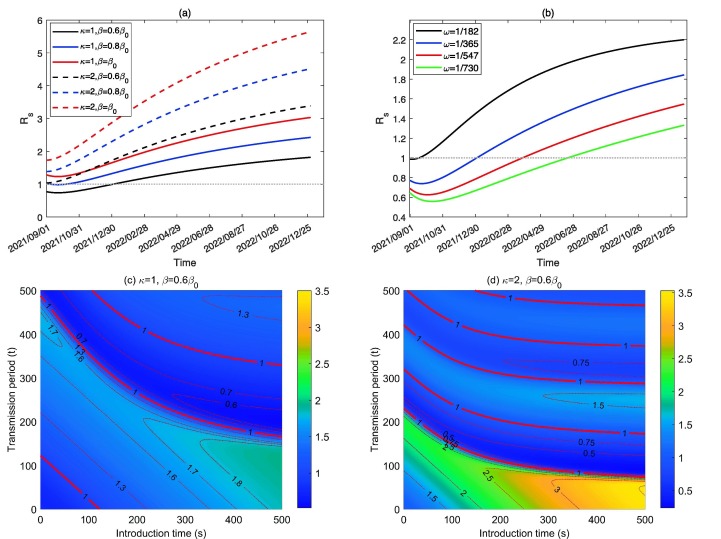
The above analysis reveals that the initial value of the effective reproduction number is greatly dependent on the introduction time, which is time-dependent due to waning immunity. Thus we defined a new reproduction number, called the invasion reproduction number, denoted by $R_s=R(s)$, to represent the invasion risk and initial transmission risk of COVID-19 in the population when infected cases are introduced into the population at time s. In Fig. 5, Fig. 5 (b), we plotted curves of $R_s$ by choosing different transmission rate $\beta$, ADE factor $\kappa$ and immunity waning rate $\omega$, from which we can see that $R_s$ is increasing over time due to waning immunity. In addition, with a higher transmission rate $\beta$ or ADE degree $\kappa$ or immunity waning rate $\omega$, the invasion reproduction number $R_s$ is always greater, indicating a higher transmission risk. The PRCCs of $R_s$ with respect to other parameters also verified this, as shown in the S4 part in SI.

Fig. 5.

(a)-(b) Effect of $\beta ,\kappa$, and $\omega$ on $R_s$, respectively. (c)-(d) Values of $R(t,s)$ with different introduction time s (taking 1 September 2021 as the initial time) and transmission period t (taking the introduction time as initial time of the transmission process).

Two time-varying reproduction numbers $R_t$ and $R_s$ have been defined. Here we defined the effective-invasion reproduction number by combining the two time-varying reproduction numbers together, denoted by $R(t,s)$, where s is the introduction time and t is the transmission period since the infected cases are introduced. It is evident that $R_s=R(0,s)$, which is the invasion reproduction number at the introduction time s, and $R_t=R(t,0)$ is the effective reproduction number at time t by taking the introduction time as the initial transmission time. With this definition, we can easily check the effective reproduction number of an epidemic that starts at different times. Particularly, Fig. 5(c) and Fig. 5(d) showed the contour plots of $R(t,s)$ with respect to varying introduction time s (taking 1 September 2021 as the initial time) and the transmission period t (taking the introduction time as the initial transmission time), with the baseline transmission rate $\beta =0.6{\beta }_0$ and ADE factor $\kappa =1$ and $\kappa =2$, respectively. The solid red curves show where $R(t,s)=1$ and the dashed red curves represent the corresponding values of $R(t,s)$ listed on the curves. The results revealed that $R(0,s)$ increases as s increases, $R(t,s)$ increases first and then fluctuates around the unit with respect to t given an arbitrary introduction time s. Furthermore, ADE ($\kappa =2$) magnifies $R(0,s)$ and makes $R(t,s)$ fluctuate more frequently and tends to stabilise. These results verified the observations in Fig. 2, Fig. 4.

3.3. Protective period evaluation and analysis

Usually, the effective reproduction number (the effective-invasion reproduction number in this study) is the only risk index revealing whether the epidemic is under control. New infections will decrease when the effective reproduction number is less than the unit. However, as illustrated in [39], the effective reproduction number less than 1 does not mean that the epidemic is totally under control or the goal of zero-COVID is achieved. Actually, it may take a long time to achieve the zero-COVID target. During this period, due to the source of infection, the COVID-19 epidemic can be easily boosted once normalized control interventions are released. Similarly, it is not reasonable to say that the disease is out of control when the effective reproduction number is greater than the unit. When several infected cases are introduced into the community, the newly confirmed cases may increase slowly, reserving enough time to carry out control measures and maintaining at a low resurgence risk. Therefore, we provide a new definition to indicate when an emerging outbreak of COVID-19 can be under control or maintained at a low level of risk.

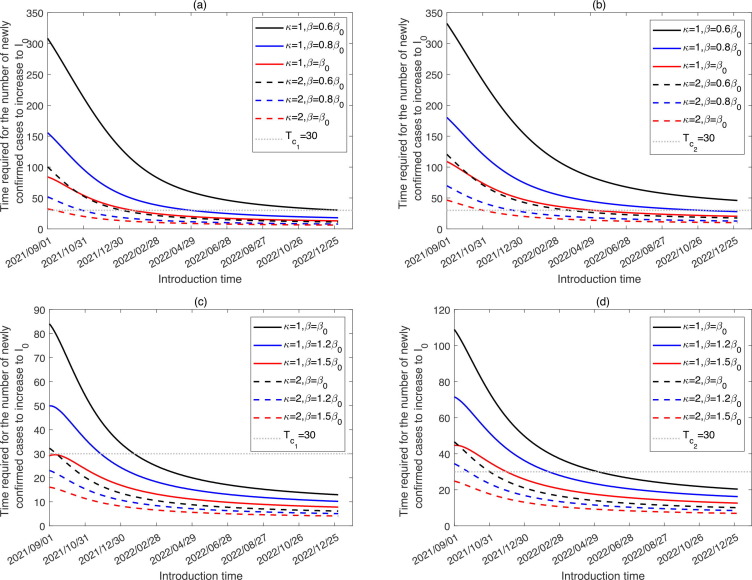
For any given number of infected cases $I_0$ introduced at time s, we have theoretically illustrated that the time required for the number of newly confirmed cases to increase to ${\mathit{kI}}_0$ ($k⩾1$ is constant) for the first time is independent of the value of $I_0$ in the S6 part in SI. Fig. 4 has told us that the later introduction time leads to faster outbreak. Based on these two information, we can define two critical introduction times $T_1$ and $T_2$ (see a graphical illustration in Fig. 3(b)). $T_1$ ($T_2$) is the time when $I_0$ infected cases are introduced into the community and the number of newly confirmed cases reaches $I_0$ (5$I_0$) for the first time on the 30th day. It’s obvious that $T_1$ and $T_2$ are independent of the value of $I_0$ and $T_2$ is certainly greater than $T_1$, Then the low-risk period is defined as the time before $T_1$, during which once the $I_0$ infected cases are introduced, the number of newly confirmed cases would always be lower than $I_0$ in the following 30 days; the medium-risk period is defined as the time interval between $T_1$ and $T_2$, during which once the $I_0$ infected cases are introduced, the number of newly confirmed cases would exceed $I_0$ but maintain lower than $5I_0$ in the following 30 days; the high-risk period is defined as the time after $T_2$, during which once the $I_0$ infected cases are introduced, the number of newly confirmed cases would exceed $5I_0$ in 30 day.

In Fig. 6 , we plotted the period required for the number of newly confirmed cases to reach $I_0$ or $5I_0$ from the introduction time. The intersection points of the curves and horizontal dash line represent the critical times $T_1$ or $T_2$. It follows from Fig. 6, Fig. 6(b) that later introduction time correlates with shorter time required for the number of newly confirmed cases to increase to $I_0$ or $5I_0$. Comparing the dash or solid curves with different colors, we observed that the increases in the transmission rate and ADE degree would bring forward the critical times $T_1$ and $T_2$, consequently shortening the low-risk period, and bringing forward the high-risk period. In the baseline situation ($\kappa =1,\beta =0.6{\beta }_0$), introducing infected cases before the end of 2022 would not quickly lead to a large outbreak (at a low-risk level). In this situation, the emerging outbreak is at low risk till 8 January 2023. With ADE ($\kappa =2$), the medium-risk period is over 1 year in advance, starting from 4 January 2022. When the transmission rate increases to $0.8{\beta }_0$ or ${\beta }_0$, corresponding to the release of normalized control interventions, the emerging outbreak is at low risk before 28 April 2022 or 22 January 2022, respectively. Furthermore, considering the higher transmissibility of the SARS-CoV-2 variants, we plotted the time required for the newly confirmed cases to reach $I_0$ or $5I_0$ from the introduction time in Fig. 6(c) and (d), using the transmission rate of $1.2{\beta }_0$ and $1.5{\beta }_0$. As illustrated in Fig. 6(c), when $\kappa =2,\beta =1.2{\beta }_0$ or $\kappa =2,\beta =1.5{\beta }_0$, the curves are always below the horizontal line from 1 September 2021. This means that the emerging outbreak of SARS-CoV-2 variants would be of medium-risk or high-risk since 1 September 2021 (Fig. 6(d)) with ADE and higher transmissible variant. Table 1 lists the critical times $T_1$ and $T_2$ under different situations with different combination of the transmission rate and ADE degree.

Fig. 6.

Time required for the newly confirmed cases to increase to $I_0$ and $5I_0$, respectively, when introducing infected cases at different times for different $\beta$ and $\kappa$.

Table 1.

The impact of the transmission rate and ADE factor on the low-risk, medium-risk and high-risk period.

Parameters	Low risk period	Medium risk period	High risk period
$\kappa =1,\beta =0.6{\beta }_0$	before 2023/01/08	-	-
$\kappa =1,\beta =0.8{\beta }_0$	before 2022/04/28	2022/04/28–2022/11/01	after 2022/11/01
$\kappa =1,\beta ={\beta }_0$	before 2022/01/22	2022/01/22–2022/05/05	after 2022/05/05
$\kappa =1,\beta =1.2{\beta }_0$	before 2021/11/26	2021/11/26–2022/02/10	after 2022/02/10
$\kappa =1,\beta =1.5{\beta }_0$	-	before 2021/11/29	after 2021/11/29
$\kappa =1.1,\beta =0.6{\beta }_0$	before 2022/09/30	after 2022/09/30	-
$\kappa =1.1,\beta =0.8{\beta }_0$	before 2022/03/21	2022/03/21–2022/08/13	after 2022/08/13
$\kappa =1.1,\beta ={\beta }_0$	before 2021/12/29	2021/12/29–2022/03/27	after 2022/03/27
$\kappa =1.1,\beta =1.2{\beta }_0$	before 2021/11/08	2021/11/08–2022/01/15	after 2022/01/15
$\kappa =1.1,\beta =1.5{\beta }_0$	-	before 2021/11/10	after 2021/11/10
$\kappa =1.2,\beta =0.6{\beta }_0$	before 2022/07/25	after 2022/07/25	-
$\kappa =1.2,\beta =0.8{\beta }_0$	before 2022/02/19	2022/02/19–2022/06/18	after 2022/06/18
$\kappa =1.2,\beta ={\beta }_0$	before 2021/12/10	2021/12/10–2022/02/24	after 2022/02/24
$\kappa =1.2,\beta =1.2{\beta }_0$	before 2021/10/24	2021/10/24–2021/12/25	after 2021/12/25
$\kappa =1.2,\beta =1.5{\beta }_0$	-	before 2021/10/27	after 2021/10/27
$\kappa =1.3,\beta =0.6{\beta }_0$	before 2022/06/07	after 2022/06/07	-
$\kappa =1.3,\beta =0.8{\beta }_0$	before 2022/01/27	2022/01/27–2022/05/07	after 2022/05/
$\kappa =1.3,\beta ={\beta }_0$	before 2021/11/24	2021/11/24–2022/01/31	after 2022/01/31
$\kappa =1.3,\beta =1.2{\beta }_0$	before 2021/10/10	2021/10/10–2021/12/07	after 2021/12/07
$\kappa =1.3,\beta =1.5{\beta }_0$	-	before 2021/10/13	after 2021/10/13
$\kappa =2,\beta =0.6{\beta }_0$	before 2022/01/04	2022/01/04–2022/03/25	after 2022/03/25
$\kappa =2,\beta =0.8{\beta }_0$	before 2021/10/30	2021/10/31–2021/12/21	after 2021/12/21
$\kappa =2,\beta ={\beta }_0$	before 2021/09/13	2021/09/13–2021/11/01	after 2021/11/01
$\kappa =2,\beta =1.2{\beta }_0$	-	before 2021/09/24	after 2021/09/24
$\kappa =2,\beta =1.5{\beta }_0$	-	-	after 2021/09/01

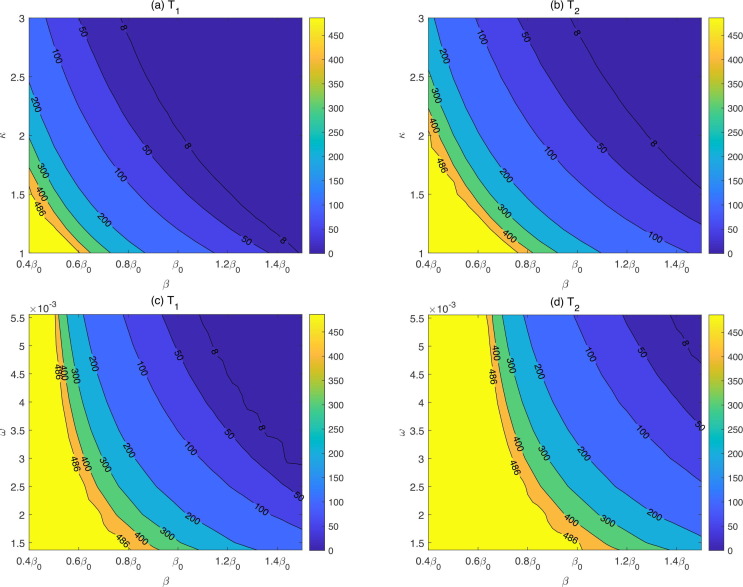
In addition, we represented the contour plots of $T_1$ and $T_2$, respectively, by regarding 1 September 2021 as the initial time in Fig. 7 , with respect to the transmission rate $\beta$ and ADE factor $\kappa$ (Fig. 7(a) and (b)), and the transmission rate $\beta$ and immunity waning rate $\omega$ (Fig. 7(c) and (d)). From Fig. 7 (a) and (b) we can see that $T_1$ and $T_2$ decrease with an increase in $\beta$ and $\kappa$, meaning that the low-risk period is shortened and the high-risk period is brought forward, verifying the results in Fig. 6. The results showed that for variants with higher transmissibility and stronger ADE degree, it is challenging to maintain the emerging outbreak at low risk given infected cases are introduced. However, with strict normalized control interventions (low transmission rate, e.g. $\beta =0.4{\beta }_0$), even if ADE is slightly feasible ($\kappa$ varies from 1 to 1.5), the emerging outbreak of introducing infected cases would be maintained at low risk until 31 December 2022. Increased immunity waning rate $\omega$ also leads to a decrease in $T_1$ and $T_2$ (Fig. 7 (c) and (d)), indicating the immunity waning would also shorten the low-risk period and bring forward the high-risk period. When the transmission rate increases to $0.8{\beta }_0$, a reduced immunity waning rate $\omega =1/180$, can ensure the emerging outbreak at a low risk level if infected cases are introduced by the end of 2022. However, when the transmission rate is sufficiently small, corresponding to the strict normalized control strategies, the emerging outbreak of introducing infected cases is maintained at low risk until 31 December 2022, regardless of the waning rate. Both contour plots illustrated that strengthening normalized control interventions protects the community from the rapid outbreak induced by imported infected cases efficiently.

Fig. 7.

Contour plots of $T_1$ and $T_2$ with respect to $\beta$ and $\kappa ,\beta$ and $\omega$, by taking 1 September 2021 as the initial time.

4. Discussion

This study discusses the COVID-19 resurgence risk in China, where local outbreaks were mainly caused by imported cases due to the strict dynamic zero-COVID policy, and herd immunity is supposed to be provided solely by COVID-19 vaccines without a significant contribution of natural infection. Evidence has shown that COVID-19 vaccines are effective on mitigating the COVID-19 spread to a certain extent [40]. However, waning immunity, ADE and the emergence of novel variants with higher transmissibility render herd immunity untenable. Imported infections may cause large outbreak. Therefore, it is critical to evaluate how long the current vaccination program can protect China at a low resurgence risk with the waning immunity, ADE and novel variants. This can provide an important decision-making basis for determining when a follow-up vaccination program should be launched.

In this study, we developed a new mathematical model describing the transmission dynamics of COVID-19 and the vaccination dynamics in China by incorporating immunity waning mechanisms and ADE effects. The proposed model was calibrated using the COVID-19 epidemic data in mainland China between 23 January and 8 April 2020 and the vaccination data from 15 December 2020 to 29 June 2021. The estimation revealed that the cumulative population with at least one dose reached 56.4% and the population with two doses reached 32.02% on 29 June 2021 (the last data collection date). A prediction indicated that vaccination coverage with at least one dose would reach 95.87%, and the proportion with two doses would reach 77.92% on 31 August 2021, which means that vaccination coverage is supposed to has reached at a high level in China up to 31 August 2021 (the vaccination stopping time we considered).

We initially assessed whether mainland China could return to the pre-COVID-19 pandemic era counting on only the mass vaccination program. We assessed if the emerging epidemics, can be controlled without other NPIs (i.e. $\beta$ is set to be ${\beta }_0$) by introducing several new cases into communities and observed that the solution is not with waning immunity. We found that the daily confirmed cases could grow exponentially in a short period after infected cases being introduced, and peak at a large number. This is directly due to waning immunity, and a large proportion of vaccinated individuals becoming susceptible again. We can intuitively see the reason from the invasion reproduction number $R_s$, which increases and exceeds the threshold of unit over time due to the immunity waning dynamic in the population. This is also why the introduction time of infected cases greatly influences the transmission dynamics of the COVID-19 (Fig. 4). Generally, the later introduction time correlates with shorter period required for the newly confirmed cases to peak. This indicates that implementation of interventions is more urgent when infected cases are imported later. One interesting phenomenon we observed is that the peak value of the outbreak is non-monotonous with respect to the introduction time, which is dependent on the ADE effect.

Occurrence of intermittent outbreaks of COVID-19 is observed in Fig. 2, Fig. 4, which is mainly attributed to waning immunity. Initially, waning immunity leads to a breakthrough in herd immunity, consequently, introducing new infected cases results in a large outbreak. In return, the outbreak can further boost herd immunity in the population level and drive the decline of the effective reproduction number, subsequently driving the decline of the epidemics. In conclusion, a loop of immunity waning and boosting in the population induced an intermittent epidemic. Furthermore, it should be mentioned that the amplitudes of the subsequent outbreaks decrease over time. This implies that a large proportion of the population will be effectively protected after several outbreaks. The result implies that boosting immunity by a booster injection of the vaccine in the population may help mitigate possible outbreaks. The optimized boosting program needs to be studied further.

Despite the effective reproduction number, we attempted to find a new index to represent whether the emerging epidemic is under control from another perspective. Thus the low-risk, medium-risk and high-risk periods were proposed along with the definition of the two critical introduction times $T_1$ and $T_2$. With our definition, it is of low risk to introduce infected cases before 22 January 2022 with the baseline transmission rate ${\beta }_0$, whereas introducing infected cases after 22 January 2022 would be of medium or high risk. This means that the vaccination program only could protect China at a low resurgence risk for a very short time. However, if the transmission rate is decreased to $0.6{\beta }_0$, which can be reached with 50% of the population maintaining normalized control interventions by wearing masks, the low-risk period can be prolonged to 8 January 2023. Thus normalized control interventions should not be discarded.

ADE occurs in individuals whose immunity has waned after obtaining the immunity through natural infection or vaccination. This is considered as a major challenge in developing and using COVID-19 vaccines. We also quantitatively evaluated the impact of ADE on the transmission dynamic of COVID-19 with the implementation of the mass vaccination program. The intuitive results are that ADE can bring forward the peak time of an outbreak and greatly increase the peak number of newly confirmed cases. Higher ADE results in an earlier peak time and larger peak value (Fig. 2). ADE can increase the frequency of intermittent outbreaks. Furthermore, as listed in Table 1, ADE would shorten the low-risk period for over 1 year (bring forward the critical time $T_1$ from 8 January 2023 to 4 January 2022) even with a normalized control intervention. Results similar to those of ADE were obtained by considering the higher transmissibility of SARS-CoV-2 variants. These results indicate that ADE and the emergence of new variants with higher transmissibility have made the controlling of the COVID-19 epidemics more challenging.

We have to emphasis that due to the lacking of the real value of ADE, we chose a range of [1], [3] following the studies on the ADE in dengue infections [17], [18], [19], [37], [38]. We used the enhancement value $\kappa =1$ and $\kappa =2$ to assess the impact of other factors in absence and presence of ADE (Fig. 4, Fig. 5, Fig. 6). However, the enhancement value might be much higher or lower, which would have a considerable impact on the outcomes. Actually, we have also explored the impact of different ADE degrees by considering the lower set ($\kappa =1.1,1.2,1.3$) in Fig. 2 and Table 1, and conducted the sensitivity analysis of $\kappa$ ranging from 1 to 3 in Fig. 7(a)(b). Another point we should note is that we didn’t consider the emergence of SARS-CoV-2 variants during the epidemic outbreak. Whether the phenomenon that the amplitudes of the subsequent outbreaks decrease over time (Fig. 2) is inevitably the case in reality depends on the particular pattern of effects in new variant. A novel variant with higher transmissibility may induce a higher subsequent wave. It’s worth mentioning that though we are focusing the resurgence risk in China, the synthesis framework could be extended to other countries that have not sought complete control.

5. Conclusion

This study focused on investigating the resurgence risk of COVID-19 after the mass vaccination program in China in the presence of waning immunity, ADE and novel variants by utilizing a mathematical model. The vaccination coverage is projected to be very high on 31 August 2021, almost reaching the requested critical level of herd immunity. However, herd immunity can easily be broken through immunity waning. Therefore, we suggest maintaining a normalized control intervention of wearing masks in the long-term, even with mass vaccination programs. By defining the risk level of an emerging outbreak, the results revealed that the current vaccination program incorporating normalized control interventions can protect China at a low level of resurgence risk until 8 January 2023. However, emerging evidence of ADE and SARS-CoV-2 variants with higher transmissibility have worsen this situation. Therefore, we should prepare for a long struggle with COVID-19 and not rely entirely on COVID-19 vaccines.

It’s worth mentioning that boosting immunity in the population may mitigate emerging outbreaks. Maintaining normalized NPIs and periodic booster injection of vaccines could help combat COVID-19 in the long-term. Optimising the periodic vaccination program incorporating NPIs implementation is significant, and falls within the scope of our future studies.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Supplementary material

The following are the Supplementary data to this article: