Significance
An increasingly high-impact application of machine learning in scientific discovery is its use in the design of novel objects with desired properties, such as the design of proteins, small molecules, and materials. Although a variety of algorithms have been developed for this purpose, it remains unclear when practitioners can trust the predictions made by learned models for designed objects, since design algorithms induce a distinctive shift between the training and test data distributions. We propose a method that provides confidence sets for designed objects, which we show satisfy finite-sample guarantees of statistical validity, for any design algorithm involving any learned regression model. Our work enables more trustworthy use of machine learning for design.
Keywords: uncertainty quantification, protein engineering, conformal prediction, machine learning
Abstract
Many applications of machine-learning methods involve an iterative protocol in which data are collected, a model is trained, and then outputs of that model are used to choose what data to consider next. For example, a data-driven approach for designing proteins is to train a regression model to predict the fitness of protein sequences and then use it to propose new sequences believed to exhibit greater fitness than observed in the training data. Since validating designed sequences in the wet laboratory is typically costly, it is important to quantify the uncertainty in the model’s predictions. This is challenging because of a characteristic type of distribution shift between the training and test data that arises in the design setting—one in which the training and test data are statistically dependent, as the latter is chosen based on the former. Consequently, the model’s error on the test data—that is, the designed sequences—has an unknown and possibly complex relationship with its error on the training data. We introduce a method to construct confidence sets for predictions in such settings, which account for the dependence between the training and test data. The confidence sets we construct have finite-sample guarantees that hold for any regression model, even when it is used to choose the test-time input distribution. As a motivating use case, we use real datasets to demonstrate how our method quantifies uncertainty for the predicted fitness of designed proteins and can therefore be used to select design algorithms that achieve acceptable tradeoffs between high predicted fitness and low predictive uncertainty.
1. Uncertainty Quantification under Feedback Loops
Consider a protein engineer who is interested in designing a protein with high fitness—some real-valued measure of its desirability, such as fluorescence or therapeutic efficacy. The engineer has a dataset of various protein sequences, denoted Xi, labeled with experimental measurements of their fitnesses, denoted Yi, for . The design problem is to propose a novel sequence, , that has higher fitness, , than any of these. To this end, the engineer trains a regression model on the dataset and then identifies a novel sequence that the model predicts to be more fit than the training sequences. Can the engineer trust the model’s prediction for the designed sequence?
This is an important question to answer, not just for the protein design problem just described, but for any deployment of machine learning where the test data depend on the training data. More broadly, settings ranging from Bayesian optimization to active learning to strategic classification involve feedback loops in which the learned model and data influence each other in turn. As feedback loops violate the standard assumptions of machine-learning algorithms, we must be able to diagnose when a model’s predictions can and cannot be trusted in their presence.
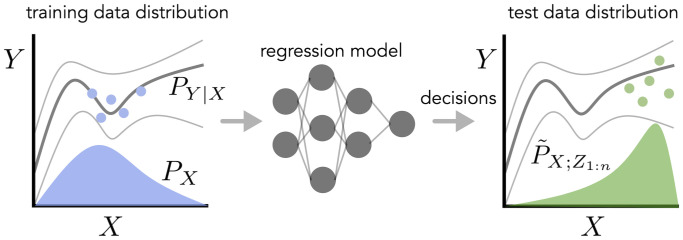
In this work, we address the problem of uncertainty quantification when the training and test data exhibit a type of dependence that we call feedback covariate shift (FCS). A joint distribution of training and test data falls under FCS if it satisfies two conditions (Fig. 1). First, the test input, , is selected based on independently and identically distributed (i.i.d.) training data, . That is, the distribution of is a function of the training data. Second, , the ground-truth distribution of the label, Y, given any input, X, does not change between the training and test data distributions. For example, returning to the example of protein design, the training data are used to select the designed protein, ; the distribution of is determined by some optimization algorithm that calls the regression model to design the protein. However, since the fitness of any given sequence is some property dictated by nature, stays fixed. Representative examples of FCS are algorithms that use predictive models to choose the test input distribution, such as in:
Fig. 1.
Illustration of feedback covariate shift. In Left graph, the blue distribution represents the training input distribution, PX. The dark gray line sandwiched by lighter gray lines represents the mean ± the SD of , the conditional distribution of the label given the input, which does not change between the training and test data distributions (Left and Right graphs, respectively). The blue dots represent training data, where , which is used to fit a regression model (Center). Algorithms that use that trained model to make decisions, such as in design problems, active learning, and Bayesian optimization, give rise to a new test–time input distribution, (Right graph, green distribution). The green dots represent test data.
-
•
The design of proteins, small molecules, and materials with favorable properties.
-
•
Active learning, adaptive experimental design, Bayesian optimization, and machine-learning-guided scientific discovery.
We anchor our discussion and experiments by focusing on protein design problems. However, the methods and insights developed herein are applicable to a variety of FCS problems.
A. Quantifying Uncertainty with Valid Confidence Sets.
Given a regression model of interest, μ, we quantify its uncertainty on an input with a confidence set. A confidence set is a function, , that maps a point from some input space, , to a set of real values that the model considers to be plausible labels.* Informally, we examine the model’s error on the training data to quantify its uncertainty about the label, , of an input, . Formally, using the notation and , our goal is to construct confidence sets that have the frequentist statistical property known as coverage.
Definition 1
Consider data points from some joint distribution, . Given a miscoverage level, , a confidence set, , which may depend on , provides coverage under if
[1] where the probability is over all data points, .
There are three important aspects of this definition. First, coverage is with respect to a particular joint distribution of the training and test data, , as the probability statement in Eq. 1 is over random draws of all n + 1 data points. That is, if one draws and constructs the confidence set for based on a regression model fit to , then the confidence set contains the true test label, , a fraction of of the time. In this work, can be any distribution captured by FCS, as we describe later in more detail.
Second, note that Eq. 1 is a finite-sample statement: It holds for any number of training data points, n. Finally, coverage is a marginal probability statement, which averages over all the randomness in the training and test data; it is not a statement about conditional probabilities, such as . We will call a family of confidence sets, , indexed by the miscoverage level, , valid if they provide coverage for all .
When the training and test data are exchangeable (e.g., independently and identically distributed), conformal prediction is an approach for constructing valid confidence sets for any regression model (1–3). Although recent work has extended the methodology to certain forms of distribution shift (4–8), to our knowledge no existing approach can produce valid confidence sets when the test data depend on the training data. Here, we generalize conformal prediction to the FCS setting, enabling uncertainty quantification under this prevalent type of dependence between training and test data.
B. Our Contributions.
First, we formalize the concept of feedback covariate shift, which describes a type of distribution shift that emerges under feedback loops between learned models and the data they operate on. Second, we introduce a generalization of conformal prediction that produces valid confidence sets under feedback covariate shift for any regression model. We also introduce randomized versions of these confidence sets that achieve a stronger property called exact coverage. Finally, we demonstrate the use of our method to quantify uncertainty for the predicted fitness of designed proteins, using several real datasets.
We recommend using our method for design algorithm selection, as it enables practitioners to identify settings of algorithm hyperparameters that achieve acceptable tradeoffs between high predictions and low predictive uncertainty.
C. Prior Work.
Our study investigates uncertainty quantification in a setting that brings together the well-studied concept of covariate shift (9–12) with feedback between learned models and data distributions, a widespread phenomenon in real-world deployments of machine learning (13, 14). Indeed, beyond the design problem, feedback covariate shift is one way of describing and generalizing the dependence between data at successive iterations of active learning, adaptive experimental design, and Bayesian optimization.
Our work builds upon conformal prediction, a framework for constructing confidence sets that satisfy the finite-sample coverage property in Eq. 1 for arbitrary model classes (2, 15, 16). Although originally based on the premise of exchangeable (e.g., independently and identically distributed) training and test data, the framework has since been generalized to handle various forms of distribution shift, including covariate shift (4, 7), label shift (8), arbitrary distribution shifts in an online setting (6), and test distributions that are nearby the training distribution (5). Conformal approaches have also been used to detect distribution shift (17–23).
We call particular attention to the work of Tibshirani et al. (4) on conformal prediction in the context of covariate shift, whose technical machinery we adapt to generalize conformal prediction to feedback covariate shift. In covariate shift, the training and test input distributions differ, but, critically, the training and test data are still independent; we henceforth refer to this setting as standard covariate shift. The chief innovation of our work is to formalize and address a ubiquitous type of dependence between training and test data that is absent from standard covariate shift and, to the best of our knowledge, absent from any other form of distribution shift to which conformal approaches have been generalized.
For the design problem, in which a regression model is used to propose new inputs—such as a protein with desired properties—it is important to consider the predictive uncertainty of the designed inputs, so that we do not enter “pathological” regions of the input space where the model’s predictions are desirable but untrustworthy (24, 25). Gaussian process regression (GPR) models are popular tools for addressing this issue, and algorithms that leverage their posterior predictive variance (26, 27) have been used to design enzymes with enhanced thermostability and catalytic activity (28, 29). Despite these successes, it is not clear how to obtain practically meaningful theoretical guarantees for the posterior predictive variance and consequently to understand in what sense we can trust it. Similarly, ensembling strategies such as in ref. 30, which are increasingly being used to quantify uncertainty for deep neural networks (24, 25, 31, 32), as well as uncertainty estimates that are explicitly learned by deep models (33) do not come with formal guarantees. A major advantage of conformal prediction is that it can be applied to any modeling strategy and can be used to calibrate any existing uncertainty quantification approach, including those aforementioned.
2. Conformal Prediction under Feedback Covariate Shift
A. Feedback Covariate Shift.
We begin by formalizing FCS, which describes a setting in which the test data depend on the training data, but the relationship between inputs and labels remains fixed.
We first set up our notation. Recall that we let , denote n i.i.d. training data points comprising inputs, , and labels, . Similarly, let denote the test data point. We use to denote the multiset of the training data, in which values are unordered but multiple instances of the same value appear according to their multiplicity. We also use the shorthand , which is a multiset of values that we refer to as the ith leave-one-out training dataset.
FCS describes a class of joint distributions over that have the dependency structure described informally in Section 1. Formally, we say that training and test data exhibit FCS when they can be generated according to the following three steps:
-
1)The training data, , are drawn i.i.d. from some distribution
-
2)
The realized training data induce a new input distribution over , denoted to emphasize its dependence on the training data, .
-
3)The test input is drawn from this new input distribution, and its label is drawn from the unchanged conditional distribution
The key object in this formulation is the test input distribution, . Prior to collecting the training data, , the specific test input distribution is not yet known. The observed training data induce a distribution of test inputs, , that the model encounters at test time (for example, through any of the mechanisms summarized in Section 1).
This is an expressive framework: The object can be an arbitrarily complicated mapping from a dataset of size n to an input distribution, as long as it is invariant to the order of the data points. There are no other constraints on this mapping; it need not exhibit any notion of smoothness, for example. In particular, FCS encapsulates any design algorithm that makes use of a regression model fitted to the training data, , to propose designed inputs.
B. Conformal Prediction for Exchangeable Data.
To explain how to construct valid confidence sets under FCS, we first walk through the intuition behind conformal prediction in the setting of exchangeable data and then present the adaptation to accommodate FCS.
Score function.
First, we introduce the notion of a score function, , which is an engineering choice that quantifies how well a given data point “conforms” to a multiset of m data points, in the sense of evaluating whether the data point comes from the same conditional distribution, , as the data points in the multiset.† A representative example is the residual score function, , where D is a multiset of m data points and μD is a regression model trained on D. A large residual signifies a data point that the model cannot easily predict, which suggests it does not obey the input-label relationship present in the training data.
More generally, we can choose the score to be any notion of uncertainty of a trained model on the point (X, Y), heuristic or otherwise, such as the posterior predictive variance of a Gaussian process regression model (28, 29), the variance of the predictions from an ensemble of neural networks (16, 30–32), uncertainty estimates learned by deep models (34), or even the outputs of other calibration procedures (35). Regardless of the choice of the score function, conformal prediction produces valid confidence sets; however, the particular choice of score function will determine the size, and therefore informativeness, of the resulting sets. Roughly speaking, a score function that better reflects the likelihood of observing the given point, (X, Y), under the true conditional distribution that governs D, , results in smaller valid confidence sets.
Imitating exchangeable scores.
At a high level, conformal prediction is based on the observation that when the training and test data are exchangeable, their scores are also exchangeable. More concretely, assume we use the residual score function, , for some regression model class. Now imagine that we know the label, , for the test input, . For each of the n + 1 training and test data points, , we can compute the score using a regression model trained on the remaining n data points; the resulting n + 1 scores are exchangeable.
In reality, of course, we do not know the true label of the test input. However, this key property—that the scores of exchangeable data yield exchangeable scores—enables us to construct valid confidence sets by including all “candidate” values of the test label, , that yield scores for the n + 1 data points (the training data points along with the candidate test data point, ) that appear to be exchangeable. For a given candidate label, the conformal approach assesses whether or not this is true by comparing the score of the candidate test data point to an appropriately chosen quantile of the training data scores.
C. Conformal Prediction under FCS.
When the training and test data are under FCS, their scores are no longer exchangeable, since the training and test inputs are neither independent nor from the same distribution. Our solution to this problem is to weight each training and test data point to take into account these two factors. Thereafter, we can proceed with the conformal approach of including all candidate labels such that the (weighted) candidate test data point is sufficiently similar to the (weighted) training data points. Toward this end, we introduce two quantities: 1) a likelihood-ratio function, which will be used to define the weights, and 2) the quantile of a distribution, which will be used to assess whether a candidate test data point conforms to the training data.
The likelihood-ratio function, which depends on a multiset of data points, D, is given by
| [2] |
where and pX denote the densities of the test and training input distributions, respectively, and the test input distribution is the particular one indexed by the dataset, D.
This quantity is the ratio of the likelihoods under these two distributions and, as such, is reminiscent of weights used to modify various statistical procedures to accommodate standard covariate shift (4, 10, 11). What distinguishes its use here is that our particular likelihood ratio is indexed by a multiset and depends on which data point is being evaluated as well as the candidate label, as will become clear shortly.
Consider a discrete distribution with probability masses located at support points , respectively, where and . We define the β-quantile of this distribution as
where is a unit point mass at si.
We now define the confidence set. For any score function, S; any miscoverage level, ; and any test input, , define the full conformal confidence set as
| [3] |
where
which are the scores for each of the training and candidate test data points, when compared to the remaining n data points, and the weights for these scores are given by
| [4] |
which are normalized such that .
In words, the confidence set in Eq. 3 includes all real values, , such that the candidate test data point, , has a score that is sufficiently similar to the scores of the training data. Specifically, the score of the candidate test data point needs to be smaller than the -quantile of the weighted scores of all n + 1 data points (the n training data points as well as the candidate test data point), where the ith data point is weighted by .
Our main result is that this confidence set provides coverage under FCS (see SI Appendix, section S1.A for the proof).
Theorem 1.
Suppose data are generated under feedback covariate shift and assume is absolutely continuous with respect to PX for all possible values of D. Then, for any miscoverage level, , the full conformal confidence set, , in Eq. 3 satisfies the coverage property in Eq. 1; namely, .
Since we can supply any domain-specific notion of uncertainty as the score function, this result implies we can interpret the condition in Eq. 3 as a calibration of the provided score function that guarantees coverage. That is, our conformal approach can complement any existing uncertainty quantification method by endowing it with coverage under FCS.
We note that although Theorem 1 provides a lower bound on the probability , one cannot establish a corresponding upper bound without further assumptions on the training and test input distributions. However, by introducing randomization to the β-quantile, we can construct a randomized version of the confidence set, , that is not conservative and satisfies , a property called exact coverage. See SI Appendix, section S1.B for details.
Estimating confidence sets in practice.
In practice, one cannot check all possible candidate labels, , to construct a confidence set. Instead, as done in previous work on conformal prediction, we estimate by defining a finite grid of candidate labels, , and checking the condition in Eq. 3 for all . Algorithm 1 outlines a generic recipe for computing for a given test input; see Section 2.D for important special cases in which can be computed more efficiently.
Algorithm 1
Pseudocode for approximately computing
Input: Training data, , where ; test input, ; finite grid of candidate labels, ; likelihood ratio function subroutine, ; and score function subroutine .
Output: Confidence set, .
- 1:
- 2:
Compute
- 3:
for do
- 4:
for do
- 5:
Compute and
- 6:
Compute
- 7:
for do
- 8:
Normalize according to (4)
- 9:
- 10:
if then
- 11:
Relationship with exchangeable and standard covariate shift settings.
The weights assigned to each score, in Eq. 4, are the distinguishing factor between the confidence sets constructed by conformal approaches for the exchangeable, standard covariate shift, and FCS settings. When the training and test data are exchangeable, these weights are simply . To accommodate standard covariate shift, where the training and test data are independent, these weights are also normalized likelihood ratios—but, importantly, the test input distribution in the numerator is fixed, rather than data dependent as in the FCS setting (4). That is, the weights are defined using one fixed likelihood-ratio function, , where is the density of the single test input distribution under consideration.
In contrast, under FCS, observe that the likelihood ratio that is evaluated in Eq. 4, , is different for each of the n + 1 training and candidate test data points and for each candidate label, . To weight the ith training score, we evaluate the likelihood ratio of Xi where the test input distribution is the one induced by ,
That is, the weights under FCS take into account not just a single test input distribution, but every test input distribution that can be induced when we treat a leave-one-out training dataset combined with a candidate test data point, , as the training data.
To further appreciate the relationship between the standard and feedback covariate shift settings, consider the weights used in the standard covariate shift approach if we treat as the test input distribution. The extent to which differs from , for any and , determines the extent to which the weights used under standard covariate shift deviate from those used under FCS. In other words, since and differ in exactly one data point, the similarity between the standard covariate shift and FCS weights depends on the “smoothness” of the mapping from D to .
Input distributions are known in the design problem.
The design problem is a unique setting in which we have control over the data-dependent test input distribution, , since we choose the procedure used to design an input. In the simplest case, some design procedures sample from a distribution whose form is explicitly chosen, such as an energy-based model whose energy function is proportional to the predictions from a trained regression model (36) or a model whose parameters are set by solving an optimization problem (e.g., the training of a generative model) (24, 25, 37–43). In either setting, we know the exact form of the test input distribution, which also absolves the need for density estimation.
In other cases, the design procedure involves iteratively applying a gradient to, or otherwise locally modifying, an initial input to produce a designed input (44–49). Due to randomness in either the initial input or the local modification rule, such procedures implicitly result in some distribution of test inputs. Although we do not have access to its explicit form, knowledge of the design procedure can enable us to estimate it much more readily than in a naive density estimation setting. For example, we can simulate the design procedure as many times as needed to sufficiently estimate the resulting density, whereas in density estimation in general, we cannot control how many test inputs we can access.
The training input distribution, PX, is also often known explicitly. In protein design problems, for example, training sequences are often generated by introducing random substitutions to a single wild-type sequence (24, 36, 49), by recombining segments of several “parent” sequences (28, 29, 50, 51), or by independently sampling the amino acid at each position from a known distribution (43, 52). Conveniently, we can then compute the weights in Eq. 4 exactly without introducing approximation error due to density ratio estimation.
Finally, we note that, by construction, the design problem tends to result in test input distributions that place considerable probability mass on regions where the training input distribution does not. The farther the test distribution is from the training distribution in this regard, the larger the resulting weights on candidate test points, and the larger the confidence set in Eq. 3 will tend to be. This phenomenon agrees with our intuition about epistemic uncertainty: We should have more uncertainty—that is, larger confidence sets—in regions of input space where there are fewer training data.
D. Efficient Computation of Confidence Sets under Feedback Covariate Shift.
Using Algorithm 1 to construct the full conformal confidence set, , requires computing the scores and weights, and , for all and all candidate labels, . When the dependence of on D arises from a model trained on D, then naively, we must train models to compute these quantities. We now describe two important, practical cases in which this computational burden can be reduced to fitting models, removing the dependence on the number of candidate labels. In such cases, we can postprocess the outputs of these models to calculate all required scores and weights (see SI Appendix, Algorithm S2 for pseudocode); we refer to this as computing the confidence set efficiently.
In the following two examples and in our experiments, we use the residual score function, , where μD is a regression model trained on the multiset D. To understand at a high level when efficient computation is possible, first let denote the regression model trained on , the ith leave-one-out training dataset combined with a candidate test data point. The scores and weights can be computed efficiently when is a computationally simple function of the candidate label, y, for all i—for example, a linear function of y. We discuss two such cases in detail.
Ridge regression.
Suppose we fit a ridge regression model, with ridge regularization hyperparameter γ, to the training data. Then, we draw the test input vector from a distribution that places more mass on regions of where the model predicts more desirable values, such as high fitness in protein design problems. Recent studies have employed this relatively simple approach to successfully design novel enzymes with enhanced catalytic efficiencies and thermostabilities (36, 50, 53).
In the ridge regression setting, the quantity can be written in closed form as
| [5] |
where the rows of the matrix are the input vectors in contains the labels in , the matrix is defined as denotes the jth column of , and denotes the jth element of .
Note that the expression in Eq. 5 is a linear function of the candidate label, y. Consequently, as formalized by SI Appendix, Algorithm S2, we first compute and store the slopes and intercepts of these linear functions for all i, which can be calculated as byproducts of fitting n + 1 ridge regression models. Using these parameters, we can then compute for all candidate labels, , by simply evaluating a linear function of y instead of retraining a regression model on . Altogether, beyond fitting ridge regression models, SI Appendix, Algorithm S2 requires additional floating-point operations to compute the scores and weights for all the candidate labels, the bulk of which can be implemented as one outer product between an n vector and a vector and one Kronecker product between an matrix and a vector.
Gaussian process regression.
Similarly, suppose we fit a Gaussian process regression model to the training data. We then select a test input vector according to a likelihood that is a function of the mean and variance of the model’s prediction; such functions are referred to as acquisition functions in the Bayesian optimization literature.
For a linear kernel, the expression for the mean prediction, , is the same as for ridge regression (Eq. 5). For arbitrary kernels, the expression can be generalized and remains a linear function of y (see SI Appendix, section S2.B for details). We can therefore mimic the computations described for the ridge regression case to compute the scores and weights efficiently.
E. Data Splitting.
For settings with abundant training data, or model classes that do not afford efficient computations of the scores and weights, one can turn to data splitting to construct valid confidence sets. To do so, we first randomly partition the labeled data into disjoint training and calibration sets. Next, we use the training data to fit a regression model, which induces a test input distribution. If we condition on the training data, thereby treating the regression model as fixed, we have a setting in which 1) the calibration and test data are drawn from different input distributions, but 2) are independent (even though the test and training data are not). Thus, data splitting returns us to the setting of standard covariate shift, under which we can use the data-splitting approach in ref. 4 to construct valid split conformal confidence intervals (SI Appendix, section S1.C).
We also introduce randomized data-splitting approaches that give exact coverage; see SI Appendix, section S1.D for details.
3. Experiments with Protein Design
To demonstrate practical applications of our work, we turn to examples of uncertainty quantification for designed proteins. Given a fitness function of interest, such as fluorescence, a typical goal of protein design is to seek a protein with high fitness—in particular, higher than we have observed in known proteins. ‡ Historically, this has been accomplished through several iterations of expensive, time-consuming experiments. Recently, efforts have been made to augment such approaches with machine-learning–based strategies; see reviews by Yang et al. (54), Sinai and Kelsic (55), and Wu et al. (56) and references therein. For example, one might train a regression model on protein sequences with experimentally measured fitnesses and then use an optimization algorithm or fit a generative model that leverages that regression model to propose promising new proteins (24, 28, 29, 36, 43, 46, 51, 53, 57–59). Special attention has been given to the single-shot case in which we are given just a single batch of training data, due to its obvious practical convenience.
The use of regression models for design involves balancing 1) the desire to explore regions of input space far from the training inputs, to find new desirable inputs, with 2) the need to stay close enough to the training inputs that we can trust the regression model. As such, estimating predictive uncertainty in this setting is important. Furthermore, the training and designed data are described by feedback covariate shift: Since the fitness is some quantity dictated by nature, the conditional distribution of fitness given any sequence stays fixed, but the distribution of designed sequences is chosen based on a trained regression model.§
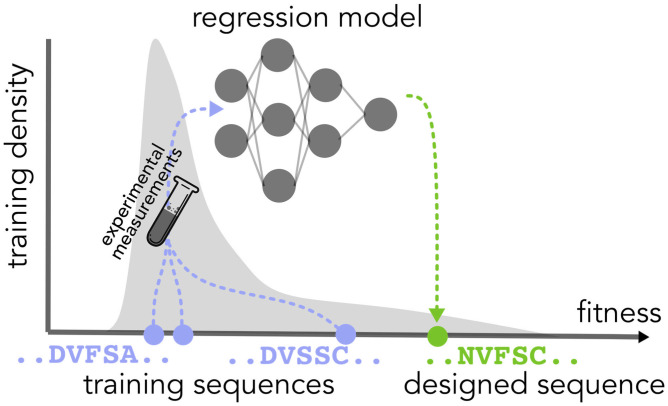
Our experimental protocol is as follows: Given training data consisting of protein sequences labeled with experimental measurements of their fitnesses, we fit a regression model, then sample test sequences (representing designed proteins) according to design algorithms used in recent work (36, 43) (Fig. 2). We then construct confidence sets with guaranteed coverage for the designed proteins and examine various characteristics of those sets to evaluate the utility of our approach. In particular, we show how our method can be used to select design algorithm hyperparameters that achieve acceptable tradeoffs between high predicted fitness and low predictive uncertainty for the designed proteins. Code reproducing these experiments is available at https://github.com/clarafy/conformal-for-design.
Fig. 2.
Illustration of single-shot protein design. The gray distribution represents the distribution of fitnesses under the training sequence distribution. The blue circles represent the fitnesses of three training sequences, and the goal is to propose a sequence with even higher fitness. To that end, we fit a regression model to the training sequences labeled with experimental measurements of their fitnesses and then deploy some design procedure that uses that trained model to propose a new sequence believed to have a higher fitness (green circle).
A. Design Experiments Using Combinatorially Complete Fluorescence Datasets.
The challenge when evaluating in silico design methods is that in general, we do not have labels for the designed sequences. One workaround, which we take here, is to make use of combinatorially complete protein datasets (57, 59–61), in which a small number of fixed positions are selected from some wild-type sequence, and all possible variants of the wild type that vary in those selected positions are measured experimentally. Such datasets enable us to simulate protein design problems where we always have labels for the designed sequences. In particular, we can use a small subset of the data for training and then deploy a design procedure that proposes novel proteins (restricted to being variants of the wild type at the selected positions), for which we have labels.
We used data of this kind from Poelwijk et al. (60), which focused on two parent fluorescent proteins that differ at exactly 13 positions in their sequences and are identical at every other position. All sequences that have the amino acid of either parent at those 13 sites (and whose remaining positions are identical to the parents) were experimentally labeled with a measurement of brightness at both a “red” wavelength and a “blue” wavelength, resulting in combinatorially complete datasets for two different fitness functions. In particular, for both wavelengths, the label for each sequence was an enrichment score based on the ratio of its counts before and after brightness-based selection through fluorescence-activated cell sorting. The enrichment scores were then normalized so that the same score reflects comparable brightness for both wavelengths.
Finally, each time we sampled from this dataset to acquire training or designed data, as described below, we added simulated measurement noise to each label by sampling from a noise distribution estimated from the combinatorially complete dataset (see SI Appendix, section S3 for details). This step simulates the fact that sampling and measuring the same sequence multiple times results in different measurements.
A.1. Protocol for design experiments.
Our training datasets consisted of n data points, , sampled uniformly at random from the combinatorially complete dataset. We used as is typical of realistic scenarios (28, 36, 51, 57, 59). We represented each sequence as a feature vector containing all first- and second-order interaction terms between the 13 variable sites and fitted a ridge regression model, , to the training data, where the regularization strength was set to 10 for and 1 otherwise. Linear models of interaction terms between sequence positions have been observed to be both theoretically justified and empirically useful as models of protein fitness functions (60–62) and thus may be particularly useful for protein design, particularly with small amounts of training data.
Sampling designed sequences.
Following ideas in refs. 36 and 43, we designed a protein by sampling from a sequence distribution whose log-likelihood is proportional to the prediction of the regression model:
| [6] |
where , the inverse temperature, is a hyperparameter. Larger values of λ result in distributions of designed sequences that are more likely to have high predicted fitnesses according to the model, but are also, for this same reason, more likely to be in regions of sequence space that are farther from the training data and over which the model is more uncertain. Analogous hyperparameters have been used in recent protein design work to control this tradeoff between exploration and exploitation (36, 39, 43, 63). We took to investigate how the behavior of our confidence sets varies along this tradeoff.
Constructing confidence sets for designed sequences.
For each setting of n and λ, we generated n training data points and one designed data point as just described T = 2, 000 times. For each of these T trials, we used SI Appendix, Algorithm S2 to construct the full conformal confidence set, , using a grid of real values between 0 and 2.2 spaced apart as the set of candidate labels, . This range contained the ranges of fitnesses in both the blue and red combinatorially complete datasets, and , respectively.¶
We used as a representative miscoverage value, corresponding to coverage of . We then computed the empirical coverage achieved by the confidence sets, defined as the fraction of the T trials where the true fitness of the designed protein was within half a grid spacing from some value in the confidence set; namely, . Based on Theorem 1, assuming is both a large and a fine enough grid to encompass all possible fitness values, the expected empirical coverage is lower bounded by . However, there is no corresponding upper bound, so it will be of interest to examine any excess in the empirical coverage, which corresponds to the confidence sets being conservative (larger than necessary). Ideally, the empirical coverage is exactly 0.9, in which case the sizes of the confidence sets reflect the minimal predictive uncertainty we can have about the designed proteins while achieving coverage.
In our experiments, the computed confidence sets tended to comprise grid-adjacent candidate labels, suggestive of confidence intervals. As such, we hereafter refer to the width of confidence intervals, defined as the grid spacing size times the number of values in the confidence set, .
A.2. Results.
Here we discuss results for the blue fluorescence dataset. Analogous results for the red fluorescence dataset are presented in SI Appendix, section S3.
Effect of inverse temperature.
First, we examined the effect of the inverse temperature, λ, on the fitnesses of designed proteins (Fig. 3A). Note that λ = 0 corresponds to a uniform distribution over all sequences in the combinatorially complete dataset (i.e., the training distribution), which mostly yields label values less than 0.5. For , we observe a considerable mass of designed proteins attaining fitnesses around 1.5, so these values of λ represent settings where the designed proteins are more likely to be fitter than the training proteins. This observation is consistent with the use of this and other analogous hyperparameters to tune the outcomes of design algorithms (36, 39, 43, 63) and is meant to provide an intuitive interpretation of the hyperparameter to readers unfamiliar with its use in design problems.
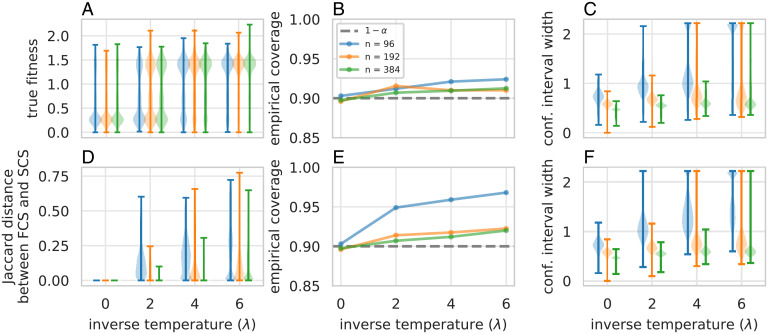
Fig. 3.
Quantifying predictive uncertainty for designed proteins, using the blue fluorescence dataset. (A) Distributions of labels of designed proteins, for different values of the inverse temperature, λ, and different amounts of training data, n. Labels surpass the fitness range observed in the combinatorially complete dataset, , due to additional simulated measurement noise. (B and C) Empirical coverage (B), compared to the theoretical lower bound of (dashed gray line), and (C) distributions of confidence interval widths achieved by full conformal prediction for feedback covariate shift (our method) over trials. In A and C, the whiskers signify the minimum and maximum observed values. (D) Distributions of Jaccard distances between the confidence intervals produced by full conformal prediction for feedback covariate shift and standard covariate shift (4). (E and F) Same as in B and C but using full conformal prediction for standard covariate shift.
Empirical coverage and confidence interval widths.
Despite the lack of a theoretical upper bound, the empirical coverage does not tend to exceed the theoretical lower bound of by much (Fig. 3B), reaching at most 0.924 for . Loosely speaking, this observation suggests that the confidence intervals are nearly as small, and therefore as informative, as they can be while achieving coverage.
As for the widths of the confidence intervals, we observe that for any value of λ, the intervals tend to be smaller for larger amounts of training data (Fig. 3C). Also, for any value of n, the intervals tend to get larger as λ increases. The first phenomenon agrees with the intuition that training a model on more data should generally reduce predictive uncertainty. The second phenomenon arises because greater values of λ lead to designed sequences with higher predicted fitnesses, which the model is more uncertain about. Indeed, for and , some confidence intervals equal the whole set of candidate labels. In these regimes, the regression model cannot glean enough information from the training data to have much certainty about the designed protein.
Comparison to standard covariate shift.
Deploying full conformal prediction as prescribed for standard covariate shift (SCS) (4), a heuristic with no formal guarantees in this setting, often results in more conservative confidence sets than those produced by our method (Fig. 3). To understand when the outputs of these two methods will differ more or less, we can compare the forms of the weights that both methods introduce on the training and candidate test data points when considering a candidate label.
First, recall that for FCS and SCS, the weight assigned to the ith training score is a normalized ratio of the likelihood of Xi under a test input distribution and the training input distribution, pX; namely,
for FCS and SCS, respectively. For FCS, the test input distribution, , is induced by a regression model trained on and therefore depends on the candidate label, y, and also differs for each of the n training inputs. Consequently, for FCS the weight on the ith training score depends on the candidate label under consideration, y. In contrast, for SCS the test input distribution, , is simply the one induced by the training data, , and is therefore fixed for all training scores and all candidate labels.
Note, however, that the SCS and FCS weights depend on datasets, and , respectively, that differ only in a single data point: The former contains Zi, while the latter contains . Therefore, the difference between the weights—and the resulting confidence sets—is a direct consequence of how sensitive the mapping from dataset to test input distribution, (given by Eq. 6 in this setting), is to changes of a single data point in D. Roughly speaking, the less sensitive this mapping is, the more similar the FCS and SCS confidence sets will be. For example, using more training data (e.g., compared to n = 96 for a fixed λ) or a lower inverse temperature (e.g., λ = 2 compared to for a fixed n) results in more similar SCS and FCS confidence sets (Fig. 3D and SI Appendix, Figs. S2D and S5). Similarly, using regression models with fewer features or stronger regularization also results in more similar confidence sets (SI Appendix, Figs. S3, S4, and S6).
One can therefore think of and use SCS confidence sets as a computationally cheaper approximation to FCS confidence sets, where the approximation is better for mappings that are less sensitive to changes in D. Conversely, the extent to which SCS confidence sets are similar to FCS confidence sets will generally reflect this sensitivity. In our protein design experiments, SCS confidence sets tend to be more conservative than their FCS counterparts, where the extent of overcoverage generally increases with fewer training data, higher inverse temperature (Fig. 3D and SI Appendix, Fig. S2D), more complex features, and weaker regularization (SI Appendix, Figs. S3 and S4).
Using uncertainty quantification to set design procedure hyperparameters.
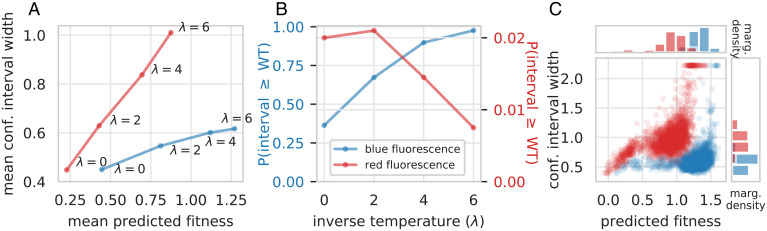
As the inverse temperature, λ, in Eq. 6 varies, there is a tradeoff between the mean predicted fitness and predictive certainty for designed proteins: Both mean predicted fitness and mean confidence interval width grow as λ increases (Fig. 4A). To demonstrate how our method might be used to inform the design procedure itself, one can visualize this tradeoff (Fig. 4) and use it to decide on a setting of λ that achieves both a mean predicted fitness and degree of certainty that one finds acceptable, given, for example, some resource budget for evaluating designed proteins in the wet laboratory. For datasets of different fitness functions, which may be better or worse approximated by our chosen regression model class and may have different amounts of measurement noise, this tradeoff—and therefore the appropriate setting of λ—will be different (Fig. 4).
Fig. 4.
Comparison of tradeoff between predicted fitness and predictive certainty on the red and blue fluorescence datasets. (A) Tradeoff between mean confidence interval width and mean predicted fitness for different values of the inverse temperature, λ, and n = 384 training data points. (B) Empirical probability that the smallest fitness value in the confidence intervals of designed proteins exceeds the true fitness of one of the wild-type parent sequences, mKate2. (C) For n = 384 and λ = 6, the distributions of both confidence interval width and predicted fitnesses of designed proteins.
For example, protein design experiments on the red fluorescence dataset result in a less favorable tradeoff between mean predicted fitness and predictive certainty than the blue fluorescence dataset: The same amount of increase in mean predicted fitness corresponds to a greater increase in mean interval width for red compared to blue fluorescence (Fig. 4A). We might therefore choose a smaller value of λ when designing proteins for the former compared to the latter. Indeed, predictive uncertainty grows so quickly for red fluorescence that, for , the empirical probability that the smallest value in the confidence interval is greater than the true fitness of a wild-type sequence decreases rather than increases (Fig. 4B), which suggests we may not want to set . In contrast, if we had looked at the mean predicted fitness alone without assessing the uncertainty of those predictions, it grows monotonically with λ (Fig. 4A), which would not suggest any harm from setting λ to a higher value.
In contrast, for blue fluorescence, although the mean interval width also grows with λ, it does so at a much slower rate than for red fluorescence (Fig. 4A); correspondingly, the empirical frequency at which the confidence interval surpasses the fitness of the wild type also grows monotonically (Fig. 4B).
We can observe these differences in the tradeoff between blue and red fluorescence even for a fixed value of λ. For example, for (Fig. 4C), observe that proteins designed for blue fluorescence (blue circles) have confidence intervals with widths mostly less than 1. That is, those with higher predicted fitnesses do not have much wider intervals than those with lower predicted fitnesses, except for a small fraction of proteins with the highest predicted fitnesses. In contrast, for red fluorescence, designed proteins with higher predicted fitnesses also tend to have wider confidence intervals.
B. Design Experiments Using Adeno-Associated Virus Capsid Packaging Data.
In contrast with Section 3.A, which represented a protein design problem with limited amounts of labeled data (at most a few hundred sequences), here we focus on a setting in which there are abundant labeled data. We can therefore employ data splitting as described in Section 2.E to construct confidence sets, as an alternative to computing full conformal confidence sets (Eq. 3) as done in Section 3.A. Specifically, we construct a randomized version of the split conformal confidence set (SI Appendix, Algorithm S1), which achieves exact coverage.
This subsection, together with the previous subsection, demonstrates that in both regimes—limited and abundant labeled data—our proposed methods provide confidence sets that give coverage, are not overly conservative, and can be used to visualize the tradeoff between predicted fitness and predictive uncertainty inherent to a design algorithm.
B.1. Protein design problem: Adeno-associated virus capsid proteins with improved packaging ability.
Adeno-associated viruses (AAVs) are a class of viruses whose capsid, the protein shell that encapsulates the viral genome, is a promising delivery vehicle for gene therapy. As such, the proteins that constitute the capsid have been modified to enhance various fitness functions, such as the ability to enter specific cell types and evade the immune system (64–66). Such efforts usually start by sampling millions of proteins from some sequence distribution and then performing an experiment that selects out the fittest sequences. Sequence distributions commonly used today have relatively high entropy, and the resulting sequence diversity can lead to successful outcomes for a myriad of downstream selection experiments (43, 49). However, most of these sequences fail to assemble into a capsid that packages the genetic payload (66–68)—a function called packaging, which is the minimum requirement of a gene therapy delivery mechanism and therefore a prerequisite to any other desiderata.
If sequence distributions could be developed with higher packaging rate, without compromising sequence diversity, then the success rate of downstream selection experiments should improve. To this end, Zhu et al. (43) use neural networks trained on sequence-packaging data to specify the parameters of DNA sequence distributions that simultaneously have high entropy and yield protein sequences with high predicted packaging ability. The protein sequences in these data varied at seven promising contiguous positions identified in previous work (65) and elsewhere matched a wild type. To accommodate commonly used DNA synthesis protocols, Zhu et al. (43) parameterized their DNA sequence distributions as independent categorical distributions over the four nucleotides at each of 21 contiguous sites, corresponding to codons at each of the seven sites of interest.
B.2. Protocol for design experiments.
We followed the methodology of Zhu et al. (43) to find sequence distributions with high mean predicted fitness—in particular, higher than that of the commonly used “NNK” sequence distribution (65). Specifically, we used their high-throughput data, which sampled millions of sequences from the NNK distribution, and labeled each with an enrichment score quantifying its packaging fitness, based on its count before and after a packaging-based selection experiment. We introduced additional simulated measurement noise to these labels, where the parameters of the noise distribution were also estimated from the pre- and postselection counts, resulting in labels ranging from –7.53 to 8.80 for 8,552,729 sequences (see SI Appendix, section S4 for details).
We then randomly selected and held out 1 million of these data points, for calibration and test purposes described shortly, and then trained a neural network on the remaining data to predict fitness from sequence. Finally, following ref. 43, we approximately solved an optimization problem that leveraged this regression model to specify the parameters of sequence distributions with high mean predicted fitness. Specifically, let denote the class of sequence distributions parameterized as independent categorical distributions over the four nucleotides at each of 21 contiguous sequence positions. We set the parameters of the designed sequence distribution by using stochastic gradient descent to approximately solve the following problem:
| [7] |
where , μ is the neural network fitted to the training data, and is an inverse temperature hyperparameter. After solving for for a range of inverse temperature values, , we sampled designed sequences from as described below and then used a randomized data-splitting approach to construct confidence sets that achieve exact coverage.
Sampling designed sequences.
Unlike in Section 3.A, here we did not have a label for every sequence in the input space—that is, all sequences that vary at the seven positions of interest and that elsewhere match a wild type. As an alternative, we used rejection sampling to sample from . Specifically, recall that we held out 1 million of the labeled sequences. The input space was sampled uniformly and densely enough by the high-throughput dataset that we treated 990,000 of these held-out labeled sequences as samples from a proposal distribution (that is, the NNK distribution) and were able to perform rejection sampling to sample designed sequences from for which we have labels.
Constructing confidence sets for designed sequences.
Note that rejection sampling results in some random number, at most 990,000, of designed sequences; in practice, this number ranged from single digits to several thousand for λ = 7 to , respectively. To account for this variability, for each value of the inverse temperature, we performed trials of the following steps. We randomly split the 1 million held-out labeled sequences into 990,000 proposal distribution sequences and 10,000 sequences to be used as calibration data. We used the former to sample some number of designed sequences and then used the latter to construct randomized staircase confidence sets (SI Appendix, Algorithm S1) for each of the designed sequences. The results we report next concern properties of these sets averaged over all trials.
B.3. Results.
Effect of inverse temperature.
The inverse temperature hyperparameter, λ, in Eq. 7 plays a similar role to that in Section 3.A: Larger values result in designed sequences with higher mean true fitness (Fig. 5A). Note that the mean true fitness for all considered values of the inverse temperature is higher than that of the training distribution (dashed black line, Fig. 5A).
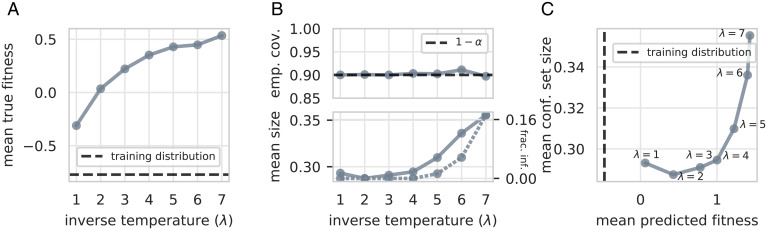
Fig. 5.
Quantifying uncertainty for predicted fitnesses of designed AAV capsid proteins. (A) Mean true fitness of designed sequences resulting from different values of the inverse temperature, . The dashed black line is the mean true fitness of sequences drawn from the NNK sequence distribution (i.e., the training distribution). (B) Top, empirical coverage of randomized staircase confidence sets (SI Appendix, section S1.D) constructed for designed sequences. The dashed black line is the expected empirical coverage of . Bottom, fraction of confidence sets with infinite size (dashed gray line) and mean size of noninfinite confidence sets (solid gray line). The set size is reported as a fraction of the range of fitnesses in all the labeled data, . (C) Tradeoff between mean predicted fitness and mean confidence set size for . The dashed black line is the mean predicted fitness for sequences from the training distribution.
Empirical coverage and confidence set sizes.
For all considered values of the inverse temperature, the empirical coverage of the confidence sets is very close to the expected value of (Fig. 5B, Top). Note that some designed sequences, which the neural network is particularly uncertain about, are given a confidence set with infinite size (Fig. 5B, Bottom). The fraction of sets with infinite size and the mean size of noninfinite sets both increase with the inverse temperature (Fig. 5B, Bottom), which is consistent with our intuition that the neural network should be less confident about predictions that are much higher than fitnesses seen in the training data.
Using uncertainty quantification to set design procedure hyperparameters.
As in Section 3.A.2, the confidence sets we construct expose a tradeoff between predicted fitness and predictive uncertainty as we vary the inverse temperature. Generally, the higher the mean predicted fitness of the sequence distributions is, the greater the mean confidence set size as well (Fig. 5C).# One can inspect this tradeoff to decide on an acceptable setting of the inverse temperature. For example, observe that the mean set size does not grow appreciably between and λ = 4, even though the mean predicted fitness monotonically increases (Fig. 5B, Bottom and C); similarly, the fraction of sets with infinite size also remains near zero for these values of λ (Fig. 5B, Bottom). However, both of these quantities start to increase for . By , for instance, more than 17% of designed sequences are given a confidence set with infinite size, suggesting that has shifted too far from the training distribution for the neural network to be reasonably certain about its predictions. Therefore, one might conclude that using achieves an acceptable balance of designed sequences with higher predicted fitness than the training sequences and low enough predictive uncertainty.
4. Discussion
The predictions made by machine-learning models are increasingly being used to make consequential decisions, which in turn influence the data that the models encounter. Our work presents a methodology that allows practitioners to trust the predictions of learned models in such settings. In particular, our protein design examples demonstrate how our approach can be used to navigate the tradeoff between desirable predictions and predictive certainty inherent to design problems.
Looking beyond the design problem, the formalism of FCS introduced here captures a range of problem settings pertinent to modern-day deployments of machine learning. In particular, FCS often occurs at each iteration of a feedback loop—for example, at each iteration of active learning, adaptive experimental design, and Bayesian optimization methods. Applications and extensions of our approach to such settings are exciting directions for future investigation.
Supplementary Material
Acknowledgments
We are grateful to Danqing Zhu and David Schaffer for generously allowing us to work with their AAV packaging data and to David H. Brookes and Akosua Busia for guidance on its analysis. We also thank David H. Brookes, Hunter Nisonoff, Tijana Zrnic, and Meena Jagadeesan for insightful discussions and feedback. C.F. was supported by a NSF Graduate Research Fellowship under Grant DGE 2146752. A.N.A. was partially supported by a NSF Graduate Research Fellowship and a Berkeley Fellowship. S.B. was supported by the Foundations of Data Science Institute and the Simons Institute.
Footnotes
Reviewers: R.A., Harvard University; and J.L., Carnegie Mellon University.
The authors declare no competing interest.
*We use the term confidence set to refer to both this function and the output of this function for a particular input; the distinction will be clear from the context.
†Since the second argument is a multiset of data points, the score function must be invariant to the order of these data points. For example, when using the residual as the score, the regression model must be trained in a way that is agnostic to the order of the data points.
‡We use the term fitness function to refer to a particular property that can be exhibited by proteins, while the fitness of a protein refers to the extent to which it exhibits that property.
§ In this section, we use “test” and “designed” interchangeably when describing data. We also sometimes say “sequence” instead of “input,” but this does not imply any constraints on how the protein is represented or featurized.
¶In general, a reasonable approach for constructing a finite grid of candidate labels, , is to span an interval beyond which one knows label values are impossible in practice, based on prior knowledge about the measurement technology. The presence or absence of any such value in a confidence set would not be informative to a practitioner. The size of the grid spacing, Δ, determines the resolution at which we evaluate coverage; that is, in terms of coverage, including a candidate label is equivalent to including the Δ-width interval centered at that label value. Generally, one should therefore set Δ as small as possible, subject to one’s computational budget.
#The exceptions are the sequence distributions corresponding to λ = 2 and λ = 3, which have a higher mean predicted fitness but on average smaller sets than λ = 1. One likely explanation is that experimental measurement noise is particularly high for very low fitnesses, making low-fitness sequences inherently difficult to predict.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2204569119/-/DCSupplemental.
Data, Materials, and Software Availability
Code and all data for reproducing our experiments are available at https://github.com/clarafy/conformal-for-design (69). Previously published data were also used for this work (60).
References
- 1.Vovk V., Gammerman A., Saunders C., “Machine -learning applications of algorithmic randomness” in Proceedings of the Sixteenth International Conference on Machine Learning, ICML ’99 Bratko I., Dzeroski S., Eds. (Morgan Kaufmann Publishers Inc., San Francisco, CA, 1999), pp. 444–453. [Google Scholar]
- 2.Vovk V., Gammerman A., Shafer G., Algorithmic Learning in a Random World (Springer, New York, NY, 2005). [Google Scholar]
- 3.Lei J., G’Sell M., Rinaldo A., Tibshirani R. J., Wasserman L., Distribution-free predictive inference for regression. J. Am. Stat. Assoc. 113, 1094–1111 (2018). [Google Scholar]
- 4.Tibshirani R. J., Foygel Barber R., Candes E., Ramdas A., Conformal prediction under covariate shift. Adv. Neural Inf. Process. Syst. 32, 2530–2540 (2019). [Google Scholar]
- 5.Cauchois M., Gupta S., Ali A., Duchi J. C., Robust validation: Confident predictions even when distributions shift. arXiv [Preprint] (2020). https://arxiv.org/abs/2008.04267 (Accessed 1 February 2022).
- 6.Gibbs I., Candès E., Adaptive conformal inference under distribution shift. Adv. Neural Inf. Process. Syst. 34, 1660–1672 (2021). [Google Scholar]
- 7.Park S., Li S., Bastani O., Lee I., “PAC confidence predictions for deep neural network classifiers” in Proceedings of the Ninth International Conference on Learning Representations (OpenReview.net, 2021).
- 8.Podkopaev A., Ramdas A., “Distribution -free uncertainty quantification for classification under label shift” in Proceedings of the 37th Uncertainty in Artificial Intelligence, C. de Campos, Maathuis M. H., Eds. (PMLR, 2021), pp. 844–853.
- 9.Shimodaira H., Improving predictive inference under covariate shift by weighting the log-likelihood function. J. Stat. Plan. Inference 90, 227–244 (2000). [Google Scholar]
- 10.Sugiyama M., Müller K. R., Input-dependent estimation of generalization error under covariate shift. Stat. Decis. 23, 249–279 (2005). [Google Scholar]
- 11.Sugiyama M., Krauledat M., Müller K. R., Covariate shift adaptation by importance weighted cross validation. J. Mach. Learn. Res. 8, 985–1005 (2007). [Google Scholar]
- 12.Quiñonero Candela J., Sugiyama M., Schwaighofer A., Lawrence N. D., Dataset Shift in Machine Learning (The MIT Press, 2009). [Google Scholar]
- 13.Hardt M., Megiddo N., Papadimitriou C., Wootters M., “Strategic classification” in Proceedings of the 2016 ACM Conference on Innovations in Theoretical Computer Science, Sudan M., Ed. (Association for Computing Machinery, New York, NY, 2016) pp. 111–122.
- 14.Perdomo J., Zrnic T., Mendler-Dünner C., Hardt M., “Performative prediction” in Proceedings of the 37th International Conference on Machine Learning, Daumé H. III, Singh A., Eds. (PMLR, 2020), vol. 119, pp. 7599–7609.
- 15.Gammerman A., Vovk V., Vapnik V., Learning by transduction. Proc. Fourteenth Conf. Uncertain. Artif. Intell. 14, 148–155 (1998). [Google Scholar]
- 16.Angelopoulos A. N., Bates S., A gentle introduction to conformal prediction and distribution-free uncertainty quantification. arXiv [Preprint] (2021). 10.48550/arXiv.2107.07511 (Accessed 1 February 2022). [DOI]
- 17.Vovk V., Testing for concept shift online. arXiv [Preprint] (2020). 10.48550/arXiv.2012.14246 (Accessed 1 February 2022). [DOI]
- 18.Hu X., Lei J., A distribution-free test of covariate shift using conformal prediction. arXiv [Preprint] (2020). 10.48550/arXiv.2010.07147 (Accessed 1 February 2022). [DOI]
- 19.Luo R., et al. , “Sample-efficient safety assurances using conformal prediction”. Workshop on Algorithmic Foundations of Robotics. arXiv [Preprint] (2022). https://arxiv.org/abs/2109.14082 (Accessed 1 February 2022).
- 20.Bates S., Candès E., Lei L., Romano Y., Sesia M., Testing for outliers with conformal p-values. arXiv [Preprint] (2021). 10.48550/arXiv.2104.08279 (Accessed 1 February 2022). [DOI]
- 21.Angelopoulos A. N., Bates S., Candès E. J., Jordan M. I., Lei L., Learn then test: Calibrating predictive algorithms to achieve risk control. arXiv [Preprint] (2021). 10.48550/arXiv.2110.01052 (Accessed 1 February 2022). [DOI]
- 22.Podkopaev A., Ramdas A., “Tracking the risk of a deployed model and detecting harmful distribution shifts” in Proceedings of the Tenth International Conference on Learning Representations (2022).
- 23.Kaur R., et al. , “iDECODe: In-distribution equivariance for conformal out-of-distribution detection” in Proceedings of the 36th AAAI Conference on Artificial Intelligence (AAAI Press, Palo Alto, CA, 2022).
- 24.Brookes D. H., Park H., Listgarten J., “Conditioning by adaptive sampling for robust design” in Proceedings of the International Conference on Machine Learning (ICML), Chaudhuri K., Salakhutdinov R., Eds. (PMLR, 2019).
- 25.Fannjiang C., Listgarten J., “Autofocused oracles for model-based design” in Advances in Neural Information Processing Systems 33 Larochelle H., Ranzato M., Hadsell R., Balcan M. F., Lin H., Eds. (Curran Associates, Inc., Red Hook, NY, 2020) pp. 12945–12956.
- 26.Auer P., Using confidence bounds for exploitation-exploration trade-offs. J. Mach. Learn. Res. 3, 397–422 (2002). [Google Scholar]
- 27.Snoek J., Larochelle H., Adams R. P., “Practical Bayesian optimization of machine learning algorithms” in Advances in Neural Information Processing Systems, Pereira F., Burges C. J. C., Bottou L., Weinberger K. Q., Eds., (Curran Associates, Inc., 2012), vol. 25, pp. 2960–2968.
- 28.Romero P. A., Krause A., Arnold F. H., Navigating the protein fitness landscape with Gaussian processes. Proc. Natl. Acad. Sci. U.S.A. 110, E193–E201 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Greenhalgh J. C., Fahlberg S. A., Pfleger B. F., Romero P. A., Machine learning-guided acyl-ACP reductase engineering for improved in vivo fatty alcohol production. Nat. Commun. 12, 5825 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lakshminarayanan B., Pritzel A., Blundell C., “Simple and scalable predictive uncertainty estimation using deep ensembles” in Advances in Neural Information Processing Systems, Guyon I., et al., Eds. (Curran Associates, Inc. Red Hook, NY, 2017), pp. 6402–6413. [Google Scholar]
- 31.Zeng H., Gifford D. K., Quantification of uncertainty in Peptide-MHC binding prediction improves high-affinity peptide selection for therapeutic design. Cell Syst. 9, 159–166.e3 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Liu G., et al. , Antibody complementarity determining region design using high-capacity machine learning. Bioinformatics 36, 2126–2133 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Soleimany A. P., et al. , Evidential deep learning for guided molecular property prediction and discovery. ACS Cent. Sci. 7, 1356–1367 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Amini A., Schwarting W., Soleimany A., Rus D., “Deep evidential regression” in Advances in Neural Information Processing Systems, Larochelle H., Ranzato M., Hadsell R., Balcan M. F., Lin H., Eds., (Curran Associates, Inc., 2020), vol. 33, pp. 14927–14937. [Google Scholar]
- 35.Kuleshov V., Fenner N., Ermon S., “Accurate uncertainties for deep learning using calibrated regression” in Proceedings of the 35th International Conference on Machine Learning, Dy J. G., Krause A., Eds. (PMLR, 2018).
- 36.Biswas S., Khimulya G., Alley E. C., Esvelt K. M., Church G. M., Low-N protein engineering with data-efficient deep learning. Nat. Methods 18, 389–396 (2021). [DOI] [PubMed] [Google Scholar]
- 37.Popova M., Isayev O., Tropsha A., Deep reinforcement learning for de novo drug design. Sci. Adv. 4, eaap7885 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kang S., Cho K., Conditional molecular design with deep generative models. J. Chem. Inf. Model. 59, 43–52 (2019). [DOI] [PubMed] [Google Scholar]
- 39.Russ W. P., et al. , An evolution-based model for designing chorismate mutase enzymes. Science 369, 440–445 (2020). [DOI] [PubMed] [Google Scholar]
- 40.Wu Z., et al. , Signal peptides generated by attention-based neural networks. ACS Synth. Biol. 9, 2154–2161 (2020). [DOI] [PubMed] [Google Scholar]
- 41.Hawkins-Hooker A., et al. , Generating functional protein variants with variational autoencoders. PLOS Comput. Biol. 17, e1008736 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shin J. E., et al. , Protein design and variant prediction using autoregressive generative models. Nat. Commun. 12, 2403 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhu D., et al. , Optimal trade-off control in machine learning-based library design, with application to adeno-associated virus (AAV) for gene therapy bioRxiv [Preprint] (2021). 10.1101/2021.11.02.467003 (Accessed 1 February 2022). [DOI] [PMC free article] [PubMed]
- 44.Killoran N., Lee L. J., Delong A., Duvenaud D., Frey B. J., “Generating and designing DNA with deep generative models” in Neural Information Processing Systems (NeurIPS) (Computational Biology Workshop, 2017). https://arxiv.org/abs/1712.06148 (Accessed 1 February 2022).
- 45.Gómez-Bombarelli R., et al. , Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 4, 268–276 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Linder J., Bogard N., Rosenberg A. B., Seelig G., A generative neural network for maximizing fitness and diversity of synthetic DNA and protein sequences. Cell Syst. 11, 49–62.e16 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Sinai S., et al. , AdaLead: A simple and robust adaptive greedy search algorithm for sequence design. arXiv [Preprint] (2020). 10.48550/arXiv.2010.02141 (Accessed 1 February 2022). [DOI]
- 48.Bashir A., et al. , Machine learning guided aptamer refinement and discovery. Nat. Commun. 12, 2366 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bryant D. H., et al. , Deep diversification of an AAV capsid protein by machine learning. Nat. Biotechnol. 39, 691–696 (2021). [DOI] [PubMed] [Google Scholar]
- 50.Li Y., et al. , A diverse family of thermostable cytochrome P450s created by recombination of stabilizing fragments. Nat. Biotechnol. 25, 1051–1056 (2007). [DOI] [PubMed] [Google Scholar]
- 51.Bedbrook C. N., et al. , Machine learning-guided channelrhodopsin engineering enables minimally invasive optogenetics. Nat. Methods 16, 1176–1184 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Weinstein E. N., et al. , “Optimal design of stochastic DNA synthesis protocols based on generative sequence models” in Proceedings of the 25th International Conference on Artificial Intelligence and Statistics, Camps-Valls G., Ruiz F. J. R., Valera I., Eds. (PMLR, 2022).
- 53.Fox R. J., et al. , Improving catalytic function by ProSAR-driven enzyme evolution. Nat. Biotechnol. 25, 338–344 (2007). [DOI] [PubMed] [Google Scholar]
- 54.Yang K. K., Wu Z., Arnold F. H., Machine-learning-guided directed evolution for protein engineering. Nat. Methods 16, 687–694 (2019). [DOI] [PubMed] [Google Scholar]
- 55.Sinai S., Kelsic E. D., A primer on model-guided exploration of fitness landscapes for biological sequence design. arXiv [Preprint] (2020). https://arxiv.org/abs/2010.10614 (Accessed 1 February 2022).
- 56.Wu Z., Johnston K. E., Arnold F. H., Yang K. K., Protein sequence design with deep generative models. Curr. Opin. Chem. Biol. 65, 18–27 (2021). [DOI] [PubMed] [Google Scholar]
- 57.Wu Z., Kan S. B. J., Lewis R. D., Wittmann B. J., Arnold F. H., Machine learning-assisted directed protein evolution with combinatorial libraries. Proc. Natl. Acad. Sci. U.S.A. 116, 8852–8858 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Angermueller C., et al. , “Model-based reinforcement learning for biological sequence design” in Proceedings of the International Conference on Learning Representations (ICLR) (OpenReview.net, 2019).
- 59.Wittmann B. J., Yue Y., Arnold F. H., Informed training set design enables efficient machine learning-assisted directed protein evolution. Cell Syst. 12, 1026–1045.e7 (2021). [DOI] [PubMed] [Google Scholar]
- 60.Poelwijk F. J., Socolich M., Ranganathan R., Learning the pattern of epistasis linking genotype and phenotype in a protein. Nat. Commun. 10, 4213 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Brookes D. H., Aghazadeh A., Listgarten J., On the sparsity of fitness functions and implications for learning. Proc. Natl. Acad. Sci. U.S.A. 119, e2109649118 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hsu C., Nisonoff H., Fannjiang C., Listgarten J., Learning protein fitness models from evolutionary and assay-labeled data. Nat. Biotechnol. 40, 1114–1122 (2022). [DOI] [PubMed] [Google Scholar]
- 63.Madani A., et al. , Deep neural language modeling enables functional protein generation across families. bioRxiv [Preprint] (2021). 10.1101/2021.07.18.452833 (Accessed 1 February 2022). [DOI]
- 64.Maheshri N., Koerber J. T., Kaspar B. K., Schaffer D. V., Directed evolution of adeno-associated virus yields enhanced gene delivery vectors. Nat. Biotechnol. 24, 198–204 (2006). [DOI] [PubMed] [Google Scholar]
- 65.Dalkara D., et al. , In vivo-directed evolution of a new adeno-associated virus for therapeutic outer retinal gene delivery from the vitreous. Sci. Transl. Med. 5, 189ra76 (2013). [DOI] [PubMed] [Google Scholar]
- 66.Tse L. V., et al. , Structure-guided evolution of antigenically distinct adeno-associated virus variants for immune evasion. Proc. Natl. Acad. Sci. U.S.A. 114, E4812–E4821 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Adachi K., Enoki T., Kawano Y., Veraz M., Nakai H., Drawing a high-resolution functional map of adeno-associated virus capsid by massively parallel sequencing. Nat. Commun. 5, 3075 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Ogden P. J., Kelsic E. D., Sinai S., Church G. M., Comprehensive AAV capsid fitness landscape reveals a viral gene and enables machine-guided design. Science 366, 1139–1143 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Fannjiang C., Data for protein design experiments, Conformal Prediction for the Design Problem. GitHub. https://github.com/clarafy/conformal-for-design. Deposited 31 May 2022.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Code and all data for reproducing our experiments are available at https://github.com/clarafy/conformal-for-design (69). Previously published data were also used for this work (60).