Significance
Humans have an extraordinary ability to learn new concepts from just a few examples, but the cognitive mechanism behind this ability remains mysterious. A long line of work in systems neuroscience has revealed that familiar concepts can be discriminated by the patterns of activity they elicit across neurons in higher-order cortical layers. How might downstream brain areas use this same neural code to learn new concepts? Here, we show that this ability is governed by key geometric properties of the neural code. We find that these geometric quantities undergo orchestrated transformations along the primate visual pathway and along artificial neural networks, so that in higher-order layers, a simple plasticity rule may allow novel concepts to be learned from few examples.
Keywords: few-shot learning, neural networks, ventral visual stream, population coding
Abstract
Understanding the neural basis of the remarkable human cognitive capacity to learn novel concepts from just one or a few sensory experiences constitutes a fundamental problem. We propose a simple, biologically plausible, mathematically tractable, and computationally powerful neural mechanism for few-shot learning of naturalistic concepts. We posit that the concepts that can be learned from few examples are defined by tightly circumscribed manifolds in the neural firing-rate space of higher-order sensory areas. We further posit that a single plastic downstream readout neuron learns to discriminate new concepts based on few examples using a simple plasticity rule. We demonstrate the computational power of our proposal by showing that it can achieve high few-shot learning accuracy on natural visual concepts using both macaque inferotemporal cortex representations and deep neural network (DNN) models of these representations and can even learn novel visual concepts specified only through linguistic descriptors. Moreover, we develop a mathematical theory of few-shot learning that links neurophysiology to predictions about behavioral outcomes by delineating several fundamental and measurable geometric properties of neural representations that can accurately predict the few-shot learning performance of naturalistic concepts across all our numerical simulations. This theory reveals, for instance, that high-dimensional manifolds enhance the ability to learn new concepts from few examples. Intriguingly, we observe striking mismatches between the geometry of manifolds in the primate visual pathway and in trained DNNs. We discuss testable predictions of our theory for psychophysics and neurophysiological experiments.
A hallmark of human intelligence is the remarkable ability to rapidly learn new concepts. Humans can effortlessly learn new visual concepts from only one or a few visual examples (1–4). Several studies have revealed the ability of humans to classify novel visual concepts with 90 to 95% accuracy, even after only a few exposures (5–7). We can even acquire visual concepts without any visual examples, by relying on cross-modal transfer from language descriptions to vision. The theoretical basis for how neural circuits can mediate this remarkable capacity for “few-shot” learning of general concepts remains mysterious, despite many years of research in concept learning across philosophy, psychology, and neuroscience (8–12).
Theories of human concept learning are at least as old as Aristotle, who proposed that concepts are represented in the mind by a set of strict definitions (13). Modern cognitive theories propose that concepts are mentally represented instead by a set of features, learned by exposure to examples of the concept. Two such foundational theories include prototype learning, which posits that features of previously encountered examples are averaged into a set of “prototypical” features (14), and exemplar learning, which posits that the features of all previously encountered examples are simply stored in memory (8). However, neither theory suggests how these features might be represented in the brain. In laboratory experiments, these features are either constructed by hand by generating synthetic stimuli that vary along a predefined set of latent features (15, 16) or are indirectly inferred from human similarity judgements (17–19).
In this work, we introduce a theory of concept learning in neural circuits based on the hypothesis that the concepts we can learn from a few examples are defined by tight geometric regions in the space of high-dimensional neural population representations in higher-level sensory brain areas. Indeed, in the case of vision, decades of research have revealed a series of representations of visual stimuli in neural population responses along the ventral visual pathway, including V1, V2, and V4, culminating in a rich object representation in the inferotemporal (IT) cortex (20–22), allowing a putative downstream neuron to infer the identity of an object based on the pattern of IT activity it elicits (23, 24).
We also hypothesize that sensory representations in IT, acquired through a lifetime of experience, are sufficient to enable rapid learning of novel visual concepts based on just a few examples, without any further plasticity in the representations themselves, by a downstream population of neurons with afferent plastic synapses that integrate a subset of nonplastic IT neural responses.
Our approach is corroborated by recent work demonstrating that artificial deep neural networks (DNNs) pretrained on a diverse array of concepts can be taught to classify new concepts from few examples by simply training linear readouts of their hidden unit representations (25–27). To understand this, we address the questions: What makes a representation good for rapidly learning novel concepts? And does the brain contain such representations? We introduce a mathematical theory, which reveals that few-shot learning performance is governed by four simple and readily measurable geometric quantities. We test our theory using neurophysiological recordings in macaques, as well as representations extracted from DNN models of the primate visual hierarchy, which have been shown to predict neural population responses in V1, V4, and IT (28, 29), the similarity structure of object representations in IT (30), and human performance at categorizing familiar objects (19, 31). We find that in both DNNs and the primate visual hierarchy, neural activity patterns undergo orchestrated geometric transformations so that few-shot learning performance increases from each layer to the next and from the retina to V1 to V4 to IT. Intriguingly, despite these common patterns in performance, our theory reveals fundamental differences in neural geometry between primate and DNN hierarchies, thereby providing key targets for improving models.
We further leverage our theory to investigate neurally plausible models of multimodal concept learning, allowing neural representations of linguistic descriptors to inform the visual system about visually novel concepts. Our theory also reveals that long-held intuitions and results about the relative performance of prototype and exemplar learning are completely reversed when moving from low-dimensional concepts with many examples, characteristic of most laboratory settings, to high-dimensional naturalistic concepts with very few examples. Finally, we make testable predictions not only about overall performance levels, but, more importantly, about salient patterns of errors, as a function of neural population geometry, that can reveal insights into the specific strategies used by humans and nonhuman primates in concept learning.
Results
A. Accurate Few-Shot Learning with Nonplastic Representations.
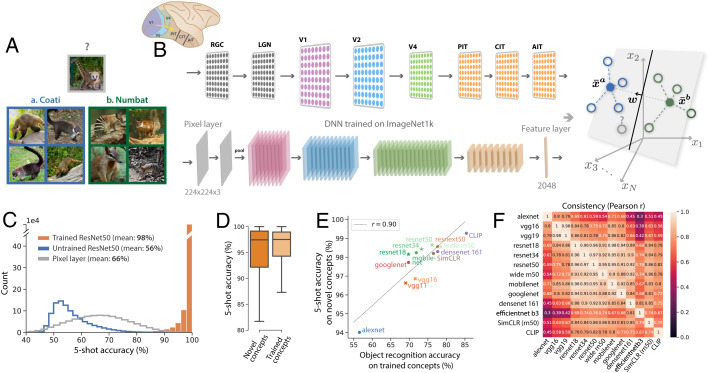
To investigate how the geometry of neural representations affects few-shot learning performance, we obtain neural representations from a DNN that has been shown to be a good model of object representations in IT cortex (32) (Fig. 1, ResNet50; Section N). The DNN is trained to classify 1,000 naturalistic visual concepts from the ImageNet1k dataset (e.g., “bee” and “acorn”). To study novel-concept learning, we select a set of 1,000 new visual concepts, never seen during training, from the ImageNet21k dataset (e.g., “coati” and “numbat”; Fig. 1A; Section J). We examine the ability to learn to discriminate each pair of new concepts, given only a few training images, by learning to classify the activity patterns these training images elicit across IT-like neurons in the feature layer of the DNN (Fig. 1B). Many decision rules are possible, but we find that in the few-shot regime, typical choices perform no better than a particularly simple, biologically plausible classification rule: prototype learning (Section H). Prototype learning is performed by averaging the activity patterns elicited by the training examples into concept prototypes, (Fig. 1B). A test image is then classified by comparing the activity pattern it elicits to each of the prototypes and identifying it with the closest prototype. This classification rule can be performed by a single downstream neuron that adjusts its synaptic weights so that its weight vector w points along the difference between the prototypes, (Fig. 1B). Despite its simplicity, prototype learning has been shown to achieve good few-shot learning performance (33), and we find that on our evaluation set of 1,000 novel concepts from the ImageNet dataset, it achieves an average test accuracy of 98.6% given only 5 training images of each concept (Fig. 1C), only slightly lower than the accuracy obtained by prototype learning on the same 1,000 familiar concepts that were used to train the DNN (Fig. 1D). When only one training example of each concept is provided (one-shot learning), prototype learning achieves a test accuracy of 92.0%. In contrast, the performance of prototype learning applied to representations in the retina-like pixel layer to the feature layer of an untrained, randomly initialized DNN is around 50 to 65% (Fig. 1C), indicating that the neural representations learned over the course of training the DNN to classify 1,000 concepts are powerful enough to facilitate highly accurate few-shot learning of novel concepts, without any further plasticity. Consistent with this, we find that DNNs that perform better on the ImageNet1k classification task also perform better at few-shot learning of novel concepts (Fig. 1E).
Fig. 1.
Concept-learning framework and model performance. (A) Example four-shot learning task: Does the test image in the gray box contain a “coati” (blue) or a “numbat” (green), given four training examples of each? (B) Each training example is presented to the ventral visual pathway (Upper), modeled by a trained DNN (Lower), eliciting a pattern of activity across IT-like neurons in the feature layer. We model concept learning as learning a linear readout to classify these activity patterns, which can be thought of as points in a high-dimensional activity space (open circles, Right). In the case of prototype learning, activity patterns are averaged into prototypes (filled circles), and is pointed along the difference between the prototypes , passing through their midpoint. To evaluate generalization accuracy, we present a test image and determine whether its neural representation (gray open circle) is correctly classified. (C) Generalization accuracy is very high across pairs of novel visual concepts from the ImageNet21k dataset (orange). In comparison, test accuracy is poor when using a randomly initialized DNN (blue) or when learning a linear classifier in the pixel space of input images (gray). (D) Test accuracy on novel concepts (dark orange) is only slightly lower than test accuracy on familiar concepts seen during training (light orange). (E) Performance on the object-recognition task used to train DNNs correlates with their ability to generalize to novel concepts, given few examples (r = 0.92, ), across a variety of DNN architectures. (F) Different DNN architectures are consistent in the pattern of errors they make across the novel concepts ().
For a finer-resolution analysis, we examine the pattern of errors each model makes across all pairs of novel concepts. We find that different models are consistent in which novel concepts they find easy/hard to learn (Fig. 1F; ; chance is zero), although the consistency is noticeably lower for older architectures (e.g., Alexnet or VGG). We also observe that good few-shot learning performance does not require pretraining on a large dataset of labeled examples, as models trained in a self-supervised or unsupervised [e.g., SimCLR (34) or CLIP (27)] manner also achieve high performance (Fig. 1E), are consistent in the patterns of errors they make (Fig. 1F), and exhibit similar representational geometry (SI Appendix, Fig. 5). Intriguingly, across models tested, the few-shot learning-error patterns reveal a pronounced asymmetry on many pairs of concepts (SI Appendix, section 7). For instance, models may be much more likely to classify a test example of a “coati” as a “numbat” than a “numbat” as a “coati” (SI Appendix, Fig. 1). Importantly, this asymmetry is not only a feature of prototype learning; diverse decision rules (e.g., exemplar learning or support vector machines) exhibit similar asymmetry in the few-shot regime (SI Appendix, Fig. 10).
These results raise several fundamental theoretical questions. Why does a DNN trained on an image-classification task also perform so well on few-shot learning? What properties of the derived neural representations empower high few-shot learning performance? Furthermore, why are some concepts easier than others to learn (Fig. 1C), and why is the pairwise classification error asymmetric (SI Appendix, Fig. 1)? We answer these questions by introducing an analytical theory that predicts the generalization error of prototype learning, based on the geometry of neural population responses.
B. A Geometric Theory of Prototype Learning.
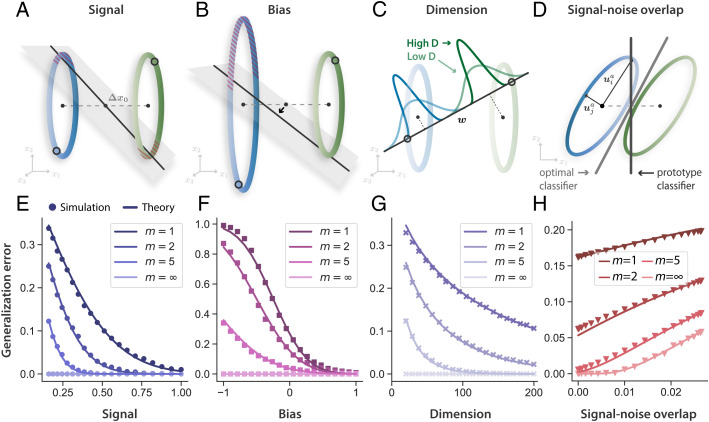
Patterns of activity evoked by examples of any particular concept define a concept manifold (Fig. 2). Although their shapes are likely complex, we find that when concept manifolds are high-dimensional, the generalization error of prototype learning can be accurately predicted based only on each manifold’s centroid, , and radii, Ri, along a set of orthonormal basis directions (SI Appendix, section 3), capturing the extent of natural variation of examples belonging to the same concept. A useful measure of the overall size of these variations is the mean squared radius .
Fig. 2.
Geometry of few-shot learning. Patterns of activity evoked by examples of each concept define a concept manifold, which we approximate as a high-dimensional ellipsoid. The generalization error (red hashed area) of a prototype classifier is governed by four geometric properties of these manifolds (Eq. 1), shown schematically in A–D. (A) Signal refers to the pairwise separation between concept manifolds, . Manifolds that are better separated are more easily discriminated by a linear classifier (gray hyperplane) given few training examples (open circles). (B) Bias: As the radius of one manifold grows relative to the other, the decision hyperplane shifts toward the manifold with the larger radius. Hence, the generalization error on the larger manifold increases, while the error on the smaller manifold decreases. Although the tilt of the decision hyperplane relative to the signal direction averages out over different draws of the training examples, this bias does not. (C) Dimension: In high dimensions, the projection of each concept manifold onto the linear readout direction concentrates around its mean. Hence, high-dimensional manifolds are easier to discriminate by a linear readout. (D) Signal–noise overlap: Pairs of manifolds whose noise directions overlap significantly with the signal direction have higher generalization error. Even in the limit of infinite training examples, , the prototype classifier (dark gray) cannot overcome signal–noise overlaps, as it has access only to the manifold centroids. An optimal linear classifier (light gray), in contrast, can overcome signal–noise overlaps using knowledge of the variability around the manifold centroids. (E–H) Behavior of generalization error (with ) in relation to each geometric quantity in A–D. Theoretical predictions are shown as dark lines, and few-shot learning experiments on synthetic ellipsoidal manifolds are shown as points. (F) When bias is large and negative, generalization error can be greater than chance (0.5). (G) Generalization error decreases when manifold variability is spread across more dimensions. (H) In the presence of signal–noise overlaps, generalization error remains nonzero, even for arbitrarily large m. Details on simulation parameters are given in Section M.
Our theory of prototype learning to discriminate pairs of new concepts (a, b) predicts that the average error of m-shot learning on test examples of concept a is given by , where is the Gaussian tail function (SI Appendix, section 3C). The quantity is the signal-to-noise ratio (SNR) for manifold a, whose dominant terms are given by,
| [1] |
A full expression and derivation are given in SI Appendix, section 3C. The SNR depends on four interpretable geometric properties, depicted schematically in Fig. 2 A–D. Their effect on the generalization error is shown in Fig. 2 E–H. The generalization error for tasks involving discriminating more than two novel concepts, derived in SI Appendix, section 3D, is governed by the same geometric properties. We now explain each of these properties.
-
1.
Signal. represents the pairwise distance between the manifolds’ centroids, and , normalized by (Fig. 2A). As the pairwise distance between manifolds increases, they become easier to separate, leading to higher SNR and lower error (Fig. 2E). We denote as the signal and as the signal direction.
-
2.
Bias. represents the average bias of the linear classifier (Fig. 2B). Importantly, when manifold a is larger than manifold b, the bias term is negative, predicting a lower SNR for manifold a. This asymmetry results from the fact that the classification hyperplane is biased toward the larger manifold (Fig. 2F) and causes the asymmetry in generalization error observed above (Section A). This bias is unique to few-shot learning. As can be seen in Eq. 1, its effect on SNR diminishes for large numbers of training examples m.
-
3.
Dimension. In our theory, , known as the “participation ratio” (35), quantifies the number of dimensions along which the concept manifold varies significantly, which is often much smaller than the number of neurons, N (Section L). Previous works have shown that low-dimensional manifolds have desirable properties for object recognition, allowing a greater number of familiar object to be perfectly classified (36, 37) and conferring robustness (38). Intriguingly, Eq. 1 reveals that for few-shot learning, high-dimensional manifolds are preferred. This enhanced performance is due to the fact that few-shot learning involves comparing a test example to the training examples of each novel concept. In low dimensions, the distance from the test example to each of the training examples varies significantly, contributing a noise term to the SNR. But in high dimensions, these distances concentrate around their typical value, and, hence, the noise term is suppressed as . Note that this benefit of high-dimensional representations is unique to few-shot learning, since the noise term can also be suppressed by averaging over many training examples (by a factor of ; Eq. 1).
-
4.
Signal–noise overlap. and quantify the overlap between the signal direction and the manifold axes of variation and (see Fig. 2D and Section L for details). Generalization error increases as the overlap between the signal and noise directions increases (Fig. 2H). We note that signal–noise overlaps decrease as the dimensionality Da increases.
Effect of number of training examples.
As the number of training examples, m, increases, the prototypes more closely match the true manifold centroids; hence, the bias and the first two noise terms in Eq. 1 decay as . However, the last noise term, , does not vanish, even when the centroids are perfectly estimated, as it originates from variability in the test examples along the signal direction (Fig. 2H; ). Thus, in the limit of a large number of examples m, the generalization error does not vanish, even if the manifolds are linearly separable. The SNR instead approaches the finite limit , highlighting the failure of prototype learning at large-m compared to an optimal linear classifier (Fig. 2D). However, in the few-shot (small-m) regime, prototype learning is close to the optimal linear classifier (Section H).
To evaluate our theory, we perform prototype learning experiments on synthetic concept manifolds, constructed as high-dimensional ellipsoids. We find good agreement between theory and experiment for the dependence of generalization error on each of the four geometric quantities and on the number of examples (see Fig. 2 E–H and Section M for details).
C. Geometric Theory Predicts the Error of Few-Shot Learning in DNNs.
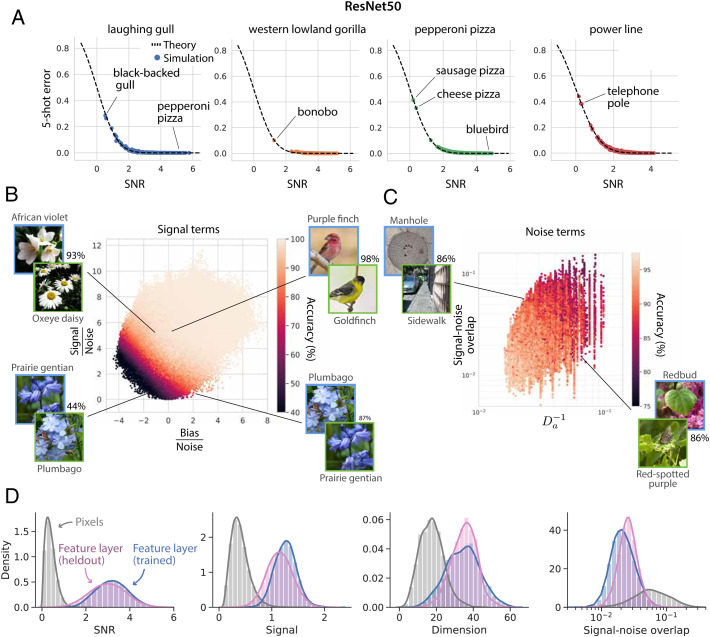
We next test whether our geometric theory accurately predicts few-shot learning performance on naturalistic visual concept manifolds, using the neural representations derived from DNNs studied in Section A. For each pair of concept manifolds, we estimate the four geometric quantities defined above (Section K) and predict generalization error via Eq. 1, finding excellent agreement between theory and numerical simulations (Fig. 3A and SI Appendix, Fig. 3), despite the obviously complex shape of these manifolds.
Fig. 3.
Geometric theory predicts the generalization error of few-shot learning in DNNs. (A) We compare the predictions of our theory to the few-shot learning experiments performed in Fig. 1. Each panel plots the generalization error of one novel visual concept (e.g., “laughing gull”) against all 999 other novel visual concepts (e.g., “black-backed gull” or “pepperoni pizza”). Each point represents the average generalization error on one such pair of concepts. x axis: SNR (Eq. 1) obtained by estimating neural manifold geometry. y axis: Empirical generalization error measured in few-shot learning experiments. Theoretical prediction (dashed line) shows a good match with experiments. Error bars, computed over many draws of the training and test examples, are smaller than the symbol size. We annotate each panel with specific examples of novel concept pairs, indicating their generalization error. Additional examples are included in SI Appendix, Fig. 3. (B) Signal terms: We dissect the generalization accuracy on each pair of novel concepts into differential contributions from the signal and bias (Eq. 1). We plot each pair of visual concepts in the resulting signal–bias plane, where both signal and bias are normalized by the noise so that one-shot learning accuracy (color, dark to light) varies smoothly across the plot. Specific examples of concept pairs are included to highlight the behavior of generalization accuracy with respect to each quantity. For example, the pair “Purple finch” vs. “Goldfinch” has a large signal and a bias close to zero and, hence, a very high one-shot accuracy (98%). The pair “African violet” vs. “Oxeye daisy”, in contrast, has a large signal, but a large negative bias; hence, its accuracy is lower (93%). Pairs with large negative bias and small signal may have very asymmetric generalization accuracy. For instance, “Prairie gentian” vs. “Plumbago” has an accuracy of 87%, while “Plumbago” vs. “Prairie gentian” has an accuracy of 44%. For each pair of concepts, test examples are drawn from the upper left concept in blue. (C) Noise terms: We dissect the contributions of dimensionality and signal–noise overlap to generalization error. Because the variability of the signal terms is much larger than that of the noise terms, we include only pairs of concepts whose signal falls within a narrow range, so that we can visually assess whether one-shot accuracy (color, dark to light) is due to large dimensionality, small signal–noise overlaps, or both. (D) We compare histograms of SNR, signal, dimension, and signal–noise overlap across all pairs of novel concepts in the retina-like pixel layer (gray) to those in the feature layer (pink, “heldout”), revealing dramatic changes in manifold geometry empowering high few-shot learning performance. We further compare to the geometry of the 1,000 concepts used to train the network (blue histograms, “trained”), indicating that the geometry of trained and heldout concepts is largely similar.
Our theory further allows us to dissect the specific contribution of each of the four geometric properties of the concept manifolds to the SNR, elucidating whether errors arise from small signal, negative bias, low dimension, or large signal–noise overlap. We dissect the contributions of signal and bias in Fig. 3B and the contributions of dimension and signal–noise overlap in Fig. 3C, along with specific illustrative examples highlighting, for instance, the strong asymmetry of few-shot learning (e.g., “Prairie gentian” vs. “Plumbago”).
DNNs perform complex nonlinear transformations to map images from the retina-like pixel layer to the feature layer. In Fig. 3D, we examine the effect these transformations have on SNR, signal, dimension, and signal–noise overlap for each pair of concepts. We find that almost all concepts become better-separated (i.e., higher signal), higher-dimensional, and more orthogonal (i.e., lower signal–noise overlap) as they are mapped from the pixel layer to the feature layer. In the following section, we study the evolution of these geometric features along the layers of DNNs.
One might suspect that because the DNN was explicitly optimized to map the 1,000 concepts on which it was trained to linearly separable regions in feature space, the geometry of these 1,000 trained concepts would differ substantially from the geometry of the 1,000 novel concepts we study in this work. Nevertheless, although the signal is slightly higher for trained concepts and the signal–noise overlaps slightly lower (Fig. 3D), the geometry is largely similar between trained and novel concepts, indicating that training on 1,000 concepts has furnished the DNN with a fairly general-purpose feature extractor. We show that novel-concept learning performance improves consistently as the number of concepts seen during training increases, due to smooth changes in manifold geometry in SI Appendix, Fig. 7.
Finally, we find that the geometry of concept manifolds in the DNN encodes a rich semantic structure, including a hierarchical organization, which reflects the hierarchical organization of visual concepts in the ImageNet dataset (SI Appendix, section 7). We examine the relationship between semantic structure and geometry in SI Appendix, Fig. 1 and provide examples of concepts with small and large manifold dimension and radius in SI Appendix, Fig. 8.
D. Concept Learning along the Visual Hierarchy.
How the ventral visual hierarchy converts low-level retinal representations into higher-level IT representations useful for downstream tasks constitutes a fundamental question in neuroscience. We first examine this transformation in models of the ventral visual hierarchy and, in the next section, compare it to the macaque hierarchy. Our theory enables us to not only investigate the performance of few-shot concept learning along successive layers of the visual hierarchy, but also obtain a finer-resolution decomposition of this performance into the geometric properties of the concept manifolds in each layer.
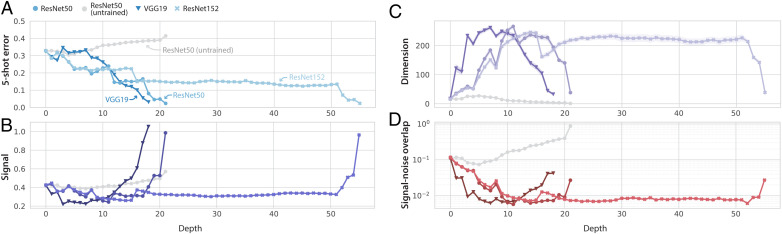
We find that, across a range of networks, the ability to learn novel concepts from few examples improves consistently along the layers of the network (Fig. 4A). In the last few layers of the network, the improvement in performance is due to a sharp increase in the signal (pairwise separability) of concept manifolds (Fig. 4B). In the earlier layers, the improvement in performance is due to a massive expansion in manifold dimensionality (Fig. 4C) and a suppression of signal–noise overlaps (Fig. 4D). We note that as the signal increases in the last few layers of the network, the dimensionality drops back down, and the signal–noise overlaps increase, perhaps reflecting a tradeoff between pairwise separability of manifolds and their dimensionality. Nonmonotonicity of dimension has also been observed by using capacity-related measures of dimension (36) and nonlinear measure of intrinsic dimensionality (39, 40). Interestingly, Fig. 4 indicates that ResNets exhibit long stretches of layers with apparently little to no change in manifold geometry.
Fig. 4.
Few-shot learning improves along the layers of a trained DNN, due to orchestrated transformations of concept manifold geometry. Each panel shows the layerwise behavior of one quantity in three different trained DNNs, as well as an untrained ResNet50 (gray). Lines and markers indicate mean value over 100 × 99 pairs of objects; surrounding shaded regions indicate 95% CIs (often smaller than the symbol size). (A) Few-shot generalization error decreases roughly monotonically along the layers of each trained DNN. (B) Signal is roughly constant across the early layers of the trained network and increases sharply in the later layers of the DNN. (C) Dimension grows dramatically in the early layers of the network and shrinks again in the late layers of network. (D) Signal–noise overlap decreases from pixel layer to feature layer, first decreasing sharply in the early layers of the network and then increasing slightly in the later layers of the network.
E. Concept Learning Using Primate Neural Representations.
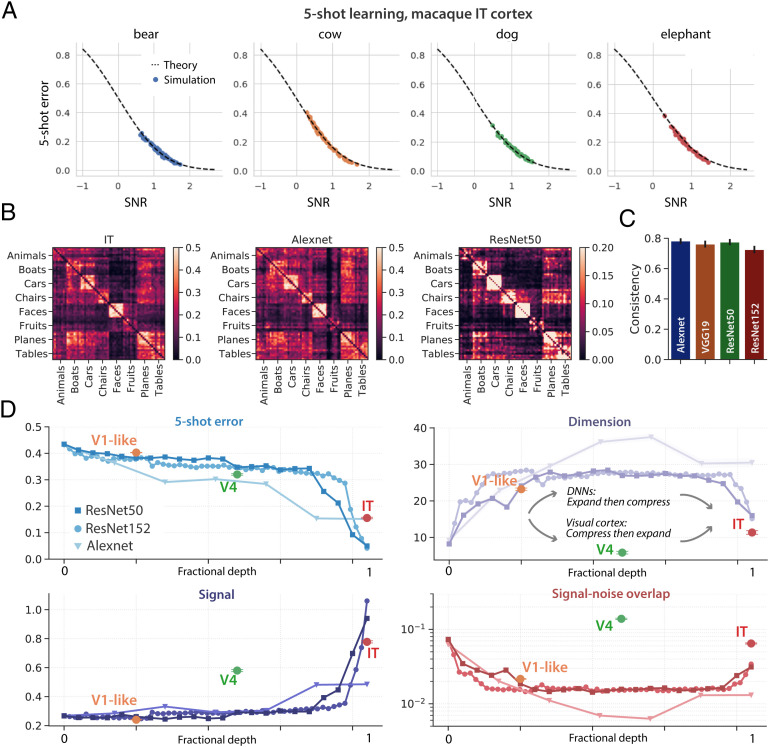
We next turn to the primate visual hierarchy and investigate the geometry of concept manifolds obtained via recordings of macaque V4 and IT in response to 64 synthetic visual concepts, designed to mimic naturalistic stimuli (24). The results in Fig. 5A show that our geometric theory is able to correctly predict the generalization error of few-shot learning simulations using the activation patterns of real neurons in the V4 and IT cortex of behaving animals. Furthermore, prototype learning achieves an average five-shot accuracy of 84% across all pairs of visual concepts; slightly better than the performance achieved by the AlexNet DNN (80%) on the same set of visual concepts and worse than ResNet50 (93%), consistent with previous experiments on object-recognition performance in primates (24). We predict that performance based on IT neurons will improve when evaluated on more naturalistic visual stimuli than the grayscale, synthetic images used here (as suggested by the increased performance of DNNs, e.g., from 80 to 94% for AlexNet when using novel stimuli from ImageNet). Beyond overall performance, we find that the error patterns in IT and DNNs are consistent (Fig. 5 B and C; ), all exhibiting a prominent block diagonal structure, reflecting the semantic structure of the visual concepts (24).
Fig. 5.
Concept learning and manifold geometry in macaque IT. (A) Five-shot prototype learning experiments performed on neural population responses of 168 recorded neurons in IT (24). Each panel shows the generalization error of one visual concept (e.g., “bear”) against all 63 other visual concepts (e.g., “cow” or “dog”). Each point represents the average generalization error on one such pair of concepts. x axis: SNR (Eq. 1) obtained by estimating manifold geometry. y axis: Empirical generalization error measured in few-shot learning experiments. The result shows a good fit to the theory (dashed line). Error bars, computed over many draws of the training and test examples, are smaller than the symbol size. (B) Error pattern of five-shot learning in IT reveals a clear block diagonal structure, similar to the error patterns in AlexNet and ResNet50. (C) Error patterns in DNNs are consistent with those in IT (Pearson r, ). Error bars are computed by measuring consistency over random subsets of 500 concept pairs. (D) Few-shot learning improves along the ventral visual hierarchy from pixels to V1 to V4 to IT, due to orchestrated transformations of concept manifold geometry. We compute the geometry of concept manifolds in IT, V4, and a simulated population of V1-like neurons (see Section E for details). Each panel shows the evolution of one geometric quantity along the visual hierarchy. The layerwise behavior of a trained ResNet50 (blue), Alexnet (light blue), and an untrained ResNet50 (gray) are included for comparison. We align V1, V4, and IT to the most similar ResNet layer under the BrainScore metric (32) (see Section E for details). Overall performance exhibits a good match between the primate visual pathway and trained DNNs, but individual geometric quantities display a marked difference. In particular, in DNNs, dimensionality expands dramatically in the early layers and contracts in the later layers, while in the primate visual pathway, dimensionality contracts from the V1-like layer to V4, then expands from V4 to IT. Similarly, in DNNs, signal–noise overlaps are suppressed in the early layers, then grow in the late layers, while in the primate visual pathway, signal–noise overlaps grow from the V1-like layer to V4, then are suppressed from V4 to IT. Lines and markers indicate mean value over 64 × 63 pairs of concepts; surrounding error bars and shaded regions indicate 95% CIs.
How does concept manifold geometry evolve along the visual hierarchy? We compute the in IT, V4, and a simulated population of V1-like neurons (Section O) and find that few-shot learning performance increases along the visual hierarchy from just above chance in the pixel layer and V1 to 69% in V4 and 84% in IT, approximately matching the corresponding layers in trained DNNs that are most predictive of each cortical area under the BrainScore metric (32) (Fig. 5D). Despite this similarity, when we decompose the SNR into its finer-grained geometric components, we find a striking mismatch between visual cortex and trained DNNs. In particular, while manifold dimensionality in DNNs undergoes a massive expansion in the early to intermediate layers, reaching its maximum in the layer most predictive of V4 (32), dimensionality in the visual hierarchy reaches its minimum in V4 (Fig. 5 D, Upper Right). A similar mismatch can be observed for signal–noise overlaps (Fig. 5 D, Lower Right). To ensure that this mismatch is not simply due to our choice to measure dimensionality using the participation ratio, we repeated these analyses using nonlinear methods for estimating intrinsic dimensionality and found consistent results (SI Appendix, Fig. 4). The lower dimensionality and larger signal–noise overlaps in V4 compared to DNNs are compensated by an enhanced signal (Fig. 5 D, Lower Left), so that overall performance is similar, despite these differences in representational geometry.
F. How Many Neurons Are Required for Concept Learning?.
Until now, we have assumed that a downstream cortical neuron has access to the entire neural representation. Can a more realistic neuron, which only receives inputs from a small fraction of IT-like neurons, still perform accurate few-shot learning? Similarly, can a neuroscientist who only records a few hundred neurons reliably estimate the geometry of concept manifolds (as we have attempted above)?
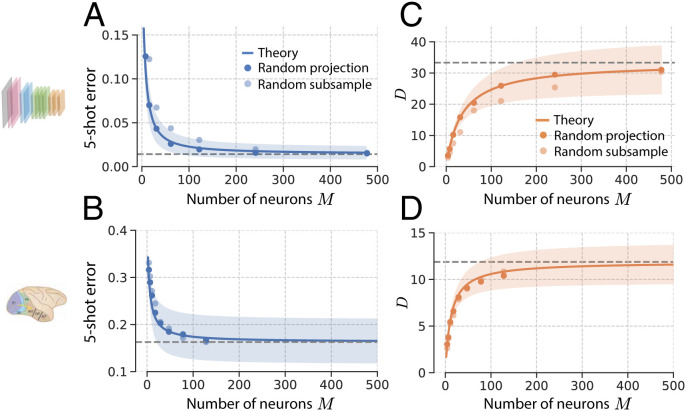
Here, we answer these questions by drawing on the theory of random projections (41–43) to estimate the effect of subsampling a small number of M neurons (see SI Appendix, section 5 for details). We find that subsampling causes distortions in the manifold geometry that decrease both the SNR and the estimated dimensionality, as a function of the number of recorded neurons M,
| [2] |
where and are the asymptotic SNR and dimensionality, given access to arbitrarily many neurons (SI Appendix, section 5). However, these distortions are negligible when M is large compared to the asymptotic dimensionality . Indeed, in both macaque IT and a trained DNN model (Fig. 6), a downstream neuron receiving inputs from only about 200 neurons performs essentially similarly to a downstream neuron receiving inputs from all available neurons (Fig. 6 A and B), and with recordings of about 200 IT neurons, the estimated dimensionality approaches its asymptotic value (Fig. 6 C and D; in the trained DNN and in the macaque IT).
Fig. 6.
Effect of number of sampled neurons on concept learning and manifold geometry. Five-shot learning experiments in ResNet50 on pairs of concepts from the ImageNet21k dataset (A) and in macaque IT on 64 × 63 pairs of novel visual concepts (24) (B), given access to only M neurons (light blue points) and given access to only M random linear combinations of the N available neurons (dark blue points). The blue curve represents the prediction from the theory of random projections (Eq. 2); the dashed line is its predicted asymptotic value, ; and the shaded region represents the SD over all pairs of concepts. In each case, the one-shot learning error remains close to its asymptotic value, provided that the number of recorded neurons M is large compared to the asymptotic manifold dimension . (C and D) The estimated manifold dimension D(M) as a function of M randomly sampled neurons (light orange points) and M random linear combinations (dark orange points) of the N neurons in the ResNet50 feature layer (C) and in macaque IT (D). The orange curve represents the prediction from the theory of random projections; the dashed line is its predicted asymptotic value, ; and the shaded region represents the SD over all pairs of concepts.
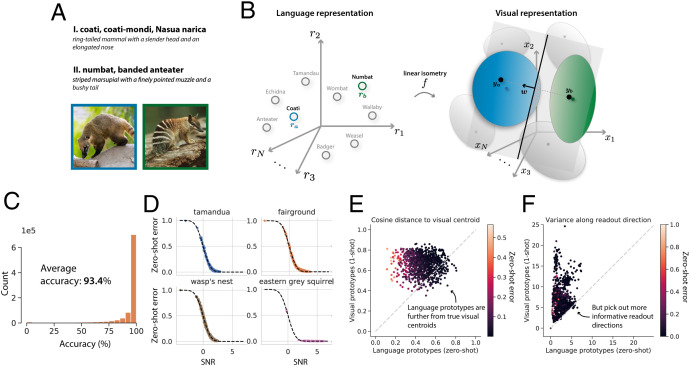
G. Visual Concept Learning Without Visual Examples.
Humans also possess the remarkable ability to learn new visual concepts using only linguistic descriptions, a phenomenon known as zero-shot learning (Fig. 7A). The rich semantic structure encoded in the geometry of visual concept manifolds (SI Appendix, Fig. 1) suggests that a simple neural mechanism might underlie this capacity, namely, learning visual concept prototypes from nonvisual language representations. To test this hypothesis, we obtain language representations for the names of the 1,000 familiar visual concepts used to train our DNN, from a standard word-vector embedding model (44) trained to produce a neural representation of all words in English based on cooccurrence statistics in a large corpus (Section P).
Fig. 7.
Visual concept learning without visual examples. (A) Example of a task showing the ability of humans to learn novel visual concepts given only language descriptions (zero-shot learning): Can you identify which image contains the “coati” and which the “numbat”? (B) To simulate this ability, we collect language representations from a word-vector embedding model (Left, gray circles) for the names of the 1,000 visual concepts used to train the DNN (e.g., “anteater” or “badger”), along with corresponding visual concept manifolds from the trained DNN (Right, gray ellipsoids). We learn a linear isometry f to map each language representation as closely as possible to its corresponding visual manifold centroid (Section P). To learn novel visual concepts (e.g., “coati” and “numbat”) without visual examples, we obtain their language representations from the language model and map them into the visual representation space via the linear isometry, . Treating the resulting representations as visual prototypes, we classify pairs of novel concepts by learning a linear classifier (gray hyperplane), which points along the difference between the prototypes, , passing through their midpoint. Generalization error (red hashed area) is evaluated by passing test images into the DNN and assessing whether their visual representations are correctly classified. (C) Generalization accuracy is high across all pairs of novel visual concepts. (D) Each panel shows the generalization error of 1 visual concept against the 999 others. Each point represents the average generalization error on one such pair of concepts. x axis: SNR (Eq. 3) obtained by estimating neural manifold geometry. y axis: Empirical generalization error measured in zero-shot learning experiments. Theoretical prediction (dashed line) shows a good match with experiments. Error bars, computed over many draws of the training and test examples, are smaller than the symbol size. (E) Visual prototypes from one-shot learning more closely match true concept manifold centroids than do language-derived prototypes, as measured by cosine similarity. (F) However, language prototypes pick out more informative readout directions: Concept manifolds vary less when projected onto readout directions derived from language prototypes than readout directions derived from one-shot visual prototypes.
Drawing inspiration from previous works that have trained mappings between visual embeddings and word embeddings (33, 45) or between word embeddings in multiple languages (46), we seek to learn a simple mapping between the language and vision domains (Fig. 7B). Remarkably, despite being optimized on independent objectives (word cooccurrence and object recognition), we find that the language and vision representations can be aligned by a simple linear isometry (rotation, translation, and overall scaling). Furthermore, this alignment generalizes to novel concepts, allowing us to construct prototypes for novel visual concepts by simply passing their names into the word-vector embedding model and applying the linear isometry. We use these language-derived prototypes to classify visual stimuli from pairs of novel visual concepts, achieving a 93.4% test accuracy (Fig. 7C). Intriguingly, this performance is slightly better than the performance of one-shot learning (92.0%), indicating that the name of a concept can provide at least as much information as a single visual example, for the purpose of classifying novel visual concepts (SI Appendix, Fig. 9).
Our geometric theory for few-shot learning extends naturally to zero-shot learning, allowing us to derive an analogous zero-shot learning SNR (SI Appendix, section 4),
| [3] |
where are the language-derived prototypes, and . This zero-shot learning SNR takes a different form from the few-shot learning SNR since language-derived prototypes are fixed, rather than varying from trial to trial. But note that the two expressions (Eqs. 1 and 3) agree in the limit where , and the language-derived prototypes perfectly match the concept manifold centroids. The signal (numerator) captures how well the language-derived prototypes match the true visual manifold centroids, while the noise (denominator) captures the extent of variation of the visual manifolds along the readout direction . Fig. 7D indicates a close match between this theory and zero-shot experiments.
To better understand why the zero-shot method performs so well (even outperforming one-shot learning), we compare the geometry of the language-derived prototypes to the geometry of the vision-derived prototypes used in one-shot learning. We find that although the vision-derived prototypes typically better match the true manifold centroids (Fig. 7E), so that the signal is in Eq. 3 is higher for vision-derived prototypes, language-derived prototypes pick out more informative readout directions, along which the visual manifolds vary less (Fig. 7F), so that the noise in Eq. 3 is smaller for language-derived prototypes. This suppression of noise is greater than the loss in signal, and, hence, language-derived prototypes perform better than one-shot vision-derived prototypes.*
H. Comparing Cognitive Learning Models on Naturalistic Tasks.
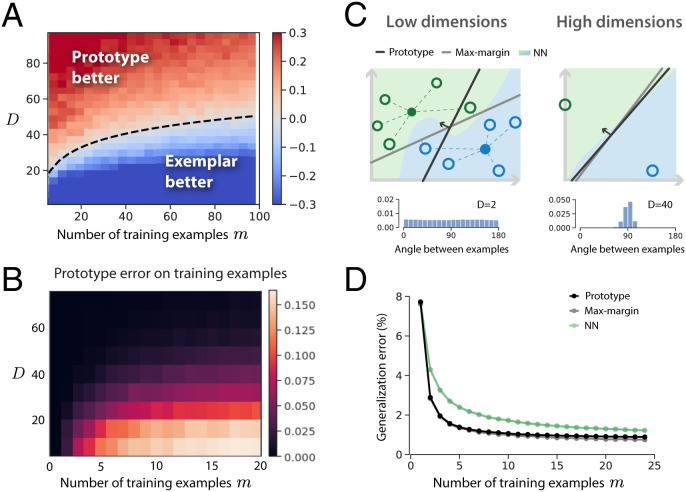
Our paradigm of using high-dimensional neural representations of naturalistic concepts as features for few-shot learning presents a unique opportunity to compare different concept-learning models, such as prototype and exemplar learning, in an ethologically relevant setting and explore their joint dependence on concept dimensionality D and the number of examples m. We formalize exemplar learning by a nearest-neighbor decision rule (NN; SI Appendix, section 6), which stores in memory the neural representation of all 2m training examples and classifies a test image according to the class membership of the nearest training example. We find that exemplar learning outperforms prototype learning when evaluated on low-dimensional concept manifolds with many training examples, consistent with past psychophysics experiments on low-dimensional artificial concepts (15, 47–49) (Fig. 8A and Section Q). However, prototype learning outperforms exemplar learning for high-dimensional naturalistic concepts and few training examples. In fact, to outperform prototype learning, exemplar learning requires a number of training examples exponential in the number of dimensions, for some constant D0 (SI Appendix, section 6). Hence, for high-dimensional manifolds, like those in trained DNNs and the macaque IT, prototype learning outperforms exemplar learning, given few examples.
Fig. 8.
Comparing cognitive learning models on naturalistic tasks. (A) We compare the performance of prototype and exemplar learning as a joint function of concept manifold dimensionality and the number of training examples, using novel visual concept manifolds from a trained ResNet50. We vary dimensionality by projecting concept manifolds onto their top D principal components. We formalize exemplar learning by NN (SI Appendix, section 6). Because the generalization error is very close to zero for m and D large, here, we plot . The dashed line demarcating the boundary is given by , reflecting the relationship predicted by our theory (SI Appendix, section 6). The constant 10 is chosen by a one-parameter fit. (B) Prototype learning error as a function of m and D when training examples are reused as test examples. A prototype classifier may misclassify one or more of the training examples themselves when concepts are low-dimensional and the number of training examples is large. However, this rarely happens in high dimensions, as illustrated in C. (C) In low dimensions, multiple training examples may overlap along the same direction (Inset histogram; distribution of angles between examples in DNN concept manifolds for D = 2). Hence, averaging these examples (open circles) to yield two prototypes (filled circles) may leave some of the training examples on the wrong side of the prototype classifier’s decision boundary (black line). In high dimensions, however, all training examples are approximately orthogonal (C, Inset histogram, D = 40), so such mistakes rarely happen. C also shows the decision boundaries of max-margin learning (gray line) and NN learning (green and blue regions), both of which perfectly classify the training examples. In low dimensions, prototype and max-margin learning may learn very different decision boundaries; however, in high dimensions, their decision boundaries are very similar, as quantified in D. (D) Empirical comparison of prototype, max-margin, and NN exemplar learning as a function of the number of training examples m (Section Q). When the number of training examples is small, prototype and SVM learning are approximately equivalent. For larger m, SVM outperforms prototype learning. NN learning performs worse than SVM and prototype learning for both small and intermediate m.
A well-known criticism of prototype learning is that averaging the training examples into a single prototype may cause the prototype learner to misclassify some of the training examples themselves (8). However, this phenomenon relies on training examples overlapping significantly along a given direction and almost never happens in high dimensions (Fig. 8B), where training examples are approximately orthogonal (Fig. 8C).
An intermediate model between prototype and exemplar learning is max-margin learning (50) (Fig. 8C). Like prototype learning, max-margin learning involves learning a linear readout; however, rather than pointing between the concept prototypes, its linear readout is chosen to maximize the distance from the decision boundary to the nearest training example of each concept (50) (SI Appendix, Fig. 12). Max-margin learning is more sophisticated than prototype learning, in that it incorporates not only the estimated manifold centroid, but also the variation around the centroid. Thus, it is able to achieve zero generalization error for large-m when concept manifolds are linearly separable, overcoming the limitation on the prototype learning SNR due to signal–noise overlaps in the large-m limit (Eq. 1 and Fig. 2D). However, like exemplar learning, it requires memory of all training examples. Comparing the three learning models on DNN concept manifolds, we find that prototype and max-margin learning are approximately equivalent for , and both outperform exemplar learning for m of small to moderate size (Fig. 8D and Section Q).
I. Discussion.
We have developed a theoretical framework that accounts for the remarkable accuracy of human few-shot learning of novel high-dimensional naturalistic concepts in terms of a simple, biologically plausible neural model of concept learning. Our framework defines the concepts that we can rapidly learn in terms of tight manifolds of neural activity patterns in a higher-order brain area. The theory provides readily measurable geometric properties of population responses (Fig. 2) and successfully links them to the few-shot learning performance of a simple prototype learning model. Our model yields remarkably high accuracy on few-shot learning of novel naturalistic concepts using DNN representations for vision (Figs. 1 and 3), which is in excellent quantitative agreement with theoretical prediction. We further show that the four geometric quantities identified by our theory undergo orchestrated transformations along the layers of trained DNNs and along the macaque ventral visual pathway, yielding a consistent improvement in performance along the system’s hierarchy (Figs. 4 and 5). We extend our theory to cross-domain learning and demonstrate that comparably powerful visual concept learning is attainable from linguistic descriptors of concepts without visual examples, using a simple map between language and visual domains (Fig. 7). We show analytically and confirm numerically that high few-shot learning performance is possible with as few as 200 IT-like neurons (Fig. 6).
A design tradeoff governing neural dimensionality.
A surprising result of our theory is that rapid concept learning is easier when the underlying variability of images belonging to the same object is spread across a large number of dimensions (Fig. 2 C and G). Thus, high-dimensional neural representations allow new concepts to be learned from fewer examples, while, as has been shown recently, low-dimensional representations allow for a greater number of familiar concepts to be classified (36, 37). Understanding the theoretical principles by which neural circuits negotiate this tradeoff constitutes an important direction for future research.
Asymmetry in few-shot learning.
We found that the pairwise generalization error of simple cognitive models, like prototype, exemplar, and max-margin learning, exhibits a dramatic asymmetry when only one or a few training examples are available (SI Appendix, Fig. 1). Our theory attributes this asymmetry to a bias arising from the inability of simple classifiers to estimate the variability of novel concepts from a few examples (Fig. 2 B and F). Investigating whether humans exhibit the same asymmetry and identifying mechanisms by which this bias could be overcome are important future directions. An interesting hypothesis is that humans construct a prior over the variability of novel concepts, based on the variability of previously learned concepts (51).
Connecting language and vision.
Remarkably, we found that machine-learning-derived language representations and visual representations, despite being optimized for different tasks across different modalities, can be linked together by an exceedingly simple linear map (Fig. 5), to enable learning novel visual concepts, given only language descriptions. Recent work has revealed that machine-learning-derived neural language representations match those in humans, as measured by both electrocorticography (ECOG) and functional MRI (fMRI) (52). Our results suggest that language and high-level visual representations of concepts in humans may indeed be related through an exceedingly simple map, a prediction that can be tested experimentally. Broadly, our results add plausibility to the tenets of dual-coding theory in human cognition (53).
Comparing brains and machines.
Computational neuroscience has recently developed increasingly complex high-dimensional machine-learning-derived models of many brain regions, including the retina (54–57); V1, V4, and IT (28, 58); motor cortex (59); prefrontal cortex (60); and entorhinal cortex (61, 62). Such increased model complexity raises foundational questions about the appropriate comparisons between brains and machine-based models (63). Previous approaches based on behavioral performance (19, 31, 64–66); neuron (54) or circuit (57) matching; linear regression between representations (28); or representational similarity analysis (30) reveal a reasonable match between the two. However, our higher-resolution decomposition of performance into a fundamental set of observable geometric properties reveals significant mismatches (Figs. 4 and 6D). For instance, intermediate representations that have previously been shown to be most predictive of responses in primate V4 are much higher-dimensional than the corresponding representations in V4. These mismatches call for a better understanding of their computational consequences and for more veridical models of the visual pathway.
Finally, our results (SI Appendix, Fig. 7) indicate that it is not only the network architecture and overall performance on object-recognition tasks that govern downstream performance and shape neural geometry, but also the number of concepts on which the model is trained. Hence, the size and structure of the dataset on which the model is trained likely play a key role when comparing brains and machines.
Comparing cognitive learning models on naturalistic concepts.
Our theory reveals that exemplar learning is superior to prototype learning given many examples of low-dimensional concepts, consistent with past laboratory experiments (15, 47, 48, 67), but is inferior to prototype learning given only a few examples of high-dimensional concepts, like those in DNNs and in primate IT (Fig. 8), shedding light on a 40-y-old debate (8). These predictions are consistent with a recent demonstration that a prototype-based rule can match the performance of an exemplar model on categorization of familiar high-dimensional stimuli (66). We go beyond prior work by 1) demonstrating that prototype learning achieves superior performance on few-shot learning of novel naturalistic concepts; 2) precisely characterizing the tradeoff as a joint function of concept manifold dimensionality and the number of training examples (Fig. 8); and 3) offering a theoretical explanation of this behavior in terms of the geometry of concept manifolds (SI Appendix, section 6).
Proposals for experimental tests of our model.
Our theory makes specific predictions that can be tested through behavioral experiments designed to evaluate human performance at learning novel visual concepts from few examples (see SI Appendix, Fig. 11 for a proposed experimental design). First, we predict a specific pattern of errors across these novel concepts, shared by neural representations in several trained DNNs (proxies for the human IT cortex), as well as neural representations in the macaque IT (Fig. 5 and SI Appendix, Fig. 11C). Second, we predict that humans will exhibit a marked asymmetry in pairwise few-shot learning performance, following the pattern derived in our theory (see SI Appendix, Fig. 11 for examples). Third, we predict how performance should scale with the number of training examples m (Fig. 8D). Matches between these predictions and experimental results would indicate that simple classifiers learned atop IT-like representations may be sufficient to account for human concept-learning performance. Deviations from these predictions may suggest that humans leverage more sophisticated higher-order processing to learn new concepts, which may incorporate human biases and priors on object-like concepts (51).
By providing fundamental links between the geometry of concept manifolds in the brain and the performance of few-shot concept learning, our theory lays the foundations for next-generation combined physiology and psychophysics experiments. Simultaneously recording neural activity and measuring behavior would allow us to test our hypothesis that the proposed neural mechanism is sufficient to explain few-shot learning performance and to test whether the four fundamental geometric quantities we identify correctly govern this performance. Furthermore, ECOG or fMRI could be used to investigate whether these four geometric quantities are invariant across primates and humans. Conceivably, our theory could even be used to design visual stimuli to infer the geometry of neural representations in primates and humans, without the need for neural recordings.
In conclusion, this work represents a significant step toward understanding the neural basis of concept learning in humans and proposes theoretically guided psychophysics and physiology experiments to further illuminate the remarkable human capacity to learn new naturalistic concepts from few examples.
Materials and Methods
J. Visual Stimuli.
Visual stimuli were selected from the ImageNet dataset, which includes 21,840 unique visual concepts. A subset of 1,000 concepts comprises the standard ImageNet1k training set used in the ImageNet Large Scale Visual Recognition Challenge (68). All DNNs studied throughout this work are trained on these 1,000 concepts alone. To evaluate few-shot learning on novel visual concepts, we gather an evaluation set of 1,000 concepts from the remaining 20,840 concepts not included in the training set, as follows. The ImageNet dataset is organized hierarchically into a semantic tree structure, with each visual concept a node in this tree. We include only the leaves of the tree (e.g., “wildebeest”) in our evaluation set, excluding all superordinate categories (e.g., “mammal”), which have many descendants. We additionally exclude leaves that correspond to abstract concepts, such as “green” and “pet.” Finally, the concepts in the ImageNet dataset vary widely in the number of examples they contain, with some concepts containing as many as 1,500 examples and others containing only a single example. Among the concepts that meet our criteria above, we select the 1,000 concepts with the greatest number of examples. From each novel concept, we choose a random set of 500 examples. A full list of the 1,000 concepts used in our evaluation set is available at GitHub (https://github.com/bsorsch/geometry-fewshot-learning).
K. Estimating the Geometry of Concept Manifolds.
Each visual stimulus elicits a pattern of activity across the sensory neurons in a high-order sensory layer, such as the IT cortex, or, analogously, the feature layer of a DNN. We collect the population responses to each of all P images in the dataset belonging to a particular visual concept in an N × P matrix X. To estimate the geometry of the underlying concept manifold, we construct the empirical covariance matrix , where is the manifold centroid. We then diagonalize the covariance matrix,
| [4] |
where are the eigenvectors of C and the associated eigenvalues. The each represent unique, potentially interpretable visual features [e.g., animate vs. inanimate, spiky vs. stubby, or short-haired vs. long-haired (22)]. Individual examples of the concept vary from the average along each of these “noise” directions. Some noise directions exhibit more variation than others, as governed by the Ri. Geometrically, the eigenvectors correspond to the principal axes of a high-dimensional ellipsoid centered at , and the Ri correspond to the radii along each axis. A useful measure of the total variation around the centroid is the mean squared radius, . R2 sets a natural length scale, which we use in our theory as a normalization constant to obtain interpretable, dimensionless quantities. Although we do not restrict the maximal number of available axes, which could be as large as the dimensionality of the ambient space, N, the number of directions along which there is significant variation is quantified by an effective dimensionality , called the participation ratio (35), which, in practical situations, is much smaller than N. The participation ratio arises as a key quantity in our theory (SI Appendix, section 3C).
L. Prototype Learning.
To simulate m-shot learning of novel concepts pairs, we present m randomly selected training examples of each concept to our model of the visual pathway, and collect their neural representations in a population of IT-like neurons. We perform prototype learning by averaging the representations of each concept into concept prototypes, . To evaluate the generalization accuracy, we present a randomly selected test example of concept a and determine whether its neural representation is closer in Euclidean distance to the correct prototype than it is to the incorrect prototype . This classification rule can be implemented by a single downstream neuron, which adjusts its synaptic weight vector to point along the difference between the two concept prototypes, , and adjusts its bias (or firing rate threshold) β to equal the average overlap of with each prototype, . We derive an analytical theory for the generalization error of prototype learning on concept manifolds in SI Appendix, section 3C, and we extend our model and theory to classification tasks involving more than two concepts in SI Appendix, section 3D.
M. Prototype Learning Experiments on Synthetic Concept Manifolds.
To evaluate our geometric theory, we perform prototype learning experiments on synthetic concept manifolds constructed with predetermined ellipsoidal geometry (Fig. 2 E–H). By default, we construct manifolds with and D = 50, and we sample the centroids and subspaces randomly under the constraint that the signal direction and the subspace directions are orthonormal, , so that the signal–noise overlaps are zero. We then vary each geometric quantity individually, over the ranges reflected in Fig. 2 E–H. To vary the signal, we vary from 1 to 2.5. To vary the bias over the interval , we fix and vary from 0 to . To vary the signal–noise overlaps, we construct ellipsoidal manifolds with one long direction, , and D – 1 short directions, . We then vary the angle θ between the signal direction and the first subspace basis vector by choosing , where . We vary θ from fully orthogonal () to fully overlapping (θ = 0).
N. DNN Concept Manifolds.
All DNNs studied throughout this work are standard architectures available in the PyTorch library (69) and are pretrained on the ImageNet1k dataset. To obtain novel visual concept manifolds, we randomly select P = 500 images from each of the never-before-seen visual concepts in our evaluation set, pass them into the DNN, and obtain their representations in the feature layer (final hidden layer). We collect these representations in an N × P response matrix Xa. for ResNet architectures. For architectures with neurons in the feature layer, we randomly project the representations down to dimensions using a random matrix . We then compute concept manifold geometry, as described in Section K. To study the layerwise behavior of manifold geometry, we collect the representations at each layer l of the trained DNN into an matrix . For the pixel layer, we unravel raw images into -dimensional vectors and randomly project down to N dimensions. Code is available at GitHub (https://github.com/bsorsch/geometry-fewshot-learning).
O. Macaque Neural Recordings.
Neural recordings of macaque V4 and IT were obtained from the dataset collected in Majaj et al. (24). This dataset contains 168 multiunit recordings in IT and 88 multiunit recordings in V4 in response to 3,200 unique visual stimuli, over presentations of each stimulus. Each visual stimulus is an image of 1 of 64 distinct synthetic three-dimensional objects, randomly rotated, positioned, and scaled atop a random naturalistic background. To obtain the concept manifold for object a, we collect the average response of IT neurons to each of the P = 50 unique images of object a in an response matrix , where , and compute the geometry of the underlying manifold, as described in Section K. We repeat for V4, obtaining a response matrix , where . We additionally simulate V1 neural responses to the same visual stimuli via a biologically constrained Gabor filter bank, as described in Dapello et al. (70) To compare with trained DNNs, we pass the same set of stimuli into each DNN and obtain a response matrix , as described in Section N. We then project this response matrix into , or dimensions to compare with IT, V4, or V1. In order to align V1, V4, and IT to corresponding layers in the trained DNN (as in Fig. 5D), we identify the DNN layers that are most predictive of V1, V4, and IT using partial least-squares regression with 25 components, as in Schrimpf et al. (32).
P. Visual Concept Learning Without Visual Examples by Aligning Visual and Language Domains.
To obtain language representations for each of the 1,000 familiar visual concepts from the ImageNet1k training dataset, we collected their embeddings in a standard pretrained word-vector embedding model (GloVe) (44). The word-vector embedding model is pretrained to produce neural representations for each word in the English language based on word cooccurrence statistics. Since concept names in the ImageNet dataset typically involve multiple words (e.g., “tamandua, tamandu, lesser anteater, Tamandua tetradactyla”), we averaged the representations for each word in the class name into a single representation , where Nl = 300 (see SI Appendix, Fig. 9 for an investigation of this choice). We collected the corresponding visual concept manifolds in a pretrained ResNet50. To align the language and vision domains, we gathered the centroids of the training manifolds into an matrix X0 and gathered the corresponding language representations into an matrix Y. We then learned a scaled linear isometry f from the language domain to the vision domain by solving the generalized Procrustes analysis problem , where , α is a scalar, is an orthogonal matrix, and is a translation.
Q. Comparing Cognitive Learning Models on Naturalistic Tasks.
In addition to prototype learning, we performed few-shot learning experiments using two other decision rules: a max-margin (SVM) classifier and a nearest-neighbors classifier (Fig. 8). Exemplar learning more generally allows for comparisons to more than just the nearest neighbor and involves the choice of a parameter β, which weights the contribution of each training example to the discrimination function. When , only the nearest neighbor contributes to the discrimination function. When β = 0, all training examples contribute equally. However, we find that the nearest-neighbors limit is close to optimal in our setting (SI Appendix, Fig. 12). Hence, we formalize exemplar learning by a nearest-neighbors decision rule. In order to study the effect of concept manifold dimensionality D on the performance of each learning rule (Fig. 8 A and B), we vary D by projecting concept manifolds onto their top D principal components.
Supplementary Material
Acknowledgments
We thank Uri Cohen, Gabriel Mel, and Daniel Yamins for helpful discussions. The work is partially supported by the Gatsby Charitable Foundation, the Swartz foundation, and the NIH (Grant 1U19NS104653). B.S. thanks the Stanford Graduate Fellowship for financial support. S.G. thanks the Simons and James S. McDonnell foundations and an NSF CAREER award.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
*But note that given two or more training examples (), vision-derived prototypes can average out this noise and achieve better overall performance (see SI Appendix, section 4B for details).
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2200800119/-/DCSupplemental.
Data, Materials, and Software Availability
Code and numerical simulations data have been deposited in GitHub (https://github.com/bsorsch/geometry-fewshot-learning) (71).
References
- 1.Smith L. B., Jones S. S., Landau B., Gershkoff-Stowe L., Samuelson L., Object name learning provides on-the-job training for attention. Psychol. Sci. 13, 13–19 (2002). [DOI] [PubMed] [Google Scholar]
- 2.Quinn P. C., Eimas P. D., Rosenkrantz S. L., Evidence for representations of perceptually similar natural categories by 3-month-old and 4-month-old infants. Perception 22, 463–475 (1993). [DOI] [PubMed] [Google Scholar]
- 3.Behl-Chadha G., Basic-level and superordinate-like categorical representations in early infancy. Cognition 60, 105–141 (1996). [DOI] [PubMed] [Google Scholar]
- 4.Carey S., Bartlett E., Acquiring a single new word in Papers and reports on child language development (1978), vol. 15, pp. 17–29. [Google Scholar]
- 5.Lake B. M., Salakhutdinov R., Tenenbaum J. B., Human-level concept learning through probabilistic program induction. Science 350, 1332–1338 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Nie W., et al., Bongard-logo: A new benchmark for human-level concept learning and reasoning. Adv. Neural Inf. Process. Syst. 33, 16468–16480 (2020). [Google Scholar]
- 7.Jiang H., et al., “Bongard-hoi: Benchmarking few-shot visual reasoning for human-object interactions” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (IEEE, Piscataway, NJ, 2022), pp. 19056–19065. [Google Scholar]
- 8.Murphy G. L., The Big Book of Concepts (MIT Press, Cambridge, MA, 2004). [Google Scholar]
- 9.Smith E. E., Medin D. L., Categories and Concepts (Harvard University Press, Cambridge, MA, 1981). [Google Scholar]
- 10.Freedman D. J., Riesenhuber M., Poggio T., Miller E. K., Experience-dependent sharpening of visual shape selectivity in inferior temporal cortex. Cereb. Cortex 16, 1631–1644 (2006). [DOI] [PubMed] [Google Scholar]
- 11.Karmarkar U. R., Dan Y., Experience-dependent plasticity in adult visual cortex. Neuron 52, 577–585 (2006). [DOI] [PubMed] [Google Scholar]
- 12.Op de Beeck H. P., Baker C. I., DiCarlo J. J., Kanwisher N. G., Discrimination training alters object representations in human extrastriate cortex. J. Neurosci. 26, 13025–13036 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Aristotle, Categories (Princeton University Press, Princeton, NJ, 1984). [Google Scholar]
- 14.Rosch E., Mervis C. B., Family resemblances: Studies in the internal structure of categories. Cognit. Psychol. 7, 573–605 (1975). [Google Scholar]
- 15.Nosofsky R. M., Similarity, frequency, and category representations. J. Exp. Psychol. Learn. Mem. Cogn. 14, 54–65 (1988). [Google Scholar]
- 16.Medin D. L., Smith E. E., Strategies and classification learning. J. Exp. Psychol. Hum. Learn. 7, 241–253 (1981). [Google Scholar]
- 17.Hebart M. N., Zheng C. Y., Pereira F., Baker C. I., Revealing the multidimensional mental representations of natural objects underlying human similarity judgements. Nat. Hum. Behav. 4, 1173–1185 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sanders C. A., Nosofsky R. M., Training deep networks to construct a psychological feature space for a natural-object category domain. Comput. Brain Behav. 3, 229–251 (2020). [Google Scholar]
- 19.Lake B. M., Zaremba W., Fergus R., Gureckis T. M., “Deep neural networks predict category typicality ratings for images” in Proceedings of the 37th Annual Meeting of the Cognitive Science Society, Noelle D. C., et al.,, Eds. (Cognitive Science Society, Austin, TX, 2015), pp. 1243–1248. [Google Scholar]
- 20.Logothetis N. K., Sheinberg D. L., Visual object recognition. Annu. Rev. Neurosci. 19, 577–621 (1996). [DOI] [PubMed] [Google Scholar]
- 21.Riesenhuber M., Poggio T., Hierarchical models of object recognition in cortex. Nat. Neurosci. 2, 1019–1025 (1999). [DOI] [PubMed] [Google Scholar]
- 22.Bao P., She L., McGill M., Tsao D. Y., A map of object space in primate inferotemporal cortex. Nature 583, 103–108 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.DiCarlo J. J., Zoccolan D., Rust N. C., How does the brain solve visual object recognition? Neuron 73, 415–434 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Majaj N. J., Hong H., Solomon E. A., DiCarlo J. J., Simple learned weighted sums of inferior temporal neuronal firing rates accurately predict human core object recognition performance. J. Neurosci. 35, 13402–13418 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dhillon G. S., Chaudhari P., Ravichandran A., Soatto S., “A baseline for few-shot image classification” in International Conference on Learning Representations (ICLR, 2020). [Google Scholar]
- 26.Tian Y., Wang Y., Krishnan D., Tenenbaum J. B., Isola P., “Rethinking few-shot image classification: a good embedding is all you need?” in European Conference on Computer Vision, Vedaldi A., Bischof H., Brox T., Frahm J. M., Eds. (Springer, Cham, 2020). pp. 266–282. [Google Scholar]
- 27.Radford A., et al., “Learning Transferable Visual Models From Natural Language Supervision” in Proceedings of the 38th International Conference on Machine Learning (PMLR), Meila M., Zhang T., Eds. (JMLR; 2021), pp. 8748–8763. [Google Scholar]
- 28.Yamins D. L., et al., Performance-optimized hierarchical models predict neural responses in higher visual cortex. Proc. Natl. Acad. Sci. U.S.A. 111, 8619–8624 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lotter W., Kreiman G., Cox D., A neural network trained for prediction mimics diverse features of biological neurons and perception. Nat. Mach. Intell. 2, 210–219 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kriegeskorte N., et al., Matching categorical object representations in inferior temporal cortex of man and monkey. Neuron 60, 1126–1141 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rajalingham R., et al., Large-scale, high-resolution comparison of the core visual object recognition behavior of humans, monkeys, and state-of-the-art deep artificial neural networks. J. Neurosci. 38, 7255–7269 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Schrimpf M., et al., Brain-score: Which artificial neural network for object recognition is most brain-like? bioRxiv [Preprint] (2018). https://www.biorxiv.org/content/10.1101/407007v2.
- 33.Snell J., Swersky K., Zemel R., Prototypical networks for few-shot learning. Adv. Neural Inf. Process. Syst. 30, 4078–4088 (2017). [Google Scholar]
- 34.Chen T., Kornblith S., Norouzi M., Hinton G., “A simple framework for contrastive learning of visual representations” in ICML’20: Proceedings of the International Conference on Machine Learning (PMLR), Daumé H., Singh A., Eds. (JMLR, 2020), pp. 1597–1607. [Google Scholar]
- 35.Gao P., et al., A theory of multineuronal dimensionality, dynamics and measurement. bioRxiv [Preprint] (2017). https://www.biorxiv.org/content/10.1101/214262v2. Accessed 15 January 2022.
- 36.Cohen U., Chung S., Lee D. D., Sompolinsky H., Separability and geometry of object manifolds in deep neural networks. Nat. Commun. 11, 746 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chung S., Lee D. D., Sompolinsky H., Classification and geometry of general perceptual manifolds. Phys. Rev. X 8, 031003 (2018). [Google Scholar]
- 38.Stringer C., Pachitariu M., Steinmetz N., Carandini M., Harris K. D., High-dimensional geometry of population responses in visual cortex. Nature 571, 361–365 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Recanatesi S., et al., Dimensionality compression and expansion in Deep Neural Networks. arXiv [Preprint] (2019). https://arxiv.org/abs/1906.00443. Accessed 15 January 2022.
- 40.Ansuini A., Laio A., Macke J. H., Zoccolan D., Intrinsic dimension of data representations in deep neural networks. arXiv [Preprint] (2019). https://arxiv.org/abs/1905.12784. Accessed 15 January 2022.
- 41.Dasgupta S., Gupta A., An elementary proof of a theorem of Johnson and Lindenstrauss. Random Structures Algorithms 22, 60–65 (2003). [Google Scholar]
- 42.Ganguli S., Sompolinsky H., Compressed sensing, sparsity, and dimensionality in neuronal information processing and data analysis. Annu. Rev. Neurosci. 35, 485–508 (2012). [DOI] [PubMed] [Google Scholar]
- 43.Trautmann E. M., et al., Accurate estimation of neural population dynamics without spike sorting. Neuron 103, 292–308.e4 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pennington J., Socher R., Manning C., GloVe: Global vectors for word representation. EMNLP 14, 1532–1543 (2014). [Google Scholar]
- 45.Socher R., et al., “Zero-shot learning through cross-modal transfer” in Advances in Neural Information Processing Systems, Pereira F., Burges C. J., Bottou L., Weinberger K. Q., Eds. (Curran Associates, Inc., 2013). [Google Scholar]
- 46.Wu S., Conneau A., Li H., Zettlemoyer L., Stoyanov V., Emerging cross-lingual structure in pretrained language models. arXiv [Preprint] (2019). https://arxiv.org/abs/1911.01464. Accessed 15 January 2022.
- 47.Reed S. K., Pattern recognition and categorization. Cognit. Psychol. 3, 382–407 (1972). [Google Scholar]
- 48.Palmeri T. J., Nosofsky R. M., Central tendencies, extreme points, and prototype enhancement effects in ill-defined perceptual categorization. Q. J. Exp. Psychol. A 54, 197–235 (2001). [DOI] [PubMed] [Google Scholar]
- 49.Smith J. D., Minda J. P., Prototypes in the mist: The early epochs of category learning. J. Exp. Psychol. Learn. Mem. Cogn. 24, 1411–1436 (1998). [Google Scholar]
- 50.Boser B. E., Guyon I. M., Vapnik V. N., “A training algorithm for optimal margin classifiers” in COLT’92: Proceedings of the Fifth Annual Workshop on Computational Learning Theory (Association for Computing Machinery, New York, 1992), pp. 144–152. [Google Scholar]
- 51.Tenenbaum J. B., Kemp C., Griffiths T. L., Goodman N. D., How to grow a mind: Statistics, structure, and abstraction. Science 331, 1279–1285 (2011). [DOI] [PubMed] [Google Scholar]
- 52.Schrimpf M., et al., The neural architecture of language: Integrative reverse-engineering converges on a model for predictive processing. bioRxiv [Preprint] (2020). https://www.biorxiv.org/content/10.1101/2020.06.26.174482v2. Accessed 15 January 2022.
- 53.Paivio A., Mental imagery in associative learning and memory. Psychol. Rev. 76, 241–263 (1969). [Google Scholar]
- 54.McIntosh L., Maheswaranathan N., Nayebi A., Ganguli S., Baccus S., “Deep learning models of the retinal response to natural scenes” in Advances in Neural Information Processing Systems, Lee D., Sugiyama M., Luxburg U., Guyon I., Garnett R., Eds. (Curran Associates, Inc., 2016), vol. 29, pp. 1369–1377. [PMC free article] [PubMed] [Google Scholar]
- 55.Ocko S. A., Lindsey J., Ganguli S., Deny S., The emergence of multiple retinal cell types through efficient coding of natural movies. Adv. Neural Inf. Process. Syst. 31, 458737 (2018). [Google Scholar]
- 56.Lindsey J., Ocko S. A., Ganguli S., Deny S., “A Unified Theory of Early Visual Representations from Retina to Cortex through Anatomically Constrained Deep CNNs” in Proceedings of the International Conference on Learning Representations (ICLR, 2019). [Google Scholar]
- 57.Tanaka H., et al., From deep learning to mechanistic understanding in neuroscience: The structure of retinal prediction. Adv. Neural Inf. Process. Syst. 32, 8537–8547 (2019). [PMC free article] [PubMed] [Google Scholar]
- 58.Yamins D. L., DiCarlo J. J., Using goal-driven deep learning models to understand sensory cortex. Nat. Neurosci. 19, 356–365 (2016). [DOI] [PubMed] [Google Scholar]
- 59.Sussillo D., Churchland M. M., Kaufman M. T., Shenoy K. V., A neural network that finds a naturalistic solution for the production of muscle activity. Nat. Neurosci. 18, 1025–1033 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Mante V., Sussillo D., Shenoy K. V., Newsome W. T., Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Sorscher B., Mel G. C., Ganguli S., Ocko S. A., A unified theory for the origin of grid cells through the lens of pattern formation. Adv. Neural Inf. Process. Syst. 32, 10003–10013 (2019). [Google Scholar]
- 62.Sorscher B., Mel G. C., Ocko S. A., Giocomo L., Ganguli S., A unified theory for the computational and mechanistic origins of grid cells. bioRxiv [Preprint] (2020). https://www.biorxiv.org/content/10.1101/2020.12.29.424583v1. Accessed 15 January 2022. [DOI] [PubMed]
- 63.Maheswaranathan N., Williams A. H., Golub M. D., Ganguli S., Sussillo D., Universality and individuality in neural dynamics across large populations of recurrent networks. Adv. Neural Inf. Process. Syst. 2019, 15629–15641 (2019). [PMC free article] [PubMed] [Google Scholar]
- 64.Singh P., Peterson J. C., Battleday R. M., Griffiths T. L., End-to-end deep prototype and exemplar models for predicting human behavior. arXiv [Preprint] (2020). https://arxiv.org/abs/2007.08723. Accessed 15 January 2022.
- 65.Sanders C. A., Nosofsky R. M., “Using deep-learning representations of complex natural stimuli as input to psychological models of classification” in Proceedings of the 40th Annual Conference of the Cognitive Science Society (Cognitive Science Society, Austin, TX, 2018), pp. 1025–1030. [Google Scholar]
- 66.Battleday R. M., Peterson J. C., Griffiths T. L., Capturing human categorization of natural images by combining deep networks and cognitive models. Nat. Commun. 11, 5418 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.McKinley S. C., Nosofsky R. M., Investigations of exemplar and decision bound models in large, ill-defined category structures. J. Exp. Psychol. Hum. Percept. Perform. 21, 128–148 (1995). [DOI] [PubMed] [Google Scholar]
- 68.Deng J., et al., “ImageNet: A large-scale hierarchical image database” in 2009 IEEE Conference on Computer Vision Pattern Recognition (IEEE, Piscataway, NJ, 2009), pp. 248–255. [Google Scholar]
- 69.Paszke A., et al., PyTorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 32, 8026–8037 (2019). [Google Scholar]
- 70.Dapello J., et al., Simulating a primary visual cortex at the front of CNNs improves robustness to image perturbations. bioRxiv [Preprint] (2020). https://www.biorxiv.org/content/10.1101/2020.06.16.154542v1. Accessed 15 January 2022.
- 71.Sorscher B., Code for: Neural representational geometry underlies few-shot concept learning. GitHub. https://github.com/bsorsch/geometry-fewshot-learning. Deposited 16 June 2021. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Code and numerical simulations data have been deposited in GitHub (https://github.com/bsorsch/geometry-fewshot-learning) (71).