PERTURBED FACTOR ANALYSIS: ACCOUNTING FOR GROUP DIFFERENCES IN EXPOSURE PROFILES

Abstract

In this article we investigate group differences in phthalate exposure profiles using NHANES data. Phthalates are a family of industrial chemicals used in plastics and as solvents. There is increasing evidence of adverse health effects of exposure to phthalates on reproduction and neurodevelopment and concern about racial disparities in exposure. We would like to identify a single set of low-dimensional factors summarizing exposure to different chemicals, while allowing differences across groups. Improving on current multigroup additive factor models, we propose a class of Perturbed Factor Analysis (PFA) models that assume a common factor structure after perturbing the data via multiplication by a group-specific matrix. Bayesian inference algorithms are defined using a matrix normal hierarchical model for the perturbation matrices. The resulting model is just as flexible as current approaches in allowing arbitrarily large differences across groups but has substantial advantages that we illustrate in simulation studies. Applying PFA to NHANES data, we learn common factors summarizing exposures to phthalates, while showing clear differences across groups.

1. Introduction.

Exposures to phthalates are ubiquitous. They are present in soft plastics, including vinyl floors, toys and food packaging. Medical supplies such as blood bags and tubes contain phthalates. They are also found in fragrant products such as soap, shampoo, lotion, perfume and scented cosmetics. There is substantial interest in studying levels of exposure of people in different groups to phthalates and in relating these exposures to health effects. This has motivated the collection of phthalate concentration data in urine in the National Health and Nutrition Examination Survey (NHANES) (https://wwwn.cdc.gov/nchs/nhanes). Excess levels of phthalates in blood/urine have been linked to a variety of health outcomes, including obesity (Kim and Park (2014), Zhang et al. (2014), Benjamin et al. (2017)) and birth outcomes (Bloom et al. (2019)). When they enter the body, phthalate parent compounds are broken down into different metabolites; assays measuring phthalate exposures target these different breakdown products. As these chemicals are often moderately to highly correlated, it is common to identify a small set of underlying factors (e.g., Weissenburger-Moser et al. (2017)). Epidemiologists are interested in interpreting these factors and in using them in analyses relating exposures to health outcomes.

However, many research groups have noticed a tendency to estimate very different factors in applying factor analysis to similar datasets or groups of individuals. For example, Maresca et al. (2016) examined data from three children’s cohorts and noted marked differences in factor structure in one of them. James-Todd et al. (2017) found variation in phthalate exposure patterns of pregnant women by race. Bloom et al. (2019) noted differences in both phthalate exposures and in associations with the birth outcomes by race. Certainly, we would like to allow for possible differences in exposures across groups; indeed, studying such differences is one of our primary interests. Such differences may relate to questions of environmental justice and may partly explain differences with ethnicity in certain health outcomes. However, even though the levels and specific sources of phthalate exposures may vary across groups, there is no reason to suspect that the fundamental relationship between levels of metabolites and latent factors would differ. Such differences in the factor structure are more likely to arise due to statistical uncertainty and sensitivity to slight differences in the data and can greatly complicate inferences on similarities and differences across groups.

To set the stage for discussing factor modeling of multigroup data, consider a typical factor model for p-variate data Y_i = (Y_i1, …, Y_ip)^T from a single group,

$$Y_i=\Lambda {\eta }_i+{ϵ}_i,{\eta }_i\sim \mathrm{N}(0,I_k),{ϵ}_i\sim \mathrm{N}(0,\Sigma ),$$ (1.1)

where it is assumed that data are centered prior to analysis, η_i = (η_i1, …, η_ik)^T are latent factors, Λ is a p × k factor loadings matrix and $\Sigma =\text{diag}({\sigma }_1^2,\dots ,{\sigma }_p^2)$ is a diagonal matrix of residual variances. Under this model, marginalizing out the latent factors η_i induces the covariance H = cov(Y_i) ΛΛ^T + Σ.

To extend (1.1) to data from multiple groups, most of the focus has been on decomposing the covariance into shared and group-specific components. A key contribution was Joint and Individual Variation Explained (JIVE) which identifies a low-rank covariance structure that is shared among multiple data types collected for the same subject (Feng, Hannig and Marron (2015), Lock et al. (2013), Feng et al. (2018)). In a Bayesian framework, Roy, Schaich-Borg and Dunson (2019) proposed Time Aligned Common and Individual Factor Analysis (TACIFA) for a related problem. More directly relevant to our phthalate application are the multistudy factor analysis (MSFA) methods of De Vito et al. (2018, 2019). These approaches replace Λη_i in (1.1) with an additive expansion containing shared and group-specific components. De Vito et al. (2018) implement a Bayesian version of MSFA (BMSFA), while De Vito et al. (2019) develop a frequentist implementation. Kim et al. (2018) propose a related approach using PCA.

The above methods are very useful in many applications but do not address our goal of improving inferences in our phthalate application by obtaining a common factor representation that holds across groups. In addition, we find that additive expansions can face issues with weak identifiability; the model can fit the data well by decreasing the contribution of the shared component and increasing that of the group-specific components. This issue can lead to slower convergence and mixing rates for sampling algorithms for implementing BMSFA and potentially higher errors in estimating the component factor loadings matrices.

We aim to identify a single set of phthalate exposure factors under the assumption that the data in different groups can be aligned to a common latent space via multiplication by a perturbation matrix. We represent the perturbed covariance in group j as $Q_j\Sigma Q_j^T$, where Σ is the common covariance and Q_j is the group-specific perturbation matrix. As in the common factor model in (1.1), the overall covariance Σ can be decomposed into a component characterizing shared structure and a residual variance. The utility of the perturbation model also extends beyond multigroup settings. In the common factor model the error terms only account for additive measurement error. We can obtain robust estimates of factor loadings from data in a single group by allowing for observation-specific perturbations. This accounts for both multiplicative and additive measurement error. In this case we define separate Q_i’s for each data vector Y_i. Here, Q_i ’s are multiplicative random effects with mean I_p. Thus, E(Q_iY_i) = E(Y_i) and the covariance structure on Q_i would determine the variability of Q_iY_i.

We take a Bayesian approach to inference using Markov chain Monte Carlo (MCMC) for posterior sampling, related to De Vito et al. (2018) but using our Perturbed Factor Analysis (PFA) approach instead of their additive BMSFA model. Model (1.1) faces well-known issues with nonidentifiability of the loadings matrix Λ (Früehwirth-Schnatter and Lopes (2018), Lopes and West (2004), Ročková and George (2016), Seber (2009)); this nonidentifiability problem is inherited by multiple group extensions such as BMSFA. It is very common in the literature to run MCMC ignoring the identifiability problem and then postprocess the samples. Aßmann, Boysen-Hogrefe and Pape (2016), McParland et al. (2014) obtain a postprocessed estimate by solving an orthogonal Procrustes problem but without uncertainty quantification (UQ). Roy, Schaich-Borg and Dunson (2019) postprocess the entire MCMC chain iteratively to draw inference with UQ. Lee, Lin and McLachlan (2018) address nonidentifiability by giving the latent factors nonsymmetric distributions, such as half-t or generalized inverse Gaussian. We instead choose heteroscedastic latent factors in the loadings matrix and postprocess based on Roy, Schaich-Borg and Dunson (2019). We find this approach can also improve accuracy in estimating the covariance, perhaps due to the flexible shrinkage prior that is induced.

The next section describes the data and the model in detail. In Section 3 prior specifications are discussed. Our computational scheme is outlined in Section 4. We study the performance of PFA in different simulation setups in Section 5. Section 6 applies PFA to NHANES data to infer a common set of factors summarizing phthalate exposures, while assessing differences in exposure profiles between ethic groups. We discuss extensions of our NHANES analysis in Section 7.

2. Data description and modeling.

NHANES is a population representative study collecting detailed individual-level data on chemical exposures, demographic factors and health outcomes. Our interest is in using NHANES to study disparities across ethnic groups in exposures. Data are available on chemical levels in urine recorded from 2009 to 2013 for 2749 individuals. We consider eight phthalate metabolites—Mono-(2-ethyl)-hexyl (MEHP), Mono-(2-ethyl-5-oxohexyl) (MEOHP), Mono-(2-ethyl-5-hydroxyhexyl) (MEHHP), Mono-2-ethyl-5-carboxypentyl (MECPP), Mono-benzyl (MBeP), Mono-ethyl (MEP),Mono-isobutyl (MiBP) and Mono-n-butyl (MnBP)—and measured in participants identifying with racial and ethnic groups: Mexican American (Mex), Other Hispanic (OH), Non-Hispanic White (N-H White), Non-Hispanic Black (N-H Black) and Other Race (Other) which includes multiracial. Previous work has shown differences across ethnic groups in patterns of use of products that contain phthalates (Taylor et al. (2018)) and in measured phthalate concentrations (James-Todd et al. (2017)). Recent work has also indicated exposure effects themselves may vary across ethnic groups (Bloom et al. (2019)), but this may be difficult to disentangle if summaries of exposure lack sufficient robustness and generalizability.

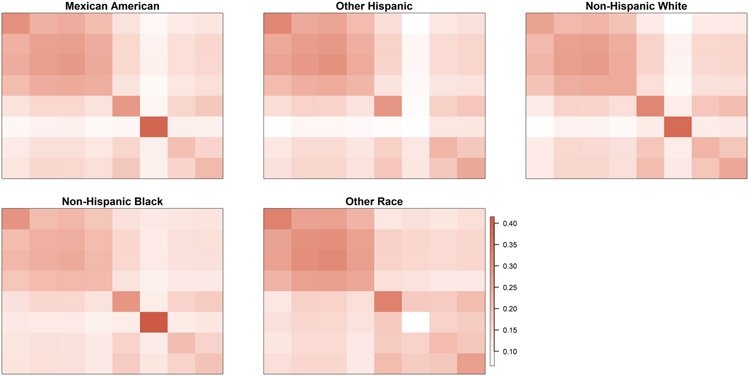
We summarize the average level of each chemical in each group in Table 1. In Table 2 we compute the Hotelling T² statistic between each pair of groups. As noted in Bloom et al. (2019), exposure levels were generally higher among non-whites. For each phthalate variable we also fit a one-way ANOVA model to assess differences across the groups taking Mexican–Americans as the baseline. The results are included in Tables 2-6 in the Supplementary Materials (Roy et al. (2021)). For the majority of phthalates, concentrations are lowest among non-Hispanic whites. We plot group-specific covariances in Figure 1. It is evident that there is shared structure with some differences across the groups.

Table 1.

NHANES data comparison across ethnic groups in terms of number of participants and average levels of different phthalate chemicals, with standard deviations in brackets

	Mex	OH	N-H White	N-H Black	Other/multi
Number of participants	566	293	1206	516	168
MnBP	3.85 (1.96)	4.31 (4.96)	3.56 (2.17)	4.21 (1.81)	3.76 (2.11)
MiBP	2.88 (1.36)	3.21 (1.70)	2.52 (1.20)	3.47 (1.67)	2.79 (1.21)
MEP	8.32 (6.64)	9.51 (6.99)	6.91 (5.43)	11.16 (9.38)	7.33 (7.57)
MBeP	2.79 (1.58)	2.78 (1.61)	2.70 (1.67)	3.06 (1.77)	2.56 (1.68)
MECPP	4.80 (3.68)	4.55 (2.68)	4.16 (2.40)	4.36 (2.38)	4.34 (2.64)
MEHHP	3.83 (3.01)	3.73 (2.59)	3.45 (2.25)	3.79 (2.26)	3.57 (2.45)
MEOHP	3.11 (2.41)	3.00 (1.92)	2.79 (1.69)	3.05 (1.71)	2.86 (1.86)
MEHP	1.58 (1.23)	1.59 (1.29)	1.33 (0.89)	1.61 (0.99)	1.58 (1.31)

Table 2.

Hotelling T² statistic between phthalate levels for each pair of groups in NHANES

	Mex	OH	N-H White	N-H Black	Other/multi
Mex	0.00	31.84	108.59	191.93	28.04
OH	31.84	0.00	156.45	63.48	28.69
N-H White	108.59	156.45	0.00	409.64	55.51
N-H Black	191.93	63.48	409.64	0.00	101.90
Other/multi	28.04	28.69	55.51	101.90	0.00

Fig. 1.

Covariance matrices of the phthalate chemicals across different ethnic groups for NHANES data.

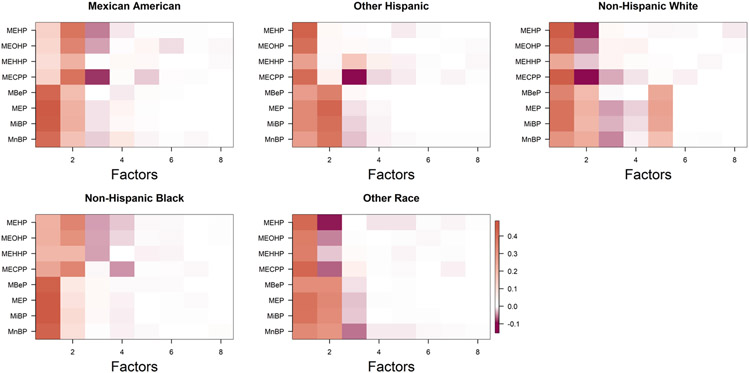
Fitting the common factor model (1.1) separately for each group, we obtain noticeably different loadings structures, as depicted in Figure 2. Throughout the article, including for Figures 1 and 2, we plot matrices using the mat2cols() function for R package IMIFA (Murphy, Viroli and Gormley (2020a, 2020b)). This function standardizes the color scale across the different matrices. We choose color palettes coral3 and deeppink4 from R package RColorBrewer (Neuwirth (2014)) for positive and negative entries, respectively. Zero entries are white, and the color gradually changes as the value moves away from zero. In the next subsection we propose a novel approach for multigroup factor analysis to identify common phthalate factors.

Fig. 2.

Estimated loadings matrices for different ethnic groups in NHANES based on applying separate Bayesian factor analyses using the approach of Bhattacharya and Dunson (2011).

2.1. Multigroup model.

We have data from multiple groups, with the groups corresponding to individuals in different racial and ethnic categories in NHANES. Each p-dimensional mean-centered response Y_ij, belonging to group G_j, for j ∈ 1 : J and i ∈ 1 : n_j, is modeled as

$$\begin{gathered} Q_j{Y}_{ij}=\Lambda {\eta }_{ij}+{ϵ}_{ij}, \\ {Q}_j\sim {\text{MN}}_{p\times p}(I_p,U,V),{\eta }_{ij}\sim \mathrm{N}(0,E), \\ {ϵ}_{ij}\sim \mathrm{N}(0,\Sigma ). \end{gathered}$$ (2.1)

The perturbation matrices Q_j are of dimension p × p, and follow a matrix normal distribution, with isotropic covariance U = V αI_p. The latent factors η_ij are heteroscedastic, so that E is diagonal with nonidentical entries such that E = diag(e₁, …, e_k) with k factors in the model and Σ = diag(σ₁, …, σ_p). We discuss advantages of choosing heteroscedastic latent factors in more detail in Section 2.3. After integrating out the latent factors, observations are marginally distributed as $Y_{ij}\sim \mathrm{N}(0,Q_j^{-1}[\Lambda E{\Lambda }^T+\Sigma ](Q_j^{-1}{)}^T)$. If we write $Q_j^{-1}=I_p+{\Psi }_j$, then Λ is the shared loadings matrix, and Ψ_jΛ is a group-specific loadings matrix. We can quantify the magnitude of perturbation as ∥Ψ_j∥_F, where ∥ · ∥_F stands for the Frobenius norm. For identifiability of Q_j ’s, we consider Q₁ = I_p and n₁ ≥ 2. We call our model Perturbed Factor Analysis (PFA).

2.1.1. Model properties.

Let Ω₁ and Ω₂ be two positive definite (p.d.) matrices. Then, there exist nonsingular matrices A and B, where Ω₁ = AA^T and Ω₂ = BB^T. By choosing E = AB⁻¹, we have Ω₁ = EΩ₂E^T. If the two matrices Ω₁ and Ω₂ are close, then E will be close to the identity. However, E is not required to be symmetric. In our multigroup model in (2.1), the Q_js allow for small perturbations around the shared covariance matrix H = ΛEΛ^T + Σ. We define the following class for the Q_j ’s:

$${\mathcal{C}}_{ϵ}=\{Q:\Vert Q-I_p{\Vert }_F\le ϵ\}.$$

The index ϵ controls the amount of deviation across groups. In (2.1) we define U = V = αI_p, for some small α, which we call the perturbation parameter. By choosing U = V to be isotropic covariances, we impose uniform perturbation across all the rows and columns around I_p. However, the perturbation matrices themselves are not required to be symmetric.

Lemma 1. P(Q_i ∉ C_ϵ) ≤ exp(−ϵ²/2α²).

The proof follows from Chebychev’s inequality. This result allows us to summarize the level of induced perturbation for any given α. Using this lemma, we can show the following result:

$$\begin{gathered} \text{KL}(\mathrm{N}(0,Q_j^{-1}[\Lambda E{\Lambda }^T+\Sigma ](Q_j^{-1}{)}^T),\mathrm{N}(0,Q_l^{-1}[\Lambda E{\Lambda }^T+\Sigma ](Q_l^{-1}{)}^T)) \\ \lesssim \mid \Vert Q_j^{-1}{\Vert }_F^2-\Vert Q_l^{-1}{\Vert }_F^2\mid . \end{gathered}$$

Therefore, the Kullback–Leibler divergence between the marginal distributions of any two groups j and l can be bounded by $\mid \Vert Q_j^{-1}{\Vert }_F^2-\Vert Q_l^{-1}{\Vert }_F^2\mid$ up to some constant. We define a divergence statistic between groups j and l as $d_{jl}=\sqrt{\frac{\mid \Vert Q_j^{-1}{\Vert }_F^2-\Vert Q_l^{-1}{\Vert }_F^2\mid }{p^2}}$. This generates a divergence matrix D = ({d_jl}), where larger d_jl implies a greater difference between the two groups.

As in other factor modeling settings, it is important to carefully choose the number of factors. This is simpler for PFA than for other multigroup factor analysis models, because we only need to select a single number of factors instead of separate values for shared and individual-specific components. Indeed, we can directly apply methods developed in the single group setting (Bhattacharya and Dunson (2011)). Due to heteroscedastic latent factors, we can directly use the posterior samples of the loading matrices without applying factor rotation. Computationally, PFA tends to be faster than multigroup factor models such as BMSFA due to a smaller number of parameters and better identifiability, leading to better mixing of Markov chain Monte Carlo (MCMC).

2.1.2. Choosing the parameter α for multigroup data.

The parameter α controls the level of perturbation across groups. We use a cross-validation technique to choose α based on 10 randomly chosen 50–50 splits. We randomly divide each group 50/50 into training and test sets 10 times. Then, for a range of α values we fit the model on the training data and calculate the average predictive log-likelihood of the test set for all the 10 random splits. After integrating out the latent factors, the predictive distribution is Q_jY_ij ∼ N(0, ΛEΛ^T Σ). If there are multiple values of α with similar predictive log-likelihoods, then the smallest α is chosen.

Alternatively, we can take a fully Bayesian approach and put a prior on α. We call this method Fully Bayesian Perturbed Factor Analysis (FBPFA). We see that FBPFA performs similarly to PFA in practice but involves a slightly more complex MCMC implementation. PFA avoids sensitivity to the prior for α but requires the computational overhead of cross-validation, ignores uncertainty in estimating α and can, potentially, be less efficient in requiring a holdout sample.

2.2. Measurement-error model.

We can modify the multigroup model to obtain improved factor estimates in single group analyses by considering observation-level perturbations. Here, we observe Y_ij ’s for j = 1, …, m_i, which are m_i, many proxies of “true” observation W_i with multiplicative measurement errors $Q_{ij}^{-1}’\mathrm{s}$ such that W_i = Q_ijY_ij. The modified model is

$$\begin{gathered} Q_{ij}{Y}_{ij}=\Lambda {\eta }_i+{ϵ}_{ij},{ϵ}_{ij}\sim \mathrm{N}(0,\Sigma ), \\ {Q}_{ij}\sim {\text{MN}}_{p\times p}(I_p,U,V),{\eta }_i\sim \mathrm{N}(0,E). \end{gathered}$$ (2.2)

In this case the Q_ij ’s apply a multiplicative perturbation to each data vector. We have $Y_{ij}=Q_{ij}^{-1}{W}_i$ where $Q_{ij}^{-1}$ is a matrix. Thus, here the measurement errors are $U_{ij}=(Q_{ij}^{-1}-I_p)W_i$ and E(U_ij∣W_i) = 0. This model is different from the multiplicative measurement error model of Sarkar et al. (2018). In their paper, observations Y_ij ’s are modeled as Y_ij = W_i ◦ U_ij, where ◦ denotes the elementwise dot product and U_ij ’s are independent of W_i with E(U_ij) = 1. Thus, the measurement error in the lth component (i.e., U_ijl) is dependent on W_i primarily through W_il. However, in our construction the measurement errors are a linear function of the entire W_i.

This is a much more general setup than Sarkar et al. (2018). With this generality comes issues in identifying parameters in the distributions of Q_ij and Y_ij. For simplicity, we again assume U = V = αI_p. In this case we have

$$\begin{gathered} E(Q_{ij}{Y}_{ij})=0, \\ V(Q_{ij}{Y}_{ij})=E(V(Q_{ij}{Y}_{ij}\mid Q_{ij}))+V(E(Q_{ij}{Y}_{ij}\mid Q_{ij})) \\ =E(V(Q_{ij}{Y}_{ij}\mid Q_{ij}))+0={\alpha }^{2}s{I}_p+H,s=\sum _{j=1}^p{H}_{jj}. \end{gathered}$$

Thus, only the diagonal elements of H are not identifiable, and the perturbation parameter α does not influence the dependence structure among the variables. Hence, with our heteroscedastic latent factors we can still recover the loading structure. To tune α, we can use the marginal distributions Q_ijY_ij ∼ N(0, α²sI_p + H) to develop a cross validation technique when m_i > 1 for all i = 1, …, n, as in Section 2.1.2. We split the data into training and testing sets. Then, fit the model in the training set, and find the α minimizing the predictive log-likelihood in the test set. We can alternatively estimate α as in FBPFA by using a weakly informative prior concentrated on small values, while assessing sensitivity to hyperparameter choice.

2.3. The special case Q_j = I_p for all j.

For data within a single group without measurement errors (in the sense considered in the previous subsection), we can modify PFA by taking Q_j = I_p for all j. Then, the model reduces to a traditional factor model with heteroscedastic latent factors,

$$\begin{gathered} Y_i=\Lambda {\eta }_i+{ϵ}_i,{ϵ}_i\sim \mathrm{N}(0,\Sigma ), \\ {\eta }_i\sim \mathrm{N}(0,E), \end{gathered}$$ (2.3)

where E is assumed to be diagonal with nonidentical entries. Integrating out the latent factors, the marginal likelihood is Y_i ∼ N(0, ΛEΛ^T + Σ). Except for the diagonal matrix E, the marginal likelihood is similar to the marginal likelihood for a traditional factor model. As E has nonidentical diagonal entries, the likelihood is no longer invariant under arbitrary rotations. For the factor model in (1.1), (Λ, _η) and (ΛR, R^T _η) have equivalent likelihoods for any orthonormal matrix R. This is not the case in our model unless R is a permutation matrix. Thus, this simple modification over the traditional factor model helps to efficiently recover the loading structure. This is demonstrated in Case 1 of Section 5. We also show that the posterior is weakly consistent in the Supplementary Materials (Roy et al. (2021)).

3. Prior specification.

As in Bhattacharya and Dunson (2011), we put the following prior on Λ to allow for automatic selection of rank and easy posterior computation:

$$\begin{gathered} {\lambda }_{lk}\mid {\varphi }_{lk},{\tau }_k\sim \mathrm{N}(0,{\varphi }_{lk}^{-1}{\tau }_k^{-1}), \\ {\varphi }_{lk}\sim \text{Gamma}(v_1,v_1),{\tau }_k=\prod _{i=1}^k{\delta }_i \\ {\delta }_1\sim \text{Gamma}({\kappa }_1,1),{\delta }_i\sim \text{Gamma}({\kappa }_2,1)\text{for}i\ge 2. \end{gathered}$$

The parameters ϕ_lk control local shrinkage of the elements in Λ, whereas τ_k controls column shrinkage of the kth column. We follow the guidelines of Durante (2017) to choose hyperparameters that ensure greater shrinkage for higher indexed columns. In particular, we let κ₁ = 2.1 and κ₂ = 3.1 which works well in all of our simulation experiments.

Suppose we initially choose the number of factors to be too large. The above prior will then tend to induce posteriors for ${\tau }_k^{-1}$ in the later columns that are concentrated near zero, leading to λ_lk ≈ 0 in those columns. The corresponding factors are then effectively deleted. In practice, one can either leave the extra factors in the model, as they will have essentially no impact, or conduct a factor selection procedure by removing factors having all their loadings within °ζ of zero. Both approaches tend to have similar performance in terms of posterior summaries of interest. We follow the second strategy, motivated by our goal of obtaining a small number of interpretable factors summarizing phthalate exposures. In particular, we apply the adaptive MCMC procedure of Bhattacharya and Dunson (2011) with ζ = 1 × 10⁻³.

For the heteroscedastic latent factors, each diagonal element of E has an independent prior,

$$e_i\sim \text{IG}(u,0.1)$$

for some constant u. In our simulations we see that u has minimal influence on the predictive performance of PFA. However, as u increases, more shrinkage is placed on the latent factors. We choose u = 10 for most of our simulations. For the residual error variance Σ, we place a weakly informative prior on the diagonal elements,

$${\sigma }_i\sim \text{IG}(0.1,0.1).$$

In our simulations a weakly informative IG(0.1,0.1) prior on α works well in terms of both predictive performance and estimation of the loading structure, including in single group analyses.

4. Computation.

Because all of the parameters have conjugate full conditional distributions, posterior inference is straightforward with a Gibbs sampler. For the model in (2.1), the full conditional of the perturbation matrix Q_j is

$$\text{vec}(Q_j)\mid Y\sim \mathrm{N}({\Gamma }_j(V\otimes U{)}^{-1}\text{vec}(I_p),{\Gamma }_j),$$

where Г_j = [(V ⊗ U)⁻¹ + S_j ⊗ H⁻¹]⁻¹ and $S_j={\sum }_i{Y}_{ij}{Y}_{ij}^T$. The notation ⊗ stands for Kronecker’s product. The full conditionals for all other parameters are described in Bhattacharya and Dunson (2011), replacing Y_ij by Q_jY_ij. For the model in (2.2), the full conditional of Q_ij is

$$\text{vec}(Q_{ij})\mid Y\sim \mathrm{N}({\Gamma }_{ij}(V\otimes U{)}^{-1}\text{vec}(I_p),{\Gamma }_{ij}),$$

where Г_ij = (V ⊗ U)⁻¹ + S_ij ⊗ H⁻¹]⁻¹ and $S_j=Y_{ij}{Y}_{ij}^T$. Other parameters can again be updated using the results in Bhattacharya and Dunson (2011), replacing Y_ij by Q_ijY_ij. To sample the entire vec(Q_ij) or vec(Q_j) together, we need to invert a p² × p² matrix at each step. Instead, we iteratively update the columns of Q_ij or Q_j which does not require matrix inversion when U = V = αI_p. For simplicity in notation, we only show the update for the columns in Q_j of the model in (2.1). The full conditional of the lth column in Q_j is

$$Q_{j,l}\mid Y\sim \mathrm{N}(M_l{V}_l,V_l),$$

where $V=1∕({\sum }_{k\in G_j}{Y}_{l,k}^2∕\text{diag}(\Sigma )+1∕\alpha )$ and M_l = −∑k∈G_j (Q_j,−l^Y−l,k − Λη_k)Y_l,k/Σ + gl/α with Σ the diagonal error covariance matrix. Here, Q_j,−l denotes the p × (p − 1) dimensional matrix removing the lth column from Q_j. Similarly, Y_−l,k denotes the response of the kth individual from group G_j, removing the lth variable and _gl the p-dimensional vector with one in the lth entry. If we put a prior on α, the posterior distribution of α is given by $\text{IG}(0.1+(J-1)p^2,0.1+{\sum }_j\Vert Q_j-I_p{)}^2{\Vert }_F^2)$ for the model in (2.1) and for the model in (2.2); the posterior distribution of α is $\text{IG}(0.1+p^2{\sum }_i{m}_i,0.1+{\sum }_{ij}\Vert Q_{ij}-I_p{)}^2{\Vert }_F^2)$. The posterior distribution of ${\sigma }_{1l}^2$ is $\text{IG}(0.1+n∕2,0.1+{\sum }_{j=1}^J{\sum }_{k\in G_j}(Q_j(l,)Y_{kj}-{\lambda }_l,{\eta }_{kj}{)}^2∕2)$, where Q_j(l,) denotes the lth row of Q_j. The posterior distribution of ${\sigma }_{2l}^2$ is $\text{IG}(0.1+n∕2,0.1+{\sum }_{j=1}^J{\sum }_{k\in G_j}{\eta }_{l,kj}^2∕2)$.

5. Simulation study.

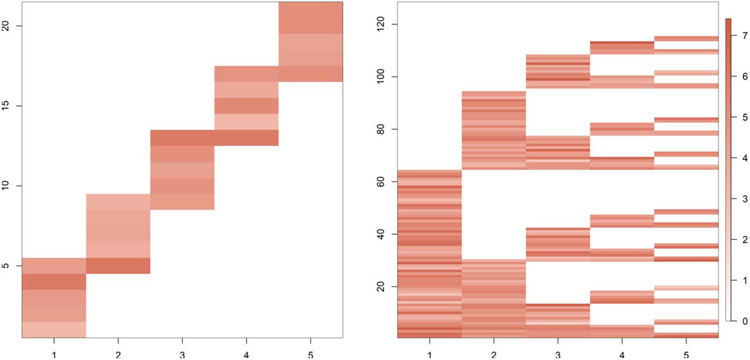
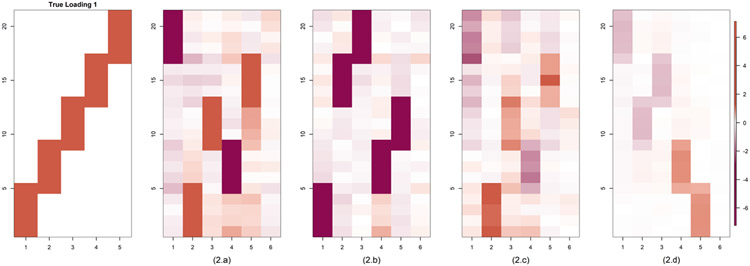
In this section we study the performance of PFA in various simulation settings. As ground truth we consider the two loading matrices given in Figure 3. These are similar to ones considered in Ročková and George (2016). R code to generate the data is provided in the github page https://github.com/royarkaprava/Perturbed-factor-model. The two matrices both have five columns, the first has 21 rows and the second has 128 rows. We compare the estimated loading matrices for different choices of the perturbation parameter α and the shape parameter u, controlling the level of shrinkage on the diagonal entries of E.

Fig. 3.

Simulation study true loading matrices of dimension 25 (Loading 1) and 128 × 5 (Loading 2), respectively.

For the single group case we compare with the method of Bhattacharya and Dunson (2011) (B&D) which corresponds to the special case of our approach that fixes the perturbation matrices and latent factor covariances equal to the identity. A point estimate of the loading matrix for B&D is calculated by postprocessing the posterior samples. We use the algorithm of Aßmann, Boysen-Hogrefe and Pape (2016) to rotationally align the samples of Λ, as in De Vito et al. (2018). In contrast, our method uses the postprocessing algorithm of Roy, Schaich-Borg and Dunson (2019). For the multigroup case we compare our estimates with Bayesian Multi-Study Factor Analysis (BMSFA). We use the MSFA package at https://github.com/rdevito/MSFA.

We compare the different methods using predictive log-likelihood. Simulated data are randomly divided 50/50 into training and test sets. After fitting each model on the training data, we calculate the predictive log-likelihood of the test set. All methods are run for 7000 iterations of the Gibbs sampler, with 2000 burn-in samples. Each simulation is replicated 30 times.

5.1. Case 1: Single group, Q_j = I_p.

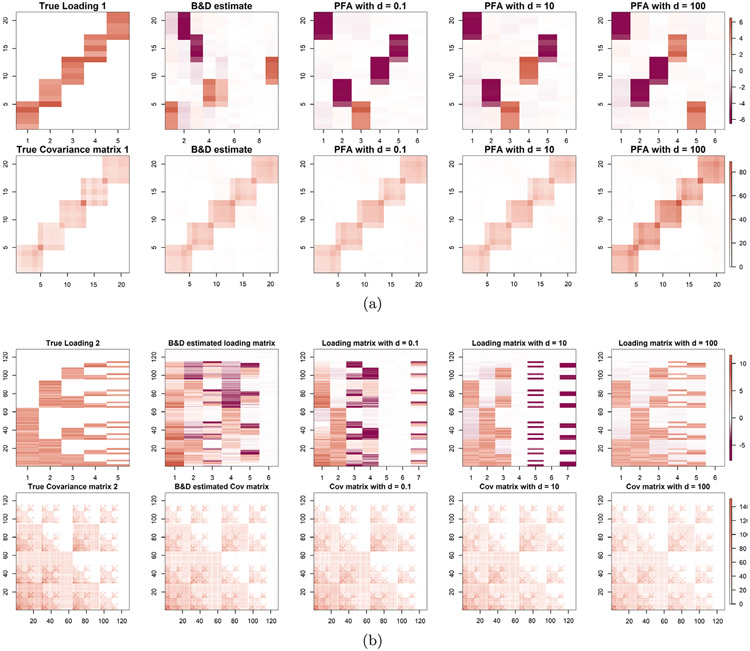
We first consider single group factor analysis. Starting with the two loading matrices in Figure 3, we simulate latent factors from N(0, I₅) and generate datasets of 500 observations, with residual variance Σ = I₅. We compare B&D with our method when Q_j = I₅, so the only adjustment is to use heteroscedastic latent factors. Note that the simulated latent factors actually have identical variances.

In Tables 3 and 4, we compare methods by MSE of the estimated vs. true covariance matrix. For the loading matrix 1, B&D had an MSE of 2.59 which is dominated by our method across a range of values of u.

Table 3.

MSE of estimated covariance matrix for loading matrix 1, across different values of u

u	MSE
0.1	1.04
10	1.32
100	1.38

Table 4.

MSE of estimated covariance matrix for loading matrix 2, across different values of u

u	MSE
0.1	5.21
10	9.45
100	10.32

For the loading matrix 2, B&D had an MSE of 10.81. Again, our method beats this across a range of values of u. The B&D model is a special case of PFA with E = I_p in (2.3). We conjecture that the gains seen for PFA are due to the more flexible induced shrinkage structure on the covariance matrix.

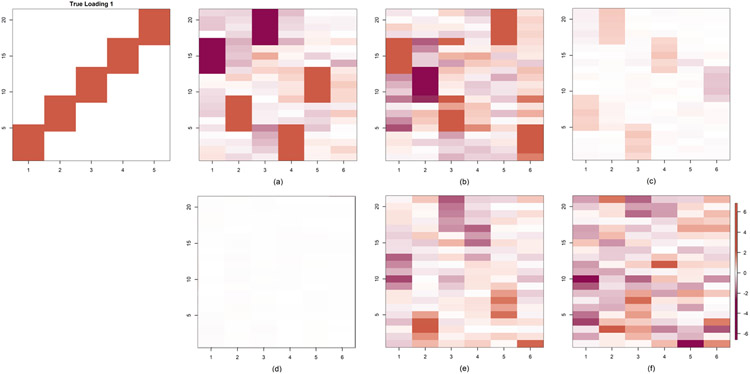
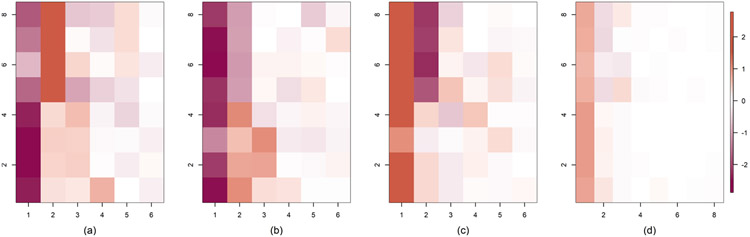
We compare the estimated and true loading matrices in Figure 4. Throughout the paper, PFA estimated loadings are based on $\widehat{\Lambda }{\widehat{E}}^{1∕2}$, where $\widehat{\Lambda }$ and $\widehat{E}$ are the estimated loading and covariance matrix of the factors, respectively. This makes the loadings comparable to methods that use identity covariance for the latent factors. PFA performs overwhelmingly better at estimating the true loading structure compared with B&D FA. The first five columns of the estimated loadings based on PFA are very close to the true loading structure under some permutation. This gain over B&D may be due to a combination of the more flexible shrinkage structure and the different postprocessing scheme. On comparing $\widehat{\Lambda }{\widehat{E}}^{1∕2}$ for different choices of u, we see that the estimates are not sensitive to the hyperparameter u. Estimation MSE is better for smaller u, but the general structure of the loadings matrix is recovered accurately for all u.

Fig. 4.

Comparison of true and estimated loading matrices and covariance matrices for Case 1. Comparison of B&D FA with our method for different choices of u. Results for loading matrix 1 are in (a) and two in (b). For all the cases, we fix Q_j = I .The color gradient added in the last image of each row holds for all the images in that row.

5.2. Case 2: Multigroup, multiplicative perturbation.

In this case we simulate data from the multigroup model in (2.1) for i = 1, …, 500. Observations Y_i are first generated using the same method as in Case 1. The data are then split into 10 groups of 50 observations such that G_j = {Y_k : 50(j – 1) ≤ k ≤ 50j} for j = 1, …, 10. The groups are perturbed using matrices Q_j0 ~ MN(I_p, α₀I_p, α₀I_p) for different choices of α₀, setting Q₁ = I_p.

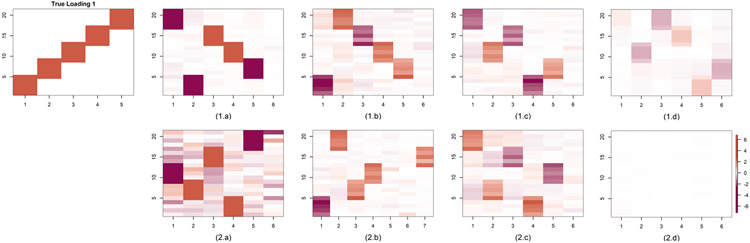
Figure 5 shows the estimated loading matrices. We obtain accurate estimates, even when assuming a higher level of perturbation than the truth, α₀ ≤ α. However, the estimates are best when α = α₀ = 10⁻⁴. Performance degrades more sharply when we underestimate the level of perturbation, as in the case where α = 10⁻⁴, α₀ = 10⁻². The BMSFA code requires an upper bound on the number of shared and group-specific factors; we choose both to be 6. The estimated loadings from PFA and FBPFA are better than BMSFA. Except for cases with a higher level of perturbation using BMSFA, the estimated loadings matrix is close to the truth under some permutation of the columns. BMSFA estimated loadings usually are of lower magnitude which may be due to the additive structure of the model. Thus they look faded in almost all the figures. The cumulative shrinkage prior used in PFA and BMSFA induces continuous shrinkage instead of exact sparsity but, nonetheless, does a good job overall of capturing the true sparsity pattern. BMSFA estimated loadings for α₀ = 10⁻² look blank as the estimated loading has all entries near zero. Results for the Case 2 loading structure are shown in Figure 5 of the Supplementary Material (Roy et al. (2021)).

Fig. 5.

Comparison of estimated loading matrix 1 in simulation Case 2 with different choices of α₀ and α where Q_j0 ∼ MN(I_p, α₀I_p, α₀I_p) and U = αI_p = V. (a) α = 10⁻⁴, α₀ = 10⁻⁴, (b) α = 10⁻², α₀ = 10⁻⁴, (c) FBPFA with α₀ = 10⁻⁴, (d) BMSFA with α₀ = 10⁻⁴, (e) α = 10⁻⁴, α₀ = 10⁻², (f) α = 10⁻², α₀ = 10⁻², (g) FBPFA with α₀ = 10⁻², (h) for BMSFA with α₀ = 10⁻². True loading matrices are plotted twice in columns 1 for easier comparison with other images.

We also apply the same simulation setting with higher error variances. Figure 6 compares the estimated loadings. All the methods identify the true structure when the residual standard deviation is 5, but only PFA with correctly specified α produces good estimates when we increase it to 10.

Fig. 6.

Comparison of estimated loading matrices in simulation Case 2 with increasing error variances and α₀ = 10⁻⁴: (a) α = 10⁻⁴ with error variance 25, (b) α = 10⁻⁴ with error variance 100, (c) BMSFA with error variance 25, (d) BMSFA with error variance 100, (e) FBPFA with error variance 25, (f) FBPFA with error variance 100.

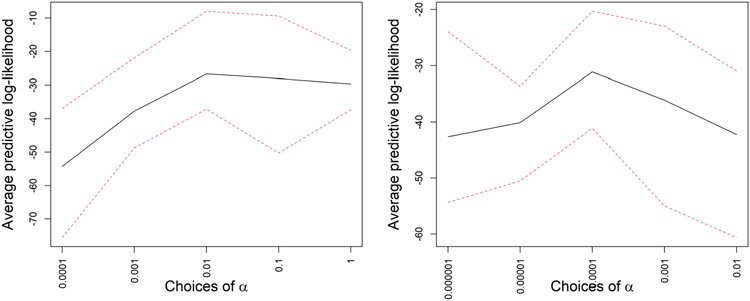
In Figure 7 we show the predictive log-likelihood averaged over all the splits under a range of α values. For each choice of α, we fit the model to a training set and calculate the predictive log-likelihood on a test set for 10 randomly chosen training-test splits. This demonstrates the utility of our cross-validation technique in finding the optimal α. In Table 5 we compare the performance of PFA with optimal α, FBPFA and BMSFA in terms of predictive likelihood. PFA and FBPFA have overwhelmingly better performance. We also show the range of predictive log-likelihoods for each choice of α in Figure 7 using dotted red lines. FBPFA is better at recovering the true loading structure for p = 21, but for the higher dimensional case with p = 128 PFA tends to be better.

Fig. 7.

Average predictive log-likelihoods in black along with two dotted red lines, denoting the range of predictive log-likelihoods across all the splits for different choices of α in simulation Case 2 for two cases—in the first case the perturbation matrices are generated using true α0 = 10⁻², and in the second case α0 = 10⁻⁴. This is based on the simulation experiment of Figure 5.

Table 5.

Average predictive log-likelihood for PFA with optimal α, FBPFA and BMSFA in simulation Case 2

True loading	α 0	PFA for optimal α	FBPFA	BMSFA
Loading 1	10−4	−31.65	−25.92	−679.36
	10−2	−30.32	−26.01	−921.76
Loading 2	10−4	−210.43	−251.13	−6871.38
	10−2	−351.42	−304.10	−25,018.50

5.2.1. Case 2.1: Partially shared factors.

We also repeat the Case 2 simulation but modified to accommodate a partially shared structure. In particular, we generated the data as in Case 2, but for the last two groups we let $Q_j{Y}_i\sim \mathrm{N}({\Lambda }_{01}{\Lambda }_{01}^T+I_p)$ for i ∈ G_j and j = 9, 10. Here, Λ₀₁ = Λ₀[, 1 : 3 is a p × 3 dimensional matrix having the first three columns from Λ₀. The choices for Λ₀ are given in Figure 3.

The estimated loading matrices are compared in Figure 8 for two levels of perturbations, α0 = 10⁻⁴, 10⁻². FBPFA works well for any level of perturbation, while BMSFA works well for only the lower perturbation level. The estimated loading in Figure 8(d) looks blank due to near zero entries. Estimated loadings for the case 2 loading structure are in Figure 6 of the Supplementary Material (Roy et al. (2021)).

Fig. 8.

Comparison of estimated loading in the partially shared modification of simulation Case 2. Row 1 corresponds to true loading structure 1 and row 2 to true loading structure 2. (a) FBPFA with α0 = 10⁻⁴, (b) FBPFA with α₀ = 10⁻², (c) BMSFA with α₀ = 10⁻⁴, (d) BMSFA with α₀ = 10⁻².

5.3. Case 3: Multigroup factor model.

In this case we generate data from the Bayesian multistudy factor analysis (BMSFA) model, as in De Vito et al. (2018),

$$\begin{gathered} Y_i=\Lambda {\eta }_{i1}+{\Psi }_j{\eta }_{i2}+{ϵ}_{1i}\text{and}{Y}_i\in G_j, \\ {ϵ}_{1i}\sim \mathrm{N}(0,\Sigma ),{\eta }_{i1},{\eta }_{i2}\sim \mathrm{N}(0,I_p), \end{gathered}$$ (5.1)

where the group-specific loadings (Ψ_j ’s) are lower in magnitude in comparison to the shared loading matrix Λ. We generate the Ψ_j s from N(−0.5, 0.8). These Ψ_j matrices are the same dimension as the shared loading matrix Λ.

Figure 9 compares the estimated loadings with the true shared loadings across different methods—PFA for two different perturbation parameters, FBPFA and BMSFA. Although we generate the data from BMFSA, all the estimates are very much comparable in Figure 9. However, PFA and FBPFA again outperform BMSFA in terms of predictive log-likelihoods, as shown in Table 6. In the Supplementary Material (Roy et al. (2021)) we present another simulation setting akin to BMSFA. There, the data generating process is similar to BMSFA with minor modifications in the shared and group-specific loading structures. Estimated loadings for the Case 2 loading structure are in Figure 7 of the Supplementary Material (Roy et al. (2021)).

Fig. 9.

Comparison of estimated loading matrices in simulation Case 3 when the true data generating process follows the model in (5.1). (a) PFA with α = 10⁻⁴, (b) PFA with α = 10⁻², (c) FBPFA, (d) BMSFA.

Table 6.

Average predictive log-likelihood for PFA for different choices of α, FBPFA and BMSFA in Simulation Case 3

Generative distribution of Ψj ’s	True loading	PFA for α = 10−2	PFA for α = 10−4	FBPFA	BMSFA
N(−0.2, 0.2)	Loading 1	−33.41	−44.10	−26.16	−500.66
	Loading 2	−336.58	−259.79	−265.77	−9547.77
N(−0.5, 0.8)	Loading 1	−49.25	−53.32	−37.89	−720.35
	Loading 2	−584.82	−308.72	−1003.02	−14,187.36

5.4. Case 4: Mimic NHANES data.

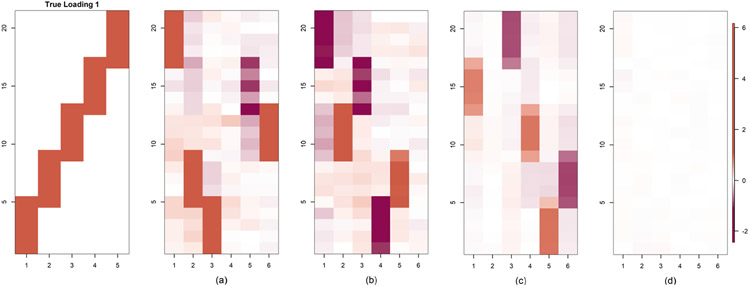
In this section we generate data from the model in (2.1). However, the model parameters Q_j ’s and Λ are first estimated on the NHANES data with α = 10⁻². Then, based on these estimated parameters, we generate the data following the same model. Figure 10 compares the estimated loadings across all the methods—PFA for different choices of α, FBPFA and BMSFA. We find that all the methods recover loading structures that match with our estimated loadings from Section 6. For PFA and FBPFA, we selected the number of factors, as described in Section 3, and hence these approaches produced fewer columns than BMSFA.

Fig. 10.

Comparison of estimated loading matrices in simulation Case 4 where the true loading matrix is PFA estimated loading with α = 10⁻² for mean-centered NHANES data and the data are simulated from the model (2.1). (a) PFA with α = 10⁻², (b) PFA with α = 10⁻⁴, (c) FBPFA, (d) BMSFA. The color gradient added in the last image holds for all the images.

6. Application to NHANES data.

We fit our model in (2.1) to the NHANES dataset, as described in Section 2, to obtain phthalate exposure factors for individuals in different ethnic groups. Before analysis the mean chemical levels across all groups are subtracted to mean-center the data. The data are then randomly split, with 2/3 in each group as a training set and 1/3 as a test set. We collect 5000 MCMC samples after a burn-in of 5000 samples. Convergence is monitored based on the predictive log-likelihood of the test set at each MCMC iteration. The hyperparameters are the same as those in Section 5. The predictive log-likelihood of the test data are used to tune α, as described in Section 2.1.2. Based on our cross-validation technique, α = 10⁻² is chosen. Note that our final estimates are based on the complete data. Our BMSFA implementation sets the upper bounds at 8 for both shared and group-specific factors. Figure 4 of the Supplementary Material (Roy et al. (2021)) depicts trace plots of the loading and perturbation matrices for FBPFA.

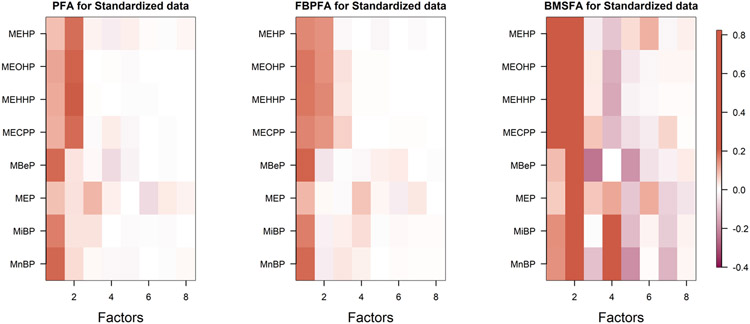
Figure 11 shows the estimated loadings using PFA, FBPFA and BMSFA. All plots show two significant factors, with some suggestions of a third factor. For PFA and FBPFA, all the chemicals load on the first factor, and the second factor is loaded on by the first four chemicals, namely MEHP, MEOHP, MEHHP and MECPP. Figure 1 also suggests that these four chemicals are related to each other more than the others. This is not surprising, as MECPP, MEHHP and MEOHP are oxidative metabolities of MEHP.

Fig. 11.

Comparison of estimated loading matrices with different methods. PFA estimates are based on α = 10⁻².

Comparing the predictive log-likelihoods for PFA, FBPFA and BMSFA, we obtain values of 4.12, 5.02 and −7.99, respectively, suggesting much better performance for the PFA-based approaches. As an alternative measure of predictive performance, we also consider test sample MSE using 2/3 of the data as training and 1/3 as test. The predictive value of the test data is estimated by averaging the predictive mean conditionally on the parameters and training data over samples generated from the training data posterior. We obtain predictive MSE values of 0.05 and 0.09 for PFA with α = 10⁻⁴ and α = 10⁻², respectively. FBPFA yields a value of 0.14, while BMSFA has a much larger error of 0.70. Considering that the data are normalized before analysis, the naive prediction that sets all the values to zero would yield an MSE of 1.0.

To explore similarities across groups, we calculate divergence scores and create the divergence matrix D. This matrix is provided in Table 7. To summarize D, we also provide a network plot between different groups in Figure 12. The plot uses greater edge widths between ethnic groups when the divergence statistic between the groups is small. In particular, the edge width between two nodes (j, l) is calculated as 60/d_jl. Thicker edges imply greater similarity. This figure implies that non-Hispanic whites differ the most in phthalate exposure profiles from the other groups, supporting the findings of our exploratory ANOVA analysis in the Section 3 of the Supplementary Material (Roy et al. (2021)) and findings in the prior literature (Bloom et al. (2019)). We find evidence of one extra factor among non-Hispanic whites relative to the other groups in Figure 2. The two Hispanic ethnicity groups are very similar in loadings as shown in Figure 2 and also their Hotelling T² distance is relatively small in Table 2. These results support our preliminary analysis, described in Section 2.

Table 7.

Estimated divergence scores for different pairs of ethnic groups based on NHANES data

	Mex	OH	N-H White	N-H Black	Other/multi
Mex	0.00	5.86	41.35	10.22	3.82
OH	5.86	0.00	40.93	8.38	4.45
N-H White	41.35	40.93	0.00	40.06	41.17
N-H Black	10.22	8.38	40.06	0.00	9.48
Other/multi	3.82	4.45	41.17	9.48	0.00

Fig. 12.

Network plot summarizing similarity between ethnic groups based on the divergence metric with thicker edges implying smaller divergence scores. Nodes correspond to different ethnic groups.

In Table 8 we show square norm differences between the group-specific loadings, estimated using BMSFA. The (i, j)-th entry of the table is calculated as $\sqrt{{\sum }_{lk}(A_{ill}-A_{jlk}{)}^2}$, where the matrices A_i and A_j are the estimated group-specific loadings for the groups i and j, respectively, using BMSFA. Based on these results, BMSFA-based inferences on differences in exposure profiles across ethnic groups are noticeably different from our PFA-based results reported above. In particular, all the groups seem to be approximately the same distance apart. The results using BMSFA from Table 8 are not consistent with Hotelling T²-based our exploratory data analysis results from Table 2 and PFA-based results from Table 7.

Table 8.

Square norm difference of the group-specific loadings, estimated using BMSFA

	Mex	OH	N-H White	N-H Black	Other/multi
Mex	0.00	0.75	0.70	0.59	0.78
OH	0.75	0.00	0.63	0.75	0.73
N-H White	0.70	0.63	0.00	0.68	0.84
N-H Black	0.59	0.75	0.68	0.00	0.91
Other/multi	0.78	0.73	0.84	0.91	0.00

7. Discussion.

In this paper our focus has been on identifying a common set of phthalate exposure factors that hold across different ehtnic groups, while also inferring differences in exposure profiles across groups. To accomplish this goal, we focused on data from NHANES which contain rich information on ethnicity and exposures. We found that our proposed perturbed factor analysis (PFA) approach had significant advantages over existing approaches in addressing our goals.

There are multiple important next steps to consider to expand on our analysis. A first is to include covariates. In addition to phthalates and ethnic group data, NHANES collects information that may be relevant to understanding ethnic differences in exposure profiles, including BMI, age, socioeconomic status, gender and other factors. Li and Jung (2017) consider a related problem of incorporating covariates into factor models for multiview data. Perhaps the simplest and most interpretable modification of our PFA model of the NHANES data is to allow the factor scores η_ij to depend on covariates X_ij = (1, X_ij2, …, X_ijq)^T through a latent factor regression. For example, we could let η_ij = βX_ij + ξ_ij, with β a k × q matrix of coefficients and ξ_ij ∼ N(0, E).

Another important direction is to extend the analysis to allow inferences on relationships between exposure profiles and health outcomes. NHANES contains rich data on a variety of outcomes that may be adversely affected by phthalate exposures. To include these outcomes in our analysis and effectively extend PFA to a supervised context, we can define separate PFA models for the exposures and outcomes, with these models having shared factors η_ij but different perturbation matrices. It is straightforward to modify the Gibbs sampler used in our analyses to this case and/or the extension described above to accommodate covariates X_ij; further modifications to mixed continuous and categorical variables can proceed as in Carvalho et al. (2008), Zhou et al. (2015) with the perturbations conducted on underlying variables. Relying on such a broad modeling and computational framework, it would be interesting to attempt to infer causal relationships between ethnicity and phthalates and adverse health outcomes. Mediation analysis may provide a useful framework in this respect.

Beyond this application the proposed PFA approach may prove useful in other contexts. The important features of PFA include both the incorporation of a multiplicative perturbation of the data and the use of heteroscedastic latent factors. These innovations are potentially useful beyond the multiple group setting to meta analysis, measurement error models, non-linear factor models (including Gaussian process latent variable models (Lawrence (2004), Lawrence and Candela (2006))) and variational autoencoders (Kingma and Welling (2014), Pu et al. (2016)) and even to obtaining improved performance in “vanilla” factor modeling lacking hierarchical structure.

Code is available for implementing the proposed approach and replicating our results from Section 5.2 at https://github.com/royarkaprava/Perturbed-factor-model and the Supplementary Material (Roy et al. (2021)).