Improved Fine-Tuning of In-Domain Transformer Model for Inferring COVID-19 Presence in Multi-Institutional Radiology Reports

Abstract

Building a document-level classifier for COVID-19 on radiology reports could help assist providers in their daily clinical routine, as well as create large numbers of labels for computer vision models. We have developed such a classifier by fine-tuning a BERT-like model initialized from RadBERT, its continuous pre-training on radiology reports that can be used on all radiology-related tasks. RadBERT outperforms all biomedical pre-trainings on this COVID-19 task (P<0.01) and helps our fine-tuned model achieve an 88.9 macro-averaged F1-score, when evaluated on both X-ray and CT reports. To build this model, we rely on a multi-institutional dataset re-sampled and enriched with concurrent lung diseases, helping the model to resist to distribution shifts. In addition, we explore a variety of fine-tuning and hyperparameter optimization techniques that accelerate fine-tuning convergence, stabilize performance, and improve accuracy, especially when data or computational resources are limited. Finally, we provide a set of visualization tools and explainability methods to better understand the performance of the model, and support its practical use in the clinical setting. Our approach offers a ready-to-use COVID-19 classifier and can be applied similarly to other radiology report classification tasks.

Supplementary Information

The online version contains supplementary material available at 10.1007/s10278-022-00714-8.

Introduction

Transformers [1], which gave birth to BERT [2], are now broadly shared through libraries like Hugging Face Transformers [3] and have reached new state-of-the-art performance.

The recent focus has been on developing BERT-like pre-trained models that work well on downstream tasks, which include various medical or radiology applications. We distinguish continuous pre-trainings, where model weights are initialized from an already pre-trained BERT and then further pre-trained on a biomedical dataset [4–6], from the from-scratch pre-trainings that seem to be even more promising but require larger amounts of data [7–9]. Other than a recent attempt at continuous pre-training on radiology reports [10], no extensive pre-training research has been done in this domain. In particular, there exists no radiology pre-training that tackles a diagnosis task such as lung disease classification.

Many radiology downstream tasks require a fine-tuning of these pre-trained models on a task-specific dataset: radiology report summarization [11, 12], generation [13, 14], and token-level or document-level classification [15, 16]. But these previous works typically do not provide diagnostic outputs. Rare attempts to classify lung diseases suffer from limited performance. For instance, CheXbert [16] labels the presence of 14 types of observations but achieves only 0.798 of macro-averaged F1-score, which limits its use in the clinical setting. To the best of our knowledge, only one previous model for COVID-19 classification has been based on radiology reports [17]. Their work is limited by a small dataset that contained only reports suspicious for COVID-19. It does not study COVID-19 in the presence of other prevalent lung diseases, nor does it rely on modern natural language processing (NLP) techniques such as transformers to maximize performance.

Limited data remains the main bottleneck for ML projects in medicine due to challenges in de-identification of text and the cost of labeling. In addition, most NLP tools for radiology reports suffer from low generalizability on multi-institutional data and are rarely optimized during hyperparameter tuning, leading to instability or under-performance.

To improve the knowledge retained from the fine-tuning step, strategies like ULMFit [18] aim to carefully design the fine-tuning process to help the transfer of knowledge, leveraging the learning rate and momentum scheduling or the unfreezing of layers. Originally designed to help fine-tune LSTM models, we can expect these methods among others [7, 19–21] to show similar improvements on the fine-tuning of BERT-like models. Similarly, many algorithms have been designed to explore the hyperparameter space, such as Bayesian optimization or population-based training [22–26].

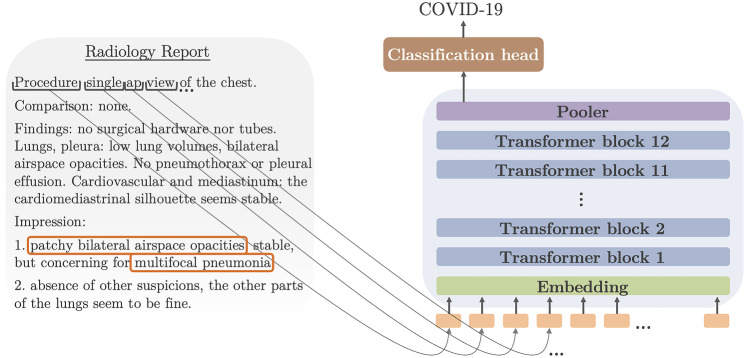
In this context, we propose new methods to develop a COVID-19 document-level classification model for radiology reports (see Fig. 1). We release RadBERT, a pre-trained BERT model on radiology reports, along with its fine-tuned version for the task of COVID-19 classification, using a multi-institutional dataset specifically labeled for this task. We provide a set of fine-tuning strategies that are helpful to better optimize the performance of a BERT model on a downstream task. This includes the comparison of several pre-trained models for tasks on radiology reports and the study of the hyperparameter space of a BERT model on radiology reports, thus suggesting methods to improve the fine-tuning performance.

Fig. 1.

Our classification task consists of consuming the text of a radiology report and generating one of three labels: COVID-19, uncertain COVID-19, and no COVID-19

COVID-19 classification is a complex task because of the need to distinguish COVID-19 from other lung diseases and other types of focal or multifocal pneumonia. Models and fine-tuning strategies that perform well on this task are likely to perform well on classification of other diseases. Our solution applies to both X-ray and CT reports and therefore represents a good benchmark to reuse its pre-processing approaches and conclusions on both planar and cross-sectional datasets. We study the performance under data and computational constraints that we often encounter in medical AI projects, making the tools and training strategies we propose reusable for other medical text classification tasks.

Materials and Methods

Data Collection and Annotation

Our BERT model for radiology reports was pre-trained on 4,056,227 reports from 608,140 unique patients being treated at Stanford Health Care from 1992 to 2014. The dataset includes more than one thousand different exam types across all body areas.

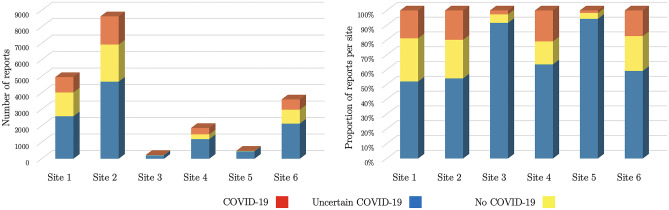
The fine-tuning dataset comprises 19,384 reports collected during 2020 in an academic health system, Penn Medicine. A total of 3520 reports were labeled by the radiologists at the time of clinical interpretation as COVID-19, 4752 as uncertain COVID-19, and 11,112 as no COVID-19. Radiologists all agreed to a consensus statement on the meaning of each label before starting the study. Due to over-representation of cases uncertain and positive for COVID-19, we resampled our subset of labeled reports among all chest reports. We included additional negative cases with co-prevalent lung diseases to approximate the actual prevalence of COVID-19. The initial dataset contained approximately 7000 negative cases, which grew to 11,000 reports after resampling. The number of reports and their balance vary across the sites of the academic health system (see Fig. 2).

Fig. 2.

Our fine-tuning dataset includes radiology reports from 6 sites within the same health academic system, Penn Medicine. The left graph shows the number of reports provided by each site, dominated by three sites. The graph on the right shows that the data imbalance remains stable across these three main sites. There is less balance in the three remaining sites

Reports from the fine-tuning dataset correspond to both X-rays and CTs of the chest: 16,432 X-rays and 2952 CTs. We split the fine-tuning data into a training set (16,876 reports), development set (838 reports), and test set (1654 reports), ensuring every patient belongs to a single split.

In addition to our fine-tuning dataset, which includes a test set of 1654 reports, we built a test set from a separate institution, unseen during training: we collected chest X-ray radiology reports from Stanford Health Care from April 1, 2020, to December 31, 2020, resulting in a total of 66,000 data points.

To label a portion of this test set, we used our baseline model described in the “Baseline Model” section to find candidate reports for each label with moderate precision but correct recall (75.3). This baseline model detected a 4% prevalence of COVID-19 cases, which means that sufficient statistical significance would require too many reports to label, based on a non-inferiority test with significance 5% and power 80% [27–29]. Leveraging our baseline model, we oversampled COVID-19 and uncertain COVID-19 candidates and randomly sampled no COVID-19 candidates among the remaining reports. This formed a test set of 300 reports from Stanford Health Care, which was hand-labeled by a radiologist from the same institution with more than 10 years of experience, after training on a data sample and agreeing on a consensus statement with a radiologist from Penn Medicine. This test set is composed of 41 COVID-19 cases, 154 uncertain COVID-19 cases, and 105 no COVID-19 cases.

Before being processed by our model, the radiology reports are pre-processed into a common format. Using rule-based parsers, we formatted the reports in a consistent manner and removed institution-specific sections that had no relevance to the task (e.g., Contrast). We chose to rely on a rule-based model that omits less important sections and clinical material to shorten the report below the 512-token threshold, whenever the reports were too long (see Supplementary Fig. 1).

Pre-training Methods

To handle our COVID-19 classification task, we develop a BERT-based approach [2] as it has been successful on numerous NLP tasks, and is supported by the availability of many pre-trainings [3].

All these BERT pre-trainings, including the ones using biomedical and clinical data, can be characterized by four main features: the pre-training dataset, the weight initialization, the vocabulary, and the training techniques. First, the pre-training datasets can be distinguished between in-domain vocabulary and structure, comprised of radiology reports, such as [10]; in-domain vocabulary only, containing any types of biomedical texts like in the case of BioBERT [5] or BlueBERT [6]; and out-of-domain vocabulary corresponding for instance to BaseBERT [2]. Second, we identify two weight initialization approaches, either from-scratch pre-trainings that are initialized with random weights or continuous pre-trainings that use weights from a previously pre-trained model. Third, each pre-training uses a pre-defined vocabulary, which can be freely chosen to correspond to the pre-training dataset for all from-scratch pre-trainings, but is imposed by the former pre-training vocabulary in case of continuous pre-trainings. Fourth, each pre-training can leverage a variety of training strategies: various self-supervised objectives [30] or generators [31].

Aside from the in-domain vocabulary and structure data, our pre-training is fairly simple, in that it follows the general guidelines from [2]. Using a weight initialization from BioBERT, itself first initialized from BaseBERT, we further pre-train for a few hundred thousand steps. In total, we adjust 109,493,006 parameters across the embeddings, 12 BERT layers (consisting of attention, linear, layer normalization, and dropout layers) and a pooler layer with tanh activation. Our output hidden dimensions have size 768. We do not consider any larger models, as they would not fit on a single GPU requiring more work and resources, and would less easily compare to other BERT models.

Fine-Tuning Methods

We assess a variety of fine-tuning strategies discussed below and provide supplemental illustrations in the Supplementary Material.

Learning Rate Strategies

We measured the impact of several learning rate strategies on model performance. Most of these approaches were developed by ULMFit when pre-trained LSTMs were the standard approach on NLP tasks.

In the equations that follow, $\alpha$ is the learning rate, modeled as a function of time t (the number of training steps or epochs so far) and the layer index l.

Discriminative learning rate consists of varying the learning rate across layers, enabling layers at the top to easily adjust their weights for the fine-tuning objective while preventing layers at the bottom to forget pre-training knowledge:

$$\begin{array}{c}\hfill {\alpha }_{t,l}={\alpha }_t{\delta }^l\end{array}$$

with $0\le l$ the layer index from top to bottom, and $0<\delta \le 1$ parameterizing the method.

One-cycle triangular scheduling enables a quick convergence to an interesting region of the parameter space before refining the weights:

$$\begin{array}{cc}\hfill {\alpha }_t& =(\frac{1}{\gamma }-1)max\alpha (\frac{t_{1/2}-t}{t_{1/2}-t_{\mathit{min}}}{\mathbb{1}}_{t\le t_{1/2}}\hfill \\ \hfill & +\frac{t-t_{1/2}}{t_{\mathit{max}}-t_{1/2}}{\mathbb{1}}_{t\ge t_{1/2}})+max\alpha \hfill \end{array}$$

with $t_{\mathit{min}}\le t\le t_{\mathit{max}}$ the training time and $1\ll \gamma$ parameterizing the method.

Slanted triangular scheduling speeds up the convergence to a region of interest in the parameter space:

$$\begin{array}{c}\hfill t_{1/2}<\frac{t_{\mathit{max}}+t_{\mathit{min}}}{2}\end{array}$$

Final decay adds a few extra training steps to choose the best parameters in a small neighborhood where the performance is satisfying:

$$\begin{array}{c}\hfill {\alpha }_t=\frac{1}{\gamma }max\alpha -\frac{1}{{\gamma }^{\beta }}\frac{t-t_{\mathit{max}}}{t_{\mathit{max}}}\end{array}$$

with $t_{\mathit{max}}<t$, $t-t_{\mathit{max}}\ll t_{\mathit{max}}$ and $1\ll \beta$ parameterizing the method.

In parallel, we also use slanted triangular momentum, which is similar in every aspect to the learning scheduling except that the variations are reversed, as found empirically (see Supplementary Fig. 2, [32]).

Unfreezing Scenarios

To avoid catastrophic forgetting phenomena and fine-tune each layer only to the extent that is needed, we include unfreezing methods in our general fine-tuning approach. We distinguish several scenarios: fine-tuning only the weights of the task-specific head, fine-tuning all the weights for the same duration, or fine-tuning different layers for different amounts of time. The latter can correspond either to the original gradual unfreezing approach suggested by [18] or to our own approach: training only the head at the beginning and then the entire transformer (see Supplementary Fig. 3).

Regularization Techniques

Following the ideas of [33] and [34], we try to use higher values of the learning rate at least at the beginning of the fine-tuning phase, then relying on our triangular scheduling with final decay to stabilize the convergence at the end of the training. As suggested by the authors, this could help speed up the convergence and fight overfitting not only by leveraging the dropout probability, but also the learning rate and the batch size. We suspect that higher values of the learning rate prevent the model from falling into local minima. Larger batch sizes smooth the gradient descent, thus achieving a similar effect as directly increasing the dropout (see Supplementary Fig. 4).

Hyperparameter Optimization

The exploration of the hyperparameter space relies on two components: a search algorithm and a trial scheduler [35]. The search algorithm uses the previously acquired knowledge, that is to say pairs of sets of hyperparameters and validation score, to suggest the next set of hyperparameters to try (hopefully converging to the ideal set of hyperparameters). The trial scheduler helps speed up this exploration by either prioritizing certain trials, early stopping others, or merging them.

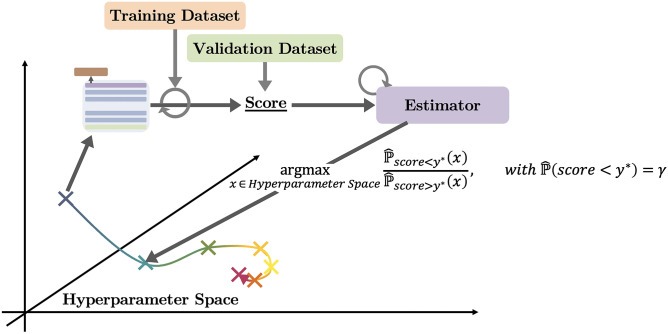
For the search algorithm, we choose to rely on Bayesian optimization [24] using a Tree-structured Parzen Estimator [22], which has the advantage of working well on continuous search spaces not too dimensionally heavy and being robust to stochastic noise. This estimator uses the validation score obtained on each hyperparameter set (viewed as a point of the hyperparameter space) to update its empirical distributions, then used to suggest the next hyperparameter set to try. More specifically, it models a distribution of good trials ${\widehat{\mathbb{P}}}_{score<y\ast }$ and a distribution of bad trials ${\widehat{\mathbb{P}}}_{score>y\ast }$ with $y\ast$ being a percentile of the total distribution of trials $\widehat{\mathbb{P}}$. Then, the ratio of these distributions is used to suggest the next of hyperparameters with maximal expected improvement:

$$\begin{array}{c}\hfill {\mathrm{argmax}}_{x\in \mathcal{X}}\frac{{\widehat{\mathbb{P}}}_{score<y\ast }(x)}{{\widehat{\mathbb{P}}}_{score>y\ast }(x)}\end{array}$$

with the empirical densities being estimated using Parzen windows (see Fig. 3).

Fig. 3.

The Tree-structured Parzen Estimator builds empirical distributions on the hyperparameter space and suggests points that are highly likely under the distribution of good trials while being highly unlikely under the distribution of bad trials

For the trial scheduler, we use a FIFO scheduler and avoid any early stopping techniques like with ASHA [26], which can give an unfair advantage to models that learn quickly over the first epochs without building solid long-term knowledge.

Explainability Methods

Our own use-case, for a COVID-19 classifier, aims at providing explanations on the model’s decision for each input report (local), using if necessary additional computations (post hoc), being as correct as possible (both sensitivity and implementation invariance) and relying on the words used in the input reports, which are easily interpretable by clinicians (feature importance) [36] propose a method called integrated gradients, which fulfills all these requirements, is gradient-based, and provides explanations that we display visually using saliency maps. In particular, we do not use attention-based methods, which ignore the weights from the other layers of the model, thus inaccurately depicting the relations between inputs and outputs.

Integrated gradients consist of examining the input in comparison to a pre-defined baseline input (in our case the dummy text made out of [PAD] tokens only). Then, following a straight line in the space of the input, we accumulate the gradients of the model going from the baseline input to the input. This measures how much and in which direction the model changes its decision, when going from a neutral text (the baseline input) to the text of interest (the input). We take the gradients relatively to each word to get scores for each one of them. This gives IG(w) the degree of importance of each word w and the direction of its impact (positive or negative) on the decision of the model:

$$\begin{array}{c}\hfill IG(w)=(w-w_0){\int }_{ϵ=0}^1\frac{\partial \mathcal{M}(T_0+ϵ(T-T_0))}{\partial w}\end{array}$$

with T being the input text, $T_0$ the baseline input text, and $w_0$ the word corresponding to w in the baseline $T_0$. As such, integrated gradients are often classified as a path method which follows the straight line, thus preserving linearity and symmetry along the path [36].

Results

Training Details

Experiments were conducted using private compute infrastructures. The pre-training takes 4 days on a single GPU NVIDIA Tesla V100 leading to an estimated 5.76 kgCO${}_2$eq of total emissions.

For the fine-tuning, each training on the full train set of $\sim$17k reports takes 2:30 min per epoch if training only the head and 8 min per epoch if training the full model (not counting $\sim$2 min of initialization of the training) on a single GPU NVIDIA Quadro P5000. During hyperparameter optimization, we explore 100 hyperparameter sets and train as many models. Using 3 GPUs NVIDIA Quadro P5000, this averages to 51 h of total training, i.e., 17 h when parallelized across the 3 GPUs (see see Supplementary Notes on implementation and Supplementary Table 1).

The total emissions to run all fine-tuning experiments are estimated to be 40.06 kgCO${}_2$eq. These estimations were conducted using an online tool [37].

Baseline Model

We develop a simple baseline approach that we evaluate on the same test set as the other models, providing context and elements of comparison for the results.

The baseline relies on a frequentist approach that starts by compiling all the words found in the reports of the training set. Then, it computes the frequency of each word among the reports of each category (COVID-19, uncertain COVID-19, and no COVID-19) and builds an empirical distribution of the vocabulary within each category. So that for each input report of the test set, the baseline assigns the category to which the report is the most likely to belong, according to the empirical distributions of the vocabulary.

In addition, we also compare our results with the scores of CheXbert [16], especially on its pneumonia task. That task is easier than ours as it does not require distinguishing among several types of pneumonia.

Evaluation Metrics

The experiments are evaluated on a test set from the same academic health system as the training data and on a test set from a different academic health system. On each test set, we report F1-score, recall, and precision on each of the three categories, namely COVID-19, uncertain COVID-19, and no COVID-19. To compare models across these three categories, we rely on macro-averaged metrics, which do not bias the scores towards the majority class (no COVID-19) as micro-averaged metrics would. Non-parametric bootstrap with 1000 bootstrap samples is used to compute both 95% percentile confidence intervals and two-tailed paired-sample Wilcoxon tests with significance level 0.05. We include the Bonferroni correction whenever testing multiple hypotheses.

Experimental Results

The results of our best model are shown in Table 1. It is trained on the full dataset of X-rays and CTs and uses both our continuous pre-training on radiology reports and all the fine-tuning methods that we presented in the “Fine-tuning Methods” section, parameterized as described in the “Training Details” section, and optimized following the Tree-structured Parzen Estimator scheme. When we evaluate it on the test set from the same institution as the training set comprising both X-rays and CTs, this model obtains a macro-averaged F1-score of 88.9 (class-wise F1-scores: COVID-19 87.6, uncertain COVID-19 84.2, and no COVID-19 94.9), with 95% confidence interval [87.5; 90.3]. The performance on X-rays only is slightly higher, with a macro-averaged F1-score of 90.5, and lower on CTs only, 79.4. This can be explained by the fact that CT reports are longer, contain more elaborate descriptions of disease, and are less prevalent in the training set than X-ray reports.

Table 1.

Our best model

Test set	COVID-19	Uncertain COVID-19	No COVID-19	Macro-average
	F1 (R., P.)	F1 (R., P.)	F1 (R., P.)	F1 (R., P.)
	Best model, known academic health system
X-rays	89.1 (90.7, 87.5)	87.1 (88.1, 86.1)	95.3 (94.3, 96.2)	90.5 (91.0, 90.0)
CTs	83.9 (86.9, 81.1)	61.7 (65.9, 58.0)	92.5 (88.5, 96.9)	79.4 (80.4, 78.7)
X-rays and CTs	87.6 (89.7, 85.7)	84.2 (85.6, 82.8)	94.9 (93.5, 96.3)	88.9 (89.6, 88.3)
	Best model with threshold, known academic health system
X-rays and CTs	91.9 (93.7, 90.2)	89.9 (89.9, 89.9)	97.3 (96.7, 97.8)	93.0 (93.4, 92.6)
	Baseline, known academic health system
X-rays and CTs	68.6 (75.3, 63.0)	65.8 (68.8, 63.0)	83.5 (79.3, 88.2)	72.6 (74.5, 71.4)
	Best model, new academic health system
X-rays	64.9 (87.8, 51.4)	53.3 (39.0, 84.5)	69.7 (87.6, 57.9)	62.6 (71.5, 64.6)

We can leverage the confidence thresholds of the best model and choose to not retain the 10% fraction of the reports where the model is the least confident: in the clinical setting, this would mean that the model handles 90% of the radiology reports and asks for additional help from a radiologist for the remaining 10%. This is very helpful for the model and helps it achieve 93.0 of macro-average F1-scores on the test set with both X-rays and CTs (all class-wise F1-scores are around 90 or more). Notice that this does not make the model less competent: we control the reports dropped by the model and ensure that it does not only drop COVID-19 reports, which are what we are interested in. When the threshold is chosen to be 10%, we can measure in the test set that the model drops 15% of COVID-19 reports, 14.5% of uncertain COVID-19, and 6.5% of no COVID-19. Dropping more or less reports allows adjustment of performance for the trade-off that best suits its use case.

If we compare these results with our frequentist baseline model, the latter achieves a macro-averaged F1-score of 72.6 on the test set from the known health system. CheXbert [16], which was trained on a classification task of several lung diseases including pneumonia using hundreds of thousands of reports, achieves a weighted F1-score of 83.5. The use of the weighted F1-score metric gives an advantage to the model as more weight is given to the majority class that is easier to classify—the reports with no symptoms. In addition, their dataset includes only X-rays, which are easier to classify than CTs. In comparison, our best model achieves a weighted F1-score of 92.2 on X-rays only, which corresponds to an almost +10 improvement, on a task that is likely more difficult. Finally, our model needs only 1+3 epochs (1 epoch training the head only, 3 epochs the full model) compared to 8 epochs for CheXbert. This shows not only the superiority of our approach on the COVID-19 classification task, where there exists no other reliable model (to the best of our knowledge), but also its potential when applied to the classification of other lung diseases.

As seen in Table 1, when evaluated within a new health academic system (Stanford Health Care), our best model achieves 62.6 macro-averaged F1-score on X-rays, with recall around 88 on both COVID-19 and no COVID-19 reports but much lower recall, 39.0, on uncertain COVID-19 reports. A radiologist from the same institution as the training data, Penn Medicine, also achieves only 82.0 macro-averaged F1-score on this test set, with the lowest recall being on uncertain COVID-19 reports. Whereas the model is able to maintain correct performance on COVID-19 and no COVID-19 reports, we observe a significant drop of performance due not only to a shift of vocabulary and report structure, but also hypothetically to a shift of definition of uncertain COVID-19. In this sense, we measured that 84% of the model mistakes were on uncertain COVID-19 reports, and leveraging confidence thresholds help improve performance on the first two classes (confidence threshold of p=0.9 leads to $\sim$ 95 recall on both of them) but do not mitigate the low performance on uncertain COVID-19 reports.

Our best model is based on our continuous pre-training on radiology reports, which was the best performing pre-training method compatible with our task, as described in Table 2. When evaluating on both X-rays and CTs, our pre-training achieves a macro-averaged F1-score of 88.9, which is approximately 1 point of F1-score higher than all other pre-trainings (P<0.01). Notice that we outperform both other continuous pre-trainings (BioBERT, BlueBERT, P<0.01) and from-scratch pre-training (PubMedBERT, P<0.01). The latter achieved the best performance on CTs only (P<0.01) but was beaten by RadBERT on X-rays (P<0.01): not seeing any radiology reports at pre-training time offsets its advantage of being a from-scratch pre-training.

Table 2.

Pretraining strategies

Pretraining	COVID-19	Uncertain COVID-19	No COVID-19	Macro-average
	F1 (R., P.)	F1 (R., P.)	F1 (R., P.)	F1 (R., P.)
	X-rays
BERT	88.6 (88.0, 89.2)	86.6 (89.2, 84.3)	95.1 (94.1, 96.2)	90.1 (90.4, 89.9)
BlueBERT	87.1 (87.5, 86.7)	86.9 (87.5, 86.3)	95.6 (95.2, 96.0)	89.9 (90.1, 89.7)
BioBERT	87.8 (91.7, 84.3)	87.2 (88.9, 85.6)	95.2 (93.2, 97.2)	90.1 (91.3, 89.0)
PubMedBERT	86.9 (89.4, 84.6)	85.4 (86.1, 84.7)	94.4 (93.3, 95.5)	88.9 (89.6, 88.3)
RadBERT (ours)	89.1 (90.7, 87.5)	87.1 (88.1, 86.1)	95.3 (94.3, 96.2)	90.5 (91.0, 90.0)
	CTs
BERT	81.1 (84.5, 78.0)	59.8 (65.9, 54.7)	91.6 (86.3, 97.6)	77.5 (78.9, 76.8)
BlueBERT	82.5 (78.6, 86.8)	54.4 (63.6, 47.5)	90.8 (88.5, 93.2)	75.9 (76.9, 75.8)
BioBERT	79.0 (78.6, 79.5)	57.1 (68.2, 49.2)	91.6 (86.3, 97.6)	75.9 (77.7, 75.4)
PubMedBERT	86.7 (85.7, 87.8)	64.1 (75.0, 55.9)	92.1 (87.8, 96.8)	81.0 (82.8, 80.2)
RadBERT (ours)	83.9 (86.9, 81.1)	61.7 (65.9, 58.0)	92.5 (88.5, 96.9)	79.4 (80.4, 78.7)
	X-rays and CTs
BERT	86.4 (87.0, 85.9)	83.5 (86.6, 80.6)	94.6 (92.9, 96.4)	88.2 (88.9, 87.6)
BlueBERT	85.9 (85.0, 86.7)	82.9 (84.9, 80.9)	94.9 (94.2, 95.6)	87.9 (88.0, 87.8)
BioBERT	85.4 (88.0, 83.0)	83.4 (86.6, 80.5)	94.7 (92.2, 97.2)	87.8 (88.9, 86.9)
PubMedBERT	86.9 (88.3, 85.5)	82.8 (84.9, 80.7)	94.1 (92.5, 95.6)	87.9 (88.6, 87.3)
RadBERT (ours)	87.6 (89.7, 85.7)	84.2 (85.6, 82.8)	94.9 (93.5, 96.3)	88.9 (89.6, 88.3)

To assess which types of reports to include in the training set, we evaluate the performance of the model trained on different compositions of the fine-tuning dataset, as depicted in Table 3. The drop in performance accounts for the fact that all fine-tuning datasets have the size of the smallest of them all, the CT dataset, which contains only 2952 reports before the split. The model trained on both X-rays and CTs achieves similar performance to the model trained on X-rays only when evaluating on X-rays only, but higher performance performance to the model trained on X-rays only when evaluating on CTs only (P<0.01); the model trained on CTs only performs poorly when evaluated on X-rays only (P<0.01). Therefore, we choose to always train on both X-rays and CTs regardless of the composition of the test set.

Table 3.

Fine-tuning datasets

Dataset	COVID-19	Uncertain COVID-19	No COVID-19	Macro-average
	F1 (R., P.)	F1 (R., P.)	F1 (R., P.)	F1 (R., P.)
	X-rays
Only X-rays	85.9 (81.5, 90.7)	83.6 (87.2, 80.3)	94.1 (93.6, 94.6)	87.9 (87.4, 88.6)
Only CTs	51.9 (37.0, 87.0)	23.9 (18.3, 34.4)	83.1 (98.0, 72.1)	53.0 (51.1, 64.5)
Both X-rays and CTs	85.3 (88.4, 82.3)	82.7 (86.1, 79.5)	93.7 (91.0, 96.5)	87.2 (88.5, 86.1)
	CTs
Only X-rays	66.3 (67.9, 64.8)	32.9 (27.3, 41.4)	83.7 (87.1, 80.7)	61.0 (60.7, 62.3)
Only CTs	86.3 (82.1, 90.8)	63.6 (77.3, 54.0)	92.9 (89.2, 96.9)	80.9 (82.9, 80.5)
Both X-rays and CTs	71.7 (73.8, 69.7)	47.7 (59.1, 40.0)	84.9 (77.0, 94.7)	68.1 (70.0, 68.1)
	X-rays and CTs
Only X-rays	80.1 (77.7, 82.6)	79.1 (80.7, 77.6)	92.5 (92.6, 92.4)	83.9 (83.7, 84.2)
Only CTs	63.7 (49.7, 88.7)	30.3 (24.8, 39.2)	84.3 (96.7, 74.7)	59.4 (57.1, 67.5)
Both X-rays and CTs	81.5 (84.3, 78.8)	78.2 (83.2, 73.8)	92.5 (88.9, 96.2)	84.1 (85.5, 83.0)

Finally, we study the impact of the fine-tuning strategies on the performance of the model and report the results in Table 4. We compare two approaches, based on the same pre-training (RadBERT): standard, where we use no advanced fine-tuning strategies as described in the “Fine-tuning Methods” section and optimize with a small grid; ours, where we use all fine-tuning strategies and the Tree-structured Parzen Estimator. When evaluated on both X-rays and CTs, the standard approach achieves a macro-averaged F1-score of 86.9 whereas ours scores 88.9 (P<0.01), in the setting where we are using the full training set with no computational constraints. If we restrict the training set to 1000 reports and limit the number of epochs to 2, our approach now outperforms the standard approach by 3 points of F1-score (P<0.01). This underlines that our fine-tuning approach has an even bigger advantage when constrained and generally converges faster. When the task becomes more difficult, such as the classification on CTs only, we observe a gap of 6 points of F1-score (P<0.01); the harder the task and the stronger the constraints, the better our fine-tuning approach.

Table 4.

Fine-tuning strategies

Strategy	COVID-19	Uncertain COVID-19	No COVID-19	Macro-average
	F1 (R., P.)	F1 (R., P.)	F1 (R., P.)	F1 (R., P.)
	X-rays
Constrained
Standard	82.5 (88.4, 77.3)	71.8 (61.1, 87.0)	91.9 (96.2, 87.9)	82.1 (81.9, 84.1)
Ours	84.3 (89.8, 79.5)	80.1 (82.8, 77.6)	93.0 (90.0, 96.2)	85.8 (87.5, 84.4)
Full
Standard	86.6 (83.8, 89.6)	85.9 (87.2, 84.6)	95.0 (95.2, 94.8)	89.2 (88.7, 89.7)
Ours	89.1 (90.7, 87.5)	87.1 (88.1, 86.1)	95.3 (94.3, 96.2)	90.5 (91.0, 90.0)
	CTs
Constrained
Standard	76.6 (85.7, 69.2)	31.2 (22.7, 50.0)	87.9 (89.2, 86.7)	65.3 (65.9, 68.6)
Ours	74.9 (83.3, 68.0)	42.4 (40.9, 43.9)	83.2 (78.4, 88.6)	66.8 (67.6, 66.8)
Full
Standard	80.9 (85.7, 76.6)	51.5 (59.1, 45.6)	88.6 (81.3, 97.4)	73.7 (75.4, 73.2)
Ours	83.9 (86.9, 81.1)	61.7 (65.9, 58.0)	92.5 (88.5, 96.9)	79.4 (80.4, 78.7)
	X-rays and CTs
Constrained
Standard	80.8 (87.7, 74.9)	67.9 (56.9, 84.2)	91.3 (95.2, 87.8)	80.0 (79.9, 82.3)
Ours	81.6 (88.0, 76.1)	76.2 (78.2, 74.4)	91.6 (88.3, 95.1)	83.1 (84.8, 81.9)
Full
Standard	84.9 (84.3, 85.5)	81.7 (84.2, 79.4)	94.1 (93.2, 95.2)	86.9 (87.2, 86.7)
Ours	87.6 (89.7, 85.7)	84.2 (85.6, 82.8)	94.9 (93.5, 96.3)	88.9 (89.6, 88.3)

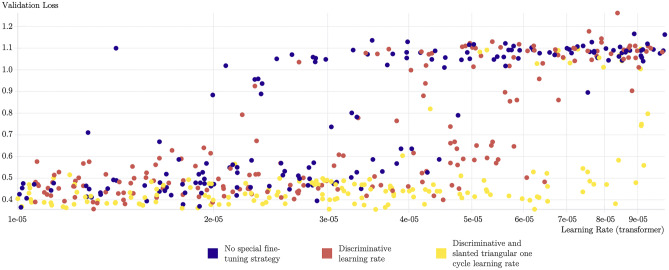
Figure 4 provides another view in which we observe the validation loss for 500 trained transformers, with or without our fine-tuning approach. The yellow runs that leverage these fine-tuning methods almost always achieve low validation scores, use higher values of the learning rate, and reach the lowest validation loss values of all runs, compared to the blue runs that follow a standard fine-tuning approach. Our fine-tuning approach provides faster and more stable training, which leads to the best performing models on the task.

Fig. 4.

Five hundred transformers using our pre-training on radiology reports and fine-tuned for the COVID-19 classification task. The yellow points, using our fine-tuning approach, perform better than the blue points in the vast majority of cases, using a standard fine-tuning procedure. This visualization was obtained using the Weights & Biases platform [39]

Discussion

Pre-Training Results

As observed in the “Experimental Results” section, our pre-trained model on radiology reports performs best on the COVID-19 classification task among the other biomedical pre-trainings: its superiority is due to the inclusion of radiology reports in the pre-training dataset. In general, according to the BLURB benchmark [8], the best pre-training on biomedical tasks is PubMedBERT, as it is a from-scratch pre-training with a biomedical vocabulary. The fact that RadBERT outperforms PubMedBERT on the X-rays and X-rays+CTs tasks, though RadBERT is a continuous per-training with general vocabulary, shows the importance of understanding well the structure of radiology reports on radiology-related tasks. We notice that PubMedBERT outperforms RadBERT on the CT-only task: the pre-training dataset of RadBERT contains mostly X-rays, and the small number of CTs seen is probably not large enough to yield an advantage over PubMedBERT. This shows the potential of from-scratch pre-training with radiology vocabulary and pre-trained on radiology reports: such a model would get the best of both worlds and probably dominate on radiology-related tasks.

In addition, we notice that BERT-base achieves surprisingly high scores on the X-ray-only task: unlike RadBERT or PubMedBERT, it is capable of leveraging the weights of an additional linear layer in the classification head to make up for its limited pre-training knowledge and improve medially by 1 point of F1-score. Nevertheless, this is not enough to handle CTs, which have much more medical content, and its performance on this task is much lower compared to RadBERT and PubMedBERT.

Fine-Tuning Approach

Out of the four unfreezing scenarios presented in the “Unfreezing Scenarios” section, the best unfreezing strategy consists of training the classification head for one epoch (along the pooler layer of the BERT model) and then unfreezing the rest of the transformer for the remaining epochs. Compared to always training the full model, the absolute best score is slightly higher with this method, although by less than 1 point of F1-score. The major difference is in training stability: the median of all the trainings following our method is 5 points of F1-score higher compared to the naive approach. Including the pooler layer in the first training epoch increases the median slightly, by 1 point of F1-score.

Comparing the other fine-tuning techniques, such as the triangular learning rate with final decay and the discriminative learning rate, we notice that all these methods help the training in three ways: stability, absolute performance, and speed of convergence. When running many models with these methods, we measure an improvement of 30 points of median F1-score across runs, compared to the standard approach. This improvement is mainly because the standard setting is much more sensitive to the value of the fixed learning rate, whereas the triangular scheduling relies on a range of values and can temporally reach higher values of the learning rate, without preventing it from converging. With this stability comes higher absolute performance, which achieves 2 additional points of F1-score when training on the full dataset, with no computational constraint and evaluating on both X-rays and CTs (see Table 4). Finally, under a limit of 2 training epochs, this set of methods achieves 3 more points of F1-score compared to the standard approach, as it allows for higher values of the learning rate (at least temporarily). Our best model uses learning rates up to 6e-05 compared to the traditional 2e-05 value recommended for BERT models, dividing by more than 2 the number of epochs required, compared to CheXbert.

The stability of the performance is a strong advantage, in particular in settings where the number of trainings is limited. Standard strategies can reach acceptable results too, though this remains less frequent and not as accurate as the best results of our approach. The fact that these methods allow for higher values of the learning rate is very beneficial for faster convergence, and may explain the superiority in settings where the data is limited, which happens frequently in the medical domain. We experimented the same approach on CheXpert dataset labeled with 14 lung diseases [38] and observed similar improvements compared to the standard fine-tuning approach. Providing a more exhaustive study of fine-tuning methods for BERT models, evaluated on a set of diverse tasks, using various optimization algorithms, could be helpful for the field and the subject of future work.

We found that with triangular scheduling, the variation of the learning rate must be controlled: when there is a smaller number of batches, the gap between the extreme values of the learning rate must be reduced to keep the training stable. The use of an additional linear layer in the classification head was in most cases useless if not counterproductive, losing 1 point of F1-score. Only when relying on BERT-base (a pre-training without biomedical knowledge) was this setting helpful. Finally, using a continuous hyperparameter space was very helpful during the hyperparameter optimization phase, compared to a discrete space.

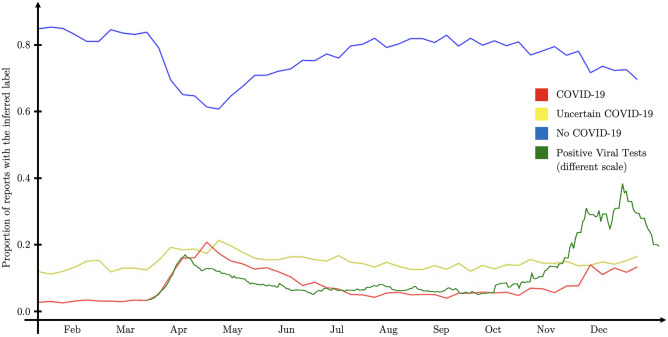
Aside from the metrics provided in the “Experimental Results” section, we can assess the performance of our model by running it on a large database of clinical reports to visualize the prevalence of disease over time. If we compare the COVID-19 presence in reports on Fig. 5 (red line) with the data from the viral tests of the same county (green line), both superimpose well. The difference in absolute values is due to the difference of scales, but probably also because COVID-19 presence in radiology reports is not directly proportional to the number of positive tests. Running similar models on medical reports from populations can be useful to gain insights on the propagation of diseases and their seasonal patterns. Other visualizations can also help compare the performance of different pre-trained and fine-tuned classifiers (see Supplementary Notes on transformer hidden-states visualization and Supplementary Fig. 5).

Fig. 5.

The red, yellow, and blue lines reflect the preponderance of COVID-19 as detected in radiology reports, all from the same health academic system, by our model. The green line represents the number of positive cases in the same county (data from the CDC COVID Tracker [40])

To compensate for the lack of interpretability of deep-learning models like BERT and to help providers in their decision process, we provide reports with post hoc explanations as computed by integrated gradients. As seen on Fig. 6, the presence of observations like “bilateral airspace opacities” or “multifocal pneumonia” are considered as good indicators of COVID-19, whereas “stable” lowers the confidence of the model in this decision (see Supplementary Notes on error analysis).

Fig. 6.

For each report and model output, integrated gradients underline in green the words that contributed positively to the decision of the model and in red the ones that contributed negatively

Conclusion

We have developed a COVID-19 document-level classifier on radiology reports, along with RadBERT, its continuous pre-training on radiology reports. First, we propose an in-domain vocabulary and structured pre-training for any radiology-related downstream task, and show its superiority over other biomedical pre-trainings on the specific COVID-19 classification task. Second, we develop a set of fine-tuning and hyperparameter optimization methods leading to more stable results, faster convergence, and better absolute performance, especially under data and computational constraints. Third, using these strategies, we further fine-tune RadBERT and achieve 88.9 of macro-averaged F1-score on the COVID-19 document-level classification task, on both X-rays and CTs. Fourth, we reinforce fine-tuned RadBERT to resist distribution shifts using a multi-institutional dataset and evaluating it in a new institution.

We hope that our COVID-19 classifier can offer intelligent assistance to radiologists and providers, as well as help monitor the spread and the evolution of the disease within the clinical setting. Our model could also serve as a weak labeler for computer vision models to detect COVID-19 on X-rays and CT scans. We believe that RadBERT can help improve the performance on all radiology-related downstream tasks, such as report generation, summarization, and classification. Finally, we aim for our fine-tuning and hyperparameter optimization approach to be reused to create successful classifiers for other lung diseases, even in the presence of a small amount of labeled data.¹

In the future, we will be gathering a much larger dataset of unlabeled radiology reports across multiple institutions and experiment with from-scratch pre-training approaches. Given the known superiority of from-scratch approaches in other settings and the potential of radiology pre-training, we believe this could further boost all text-based transformer models on radiology-related tasks.²

Supplementary Information

Below is the link to the electronic supplementary material.

Author Contribution

Guarantors of integrity of entire study, P.J.C., T.S.C., C.P.L.; study concepts/study design or data acquisition or data analysis/interpretation, all authors; manuscript drafting or manuscript revision for important intellectual content, all authors; approval of final version of submitted manuscript, all authors; agrees to ensure any questions related to the work are appropriately resolved, all authors; literature research, P.J.C.; experimental studies, P.J.C.; statistical analysis, P.J.C.; and manuscript editing, all authors.

Funding

This research was made possible by the National Institute of Biomedical Imaging and Bioengineering (NIBIB) of the National Institutes of Health under contracts 75N92020C00008 and 75N92020C00021. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Data Availability

The data of the results are available in the tables attached to this study. The raw data used for model training, development, and testing cannot unfortunately be made available due to privacy concerns. De-identification and specific data-share agreements might be possible for research purposes upon request to the authors.

Code Availability

The code will be made available in a GitHub repository upon publication. The model weights of both RadBERT and its fine-tuned version for COVID-19 classification are available on Hugging Face.

Declarations

Ethics Approval and Consent

This study involves human subjects and was approved by Stanford University and University of Pennsylvania IRBs. The IRBs determined that no consent was necessary.

Competing Interests

Personal financial interests: Board of directors and shareholder, Bunkerhill Health; Option holder, whiterabbit.ai; Advisor and option holder, GalileoCDS; Advisor and option holder, Sirona Medical; Advisor and option holder, Adra; Advisor and option holder, Kheiron; Advisor, Sixth Street; Chair, SIIM Board of Directors; Member at Large, Board of Directors of the Pennsylvania Radiological Society; Member at Large, Board of Directors of the Philadelphia Roentgen Ray Society; Member at Large, Board of Directors of the Association of University Radiologists (term just ended in June); Honoraria, Sectra (webinars); Honoraria, British Journal of Radiology (section editor); Speaker honorarium, Icahn School of Medicine (conference speaker); Speaker honorarium, MGH (conference speaker). Recent grant and gift support paid to academic institutions involved: Carestream; Clairity; GE Healthcare; Google Cloud; IBM; IDEXX; Hospital Israelita Albert Einstein; Kheiron; Lambda; Lunit; Microsoft; Nightingale Open Science; Nines; Philips; Subtle Medical; VinBrain; Whiterabbit.ai; Lowenstein Foundation; Gordon and Betty Moore Foundation; Paustenbach Fund. Grant funding: NIH; Independence Blue Cross; RSNA.