A novel pipeline leveraging surface-based features of small subcortical structures to classify individuals with autism spectrum disorder

Abstract

Autism spectrum disorder (ASD) is accompanied with widespread impairment in social-emotional functioning. Classification of ASD using sensitive morphological features derived from structural magnetic resonance imaging (MRI) of the brain may help us to better understand ASD-related mechanisms and improve related automatic diagnosis. Previous studies using T1 MRI scans in large heterogeneous ABIDE dataset with typical development (TD) controls reported poor classification accuracies (around 60%). This may because they only considered surface-based morphometry (SBM) as scalar estimates (such as cortical thickness and surface area) and ignored the neighboring intrinsic geometry information among features. In recent years, the shape-related SBM achieves great success in discovering the disease burden and progression of other brain diseases. However, when focusing on local geometry information, its high dimensionality requires careful treatment in its application to machine learning. To address the above challenges, we propose a novel pipeline for ASD classification, which mainly includes the generation of surface-based features, patch-based surface sparse coding and dictionary learning, Max-pooling and ensemble classifiers based on adaptive optimizers. The proposed pipeline may leverage the sensitivity of brain surface morphometry statistics and the efficiency of sparse coding and Max-pooling. By introducing only the surface features of bilateral hippocampus that derived from 364 male subjects with ASD and 381 age-matched TD males, this pipeline outperformed five recent MRI-based ASD classification studies with > 80% accuracy in discriminating individuals with ASD from TD controls. Our results suggest shape-related SBM features may further boost the classification performance of MRI between ASD and TD.

1. Introduction

Autism spectrum disorder (ASD) is associated with a range of phenotypes that vary in severity of social, communicative and sensorimotor deficits, of which morbidity increased from 1 in 68 children (Autism and Investigators, 2014) to 1 in 59 children (Control and Prevention, 2018) in recent years. Therefore, computer-aided diagnosis is increasingly needed using biomarkers based on neuroimaging and other measurements to more adequately distinguish between ASD and typical development (TD) groups. Among various neuroimaging techniques, volumetric T1-weighted magnetic resonance imaging (MRI) has been the focus of many studies, especially given its stability in repeated measurements and the vast number of features available in a 3D brain image.

Distinguishing individuals with ASD and TD subjects has been a challenging topic since the pathological effects of ASD on brain morphology are always more obscure relative to brain diseases such as Alzheimer's disease (AD) or Parkinson's disease (PD). Early ASD studies mainly relied on the volumes or areas of whole gray, white matter or whole brain to describe the structural brain differences between ASD and TD groups (Courchesne et al., 2003; Herbert et al., 2004; Lotspeich et al., 2004; Hazlett et al., 2006). These features achieved good classification accuracy in small and homogeneous dataset (Akshoomoff et al., 2004). Later, the cortical thickness (Hutsler et al., 2007) and gradually the voxel-based morphometry (VBM) (Hyde et al., 2010; Nickl-Jockschat et al., 2012) became the new biomarkers as they may provide more sensitive geometric information. For example, adopting thickness-based classification with logistic model trees (LMTs), Jiao et al. (2010) achieved the accuracy of 87% in 22 ASD and 16 TD subjects; using VBM along with a novel multivariate pattern analysis approach and searchlight algorithm, Uddin et al. (2011) achieved the accuracy of approximately 90% in 24 ASD children subjects and 24 TD children subjects.

However, VBM also has some potential disadvantages. For example, it cannot directly measure the cerebral cortex which is a 2-D sheet with a highly folded and curved geometry (Jiao et al., 2010). Some early studies (Thompson et al., 1998a; Fischl et al., 1999; Van Essen et al., 2001) have demonstrated that surface-based morphometry (SBM) may offer advantages over VBM as a method to study the structural features of the brain, such as surface deformation, as well as the complexity and change patterns in the brain due to disease or developmental processes.

Statistics derived from anatomical surface models, such as radial distance analysis (RD, distances from the medial core to each surface point) (Pizer et al., 1999; Pitiot et al., 2004), spherical harmonic analysis (Styner et al., 2006; Gutman et al., 2009) and local area differences (related to the determinant of the Jacobian matrix) (Woods, 2003) also have been applied to analyze the shape and geometry of various brain structures.

Surface tensor-based morphometry (TBM) (Thompson et al., 1998a; Woods, 2003; Chung et al., 2008) is an intrinsic surface statistic that examines spatial derivatives of the deformation maps that register brains to a common template and construct morphological tensor maps. More specifically, the eigenvalues of the deformation tensor are determined by the size of the deformation in the direction of the associated eigenvectors. Our previous studies also showed that surface multivariate TBM (mTBM) (Wang et al., 2010; Wang et al., 2011; Shi et al., 2013a; Shi et al., 2013b; Lao et al., 2016) was more sensitive for detecting group differences than other standard TBM-based statistics. Later, we found the combination of surface RD and mTBM, which termed the multivariate morphometry statistics (MMS), could give the most powerful statistic results than RD or mTBM (Wang et al., 2011; Wang et al., 2012).

Although surface-based morphometry achieved great success in population-based analyses and discovered the general trend of disease burden and progression in a more sensitive way (Thompson et al., 1998b; Wang et al., 2011; Lao et al., 2016), few studies have investigated the use of surface-based morphometry features for brain disease classification on an individual basis. A potential reason, no matter for TBM (N × 1), mTBM (N × 3), or MMS (N × 4), is that they all belong to high-dimensional shape descriptors (HDSD). Though HDSD is a useful source for disease biomarkers, it requires careful treatment in its application to machine learning to mitigate the curse of dimensionality (Wade et al., 2017). That means, when we use surface-based features such as MMS to classify, the feature dimension is usually much larger than the number of subjects, i.e., the so-called “high dimension, small sample size problem”. When a vast number of variables measured from a small number of subjects, it is often necessary to reduce their high dimensional features to a relatively lower dimension. By doing so, we may be able to truly stimulate the potential of MMS features in terms of classification.

The first aim of this study is to reduce the dimensionality of these high-dimensional surface-based features and therefore makes the process of classification easier. To the best of our knowledge, existing feature dimension reduction approaches mainly include feature selection (Jain and Zongker, 1997; Fan et al., 2005), feature extraction (Guyon et al., 2008; Abdi and Williams, 2010) and sparse learning methods (Donoho, 2006; Vounou et al., 2010). In most cases, the information was lost by mapping into a lower-dimensional space. In fact, the discarded information may be compensated by a better defined subspace (or features) — this forms the idea of sparse coding and dictionary learning. Sparse coding and dictionary learning has been previously proposed to learn an over-complete set of basis vectors (also called dictionary) to represent input vectors efficiently and concisely (Donoho and Elad, 2003). Previous studies have shown that sparse coding and dictionary learning was efficient enough for many tasks such as image imprinting (Moody et al., 2012), super-resolution (Yang et al., 2008), functional connectivity (Lv et al., 2014; Lv et al., 2017) and structural morphometry analysis (Zhang et al., 2017b). Since sparse coding and dictionary learning was demonstrated can generate state-of-the-art results (Mairal et al., 2009; Zhang and Li, 2010; Lv et al., 2017; Zhang et al., 2017b) in the field of computer vision, medical imaging and bioinformatics applications, it is suggested this method may also boost the power in the dimensionality reduction of our MMS features.

Our second aim is to compare and select the most suitable classifiers and optimizers with our MMS features after dimensionality reduction. Based on this, we can illustrate which classifiers or optimizers may achieve a higher classification accuracy between ASD and TD groups, and may better cooperate with our final features.

Many previous ASD classification studies (Ecker et al., 2010; Jiao et al., 2010; Uddin et al., 2011) based on small samples and heterogeneous features generated in MRIs, which may limit their generalization performance in ASD diagnosis at different sites with different scanners. A much larger ASD dataset is needed to overcome the previous heterogeneous findings and extract more universal classification features. The emergence of the Autism Brain Imaging Data Exchange I (ABIDE I) dataset (Di Martino et al., 2014) provides this chance. Therefore, the third aim of this study is to test our final classification pipeline in the large multi-site dataset, and to obtain a more general and reproducible basis for ASD classification with different scanners and scan parameters.

In this paper, we finally propose a novel and automated classification pipeline for ASD classification, which mainly includes the generation of surface-based features, dimension reduction based on sparse coding and dictionary learning, Max-pooling and ensemble classifiers based on adaptive optimizers. This pipeline is specially designed for subcortical structures with high-dimensional morphological features. Subcortical structure surfaces usually do not have strong curvature contrasts, but most of them partially have a tube-like shape. We include hippocampus in our manuscript because it is a very representative tube-like subcortical structure among all of the subcortical structures. We hypothesize that our novel pipeline would improve the accuracy of ASD classification based on surface morphological features of bilateral hippocampus. We will also discuss the potential of this pipeline and its improvable directions in future applications and studies.

2. Materials and methods

2.1. ABIDE subjects

This study analyzes T1-weighted anatomical images from the ABIDE, which includes 539 individuals with ASD and 573 TD participants (Di Martino et al., 2014), aged 6.47–64, collected as part of 20 studies at 17 different sites. All images were obtained with informed consent according to procedures established by human subjects' research boards at each participating institution. Details of acquisition, informed consent, and site-specific protocols are available at http://fcon_1000.projects.nitrc.org/indi/abide/. As not all sites collected female participants and the sampling was extremely sparse than male group, this study only included male participants between the age of 6 and 34. It would be beneficial to do so as there is increasing evidence that both the biological and behavioral features of ASD may be substantially different in male and female individuals (Lai et al., 2017; Ferri et al., 2018). To ensure the quality of segmentation, only these male participants with hippocampus that could be normally segmented and with good to excellent segmentation quality were retained. According to age, gender and quality controls, the final sample consisted of 364 ASD and 381 TD male participants. The demographic information of studied participants is shown in Table 1.

Table 1.

Demographic information of subjects in each site.

Site	Scanner	Male Subjects
				Age			Age
		N	ASD	Mean	SD	TD	Mean	SD	P*
CALTECH	SIEMENS Trio	16	7	23.5	3.5	9	23.3	5.2	0.95
CMU	SIEMENS Verio	17	8	23.6	3.4	9	25.6	4.4	0.30
KKI	Philips Achieva	36	15	10.0	1.3	21	10.3	1.3	0.58
Leuven 1	Philips INTERA	27	13	22.1	4.2	14	23.4	3.0	0.34
Leuven 2	Philips INTERA	21	10	13.8	1.5	11	14.1	1.5	0.73
Max Munich	SIEMENS Verio	29	12	17.7	8.4	17	23.3	6.3	0.05
NYU	Philips Allegra	131	63	13.5	5.8	68	16.4	6.4	< 0.05*
OHSU	SIEMENS Trio	23	10	11.3	2.3	13	10.2	1.0	0.12
OLIN	SIEMENS Allegra	27	14	15.8	2.9	13	17.2	3.8	0.30
PITT	SIEMENS Allegra	36	18	17.8	6.0	18	20.2	7.4	0.30
SBL	Philips INTERA	7	2	23.5	5.0	5	27.8	3.7	0.25
SDSU	GE MR750	20	7	14.7	1.9	13	14.7	1.6	0.95
Stanford	GE Signa	22	12	10.2	1.5	10	10.2	1.8	0.99
Trinity	Philips Achieva	36	15	16.5	3.1	21	17.4	3.9	0.51
UCLA 1	SIEMENS Trio	59	34	13.2	2.5	25	13.1	2.3	0.86
UCLA 2	SIEMENS Trio	21	12	12.5	1.8	9	12.2	1.3	0.64
UM 1	GE Signa	67	32	12.6	2.4	35	13.4	3.2	0.26
UM 2	GE Signa	28	11	14.7	1.6	17	17.1	4.3	0.10
USM	SIEMENS Trio	87	50	21.1	5.8	37	20.8	6.9	0.82
Yale	SIEMENS Trio	35	16	13.4	2.8	19	12.3	2.9	0.26

N = number of subjects; SD = Standard Deviation; P* were calculated by Student's t-test; P* values survived the pre-defined statistical threshold of 0.05 were denoted in bold.

2.2. Image preprocessing

All made subjects' bilateral hippocampus were automatically segmented from T1 images using FIRST (available at https://fmrib.ox.ac.uk/fsl/fslwiki/FIRST/), which is an integrated tool developed as a part of the FSL library. Relative to Freesurfer, FSL can achieve higher accuracy and lower failed rate in the segmentation of subcortical structures (Mulder et al., 2014; Perlaki et al., 2017). After the segmentation, the output results were strictly checked to verify their quality. When obtaining the binary segmentations of the hippocampus, we used a topology-preserving level set method (Han et al., 2003) to build surface models. Based on that, the marching cube algorithm (Lorensen and Cline, 1987) was applied to construct triangular surface meshes. Then, to reduce the noise from MR image scanning and to overcome the partial volume effects, surface smoothing was applied consistently to all surfaces. Our surface smoothing process consists of mesh simplification using “progressive meshes” (Hoppe, 1996) and meshes refinement by loop subdivision surface (Loop, 1987). Similar procedures were adopted in a number of prior studies of our group (Wang et al., 2010; Wang et al., 2011; Colom et al., 2013; Shi et al., 2013a; Shi et al., 2015), which have shown that the smoothed meshes are accurate approximations to the original surfaces with higher signal-to-noise ratio (SNR) (Shi et al., 2013a).

To facilitate hippocampal shape analysis, we generated a conformal grid on each surface, which is used as a canonical space for surface registration (Wang et al., 2008). On each hippocampal surface, we computed its conformal grid with holomorphic 1-form basis (Wang et al., 2007; Wang et al., 2010). We adopted surface conformal representation (Shi et al., 2013a) to obtain surface geometric features for automatic surface registration. It consists of the conformal factor and mean curvature, encoding both intrinsic surface structure and information on its 3D embedding. After capturing these two local features on each surface point, we computed their summation and then linearly scaled the dynamic range of the summation into [0, 255] to obtain a feature image for the surface. Finally, we further registered each hippocampal surface to an existing common template surface. With surface conformal parameterization and conformal representation, we generalized the well-studied image fluid registration algorithm (Bro-Nielsen and Gramkow, 1996; D'agostino et al., 2003) to general surfaces. Furthermore, most of the image registration algorithms in the literature are not symmetric, i.e., the correspondences established between the two images depending on which image is assigned as the deforming image and which one is the non-deforming target image. An asymmetric algorithm can be problematic as it tends to penalize the expansion of image regions more than shrinkage (Rey et al., 2002). In our system, to address this issue, we further extended the surface fluid registration method to an inverse-consistent framework (Leow et al., 2005). Therefore, the obtained surface registration is diffeomorphic. Details of our inverse-consistent surface fluid registration method can be found in (Shi et al., 2013a).

Together, these above steps allow us to compare and analyze surface data effectively on a simpler parameter domain, which avoids considering the complicated brain surfaces (Wang et al., 2013). In other words, it is usually hard to handle surfaces with complicated topologies (boundaries and landmarks) without singularities. The one-to-one correspondence achieved between vertices allows us to accurately analyze localized information on the surfaces of the hippocampus.

The a-d subplots of Fig. 1 illustrate the whole pipeline applied in this paper, which includes the segmentation of hippocampus, surface reconstruction, surface registration and the extraction of high-dimensional surface-based features.

Fig. 1.

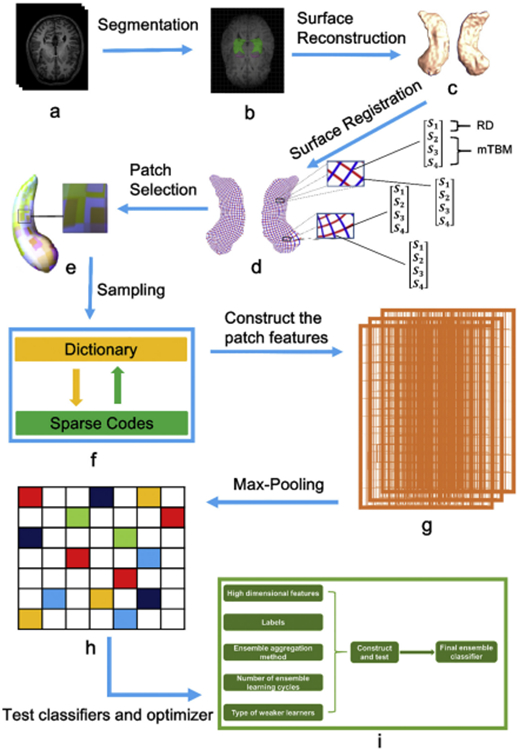
The whole pipeline applied in this paper. Subplots: (a) T1 MRIs; (b) segmentation of bilateral hippocampus; (c) reconstruction of 3D surface models; (d) one to one correspondence obtained from surface registration (the red curves are the isoparametric curves and therefore they are perpendicular to the medial axis; the intersection of each red curve and blue curve represents a surface vertex; each vertex contains a 4 × 1 vector that represents by S₁, S₂, S₃ and S₄); (e) selection of patches; (f) sparse coding and dictionary learning; (g) construction of patch features; (h) Max-pooling; (i) selection of suitable ensemble classifiers and optimizers.

2.3. Capturing the surface-based features

This study adopted 2 novel features: the radial distance (RD) and the multivariate tensor-based morphometry (mTBM), which formed the final joint feature — the surface multivariate morphometry statistics (MMS). Here we make a brief introduction for RD and mTBM as follows:

1. The RD (1 × 1 vector): radial distance, refers to the distance from a medial axis to a vertex on the surface — which represents the thickness of the shape at each vertex to the medial axis (Pizer et al., 1999; Thompson et al., 2004). The isoparametric curve (see red curves in Fig. 1d) is perpendicular to the medial axis (usually the medial axis is determined by calculating the geometric center of each red annulus) on the computed conformal grid (Wang et al., 2011), after which RD value is easily found at each vertex.

2. The surface mTBM (3 × 1 vector) has been widely studied in our prior work (Wang et al., 2009; Wang et al., 2010; Shi et al., 2013b; Shi et al., 2015), which usually describes a set of multivariate statistics that computed by analyzing the local deformations. Details about mTBM can be found in our previous papers (Wang et al., 2009; Wang et al., 2013).

The joint feature MMS has an obvious advantage as the mTBM describes the surface deformation along the surface tangent plane while RD reflects surface differences along the surface normal directions. Therefore, for each vertex, the MMS is constructed as a 4 × 1 vector consisting of the both RD and mTBM.

2.4. Patch-based surface sparse coding and Max-pooling for surface feature dimension reduction

2.4.1. Patch selection on vertex-wise surface morphometry features

In surface-based brain morphometry research, after establishing a one-to-one correspondence map between surfaces of subcortical structures (e.g., the subject 1's left hippocampus and subject 2's left hippocampus), the Jacobian matrix J of the map is determined. As introduced by some prior studies of our group (Zhang et al., 2016a; Zhang et al., 2017a), Surface TBM (Davatzikos, 1996; Thompson et al., 1998a; Woods, 2003; Chung et al., 2008) and its variant, mTBM (Wang et al., 2009; Wang et al., 2011), are further defined to measure local surface deformation based on the local surface metric tensor changes. Such vertex-wise surface morphometry features can help improve local deformation measure accuracy and may offer better localization and visualization of regional atrophy/expansion (Yao et al., 2018) and development (Thompson et al., 1998a). However, classification using vertex-wise high-dimensional neuroimaging features is likely to be plagued by the curse of dimensionality (Wade et al., 2017). Prior studies on surface feature-based (Sun et al., 2009; Wang et al., 2013) or voxel-based (Davatzikos et al., 2008; Uddin et al., 2011) classification mainly depended on direct feature dimension reduction or without dimension reduction, and then do the predict. Actually, such approaches do not exploit the possible relationships among features and may ignore the intrinsic properties of a structure's regional morphometry. For example, if a surface point carries strong statistical power for classification, most likely its neighboring surface points also have certain statistical discrimination power. More importantly, a single surface vertex may not carry strong statistical power, but a set of such correlated points may do so. In other words, our aim is to establish an association mapping among vertices and this may “borrow strength” from correlated phenotypes and can potentially yield higher statistical power. In computer vision and medical imaging research, patch-based local analysis has been frequently adopted for image classification and segmentation (Mairal et al., 2008; Lin et al., 2014). These prior patch-based studies, along with the potential advantages of conformal parameterization method (Wang et al., 2007) proposed in our prior research, inspired us to generalize patch-based analysis to anatomical surfaces of human subcortical structures.

Specifically, with regular surface parameterization obtained in our surface fluid registration research (Shi et al., 2013a), we randomly generated a number of p-vertex square windows on each registered surface to obtain a collection of small surface patches with different amounts of overlapping. These patches are allowed to overlap, so a vertex may be contained in several patches. We allow patches with overlapping vertices for the purpose that ensure every vertex can be learned at least once in the learning stage (therefore all vertices participate in the formation of the final features). The e subplot of Fig. 1 shows overlapping areas on selected patches from a hippocampal surface. Based on this method, we can get a much smaller feature dimension than vertex-wise features for each input sample. Meanwhile, we are still able to keep the surface spatial structure and learn the mesh structures. We finally transferred the original high-dimensional hippocampal surface features into 1008 overlapping patches, as the same as our previous studies (Zhang et al., 2016b; Wu et al., 2018). Based on our prior experience, the total number of surface patches is usually the most suitable for the hippocampus when it is equal to 1008.

2.4.2. Setting the appropriate patch size

As introduced in our previous studies (Zhang et al., 2016a; Zhang et al., 2017a), setting a suitable patch size can be an intriguing problem in our system. Ordinarily this problem can be solved empirically by exploiting the relationship between the classification performance and patch sizes. In the classification evaluation stage, for each patch size, a 10-fold cross validation protocol (9 folds for training and 1 fold for test, repeatedly) was adopted to determine the most suitable patch size (with the best classification performance). In our experiment, with 5 as the iteration interval, we tried all window sizes from 5 × 5 to 30 × 30 and finally found that the size of 20 × 20 had the best classification performance between ASD and TD groups. That means we got the best patch size which is 20 × 20 window. The relationship between surface patch size and classification accuracy is showed in Fig. 2.

Fig. 2.

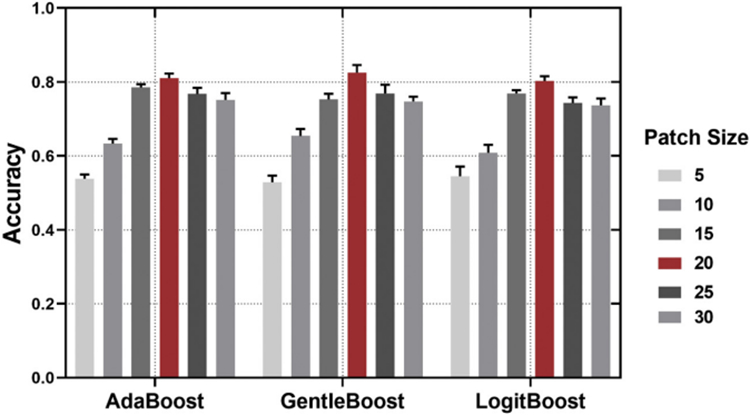
The relationship between surface patch size and classification accuracy. Patch size of 20 × 20 (red bar) was used in this study. Error bars signify SEM (Standard error of mean).

2.4.3. Sparse coding and dictionary learning

After illustrating these patches, we used the technique of sparse coding and dictionary learning (Mairal et al., 2009) to learn a sparse representation of patch features. In this way, the feature dimension can be further reduced. To our knowledge, solving sparse coding remains a computationally challenging problem, especially when dealing with large-scale datasets and learning large size dictionaries. Here, the Stochastic Coordinate Coding (SCC) (Lin et al., 2014) was adopted on our surface patches to construct the dictionary because of its computational efficiency.

In brief, the sparse coding and dictionary learning techniques (Olshausen and Field, 1997; Lee et al., 2006) consider a finite training set of signals/image patches X = (x₁, x₂, …, x_n) in R^{p × n}. In our work, X is a set of surface patches and each surface patch x_i ∈ R^p, i = 1, 2, …, n, where p is the dimension of the surface patch (p-vertex) and n is the number of surface patches. We aim to optimize the empirical cost function

$$f(D)\triangleq \frac{1}{n}\sum _{i=1}^{n}l(x_i,D)$$ (1)

where D ∈ R^{p × m} (n)m) is the dictionary, each column (atom) representing a basis vector, and l is a loss function such that l(x_i, D) should be small if D is “good” at representing the surface patch x_i. Specifically, suppose there are m atoms d_j ∈ R^p, j = 1, 2, …, m, then x_i can be represented into

$$x_i=D{z}_i$$ (2)

where x_i is approximated by both d_j (atoms of dictionary) and z_{i, j} (sparse codes). In this way, the p-dimensional vector x_i is represented by an m-dimensional vector z_i = (z_{i, 1}, z_{i, 2}, ..., z_{i, m})^T. Then, we define l (x_i, D) as the optimal value of the l₁- sparse coding problem:

$$l(x_i,D)\triangleq \underset{z_i\in R^m}{\text{min}}\frac{1}{2}\mid \mid D{z}_i-x_i\mid {\mid }_2^2+\lambda \Vert z_i{\Vert }_1$$ (3)

where λ is a regularization parameter which is usually taken to avoid the overfitting of the regression, ∥ · ∥ is the standard Euclidean norm. This problem is also known as “Lasso problem” (Fu, 1998), which is a convex problem.

Then, we can incorporate the idea of n surface patches into eq. (3) and have the following optimization problem:

$$\underset{D,z_i}{\text{min}}\frac{1}{2}\sum _{i=1}^n\Vert D{z}_i-x_i{\Vert }_2^2+\lambda \sum _{i=1}^n\Vert z_i{\Vert }_1$$ (4)

where ∥z_i∥₁ = Σ_{j = 1}^m ∣z_{i, j}∣. The first term of eq. (4) measures the degree of goodness representing the surface patches. The second term ensures the sparsity of the learned feature z_i. D = (d₁, d₂, …, d_m) ∈ R^{p × m} is the dictionary, where d_j ∈ R^p, j = 1, …, m. The second term of eq. (4) is also called l₁ penalty (Fu, 1998). It is well known that the l₁ penalty yields a sparse solution for Z. However, there is no link between the value of λ and the l₁ penalty. To prevent D from being arbitrarily large and leading to arbitrary scaling of the sparse codes, one may constrain its columns (d_i)_{j = 1}^k to have l₂ norm less than or equal to one. We will let C become the convex set of matrices verifying the constraint:

$$C\triangleq \{D\in R^{p\times m},s.t.\forall j=1,2,\dots ,m,d_j^T{d}_j\le 1\}$$ (5)

Therefore, our objective function in this work can be written into following matrix notation:

$$\underset{D\in C,Z\in R^{m\times n}}{\text{min}}\mid \mid DZ-X\mid {\mid }_F^2+\lambda \mid \mid Z\mid {\mid }_1$$ (6)

where the first term is Frobenius norm, the matrix F-norm is defined as the square root of the sum of the absolute squares of its elements. Eq. (6) is a non-convex problem with respect to joint parameters in the dictionary D and the sparse codes Z. However, it is a convex problem when either D or Z is fixed. When the dictionary D is fixed, solving sparse codes Z is a Lasso problem (Fu, 1998). On the other hand, when the sparse code Z is fixed, optimizing D is a quadratic problem. However, either solving D or Z in sparse coding problem requires much time (Lin et al., 2014) when dealing with large-scale data sets and a large sized dictionary. Thus, we choose the stochastic coordinate coding (SCC) algorithm (Lin et al., 2014), which can dramatically reduce the computational cost of the sparse coding while keeping a comparable performance.

2.4.4. Pooling operation

In practice, we could directly use all learned surface patch features computed by the previous sparse coding step as input features with a suitable classifier. However, we found the classification accuracy was relatively lower and it was more challenging in computation if we do so. To describe our surface features efficiently, one natural approach is to aggregate statistics of these features at various locations. Therefore, we introduced the pooling operation. Commonly used pooling operations include Max-pooling and Average-pooling. As a key component of deep learning models in recent years, Max-pooling takes the most responsive node (usually the biggest in value) of a given region of interest (Boureau et al., 2010), which therefore can better retain the texture features of this region. Average-pooling is widely used for image retrieval (Gu et al., 2018), which has certain advantages in maintaining the overall characteristics of a region.

Although Max-pooling and Average-pooling both down sampled the data, the idea of Max-pooling is more like feature extraction, as the features with better classification recognition are selected. Therefore, we finally used Max-pooling in our pooling operation. As displayed in Fig. 3, Max-pooling usually takes each max value over four numbers (little 2 × 2 squares with the same colors) and the feature dimension is then reduced to one fourth, when we set the stride as 2.

Fig. 3.

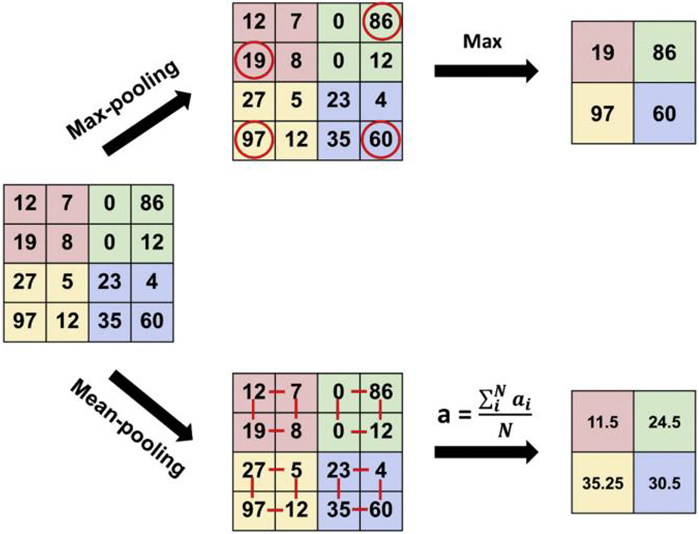
The process of Max-pooling and Average-pooling.

2.5. Choosing the most suitable ensemble classifier

Despite a series of dimension reduction and feature extraction methods were applied, the final feature dimension for bilateral hippocampus still remain 8000 — a huge number which is challenging for usual single classifiers such as SVM, decision tree or Naive Bayes. To better solve the curse of dimensionality in subcortical brain surface morphometry, here we introduced and compared a series of ensemble classifiers.

Like a “committee” of weak classifiers, ensemble classifiers (Rodriguez et al., 2006; Pratama et al., 2018) can usually achieve higher accuracy and stronger statistical ability than any individual classifier and are especially suitable for data sets with high-dimensional distribution patterns. After sparse coding and max-pooling, the diversification of our sparse surface features becomes more subtle — this give ensemble classifier chance to better detect these subtle differences between groups. How to construct a high-quality ensemble classifier/predictor is a critical topic here, and the framework of construction is introduced in Fig. 4, which mainly includes ensemble aggregation method, number of iterations and type selection of weaker learners. Generally, there are many ensemble algorithms for solving the binary classification problem, such as boost learning series (subtypes include: AdaBoost, LogitBoost, GentleBoost and RUSBoost) (Freund and Schapire, 1997; Friedman, 2001; Freund, 2009), Subspace (Barandiaran, 1998) and Bagging (Breiman, 1996).

Fig. 4.

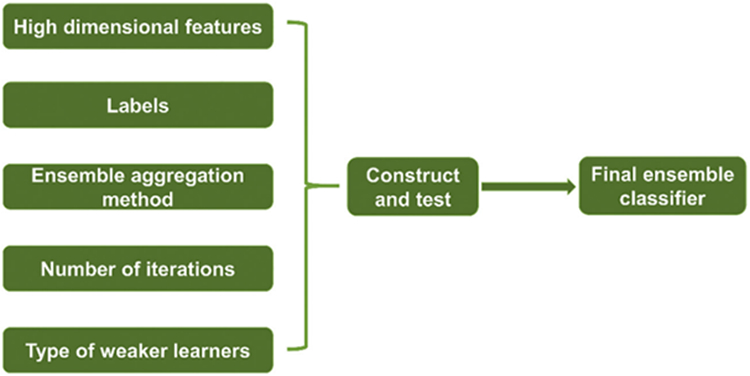
The framework of constructing a suitable ensemble classifier.

To choose the most suitable ensemble classifier for our patch-based surface features, we plan to compare the performance of all the above ensemble algorithms (see Table 2 and Table 3) and meanwhile retain other parameter consistent (e.g., all of them use tree as weak learners and adopt the same number of iterations). Here we use tree as weak learners rather than the SVM which applied in our prior studies (Zhang et al., 2016a; Zhang et al., 2017a) because our recent research discovered that tree (which may construct the random forest or even deep forest) had very stable performance in patch-based features of our ASD datasets. A possible explanation is that ensemble classifier with trees as weak learners can handle high-dimensional features without variable deletion and it can always run efficiently on large databases. Different with SVM-based ensemble classifier, it doesn't need to do a lot of parameter tuning, which, in some degree, guarantees the universality of our model. Meanwhile, a previous study has pointed out that random forest, which constructed by trees, had the most stable classification performance in high-dimensional shape descriptors (Wade et al., 2017).

Table 2.

Classification results of different ensemble classifiers based on Bayesian optimization.

	AdaBoost	RUSBoost	Bagging	GentleBoost	LogitBoost	Subspace
ACC	0.81 ± 0.04	0.69 ± 0.04	0.76 ± 0.06	0.83 ± 0.07	0.80 ± 0.04	0.50 ± 0.05
SEN	0.78 ± 0.09	0.62 ± 0.07	0.70 ± 0.07	0.80 ± 0.10	0.77 ± 0.04	0.92 ± 0.08
SPE	0.84 ± 0.06	0.75 ± 0.05	0.81 ± 0.09	0.85 ± 0.06	0.84 ± 0.06	0.11 ± 0.12
PPV	0.82 ± 0.08	0.70 ± 0.07	0.78 ± 0.10	0.84 ± 0.06	0.81 ± 0.09	0.50 ± 0.04
NPV	0.81 ± 0.08	0.68 ± 0.05	0.74 ± 0.07	0.82 ± 0.08	0.79 ± 0.06	0.44 ± 0.32

ACC = Accuracy; SEN = Sensitivity; SPE = Specificity; PPV = Positive predictive value; NPV = Negative predictive value. All of the values are denoted by Mean with SD. The ensemble classifiers with ACC greater than 80% are denoted in bold.

Table 3.

Classification results of different ensemble classifiers based on random search.

	AdaBoost	RUSBoost	Bagging	GentleBoost	LogitBoost	Subspace
ACC	0.81 ± 0.06	0.70 ± 0.03	0.75 ± 0.06	0.81 ± 0.07	0.80 ± 0.03	0.49 ± 0.05
SEN	0.78 ± 0.11	0.66 ± 0.08	0.68 ± 0.08	0.78 ± 0.10	0.75 ± 0.05	0.89 ± 0.10
SPE	0.85 ± 0.07	0.73 ± 0.11	0.83 ± 0.06	0.83 ± 0.08	0.84 ± 0.06	0.12 ± 0.08
PPV	0.83 ± 0.06	0.71 ± 0.06	0.79 ± 0.07	0.82 ± 0.07	0.82 ± 0.06	0.45 ± 0.05
NPV	0.80 ± 0.09	0.69 ± 0.03	0.73 ± 0.08	0.79 ± 0.10	0.78 ± 0.06	0.59 ± 0.23

ACC = Accuracy; SEN = Sensitivity; SPE = Specificity; PPV = Positive predictive value; NPV = Negative predictive value. All of the values are denoted by Mean with SD. The ensemble classifiers with ACC greater than 80% are denoted in bold.

In the final performance evaluation stage, a 10-fold cross validation protocol is adopted on the experiments of all ensemble classifiers to estimate the classification accuracy. We repeat this procedure for 10 times and estimate their average results. Five performance measures Accuracy (ACC), Sensitivity (SEN), Specificity (SPE), Positive predictive value (PPV) and Negative predictive value (NPV) are used to evaluate the classification performance (see Table 2 and Table 3). We also illustrate the area-under-the-curve (AUC) of the receiver operating characteristic (ROC), which is based on the results of the last fold in the last time experiment of all ensemble classifiers.

2.6. Selecting the best optimizer for our patch-based dataset and classifier

After choosing the most suitable ensemble classifier, a key point for boosting the power of this classifier is to select a best suitable optimizer, and this is also a component of optimization for hyperparameters. Although our model can search of network hyperparameters automatically, we still should predefine a specific search method. Generally, there are three kinds of automated methods for searching the hyperparameters — Bayesian optimization, grid search and random search. Here, the grid search is actually an exhaustive search and therefore it is expensive (Keerthi et al., 2007). Particularly, when the number of train examples is very large, this search is so time-consuming relative to Bayesian optimization or random search. In terms of effectiveness, previous study (Bergstra and Bengio, 2012) showed empirically and theoretically that randomly chosen trials (random search) are more efficient for hyperparameter optimization than trials on a grid (grid search). Due to the poor performance of grid search in high-dimensional large samples, this section finally compared the Bayesian optimization and random search.

Bayesian optimization is a powerful tool for optimizing objective functions which are very costly or slowly to evaluate (Martinez-Cantin et al., 2007; Snoek et al., 2012). Mathematically, we are considering the problem of finding a global maximizer (or minimizer) of an unknown objective function f

$$x^{\ast }=\text{arg}\underset{x\in \chi }{\max }f(\mathrm{x})$$ (7)

where χ is some design space of interest; in global optimization, χ is often a compact subset of ${\mathbb{R}}^d$ but the Bayesian optimization framework can be applied to more unusual search spaces that involve categorical or conditional inputs, or even combinatorial search spaces with multiple categorical inputs (Shahriari et al., 2015). Bayesian optimization can usually find an acceptable hyperparameter value quickly and it needs fewer iterations (relative to grid search), even its disadvantage is that it is not easy to find the global optimal solution.

In random search, we can express the hyper-parameter optimization problem (Snoek et al., 2012) in terms of a hyper-parameter response function Ψ by:

$${\lambda }^{\ast }=\text{arg}\underset{\lambda \in \Lambda }{\max }\Psi (\lambda )$$ (8)

$$\approx \text{arg}\underset{\lambda \in \{{\lambda }^{(1)}\cdots {\lambda }^{(S)}\}}{\max }\Psi (\lambda )\equiv \widehat{\lambda }$$

where λ is a hyper-parameter which identified by a good value; λ ∈ Λ and Λ represents a specific dataset. Hyper-parameter optimization is the maximization or minimization of Ψ(λ) over λ ∈ Λ. The dominant strategy for finding a good λ is to choose some number (S) of trial points {λ⁽¹⁾⋯λ^(S)}, to evaluate Ψ(λ) for each one, and return the λ⁽ⁱ⁾ that worked the best as $\widehat{\lambda }$. Previous study (Snoek et al., 2012) has shown that random search is more efficient than grid search in high-dimensional spaces if functions Ψ of interest have a low effective dimensionality. In particular, if a function f of two variables could be approximated by another function of one variable (f(x₁, x₂) ≈ g(x₁)), we could say that f has a low effective dimension. Obviously, random search also has huge potential for our high-dimensional features.

Later, we compare the optimizer performance of Bayesian optimization and random search in all ensemble classifiers, and try to evaluate which one is better.

3. Results and validations

3.1. Demographic characteristics

The demographic characteristics of all the male subjects are summarized in Table 1, which includes site name, information of scanner, mean and standard deviation (SD) of the age of male subjects. Among the 20 sites, only the NYU site has significant difference in age distribution between ASD and TD groups (p < 0.05). Put aside different sites, all of the 364 ASD and 381 TD male participants are age-matched.

3.2. Classification results and the selection of suitable ensemble classifiers

Classification results of these ensemble classifiers are displayed in Table 2 and Table 3. When adopting the same optimizer (e.g. Bayesian optimization), the GentleBoost outperformed than other ensemble classifiers in ACC, SEN, SPE, PPV and NPV. Subspace is found not suitable for our features and pipeline (ACC ≈ 0.50). Except for the Subspace, the impact of different optimizers (Bayesian optimization vs. random search) on the final classification accuracy is very limited, which usually less than 1% in changes of ACC, 4% in changes of SEN, 2% in changes of SPE, 2% in changes of PPV and 3% in changes of NPV.

No matter what optimizer is used, the classification accuracy of the three ensemble classifiers — include Adaboost, GentleBoost and LogitBoost, are steadily greater than or equal to 80%. We illustrating 5 best and representative optimization performances for each ensemble classifier under the same number of iterations (Fig. 5) based on Bayesian optimization. Results show that in the optimization process of all ensemble classifiers, the Adaboost, GentleBoost and LogitBoost are easier to find acceptable minimum estimated values relative to minimum observed value. In other classification metrics, such as SEN, SPE, PPV and NPV, the three ensemble classifiers displayed very similar patterns.

Fig. 5.

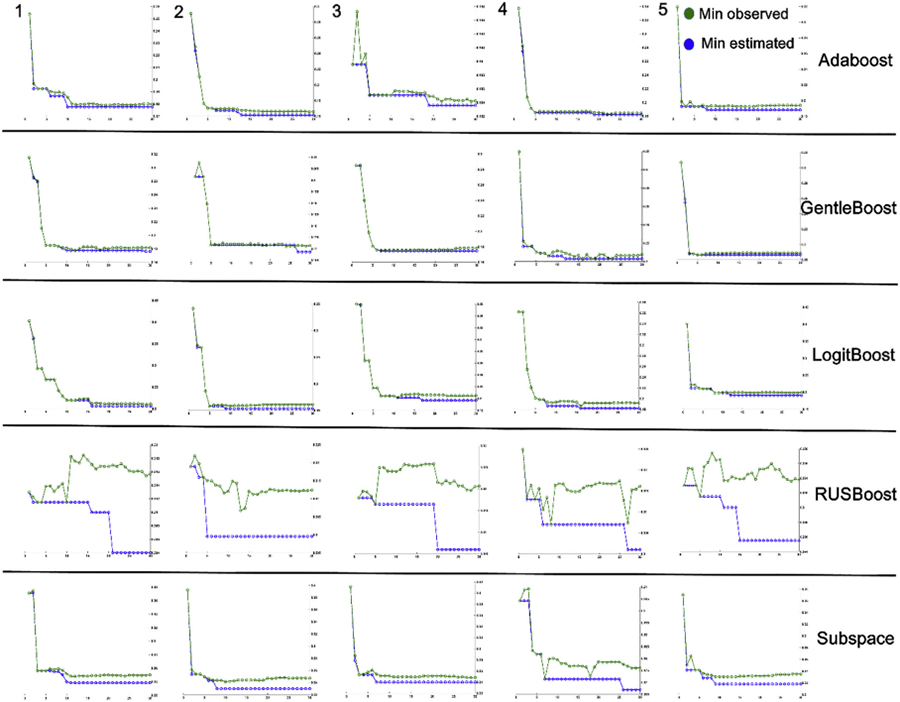
The 5 best and representative optimization performance for each ensemble classifier under the same number of iterations.

Note that the ROC results in Fig. 6 are derived on the results of the last fold in the last time experiment of all ensemble classifiers (not directly choosing the best ROC), because our aim is just simply display which ensemble classifiers might be better. In conclusion, the Adaboost, GentleBoost and LogitBoost ensemble classifiers might work well with our pipeline.

Fig. 6.

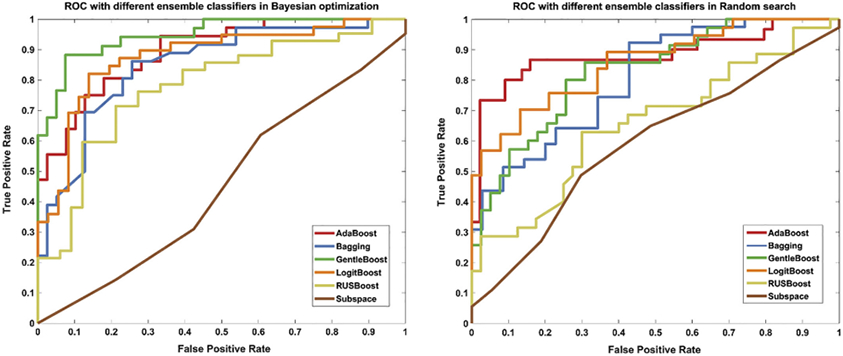
The ROC of the six ensemble classifiers based on Bayesian optimization (left) and Random search (right).

In the best case, when combining GentleBoost ensemble classifier with Bayesian optimization, this pipeline can achieve 83% accuracy, 80% sensitivity, 85% specificity for the classification of ASD vs. TD, though it only used morphological features from bilateral hippocampus.

3.3. Validations of classification performances

3.3.1. Classification performance of this pipeline in a single site

We also added a single site experiment to test the classification performance of our pipeline on subjects with the same scan parameters. Considering the number of subjects and the matching degree of age, we extracted subjects from the USM site (rather than NYU site) to perform this verification process. The USM site contains 87 of 745 male subjects, which consisting of 50 male subjects with ASD and 37 TD male subjects. GentleBoost ensemble classifier with Bayesian optimization was applied here because of its better performance in ABIDE multi-site classification. Due to the much smaller sample size, here we used a 20-fold cross-validation protocol and repeated this procedure for 10 times. As shown in Fig. 7, USM site dataset outperformed than multi-site dataset in the mean values of ACC (86% > 83%), SEN (92% > 80%), PPV (88% > 84%) and NPV (86% > 82%), but displayed lower SPE (81% < 85%).

Fig. 7.

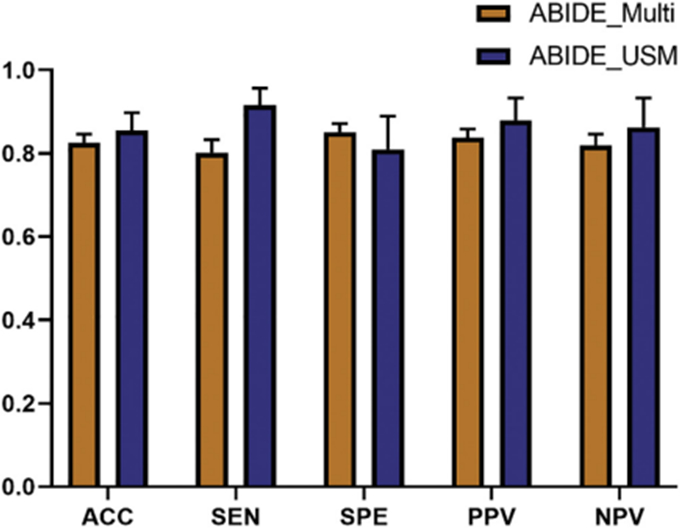
The classification performance of USM site vs. ABIDE multi-site. Error bars signify SEM.

3.3.2. Classification performance of this pipeline when only using RD features

The advantage of MMS feature is it contains both RD (from surface normal direction) and mTBM (form surface tangent direction) in each surface vertex. Combining features from both directions usually makes the classification results better. In this section, we also evaluated the average classification performance of using only the RD features with a 10-fold cross-validation protocol. We repeated this experiment in AdaBoost, GentleBoost and LogitBoost ensemble classifiers. All of the performances of using RD features are significantly worse than using MMS features (Table 4).

Table 4.

Classification performances of three ensemble classifiers based on MMS features vs. RD features.

	AdaBoost	AdaBoost_RD	GentleBoost	GentleBoost_RD	LogitBoost	LogitBoost _RD
ACC	0.81 ± 0.04	0.68 ± 0.04	0.83 ± 0.07	0.63 ± 0.05	0.80 ± 0.04	0.61 ± 0.05
SEN	0.78 ± 0.09	0.66 ± 0.07	0.80 ± 0.10	0.59 ± 0.11	0.77 ± 0.04	0.63 ± 0.09
SPE	0.84 ± 0.06	0.70 ± 0.09	0.85 ± 0.06	0.67 ± 0.05	0.84 ± 0.06	0.60 ± 0.06
PPV	0.82 ± 0.08	0.68 ± 0.07	0.84 ± 0.06	0.63 ± 0.08	0.81 ± 0.09	0.60 ± 0.08
NPV	0.81 ± 0.08	0.68 ± 0.07	0.82 ± 0.08	0.63 ± 0.09	0.79 ± 0.06	0.63 ± 0.06

ACC = Accuracy; SEN = Sensitivity; SPE = Specificity; PPV = Positive predictive value; NPV = Negative predictive value. All of the values are denoted by Mean with SD. Results based on RD features are denoted by bold.

3.3.3. Classification performance of this pipeline based on direct feature reduction

As a classical feature dimensionality reduction method, Principal Component Analysis (PCA) is usually used as a representative method for the direct feature reduction. While maintaining the contribution rate of 90%, we reduced the original features with 120,000 dimensions to the final 145 dimensions. We repeated this experiment in AdaBoost, GentleBoost and LogitBoost ensemble classifiers and found the classification results based on PCA feature reduction were much worse than our method (see Table 5).

Table 5.

Classification results of the three ensemble classifiers based on PCA feature reduction.

	AdaBoost	AdaBoost_PCA	GentleBoost	GentleBoost_PCA	LogitBoost	LogitBoost _PCA
ACC	0.81 ± 0.04	0.52 ± 0.07	0.83 ± 0.07	0.53 ± 0.05	0.80 ± 0.04	0.51 ± 0.04
SEN	0.78 ± 0.09	0.44 ± 0.12	0.80 ± 0.10	0.48 ± 0.09	0.77 ± 0.04	0.44 ± 0.15
SPE	0.84 ± 0.06	0.60 ± 0.02	0.85 ± 0.06	0.58 ± 0.09	0.84 ± 0.06	0.58 ± 0.10
PPV	0.82 ± 0.08	0.51 ± 0.12	0.84 ± 0.06	0.52 ± 0.06	0.81 ± 0.09	0.50 ± 0.07
NPV	0.81 ± 0.08	0.53 ± 0.06	0.82 ± 0.08	0.54 ± 0.10	0.79 ± 0.06	0.53 ± 0.07

ACC = Accuracy; SEN = Sensitivity; SPE = Specificity; PPV = Positive predictive value; NPV = Negative predictive value. All of the values are denoted by Mean with SD. Results based on PCA feature reduction are denoted by bold.

4. Discussion

This study has four main findings. Firstly, we make the high-dimensional surface-based features of bilateral hippocampus more feasible for classification and achieved good accuracy. In fact, surface-based features, especially derived from subcortical structures, are challenging in feature extraction — small errors or uncaptured deformations may cause worse accuracy. This solution mainly relies on our novel pipeline for ASD classification, which includes the generation of surface-based features, dimension reduction based on sparse coding and dictionary learning, Max-pooling and classifier selection based on adaptive optimizer.

Secondly, we find our multivariate morphometry statistics (MMS), which consists of surface multivariate tensor-based morphometry and radial distance, are applicable for prediction and classification research of ASD. This discovery implies that when analyzing ASD-related morphological changes in subcortical structures, it may be highly beneficial if we simultaneously consider the surface normal direction and surface tangent direction. Our supplementary experiment in Section 3.3.2 also confirms that classification results included morphological features in only one direction usually perform worse.

Thirdly, by leveraging the multi-site international dataset (ABIDE), we show that our pipeline is stable and has good generalization in MRI data with long span of ages, strong heterogeneity in scan parameters and scanners. This also means our pipeline may produce more attractive results in data sets with less heterogeneity (e.g. more closely matched in age, IQ and use the same scanner and the same scan parameters). Our supplementary experiment in Section 3.3.1 has provided a preliminary evidence.

Fourthly, our pipeline demonstrates that high-dimensional surface-based features of subcortical structures may provide stronger statistical power in ASD-related classification and diagnosis if we encode a great deal of neighboring intrinsic geometry information that might be overlooked in previous studies. As for comparison, the traditional feature reduction method (e.g., PCA, see Section 3.3.3) works much worse than our method.

4.1. The tradeoff of high-dimensional surface-based features and classification accuracy

One of the original intentions of this paper is to make a tradeoff between high-dimensional surface-based features and classification accuracy. The high-dimensional surface-based features, such as SPHARM, RD, mTBM, MMS and so on (Woods, 2003; Pitiot et al., 2004; Styner et al., 2006; Chung et al., 2008; Gutman et al., 2009; Wang et al., 2010; Shi et al., 2013a), are usually more sensitive than volume, surface area or VBM (Jiao et al., 2010; Wang et al., 2011; Yao et al., 2018). However, these high-dimensional surface-based features have different degrees of sensitivity in capturing local deformations. For example, the surface multivariate TBM (mTBM) was demonstrated outperformed than SPHARM (Shi et al., 2011).

The MMS features adopted in this research may capture richer details in local morphometry than using only RD or mTBM (Wang et al., 2011; Wang et al., 2012), therefore it is sensitive enough among existing surface-based features. However, this “sensitivity” is not always a good thing — simultaneously includes features in surface normal direction and surface tangent direction make MMS a bit noisier (Lao et al., 2016; Yao et al., 2018). In order to prove that our proposed pipeline is novel and effective, we also need to ensure that the final classification accuracy is stable and can achieve similar or better results than these current classification schemes.

After image preprocessing, a pair of hippocampus includes totally 30,000 vertices on their surface, while MMS feature at each surface vertex is a 4 × 1 vector, therefore the final original feature dimension is up to 120,000 dimensions. In the initial of this study, we tried to classify directly with the original high-dimensional features or do some traditional dimensionality reduction method such as PCA (see Section 3.3.3), but obtained poor classification performance. Then we considered patch-based analysis, as a single surface vertex may not carry strong statistical power and is too sensitive to noise. We found the best patch size is 20 × 20 since it may generate the best prediction performance between ASD and TD groups. This is slightly different from our previous experience, as our previous research found that 10 × 10 window is the most suitable for the classification between Alzheimer's disease (AD) group and cognitive unimpaired (CU) group (Zhang et al., 2016b; Zhang et al., 2017a). We speculate the underlying reason may be that the overall degree of hippocampal morphological changes caused by ASD is relatively weaker or the recognizable areas between the two groups on bilateral hippocampus are more dispersive (as for comparison, morphological changes in hippocampus of AD are obviously more extensive). In practical analysis, it may be rewarding to consider the association of patch sizes and classification accuracies.

In terms of improving the classification accuracy, we compared six classical ensemble classifiers, and found three of them may produce good classification results. We also demonstrated that our pipeline seems not very sensitive to the selection of different optimizers. In the future, we may discuss the underlying causes of this phenomenon.

4.2. Comparison with other ASD classification research based on MRI data of ABIDE dataset

Considering the contrast, it may be advantageous to list some prior classification research based on T1-weighted MRIs of ABIDE dataset. Using autism, classification and ABIDE as key words simultaneously, we got five ASD classification studies from the Google Scholar. The time range we conducted is from 2014 to 2019. We found that the topic of ASD classification becomes hotter in recent years. We summarized these state-of-the-art MRI-based classification studies (Haar et al., 2014; Katuwal et al., 2015; Sabuncu et al., 2015; Katuwal et al., 2016; Zheng et al., 2019) and this study in Table 6 for comparison. From this table, we can see that 1) our experiments are conducted with a large dataset and heterogeneous subjects; 2) our experimental results show the superiority of the proposed pipeline over the state-of-the-art morphometry classification methods; 3) our pipeline may be more expandable in future research (because we only used patch-based features derived from the bilateral hippocampus, and a large number of features in the brain were not include).

Table 6.

Comparison with other ASD classification research based on MRI data of ABIDE dataset.

Ref	ASD group			TD group			sMRI features	Classification method	Classification accuracy	Note
	Age	Gender	Size	Age	Gender	Size
Haar et al. (2014)	6–35	Male only	453	6–35	Male only	453	Regional volume, surface area and cortical thickness	LDA, QDA	< 60%	Performed two analyses, based on strict/relaxed criteria.
Sabuncu et al. (2015)	17.8 ± 7.4	88.6% Male	325	17.9 ± 7.4	88.6% Male	325	Regional volume, surface area and cortical thickness	SVM, NAF, RVM	< 60%	None.
Katuwal et al. (2015)	Unknown	Male only	373	Unknown	Male only	361	Volume, surface area, cortical thickness, thickness std., mean curvature, Gaussian curvature, folding index	RF, GBM, SVM	60%	None.
Katuwal et al. (2016)	17.9 ± 8.7	Male only	361	18.1 ± 8.2	Male only	373	Curvature and folding index	GBM	60%	Adding VIQ and age to morphometric features.
Zheng et al. (2019)	Depends on site	Depends on site	66	Depends on site	Depends on site	66	Seven morphological features of each of the 360 brain regions, elastic network, multi-feature-based networks	SVM	78.63%	High-functioning adults with ASD.
This study	6–34	Male only	364	6–34	Male only	381	Patch-based features derived from hippocampus	Six ensemble classifiers	> 80%	None.

LDA = Linear Discriminant Classifier; QDA = Quadratic Discriminant Classifier; SVM = Support Vector Machine; NAF = Neighborhood Approximation Forest; RVM = Bayesian Relevance Vector Machine; RF = Random Forest; GBM = Gradient Boosting Machine.

4.3. Limitations and potential future improvements

Although the current work drew on the experience of our previous studies (Zhang et al., 2016b; Zhang et al., 2017a) and its performance is tested in both AD and ASD groups, this pipeline is still on its preliminary stage. This study has three main limitations. First, because of the overlaps in patch selection and the max-pooling scheme, we generally cannot visualize the selected features and it decreases the comprehensibility of this pipeline. Usually an alternative solution is that we may visualize these statistically significant regions based on our previous analysis framework for group difference (Shi et al., 2013a; Wang et al., 2013; Yao et al., 2018). Second, we only tested the performance of six classical ensemble classifiers and two automated methods for searching the hyperparameters. Using more novel classifiers and optimizers in experiment may find more attractive results. Third, MRIs of ABIDE were obtained from different sites, with different scanning parameters, have large age spans and different phenotypic characteristics. When these factors are mixed, they may weaken the classification ability of our pipeline. Since ASD is a “spectrum” disorder, there are a large array of different phenotypic characteristics that may classify an individual as having ASD. For example, the lower accuracies achieved when classifying ASD in comparison to other disorders may be caused by the wide variety of individuals who fall under the categorization of ASD (Mathur and Lindberg, n.d.).

In the future, there are at least two improvements worth exploring with our pipeline. First, no matter in our previous AD classification studies or this ASD classification study, we only used patch-based features that derived from hippocampal morphometry. As we know, there are many subcortical structures and cortical structures in the human brain that are pathologically related to ASD, hence the joint features from these multiple structures may further boost the classification potential of our pipeline. Second, the ASD subjects included in this study are very heterogeneous. A better alternative in the future, as pointed out by Katuwal et al. (2016), may be to focus on the classification in relatively more homogenous sub-groups defined by a number of criteria such as age, sex, IQs, handedness, severity, etc.

5. Conclusion

In the present study, we illustrated a novel pipeline that leverages surface multivariate morphometry statistics with surface sparse coding and max-pooling for the ASD classification. We discussed the selection of patch sizes, ensemble classifiers and automated optimizers. We compared our classification results with previous MRI-based classification studies using ABIDE dataset and found our pipeline had superiority in both accuracy and expansibility. Software source code of sparse coding and dictionary learning were also released on our website for public access (available at: http://gsl.lab.asu.edu/software). In future, we plan to apply our pipeline to more cortical and subcortical surface data and further improve the comprehensibility of this framework by visualizing morphometry features selected in classification.