Integrating multidimensional data for clustering analysis with applications to cancer patient data

Abstract

Advances in high-throughput genomic technologies coupled with large-scale studies including The Cancer Genome Atlas (TCGA) project have generated rich resources of diverse types of omics data to better understand cancer etiology and treatment responses. Clustering patients into subtypes with similar disease etiologies and/or treatment responses using multiple omics data types has the potential to improve the precision of clustering than using a single data type. However, in practice, patient clustering is still mostly based on a single type of omics data or ad hoc integration of clustering results from individual data types, leading to potential loss of information. By treating each omics data type as a different informative representation from patients, we propose a novel multi-view spectral clustering framework to integrate different omics data types measured from the same subject. We learn the weight of each data type as well as a similarity measure between patients via a non-convex optimization framework. We solve the proposed non-convex problem iteratively using the ADMM algorithm and show the convergence of the algorithm. The accuracy and robustness of the proposed clustering method is studied both in theory and through various synthetic data. When our method is applied to the TCGA data, the patient clusters inferred by our method show more significant differences in survival times between clusters than those inferred from existing clustering methods.

1. Introduction

Identifying cancer patient subtypes based on their genomics profiles has proved useful for tumor classification, and it has been successfully applied to many cancer types (Perou et al., 2000; Verhaak et al., 2010; Markert et al., 2011; Guinney et al., 2015; Cristescu et al., 2015; Liu et al., 2017). For example, for breast cancer, PAM50-based subtypes are commonly used to predict patient prognosis and guide patient treatment in clinical care (Parker et al., 2009; Bastien et al., 2012). As more technologies and platforms are being developed and applied to characterize patients’ molecular profiles, there is a need to develop accurate clustering algorithms to integrate diverse types of data to identify patients having different tumor subtypes (Kristensen et al., 2014; Bailey et al., 2016). Many projects, such as The Cancer Genome Atlas (TCGA) project (Weinstein et al., 2013), have generated rich resources of multi-dimensional omics data. Despite its importance, due to the lack of statistical methods for data integration, clustering patients is still mostly based on a single type of omics data (e.g., gene expression data) in practice (Verhaak et al., 2010; Markert et al., 2011; Chen et al., 2013; Guinney et al., 2015; Cristescu et al., 2015; Netanely et al., 2016), and to the best of our knowledge there have been limited studies comprehensively considering the combination of multiple omic profiles for identifying tumor subtypes (Liu et al., 2013; Serra et al., 2015; Imangaliyev et al., 2017). Because different tumor subtypes may exhibit heterogeneity-relevant signals from different pathways via different mechanisms, different subtypes may only be identified when different data types are analyzed together (Kristensen et al., 2014).

One challenge in integrating different data sets is that they have different degrees of quality and information on patient heterogeneity and subtypes. Some data may be more noisy due to sample processing and measurement errors, and their inclusion in clustering may add limited information on patient clustering. In addition, as various omics data sets reveal patient heterogeneity from different perspectives, each data set must be used with caution. However, this aspect has mostly been overlooked in the multi-view clustering literature where all representations are equally considered (Shen et al., 2009; Zhang et al., 2012; Liu et al., 2017). On the other hand, manual integration (e.g., consensus clustering (Monti et al., 2003)) of clustering results from different data sets tends to be subjective, and it is difficult to capture both concordant and unique alterations across data types (Shen et al., 2009).

In this article, we propose a kernel-learning method to iteratively update the importance of each view (data set) and perform refined clustering analysis by aggregating multiple omics data sets that include a large number of molecular features. We adopt the spectral clustering framework with sparse structures on the target matrices. Spectral clustering is a popular clustering method utilizing the eigenvectors of a graph Laplacian that is derived from the data for clustering. It often outperforms traditional clustering methods such as k-means clustering (von Luxburg, 2007), and can be computed efficiently by standard linear algebra software. The main reason for adopting spectral clustering is that once a similarity measure is constructed between samples for each data type, these similarity structures can be easily shared across different data types through our proposed multi-view spectral clustering framework (which is described in Section 2.3) to improve clustering accuracy. One limitation of spectral clustering is that the results of spectral clustering may be sensitive to the choice of similarity measures, and there are no clear criteria for determining an appropriate similarity measure from data (Wang et al., 2017). In this paper, to allow for more flexibility in choosing similarity measures, we update similarities between subjects from multiple Gaussian kernels for each data set, which alleviates the user from having to choose the best kernel functions and kernel parameters for each data set beforehand. The weights for different data sets and kernels are learned simultaneously in the optimization procedure, where the weight assigned to each data set indicates its quality in clustering analysis, while the weight assigned to a kernel represents the quality of the corresponding view’s information. Our proposed method is able to assign larger weights to the data sets and kernels with more information about clustering. We assess the performance of the proposed clustering method through both simulations and applications to 22 major cancer types of TCGA in terms of survival outcomes.

2. Methods

2.1. Sparse spectral clustering

Given a set of data points $X={\left[x_1,\cdots ,x_n\right]}^T\in {ℝ}^{n\times p}$ spectral clustering (von Luxburg, 2007) uses the symmetric similarity matrix $S=\left(s_{ij}\right)\in {ℝ}^{n\times n}$, where p is the number of features, n is the number of samples, and $s_{ij}\ge 0$ represents a similarity measure between data points x_i and x_j. For spectral clustering (SC) to perform well, it is important to choose an appropriate similarity matrix S. Gaussian kernel is one of the most commonly used functions to construct S = (s_ij) with $s_{i,j}=\exp \left(-{‖x_i-x_j‖}^2/\left(2{\sigma }^2\right)\right)$, where $‖x_i-x_j‖$ is the Euclidean distance between x_i and x_j, and σ controls the width of the neighborhoods.

SC solves the following problem: for a target clustering number C,

$$\underset{L\in {ℝ}^{n\times C}}{\min }\text{tr}\left\{L^T\left(I_n-W\right)L\right\}\hspace{1em}\text{s}.\text{t}.\hspace{1em}{L}^{T}L=I_C,$$

where $W=D^{-1/2}S{D}^{-1/2}$ is the normalized similarity matrix, and $D=\text{diag}\left(d_{11},\cdots ,d_{nn}\right)$ is a diagonal matrix with $d_{ii}=\sum _{j=1}^n{s}_{ij}$. Finally, each row of the optimal L is treated as a point in ${ℝ}^c$, and clustered into C groups by k-means. Note that $I_n-W$ is called a normalized graph Laplacian (Andrew et al., 2001; von Luxburg, 2007), and solving the above optimization is equivalent to finding C eigenvectors of I_n –W corresponding to the C smallest eigenvalues (or C eigenvectors of W corresponding to the C largest eigenvalues). Note that in the ideal case in which C is the underlying clustering number and W fully reflects similarities between samples, i.e., w_ij > 0 if and only if the ith and jth samples belong to the same underlying cluster, the optimum L encodes true clustering membership such that L_ik ≠ 0 if and only if the ith sample belongs to the kth cluster. For detailed properties of SC, see von Luxburg (2007).

There are equivalent forms of SC as follows. Under the constraint L^TL=I_C, we have

$$\text{tr}\left(L^T\left(I_n-W\right)L\right)=\text{tr}\left(L^{T}L\right)-\text{tr}\left(L^{T}WL\right)=C-\text{tr}\left(WL{L}^T\right)=C-〈W,L{L}^T〉,$$

where $〈A,B〉=\text{tr}\left(A^{T}B\right)$ for two matrices A and B. Since C is a constant, the minimizer of the original optimization of SC is equivalent to the minimizer of the following problem:

$$\underset{L\in {ℝ}^{n\times C}}{\min }-〈W,L{L}^T〉\hspace{1em}\text{s}.\text{t}.\hspace{1em}{L}^{T}L=I_C.$$

Moreover, it holds that

$${‖L{L}^T‖}_F^2=\text{tr}\left({\left(L{L}^T\right)}^T\left(L{L}^T\right)\right)=\text{tr}\left(\left(L{L}^T\right)L{L}^T\right)=\text{tr}\left(L{L}^T\right)=\text{tr}\left(L^{T}L\right)=\text{tr}\left(I_C\right)=C,$$

where the first equality holds due to ${‖A‖}_F^2=\text{tr}\left(A^{T}A\right)$ for any matrix A, thus ${‖L{L}^T‖}_F^2$ has a constant value C as long as L^T L = I_C holds. Hence, the minimizer of the original optimization of SC is also equivalent to the minimizer of

$$\underset{L\in {ℝ}^{n\times C}}{\min }ϵ{‖L{L}^T‖}_F^2-〈W,L{L}^T〉\hspace{1em}\text{s}.\text{t}.\hspace{1em}{L}^{T}L=I_C$$

for any $ϵ\ge 0$. We will use this optimization for further variations. Note that the term ${‖L{L}^T‖}_F^2$ plays an important role in the computational convergence of the proposed optimization, which will be given in Section 2.3. The role of ϵ is to control the effect of the term ${‖L{L}^T‖}_F^2$, and a small ϵ > 0 guarantees a convergence of the algorithm (Theorem 2) and also leads to slightly better clustering results in our settings. In the ideal case in which w_ij > 0 if and only if the ith and jth samples belong to the same underlying cluster, the obtained $L{L}^T\in {ℝ}^{n\times n}$ has a block diagonal structure and thus sparse (Lu et al., 2016). Motivated by this observation, we can modify the sparse spectral clustering (Lu et al., 2016) as follows:

$$\underset{L\in {ℝ}^{n\times C}}{\min }ϵ{‖L{L}^T‖}_F^2-〈W,L{L}^T〉+\lambda {‖L{L}^T‖}_1\hspace{1em}\text{s}.\text{t}.\hspace{1em}{L}^{T}L=I_C.$$ (1)

Note that (1) includes a nonlinear constraint and is not convex. Instead of using the nonlinear constraint L^T L = I_C , we add the relaxed convex constraint tr(LL^T ) = C and 0 LL^T I to address the computational issue of the nonconvex model. It is known that the set {P : tr(P) = C, 0 P I}, called the Fantope (Dattorro, 2005), is a convex hull of the set {P = LL^T : L^T L = I_C } (Dattorro, 2005; Vu et al., 2013). Hence we consider the following convex optimization problem

$$\underset{P\in {ℝ}^{n\times n}}{\min }ϵ{‖P‖}_F^2-〈W,P〉+\lambda {‖P‖}_1\hspace{1em}\text{s}.\text{t}.\hspace{1em}\text{tr}\left(P\right)=C,0\hspace{1em}P\hspace{1em}I,$$ (2)

which can be efficiently solved using the ADMM algorithm (Boyd et al., 2011). Note that the computational convergence of the proposed algorithm, which will be given later (Theorem 2), is achieved only when $ϵ>0$.

Let $\widehat{P}$ be the solution to the convex sparse spectral clustering problem as formulated in (2). Theorem S1 of the Supplementary materials shows that the clustering result obtained by the C leading eigenvectors of $\widehat{P}$ accurately estimates the underlying clusters when there exists C clusters under some regularity conditions. This result implies that even with the approximation error due to convex relaxation of (2) with regard to (1), the estimated target matrix $\widehat{P}$ preserves the true clustering membership. Proofs are deferred to the Supplementary materials. Throughout the paper, let C* be the underlying number of clusters, $f\left(i\right)\in \left\{1,\cdots ,C^{\ast }\right\}$ be the clustering membership of the ith sample, T_k = {i ϵ [n]: f (i) = k} be the set of the sample indices in the kth cluster for $k=1,\cdots ,C^{\ast }$, and N_g (i) be the collection of g nearest neighbors of the ith sample. Recall that the ψ₂ norm of a random variable Z is defined by ${‖Z‖}_{{\psi }_2}=\inf \left\{t:E\left[\exp \left(Z^2/t^2\right)\right]\le 2\right\}$ (Rudelson and Vershynin, 2013).

2.2. Multiple kernel learning

As shown in Theorem S1, an appropriate Gaussian kernel can produce an accurate clustering result under some regularity conditions. In our proposed method with multi-view clustering framework, we utilize multiple Gaussian kernels to learn the similarities between samples because in practice a single similarity matrix may not generalize many biological experiments. We consider the following Gaussian kernels (Wang et al., 2017): for samples i and j,

$$K_{\sigma ,g}\left(x_i,x_j\right)=\left\{\begin{array}{ll}\exp \left(-\frac{{‖x_i-x_j‖}^2}{2{ϵ}_{ij}^2}\right)\hfill & \text{if}\hspace{0.33em}i\in N_g\left(j\right)\hspace{0.33em}\text{or}\hspace{0.33em}j\in N_g\left(i\right)\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}\right.$$

$${ϵ}_{ij}=\frac{\sigma \left({\mu }_i+{\mu }_j\right)}{2},\hspace{1em}{\mu }_i=\frac{\sum _{j\in N_g\left(i\right)}‖x_i-x_j‖}{g}$$

for some fixed σ and g. Note that this similarity measure only considers the distances of each sample to at most 2g other samples, including its g nearest neighbors. The motivation behind using a few nearest neighbors for each sample is that in high dimensional space the ranking of samples based on distance is still meaningful though the primary similarity measure might not (Houle et al., 2010). We consider $\sigma \in \left\{1,1.25,\cdots ,2\right\}$ and $g\in \left\{10,12,\cdots ,30\right\}$ and learn the similarity matrix using the 55 Gaussian kernel functions. More specifically, let $S_{\sigma ,g}\in {ℝ}^{n\times n}$ be the similarity matrix constructed by the kernel function $K_{\sigma ,g}$. Let D_σ ,_g be the corresponding degree matrix such that $D_{\sigma ,g}=\text{diag}\left(d_1,\cdots ,d_n\right)$ is a diagonal matrix with $d_i=\sum _{j=1}^n{\left(S_{\sigma ,g}\right)}_{ij}$. We use the following unified normalized similarity matrix S:

$$S=\sum _{\sigma ,g}{w}_{\sigma ,g}{G}_{\sigma ,g},\hspace{1em}\sum _{\sigma ,g}{w}_{\sigma ,g}=1,\hspace{1em}{w}_{\sigma ,g}\ge 0,\hspace{1em}{G}_{\sigma ,g}=D_{\sigma ,g}^{-1/2}{S}_{\sigma ,g}{D}_{\sigma ,g}^{-1/2},$$

where G_{σ ,g} is the normalized similarity matrix and the weights w_{σ ,g} are learned in the optimization step. Note that this multiple kernels framework is often more flexible than that using a single affinity matrix and relying on a single conventional similarity (Beyer et al., 1999).

2.3. Multi-view clustering

Consider a total of M data sets $X^{\left(1\right)},\cdots ,X^{\left(M\right)}$, where the mth data set $X^{\left(m\right)}={\left[x_1^{\left(m\right)},\cdots ,x_n^{\left(m\right)}\right]}^T$ has p_m features for n subjects. For a multi-view case in which multiple data sets are available for clustering analysis, one naive approach is to concatenate all the features together and perform clustering on the concatenated features or to manually integrate the clustering results from each data set (The Cancer Genome Atlas Network, 2012; Zhang et al., 2013; Hoadley et al., 2014; Liu et al., 2017). However, more informative and less informative data sets are treated equally by these approaches. Since we jointly consider the M data sets $X^{\left(m\right)}\in {ℝ}^{n\times p_m}$ for $m=1,\cdots ,M$, we utilize the multi-view version of (2) by allowing different importance to X^(m) in the sense that the objective function of the convex sparse spectral clustering is differently weighted by c_m for the mth data set as follows: for the set of similarity matrices $\left\{S_1,\cdots ,S_M\right\}$ and some positive constant ϵ,

$$\begin{array}{l}\underset{\left\{P_m\right\},\left\{c_m\right\}}{\mathrm{m}}ϵ\sum _m{c}_m{‖P_m‖}_F^2-\sum _m{c}_m〈S_m,P_m〉+\lambda \sum _m{c}_m{‖P_m‖}_1+\mu \sum _{m\ne j}{‖P_m-P_j‖}_F^2+\sum _m{g}_c\left(c_m\right)\\ \text{s}.\text{t}.\hspace{0.33em}\hspace{0.33em}\text{tr}\left(P_m\right)=C,0\hspace{1em}{P}_m\hspace{1em}I,\hspace{0.33em}\hspace{0.33em}{c}_m\ge 0,\hspace{0.33em}\sum c_m=M,\end{array}$$ (3)

where $g_c\left(\cdot \right)$ is some penalty function, and $P_m\in {ℝ}^{n\times n}$ and $c_m\in ℝ$. This optimization allows us to give a flexible weight to the target matrix P_m (corresponding to the data set X ^(m) ) such that more informative data sets will play a more important role in clustering by allowing larger c_m. Note that the fourth term in (3) plays a role for fusing the sample-by-sample similarity information of different data sets.

Together with (3) and the unified normalized similarity matrix as in Section 2.2, we consider the following optimization problem:

$$\begin{array}{l}\underset{\left\{P_m\right\},\left\{c_m\right\},\left\{w_{ml}\right\}}{\min }ϵ\sum _m{c}_m{‖P_m‖}_F^2-\sum _m{c}_m〈S_m,P_m〉+\lambda \sum _m{c}_m{‖P_m‖}_1+\mu \sum _{m\ne j}{‖P_m-P_j‖}_F^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\sum _m{g}_c\left(c_m\right)+\sum _m\sum _l{g}_w\left(w_{ml}\right)\\ \text{s}.\text{t}.\hspace{0.33em}\text{tr}\left(P_m\right)=C,0\hspace{1em}{P}_m\hspace{1em}I,S_m=\sum _l{w}_{ml}{G}_{ml},\hspace{0.33em}{w}_{ml},c_m\ge 0,\hspace{0.33em}\sum _l{w}_{ml}=1,\hspace{0.33em}\sum _m{c}_m=M,\end{array}$$ (4)

where $g_c\left(\cdot \right)$ and $g_w\left(\cdot \right)$ are some penalty functions, G_ml is the normalized similarity matrix by the lth kernel in X ^(m) , and $P_m\in {ℝ}^{n\times n}$ and $c_m\in ℝ$. Here, for $1\le l\le \ell =55$ and 1 ≤ m ≤ M , w_ml is the weight on the lth kernel for the mth data set that represents the importance of these factors for clustering.

For the penalty functions, we use the entropy function with the same penalty parameter to reduce the complexity of the optimization problem: for nonnegative x,

$$g_c\left(x\right)=g_w\left(x\right)=\rho x\log x$$

for some penalty parameter ρ > 0 . This entropy penalty function avoids the case that the weight from one data set dominates those from the other data sets so that we give nonzero weights to many variables. One can use other penalty functions, but the entropy penalty yields a closed-form solution for updating the weights that reduces computation time. Moreover, we have observed in our simulations that our method can effectively distinguish more important data types from less important ones by assigning different weights (Section 3.4). More importantly, we have theoretically proved that the proposed clustering method (4) using the entropy penalty function enjoys clustering consistency (Theorem 1).

Let $\left\{{\widehat{P}}_m\right\}$ and $\left\{{\widehat{c}}_m\right\}$ be the solutions to the convex optimization (4). Sample clustering is performed using ${\widehat{L}}_m\in {ℝ}^{n\times C}$, which consists of the C eigenvectors corresponding to the C largest eigenvalues of ${\widehat{P}}_m$. We construct $\widehat{L}=\left[{\widehat{c}}_1{\widehat{L}}_1,\cdots ,{\widehat{c}}_M{\widehat{L}}_M\right]\in {ℝ}^{n\times MC}$ by incorporating the obtained weights ${\widehat{c}}_m$ such that the data sets with larger ${\widehat{c}}_m$ play more important roles in clustering. We apply k-means clustering with the target number of clusters C to the normalized rows of $\widehat{L}$ to infer the membership of the n samples.

Theorem 1 shows that the proposed multi-view spectral clustering method enjoys consistency property under some regularity conditions. Proofs are deferred to the Supplementary materials.

Theorem 1. Suppose that for the mth data set $X^{\left(m\right)}={\left[x_1^{\left(m\right)},\cdots ,x_n^{\left(m\right)}\right]}^T$, the n datapoints follow the following sub-Gaussian distribution:

$$x_i^{\left(m\right)}={\mu }_{f\left(i\right)}^{\left(m\right)}+z_i^{\left(m\right)}\hspace{1em}\text{for}\hspace{1em}m=1,\cdots ,M\hspace{1em}\text{and}\hspace{1em}i=1,\cdots ,n,$$

where $z_i^{\left(m\right)}={\left(z_{i1}^{\left(m\right)},\cdots ,z_{i{p}_m}^{\left(m\right)}\right)}^T\in {ℝ}^{p_m}$ is a random vector with independent component satisfying $E\left[z_{ij}^{\left(m\right)}\right]=0$, $E\left[{\left(z_{ij}^{\left(m\right)}\right)}^2\right]={\sigma }_m^2$, and ${‖z_{ij}^{\left(m\right)}‖}_{{\psi }_2}\le {\sigma }_m\psi$ for some $\psi >0$. Let ${\sigma }^2={\max }_m{\sigma }_m^2$ and $p={\max }_m{p}_m$. Suppose for any $\tilde{k}\in \left\{1,\cdots ,C^{\ast }\right\}$,

$$\underset{m}{\max \hspace{0.33em}}\underset{k\ne \tilde{k}}{\min }{‖{\mu }_{\tilde{k}}^{\left(m\right)}-{\mu }_k^{\left(m\right)}‖}_2^2\ge 8p{\sigma }^2+64{\sigma }^2{\psi }^2\log n/c$$

for some constant c > 0. Assume $c_{1}n\le \left|T_k\right|\le \left(1-c_1\right)n$ for some constant $c_1\in \left(0,1/2\right)$ and $M\le \exp \left(3C^{\ast }\right)$. Let $\left\{{\widehat{P}}_m\right\}$ and $\left\{{\widehat{c}}_m\right\}$ be the solution to (4) with $\lambda =C^{\ast }/n^2$, $\mu =\sqrt{n}\lambda /\left(C^{\ast }M\right)$, $ϵ=1/n^3$, ρ = 1, and C = C* with multiple Gaussian kernels as presented in Section 2.2. Let ${\widehat{L}}_m\in {ℝ}^{n\times C^{\ast }}$ be the C* eigenvectors corresponding to the C* largest eigenvalues of ${\widehat{P}}_m$. Then, with probability $1-2\ell {\left(C^{\ast }\right)}^2/n$, k-means clustering to the normalized row vectors of $\widehat{L}=\left[{\widehat{c}}_1{\widehat{L}}_1,\cdots ,{\widehat{c}}_M{\widehat{L}}_M\right]\in {ℝ}^{n\times M{C}^{\ast }}$ guarantees the exact clustering results.

Theorem 1 implies that when λ, µ , and ϵ are set to some functions of known parameters n and M, and the unknown parameter C* , then the proposed method provides consistent clustering results under some regularity conditions. In the implementation of (4), we exploit these relationships to infer C* in a data-dependent manner. Specifically, by treating C as the underlying number of clusters C* , we set λ, µ , and ϵ by the functions of C, and determine C via sensitivity analysis with respect to small additive noise. We add $N\left(0,{\sigma }_X^2\right)$ noise to X, where σ_X is the standard deviation of all the entries in X, to create a perturbed data set on which to apply the proposed clustering method by varying number of clusters C. This method is motivated by the observation that if the underlying clustering structure is strong, we would expect that sample assignment would be robust from adding small noises. See Section 2.5 for details.

2.4. Algorithm

Let F({P_m},{c_m},{w_ml }) be the objective function of (4), where $\left\{P_m\right\}=\left\{P_1,\cdots ,P_M\right\}$, $\left\{c_m\right\}=\left\{c_1,\cdots ,c_M\right\}$, and $\left\{w_{ml}\right\}=\left\{w_{11},\cdots ,w_{M\ell }\right\}$. Although $F\left(\cdot \right)$ is not a jointly convex function, it is convex for one parameter conditional on the other variables. Hence we iteratively solve (4) as follows: at the ith iteration of each update,

$${\left\{c_m\right\}}_i=\underset{\left\{c_m\right\}}{\text{argmin}}F\left({\left\{P_m\right\}}_{i-1},\left\{c_m\right\},{\left\{w_{ml}\right\}}_{i-1}\right)$$ (5)

$${\left\{w_{ml}\right\}}_i=\underset{\left\{w_{ml}\right\}}{\text{argmin}}F\left({\left\{P_m\right\}}_{i-1},{\left\{c_m\right\}}_i,\left\{w_{ml}\right\}\right)$$ (6)

$${\left\{P_m\right\}}_i=\underset{\left\{P_m\right\}}{\text{argmin}}F\left(\left\{P_m\right\},{\left\{c_m\right\}}_i,{\left\{w_{ml}\right\}}_i\right)$$ (7)

until convergence, where ${\left\{P_m\right\}}_i=\left\{P_1^{\left(i\right)},\cdots ,P_M^{\left(i\right)}\right\}$, ${\left\{c_m\right\}}_i=\left\{c_1^{\left(i\right)},\cdots ,c_M^{\left(i\right)}\right\}$, and ${\left\{w_{ml}\right\}}_i=\left\{w_{11}^{\left(i\right)},\cdots ,w_{M\ell }^{\left(i\right)}\right\}$. Note that (5)-(7) are convex optimizations, and (5) and (6) have closed-form solutions. The optimization problem (7) can be solved using the ADMM algorithm (Gabay and Mercier, 1976). See Section A of the Supplementary materials for details of the algorithm. Throughout the paper, we write $a\lesssim b$ if $a\le C_{1}b$ for some positive absolute constant C₁. We use $a\asymp b$ when $a\lesssim b$ and $b\lesssim a$.

Theorem 2 shows that the algorithm enjoys a computational convergence property.

Theorem 2. Let F({P_m},{c_m},{w_ml}) be the objective function of (4). Let ${\left\{{\widehat{P}}_m\right\}}_i$, ${\left\{{\widehat{c}}_m\right\}}_i$, ${\left\{{\widehat{w}}_{ml}\right\}}_i$ be the obtained iterates of the proposed algorithm, where ${\left\{{\widehat{P}}_m\right\}}_i$ is the t_i-th iterate of the ADMM in (7). Then ${\left\{{\widehat{P}}_m\right\}}_i$, ${\left\{{\widehat{c}}_m\right\}}_i$, ${\left\{{\widehat{w}}_{ml}\right\}}_i$ converge to some stationary point $\left\{P_m^{\ast }\right\}$, $\left\{c_m^{\ast }\right\}$, of F in the sense that for a fixed tolerance parameter $\delta \in \left(0,1\right)$, it holds that

$$\sum _m{‖{\widehat{P}}_m^{\left(i^{\ast }\right)}-P_m^{\ast }‖}_F+\sum _m‖{\widehat{c}}_m^{\left(i^{\ast }\right)}-c_m^{\ast }‖+\sum _m\sum _l\left|{\widehat{w}}_{ml}^{\left(i^{\ast }\right)}-w_{ml}^{\ast }\right|\le C_2\delta$$

with the iterate number $i^{\ast }\asymp {\delta }^{-\left(2\theta -1\right)/\left(1-\theta \right)}$, and the iterate number of ADMM for (7) being $t_{i^{\ast }}\asymp \log \left(\delta /i^{\ast }\right)/\log \left(\mu \right)$ and $t_{i^{\ast }-k}\asymp t_{i^{\ast }}{\left(t_{i^{\ast }}+1\right)}^{k-1}$ for all $1\le k\le i^{\ast }-1$, where $C_2>0,1/2<\theta <1$, and ${\delta }^{\theta /\left(1-\theta \right)}<\mu <1$ are some absolute constants.

Theorem 2 essentially follows from the global convergence properties of the block coordinate descent method (Xu and Yin, 2013) and the ADMM in (7), and the fact that the objective function F is strictly convex for one variable providing that the remaining variables are fixed among {P_m},{c_m},{w_ml }. It is worth noting that the convergence of the proposed algorithm is achieved when ϵ > 0 proofs are deferred to Section C of the Supplementary materials.

2.5. Choosing the number of clusters

The proposed clustering method requires a target number of clusters. We choose the number of clusters (C) that produces the most stable and reproducible results under additive noises on the original data X. Specifically, we add i.i.d. $N\left(0,{\sigma }_X^2\right)$ noise, where σ_X is the standard deviation of all the entries in X, to create a perturbed data set on which to apply the proposed clustering method by varying the target number of clusters. We compute the adjusted Purity between the baseline clustering and the one obtained on the perturbed data over 100 runs with setting λ, µ , and ϵ by the functions of C based on the results of Theorem 1, and choose the number that has the highest performance value. Note that the adjusted Purity between the clustering results U and V using the target number of clusters C is

$$\text{Purity}\left(U,V\right)/{\mu }_{\text{Purity}}\left(C\right),$$

where µ_Purity (C) is the expected value of the Purity between any two random partitions having C clusters. See Section F of the Supplementary materials for the definition of the Purity.

3. Results

3.1. Evaluation metrics

We use the following three performance metrics to evaluate the consistency between the inferred clusters and the true labels: Normalized Mutual Information (NMI) (Strehl and Ghosh, 2003), Purity (Wagner and Wagner, 2007), and Adjusted Rand Index (ARI) (Wagner and Wagner, 2007). See Section F of the Supplementary materials for the details of these metrics. Note that NMI and Purity take on values between 0 and 1, whereas ARI can yield negative values. These metrics measure the concordance of two clustering labels such that higher values suggest higher concordance between two labels.

3.2. Data

We collected data from 22 major cancer types with sufficient numbers of patients from the TCGA project, with the following three molecular profiles: RNA expression (RNA-seq V2), miRNA, and copy number alterations (CNA). To reduce the batch effects, we considered each molecular profile from one platform. The RNA data sets are from the Illumina sequencing technology with the log₂(x+1) transformed RSEM (RNA-Seq by Expectation Maximization) values, the miRNA mature strand expression data sets are measured by Illumina miRNA-seq, and the CNA have discrete values which are estimated using the GISTIC2 threshold method and compiled using data from all TCGA cohorts (Weinstein et al., 2013). Note that CNA data have values −2, −1, 0, 1, or 2, depending on corresponding gene copy levels (Mermel et al., 2011). See Supplementary Section G for details. Patients with missing molecular profiles were removed, resulting in a total of 6,976 patients included in the clustering and survival analysis. See Section G of the Supplementary materials for the details of the 22 data sets.

3.3. Other methods compared

To demonstrate the advantages of the proposed clustering method, we compare its performance with the following clustering methods for a specified number of clusters C:

• Consensus clustering (‘Cons-R’, ‘Cons-M’, ‘Cons-C’, ‘Cons-A’): We consider the consensus clustering proposed by Liu et al. (2017) using each omics data set individually and the three data sets (multi-view) together, respectively. Note that consensus clustering can naturally integrate multiple molecular data types measured from the same set of subjects.

• Spectral clustering (‘S-R’, ‘S-C’, ‘S-M’, ‘S-A’): We consider spectral clustering (Andrew et al., 2001) using each omics data set X ^{(k )} for k = 1, 2, 3, as well as all three data sets by applying k-means to the combined matrix [Q₁,Q₂ ,Q₃ ] , where Q_k is the n by C matrix whose columns consist of C eigenvectors corresponding to the C smallest eigenvalues of normalized graph Laplacian of the X ^{(k )} .

• k-means clustering (‘K-R’, ‘K-C’, ‘K-M’, ‘K-A’ ): We consider k-means clustering using each omics data set as well as all three data sets by simply merging the data.

• Kernel addition (‘Ker-A’ ): We consider combining different kernels by adding them, and then running our multi-view clustering. By comparing the performance of this method with our proposed method, we can investigate the effect of learning multiple kernels.

• SIMLR (‘SIM-R’, ‘SIM-C’, ‘SIM-M’, ‘SIM-A’ ): We consider a clustering method using the multi-kernel-learning technique proposed by Wang et al. (2017). ‘SIM-A’ uses all three data sets by integrating the obtained C eigenvectors corresponding to the three obtained target matrices from single-view SIMLR.

• Multi-view pairwise sparse spectral clustering (‘SS-R’, ‘SS-C’, ‘SS-M’, ‘SS-A’ ): We consider the multi-view clustering method that adopts a sparse spectral clustering proposed by Lu et al. (2016).

• Co-regularized clustering (‘C-A’, ‘P-A’) : We consider the multi-view clustering methods that adopt a co-regularized spectral clustering framework proposed by Kumar et al. (2011). ‘C-A’ and ‘P-A’ are centroid and pairwise based, respectively.

• iCluster (‘iCluster-A’): We consider the iCluster algorithm (Shen et al., 2009) that incorporates flexible modeling of the associations between different omics data types and the variance-covariance structure.

• The proposed multi-view clustering methods (‘MKerW-A’, ‘MKer-A’): ‘MKerW-A’ is our proposed multi-view clustering with multiple kernels and learning weights of data sets as in (4). ‘MKer-A’ is our clustering method without learning weights of data, i.e., cm = 1 in (4).

Across all methods considered, we include ‘-R’, ‘-M’, ‘-C’, and ‘-A’ at the end of each method, to denote that the method is applied to RNA, miRNA, CNA, and all the three data types together, respectively.

3.4. Identifying a cancer type

In this subsection, we consider 22 cancer types to illustrate the performances of the proposed method in identifying different cancer types. In the first implementation, all the patients are included in clustering analysis. In the second implementation, about half of the patients from each cancer type are randomly selected for clustering analysis. For example, 200 and 370 patients are randomly chosen from Bladder Cancer (BLCA) and Breast Invasive Carcinoma (BRCA), respectively, in each experiment. We repeat this procedure 50 times and record the accuracy of clustering methods. In the third implementation, we consider the balanced sample case such that 30 patients are randomly selected from each of the 22 cancer types, thus a total of 660 patients are chosen. We also repeat this procedure 50 times. In the main paper, we focus on the third implementation case. See the Supplementary materials for the results of the first two cases.

Figure S1 of the Supplementary materials shows the heatmap of the similarity measures between patients obtained by one of the Gaussian kernel functions based on each of the three molecular data types. We observe that RNA and miRNA clearly show 22 block-diagonal matrices compared to CNA. In this setting, we can see the performance of the proposed method ‘MKerW-A’ if one of the data types (e.g., CNA) does not provide correct information in terms of exact clustering.

Figure 1(A) shows the average and one standard deviation of the assigned weights of the three data set in the proposed method based on 50 randomly generated data sets. We can see that RNA and miRNA contribute more to clustering compared to CNA, which suggests that the proposed clustering method tends to give higher weights to data including clearer clustering structure. We further investigate this by considering partially corrupted data sets by adding significant Gaussian noises to the observed data. Figures 1(B)-(D) show the results when RNA, miRNA, or CNA are corrupted, respectively, while the other two data types remain the same. It can be seen that the corrupted data type becomes less important than the other two data types, demonstrating that the entropy based penalty function can distinguish data types of different degrees of information.

Fig. 1.

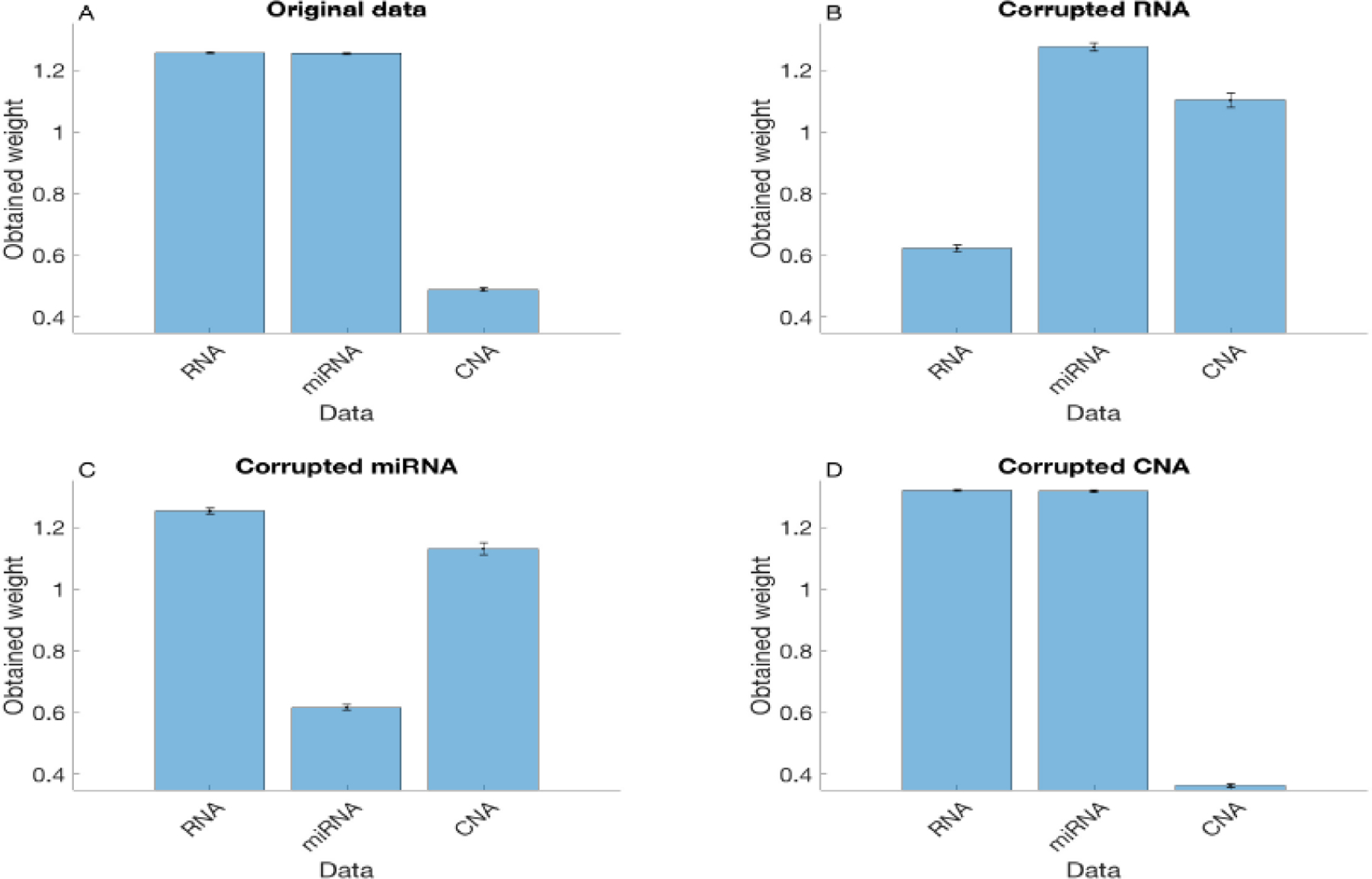
The average of assigned weights of the three data sets when 30 patients were randomly selected from 22 cancer types resulting in a total of 660 patients. A total of 50 experiments were run. We considered four sets of data: (A) the original data sets; (B) the RNA data that were corrupted by significant additive noise; (C) the miRNA data that were corrupted by significant additive noise; and (D) the CNA data that were corrupted by significant additive noise. The error bars represent one standard deviation.

Figure 2 shows the average adjusted Purity value for different target numbers of clusters C over 2 ≤ C ≤ 30 , with $\lambda =C/n^2$, $\mu =\sqrt{n}\lambda /\left(CM\right)$, and $ϵ=1/n^3$, based on the results of Theorem 1. We can see that the highest mean value with the smallest standard deviation is achieved at the true number of clusters 22 (i.e., number of cancer types). Based on this, we set C = 22 as the target number of clusters in the following analysis.

Fig. 2.

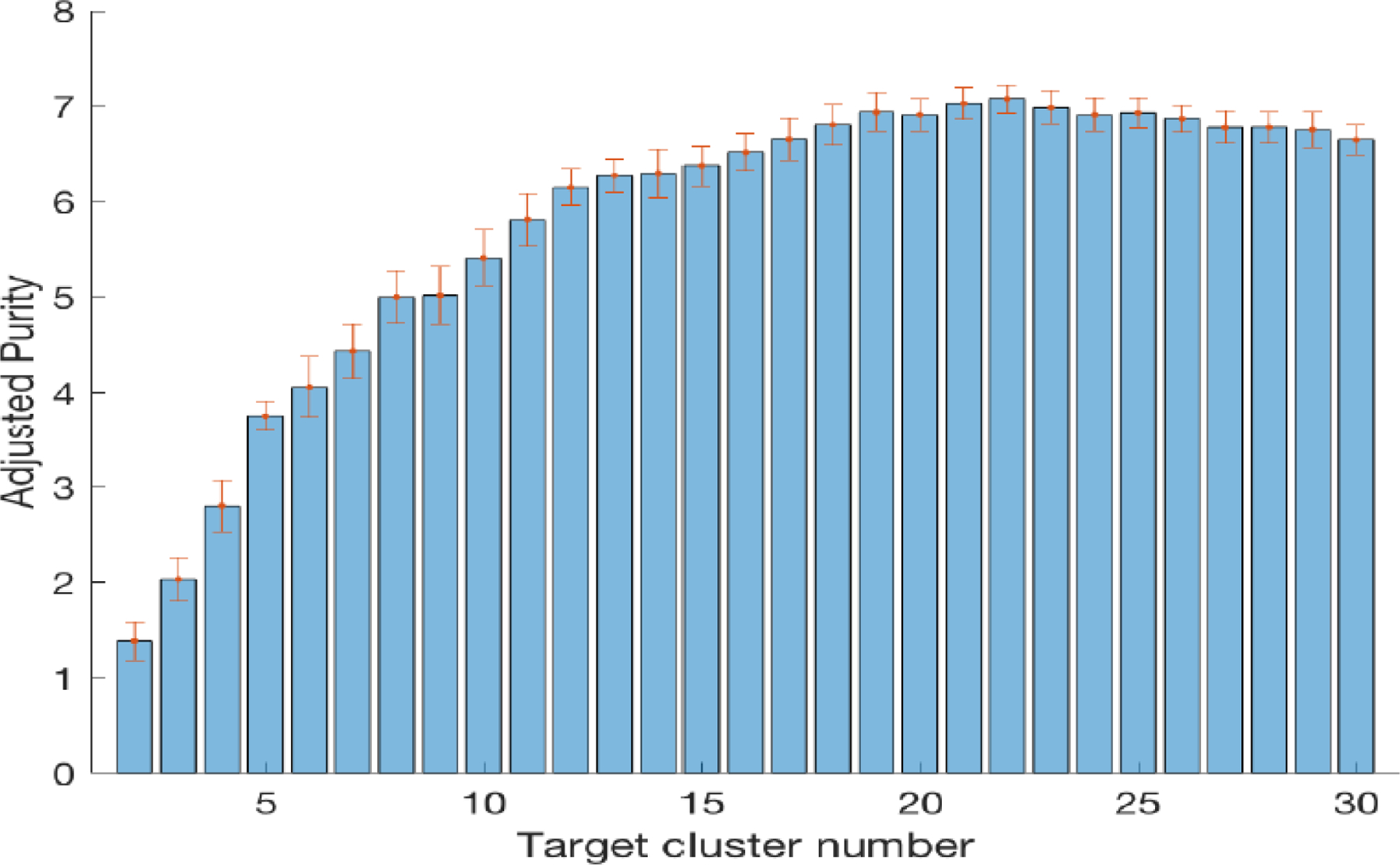
Robustness of clustering analysis for additive noise when the target number of clusters is varied between 2 and 30 when 30 patients were randomly selected from each of the 22 cancer types. The adjusted Purity values were averaged over 100 runs for each target number of clusters. The error bars represent one standard deviation.

Figure 3 shows the average NMI of ‘MKerW-A’ against the other clustering methods over 50 replicates based on randomly selected patients. We can see that ‘MKerW-A’ outperformed the other methods in terms of NMI as well as Purity and ARI measures (Supplementary Figures S2-S3). The differences between the results from ‘MKerW-A’ and ‘MKer-A’ suggest that learning weights on different data types may lead to more accurate clustering results than assigning equal weight to each data type.

Fig. 3.

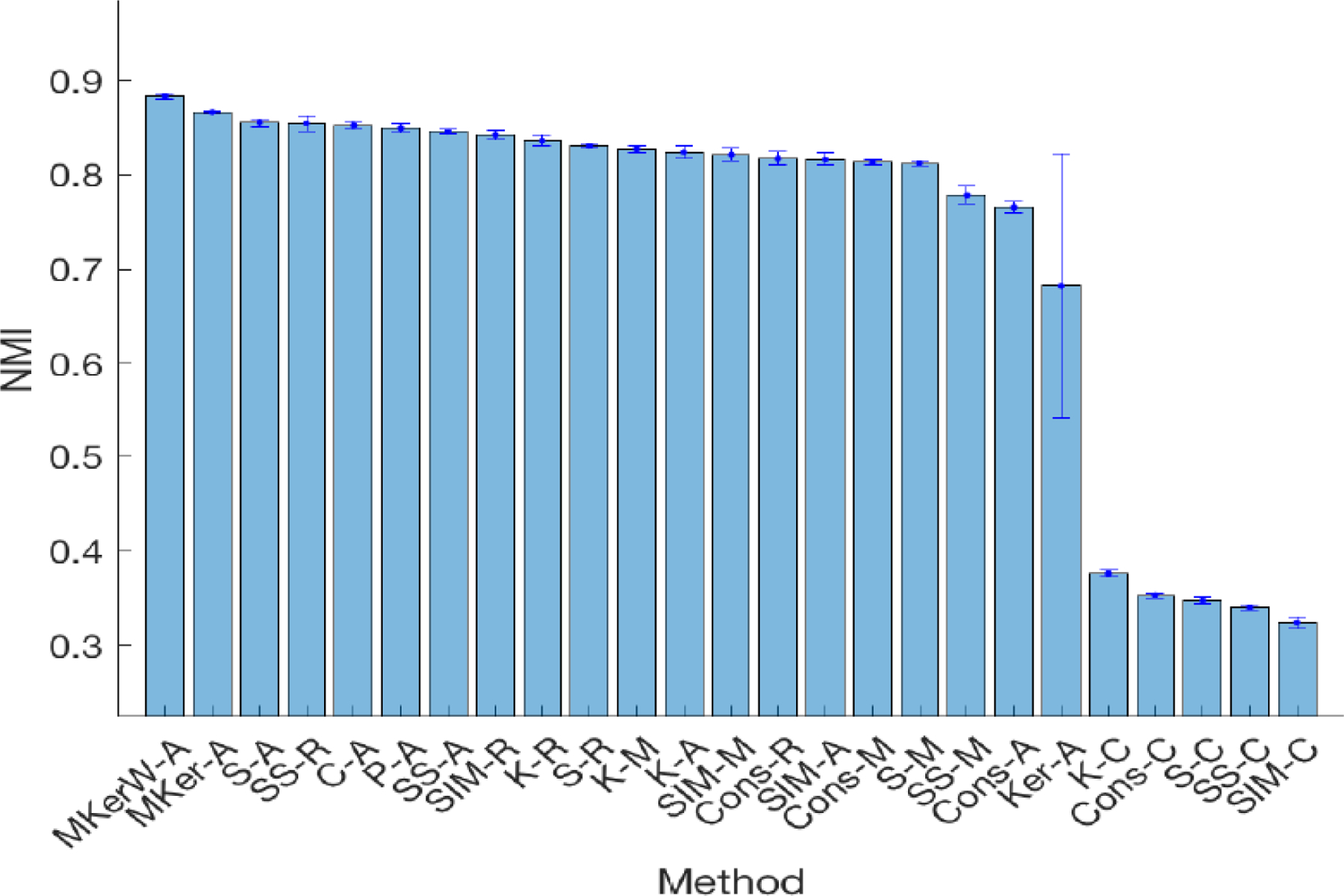
The average NMI and one standard deviation of 50 replicates for the 25 clustering methods when 30 patients were randomly selected from each of the 22 cancer types. The methods are ordered according to the NMI values.

When all patients were included in the clustering analysis or when about half of the patients were randomly selected from each of the 22 cancer types, ‘MKerW-A ‘ still provided the most accurate clustering results in terms of the three performance metrics, followed by ‘MKer-A’ (Supplementary Figures S4-S6 and S7-S9, respectively). We also observe that the proposed method can correctly infer the underlying number of clusters 22 (Supplementary Figures S10 and S11) for these two cases as well.

3.5. Survival analysis

If clustering analysis is effective in identifying cancer subtypes, we would expect to see that the subgroups of patients identified by ‘MKerW-A’ would show differences in clinical features as reflected in the heterogeneity of their genomic profiles. In this article, we consider patient’s survival outcome to compare ‘MKerW-A’ with other clustering methods (See Section 3.3), because we expect that subjects in different clusters inferred by ‘MKerW-A’ will have different survival distributions. We apply the clustering methods to each cancer type with the target number of clusters (See Section G of the Supplementary materials). We then consider the following two metrics to measure the differences in survival distributions between identified subtypes:

• Area between two curves: we consider the ten year survival distribution (120 months) from the time the patient on treatment, i.e., ${\int }_0^{120}\left|w_i\left(t\right)-w_j\left(t\right)\right|\text{dt}$, where t represents a monthly basis time and w_i (t) is the fitted survival curve using the Weibull distribution for the subjects in Cluster i. To quantify the degree to which two curves intersect, we use ‘Area_Min’, defined by ${\min }_{i\ne j}{A}_{ij}$, where $A_{ij}=\frac{\left|{\int }_0^{120}\left(w_i\left(t\right)-w_j\left(t\right)\right)\text{dt}\right|}{{\int }_0^{120}\left|w_i\left(t\right)-w_j\left(t\right)\right|\text{dt}}$.

• Log-rank test: this is a nonparametric test to compare the survival distributions of two or more groups. We record the log p-value of the log-rank test to measure the heterogeneity of survival outcomes among identified clusters.

The larger ${\min }_{i\ne j}{A}_{ij}$, the more heterogeneity between the survival curves of the identified clusters, while a smaller p-value for the log-rank test suggests more difference between the curves.

We record these measures for the 25 clustering methods across 22 cancer types. For ‘Area_Min’, the proposed ‘MKerW-A’ has the highest mean values over the 22 cancers, and the differences of the mean values from the other methods are statistically significant (paired t-test p-value < 0.05 for the 23 clustering methods, while the p-value of ‘MKerW-A’ versus ‘MKer-A’ is close to 0.1). For the log-rank test, ‘MKerW-A’ also has the smallest mean p-value over the 22 cancer types.

Figure 4 and Figure S12 of the Supplementary materials show the heatmaps of the two measures for 25 clustering methods over 22 cancer types. We can see that for most data sets, ‘MKerW-A’ is superior to the other clustering methods in terms of the heterogeneity of the distributions of the survival outcomes. The relative performances of the 25 clustering methods is different across the two metrics because these two metrics capture different aspects of heterogeneity of survival outcomes. For example, when we rank the 25 clustering methods based on each of the average values of the measures, ‘P-A’ is ranked the 4th and 9th based on Area_Min and Log-Rank, respectively. So, it would be more robust to assess the clustering methods based on these measures simultaneously instead of relying on one measure.

Fig. 4.

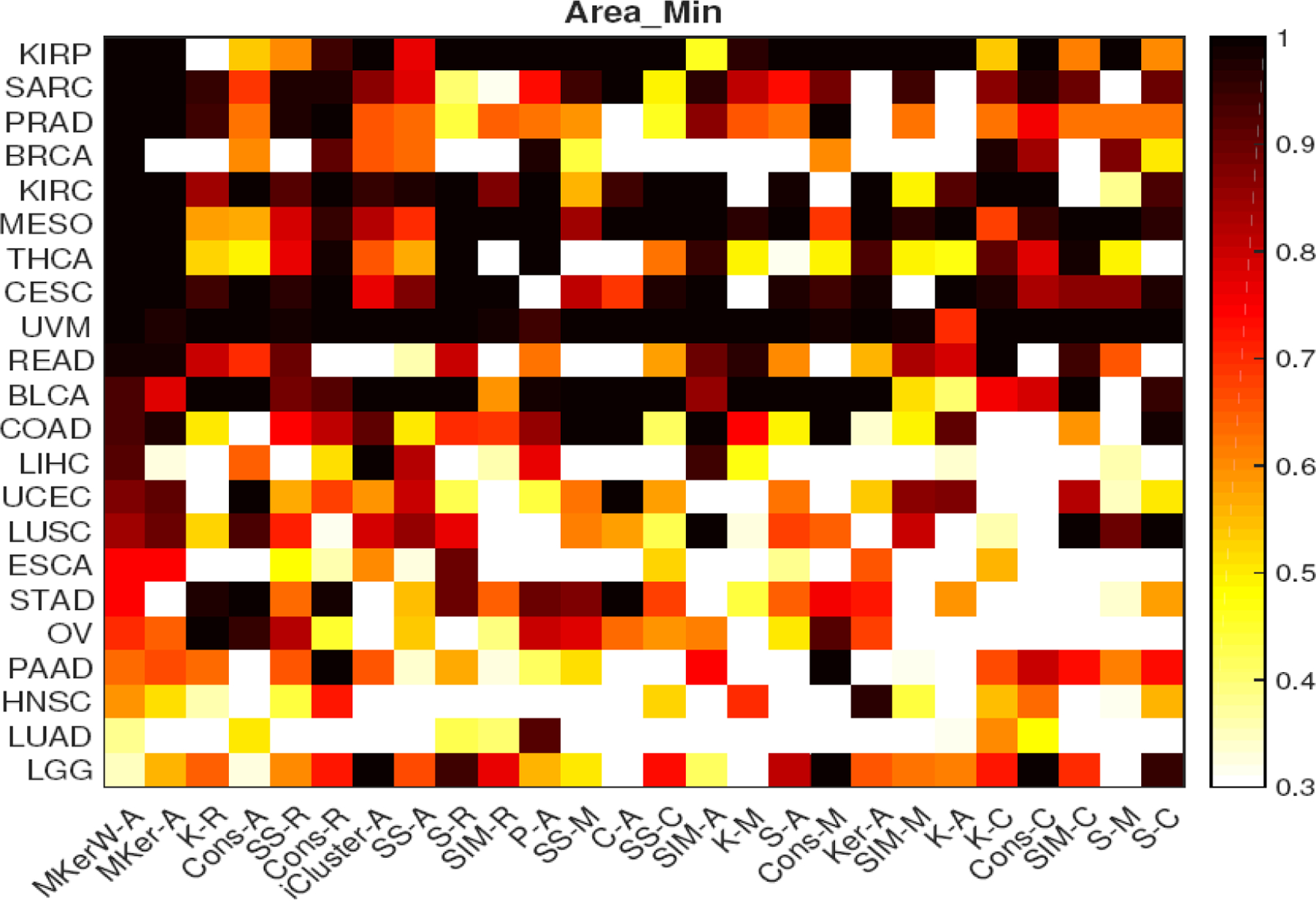
Heatmap of the minimum survival curves area proportion. Abbreviations of the cancer types and clustering methods are given on the left and bottom. Legend for the shades is given on the right. For details of abbreviations of the 22 cancer types, see Section G of the Supplementary materials.

We highlight the fact that integrating multiple omics data types does not always yield better results. For example, based on the log-rank test, the best method among the k-means clusterings is the one using the RNA data only, whereas the average p-value of k-means using RNA only and the three omics data types is 0.12 and 0.24, respectively. Spectral clustering shows similar patterns, where the mean p-value using RNA only and all the three omics data types is 0.15 and 0.22, respectively. Another kernel-learning based clustering method SIMLR performs worse when using all three omics data types than the one using the RNA data only. The inferior results of the other clustering methods with multiple omics data types suggests that care is needed when integrating multiple omics data for clustering analysis, and there is no guarantee that integrating more data sets will lead to improved clustering results.

In terms of ‘Area_Min’, using RNA data generally has better results than using the other two data types, miRNA and CNA, which suggests that the three data types contribute differently to clustering results, justifying the need to weigh each data type differently. There is also evidence by comparing the results of ‘MKerW-A’ and ‘MKer-A’, where the former learns the weights of data in the optimization procedure and the latter gives the same weights to different data types. Based on Area_Min and the log-rank test, ‘MKerW-A’ performs better than ‘MKer-A’ in 17 and 15 cancer types, respectively. Hence, there is benefit to learn the weights from the data, and it is expected that RNA has a higher weight than the other two data types.

Figure 5 shows the learned weight of the three data types across 22 cancer types. We can see that RNA data generally have the largest weight, followed by miRNA and CNA. Average learned weights of RNA, miRNA, and CNA are 40%, 35%, and 25%, respectively, and the differences of these learned weights of the three data types are statistically significant (paired t-test p-value < 10⁻⁵).

Fig. 5.

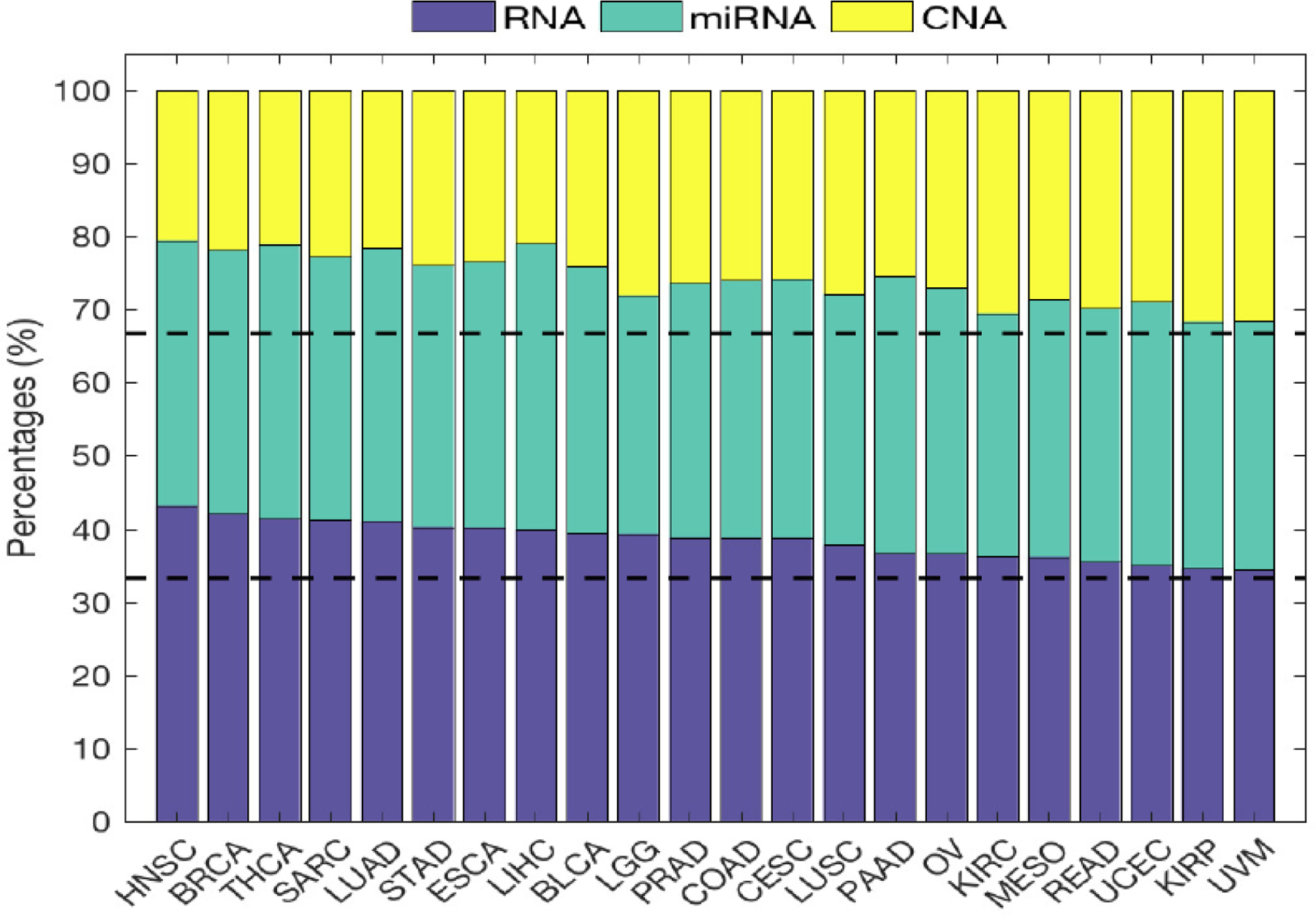
The relative learned weights $100\times \frac{c_i}{c_1+c_2+c_3}$ for i = 1, 2, 3 on the RNA, miRNA, and CNA data for ‘MKerW-A across 22 cancer types, where the c_m are obtained by solving (4). The cancers are ordered decreasingly according to the weights on the RNA data.

‘MKerW-A’ and ‘MKer-A’ generally performed better than ‘iCluster’ and other mutli-view clustering methods considered. In terms of ‘Area_Min’, the differences between ‘MkerW-A’ and the other multi-view methods are all statistically significant at the 0.05 level. Overall, ‘MKerW-A’ showed better stability in separating patients with different survival times than other clustering methods. In the next three subsections, we provide more details on breast cancer, low grade glioma, and pancreatic cancer.

3.6. Breast Cancer

To gain further insights into the molecular subtypes generated by the ‘MKerW-A’, we compare the identified clusters with the subtypes defined by PAM50, which consist of “Luminal A” (LumA), “Luminal B” (LumB), “Her2-enriched” (Her2), “ Basal-like” (Basal), and “Normal-like” (Normal), based on the expression profiles of 50 signature genes, where the “Basal” and “Her2” subtypes are more difficult to treat than the other subtypes (Parker et al., 2009; Bastien et al., 2012). Figure 6(A) shows the frequency of PAM50 subtypes for each of the four identified clusters based on ‘MKerW-A’. It can be seen that although there is good correspondence between the subtypes identified by these two approaches, there are clear differences with Chi-square p-value < 0.05.

Fig. 6.

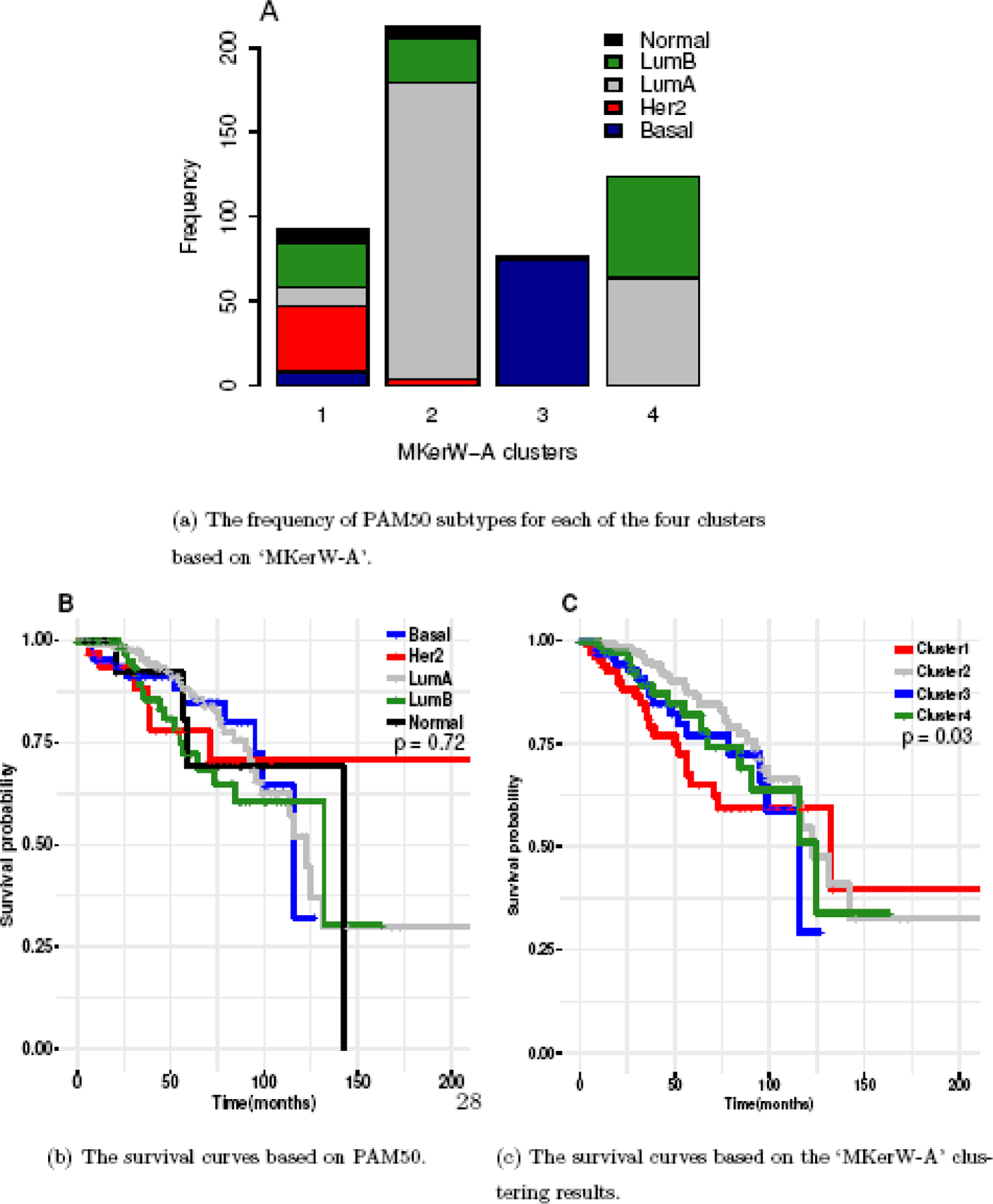
Application to breast cancer.

The majority of samples in Cluster 1 are from Her2 and LumB, with most Her2 patients assigned to Cluster 1. More than 75% of Cluster 2 patients are from LumA, with about 50% of LumA patients assigned to Cluster 2. Cluster 3 and Basal consist of mostly the same patients, while Cluster 4 includes some patients from LumA and LumB, and 50% of LumB patients are in Cluster 4. The survival curves for the five PAM50 subtypes are not separated very well, where the p-value of log-rank test is not significant (p-value=0.72, Figure 6(B)). However there are significant differences in the survival distributions across clusters based on ‘MKerW-A’ (p-value =0.03, Figure 6(C)). Specifically, the Cluster 1 (Her2-like) subtype has worse survival, patients in Cluster 2 have better survival than those in the other clusters, and patients in Clusters 3 and 4 have similar survival outcomes. Our results suggest that the molecular subtypes identified by ‘MKerW-A’ could complement the PAM50-defined subtypes to more accurately predict patient prognosis.

3.7. Lower Grade Glioma

Lower grade glioma (LGG) develops in the glial cells of the brain. LGG could be classified into grades I, II, III, or IV based on the histological information defined by the World Health Organization (Vigneswaran et al., 2015). The TCGA LGG data set includes information of grades II and III, which are treated as low grade and high grade in this study. The subtypes identified by ‘MKerW-A’ are closely associated with the histological classification system. Figure 7(A) shows the frequency of grades-subtypes for each of the four obtained clusters based on ‘MKerW-A’. Most samples in Cluster 1 identified by ‘MKerW-A’ consist of high grade LGG patients than the other three clusters. Figure 7(B) shows the survival curves with the grades information of LGG, and there are significant differences between the two curves. Figure 7(C) shows the fitted survival curves with the obtained clusters by ‘MKerW-A’, and Cluster 1 has worse survival than the other three clusters as the majority of Cluster 1 are from low grade patients.

Fig. 7.

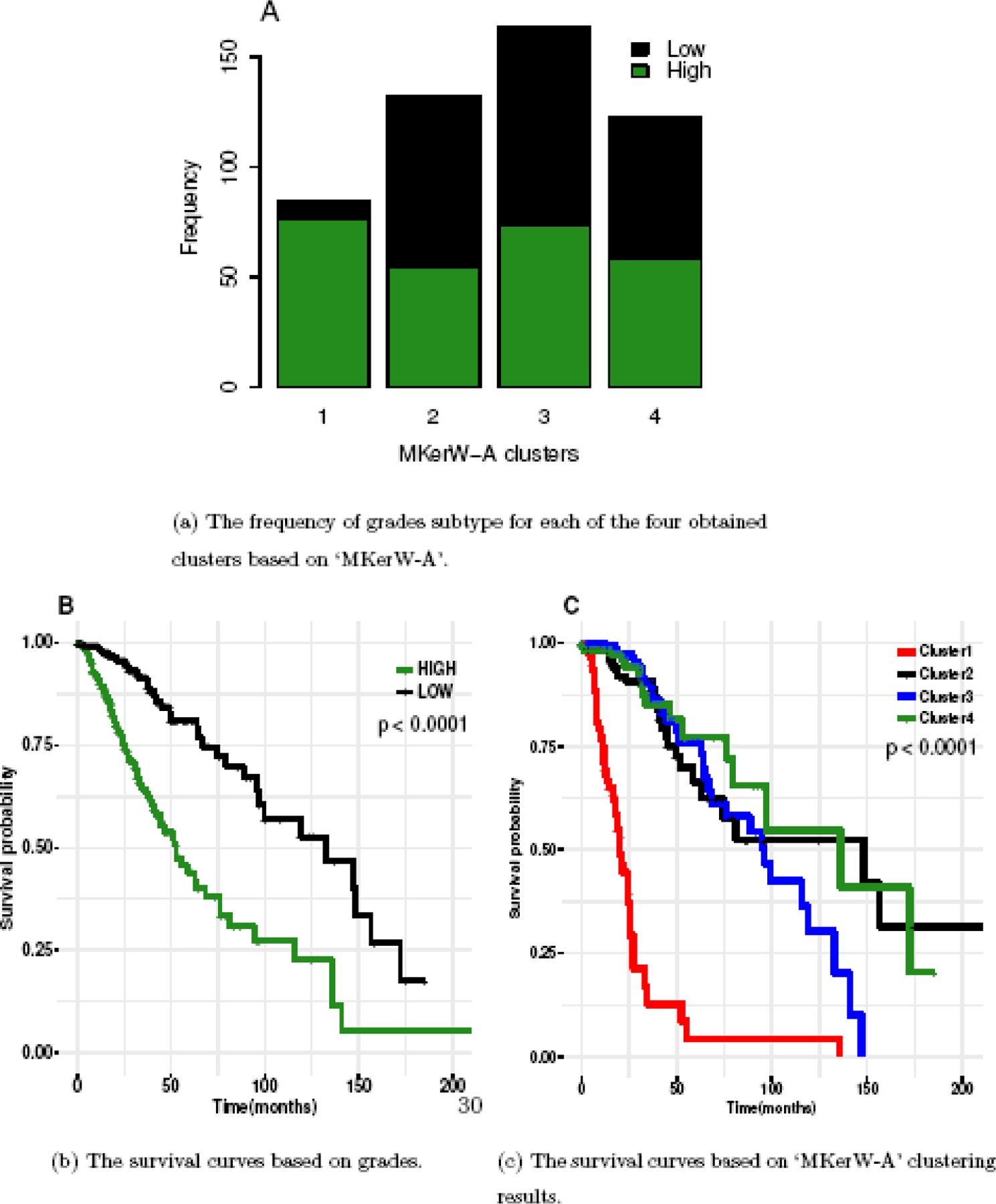
Application to Lower Grade Glioma.

3.8. Pancreatic Cancer

Pancreatic cancer is the third most aggressive cause of cancer deaths in the world and the fourth in the United States (Matsuoka and Yashiro, 2016; Raphael et al., 2017). The high mortality of pancreatic cancer is mostly due to the low response rate to treatment, which may be related to the heterogeneous nature of the disease (Matsuoka and Yashiro, 2016; Raphael et al., 2017). Erlotinib is the only targeted therapy approved by FDA for pancreatic adenocarcinoma, the most common type of pancreatic cancer (Matsuoka and Yashiro, 2016). The treatment data are provided in the TCGA data portal and all samples have treatment information in the clinical file, i.e. “Yes” or “No” values. Among 176 patients, 14 patients do not have the treatment information, and these patients were not considered.

We have investigated how patients of the individual clusters, identified by the proposed method ‘MKerW-A’, respond to molecular targeted therapy. Figure S13 of the Supplementary materials shows the survival distribution of pancreatic cancer patients treated versus untreated for each inferred cluster, and Figure S14 of the Supplementary materials shows the difference of survival time of patients treated versus those not treated with molecular targeted therapy. We observe that the targeted therapy is effective for pancreatic cancers. However, when we look further into each identified cluster, these effects are different among the four clusters, with the targeted therapy seems to be effective only in Cluster 3 and Cluster 4. Patients in these two clusters have significantly increased survival time when treated with targeted therapy (corrected log-rank test p-value < 0.001). However, for patients in Cluster 1 and Cluster 2, we do not detect significant differences in survival time between those treated and those untreated. Similar results can also be found in the STAD data set, which also suggests that the identified clusters have different responses to the Radiotherapy (Supplementary Section I). To sum up, the inferred clusters could be helpful for choosing the the right therapies for the patients.

To investigate whether certain gene expression or gene copy number could be predictive markers for survival benefit from the targeted therapy, we have performed a two-sample t-test for each gene by treating Clusters 1 and 2 as one group and Clusters 3 and 4 as another group. Among the 20 most frequently mutated genes in pancreatic cancer provided in the TCGA data portal, we observe that “SCN5A”, “GLI3”, “CSMD3”, and “EGFR” are significantly over-expressed in Clusters 3 and 4, while “GNAS” and “GSK3A” are significantly under-expressed in Clusters 3 and 4, i.e., expression status of these genes could be potential predictive markers for survival benefit from the targeted therapy. On the other hand, we observe that “CSMD3”, “TP53”, “SMAD4”, and “CDKN2A” copy numbers could be potential predictive markers (t-test p-value < 0.05).

Specifically, we observe that patients with “EGFR” mutations are mostly assigned to Clusters 3 and 4, which is consistent with the finding that the targeted therapy is more effective for patients with “EGFR” mutations (Wang et al., 2015). On the other hand, “KRAS”, known as the most frequent gene mutations in pancreatic cancer (Lee et al., 2007), is not significantly differentially expressed in different groups, which is consistent with the results in Wang et al. (2015). However, note that whether “KRAS” is associated with the targeted therapy in pancreatic cancer patients remains controversial (da Cunha Santos G et al., 2010). It is worth studying further, both clinically and biologically.

4. Discussion

In this article, we have introduced a novel multi-vew clustering algorithm that allows different weights on the data sets, motivated by the fact that some of the available data sets may be more informative than others in revealing the true structure of the data. We have investigated the statistical properties of the proposed multi-vew clustering method and showed that it can accurately infer the underlying clusters under some regularity conditions. From various simulations, we showed the improved performance of our clustering method compared with other single-view and multi-view clustering methods. For cancer data, we observed that the identified subtypes based on our proposed clustering method can better characterize tumor heterogeneity as reflected in better separations of survival distributions for patients between the identified clusters. In our method, we solve the proposed non-convex problem iteratively with the embedded ADMM algorithm, and we also prove the convergence of the algorithm. We also proposed data-driven approaches for choosing the parameters.

Note that some data types may not be informative in clustering analysis. In our simulations, we considered the case in which some data are not informative for clustering analysis, and we investigate its assigned weight in the proposed method. We observed that the proposed method using the entropy penalty function does distinguish the less informative data by giving lower weight compared to informative data. In the software, we give an option to users to set the weights of data types, i.e., cm, freely as they want to add more flexibility to user.