Observation of high-order imaginary Poynting momentum optomechanics in structured light

Significance

Optical forces on small particles are conventionally produced from the intensity or phase gradient of light. Harnessing the imaginary Poynting momentum (IPM) of light to generate nontrivial forces would unlock the full potential of optical manipulation techniques, but so far, it is demonstrated only for dipolar magnetoelectric particles. Here, we show that the IPM can be coupled to the force via the interplay of multipoles higher than dipoles, giving rise to high-order IPM forces that can be exerted on a large variety of Mie particles. The high-order concept and theory can be extended to the well-known optical gradient force and radiation pressure, and may inspire new insights for studying the interaction of matter with other classic waves, such as acoustics.

Abstract

The imaginary Poynting momentum (IPM) of light has been captivated as an unusual origin of optical forces. However, the IPM force is predicted only for dipolar magnetoelectric particles that are hardly used in optical manipulation experiments. Here, we report a whole family of high-order IPM forces for not only magnetoelectric but also generic Mie particles, assisted with their excited higher multipoles within. Such optomechanical manifestations derive from a nonlocal contribution of the IPM to the optical force, which can be remarkable even when the incident IPM is small. We observe the high-order optomechanics in a structured light beam, which, despite carrying no angular momentum, is able to set normal microparticles into continuous rotation. Our results provide unambiguous evidence of the ponderomotive nature of the IPM, expand the classification of optical forces, and open new possibilities for levitated optomechanics and micromanipulations.

The complex Poynting vector, Π = (E* × H)/2, is a fundamental characteristic quantity of Maxwell waves (1), and it plays a crucial role in light-matter interactions. For example, its real part, Re(Π), represents the density of time-averaged electromagnetic energy flux and determines, up to a dimensional constant, an important dynamic property of light, namely, its time-averaged momentum. When light interacts with small objects, the incident momentum gives rise to the radiation pressure, with implications spanning over the areas of laser cooling (2, 3), optical micromanipulation (4, 5), and optomechanical systems (6).

The physical meaning of Re(Π) is so straightforward that its imaginary counterpart, Im(Π), has sometimes been forgotten or even neglected in optical physics. The flow of the latter is usually interpreted as the reactive power (1), which used to be a topic only of interest to engineering researchers in radio frequency antenna design and in the electric power industry (7, 8). However, the imaginary Poynting vector has, in recent years, gained a growing interest in the burgeoning area of nanophotonics, and it is associated with the concept of imaginary Poynting momentum (IPM) (9–12). This increased attention can be traced primarily to its influence in optical force theory (13), which shows that the IPM of the illumination can be coupled to a recoiling force via the interplay between electric and magnetic dipoles induced in the particles. Because the IPM force, in general, is linearly independent of the extinction force that consists of the optical radiation pressure and intensity-gradient force, it offers a distinct degree of freedom for optically manipulating particles. Such a profound implication has been theoretically highlighted in different configurations, like optical tweezers (14), vector beams (12, 15), and evanescent (9, 16) and two-wave interference fields (10, 16, 17). Moreover, because the generation of this force is accompanied with asymmetric light scattering by the particle (13), it could be exploited for the design of advanced optical nanoantennas and sources (18–20).

Despite this progress, there is not yet experimental evidence of the IPM force, which is weak and masked in observations (11) of the overall mechanical effect of light by observing the deflection of a nanocantilever probe in the evanescent field, so that such a deflection could not directly signal the IPM force, due to the coexisting, stronger transverse radiation pressure (9, 11), and potential torque effects caused by the anisotropy of the rod-like probe (21, 22).

In fact, so far, the knowledge of the IPM force is well established only for those particles that can be treated as magnetoelectric dipoles, but nothing is known of its role beyond the dipole approximation. In this context, we are naturally led to the following questions: (i) How can one discriminate and thus observe the IPM force independently? (ii) Can the IPM be coupled to the optical force via multipolar effects? Then, can this force be observed in particles with no magnetic (or electric) response? Under which circumstances?

Regarding (i), one may search for a wavefield in which the IPM can be separated from all other field quantities that could have mechanical effects. We have previously shown a paraxial cylindrical vector (CV) beam, with IPM streamlines looping around the beam axis and orthogonal to both the optical momentum and intensity gradient (12). Such a vortex structure, therefore, serves as a potential candidate to test the IPM force in the azimuthal direction. In this paper, we will deal with the IPM vortex of tightly focused (or nonparaxial) beams that can be applied to practical optical trapping and manipulation experiments. In addition, we now establish a useful multipolar model of optical force, which accounts for the relationship of the field quantities (including the IPM) with the force due to the multipolar interplay. This reveals a nonlocal field-to-force coupling, which is absent in the dipole approximation and that leads to the high-order IPM force. Also, it uncovers a so-far-unknown magnetoelectric response of plasmonic particles to incident light concerning the emergence of the optical force.

Results

IPM Vortex in Tightly Focused Beams.

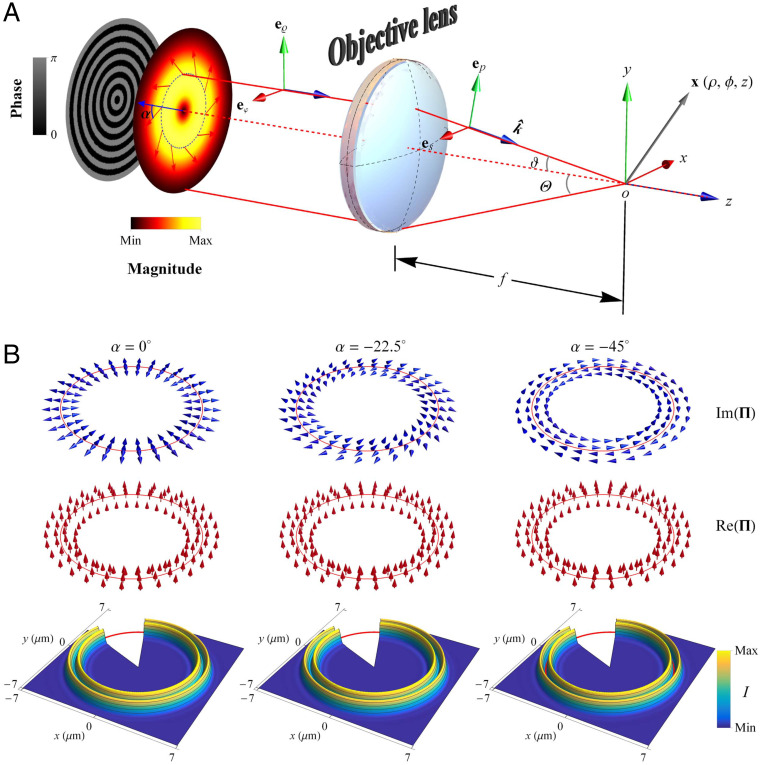
The geometry of the focusing problem is depicted in Fig. 1A, where a CV illumination with free space wavelength λ is focused by a high numerical aperture (NA) objective lens into a nondissipative medium, with permittivity ε and permeability μ. The input electric field can be written in the pupil plane polar coordinates (ϱ, φ) as (23)

$${\mathbf{A}}_0(\varrho ,\phi )=(\cos \alpha {\mathbf{e}}_{\varrho }+\sin \alpha {\mathbf{e}}_{\phi }){\mathcal{A}}_0(\vartheta ),$$ [1]

where (e_ϱ, e_φ) are unit vectors along radial and azimuthal directions, and ${\mathcal{A}}_0(\vartheta )$ denotes the radial dependence of the field amplitude, with ϑ = arcsin(ϱ/f) and f referring to the focal length; the parameter α ∈ (−90°, 90°) characterizes the polarization state of the incident field: α = 0 and ±90° correspond to the typical radial and azimuthal polarizations, respectively. Throughout the paper, ${\mathcal{A}}_0(\vartheta )$ is taken to be real-valued as also employed in our experiments.

Fig. 1.

The IPM in nonparaxial CV beams. (A) Geometry for analyzing the focusing property of CV beams. (B) Calculated fields (λ = 1.064 μm) focused with NA = 1.26, for different polarization parameter α. The refractive index of the ambient medium in image space is assumed to be n_med = 1.33 (water). Red circles with radius of 5.5 μm indicate the positions of local minima (min) between intensity maxima (max).

Upon apodization, the field can be expressed by its s- and p-polarization components along e_s and e_p, and employing the Richards-Wolf integral (24–26), one may formulate the electric vector in the vicinity of the focus as (see SI Appendix, Note 1 for details)

$$\mathbf{E}(\mathbf{x})=-i\frac{\cos \alpha }{k}{\partial }_{z}U(\rho ,z){\mathbf{e}}_{\rho }+U(\rho ,z)\sin \alpha {\mathbf{e}}_{\varphi }+i\frac{\cos \alpha }{k}\left({\partial }_{\rho }+\frac{1}{\rho }\right)U(\rho ,z){\mathbf{e}}_z,$$ [2]

where (e_ρ, e_ϕ, e_z) are the unit vectors for the cylindrical coordinates x = (ρ, ϕ, z) in image space, and k is the wavenumber in medium; U is a function given by:

$$U(\rho ,z)=-kf{\displaystyle {\int }_0^{\mathrm{\Theta }}\sqrt{\cos \vartheta }{\mathcal{A}}_0(\vartheta )J_1(k\rho \sin \vartheta )e^{\mathit{ikz}\cos \vartheta }\sin \vartheta d\vartheta },$$ [3]

with J₁(⋅) the Bessel function of the first kind of order one and Θ = arcsin(NA/n_med) the maximal converging angle (n_med the refractive index of ambient medium).

Eq. 2 holds exactly without any approximation (25). With [2] and Maxwell’s equations, it is shown that the azimuthal component Π_ϕ of the complex Poynting vector is purely imaginary over the whole focal volume (see SI Appendix, Note 1), and the imaginary Poynting vector at the focal plane takes the form

$$\mathrm{Im}(\mathbf{\Pi })=\frac{1}{2\mu c}\left\{\frac{\cos 2\alpha }{k}\left(\frac{1}{\rho }|U{|}^2+\frac{1}{2}{\partial }_{\rho }|U{|}^2\right){\mathbf{e}}_{\rho }+\frac{\sin 2\alpha }{k^2}\mathrm{Im}\left[\frac{1}{\rho }{\partial }_{\rho }\left(\rho U^{\ast }\right){\partial }_{z}U\right]{\mathbf{e}}_{\varphi }\right\},$$ [4]

where c is the light speed in the medium, and we have made use of Im(U) = 0, which holds for the field at the focal plane. Eq. 4 is a main theoretical result of this paper, which describes the rotational dynamics of the IPM for a generic CV beam. Applying the paraxial approximation ∂_zU ∼ ikU, one can produce from Eq. 4 the result for paraxial CV beams (12). From the α-dependent terms, it is deduced that the IPM will form a vortex structure at α = ±45°, for which Im(Π_ϕ) assumes the maximal value and Im(Π_ρ) is zero.

As an illustration, Fig. 1B shows the calculated focused fields with different polarization parameters. The amplitude function ${\mathcal{A}}_0(\vartheta )$ of the input field has a magnitude of standard CV beams, but modulated by a radially varying phase profile (see insets in Fig. 1A, or Methods for details) to prevent the focused field from being localized near the beam axis. We see that the field intensity distribution, in either case, is characterized by a sharp dual ring-like profile. As the field is axially symmetrical, its intensity gradient should exist only in the radial direction. The longitudinal real Poynting vector, Re(Π), indicates that the field carries no net angular momentum. However, the IPM, Im(Π), has azimuthal component for α ≠ 0. Specially, for α = −45°, this momentum circulates around the axis in a bidirectional manner, as shown in Fig. 1B (Top Right panel) where the IPM is clearly in opposite directions on the inner and outer sides of the annular field. Such a bichiral vortex structure is attributed to the spatial dependence of Im(Π_ϕ), whose sign is changed by the radial position ρ (see Eq. 4).

Multipolar Effects on the IPM Force.

An unambiguous observation of the IPM mechanical action requires comprehensive knowledge of the IPM force. In the dipole limit, this force can be written as (13)

$${\mathbf{F}}_{\text{IPM}}^{(1)}=A_{1,1}\mathrm{Im}\left({\mathbf{E}}^{\ast }\times \mathbf{H}\right),$$ [5]

where the prefactor $A_{1,1}=\mu k^4\mathrm{Im}\left[{\gamma }_{\text{elec}}^{\left(1\right)*}{\gamma }_{\mathrm{mag}}^{\left(1\right)}\right]/\left(12\pi \epsilon c\right)$ is determined by the electric and magnetic dipolar polarizabilities, ${\gamma }_{\text{elec}}^{(1)}$ and ${\gamma }_{\mathrm{mag}}^{\left(1\right)}$, of the particle; E and H are the incident field vectors in the particle center. It follows from Eq. 5 that an azimuthal force can be generated by azimuthal IPM incidence. For those particles that can support multipolar responses, the force associated with the IPM can be formulated, by a multipole moment expansion technique (27–29) and the angular spectrum representation, as (see Methods for details):

$${\mathbf{F}}_{\text{IPM}}^{(N)}=\sum _{l=1}^N{A}_{N,l}{\left(k^2+\frac{\mathrm{\Delta }}{2}\right)}^{l-1}\mathrm{Im}\left({\mathbf{E}}^{\ast }\times \mathbf{H}\right),$$ [6]

where Δ is the Laplacian operator and exponent means operator applied l−1 times; the coefficient A_N,l is determined by the particle properties (see Eqs. 19). The positive integer N denotes the truncation index used in the calculations, that is, the highest order of the multipole included; the larger the value of N, the more the higher-order components of force are involved.

Eq. 6 is the second major theoretical result of this paper, which generalizes the IPM force to the multipolar regime. For dipolar particles (N = 1), it reproduces Eq. 5 that is directly proportional to the IPM. However, the Laplacian Δ involved in the case of N > 1 indicates that the proportionality is invalid in the presence of multipoles. The force thus depends on derivatives of the IPM with respect to space, so that the particle is able to feel not only the local field, but its neighborhood. Such nonlocal effects, which are unique to the higher-order terms, also contribute to the azimuthal force, because the Laplacian action on the azimuthal IPM will not alter its direction, but just impose a modulation on its magnitude: ${\mathrm{\Delta }}^l\left(\text{Im}{\mathit{\Pi }}_{\varphi }{\mathbf{e}}_{\varphi }\right)={\mathbf{e}}_{\varphi }{\tilde{\mathrm{\Delta }}}^l\text{Im}{\mathit{\Pi }}_{\varphi }$, where $\tilde{\mathrm{\Delta }}\equiv \left[{\left({\partial }_{\rho }\right)}^2+(1/\rho ){\partial }_{\rho }-{1/\rho }^2+{\left({\partial }_z\right)}^2\right]$. Additionally, one may deduce from Eqs. 18 in Methods that the intensity-gradient force and the radiation pressure have no azimuthal component for the fields shown in Fig. 1B. It is evident from the above considerations that the IPM vortex beam is an ideal platform to isolate the IPM force in the azimuthal direction, even in the multipolar scenario.

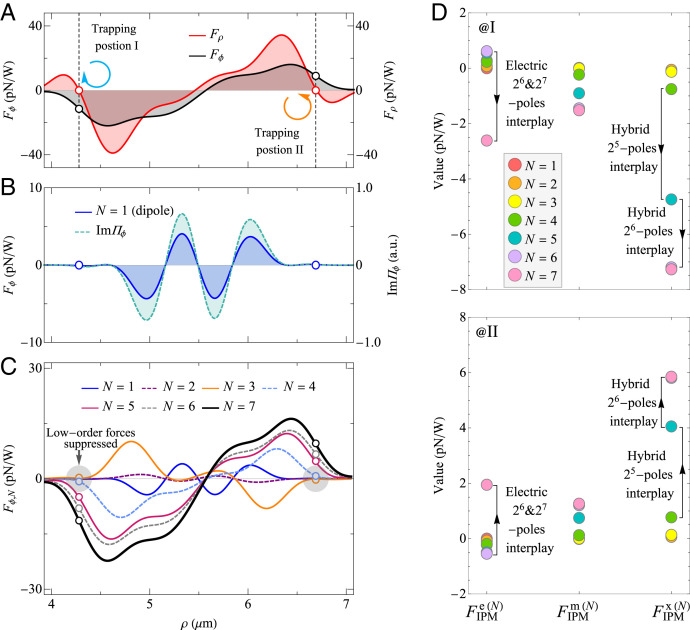
To know the multipolar effects excited by the IPM vortex beam, optical forces were calculated by the Lorenz-Mie theory (30) over a gold sphere placed on the focal plane of the field with α = −45° (i.e., the IPM vortex condition). The radius and refractive index of the sphere is set as 0.75 μm and 0.26 + 6.97i (the value at λ = 1,064 nm). Fig. 2A presents the total azimuthal and radial forces acting on the particle. Two equilibrium positions (I and II) can be identified, where F_ϕ is significant and takes opposite signs. It means that the particle tends to rotate clockwise and anticlockwise about the beam axis for the trapping positions I and II, respectively.

Fig. 2.

Theoretical results of optical forces for α = −45° (the IPM vortex condition). (A) Radial and azimuthal forces, F_ρ and F_ϕ, versus the radial displacement of the gold sphere. The truncation index in these calculations is N = 7, which is large enough to ensure the convergence of the Mie series. Hollow dots mark the values at radial equilibrium positions I and II, where the radial force vanishes with a negative derivative. (B) Comparison of the dipolar component of F_ϕ with incident IPM. (C) Azimuthal force for different N showing that low-order contributions are small at the equilibrium positions. (D) Calculated electric $F_{\mathrm{IPM}}^{\mathrm{e}\left(N\right)}$, magnetic $F_{\mathrm{IPM}}^{\mathrm{m}\left(N\right)}$, and hybrid $F_{\mathrm{IPM}}^{\mathrm{x}\left(N\right)}$ components of the IPM force at the trapping positions I and II, for different N. All components are in the azimuthal direction. In each channel, the difference between the components with adjacent N indicates the contribution from specific multipolar interaction: $F_{\mathrm{IPM}}^{\mathrm{e}\left(N\right)}-F_{\mathrm{IPM}}^{\mathrm{e}(N-1)}$ (or $F_{\mathrm{IPM}}^{\mathrm{m}\left(N\right)}-F_{\mathrm{IPM}}^{\mathrm{m}(N-1)}$) represents the electric (or magnetic) IPM force, due to the interplay of the electric (or magnetic) 2^N-pole with 2^N−1-pole; $F_{\mathrm{IPM}}^{\mathrm{x}\left(N\right)}-F_{\mathrm{IPM}}^{\mathrm{x}(N-1)}$ gives the hybrid IPM force caused by the interference between electric and magnetic 2^N-poles.

As discussed above, F_ϕ should be provided by the IPM force. Fig. 2B shows the dipolar component of F_ϕ, calculated with truncation index N = 1, together with the distribution of the azimuthal IPM of illumination. It stands out that the dipolar component is proportional to the IPM, as expected from Eq. 5, but it is negligible at the equilibrium positions where the IPM is vanishingly small. However, the proportionality relationship is absent for N > 1, as shown in Fig. 2C. This can be explained by including the high-order terms in Eq. 6, which allows the particle to respond to the incident IPM of the surroundings. Thanks to the nonlocal effect, a marked azimuthal force can be produced at each trapping position for N > 4. Such a radial trapping, with suppressed low-order IPM components, facilitates our experimental observation of the high-order IPM force.

The Lorenz-Mie theory results in Fig. 2C are reproduced by directly computing the IPM force using Eqs. 6 or 20 (see SI Appendix, Fig. S3 for details). Also, by decomposing the total IPM force into its electric, magnetic, and hybrid components (see Eq. 20), ${\mathbf{F}}_{\mathrm{IPM}}^{\left(N\right)}={\mathbf{F}}_{\mathrm{IPM}}^{\mathrm{e}\left(N\right)}+{\mathbf{F}}_{\mathrm{IPM}}^{\mathrm{m}\left(N\right)}+{\mathbf{F}}_{\mathrm{IPM}}^{\mathrm{x}\left(N\right)}$, we are able to know the specific types of interaction that dominate the azimuthal force. Fig. 2D shows the values of the different components calculated at the trapping positions. For both positions, the electric IPM force $F_{\mathrm{IPM}}^{\mathrm{e}\left(N\right)}$ is almost unchanged as N runs from 1 to 6, but a dramatic change occurs when N increases from 6 to 7. Namely, $F_{\mathrm{IPM}}^{\mathrm{e}\left(7\right)}-F_{\mathrm{IPM}}^{\mathrm{e}\left(6\right)}$, is significant, so that the electric IPM force mainly stems from the interplay of the electric 2⁶-pole with 2⁷-pole.

Likewise, we can identify, in the hybrid channel $F_{\mathrm{IPM}}^{\mathrm{x}\left(N\right)}$, the remarkable contribution from the interaction between the electric and magnetic 2⁵-poles and that between the electric and magnetic 2⁶-poles. Although individual magnetic multipolar interactions contribute only a small amount of force ($F_{\mathrm{IPM}}^{\mathrm{m}\left(N\right)}-F_{\mathrm{IPM}}^{\mathrm{m}(N-1)}$ is small for all N), their accumulation $F_{\mathrm{IPM}}^{\mathrm{m}\left(7\right)}$ is nonnegligible. This is remarkable, as it indicates a so-far-unknown magnetoelectric response of plasmonic particles to the action of light as regards the build-up of the optical force. Ultimately, we see from Fig. 2D that actually the low-order multipolar interplay is restrained for each component of the IPM force.

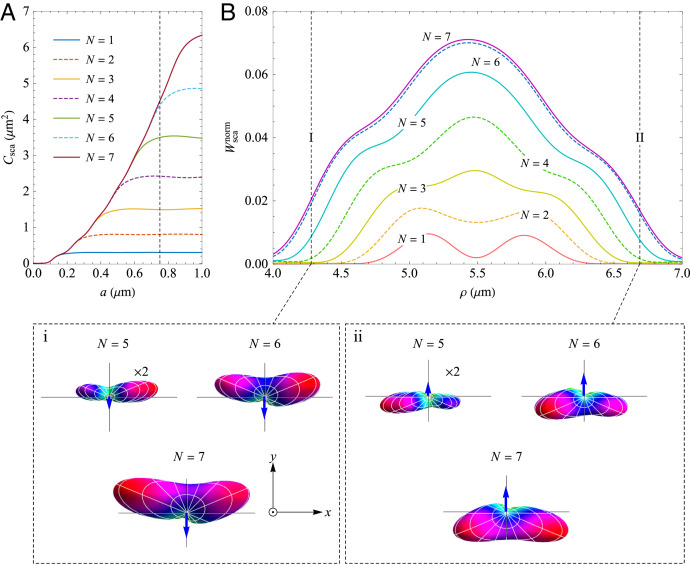
The structure of the incident field is crucial to the selective multipolar excitation. In fact, the low-order responses cannot be well suppressed under illumination with a plane wave. As shown in Fig. 3A, while the particle on use (a = 0.75 μm) supports rich multipoles up to seventh order, its scattering cross-section remains significant when the truncation index N is lowered to 4 and the dipolar response, although relatively weak, is nonnegligible. For comparison, Fig. 3B shows the scattering property of the particle excited by the IPM vortex beam. Here, in consideration of the inhomogenous illuminating field, we evaluate the normalized scattered power $W_{\mathrm{sca}}^{\mathrm{norm}}$ from the particle (see Eq. 22 in Methods), instead of the scattering cross-section. This quantity highly depends on ρ. At the trapping positions, $W_{\mathrm{sca}}^{\mathrm{norm}}$ is extremely small for N < 5, consistent with the force results of Fig. 2C.

Fig. 3.

Multipolar analysis of the particle’s response. (A) Scattering cross-section of an Au particle with different sizes for plane-wave incidence. (B) Normalized scattered power from the particle of radius a = 0.75 μm, placed on the focal plane of the IPM vortex beam, versus its radial position for different N. Note the two vertical broken lines indicating the trapping positions I and II shown in Fig. 2A. The insets i and ii depict the angular distribution of scattered intensity in the far field for N > 4, when the particle is located at these trapping positions on the positive x axis, respectively. Because the scattered intensity for N = 5 is small, the size of its patterns is doubled to ease reading. Blue arrows illustrate the directions of the azimuthal recoiling force expected from the asymmetry of the pattern.

It should be remarked, however, that by observing just the scattered power $W_{\mathrm{sca}}^{\mathrm{norm}}$, one fails to understand how the azimuthal IPM force in Fig. 2C acquires opposite signs at the two trapping positions. In this regard, it is worth noting that $W_{\mathrm{sca}}^{\mathrm{norm}}$ is a linear superposition of the scattering coefficients of sole multipoles (see Eq. 22) and thus independent of the interference between different multipoles, which accounts for the asymmetric scattering behavior of the particle (13).

In view of the momentum conservation, the IPM force can be explained by the recoiling effect due to the asymmetric scattering (13, 28, 29). Therefore, this force is associated not only with the scattering strength, but also with the scattering pattern. Insets i and ii of Fig. 3B show the calculated differentiate scattering power (i.e., the far-field distribution of scattered intensity) from the particle located at the trapping positions I and II. From these patterns, one can respectively expect for I and II a recoiling force in the anti-azimuthal and azimuthal directions, in agreement with Fig. 2C.

Experimental Observation of the High-Order IPM Force.

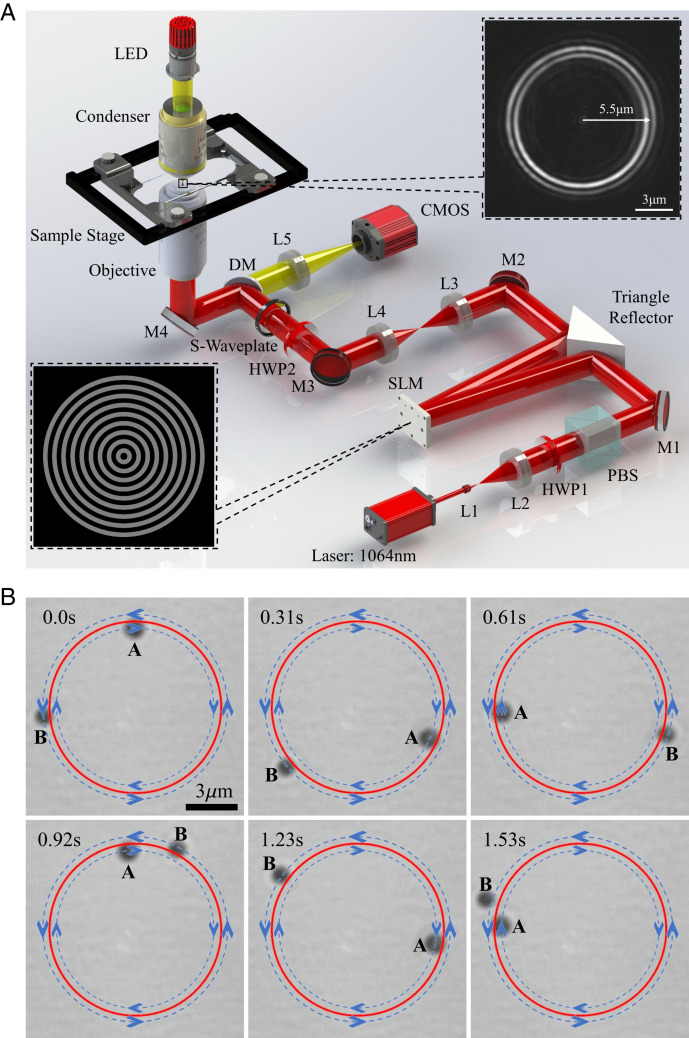
The experimental configuration is shown in Fig. 4A. A spatial light modulator (SLM) and a polarization converter (S-Waveplate) are used to modulate the input field phase and polarization, respectively (see Methods for detailed descriptions). The hologram loaded onto the SLM is shown in inset I, which is consistent with that used in our theoretical calculations. Inset II shows the measured intensity distribution at the focal plane, featuring a double-ring profile with a radius of about 5.5 μm. In line with the numerical simulations, we use Au spheres (diameter: 1.5 μm; immersed in water) to probe the optical force. These metallic particles can experience repulsive radiation pressure in the longitudinal direction, which cannot be overcome by the intensity-gradient force and their gravity. In our experiments, the longitudinal repulsive effect was compensated by the surface of the glass cover, so that the motion of the spheres was limited in two dimensions.

Fig. 4.

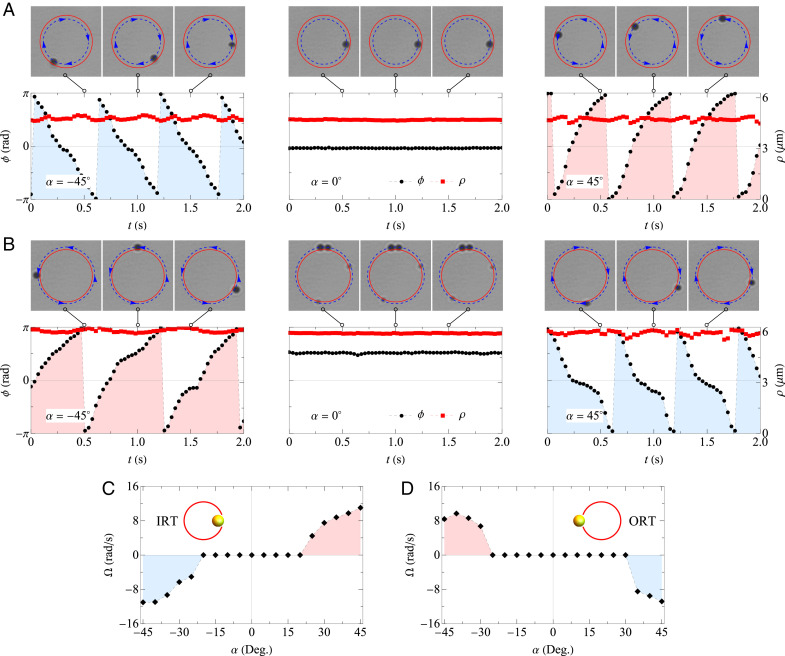
Particle rotation in the focused IPM vortex beam. (A) Schematics of experimental set-ups. L, Lens; HWP, half-wave plate; PBS, polarizing beam splitter; M, mirror; SLM, spatial light modular; DM, dichroic mirror; CMOS, complementary metal oxide semiconductor camera. The polarization parameter α is controlled by S-Waveplate. Insets I and II show the phase mask profile on the SLM and the measured intensity profile at the focal plane, respectively. (B) Successive images showing two Au particles trapped and rotated by the IPM vortex beam with polarization parameter α = –45°. Red circles with a radius of 5.5 μm illustrate the beam profile. The rotation direction of the spheres is indicated by arrows.

We exemplify in Fig. 4B (SI Appendix, Movie S1) the off-axis dual trapping using two spheres (A and B), which are radially confined, inner and outer, respectively, to the red circle that illustrates the focused beam. For both the inner (IRT) and outer radial trapping (ORT), the spheres are shown to revolve about the beam axis, as a manifestation of the high-order IPM force, which acts in the azimuthal direction. However, their rotational behaviors are quite different: the sphere A rotates clockwise, while the sphere B rotates anticlockwise. The rotation directions, opposite with respect to each other, agree well with our theoretical results that the azimuthal forces at the two distinct positions of radial equilibrium have opposite signs (Fig. 2C). This rotation ability of the IPM vortex beam is in sharp contrast with that of the conventional optical spanner based on a phase vortex (31–33), in which the particles usually orbit in the same sense.

It was shown previously that metallic microparticles in tightly focused beams with a point focal pattern may generate bubbles due to light-induced heating (34). We did not observe the bubble formation in the experiments, suggesting that the ring-like focal pattern of the IPM vortex beam alleviates the heating effects. The particle could also undergo a photophoretic force produced by inhomogeneous heating of the particle’s surface (35). Nevertheless, a careful consideration (SI Appendix, Note 2) shows that the photophoretic force is small in our case, and its azimuthal component is opposite to the rotation direction of the particle, for both the IRT and ORT. For these reasons, the particle rotation can be attributed exclusively to the azimuthal IPM force.

To experimentally examine the polarization-dependent property of the IPM force, the particle’s trajectories were recorded at varying α. Note that, here, a single sphere is used in order to avoid possible interparticle interactions. Fig. 5A shows the results for the IRT (SI Appendix, Movie S2). The clockwise motion occurring at α = −45° is halted when α is switched to 0, and a rotation of reversed direction is driven at α = 45°. The sensitivity of the rotation to the field polarization is also remarkable for the ORT (Fig. 5B and SI Appendix, Movie S3). However, the ORT yields a rotation direction, which is always opposite to that for the IRT, as it should be. Fig. 5 C and D show the experimentally measured averaged angular speed Ω of the sphere as a function of α, for the IRT and ORT, respectively. The speed profile in either case is almost symmetric, with a sinusoidal-like region around α = ±45°. This is a typical signature of the IPM force, as can be seen by the factor sin(2α) in Eq. 4. However, we did not observe a significant rotation when |α| or |sin(2α)| is small, although the azimuthal IPM of illumination can be nonzero in these conditions. We ascribe the stationary phenomena to the resistance arising from the glass cover. Namely, since the sphere is trapped against the surface of the glass cover, it should experience a frictional force that could surpass the IPM force, especially when |sin(2α)| is small.

Fig. 5.

Dependence of the particle rotation on the polarization. (A and B) Real-time positions of a single sphere for the IRT (A) and ORT (B) for different values of the polarization parameter α. Insets show experimental snapshots of the rotating sphere at selected time points. (C and D) Measured angular speed of the sphere versus α for the IRT (C) and ORT (D).

Discussion

We have demonstrated, both numerically and experimentally, the direct observation of the IPM force, by utilizing the IPM vorticity in a structured light beam and the high-order Mie responses of gold microparticles. It indicates that the IPM force, a long time overlooked mechanical effect of light (4, 16, 36), is actually ubiquitous, being exerted on a large variety of Mie particles (37–39). This force is shown to be remarkable, as the dynamics of the particles can be effectively controlled by this force alone. It functions in the beam as a peculiar optical spanner that sets the particles into bidirectional rotation, which endows itself with novel characteristics for applications in optical manipulation.

Moreover, our theoretical model describes the multipolar contributions to the optical force derived from various field quantities of interest. It tells us that the optical force on a generic Mie particle can be classified into four fundamental types, which are associated with the intensity gradient, canonical momentum, time-averaged momentum, and IPM, respectively. This is akin to the landscape in the dipolar approximation (9–13). However, one should draw special attention to those high-order terms, in which the Laplacian couples the nonlocal field to the force. The nonlocal effects may open new opportunities for tailoring light-matter interactions and should empower advanced applications in plasmonics and in the emerging area of Mie-tronics (38, 39).

Materials and Methods

Phase Modulation on the Input Field.

The amplitude function of the CV input field can be expressed as

$${\mathcal{A}}_0(\vartheta )=E_0{\mathcal{P}}_{\text{Mod}}(\vartheta )e^{-{\beta }_0^2{(\sin \vartheta /\sin \text{Θ})}^2}{J}_1\left(2{\beta }_0\frac{\sin \vartheta }{\sin \text{Θ}}\right),$$ [7]

where E₀ is the peak field amplitude and a small parameter β₀ is typically used (β₀ = 1.5 in our case) so that the input field can fill the aperture. The radial modulation function, ${\mathcal{P}}_{\text{Mod}}(\vartheta )$, is used to shape the focused field. The case ${\mathcal{P}}_{\text{Mod}}(\vartheta )$ = 1 corresponds to a normal CV input field (23), tight focusing of which will cause the obtained IPM vortex to be concentrated in an immediate vicinity of the beam axis (see SI Appendix, Note 3 for details). To localize the field away from the axis, we have resorted to perfect vortex generation technique, in which an additional radially varying modulation factor is introduced, to create an annular intensity profile (40). For our application, we use

$${\mathcal{P}}_{\text{Mod}}(\vartheta )=\mathrm{sign}\left[J_0(k_1{\rho }_0\sin \vartheta )\right],$$ [8]

This phase modulation will split the input field into a diverging spherical wave and a converging spherical wave, thereby their interfering results in an annular pattern in the focal plane. The focused field obtained by this modulation factor will be of an annular pattern of radius ∼ρ₀. In our work, ρ₀ is set to be 5.5 μm.

High-Order Theory of IPM Force, Intensity-Gradient Force, and Radiation Pressure.

Our theory is developed based on the optical force model established by Lin et al. (27–29, 41, 42). In this model, the optical force on a generic sphere is described by a set of incident field moments:

$$\begin{array}{l}{\mathbf{S}}_{\text{em}}^{(n)}=\left[\left({\nabla }^{(n-1)}{\mathbf{E}}^{*}\right)\stackrel{(n-1)}{:}\left({\nabla }^{(n-1)}\mathbf{H}\right)\right]\stackrel{(2)}{:}{\mathbf{ϵ}}^{(3)},\\ D_{\text{e}}^{(n)}=\left({\nabla }^{(n-1)}{\mathbf{E}}^{*}\right)\stackrel{(n)}{:}\left({\nabla }^{(n-1)}\mathbf{E}\right),\\ D_{\text{m}}^{(n)}=\left({\nabla }^{(n-1)}{\mathbf{H}}^{*}\right)\stackrel{(n)}{:}\left({\nabla }^{(n-1)}\mathbf{H}\right),\\ {\mathbf{S}}_{\text{e}}^{(n)}=\left[\left({\nabla }^{(n-1)}{\mathbf{E}}^{*}\right)\stackrel{(n-1)}{:}\left({\nabla }^{(n-1)}\mathbf{E}\right)\right]\stackrel{(2)}{:}{\mathbf{ϵ}}^{(3)},\\ {\mathbf{S}}_{\text{m}}^{(n)}=\left[\left({\nabla }^{(n-1)}{\mathbf{H}}^{*}\right)\stackrel{(n-1)}{:}\left({\nabla }^{(n-1)}\mathbf{H}\right)\right]\stackrel{(2)}{:}{\mathbf{ϵ}}^{(3)},\end{array}$$ [9]

where ϵ ⁽³⁾ is the Levi-Civita tensor, and the integer 1 ≤ n ≤ N denotes the order of the moments. In Eq. 9, the notation ${\mathbb{A}}^{\left(n\right)}\stackrel{(m)}{:}{\mathbb{B}}^{\left(n\prime \right)}$ denotes the second kind of m-fold contraction of tensors ${\mathbb{A}}^{\left(n\right)}$ and ${\mathbb{B}}^{\left(n\prime \right)}$ (28).

Although the model involves complicated formulas, it is not difficult to observe from ref. 28. or 29 that the force can be arranged into a series over these moments:

$${\mathbf{F}}^{\left(N\right)}=\sum _{l=1}^N\left\{\begin{array}{c}{A}_{N,l}\mathrm{Im}{\mathbf{S}}_{\text{em}}^{\left(l\right)}+B_{N,l}\nabla D_{\text{e}}^{\left(l\right)}+C_{N,l}\nabla D_{\text{m}}^{\left(l\right)}+\\ D_{N,l}\mathrm{Re}{\mathbf{S}}_{\text{em}}^{\left(l\right)}+E_{N,l}{\mathbf{P}}_{\text{e}}^{\left(l\right)}+F_{N,l}{\mathbf{P}}_{\text{m}}^{\left(l\right)}\end{array}\right\},$$ [10]

where the truncation index N denotes the highest order of multipole included, and we have introduced the moments:

$${\mathbf{P}}_{\text{e}}^{\left(n\right)}=\omega {\mathrm{ReS}}_{\text{em}}^{\left(n\right)}+i\nabla \times {\mathbf{S}}_{\text{e}}^{\left(n\right)}/2,{\mathbf{P}}_{\text{m}}^{\left(n\right)}=\omega {\mathrm{ReS}}_{\text{em}}^{\left(n\right)}/c^2+i\nabla \times {\mathbf{S}}_{\text{m}}^{\left(n\right)}/2.$$ [11]

The coefficients A_N,l ∼ F_N,l are determined by both N and the polarizabilities of the particle. For N = 1, Eq. 10 gives the well-known dipolar optical force (13), which can be decomposed into the IPM force, intensity-gradient force, and radiation pressure. In the following section, we will generalize these concepts to the case of N > 1.

To proceed, we turn to k-space, in which the incident fields E and H are represented by the angular spectrum of plane-wave components (16, 43, 44):

$$\mathbf{E}(\mathbf{x})={\displaystyle {\int }_{-\infty }^{+\infty }\mathbf{f}}(\mathbf{u})e^{i\mathbf{k}\cdot \mathbf{x}}{\text{d}}^{2}K, \mathbf{H}(\mathbf{x})={\displaystyle {\int }_{-\infty }^{+\infty }\mathbf{h}}(\mathbf{u})e^{i\mathbf{k}\cdot \mathbf{x}}{\text{d}}^{2}K,$$ [12]

where k = (k_x, k_y, k_z), $\mathbf{k}·\mathbf{k}=k^2$, u = (k_x, k_y), and d²K = dk_xdk_y. Using this representation, we find

$${\mathbf{S}}_{\text{em}}^{(n)}(\mathbf{x})={\displaystyle \iint {\left({\mathbf{k}}_1^{*}\cdot {\mathbf{k}}_2\right)}^{n-1}}\left[{\mathbf{f}}^{*}({\mathbf{u}}_1)\times \mathbf{h}({\mathbf{u}}_2)\right]e^{-i{\mathbf{k}}_{12}\cdot \mathbf{x}}{\text{d}}^2{K}_1{\text{d}}^2{K}_2,$$ [13]

with k₁₂ ≡ k₁* − k₂. The key step is to note the equality: (k₁* · k₂) = k² − (k₁₂)²/2, which yields

$${\left({\mathbf{k}}_1^{*}\cdot {\mathbf{k}}_2\right)}^{n-1}={\left[k^2-\frac{{\left({\mathbf{k}}_{12}\right)}^2}{2}\right]}^{n-1}={\displaystyle \sum _{j=0}^{n-1}{C}_{n,j}}(k){\left({\mathbf{k}}_{12}\right)}^{2j},$$ [14]

where

$$C_{n,j}(k)={\left(-\frac{1}{2}\right)}^j\frac{(n-1)!}{j!(n-1-j)!}{k}^{2n-2j-2}.$$

Upon substitution, we have

$${\mathbf{S}}_{\text{em}}^{\left(n\right)}=\sum _{j=0}^{n-1}{C}_{n,j}\left(k\right)\iint {\left({\mathbf{k}}_{12}\right)}^{2j}[{\mathbf{f}}^{*}\left({\mathbf{u}}_1\right)\times \mathbf{h}\left({\mathbf{u}}_2\right)]e^{-i{\mathbf{k}}_{12}\cdot \mathbf{x}}{\text{d}}^2{K}_1{\text{d}}^2{K}_2.$$ [15]

We observe that the role of (k₁₂)^2j in the integrand is equivalent to the negative Laplacian −Δ = −∇², which is operated in the x-space. Eq. 15 can thus be rewritten as

$$\begin{array}{c}{\mathbf{S}}_{\text{em}}^{(n)}={\displaystyle \sum _{j=0}^{n-1}{(-\mathrm{\Delta })}^j}{C}_{n,j}(k){\displaystyle \iint \left[{\mathbf{f}}^{*}\left({\mathbf{u}}_1\right)\times \mathbf{h}\left({\mathbf{u}}_2\right)\right]}{e}^{-i{\mathbf{k}}_{12}\cdot \mathbf{x}}{\text{d}}^2{K}_1{\text{d}}^2{K}_2\\ ={\displaystyle \sum _{j=0}^{n-1}{(-\mathrm{\Delta })}^j}{C}_{n,j}(k){\mathbf{S}}_{\text{em}}^{(1)}={\left(k^2+\frac{\mathrm{\Delta }}{2}\right)}^{n-1}{\mathbf{S}}_{\text{em}}^{(1)}.\end{array}$$ [16]

In a development paralleling the steps from Eqs. 12–16, we obtain the results for the other field moments in Eq. 10:

$$\begin{array}{c}{D}_{\text{e}}^{(n)}={\left(k^2+\frac{\mathrm{\Delta }}{2}\right)}^{n-1}{D}_{\text{e}}^{(1)},D_{\text{m}}^{(n)}={\left(k^2+\frac{\mathrm{\Delta }}{2}\right)}^{n-1}{D}_{\text{m}}^{(1)},\\ {\mathbf{P}}_{\text{e}}^{(n)}={\left(k^2+\frac{\mathrm{\Delta }}{2}\right)}^{n-1}{\mathbf{P}}_{\text{e}}^{(1)},{\mathbf{P}}_{\text{m}}^{(n)}={\left(k^2+\frac{\mathrm{\Delta }}{2}\right)}^{n-1}{\mathbf{P}}_{\text{m}}^{(1)}.\end{array}$$ [17]

Eqs. 16 and 17 link the field moments of arbitrary orders to their lowest order counterparts, whose physical meaning is quite straightforward: $D_{\text{e}}^{(1)}=|\mathbf{E}{|}^2$ (electric intensity); $D_{\text{m}}^{(1)}=|\mathbf{H}{|}^2$ (magnetic intensity); ${\mathbf{P}}_{\text{e}}^{(1)}=\mathrm{Im}[{\mathbf{E}}^{*}\cdot (\nabla )\mathbf{E}]$ (electric orbital momentum); ${\mathbf{P}}_{\text{m}}^{(1)}=\mathrm{Im}[{\mathbf{H}}^{*}\cdot (\nabla )\mathbf{H}]$ (magnetic orbital momentum); and ${\mathbf{S}}_{\mathrm{em}}^{\left(1\right)}={\mathbf{E}}^{*}\times \mathbf{H}$ (complex Poynting vector). Substituting these results into Eq. 10, and according to field-related characteristics, one may categorize the force into four parts: ${\mathbf{F}}^{(N)}={\mathbf{F}}_{\text{IPM}}^{(N)}+{\mathbf{F}}_{\text{G}}^{(N)}+{\mathbf{F}}_{\text{RP}}^{(N)}+{\mathbf{F}}_{\text{CRP}}^{(N)}$, where

$$\begin{array}{c}{\mathbf{F}}_{\text{IPM}}^{(N)}={\displaystyle \sum _{l=1}^N{A}_{N,l}}{\left(k^2+\frac{\mathrm{\Delta }}{2}\right)}^{l-1}\mathrm{Im}{\mathbf{S}}_{\text{em}}^{(1)},\\ {\mathbf{F}}_{\text{G}}^{(N)}={\displaystyle \sum _{l=1}^N{\left(k^2+\frac{\mathrm{\Delta }}{2}\right)}^{l-1}}\left[B_{N,l}\nabla D_{\text{e}}^{(1)}+C_{N,l}\nabla D_{\text{m}}^{(1)}\right],\\ {\mathbf{F}}_{\text{RP}}^{(N)}={\displaystyle \sum _{l=1}^N{D}_{N,l}}{\left(k^2+\frac{\mathrm{\Delta }}{2}\right)}^{l-1}\mathrm{Re}\left[{\mathbf{S}}_{\text{em}}^{(1)}\right],\\ {\mathbf{F}}_{\text{CRP}}^{(N)}={\displaystyle \sum _{l=1}^N{\left(k^2+\frac{\mathrm{\Delta }}{2}\right)}^{l-1}}\left[E_{N,l}{\mathbf{P}}_{\text{e}}^{(1)}+F_{N,l}{\mathbf{P}}_{\text{m}}^{(1)}\right].\end{array}$$ [18]

We call ${\mathbf{F}}_{\text{IPM}}^{(N)}$ the generalized IPM force, as it originates from the IPM of illumination. The second and third rows can be identified as the generalized intensity-gradient force and generalized radiation pressure, induced by the optical intensity inhomogeneity and momentum, respectively. However, it is worth noting that the electric and magnetic fields contribute differently to these two forces. The last term, ${\mathbf{F}}_{\text{CRP}}^{(N)}$, is also a type of radiation pressure, as the orbital momentum represents the canonical part of the optical field momentum (9). For this reason, we coin it the generalized canonical radiation pressure. We remark that the above generalization is self-consistent, because for N = 1, all the terms in Eq. 18 reduce to their dipolar counterparts (13).

So far, we have not dealt with the coefficients A_N,l ∼ F_N,l. These coefficients can be worked out with proper index substitution for Eqs. 11–22 in ref. 29. (see SI Appendix, Note 4 for details). As the main goal of this paper is the IPM force, we present the result for $A_{N,l}=A_{N,l}^{\text{e}}+A_{N,l}^{\text{m}}+A_{N,l}^{\text{x}}$:

$$\begin{array}{c}{A}_{N,l}^{\text{e}}=\frac{\mu \omega }{4\pi \epsilon }\left\{{\displaystyle \sum _{j=0}^{\lfloor \frac{N-l-1}{2}\rfloor }{\Lambda }_{l+2j,j}}\mathrm{Im}\left[{\gamma }_{\text{elec} }^{(l+2j)}{\gamma }_{\text{elec} }^{(l+2j+1)*}\right]+{\displaystyle \sum _{j=0}^{\lfloor \frac{N-l-2}{2}\rfloor }{\mathit{\Omega }}_{l+2j+1,j}}\mathrm{Im}\left[{\gamma }_{\text{elec} }^{(l+2j+1)}{\gamma }_{\text{elec} }^{(l+2j+2)*}\right]\right\},\\ A_{N,l}^{\text{m}}=-\frac{\mu \omega }{4\pi \epsilon c^4}\left\{{\displaystyle \sum _{j=0}^{\lfloor \frac{N-l-1}{2}\rfloor }{\Lambda }_{l+2j,j}}\mathrm{Im}\left[{\gamma }_{\text{mag} }^{(l+2j)}{\gamma }_{\text{mag} }^{(l+2j+1)*}\right]+{\displaystyle \sum _{j=0}^{\lfloor \frac{N-l-2}{2}\rfloor }{\mathit{\Omega }}_{l+2j+1,j}}\mathrm{Im}\left[{\gamma }_{\text{mag} }^{(l+2j+1)}{\gamma }_{\text{mag} }^{(l+2j+2)*}\right]\right\},\\ A_{N,l}^{\text{x}}=\frac{\mu }{4\pi \epsilon c}\{{\displaystyle \sum _{j=0}^{\lfloor \frac{N-l}{2}\rfloor }{M}_{l+2j,j}}\mathrm{Im}\left[{\gamma }_{\text{elec}}^{(l+2j)*}{\gamma }_{\text{mag} }^{(l+2j)}\right]-\frac{l{k}^2}{{(l+1)}^2}{\displaystyle \sum _{j=0}^{\lfloor \frac{N-l-1}{2}\rfloor }{M}_{l+2j+1,j}}\mathrm{Im}\left[{\gamma }_{\text{elec} }^{(l+2j+1)*}{\gamma }_{\text{mag} }^{(l+2j+1)}\right]\\ -\frac{l(l+1)k^4}{{(l+2)}^2}{\displaystyle \sum _{j=0}^{\lfloor \frac{N-l-2}{2}\rfloor }{M}_{l+2j+2,j}}\mathrm{Im}\left[{\gamma }_{\text{elec}}^{(l+2j+2)*}{\gamma }_{\text{mag} }^{(l+2j+2)}\right]\},\end{array}$$ [19]

where ${\gamma }_{\text{elec}}^{\left(n\right)}$ and ${\gamma }_{\text{mag}}^{\left(n\right)}$ are the electric and magnetic 2ⁿ-polar polarizabilities, and the related parameters (Λ_n,m, Ω_n,m, and Μ_n,m) are given by SI Appendix, Eq. S4.12. To gain insight into the physics underneath the IPM force, we have decomposed A_N,l into three parts:

$${\mathbf{F}}_{\text{IPM}}^{(N)}={\mathbf{F}}_{\text{IPM}}^{\text{e}(N)}+{\mathbf{F}}_{\text{IPM}}^{\text{m}(N)}+{\mathbf{F}}_{\text{IPM}}^{\text{x}(N)}={\displaystyle \sum _{l=1}^N{A}_{N,l}^{\text{e}}}\mathrm{Im}{\mathbf{S}}_{\text{em}}^{(l)}+{\displaystyle \sum _{l=1}^N{A}_{N,l}^{\text{m}}}\mathrm{Im}{\mathbf{S}}_{\text{em}}^{(l)}+{\displaystyle \sum _{l=1}^N{A}_{N,l}^{\text{x}}}\mathrm{Im}{\mathbf{S}}_{\text{em}}^{(l)},$$ [20]

which underlines the components linked to different multipolar interplay processes. In the dipole limit (N = 1), this interaction is simply the hybrid coupling between the electric and magnetic dipoles (9–14), as $A_{1,1}^{\mathrm{e}}=A_{1,1}^{\mathrm{m}}=0$ while $A_{1,1}^{\mathrm{x}}\ne 0$ (in general); for a generic Mie particle, the interactions also include the electric-electric coupling and magnetic-magnetic coupling.

From Eqs. 18–20, we see that ${\mathbf{F}}_{\mathrm{IPM}}^{\mathrm{e}\left(N\right)}$ (or ${\mathbf{F}}_{\mathrm{IPM}}^{\mathrm{m}\left(N\right)}$) represents the purely electric (or magnetic) IPM force resulting from the interaction of electric (or magnetic) multipoles with adjacent orders, while ${\mathbf{F}}_{\mathrm{IPM}}^{\mathrm{x}\left(N\right)}$ is the hybrid magnetoelectric IPM force derived from the interference between electric and magnetic multipoles of the same order. As an illustration, we consider the case shown in Fig. 2C and make a decomposition of the azimuthal IPM force into the three parts using Eq. 20. The results are shown in SI Appendix, Fig. S3, from which the data at the trapping positions are extracted, and they are presented in Fig. 2D.

As a closing remark, we would stress that the generation of the IPM force requires the breaking of electric-magnetic symmetry (41), as ${\mathbf{F}}_{\mathrm{IPM}}^{\left(N\right)}$ vanishes when ${\gamma }_{\mathrm{elec}}^{\left(n\right)}={\gamma }_{\mathrm{mag}}^{\left(n\right)}$ for all n. However, it should be noted that such a dual asymmetry does not necessarily lead to the IPM force. For instance, an electric dipole (${\gamma }_{\mathrm{elec}}^{\left(1\right)}\ne 0$, ${\gamma }_{\mathrm{elec}}^{\left(n\right)}=0$ for n > 1, and ${\gamma }_{\mathrm{mag}}^{\left(n\right)}=0$ for all n) will never experience this force, although it sustains the dual asymmetry, ${\gamma }_{\mathrm{elec}}^{\left(1\right)}\ne {\gamma }_{\mathrm{mag}}^{\left(1\right)}$.

Scattering Property Calculations.

It is common to study the particle multipolar scattering on plane-wave excitation by means of the scattering cross-section (45),

$$C_{\mathrm{sca}}=\frac{1}{k^2{\left|\mathbf{E}\right|}^2}\sum _{l=1}^N\sum _{m=-l}^l({\left|p_{l,m}\right|}^2+{\left|q_{l,m}\right|}^2),$$ [21]

where p_l,m and q_l,m are the electric and magnetic multipolar coefficients of the scattered field (see SI Appendix, Eq. S4.1 in Note 4). The summation term in Eq. [21] (multiplied by a dimensional constant) denotes the optical power scattered off the particle and holds for a generic incident field. However, we notice that Eq. 21 may not make sense for inhomogenous fields whose local incident power density, or intensity |E|², is not a constant and in some cases, it can be zero, yielding Eq. 21 a divergent result.

Therefore, to properly quantify the particle-scattering property in our case, we shall use the scattered power normalized by the total incident power W_inc, namely

$$W_{\text{sca}}^{\text{norm}}=\frac{\epsilon c}{2k^2{W}_{\mathit{inc}}}{\displaystyle \sum _{l=1}^N{\displaystyle \sum _{m=-l}^l\left({\left|p_{l,m}\right|}^2+{\left|q_{l,m}\right|}^2\right)}}.$$ [22]

In doing so, we are able to characterize the absolute scattering strength of the particle at different positions in the illumination field. However, it should be mentioned that Eq. 22, which is adequate for beams or focused fields, does not apply to infinitely extended wavefields like, e.g., plane waves, since evidently the total incident power of the latter is infinite. Hence, Eqs. 21 and 22 have different use depending on the characteristics of the incident field.

Experimental Setup.

Our experiments were performed based on home-built holographic optical tweezers (Fig. 4A). A linearly polarized beam (λ = 1,064 nm) was expanded and collimated by a telescope consisting of L1 and L2. After passing through a half-wave plate (HWP1) and a polarizing beam splitter, the input beam becomes horizontally polarized. To miniaturize the size of the setup, a specially designed 96° triangle reflector is employed to reflect the input beam onto an SLM (Pluto-HED6010-NIR-049-C, Holoeye Photonics AG, Inc., 1920 × 1080 pixels, pixel pitch: 8.0 μm, frame rate: 60 Hz). The modulated beam was relayed into the back aperture of the objective (100×, NA 1.4, Oil-immersion, CFI Plan Apo, Nikon, Inc.) by a 4f system consisting of L3 and L4. After L4, a half-wave plate (HWP2) and an S-Waveplate (RPC-1064–08-334, Workshop of Photonics, Inc.) were used to convert the linearly polarized beam into a vector beam.

It is known that the S-Waveplate can be considered as a half-wave plate with space variant direction of fast-axis. To control the polarization direction, i.e., the polarization angle α, of the generated vector beam with respect to the radial direction, the HWP2 was arranged into a stepper motor rotation mount (K10CR1/M, Thorlabs, Inc.) to rotate the polarization direction of the linearly polarized beam incident onto the S-Waveplate. The generated beam can be considered as a linearly polarized vector Bessel-Gauss beam and then focused by the objective. The objective was also employed for the sample imaging, and a CMOS (complementary metal oxide semiconductor) camera (Point Gray GS3-U3-41C6M-C, FLIR System, Inc., 2048 × 2048 pixels, pixel pitch: 5.5 μm, frame rate: 90 fps) was used to monitor and record the manipulation process.

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.