Abstract
The cyclic coordinate descent (CCD) method is a popular loop closure method in protein structure modeling. It is a robotics algorithm originally developed for inverse kinematic applications. We demonstrate an effective method of building the backbone of protein structure models using the principle of CCD and a guiding trace. For medium-resolution 3-dimensional (3D) images derived using cryo-electron microscopy (cryo-EM), it is possible to obtain guiding traces of secondary structures and their skeleton connections. Our new method, constrained cyclic coordinate descent (CCCD), builds α-helices, β-strands, and loops quickly and fairly accurately along predefined traces. We show that it is possible to build the entire backbone of a protein fairly accurately when the guiding traces are accurate. In a test of 10 proteins, the models constructed using CCCD show an average of 3.91Å of backbone root mean square deviation (RMSD). When the CCCD method is incorporated in a simulated annealing framework to sample possible shift, translation, and rotation freedom, the models built with the true topology were ranked high on the list, with an average backbone RMSD100 of 3.76Å. CCCD is an effective method for modeling atomic structures after secondary structure traces and skeletons are extracted from 3D cryo-EM images.
Keywords: Inverse Kinematics, Cryo-electron microscopy, Image, Skeleton, Protein Structure, Loop Modeling, Cyclic Coordinate Descent
1. Introduction
The cyclic coordinate descent (CCD) method is a loop closure method that addresses inverse kinematic problems in which a robot's hand is moved to a target via a series of arm rotations around multiple joints.1 CCD has been widely used in protein structure modeling.2-4 A loop often consists of four or more amino acids and is part of a protein chain. Each amino acid contains multiple rotatable bonds that resemble multiple joints of a robot's arm. Given the location of two anchor amino acids and the number of amino acids between the anchors, a loop closure method aims to generate a loop that connects the two anchors. This problem is similar to sample-based motion planning in robotics. Many analytical and optimization methods have been developed to address this problem.5-9 Some of the analytical methods have solved the problem for three residues using spherical geometry and polynomial equations.10-12 The optimization approach has been used for loops with more than six degrees of freedom. These methods search for an approximate solution by iteratively changing the backbone torsion angles until the desired distance between the end of the loop and the anchor is reached. Two such methods are the random tweak method13, 14 and the CCD method.4, 15 Some loop modeling approaches and tools are based on the random tweak method, such as Drawbridge16 and LOOPY.17 In protein modeling, many possible conformations of a loop can be built quickly using CCD. Such loops are eventually selected based on the energetic stability of the entire chain.
Cryo-electron microscopy (cryo-EM) is an emerging technique that produces 3-dimensional (3D) images of molecules at a wide range of resolutions.18-21 Although more and more cryo-EM images are produced at resolutions around 3Å, at which atomic structure can be determined from the image,22-26 many more have been deposited in the Electron Microscopy Data Bank (EMDB) at a lower, less workable “medium” resolution.27 At the medium resolutions, such as 5–8Å, neither the backbone nor the characteristic features of amino acids are resolved. It is challenging to derive the atomic structure from such an image. One approach is to fit a known atomic structure or a homologous structural model in the cryo-EM map using rigid-body or flexible fitting.28-37 The limitation here is the need for atomic structures that are either components of or homologous to the target protein. The de novo approach aims to derive atomic models without the dependence of a known atomic structure. Although it is a challenging problem without a template, recent advances show that the de novo approach is increasingly likely to be successful. Such advances include more computational methods to extract structural patterns from cryo-EM images,38-40 effective computational methods to derive topologies in large and more complicated proteins,41-44 effective computational methods to handle errors and large data,45-47 and effective construction of initial backbone models. 48
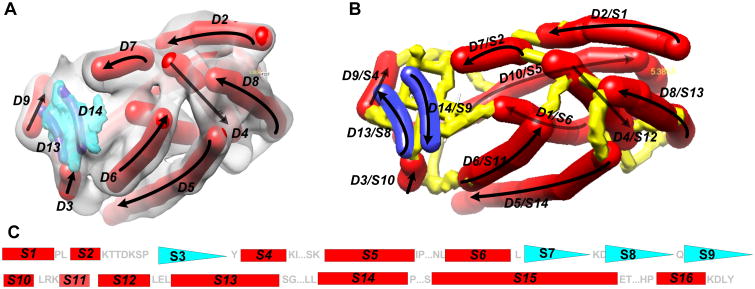
At the medium resolution range, the location and orientation of major secondary structures, such as helices and β-sheets, are detectable using various image processing tools.38, 40, 49-54 A helix appears as a cylinder (red in Figure 1A) and a β-sheet appears to have a thin layer of density (blue in Figure 1A). Image processing tools such as SSETracer utilize such characteristics to detect helices and β-sheets55 (Figure 1). A detected helix can be represented by the trace of its central axis, referred to as an α-trace. For easy visualization, an α-trace is shown as a red cylinder (Figure 1A and B). We recently showed that it is possible to detect β-strands from β-sheet density image using StrandTwister.39 StrandTwister predicts a small set of possible β-traces using the principle of right-handed β-twist.39 A detected β-strand is represented as its central line, referred to as a β-trace (navy blue in Figure 1A and B). Secondary structure traces of major α-helixes and β-strands provide important constraints for building initial backbone models of the protein.
Figure 1. Secondary structure traces, skeleton, and topology.
(A) The 3D image (gray) was simulated to 10 Å resolution using atomic structure 3PBA from the Protein Data Bank (PDB) and EMAN software.73 Secondary structure traces (red sticks: α-traces; purple: β-strands) were detected using SSETracer55 and StrandTwister39 and viewed using Chimera.76 See the detected β-traces (blue) in (B) for clear viewing. Only those at the front of the structure are labeled. Arrows: the direction of the protein sequence; (B) The skeleton (yellow) derived from the image is superimposed on the traces of helices (red) and β-strands (blue). (C) The amino acid sequence of protein 3PBA is annotated with secondary structures using red rectangles (helices) and blue triangles (β-strands). The two smaller triangles S3 and S7 were not detected in the image. Loops longer than two amino acids are indicated using “…”.
In addition to major secondary structures detectable in the image, a density skeleton (yellow in Figure 1B) can also be detected. Gorgon uses thinning and pruning techniques44, 56 and SkelEM derives a skeleton by processing local maxima.57 A skeleton represents the voxels that are connected with relatively high density values in the 3D image. Depending on the quality of the image, a skeleton may have gaps or wrong connections. In spite of the possible errors in skeletons, they suggest possible connections between two secondary structure traces. Such connection information is another source of constraints for building the initial backbone of the protein.
The locations of α-traces, β-traces, and the skeleton represent the pattern of a protein from the 3D image. The locations of helices and β-strands in the amino acid sequence can be predicted using various secondary structure prediction tools.58-60 An example of secondary structure locations on a protein sequence is shown in Figure 1C. In the 3D image, different helices and β-strands may have different lengths and may be separated from each other by different distances. It is possible to derive the topology of the α-traces and β-traces by mapping the secondary structure information in the 3D image with that in the 1D amino acid sequence.42, 43, 61 A topology of the α-traces and β-traces refers to the order of the traces along the protein sequence and the direction of each trace. The topology of α-traces and β-traces indicates how the amino acid sequence threads through the secondary structure traces. For example, the true topology in Figure 1B encodes an order of secondary structure traces as (D2, D7, D9, D10, D1, D13, D14, D3, D6, D4, D8, D5, D11, D12). Traveling along the direction of the protein sequence, α-trace D2 is mapped to helix S1. After a short segment of the skeleton trace, D7 is mapped to S2 (Figure 1B). Note that the majority of the helices and β-strands can be detected, but small helices shorter than two turns and two-stranded β-sheets are still challenging to detect.
2. Related Work
This paper addresses the problem of constructing fragments and/or a backbone using guiding traces of secondary structures and skeletons. Current methods to construct initial backbones generally belong to two categories. One category employs the comparative modeling principle to utilize templates that are selected from proteins with known atomic structures.62, 63 The other category uses the ab initio principle to build the entire chain by selecting fragments of 3 to 15 amino acids long from a fragment library. Fragment libraries consist of short pieces extracted from known structures.64, 65 Constrained CCD (CCCD) is a method that differs from the above two categories in that it builds backbone models using guiding traces that represent the overall location of secondary structures and their connections.
Previous de novo modeling methods either rely on an existing ab initio protein structure prediction method or on high-resolution image data. Gorgon is a semi-automatic method to place Cα atoms of the protein in the image. A user is involved in the selection of Cα positions among possible pseudo-atoms suggested by the tool.41 EM-fold uses Rosetta to construct conformations of the protein for each possible topology of the secondary structure traces.66, 67 Rosetta docks the initial model into the image and identifies regions that displace from it. Rosetta iteratively resamples the conformations in these regions, scoring each potential conformation with an energy function that considers the fitting of the model in the image. Pathwalking derives cluster points from the 3D image that are possible locations of amino acids. It then uses a constraint solver to find an optimal path that goes through the cluster points.68 Because it relies on the accuracy of the cluster points, it appears to be successful in 3D images with resolutions higher than 5Å, but it fails with lower resolution images. The problem of filling the gap in an incomplete model using a 3D image from X-ray crystallography is addressed in the work by Lotan et al.69 That problem is slightly different because X-ray crystallography data provide much higher resolution than medium-resolution images from cryo-EM; therefore, they demand more accurate loops. As mentioned in the paper, it may take 30 minutes to build short loops (with ∼4 amino acids) and 178 minutes for longer loops (with ∼15 amino acids).69 We present a simple and effective method, unlike our previous ab initio approach70, that is particularly suitable to construct any kind of fragment along a guiding trace for medium-resolution images.
Although CCD has been widely used to construct loops, it is often used without a guiding trace.4 We previously developed forward backward CCD (FBCCD), which is a fast approximate loop closure method.71 It does not use guiding traces; rather, it generates structure fragments that approximately fill the gap. The CCCD method uses guiding traces and utilizes FBCCD as a sub-program to generate a backbone along the guiding trace. We showed that it is possible to build entire backbone sequentially using skeleton traces as a guide.72 In this paper, we propose CCCD as a methodology for efficient construction of protein backbone fragments as long as the guiding traces are available. This paper provides in-depth analysis of the accuracy and runtime of the method as well as two kinds of applications. To our knowledge, CCCD is the first effective model-building method that uses the principle of CCD to construct an initial backbone directly from the traces of secondary structures and a skeleton.
3. Methods
3.1 Constrained CCD
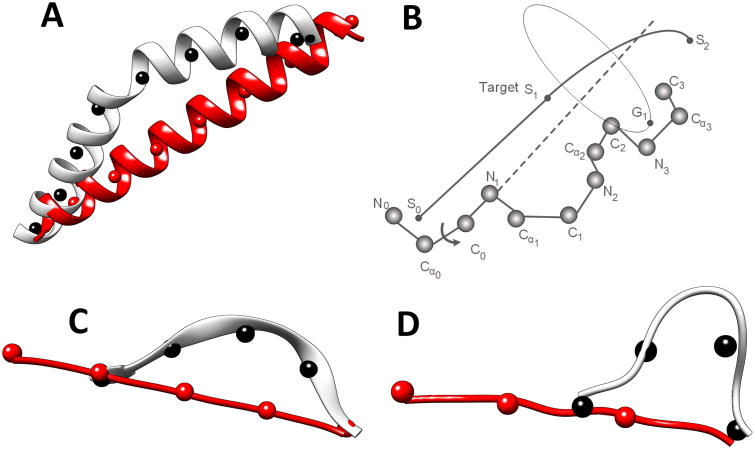
CCCD is designed to utilize the effectiveness of CCD and to force structure fragments along a guiding trace. The idea is to break the guiding trace into short segments and to break the fragment, which is to be built, into sub-fragments. CCCD requires each sub-fragment of the model to reach the approximate location of the corresponding trace segment. In this way, the entire model aligns with the guiding trace because each sub-fragment aligns with its trace segment. A guiding trace is first divided into short segments of 6Å long (by default), although results are reported using 9Å and 12Å segments (see Results). The number of amino acids in each sub-fragment is determined by the total number of amino acids in the fragment and the number of trace segments. To align each sub-fragment to a trace segment, the principle of CCD was applied to move the ending point of the sub-fragment to the target point on the trace, except for the last trace segment. FBCCD was used to align the last sub-fragment to the last trace segment. As shown in Figure 2B, a sub-fragment of four amino acids is to be built such that the geometric center of the first three atoms is aligned with segment point S0, and the geometric center of the last three atoms, G1, is moved closest to segment point S1 through sequential updates of torsion angles. Once the first sub-fragment converges to the trace segment (i.e., S0S1), the next sub-fragment is built using the next trace segment (i.e., S1S2).
Figure 2. Constrained CCD for building an α-helix, a β-strand, and a loop.
A guiding trace is divided into segments indicated using segment points (black spheres) for an α-helix in (A), a β-strand in (C), and a turn in (D). The initial ideal fragment is divided into the same number of sub-fragments (indicated using red spheres) as the number of segments. (B) The principle of aligning a sub-fragment to a segment. The segment points are labeled S0, S1, and S2. The geometric center of the last three atoms on the sub-fragment is labeled G1.
CCCD is a general method to build any kind of fragments, as long as the guiding trace is provided. α-helices, β-strands, and loops were built using same principle but with different parameters. The process of building an α-helix is similar to that for building a β-strand. It starts with a straight α-helix (or a straight β-strand) using the torsion angle (φ, ψ) = (-57°, -47°) for a helix or (φ, ψ) = (-139°, 135°) for a β-strand. The number of amino acids in the perfect secondary structure was calculated using the length of the trace segment and the rise of 1.5Å for an α-helix and of 3Å for a β-strand. The number of points on the trace (marked by black points in Figure 2 A, C, and D) is required to be the same as that on the central line of the straight α-helix/β-strand (red points in Figure 2 A, C, and D). To preserve the structure character of an α-helix/β-strand, an update is accepted if a new torsion angle is within the predefined range of a helix (i.e., φ∈ [-80°, -40°] and ψ∈[-60°, -20°]) or a β-sheet (i.e., φ∈ [-170°, -60°] and ψ∈[90°, 175°]). The process terminates either when the maximum number of cycles is reached or when the cutoff distance from the target is reached. The maximum number of cycles is 100 and the cutoff distance is 0.1Å in the current implementation.
CCCD uses FBCCD to generate the last sub-fragment that aligns with the last trace segment. FBCCD is a fast approximate loop closure method.71 It does not require the convergence of the loop; yet it ensures the accuracy of the downstream backbone. Both the forward and backward cycles use the principle of CCD; however, the target points of the backward cycle consist of points from the downstream portion of the backbone. The forward cycle brings the moving end of the loop quickly to the proximity of the target. Instead of spending many more forward cycles to bring the moving end closer to the target, FBCCD connects the moving end to the backbone and uses the backward cycle to adjust the torsion angles of the fragments so that the downstream backbone returns to the original position. FBCCD is shown to generate loops of comparable accuracy in fewer cycles compared to CCD.71
3.2. Sequential construction of the entire backbone
To test the feasibility of building the entire backbone directly from traces, major α-traces and β-traces derived from the native structure were used to construct α-helices and β-strands. Such traces are expected to be more accurate than those detected directly from the 3D image. Those traces from helices shorter than seven amino acids and β-strands shorter than four amino acids were not used. This was done to simulate the fact that shorter helices and strands are often not detected from images at medium resolutions. Native structures were simulated to a 3D image using EMAN,73 and the skeleton was derived using SkelEM.57 EMAN is a scientific image processing suite with a primary focus on processing data obtained from transmission electron microscopes. SkelEM is a software package we previously developed to extract the skeleton of cryo-EM 3D images. The traces of loops were derived from the skeleton. The entire backbone of a protein was constructed sequentially from the N to the C terminal of the chain. CCCD was applied to build helices, β-strands, and loops. Each newly constructed fragment was screened for any collision in the local environment. In this experiment, the true amino acid sequence segments of helices and β-strands were used in constructing the model.
3.3. Constructing full models of the protein using simulated annealing
A guiding trace represents the central line of a helix/β-strand/loop. Since it is almost impossible to detect secondary structure locations accurately in either the 3D image or the protein sequence, alternative positions are needed in the construction of a chain. We developed a simulated annealing process that samples the translation, rotation, and shift of secondary structure positions. The translation, T, is the distance to translate a helix along the central axis. The rotation is the angle to rotate a helix around the central axis. In principle, the starting position of a helix is determined by the translation and rotation parameters. The shift parameter, S, is used to simulate the error of the secondary structure prediction on the protein sequence. We noticed that the position of a helix can be approximated using two parameters (T, S) without the rotation parameter (data not shown), presumably due to the helical nature. Our simulation eliminated the rotation parameter to reduce the computation. We used T ∈ [−3Å, 3Å] and S ∈ [−2, 2] amino acid positions.
The 3D image of a protein was simulated using its native protein structure and EMAN software.73 The helices were detected from the 3D image using SSETracer.55 SSETracer characterizes each voxel of the 3D image based on multiple local geometrical features. The output is the central axes of helices and voxels of β-sheets of the protein. The top 100 topologies were generated using DP-TOSS,43 a constrained K-shortest-paths algorithm for a topology graph. The input of the program consists of the detected secondary structure traces and the amino acid segments of the secondary structures. The output is a list of ranked topologies of the secondary structure traces. For each possible topology, 100 backbone conformations were constructed using CCCD. The current implementation applies to α-proteins that do not contain β-strands. To generate each backbone, helices were built first and then loops were built to connect the helices. A full model is a model that includes both backbone atoms and side chain atoms except hydrogen atoms. Once a backbone was generated, side chains were added using R3 algorithm.74 The full models were ranked using a multi-well energy function.75 This is a contact pair-specific and distance-specific function based on statistical characterization of the side chains of proteins
4. Results and Discussion
4.1 Accuracy and time to build a helix, a β-strand, and a loop using CCCD
Many long helices are bent and many β-strands deviate from their ideal curvature. We addressed the question: Can a fragment of a backbone be accurately built if the trace is fairly accurate? A dataset containing five helices, six β-strands, and six loops wasused to test the performance. The trace of a helix/β-strand was derived from the native structure, and therefore they are fairly accurate. CCCD was able to build a helix/β-strand fairly accurately (Table I) for a dataset that contains random proteins with different lengths of secondary structures. We noticed that the length of the segment affects both the accuracy and time. It is expected that the segment cannot be too long in order for CCD to follow a trace. Among the three lengths tested, 12Å appears to be the best for 16 of the 17 cases of α-helices, β-strands, and loops tested. This segment length gives the best accuracy and run time among the three lengths tested. It is faster to build using this segment length than using shorter lengths. This is expected because longer fragments generally converge faster in CCD. A 12Å long segment corresponds to about eight amino acids or about two turns in an α-helix or about four amino acids for a β-strand or a loop. Using 12Å as the segment length, the RMSD of backbone atoms is between 0.47Å and 1.56Å for all the helix cases, most of which have RMSDs of about 1Å (Table I, rows 1–5). For the helix in 1OXJ (Figure 3A and row 5 of Table I), the model has 1.62Å in RMSD compared to the native helix when the segment length of 6Å was used. For a β-strand in 3CAU (Figure 3B and row 10 in Table I), the model constructed using CCCD has RMSD of 1.65Å when the segment length of 6Å was used. The accuracy of the constructed β-strand models is fairly good, with an RMSD between 0.61Å and 1.96Å, although it is slightly higher than that for a helix. The experiment was performed using a desktop Dell Dimension E520 machine with a 2.13 GHz Intel core (2) processor and 6 GB of memory. CCCD is an efficient method to build an individual helix, a β-strand, and a loop. It takes less than 50 ms to build a fragment for 15 of the 17 cases when fragment length of 12Å was used. We noticed that it generally took less time to build a helix or a β-strand than to build a loop.
Table I.
The performance of constrained CCD in building α-helices, β-strands, and loops.
| Index | IDa | Typeb | Sequencec | Lengthd | 6Åe | 9Åf | 12Åg | |||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSD | Time (ms) | RMSD | Time (ms) | RMSD | Time (ms) | |||||
| 1 | 2Y4Z | H | 89–96 | 8 | 0.87 | 15 | 0.93 | 14 | 0.63 | 1 |
| 2 | 1OZ9 | H | 50–61 | 12 | 0.93 | 4 | 0.69 | 4 | 0.86 | 2 |
| 3 | 4V68 | H | 37–58 | 22 | 1.95 | 31 | 1.67 | 24 | 1.56 | 24 |
| 4 | 2Y4Z | H | 108–134 | 27 | 0.53 | 10 | 0.53 | 11 | 0.47 | 19 |
| 5 | 1OXJ | H | 639–669 | 31 | 1.62 | 55 | 1.47 | 30 | 1.21 | 27 |
| 6 | 2Y4Z | S | 10–13 | 4 | 0.71 | 11 | 0.61 | 1 | 0.61 | <1 |
| 7 | 1OZ9 | S | 69–74 | 6 | 0.81 | 26 | 0.94 | 14 | 0.87 | 13 |
| 8 | 4V68 | S | 111–115 | 5 | 1.35 | 14 | 1.47 | 3 | 1.50 | 3 |
| 9 | 1ICX | S | 52–58 | 7 | 0.84 | 27 | 0.79 | 14 | 0.77 | 13 |
| 10 | 3CAU | S | 318–325 | 8 | 1.65 | 25 | 1.42 | 14 | 1.34 | 12 |
| 11 | 1ICX | S | 94–105 | 12 | 2.04 | 66 | 1.92 | 42 | 1.96 | 30 |
| 12 | 2Y4Z | L | 4–9 | 6 | 1.86 | 25 | 1.86 | 22 | 1.86 | 22 |
| 13 | 1A7D | L | 87–92 | 6 | 2.01 | 43 | 1.87 | 37 | 1.72 | 38 |
| 14 | 2RU9 | L | 13–21 | 9 | 2.47 | 30 | 2.29 | 6 | 2.01 | 2 |
| 15 | 4V68 | L | 101–110 | 10 | 2.08 | 150 | 2.08 | 108 | 1.95 | 135 |
| 16 | 2Y4Z | L | 97–107 | 11 | 3.23 | 70 | 2.03 | 34 | 2.19 | 18 |
| 17 | 4OXW | L | 57–73 | 17 | 5.42 | 440 | 3.9 | 362 | 3.7 | 108 |
The PDB ID of the protein.
The type of the secondary structure; H for helix, S for β-strand, and L for Loop/turn.
The amino acid index for the start and the end of the sequence segment.
The length of the secondary structure.
The backbone RMSD (Å) from the native, the time (millisecond) to build, the length of trace segment: 6Å.
The backbone RMSD (Å) from the native, time (millisecond) to build, the length of trace segment: 9Å.
The backbone RMSD (Å) from the native, the time (millisecond) to build, the length of trace segment:12Å.
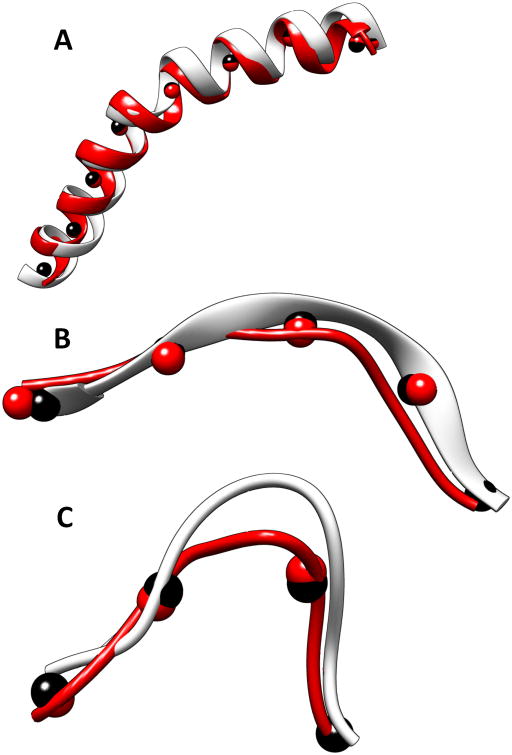
Figure 3. Backbone fragments constructed using CCCD.
Fragments built using CCCD for (A) a helix (639-669) in 1OXJ (PDB ID), (B) a β-strand (318-325) in 3ACU (PDB ID), and (C) a loop (13–21) in 3RU9 (PDB ID). The native structures are shown in silver and the constructed fragments are shown in red. Trace points (black spheres) derived from the true structure and the fragment points (red spheres) of the model are shown.
The trace derived directly from the structure of a helix/β-strand approximates an ideal trace for the helix/β-strand. In reality, the traces are to be detected from a 3D image. We generated 3D images to 10Å resolution using native structures and EMAN software.73 Given a structure in the Protein Data Bank (PDB), EMAN was used to produce an image using the position of atoms and to blur it to the resolution given. Note that in principle, it is challenging to simulate all errors that exist in an experimentally obtained cryo-EM image. The simulated images are used to test if the CCCD methodology works; additional tests using cryo-EM data are need. SkelEM43 was used to detect the skeleton in the image. The portion of the skeleton that corresponds to a loop was extracted and was used as the trace for building the loop. It is expected to be less accurate than the trace that is directly derived from a helix/β-strand, but it more realistic. In the test involving loops from length 6 to length 17, the constructed loops have between 1.72Å RMSD and 3.7Å RMSD from the native structure when the segment length of 12Å was used. The higher RMSD in the loop models, relative to that of a helix or a β-strand, may be due to less accurate traces of the loops or the fact that loop conformations have more freedom.
4.2 Backbone models of protein chains constructed using CCCD
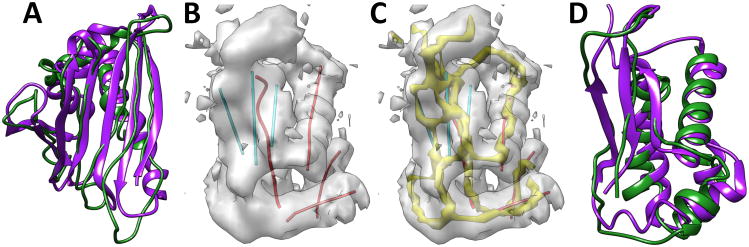
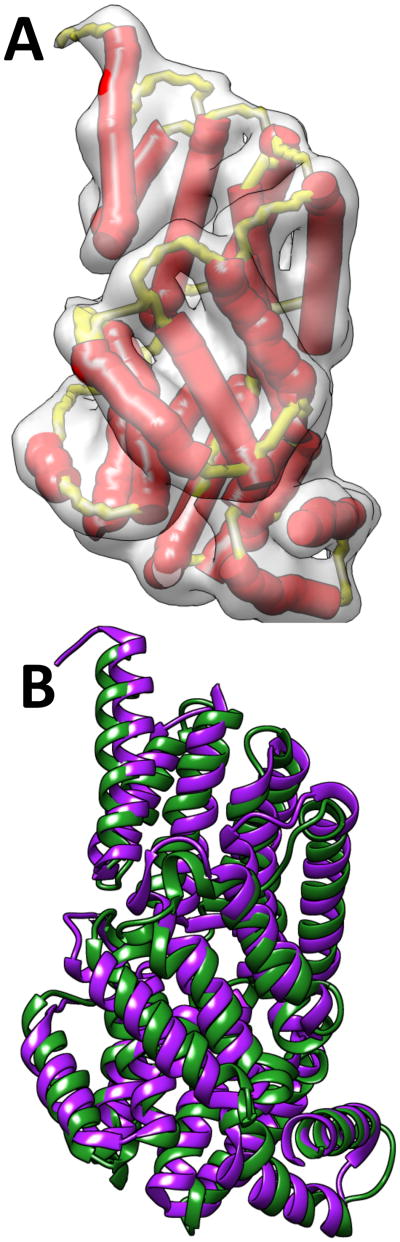
Building the model of an entire protein backbone is in principle the same as building individual fragments. However, a few additional problems must be dealt with. Although building an individual fragment is quite fast, collision checking has significant overhead when building an entire chain. Each possible conformation of the fragment has to be checked for collision. The skeleton trace derived from the 3D image may not be continuous. When there is a gap in the skeleton, the trace of a loop may not be accurate. The model built for 1ICX (green in Figure 4A and row 9 of Table II) has RMSD100 of 3.47Å from the native structure. In this case, there are seven helices in the PDB structure, three of which have at least six amino acids in the helix. The traces used for CCCD include the central line of the three longer helices and seven β-strands, as well as the skeleton derived from the 3D image for loops and short helices. The constructed backbone appears to follow the true backbone in most of the regions, but it differs in small helix regions and some loop regions. Note that β-strands were constructed individually according to the β-traces. In order to form a β-sheet, adjustment is needed in the future so that hydrogen bonds are formed between neighboring strands. Using a dataset of 10 proteins, the collision-free model of the entire chain has RMSD100 between 3.19Å and 4.8Å.
Figure 4. Backbone models constructed using CCCD.
The models (green) are superimposed with the corresponding PDB structure (purple) respectively for 1ICX in (A) and 4V68_BR in (D). (B) The 3D cryo-EM image (gray) extracted from 5030 (EMDB ID) for 4V68_BR (PDB ID) and the detected traces for α-helices (in red) and β-strands (in cyan). (C) The skeleton (yellow) of the 3D image is shown in addition to those shown in B.
Table II.
Backbone models constructed using true positions of secondary structure traces.
| Index | ID/EMDa | #AAb | HlxSeqc | StrSeqd | HlxMape | StrMapf | RMSDg |
|---|---|---|---|---|---|---|---|
| 1 | 1A7D | 118 | 6 | 0 | 4 | 0 | 4.80 |
| 2 | 1BZ4 | 144 | 5 | 0 | 5 | 0 | 4.30 |
| 3 | 4V68_BR/5030 | 117 | 4 | 3 | 4 | 3 | 4.04 |
| 4 | 1HZ4 | 373 | 21 | 0 | 19 | 0 | 3.19 |
| 5 | 3LTJ | 201 | 16 | 0 | 12 | 0 | 3.32 |
| 6 | 4OXW | 119 | 5 | 3 | 3 | 3 | 4.21 |
| 7 | 1YD0 | 96 | 5 | 4 | 3 | 3 | 4.01 |
| 8 | 1OZ9 | 150 | 5 | 5 | 5 | 4 | 3.61 |
| 9 | 1ICX | 155 | 6 | 7 | 3 | 7 | 3.47 |
| 10 | 2Y4Z | 140 | 6 | 2 | 6 | 2 | 4.10 |
| Average | 3.91 | ||||||
The protein ID of PDB/experimental image EMD ID.
The number of amino acids in the protein.
The number of helices in the native structure.
The number of strands in the native structure
The number of helices detected from the 3D image.
The number of strands detected from the 3D image.
The backbone RMSD100 (Å) of the constructed model with the native structure.
We performed an experiment to construct the backbone using an experimentally derived cryo-EM image EMD-5030 (EMDB ID) and its fitted structure 4V68_BR (PDB ID). The protein structure has four helices and one β-sheet that contains three β-strands. All four helices were detected using SSETracer (red lines in Figure 4B).55 The traces of the β-strands (cyan lines in Figure 4B) were extracted directly from the PDB structure because the β-sheet region detected using StrandTwister is smaller, and only two β-strands were detected when StrandTwister was used. The skeleton connection was derived using SkelEM. The skeleton detected from a cryo-EM image is often less accurate than that detected from a simulated image. Yet the model built has backbone RMSD100 of 4.04Å from the native structure (Figure 4 D and row 3 or Table II).
4.3 Full models constructed using CCCD and simulated annealing
We investigate the entire process of generating full models using the 3D image and amino acid sequence of the protein. The method of building the entire backbone proposed in Section 3.2 requires precise traces. In reality, there can be errors in the detection of the traces and in the prediction of secondary structures from the amino acid sequence. As a result, multiple slightly different positions of the secondary structures need to be sampled in the 3D image and in the 1D amino acid sequence. A critical step in building a model of a protein is to know the topology of the secondary structures. In Section 3.2, it is assumed that the true topology has already been identified. In reality, the true topology can often be ranked near the top of the list using DP-TOSS but not necessarily the top one. For example, the true topology for 1HZ4 (Figure 5) was ranked second using DP-TOSS (row 8 of Table III). There are 21 helices in the native structure, out of which 19 longer ones were detected using SSETracer. The detected helices are often located approximately where native helices are, yet they may be slightly shorter, longer, or shifted. Therefore, the α-traces in this test are generally not as accurate as those used in Section 3.3. The simulated annealing process uses CCCD to build 100 models for each of the top 100 topologies, and thus 10,000 full models were constructed for each protein. For each backbone constructed using CCCD, side chains were added. The full models were evaluated using the multi-well energy function.75 The best model with the true topology was ranked second for 1HZ4, with an RMSD100 of 3.87Å from the native structure. Of the eight cases tested, the average RMSD100 of the best model with the true topology is 3.76Å.
Figure 5. The full model built for the true topology of 1HZ4 (PDB ID).
(A) The α-traces (red sticks) and the skeleton (yellow) detected from the image are superimposed with the density image of the protein. (B) The superimposition of the native protein structure (green) and the model (purple). The full model includes both backbone and side chain atoms.
Table III.
Full models constructed using constrained CCD, FBCCD, and simulated annealing.
| Index | IDa | #AAb | #hlxc | #α-Trcd | Topology Ranke | Rankf | RMSD100g |
|---|---|---|---|---|---|---|---|
| 1 | 2PSR | 100 | 5 | 4 | 31 | 21 | 5.45 |
| 2 | 1A7D | 118 | 6 | 4 | 1 | 6 | 3.87 |
| 3 | 1NG6 | 148 | 9 | 7 | 2 | 33 | 3.63 |
| 4 | 2XB5 | 207 | 13 | 9 | 11 | 10 | 3.49 |
| 5 | 3ACW | 293 | 17 | 14 | 32 | 43 | 3.29 |
| 6 | 1Z1L | 345 | 23 | 14 | 11 | 114 | 3.51 |
| 7 | 3HJL | 329 | 20 | 20 | 1 | 37 | 2.99 |
| 8 | 1HZ4 | 373 | 21 | 19 | 2 | 2 | 3.87 |
| Average RMSD100 | 3.76 | ||||||
The PDB ID.
The number of amino acids in the protein.
The number of helices in the native structure.
The number of detected helices from the 3D image.
The rank of the true topology using DP-TOSS.
The highest rank of the model with the correct topology evaluated using the multi-well energy function.
The RMSD100 (Å) of backbone atoms for the best ranked model (with the true topology) based on potential energy.
Errors are inevitable in the detection of secondary structure traces and their connection skeleton from a medium-resolution image. We showed that CCCD produces a fairly accurate model if the traces are accurate. In principle, CCCD is limited to the accuracy of the traces and the skeleton, but it is less affected when it is combined with modeling methods to sample alternatives and to evaluate from an energy point of view. Our test using simulated annealing and CCCD suggests that the best practice is to develop a good sampling strategy and an evaluation method to select models.
5. Conclusion
Deriving atomic structures from medium-resolution 3D images produced using the cryo-EM technique is challenging, particularly when there are no suitable template structures are available. Many alternative models have to be constructed and they are evaluated based on energetic stability of the model and the fitting of the model in the image. This paper addressed the problem of effective construction of alternative models. One approach is to construct alternative models using the amino acid sequence information and fragment libraries. Another approach is to construct alternative models from the 3D image. CCCD combines both the sequence information and the 3D image information in the construction of alternative models. CCCD approach uses the traces extracted from the 3D image in the construction of alternative backbone models.
We describe CCCD, a simple and effective method that is inspired by a robotics algorithm. It does not require the process of extracting potential Cα atoms from the 3D image, a step that demands high-resolution images. Our approach only requires the extraction of the central line of a helix, a β-strand, or a loop at the secondary structure level. The idea is to sample backbone conformations fragment by fragment and to align them with the corresponding guiding traces. CCCD combines the effectiveness of CCD in sampling multiple conformations and the restrictive nature of the guiding traces derived from the image.
The results show that individual fragments of α-helices, β-strands, and loops can be built fairly accurately if the traces are fairly accurate. Chopping a trace into segments of 12Å appears to result in the best accuracy and run time among the three lengths tested. When using accurate secondary structure traces derived from the PDB structure and the skeleton derived from the simulated images, the backbones constructed using CCCD have an average of 3.9Å RMSD in a dataset of 10 cases. This result suggests that CCCD is an effective method to construct the initial backbone if traces are fairly accurate. We further tested the use of secondary structure traces and the skeleton directly detected from the simulated image. Although such detected traces often have errors, simulated annealing was successfully used to sample alternative positions, and an average of 3.76Å RMSD was achieved in a dataset including eight test cases of α-proteins. This result demonstrates the potential of CCCD in building the entire backbone of a protein. We also demonstrate that when the CCD robotics algorithm is applied to a guided trace, it becomes an effective method for modeling protein structures using cryo-EM images.
Acknowledgments
The work in this paper was partially supported by NSF DBI-1356621 (to JH), NSF RIA-1600919 (to KA), NIH R01-GM062968, and the FP3 fund of the Old Dominion University.
Footnotes
Authors' contributions: KA and JH developed the method. KA implemented the method and conducted the tests. KA and JH wrote the manuscript.
References
- 1.Canutescu AA, Dunbrack RL., Jr Cyclic coordinate descent: A robotics algorithm for protein loop closure. Protein Sci. 2003;12(5):963–972. doi: 10.1110/ps.0242703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang C, Bradley P, Baker D. Protein-protein docking with backbone flexibility. J Mol Biol. 2007;373(2):503–519. doi: 10.1016/j.jmb.2007.07.050. [DOI] [PubMed] [Google Scholar]
- 3.Mandell DJ, Coutsias EA, Kortemme T. Sub-angstrom accuracy in protein loop reconstruction by robotics-inspired conformational sampling. Nature Methods. 2009;6(8):551–552. doi: 10.1038/nmeth0809-551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nasr K, He J. Deriving Protein Backbone Using Traces Extracted from Density Maps at Medium Resolutions. In: Harrison R, Li Y, Măndoiu I, editors. Bioinformatics Research and Applications. Springer International Publishing; 2015. pp. 1–11. [Google Scholar]
- 5.Kavraki LE, Svestka P, Latombe JC, Overmars MH. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Tansactions on Robotics and Automation. 1996;12(4):566–580. [Google Scholar]
- 6.Biswas A, Ranjan D, Zubair M, He J. A Novel Computational Method for Deriving Protein Secondary Structure Topologies Using Cryo-EM Density Maps and Multiple Secondary Structure Predictions. In: Harrison R, Li Y, Măndoiu I, editors. Bioinformatics Research and Applications. Springer International Publishing; 2015. pp. 60–71. [Google Scholar]
- 7.Rusu M, Starosolski Z, Wahle M, Rigort A, Wriggers W. Automated tracing of filaments in 3D electron tomography reconstructions using Sculptor and Situs. Journal of structural biology. 2012;178(2):121–128. doi: 10.1016/j.jsb.2012.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Birmanns S, Rusu M, Wriggers W. Using Sculptor and Situs for simultaneous assembly of atomic components into low-resolution shapes. Journal of structural biology. 2011;173(3):428–435. doi: 10.1016/j.jsb.2010.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yakey JH, LaValle SM, Kavraki LE. Randomized path planning for linkages with closed kinematic chains. IEEE Transactions on Robotics and Automation. 2001;17(6):951–958. [Google Scholar]
- 10.Wedemeyer WJ, Scheraga HA. Exact analytical loop closure in proteins using polynomial equations. J Comput Chem. 1999;20:819–844. doi: 10.1002/(SICI)1096-987X(199906)20:8<819::AID-JCC8>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 11.Shehu A, Clementi C, Kavraki LE. Modeling protein conformational ensembles: From missing loops to equilibrium Fluctuations. Proteins: Structures, Functions, and Bioinformatics. 2006;65(1):164–179. doi: 10.1002/prot.21060. [DOI] [PubMed] [Google Scholar]
- 12.Coutsias EA, Seok C, Jacobson MP, Dill KA. A kinematic view of loop closure. J Comput Chem. 2004;25:510–528. doi: 10.1002/jcc.10416. [DOI] [PubMed] [Google Scholar]
- 13.Fine RM, Wang H, Shenkin PS, Yarmush DL, Levinthal C. Predicting antibody hypervariable loop conformations. II: Minimization and molecular dynamics studies of MCPC603 from many randomly generated loop conformations. Proteins. 1986;1(4):342–362. doi: 10.1002/prot.340010408. [DOI] [PubMed] [Google Scholar]
- 14.Shenkin PS, Yarmush DL, Fine RM, Wang HJ, Levinthal C. Predicting antibody hypervariable loop conformation. 1. ensembles of random conformations for ring-like structure. Biopolymers. 1987;26:2053–2085. doi: 10.1002/bip.360261207. [DOI] [PubMed] [Google Scholar]
- 15.Wang LT, Chen CC. A combined optimization method for solving the inverse kinematics problem of mechanical manipulators. IEEE Trans Robot Autom. 1991;7:489–499. [Google Scholar]
- 16.Ring CS, Kneller DG, Langridge R, Cohen FE. Taxonomy and conformational analysis of loops in proteins. J Mol Biol. 1992;224:685–699. doi: 10.1016/0022-2836(92)90553-v. [DOI] [PubMed] [Google Scholar]
- 17.Si D, He J. Proceedings of the 5th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics. ACM; Newport Beach, California: 2014. Orientations of beta-strand traces and near maximum twist; pp. 690–694. [Google Scholar]
- 18.Ludtke CD, S J, Song JL, Chuang DT, Chiu W. Seeing GroEL at 6 A resolution by single particle electron cryomicroscopy. Structure. 2004;12(7):1129–1136. doi: 10.1016/j.str.2004.05.006. [DOI] [PubMed] [Google Scholar]
- 19.Chiu W, Schmid MF. Pushing back the limits of electron cryomicroscopy. Nature Struct Biol. 1997;4:331–333. doi: 10.1038/nsb0597-331. [DOI] [PubMed] [Google Scholar]
- 20.Chiu W, Baker ML, Jiang W, Zhou ZH. Deriving folds of macromolecular complexes through electron cryomicroscopy and bioinformatics approaches. Curr Opin Struct Biol. 2002;12(2):263–269. doi: 10.1016/s0959-440x(02)00319-6. [DOI] [PubMed] [Google Scholar]
- 21.Zhou ZH, Dougherty M, Jakana J, He J, Rixon FJ, Chiu W. Seeing the herpesvirus capsid at 8.5 A. Science. 2000;288(5467):877–880. doi: 10.1126/science.288.5467.877. [DOI] [PubMed] [Google Scholar]
- 22.Lasker K, Topf M, Sali A, Wolfson HJ. Inferential Optimization for Simultaneous Fitting of Multiple Components into a CryoEM Map of Their Assembly. Journal of Molecular Biology. 2009;388(1):180–194. doi: 10.1016/j.jmb.2009.02.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cheng L, Sun J, Zhang K, Mou Z, Huang X, Ji G, Sun F, Zhang J, Zhu P. Atomic model of a cypovirus built from cryo-EM structure provides insight into the mechanism of mRNA capping. Proceedings of the National Academy of Sciences. 2011;108(4):1373–1378. doi: 10.1073/pnas.1014995108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Biswas A, Ranjan D, Zubair M, He J. A Dynamic Programming Algorithm for Finding the Optimal Placement of a Secondary Structure Topology in Cryo-EM Data. Journal of Computational Biology. 2015;22(9):837–843. doi: 10.1089/cmb.2015.0120. [DOI] [PubMed] [Google Scholar]
- 25.Nasr KA, He J. Proceedings of the 5th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics. ACM; Newport Beach, California: 2014. Construction of protein backbone pieces using segment-based FBCCD and Cryo-EM skeleton; pp. 711–716. [Google Scholar]
- 26.Al Nasr K, Chen L, Si D, Ranjan D, Zubair M, He J. Proceedings of the ACM Conference on Bioinformatics, Computational Biology and Biomedicine. ACM; Orlando, Florida: 2012. Building the initial chain of the proteins through de novo modeling of the cryo-electron microscopy volume data at the medium resolutions; pp. 490–497. [Google Scholar]
- 27.Lawson CL, Baker ML, Best C, Bi C, Dougherty M, Feng P, van Ginkel G, Devkota B, Lagerstedt I, Ludtke SJ, Newman RH, Oldfield TJ, Rees I, Sahni G, Sala R, Velankar S, Warren J, Westbrook JD, Henrick K, Kleywegt GJ, Berman HM, Chiu W. EMDataBank.org: unified data resource for CryoEM. Nucleic acids research. 2011;39(suppl 1):D456–464. doi: 10.1093/nar/gkq880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Al Nasr K, He J. Deriving Protein Backbone Using Traces Extracted from Density Maps at Medium Resolutions. Lect N Bioinformat. 2015;9096:1–11. [Google Scholar]
- 29.Topf M, Lasker K, Webb B, Wolfson H, Chiu W, Sali A. Protein structure fitting and refinement guided by cryo-EM density. Structure. 2008;16(2):295–307. doi: 10.1016/j.str.2007.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tama F, Miyashita O, Brooks CL. Normal mode based flexible fitting of high-resolution structure into low-resolution experimental data from cryo-EM. Journal of Structural Biology. 2004;147(3):315–326. doi: 10.1016/j.jsb.2004.03.002. [DOI] [PubMed] [Google Scholar]
- 31.Pandurangan AP, Topf M. Finding rigid bodies in protein structures: Application to flexible fitting into cryoEM maps. Journal of structural biology. 2012;177(2):520–531. doi: 10.1016/j.jsb.2011.10.011. [DOI] [PubMed] [Google Scholar]
- 32.Suhre K, Navazab J, Sanejouand YH. NORMA: a tool for flexible fitting of high-resolution protein structures into low-resolution electron-microscopy-derived density maps. Acta crystallographica Section D, Biological crystallography. 2006;62(Pt 9):1098–1100. doi: 10.1107/S090744490602244X. [DOI] [PubMed] [Google Scholar]
- 33.Velazquez-Muriel JA, Carazo JM. Flexible fitting in 3D-EM with incomplete data on superfamily variability. Journal of structural biology. 2007;158(2):165–181. doi: 10.1016/j.jsb.2006.10.014. [DOI] [PubMed] [Google Scholar]
- 34.Wriggers W, He J. Numerical geometry of map and model assessment. Journal of structural biology. 2015;192(2):255–261. doi: 10.1016/j.jsb.2015.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wriggers W, Birmanns S. Using situs for flexible and rigid-body fitting of multiresolution single-molecule data. Journal of Structural Biology. 2001;133(2-3):193–202. doi: 10.1006/jsbi.2000.4350. [DOI] [PubMed] [Google Scholar]
- 36.Wriggers W. Using Situs for the integration of multi-resolution structures. Biophysical Reviews. 2010;2(1):21–27. doi: 10.1007/s12551-009-0026-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Topf M, Baker ML, Marti-Renom MA, Chiu W, Sali A. Refinement of protein structures by iterative comparative modeling and CryoEM density fitting. J Mol Biol. 2006;357(5):1655–1668. doi: 10.1016/j.jmb.2006.01.062. [DOI] [PubMed] [Google Scholar]
- 38.Baker ML, Ju T, Chiu W. Identification of secondary structure elements in intermediate-resolution density maps. Structure. 2007;15(1):7–19. doi: 10.1016/j.str.2006.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Si D, He J. Tracing Beta Strands Using StrandTwister from Cryo-EM Density Maps at Medium Resolutions. Structure. 2014;22(11):1665–1676. doi: 10.1016/j.str.2014.08.017. [DOI] [PubMed] [Google Scholar]
- 40.Biswas A, Ranjan D, Zubair M, Zeil S, Nasr KA, He J. An Effective Computational Method Incorporating Multiple Secondary Structure Predictions in Topology Determination for Cryo-EM Images. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2016;14(3):578–586. doi: 10.1109/TCBB.2016.2543721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Baker ML, Abeysinghe SS, Schuh S, Coleman RA, Abrams A, Marsh MP, Hryc CF, Ruths T, Chiu W, Ju T. Modeling protein structure at near atomic resolutions with Gorgon. Journal of structural biology. 2011;174(2):360–373. doi: 10.1016/j.jsb.2011.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Al Nasr K, Ranjan D, Zubair M, He J. Ranking valid topologies of the secondary structure elements using a constraint graph. J Bioinform Comput Biol. 2011;9(3):415–430. doi: 10.1142/s0219720011005604. [DOI] [PubMed] [Google Scholar]
- 43.Al Nasr K, Ranjan D, Zubair M, Chen L, He J. Solving the Secondary Structure Matching Problem in Cryo-EM De Novo Modeling Using a Constrained K-Shortest Path Graph Algorithm. Computational Biology and Bioinformatics, IEEE/ACM Transactions on. 2014;11(2):419–430. doi: 10.1109/TCBB.2014.2302803. [DOI] [PubMed] [Google Scholar]
- 44.Ju T, Baker ML, Chiu W. Computing a family of skeletons of volumetric models for shape description. Computer-Aided Design. 2007;39(5):352–360. doi: 10.1016/j.cad.2007.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Al Nasr K, He J. Constrained cyclic coordinate descent for cryo-EM images at medium resolutions: beyond the protein loop closure problem. Robotica. 2016;34(08):1777–1790. doi: 10.1017/s0263574716000242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Biswas A, Ranjan D, Zubair M, He J. A Dynamic Programming Algorithm for Finding the Optimal Placement of a Secondary Structure Topology in Cryo-EM Data. Journal of Computational Biology. 2015 doi: 10.1089/cmb.2015.0120. [DOI] [PubMed] [Google Scholar]
- 47.Biswas A, Ranjan D, Zubair M, He J. A Novel Computational Method for Deriving Protein Secondary Structure Topologies Using Cryo-EM Density Maps and Multiple Secondary Structure Predictions. LNCS, Bioinformatics Research and Applications. 2015;9096:60–71. [Google Scholar]
- 48.Al Nasr K, Chen L, Si D, Ranjan D, Zubair M, He J. Proceedings of the ACM Conference on Bioinformatics, Computational Biology and Biomedicine, Orlando, Florida. 2012. Building the initial chain of the proteins through de novo modeling of the cryo-electron microscopy volume data at the medium resolutions; pp. 490–497. [Google Scholar]
- 49.Jiang W, Baker ML, Ludtke SJ, Chiu W. Bridging the information gap: computational tools for intermediate resolution structure interpretation. J Mol Biol. 2001;308(5):1033–1044. doi: 10.1006/jmbi.2001.4633. [DOI] [PubMed] [Google Scholar]
- 50.Anger AM, Armache JP, Berninghausen O, Habeck M, Subklewe M, Wilson DN, Beckmann R. Structures of the human and Drosophila 80S ribosome. Nature. 2013;497(7447):80–85. doi: 10.1038/nature12104. [DOI] [PubMed] [Google Scholar]
- 51.Rusu M, Wriggers W. Evolutionary bidirectional expansion for the tracing of alpha helices in cryo-electron microscopy reconstructions. Journal of Structural Biology. 2012;177(2):410–419. doi: 10.1016/j.jsb.2011.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kong Y, Ma J. A structural-informatics approach for mining beta-sheets: locating sheets in intermediate-resolution density maps. J Mol Biol. 2003;332(2):399–413. doi: 10.1016/s0022-2836(03)00859-3. [DOI] [PubMed] [Google Scholar]
- 53.Kong Y, Zhang X, Baker TS, Ma J. A Structural-informatics approach for tracing beta-sheets: building pseudo-C(alpha) traces for beta-strands in intermediate-resolution density maps. J Mol Biol. 2004;339(1):117–130. doi: 10.1016/j.jmb.2004.03.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zhang X, Ge P, Yu X, Brannan JM, Bi G, Zhang Q, Schein S, Zhou ZH. Cryo-EM structure of the mature dengue virus at 3.5-A resolution. Nature structural & molecular biology. 2013;20(1):105–110. doi: 10.1038/nsmb.2463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Si D, He J. Beta-sheet Detection and Representation from Medium Resolution Cryo-EM Density Maps. BCB'13: Proceedings of ACM Conference on Bioinformatics, Computational Biology and Biomedical Informatics; Washington, D.C.. September 22-25; 2013. [Google Scholar]
- 56.Chothia C. Conformation of twisted beta-pleated sheets in proteins. J Mol Biol. 1973;75(2):295–302. doi: 10.1016/0022-2836(73)90022-3. [DOI] [PubMed] [Google Scholar]
- 57.Al Nasr K, Liu C, Rwebangira M, Burge L, He J. Intensity-Based Skeletonization of CryoEM Gray-Scale Images Using a True Segmentation-Free Algorithm. IEEE/ACM Trans Comput Biol Bioinformatics. 2013;10(5):1289–1298. doi: 10.1109/TCBB.2013.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Cuff JA, Clamp ME, Siddiqui AS, Finlay M, Barton GJ. JPred: a consensus secondary structure prediction server. Bioinformatics. 1998;14(10):892–893. doi: 10.1093/bioinformatics/14.10.892. [DOI] [PubMed] [Google Scholar]
- 59.Pollastri G, McLysaght A. Porter: a new, accurate server for protein secondary structure prediction. Bioinformatics. 2005;21(8):1719–1720. doi: 10.1093/bioinformatics/bti203. [DOI] [PubMed] [Google Scholar]
- 60.Jones DT. Protein secondary structure prediction based on position-specific scoring matrices. J Mol Biol. 1999;292(2):195–202. doi: 10.1006/jmbi.1999.3091. [DOI] [PubMed] [Google Scholar]
- 61.Abeysinghe S, Ju T, Baker ML, Chiu W. Shape modeling and matching in identifying 3D protein structures. Computer-Aided Design. 2008;40(6):708–720. [Google Scholar]
- 62.Ginalski K. Comparative modeling for protein structure prediction. Current Opinion in Structural Biology. 2006;16(2):172–177. doi: 10.1016/j.sbi.2006.02.003. [DOI] [PubMed] [Google Scholar]
- 63.Fiser A, Šali A. Modeller: generation and refinement of homology-based protein structure models. Methods in Enzymology. 2003;374:461–491. doi: 10.1016/S0076-6879(03)74020-8. [DOI] [PubMed] [Google Scholar]
- 64.Simons KT, Kooperberg C, Huang E, Baker D. Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and Bayesian scoring functions. J Mol Biol. 1997;268(1):209–225. doi: 10.1006/jmbi.1997.0959. [DOI] [PubMed] [Google Scholar]
- 65.Rohl CA, Strauss CE, Misura KM, Baker D. Protein structure prediction using Rosetta. Methods in enzymology. 2004;383:66–93. doi: 10.1016/S0076-6879(04)83004-0. [DOI] [PubMed] [Google Scholar]
- 66.Deming WE. The statistical procedure in the SENIC Project. American journal of epidemiology. 1980;111(5):470–471. doi: 10.1093/oxfordjournals.aje.a112927. [DOI] [PubMed] [Google Scholar]
- 67.Lindert S, Staritzbichler R, Wötzel N, Karakas M, Stewart PL, Meiler J. EM-fold: De novo folding of alpha-helical proteins guided by intermediate-resolution electron microscopy density maps. Structure. 2009;17(7):990–1003. doi: 10.1016/j.str.2009.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Duckham M, Kulik L, Worboys M, Galton A. Efficient generation of simple polygons for characterizing the shape of a set of points in the plane. Pattern Recogn. 2008;41(10):3224–3236. [Google Scholar]
- 69.Lotan I, van den Bedem H, Deacon AM, Latombe JC. Computing Protein Structures form Electron Density Maps: The Missing Fragment Problem Algorithmic Foundations of Robotics VI. Springer Tracts in Advanced Robotics. 2005;17:345–360. [Google Scholar]
- 70.Lu Y, He J, Strauss CE. Deriving topology and sequence alignment for the helix skeleton in low-resolution protein density maps. Journal of bioinformatics and computational biology. 2008;6(1):183–201. doi: 10.1142/s0219720008003357. [DOI] [PubMed] [Google Scholar]
- 71.Al Nasr K, He J. An effective convergence independent loop closure method using Forward-Backward Cyclic Coordinate Descent. International Journal of Data Mining and Bioinformatics. 2009;3(3):346–361. doi: 10.1504/ijdmb.2009.026712. [DOI] [PubMed] [Google Scholar]
- 72.Nasr KA, He J. Deriving Protein Backbone Using Traces Extracted from Density Maps at Medium Resolutions. 2015:1–11. [Google Scholar]
- 73.Ludtke SJ, Baldwin PR, Chiu W. EMAN: Semi-automated software for high resolution single particle reconstructions. Journal of Structural Biology. 1999;128(1):82–97. doi: 10.1006/jsbi.1999.4174. [DOI] [PubMed] [Google Scholar]
- 74.Xie W, Sahinidis NV. Residue-rotamer-reduction algorithm for the protein side-chain conformation problem. Bioinformatics. 2006;22(2):p188–194. doi: 10.1093/bioinformatics/bti763. [DOI] [PubMed] [Google Scholar]
- 75.Sun W, He J. Native secondary structure topology has near minimum contact energy among all possible geometrically constrained topologies. Proteins. 2009;77(1):159–173. doi: 10.1002/prot.22427. [DOI] [PubMed] [Google Scholar]
- 76.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera—A visualization system for exploratory research and analysis. Journal of Computational Chemistry. 2004;25(13):1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]