A multi‐model approach to predict efficacious clinical dose for an anti‐TGF‐β antibody (GC2008) in the treatment of osteogenesis imperfecta

Abstract

Osteogenesis imperfecta (OI) is a heterogeneous group of inherited bone dysplasias characterized by reduced skeletal mass and bone fragility. Although the primary manifestation of the disease involves the skeleton, OI is a generalized connective tissue disorder that requires a multidisciplinary treatment approach. Recent studies indicate that application of a transforming growth factor beta (TGF‐β) neutralizing antibody increased bone volume fraction (BVF) and strength in an OI mouse model and improved bone mineral density (BMD) in a small cohort of patients with OI. In this work, we have developed a multitiered quantitative pharmacology approach to predict human efficacious dose of a new anti‐TGF‐β antibody drug candidate (GC2008). This method aims to translate GC2008 pharmacokinetic/pharmacodynamic (PK/PD) relationship in patients, using a number of appropriate mathematical models and available preclinical and clinical data. Compartmental PK linked with an indirect PD effect model was used to characterize both pre‐clinical and clinical PK/PD data and predict a GC2008 dose that would significantly increase BMD or BVF in patients with OI. Furthermore, a physiologically‐based pharmacokinetic model incorporating GC2008 and the body's physiological properties was developed and used to predict a GC2008 dose that would decrease the TGF‐β level in bone to that of healthy individuals. By using multiple models, we aim to reveal information for different aspects of OI disease that will ultimately lead to a more informed dose projection of GC2008 in humans. The different modeling efforts predicted a similar range of pharmacologically relevant doses in patients with OI providing an informed approach for an early clinical dose setting.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Efficacious human dose prediction is a complex process as compound's biopharmaceutical, pharmacokinetic (PK), and pharmacodynamic (PD) properties informed from preclinical species must be projected to humans. The current knowledge gap was translating pharmacology for patients with osteogenesis imperfecta (OI) because there is not current TGF‐β directed treatment.

WHAT QUESTION DID THIS STUDY ADDRESS?

Evaluation of efficacious dose for a new anti‐TGF‐β antibody drug candidate (GC2008), for the treatment of OI.

WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

In this study, we propose the use of a multi‐model approach to inform on projected human doses. The tiered modeling approach shown in this work is based on preclinical and sparse clinical PK/PD data in which targeting TGF‐β was investigated for the treatment of OI.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

Use of a tiered multi‐model approach incorporating mathematical models that evaluate different aspects of disease, can be sued to build confidence in translation projected pharmacology for the treatment of OI.

INTRODUCTION

Osteogenesis imperfecta (OI), also known as brittle bone disease, is a connective tissue disorder characterized by increased bone fragility, low bone mass, and other skeletal abnormalities. ¹ , ² It is a genetically and clinically heterogeneous bone disease with a prevalence of 1 in 10,000 to 1 in 20,000. ² , ³ OI is considered a collagen‐related disorder with about 85%–90% of cases caused by mutations of collagen type I genes (COL1A1 or COL1A2), ⁴ , ⁵ yet it is unknown how these genetic disorders ultimately lead to abnormal bone quantity and quality. Recent studies in OI mice suggest that increased concentrations of transforming growth factor‐beta (TGF‐β) in bones may be a causative factor leading to an impairment in the bone remodeling process, and that restoring levels to their homeostatic value enables improvements in bone strength and volume. ⁶

Bone remodeling is a fundamental process coordinated by a team of bone cells known as basic multicellular units, by which skeleton tissue is renewed to maintain the integrity of bone, and support its role in mineral homeostasis. ⁷ There are five steps in the bone remodeling process, namely activation, resorption, reversal, formation, and termination, that primarily regulate the osteoclast mediated digestion of old bone, and osteoblast mediated lay down of new bone. ⁸ TGF‐β signaling plays a key role in the temporal and spatial regulation of bone remodeling by recruiting mesenchymal stem cells to the bone resorptive sites to undergo osteoblastic differentiation and form new bone. ⁹ The importance of TGF‐β regulation in bone homeostasis and the necessity to be dynamically regulated in the different bone remodeling phases has been shown in multiple genetic models. ¹⁰ , ¹¹ , ¹² In addition, blockade of TGF‐β signaling in vivo by 1D11, a murine pan TGF‐β monoclonal antibody, has been shown to exert significant effects on bone development in mice. ¹³ , ¹⁴ The work of Yang et al. ¹⁵ further showed that in vivo administration of 1D11 improved the low bone mass of severely osteopenic mice. Interestingly, Grafe et al. ⁶ showed that excessive TGF‐ β signaling occurs in OI and treatment with 1D11 corrects the bone phenotype and improves the lung abnormalities in OI mice. In humans, Fresolimumab (GC1008), a human anti‐TGF‐β antibody with similar affinity and epitope binding as 1D11, has been tested in a small number of patients and initial results indicated a potential disease‐specific therapy with dose‐dependent effects on bone mineral density (BMD), ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ which is an accepted clinical end point in numerous clinical studies to date (https://clinicaltrials.gov/ct2/show/NCT03064074, https://clinicaltrials.gov/ct2/show/NCT00063479, https://clinicaltrials.gov/ct2/show/NCT05125809, and https://clinicaltrials.gov/ct2/show/NCT03638128).

In this work, we used available pharmacokinetic/pharmacodynamic (PK/PD) information from preclinical and clinical studies of anti‐TGF‐β antibodies 1D11 and GC1008, to predict pharmacologically relevant doses of a second generation human anti‐TGF‐β GC2008, for patients with OI. PK/PD and physiologically‐based pharmacokinetic (PBPK) modeling was used to characterize the concentration response relationship of 1D11, GC1008, GC2008, and its impact on BMD, bone volume fraction (BVF = bone volume/total volume [BV/TV]), and TGF‐β levels in patients with OI. Using a multi‐model approach that is based upon multiple preclinical and clinical data of anti‐TGF‐β antibodies that share similar affinity to TGF‐β, we aim to build confidence on our model‐based efficacious dose prediction for the treatment of OI considering different disease outcomes.

MATERIALS AND METHODS

In this work, nonclinical PK/PD modeling was conducted using 1D11, whereas clinical modeling using Fresolimumab (GC1008), or GC2008 that was used during first‐in‐human studies. Detailed description of the preclinical and clinical PK/PD data used in this work were published previously and are briefly discussed here. ⁶ , ¹⁶ , ¹⁷ , ¹⁹ , ²⁰ , ²¹ Summaries of the available PK/PD data used in our multi‐model approach are shown in Table 1. GC2008 is a second generation human anti‐TGF‐β, differing only by a single amino acid substitution in the heavy chain (S228P) of GC1008. Therefore, GC2008 and Fresolimumab (GC1008) have identical complementarity determining region amino acid sequences. The 1D11, Fresolimumab (GC1008), and GC2008 retain the same affinity for TGF‐β and would expect to have the same mode of action.

TABLE 1.

Anti‐TGF‐β antibodies’ preclinical and clinical PK/PD studies, and corresponding data used for the presented multi‐model approach

Molecule name	Species/patients	Study/available data	Dosing scheme – doses	Source
1D11	OI mice	PK	Single dose i.p. – 5 mg/kg	Figure S2
		PD/BVF	Dose i.p. three times weekly – 0.3, 1, 5 mg/kg Dose i.p. administered three times weekly, one time weekly, one time every 2 weeks, one time every 4 weeks – 5 mg/kg	[20]
Fresolimumab (GC1008)	Adult patients with cancer	PK	I.V. infusion – 0.3, 1, 2, 4 mg/kg	[16]
	Adults with OI	PD/BMD	I.V. infusion – 1, 4 mg/kg	[19]
GC2008	Adult patients with cancer	PK	30 min i.v. infusion once every 2 weeks – 0.05, 0.25, 1, 3, 10, 15 mg/kg	https://clinicaltrials.gov/ct2/show/NCT03192345

Abbreviations: BMD, bone mineral density; BVF, bone volume fraction; OI, osteogenesis imperfecta; PD, pharmacodynamic; PK, pharmacokinetic.

1D11 PK study in OI mouse model

A single dose of 5 mg/kg 1D11 was administered i.p. in the G610C OI mice (six female and six male mice, 8 weeks old) and blood was collected at 4, 48, 168, 360, 528, and 1032 h postdose. All samples were processed for serum, placed on dry ice, and transferred to less than or equal to −60°C prior to analysis.

The circulating drug levels in serum were determined using an enzyme‐linked immunosorbent assay‐based bioanalytical method. Briefly, G610C mouse serum samples containing 1D11 were diluted in the buffer (phosphate‐buffered saline, 0.05% Tween‐20, 0.05% Triton X‐100, 0.01% bovine serum albumin) at a 10,000‐fold dilution except those from the last timepoint (1032 h) which was diluted 1000‐fold. The 96‐well plate was coated with TGF‐β2 and mouse serum samples applied to the plate to capture 1D11. A detection antibody of goat anti‐mouse horseradish peroxidase conjugate (A0168/095M4759V; Sigma) was applied, and the optical density was read at 450 nm and 570 nm in Spectramax plus (Molecular Devices). A standard curve was generated and serum 1D11 concentrations were obtained. The low limit of detection of the assay was 1.0 μg/ml. The PK response of 1D11 is shown in Figure S2.

In vivo pharmacology study with 1D11 in OI mice

Animals were provided ad libitum access to food (Auto KF 5 K 52; Lab Diet) and water and gang‐housed in pathogen‐free, climate‐controlled facilities with 12‐h light/dark cycles. Male and female G610C OI (Stock no. 007248; Jackson Labs, hereafter referred to as OI mouse) mice were administered 1D11 i.p. at 0.3, 1, or 5 mg/kg at a dosing frequency of TIW over an 8‐week period (n = 4–8 males and 5–8 females per group). The PD effect of 1D11 measured was BVF and maximum force to failure and was assessed across various doses. A dose‐frequency study at a dose of 5 mg/kg of 1D11, administered i.p. three times weekly, one time weekly, one time every 2 weeks, or one time every 4 weeks, for a total of 12 weeks was evaluated (n = 5–8 for both uCT and biomechanics). ²⁰

Exposure of Fresolimumab (GC1008) in humans and PK evaluation

The PK of Fresolimumab (GC1008), was evaluated during an open label, dose ranging, first‐in‐human study conducted in patients with biopsy confirmed, treatment resistant, primary focal segmental glomerulosclerosis (FSGS). Sixteen patients received one of four single‐dose levels of Fresolimumab (GC1008; 0.3, 1, 2, and 4 mg/kg) and were followed for 112 days, with rich sampling PK. The mean age of the patients was 37 ± 12 years, mean FSGS duration was 3.0 ± 2.1 years, half were men, 13 were White, and three were Black. ¹⁶ Serum PK of Fresolimumab (GC1008) was best described by a two‐compartment model with linear clearance. ¹⁶ Patient weight was the only significant covariate identified as being predictive of PK variability. The estimated half‐life was 14 days and did not change with dose. The PK model parameters are shown in Table S1.

Fresolimumab (GC1008) phase 1 study in patients with OI

A phase I study with a single administration of Fresolimumab (GC1008) was conducted in eight adults with OI. The study involved a single infusion of Fresolimumab (GC1008; 1 mg/kg body weight and 4 mg/kg body weight; n = 4 in each dose‐cohort). The study's primary outcome was the safety of Fresolimumab (GC1008) after a single administration, whereas the effects of Fresolimumab (GC1008) on bone remodeling biomarkers and lumbar spine areal bone mineral density (LS aBMD) were also obtained and analyzed as secondary outcomes over a 6‐month time period. ¹⁹

Phase I study of GC2008 and PK evaluation

The PK of GC2008 was evaluated during an open label, dose escalation, and expansion first‐in‐human study (NCT03192345), in patients with cancer treated with GC2008 alone (part A) or treated with GC2008 in combination with cemiplimab (part B). A total of 52 patients received GC2008 30‐min i.v. infusions, from 0.05 up to 15 mg/kg every 2 weeks (Q2W) or at 22.5 mg/kg every 3 weeks (Q3W). ²¹ The PK of GC2008 was similar to Fresolimumab (GC1008) and was described by a two‐compartment model with linear clearance (Figure S1). The PK parameters are shown in Table S2.

Development of a multi‐model approach to evaluate efficacious dose of GC2008

The tiered modeling approach followed in this work is shown in Figure 1.

FIGURE 1.

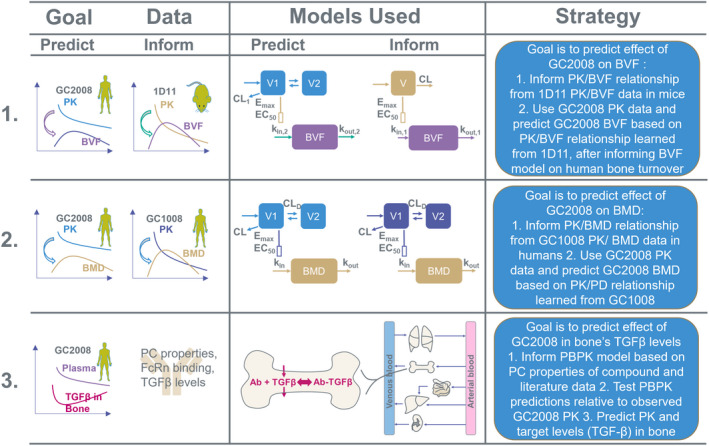
Schematic of the multi‐model strategy followed to predict efficacious human dose of the anti‐TGF‐β antibody (GC2008) for the treatment of OI. In the first modeling approach the goal was to predict efficacious dose based on the effect of GC2008 on bone volume fraction (BVF = bone volume/total volume BV/TV). In this, a PK/PD (BVF) relationship was established from 1D11 PK/BVF data in mice. To predict the response for GC2008 in humans, the PK component of the model was replaced to represent GC2008 PK, and the PD parameters governing the half‐life were replaced to represent human bone turnover rate. The model was then used to predict the dose of GC2008 that will lead to a 5% increase in BVF. In the second modeling approach, the goal was to predict the efficacious dose based on the effect of GC2008 on BMD. In this, a PK/PD (BMD) relationship was established from Fresolimumab (GC1008) PK/BMD data. Next, PK data from GC2008 was used along with the Fresolimumab (GC1008) PD‐related parameters to provide a dose that results in a 5% increase in BMD. In the third modeling approach a PBPK model was informed based on drug's physicochemical (PC) properties, TGF‐β levels, and human physiology. After checking the validity of PBPK model's predictions by comparing with GC2008 PK data, the PBPK model was used to evaluate the dose that will decrease OI‐related TGF‐β levels back to their homeostatic concentration. BMD, bone mineral density; CL, clearance; EC₅₀, half‐maximal effective concentration; E _max, maximum effect; OI, osteogenesis imperfecta; PBPK, physiologically‐based pharmacokinetic; PD, pharmacodynamic; PK, pharmacokinetic.

Development of a PK/PD model to describe GC2008 effect on BVF in humans

The first modeling approach aims to predict the effect of GC2008 on BVF. Toward this goal, a PK/BVF relationship was initially established for 1D11 in mice based on available PK/BVF data. The 1D11 PK was described by a one‐compartment model (Figure S2, Table S3) and the dynamics of BVF by a type III indirect response model where 1D11 concentration stimulates the input rate of BVF (Figure 1). The k _in/k _out were set according to bone turnover, and BVF baseline in mice. The maximum effect/half‐maximal effective concentration (E _max/EC₅₀) were optimized based on the available BVF data. To translate the PK/PD relationship to humans, GC2008 population PK (PopPK) model was used (Figure S1), and the mouse bone turnover rate (~3 weeks) was replaced by the human bone turnover rate (~3 months), whereas the PD related parameters E _max and EC₅₀, were kept constant. The model was then used to predict GC2008 dose/response (BVF) relationship and evaluate the dose that will ultimately lead to a 5% increase in BVF. PK/PD modeling for 1D11 and its forward translation to humans was performed in Matlab R2019a using ode45 solver for ordinary differential equations.

Development of a PK/PD model to describe GC2008 effect on BMD in humans

In the second modeling approach, a PK/PD model was initially developed to evaluate the PK/BMD relationship of Fresolimumab (GC1008) using the PopPK model of Fresolimumab (GC1008) fitted to the according Fresolimumab (GC1008) PK data and performed in earlier studies. ¹⁶ The BMD dynamics were described by a type III indirect response model that simulates a PK‐related increase in BMD through induction of the input rate of the effect compartment. ²² Due to the low number of BMD data (4 subjects), their sparsity, and their high variability, the E _max/EC₅₀ parameters of the PD model were optimized according to the average BMD value for each timepoint, whereas k _in/k _out were set based on bone turnover, and BMD baseline in humans. After informing the PD‐related parameters with the available BMD data, ¹⁹ Fresolimumab (GC1008) PK was replaced by the two‐compartment PK model of GC2008 (Figure S1) and based on the PK/PD relationship informed by Fresolimumab (GC1008), the model was used to provide predictions for the GC2008 dose/response (BMD) relationship and ultimately evaluate the dose that will result in a 5% increase in BMD. Population PK analysis of Fresolimumab (GC1008) and GC2008 was performed using NONMEM and Monolix, respectively. ²³ PK/PD modeling was performed in Matlab R2019a using ode45 solver for ordinary differential equations.

Development of a PBPK model to describe GC2008 effect on TGF‐β levels in human bone

Last, a PBPK modeling approach was used to evaluate GC2008 PK in bone, and the corresponding TGF‐β response in humans. Given their significance in model‐based drug development, there are several commercial platforms that integrate physiologically based methodologies, such as Simcyp (https://www.certara.com/software/simcyp‐pbpk/), GastroPlus (https://www.simulations‐plus.com/software/gastroplus/), SimBiology (https://www.mathworks.com/products/simbiology.html), and PK‐Sim (http://www.open‐systems‐pharmacology.org/). In this work, we used the PK‐Sim platform due to its relative ease of incorporating target binding in the tissue of interest, which was eventually the objective of this approach. ²⁴ , ²⁵ The distribution model that was used to describe the kinetics of GC2008 was based on the two‐pore formalism and is described elsewhere. ²⁶ The physiology‐related parameters were kept constant to the ones provided as typical values from the software, and the only parameters changed were the ones related to the drug and target of interest. In specific, the parameters informed based on the specific project were the baseline concentration of TGF‐β in plasma and bone, the binding affinities to TGF‐β and FcRn, and the molecular weight of GC2008. These parameters were informed based on literature and no fitting was performed in this work (Table S4). ²⁷ , ²⁸ , ⁴⁹ , ⁵⁰ , ⁵¹ To evaluate PBPK predictions, GC2008 clinical PK data were compared with PBPK predictions for the according scenarios. After validation, the PBPK model was used to evaluate PBPK/TGF‐β response in human plasma and bone tissue and ultimately evaluate the dose that will decrease OI related TGF‐β back to their homeostatic values.

RESULTS

A one‐compartment PK model linked to an indirect effect model was used to describe the concentration response data in OI mice after 1D11 treatment. Figure 2 shows the PK/BVF response after i.p. administration of 5 mg/kg 1D11 at various regimens. Comparing the simulated (solid lines) with the experimental observations (symbols), the model was able to describe the observed PD data satisfactorily. The model further predicts that more frequent administration of the same dose leads to a faster time to reach steady‐state of the PD response. Comparison of the model's response with the available PK data are shown in Figure S1.

FIGURE 2.

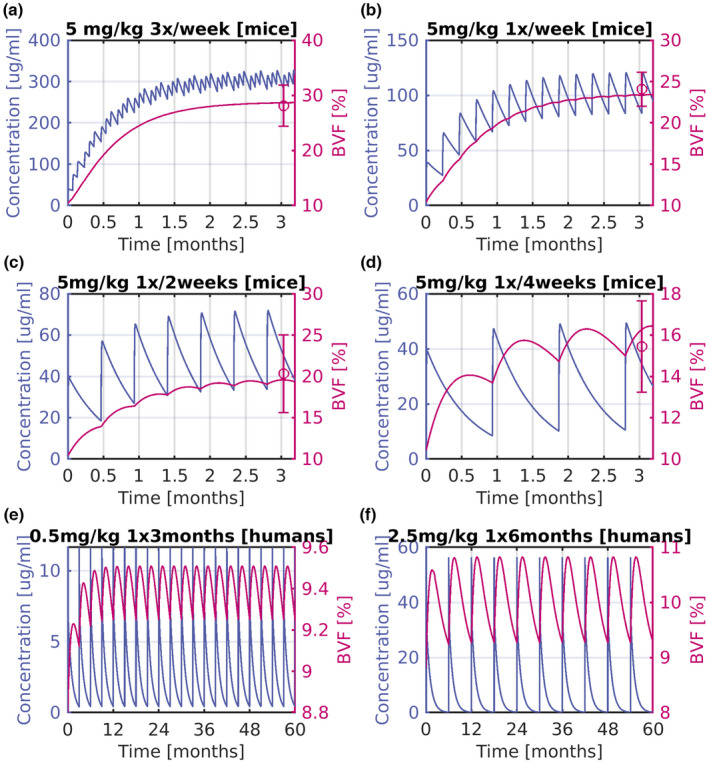
Mice 1D11 PK/BVF for different dosing scenarios, and predictions of GC2008 PK/PD response in humans. Shown as concentration versus time (left‐axis), and BVF; (right‐axis) (a) for 5 mg/kg administration three times per week in mice. (b) For 5 mg/kg administration weekly in mice. (c) For 5 mg/kg administration every 2 weeks in mice. (d) For 5 mg/kg administration every 4 weeks in mice. (e) For 0.5 mg/kg administration every 3 months in humans. (f) For 2.5 mg/kg administration every 6 months in humans. Symbols are average BVF data, and error bars depict their SD. Solid lines indicate the model's predictions. BVF, bone volume fraction; PD, pharmacodynamic; PK, pharmacokinetic.

This indirect effect model was also used to predict BVF response in humans. A two‐compartment PK model developed for GC2008 was used, and the baseline along with turnover rate parameters of the BVF‐PD preclinical model were changed to represent human values of BVF and bone turnover accordingly. Figure 2e,f depict model‐based PK/BVF predictions for 0.5 mg/kg i.v. administration once per 3 months, and 2.5 mg/kg i.v. administration every 6 months in humans, respectively. These doses result in a 5% increase on BVF.

In the second modeling approach, a PK/PD model was developed to describe the concentration time response data of BMD in response to administration of Fresolimumab (GC1008) in patients with OI. Figure 3 shows the PK/BMD dynamics, along with the respective BMD data for single dose of 1 and 4 mg/kg Fresolimumab (GC1008), in patients with OI. ¹⁹ Parameters of the PD model were fit to the BMD data after administration of 1 (Figure 3a) and 4 mg/kg (Figure 3b) Fresolimumab (GC1008). For BMD, administration of 1 mg/kg had minimal effect on the dynamics, as shown in Figure 3a. The simulations suggest a more profound increase in the initial period after a 4 mg/kg i.v. dose. In both dose groups, the number of patients enrolled in the study was low and their BMD values maintained significant variability. Therefore, this posed a challenge in using this data alone for translational purposes.

FIGURE 3.

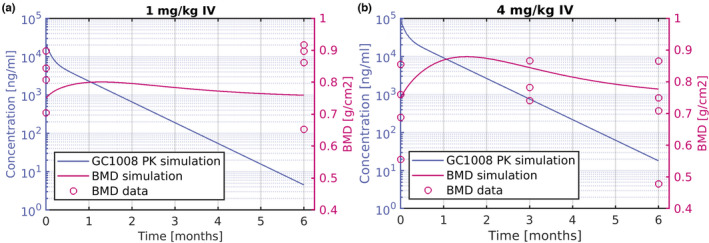
PK/BMD response of Fresolimumab (GC1008) in patients with OI shown as concentration versus time (left‐axis), and BMD (right‐axis) response (a) after 1 mg/kg single i.v. administration of Fresolimumab (GC1008). (b) After 4 mg/kg single i.v. administration of Fresolimumab (GC1008). Solid lines represent simulation and symbols human data. BMD, bone mineral density; OI, osteogenesis imperfecta; PK, pharmacokinetic.

To predict the effects of GC2008 on BMD, the PK/PD model described above for GC1008 was utilized by informing the PK model inputs from the GC2008 PK data, whereas the PD parameters were kept constant. Figure 4 shows the PK/BMD simulated response of GC2008 when administered i.v. as 0.4 mg/kg every 3 months (Figure 4a), and 2 mg/kg every 6 months (Figure 4b). The doses shown in Figure 4 are the doses resulting in a 5% increase in the BMD.

FIGURE 4.

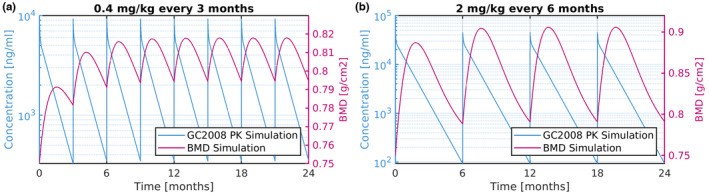
PK/BMD response of GC2008 shown as concentration vs time (left‐axis), and BMD (right‐axis) response (a) for 0.4 mg/kg i.v. administration of GC2008 every 3 months and (b) for 2 mg/kg i.v. administration of GC2008 every 6 months. BMD, bone mineral density; PK, pharmacokinetic.

In the last modeling approach, a PBPK model was developed for GC2008, and used to predict the dose needed to reduce TGF‐β in bone to its physiological level. Figure 5 shows validation of the PBPK model and its forward predictions of GC2008 PK data. Figure 5a illustrates the response of the PBPK model for different doses of GC2008. Solid lines depict model‐based predictions and open circles the individual clinical PK data for the different doses. Comparison between simulations and the PK data indicates that the PBPK model predicts drug exposure in humans well, for scenarios that were not used to train the model. Figure 5b depicts the distribution of GC2008 in plasma (solid line) and bone (dotted line), for 0.05 mg/kg i.v. administration of GC2008. The PBPK model predicts that drug concentration in bone is nearly 5% of that in plasma. To simulate an OI scenario, TGF‐β expression was increased three‐fold to represent the higher concentration of TGF‐β that have been reported in the patients with OI. ²⁷ , ²⁸ Figure 5c further depicts PBPK model‐based PK prediction of patients with OI, where 0.35 and 2.5 mg/kg i.v. administration of GC2008 was administered every 3 and 6 months, respectively. These doses were found to decrease TGF‐β levels to their physiological values for the according dosing schemes. Figure 5d further depicts the corresponding TGF‐β target levels after 0.35 and 2.5 mg/kg i.v. administration of GC2008 every 3 and 6 months.

FIGURE 5.

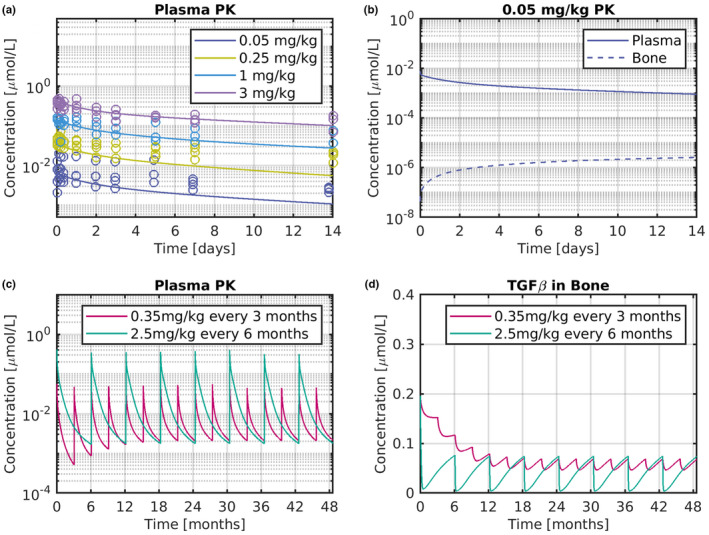
GC2008 human PBPK model validation and predictions. (a) Concentration of GC2008 for 0.05, 0.25, 1, and 3 mg/kg single i.v. administration. Symbols are individual subject data, and lines depict predictions of PBPK model. (b) Comparison of GC2008 in plasma (solid line) and bone (dotted line) PK for a single i.v. administration of 0.05 mg/kg GC2008. (c) Plasma PK prediction of 0.35 mg/kg administration every 3 months and 2.5 mg/kg administration every 6 months. (d) TGF‐β target dynamics in bone, after 0.35 mg/kg administration every 3 months, or 2.5 mg/kg administration every 6 months of GC2008. Solid lines indicate PBPK model predictions. PBPK, physiologically‐based pharmacokinetic; PK, pharmacokinetic.

DISCUSSION

In view of the wide variety of bone diseases, such as OI, and the complexity underlying the biochemical processes involved, there has been a significant increase in the use of mathematical modeling to better understand bone behavior. ²⁹ Among these, intensive efforts were made to develop PK/PD models permitting the prediction of treatment dynamics and their forward effects on bone performance. ³⁰ , ³¹ This work is focused on the translational model‐based approaches for predicting a human efficacious dose range for GC2008 in patients with OI. Multiple data sets of 1D11 in a preclinical model and a small clinical study of GC1008 in patients with OI were available for the development of a multi‐model approach to understand the concentration‐response relationship of an anti‐TGF‐β treatment (GC2008) with BMD or BVF. The aim of applying multiple PK/PD models that incorporate different assumptions and different PD end points, is to gain confidence in predicting a pharmacologically relevant dose range for GC2008 and temper the limitations imposed by highly variable and sparse datasets in particular for PD end points, such as BMD and BVF.

To date, there are several studies investigating the effects of various treatments to BMD in patients with OI. In a clinical study involved 23 men and 23 premenopausal women with OI, Adami et al. ³² tested the effect of neridronate, an amino‐bisphosphonate, when administered every 3 months. Within the first 12 months of treatment, spine and hip BMD rose by 3% and 4.3%, respectively, and during the second year of follow‐up additional 3.91% and 1.49% increases were observed. The magnitude of these changes was considered clinically relevant based on the relationship between BMD changes and fracture risk reduction. ³³ In the clinical trial of Orwoll et al., 79 adults with OI were randomized at a 1:1 ratio to receive subcutaneous 20 μg/day teriparatide or placebo. Compared to the placebo group, the treatment group showed a 6.1% increase in LS aBMD versus 2.8%, and total hip aBMD 2.6% versus −2.4%. Furthermore, vertebral BMD (vBMD) and strength improved with the treatment but declined with placebo. ³⁴ Overall, the results indicated that adults with OI displayed an increased hip and spine aBMD, vBMD, and estimated strength. In the retrospective analysis of Kuhn et al., ³⁵ the effect of the new physiotherapy approach including side alternating whole body vibration on motor function was analyzed in 53 children with OI. After 12 months, the children showed a significant increase of motor function and walking distance that was accompanied with an increase of the aBMD from 0.4357 to 0.48 (~10%) and of the BMD of the total body without the head from 0.5382 to 0.5529 (~3%). Finally, in a later study, Kuhn et al. ³⁶ showed that Denosumab, a RANK ligand antibody inhibiting osteoclast maturation, led to a 19% increase in the lumbar aBMD in 10 children with OI. In summary, current data indicate that significant amelioration in clinical outcome is expected for 5% or greater increase in BMD.

In the first modeling approach (Figure 1), available preclinical data of 1D11 were taken into consideration. The PK of 1D11 was described using a one‐compartment model with linear clearance. To describe the BVF dynamics in OI mice, a type III indirect response model was used (Figure 2a–d). As seen in Figure 2, the 1D11 mice PK/PD model was able to satisfactorily describe the available data. Of note, BVF measurements were only available at one timepoint limiting the predicting capacity of the model especially for the intermediate timepoints. The type III indirect response model assumes that the concentration of 1D11 induces an increase in the input rate of BVF. The choice of the indirect PD model was based on the available BVF and BMD data in mice and humans, which indicate an increase of both BVF and BMD when an anti‐TGF‐β agent is introduced. Although a type II model that represents drug response accruing form inhibition of the dissipation of the response could also be used to model the BMD data, a type III model was preferred based on the underlying physiology where anti‐TGF‐β treatment ultimately blocks the mechanism inducing BMD. ³⁷ Overall, indirect response models represent a simplified abstraction of the underlying physiological process and are appropriate for this work where bone turnover is known, but specific data for the effect of GC2008 on the bone remodeling system components were missing. Although system‐based models incorporating more mechanistic details for bone remodeling are available, ²⁹ , ³⁸ , ³⁹ , ⁴⁰ in this work, we intended to predict GC2008 PK/PD response and efficacious dose with a more simplified modeling approach that could be based on available PK/PD, and target concentration data.

To translate the mice 1D11 PK/PD model to GC2008 PK/PD in humans, three steps were taken. Initially, the 1D11 PK model was replaced by the GC2008 PK model evaluated previously (Figure S1). Furthermore, the mice BVF baseline was replaced by the literature‐based value of BVF in patients with OI, ⁴¹ , ⁴² and the bone turnover of mice, which is nearly 3 weeks, was replaced by the nearly 3 months value of the human bone turnover. ⁴³ Based on these changes, the model was used to evaluate the PK/PD response of GC2008, as shown in Figure 2e,f. To achieve a 5% increase in BVF, PK/PD model predicts administration of 0.5 mg/kg every 3 months, or 2.5 mg/kg bi‐annually.

Fresolimumab (GC1008) PK behavior in FSGS was similar in two other disease populations, namely idiopathic pulmonary fibrosis and advanced malignancy. ¹⁷ The underlying hypothesis in this work is that Fresolimumab (GC1008) is expected to have a similar PK profile in patients with OI (confirmed by in‐house unpublished preliminary PK data in OI) and therefore the PK parameters derived from the PopPK analysis of Fresolimumab (GC1008) in patients with cancer can be used to describe the PK of Fresolimumab (GC1008) in patients with OI. For modeling the PDs after Fresolimumab (GC1008) administration, similar to the first modeling approach, a type III PD model was used. This model described drug response that accrues from stimulation of the factors controlling the production of the response variable, which in this case is BMD. ²² The model predicted minimal effect on BMD after a single dose of 1 mg/kg Fresolimumab (GC1008), whereas administration of 4 mg/kg induced a stronger effect with a more pronounced increase of BMD in the first 100 days. The BMD response after GC2008 administration was assumed to follow the same dynamics (same PD‐model, and related parameters) as the ones informed from fitting PK/BMD of Fresolimumab (GC1008). Therefore, using the PopPK derived parameters of GC2008, and the BMD‐related parameters identified in the first step of this modeling approach, our model provided predictions of the PK/PD response of GC2008 (Figure 4a,b). Based on the model‐based prediction of GC2008 PK/BMD, a 5% BMD increase could be achieved after a 0.4 mg/kg dose of GC2008 administered once every 3 months (Figure 4a), or a 2 mg/kg dose administered every 6 months (Figure 4b).

Finally, a PBPK approach was implemented to predict the effect of GC2008 on the levels of TGF‐β in bone. PBPK models retain a mathematical framework based on which distribution of drug in the different tissues is predicted depending on physiology‐based mass balances and transport phenomena. ⁴⁴ The input to PBPK can be generally divided to drug‐specific and organism‐specific parameters. Drug‐specific parameters are related to the physicochemical properties of the compound, such as molecular weight, affinity to FcRn, affinity to the target of interest, and others. Organism‐specific parameters are related to physiological characteristics of the body, such as tissue volumes and tissue blood flows, which are mostly based on literature and generally incorporated in the model platform used. To evaluate the predictive capacity of the model, simulations were compared with the available PK data of GC2008 (Figure 5a). Model‐based predictions were able to describe the available data well despite the model not being previously trained on the GC2008 PK data. Although the bone GC2008 PK was not available to compare the predicted distribution, our PBPK predictions were well aligned with the literature indicating an average of 7% distribution of large molecules to bone (Figure 5b, AUC_Bone/AUC_plasma). ⁴⁵ After establishing confidence in the PBPK model predictions, a scenario of increased TGF‐β concentration was implemented. Based on the available literature evidence, patients with OI showed three times higher concentration of TGF‐β in plasma and bone relative to healthy individuals. ⁶ , ²⁷ , ⁴⁶ Based on these data, the TGF‐β expression in plasma and bone was increased in accordance with literature in order to simulated TGF‐β changes in patients with OI. We intended to project the dose of GC2008 that reduces the free TGF‐β levels back to their healthy value in patients with OI. Due to limited data on specific physiological changes in OI physiology other than the increased TGF‐β levels in plasma and peripheral tissues, the rest of the PBPK parameters were kept equal to the ones of a healthy individual. The underlying assumption is that OI‐related changes in body physiology (i.e., reduced bone volume and lung abnormalities) do not significantly impact GC2008 PK. Based on the PBPK analysis, administration of 0.35 mg/kg every 3 months or 2.5 mg/kg every 6 months (Figure 5c) would decrease the free TGF‐β levels in bone to their physiological values reported for healthy individuals (Figure 5d). Interestingly, the PBPK analysis indicated that a 2.5 mg/kg administration bi‐annually decreases the total amount of free TGF‐β in bone when GC2008 concentration reaches its peak. This further unveils a constraint for possible dosing designs where administration should be optimized to account for this implication.

Model‐based PK/PD assessment is an essential tool in drug research and development to gain an integrated understanding of the available PK/PD data. Nonlinear mixed effect modeling is applied in situations of sparse sampling to gain a better understanding of PK/PD parameter estimates and their according variability. ⁴⁷ In preclinical research, however, there is typically no information of a drug's behavior in the clinic. Furthermore, for the case of complex diseases, such as OI, that involves multiple tissues linked with various bone‐remodeling steps and forward signaling pathways that take place in different time scales, the development of a system‐model that captures all mechanistic insights can be cumbersome and very time‐consuming for drug development timelines. These embedded constraints urge for more creative model‐based strategies to gain confidence in predicting clinical PK/PD. The aim of this work is not the development of a fully mechanistic model that captures all disease's aspects, but rather a proposal for using different in silico experiments that involve simple PK/PD models with different assumptions to increase the confidence in predicting a pharmacologically relevant dose range for planning clinical studies.

In conclusion, the three modeling approaches implemented in this work provide a similar dose estimate for predicting GC2008 clinically relevant PD effects. In particular, the first approach uses preclinical data of 1D11 predicted a 0.5 mg/kg administration every 3 months and 2.5 mg/kg administration bi‐annually to increase BVF 5%. The second approach which further uses Fresolimumab (GC1008) clinical PK/PD data predicted a 0.4 mg/kg administration every 3 months or 2 mg/kg bi‐annually to increase the BMD 5%. Finally, PBPK modeling predicts a 0.35 mg/kg administration every 3 months or 2.5 mg/kg administration bi‐annually to decrease OI‐related TGF‐β levels back to their physiological values. Correspondence of the three approaches increased the confidence for the translation of the PK/PD relationship of GC2008 and provided a robust model‐based evaluation for predicting clinical efficacy.

AUTHOR CONTRIBUTIONS

P.D.M., N.P., Q.W., C.P., B.G., and J.F. wrote the manuscript. P.D.M. designed the research. P.D.M., N.P., Q.W., and J.F. performed the research. P.D.M., N.P., and Q.W. analyzed the data. P.D.M. and N.P. contributed new analytical tools.

FUNDING INFORMATION

This study was funded by Sanofi.

CONFLICT OF INTEREST

The authors declared no competing interests for this work.

Supporting information

Appendix S1

Mavroudis PD, Pillai N, Wang Q, Pouzin C, Greene B, Fretland J. A multi‐model approach to predict efficacious clinical dose for an anti‐TGF‐β antibody (GC2008) in the treatment of osteogenesis imperfecta. CPT Pharmacometrics Syst Pharmacol. 2022;11:1485‐1496. doi: 10.1002/psp4.12857