Abstract
Numerous machine learning and image processing algorithms, most recently deep learning, allow the recognition and classification of COVID-19 disease in medical images. However, feature extraction, or the semantic gap between low-level visual information collected by imaging modalities and high-level semantics, is the fundamental shortcoming of these techniques. On the other hand, several techniques focused on the first-order feature extraction of the chest X-Ray thus making the employed models less accurate and robust. This study presents Dual_Pachi: Attention Based Dual Path Framework with Intermediate Second Order-Pooling for more accurate and robust Chest X-ray feature extraction for Covid-19 detection. Dual_Pachi consists of 4 main building Blocks; Block one converts the received chest X-Ray image to CIE LAB coordinates (L & AB channels which are separated at the first three layers of a modified Inception V3 Architecture.). Block two further exploit the global features extracted from block one via a global second-order pooling while block three focuses on the low-level visual information and the high-level semantics of Chest X-ray image features using a multi-head self-attention and an MLP Layer without sacrificing performance. Finally, the fourth block is the classification block where classification is done using fully connected layers and SoftMax activation. Dual_Pachi is designed and trained in an end-to-end manner. According to the results, Dual_Pachi outperforms traditional deep learning models and other state-of-the-art approaches described in the literature with an accuracy of 0.96656 (Data_A) and 0.97867 (Data_B) for the Dual_Pachi approach and an accuracy of 0.95987 (Data_A) and 0.968 (Data_B) for the Dual_Pachi without attention block model. A Grad-CAM-based visualization is also built to highlight where the applied attention mechanism is concentrated.
Keywords: Deep learning, COVID-19 detection, Chest X-rays images, Feature extraction, Attention mechanism, Global second-order pooling
1. Introduction
The advent of a pathological member of the coronavirus class called severe acute respiratory syndrome coronavirus-2 (SAR-CoV-2) was discovered around December 2019 and has since infected millions globally [1]. The syndrome characterized by SAR-CoV-2 is known as COVID-19 and was classified as a pandemic in February 2020 by the World Health Organization (WHO) [2]. The coronavirus family is made up of a lot of different viruses that can cause moderate-to-extreme respiratory illnesses like Middle East respiratory syndrome (MERS), among others [3]. Since the emergence of the virus, more than five million infections and 355,000 deaths have been recorded worldwide. COVID-19 is a highly contagious virus that mostly affects the lungs. Most people with COVID-19 have a fever, cough, tiredness, trouble breathing, etc. The disease can spread to the lower respiratory system and cause pneumonia, which is a severe inflammation of the lungs. People with this illness often result from cytokine release syndrome, which in turn leads to the failure of multiple organs causing Acute Respiratory Distress Syndrome (ARDS) which in many cases leads to death [4,5]. When this influx suddenly, a tremendous burden is mounted on the inadequate medical resources in most developing countries making the facilities inaccessible to the needy. Covid-19 spreads through aerosols or droplets that come out of an infected patient's mouth or nose when they cough, talk, touch, etc. Therefore, to stop the spread of the infectious virus, medical practitioners have lined-up fundamental preventive measures like social distancing, mandatory face mask usage, constant hand washing or sanitizing with alcoholic-based sanitizers, and quarantine [6] if necessary. With new strains and waves sweeping across various countries and wreaking havoc now and then, there is a need for a reliable and efficient system for detecting COVID-19 in the lungs. Effective testing and detection can help alleviate the spread eventually. Detecting Covid-19 in its early days was based on an antibody test and reverse transcription (RT) - polymerase chain reaction (PCR) [7] approaches. These approaches have seen many drawbacks, including the scarcity of testing kits, and false or negative results with RT-PCR-based approaches among others. An antibody test may only be performed after a specified length of infection and is not a safe choice [8]. Instead, computerized tomography (CT) scans and X-rays are employed for this procedure [9]. The radiation released by CT scans is much more damaging to an individual's health than those emitted by advanced technological operations of radiographic imaging such as X-rays [10]. This is why, in contrast, chest X-rays are much more dependable, safe, and efficient.
Deep learning (DL) techniques have grown in prominence in recent years due to their ability to learn without aid and produce previously unseen extremely efficient accuracy index [11]. As a result, DL is being used in several fields, including medical imaging, computer vision, etc. DL is used to forecast pneumonia using chest x-rays (CXRs), segment MRI images, and analyze CT scans [[12], [13], [14], [15]] in the medical imaging domain. DL is therefore the most desired research field for identifying Covid-19 in chest X-rays. Currently, only specialized radiologists can analyze and interpret the complicated patterns of Chest X-rays data or images [16]. Sadly, this number remains insignificant, particularly in underdeveloped areas worldwide, compared to the enormous need for daily Coronavirus testing [17]. Therefore, it is necessary to develop a more efficient method to detect COVID-19 infections among mammals leading to timely recovery [18] and lessening the burden on physicians and radiologists across the world. Image preparation and preprocessing play a vital role in enhancing the performance of a classifier. Improving the image quality of the training data may help improve the accuracy of the algorithms. Several metaheuristic-based optimization approaches [19] have been shown to enhance image quality. Recently, studies have been conducted on multi-modal medical image fusion using meta-heuristic-based optimization [20] because it improves the quality of fused images while conserving vital information from the input images.
Convolutional Neural Networks (CNN) models are very effective in computer vision and are often used in medical imaging [21]. This is because CNN models demonstrated effectiveness in predicting output by analyzing and mapping visuals to the desired output [22]. Different COVID-19 detections based on DL models have been developed and applied successfully [23]. Well-established CNN models such as inception, GoogleNet, and, Xception, have been adopted with advanced transfer learning (TL) technologies [24,25]. In using X-ray images, the authors of [26] proposed a network-based COVID model to detect COVID-19 patients. The proposed network model reached a good degree of precision and an average sensitivity; likewise [27], designing the COVID-CAPS model with better accuracy and a good detection rate. However, the above-mentioned models acquired a poor detection rate due to an inadequate number of COVID-19-labeled data sets. In biomedical imaging, enhancing computational efficiency is a vital tool for producing realistic mathematical results. However, DL methods are often computationally intensive, making their systems unfeasible. Therefore, TL has been added to state-of-the-art algorithms and fine-tuned using a chest X-ray dataset unique to solve these specific problems. In Ref. [28], a cutting-edge inception model using TL has been used to filter COVID-19 with a truncated accuracy of 89.5%. Similarly, the pre-trained ResNet-50 CNN has been used on a small number of samples and has attained a better accuracy [29]. The pre-trained models are trained on the massive “ImageNet” dataset, which includes over 14 million input data and 1000 classifications. Using TL with these models yields successful outcomes, even when applied to distinct datasets. Recently, COVID-19 is being detected in mammals using ResNet18, DensNet20, and SqueezeNet. These models were calibrated again with TL on the "COVID-Xray-5k" dataset and returned a better accuracy [30]. All of the aforementioned models were implemented on a SoftMax classifier for detecting COVID-19 patients, and as a result, only the empirical risk reduction benefit was reached.
This study saw the integration of the conventional and recent advancement deep learning models to tackle the issue of accurate and robust feature extraction in chest x-ray images termed Dual_Pachi: Attention Based Dual Path Framework with Intermediate Second Order-Pooling for Covid-19 Detection from Chest X-Ray Images. Specifically, Dual_Pachi is a four-block component deep learning model comprising dual-part CNN techniques, second-order pooling techniques and a multi-head attention mechanism. First, an enhanced texture and patterns of COVID-19-specific X-ray features are extracted using a dual-part CNN by first converting the RGB Input image to a CIE LAB separate coordinates (L and AB branch) in the first block. The L branch focuses on the texture and edge features of the Chest X-ray images while the AB channel focused on the color findings. The second block applies a global second-order pooling operation to the extracted output features of the first block thereby focusing on the high and low characteristics of the images After this comes the third block which applies the Multi-head self-attention to avoid highly complex parameter optimization and simulates the discriminative and relevant features before being applied to the fourth block which is the classification Block. Finally, the low-level visual information and the high-level semantics of Chest X-ray image features are used for the detection and result generalization without sacrificing performance. The primary contributions of our research are listed below;
-
1.
Dual_Pachi, an End-to-End framework that generalizes COVID-19, Pneumonia, Lung opacity and Normal images, is proposed for COVID-19 identification. Four extremely distinctive Block makes up the proposed Dual_Pachi. The first block consists of dual channel Convolution layers at the first three convolution layer which accepts transformed RGB images into CIE LAB coordinates (L and AB channels where the L channel focuses on the texture and edge of the chest X-ray images and the AB channel focuses on the color features). The first block is followed by the second block which is a global high-order pooling method that concentrates on the higher representation of the extracted block one feature enriching them before sending it to the third block which is the multi-head self-attention block and MLP block that focuses on the overlooked edges and tiny features of the chest x-ray images. The last block is the classification block where the learned features are used for the identification Dual_Pachi using the SoftMax activation function.
-
2.
An extensive experiment was carried out using two Loss functions (categorical cross-entropy and categorical smooth loss) and learning rates (0.001 and 0.0001) to examine the optimal performance of Dual_Pachi.
This paper is divided into the following sections; section 2 contains the related studies while section 3 contains the detailed comprehensive working processes of the Dual_Pachi model. Section 4 contains the experimental results, data, data analysis and evaluation metrics while section 5 contains the results obtained. Section 6 is the result discussion, ablation studies and comparison with related works, limitations and future works and we conclude in section 7.
2. Related works
Ever since the WHO declared Coronavirus a pandemic in February 2020, worldwide efforts from academia and medical research industries have been focused on developing scientific formulations and applications to detect the virus. DL algorithms have been applied to Chest X-rays extensively to efficiently detect Coronavirus but due to the unavailability of covid-19-related datasets, most models proposed are unrealistic in the real world.
Jain et al. [31], compared and analyze the accuracy of InceptionV3, Xception, and ResNet models using the 6432 chest X-ray image dataset. The authors asserted that the Xception model had the best accuracy at 97.97%. As a unique strategy, they used the LeakyReLU instead of the conventional ReLU as the activation function although they observed that there was overfitting during the training phase that lead to high accuracy. Jain et al. [31], in their conclusion, suggested further consideration of huge datasets to verify their proposed paradigm. TL was adopted in a multi-class approach by Apostolopoulos and Mpesiana [32], combining VGG19 and MobileNetV2 to classify COVID-19, Pneumonia, and Normal cases. The accuracy index established was far more encouraging than the contemporary studies at that time. Similar to Ref. [33], the authors presented Domain Extension TL (DETL) and affirms the need for a vast amount of data when training a CNN model from scratch. Following a 5-fold Cross-Validation, the stated accuracy for AlexNet was 82.98%, VGGNet was 90.13%, and ResNet was 85.98%. The authors also used the Grad-CAM (Gradient Class Activation Map) concept to determine whether or not a model paid more attention during classification. A TL-based nCovNet was designed by Panwar et al. [34], in a way that the input layer is followed by ReLU activation, 18 convolutional, and max-pooling layers from the pre-trained VGG16 model. The 2nd phase of nCovNet incorporated five (5) additional specific head layers. A total of 337 X-ray scans were used, of which 192 samples are scanned with COVID-positive images. The training accuracy saw a better performance index, whereas the validation accuracy on coronavirus-positive patients was 97.62%. Authors fear for data-leakage due to their manual annotation. In Ref. [24], Ozturk et al. also used the 5-fold cross-validation on a pre-trained model based on 3 CNN architectures that obtained 98% accuracy. Sethy et al. [35], discovered that COVID-19 CXR sample categorization combining ResNet50 and SVM classifier achieved better accuracy. Asif et al. [36]. classified COVID-19 infection in CXR samples using a deep CNN model. A Covid-19 detecting model based on ConvNet was labeled as “EfficientNet” using CXR images that recorded positive covid-19 accuracy of 93.9%, with 5–30 times fewer parameters recorded with no false prediction [37]. A dataset of 13,569 X-ray samples of healthy individuals, COVID-19 pneumonia, and non-COVID-19 pneumonia cases was utilized to train the proposed techniques and the 5 competing designs. A hierarchical method and cross-dataset analysis were used. The evaluation of many datasets indicated that even the most sophisticated models lack generalization capability. As can be observed, this research only covered a limited number of photos of Covid-19-positive individuals. The authors evaluated the performance of the proposed models on a large and diverse dataset.
In addition, Hussain et al. [38], proposed a 22-layer CNN-based model labeled CoroDet and used both Chest X-rays and CT Scan Datasets for 2, 3, and 4 classes, i.e., COVID, Normal, non-COVID bacterial pneumonia, and non-COVID viral pneumonia. With the CoroDet Model on X-ray Dataset, they could get an accuracy of 99.1%, 94.2%, and 91.2% for classifying 2,3, and 4 classes, respectively. Karakanis et al. [39] suggested two lightweight models, one for binary classification as well as one for three-class classification, and compared it to the ResNet8 Pre-trained structure, which is the current state of the art. Due to the lack of datasets, they have also used Conditional Generative Adversarial Networks (cGANs) to produce synthetic pictures. They attained an accuracy of 96.5% with the suggested binary class model and 94.3% with the multiclass model. Using cGANs, the accuracy of binary and multiclass Models increased to 98.7% and 98.3%, respectively. Hammoudi et al. [40], proposed individualized DL algorithms for identifying pneumonia-infected individuals from chest X-rays. Cases of viral pneumonia detected during COVID-19 had a high risk of developing COVID-19 infections, according to the author. DenseNet169 obtained 95.72% accuracy, surpassing other models such as ResNet34 and ResNet50. Recently, hybrid DL mechanisms have been explored for detecting Covid-19. Khan et al. [41], suggest two deep learning frameworks for detecting Covid-19: Deep Hybrid Learning (DHL) and Deep Boosted Hybrid Learning (DBHL). The dataset employed for binary classification in this study consisted of 3224 Covid-19 and 3224 Normal Chest X-ray pictures. The proposed DHL framework makes use of COVID-ResNet 1&2 models to extract deep features, which are then fed individually via an SVM classifier for Covid-19 identification. Edge- and region-based techniques are used in COVID-RENet models to extract region and boundary characteristics. In the proposed DBHL framework, the feature spaces are concatenated to fine-tune COVID-RENet models. According to the authors, the suggested approaches dramatically minimize the number of false negatives and false positives in comparison to earlier research. In Ref. [42], Muhammad et al. used a reconstruction-independent component analysis (RICA) to supplement labeled data. Covid-19 was detected using CNN-BiLSTM. CNN helps extract high-level information, whereas augmentation offers low-dimensional features. BiLSTM classifies processed data. On three Covid-19 datasets, our new methodology outperformed earlier techniques. Visualizing findings using PCA and t-SNE. A thorough performance comparison study was conducted by V.K. Shrivastava and M. K. Pradhan [43] on 16 cutting-edge models that they trained using scratch learning, transfer learning, and fine-tuning. They conducted their investigation using two scenarios: multiclass classification and binary classification. Techniques for teaching that take into account costs were utilized to address the issue of class imbalance. Among all models taken into consideration, the InceptionResNetV2 model using a fine-tuning method earned the greatest classification accuracy, with a binary classification accuracy of 99.20%, and the Xception model with a multiclass classification accuracy of 89.33%. The DarkCovidNet model, which is built on CNN, was updated by D. K. Redie et al. [44] and they showed the experimental outcomes for two scenarios: binary classification (and multi-class classification. The model's average accuracy for binary and multi-class classification was 99.53% and 94.18%, respectively. Extensive feature extraction, twerking of pre-trained CNN, and end-to-end training of a built CNN model was employed by A. M. Ismael and A. Engür [45] to categorize COVID-19 and standard chest X-ray images. Deep CNN models (ResNet18, ResNet50, ResNet101, VGG16, and VGG19) that have already undergone training were employed for deep feature extraction, while the Support Vector Machines (SVM) classifier was used using a variety of kernel functions, including quadratic, gaussian, linear and cubic. The ensemble of the ResNet50 model with SVM classifier via Linear kernel function had the greatest classification accuracy (94.7%), followed by the twerked ResNet50 model with a result of 92.6% and the constructed CNN model with a result of 91.6% after end-to-end training. F. Demir [46] introduced a unique method based on the DeepCovNet deep learning model to categorize COVID-19, normal, and pneumonia classes in chest X-ray pictures. DeepCovNet is an ensemble of convolutional-autoencoder and an SVM classifier with various kernel functions. With an innovative and reliable approach called SDAR, the distinct features were chosen from the deep feature set and yielded an accuracy of 99.75%.
The above-mentioned studies so far have a common factor: it has been implemented on datasets that were insufficient in size owing to the lack of unavailable data. This becomes impractical in real-world implementation, even if the performance accuracy is convincing. In other circumstances, even though the dataset was big enough, the model's accuracy and efficiency were not well balanced. However, in this study, we presented a well-designed architecture with a remarkable and efficient performance index in identifying covid-19 using a standard Chest X-ray dataset which will be feasible in a real-world implementation.
3. Proposed methodology
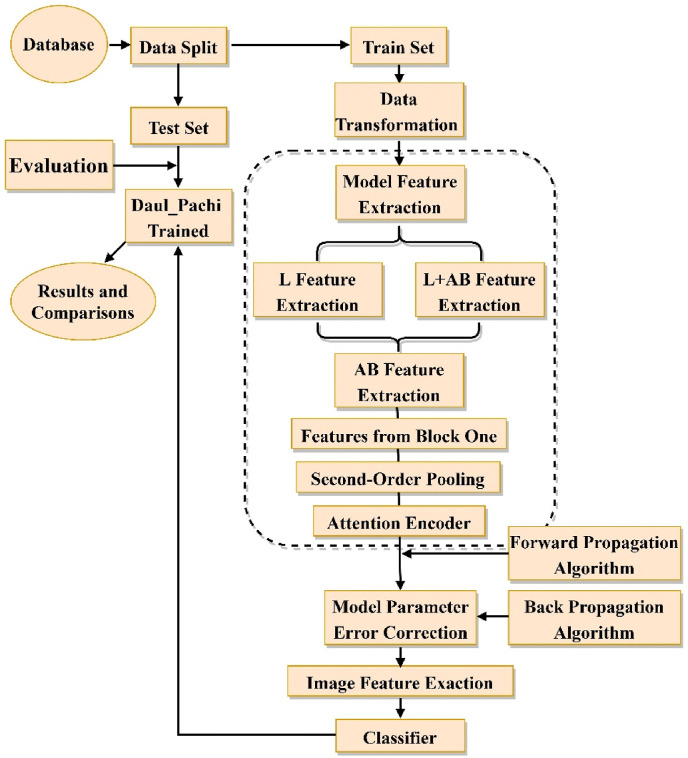
This section illustrates the flow chart of the Dual_Pachi implementation in Fig. 1 . The process begins with data split to train/validation and test set. The train set undergoes data transformation before being fed into Dual_Pachi for feature extraction, model parameter error correction to the use of the learned features for prediction by the classifier. The Dual_Pachi model is saved as a.tf file before introducing the test set for evaluation and result comparisons. Further details on the proposed methodology are described below.
Fig. 1.
Flow Chart of the Dual_Pachi implementation. In the data splitting, we split int train set, validation set and test set. the trained model is saved as a.tf file.
3.1. Dual_Pachi model
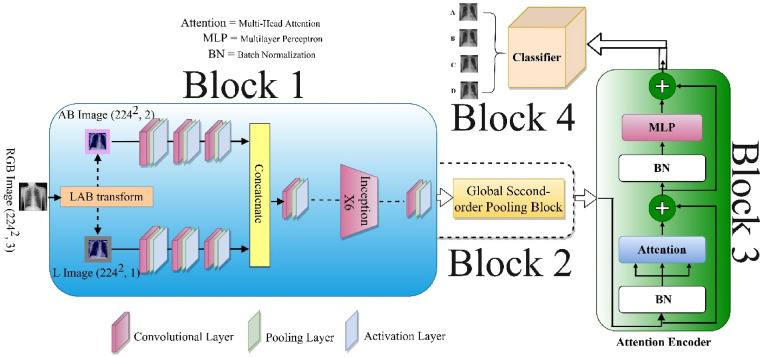
Fig. 2 illustrates the Dual_Pachi architecture. The Dual_Pachi model is broken down into four Blocks. The first block emulates the inception v3 variation proposed by Toda & Okuras [47]. The identified property of the inception v3 variation got rid of the last 5 mixed layers out of 11 layers. The second Block emulates the Global second-order pooling which adds a variety of neighboring features via covariance matrix to the conventional second-order pooling thus learning the attention filter. The third block is the encoder which comprises multiple self-attention heads MLP blocks both of which are built utilizing a shortcut connection and normalizing layer. The fourth and last block is the classification block which makes use of the extracted and learned feature for prediction.
Fig. 2.
Proposed Dual_Pachi Architecture. The proposed architecture consists of four blocks as seen in the diagram. The 1st block is the dual inceptionv3 variation, block 2 is the global second-order pooling, the 3rd is the Encoder which comprises the multi-head self-attention network and the MLP layer while the last Block i.e the 4th block is the classification layer.
Block One: First, the RGB input image is transformed to CIE LAB coordinates where the L channel is been treated separately and the AB channel is treated likewise before the features are joined together. From the diagram, the first three layers of the Inception V3 architecture [47] are modified into two branches to accept the L and AB channels independently. This approach saves from 1/3 to 1/2 of the parameters in the separated branches. After the L and AB features are treated separately by the first three convolutional layers, the features are concatenated and the rest of the network setting remains the same as the Inception V3 architecture.
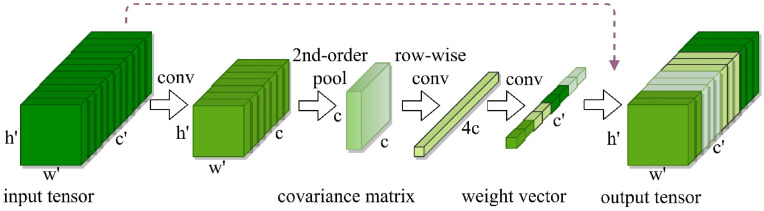
Block Two: we also refer to this block as the Global Second-Order Pooling block which defers from the traditional Second-Order Pooling by the addition of neighborhood pixels. A covariance matrix is applied to all the nearby pixels to learn the attention filters while a normalization was first introduced to reduce the input features scale dependency.
| (1) |
Where = node-sets neighborhood pixels' covariance matrix mathematically represented as The similarity between each neighboring pixel and the core pixel is determined via an adaptable cosine neighborhood function with the description of the corresponding formula;
| (2) |
The stochastic pixel vector close by is denoted as when the core pixel vector inside the neighborhood is denoted as , where , and is an additional symmetric matrix making trainable. It is believed to be more effective to utilize pixel vectors from to compute as offers information on the spatial frequency similarity of two pixels at various places. The attention weights are then standardized into a single without unit addition using a SoftMax function, which is demonstrated to produce higher convergence.
| (3) |
Where = bias, = diagonal weight matrix created based on = 1 for . The entire parameter implementation of Block two is mathematically expressed as;
| (4) |
| (5) |
The second Block expresses second-order information while simply introducing the variability of surrounding pixels by using a data-adaptive and trainable weighting scheme. Smaller weighted pixels have less of an effect on this process while larger weighted pixels are more significant. Block three is diagrammatically represented as seen in Fig. 3 .
Fig. 3.
The first Block's obtained features after dimension reduction form the input tensor of the second block which computes the covariance matrix before completing two successive operations of sequential convolution and quasi-activation to produce the output tensor (Multiplication of the input along the channel axis).
Block Three: The dimension of the second block output is tweaked to enable the encoder to accept the features. The final features to be input into the encoder are implemented using two separate layers, the Multi-Head Self-Attention layer and the MLP layers, both of which are built utilizing a shortcut connection and normalizing layer as shown in Eq. (6).
| (6) |
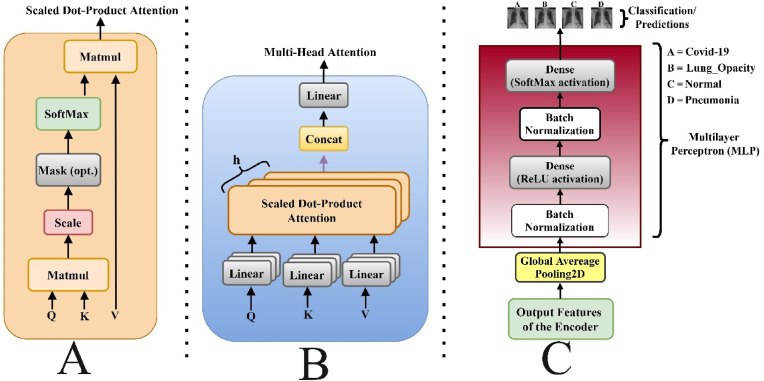
In Eq. (6), is the layer input and layer output, is the normalization layer, is either the multi-head attention or MLP . The multi-head self-attention layer is based on scaled dot-product attention (Fig. 4 ), which attempts to query information from the source sequence that is relevant to the target sequence as shown in Eq. (7).
| (7) |
Where the row-wise SoftMax is represented . One scale dot-product attention attends only one position in each row hence to attend to multiple positions, the multi-head attention was employed via multiple scaled dot-product attention in parallel as shown in Fig. 4. B and mathematically represented as;
| (8) |
Where , depicts the number of attention heads, represent the learnable entities. From Fig. 4. C. the MLP block is of two layers; the non-linear function and the parameters mathematically calculated as thus;
| (9) |
Fig. 4.
A illustrates the Scale Dot Product attention, B. illustrates the implemented Multi-head Self-Attention network showing the several attention layers running in parallel and C. shows the implemented MLP Block.
From Equation (5), the extracted feature coming from Block one is depicted as , the attention layer configuration calculates outputs as shown in equation (10) whereas the MLP layer configuration calculates the output as shown in equation (11).
| (10) |
| (11) |
Block Four: The GeLu activation [49] function was employed after a 1D Global Average Pooling, whereas the SoftMax activation function was utilized after Batch Normalization [48] in the second block, as shown in Fig. 4 (C). The Adam and SGD optimizers serve as the optimization method whereas the categorical smooth loss and a categorically cross-entropy loss serve as the loss function.
4. Experiments
A thorough analysis of the dataset, data preparation, evaluation metric, and experimental settings are done in this part.
4.1. Dataset
Some existing works use proprietary datasets to evaluate their approaches, while others mix data from many publicly available sources. Two huge publicly available datasets were used in this work, as stated below:
-
•
Data A: This dataset (COVID-19 Radiography Dataset [50]) contains four unique classes of medical Chest X-ray images: Normal, Pneumonia, Lung Opacity, and COVID-19, which were collected by researchers from Qatar University Doha Qatar, University of Dhaka, Bangladesh, and medical professionals and researchers from Pakistan and Malaysia. It contains 3616 COVID-19 samples, 10,192 Normal samples, 6012 Lung Opacity samples, and 1345 Pneumonia samples. The images have a resolution of 299 x 299 pixels and are in the Portable Network Graphics file format. In this paper, only 3000 images per class were collected for training, 300 for validation, and 300 for testing. We used the Python Augmentor process to augment the data to get the number of samples needed for the experiment because the Pneumonia samples were less than 3000.
-
•
Data B: The ChestX-ray-15k dataset was acquired by Badawi et al. [51] from eleven different sources. This dataset contains a balanced amount of Chest X-ray images for training/validation and testing, with 3500 and 1500 images, respectively. The three unique chest X-ray categories are normal, COVID-19, and pneumonia. The images in this category are all in portable network graphics format, however at varied spatial resolutions. The validation set included 500 images from each test set class.
These datasets are utilized to perform a multi-class prediction study for COVID-19 detection and to address the multi-class scarcity problem. All of the images were scaled to 224 by 224 pixels using bilinear interpolation. To increase the number of images in each class, the data transformations zoom range = 0.2, rotation range = 1, and horizontal flip = True were carried out. For each of the classes, Fig. 5 displays multiple illustrations of different visual views. The distribution splits of the dataset by class are shown in Table 1 . For each class, a random selection from the dataset is used to determine the training set, validation set, and testing set.
Fig. 5.
Sample of the employed dataset.
Table 1.
Employed dataset distribution.
| Partition | Normal | Pneumonia | COVID-19 | Lung Opacity | Total | Total | |
|---|---|---|---|---|---|---|---|
| Data_A | Training | 3000 | 3000 | 3000 | 3000 | 12000 | 14400 |
| Validation | 300 | 300 | 300 | 300 | 1200 | ||
| Testing | 300 | 300 | 300 | 300 | 1200 | ||
| Data_B | Training | 3500 | 3500 | 3500 | – | 10500 | |
| Validation | 500 | 500 | 500 | – | 1500 | 1500 | |
| Testing | 1000 | 1000 | 1000 | – | 3000 |
4.2. Evaluation metrics
Several assessment metrics were used to gauge how robust the proposed model was. ROC curve, PR curve, F1-score, specificity, accuracy, and precision. True Positive, False Positive, True Negative and False Negative are all abbreviated as TP, FP, TN, and FN, respectively. The probability curve created by plotting at various threshold levels is referred to as the ROC (Receiver Operating Characteristic). The following are the metrics we used;
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
4.3. Experimental setup
This experiment was carried out on Desktop Computer with 64.0 GB RAM and an NVIDIA GEFORCE RTX-3060 12 GB graphics processing unit with a CPU (AMD RYZEN 9 5900X). This paper utilizes the open-source library of Keras and TensorFlow for implementation. Table 2 summarized the training hyperparameters used in this study. This study further explored the effects of the following hyperparameters on the proposed model.
Table 2.
Experiment with hyperparameters optimization and settings.
| Hyperparameters and Settings | ||||||||
|---|---|---|---|---|---|---|---|---|
| Loss Function |
Categorical Smooth Loss |
Categorical Cross-Entropy |
||||||
| Optimizers |
Adam |
SGD |
Adam |
SGD |
||||
| Learning rate | 0.0001 | 0.001 | 0.0001 | 0.001 | 0.0001 | 0.001 | 0.0001 | 0.001 |
| Batch size | 8 | 8 | 8 | 8 | ||||
| Reduce Learning Rate | 0.2 | 0.2 | 0.2 | 0.2 | ||||
| Epsilon | 0.001 | 0.001 | 0.001 | 0.001 | ||||
| Patience | 10 | 10 | 10 | 10 | ||||
| Verbose | 1 | 1 | 1 | 1 | ||||
| Es-Callback (Patience) | 10 | 10 | 10 | 10 | ||||
| Clip Value | 0.2 | 0.2 | 0.2 | 0.2 | ||||
| Epoch | 100 | 100 | 100 | 100 | ||||
| Patch Size | (2, 2) | (2, 2) | (2, 2) | (2, 2) | ||||
| Drop Rate | 0.01 | 0.01 | 0.01 | 0.01 | ||||
| Number of Heads | 8 | 8 | 8 | 8 | ||||
| Embed_dim | 64 | 64 | 64 | 64 | ||||
| Num_MLP | 256 | 256 | 256 | 256 | ||||
| Window Size | Window Size//2 | Window Size//2 | Window Size//2 | Window Size//2 | ||||
| Input Size | (224 x 224) | (224 x 224) | (224 x 224) | (224 x 224) | ||||
4.3.1. Loss function (Lf)
Simply put, the Lf calculates how well the model can forecast using a given set of inputs. The difference between the model's estimate using a set of specified values and the measured ground truth is the computed result, which is the loss or failure. Categorical cross-entropy loss and categorical smooth loss function were employed in this study's analysis.
4.3.2. Optimizer (Opt)
By making model parameter updates in response to the results of the loss function, the Opt executes loss function minimization, producing a global minimum with the smallest and most accurate result. This paper utilized the Stochastic Gradient Descent (SGD) and Adaptive Moment Estimation (Adam).
4.3.3. Learning rate (Lr)
The Lr is a parameter that determines how much the model should modify each time the model weights are changed in response to the projected mistake. In this paper, the Lr of 1 × 10−4 and 1 × 10−3 are explored.
5. Results
This section discusses the classification results of the various approaches implemented in this paper starting with the classification performance of the base model (Inception v3), followed by the proposed approach result down to the Ablation studies and lastly comparison with the state-of-the-art models.
5.1. Baseline experiment
As stated earlier, this paper studied the behavior of dual optimizer, learning rate and loss function on the proposed model. However, we will report only the hyperparameter settings that give promising results hence we set an accuracy of 90% as a benchmark in reporting the various performance of the model. Since Dual_Pachi's first block is a modified inceptionV3 model, this report starts with the performance of the original InceptionV3 as the performance baseline. Table 3 shows the obtained result which was recorded using accuracy, sensitivity, specificity, precision, F1-score and AUC. Various hyperparameter settings with that of Adam optimizer recorded an accuracy above 90% except for the settings with learning rate and categorical cross-entropy loss while that of SGD optimizer all recorded an accuracy lower than 90% except that of categorical cross-entropy loss and learning rate. From the experimented settings the setting using Adam optimizer, Categorical Cross-Entropy loss and Lr yielded the best classification performance with an accuracy of 0.91973, sensitivity of 0.84466, specificity of 0.94713, precision of 0.85426, F1-score of 0.84114 and AUC of 0.89426 while the rest recorded settings in Table 3 also performed well with accuracy above 90% with the minimal difference among their results. Comparing the performance of the two-loss functions, the categorical entropy loss is preferred to that of the categorically smooth loss as it yields much better accuracy.
Table 3.
Baseline classification result. Opt signifies optimizer, Lr signifies learning rate, Adam signifies adaptive moment estimation while SGD signifies stochastic gradient descent, and Lf signifies loss function.
| Models | Accuracy (%) | Sensitivity (%) | Specificity (%) | Precision (%) | F1 Score | AUC |
|---|---|---|---|---|---|---|
| Opt: Adam, Lf: Categorical Smooth Loss, Lr: | ||||||
| Baseline | 0.90468 | 0.81116 | 0.93631 | 0.83653 | 0.81355 | 0.87373 |
| Opt: Adam, Lf: Categorical Smooth Loss, Lr: | ||||||
| Baseline | 0.9097 | 0.81579 | 0.93941 | 0.83356 | 0.81979 | 0.87881 |
| Opt: Adam, Lf: Categorical Cross-Entropy, Lr: | ||||||
| Baseline | 0.91973 | 0.84466 | 0.94713 | 0.85426 | 0.84114 | 0.89426 |
| Opt: SGD, Lf: Categorical Cross-Entropy, Lr: | ||||||
| Baseline | 0.90301 | 0.80312 | 0.93645 | 0.81609 | 0.80225 | 0.8729 |
5.2. Dual_Pachi experimental result (Data_A)
Attention mechanisms have gained a lot of focus in computer vision tasks recently hence Dual_Pachi Block 3 incorporates a multi-head self-attention network and MLP block. During our experiment, we implemented the proposed Dual_Pachi model with and without the Attention block (Block 3) to analyze how trustworthy attention mechanism performance is in vision tasks. Table 4 illustrates the recorded results on the Adam optimizer using accuracy, sensitivity, specificity, precision, F1-score and AUC. Only the hyperparameter settings performance above 90% accuracy is recorded for discussion. The results show the effect of the tuning parameters in the yielded results. Using the learning rate and categorical_smooth_loss function vs. categorical cross-entropy loss, the Dual_Pachi performance is good with minimal difference. However, its superiority was significant when using the Lr and categorical cross-entropy loss function with an accuracy of 0.90134, sensitivity of 0.8057, specificity of 0.93499, precision of 0.83318, F1-score of 0.80354 and AUC of 0.86999 over 0.82441 accuracy, 0.65074 sensitivity, 0.88223 specificity, 0.76553 precision, 0.63804 F1-score and 0.76446 AUC of the Model without the attention Block (Block 3). The best performance of the Dual_Pachi without Block 3 (Attention Block) is seen using the learning rate of and categorical_smooth_loss function with an accuracy of 0.95819, sensitivity of 0.91672, specificity of 0.97106, precision of 0.92882, F1-score of 0.92002 and AUC of 0.94211. In summary of the Adam optimizer settings, the Dual_Pachi performed much better than when the attention block is removed with a +0.01–0.05% difference in all the implemented evaluation metrics supporting the claims of the superb contribution of the attention mechanism in vision tasks.
Table 4.
Classification Performance of Dual_Pachi on Data_A using the Adam Optimizer. The Analyzed hyperparameter includes; learning rate (Lr): and , loss function (Lf); categorical_smooth_loss and categorical cross-entropy.
| Accuracy (%) | Sensitivity (%) | Specificity (%) | Precision (%) | F1 Score | AUC | |
|---|---|---|---|---|---|---|
| Opt: Adam, Lr: , Lf: categorical_smooth_loss | ||||||
| Without Bl. 3 | 0.95819 | 0.91672 | 0.97106 | 0.92882 | 0.92002 | 0.94211 |
| Dual_Pachi | 0.96656 | 0.93315 | 0.97774 | 0.93905 | 0.93389 | 0.95547 |
| Opt: Adam, Lr:, Lf: categorical_smooth_loss | ||||||
| Without Bl. 3 | 0.9097 | 0.82806 | 0.94174 | 0.82548 | 0.81511 | 0.88349 |
| Dual_Pachi | 0.95318 | 0.90794 | 0.96911 | 0.90699 | 0.90518 | 0.93822 |
| Opt: Adam, Lr:, Lf: categorical cross-entropy | ||||||
| Without Bl. 3 | 0.95485 | 0.91232 | 0.96878 | 0.92109 | 0.9132 | 0.93756 |
| Dual_Pachi | 0.95987 | 0.91747 | 0.97255 | 0.93502 | 0.92233 | 0.9451 |
Table 5 shows the Receiver operating characteristics (ROC) curve and the precision-recall curve (PR) for the individual class performance of the analyzed Table 4. For the Dual_Pachi without Block 3 model, the class performance is affected by the training hyperparameters. For the categorical_smooth_loss, training with learning rate, the Lung opacity had a better area (0.98) followed by COVID-19 (0.96), while the Normal and the Pneumonia class had the same area (0.92). Training with learning rate, the COVID-19 class had an area of 0.94 followed by Lung opacity (0.93), Pneumonia class (0.89) and lastly the Normal class (0.78). For the categorical cross-entropy loss function, and learning rate, the Lung opacity class have the best area (0.99) followed by the COVID-19 class (0.95), and the Normal class (0.92) while the pneumonia class had the least area (0.91). The AP performance of the Dual_Pachi without Block 3 is in synchronization with the ROC Performance. However, the Highest AP in all the implemented settings is seen in the Lung opacity class (0.92) via learning rate and categorical_smooth_loss function while the least AP is seen in the Normal Class with an AP of 0.55 via learning rate and categorical_smooth_loss.
Table 5.
Receiver Operating Characteristic (ROC) and Precision-Recall (PR) performance of Dual_Pachi on the Adam Optimizer (Opt). The parameter employed includes learning rate (Lr); and , Loss function (Lf); Categorical_smooth_loss and categorical cross-entropy.
| ROC (Area) | Macro-Average | Micro-Average | COVID-19 | Lung Opacity | Normal | Pneumonia |
|---|---|---|---|---|---|---|
| Opt: Adam, Lr: , Lf: categorical_smooth_loss | ||||||
| Without Bl. 3 | 0.94 | 0.94 | 0.96 | 0.98 | 0.92 | 0.92 |
| Dual_Pachi | 0.96 | 0.96 | 0.98 | 0.96 | 0.95 | 0.94 |
| Opt: Adam, Lr:, Lf: categorical_smooth_loss | ||||||
| Without Bl. 3 | 0.88 | 0.88 | 0.94 | 0.93 | 0.78 | 0.89 |
| Dual_Pachi | 0.94 | 0.94 | 0.95 | 0.97 | 0.89 | 0.96 |
| Opt: Adam, Lr:, Lf: categorical cross-entropy | ||||||
| Without Bl. 3 | 0.94 | 0.94 | 0.95 | 0.99 | 0.92 | 0.91 |
| Dual_Pachi | 0.95 | 0.95 | 0.95 | 0.94 | 0.93 | 0.97 |
| Precision-Recall (AP) | Micro-Average | COVID-19 | Lung Opacity | Normal | Pneumonia |
|---|---|---|---|---|---|
| Opt: Adam, Lr:, Lf: categorical_smooth_loss | |||||
| Without Bl. 3 | 0.86 | 0.90 | 0.92 | 0.79 | 0.87 |
| Dual_Pachi | 0.89 | 0.95 | 0.92 | 0.80 | 0.89 |
| Opt: Adam, Lr:, Lf: categorical_smooth_loss | |||||
| Without Bl. 3 | 0.72 | 0.67 | 0.85 | 0.55 | 0.84 |
| Dual_Pachi | 0.84 | 0.84 | 0.84 | 0.77 | 0.93 |
| Opt: Adam, Lr:, Lf: categorical cross-entropy | |||||
| Without Bl. 3 | 0.85 | 0.87 | 0.92 | 0.79 | 0.86 |
| Dual_Pachi | 0.87 | 0.80 | 0.88 | 0.88 | 0.95 |
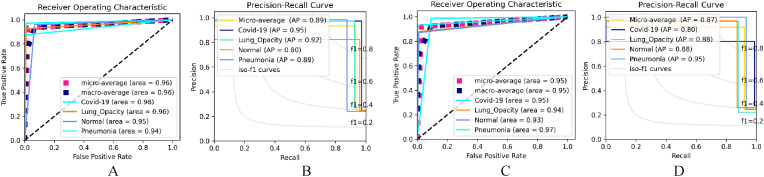
The Dual_Pachi ROC and AP are also seen in Table 5. For the categorical_smooth_loss, training with learning rate, the COVID-19 class had a better area (0.98), followed by the Lung opacity (0.96), Normal class (0.95) and the Pneumonia class (0.94). However, training with learning rate, the Lung opacity class and the Pneumonia class are the two preferred as they had an area of 0.97 and 0.96 respectively. The COVID-19 class followed with an area of 0.95 while the Normal yielded the least area (0.89). For the categorical cross-entropy loss function, and learning rate of , the pneumonia class had a better area (0.97), followed by the COVID-19 class (0.95), the Lung Opacity class (0.94) and the Normal class (0.93). The Precision-Recall curve of the Dual_Pachi models depicts that the COVID-19 class had a better AP (0.95) followed by the Lung opacity class (0.92), the Pneumonia class (0.89) and the Normal class with (0.80) for the learning rate and categorical_smooth_loss which is the highest recorded AP in this experiment.
Analyzing the performance of the Dual_Pachi performance using the SGD Optimizer, we only recorded the best performance of the model which is found to be at the learning rate of , and categorical cross-entropy loss function. Dual_Pachi recorded an accuracy of 0.95151, a sensitivity of 0.90316, a specificity of 0.96772, a precision of 0.90625, an F1-score of 0.90127 and an AUC of 0.93545 as seen in Table 6 . A huge difference is noted between Dual_Pachi's performance and when Dual_Pachi is trained without the attention Block. The SGD Optimizer Receiver Operating Characteristic (ROC) and Precision-Recall (PR) of the Dual_Pachi are also seen in Table 6. The best ROC Area is seen in the Pneumonia class (0.97) while the Normal class (0.93) recorded the least. In general, the Dual_Pachi model recorded an area of 0.95 for the COVID-19 class, 0.94 for the lung opacity class, 0.97 for the Pneumonia class and 0.93 for the Normal class. The best Class Ap is seen in the Pneumonia class (0.95) while its worst AP is in the COVID-19 class (0.80). In general, Dual_Pachi yielded an AP of 0.95 for the pneumonia class, 0.88 for the lung opacity class, 0.80 for the COVID-19 class and 0.88 for the Normal class. Fig. 6 depicts the best ROC and Ap performance of the proposed aproach on data_A for both Adam and SGD optimizer.
Table 6.
Data_A SGD Optimizer Receiver Operating Characteristic (ROC) and Precision-Recall (PR) Result. The parameter employed includes Learning rate (Lr): , categorical cross-entropy.
| Opt: SGD, Lr: , Lf: categorical cross-entropy | ||||||
|---|---|---|---|---|---|---|
| Without Bl. 3 | 0.85284 | 0.71417 | 0.90233 | 0.70741 | 0.70447 | 0.80465 |
| Dual_Pachi | 0.95151 | 0.90316 | 0.96772 | 0.90625 | 0.90127 | 0.93545 |
| ROC (Area) | Macro-Average | Micro-Average | COVID-19 | Lung Opacity | Normal | Pneumonia |
|---|---|---|---|---|---|---|
| Without Bl. 3 | 0.80 | 0.81 | 0.73 | 0.81 | 0.80 | 0.90 |
| Dual_Pachi | 0.95 | 0.95 | 0.95 | 0.94 | 0.93 | 0.97 |
| Precision-Recall (AP) | Micro-Average | COVID-19 | Lung Opacity | Normal | Pneumonia |
|---|---|---|---|---|---|
| Opt: SGD, Lr:, Lf: categorical cross-entropy | |||||
| Without Bl. 3 | 0.57 | 0.52 | 0.53 | 0.55 | 0.71 |
| Dual_Pachi | 0.87 | 0.80 | 0.88 | 0.88 | 0.95 |
Fig. 6.
The selected best ROC and Precision-Recall Curve of the Dual_Pachi on Data_A. A & B depicts the ROC and AP using the Adam optimizer, a learning rate of , and categorical smooth loss while C & D depicts that of SGD Optimizer, a learning rate of , and categorical cross-entropy loss.
5.3. Dual_Pachi experimental result (Data_B)
This section explains the result of the implemented models on Data_B. In line with the performance evaluation of Data_A, the same evaluation metrics and implementation stargates were used here. Just as in dataset_A, the Dual_Pachi model without the attention Block performance was improved with little to no change using the Adam Opt, learning rate (Lr), and categorical smooth loss function. However, when using Adam Opt, Lr and categorical cross-entropy loss function, its superiority was significant with an accuracy of 0.968, a sensitivity of 0.95203, specificity of 0.97594, precision of 0.95234, F1-score of 0.95208, and AUC of 0.96391 over 0.93067 accuracies, 0.89867 sensitivity, 0.94839 specificities, 0.90341 precision, 0.89684 F1-score and 0.92258 AUC. The Adam Opt, Lr and categorical smooth loss function provide the best performance. With a +0.01–0.04% difference in each of the implemented evaluation measures, the Dual_Pachi model outperformed the without attention Block model in all of the Adam optimizer (Opt) experiments.
With the SGD Opt, Lr and categorical smooth loss function, Dual_Pachi exhibits the best performance with an accuracy of 0.95822, a sensitivity of 0.93667, specificity of 0.96869, precision of 0.93759, F1-score of 0.93631, and AUC of 0.95304. According to Table 7 , the best performance for the Adam Opt Dual_Pachi model is at Lr and categorical smooth loss and Lr and categorical cross-entropy loss whereas the greatest performance for SGD is at the Lr. and categorical cross-entropy loss and Lr and categorical smooth loss.
Table 7.
Dual_Pachi Data_B classification Result. The optimizers employed include Adam and SGD, Lr; and , Loss function; Categorical_smooth_loss and categorical cross-entropy.
| Accuracy (%) | Sensitivity (%) | Specificity (%) | Precision (%) | F1 Score | AUC | |
|---|---|---|---|---|---|---|
| Opt: Adam, Lr: , Lf: categorical_smooth_loss | ||||||
| Without Bl. 3 | 0.95111 | 0.92693 | 0.96355 | 0.92656 | 0.92635 | 0.94532 |
| Dual_Pachi | 0.96356 | 0.94526 | 0.97239 | 0.94721 | 0.94578 | 0.95859 |
| Opt: Adam, Lr:, Lf: categorical_smooth_loss | ||||||
| Without Bl. 3 | 0.968 | 0.95206 | 0.97582 | 0.95273 | 0.95236 | 0.96373 |
| Dual_Pachi | 0.97867 | 0.96786 | 0.984 | 0.96803 | 0.96787 | 0.976 |
| Opt: Adam, Lr:, Lf: categorical cross-entropy | ||||||
| Without Bl. 3 | 0.92356 | 0.88615 | 0.94285 | 0.89449 | 0.88529 | 0.91428 |
| Dual_Pachi | 0.96356 | 0.94466 | 0.97263 | 0.94825 | 0.94431 | 0.95895 |
| Opt: Adam, Lr:, Lf: categorical cross-entropy | ||||||
| Without Bl. 3 | 0.93067 | 0.89867 | 0.94839 | 0.90341 | 0.89684 | 0.92258 |
| Dual_Pachi | 0.96800 | 0.95203 | 0.97594 | 0.95234 | 0.95208 | 0.96391 |
| Opt: SGD, Lr:, Lf: categorical_smooth_loss | ||||||
| Without Bl. 3 | 0.92533 | 0.88855 | 0.94388 | 0.89242 | 0.88831 | 0.91581 |
| Dual_Pachi | 0.95822 | 0.93667 | 0.96869 | 0.93759 | 0.93631 | 0.95304 |
| Opt: SGD, Lr:, Lf: categorical_smooth_loss | ||||||
| Without Bl. 3 | 0.88000 | 0.82111 | 0.91016 | 0.82465 | 0.81777 | 0.86524 |
| Dual_Pachi | 0.91556 | 0.87352 | 0.93677 | 0.87937 | 0.86920 | 0.90516 |
| Opt: SGD, Lr:, Lf: categorical cross-entropy | ||||||
| Without Bl. 3 | 0.93422 | 0.90223 | 0.95093 | 0.90577 | 0.90115 | 0.92640 |
| Dual_Pachi | 0.95022 | 0.92666 | 0.96309 | 0.92807 | 0.92547 | 0.94464 |
| Opt: SGD, Lr:, Lf: categorical cross-entropy | ||||||
| Without Bl. 3 | 0.91822 | 0.87731 | 0.93854 | 0.87891 | 0.87610 | 0.90781 |
| Dual_Pachi | 0.91911 | 0.87253 | 0.93767 | 0.89032 | 0.87594 | 0.90651 |
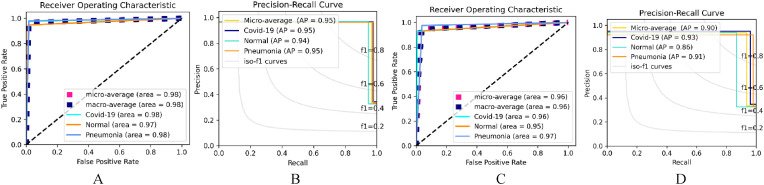
Table 8 shows the class performance of each model using the Receiver operating characteristics (ROC) curve and the precision-recall curve (PR) via the Adam Optimizer. For the categorical_smooth_loss, training with Lr, The Pneumonia class had a better area (0.97) followed by the COVID-19 class (0.96) and lastly the Normal class (0.95) which follows the same performance with Lr. For the categorical cross-entropy loss function, and Lr, the Pneumonia class had the best area (0.96), followed by the Normal class (0.90), and lastly the COVID-19 class (0.89) while training with Lr, the Normal class and the Pneumonia class had the same area (0.92) while the COVID-19 class had a better area (0.97). The AP performance is in synchronization with the ROC Performance. However, the Highest AP in all the implemented settings is seen in the COVID-19 class (0.95) via Lr and categorical_smooth_loss function and categorical cross-entropy. Also, the Pneumonia class (0.95) Lr and categorical_smooth_loss function while the least AP is seen in the Normal Class with an AP of 0.75 via Lr and categorical cross-entropy.
Table 8.
Dual_Pachi Adam optimizer implementation Receiver Operating Characteristic (ROC) and Precision-Recall (PR) classification Result. The parameter employed includes Lr: and , Lf: Categorical_smooth_loss and categorical cross-entropy.
| ROC (Area) | Macro-Average | Micro-Average | COVID-19 | Normal | Pneumonia |
|---|---|---|---|---|---|
| Opt: Adam, Lr: , Lf: categorical_smooth_loss | |||||
| Without Bl. 3 | 0.95 | 0.95 | 0.94 | 0.93 | 0.96 |
| Dual_Pachi | 0.96 | 0.96 | 0.96 | 0.95 | 0.97 |
| Opt: Adam, Lr:, Lf: categorical_smooth_loss | |||||
| Without Bl. 3 | 0.96 | 0.96 | 0.96 | 0.95 | 0.97 |
| Dual_Pachi | 0.98 | 0.98 | 0.98 | 0.97 | 0.98 |
| Opt: Adam, Lr:, Lf: categorical cross-entropy | |||||
| Without Bl. 3 | 0.91 | 0.91 | 0.89 | 0.90 | 0.96 |
| Dual_Pachi | 0.96 | 0.96 | 0.98 | 0.92 | 0.97 |
| Opt: Adam, Lr:, Lf: categorical cross-entropy | |||||
| Without Bl. 3 | 0.92 | 0.92 | 0.94 | 0.89 | 0.94 |
| Dual_Pachi | 0.96 | 0.96 | 0.97 | 0.96 | 0.96 |
| Precision-Recall (AP) | Micro-Average | COVID-19 | Normal | Pneumonia |
|---|---|---|---|---|
| Opt: Adam, Lr:, Lf: categorical_smooth_loss | ||||
| Without Bl. 3 | 0.88 | 0.86 | 0.87 | 0.92 |
| Dual_Pachi | 0.91 | 0.93 | 0.89 | 0.91 |
| Opt: Adam, Lr:, Lf: categorical_smooth_loss | ||||
| Without Bl. 3 | 0.92 | 0.92 | 0.90 | 0.95 |
| Dual_Pachi | 0.95 | 0.95 | 0.94 | 0.95 |
| Opt: Adam, Lr:, Lf: categorical cross-entropy | ||||
| Without Bl. 3 | 0.82 | 0.84 | 0.75 | 0.89 |
| Dual_Pachi | 0.91 | 0.95 | 0.89 | 0.90 |
| Opt: Adam, Lr:, Lf: categorical cross-entropy | ||||
| Without Bl. 3 | 0.84 | 0.81 | 0.80 | 0.91 |
| Dual_Pachi | 0.92 | 0.95 | 0.91 | 0.91 |
For the without-attention Block approach, using categorical_smooth_loss, training with and Lr, the Pneumonia class had a better area (0.97), followed by the COVID-19 class (0.96) and then the Normal class (0.95). For the categorical cross-entropy loss function, and Lr, the normal class had the least area (0.92) with the COVID-19 class having the highest (0.98), followed by the Pneumonia class (0.90). Using the Lr of , the COVID-19 and Pneumonia class had a better area (0.94), while the Normal class yielded the least result (0.89). The Precision-Recall curve depicts that the Pneumonia and the COVID-19 class had the highest AP recording an AP of 0.95 respectively but in a different training settings. The least AP was the Normal class (0.75) at the Lr of and categorical cross-entropy function. Generally, the best AP was seen at the Lr of and categorical_smooth_loss function with the COVID-19 class recording an AP of 0.92, Pneumonia recoding 0.95 and the normal class recording 0.90 while the worst AP is seen at the Lr of and categorical cross-entropy function with an AP of 0.81 (COVID-19), 0.80 (Normal class) and 0.91 (Pneumonia class).
Table 9 shows the ROC area and the AP of the Dual_Pachi using the SGD optimizer. The highest ROC area was seen in the Lr of and categorical_smooth_loss function which also yielded the best AP. However, the least ROC area was seen Lr of and categorical_smooth_loss function which also had the least AP. Among all the implemented setups, the COVID-19 and the Pneumonia class had the highest area (0.97) each while the COVID-19 recorded the best AP. Fig. 7 depicts the best ROC and Ap performance of the proposed aproach on data_A for both Adam and SGD optimizer.
Table 9.
Dual_Pachi SGD optimizer implementation Receiver Operating Characteristic (ROC) and Precision-Recall (PR) classification Result. The parameter employed includes Lr; and , Loss function; Categorical_smooth_loss and categorical cross-entropy.
| ROC (Area) | Macro-Average | Micro-Average | COVID-19 | Normal | Pneumonia |
|---|---|---|---|---|---|
| Optimizer: SGD, Lr: , Lf: categorical_smooth_loss | |||||
| Without Bl. 3 | 0.92 | 0.92 | 0.93 | 0.88 | 0.93 |
| Dual_Pachi | 0.95 | 0.95 | 0.97 | 0.92 | 0.97 |
| Opt: SGD, Lr:, Lf: categorical_smooth_loss | |||||
| Without Bl. 3 | 0.86 | 0.87 | 0.90 | 0.82 | 0.88 |
| Dual_Pachi | 0.90 | 0.91 | 0.94 | 0.84 | 0.93 |
| Opt: SGD, Lr:, Lf: categorical cross-entropy | |||||
| Without Bl. 3 | 0.93 | 0.93 | 0.96 | 0.90 | 0.92 |
| Dual_Pachi | 0.94 | 0.94 | 0.93 | 0.93 | 0.97 |
| Opt: SGD, Lr:, Lf: categorical cross-entropy | |||||
| Without Bl. 3 | 0.91 | 0.91 | 0.93 | 0.87 | 0.92 |
| Dual_Pachi | 0.91 | 0.91 | 0.93 | 0.87 | 0.92 |
| Precision-Recall (AP) | Micro-Average | COVID-19 | Normal | Pneumonia |
|---|---|---|---|---|
| Opt: SGD, Lr:, Lf: categorical_smooth_loss | ||||
| Without Bl. 3 | 0.83 | 0.81 | 0.79 | 0.88 |
| Dual_Pachi | 0.90 | 0.93 | 0.86 | 0.91 |
| Opt: SGD, Lr:, Lf: categorical_smooth_loss | ||||
| Without Bl. 3 | 0.73 | 0.75 | 0.71 | 0.75 |
| Dual_Pachi | 0.80 | 0.85 | 0.76 | 0.81 |
| Opt: SGD, Lr:, Lf: categorical cross-entropy | ||||
| Without Bl. 3 | 0.85 | 0.86 | 0.79 | 0.89 |
| Dual_Pachi | 0.88 | 0.89 | 0.82 | 0.93 |
| Opt: SGD, Lr:, Lf: categorical cross-entropy | ||||
| Without Bl. 3 | 0.81 | 0.83 | 0.77 | 0.83 |
| Dual_Pachi | 0.81 | 0.81 | 0.79 | 0.84 |
Fig. 7.
The selected best ROC and Precision-Recall Curve of the Dual_Pachi on Data_B. A & B depicts the Adam optimizer ROC and AP while C & D depicts the SGD optimizer.
6. Discussions
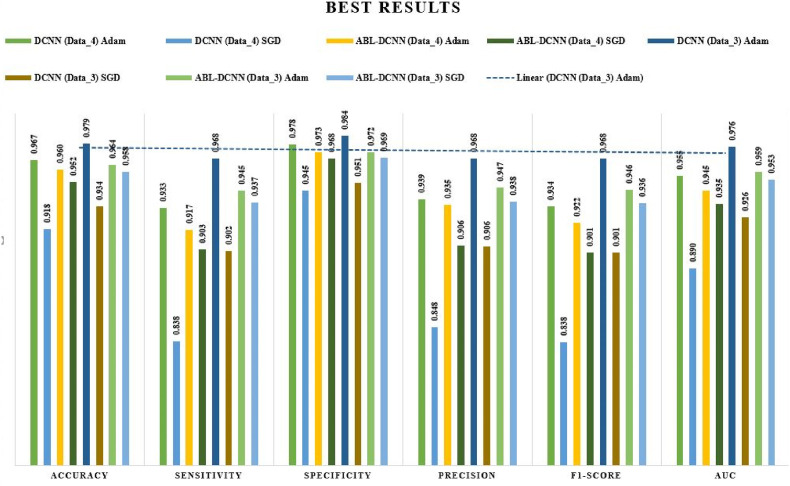
This paper focused its discussion mainly on the effects of the hyperparameters used in the training of the models. As seen in Fig. 2, Dual_Pachi is made up of four blocks the attention mechanism being the 3rd block. As discussed earlier, in the field of computer vision, attention mechanisms have proven to be a promising approach to tackling the task with feature extraction difficulties. Thus, we experimented on the proposed Dual_Pachi with and without the attention mechanism block to verify its contribution to the performance of the Daul_Pachi model. Fig. 8 summarizes all the results. From Table 4, it was noticed that the Dual_Pachi model without the attention block performs much better on Data_A when trained with the Adam optimizer, with a learning rate of on both categorical_smooth_loss and categorical cross-entropy loss functions. However, the Dual_Pachi outperformed the without-attention block approach in all the experiments (Adam and SGD optimizer.). The best Dual_Pachi without the attention block result on data_A yielded an accuracy of 0.96656, sensitivity of 0.93315, specificity of 0.97774, precision of 0.93905, F1-score of 0.93389 and AUC of 0.95547 while that of Dual_Pachi yielded an 0.95987 accuracy, 0.91747 sensitivity, 0.97255 specificity, 0.93502 precision, 0.92233 F1-score and 0.9451 AUC.
Fig. 8.
Graphical illustration of the optimal hyperparameters for the two proposed approaches on both datasets.
Notwithstanding, the Dual_Pachi results show that the optimal best hyperparameter settings were not met as the different implementation setups all yielded an accuracy of 0.95 except for the Adam optimizer, a learning rate of , categorical cross-entropy loss function with all the SGD optimizer experiments exclusively of SGD optimizer, a learning rate of and categorical cross-entropy loss. Dual_Pachi model results indicate that little finetuning of the number of heads and MLP will yield a better result as recorded in the table. Comparing the Area and AP of the individual classes, the COVID-19 class was in competition with the lung opacity class for the best results in all the experiments carried out while pneumonia and the normal class remain the least AP and area although the Pneumonia class was much better than the normal class. This also entails that the proposed model is robust enough to classify the classes differently.
The results obtained on Data_B are also in line with the results of Data_A. The without-attention block approach using the Adam optimizer, a learning rate of on both categorical_smooth_loss and categorical cross-entropy loss function is in uniformity with the Dual_Pachi model with +0.01%–0.02%. However, the Dual_Pachi supersedes all other experimental setup results. the best and worst result for the without attention block is seen at the Adam optimizer, a learning rate of and categorical_smooth_loss and SGD optimizer, a learning rate of and categorical smooth loss which is also the same as that of the Dual_Pachi. An obvious remark is seen between the performance of the without attention block and the Dual_Pachi which is the lowest yielded result of the Dual_Pachi is +0.1–0.5% higher. We summarize this discussion by strongly believing that the Dual_Pachi model when trained with its optimal hyperparameters supersedes the without-attention block approach.
6.1. Ablation studies of the implemented models (Data_A)
The quantitative ablation studies are examined in this section between the baseline, the without attention block and the Dual_Pachi model as shown in Table 10 . Data_A is chosen for this experiment as models tend to perform poorly when multiple classes with fewer samples are used for training. Hence robust models are designed to perform well irrespective of the number of training samples involved. The quantitative studies also saw the differently implemented hyperparameters (optimizer, learning rate and Loss function). From Table 10, there are significant contributions with +0.03512 in accuracy, +0.07574 in sensitivity, +0.02281 in specificity, +0.06488 in precision, +0.07308 in F1-Score, and +0.07971 AUC by the without attention block. 3 while the Dual_Pachi had a +0.05351 in accuracy, +0.10556 in sensitivity, +0.03475 in specificity, +0.09229 in precision, +0.10647 in F1-score and +0.06838 in AUC. For the experiment using the Adam optimizer, the contribution of the two approaches is a significant sequel to the training setups.
Table 10.
Dual_Pachi Quantitative Ablation studies illustrate the contribution of each part in the model performance using Data_A.
| Accuracy (%) | Sensitivity (%) | Specificity (%) | Precision (%) | F1 Score | AUC | |
|---|---|---|---|---|---|---|
| Opt: Adam, Lr: , Lf: categorical_smooth_loss | ||||||
| Baseline | 0.90468 | 0.81116 | 0.93631 | 0.83653 | 0.81355 | 0.87373 |
| Without Bl. 3 | +0.05351 | +0.10556 | +0.03475 | +0.09229 | +0.10647 | +0.06838 |
| Dual_Pachi | +0.06188 | +0.12199 | +0.04143 | +0.10252 | +0.12034 | +0.08174 |
| Opt: Adam, Lr:, Lf: categorical cross-entropy | ||||||
| Baseline | 0.91973 | 0.84466 | 0.94713 | 0.85426 | 0.84114 | 0.89426 |
| Without Bl. 3 | +0.03512 | +0.06766 | +0.02165 | +0.06683 | +0.07206 | +0.0433 |
| Dual_Pachi | +0.04014 | +0.07281 | +0.02542 | +0.08076 | +0.08119 | +0.05084 |
| Opt: SGD, Lr:, Lf: categorical_smooth_loss | ||||||
| Baseline | 0.88294 | 0.76244 | 0.92221 | 0.78338 | 0.76471 | 0.84442 |
| Without Bl. 3 | +0.03512 | +0.07574 | +0.02281 | +0.06488 | +0.07308 | +0.07971 |
| Dual_Pachi | +0.05184 | +0.10519 | +0.03412 | +0.09559 | +0.10359 | +0.06823 |
We further visualize the role of the implemented attention mechanism of the Dual_Pachi model as shown in Fig. 9 . The implemented attention mechanism is a multi-head attention mechanism and it involved dividing the input images into patches and embeddings. The embedding retains the potions of the images that were divided into patches by so doing helps the model to remember the initial input structure during output. 2D learnable convolutions were used for the patch conversions. In addition, the attention mechanism proximity increases as the depth of the network increase too. Fig. 9 depicts the area where the attention mechanism model focuses via the input image relevant for recognition and classification.
Fig. 9.
The proposed attention mechanism helps the model to focus on the semantic information in the Chest X-Ray image that is relevant for identification.
6.2. Comparison with the state-of-the-art deep learning models
Comparison with the state-of-the-art was done with the optimal setting result of the implemented models. We compared the models on Data_A and Data_B results. With the Dual_Pachi model, we recorded 0.96656 accuracy, 0.93315 sensitivity, 0.97774 specificity, 0.93905 precision, 0.93389 F-1 score and 0.95547 AUC score on Data_A and 0.97867 accuracy, 0.96786 sensitivity, 0.984 specificity, 0.96803 precision, 0.96787 F-1 score and 0.976 AUC score on Data_B while the without attention block model achieve 0.95987 accuracy, 0.91747 sensitivity, 0.97255 specificity, 0.93502 precision, 0.92233 F-1 score and 0.9451 AUC score on Data_A and 0.968 accuracy, 0.95206 sensitivity, 0.97582 specificity, 0.95273 precision, 0.95236 F-1 score and 0.96373 AUC score on Data_B. We first compared with models that used the same dataset as ours as shown in Table 11, Table 12 .
Table 11.
Deep_Pachi comparison with state-of-the-art data_A.
| Ref | Year | Model | Accuracy | Precision | Sensitivity | F1-Score |
|---|---|---|---|---|---|---|
| Khan et al. (Strategy 1) [56] | 2022 | EfficientNetB1 | 92 | 91.75 | 94.50 | 92.75 |
| NasNetMobile | 89.30 | 89.25 | 91.75 | 91 | ||
| MobileNetV2 | 90.03 | 92.25 | 92 | 91.75 | ||
| Khan et al. (Strategy 2) [56] | 2022 | EfficientNetB1 | 96.13 | 97.25 | 96.50 | 97.50 |
| NasNetMobile | 94.81 | 95.50 | 95 | 95.25 | ||
| MobileNetV2 | 93.96 | 94.50 | 95 | 94.50 | ||
| Mondal et al. [54] | 2022 | Local Global Attention Network | 95.87 | 95.56 | 95.99 | 95.74 |
| Shi et al. [55] | 2021 | Teacher Student Attention | 91.38 | 91.65 | 90.86 | 91.24 |
| Li et al. [53] | 2021 | Mag-SD | 92.35 | 92.50 | 92.20 | 92.34 |
| Khan et al. [52] | 2020 | CoroNet | 89.6 | 90.0 | 96.4 | 89.8 |
| Wang et al. [26] | 2020 | COVIDNet | 90.78 | 91.1 | 90.56 | 90.81 |
| Ours | 2022 | Dual_Pachi | 96.65 | 93.90 | 93.31 | 93.38 |
| Ours | 2022 | Without attention Block | 95.98 | 93.50 | 91.74 | 92.23 |
Table 12.
State-of-the-art model comparison on Data_B.
| Ref | Year | Model | Accuracy | Precision | Sensitivity | F1-Score |
|---|---|---|---|---|---|---|
| Luz et al. [37] | 2021 | EfficientNet-B0 | 0.89 | 0.88 | 0.89 | 0.88 |
| Shome et al. [57] | 2021 | COVID-Transformer | 0.92 | 0.93 | 0.89 | 0.91 |
| M.-L. Huang et al., 2022 [58] | (First Approach) | InceptionV3 | 96.5 | 96.7 | 96.8 | 96.7 |
| ResNet50v2 | 95.1 | 95.2 | 95.1 | 95.1 | ||
| Xception | 95.9 | 96.5 | 96.0 | 96.5 | ||
| DenseNet121 | 94.7 | 94.7 | 94.6 | 95.0 | ||
| MobileNetV2 | 96.4 | 96.3 | 96.3 | 96.0 | ||
| EfficientNet-B0 | 94.8 | 94.5 | 94.5 | 94.5 | ||
| EfficientNetV2-S | 94.8 | 94.8 | 94.8 | 94.6 | ||
| 3 Classes (Second Approach) | InceptionV3 | 97.7 | 96.7 | 96.7 | 96.8 | |
| ResNet50v2 | 97.1 | 96.8 | 96.9 | 96.9 | ||
| Xception | 97.3 | 96.5 | 96.4 | 96.2 | ||
| DenseNet121 | 95.4 | 95.1 | 95.3 | 95.2 | ||
| MobileNetV2 | 97.7 | 96.6 | 96.7 | 96.4 | ||
| EfficientNet-B0 | 96.8 | 96.7 | 96.6 | 96.6 | ||
| EfficientNetV2-S | 96.7 | 96.8 | 96.8 | 96.7 | ||
| Ours | 2022 | Dual_Pachi | 0.98 | 0.97 | 0.97 | 0.97 |
| Ours | 2022 | Without Attention Block | 0.97 | 0.95 | 0.95 | 0.95 |
A comparison of Data_A utilizing accuracy, precision, sensitivity, and F1-score is shown in Table 11. For COVID-19 multiclassification, Wang et al. [26] recommended using COVIDNet, but Khan et al. [52] suggested using CoroNet. However, the COVIDNet model beats the CoroNet model, with an accuracy of 90.78%, precision of 91.18%, and F1-Score of 90.81% compared to 89.68%, precision of 90.08%, and F1-Score of 89.88%. However, in terms of sensitivity, the CoroNet model beat the COVIDNet model (96.4%). The Mag-SD model was suggested by Li et al. [53] who also attained 92.35% accuracy, 92.50% precision, 92.20% sensitivity, and 92.34% F1-Score. The use of an attention mechanism was suggested by Mondal et al. [54] and Shi et al. [55] to enhance feature extraction understanding of Chest X-ray images. The Teacher-Student Attention Scale was presented by Shi et al. [55]. The accuracy was higher than with the earlier methods, reaching 91.38%. The Local-Global Attention Network was developed by Mondal et al. [54] and surpassed earlier state-of-the-art models in terms of classification accuracy (95.87%), precision (95.56%), sensitivity (95.99%), and F1-score (95.74%). The author of Ref. [56] utilized the same dataset and two different CXr classification algorithms in this work. The EfficientNetB1 (Strategy 2) produced the greatest classification results, with 92% accuracy, 91.75% precision, 94.50% sensitivity, and 92.75% F1-Score. Both strategies used NasNetMobile, MobileNetV2, and EfficientNetB1. As seen in Table 11, the model we used in this investigation performed better in terms of accuracy. However, due to the number of training sets used from this dataset, we obtained an acceptable sensitivity, Precision and F1-Score.
The EfficientNet-B0 was used by Luz et al. [37], however, the recorded result is not encouraging. The COVID-Transformer network was utilized by Shome et al. [57] to achieve 92% accuracy, 93% precision, 89% sensitivity, and 91% F1 score. Seven pre-trained deep learning models were used by Huang et al. [58] in two situations. He first adjusted without paying attention to how to make the models' computations simpler, and then he did so while paying attention to the models' computational complexity. His results showed that the less computationally difficult model produced better outcomes than the traditional approach, which is a step forward for the medical industry. The Dual_Pachi first block is designed keeping in mind the goal of creating models with a lower computational cost while producing better accuracy and precision. In conclusion, the Dual_Pachi showed the greatest degree of precision, indicating that the proposed classifier seldom misclassifies negative samples as positive values. The classifier can recognize the majority of positive samples that belong to each class, as evidenced by the fact that we obtained the highest recall score. When compared to baseline techniques, the recommended method has the highest F1 score, which suggests that it is the most balanced in terms of precision and sensitivity.
6.3. Limitations and future works
Notwithstanding, this paper identified some limitations of the proposed approach. First, the result of the Dual_Pachi shows that the optimal sensitivity parameter setting was not met for the performance of the model due to the available resources for the experiment. Secondly, the suggested model did not take any Image Feature enhancement approaches into account such as Multi-Scale Retinex with Color Restoration (MSRCR), Contrast Limited Adaptive Histogram Equalization (CLAHE) and Multi-Scale Retinex with chromaticity preservation (MSRCP). Thirdly, the severity of COVID-19 illness was not considered a sub-classification (mild, moderate, or severe disease). We also observe that the chest X-ray dataset only shows one series for a patient, supporting the claim made by Ref. [34] that a small dataset (one chest x-ray series for a patient) cannot be used to predict whether a patient would develop a radiographic abnormality as the disease advances.
As a future study, this study will address the highlighted shortcomings. Before using feature extraction models, image-enhancing techniques such as Contrast Limited AHE (CLAHE), Canny edge detection, import local binary pattern, and so on will be applied to the input image. Other medical image modalities will be used to assess the robustness of the model in medical image disease classification. Furthermore, we will incorporate the use of automatic data annotation [59] by utilizing discretization learning and contemporary Neural Network topologies to evaluate prediction variance as well as demonstrate the ability of the proposed model in classifying distorted images after being trained on a real image.
7. Conclusion
In this study, a new Attention Based Dual Path Framework with Intermediate Second Order-Pooling termed Dual_Pachi is proposed for early detection and accurate feature extraction of Chest X-ray images for COVID-19 detection. Two new architectures are explored in this study. Dual_Pachi with attention block and Dual_Pachi without attention block. These two models were experimented with using two large publicly available datasets; COVID-19 Radiography Dataset [48] (Data_A) and ChestX-ray-15k dataset [49] (Data_B) and evaluated using accuracy, sensitivity, specificity, precision, F1-score and AUC evaluation metrics. The proposed model performance supports the claims of its robust feature extraction of the chest X-ray Images. The two-branch channel treatment (L channel and AB channel) in addition to the global second-order pooling and attention mechanism (Multi-head self-attention) focused on the low-level visual information and the high-level semantics of Chest X-ray image features without sacrificing performance. According to the experimental results, the proposed models yielded an acceptable result with an accuracy of 0.96656 (Data_A) and 0.97867 (Data_B) for the Dual_Pachi approach and an accuracy of 0.95987 (Data_A) and 0.968 (Data_B) for the Dual_Pachi without attention block model. From the established result, we saw the contribution of the attention mechanism in the proposed Dual_Pachi model. According to the results, the proposed models outperform traditional deep learning models and other state-of-the-art approaches described in the literature in terms of COVID-19 identification. A Grad-CAM-based visualization is also built to highlight where the applied attention mechanism is concentrating for suitable low and high-level semantic feature extraction of the chest x-ray images.
Code availability/Availability of data
Both https://github.com/abeerbadawi/COVID-ChestXray15k-Dataset-Transfer-Learning (retrieved: August 17, 2022). and https://www.kaggle.com/datasets/tawsifurrahman/covid19-radiography-database (retrieved: 12 August 2022) provides access to the dataset utilized in this study. The TensorFlow/Keras code we utilized in our experiment is not currently accessible to the general public, but it will be when the study is published.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Informed consent
Informed consent was obtained from all participants included in the study.
Declaration of competing interest
All authors declare that they have no conflict of interest.
Acknowledgments
This research is supported by the National Science Foundation of China (NSFC) under the project “Development of fetal heart-oriented heart sound echocardiography multimodal auxiliary diagnostic equipment” (62027827). We also acknowledge the Network and Data Security Key Laboratory of Sichuan for providing us with a good environment for the study.
References
- 1.Pang L., Liu S., Zhang X., Tian T., Zhao Z. Transmission dynamics and control strategies of COVID-19 in Wuhan, China. J. Biol. Syst. 2020;28(3):543–560. doi: 10.1142/S0218339020500096. [DOI] [Google Scholar]
- 2.Zheng J. SARS-coV-2: an emerging coronavirus that causes a global threat. Int. J. Biol. Sci. 2020;16(10):1678–1685. doi: 10.7150/ijbs.45053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shereen M.A., Khan S., Kazmi A., Bashir N., Siddique R. COVID-19 infection: origin, transmission, and characteristics of human coronaviruses. J. Adv. Res. 2020;24:91–98. doi: 10.1016/j.jare.2020.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zaim S., Chong J.H., Sankaranarayanan V., Harky A. COVID-19 and multiorgan response. Curr. Probl. Cardiol. 2020;45(8) doi: 10.1016/j.cpcardiol.2020.100618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hani C., et al. COVID-19 pneumonia: a review of typical CT findings and differential diagnosis. Diagnos. Interven. Imag. 2020;101(5):263–268. doi: 10.1016/j.diii.2020.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lewnard J.A., Lo N.C. Scientific and ethical basis for social-distancing interventions against COVID-19. Lancet Infect. Dis. 2020;20(6):631–633. doi: 10.1016/S1473-3099(20)30190-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang Y., Kang H., Liu X., Tong Z. Combination of RT-qPCR testing and clinical features for diagnosis of COVID-19 facilitates management of SARS-CoV-2 outbreak. J. Med. Virol. 2020;92(6):538–539. doi: 10.1002/jmv.25721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li Y., et al. Stability issues of RT-PCR testing of SARS-CoV-2 for hospitalized patients clinically diagnosed with COVID-19. J. Med. Virol. 2020;92(7):903–908. doi: 10.1002/jmv.25786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ai T., et al. Correlation of chest CT and RT-PCR testing for coronavirus disease 2019 (COVID-19) in China: a report of 1014 cases. Radiology. 2020;296(2):E32–E40. doi: 10.1148/radiol.2020200642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nelson R.C., Feuerlein S., Boll D.T. New iterative reconstruction techniques for cardiovascular computed tomography: how do they work, and what are the advantages and disadvantages. J. Cardiovasc. Comput. Tomogr. 2011;5(5):286–292. doi: 10.1016/j.jcct.2011.07.001. [DOI] [PubMed] [Google Scholar]
- 11.Ukwuoma C.C., Zhiguang Q., Hossin M.A., Cobbinah B.M., Oluwasanmi A., Chikwendu I.A., Ejiyi C.J., Abubakar H.S. 2021 4th International Conference on Pattern Recognition and Artificial Intelligence (PRAI) Aug. 2021. Holistic attention on pooling based cascaded partial decoder for real-time salient object detection. [DOI] [Google Scholar]
- 12.Akkus Z., Galimzianova A., Hoogi A., Rubin D.L., Erickson B.J. Deep learning for brain MRI segmentation: state of the art and future directions. J. Digit. Imag. 2017;30(4):449–459. doi: 10.1007/s10278-017-9983-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yamanakkanavar N., Choi J.Y., Lee B. MRI segmentation and classification of the human brain using deep learning for diagnosis of Alzheimer's disease: a survey. Sensors. 2020;20(11):1–31. doi: 10.3390/s20113243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ardakani A.A., Kanafi A.R., Acharya U.R., Khadem N., Mohammadi A. Application of deep learning technique to manage COVID-19 in routine clinical practice using CT images: results of 10 convolutional neural networks. Comput. Biol. Med. 2020;121 doi: 10.1016/j.compbiomed.2020.103795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hesamian M.H., Jia W., He X., Kennedy P. Deep learning techniques for medical image segmentation: achievements and challenges. J. Digit. Imag. 2019;32(4):582–596. doi: 10.1007/s10278-019-00227-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Das D., Santosh K.C., Pal U. Truncated inception net: COVID-19 outbreak screening using chest X-rays. Phys. Eng. Sci. Med. 2020;43(3):915–925. doi: 10.1007/s13246-020-00888-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chin E.T., Huynh B.Q., Chapman L.A.C., Murrill M., Basu S., Lo N.C. Frequency of routine testing for coronavirus disease 2019 (COVID-19) in high-risk healthcare environments to reduce outbreaks. Clin. Infect. Dis. 2021;73(9):E3127–E3129. doi: 10.1093/cid/ciaa1383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mahmud T., Rahman M.A., Fattah S.A. CovXNet: a multi-dilation convolutional neural network for automatic COVID-19 and other pneumonia detection from chest X-ray images with transferable multi-receptive feature optimization. Comput. Biol. Med. 2020;122 doi: 10.1016/j.compbiomed.2020.103869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dinh P.H. Combining Gabor energy with equilibrium Opt algorithm for multi-modality medical image fusion. Biomed. Signal Process Control. 2021;68 doi: 10.1016/j.bspc.2021.102696. [DOI] [Google Scholar]
- 20.Dinh P.H. A novel approach based on Grasshopper optimization algorithm for medical image fusion. Expert Syst. Appl. 2021;171 doi: 10.1016/j.eswa.2021.114576. [DOI] [Google Scholar]
- 21.Ukwuoma C.C., Hossain M.A., Jackson J.K., Nneji G.U., Monday H.N., Qin Z. Multi classification of breast cancer lesions in histopathological images using DEEP_pachi: multiple self-attention head. Diagnostics. May 2022;12(5):1152. doi: 10.3390/diagnostics12051152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ukwuoma C.C., Qin Z., Yussif S.B., Happy M.N., Nneji G.U., Urama G.C., Ukwuoma C.D., Darkwa N.B., Agobah H. Animal species detection and classification framework based on modified multiscale attention mechanism and feature pyramid network. Sci. Afr. Jul. 2022;16 doi: 10.1016/j.sciaf.2022.e01151. [DOI] [Google Scholar]
- 23.Wang Z., et al. Automatically discriminating and localizing COVID-19 from community-acquired pneumonia on chest X-rays. Pattern Recogn. 2021;110 doi: 10.1016/j.patcog.2020.107613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ozturk T., Talo M., Yildirim E.A., Baloglu U.B., Yildirim O., Rajendra Acharya U. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Comput. Biol. Med. 2020;121 doi: 10.1016/j.compbiomed.2020.103792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Khan S.H., Sohail A., Zafar M.M., Khan A. Coronavirus disease analysis using chest X-ray images and a novel deep convolutional neural network. Photodiagnosis Photodyn. Ther. 2021;35 doi: 10.1016/j.pdpdt.2021.102473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wang L., Lin Z.Q., Wong A. COVID-Net: a tailored deep convolutional neural network design for detection of COVID-19 cases from chest X-ray images. Sci. Rep. 2020;10(1) doi: 10.1038/s41598-020-76550-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Afshar P., Heidarian S., Naderkhani F., Oikonomou A., Plataniotis K.N., Mohammadi A. COVID-CAPS: a capsule network-based framework for identification of COVID-19 cases from X-ray images. Pattern Recogn. Lett. 2020;138:638–643. doi: 10.1016/j.patrec.2020.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wang S., et al. A deep learning algorithm using CT images to screen for Coronavirus disease (COVID-19) Eur. Radiol. 2021;31(8):6096–6104. doi: 10.1007/s00330-021-07715-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Narin A., Kaya C., Pamuk Z. Automatic detection of coronavirus disease (COVID-19) using X-ray images and deep convolutional neural networks. Pattern Anal. Appl. 2021;24(3):1207–1220. doi: 10.1007/s10044-021-00984-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Minaee S., Kafieh R., Sonka M., Yazdani S., Jamalipour Soufi G. Deep-COVID: predicting COVID-19 from chest X-ray images using deep transfer learning. Med. Image Anal. 2020;65 doi: 10.1016/j.media.2020.101794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jain R., Gupta M., Taneja S., Hemanth D.J. Deep learning-based detection and analysis of COVID-19 on chest X-ray images. Appl. Intell. 2021;51(3):1690–1700. doi: 10.1007/s10489-020-01902-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Apostolopoulos I.D., Mpesiana T.A. Covid-19: automatic detection from X-ray images utilizing transfer learning with convolutional neural networks. Phys. Eng. Sci. Med. 2020;43(2):635–640. doi: 10.1007/s13246-020-00865-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Basu S., Mitra S., Saha N. 2020 IEEE Symposium Series on Computational Intelligence, SSCI 2020. 2020. Deep learning for screening COVID-19 using chest X-ray images; pp. 2521–2527. [DOI] [Google Scholar]
- 34.Panwar H., Gupta P.K., Siddiqui M.K., Morales-Menendez R., Singh V. Application of deep learning for fast detection of COVID-19 in X-Rays using nCOVnet. Chaos, Solit. Fractals. 2020;138 doi: 10.1016/j.chaos.2020.109944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sethy P.K., Behera S.K., Ratha P.K., Biswas P. Detection of coronavirus disease (COVID-19) based on deep features and support vector machine. Int. J. Math. Eng. Manag. Sci. 2020;5(4):643–651. doi: 10.33889/IJMEMS.2020.5.4.052. [DOI] [Google Scholar]
- 36.Asif S., Wenhui Y., Jin H., Jinhai S. 2020 IEEE 6th International Conference on Computer and Communications. ICCC; 2020. Classification of COVID-19 from chest X-ray images using deep convolutional neural network; pp. 426–433. [DOI] [Google Scholar]
- 37.Luz E., et al. Towards an effective and efficient deep learning model for COVID-19 patterns detection in X-ray images. Res. Biomed. Eng. 2022;38(1):149–162. doi: 10.1007/s42600-021-00151-6. [DOI] [Google Scholar]
- 38.Hussain E., Hasan M., Rahman M.A., Lee I., Tamanna T., Parvez M.Z. CoroDet: a deep learning based classification for COVID-19 detection using chest X-ray images. Chaos, Solit. Fractals. 2021;142 doi: 10.1016/j.chaos.2020.110495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Karakanis S., Leontidis G. Lightweight deep learning models for detecting COVID-19 from chest X-ray images. Comput. Biol. Med. 2021;130 doi: 10.1016/j.compbiomed.2020.104181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hammoudi K., et al. Deep learning on chest X-ray images to detect and evaluate pneumonia cases at the era of COVID-19. J. Med. Syst. 2021;45(7) doi: 10.1007/s10916-021-01745-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Khan S.H., et al. COVID-19 detection in chest X-ray images using deep boosted hybrid learning. Comput. Biol. Med. 2021;137 doi: 10.1016/j.compbiomed.2021.104816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Muhammad U., Hoque M.Z., Oussalah M., Keskinarkaus A., Seppänen T., Sarder P. SAM: self-augmentation mechanism for COVID-19 detection using chest X-ray images. Knowl. Base Syst. 2022;241 doi: 10.1016/j.knosys.2022.108207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shrivastava V.K., Pradhan M.K. Diagnosis of COVID-19 based on chest X-ray images using pre-trained deep convolutional neural networks. Intell. Decis. Technol. Apr. 2022;16(1):169–180. doi: 10.3233/idt-210002. [DOI] [Google Scholar]
- 44.Redie D.K., et al. Diagnosis of COVID-19 using chest X-ray images based on modified DarkCovidNet model. Evolution. Intell. Mar. 2022 doi: 10.1007/s12065-021-00679-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ismael A.M., Şengür A. Deep learning approaches for COVID-19 detection based on chest X-ray images. Expert Syst. Appl. Feb. 2021;164 doi: 10.1016/j.eswa.2020.114054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Demir F., Demir K., Şengür A. DeepCov19Net: automated COVID-19 disease detection with a robust and effective technique deep learning approach. New Generat. Comput. Jan. 2022 doi: 10.1007/s00354-021-00152-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Toda Y., Okura F. How convolutional neural networks diagnose plant disease. Plant Phenomics. Mar. 2019:1–14. doi: 10.34133/2019/9237136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sergey I., Szegedy C. International Conference on Machine Learning. PMLR; Lille, France: 2015. Batch normalization: accelerating deep network training by reducing internal covariate shift; pp. 448–456. [Google Scholar]
- 49.H. Dan, and K. Gimpel. Gaussian Error Linear Units (Gelus). arXiv 2016, arXiv:1606.08415.
- 50.Chowdhury M.E.H., Rahman T., Khandakar A., Mazhar R., Kadir M.A., Mahbub Z.B., Islam K.R., Khan M.S., Iqbal A., Emadi N.A., Reaz M.B.I., Islam M.T. Can AI help in screening viral and COVID-19 pneumonia? IEEE Access. 2020;8:132665–132676. doi: 10.1109/ACCESS.2020.3010287. [DOI] [Google Scholar]
- 51.Badawi A., Elgazzar K. Detecting coronavirus from chest X-rays using transfer learning. COVID. Sep. 2021;1(1):403–415. doi: 10.3390/covid1010034. [DOI] [Google Scholar]
- 52.Khan A.I., Shah J.L., Bhat M.M. CoroNet: a deep neural network for detection and diagnosis of COVID-19 from chest x-ray images. Comput. Methods Progr. Biomed. Nov. 2020;196 doi: 10.1016/j.cmpb.2020.105581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Li J., Wang Y., Wang S., Wang J., Liu J., Jin Q., Sun L. Multiscale Attention guided network for COVID-19 diagnosis using chest X-ray images. IEEE J. Biomed. Health Inform. May 2021;25(5):1336–1346. doi: 10.1109/JBHI.2021.3058293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Mondal A.K. COVID-19 prognosis using limited chest X-ray images. Appl. Soft Comput. Jun. 2022;122 doi: 10.1016/j.asoc.2022.108867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Shi W., Tong L., Zhu Y., Wang M.D. COVID-19 automatic diagnosis with radiographic imaging: explainable attention transfer deep neural networks. IEEE J. Biomed. Health Inform. Jul. 2021;25(7):2376–2387. doi: 10.1109/JBHI.2021.3074893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Khan E., Rehman M.Z.U., Ahmed F., Alfouzan F.A., Alzahrani N.M., Ahmad J. Chest X-ray classification for the detection of COVID-19 using deep learning techniques. Sensors. Feb. 2022;22(3):1211. doi: 10.3390/s22031211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Shome D., Kar T., Mohanty S., Tiwari P., Muhammad K., AlTameem A., Zhang Y., Saudagar A. COVID-transformer: interpretable COVID-19 detection using vision transformer for healthcare. Int. J. Environ. Res. Publ. Health. Oct. 2021;18(21):11086. doi: 10.3390/ijerph182111086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Huang M.-L., Liao Y.-C. A lightweight CNN-based network on COVID-19 detection using X-ray and CT images. Comput. Biol. Med. Jul. 2022;146 doi: 10.1016/j.compbiomed.2022.105604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.De Sousa Ribeiro F., Calivá F., Swainson M., Gudmundsson K., Leontidis G., Kollias S. Deep bayesian self-training. Neural Comput. Appl. Jul. 2019;32(9):4275–4291. doi: 10.1007/s00521-019-04332-4. [DOI] [Google Scholar]