Localization of Craniomaxillofacial Landmarks on CBCT Images Using 3D Mask R-CNN and Local Dependency Learning

Abstract

Cephalometric analysis relies on accurate detection of craniomaxillofacial (CMF) landmarks from cone-beam computed tomography (CBCT) images. However, due to the complexity of CMF bony structures, it is difficult to localize landmarks efficiently and accurately. In this paper, we propose a deep learning framework to tackle this challenge by jointly digitalizing 105 CMF landmarks on CBCT images. By explicitly learning the local geometrical relationships between the landmarks, our approach extends Mask R-CNN for end-to-end prediction of landmark locations. Specifically, we first apply a detection network on a down-sampled 3D image to leverage global contextual information to predict the approximate locations of the landmarks. We subsequently leverage local information provided by higher-resolution image patches to refine the landmark locations. On patients with varying non-syndromic jaw deformities, our method achieves an average detection accuracy of 1.38±0.95 mm, outperforming a related state-of-the-art method.

I. INTRODUCTION

CRANIOMAXILLOFACIAL (CMF) surgery repositions displaced bones and reconstructs deformed or missing skeletons [1]. For accurate surgical planning, the deformity of CMF anatomy is quantitatively analyzed via cephalometric analysis based on bony landmarks detected using cone-beam computed tomography (CBCT) scans. An automatic system described in [1] utilizes the detected landmarks to analyze deformity, and creates a 3D prediction of the patient’s surgical outcomes. More than 100 anatomical landmarks need to be manually localized (digitized) by surgeons or experienced technicians [1]. This is a time-consuming process, thus automated landmark digitization methods are highly desirable to speed up surgical planning.

Automated landmark detection has been comprehensively studied in the computer vision community [2]–[4]. Application of these methods to medical images requires the following considerations: 1) Natural and medical images differ significantly in appearance, dimensionality, and scale, and 2) Network training using medical image volumes is limited by memory capacity and sample size. Over the years, traditional machine learning-based algorithms have been used for locations of landmarks in medical images [5]–[7]. They typically extract handcrafted features to train a classification or regression model, which often results in suboptimal detection performance due to the inconsistency between feature extraction and model construction. More recently, deep learning-based methods have been proposed for localizing anatomical landmarks [8]–[11]. The performance of these methods is limited by small training datasets and large computational consumption when trained with whole images in an end-to-end manner. Implementing networks with high-resolution image patches can potentially avoid this problem. However, global anatomical information is neglected, consequently leading to miss-detections.

Existing learning-based methods typically ignore inter-landmark dependency. The relative locations of CMF landmarks are relatively stable; therefore effectively modeling the inner landmark dependency can reduce misdetections, especially for landmarks located on bony structures with similar appearances.

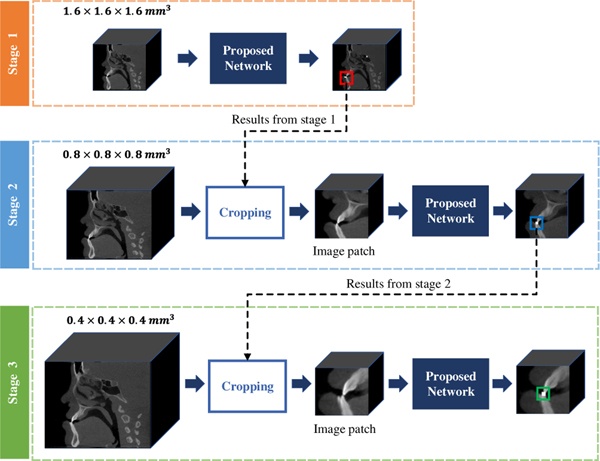
In this work, a deep learning method is proposed for the automated localization of CMF landmarks on CBCT images (Fig. 1). Specifically, we first use the down-sampled CBCT images to train an initial shallow network, which leverages the global anatomical information to coarsely predict the location of each landmark. Then, around the rough locations, we crop a set of image patches from medium- and higher-resolution images to train another two detection networks, which leverage the local appearance for further refinement. The proposed detection network in each step is an extension of the state-of-the-art Mask Region-based Convolutional Neural Network (Mask R-CNN) [12]. In addition, we learn local landmark dependencies as an auxiliary task to provide additional guidance for the accurate localization.

Fig. 1:

Our coarse-to-fine framework for CMF landmark localization in CBCT images.

A preliminary version of this work has been reported in [13]. New contributions in this paper are as follows: 1) A new region proposal network is introduced to simplify the training procedure and stabilize detection results; 2) A more stable inner-landmark dependency model is proposed to boost the performance on patients with defects; 3) The proposed method is evaluated on more patients with severe deformities and is compared with several state-of-the-art methods; 4) Eeffectiveness of the proposed Multi-RPN and landmark dependency model is evaluated. Experimental results on real patient data show that the average detection error of 105 landmarks is 1.38 ± 0.95 mm, which can be achieved with less than 4 minutes of computation time. Both the accuracy and efficiency of our method meet the clinical requirements of surgical planning to correct for CMF deformities.

II. RELATED WORK

A. Anatomical Landmark Detection

Learning-based methods have been extensively applied for anatomical landmark localization in medical images. Generally, these methods can be based on traditional machine learning or deep learning. For methods based on traditional machine learning, handcrafted features [14]–[17] are typically extracted from local image patches to train a patch-wise classifier [18], [19], [21]–[23] to identify whether the central voxel is close to a landmark. For example, Mahapatra et al. [22] first predict a set of potential landmarks using morphological operations and graph cut segmentation [24], and then identify the landmarks via a random forest model [25]. State-of-the-art methods based on machine learning are summarized in [26] and [27].

Handcrafted features can be used to learn a regression model that predicts the displacement between an input image patch and a target landmark [28], [29]. The landmark location is then determined by aggregating the predictions from all image patches (e.g., via majority voting). For example, Gao et al. [28] introduced a two-layer regression model, the first layer predicts displacement fields for each landmark individually, then context features extracted from these fields are used to jointly refine the coarse landmark results. Darko et al. [29] predict ambiguous landmarks using a Regression Random Forest (RRF) and then apply back-projection to select pixels to train another RRF in combination with a Markov Random Field model for locating landmarks with high accuracy.

Deep learning methods, such as convolutional neural networks (CNNs), have been proposed to learn task-oriented features for anatomical landmark localization. For example, Payer et al. [8] formulate landmark localization as a heatmap regression problem, where a fully convolutional network (FCN) [30] is applied to predict the corresponding heatmap for each landmark. Payer et al. [32] further refine the results by combining information of local appearance and spatial configuration into a single end-to-end trained network for anatomical landmark localization. Wang et al. [31] developed a multi-task network for segmentation and landmark localization in prenatal ultrasound volumes. An adversarial module is leveraged to emphasize the correspondence between segmentation and landmark localization. In [9], a cascade of two U-Nets is employed to detect multiple anatomical landmarks, where the first FCN predicts the 3D displacements from each voxel to target landmarks, and the second FCN combines 3D displacements with input image patches to regress the landmark heatmaps. Although this method yields promising results for the prediction of 15 landmarks, it cannot handle larger-scale landmark localization due to the significant memory consumption. Additionally, solely using image patches may lead to misdetections, where the global anatomical information from the whole image is ignored. Misdetections frequently occur in areas where anatomical structures are not prominent (e.g., temporomandibular joints), causing landmarks with similar local appearances to be indistinguishable.

Torosdagli et al. [40] proposed a CNN-based method to detect 9 mandibular landmarks, where a FCN is learned to detect sparsely-spaced landmarks in the geodesic space from a pre-segmented mandible. A long short-term memory network is subsequently learned to detect closed-spaced landmarks. This method relies heavily on the results of presegmentation mandible, and the localization accuracy of the closed-spaced landmarks are affected by the results of the sparsely-spaced landmarks. To address these issues, Relational Reasoning Network (RRN) was proposed in [41] to learn landmark dependency for improving accuracy. Specifically, given a few landmarks as input, RRN learns the representations of the landmark relations. By utilizing the learned relations, RNN subsequently localizes the remaining landmarks. Since only the relationships of the primary (known) landmarks are learned, with the relationships of primary-secondary and secondary-secondary landmarks not considered, this method relies on the selection of the primary landmarks.

B. Object Detection Network

Mask R-CNN [12] is designed for object detection in an end-to-end manner. It first generates several region proposals for the target through a region proposal network, then jointly outputs the location, category, and segmentation of the target object in a multi-task learning framework. Recently, Mask R-CNN has been used for localizing key-points from a detected object by modeling each key-point location as a one-hot mask [12]. Similar to most existing landmark detection methods, the original Mask R-CNN for general object detection treats different targets independently, ignoring their inter-dependency.

In recent years, several RPN-based methods have been proposed for landmark detection. Liu et al. [44] directly applied Faster R-CNN for misshapen pelvis landmark detection, where an RPN proposes landmark neighborhoods and a fast R-CNN regresses the coordinates of the target landmarks. Xu et al. [45] proposed to detect multiple organs from CT images using an RPN that generates class-specific proposals for each object. The bounding box of each organ was calculated by a multicandidate fusion strategy. However, this method is based on the assumption that at least one instance for each organ exists and therefore cannot handle missing landmarks.

Deep Reinforcement Learning (DRL) methods have been recently proposed for localizing landmarks. In [43], an optimal path from the initial position to the target location is learned by maximizing the cumulative rewards. Vlontzos et al. [42] extended this work with a multi-agent module to detect multiple landmarks. However, DRL methods are limited to localizing a small number of landmarks simultaneously due to GPU limitations.

III. METHODS

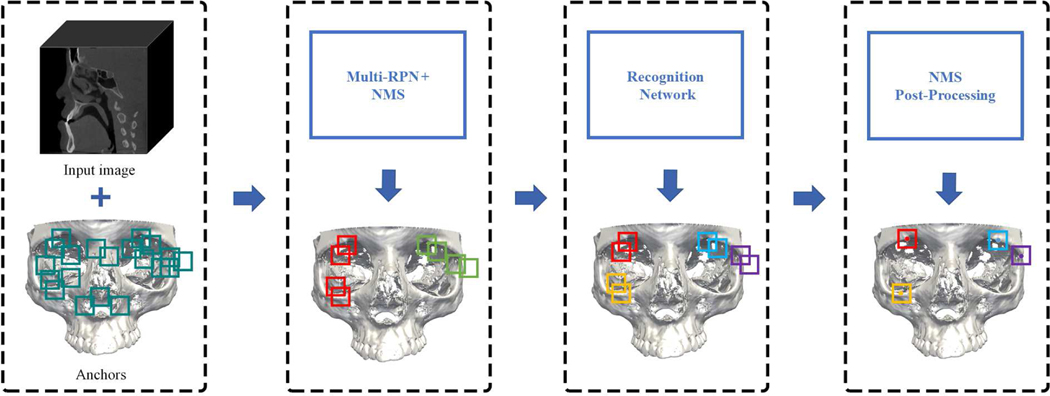
For CMF landmark localization in CBCT images, we gradually refine the landmark positions predicted by a cascade of multi-task detection networks in a coarse-to-fine manner. The proposed network is an extension of the standard Mask R-CNN by including the explicit modeling of landmark dependencies as guidance to assist the joint prediction of landmark locations. Fig. 2 shows the architecture of our detection network. First, given a CBCT image and a set of anchors, a Multi-Region Proposal Network (Multi-RPN) generates several location proposals for each landmark. Non-Maximum Suppression (NMS) is applied to reduce redundant proposals. Then, a recognition network predicts the landmark location from each location proposal under multi-task supervision. Finally, another NMS with a different threshold is performed to further refine detection.

Fig. 2:

Our workflow for CMF landmark detection, illustrated for detecting four landmarks in two anatomical regions. The Multi-RPN generates several location proposals with anatomical region labels (illustrated by two different colors), which are processed by NMS. Then, a recognition network detects each landmark from the proposals in the form of a regressed bounding box and a corresponding landmark label (illustrated by four different colors). Finally, NMS post-processing is applied to further filter out redundant bounding boxes.

A. Multi-Region Proposal Network

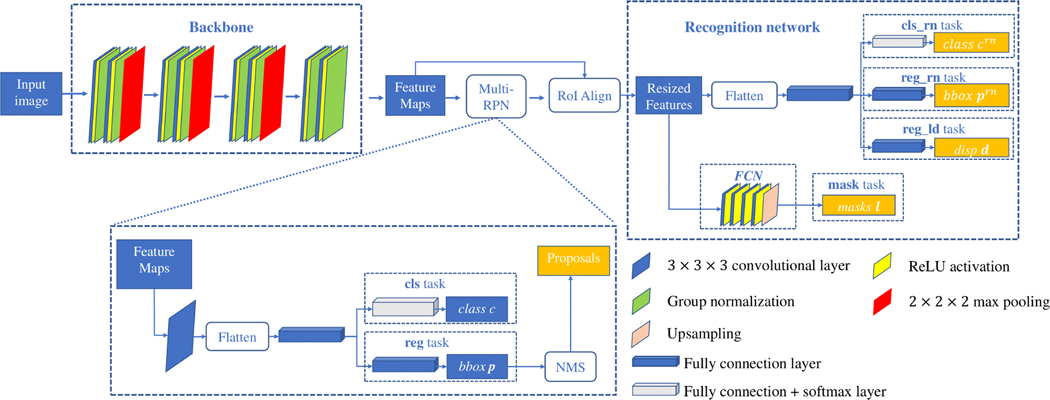
The multi-region proposal network (Multi-RPN) generates several proposals for landmark positions (Fig. 3). The backbone consists of four residual blocks [33]. A set of anchors with different sizes are defined on each voxel of the produced feature maps to generate proposal boxes for landmarks. For each anchor, the features of voxels located in the anchor region are gathered and reshaped to a feature vector, which is then mapped by a Full Connected (FC) layer for two tasks: 1) a multi-classification (cls) task, where the output $c=\{0,1,2,\dots ,C\}$. c = 0 indicates that this anchor contains no landmarks (negative). C is the number of the predefined anatomical regions. This task assign each anchor with the label of anatomical region; and 2) a regression (reg) task that predicts offsets for regressing the coordinates of positive proposal regions. Specifically, the output p is a 6-dimensional vector including the offset of the center coordinates (3-dimensional), and the offset of the anchor size (3-dimensional). NMS is applied to keep P proposals by removing the redundant proposals in association with each landmark. The loss for Multi-RPN is

$$\begin{array}{l}{L}^{\text{RPN}}\left(\left\{c_i\right\},\left\{p_i\right\}\right)=\frac{1}{A}\sum _{i=0}^A{L}_{\text{cls}}^{\text{RPN}}\left(c_i,c_i^{\ast }\right)\\ +\frac{\lambda }{A}\sum _{i=0}^A{L}_{\text{reg}}^{\text{RPN}}\left({\mathbf{\text{p}}}_i,{\mathbf{\text{p}}}_i^{\ast }\right).\end{array}$$ (1)

We use three ratios 0.5, 1.0, and 1.5, and three scales 48, 64, and 80 to generate anchors, so that each anchor has 27 different sizes. The ratios and scales are chosen empirically. A = 27 × W × H × D is the number of anchors, where W ×H ×D is the size of each feature map produced by the backbone. The classification term $L_{\text{cls}}^{\text{RPN}}$ is a cross-entropy loss, where c_i is the probability of the i-th anchor being an positive proposal, and $c_i^{\ast }$ is the corresponding ground truth. The regression term $L_{\text{reg}}^{\text{RPN}}$ is an ${𝓁}_1$-norm loss [35], where p_i is a 6-dimensional vector representing the parameterized coordinates (displacements of the center and ratios of the sizes), and ${\mathbf{\text{p}}}_i^{\ast }$ is the respective ground truth. The classification and regression tasks are balanced by λ. The settings of Multi-RPN are provided in Table I.

Fig. 3:

Architecture of the proposed Mask R-CNN for detecting landmarks.

TABLE I:

Specifications of the Multi-RPN.

Layer	Number of Feature Maps
Input	1
Residual block + maxpooling	32
Residual block + maxpooling	64
Residual block + maxpooling	128
Residual block + maxpooling	128
3×3×3 Convolution	128
FC layer	256
reg task	6×A
cls task	(C +1)×A

B. Recognition Network

The architecture of the recognition network (RN) for localizing N landmarks is shown in Fig. 3. According to the proposals generated by Multi-RPN, the Region of Interest Align (ROIAlign) [12] operation crops patches from the feature maps produced by the backbone, and resizes them to a common size of 14×14×14. Each cropped patch is reshaped and mapped by a FC layer. The output of FC layer is then fed into a classification task (cls_rn) and a regression task (reg_rn), respectively. cls_rn predicts the landmark label $c^{\text{rn}}=\{0,1,2,\dots N\}$ for the proposal box, where N is the number of the landmarks. c^rn = 0 indicates that the landmark does not exist. reg_rn outputs the displacement vector p^rn indicating the offset from the proposal box center to the ground-truth box center. In addition, the cropped feature patches are fed into a lightweight FCN to predict the bony masks l, capturing the structural information of the bones around a landmark. The ground truth of the predicted bony mask $l^{\ast }$ is generated by performing RoIAlign operation on the whole bony mask according to the location of the proposal. The FCN contains four 3×3×3 conv + ReLU layers followed by an upsampling layer. The loss function is

$$\begin{array}{l}{L}^{\text{RN}}\left(\left\{c_i^{\text{rn}}\right\},\left\{{\mathbf{\text{p}}}_i^{\text{rn}}\right\},\left\{l_i\right\}\right)=\frac{1}{P}\sum _{i=0}^P\{L_{\text{cls}}^{\text{RN}}\left(c_i^{\text{rn}},c_i^{{\text{rn}}^{\ast }}\right)\\ +L_{\text{reg}}^{\text{RN}}\left({\mathbf{\text{p}}}_i^{\text{rn}},{\mathbf{\text{p}}}_i^{{\text{rn}}^{\ast }}\right)+L_{\text{seg}}^{\text{RN}}\left(l_i,l_i^{\ast }\right)\},\end{array}$$ (2)

where $c^{{\text{rn}}^{\ast }}$, ${\mathbf{\text{p}}}^{{\text{rn}}^{\ast }}$, $l^{\ast }$ are the ground truth for c^rn, p^rn, and l, respectively. We employ cross-entropy losses for $L_{\text{cls}}^{\text{RN}}$ and $L_{\text{seg}}^{\text{RN}}$, and the ${𝓁}_1$-norm loss for $L_{\text{reg}}^{\text{RN}}$.

C. Landmark Dependencies

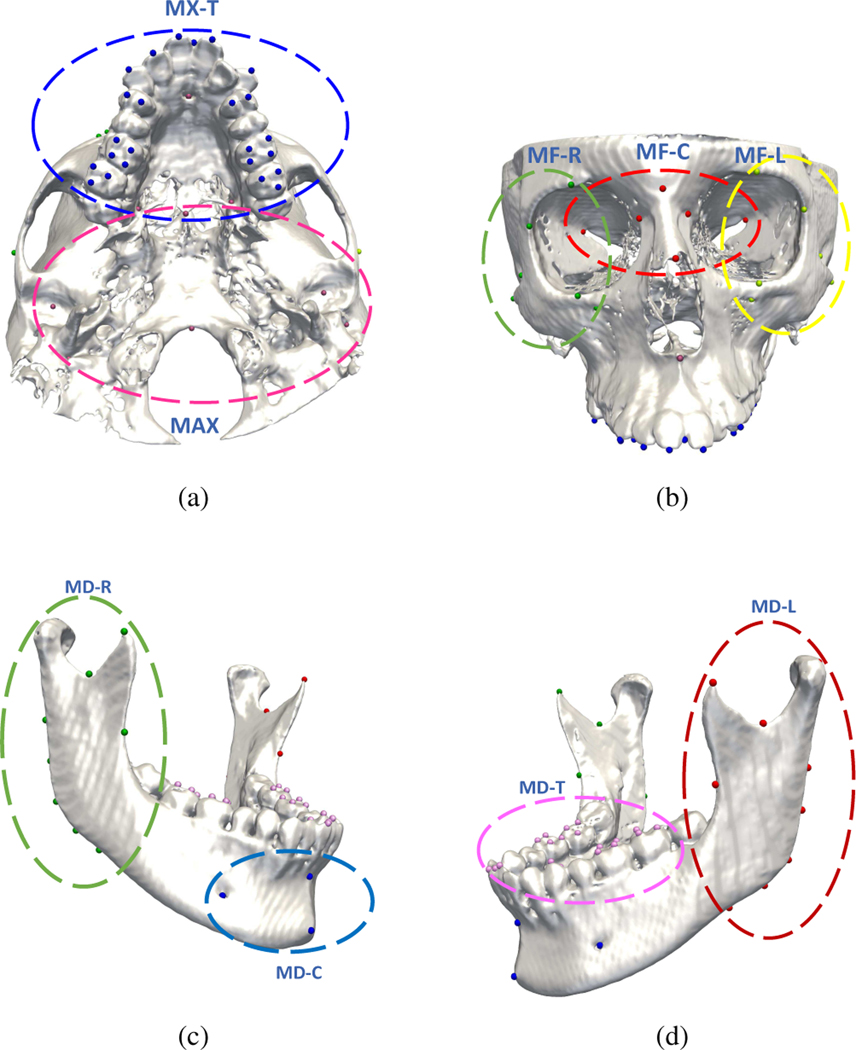
CMF landmarks in the same local region have relatively consistent spatial relationships that can be leveraged to improve localization. Therefore, as shown in Fig. 4 (a)–(d), we group the total 105 CMF landmarks according to C = 9 anatomical regions: Midface-Left (MF-L), Midface-Central (MF-C), Midface-Right (MF-R), Maxilla (MAX), Maxillary-Teeth (MX-T), Mandible-Left (MD-L), Mandible-Right (MDR), Mandible-Central (MD-C), and Mandibular-Teeth (MD-T). In [13], to capture local dependencies, the landmarks located in the same region are empirically defined as a tree structure, i.e., the landmark at the center of the region is defined as the root node, and the others as leaf nodes. A potential problem with this approach is that root landmarks can be mis-detected, consequently compromising locations of leaf landmarks. It is also common in CMF patients with partial defects that the root landmark can be missing. This approach also ignores the geometrical relationships between leaf landmarks. To more reliably encode the geometrical structure, we include an auxiliary task in the recognition network to model the dependencies between each pair of landmarks in the same anatomical area, i.e., reg_ld task that predicts the average displacement of the detected landmark to other landmarks in the same region. The corresponding loss function L^LD is defined as

$$L^{\text{LD}}\left({\mathbf{\text{d}}}_i\right)=\frac{1}{P}\sum _{i=1}^P{L}_{\text{reg}}^{\text{LD}}\left({\mathbf{\text{d}}}_i,{\mathbf{\text{d}}}_i^{\ast }\right),$$ (3)

where ${\mathbf{\text{d}}}_i^{\ast }$ and d_i are the ground-truth and predicted displacements for the i-th proposal, respectively, P is the number of proposals generated by Multi-RPN. ${\mathbf{\text{d}}}_i^{\ast }$ is calculated by

$${\mathbf{\text{d}}}_i^{\ast }=\frac{1}{N^c-1}\sum _{j\ne i}^{N^c-1}{\mathbf{\text{d}}}_{ij},$$ (4)

where N^c is the number of landmarks in an anatomical region, ${\mathbf{\text{d}}}_{ij}=\left[{\delta }_{z_{ij}},{\delta }_{y_{ij}},{\delta }_{x_{ij}}\right]$ is a 3-dimensional displacement vector, $L_{\text{reg}}^{\text{LD}}$ is defined as the ${𝓁}_1$-norm. Additional information on the recognition network is provided in Table II.

Fig. 4:

Predefined anatomical landmark regions with landmarks in the same anatomical region marked with the same colors.

TABLE II:

Specifications of the recognition network.

Layer	Number of Feature Maps
Input	128
RoI Align Layer	128
FC layer	1024
Cls_rn task	N
reg_rn task	6×N
reg_ld task	3×N
3×3×3 Convolution block	64
Transition up	N
mask task	N

D. Coarse-to-Fine Framework

We apply a three-stage coarse-to-fine framework to gradually refine the localization results on high-resolution CBCT images. The proposed network is integrated in each stage, and trained by minimizing the combination of the losses defined in (1), (2), and (3), i.e.,

$$L={\lambda }_{\text{r}}{L}^{\text{RPN}}+{\lambda }_{\text{rn}}{L}^{\text{RN}}+{\lambda }_{\text{ld}}{L}^{\text{LD}}.$$ (5)

To train the model in the first stage, the original CBCT image (0.4 × 0.4 × 0.4 mm³) is down-sampled (1.6 × 1.6 × 1.6 mm³) and padded to have the size of 128 × 128 × 128. In the following two stages, the image resolutions are up-sampled to be 0.8 × 0.8 × 0.8 mm³ and 0.4 × 0.4 × 0.4 mm³, respectively. 100 image patches (64 × 64 × 64) are sampled around each predicted landmark and taken as inputs. Since the size of the bounding box used as ground truth for each landmark is hard to determine, we use anchors with multi-scale sizes of 32 × 32 × 32, 40 × 40 × 40, and 48 × 48 × 48 for each landmark for greater robustness.

E. Network Implementation and Inference

At each stage, our model was trained via the SGD optimizer with an initial learning rate of 0.01, decaying by 20% after every 5 epochs. The network was trained for 25 epochs (6,000 iterations in each epoch), taking around 3 days to complete. To balance the training speed and the number of proposals, the Multi-RPN was set to produce P = 500 proposal boxes for each input. For the first 10 epochs, the training weights in (5) were set to λ_r = 1.0, λ_rn = 0.3 and λ_ld = 0.3. After that, the RPN weight λ_r was reduce to 0.3, while λ_rn and λ_ld were increased to 1.0 to focus on the training of the recognition network.

During inference, the first stage simultaneously outputs coarse positions of all landmarks. Starting from the second stage, only image patches centered at the coarse landmarks were sampled and used as inputs for refining, as the results from the first stage are very close to the ground truth. The maximum number of proposals were dropped to P = 50. The threshold of NMS processing for refining proposal boxes is set to 0.1. The trained model takes less than 2 minutes to process a CBCT volume with a size larger than 536 × 536 × 440 for detecting 105 landmarks. The network was implemented based on Tensorflow and evaluated on a 11 GB GTX 1080Ti GPU and a 64 GB RAM.

IV. EXPERIMENTAL RESULTS

A. Experimental Data

Our method was evaluated qualitatively and quantitatively on 50 patients of CBCT images (0.4 × 0.4 × 0.4 mm³ or 0.3×0.3×0.3 mm³ with size larger than 536×536×440) with personal information removed via 5-fold cross-validation. The age ranges from 37 to 80. All images were acquired from patients with non-syndromic jaw deformities, where 20 patients in our CBCT dataset are with CMF defects. Each subject had 105 landmarks (59 on the midface and 46 on the mandible) digitized and verified by two experienced CMF surgeons using AnatomicAligner [7]. The segmentation of the midface and the mandible was also provided by the same surgeons. The inter-rater agreement value of the landmark annotations was approximately 2.5 mm. These manually digitized landmarks serve as the ground truth.

Since CT images of normal people have a better resolution than CBCT images, and the landmarks are relatively stable, we first use CT images to pre-train a model to better capture contextual features and learn local landmark dependency for accelerating the network training. In this work, 45 sets of normal spiral CT images [36] with resolution 0.49×0.49×1.25 mm³ were used for pre-training in a 5-fold cross-validation manner. Specifically, the network was trained via the SGD optimizer with an initial learning rate of 0.01 for 10 epochs (6,000 iterations in each epoch).

We performed data augmentation on each pair of the input image and the corresponding landmark ground truth (coordinates) by the same rotation, translation and scaling. Specifically, each subject including the image and its landmark coordinates has a 50% possibility to be translated with a displacement in [−20, 20] and scale with a ratio in [0.8, 1.2] along each axis. In addition, each subject has a 50% possibility to be rotated by an angle in $\left[-\frac{\pi }{12},\frac{\pi }{12}\right]$. The augmentation was performed 50 times on each subject to enlarge the training set. Histogram matching and Gaussian normalization constant were performed to normalize the dateset as a whole.

B. Competing Methods

We quantitatively and qualitatively compared our method with six baseline methods:

• U-Net: A standard U-Net [8] for predicting a heatmap from an image. We adopted the same residual blocks that are used in our method to construct the contraction path of this network. Considering the limited GPU memory, only four residual blocks with the output size of 32, 64, 128, and 256 were used for extracting high-level features. The expansion path consists of three convolutional blocks, each block consists of two 3×3×3 conv + ReLU activation layers. The size of input from coarse stage to refine stage is 128×128×128 (resolution: 0.4 mm isotropic, whole image), 96×96×96 (resolution: 0.8 mm isotropic, image patch) and 64×64×64 (resolution: 0.4 mm isotropic, image patch), respectively.

• DI-U-Net: A dual-input U-Net (same architecture as [8]) that uses both image patches and bony segmentations as input.

• JSD: A state-of-the-art deep-learning method that jointly performs bone segmentation and landmark digitization [9]. We trained the network for landmark localization using the same architecture and paremeter setting as described in [9]. During training, the input sizes for the three stages are 128×128×128 whole image (resolution: 0.4 mm isotropic), 96×96×96 image patches (resolution: 0.8 mm isotropic), and 64×64×64 image patches (resolution: 0.4 mm isotropic), respectively.

• DQN: We trained this network to detected no more than 4 lanmdarks in each anatomical region simultaneously due to GPU limitation. The parameter settings are the as described in [42].

• Method in [40]: This network first localizes some sparsely-located landmarks, then detects closely-located landmarks by using a long short-term memory (LSTM) network according to the localization results of sparsely-located landmarks. To apply this network on our dataset, the 105 landmarks are predicted separately by regions. Specifically, due to different landmark numbers in each region, we defined 5 landmarks in MD-L, MD-R, MD-T, MX-T and MAX, 3 landmarks in MF-C, MF-L and MF-R, and 2 landmarks in MD-C as sparsely-spaced landmarks since they are sparsely located in these regions. The rest of the landmarks in each region are defined as closely-spaced landmarks. The parameter setting and network architecture are as described in [40].

• RRN in [41]: This network first learns the relationships of each pair of input landmarks, then takes the learned relationships as input, to regress the coordinates of the other landmarks. To compare with this method, in each anatomical region, half of the landmarks were annotated as inputs to predict the other landmarks. Specifically, only 5 dental landmarks were annotated as inputs in MX-T and MD-T due to the large amount of dental landmarks. The parameter settings are kept the same as described in [41].

For each method, two models were trained to predict the locations of the landmarks on the midface and the mandible separately.

C. Results

The accuracy of landmark localization was evaluated via Mean Squared Error (MSE). The overall quantitative results of landmark localization in 9 anatomical areas are summarized in Table III. Among the six compared methods, U-Net results in the largest MSE (2.46 mm) in all anatomical areas. The reason is two-fold:

TABLE III:

The mean squared error (mm) for landmark localization using five methods in 9 anatomical regions.

Method	MF-L	MF-C	MF-R	MAX	MX-T	MD-L	MD-R	MD-C	MD-T	Overall
U-Net	2.72±1.35	2.17±1.25	2.61±1.28	2.14±1.36	2.61±1.35	2.53±1.68	2.44±1.72	2.30±1.21	2.77±1.64	2.46±1.42
DI-U-Net	2.42±1.32	2.05±1.27	2.26±1.25	2.01±1.37	2.29±1.17	2.43±1.58	2.11±1.49	2.02±1.05	2.34±1.33	2.18±1.31
JSD	1.70±0.66	1.53±0.88	1.86±0.52	1.54±0.63	1.98±1.11	1.93±1.07	1.85±1.14	1.56±1.23	1.64±0.96	1.92±0.91
Mask R-CNN	1.53±0.46	1.50±0.98	1.51±0.56	1.55±0.79	2.03±1.12	1.66±1.11	1.63±1.16	1.61±1.26	1.74±0.76	1.68±1.02
DQN	1.89±0.58	2.10±0.93	2.23±0.76	2.07±0.74	2.31±1.05	1.97±0.87	2.18±0.77	1.78±1.05	1.93±0.88	2.05±0.75
RNN	1.46±0.53	1.67±0.78	1.42±0.68	1.59±0.83	2.53±1.16	1.52±0.85	1.67±1.05	1.49±1.32	2.68±1.44	1.78±0.96
Method in [40]	1.55±0.64	1.88±0.76	1.57±0.56	1.52±0.86	2.67±1.09	1.58±0.92	1.68±1.03	1.58±1.01	2.77±1.89	1.86±0.97
Our method	1.28±0.44	1.47±0.95	1.25±0.44	1.49±0.76	1.86±1.04	1.43±1.03	1.58±1.15	1.45±1.13	1.66±0.77	1.38±0.95

• Since no bony segmentation information was involved in training, landmarks located close to each other or on smooth surfaces were difficult to distinguish, consequently yielding large errors or misdetections (e.g., MF-C/MD-C);

• By fixing the number of output landmarks, U-Net is not able to cope with the missing landmarks in patients with defects and attempts to localize landmarks that do not actually exist.

DI-U-Net improves the accuracy (2.18 mm) over the standard U-Net (p < 0.05), indicating the usefulness of segmentation information. The JSD method first predicts a displacement map from all voxels to each target landmark. The learned displacement maps are used as spatial context information to further regress landmark locations. An average error of 1.92 mm achieved by JSD suggests that the displacement map provides useful information to reduce prediction error. Specifically, the MSE of JSD reduces to 1.53 mm, 1.54 mm, and 1.56 mm in MF-C, MAX, and MD-C, respectively. However, JSD still results in a 100% FN rate since the outputs are regressed heatmaps, without any post-processing on determining the existence of each landmark, yielding high MSE in the MF-L/MF-R and MD-L/MD-R.

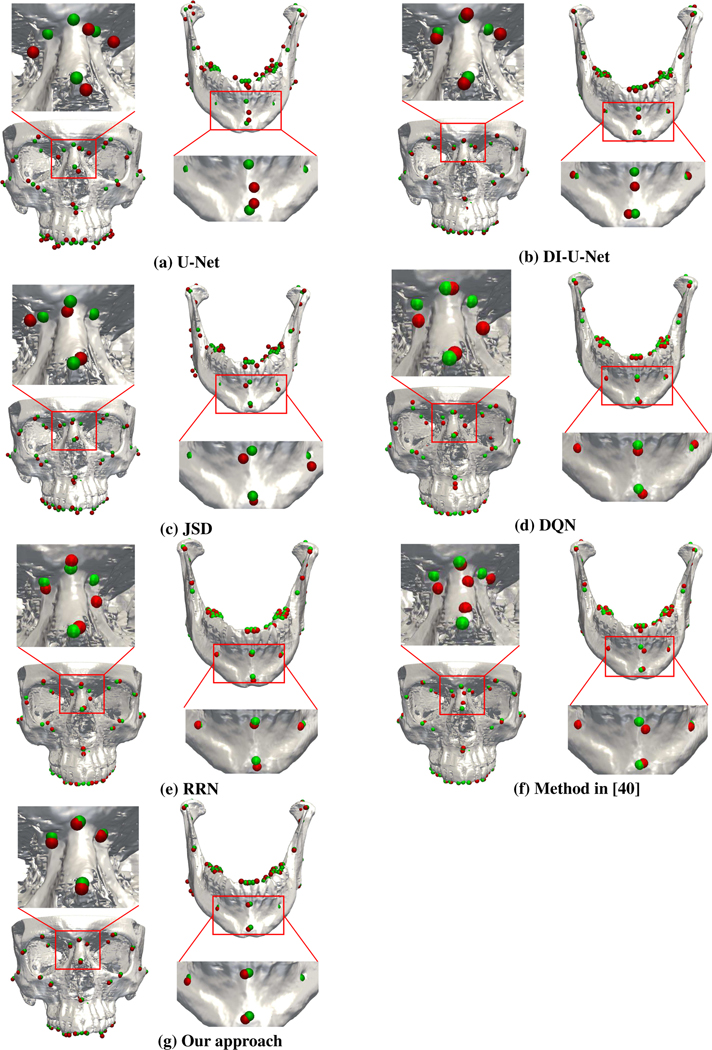
DQN achieves an average MSE error of 2.05 mm. Besides the fact that training DQN for all 105 landmarks is time-consuming, some detected landmarks are not attached to bones because the corresponding agents are trapped in local optima. RRN achieves an average MSE of 1.78 mm. It is worth noting that RRN yields a high accuracy in most regions (< 2 mm), confirming the benefits of learning landmark relationships. However, RRN only learns the relationships between a few known landmarks, resulting in low accuracy when handling regions with a large amount of landmarks (2.53 mm in MX-T and 2.68 mm in MD-T). The method described in [40] achieves an average MSE of 1.86 mm. High errors occur in tooth areas due to the same reason as RRN. The accuracy in other regions are lower than RNN because errors of sparsely-spaced landmarks affect the detection results of closely-spaced landmarks. It can be observed that additional landmarks were detected in the MF-C region (Fig. 5).

Fig. 5:

Example landmark localization results.

Our method is more accurate than all compared methods (p < 0.05) with error as low as 1.38 mm, confirming the benefits of the explicit modeling of landmark dependency. Unlike RRN, which only learns partial landmark dependency between a few known landmarks, our method learns the relations between each pair of landmarks in every anatomical region, making our method more robust to the number of landmarks. Specifically, the MSE achieved by our approach is significantly reduced to 1.47 mm, 1.49 mm, and 1.45 mm in MF-C, MAX and MD-C, respectively. Besides, in MF-L/MF-R and MD-L/MD-R, our approach reduces the MSEs to 1.28 mm, 1.25 mm, 1.43 mm, and 1.58 mm, respectively. These results show that our approach can more precisely localize landmarks in the anatomical areas where landmarks might be missing. It is also worth noting that our approach achieves an MSE of 1.86 mm and 1.66 mm in MX-T and MD-T, indicating that it can robustly localize tooth landmarks. Our method shows no significant differences within the age range of our dataset. Experimental results for all compared methods are shown in Fig. 5.

V. DISCUSSION

A. Landmark Dependency

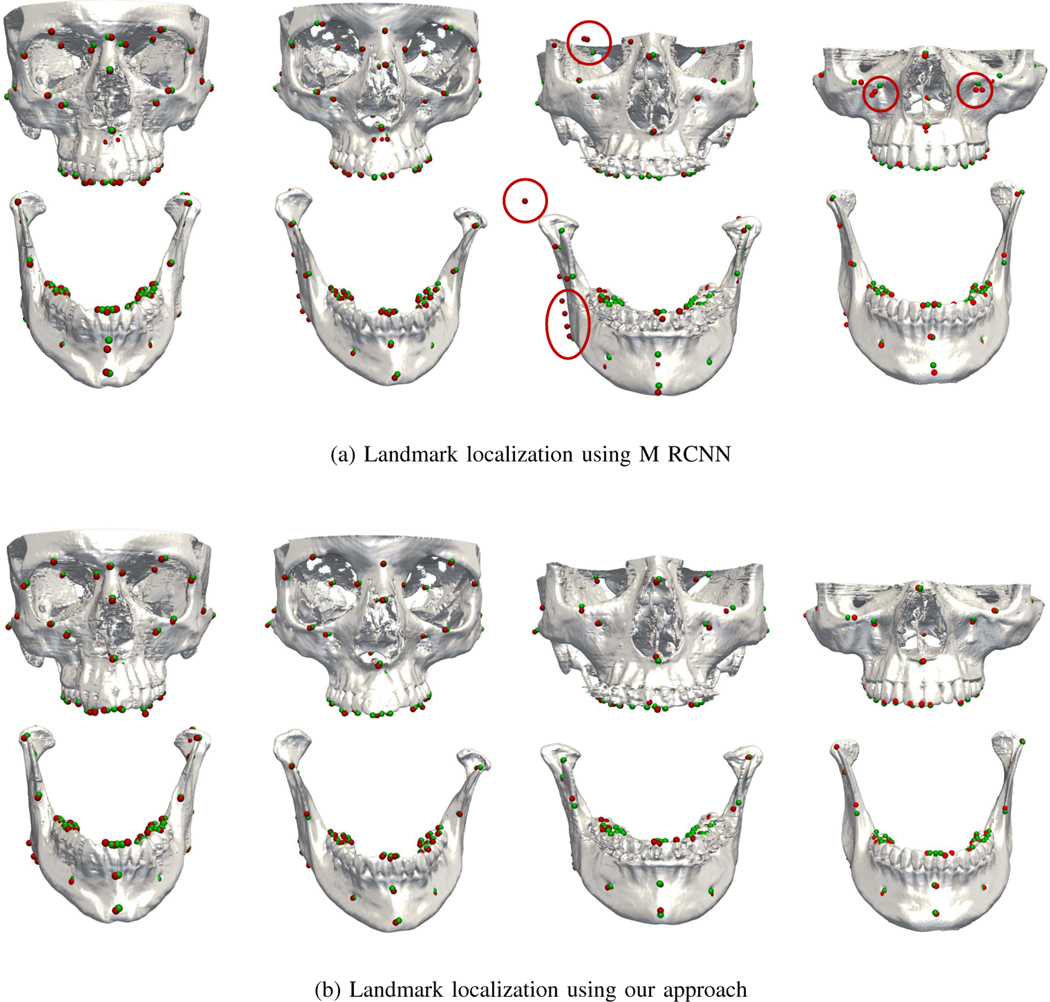
We compared our approach with the extended Mask R-CNN described in [13]. The landmark dependency is represented by a tree structure, where the root node is associated with one landmark and the leaf nodes are associated with other landmarks in the anatomical regions [13]. We trained the extended Mask R-CNN by using the same parameters as described in [13]. The input sizes from the coarse stage to refine stage are 128×128×128 (resolution: 0.4 mm isotropic, whole image), 64×64×64 (resolution: 0.8 mm isotropic, image patch), and 64×64×64 (resolution: 0.4 mm isotropic, image patch). The results for each region are summarized in Table III. Specifically, comparison was performed for patients with slight deformities, severe deformities, and defects.

We can observe from Table IV that our approach gains significant improvements for the three types of deformities. Particularly, for patients with slight and severe deformities, our approach reduces the MSE from 1.63 mm/1.65 mm to 1.32 mm/1.35 mm. Since there are no missing landmarks in these patients, we did not calculate the FN rate. For patients with defects, the improvement is significant. Specifically, the extended Mask R-CNN results in high MSE and FN rate if root landmarks are missing. Our approach reduces the MSE from 2.41 mm to 1.42 mm and lowers the FP/FN rate from 5%/90% to 2%/40%, indicating that our model is robust in cases with defects. The improvements can be attributed to two factors: 1) The existence of missing landmarks in the defect region can be detected with the Multi-RPN; 2) For the existing landmarks in the same region, the local relations can still be calculated with the other remaining landmarks since the landmark dependency is calculated as the mean of the displacement vectors from the current landmark to its neighbors. Fig. 6 shows obvious misdetections.

TABLE IV:

The mean squared errors (mm), FP rates, and FN rates for landmark detection on patients with three different types of deformities.

Condition	Method	MSE±SD	FP rate	FN rate
Slight Deformity	Mask RCNN	1.63±1.01	3%	N/A
	Our method	1.32±1.05	1%	N/A
Severe Deformity	Mask RCNN	1.65±1.11	6%	N/A
	Our method	1.35±1.08	2%	N/A
Defect	Mask RCNN	2.41±1.02	5%	90%
	Our method	1.42±0.95	2%	40%

Fig. 6:

Landmark localization for four patients with slight deformity (left), severe deformity (middle), and defects (right).

B. Multi-RPN

We performed an ablation study to evaluate the effectiveness of the Multi-RPN in localizing landmarks from pre-clustered proposals. We implemented a variant of our approach by adopting the standard RPN [13], which only classifies each anchor as negative (no landmark exists) or positive (landmark exists). The recognition network of this variant was similar to that used in [13] except that the landmark dependency was replaced by ours.

The accuracy of localization results of using the Multi-RPN and the standard RPN for 5-fold cross-validation are summarized in Table VI. The variant with standard RPN yields a large MSE of 1.65 mm. This is partly due to the misdetections caused by the standard RPN, where positive proposals were classified as negative proposals, causing some undetected landmarks. The Multi-RPN significantly improves performance and reduces the MSE to 1.38 mm. Since the recognition network only works on positive proposals, pre-clustering the proposals as multiple anatomical regions by the Multi-RPN can help reduce the misdetection rate. Notably, the FP rate is reduced by 6%, suggesting improved robustness when using the Multi-RPN.

TABLE VI:

Mean squared error (mm) of landmark localization with and without the Multi-RPN.

Method	MSE ± SD	FP Rate
Standard RPN	1.65±1.02	8%
Multi-RPN	1.38±0.95	2%

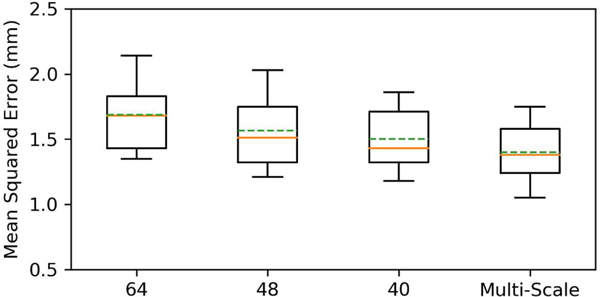
C. Multi-Scale Bounding Boxes

To evaluate the effectiveness of multi-scale bounding boxes, we modified our approach to use single-scale bounding boxes for comparison. Specifically, we evaluated different bounding box sizes: 64×64×64, 48×48×48, and 40×40×40. Fig. 7 shows that the modified method yields a minimum MSE of 1.45 mm with the bounding box size 40×40×40. However, a high FP rate of 10% still occurs because some landmarks are not covered by the anchors. Our original method reduces the MSE to 1.38 mm, and lowers the FP rate to 2%, suggesting that multi-scale bounding boxes improve robustness.

Fig. 7:

Detection errors for bounding boxes of different sizes.

D. Coarse-to-fine strategy

Our work applied a coarse-to-fine strategy to train the network. Table V lists the detection results of each anatomical region from each stage. Since the input of our network in the coarse stage has been down-sampled to a low resolution (1.6 × 1.6 × 1.6 mm³) due to GPU memory limitations, a lot of structural information has been lost, causing an average MSE of 2.87 mm, which cannot meet clinical requirements. However, the coarse results can approximately predict the location of each landmark, and the miss-detection rate (FN/FP rates) have been significantly reduced by landmark dependency learning and the Multi-RPN as discussed before. In the second stage, multiple high-resolution image patches with more local details of structural information are sampled around each coarse result as inputs to the refinement network, yielding a lower MSE of 1.45 mm. During the test, we only consider the result of the landmark where the input image patch is sampled from, thus even though the sampled image patch contains multiple landmarks (specially in the tooth region), the final results will not be affected.

TABLE V:

The mean squared error (mm) for landmark localization using our approach in 3 stages.

Method	MF-L	MF-C	MF-R	MAX	MX-T	MD-L	MD-R	MD-C	MD-T	Overall
Stage 1	2.89±1.65	2.78±1.64	2.79±1.55	2.64±1.56	2.95±1.65	3.13±1.68	2.81±1.77	2.97±1.79	2.86±1.74	2.87±1.67
Stage 2	1.52±1.02	1.77±0.75	1.64±0.72	1.71±0.62	2.19±0.87	1.71±0.79	1.88±0.82	1.67±0.71	2.12±0.98	1.80±0.81
Stage 3	1.28±0.44	1.47±0.95	1.25±0.44	1.49±0.76	1.86±1.04	1.43±1.03	1.58±1.15	1.45±1.13	1.66±0.77	1.38±0.95

VI. CONCLUSION

In this work, we have proposed a deep learning method to gradually and jointly localize a total of 105 CMF landmarks from CBCT images. Our method achieves start-of-the-art performance in the challenging task of localizing CMF landmarks from CBCT images. Unlike the original Mask R-CNN, our network explicitly learns landmark dependency to enhance localization of landmarks. Our method is robust to deformities in patients and improves localization accuracy. The results show that the proposed method outperforms state-of-the-art methods quantitatively and qualitatively.

Our method has some potential limitations. First, we treated all landmarks equally and assigned to them bounding boxes of the same size. However, the localization of landmarks in different areas may require different receptive fields. A large receptive field is needed for landmarks located on smooth surfaces and a relatively small receptive field is needed for tooth landmarks typically located on tips or valleys. Second, we only considered the geometrical relationship between each landmark and its neighbors in the same anatomical region, but ignore the relationships between landmarks in different regions. In the future, we will investigate encoding the relationships of all landmarks, for example, using graph convolutional networks (GCN) [37].