Deciphering deamidation and isomerization in therapeutic proteins: Effect of neighboring residue

ABSTRACT

Deamidation of asparagine (Asn) and isomerization of aspartic acid (Asp) residues are among the most commonly observed spontaneous post-translational modifications (PTMs) in proteins. Understanding and predicting a protein sequence’s propensity for such PTMs can help expedite protein therapeutic discovery and development. In this study, we used proton-affinity calculations with semi-empirical quantum mechanics and microsecond long equilibrium molecular dynamics simulations to investigate mechanistic roles of structural conformation and chemical environment in dictating spontaneous degradation of Asn and Asp residues in 131 clinical-stage therapeutic antibodies. Backbone secondary structure, side-chain rotamer conformation and solvent accessibility were found to be key molecular indicators of Asp isomerization and Asn deamidation. Comparative analysis of backbone dihedral angles along with N-H proton affinity calculations provides a mechanistic explanation for the strong influence of the identity of the n + 1 residue on the rate of Asn/Asp degradation. With these findings, we propose a minimalistic physics-based classification model that can be leveraged to predict deamidation and isomerization propensity of proteins.

Introduction

Protein stability is at the center of biological mechanisms spanning molecular pathways and therapeutic interventions.^1–3 Proteins are subject to various post-translational modifications (PTM) that are essential for their function, e.g., glycosylation, acylation. Some of these PTMs are spontaneous chemical reactions that lead to degradation, such as deamidation of asparagine (Asn→Asp/iso-Asp), isomerization of aspartic acid (Asp→iso-Asp) and oxidation of Met/Trp residues.^4,5 These spontaneous chemical modifications often serve as a key indicator of stress that elicits a physiological response.⁶ Bio-manufactured therapeutic proteins, including peptides, vaccines, monoclonal antibodies (mAbs), and viral capsids, are subject to physical and chemical stressors during manufacturing that result in accumulation of various PTMs.^7–11 Spontaneous chemical modification can negatively impact the biomolecule’s therapeutic efficacy, quality and developability by altering the structure and/or molecular properties of the protein. For instance, isomerization of an Asp residue alters the backbone connectivity and deamidation of an Asn residue imparts a negative charge (Figure 1), both of which can result in altered functional consequences.^12,13 Often protein engineering strategies are used to mitigate the negative impacts of such chemical modifications, but this is carried out in an iterative manner, which leads to prolonged development cycle for therapeutic proteins.^14–16 Understanding and predicting the propensity of a therapeutic protein to undergo chemical degradation can expedite development timelines.^17–20

Figure 1.

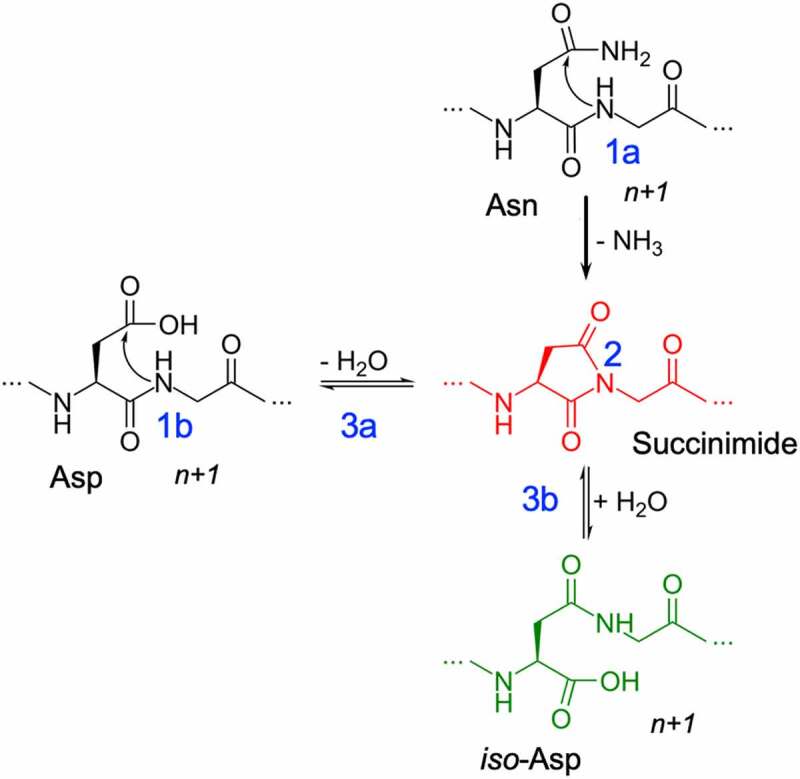
Deamidation (1a) and Isomerization (1b) reaction mechanisms showing deprotonation (1) of the n + 1 amide leading to the formation of succinimide intermediate (2) and hydrolysis of succinimide (3) into aspartic acid (3a) or iso-aspartic acid (3b).

Deamidation of an Asn residue has been experimentally well characterized.^21–23 Among the multiple pathways that are feasible, pH-dependent base-catalyzed nucleophilic attack has been shown to be the predominant pathway.^23–26 The reaction is irreversible and proceeds via a 3-step process: 1) base-catalyzed deprotonation of the n + 1 amide, 2) nucleophilic attack of the anionic nitrogen on the side-chain carbonyl group and a subsequent ring closure that leads to the formation of a succinimide intermediate, and 3) hydrolysis of the succinimide into Asp or iso-Asp (Figure 1). Similarly, the isomerization reaction can proceed from an Asn or Asp residue via the same succinimide intermediate pathway. There are mechanistic parallels and kinetic dissimilarities between the isomerization and deamidation reactions.^13,27,28 Experimentally, it has been shown that the degradation half-times of Asn (or Asp) residue in small peptides can vary by orders of magnitude depending on the residue at n + 1 position on the C-terminal end.^21,29–32 Previous studies using pentapeptides by Robinson et al.³³ have shown a higher likelihood of chemical degradation if the n + 1 neighboring residue of the Asn residue is a Gly, Ala, Ser or Thr. Based on these peptide-level studies, the NX and DX (where X could be G/A/S/T) are often considered hotspots for degradation in proteins. However, such peptide-level sequence rules are not necessarily applicable to folded proteins. For example, a recent study by Lu et al.³⁴ reported an experimental survey of 131 clinical-stage therapeutic antibodies (henceforth referenced as the Adimab dataset), which revealed vast discrepancies in the range of deamidation and isomerization propensities among antibodies that did not follow the sequence-dependent hotspot rules. For instance, there were 27 deamidation sites with the hotspot NG sequence in the complementary-determining region (CDR), of which only 14 underwent deamidation. A similar trend was observed in the case of isomerization (16 of 44 DG sites isomerized). Furthermore, chemical degradation was observed at NY, NW, DR and DY motifs that are not considered hotspots based on the peptide-level studies. The results reported in Lu et al. indicate a gap in our knowledge of how the neighboring residues contribute to the chemical degradation propensity in proteins.

Multiple computational strategies, from physics-based approaches (e.g., quantum mechanics/molecular mechanics (QM/MM), molecular dynamics (MD) simulations)^29,30,35,36 along with machine-learning models,^17,20,37 have been developed over the past two decades to predict deamidation and isomerization in peptides and proteins. Several detailed computational models explored site-specific effects using QM/MM calculations at the peptide level. For example, ab initio calculations on Gly-containing peptide mimetic model compound (N-formyl-glycinamide) revealed how the conformation of the molecule affects the proton-affinity of the backbone amide (Figure 2). ³⁸ However, it is unclear if this trend is generalizable to Asp and Asn residues where the n + 1 residue is not Gly. Multiple machine learning (ML) models have been proposed that were trained on a number of structure-based features such as secondary structure, local flexibility, size of the neighboring residue, and solvent exposure.^17,20,37,38 While computationally facile and practical in nature, ML-based models often focus exclusively on prediction without necessarily offering mechanistic insight into causality. Sometimes important mechanistic and structural details such as conformational dynamics, key for the reaction’s feasibility, are neglected. Lastly, given that these models are trained on a limited set of data points using pre-assumed input features, their generalizability to new datasets remain unclear.

Figure 2.

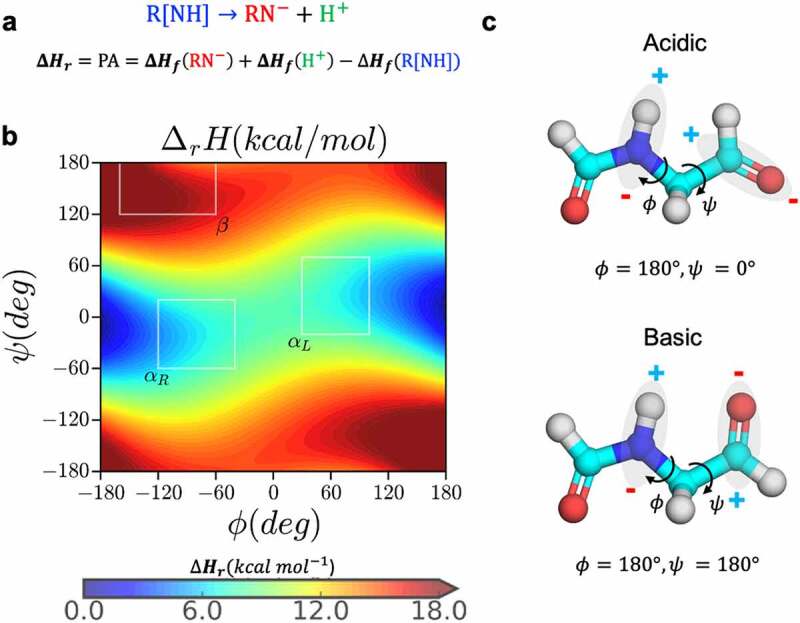
Dependence of proton affinity of small molecule N-formyl-glycinamide on backbone conformation. (a) the deprotonation reaction and calculation of proton affinity as the heat of formation of the forward reaction, (b) the proton affinity distribution of the small molecule N-formyl-glycinamide as a function of the backbone dihedral angles, and (c) the most acidic and basic conformations based on the proton affinity distribution.

Here, we used proton-affinity calculations with semi-empirical QM, microsecond long equilibrium MD simulations, and a conformational analysis of all of the antibody structures in the Protein Data Bank (PDB; www.rcsb.org) to provide insight into the effect of neighboring residues in dictating the chemical degradation at Asn/Asp site of proteins. Based on the analysis of a large set of the Adimab dataset, including 1000+ Asn/Asp sites in the CDR region, we propose a physics-based classifier model that can accurately predict the propensity of deamidation and isomerization of a protein sequence. The model relies on decomposing the major steps of the reaction (deprotonation, nucleophilic attack, and hydrolysis) as conformational degrees of freedom and inferring the reaction propensity based on the thermodynamic feasibility of exploring those conformations.

Results

Conformational determinants of deprotonation

Peptide backbone conformation and amide acidity. Deprotonation of the amide nitrogen in proteins has been experimentally characterized to proceed via a base-catalyzed reaction that is quite spontaneous even at acidic conditions.^31,39–41 Several studies have investigated the dependence of backbone amide acidity on the conformation and chemical environment using QM/QMMM calculations.^{29,30,35–37} In pioneering studies, Radkiewicz et al.^26,27 used N-formyl-glycinamide as a model compound representing a peptide bond to calculate the relative proton affinity as a function of the ϕ and ψ dihedral angles (using HF/6-31 + G*//HF/3-21 G). The calculations showed that conformations along the ψ dihedral angle had a larger impact on the backbone acidity of peptide bond relative to the ϕ angle. Here, we carried out density functional theory (DFT) calculation to estimate proton affinity for the same model compound at the M062X/6-311++G (d, p) level of theory in both gas phase and aqueous phase continuum SMD (Solvation Model Based on Density) solvent environment. Our results agree with the earlier studies: proton affinity of backbone amide varies significantly with respect to changes in the backbone conformation (Figure 2b and S1). Specifically, in α-helical conformation the proton bonded to the amide experiences a repulsive force from the adjacent carbonyl carbon as a result of a di-electric instability with the amide nitrogen (Figure 2c) i.e., proton affinity of the model compound is lower in the α-helical conformation centered around −60° ≤ ψ ≤ 60°, Figure 2b. The gas phase semi-empirical QM calculations using MOPAC with PM6-D3H4,47 PM7 and RM1 Hamiltonians (see methods and Figure S1) are also consistent with DFT results.

To better understand the mechanism by which peptide backbone conformation affects amide acidity, we extended the proton affinity calculations as a function of backbone ϕ & ψ dihedral angles to different DX and NX dipeptides, Figure 3 and Figures S2-S16. As reported previously,³³ fold differences are observed in reaction half-lives of pentapeptides due to the variations in the n + 1 residue. For instance, an interesting comparison can be made between Gly and Ala as n + 1 residue. In solution, GGNGG and GGNAG peptides show high propensity to adopt an α-helical conformation,^41,42 yet their deamidation half-lives are an order of magnitude different (1.03 and 21.1 d, respectively).³³ From the proton affinity calculations, we observed that the amides in both NG and NA are indeed acidic around −60° ≤ ψ ≤ 60° conformations (Figure 3a). However, the amide proton affinity in the NA peptide significantly changes as a function of the ϕ angle. Specifically, the backbone amide of the NA residue is more acidic in conformations where ϕ > 0 compared to ϕ < 0 within the same boundary of −60° ≤ ψ ≤ 60°. In other words, the proton affinity of NA peptide is also dependent on the type of the helical conformation (right-handed α-helix versus left-handed α-helix). A right-handed α-helix conformation places the methyl side-chain group in close proximity to the backbone amide that offers protection from exposure to the base and/or hydrolysis (Figure 3b, conformation 2).

Figure 3.

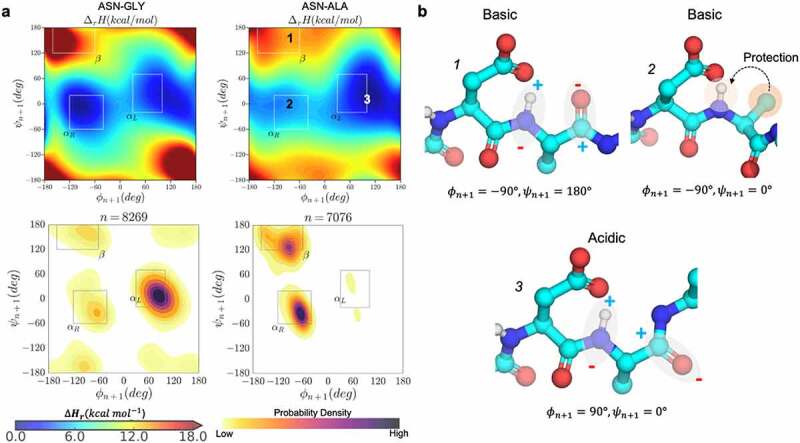
Conformational determinants of proton affinity in NG and NA dipeptides. a) the gas-phase proton-affinity calculated with the semi-empirical PM6 Hamiltonian as a function of ϕ & ψ angles (upper panels) and the kernel density estimation plots of ϕ & ψ angles for the respective NG and NA motifs observed in the PDB database of crystallized antibodies (lower panels). b) Representative conformations and the possible ways in which the values of ϕ & ψ affects proton affinity: beta sheet (b1, basic), right-handed helix (b2, basic), and left-handed helix (b3, acidic).

Similarly, it can be inferred from the proton affinity plots for different [N/D]X dipeptides (Figures S2-S16) that amide acidity in right-handed α-helix conformations is affected by the side chain of the n + 1 residue. The side chain-mediated protection increases with increasing the size of nonpolar, hydrophobic (i.e., Phe > Ile > Leu > Val > Ala). On the other hand, the presence of a polar hydroxyl or carbonyl groups in the n + 1 side chain (as in Asp, Ser, Thr, Asn, Tyr) facilitates the deprotonation of the amide by solvent-mediated electrostatic interactions. In any left-handed α-helix conformation, or in the case of Gly, the protection from the n + 1 residue is completely lost (Figure 3b, conformation 3), which is consistent with the previous results based on the model compound.^26,27

Crystal structure analysis. It must be noted that a large fraction of combinations of ϕ & ψ dihedral angles explored in the dipeptide models are energetically inaccessible in folded proteins. To identify the relevant secondary structures for the NX and DX motifs in proteins, we collected ϕ & ψ angle distribution from all the antibody crystal structures available in the PDB. These distributions were analyzed using kernel density estimation (KDE) to arrive at the probability density function (PDF) of conformational preference for [N/D]X residues in ϕ & ψ space (Figure 3a and Figures S2-S16). Comparing the proton affinity calculations with the conformational PDF reveals that [N/D]G sites mainly populate the acidic left-handed α-helical conformations, whereas [N/D]A sites largely favor the basic right-handed helix (ϕ < 0 region) or the beta sheet. The latter agrees with a previous work showing that a steric interaction between the methyl group and the terminal carbonyl oxygen destabilizes all structures with ϕ ~ 120°, relative to glycine dipeptides.⁴³ These results clearly explain why [N/D]A sites are often orders of magnitude less prone to degradation than [N/D]G sites.

A comprehensive analysis of the proton affinity calculations and conformational PDF (Probability Density Function) in ϕ & ψ space for all the [N/D]X sites (Figures S2-S16) revealed that the frequency of observing a residue in the acidic region from the PDB is strongly correlated with the likelihood of the residues to undergo degradation. In particular, we observed that the most frequently modified, or canonical, [N/D]X sequences based on various reports (i.e., DG,^44–46 DS,^14,47,48 DD,⁴⁸ DT,²⁰ DH,⁴⁹ NG, NS, NN, and NT^12,20,33,44) mainly favor the left-handed helix in the Ramachandran plot, i.e., the backbone is acidic and any side-chain protection by the n + 1 residue is completely lost (Figure 3b, conformation 3). Interestingly, the strongest left-handed helix population is seen for DG and DS, followed by DH, DD, and DN. Similarly, for deamidation motifs, a decreasing population of left-handed helix is observed in the order of NG, NS, NN and NT.

To better illustrate this point, we plotted the normalized probability of secondary structure conformations (area under the PDF surface bound by the region in ϕ & ψ space) for [N/D]X motifs in all of the antibodies in the PDB against the normalized minimum proton affinity calculated for the corresponding dipeptides in the same conformational region (Figure 4, S17 and S18). The canonical NX motifs (NG, NS, NN, and NT^12,20,33,44) clearly aggregate in the bottom right quadrant of the plot (yellow boxes in Figure 4), which corresponds to a high probability of adapting a low proton affinity conformation within each bounding box (α_R,α_L and β) defined in Figure 3. In contrast, non-canonical motifs (e.g., NV, NL, NM, NC, NI, NF, NE, ND) either largely favor a basic beta-sheet conformation (Figure 4c, top-right quadrant), or a basic right-handed helix (e.g., NI, NM, and ND in Figure 4a, top-right quadrant). A similar trend is observed for DX motifs (Figure 4d-4f, S19 and S20), canonical motifs such as DG, DS and DD fall either within or very close to the high-risk quadrants. A few exceptions to this trend are DY, DF and DL that are unexpectedly placed in the low proton affinity region of the beta sheet conformation, Figure 4d. However, a side-by-side comparison of the proton affinity calculation plots and conformational PDF plots for these three residues (Figures S11, S14 and S15) suggests that: 1) these motifs indeed highly favor a β-sheet conformation, and 2) on average, the proton affinity is still much higher in the β-sheet region compared to α_R and α_L. In fact, the minimum proton affinity value for these three motifs (Figure 4d) is defined by an abrupt decrease in the rough proton affinity surface, and it is not representative of the overall trend.

Figure 4.

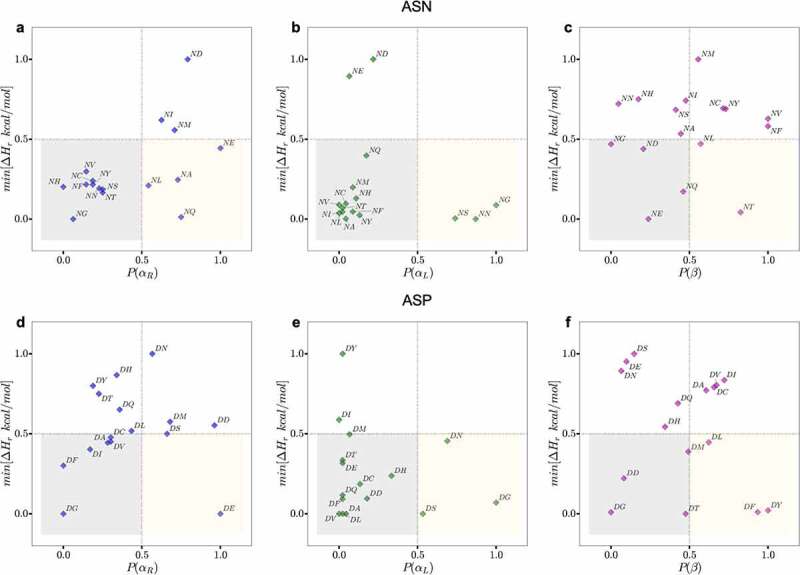
Plots of the normalized probability of secondary structure conformations for NX (upper panels) or DX (lower panels) motifs for antibody structures in PDB (X-axis) and the normalized minimum PM6 proton affinity heat of formation observed in the same region in Y-axis. The yellow boxes show motifs that are likely to adapt the corresponding conformation (X-axis) resulting in a low relative proton affinity. The gray boxes highlight motifs that are less likely to adapt the corresponding conformation but will result in a low proton affinity. The regions outside gray and yellow represent high proton affinity motifs and conformations (less prone to degradation). The residues in the yellow boxes are most often the hot spot residues.

Overall, Figure 4 demonstrates the role of a combined effect of secondary structure and the identity of the n + 1 amino acid side chains in impacting chemical degradation. Therefore, we use the ϕ & ψ backbone dihedral angle of the peptide bond at an [N/D]’s n + 1 position as a metric to identify sites that have higher propensity to deprotonate: 1) β-sheet conformation is less deprotonation prone, 2) the left-handed α-helix regions (−60° ≤ ψ ≤ 60°, ϕ > 0°) is acidic for all amino acids that have a nonpolar (A, V, L, I) or bulkier side-chain groups (F, W), and 3) on the contrary, for small polar amino acids (G, S, T, D) both the left and right-handed α-helix (−60° ≤ ψ ≤ 60°) conformations are acidic.

Application to therapeutic antibodies. Next, we explored the relationship between backbone conformations of the [N/D]X sites in the CDR regions of 131 therapeutic mAbs and their reported degradation rates. This dataset corresponds to 1039 [N/D] X sites (498 Asp and 541 Asn) of which 30 DX and 39 NX sites were prone to degradation (reactive). To obtain the backbone conformation preference, we calculated the conformational free energy surface (FES) in the ϕ & ψ space for the n + 1 residue from microsecond long equilibrium MD simulations of the antigen-binding fragment (Fab) structures. We arbitrarily chose a value of 2k_BT energy barrier or ~1 kcal/mol to define energetically favorable conformations, i.e., in the FES, a region whose energy values are <1 kcal/mol are likely to be sampled under equilibrium conditions. The n + 1 residues were considered to be in a left-handed or right-handed α-helix if the minimum energy values in the regions of FES where −60° ≤ψ ≤ 60° and ϕ > 0, or ϕ < 0, were <1 kcal/mol.

Figure 5 shows that the calculated conformational distribution (PDF) of reactive and non-reactive residues correspond very well with the expected conformational preference seen in proton affinity calculations. The experimentally reported non-reactive residues show a preference to the right-handed α-helix or the β-sheet conformation, while the reactive residues show large preference to the left-handed helical conformation. Figure 7 (D1) reveals a correlation between the rate of degradation and the probability of the backbone amide being found in the acidic regions. With the exception of two sites, the degradation rates fall below the desirable 5% cutoff for all the [N/D]X sites that are in a basic backbone conformation (i.e., Free Energy >1 kcal/mol, which corresponds to either a beta-sheet or a right-handed helix when the n + 1 residue is nonpolar). However, the results in Figure 7 (D1) suggest that an acidic backbone conformation (Free Energy < 1 kcal/mol) does not always result in high degradation rates (% Degraded > 5). A high propensity for a basic conformation can prevent the site from degradation, but lack thereof is not sufficient for degradation.

Figure 5.

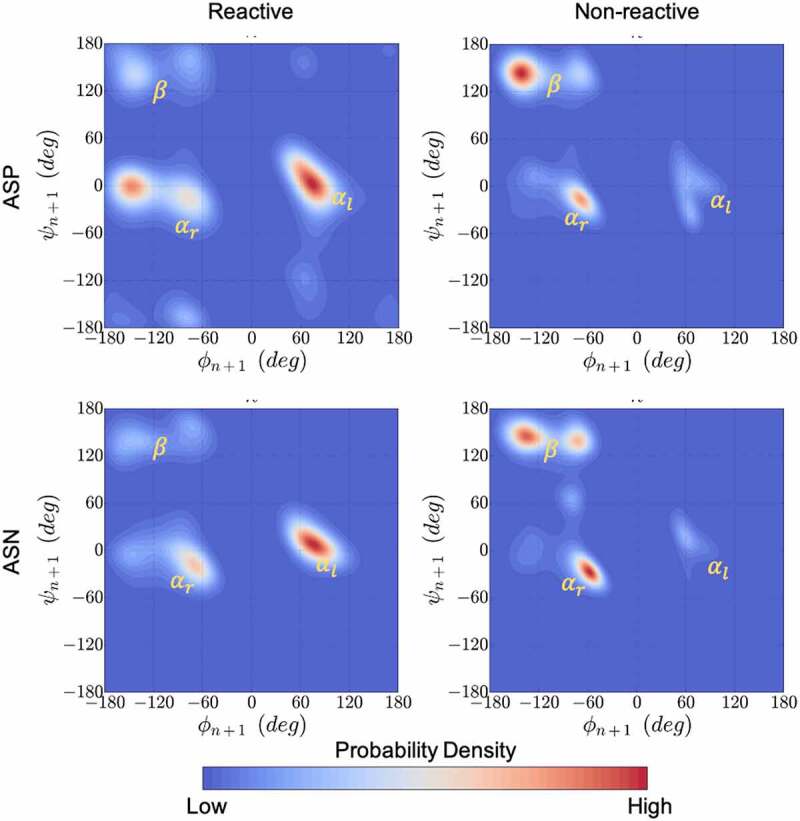
Kernel density estimation plots for the ϕ & ψ dihedral angles populated in MD simulations combined for all 1039 residues that neighbor Asp (top) or Asn (bottom) in the Adimab dataset. The ϕ & ψ angle distributions were collected from μs long equilibrium MD simulations and classified as reactive (left) and non-reactive (right) based on the measurements reported in the Adimab dataset. A clear pattern emerges around the left-handed α-helix conformation in reactive cases that is distinct from the non-reactive cases on the right.

Figure 7.

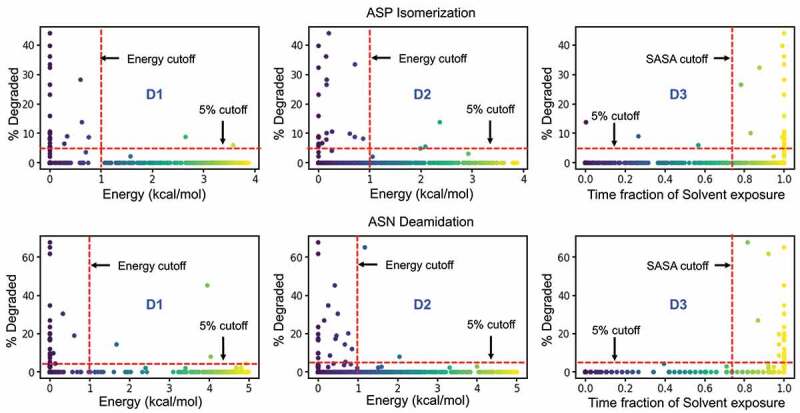
Performance of individual descriptors in discriminating degraded Asp (top) and Asn (bottom) residues from the Adimab dataset. The percentage degradation values reported in the Adimab study are represented on the X-axis. The Y-axis in the leftmost panel (D1) is the free-energy barrier at the deprotonation prone backbone helical conformation of the n + 1 residue. The Y-axis in the middle panel (D2) is the free-energy barrier at the near-attack conformation defined by the ψ & χ angles. The Y-axis in the rightmost panel (D3) is the time fraction when the Asp/Asn residue remains solvent accessible. The red cutoff markers indicate the values that determine if a residue is prone to degradation or not. The blue shaded regions indicate the false negative predictions (experimentally observed to degrade but classified as non-reactive) and the gray shaded region indicates the false positives (predicted reactive but not evidenced experimentally).

The backbone conformational preference of NX and DX residues under equilibrium conditions as a single descriptor was found to classify the reactive vs non-reactive residues at 65% accuracy (Table 1). This shows that proton affinity inferred from the secondary structure of n + 1 residue is a decisive descriptor to predict degradation propensity of NX and DX sites.

Table 1.

Performance analysis for the physics-based classifier model using different combinations of the descriptors: (D1) backbone dihedral conformation of the n + 1 residue, (D2) side-chain dihedral conformation of Asn/Asp residue, (D3) fraction of time the Asn/Asp residue remains solvent accessible. Combinations are represented by DXX where the X represents the descriptors.

Type	TP*	FN*	FP*	TN*	Accuracy	Accuracy†	Precision	Recall	F1 Score	F0.5 Score	MCC‡	CKS§
ASN-D1	20	3	173	345	0.67	0.77	0.95	0.67	0.77	0.87	0.23	0.12
ASN-D2	21	2	301	217	0.44	0.67	0.95	0.44	0.57	0.75	0.14	0.05
ASN-D3	23	0	316	202	0.42	0.69	0.96	0.42	0.54	0.73	0.16	0.05
ASN-D12	19	4	130	388	0.75	0.79	0.95	0.75	0.83	0.90	0.26	0.16
ASN-D13	20	3	92	426	0.82	0.85	0.96	0.82	0.87	0.92	0.34	0.24
ASN-D23	21	2	183	335	0.66	0.78	0.96	0.66	0.76	0.86	0.23	0.12
ASN-naïve	0	23	0	518	0.96	0.50	0.92	0.96	0.94	0.92	0.00	0.00
ASN-D123	19	4	62	456	0.88	0.85	0.96	0.88	0.91	0.94	0.40	0.32
ASP-D1	22	2	186	288	0.62	0.76	0.95	0.62	0.73	0.84	0.23	0.11
ASP-D2	22	2	318	156	0.36	0.62	0.94	0.36	0.48	0.68	0.11	0.03
ASP-D3	21	3	312	162	0.37	0.61	0.94	0.37	0.49	0.68	0.10	0.03
ASP-D12	20	4	118	356	0.76	0.79	0.95	0.76	0.82	0.89	0.28	0.18
ASP-D13	20	4	133	341	0.72	0.78	0.95	0.72	0.80	0.88	0.26	0.16
ASP-D23	20	4	205	269	0.58	0.70	0.94	0.58	0.69	0.82	0.17	0.08
ASP-naïve	0	24	0	474	0.95	0.50	0.91	0.95	0.93	0.91	0.00	0.00
ASP-D123	19	5	77	397	0.84	0.81	0.95	0.84	0.88	0.92	0.34	0.26
ALL-D1	42	5	359	633	0.65	0.77	0.95	0.65	0.75	0.86	0.23	0.12
ALL-D2	43	4	619	373	0.40	0.65	0.95	0.40	0.53	0.72	0.13	0.04
ALL-D3	44	3	628	364	0.39	0.65	0.95	0.39	0.52	0.71	0.13	0.04
ALL-D12	39	8	248	744	0.75	0.79	0.95	0.75	0.83	0.90	0.27	0.17
ALL-D13	40	7	225	767	0.78	0.81	0.95	0.78	0.84	0.90	0.30	0.19
ALL-D23	41	6	388	604	0.62	0.74	0.95	0.62	0.73	0.85	0.20	0.10
ALL-naïve	0	47	0	992	0.95	0.50	0.91	0.95	0.93	0.92	0.00	0.00
ALL-D123	38	9	139	853	0.86	0.83	0.95	0.86	0.89	0.93	0.37	0.29

*TP – True positive, FN – False Negative, FP – False positive and TN – True Negative. † Balanced accuracy calculated with weighted distribution of positives and negatives. ‡ Matthew’s Correlation Coefficient ranges from −1.0 to +1.0, where the negative values indicate a bad predictor. § Cohen Kappa Score ranges from −1.0 to +1.0, similar to the MCC statistic but a better indicator to compare an imbalanced dataset.

Conformational determinants of cyclization

Once deprotonation is enabled by the acidity of the backbone, the next step in the reaction is ring closure leading to succinimide formation via nucleophilic attack between N- atom of the n + 1 residue and Cγ of the ASN/ASP residue (Figure 1). In order for the nucleophilic attack to be feasible, the N- and Cγ should come closer than distances of 3.0 Å (near-attack conformation).^29,30 In folded proteins, side-chain interactions, including hydrogen bond formation, can limit the conformational flexibility of Asn/Asp residues to visit near attack conformations. This in turn can disfavor succinimide formation. Multiple side-chain orientations can result in the near attack conformation (Figure 6a). Conformational degrees of freedom affecting the distance between Cγ and N_n+1 can be defined as a function of the two dihedral angles ψ & χ₁.

Figure 6.

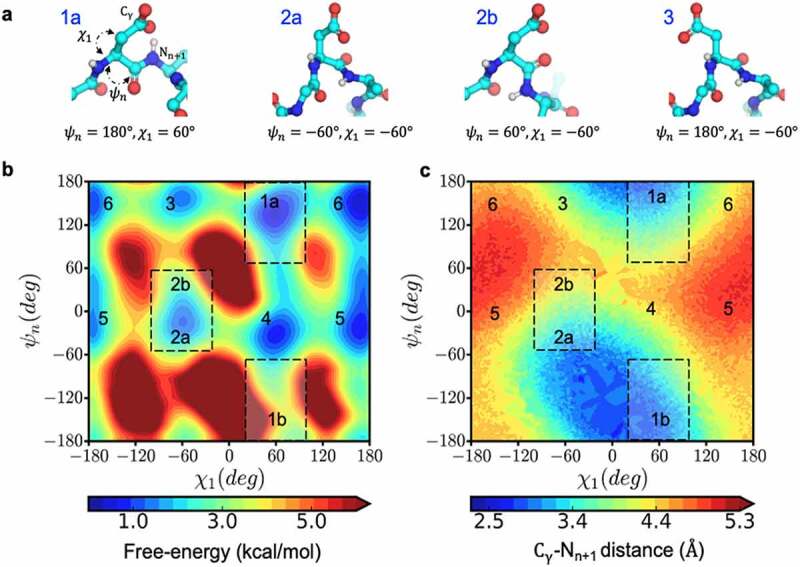
Conformational space that enables near-attack distances increasing the propensity for succinimide formation. a) The structural orientation of the reactive (1a and 2a) and non-reactive (2b and 3) side-chain conformations, characterized by ψ & χ, for an aspartic acid residue shown in ball and stick representation. b) Free-energy surface in the space of ψ & χ dihedral angles and c) the corresponding distance between Cγ and the n + 1 amide nitrogen calculated from metadynamics simulation of Ace-GGNAG-Nme pentapeptide.

To identify the relevant conformations that enable a nucleophilic attack distance, we sampled the free energy space of ψ & χ₁ angles in Ace-GGNAG-Nme pentapeptide using Metadynamics simulations. By applying an additive historical bias, Metadynamics pushes the system to explore conformations that are kinetically limited in an equilibrium simulation⁵⁰. There are six low energy states in the ψ & χ₁ space (Figure 6b), of which two regions are coincident with the near attack conformation distance (Figure 6c). With this information, we looked at the correlation between the near attack side-chain conformation and the experimental rates reported in the Adimab dataset. As with the backbone conformation, we looked at the FES from the equilibrium MD simulation. The side chains were considered to be in a near-attack conformation if the minimum energy values in the regions of FES where −100 < χ₁< −20 and −60 < ψ < 60 (Figure 2b, region 2), or 20 < χ₁ < 100 and ψ < −60 or ψ > 60 (Figure 2b, region 1), were <1 kcal/mol.

Figure 7, D2 shows that when the side chain is not in a near-attack conformation (i.e., Free Energy > 1 kcal/mol), the reaction rates largely remain below the 5% cutoff, with a few exceptions. Otherwise, the residue may or may not be reactive, as suggested by the large number of data points below and above 5% for Free Energy <1 kcal/mol. Therefore, the side-chain conformation indeed proved to be a useful descriptor in identifying reactive residues (Figure 7, D2). The overall accuracy of the prediction was at 40%, but when used in combination with the backbone conformation rule, i.e., both the acidic conformation and the near attack conformations are energetically feasible, the accuracy of the classification model improves to 75% (Table 1).

Solvent accessibility

Water plays an important role in the deamidation and isomerization reaction as a proton donor/acceptor. Both the base catalyzed deprotonation and hydrolysis of succinimide intermediate to Asp/iso-Asp are only feasible in the presence of water molecules (Figure 1). In previous studies, solvent accessibility weakly predicted the reaction propensity.^19,20,33 These previous calculations were done on static protein structures that lacked proper structural relaxations that may affect solvent accessibility calculations. Our solvent accessibility calculations use a dynamic approach in combination with intuitions about the reaction. Here, we calculated the solvent accessibility at a residue level. In order to capture the dynamic aspect of the solvent occupancy, we represented solvent accessibility as a fraction of time in which the Asn/Asp residue remained accessible (see methods). Using this value, we once again sought to classify the Asn/Asp residues in the Adimab set as reactive vs non-reactive. Figure 7, D3 shows that solvent-inaccessible side chains (time fraction of solvent exposure < 75%) are indeed protected from the reaction. However, a large number of both reactive and non-reactive cases are seen in the solvent-accessible region (time fraction of solvent exposure > 75%). The overall accuracy in predicting the reactivity using the solvent-accessible surface area as a single descriptor is 39%, which is no better than the performance of the near attack conformation metric.

Combined model

As discussed above, deamination and isomerization reactions can be described in the three consecutive steps: deprotonation, cyclization, and hydrolysis. Using a multiscale computational approach, we were able to test the propensity of degradation in the Adimab dataset using these physics-based metrics. Since all three steps are essential for the reaction, we sought to check if a combination of the three metrics would improve the classification accuracy: (D1) deprotonation – as represented by the free-energy profile of ϕ, ψ angles of the n + 1 residue recovered from the MD simulation, (D2) cyclization – as represented by the free-energy profile of χ₁, ψ angles also recovered from the MD simulation, and (D3) hydrolysis – as represented by the solvent accessibility calculated as the fraction of solvent occupied state in MD trajectory. The decision tree that we used to classify if an Asn/Asp residue is likely to degrade is shown in Figure 8. The Adimab dataset discussed herein is disproportionately distributed toward true negatives (non-reactive) vs true positives (reactive), so this presented a challenge to interpreting common statistical measures such as accuracy. We instead chose to use balanced accuracy, Matthew’s correlation coefficient (MCC) and Cohen’s Kappa score (CKS) as the statistic to compare the three individual descriptors, as well as combinations. We also created a naïve predictor that would predict all the residues as non-reactive; this naïve predictor will score 0 on both the MCC and CSK statistic. As can be seen from Table 1, the physics-based classifier model based on the three descriptors offers an overall balanced accuracy of 83% in predicting the isomerization and deamidation sites. All three descriptors have a better MCC and CKS score compared to the naïve predictor. Similarly, any combination of two descriptors performed moderately better than a single predictor. The combined model using all three descriptors is better at predicting non-reactive residues over reactive residues, which could be useful in a therapeutic manufacturing setting where the cost of predicting a reactive residue as non-reactive is higher. This combined mechanistic model acts as a good screening criterion in identifying antibodies that are prone to chemical degradation via deamidation or isomerization.

Figure 8.

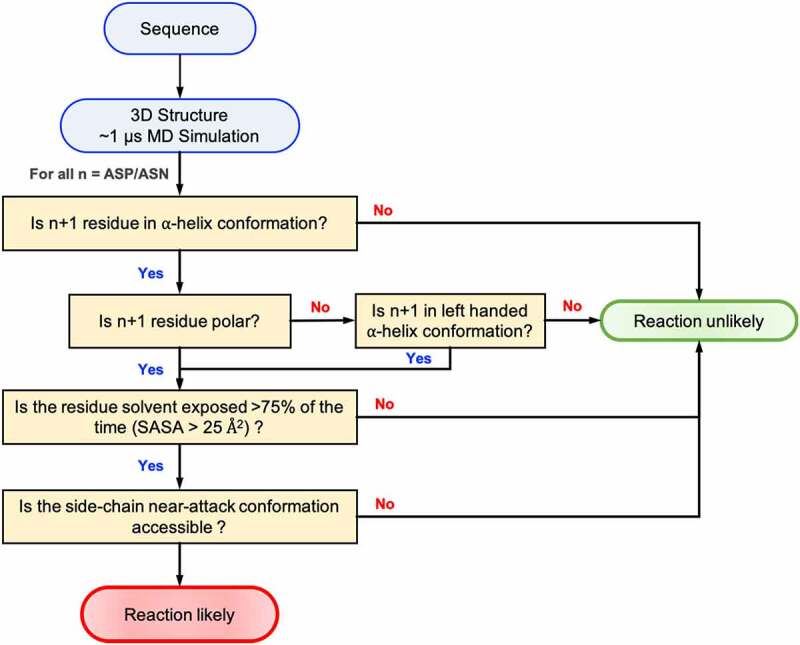
Flowchart showing the decision scheme used to determine if a given Asn/Asp residue is likely to degrade in folded proteins.

Finally, we investigated the impact of simulation sampling time and number of replicates on the reliability of the prediction results. Both the sampling time and conformation sourced from multiple replicates have a direct impact on the probability of observing kinetically limited events in equilibrium simulations. We calculated accuracy metrics: MCC, specificity, sensitivity, and accuracy, as a function of different simulation lengths and numbers of replicas (Figure 9). We find that accuracy and specificity plateau in the 10-to-100 ns regime, whereas more robust performance indicators such as MCC and sensitivity show improvement with longer simulations, regardless of the number of replicates. Furthermore, predictions were more reliable when the conformations were collected from multiple short replicates over conformations from one long simulation. This is directly attributable to a decrease in the number of false positives with increased number of replicas that has been observed in similar studies performed by others.⁵¹ Overall, our method is robust when conformations are sourced from at least three replicate simulations of the system each at least 100 ns long. This replication and duration give an optimal trade-off between accuracy and computational investment.

Figure 9.

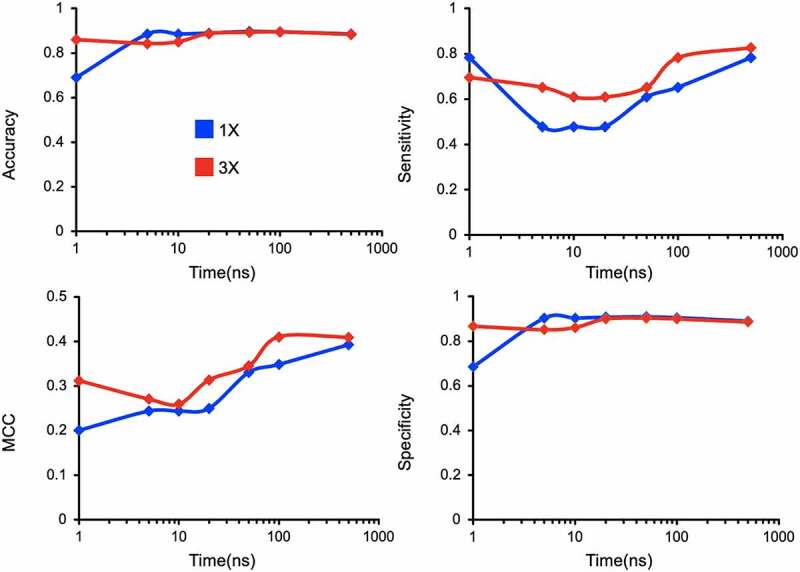
Assessing sensitivity of model accuracy to the variations in simulation length (1–500 ns) and replicas (1 and 3).

Discussion

Spontaneous chemical degradation at the Asn/Asp residues is an important problem that affects the developability of the protein therapeutics. Typically, the issues of chemical degradation are encountered at later stages in the development, at which point iterative protein-engineering efforts are used to mitigate these modifications. Such iterative efforts prolong development timelines and delay the delivery of lifesaving therapeutics to patients. Multiple computational strategies ranging from QM calculations to machine learning models have been proposed to predict degradation in Asn/Asp. Very few such tools (if any) generalize for high-throughput screening. We leveraged prior theoretical and experimental findings on the Asn/Asp degradation reactions to carry out multiscale analysis to comprehensively evaluate the chemical degradation in 1039 residues (498 Asp and 541 Asn) spanning 131 therapeutic mAbs. In doing so we made several notable observations. First, amide acidity in right-handed α-helix conformations is highly dependent on the n + 1 residue; a nonpolar n + 1 side chain decreases the amide acidity through protection from exposure to the base and/or hydrolysis. The protection from the n + 1 side chain is completely lost in left-handed α-helix conformations, as well as in the case of Gly. Second, specific regions of the Asn/Asp’s side-chain conformational space facilitate a near-attack conformation and are energetically more favorable in reactive sites. Third, solvent-inaccessible side chains are protected from the reaction. From an experimentally validated set, we were able to connect molecular intuition from the reaction mechanism to a real-life scenario. Using just three descriptors that are fundamental to the protein structure one can heuristically classify the likelihood of the protein to undergo chemical degradation at the ASN/ASP sites. Although we have exclusively examined mAbs in this study, we believe that the structural and chemical insights described herein are broadly applicable and generalizable to all proteins and protein-based therapeutics.

Materials and methods

Experimental dataset

The validation data contained 498 Asp and 541 Asn residues in the CDR loops of 131 therapeutic mAbs published by Lu et al.³⁴ The isomerization events were analyzed at low pH stress (pH 5.5) for 2 weeks at 40°C. A total of 31 isomerization sites were identified with total modification measurements ranging from 2.1% to 44.0%. The deamidation data were obtained at high pH stress (pH 8.5) for 1 week at 40°C. A total of 39 deamidation sites were reported with degradation levels ranging from 2.0% to 67.7%. We used a threshold cutoff of 5.0% for both isomerization and deamidation events to classify reactive versus non-reactive.

QM calculations

Semi-empirical QM (SQM) calculations to calculate proton affinity were performed using GAUSSIAN09⁵² and MOPAC2016⁵³ software packages. To rule out any uncertainties in the proton affinity calculations, we carried out DFT calculation of proton affinity for N-formyl-glycinamide at M062X/6-311++G(d,p) level of theory in both gas phase and aqueous phase continuum SMD solvent environment.⁵⁴ The gas phase calculations where then repeated in MOPAC with PM6-D3H4,⁵⁵ PM7 and RM1 semi-empirical methods (SI).⁵⁴ The regions of proton affinity qualitatively matched across DFT and SQM levels of theory, albeit with variations in the energy values as expected due to variations in the theory and the Hamiltonian. DFT, although accurate, remained prohibitive for exploring conformations across all dipeptides. Semi-empirical QM methods PM6-D3H4, RM1 and PM7 each had discontinuities and convergence issues in sampling conformations of polar side chains. The choice of the SQM functional had a direct impact on how the proton-affinity of a specific conformation is interpreted. We chose to err on the side of caution and took a consensus of the proton-affinity plots from all three functionals to make interpretations. SQM functional are in constant improvement and being corrected for short range interactions, recalculating proton-affinity with those improved potentials can improve interpretations. Overall, we tried to make only qualitative inferences from the QM calculations and we refrained from interpreting the exact energy, as that is beyond the scope of this study.

Dipeptides of the Ace-NX-Nme and Ace-DX-Nme, as well as their corresponding deprotonated anions (where X can be single letter code of all 20 amino acids), were generated using OpenBabel.⁵⁶ The generated structures were subject to geometry optimization under PM6 level of theory to arrive at an initial structure. A 2D PES scan at PM6-D3H4, PM7 and RM1 levels of theory. The scan was performed at 10^° intervals spanning the entire Ramachandran region. A total of 1369 data points were scanned for each dipeptide and its corresponding anion. At each step, geometry optimization was requested to adhere to TIGHT convergence criterion while the angles being scanned would be kept constant. The resulting PES were used to arrive at the proton affinity expressed in the heat of formation for the forward reaction as described in Figure 2. The discrete energy points were interpolated and plotted using linear spline interpolation as implemented in the sklearn and matplotlib⁵⁷ python packages.

PDB library

We downloaded the PDB file of all the antibody (and antibody-like molecules such as Fab, scFv) that have crystal structure deposited in the PDB from SAbDab (The Structural Antibody Database http://opig.stats.ox.ac.uk/webapps/newsabdab/sabdab/).^58,59 We arrived at 3493 structures, which were then cleaned, energy minimized and isolated from any other ligands. Using these structures, we calculated backbone dihedral angles of all Nx and Dx residues from the Fab domain. All the PDB handling was performed using MDanalysis⁶⁰ and PyTraj⁶¹ python tools. The backbone dihedral angle distribution from this data was used for calculating 2D kernel density estimation using the SciKit-Learn python package.⁶²

KDE calculation

In order to compare the KDEs that were calculated from the PDB and the backbone dihedral angles observed in the MD simulations, we first classified each [N/D]X site as reactive or non-reactive based on the deprotonation metric. We collected the ϕ & ψ angle distribution for all these sites across all MD trajectories. This data was used to calculate the second kernel density estimation plot in Figure 5, using the same scikit-learn package as before.

Molecular dynamics simulation

Molecular Operating Environment (MOE)⁶³ software from Chemical Computing Group was used to homology model each of the Fab domain of all the antibodies accessed in the Adimab dataset. The Fab homology modeling tool in MOE constructs the full Fab domain using only the Fv sequences from the Adimab set as input. The Fab structures were energy minimized to remove any steric clashes. The energy minimization was performed using SANDER program in Amber2015.⁶⁴ The protonation states at pH 5.5 and 8.5 were assigned using the PDB2PQR tool. The two pH values mimic the buffer conditions in which the reactivity was estimated in the Adimab experiment.

Energy-minimized Fab structures were then prepared for equilibrium MD simulations by solvating the structure in a cubic box of TIP3P explicit water (model).⁶⁵ It was ensured such that the Fab was positioned at a minimum 10 Å distance from the edge of the box. The system was then adjusted to have a net neutral charge by adding Na+ and Cl- counter ions. Hydrogen Mass Repartitioning was performed on the solute atoms to enable long simulation time steps of 4 fs.⁶⁶

The GPU implementation of Amber 2015 MD software package⁶⁴ with the SPFP precision model was used for the MD simulation. The simulations proceeded by relaxing the system with 2000 steps of conjugate-gradient energy minimization. Harmonic restraining potentials with the force constant of 10 kcal/mol/Ų were imposed to restrain the solute to its initial structure, post which the system was brought to an NPT ensemble with the pressure maintained at 1 atm and the thermostat set to 300 K over the course of 200 ps, while the protein was restrained using a harmonic positional restraint of 10 kcal/mol/Ų. The system was then equilibrated for 1 ns with a restraint force constant of 1 kcal/mol/Ų on the protein structure maintaining the pressure and temperature at the same levels. The system was then subject to equilibrium MD simulation at NPT ensemble without any restraints at a time step of 4 fs. Long-range interactions were cut off at 9 Å and restricted range limited interactions. Coulombic interaction was calculated using the Particle Mesh Ewald algorithm for long-range electrostatics. The thermostat was maintained at 300 K with Langevin dynamics and collision frequency set to 1 ps⁻¹. The simulation was carried out for 500 ns during which the SHAKE algorithm was applied to constrain all bonds involving hydrogen atoms. Two other replicates of the 500 ns simulation were performed instantiated with a different random number to bring the combined sampling time to 1.5 μs. Trajectory snapshots were saved at 10 ps intervals and used for downstream analysis. The combined trajectories from three simulations were used for the analysis.

CPPTRAJ software in AmberTools⁶⁴ was used to analyze the trajectories. The FES in the space of ψ and ϕ dihedral angles were calculated from bin populations using G_i = -k_B T ln(N_i/N_max), where k_B is Boltzmann’s constant, T is the temperature, N_i is the population of bin i and N_max is the population of the most populated bin.

Bins with no population were given an artificial barrier equivalent to a population of 0.5. Solvent-accessible surface area was calculated using the MSMS package⁶⁷ using a probe radius of 1.4 and triangle density of 3.

Advanced sampling using metadynamics

Metadynamics simulations were carried out using the GROMACS2018⁶⁸ MD engine patched to interface with PLUMED.⁶⁹ Metadynamics was performed in the well-tempered⁵⁰ scheme along the conformational space of ψ & χ angles, as collective variables, of the pentapeptide Ace-GGNAG-Nme. The choice of collective variables was based on the atoms connecting the dihedral angles that will affect the distance between n + 1 amide and the side-chain gamma carbon. The simulations used the same forcefield and MD parameters with 2 fs time steps. Bias was added at every 500 steps with a sigma of 0.1 and bias of 1.0 kcal/mol. The simulation was carried out for 1 μs and the trajectory was analyzed after unbiasing the simulation using the standard reweighting⁷⁰ procedure implemented in PLUMED. The free energy surface and corresponding distance distribution was plotted using matplotlib.

Funding Statement

The author(s) reported there is no funding associated with the work featured in this article.

Abbreviations

QM – Quantum Mechanics

PTM – Post-translational modification

CST – Clinical stage therapeutics

CDR – Complementarity-determining regions

QMMM – Quantum mechanics molecular mechanics

KDE – Kernel density estimation

PDF – Probability density function

FES – Free energy surface

MD – Molecular Dynamics

MCC – Matthew’s correlation coefficient

CKS – Cohen’s Kappa score

Fab – Fragment-antigen binding domain

DFT – Density functional theory.

SQM – Semi-empirical quantum mechanics.

SASA – Solvent accessible surface area

Disclosure statement

FJI and SI are co-inventors on the provisional patent application describing the computational method discussed in the manuscript

Supporting information

The supporting information provides the proton affinity calculations and the corresponding KDE plots for DX and NX dipeptides using different QM models.

Contact

All correspondence and data requests should be directed to the corresponding author.

Supplementary material

Supplemental data for this article can be accessed online at https://doi.org/10.1080/19420862.2022.2143006.