Liability-scale heritability estimation for biobank studies of low-prevalence disease

Summary

Theory for liability-scale models of the underlying genetic basis of complex disease provides an important way to interpret, compare, and understand results generated from biological studies. In particular, through estimation of the liability-scale heritability (LSH), liability models facilitate an understanding and comparison of the relative importance of genetic and environmental risk factors that shape different clinically important disease outcomes. Increasingly, large-scale biobank studies that link genetic information to electronic health records, containing hundreds of disease diagnosis indicators that mostly occur infrequently within the sample, are becoming available. Here, we propose an extension of the existing liability-scale model theory suitable for estimating LSH in biobank studies of low-prevalence disease. In a simulation study, we find that our derived expression yields lower mean square error (MSE) and is less sensitive to prevalence misspecification as compared to previous transformations for diseases with $\le 2\text{\%}$ population prevalence and LSH of $\le 0.45$, especially if the biobank sample prevalence is less than that of the wider population. Applying our expression to 13 diagnostic outcomes of $\le 3\text{\%}$ prevalence in the UK Biobank study revealed important differences in LSH obtained from the different theoretical expressions that impact the conclusions made when comparing LSH across disease outcomes. This demonstrates the importance of careful consideration for estimation and prediction of low-prevalence disease outcomes and facilitates improved inference of the underlying genetic basis of $\le 2\text{\%}$ population prevalence diseases, especially where biobank sample ascertainment results in a healthier sample population.

Estimating the heritability of low-prevalence diseases in biobanks can lead to inconsistent and unrealistic results because of high estimator variance. Here, we propose a simple alternative that increases the heritability estimation accuracy for low-prevalence traits that is also suitable for ascertained samples.

Introduction

Genetically informed deep-phenotyped biobanks are an increasingly available important research resource. From these data, estimates of SNP heritability, $h_{SNP}^2$, can be obtained, a quantity describing the proportion of phenotypic variance attributable to the genetic marker data.¹ Linked electronic health records provide a large number of binary, presence/absence disease diagnosis indicators and it is important to be able to compare $h_{SNP}^2$ estimates in order to infer the relative importance of genetic and environmental risk factors that shape different clinically important disease outcomes.

To better describe the genetics of such binary traits, the notion of liability-scale heritability (LSH) has been coined² to reflect the underlying continuous nature of additive genetic effects. Falconer defines liability to a disease as “an underlying gradation of some attribute immediately related to the causation of the disease,”² however in practice one instead observes the binary disease trait defined as the liability exceeding or not exceeding some threshold. It is possible to estimate the heritability on the observed binary scale, however as this will be dependent on the disease prevalence, it is preferred to transform the observed scale heritability into LSH. Therefore, LSH is defined as the ratio of genetic variance and the total phenotypic variance on the previously described latent liability scale. An initial derivation for LSH was given by Alan Robertson in the Appendix of Dempster and Lerner³ for the scenario where the case-control ratio was the same in the sample and the population. Lee et al.⁴ proposed an extended derivation to account for the fact that, in a case-control study, cases tend to be over-represented compared to the population prevalence, arriving at the following expression for the LSH:

$$h_{liab}^2=h_{obs}^2\frac{K\left(1-K\right)}{\phi {\left({\text{Φ}}^{-1}\left(K\right)\right)}^2}\frac{K\left(1-K\right)}{P\left(1-P\right)},$$ (Equation 1)

where $h_{obs}^2$ is the observed scale heritability, K is the prevalence of the binary trait in the full population, P is the prevalence of the binary trait in the sampled subpopulation, and the denominator of the first fraction is the squared probability density function of the standard normal distribution evaluated at the Kth quantile of the inverse cumulative density function of the standard normal distribution. This expression was derived under the assumption that sample prevalence is greater than or equal to population prevalence ($P\ge K$).

The problem of accurately estimating LSH was further investigated by Golan et al.,⁵ who noted that in the common setting of sample prevalence exceeding population prevalence ($P>K$), Equation 1 applied on REML estimates underestimates LSH. To account for this, they proposed phenotype correlation-genotype correlation (PCGC) regression, which generalizes a Haseman-Elston regression and yields unbiased estimates of LSH in simulations. In many settings, especially if there are individual-level data available and the sole goal of the analysis is to estimate the LSH, it is recommended to use PCGC or its extension to summary statistic data.⁶ However, often summary-level marginal SNP regression coefficients from biobank studies are used in methods such as LD score regression⁷ or high-definition likelihood⁸ to indirectly infer $h_{SNP}^2$. Furthermore, the observed scale heritability estimate could be a hyper-parameter embedded into effect size estimation (BayesRR-RC⁹) or GREML¹⁰ is used to directly infer the observed scale heritability. Therefore, it remains important to facilitate the transformation of observed scaled heritability into LSH.

The structure of the biobank datasets creates additional problems. Firstly, they often represent a subset of the population that often is healthier, younger, or has higher socio-economic background than the average population. Because of this, many, if not most, binary disease traits have a lower sample prevalence compared to the population prevalence ($P<K$). The classical expression in Equation 1 has been derived and tested for situations where $P\ge K$, and this can result in estimates with inflated variance for situations where $P<K$. Secondly, the disease prevalence in biobank-scale studies can be small and measurement errors of such a small quantity could greatly amplify the variance of the LSH estimate. In practice, as biobanks include people born during different decades, cohorts have usually not reached the end of their lifespan, and as disease prevalences change across time, it seems appropriate to accompany the prevalence estimates with error estimates when arriving at an LSH estimate. Furthermore, although Equation 1 has solid theoretical justification, it does not guarantee that the LSH estimate will be lower than or equal to 1, and even if the LSH estimate is bounded, it can still have high variance in the biobank setting, especially if the model is imperfectly specified or there are greater deviations away from the assumption of the existence of latent genetic liability.

Here, we propose an alternative expression to address some of those issues. Firstly, the suggested expression will guarantee that the LSH estimate will be bounded between 0 and 1, and secondly, we demonstrate that for low prevalences ($K\le 0.02$), our formula results in lower mean square error (MSE) compared to the classical expression. Thirdly, we show that our formula limits the inflation in MSE if we take into account the uncertainty in the prevalence estimation. We further provide an adjusted expression for ascertained samples. Although the suggested expressions can result in a small downwards bias, we argue that for many biobank-based studies for which $P\le 1.5K$ and $K\le 0.02$, this still is preferred to inhibit the emergence of unrealistic estimates due to large MSE. Finally, we apply our proposed expressions to 13 disease outcomes with low sample prevalence in the UK Biobank and we compare the LSH estimates obtained by our expression to those of Equation 1. We also provide a shiny app, https://medical-genomics-group.shinyapps.io/h2liab/.

Material and methods

Derivation of the expression

Suppose that we have a binary trait with a frequency of K in the population, and a frequency of P in the sample is here equal to K. Suppose that a liability model holds meaning that there exists a latent liability l that is defined as a sum of genetic (g) and error (e) components, $l=g+e$. We assume that l has a variance of 1 and that g and e come from normal distributions: $g\sim N\left(0\text{,}{h}_l^2\right)$, $e\sim N\left(0\text{,}1-h_l^2\right)$, where $h_l^2$ is the LSH. Then we assume that the binary disease trait y is associated with l such that $y=1$ if $l>t$ and $y=0$ if $l\le t$, where t is some liability-scale threshold defining the required liability value for disease occurrence, and $t={\text{Φ}}^{-1}\left(1-K\right)$.

We first write the expression of how is the observed scale heritability associated with LSH. As shown by Dempster and Lerner,³

$$h_o^2=\frac{h_l^2\phi {\left({\text{Φ}}^{-1}\left(K\right)\right)}^2}{K\left(1-K\right)},$$ (Equation 2)

where $h_o^2$ is the observed scale heritability. We recognize that the numerator represents the observed scale genetic variance and the denominator represents the total observed scale phenotypic variance. Our idea is to replace the total phenotypic variance estimate $K\left(1-K\right)$ with the sum of genetic and error variances and that by definition will guarantee that the LSH estimate remains bounded. Thus, we need to rewrite the total phenotypic variance by using the error variance $E\left(Var\left(y|c+zg\right)\right)$:

$$Var\left(y\right)=h_l^2\phi {\left({\text{Φ}}^{-1}\left(K\right)\right)}^2+E\left(Var\left(y|c+zg\right)\right).$$ (Equation 3)

We find (see supplemental information) that the error variance is expressed as

$$E\left(Var\left(y|c+zg\right)\right)=K-\widetilde{\text{Φ}}\left({\text{Φ}}^{-1}\left(K\right)\text{,}{\text{Φ}}^{-1}\left(K\right)\text{,}{h}_l^2\right),$$ (Equation 4)

where $\widetilde{\text{Φ}}\left(x_1\text{,}{x}_2\text{,}\rho \right)$ is the cumulative distribution function of a bivariate normal distribution with a mean of 0, variance of 1, and correlation ρ evaluated at $\left(x_1\text{,}{x}_2\right)$. That gives us the expression for observed scale heritability

$$h_o^2=\frac{h_l^2\phi {\left({\text{Φ}}^{-1}\left(K\right)\right)}^2}{h_l^2\phi {\left({\text{Φ}}^{-1}\left(K\right)\right)}^2+K-\widetilde{\text{Φ}}\left({\text{Φ}}^{-1}\left(K\right)\text{,}{\text{Φ}}^{-1}\left(K\right)\text{,}{h}_l^2\right)}=u\left(h_l^2\right).$$ (Equation 5)

It is impossible to find the closed expression for $h_l^2$ from the last expression, however, we can still plug in values for K and $h_o^2$ and solve Equation 5 numerically for $h_l^2$.

We derive the variance for $h_l^2$ from the last expression by using the delta method. Suppose that we know $Var\left(h_l^2\right)$ and we would like to find $Var\left(h_o^2\right)$. For this, we need to differentiate Equation 5 with respect to $h_l^2$ and that results in

$$\begin{array}{l}\frac{d}{d{h}_l^2}u\left(h_l^2\right)=\frac{d}{d{h}_l^2}{\left(1+\frac{K-\widetilde{\text{Φ}}\left(-t\text{,}-t\text{,}{h}_l^2\right)}{h_l^2\phi {\left(-t\right)}^2}\right)}^{-1}=-{\left(1+\frac{K-\widetilde{\text{Φ}}\left(-t\text{,}-t\text{,}{h}_l^2\right)}{h_l^2\phi {\left(-t\right)}^2}\right)}^{-2}\frac{-{\widetilde{\text{Φ}}}^{\text{′}}\left(-t\text{,}-t\text{,}{h}_l^2\right)h_l^2\phi {\left(-t\right)}^2-\phi {\left(-t\right)}^2\left(K-\widetilde{\text{Φ}}\left(-t\text{,}-t\text{,}{h}_l^2\right)\right)}{{\left(h_l^2\phi {\left(-t\right)}^2\right)}^2}\\ =\frac{{\widetilde{\text{Φ}}}^{\text{′}}\left(-t\text{,}-t\text{,}{h}_l^2\right)h_l^2\phi {\left(-t\right)}^2+\phi {\left(-t\right)}^2\left(K-\widetilde{\text{Φ}}\left(-t\text{,}-t\text{,}{h}_l^2\right)\right)}{{\left(h_l^2\phi {\left(-t\right)}^2+K-\widetilde{\text{Φ}}\left(-t\text{,}-t\text{,}{h}_l^2\right)\right)}^2},\end{array}$$ (Equation 6)

where we have denoted ${\text{Φ}}^{-1}\left(K\right)=-t$ (negative of the disease defining threshold), ${\widetilde{\text{Φ}}}^{\text{′}}\left(-t\text{,}-t\text{,}{h}_l^2\right)$ is the partial derivative of $\widetilde{\text{Φ}}\left(-t\text{,}-t\text{,}{h}_l^2\right)$ with respect to $h_l^2$, and as demonstrated by Drezner and Wesolowsky,¹¹

$${\widetilde{\text{Φ}}}^{\text{′}}\left(-t\text{,}-t\text{,}{h}_l^2\right)=\frac{1}{2\pi \sqrt{1-{\left(h_l^2\right)}^2}}\text{exp}\left(-\frac{t^2}{1+h_l^2}\right).$$ (Equation 7)

The variance can thus be expressed from the delta method as

$$Var\left(h_o^2\right)=Var\left(u\left(h_l^2\right)\right)\approx {\left(\frac{d}{d{h}_l^2}u\left(h_l^2\right)\right)}^{2}Var\left(h_l^2\right)$$ (Equation 8)

and conversely for the $h_l^2$ as

$$Var\left(h_l^2\right)\approx {\left(\frac{d}{d{h}_l^2}u\left(h_l^2\right)\right)}^{-2}Var\left(h_o^2\right).$$ (Equation 9)

Adjustment for ascertained samples

Knowing that it is possible to write the total phenotypic variance as a sum of genetic and error variances $h_l^2\phi {\left({\text{Φ}}^{-1}\left(K\right)\right)}^2+K-\widetilde{\text{Φ}}\left({\text{Φ}}^{-1}\left(K\right)\text{,}{\text{Φ}}^{-1}\left(K\right)\text{,}{h}_l^2\right)$, we can plug in the Equation 1 to replace the term $K\left(1-K\right)$. That gives us the expression

$$h_l^2=h_o^2\frac{{\left(h_l^2\phi {\left({\text{Φ}}^{-1}\left(K\right)\right)}^2+K-\widetilde{\text{Φ}}\left({\text{Φ}}^{-1}\left(K\right)\text{,}{\text{Φ}}^{-1}\left(K\right)\text{,}{h}_l^2\right)\right)}^2}{\phi {\left({\text{Φ}}^{-1}\left(K\right)\right)}^{2}P\left(1-P\right)},$$ (Equation 10)

and we can solve this for $h_l^2$ to get an estimate of liability-scale heritability under stronger ascertainment. Similar to as with the previous case of no ascertainment, we will derive an expression for the variance of this estimator by using the delta method. From Equation 10, we can write that

$$h_o^2=v\left(h_l^2\right)=\frac{h_l^2\phi {\left(-t\right)}^{2}P\left(1-P\right)}{{\left[h_l^2\phi {\left(-t\right)}^2+K-\widetilde{\text{Φ}}\left(-t\text{,}-t\text{,}{h}_l^2\right)\right]}^2}.$$ (Equation 11)

The derivative of $v\left(h_l^2\right)$ is

$$\begin{array}{l}\frac{d}{d{h}_l^2}v\left(h_l^2\right)=\frac{d}{d{h}_l^2}\left(\frac{h_l^2\phi {\left(-t\right)}^{2}P\left(1-P\right)}{{\left[h_l^2\phi {\left(-t\right)}^2+K-\widetilde{\text{Φ}}\left(-t\text{,}-t\text{,}{h}_l^2\right)\right]}^2}\right)\hfill \\ =\phi {\left(-t\right)}^{2}P\left(1-P\right)\frac{2h_l^2{\widetilde{\text{Φ}}}^{\text{′}}\left(-t\text{,}-t\text{,}{h}_l^2\right)-\phi {\left(-t\right)}^2{h}_l^2+K-\widetilde{\text{Φ}}\left(-t\text{,}-t\text{,}{h}_l^2\right)}{{\left(\phi {\left(-t\right)}^2{h}_l^2+K-\widetilde{\text{Φ}}\left(-t\text{,}-t\text{,}{h}_l^2\right)\right)}^3},\hfill \end{array}$$ (Equation 12)

where the derivative of ${\widetilde{\text{Φ}}}^{\text{′}}\left(-t\text{,}-t\text{,}{h}_l^2\right)$ is given in Equation 7. From the delta method, we can thus write the expression for $Var\left(h_o^2\right)$ exactly the same way as shown in Equations 8 and 9 by simply replacing $u\left(h_l^2\right)$ with $v\left(h_l^2\right)$.

Results

Simulation study

We executed two simulation settings. Simulation 1 followed the strategy of Lee et al.,⁴ and we used it to demonstrate the implications of the uncertainty of prevalence estimates to the outcome in the absence of ascertainment. There, we used a sample size of 20,000 and we created a low level of relatedness by simulating individuals in independent batches of 100 with genetic values (g) drawn from a multivariate normal distribution given a $100\times 100$ covariance matrix with off-diagonal elements in the covariance matrix that were $0.05h_l^2$ and $h_l^2$ for the diagonals. Error term e was simulated from a normal distribution $N\left(0\text{,}{\sigma }_e^2\right)$ such that the variance of the liability $l=g+e$ would be $Var\left(l\right)=h_l^2+{\sigma }_e^2=1$. The corresponding observed binary phenotype was defined as

$$y=\{\begin{array}{ll}0,\hfill & \text{if }l<{\text{Φ}}^{-1}\left(1-K\right)\hfill \\ 1,\hfill & \text{if }l\ge {\text{Φ}}^{-1}\left(1-K\right)\hfill \end{array}.$$ (Equation 13)

We varied the true LSH from 0.15 to 0.65 with a step of 0.1, and we varied prevalence between $K=$ 0.001, 0.005, 0.01, 0.05, 0.1, 0.5. In addition, to mimic the potential uncertainty coming from the heterogeneity across estimates, at each step when estimating the LSH, we drew the value for $\hat{K}$ from a normal distribution $N\left(K\text{,}{\left(0.1K\right)}^2\right)$ yielding a coefficient of variation of $10\text{\%}$. The number of simulation replicates was 2,000.

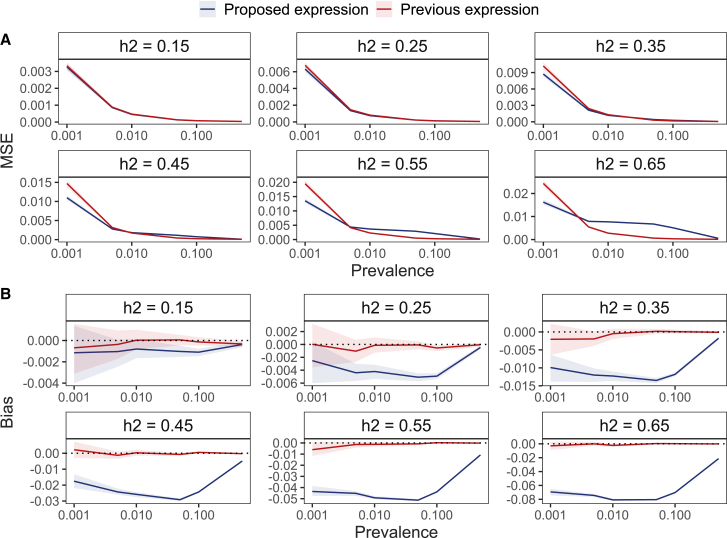
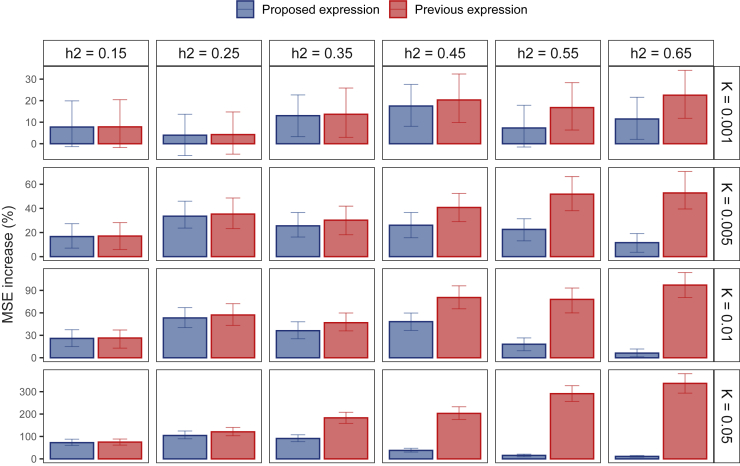
For low-prevalence traits, our proposed formula results in a more accurate result in terms of MSE in many common settings where the LSH is smaller than 0.55 and the prevalence less than 2% (Figure 1A). However, we note caution that if the underlying LSH is higher than 0.45, then bounding the LSH estimate below 1 results in a small bias that becomes more noticeable with higher values of heritability (Figure 1B), but we expect this to be less common for real-world disease outcomes. For example, at a liability-scale heritability of 0.45 and disease prevalence of 0.001, the relative downwards bias is 4%. Using an inaccurately measured prevalence results in increased MSE, and the proposed formula is more robust to this kind of misspecification, as it generally yields a lower MSE increase across all scenarios (Figure 2).

Figure 1.

MSE and bias of previous and proposed formula in the case of no ascertainment and no measurement error for the prevalence across different values for the liability-scale heritability

(A) The proposed estimate yields lower MSE in the settings where the prevalence is low ($K<0.01$). The benefit of using the proposed formula decreases as the underlying liability-scale heritability increases, stemming from (B) the small bias introduced in the proposed estimate that is also bounding the estimate below 1. For example, for moderate size liability-scale heritability $h_l^2=0.45$, the relative downward bias is 4%. For datasets created under simulation scenario 1, the ribbon around the line indicates the 95% CI via a bootstrapping procedure with 250 replicates.

Figure 2.

Increase in MSE due to measurement error of prevalence

Using prevalence that has not been completely accurately measured results in an increase in the mean squared error. However, the proposed formula is more robust to this kind of misspecification, as it yields a lower MSE increase across all scenarios. For datasets created under simulation scenario 1, the error bar indicates the 95% CI via a bootstrapping procedure with 250 replicates.

Simulation 2 examined a more realistic scenario similarly to Golan et al.⁵ The final sample size was again 20,000, but here we created the genetic values by using SNP data of 10,000 markers. For each of the 10,000 SNPs, we simulated the SNP minor allele frequency (MAF) from a uniform distribution $U\left(0.05\text{,}0.5\right)$, and the minor allele counts $x_{ij}$ for individual i at SNP j were simulated from a binomial distribution $B\left(2\text{,}MA{F}_j\right)$. The effect size for each SNP j was drawn from a normal distribution such that ${\beta }_j\sim N\left(0\text{,}\frac{h_l^2}{\mathrm{10,000}}\right)$. The genetic value for an individual i $g_i$ was calculated as $g_i=x_i^{\text{′}}\beta$ and the error term $e_i$ was simulated from $N\left(0\text{,}{\sigma }_e^2\right)$ such that the variance of the liability $l_i=g_i+e_i$ would be $Var\left(l_i\right)=h_l^2+{\sigma }_e^2=1$. The liability-scale phenotype $l_i$ was translated into binary phenotype $y_i$ as shown in Equation 13. To create suitably ascertained samples, we first simulated a slightly larger population of $\tilde{N}(>20\text{,}000$) that has a case prevalence (in population) of K, and then we randomly selected $N\cdot P$ cases and $N\cdot \left(1-P\right)$ controls to achieve case prevalence (in sample) of P. We used GREML¹⁰ from GCTA¹² to estimate the observed scale heritability that was transformed to the liability scale by either using the classical expression (Equation 1), proposed adjusted (Equation 10), or proposed unadjusted expression (Equation 5). Additionally, we compared the GREML results with the summary statistic version of PCGC⁶ that directly estimates the LSH. We used the same values for heritability, we varied the K between 0.005, 0.01, 0.02, and 0.05, and we used P as a factor of 0.25, 0.5, 0.75, 0.9, 1, 1.25, 1.5, 2, and 4 of the K value. As a result of the increased computational complexity, we resorted to 100 simulation replicates.

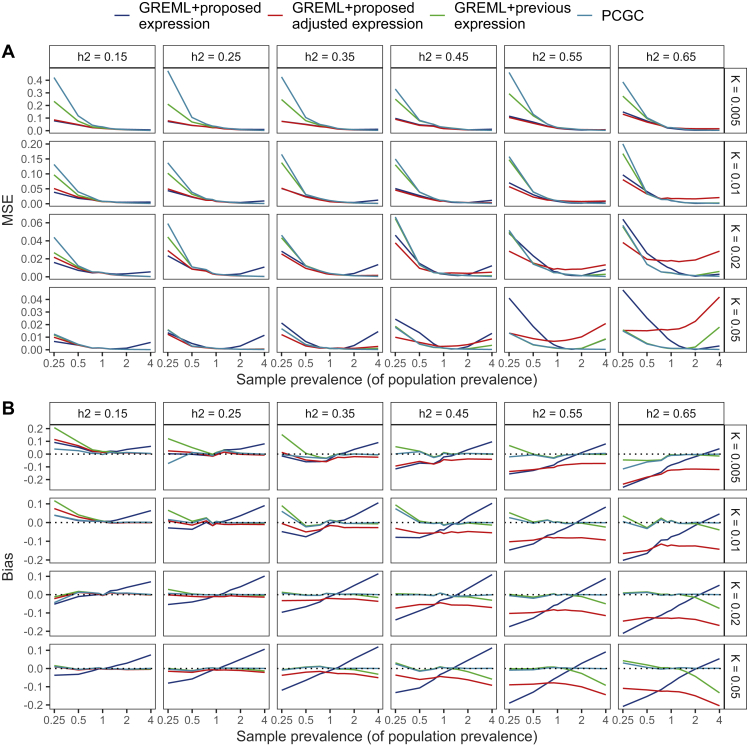
Here, we find the GREML along with proposed expression for unascertained (Equation 5) and the proposed expression for ascertained samples (Equation 10) to result in lower MSE (Figure 3A, Data S1) at lower population prevalence ($K\le 0.02$) and with moderate or low LSH values (LSH $\le 0.45$) as compared to the classical expression of Equation 1, supporting the results of the first simulation setting. Importantly, the proposed expressions of Equation 5 and Equation 10 can result in a small downwards bias for the scenarios with higher LSH (Figure 3B, Data S1). The proposed adjusted expression keeps bias similar across different ascertainment levels, whereas the bias from the proposed unadjusted expression changes linearly with downwards bias with $P<K$ and upwards bias with $P>K$ scenario. The PCGC method works well in situations where the sample prevalence exceeds the population prevalence, giving virtually unbiased results but resulting in greatly increased MSE values if the population prevalence is small and $P\le K$. Given the simulation results, we propose that for biobank studies of diseases with $\le 2\text{\%}$ population prevalence, especially where the sample prevalence is less than that of the wider population, Equation 5 or Equation 10 for moderately ascertained samples should be preferred over Equation 1 or PCGC. Although this can result in a small downwards bias, we believe that giving a slightly more conservative but more accurate estimate is useful for characterizing low-prevalence traits.

Figure 3.

MSE and bias given different values of liability-scale heritability, population prevalence, and sample prevalence

Results about MSE and bias are shown in (A) and (B), respectively. We observe that for the scenarios of small to moderate heritability ($h^2<0.5$), small population prevalence ($K\le 0.02$) and sample prevalence smaller or slightly larger than the population prevalence ($P\le 1.25K$), it is preferred to use our proposed expression, as it gives a lower MSE while not increasing the bias too much. In the case of ascertainment, we suggest using the proposed expression with the adjustment. We evaluated the observed scale heritability using GREML and then transformed it to the liability scale either by using the previous expression from Lee et al., by our proposed expression without adjustment for ascertainment, and by our proposed adjustment with ascertainment adjustment. In addition, we directly estimated the liability-scale heritability by using the PCGC method with summary statistics. Datasets were created under simulation scenario 2, and the number of simulation replicates was 100. 95% CI for MSE and bias values are provided in Data S1.

Empirical data analysis

We then analyzed 13 ICD-10 binary disease outcomes with $\le 3\text{\%}$ sample prevalence in UK Biobank (Table 1) with our recently proposed GMRM software to obtain observed scale heritability estimates, accounting for marker effect size differences across SNPs of different minor allele frequencies, linkage disequilibrium, and functional annotation,^9,13 by using 2,174,071 SNP markers and 382,390 individuals of SNP marker relatedness ($\le 0.05$). To attempt to control for environmental confounding before analysis, we adjusted for the leading 20 principal components as supplied by the UK Biobank, sex as a binary factor, age as a linear and quadratic term, east and north coordinate of residence, recruitment center, and genotype batch. We estimated the posterior mean observed scale heritability from the last 1,500 sampling iterations after stabilization of the running mean and then compared the liability-scale estimates produced with either the classical expression of Equation 1 or our proposed expressions of Equation 5 and Equation 10 for unascertained and ascertained samples, respectively.

Table 1.

13 selected disease outcomes recorded in the UK Biobank of <3% sample prevalence with higher prevalence in the general UK population

Disease	ICD-10 code	Sample prevalence	Estimated population prevalence	$h_{\mathbf{obs}}^2$95% CI	Proposed SNP-$h_{\mathbf{liab}}^2$95% CI	Classic SNP-$h_{\mathbf{liab}}^2$95% CI	Reduction in 95% CI
Carpal tunnel syndrome	G56	2.8%	5.0%14	0.038 (0.031, 0.044)	0.277 (0.232, 0.316)	0.291 (0.240, 0.338)	14%
Chronic obstructive pulmonary disease	J44	2.6%	4.6%15	0.036 (0.029, 0.043)	0.276 (0.227, 0.320)	0.291 (0.235, 0.344)	15%
Oesophagitis	K20	2.5%	2.5%∗	0.026 (0.020, 0.032)	0.180 (0.138, 0.220)	0.182 (0.139, 0.223)	2%
Iron deficient anaemia	D50	2.4%	5.5%16	0.021 (0.015, 0.027)	0.188 (0.140, 0.235)	0.192 (0.141, 0.244)	8%
Atherosclerosis	I70-I79	2.3%	2.3%∗	0.025 (0.020, 0.031)	0.191 (0.153, 0.234)	0.193 (0.154, 0.239)	5%
Osteoporosis	M80-M82	2.1%	5.1%17	0.028 (0.022, 0.034)	0.270 (0.220, 0.320)	0.284 (0.227, 0.344)	15%
Cellulitis	L03	2.1%	2.1%∗	0.023 (0.017, 0.029)	0.186 (0.141, 0.229)	0.188 (0.141, 0.233)	4%
Endometriosis	N80	1.8%	10.0%18	0.043 (0.034, 0.051)	0.528 (0.445, 0.594)	0.634 (0.504, 0.758)	41%
Acute renal failure	N17	1.8%	1.8%∗	0.022 (0.018, 0.028)	0.197 (0.156, 0.248)	0.199 (0.157, 0.253)	4%
Glaucoma	H40	1.4%	2.5%19	0.030 (0.025, 0.037)	0.341 (0.286, 0.399)	0.370 (0.302, 0.448)	23%
Macular degeneration	H35.3	0.8%	3.4%20	0.025 (0.020, 0.032)	0.508 (0.428, 0.584)	0.624 (0.491, 0.783)	47%
Hyperthyroidism	E05	0.5%	0.8%21	0.027 (0.022, 0.032)	0.536 (0.466, 0.596)	0.656 (0.535, 0.786)	48%
Hypertensive renal disease	I12	0.4%	0.4%∗	0.027 (0.021, 0.032)	0.679 (0.581, 0.743)	0.817 (0.650, 0.961)	48%

Columns of the table give the commonly used disease name, the ICD-10 code, the UK Biobank sample prevalence, the estimated UK population prevalence with the corresponding reference (“^∗” denotes that we used the UK Biobank prevalence as a result of unavailability or vast heterogeneity in the estimates), the posterior mean 0/1 observed scale single-nucleotide polymorphism (SNP) heritability with 95% credible interval, the posterior mean liability-scale SNP heritability with 95% credible interval via the proposed transformation, the posterior mean liability-scale SNP heritability with 95% credible interval via the classic transformation, and the reduction in the width of the 95% CI via the proposed transformation

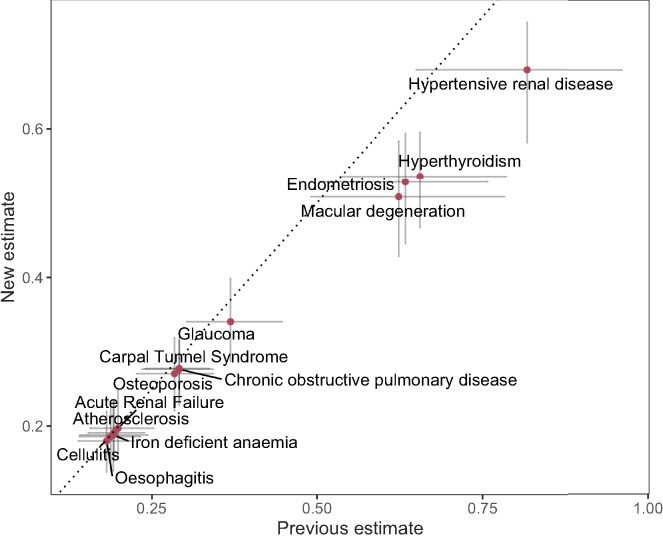
Liability-scale heritability estimates obtained by Equation 5 or Equation 10 were lower than the classical expression of Equation 1 (Figure 4). For disease outcomes where we assume that the UK Biobank sample prevalence is identical to the wider population prevalence, the estimates from either equation are in agreement (Figure 4). However, once the sample prevalence was $\le 1\text{\%}$, and when it was lower than that estimated in the wider population from which it was drawn, we observe substantially lower liability-scale estimates from Equation 5 or Equation 10 (Figure 4). For example, LSH estimate differed by 0.11 for endometriosis and 0.12 for macular degeneration. Even though we assumed equal sample and population prevalence for hypertensive renal disease, we still get a difference of 0.14 between the classical and proposed estimates. This is accompanied by a narrower 95% CI for the proposed estimate for each of the analyzed traits (Table 1) with the reduction in CI ranging from 2% for oesophagitis to 48% for hypertensive renal disease (15% of median reduction in 95% CI length). These differences influence the inference made, as Equation 10 estimates a borderline significant difference of LSH between hypertensive renal disease and macular degeneration, in contrast to the clearly overlapping credible interval that would be obtained from Equation 1 (Figure 4). Therefore, the lower MSE of our proposed estimate across many common settings translates to real-world differences in inference for low-prevalence diseases within biobank studies.

Figure 4.

Comparison of previous and proposed liability-scale heritability estimates with 95% CI for 13 ICD-10 binary disease outcomes with $\le 3\text{\%}$ sample prevalence in the UK Biobank

Table 1 gives the full disease names, codes, sample prevalence, population prevalence, observed-scale estimates, and liability-scale conversions. We analyzed the 13 traits with our recently proposed GMRM software to obtain observed scale heritability estimates, accounting for marker effect size differences across SNPs of different minor allele frequency, linkage disequilibrium, and functional annotation in 382,390 unrelated UK Biobank individuals. We estimated the posterior mean observed scale heritability and plot the liability-scale estimates produced with either the classical expression of Equation 1 on the x axis or our proposed expressions of Equation 5 and Equation 10 on the y axis.

Discussion

Using biobank-scale datasets to infer the heritability of rare traits is increasingly important because of the general difficulties of collecting case-control samples for rare diseases. However, our results demonstrate the importance of treating low prevalence traits with extra care. Moreover, the advantage of using our proposed estimate is even greater if we take into account the uncertainty or heterogeneity in the lifetime prevalence estimates. Heterogeneity in the lifetime prevalence estimates is very common and stems from regional differences, differences in the time of the study, methodology, usage of subpopulations, and that often the lifetime prevalence estimate is simply unavailable or some proxies are used. All this amounts to a considerable amount of uncertainty, and unfortunately, the most common way to handle this is to simply pick one of the prevalence estimates and not take into account the uncertainty. Our proposed approach limits the error that stems from uncertainty, and we argue that future analyses using lifetime population prevalence should reflect the uncertainty in the estimates.

The analysis of empirical data in UK Biobank calculating SNP heritability demonstrated that in many settings the classical expression could lead to likely, if not clear, overestimates. For example, for hypertensive renal disease, the classic formula gave an LSH estimate of 0.82 (95% CI: 0.65, 0.96), whereas the proposed formula estimated an LSH of 0.68 (95% CI: 0.58, 0.74). For a similar trait of chronic kidney disease, the heritability values have been estimated between 0.30 to 0.75,²² suggesting that the classical estimate might be unrealistically high. We also observe a similar effect for macular degeneration where the classical formula also yields a likely overestimate of 0.62 (95% CI: 0.49, 0.78), whereas the literature suggests SNP heritability of 0.47 that had been calculated on a larger case count.²³ Such high estimates in empirical data are likely to be driven by greater estimator variance, which is still problematic. Even if, on average, the bias is small or non-existing with the previous estimator, a high estimator variance can yield estimates that greatly miss the actual value. However, it should be acknowledged that it is not fully clear whether the observed differences in empirical data analysis are from improvement in accuracy or differences in bias under potential model violations. Instead, it is likely to be a combination of the two, as the proposed expression has a narrower credible interval and overlapping yet ranked confidence intervals between the two methods do not prove the existence nor eliminate the possibility of bias. In conclusion, we believe that no one model is best for every scenario and that models can perform suboptimally under certain conditions. Therefore, LSH estimation would benefit from careful consideration of the modeling assumptions, and different LSH estimators could be compared within sensitivity analysis to achieve a more reliable understanding of the estimate.

In general, there seems to be a switch point in prevalence after which the classical expression (Equation 1) tends to become more effective. That is probably because $K\left(1-K\right)$ is a good estimator for the total phenotypic variance with high K values (as in Equation 2), but with small K values, that product $K\left(1-K\right)$ becomes tiny and the expressions using the inverse $\frac{1}{K\left(1-K\right)}$ will become highly sensitive to the observed scale heritability estimation error. Our proposed expressions make the total phenotypic variance dependent on the estimated observed genetic variance and thus control better for the mismatch between the total phenotypic and genotypic variances in the classical expression.

There are important caveats to our proposed formulas. Even though we manage to effectively constrain the heritability between 0 and 1, it also introduces a small downward bias that becomes more visible with higher values of prevalence and true liability-scale heritability (>0.6). Nevertheless, we argue that this will most likely be the exception for real-world disease outcomes. Any transformation of scale will be an approximation made under a set of theoretical assumptions, and our aim here is to simply provide an approach that facilitates comparisons of the proportion of variance attributable to the SNP markers for low-prevalence diseases with as low MSE as possible. We additionally find that for the scenario with stronger case oversampling ($P>1.5K$), moderate to high LSH and population prevalence above 2% our proposed formulas do not give a more precise estimate in terms of MSE compared to the previous classical Equation 1 or PCGC,⁶ and in these cases, the user could use other methods. Regardless, we advocate using the proposed expressions for scenarios with low prevalence, small to moderate LSH, and small case oversampling. Especially for the scenario where the cases are underrepresented compared to the population, we find the proposed expressions to be a lot more precise in terms of MSE compared to other compared methods.

Here, we have proposed expressions for calculating LSH suitable for traits with low prevalence. We have shown that our proposed formulas result in a more accurate LSH estimator in terms of MSE in many common settings and in general results in slightly more conservative estimates that can result in more accurate estimates of liability-scale heritability. Hopefully, it can lead to a more realistic quantification of rare trait heritabilities, many of which are still yet to be explored.

Published: October 19, 2022

Data and code availability

The shiny app for calculating liability-scale heritability can be found at https://medical-genomics-group.shinyapps.io/h2liab/. This project uses UK Biobank data under project 35520. UK Biobank genotypic and phenotypic data are available through a formal request at http://www.ukbiobank.ac.uk. The UK Biobank has ethics approval from the North West Multi-centre Research Ethics Committee (MREC). The GMRM model was executed with the GMRM software, and full open source code is available at https://github.com/medical-genomics-group/gmrm. The code generated during this study is available at https://github.com/svenojavee/LSH.