Effects of vimentin on the migration, search efficiency, and mechanical resilience of dendritic cells

Abstract

Dendritic cells use amoeboid migration to pass through narrow passages in the extracellular matrix and confined tissue in search for pathogens and to reach the lymph nodes and alert the immune system. Amoeboid migration is a migration mode that, instead of relying on cell adhesion, is based on mechanical resilience and friction. To better understand the role of intermediate filaments in ameboid migration, we studied the effects of vimentin on the migration of dendritic cells. We show that the lymph node homing of vimentin-deficient cells is reduced in our in vivo experiments in mice. Lack of vimentin also reduces the cell stiffness, the number of migrating cells, and the migration speed in vitro in both 1D and 2D confined environments. Moreover, we find that lack of vimentin weakens the correlation between directional persistence and migration speed. Thus, vimentin-expressing dendritic cells move faster in straighter lines. Our numerical simulations of persistent random search in confined geometries verify that the reduced migration speed and the weaker correlation between the speed and direction of motion result in longer search times to find regularly located targets. Together, these observations show that vimentin enhances the ameboid migration of dendritic cells, which is relevant for the efficiency of their random search for pathogens.

Significance

Dendritic immune cells are responsible for finding pathogens in tissues and for alerting the immune system by migrating toward lymph nodes. A successful immune response depends crucially on the navigation and search efficiency of these cells. Here, we show that the loss of the intermediate filament vimentin compromises the in vivo migration of dendritic cells toward lymph nodes. In our in vitro experiments, vimentin-expressing cells migrate faster in straighter lines compared with vimentin-deficient cells. Our numerical simulations reveal that a reduced speed and a weaker correlation between the local speed and direction of migration result in a considerable reduction in the efficiency of finding regularly located targets in stochastic persistent search processes.

Introduction

The cytoskeleton of the cell comprises a highly complex and dynamic biomechanical structure, including intermediate filaments (IFs), microtubules, and actin filaments. IFs are polymers with homologous assembly properties, forming filamentous networks that contribute to mechanical resistance, signaling, adhesion, and migration in different cellular systems. Vimentin is the major IF protein that is constitutively expressed in connective tissues and motile cells of mesenchymal origin, such as endothelial cells, leukocytes, and fibroblasts.

There have been studies to understand the contribution of IFs to the mechanical properties of the cell (1, 2, 3, 4, 5). It is known so far that IFs are involved in the organization of traction forces (6) (for example, vimentin orients traction stresses in fibroblasts (1,7)). Although the roles of microfilaments, microtubules, and even cytoskeletal cross-linkers and motor proteins in the mechanical response of the cell have been extensively investigated (see, e.g., (8) for overview), further studies are needed to better understand the detailed mechanisms underlying the roles of IFs in cell mechanics (9).

The role of IFs in cell motility and migration is also a matter of ongoing research (7,10, 11, 12, 13, 14, 15, 16, 17, 18). Motile immune cells exhibit two main modes of migration: slow mesenchymal mode—characterized by actin stress fibers and focal adhesions that connect the cell to the extracellular matrix (19,20)—and fast ameboid mode—characterized by minimal adhesion, high contractility, and fast shape remodeling (21,22)—which depends on friction forces with the environment (23). Vimentin has been implicated in different migratory functions of adherent cells, especially in relation to the organization and functionality of actomyosin complexes (7,10,11). Injection of vimentin into MCF-7 mammary duct carcinoma cells results in rapid cell polarization and a subsequent increase in cell motility (12). Moreover, vimentin influences leukocyte diapedesis by organizing the surface molecules that are crucial for cell adhesion and transmigration (13). Overexpression of vimentin in cancer cells is often associated with an increased cell motility and a greater cell malignancy (14,15). While the impact of vimentin on the migration of adherent cells on surfaces has been studied in some depth (16,17,24), there is little information on how vimentin influences low-adhesion ameboid migration.

Studies have shown that the mechanisms by which IFs affect cell mechanics and migration have common origins. The observed cytoplasmic localization of vimentin in lymphocytes (25) suggests that vimentin provides mechanical stability to the cell body to enable transmigration through the endothelium. We have previously shown that the mechanical properties of suspended and adherent cells are fundamentally different (26); in suspended cells, the cytoskeleton is adapted to the low-adhesive state of the cell, and the cytoskeletal control of cellular mechanics is likely to be different from that of adherent cells. We hypothesize that the vimentin network governs the dynamic regulation of the stiffness and elasticity of cellular regions, thereby generating the forces that underlie the ameboid migration of low-adherence immune cells.

Migrating immune cells—such as dendritic and T cells—explore the environment to fulfill specific tasks. Dendritic cells (DCs) are mainly located in peripheral tissues. Mature DCs are sensitive to hydraulic resistance and try to find the shortest path toward lymph nodes where they interact with other immune cells (27,28). Conversely, immature DCs migrate through highly confined spaces and patrol the environment in search for pathogens (28, 29, 30). To this aim, DCs constantly adapt their shape, which implies rearrangements of their cytoskeleton. According to our previous experiments, actin waves are involved in the motion of immature bone-marrow-derived dendritic cells (BMDCs) (31). Actin retrograde flows—generated by asymmetric spatial distributions of either actin polymerization regulators or activators of contractility—mediate a universal coupling between the speed and directional persistence of DCs (32) and we recently verified that this correlated motion enhances the search efficiency of DCs (33). Notably, the degree of persistence-speed coupling—i.e., the ability to correlate the local curvature of the path to the instantaneous speed—varies from cell to cell. A crucial question that arises is whether the ability of the cell to generate actin flows and induces the correlated dynamics depends on factors—such as the presence of vimentin—which influence the cell mechanics.

The present study aims to provide a better understanding of the role of vimentin in ameboid cell migration and search through confined spaces. As a model system, we have chosen primary BMDCs from vimentin wild-type (WT) and vimentin knockout (KO) mice. These cells migrate through narrow passages and are required for the immune response. We compare two extreme cases—i.e., full presence versus full absence of vimentin—to be able to detect even weak effects of vimentin on the quantities of interest. By analyzing immature BMDC migration in vitro in 1D microchannels and 2D confining geometries between two parallel plates, we show that the persistence-speed coupling is weaker in KO cells than in WT ones. This leads to a substantial reduction of the stochastic search efficiency of KO cells according to our Monte Carlo simulation results. (To quantify the search efficiency, we have measured the mean-first-passage time [MFPT], which is the average time it takes for a random searcher to reach a target position for the first time.) Our in vivo experiments reveal that BMDC homing to lymph nodes is also impaired in KO cells. Moreover, by quantifying the mechanical properties of BMDCs, we show that KO cells are softer than WT cells. Our findings suggest that vimentin IFs influence DCs’ capacity for ameboid migration and search for pathogens in confined spaces.

Materials and methods

Cells

Primary DCs were differentiated from bone-marrow precursors extracted from WT and KO mice. BMDCs were generated (as described previously in (34)) using Iscove’s modified Dulbecco’s medium with $10\text{\%}$ fetal calf serum, 2 mM glutamine, $100{\text{U.mL}}^{-1}$ penicillin, $100\mu {\text{g.mL}}^{-1}$ streptomycin, $50\mu \text{M}$ 2-mercaptoethanol, and $50{\text{ng.mL}}^{-1}$ granulocyte macrophage colony-stimulating factor, and containing supernatant obtained from transfected J558 cells. The semi-adherent cell fraction, corresponding to the $\text{CD}{86}^{+}$ cells, was gently flushed from the cell culture dishes. All the experiments were performed on days 10–12 of cell differentiation. All of the reagents used for cell culture were from Thermo Fisher Scientific (Waltham, MA). Vimentin was reported to have even profound effects on the differentiation of some cells, e.g., the stem cell lineages (35). However, for the differentiation of DCs we observed no obvious effects on cellular phenotype.

Mice

Vimentin heterozygous mice (129/Sv $\times$ C57BL/6) were used to generate vimentin knock-out homozygotes (${\text{VIM}}^{-/-}$) and WT offspring. Both WT and KO mice used for bone marrow extraction were maintained in the Animal Facility of Biocity (Turku, Finland) under permit 7284/04.10.03/2012 and protocol number 197/04.10.07/2013 of the Ethical Committee for Animal Experiments of the University of Turku. The regular molecular cloning and other GMO1-related research work were performed under the permit of the Board of Gene Technology, Finland (GTLK), with notification number 038/M/2007.

Antibodies and chemicals

The antibodies used for immunostaining were the anti-vimentin monoclonal antibody (D21H3; Cell Signaling Technology, Danvers, MA) combined with Alexa 647-conjugated secondary antibodies (Abcam, Cambridge, UK). For actin staining, we used phalloidin conjugated with tetramethyl rhodamine B isothiocyanate (Sigma Aldrich, St Louis, MO) and, for nuclear staining, we used Hoechst 34580 (Sigma Aldrich). The antibodies used for western blotting were anti-vimentin monoclonal antibody (D21H3; Cell Signaling Technology), combined with the secondary anti-horse radish peroxidase anti-rabbit antibody (Bio-Rad, Hercules, CA) and an anti-biotin monoclonal antibody (Hsc70; 1B5; Enzo Life Sciences, Plymouth, PA).

Channels

The microchannels used in the 1D migration experiments were manufactured according to previously published procedures (36,37). In brief, poly(dimethylsiloxane) (PDMS) (RTV-615; Momentive Performance Materials) was mixed with the curing agent (10:1), degassed, and polymerized at 75°C in the specific custom-made microfabricated molds of a positive channel imprint made by photolithography. The resulting 1D channels of $5\mu \text{m}$ height and $5\mu \text{m}$ width were sealed in 35-mm glass-bottomed cell culture dishes (World Precision Instruments, Sarasota, FL) using plasma surface activation. The assembled structure was coated with $20\mu {\text{g.mL}}^{-1}$ fibronectin (Sigma-Aldrich) and incubated with cell culture medium for $60\text{min}$ (coating with poly(L-lysine)-graft-poly(ethylene glycol) (PLL-PEG) led to a very small number of cells that managed to enter the microchannels). The cells were plated at the channel entry at a concentration of $2\times {10}^7$ ${\text{cells.mL}}^{-1}$. The lateral size of the manufactured microchannel was sufficiently smaller than the typical cell size of nearly $10\mu \text{m}$ in our experiments; thus, it provided a 1D confinement that restricted the cell shape by preventing lateral cell spreading.

Plate-plate geometries

The cell-confining plate “roofs” were prepared as described previously (38,39). The mold for the coverslip PDMS (RTV-615; Momentive Performance Materials) coating was produced by photolithography, and consisted of pillars of $3\mu \text{m}$ height and $440\mu \text{m}$ diameter, spaced at $1000\mu \text{m}$ from each other. The confining geometry was assembled in glass-bottomed six-well plates (Mattek, Ashland, MA). The roof of the 3-$\mu \text{m}$ height spacers was covered by a 10-mm coverslip. The roof was adhered to the culture dish lid using a softer, deformable PDMS pillar (with a mixing PDMS to cross-linker ratio of 35:1), which was later closed and fixed with adhesive tape. Before the experiments, both the cell culture dishes and the roofs were coated with $0.5{\text{mg.mL}}^{-1}$ PLL-PEG (SuSoS, Dübendorf, Switzerland) to avoid cell adhesion. The mounted device was incubated in culture medium before the experiment for at least 4 h to equilibrate the PDMS. Cell recording started 2 h after the cell confinement.

Migration assays and cell trajectories

Cell nuclei were stained with $200{\text{ng.mL}}^{-1}$ Hoechst 34580 (Sigma Aldrich), for 30 min, and cell migration was recorded using epifluorescence microscopy, over at least 6 h. The cells were kept at a constant atmosphere of 37°C and $5\text{\%}$ ${\text{CO}}_2$ (Okolab, Italy) during the entire experiment. Images were obtained using an inverted microscope system (eclipse Ti-E; Nikon, Tokyo, Japan) equipped with fluorescent illumination. Cell trajectories were tracked using the custom-made software described in (40); in brief, for cell tracking a geometric center was assigned to each cell in each image frame. The cell center was determined by identifying the nucleus boundary, segmenting the nucleus image into stripes, and calculating the overall geometric center. The cell speed was extracted by tracking the geometric center with a global minimization algorithm to automatically track individual cell displacements. With a sampling rate of $20\text{frames}/\text{min}$, the time interval between successive recorded positions along the cell trajectory was Δt = 3 s. Every two successive recorded positions at times t and $t+\text{Δ}t$ were used to calculate the local displacement $\text{Δ}\mathit{r}\left(t\right)$ and the local velocity $\mathit{v}\left(t\right)=\text{Δ}\mathit{r}\left(t\right)/\text{Δ}t$ of the cell. For the analysis, all trajectories were filtered to exclude those shorter than 25$\mu \text{m}$ length or 30 min duration. The number of migrating cells was then measured as the number of remaining tracks, according to these thresholds.

In vivo lymph node homing assay

The in vivo migration assay was performed according to (41) with some modifications. Before injection of the mice, BMDCs from WT and KO mice were treated with $100{\text{ng.mL}}^{-1}$ lipopolysaccharide for 30 min, and fluorescently labeled with a cell tracer (Oregon 488; Thermo Fisher Scientific), according to the manufacturer’s protocol. A total of $1\times {10}^6$ fluorescently tagged cells diluted in phosphate-buffered saline to a final volume of $40\mu \text{L}$ was injected subcutaneously into the hind footpads of mice aged between 6 and 10 weeks old. The mice were killed 36 h after BMDC injection, and the popliteal lymph node was extracted. The lymph nodes were then mechanically disrupted and digested using collagenase D (Roche, Basel, Switzerland) and DNAse1 (Roche) for 30 min at 37°C. The homogenate was filtered through a 77-$\mu \text{m}$ silk filter. The purified cells were mounted on a microscope slide, and the ratio between the fluorescent and nontagged cells was estimated. This ratio was normalized to the ratio of WT cells that had arrived in the lymph nodes.

Immunofluorescence

The cells were fixed for $10\text{min}$ with $4\text{\%}$ paraformaldehyde (Sigma Aldrich), and permeabilized with $0.5\text{\%}$ Triton X-100 (Sigma Aldrich) for 10 min. Protein blocking was achieved by incubating the cells with $3\text{\%}$ bovine serum albumin (BSA) for 1 h. Primary antibodies were diluted 1:200 in BSA $3\text{\%}$ and incubated overnight at 4°C. Secondary antibodies were diluted at a 1:1000 ratio in $3\text{\%}$ BSA and incubated for 1 h at room temperature. The actin staining used phalloidin conjugated with rhodamine (1 mM final).

SDS-PAGE and western blotting

Whole-cell lysates were extracted using Laemmli sample buffer (150 mM Tris-Cl/[pH 6.8]; 300 mM DTT [β-mercaptoethanol $15\text{\%}$]; $6\text{\%}$ SDS; 0.3% bromophenol blue; $30\text{\%}$ glycerol). Protein separation was carried out by SDS-PAGE in $10\text{\%}$ bis-acrylamide gels, and proteins were then transferred to nitrocellulose membranes (Amersham Protran; pore size, $0.45\mu \text{m}$; GE Healthcare, Chicago, IL) according to standard protocols (42). The membranes were blocked with $5\text{\%}$ fat free milk in 20 mM Tris-buffered saline and incubated overnight at 4°C with the anti-vimentin antibody (dilution 1:1000 in $5\text{\%}$ BSA) or with the loading control HSC70 (dilution 1:1000 in $5\text{\%}$ BSA); see the antibodies used in the assay in the “antibodies and chemicals” subsection. Proteins were detected using enhanced chemiluminescence (Western Lightning Plus-ECL; PerkinElmer, Waltham, MA).

Confocal microscopy

Confocal images were obtained using a spinning disk unit (CSU W1; Yokogawa; Andor Technology, Belfast, UK) with a pinhole size of $50\mu \text{m}$ coupled to the inverted microscope system (Eclipse Ti-E; Nikon). Images were recorded using a Flash 4.0 camera with a 6.5-$\mu \text{m}$ pixel size (Hamamatsu, Hamamatsu City, Japan). Image treatment and Z maximum projection were carried out using ImageJ software (FIJI) (43).

Atomic force microscopy

To measure the mechanical response of the bulk of the cells in suspension, tipless cantilevers (MLCT-010, cantilever F) with a spring constant of 0.3–1.2 (nominal: 0.6) ${\text{Nm}}^{-1}$ (Bruker, Billerica, MA) were wedged (according to (44)) to correct the 10° cantilever tilt. This provided a flat surface to probe the cells. The tipless cantilevers were pressed against drops of adhesive (Norland Optical Adhesive 63; NOA63; Thorlabs, Newton, NJ) placed on a silicone-coated coverslip. NOA63 was cured with UV light for 60 s, gently detached from the silicone-coated coverslip, and cured for an additional 300 s. The flatness and integrity of the wedged cantilevers were assessed using electron microscopy. Atomic force microscopy (AFM) measurements were carried out using a JPK Cell Hesion 200 (JPK Instruments, Berlin, Germany) mounted on an inverted microscope system (Eclipse Ti-E; Nikon). The sensitivity was calibrated by acquiring a force curve on the dish surface, and the spring constant was calibrated by the thermal noise fluctuation method using the built-in function of the JPK software. For measurements, the cantilever was lowered at a speed of $0.5\mu {\text{m.s}}^{-1}$ with a setpoint force of $4\text{nN}$. Measurements consisted of four subsequent compressions of 1 μm for 60 s each. During compressions, the height was kept constant and the cell force was recorded for all extents (total time, 300 s). Bright-field images were taken for all of the steps of the measurements (magnify 40 $\times$ plus 1.5 $\times$ zoom, to calculate the size and contact area of the cells without cellular protrusions). The cells were kept at 37°C during the measurements, and the culture medium was supplemented with $200{\text{mg.mL}}^{-1}$ Hepes buffer (Gibco HEPES 1 M Gibco 15630056). The Young’s modulus was calculated using the elastic Hertz model on each extent (45). This enabled us to compare the elastic response of WT and KO cells relative to each other, which was sufficient for our purposes (to obtain the absolute value of the Young’s modulus, the viscoelasticity of the cell needs to be incorporated into the models, leading to more sophisticated approaches such as the one presented in (46)).

Real-time deformability cytometry

High-throughput measurements of cell mechanics were performed using real-time deformability cytometry (RT-DC) according to previously described procedures (47). In brief, the cells were suspended in 100 μL viscosity-adjusted measurement buffer ($0.5\text{\%}$ [w/v] methylcellulose (4000 cPs, Alfa Aesar, Germany) in phosphate-buffered saline without ${\text{Mg}}^{2+}$ and ${\text{Ca}}^{2+}$; final viscosity of $15{\text{mPa.s}}^{-1}$ as measured by a HAAKE Falling Ball Viscometer type C (Thermo Fisher Scientific) using ball number 3, and flushed through a 300-$\mu \text{m}$-long microfluidic channel with a $30\times 30\mu \text{m}$ square cross-section, at flow rates of $0.16\mu {\text{L.s}}^{-1}$ (Fr1) and $0.32\mu {\text{L.s}}^{-1}$ (Fr2). Images of the deformed cells were acquired at $2000{\text{frames.s}}^{-1}$ within a region of interest close to the channel end. Cell deformation and cross-sectional area were evaluated in real time based on contours fitted to the cells by an in-house developed image processing algorithm (48). The obtained data were filtered for cell areas of 50 to 400 μm², and area ratios of $1.00-1.05$. Area ratio—defined as the ratio between the area enclosed by the convex hull of the contour and the area enclosed by the raw contour—allowed the discarding of cells with rough or incompletely fitted contours. Young’s modulus values were assigned to each cell with the aid of the ShapeOut analysis software, version 0.8.7 (available at https://github.com/ZELLMECHANIK-DRESDEN/ShapeOut). ShapeOut utilized a look-up table, generated in numerical simulations modeling isotropic elastic spheres passing through a microfluidic channel of dimensions corresponding to those used in the experiments (49). The look-up table related the measured cell area and deformation to the Young’s modulus value. More than 1000 events within the specified filters were collected per condition in each experiment (see Table S2 for details), with five experiments carried out. We were able to extract Young’s modulus for 60–$90\text{\%}$ of the events within the validity of the look-up table. Statistical analysis was performed using linear mixed effect models, as described in detail elsewhere (50).

Simulation method

Monte Carlo simulations were performed to compare the efficiency of the stochastic search of WT and KO cells for regularly located targets. The experimental mean values of the persistence-speed coupling strength for both categories of cells—i.e., $c_{\text{WT}}\left(p\text{,}v\right)$ and $c_{\text{KO}}\left(p\text{,}v\right)$—and the speed distributions $F_{\text{WT}}\left(v\right)$ and $F_{\text{KO}}\left(v\right)$ were used as input for simulations. In each simulation, a single random target was considered in a square box of size L (using the target size as the length unit) with periodic boundary conditions. A persistent random walker (being in either WT or KO state) with a random initial position and orientation was supposed to search for the target. At each time step, the instantaneous speed v of the searcher was drawn from the speed distribution $F\left(v\right)$. Then, the local persistence $p\left(\in \left[-1\text{,}1\right]\right)$ was stochastically deduced according to the correlation value $c\left(p\text{,}v\right)$ using the sum-of-uniforms algorithm (33). This algorithm allowed for variation of p in such a way that the mean value of the actual persistence-speed coupling was equal to the experimental $c\left(p\text{,}v\right)$ value. Next, the turning angle θ was obtained via $\theta =\text{arccos}\left(p\right)$ (51). For instance, p = 1 or −1 resulted in continuing along the previous direction of motion ($\theta =0$) or reversing it ($\theta =\pi$). The algorithm has been extended to multistate processes such as run-and-tumble dynamics (52,53). By obtaining the first-passage time to visit the target for the first time and repeating the procedure for an ensemble of initial positions and orientations, the MFPT τ was obtained for the given correlation value $c_{\text{WT}}\left(p\text{,}v\right)$ or $c_{\text{KO}}\left(p\text{,}v\right)$.

Results

In vitro migration of BMDCs

It is known that confinement governs the migration of DCs (29). To better understand the role of vimentin in cell migration in different spatial confinements, we perform in vitro migration experiments of BMDCs under conditions that mimic the confined physiological environment of BMDCs in vivo, as described in previous studies (32,38,39). To confine the cells in a reproducible manner and acquire large data sets of trajectories, we produce 1D confining microchannels (Fig. 1 A) and 2D confining geometries between two parallel plates (Fig. 1 B), using microfabrication methods (36,54). These devices enable us to analyze the ability of BMDCs to migrate in 1D and 2D spaces.

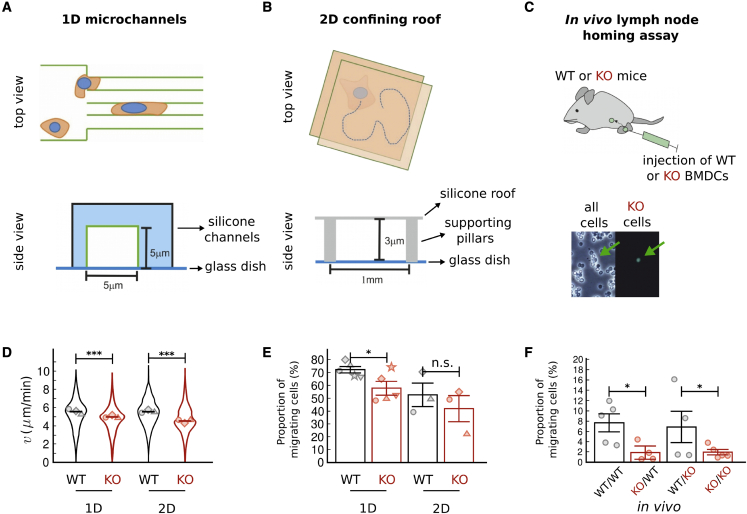
Figure 1.

Ameboid migration of BMDCs with (WT) or without (KO) vimentin. (A and B) Top and side views of the 1D microchannels and 2D confining roof setup. (C) Top: scheme of the lymph node homing assay. Bottom: representative phase contrast (left) and fluorescence (right) microscopy images, which are used to count the fluorescently labeled WT and KO cells that reached the lymph node. Green arrows indicate a KO cell that was injected into the footpad of the mouse. (D) Violin plots of migration speed v of WT and KO cells in 1D (3 independent experiments with 1139 total tracks for WT and 562 for KO cells) and 2D (3 independent experiments with 2428 total tracks for WT and 2409 for KO cells) setups. The horizontal lines indicate the medians. Symbols represent the mean values of individual experiments to incorporate the variability from independent experiments (55). (E) Proportion ($\text{\%}$) of migrating WT and KO cells in 1D (5 independent experiments) and 2D (3 independent experiments) setups. Symbols denote the mean values of individual experiments. The data in (D) and (E) are also available in Table S1. (F) Proportions ($\text{\%}$) of injected WT and KO cells arriving at a lymph node in WT (WT/WT and KO/WT) or KO (WT/KO and KO/KO) mice (WT/WT: n = 5 mice; KO/WT: n = 4 mice; WT/KO: n = 4 mice; KO/KO: n = 5 mice). Symbols represent the mean values for each mouse. The data in (E) and (F) represent mean $\pm$ standard error. Statistical analysis in (D) and (E) is performed using a t test over all data points. $\text{∗}p<0.05$, $\ast \ast \ast p<0.001$; n.s., not significant. To see this figure in color, go online.

To determine the ameboid migration of vimentin-deficient cells, we generate BMDCs from WT and vimentin KO mice, as described in the “materials and methods” section. Upon loss of vimentin, the migration speed v in 1D and 2D is reduced ($v_{\text{WT}}/v_{v_{\text{KO}}}\simeq 1.11$ and 1.22 in 1D and 2D confinements, respectively); see Fig. 1 D and Table S1. Furthermore, loss of vimentin decreases the proportion of the cells that manage to migrate (Fig. 1 E). Note that being motile has been used here as the minimum requirement for a (partially) successful migration, since the aim of migration of immature DCs is to explore the environment. Taken together, these data indicate that vimentin is beneficial for BMDCs to be able to migrate and to achieve a larger migration speed in 1D or 2D confined environments.

In vivo migration of BMDCs to lymph nodes

To determine whether vimentin also influences the in vivo migration of mature DCs, we perform lymph node homing assays (as described in the “materials and methods” section and previous studies (56)). Only mature DCs, i.e., those encountering pathogens, have the ability to migrate toward the lymph nodes to communicate with the immune system. Thus, our BMDCs are first treated with lipopolysaccharide—which is a membrane component of bacteria—and then injected into the footpads of mice (see Fig. 1 C). By counting the numbers of BMDCs in the closest lymph node (popliteal lymph node) after 36 h, we check whether a lack of vimentin can affect the migration of mature BMDCs. Note that reaching a lymph node is taken as the definition of a successful migration in our in vivo experiments, which is different from the definition used in the previous section for immature BMDCs. The proportions of the injected WT or KO BMDCs that arrive at the lymph nodes of WT or KO mice are shown in Fig. 1 F. Lymph node homing (in either WT or KO mice) is notably less successful for KO BMDCs than for WT cells. These data show that the observed deficiencies of KO BMDCs are not due to the vimentin levels in the surrounding microenvironment and/or the receiving tissue(s). Taken together, our observations indicate that vimentin promotes the in vivo BMDC homing rate.

Search efficiency of migrating BMDCs

A major function of immature DCs is the detection of harmful pathogens, for which they need to explore the environment efficiently. The reductions in the proportion and speed of migrating BMDCs with the loss of vimentin indicates that the overall time required to patrol the environment is relatively longer for KO BMDCs compared with WT cells. To quantify and compare the search time of WT and KO BMDCs, we consider the MFPT of individual cells. In addition to the migration speed v, the MFPT depends on the directional persistence p and the persistence-speed coupling $c\left(p\text{,}v\right)$ (33,57). Thus, in the following we investigate whether the loss of vimentin affects these aspects of the BMDC dynamics in the 2D confining setup. We note that in the present study the search problem is limited to finding regularly located targets, which has similarities with the task of DCs to explore tissues to find pathogens. Similar conclusions can be drawn for correlated stochastic searches in the presence of biochemical or other environmental cues.

Each experimental cell trajectory comprises a regularly recorded set of cell positions. From the turning angle ${\theta }_{\text{i}}$ at each cell position i (see Fig. 2 A), a local directional persistence $p_{\text{i}}$ can be deduced as $p_{\text{i}}=\text{cos}\left({\theta }_{\text{i}}\right)$. The mean value p of the local directional persistence $\left(p\in \left[-1\text{,}1\right]\right)$ effectively reflects the cell diffusivity (58) and governs the MFPT (57). We obtain the turning-angle distribution $P\left(\theta \right)$ for WT and KO BMDCs over all cell trajectories. The distributions are qualitatively similar, with mean values of approximately zero (${⟨\theta ⟩}_{\text{WT}}=0.1\pm 1.2°$ and ${⟨\theta ⟩}_{\text{KO}}=0.0\pm 0.9°$; see Fig. S1 A). The resulting mean local persistence $p=⟨\text{cos}\left(\theta \right)⟩={\int }_{-\pi }^{\pi }\text{cos}\left(\theta \right)P\left(\theta \right)\text{d}\theta$ is very close for both categories of cells ($p_{\text{WT}}=0.44\pm 0.02$ and $p_{\text{KO}}=0.47\pm 0.02$; Fig. 2 B). A similar behavior is observed for the apparent persistence of individual trajectories—defined as the end-to-end distance divided by the actual length of the cell trajectory—as presented in Table S1. Thus, vimentin-deficient cells are able to retain their directional persistence. The relatively small difference between the persistence of WT and KO BMDCs can induce only a negligible difference between their MFPTs (57).

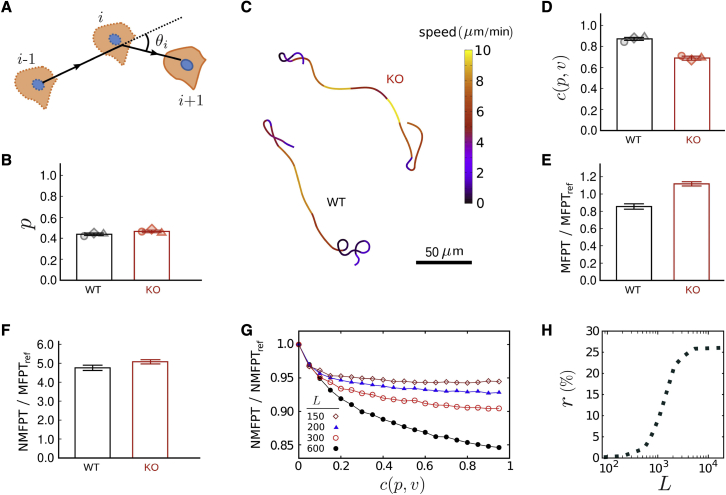
Figure 2.

Search efficiency of BMDCs with (WT) or without (KO) vimentin in 2D confinement. (A) Sketch of the migration path. (B) Directional persistence p (extracted from 3 independent experiments for each cell category; total tracks: $\sim 3700$ for WT and 6500 for KO cells). The data represent mean $\pm$ standard error and symbols are the mean values of individual experiments. (C) Sample cell trajectories, color coded with respect to cell speed. (D) Persistence-speed correlation $c\left(p\text{,}v\right)$ for both cell categories. Symbols denote the mean values of individual experiments. (E) MFPT of WT and KO cells in a confinement with lateral size $L=600$ (with the target size being the length unit). As a reference for comparison, the MFPTs are scaled by the search time ${\text{MFPT}}_{\text{ref}}$ of an uncorrelated persistent searcher (i.e., with $c\left(p\text{,}v\right)=0$) that moves with the same mean persistence and speed as WT cells. (F) Normalized MFPT with respect to mean cell speed, NMFPT, for both cell categories. (G) NMFPT, scaled by ${\text{NMFPT}}_{\text{ref}}$, in terms of $c\left(p\text{,}v\right)$ for different system sizes. (H) Relative difference r between the NMFPT of WT and KO BMDCs, $r=\frac{{\text{NMFPT}}_{\text{KO}}}{{\text{NMFPT}}_{\text{WT}}}-1\left(\%\right)$, in terms of the system size L. To see this figure in color, go online.

Next we analyze the persistence-speed coupling $c\left(p\text{,}v\right)$ as another factor that can influence the search efficiency. As shown in the typical trajectories depicted in Fig. 2 C, KO BMDCs exhibit reduced ability to correlate the local curvature of their path to the instantaneous migration speed (see also Fig. S1 B). By calculating the correlation coefficient $c\left(p\text{,}v\right)\left(\in \left[-1\text{,}1\right]\right)$, we find that the persistence and speed of KO BMDCs are less correlated compared with WT cells ($c_{\text{KO}}\left(p\text{,}v\right)=0.69\pm 0.04$ vs. $c_{\text{WT}}\left(p\text{,}v\right)=0.87\pm 0.03$, as shown in Fig. 2 D). The difference is ∼ $20\text{\%}$, which is expected to induce a considerable difference between the MFPTs of the two categories of cells (33).

To evaluate the relative importance of each of the two key factors—i.e., a weaker coupling strength $c\left(p\text{,}v\right)$ and a lower migration speed v—on the MFPT of KO BMDCs to find regularly distributed targets, we perform extensive Monte Carlo simulations of a correlated active search process in a confinement with periodic boundary conditions. We extract the instantaneous speed of the random walker at each time step from the experimental speed distribution $F_{\text{WT}}\left(v\right)$ or $F_{\text{KO}}\left(v\right)$. Then, we calculate the local persistence according to the experimental coupling strength $c_{\text{WT}}\left(p\text{,}v\right)$ or $c_{\text{KO}}\left(p\text{,}v\right)$, and update the new direction of motion θ (see the “materials and methods” section for details). For each starting position and direction of motion, the walker continues the search until the target is found. The MFPT is obtained by averaging over an ensemble of initial conditions. The simulation results shown in Fig. 2 E (for a confinement of lateral size $L=600$ in the units of the target size) reveal that the MFPT is nearly $30\text{\%}$ higher for KO BMDCs. To exclude the contribution of the migration speed to the MFPT, we introduce a characteristic time $\tau =1/v$ to travel a unit of length with speed v. Then, we scale the MFPT by τ to obtain a normalized search time as $\text{NMFPT}=\text{MFPT}/\tau$. Fig. 2 F shows that the NMFPT of KO BMDCs is still higher than that of WT cells (${\text{NMFPT}}_{\text{KO}}/{\text{NMFPT}}_{\text{WT}}\simeq 1.06$), which is due to the weaker $p$-v coupling of KO BMDCs.

For an arbitrary choice of speed v in simulations, the NMFPT monotonically decreases by increasing $c\left(p\text{,}v\right)$ (Fig. 2 G). However, this effect weakens when the confinement size L is decreased. The reason is that, by decreasing L at a given persistence, the relative persistence length of the searcher (compared with L) increases and approaches the optimal value for search with constant persistence (57). The search with $p$-v correlated dynamics is always less efficient than the optimal constant-persistence search (33). By approaching the optimal relative persistence, the correlated search strategy becomes less beneficial. Therefore, the relative difference between the search efficiencies of moving with $c_{\text{KO}}\left(p\text{,}v\right)\simeq 0.69$ or $c_{\text{WT}}\left(p\text{,}v\right)=0.87$ depends on L. The question arises whether in the natural living environments of immature BMDCs the difference in $c\left(p\text{,}v\right)$ of WT and KO cells leads to a considerable difference between their NMFPTs. To answer this question, we perform simulations where L is varied while $c\left(p\text{,}v\right)$ of WT and KO BMDCs is kept fixed at their experimental values. Fig. 2 H shows that the relative NMFPT difference of WT and KO BMDCs increases with L and can even exceed $25\text{\%}$. The larger the searching environment a BMDC has to patrol, the stronger the effects of vimentin on search efficiency. We have checked that changing the size of the target or the searcher in our simulations does not influence the reported trends or our conclusions. We note that using periodic or mirror-like reflective boundary conditions yields analogous MFPT trends (57). (A reflective boundary condition corresponds to mirror imaging the simulation box when crossing the border, which leads to slight differences with the periodic boundary condition. The latter is equivalent to regularly spaced targets on an infinite plane.)

Viscoelastic response of BMDCs

We previously showed that cell mechanics and migration are strongly interdependent cell features (59). The mechanical properties of cells are known to be influenced by the presence of vimentin (1,9), even though the roles of vimentin and actin cortex in cell mechanics are not clearly differentiated. In an attempt to clarify this point, we determine the subcellular localization of actin and vimentin IFs in immature BMDCs 24 h after seeding on glass. The results shown in Fig. S2 B reveal a predominantly cytoplasmic subcellular localization of vimentin filaments, with no detectable vimentin at the cell periphery or in cell protrusions. We also image the cells in 1D microchannels to mimic the in vivo migration of DCs through highly confined spaces caused by other cells and the extracellular matrix (29,60). Similarly, there is no vimentin signal at the periphery or in cellular protrusions (Fig. S2 C). These observations are in line with earlier reports of vimentin localization around cell nuclei (9). The question arises whether vimentin mainly influences the mechanical properties of the cytoplasmic, and not the peripheral, regions of DCs. To answer this question, we analyze the mechanical properties of BMDCs with and without vimentin subjected to low or high shear strain.

RT-DC is a high-throughput method to deform cells with a hydrodynamic shear flow on a millisecond timescale (see Fig. 3 A and (48)). The characteristics of this method make it a suitable technique to probe the outer cortical region of the cell. The applied shear flow can be adapted to tune the deformation force imposed on the cell. We use this technique to measure the mechanical response of the cells under low deformation. We quantify cell deformation as $\xi =1-2\sqrt{\pi A}/\delta$ (48), with A and δ being the projected cell area and perimeter, respectively. The dimensionless quantity ξ ($\in \left[0\text{,}1\right]$) increases with deviation from a round shape. Under a flow rate of 0.16 $\mu {\text{L.s}}^{-1}$, only a minor difference between the deformation of WT and KO BMDCs is observed (Fig. S3 C and Table S2). Since KO cells are on average smaller than WT cells (Fig. S3 E), they experience lower shear forces in the microfluidic channel. Thus, it is not ideal to compare their mechanical properties based on the deformation value alone. To compare the mechanical properties of the two cell classes, we utilize an established look-up table based on numerical simulations (49) to assign the Young’s modulus values to the cells based on their area and deformation. As shown in Fig. 3 B, the Young’s modulus of KO BMDCs is ∼ 70 Pa lower than that of WT cells, which is substantial (for comparison, the decrease in Young’s modulus due to depletion of various Rho-signaling-related molecules in mitotic Kc167 cells rarely surpasses 100 Pa (61)). Increasing the flow rate to 0.32 $\mu {\text{L.s}}^{-1}$ exerts stronger shear forces, induces larger deformation of cells, and increases the observed difference in deformation between WT and KO cells (Fig. S3 C). The cell sizes are not dramatically affected by the shear flow rate, as the cells can be considered incompressible. Both cell categories exhibit a higher Young’s modulus under larger deformation (Fig. S3 D) due to strain-stiffening characteristics typical of biological materials (62); nevertheless, WT BMDCs are stiffer than KO cells independent of the flow rate.

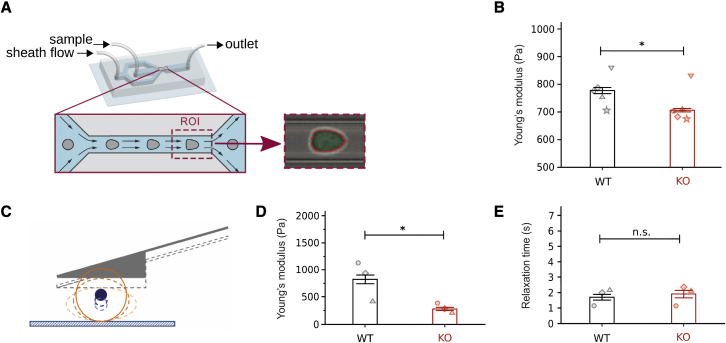
Figure 3.

Viscoelastic response of BMDCs with (WT) or without (KO) vimentin. (A) A schematic overview of microfluidics-based RT-DC measurements. (B) Young’s moduli of WT and KO BMDCs obtained from RT-DC measurements performed at a flow rate of 0.16 $\mu {\text{L.s}}^{-1}$. The data represent the median $\pm$ absolute deviation. Circles denote the median values of five independent experiments. (C) Scheme of a wedged cantilever compressing a cell. (D and E) Young’s moduli and relaxation times of WT and KO BMDCs measured at the first extent in AFM experiments. The data represent the mean $\pm$ standard error. Circles represent the mean values of three independent experiments. Statistical analysis is performed using the linear mixed effects model (B) or the t test (D and E). $\text{∗}p<0.05$; n.s., not significant. To see this figure in color, go online.

To examine the influence of vimentin on the mechanical properties of the bulk (i.e., cytoplasmic regions) of BMDCs, we use AFM, which is a low-throughput method and offers better control of cell-indentation speed and depth compared with RT-DC. We place the cells in nonadhesive PEG-coated dishes and compress them using wedged tipless cantilevers (see Figs. 3 C, S4 A, and (44)). By analyzing the deformation curves for an indentation of 4 nN, we obtain the Young’s modulus. We use the elastic Hertz model for simplicity since the ratio between the Young’s moduli of WT and KO cells is of interest. The similarity of the Hertz model with the viscoelastic model of (46) is a linear relationship between the Young’s modulus and the AFM measured force in both models. However, the prefactor of the linear relation in the viscoelastic model depends on the viscosity properties of the cell, such as the relaxation functions. We show in the following that the force relaxation time is not considerably different in WT and KO cells. Assuming that the viscosity properties of the cells are not affected by the lack of vimentin, the resulting ratio between the Young’s moduli of WT and KO cells from the viscoelastic model is the same as that obtained from the elastic Hertz model. In general, however, the viscosity properties of WT and KO cells can be slightly different and microrheological experiments are required to precisely evaluate their elastic responses. Fig. 3 D shows that WT cells are stiffer than KO cells, in agreement with the RT-DC measurements (here the difference is even larger, i.e., a nearly three times higher Young’s modulus for WT cells). This trend also persists for higher indentation depths which induce larger deformations (see Fig. S4 and Table S3).

Next, to examine whether vimentin influences the viscous properties of cells, we analyze the relaxation times of WT and KO BMDCs, using AFM. A higher relaxation time indicates a higher viscosity. Fig. 3 E shows only a minor difference between the relaxation time of WT and KO BMDCs (see also Fig. S4 D and Table S3). These data suggest that, while vimentin influences the elastic properties, its presence is not important for the viscous properties of BMDCs. However, it was recently shown that individual vimentin filaments are able to highly dissipate the input energy and display tensile memory (63). The origin of the energy dissipation is attributed to the unfolding/folding cycles of α helices in the vimentin monomers. The resulting rough energy landscape of the unfolded state gives rise to the viscoelastic relaxation behavior of vimentin filaments (64). We attribute the discrepancy to the complexity of the entire cell compared with the simplified in vitro conditions of individual vimentin filaments. The single filament properties may not necessarily play a major role in the complex living cell.

Discussion

Adaptive immune responses rely on the migration of DCs to lymph nodes or a site of inflammation using a type of migration that can rapidly integrate spatiotemporal signals and adapt to the environment (65). Although many aspects of migratory processes are well understood, little is known about the mechanisms that underlie the actual migration and passage of these cells through complex tissue settings and highly confined spaces. It is clear that the involved migratory processes require active engagement of the cytoskeleton. A number of studies have demonstrated specific roles of microtubules and microfilaments (66,67). The migration of DCs is expected to be influenced by vimentin, as it has been demonstrated to have an essential role in leukocyte homing (13). Our goal has been to better understand the contribution of vimentin to the biomechanics required for BMDC migration.

We have studied confined ameboid migration using 1D and 2D techniques that allows for long (15 h) periods of observation. While 2D migration allows for the investigation of the navigation abilities of cells, 1D migration through microchannels enforces confinement all around the sides of the cell, which might be more reflective of the local geometries that they encounter during in vivo migration through very tight spaces. It should be noted that the required degree of lateral confinement to have a 1D or 2D ameboid migration differs from that of an adherent mesenchymal migration (68,69) as the migration mechanisms are different: while the cells use integrins to adhere, transmit forces, and move in the mesenchymal migration, nonspecific friction forces are used in the ameboid migration mode (23,70). The cross section size of the microchannel in our 1D setup or the spacing between the parallel plates in the 2D setup should be small enough that the BDMCs can form the required frictional contacts with walls; otherwise the cells remain immobile. We observe that the speed of KO BMDCs is lower than that in WT cells in both the 1D and 2D setups; thus, vimentin influences the motility of BMDCs (as was also suggested for mesenchymal cell migration (17,71)).

The universal coupling between the migration speed and directional persistence has been observed for a range of different cell types (32,72). It shows that the local curvature of the cell trajectory depends on the instantaneous migration speed (such that the cell has a straighter path when it moves faster), in contrast to uncorrelated persistence-speed dynamics. Such a correlated active motion enables active searchers to reduce their search time (33). In our 2D experiments, the persistence-speed coupling is lower for KO BMDCs compared with WT cells. By Monte Carlo simulations we have investigated the influence of the lower migration speed and the weaker persistence-speed coupling strength on the search time of KO BMDCs to find regularly distributed targets such as pathogens. For instance, we consider dermal DCs in the skin or DCs in small intrapulmonary airways, where the density of DCs reaches a few hundred cells per ${\text{mm}}^2$ (73,74). Our numerical results suggest that loss of vimentin causes up to $30\text{\%}$ longer search times for DCs in these environments. Previous studies primarily from mesenchymal systems have shown that vimentin affects actin flow. It is possible that vimentin similarly affects actin retrograde flow in ameboid migration, as our preliminary observations evidence alterations in actin-driven processes when vimentin is depleted. Overall, however, the mechanisms behind vimentin-mediated effects on retrograde flow are still to be resolved at the molecular level and several paradigms have been presented, including the possibility that vimentin reacts upstream of actin dynamics on the ROCK pathway (10,75).

According to Fig. 1, E and F, the reduction of the migration success rate in the absence of vimentin is more pronounced for in vivo experiments; nearly $30\text{\%}$ of the vimentin-KO cells arrive at the lymph node, while $\sim 80\text{\%}$ of the vimentin-KO cells manage to migrate in vitro. Although the in vivo conditions are more complex and additional mechanisms may be involved, a major source of difference between the results is the difference between the definitions of migration: reaching a lymph node is used as the definition of a successful in vivo migration of mature DCs, but being motile is taken as the minimum requirement for in vitro migration of immature DCs (since the aim of migration of immature DCs is tissue patrolling and antigen capture). If we choose reaching a target as the definition of a successful migration in both cases, then the results get closer to each other. For comparison, we estimate the overall ability of vimentin-KO cells to reach a far target position in vitro. According to Fig. 2, E–H, each of a slower speed or a weaker p-v coupling can increase the search time up to $25\text{\%}$. This indicates that the rate of arrival at a target position during a given time period may be reduced even to $\sim 75\text{\%}$ due to either a lower speed or a lower p-v coupling. Therefore, the overall success rate can be 80 × 75 × 75% = 45%, which is appreciably close to the in vivo situation in Fig. 1 F despite all differences between the two cases.

In this study, we have compared two extreme limits of full presence and full absence of vimentin. It would be attractive to modulate the vimentin level in a desired direction to a desired level. However, this is indeed a serious challenge. We use primary DCs to obtain maximal physiological relevance and also because these cells display a highly clean ameboid migration modality (in contrast to, e.g., cancer cells that display a mix of mesenchymal and ameboid modalities (18)). Nevertheless, primary DCs are notoriously difficult to transfect. Furthermore, vimentin is an extremely stable protein. Silencing vimentin by siRNA (18,76) requires at least two rounds to achieve as little as $40\text{\%}$ of reduction of the protein. Two rounds of silencing would take longer than the time ($\sim$10 days) between obtaining bone marrow and its differentiation into DCs.

We have shown that loss of vimentin affects the elasticity of BMDCs at both low and high strain. Thus, vimentin contributes to the elasticity that is required for these suspended BMDCs to deform or squeeze through confined environments. This is consistent with previous observations in adherent cells (9,77). In vitro rheology analyses of cytoskeletal filaments have revealed that vimentin is more stretchable and also more resistant to breakage at high strain compared with actin or microtubules; the latter feature provides a greater toughness to living cells (4,78).

The role of vimentin has also been investigated in mesenchymal fibroblasts recently (2), where hyperelastic properties are reported for vimentin filaments; vimentin-deficient and vimentin-enriched cells have a lower or higher force relaxation than WT cells, respectively. This suggests that vimentin is a hyperelastic fiber, i.e., it responds elastically even under large deformation. This indirectly contributes to cell viscoelasticity and mesenchymal migration (1,2,79). Hyperelasticity has also been reported in epithelial sheets (80): it is induced by microscopic instabilities that are triggered by stretch-induced dilution of the actin cortex and rescued by the IFs.

As vimentin organization is dynamically regulated by constitutive phosphorylation and dephosphorylation cycles, this will provide the dynamic properties needed for meaningful contributions to the required forces for migration (81, 82, 83). The differences between migration behavior of mesenchymal and ameboid migrating cells under the loss of vimentin can be seen by comparison of our data to a recent study that investigated the 1D and 2D migration of fibroblasts that lacked vimentin (71). These fibroblasts showed a lower migration speed similar to BMDCs on 2D surfaces, but an opposite effect in 1D microchannels (i.e., an increased migration speed). This emphasizes the differences between these two migration types, which become particularly evident in one dimension. Moreover, it has been shown in adherent cells that vimentin provides localized increases in cell stiffness and protects the nucleus from rupture (77). For this reason, vimentin-deficient cells can show stronger deformation of the nucleus itself in confined spaces, which accelerates mesenchymal cells in 1D microchannels (71). Considering that vimentin filaments in migrating DCs are localized mainly in the cytoplasm, we suggest that vimentin reinforces these subcellular regions against strong compressive stresses. This idea is supported by Patteson et al. (77), who showed that the absence of vimentin results in an unstable nuclear shape and increased DNA damage during migration through a 3D collagen mesh. Since vimentin protects against DNA damage and nuclear deformation and instability (77,84), we can assume a role for vimentin in the modulation of gene expression, i.e., vimentin may indirectly regulate gene expression and, as a consequence, the differentiation, maturation, and migration of DCs.

Author contributions

L.S., E.T., J.E.E., and F.L. conceived the experiments. L.S., M.U., D.A.D.F., E.T., and F.C. performed the experiments. L.S., M.U., and M.R.S. analyzed the data. M.R.S. designed and performed the numerical simulations. L.S., D.V., M.R.S., A.K.B.G., and E.T. wrote the manuscript. L.S., D.V., and M.R.S. drafted the figures. M.R.S., J.E.E., and F.L. revised the manuscript. M.R.S., L.S., and D.V. contributed equally to this work. J.E.E. and F.L. contributed equally to this work.

Editor: Timo Betz.