Diagnosing and mitigating method-based avidity artifacts that confound polyubiquitin-binding assays

Abstract

Polyubiquitination is a complex form of posttranslational modification responsible for the control of numerous cellular processes. Many ubiquitin-binding proteins recognize distinct polyubiquitin chain types, and these associations help drive ubiquitin-signaling pathways. There is considerable interest in understanding the specificity of ubiquitin-binding proteins; however, because of the multivalent nature of polyubiquitin, affinity measurements of these interactions that rely on affixing ubiquitin-binding proteins to a surface can display artifactual, method-dependent avidity, or “bridging.” This artifact, which is distinct from biologically relevant, avid interactions with polyubiquitin, is commonplace in such polyubiquitin-binding measurements and can lead to dramatic overestimations of binding affinities for particular chain types, and thus, incorrect conclusions about specificity. Here, we use surface-based measurements of ubiquitin binding in three model systems to illustrate bridging and lay out practical ways of identifying and mitigating it. Specifically, we describe a simple fitting model that enables researchers to diagnose the severity of bridging artifacts, determine whether they can be minimized, and more accurately evaluate polyubiquitin-binding specificity.

Why it matters

Recognition of specific polyubiquitin chain linkages by ubiquitin-binding proteins helps drive ubiquitin-signaling pathways in the cell. Quantitative affinity measurements are critical to determining the specificity of these ubiquitin-binding proteins, and surface-based techniques like surface plasmon resonance and biolayer interferometry are attractive methods for these studies. Although these biophysical methods are rapid and quantitative, the multivalent nature of polyubiquitin makes them subject to surface-dependent avidity artifacts that we term “bridging”—an important issue that, to date, has been largely under-appreciated in polyubiqutin-binding studies. Here, we demonstrate how prevalent bridging artifacts easily skew affinity measurements and specificity determinations and provide a set of practical, easy-to-apply techniques for recognizing and mitigating these artifacts in such biophysical measurements.

Introduction

Ubiquitination—the covalent attachment of the small protein ubiquitin to target proteins—is one of the most crucial and complex forms of posttranslational modification in eukaryotic cells (1, 2, 3, 4). In humans, hundreds of proteins are involved in the ubiquitination and deubiquitination of diverse targets, and hundreds more are responsible for recognizing the resulting modified proteins and governing their fates (3, 4, 5). Ubiquitin itself is a simple, 76-residue globular protein, but it gains tremendous complexity as a posttranslational modification through its ability to form a diverse array of polyubiquitin chains via its lysines (K6, K11, K27, K29, K33, K48, K63) (3,6,7). In addition, linear ubiquitin chains may be formed by linking ubiquitin monomers head-to-tail (N-to-C-termini) (8). The structural differences inherent in each ubiquitin chain type provide a means for ubiquitin-binding proteins to recognize different polyubiquitin species. For example, a protein may recognize a local environment unique to a particular linkage type, such as an exposed surface residue or the structural context of the isopeptide bond. A second, sometimes complementary, mode of polyubiquitin recognition occurs through linkage-specific avidity. In these cases, the spatial arrangement of ubiquitin monomers in a chain is exploited by a complementary spacing of multiple ubiquitin-binding elements in the partner protein (9).

Determining the length and linkage specificity of ubiquitin-binding proteins is an active area of research and important to our molecular understanding of ubiquitin signaling. The difficulty of preparing pure, linkage-specific polyubiquitin chains makes biophysical techniques like surface plasmon resonance (SPR) and biolayer interferometry (BLI) very attractive methods for studying these proteins. Both methods require relatively small amounts of material, are rapid and quantitative, and provide kinetic as well as equilibrium information. A key experimental limitation, however, is that these techniques involve attaching one molecule (known as the ligand) to a surface and measuring a change in signal (refractive index, optical interference) upon the introduction of a second molecule (the analyte) in solution. Because of this dependence on affixing the ligand to the experimental surface, these techniques are subject to method-dependent avidity artifacts when applied to a multivalent-binding analyte such as polyubiquitin.

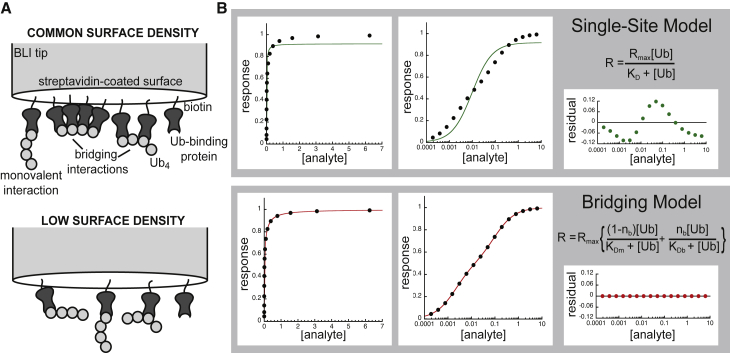
Take, for example, a biotinylated monoubiquitin-binding protein (Fig. 1 A, top panel). When a streptavidin-coated surface is immersed in a solution of these biotinylated proteins, the individual molecules will sit down randomly on the tip surface. Some will end up very close to their nearest neighbors, whereas others will be farther apart. If a polyubiquitin chain is then added to the solution as analyte, some of these chains will be able to interact with two or more immobilized ubiquitin-binding elements at once. But this interaction occurs simply because the binding elements are the right distance apart on the tip surface for a polyubiquitin chain to physically bridge between them, rather than due to a meaningful biological event. As such, these interactions should not be confused with avidity-based recognition mechanisms like those introduced above, in which the geometry of ubiquitin-binding elements within a protein or complex enables multivalent recognition of a polyubiquitin chain. In light of this, we term this type of experimental artifact “bridging,” to clearly distinguish it from the biologically significant, linkage-specific avidity that, unlike bridging, can be observed in solution-based measurements.

Figure 1.

Bridging artifacts in surface-based polyubiquitin affinity measurements. (A) Schematic representation of a biotinylated, monoubiquitin-binding protein (dark gray) associating with linear tetraubiquitin (light gray circles) on a streptavidin coated BLI tip at two different surface saturation levels. (B) Theoretical bridging-biased data generated for system with 50/50 split between bridging and monovalent interactions, in which the bridging affinity is 50-fold tighter than the monovalent affinity (K_Db = 0.002 μM and K_Dm = 0.1 μM, respectively). Data plotted with linear (left panel) and logarithmic (middle panel) x axes and fit to single-site-binding model (top row) or bridging model (bottom row) used to generate the data. In this theoretical example, R_min is set to zero so ΔR_max simplifies to just R_max in Eq. 2 (see Materials and methods). Residuals from the nonlinear fits also plotted (right panel).

Although these two types of avidity differ in their relevance to biological function, the underlying biophysical principles remain much the same. Analogous to a functionally relevant avid interaction, bridging relies on increases in local concentration to enhance an otherwise lower affinity. In other words, using our above example, the association of the first ubiquitin monomer in the chain with an immobilized ubiquitin-binding element brings the rest of the ubiquitin chain close to the surface, and therefore, close to more ubiquitin-binding elements. This boosts the local concentrations of the binding partners, which leads to a greatly enhanced apparent affinity (10). Bridges are more likely to form on highly saturated surfaces, where the chance of finding two or more binding elements with the right spacing is much higher. At lower surface saturation, the immobilized proteins are more sparsely spaced, and bridging interactions are reduced or eliminated (Fig. 1 A, bottom panel).

When using surface-based biophysical techniques like SPR or BLI to study multivalent binding analytes such as polyubiquitin, it is crucial to recognize that these two types of avidity are distinct. By definition, bridging events are artifacts built into the experimental system. Moreover, bridging is not merely a theoretical possibility, but a frequent artifact under routine experimental conditions that can dominate measurements of multivalent interactions. Bridging is a common consideration in surface-based antibody binding experiments, where bivalent antibodies are standardly captured on the surface to serve as ligands instead of being used as analytes to avoid confounding avidity effects (11). Although bridging has been noted in the field of polyubiquitin binding before, there has been no means to quantitatively assess its impact on binding data or recover meaningful information from bridging-encumbered data. Here, we present three case studies of ubiquitin-binding proteins (NF-κB essential modulator (NEMO), cellular inhibitor of apoptosis protein 1 (cIAP1), and A20) to clearly demonstrate bridging and describe practical methods for detecting, quantifying, and avoiding these artifacts in surface-based polyubiquitin-binding studies.

Materials and methods

Protein expression and purification

A truncated, mutant form of cIAP1 (cIAP1-B3R) was cloned, expressed, and purified as described previously (12). A biotinylated version of cIAP1-B3R was achieved by fusing the cIAP1-B3R construct to an N-terminal sequence encoding a hexahistidine tag followed by a Tobacco Etch Virus (TEV) protease cleavage site, an Avi-tag (amino acid sequence GLNDIFEAQKIEWHE) and a GlySer or Glycine-Serine (GS)-linker before the start of the target protein construct (Avidity, Aurora, CO). Protein was coexpressed with BirA for specific biotinylation of the Avi-tag (13) and purified as described previously (14). Singly biotinylated forms of the ubiquitin-binding domain of NEMO (NEMO_UBAN: G257-S346), and select zinc finger domains of human A20 (ZnF1; ZnF4: S592-K635, with and without the C624A/C627A binding mutation; ZnF7: P758-G790) were also expressed and purified as described previously (14, 15, 16). Linear, K48-linked and K63-linked ubiquitin chains of various lengths were prepared and purified as described previously (17). Singly biotinylated ubiquitin chains were prepared by cotransforming Avi-tagged ubiquitin vectors (see above) with BirA expression vectors and expressing protein as described above. Protein was purified in the same way as untagged constructs. The presence of covalently attached biotin was confirmed by mass spectrometry.

Biolayer interferometry measurements

All data were collected on a ForteBio Octet Red384 instrument using streptavidin (SA) tips, also from ForteBio (Menlo Park, CA). For measurements of cIAP1-B3R and NEMO_UBAN binding to ubiquitin, the assay buffer was 25 mM Tris (pH 8.0), 300 mM NaCl, 0.5 mM TCEP, 0.1 mg/mL bovine serum albumin 0.02% (v/v) Tween-20. Measurements of A20-ubiquitin binding were carried out in A20-binding buffer (20 mM MES pH 6.0, 150 mM NaCl, 10% glycerol, 0.2 mM DTT, 0.01% (v/v) Tween-20, 0.1 mg/mL human serum albumin).

Tips were first soaked in assay buffer for at least 5 min. To perform the measurement, tips were then incubated in fresh buffer for 60–120 s and biotinylated protein was then loaded to the desired surface saturation (also termed loading density). Tips were then washed in assay buffer for 60–300 s and introduced to analyte for 600–1200 s, until the signal was fully saturated. Dissociation phases were accomplished in buffer alone and carried out for 600–1200 s.

All data were aligned by the last 10 s of the postloading baseline. Response values were averaged from the last 10 s of the saturated association step and plotted versus analyte concentration using Kaleidagraph (Synergy Software; Reading, PA). All nonlinear fitting was performed in Kaleidagraph.

Isothermal titration calorimetry measurements

Titrations were performed using a MicroCal PEAQ-ITC automated calorimeter (Malvern Panalytical, Worcestershire, UK) at 25°C, where the stirred cell contained 20–40 μM NEMO_UBAN dimer and the syringe held 400 μM linear tetraubiquitin (both in assay buffer containing 25 mM Tris (pH 8.0), 300 mM NaCl, 0.5 mM TCEP). Each titration was fit to a one-site model using MicroCal PEAQ-ITC Analysis software (Malvern Panalytical, Worcestershire, UK). K_D- and stoichiometry values reported are averages (±standard deviation) from three independent titrations.

Nonlinear fitting to diagnose bridging artifacts

Because BLI ligands are affixed to a surface, one may assume some sites are not available for bridging interactions based on 1) their distance from an appropriate partner site or 2) the relative saturation of nearby sites (see Fig. 1 A). It is impossible to know the relative composition of bridging versus monovalent interactions, but if these interactions are sufficiently different in affinity, we reasoned it would be possible to estimate their relative levels empirically. In effect, the two types of interactions behave like two classes of independent-binding sites, and so we can model them using an independent, nonequivalent two-site model (18):

$$R=\text{Δ}{R}_{max}\left\{\frac{n_m\left[Ub\right]}{K_{Dm}+\left[Ub\right]}+\frac{n_b\left[Ub\right]}{K_{Db}+\left[Ub\right]}\right\}+R_{min}.$$ (1)

In this version of the independent sites model, R represents the equilibrium BLI signal, [A] is the analyte concentration, ΔR_max (R_max – R_min) is the extrapolated maximal change in signal, n_m represents the fractional contribution of monovalent-binding interactions to the signal, K_Dm is the affinity of those monovalent interactions, n_b is the fractional contribution of bridging interactions to the signal, K_Db is the apparent affinity of those interactions and R_min is the minimum or “zero-analyte” signal offset (which can be used when the data warrant a background correction).

This model makes a number of simplifying assumptions. First, it is very important to understand that K_Db is not a true equilibrium constant. It is better thought of as a composite value encompassing many interactions of indistinguishably high affinity. It is a metric for the severity of bridging rather than a binding affinity explicitly describing the strength of the bridging interaction. It is also important to note that n_m and n_b do not necessarily reflect the number of monovalent or bridging interactions. Because BLI signal depends on conformation as well as mass, it is impossible to know the precise contributions each type of binding event makes to the overall signal. Thus, just as K_Db is a composite factor comprising multiple affinity constants, n_m and n_b are composite factors comprising the relative saturations of monovalent and bridging sites as well as the different (and unknown) contributions the conformations of these complexes make to the overall BLI signal. Furthermore, we include an R_min-value to account for the fact that not all researchers subtract a “zero-analyte” point from their data, but this term may be removed if the data have already been adjusted to the theoretical baseline. These simplifications are useful to avoid overfitting of the data. Explicitly accounting for the different modes of bridging interactions would more precisely reflect the system, but whether the data would support such complexity is questionable.

We can further stabilize this analysis by assuming that at any given analyte concentration, all possible bridging interactions will be formed. That is, if a multivalent analyte can find a second, third, or fourth binding partner on the surface of the tip, it will do so. Only those ligands that lack adjacent sites because of local saturation effects or the distribution of ligands on the tip will form monovalent interactions. We can then link the fractional saturation of bridging and monovalent interactions as follows:

$$R=\text{Δ}{R}_{max}\left\{\frac{\left(1-n_b\right)\left[Ub\right]}{K_{Dm}+\left[Ub\right]}+\frac{n_b\left[Ub\right]}{K_{Db}+\left[Ub\right]}\right\}+R_{min}.$$ (2)

Here, n_m has been replaced with (1−n_b), reflecting our assumption that the relative saturations of monovalent and bridging interactions are interdependent.

Results

In a system with surface-based method-dependent avidity, the resulting data will reflect two classes of interactions: physiologically relevant monovalent interactions and artifactual bridging interactions (19). In most polyubiquitin-binding systems, bridging interactions will be much stronger than the typically micromolar-range biologically pertinent interactions. Furthermore, because of the stochastic distributions of ligands on a binding surface, even the much stronger bridging interactions will never dominate completely. Accordingly, we reasoned that these data may be described using a simple variant of the independent multisite binding equation (Fig. 1 B, see Materials and methods for details) (18). To test whether this assumption holds true for real BLI data, we used three model systems of ubiquitin-binding proteins associating with various forms of polyubiquitin. Our data demonstrate how unmitigated bridging artifacts can lead to incorrect conclusions not only about the strength of a protein’s affinity for polyubiquitin, but also its specificity for particular polyubiquitin chain linkages or lengths. We further show how our model can be used to quantitate the extent of bridging and find conditions in which it is minimized.

Diagnosing artifactual length-dependent specificity: NEMO and linear polyubiquitin binding

Our first example, NEMO, is a member of the canonical IKK complex that plays a role in cellular responses to inflammation and DNA damage (20, 21, 22, 23). NEMO contains a diubiquitin-binding domain called a ubiquitin binding in ABIN and NEMO (UBAN) motif that has been shown to selectively bind linear diubiquitin and is critical for NEMO’s function in regulating inflammatory signaling (24, 25, 26). Crystal structures of NEMO-diubiquitin complexes reveal that linkage selectivity likely stems from the UBAN motif’s recognition of particular exposed surface patches present in extended diubiquitin conformations like those found in linear and K63-linked ubiquitin dimers (see Fig. 2 A) (24,27). Based on these prior observations, we would expect NEMO_UBAN to display higher binding affinity for linear diubiquitin than for monoubiquitin, but we would not expect it to display a dramatic increase in affinity for tri-or-tetraubiquitin substrates compared with diubiquitin.

Figure 2.

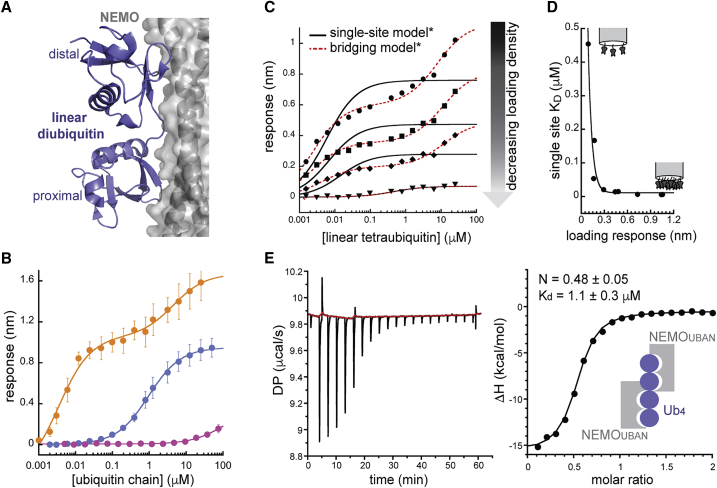
Ubiquitin binding by NEMO_UBAN. (A) NEMO_UBAN (gray cartoon and surface) selectively recognizes linear diubiquitin (blue cartoon) as a single binding unit (Protein Data Bank (PDB): 2ZVO). (B) BLI measurements of monobiotinylated NEMO_UBAN binding to discrete ubiquitin species. Error bars represent standard deviations from three measurements. Fits to single-site binding model (mono- and diubiquitin) or bridging model (tetraubiquitin) shown. For visual clarity, the data here are fit with R_min set to zero (see Figs. S1, c and d for a comprehensive analysis of single-site and bridging model fits, including comparisons of fitting models with and without R_min as a fitted parameter) (C) Linear tetraubiquitin binding singly biotinylated NEMO_UBAN at various loading densities: 1.0 nm (circles), 0.73 nm (squares), 0.44 nm (diamonds), and 0.09 nm (triangles) loading response. Fits to single-site binding equation or bridging model shown. (D) Apparent K_D-values derived from single-site model change as a function of loading density. Data fit to an exponential decay equation to guide the eye. (E) ITC analysis of NEMO_UBAN binding to linear tetraubiquitin. A representative titration is shown both as raw injection heats over the titration time course (left panel) and as integrated and normalized heats per titration step (right panel), with the latter fit to a single-site-binding model (solid line). Average K_D and complex stoichiometry values are reported with standard deviations (n = 3) and support a 2:1 model of NEMO_UBAN/tetraubiquitin binding. All fitting parameters from fits of these BLI data may be found in Table S1.

We prepared a biotinylated form of the diubiquitin-binding domain of NEMO (NEMO_UBAN) and tested its binding to monoubiquitin and linear di- and tetraubiquitin using BLI (Fig. 2 B). At routine loading densities (∼1 nm loading response), the binding data for monoubiquitin and linear diubiquitin fit well to a single-site binding model and demonstrate the protein’s previously reported 100-fold (or greater) specificity for linear diubiquitin over ubiquitin monomer (14) (Fig. S1 A, right-hand panel, blue and purple curves; Table S1). However, when we fit the tetraubiquitin binding data to a single-site binding model, we found a dramatically decreased apparent K_D of 9 nM, ∼100-fold tighter than the ∼1 μM value for diubiquitin, suggesting that NEMO has a strong preference for tetraubiquitin (Fig. S1 A, right-hand panel, orange curve). This result is incongruent with prior data and, as we describe below, is a result of bridging artifacts.

In contrast to the diubiquitin-binding data, the tetraubiquitin binding curve is highly biphasic, with a pronounced “humped” shape characteristic of nonequivalent two-site binding in which the two affinities are very different. These data are not well-described by a single-site binding model (despite technically converging during nonlinear fitting, Fig. S1 A), but they are fit well by the bridging model (Figs. 2 B and Document S1. Figs. S1–S6 and Table S1 and S2, Document S2. Article plus supporting materials A). It is further important to note that had we stopped collecting response data at 1 μM tetraubiquitin, the biphasic character of the curve would have been easy to miss, and the data might have appeared to better fit the single-site model (Fig. S1 B). When fit to the fully saturated data, the bridging model returns a monovalent K_D (K_Dm) of 4 μM, the same order of magnitude as the 1 μM K_D previously reported for NEMO binding to linear diubiquitin (14). The bridging affinity, on the other hand, is 1000-fold tighter (K_Db = 4 nM), comparable with the apparent K_D returned by the single-site model fit (Table S1).

Because NEMO’s UBAN motif consists of a coiled-coil, which dimerizes to form two symmetric diubiquitin-binding sites (24,28) on opposite faces of the protein, it is formally possible that the higher affinity interaction we ascribe to artifactual avidity is in fact due to linear tetraubiquitin interacting with both diubiquitin-binding sites at once, rather than to bridging between separate NEMO_UBAN dimers on the surface of the BLI tip. Both scenarios would fit equally well to the bridging model equation; however, only bridging would be sensitive to the surface loading density of NEMO_UBAN. To determine whether the high-affinity binding observed for linear tetraubiquitin was a result of bridging artifacts, we repeated the tetraubiquitin binding experiment at various surface saturations of NEMO_UBAN, and found that the biphasic character of the curves indeed diminishes as surface saturation decreases (Fig. 2 C; Fig. S1, C and D). Furthermore, the apparent K_D (single-site model) increases with decreasing surface saturation (Fig. 2 D). Although we were not able to go low enough in loading density (and maintain adequate binding signal) for this apparent K_D to converge on a stable value, it did begin to approach the ∼1 μM affinity of NEMO_UBAN for linear diubiquitin as bridging was reduced in the experiment. Importantly, although the K_D-values from the single-site fits changed 100-fold as loading density was reduced, the bridging model fits returned K_Dm-values within error of each other regardless of loading density, provided signal was strong enough for a stable fit (Table S1). To further confirm the validity of this low micromolar binding affinity in our hands, we independently determined that NEMO_UBAN binds to linear tetraubiquitin, with a 2:1 stoichiometry and an affinity of 1.1 μM, using isothermal titration calorimetry (ITC)—a solution-based methodology that is not subject to surface-based bridging artifacts (Fig. 2 E).

This case study demonstrates how polyubiquitin length-dependent binding specificities may be dramatically (1000-fold) in error when bridging artifacts confound binding measurements. Furthermore, it demonstrates that when there is sufficient difference between single-site and bridging affinities, our model returns single-site K_D-values and specificity determinations that approach the results determined from unencumbered solution-based measurements.

Diagnosing artifactual length-dependent specificity: cIAP1 and linear polyubiquitin binding

For our second case study, we considered cIAP1, a ubiquitin-binding protein and ligase involved in the control of programmed cell death (29). In its ligase-inactive, monomeric state cIAP1 contains a single ubiquitin-associated (UBA) domain, a motif known to bind monoubiquitin (30,31). It has been suggested from pulldown experiments that cIAP1 binds preferentially to polyubiquitin chains of four or more units (30), but because some of these pulldowns were performed with a Glutathione S-transferase (GST)-fused form of cIAP1 bound to glutathione sepharose resin, it is possible that bridging artifacts might play a role in this result. We sought to quantitatively determine whether monomeric cIAP1 displays any preference for ubiquitin chain length.

We prepared a truncated form of singly biotinylated, monomeric cIAP1, referred to henceforth as cIAP1-B3R, and measured its binding to linear di-, tri- and tetraubiquitin using BLI (see Materials and methods). Initial inspection of the response data suggests cIAP1-B3R to have a strong preference for the tri- and tetraubiquitin chains (Fig. 3 A). The binding curves of these polyubiquitin chains are considerably shifted to higher affinity compared with that of linear diubiquitin; yet, the binding data from the longer chains are biphasic, suggesting that bridging artifacts might account for the higher affinity observed for these multivalent analytes. Consistent with this hypothesis, the tri- and tetraubiquitin data are fit well by the bridging model compared to a single-site binding model (Fig. S2 A).

Figure 3.

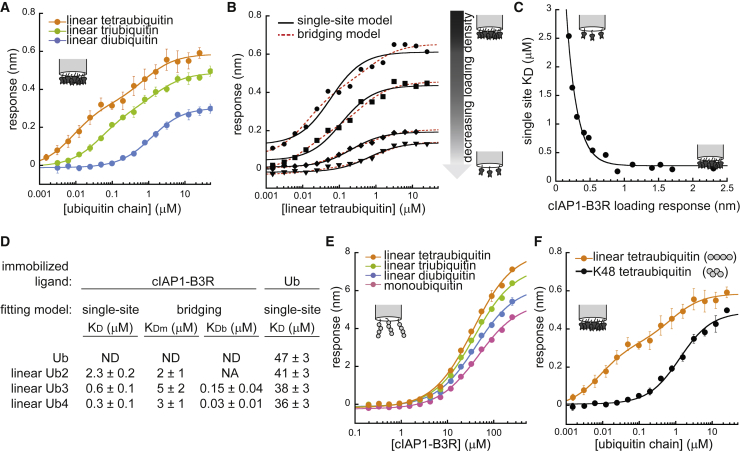
Ubiquitin binding by cIAP1-B3R. (A) BLI measurements of linear ubiquitin chains binding to monobiotinylated cIAP1-B3R. Curves represent fit of the bridging model to the data. Error bars indicate the standard deviation of three experiments. (B) BLI data collected at four different cIAP1-B3R surface saturation levels: 1.4 nm (circles), 0.73 nm (squares), 0.41 nm (diamonds), and 0.19 nm (triangles) loading response. Fits to single-site binding equation or bridging model shown. (C) Apparent K_Ds of linear tetraubiquitin binding cIAP1-B3R (fits from single-site model) change as a function of cIAP1-B3R surface saturation. Data fit to an exponential decay equation as a guide to the eye. (D) Summary of K_D-values from different data collection and analysis strategies. Note that for the immobilized cIAP1-B3R studies, K_D-, K_Dm-, and K_Db-values are normalized to the reflect number of ubiquitin sites in solution; for example, the K_D for tetraubiquitin binding has been multiplied by four to account for the mass action of four ubiquitins in a single chain. (E) BLI measurements of cIAP1-B3R binding to singly biotinylated ubiquitin species. Error bars indicate the standard deviations from three experiments. Fits to single-site binding model shown. (F) cIAP1-B3R binding to linear (bridging model fit) and K48-linked (single-site model fit) tetraubiquitin. Error bars indicate the standard deviations from three experiments. See Fig. S2 for comprehensive analysis of single-site and bridging model fits and residuals. All fitting parameters from these fits may be found in Table S1.

To confirm the presence of bridging artifacts, we altered the surface saturation of the tips, affixing biotinylated cIAP1-B3R to streptavidin tips at different surface saturation levels and performing linear tetraubiquitin binding titrations. The binding curves gradually became more monophasic as we decreased the surface saturation (Fig. 3 B; Fig. S2 B), whereas the apparent K_D (single-site model) increased (Fig. 3 C). As with the NEMO_UBAN studies, we were not able to achieve low enough tip saturation (due to signal-to-noise limitations) such that the apparent K_D converged to a stable plateau, but the apparent K_D from single-site binding model fits did approach the 3 μM K_Dm-value returned by the bridging model (Table S1).

By conducting experiments at different loading densities, we confirmed that the cIAP1-B3R-binding data are encumbered by bridging artifacts, and the apparent preference of cIAP1-B3R for longer polyubiquitin chains may be artifactual. Congruent with this hypothesis, fits of the binding curves in Fig. 3 A to the bridging model return similar monovalent affinities (K_Dm-values) for the different chain species, suggesting no significant length preference in the binding of cIAP1-B3R to linear polyubiquitin (Fig. 3 D; Table S1). To determine whether these K_Dm values were able to approximate the true affinity and specificity of the interaction in this system, we next reversed the biotinylation scheme in our experimental protocol, using singly biotinylated linear ubiquitin chains as the surface-bound ligands and nonbiotinylated, monovalent cIAP1-B3R as the analyte. As shown in Fig. 3 E and Fig. S2 C, the response data for monoubiquitin and linear di-, tri-, and tetraubiquitin collapse to a similar binding isotherm that is more consistent with the single-site model, in contrast to the original binding curves presented in Fig. 3 A and Fig. S2 A. We find only minor differences among K_D-values for monoubiquitin and linear di-, tri-, and tetraubiquitin binding to cIAP1-B3R using this method, whereas single-site fits of the original data trend toward substantially higher affinities with longer polyubiquitin analytes (Fig. 3 D, right and left panels, respectively, Table S1).

The K_D-values determined using the reversed attachment scheme, however, are ∼10-fold weaker than the K_Dm-values returned by the bridging fit of the original bridging-biased data. This incongruity may be explained by the smaller (10- to 100-fold) difference between the monovalent and bridging affinities (K_Dm- and K_Db-values, respectively), which makes it difficult for the bridging model to distinguish between the two phases in the equilibrium binding data. It is also possible that attachment artifacts distinct from bridging impact the two experimental regimes, making one artifactually weaker (e.g., steric clash with the tip surface when the smaller ubiquitin species are loaded). In addition, the lack of flow and thus the greater chance for analyte rebinding in BLI measurements (as opposed to SPR measurements, for example) may differentially confound the data in these two attachment schemes. Nevertheless, the bridging model succeeds in correctly capturing the lack of length-dependent specificity in these monomeric cIAP1-polyubiquitin interactions. We note that the case may be different for the activated, dimeric form of cIAP1, which could display a preference for longer polyubiquitin chains (30). Similar to our NEMO case study, this case study demonstrates how bridging artifacts can lead to incorrect conclusions about the specificity of ubiquitin-binding proteins for particular polyubiquitin chain lengths.

Diagnosing artifactual linkage-dependent specificity: cIAP1 and tetraubiquitin binding

Thus far we have focused on evaluating bridging as a function of increasing ubiquitin chain length, yet these surface-based artifacts can also influence comparisons of different polyubiquitin linkage types that contain equivalent numbers of ubiquitin protomers. Take for instance, BLI response data for cIAP1-B3R binding to linear versus K48-linked tetraubiquitin analytes (Fig. 3 F; Fig. S2 D). Initial inspection would suggest that cIAP1-B3R has a strong preference for linear tetramers over K48-linked tetramers. However, as discussed previously, the linear tetraubiquitin data are biphasic and heavily skewed by bridging artifacts. By contrast, the data for the more structurally compact K48-linked chains (32,33) fit well to the single-site model and do not appear to have any pronounced bridging pathologies (Fig. S2 D). The monovalent binding affinity (K_Dm) of linear tetraubiquitin returned by a fit to the bridging model is close to the K_D returned by a single-site fit to the K48 tetraubiquitin binding data (1.3 μM), suggesting that, as anticipated, monomeric cIAP1 has no strong preference between these two ubiquitin chain types (Table S1).

Diagnosing artifactual linkage-dependent specificity in a multisite binding system: A20 and triubiquitin binding

For our third case study, we considered a ubiquitin-binding protein that is known to have true multisite binding. A20, otherwise known as TNFα-induced protein 3 (TNFAIP3), is a ubiquitin-editing enzyme that regulates NF-κB signaling (15,34, 35, 36, 37). The protein exhibits deubiquitinating activity and contains an ovarian tumor-like deubiquitinating domain and seven zinc fingers (34,38,39). Two of these zinc fingers—ZnF4 and ZnF7—have been shown to bind polyubiquitin in a linkage-specific manner (40,41). We sought to determine the binding affinities of these zinc fingers for different types of triubiquitin chains. As a negative control, we also studied a mutant form of ZnF4 (ZnF4-C624A/C627A), which is unable to bind ubiquitin in any form (15).

We prepared monobiotinylated forms of these A20 ZnFs and tested their binding to linear, K63-linked and K48-linked triubiquitin using BLI (Fig. 4 A). Previous studies have established that ZnF4 has negligible affinity for linear triubiquitin, whereas ZnF7 has negligible affinity for K63-linked triubiquitin, but our initial measurements showed both interactions to be significant (40,41). Additionally, all three zinc fingers, even the binding-defective mutant, unexpectedly bound K48-linked triubiquitin, albeit with relatively weak affinities. Importantly, the plots of ZnF4 binding to linear triubiquitin (Fig. 4 A, right panel, purple curve), ZnF7 binding to K63-linked triubiquitin (Fig. 4 A, middle panel, blue curve), and K48-linked triubiqutin binding to all Zn fingers do not display the unambiguous biphasic character that might alert experimenters to bridging artifacts unless single-site model fits and residuals are closely examined and compared with the bridging model fits. This is particularly true of the ZnF4/linear triubiquitin interaction. (See Fig. S3 for a comprehensive display of fitted data). Given the potential for artifactual avidity in this system and the more clearly biphasic curves associated with the ZnF7/linear triubiquitin and ZnF4/K63-linked triubiquitin binding data, we suspected bridging accounted for these results.

Figure 4.

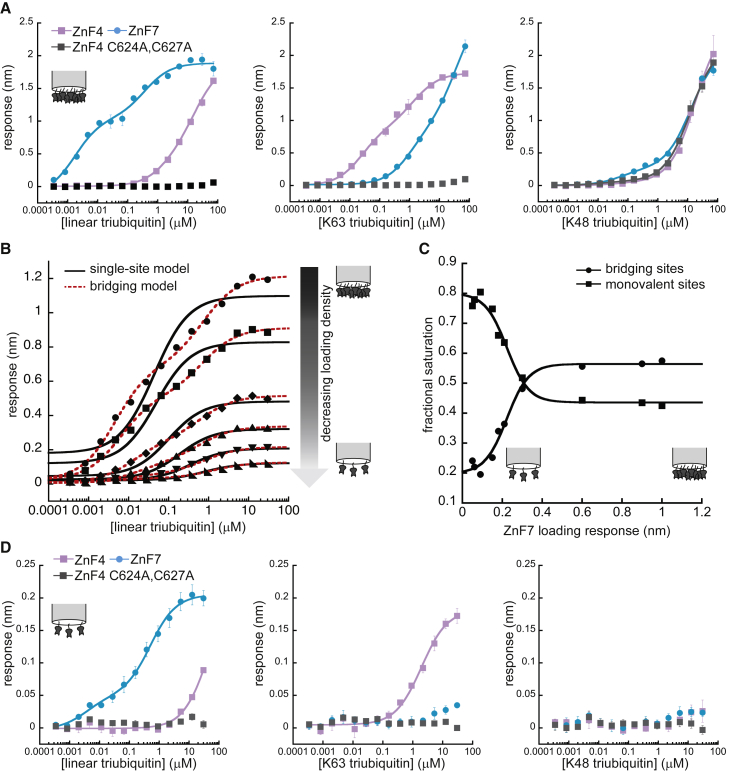
Ubiquitin binding by A20 ZnF domains. (A) Linear (left), K63-linked (center) and K48-linked (right) triubiquitin binding to monobiotinylated A20 ZnF domains, at ∼1-nm loading response. Data were fit to the bridging model. Error bars indicate the standard deviations from three experiments. (B) Linear triubiquitin-binding ZnF7 at various ZnF7 surface saturation levels: from top to bottom, 1.0-, 0.90-, 0.60-, 0.30-, 0.18-, and 0.090-nm loading response. Fits to single-site binding equation or bridging model shown. (C) Relative bridging (circles) and monovalent (squares) site saturations returned by the bridging model for linear triubiquitin-binding ZnF7 at a range of ZnF7 surface saturation levels. Data fit to a sigmoidal function as a guide to the eye. (D) Linear (left), K63-linked (center) and K48-linked (right) triubiquitin binding to A20 ZnF domains, at ∼0.1-nm loading response. Data are fit to either single-site model (ZnF4) or an independent two-site model (ZnF7) (see Materials and methods), with ZnF4- and ZnF7-binding curves reproduced with permission of Nature (16). Error bars indicate the standard deviations from three experiments. See Figs. S3 and S4 for comprehensive analysis of fitting models with residuals. All fitting parameters from these fits may be found in Tables S1 and S2.

Using ZnF7 and linear triubiquitin as a test case, we performed BLI measurements with decreasing levels of biotinylated ZnF7 affixed to streptavidin tips (Fig. 4 B; Fig. S4 A). As observed with NEMO_UBAN and cIAP1-B3R, the ZnF7 binding curves lose their obvious biphasic shape with decreasing loading density, consistent with the reduction of bridging artifacts. By fitting these data to the bridging model, we were able to determine the relative abundance of bridging sites versus monovalent sites as a function of loading response (Fig. 4 C). Below a surface saturation of 0.1 nm loading response, the contribution from bridging interactions appears to reach a minimum of ∼20%, and, unlike the previous test cases described, there is enough signal remaining to accurately monitor binding.

Because the fitting parameters are no longer sensitive to loading density below 0.1-nm loading response, we reasoned that bridging was no longer impacting the system in these conditions, and we repeated all of our measurements at low surface saturation. As shown in Fig. 4 D and Fig. S4, B and C, the new measurements are in much better agreement with published results. ZnF7 binds only to linear triubiquitin, ZnF4 binds strongly to K63-linked triubiquitin (K_D = ∼2 μM) and negligibly to linear triubiquitin, and neither of the zinc fingers bind K48-linked triubiquitin (Table S1). ZnF4-C624A/C627A, as expected, shows no binding to any form of triubiquitin (41). However, unlike in our previous case studies, in which our data at low loading density are fit better by the single-site model and fits to the bridging model cease to be meaningful, the ZnF7/linear triubiquitin binding data are still well-fit by the bridging equation even at low loading densities. Because the bridging model is, in effect, an independent two-site binding model, one explanation for this result is that ZnF7 does in fact possess multiple nonequivalent ubiquitin-binding sites. This residual saturation of “bridging sites” would thus reflect the existence of a nonequivalent, biologically relevant site. Crystallographic evidence supports this two-site hypothesis, showing the association of monoubiquitin with the ZnF4 homolog at multiple sites (40). As expected, the data are fit equally well by the bridging model and the nonequivalent sites model (Fig. S4 B), but the fact that the two binding phases are unequally saturated in this case requires some explanation: Unlike SPR, BLI data are sensitive to conformational changes and surface density, and there is no reason to suppose that two binding partners of equal mass will yield the same signal if they bind to different sites on a partner. An additional alternate explanation might be that negative cooperativity influences polyubiquitin binding in this system. To address this possibility, we fit our data to the Hill equation, which did return a Hill coefficient less than 1, albeit with reduced goodness-of-fit compared to the nonequivalent sites model (Fig. S4 B; Table S2).

This case study demonstrates how the bridging model can be used to pinpoint experimental conditions that mitigate bridging artifacts even in a case where multiple, independent binding sites exist. It also demonstrates how bridging interactions can generate seemingly uncomplicated single-site binding data that are in fact due almost entirely to artifactual avidity.

Discussion

Ubiquitination triggers many diverse, biologically important events. The breadth and specificity of biochemical outcomes driven by polyubiquitination is due in part to the multivalent nature of polyubiquitin, which can vary in length and linkage topology. Physical differences in polyubiquitins are exploited by polyubiquitin-binding proteins and complexes, which gain specificity and accumulated strength through avidity, even when individual interactions with single ubiquitin monomers are relatively weak. This mechanism is evident in multivalent ubiquitin receptors and in the clustering of binding partners in large, ubiquitinated signaling complexes. Multivalency, however, poses a significant technical problem to researchers wishing to understand polyubiquitin-binding systems. When one of the partners in such a system is artificially multimerized—either through oligomeric affinity tags or immobilization on a bead or surface—artifactual, method-dependent avidity (bridging) can occur. Many methods commonly used to study polyubiquitin-binding interactions (pulldowns, SPR, BLI) fall into this category; indeed, bridging artifacts have already been demonstrated for a specificity study of UBA domains. In this case, UBA domains were artificially multimerized through a fused GST tag, leading to the appearance of K63-specific binding that turned out to be entirely depended on the dimeric GST tag (42,43). Despite published studies highlighting artifacts such as these, surface-based polyubiquitin-binding assays with attachment schemes subject to method-dependent avidity are not routinely assessed for bridging. Even in studies where the potential for bridging is noted, the impact bridging has on the data is not quantified or fully remedied (44).

A mathematical description of biologically relevant avidity exists and can be used to determine avid and nonavid binding affinities in a multivalent system with known binding sites. This model, however, does not accurately describe the bridging that occurs in methods involving surface-immobilization because the number and affinity of avid binding sites in such experiments are dependent on the geography of ligands bound to a surface. One can apply models that account for the effect of surface saturation on artificially avid interactions, but even detailed knowledge of the structure of the macromolecules is insufficient to define, a priori, the effective distance at which two surface-bound ligands may engage a bivalent analyte (19). An analysis of this kind thus requires detailed computation and experimentation for each new system. Furthermore, in the case of polyubiquitin, one is often dealing with ubiquitin chains of three, four, or more units, making the analysis even more complex. We therefore sought to derive a facile, universally applicable model that diagnoses, rather than accounts for, bridging artifacts.

Here, we have established that quantitative surface-based measurements of polyubiquitin binding using BLI are readily susceptible to bridging artifacts. We find that more extended polyubiquitin chain types (such as K63-linked and linear polyubiquitin) (45) are more prone to these artifacts, a situation that can lead to erroneous conclusions about the length and linkage specificity of ubiquitin-binding proteins. Using solution-based binding methods or switching the surface attachment such that the polyubiquitin is the ligand (not the analyte) can avoid these issues. In some cases, however, even switching the immobilized binding partner does not resolve the issue. The ubiquitin-binding protein itself may have multiple ubiquitin-binding sites or may have engineered tags (such as GST tags) that cause it to multimerize. Attachment artifacts or technical limitations in protein production may make immobilization of one partner unfeasible. In such cases, if an assay cannot be designed to avoid bridging entirely, it may be possible to take steps to mitigate the impact of bridging artifacts.

First, the bridging model presented here may be used as a quantitative diagnostic tool when used along with fits to other warranted models (Fig. S5). Bridging artifacts are usually apparent in the kinetic data returned by BLI instruments; bridging-encumbered systems often display sensograms in which the dissociation phase does not return to baseline (Fig. S6). This pathology, however, can be mistaken for a consequence of nonspecific binding or analyte rebinding to the BLI tip. The clearest indication that bridging is in fact occurring is in the biphasic shape of equilibrium binding curve, but as we have shown here, this biphasic shape can be easy to miss if data are not saturated (Fig. 1 B), and it can sometimes be mistaken for nonspecific binding or cooperativity (Fig. S5). Qualitative “curve shape” recognition of bridging is also difficult when the monovalent K_D is strong with respect to the bridging interactions (as in our cIAP1 case study; see Fig. 3), or when the artifactual interaction is the only one that can be feasibly detected (as in our A20 case study; see Fig. 4). However, in many cases, even a seemingly monophasic equilibrium titration can be fit to the bridging model presented here, and standard practices for evaluating goodness-of-fit (inspection of residuals, comparison of χ²-values) can help experimenters evaluate whether bridging is occurring. Unambiguous confirmation of the presence of bridging can then be obtained by conducting the binding experiment at different loading densities and assessing whether this change has any effect on the bridging model parameters, particularly n_b. A decrease in n_b as loading density is decreased is a strong indicator that the biphasic character of the equilibrium binding curve is due to bridging artifacts rather than biologically relevant nonequivalent binding sites.

If bridging is detected, it might then be possible to lower the surface saturation of the ligand to a point at which these artifacts are negligible. This level must be determined empirically for every system by performing equilibrium binding titrations at a range of different surface saturations and assessing the associated change in the fraction of bridging sites (n_b; as in Fig. 4 C) and K_D from a single-site (or other appropriate) model (as in Fig. 2 D; Fig. 3 C). If loading density can be reduced to a point past which these values plateau, bridging artifacts have likely been mitigated as much as is technically feasible for the system in question. Another indicator that bridging has been mitigated is the failure of the bridging model fit to return sensible values for bridging fraction; a negative n_b is a strong indicator that there is no detectable bridging. Fits to a single-site binding model (or other appropriate model) may then be used to evaluate data collected at this low-loading density. This method allows researchers to identify the highest-signal-to-noise assay conditions they may safely use to estimate binding affinity. We must stress that one should still treat affinities collected in this way as approximate because it is likely impossible to eliminate bridging entirely, but as demonstrated in our analyses here, these values may be sufficiently unencumbered by bridging to allow for relative affinities and thus specificities to be approximated.

If the above experimental methods for reducing bridging are not achievable, one might be able to make a very rough estimate of binding affinity using the bridging model to fit data collected at high-loading densities. The higher the ratio between K_Dm and K_Db, the more pronounced the biphasic shape of the curve will be, the more reliably the fit will converge, and the better the estimate of the true K_D is likely to be. In our experience, a difference of 1000-fold in K_Dm and K_Db, as well as a bridging fraction (n_b) near 0.5 are more likely to yield strong fits and more reliable K_Dm estimates. An example of such a case is the NEMO_UBAN-polyubiquitin-binding data collected here, for which the K_Dm and K_Db values differed by 1000-fold, and the value for K_Dm approached the solution K_D. Nevertheless, it is important to note that even in cases with dramatic differences between K_Dm- and K_Db-values, we do not believe the bridging model is precise enough to completely account for all possible artifactual contributions to the observed binding signal. This is particularly true in BLI data, where response values are sensitive to changes in both mass and conformational states of the ligand and/or analyte upon binding (i.e., density changes).

Finally, because the bridging model described here is completely naive to any sort of structural information and requires no knowledge of the distance between binding elements, it may be applied to any multivalent system as a diagnostic to detect bridging. It may also be used in cases for which the stoichiometry of binding is unknown, as the procedure of reducing loading density serves as an unambiguous quantitative diagnostic for bridging artifacts irrespective of the biological system. In this context, it is important to reiterate that because the bridging model is in effect an independent two-site model, it is not capable of distinguishing bridging from true independent two-site binding. Researchers should use their best judgment and appropriate controls to confirm that bridging is in fact occurring. In making this model more generally applicable, we have lost much of the precision we might otherwise have included, but we also avoid overfitting the data, and we gain a diagnostic method that is simple to apply to a wide variety of systems.

Author contributions

A.J.S. and E.C.D. designed the study and interpreted the results. A.J.S., E.H., and N.P. performed protein expression and purification. A.J.S., E.C.D., and E.H. performed BLI measurements. E.C.D. performed ITC experiments. A.J.S. and E.C.D. drafted the manuscript. All authors contributed to the final version.

Declaration of interests

E.C.D., E.H., and N.P. are employees of Genentech.

Editor: Hagen Hofmann.