Highlights
-
•
We determined how motion management strategies influence treatment margins.
-
•
A simple recipe was found to determine the margin when intrafraction motion is constrained.
-
•
For a continuous drift, the margin was well approximated by assuming the target is at ¾ of the drift.
-
•
Our analysis can be used to study the benefit of different motion management strategies.
Keywords: Intra-fraction motion, Treatment margins, Margin recipe, Motion management
Abstract
Background and purpose
Strategies to limit the impact of intra-fraction motion during treatment are common in radiotherapy. Margin recipes, however, are not designed to incorporate these strategies. This work aimed to provide a framework to determine how motion management strategies influence treatment margins.
Materials and methods
Two models of intra-fraction motion were considered. In model 1 motion was instantaneous, before treatment starts and in model 2 motion was a continuous drift during treatment. Motion management strategies were modelled by truncating the underlying error distribution at cσ, with σ the standard deviation of the distribution and c a free parameter. Using Monte Carlo simulations, we determined how motion management changed the required margin. The analysis was performed for different number of treatment fractions and different standard deviations of the underlying random and systematic errors.
Results
The required margin for a continuous drift was found to be well approximated by an average position of the target at ¾ of the drift. Introducing a truncation at cσ, the relative change in the margin was equal to 0.3c. This result held for both models, was independent of σ or the number of fractions and naturally generalizes to the situation with a residual (systematic) error.
Conclusion
Treatment margins can be determined when motion management strategies are applied. Moreover, our analysis can be used to study the potential benefit of different motion management strategies. This allows to discuss and determine the most appropriate strategy for margin reduction.
1. Introduction
Expanding the clinical target volume (CTV) to a planning target volume (PTV) to account for treatment uncertainties is a standard practice in radiotherapy [1]. To reduce margins and therefore reduce the irradiation of healthy tissue, improved image guidance, and adaptive radiotherapy have been developed, currently resulting in daily online adaptation using either magnetic resonance imaging or cone-beam computed-tomography guidance [2], [3], [4].
In an online adaptive workflow, essentially all preparation errors become daily execution errors. This includes random, systematic or periodic intra-fraction motion of the target and daily delineation uncertainty. Intra-fraction motion during treatment can still be substantial [5], [6], [7], [8]. Therefore, intervention strategies have been developed to limit too substantial movements, both for online adaptive as well as conventional radiotherapy. These interventions include gating, tracking and trailing, but also a manual approach where target motion is monitored and treatment is manually interrupted if the motion exceeds a certain threshold [9], [10], [11], [12], [13], [14].
Online motion management strategies aim to narrow the error distribution, thereby reducing the PTV margins. However, they can also change the underlying shape of the error distribution and thereby invalidate the assumptions of the common margin recipes. Moreover, there currently is no relation known between an intervention strategy and the resulting margin reduction. Published margins for online adaptive radiotherapy are determined using heuristic estimates, but lack an underlying framework to systematically assess the impact of motion management strategies [15], [16]. Therefore, an open question remains how to determine the margin upon introducing (online) motion management. The aim of the current work was to develop a margin recipe for this purpose.
2. Materials and methods
We studied two models for online motion management that captured the essentials of most motion patterns and motion management strategies. For both models, we determined how the required treatment margin changes due to the motion management strategy.
For clarity, we focused our analysis assuming no systematic error. However, we also showed how our results generalize to the case of a non-zero residual systematic error.
2.1. Model description
The well-known Van Herk recipe for CTV-PTV margins [17] assumes treatment uncertainties to be normally distributed and then studies the population histogram to ensure that 90 % of patients receive 95 % of the prescribed dose.
Our approach to calculate margins was similar to the Van Herk approach: we assumed a spherical target, with a homogeneous, spherical dose distribution, convolved with a Gaussian penumbra of width σp = 3.2 mm. We assumed systematic errors to be absent and random intra-fraction errors to be Gaussian distributed with width σ.1 We assumed an online intervention at a threshold c to change the error distribution to a truncated Gaussian, with width σ and truncation at ± cσ. (See supplement A). We considered a margin adequate when the minimal target dose is 95 % of the prescribed dose in 90 % of the population. Table C1 in the supplementary material provides an overview of the notation used.
With this approach, we considered two different models.
2.1.1. Model 1
We considered intra-fraction motion to be a discrete target displacement along a vector . Every fraction, was sampled from a (truncated) Gaussian distribution of width σ and truncation c. This can be interpreted as a random residual displacement after image guidance or plan adaptation, with no additional motion after the irradiation starts. The truncation can be interpreted as a threshold used as a check, just prior to irradiation, what residual displacement would still be acceptable. Such an approach is common practice in many image guidance workflows, with or without online adaptation.
2.1.2. Model 2
We considered intra-fraction motion to be a continuous target displacement linearly increasing with time to vector . Every fraction, was sampled from a (truncated) Gaussian distribution of width σ and truncation c. We assumed the full dose to be delivered at a constant rate during this movement and ignored interplay effects. This model is applicable for intra-fraction motion during irradiation. While the precise results will depend on the trajectory (we assumed a straight line) and speed (we assumed to be constant), these can be expected to be higher order corrections. The interpretation of the truncation in this case is a threshold used in intra-fraction motion monitoring.
We considered two variations in order to generalize our results to the situation of a non-homogeneous dose prescription and a non-zero residual systematic error. These variations were only considered for model 1, since the effect of the variations will be similar for both models.
2.1.3. Variation 1
We changed the prescription isodose to 80 % instead of 95 %. This made the dose distribution in the target more inhomogeneous. This is common practice in stereotactic body radiation therapy [18].
2.1.4. Variation 2
We considered the case where a residual systematic error was present. We considered this error to be a target displacement that was sampled once for every patient from a Gaussian distribution of width Σ.
2.2. Analytic approximations
We derived analytic approximations to supplement our analysis (see supplement B for details). The approximation followed the same approach as the van Herk margin recipe [17]. To take into account the finite number of fractions N, the error σ effectively results in a ‘random’ component σN and a ‘systematic’ component ΣN [19], [20], [21]:
| (1) |
| (2) |
To model the effect of the motion management, σ was replaced with the standard deviation of the truncated distribution: σC (see supplement A). Equivalent to equation (1) this resulted in σN,c. The margin mc was given by
| (3) |
The systematic factor αc was determined by equation (B.7) from supplement B, independent of N. αc = 2.5 when no truncation was present and changed to 2.4, 1.8 and 1.0 for c equals 3, 2 and 1, respectively. The random factor β followed from equation (B.6). β = 1.64 for a prescription of 95 % and β = 0.84 for a prescription of 80 %.
The random factor in equation (3) is only approximately correct for both a finite number of fractions and in the presence of truncation. The calculation of the random component assumed that the net effect of fractionation was a Gaussian blur, however this is not true for a finite number of fractions. Since the worst 10 % of cases are ignored in the van Herk margin recipe and σN and ΣN are correlated via equations (1), (2), the margin is determined by those patients with the smaller blur, causing equation (3) to give an under-estimation of the margin for this problem. The Gaussian blur is also incorrect in the presence of truncation since the Gaussian convolution of a truncated Gaussian is not anymore Gaussian, but more peaked. This resulted in a different functional form, causing equation (3) to give a slight over-estimation of the margin for this problem.
For model 2, we used the additional assumption that the effective displacement due to the movement changes σ to εσ, where ε is a free parameter we fitted using the Monte Carlo results. This correction applied via equations (1), (2) both to σN and ΣN.
2.3. Monte Carlo simulations
We used Monte Carlo simulations to determine the required margin. In all experiments we sampled a spherical surface of radius 30 mm with 300 points for 5000 patients. These values were chosen such that the simulation produced stable results. The random displacements used in the simulations were obtained from a 3D Gaussian random number generator (Numpy v1.19.2, Python v3.8.5). When truncated normal variables were needed, first, a large number of Gaussian distributed 3D vectors were sampled and those with a vector length above the desired truncation were discarded.
We assumed that the accumulated minimum dose to the target was always located at its surface. Therefore, to determine the minimum dose, dose only needed to be calculated in points distributed on a spherical surface. The points were sampled using a Fibonacci sphere algorithm to distribute them approximately evenly over the sphere.
We determined the margin using the following pseudo-code (for model 1).
Loop over margins, starting at 0 mm
For each patient:
For each fraction:
Sample a random displacement from the (truncated) distribution
Calculate the dose in all points on the sphere using the 3D Cartesian equivalent of Eq. A.11
Sum all fractions
Determine the minimum dose
Determine the number of patients for which the minimum dose is > 95 %
If the relative number of patients is > 90 %:
The used margin is the required margin
Else:
Increase the margin with 0.1 mm and repeat.
For model 2, we additionally divided each fraction in 10 timepoints over which the target moves linearly.
2.4. Experiments
We performed the following experiments, for both models.
-
1.
Using the Monte Carlo code, we determined the margin required for a range of parameter values. σ = {1, 2.5, 5, 7.5} mm; N = {1, 2, …, 20}; c = {1, 2, 3, inf}. We also determined the accuracy of the analytic approximation from equation (3). For model 2 we determined parameter ε by minimizing the relative distance between equation (3) and the Monte Carlo results for σ = {1, 2.5, 5} mm, N = {1,3,5,20} and no truncation (c = inf).
-
2.
We determined a margin recipe for the relative change of the margin as a function of the truncation c, for the different values of σ and N. We considered a linear fit mc / m = ω c and determined ω for the fit of σ = {1, 2.5, 5} mm, N = {1,3,5,20}.
In the presence of a systematic error Σ (variation 2), the margin m0 required for c = 0 was 2.5Σ. The fit used was the equivalent of the linear fit without systematic errors:
| (4) |
3. Results
3.1. Determination of required margins
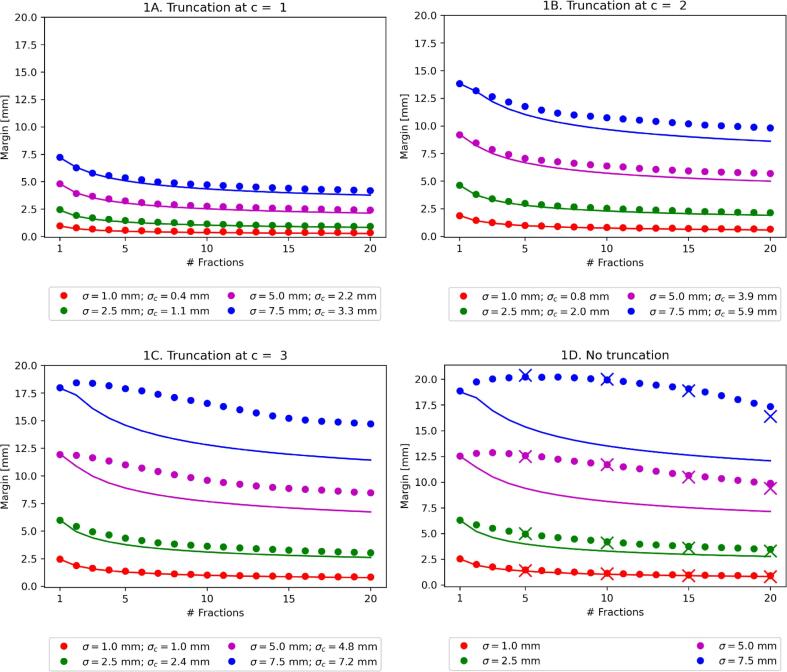
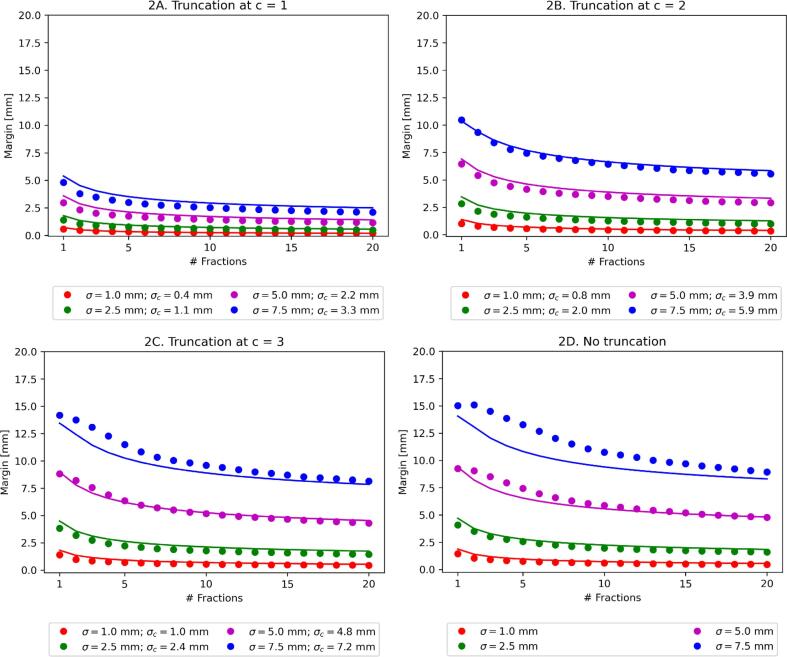
The disagreement between the analytic and Monte Carlo results decreased for model 1 with decreasing c from < 5.3 mm without truncation to < 0.4 mm with c = 1 for the parameters studied (Fig. 1; Tables 1 (accuracy of approximation) and C2 (full numerical results)). This effect was considerably less pronounced for model 2, where the results where < 2.5 mm and < 0.6 mm respectively (Fig. 2; Tables 1 and C3).
Fig. 1.
Margin required for different values of standard deviation σ, truncation parameter c and number of fractions N for model 1 (discrete displacement). Dots show the Monte Carlo simulation result and the solid line shows the analytic approximation given by the van Herk margin formula, corrected for finite fractions and truncation (equation (3)). σc is the standard deviation of the truncated distribution (given by equation A7). Crosses in Fig. 1D are the Monte Carlo results from [19] for reference.
Table 1.
Monte Carlo (MC) and analytic results of the required margin for different values of the standard deviation σ, the number of fractions N, and the truncation parameter c. Results are shown for model 1 (discrete displacement) and model 2 (continuous movement).
|
MC result (mm) |
analytic model (mm) |
absolute difference (mm) |
relative difference |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| model 1 | σ (mm) | N = 1 | N = 3 | N = 5 | N = 20 | N = 1 | N = 3 | N = 5 | N = 20 | N = 1 | N = 3 | N = 5 | N = 20 | N = 1 | N = 3 | N = 5 | N = 20 |
| c = 1 | 1 | 1.0 | 0.7 | 0.6 | 0.4 | 1.0 | 0.6 | 0.5 | 0.3 | 0.0 | 0.1 | 0.1 | 0.1 | 0.02 | 0.15 | 0.18 | 0.24 |
| 2.5 | 2.4 | 1.7 | 1.5 | 0.9 | 2.4 | 1.6 | 1.3 | 0.8 | 0.0 | 0.1 | 0.1 | 0.1 | 0.02 | 0.07 | 0.10 | 0.11 | |
| 5 | 4.8 | 3.7 | 3.2 | 2.4 | 4.8 | 3.5 | 3.0 | 2.1 | 0.0 | 0.1 | 0.2 | 0.3 | 0.00 | 0.04 | 0.06 | 0.12 | |
| 7.5 | 7.2 | 5.8 | 5.3 | 4.2 | 7.2 | 5.7 | 5.1 | 3.8 | 0.0 | 0.0 | 0.3 | 0.4 | 0.00 | 0.01 | 0.05 | 0.10 | |
| c = 2 | 1 | 1.9 | 1.2 | 1.0 | 0.7 | 1.9 | 1.2 | 1.0 | 0.6 | 0.0 | 0.0 | 0.0 | 0.1 | −0.01 | 0.03 | 0.01 | 0.13 |
| 2.5 | 4.7 | 3.4 | 3.0 | 2.1 | 4.6 | 3.3 | 2.8 | 1.9 | 0.0 | 0.1 | 0.2 | 0.2 | 0.01 | 0.04 | 0.06 | 0.10 | |
| 5 | 9.2 | 7.9 | 7.1 | 5.7 | 9.2 | 7.5 | 6.7 | 5.0 | 0.0 | 0.4 | 0.4 | 0.7 | 0.00 | 0.05 | 0.06 | 0.12 | |
| 7.5 | 13.8 | 12.7 | 11.8 | 9.8 | 13.8 | 12.2 | 11.0 | 8.6 | 0.0 | 0.5 | 0.7 | 1.2 | 0.00 | 0.04 | 0.06 | 0.12 | |
| c = 3 | 1 | 2.5 | 1.6 | 1.4 | 0.8 | 2.4 | 1.6 | 1.3 | 0.8 | 0.0 | 0.1 | 0.1 | 0.1 | 0.00 | 0.04 | 0.06 | 0.08 |
| 2.5 | 5.9 | 5.0 | 4.4 | 3.0 | 6.0 | 4.4 | 3.8 | 2.6 | −0.1 | 0.6 | 0.6 | 0.4 | −0.01 | 0.12 | 0.14 | 0.14 | |
| 5 | 12.0 | 11.6 | 11.0 | 8.5 | 12.0 | 10.0 | 8.9 | 6.7 | 0.0 | 1.7 | 2.1 | 1.7 | 0.00 | 0.14 | 0.19 | 0.20 | |
| 7.5 | 18.0 | 18.3 | 17.8 | 14.7 | 18.0 | 16.1 | 14.6 | 11.4 | 0.0 | 2.2 | 3.3 | 3.3 | 0.00 | 0.12 | 0.18 | 0.22 | |
| no truncation | 1 | 2.6 | 1.8 | 1.5 | 0.9 | 2.5 | 1.6 | 1.3 | 0.8 | 0.0 | 0.1 | 0.1 | 0.1 | 0.01 | 0.08 | 0.09 | 0.09 |
| 2.5 | 6.3 | 5.5 | 5.0 | 3.5 | 6.3 | 4.6 | 4.0 | 2.8 | 0.0 | 0.9 | 1.0 | 0.7 | −0.01 | 0.16 | 0.20 | 0.21 | |
| 5 | 12.6 | 12.9 | 12.7 | 9.8 | 12.5 | 10.5 | 9.4 | 7.1 | 0.1 | 2.4 | 3.3 | 2.7 | 0.01 | 0.18 | 0.26 | 0.27 | |
| 7.5 | 18.7 | 20.3 | 20.3 | 17.3 | 18.8 | 16.9 | 15.4 | 12.1 | −0.1 | 3.3 | 4.9 | 5.3 | −0.01 | 0.16 | 0.24 | 0.30 | |
| model 2 | |||||||||||||||||
| c = 1 | 1 | 0.6 | 0.4 | 0.3 | 0.2 | 0.7 | 0.4 | 0.3 | 0.2 | −0.1 | 0.0 | 0.0 | 0.0 | −0.21 | −0.08 | −0.04 | 0.03 |
| 2.5 | 1.4 | 0.9 | 0.8 | 0.5 | 1.8 | 1.1 | 0.9 | 0.6 | −0.4 | −0.2 | −0.2 | −0.1 | −0.28 | −0.27 | −0.22 | −0.13 | |
| 5 | 3.0 | 2.0 | 1.8 | 1.2 | 3.6 | 2.5 | 2.1 | 1.4 | −0.6 | −0.5 | −0.4 | −0.3 | −0.21 | −0.25 | −0.21 | −0.23 | |
| 7.5 | 4.8 | 3.5 | 3.0 | 2.1 | 5.4 | 4.0 | 3.5 | 2.5 | −0.6 | −0.6 | −0.5 | −0.4 | −0.12 | −0.16 | −0.18 | −0.19 | |
| c = 2 | 1 | 1.0 | 0.7 | 0.6 | 0.4 | 1.4 | 0.9 | 0.7 | 0.4 | −0.4 | −0.2 | −0.1 | 0.0 | −0.39 | −0.27 | −0.22 | −0.12 |
| 2.5 | 2.8 | 1.9 | 1.6 | 1.0 | 3.5 | 2.3 | 2.0 | 1.3 | −0.6 | −0.5 | −0.4 | −0.3 | −0.22 | −0.26 | −0.23 | −0.29 | |
| 5 | 6.5 | 4.7 | 4.2 | 2.9 | 6.9 | 5.3 | 4.6 | 3.3 | −0.5 | −0.6 | −0.5 | −0.4 | −0.07 | −0.12 | −0.11 | −0.14 | |
| 7.5 | 10.5 | 8.4 | 7.4 | 5.6 | 10.4 | 8.6 | 7.7 | 5.8 | 0.1 | −0.2 | −0.3 | −0.3 | 0.01 | −0.03 | −0.03 | −0.05 | |
| c = 3 | 1 | 1.4 | 0.8 | 0.7 | 0.4 | 1.8 | 1.1 | 0.9 | 0.5 | −0.4 | −0.3 | −0.2 | −0.1 | −0.30 | −0.35 | −0.30 | −0.19 |
| 2.5 | 3.8 | 2.7 | 2.2 | 1.5 | 4.5 | 3.1 | 2.6 | 1.7 | −0.7 | −0.4 | −0.4 | −0.3 | −0.17 | −0.14 | −0.18 | −0.20 | |
| 5 | 8.8 | 7.6 | 6.4 | 4.3 | 9.0 | 7.1 | 6.2 | 4.5 | −0.2 | 0.5 | 0.2 | −0.2 | −0.02 | 0.07 | 0.02 | −0.06 | |
| 7.5 | 14.2 | 13.1 | 11.5 | 8.1 | 13.5 | 11.4 | 10.3 | 7.8 | 0.7 | 1.6 | 1.2 | 0.3 | 0.05 | 0.13 | 0.11 | 0.04 | |
| no truncation | 1 | 1.4 | 0.9 | 0.8 | 0.5 | 1.9 | 1.2 | 1.0 | 0.6 | −0.4 | −0.3 | −0.2 | −0.1 | −0.30 | −0.31 | −0.26 | −0.18 |
| 2.5 | 4.1 | 3.0 | 2.6 | 1.6 | 4.7 | 3.3 | 2.8 | 1.8 | −0.6 | −0.3 | −0.2 | −0.2 | −0.15 | −0.09 | −0.09 | −0.16 | |
| 5 | 9.3 | 8.5 | 7.5 | 4.8 | 9.4 | 7.4 | 6.6 | 4.8 | −0.1 | 1.1 | 0.9 | 0.0 | −0.01 | 0.13 | 0.12 | 0.00 | |
| 7.5 | 15.0 | 14.5 | 13.3 | 9.0 | 14.1 | 12.1 | 10.8 | 8.3 | 1.0 | 2.4 | 2.5 | 0.6 | 0.06 | 0.17 | 0.19 | 0.07 | |
Fig. 2.
Margin required for different values of standard deviation σ, truncation parameter c and number of fractions N for model 2 (continuous movement). Dots show the Monte Carlo simulation result and the solid line shows the analytic approximation given by the van Herk margin formula, corrected for finite fractions and truncation (equation (3)), using σ → 0.75 σ. σc is the standard deviation of the truncated distribution (given by equation A7).
For model 2, the parameter ε, determining the effective change in σ due to the continuous motion, was fitted to be ε = 0.75.
When prescribing on the 80 % isodose, the smaller value of β in equation (3) resulted in a relatively smaller margin when N increases (Fig. D1).
3.2. Relative change of the margin in the presence of truncation
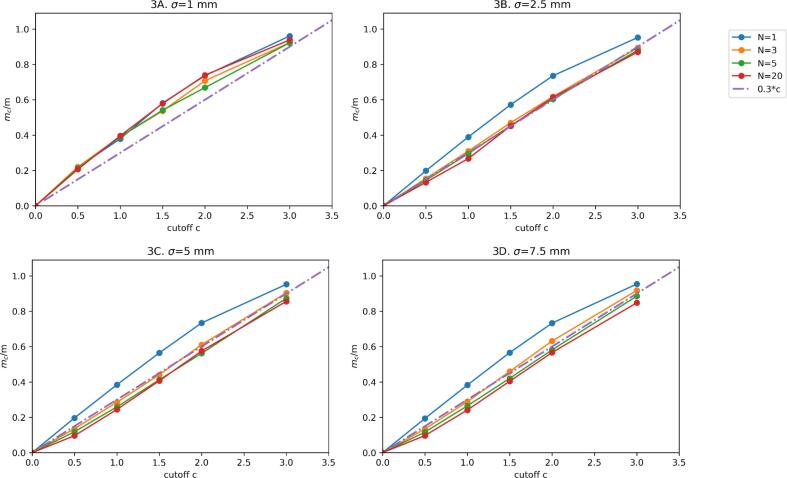
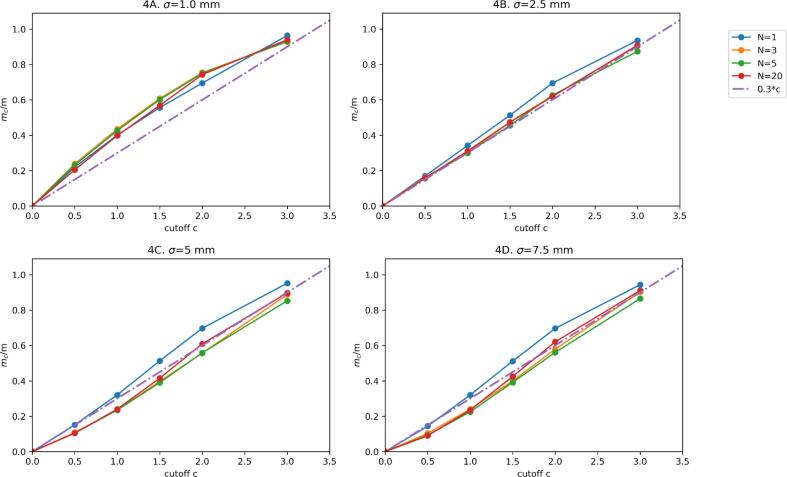
The ratio mc/m was approximately linear in c in the regime of interest, justifying the fit mc / m = ω c. The fit for ω resulted for model 1 in an average value of 0.32 (range: 0.28–0.35; Fig. 3) and for model 2 in 0.31 (range 0.28–0.35; Fig. 4), which we approximated for simplicity with ω = 0.3 for both models.
Fig. 3.
Margin relative to the original (no truncation) margin (mc / m) for different values of the standard deviation σ and number of fractions N as a function of the truncation parameter c for model 1 (discrete displacement). Dots are the Monte Carlo result and the solid lines are a linear interpolation. The dash-dotted line is the linear relation with mc / m = 0.3c.
Fig. 4.
Margin relative to the original (no truncation) margin (mc / m) for different values of the standard deviation σ and number of fractions N as a function of the truncation parameter c for model 2 (continuous movement). Dots are the Monte Carlo result and the solid lines are a linear interpolation. The dash-dotted line is the linear relation with mc / m = 0.3c.
The upper quartile error of this fit for mc / m, evaluated over the range c = {0,3}, was ≤ 0.12 and ≤ 0.15 for model 1 and model 2 respectively (Table 2). The upper quartile error for mc was ≤ 0.10 mm and ≤ 0.04 mm for model 1 and model 2 respectively (Table C4).
Table 2.
Difference in the margin relative to the original (no cut-off) margin (mc / m) between the Monte Carlo calculation and linear fit mc / m = 0.3c, for different values of the standard deviation σ and number of fractions N. The difference is calculated over the range of the truncation parameter c = {0…3} and the reported values are the median (lower quartile; upper quartile).
| Model 1 | σ (mm) | N = 1 | N = 3 | N = 5 | N = 20 |
|---|---|---|---|---|---|
| 1 | 0.09 (0.07; 0.12) | 0.08 (0.06; 0.09) | 0.07 (0.04; 0.08) | 0.09 (0.06; 0.12) | |
| 2,5 | 0.09 (0.06; 0.12) | 0.01 (0.00; 0.02) | −0.00 (-0.01; 0.00) | −0.01 (-0.02; 0.00) | |
| 5 | 0.09 (0.06; 0.11) | −0.00 (-0.01; 0.01) | −0.04 (-0.04; −0.03) | −0.04 (-0.05; −0.03) | |
| 7,5 | 0.09 (0.06; 0.11) | 0.01 (-0.01; 0.02) | −0.02 (-0.03; −0.02) | −0.05 (-0.05; −0.04) | |
| Model 2 | |||||
| 1 | 0.09 (0.07; 0.10) | 0.12 (0.07; 0.15) | 0.11 (0.07; 0.14) | 0.10 (0.06; 0.12) | |
| 2,5 | 0.05 (0.03; 0.07) | 0.01 (0.01; 0.02) | 0.00 (0.00; 0.01) | 0.01 (0.01; 0.02) | |
| 5 | 0.06 (0.01; 0.08) | −0.04 (-0.05; −0.03) | −0.05 (-0.06; −0.04) | −0.02 (-0.05; 0.00) | |
| 7,5 | 0.05 (0.01; 0.07) | −0.03 (-0.05; −0.01) | −0.04 (-0.06; −0.04) | −0.02 (-0.05; 0.01) | |
mc /m was approximately independent from σ and N (for N large enough), which is evident from the graphs. In the supplement (sections B.3.1 and B.3.2) we provide a heuristic argument for this.
The results for using the 80 % isodose prescription were equivalent and are provided in the supplementary material (Fig. D2).
When a residual systematic error was introduced of Σ = 3 mm,. the linear fit (equation (4)) again resulted in ω = 0.3 (Fig. D3).
4. Discussion
In this work, we analyzed the margins required for intra-fraction motion in the presence of online interventions. Our main finding was that the relative change in the margin was accurately described by a simple linear relation, mc/m = 0.3c, independent of the standard deviation and number of fractions (for N > 1). This relation held for both models of intra-fraction motion we studied. To appreciate this finding, consider a treatment given in 5 fractions, with intra-fraction motion characterized by σ = 5 mm. In this case, a margin of 12.7 mm is required. If motion management is introduced, such that all movement is limited to be < 10 mm (c = 2), the new margin is easily determined to be 7.6 mm.
While the linear fit for mc/m showed discrepancies of up to 0.15 for σ = 1 mm, the margin m in this case was only 2–3 mm and these errors were thus < 1 mm. Therefore, we believe our results ensure sufficient coverage (with the same caveats as the Van Herk recipe). The exception was for N = 1 and relatively large σ. In that case the error could be up to 2 mm for the parameters studied.
We found that the effective standard deviation for intra-fraction motion in the case of a constant drift was ¾ of the standard deviation of the full displacement. In practice, intra-fraction motion is often determined by calculating the standard deviation of the displacement between a pre-treatment and post-treatment scan. As input for the margin either the full displacement (as a worst case scenario) or half of the displacement (assuming this is the average position) can be used [22]. It has been argued [23] that an appropriate margin could be to leave the random factor as is but only change the systematic component. However, the kernel of the random blur of a continuous motion is effectively more peaked at zero, since the motion always starts at zero. Therefore it is natural to change both components and our results indicated that simply evaluating σ at ¾ of the full displacement resulted in accurate results.
Changes to the van Herk margin recipe for a finite number of fractions have been studied before by Gordon et al. [21] and by Herschtal et al. [20]. We plotted the Monte Carlo results from Gordon et al. in Fig. 1D, showing our Monte Carlo results were identical. For model 1 (Fig. 1), the analytic approximation was exact for N = 1. In this case all errors were effectively systematic and their contribution to the margin via equation (3) could be calculated exactly for all values of c (using equations (A.4) and (B.7) from the supplementary material). For larger values of N, the analytic approximation in the case of no truncation showed errors of < 5.3 mm for model 1 for the parameters studied. The lack of correspondence is known and substantial improvements are feasible [20], [21]. However, we found that the simple analytic approximation given by equations (1)-(3) already substantially improved in cases where the underlying distribution is truncated and/or the underlying motion was continuous. Both conditions are in practice often fulfilled and therefore our analysis considerably broadens the applicability of these approximations.
The improvement in the analytic approximation due to truncation decreased the error to < 3.3 mm, <1.2 mm and < 0.4 mm for c equals 3, 2 and 1 respectively for model 1. This improvement was not solely due to the fact that σc < σ, as could be seen from the values of σc provided in the figures. For example, the approximation for c = 2 with σ = 7.5 mm (σc = 5.9 mm) was considerably better compared to σ = 5 mm without truncation. The underlying reason for this was probably that the analytic approximation used the fully convolved dose distribution to reach a closed form result. With a finite number of fractions, the probability that this was a reasonable assumption increases when there are less outliers in the underlying distribution, i.e. in the presence of truncation. The analytic approximation when considering continuous motion (model 2) was considerably better compared to model 1 (see Fig. 1, Fig. 2). The likely reason here was that the motion provides an additional blur and therefore improved the approximation of the fully convolved dose distribution.
The two models we considered are an approximation of actual intra-fraction motion. A limitation of the interpretation of model 2 is that the model assumed all dose to be delivered during a constant drift. In practice, however, if one interrupts the treatment, the remaining dose still needs to be delivered after correction. This causes the required margins to be smaller compared to our results, since the effective distribution will be more peaked around zero (with the exception of the case where the interruption is exactly halfway; then the result will be identical).
Another limitation in our models is the assumption that intra-fraction motion is random and isotropic since intra-fraction motion can have a preferred direction. For example liver lesions drift primarily dorsal during treatment [24]. In these situations, the margins required will be larger compared to our results. However, since our result for finite N also included a systematic component ΣN and the dependency of mc/m was independent of N, a systematic component in the drift does not change the simple linear dependency of the relative margin on c.
In summary, in this work we analyzed how treatment margins are to be adapted when motion management strategies are applied and found a simple linear relation mc/m = 0.3c to be sufficient. Based on the results, treatment margins can be determined when motion management strategies are applied. Moreover, our analysis can be used to study the potential benefit of different motion management strategies for different treatment sites. This allows to discuss and determine the most appropriate strategy for margin reduction.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
An argument for this assumption is the applicability of the central limit theorem.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.phro.2022.11.008.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Grégoire V., Mackie T., De Neve W., Gospodarowicz M., Purdy J.A., van Herk M., et al. ICRU Report 83. J ICRU. 2010;10:1–106. [Google Scholar]
- 2.Winkel D., Bol G.H., Kroon P.S., van Asselen B., Hackett S.S., Werensteijn-Honingh A.M., et al. Adaptive radiotherapy: The Elekta Unity MR-linac concept. Clin Transl Radiat Oncol. 2019;18:54–59. doi: 10.1016/j.ctro.2019.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Acharya S., Fischer-Valuck B.W., Kashani R., Parikh P., Yang D., Zhao T., et al. Online Magnetic Resonance Image Guided Adaptive Radiation Therapy: First Clinical Applications. Int J Radiat Oncol Biol Phys. 2016;94:394–403. doi: 10.1016/j.ijrobp.2015.10.015. [DOI] [PubMed] [Google Scholar]
- 4.Sibolt P., Andersson L.M., Calmels L., Sjöström D., Bjelkengren U., Geertsen P., et al. Clinical implementation of artificial intelligence-driven cone-beam computed tomography-guided online adaptive radiotherapy in the pelvic region. Phys Imaging Radiat Oncol. 2021;17:1–7. doi: 10.1016/j.phro.2020.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Intven MPW, de Mol van Otterloo SR, Mook S, Doornaert PAH, de Groot-van Breugel EN, Sikkes GG, et al. Online adaptive MR-guided radiotherapy for rectal cancer; feasibility of the workflow on a 1.5T MR-linac: clinical implementation and initial experience. Radiother Oncol 2021;154:172–8. https://doi.org/10.1016/j.radonc.2020.09.024. [DOI] [PubMed]
- 6.Foroudi F., Pham D., Bressel M., Gill S., Kron T. Intrafraction bladder motion in radiation therapy estimated from pretreatment and posttreatment volumetric imaging. Int J Radiat Oncol Biol Phys. 2013;86:77–82. doi: 10.1016/j.ijrobp.2012.11.035. [DOI] [PubMed] [Google Scholar]
- 7.van de Lindt T., Janssen T., Witte M., van Pelt V., Betgen A., Nowee M., et al. PO-1575 Evaluation of accumulated dose with residual uncertainties: an example with 4D-MRI guided liver SBRT. Radiother Oncol. 2021;161:S1300–S1301. doi: 10.1016/s0167-8140(21)08026-9. [DOI] [Google Scholar]
- 8.Pang E.P.P., Knight K., Fan Q., Tan S.X.F., Ang K.W., Master Z., et al. Analysis of intra-fraction prostate motion and derivation of duration-dependent margins for radiotherapy using real-time 4D ultrasound. Phys Imaging Radiat Oncol. 2018;5:102–107. doi: 10.1016/j.phro.2018.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bertholet J., Knopf A., Eiben B., McClelland J., Grimwood A., Harris E., et al. Real-time intrafraction motion monitoring in external beam radiotherapy. Phys Med Biol. 2019;64 doi: 10.1088/1361-6560/ab2ba8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Shirato H., Shimizu S., Kunieda T., Kitamura K., Van Herk M., Kagei K., et al. Physical aspects of a real-time tumor-tracking system for gated radiotherapy. Int J Radiat Oncol Biol Phys. 2000;48:1187–1195. doi: 10.1016/S0360-3016(00)00748-3. [DOI] [PubMed] [Google Scholar]
- 11.D’Souza W.D., Naqvi S.A., Yu C.X. Real-time intra-fraction-motion tracking using the treatment couch: A feasibility study. Phys Med Biol. 2005;50:4021–4033. doi: 10.1088/0031-9155/50/17/007. [DOI] [PubMed] [Google Scholar]
- 12.Wilbert J., Meyer J., Baier K., Guckenberger M., Herrmann C., Heß R., et al. Tumor tracking and motion compensation with an adaptive tumor tracking system (ATTS): System description and prototype testing. Med Phys. 2008;35:3911–3921. doi: 10.1118/1.2964090. [DOI] [PubMed] [Google Scholar]
- 13.Fast M., van de Schoot A., van de Lindt T., Carbaat C., van der Heide U., Sonke J.J. Tumor Trailing for Liver SBRT on the MR-Linac. Int J Radiat Oncol Biol Phys. 2019;103:468–478. doi: 10.1016/j.ijrobp.2018.09.011. [DOI] [PubMed] [Google Scholar]
- 14.Poels K., Dhont J., Verellen D., Blanck O., Ernst F., Vandemeulebroucke J., et al. A comparison of two clinical correlation models used for real-time tumor tracking of semi-periodic motion: A focus on geometrical accuracy in lung and liver cancer patients. Radiother Oncol. 2015;115:419–424. doi: 10.1016/j.radonc.2015.05.004. [DOI] [PubMed] [Google Scholar]
- 15.Ahmad R., Bondar L., Voet P., Mens J.W., Quint S., Dhawtal G., et al. A margin-of-the-day online adaptive intensity-modulated radiotherapy strategy for cervical cancer provides superior treatment accuracy compared to clinically recommended margins: A dosimetric evaluation. Acta Oncol. 2013;52:1430–1436. doi: 10.3109/0284186X.2013.813640. [DOI] [PubMed] [Google Scholar]
- 16.Ray X., Moazzezi M., Bojechko C., Moore K.L. Data-Driven Margin Determination for Online Adaptive Radiotherapy Using Batch Automated Planning. Int J Radiat Oncol Biol Phys. 2020;108:e370. [Google Scholar]
- 17.Van Herk M., Remeijer P., Rasch C., Lebesque J.V. The probability of correct target dosage: Dose-population histograms for deriving treatment margins in radiotherapy. Int J Radiat Oncol Biol Phys. 2000;47:1121–1135. doi: 10.1016/S0360-3016(00)00518-6. [DOI] [PubMed] [Google Scholar]
- 18.Peulen H., Belderbos J., Rossi M., Sonke J.J. Mid-ventilation based PTV margins in Stereotactic Body Radiotherapy (SBRT): A clinical evaluation. Radiother Oncol. 2014;110:511–516. doi: 10.1016/j.radonc.2014.01.010. [DOI] [PubMed] [Google Scholar]
- 19.De Boer H.C.J., Heijmen B.J.M. A protocol for the reduction of systematic patient setup errors with minimal portal imaging workload. Int J Radiat Oncol Biol Phys. 2001;50:1350–1365. doi: 10.1016/S0360-3016(01)01624-8. [DOI] [PubMed] [Google Scholar]
- 20.Herschtal A., Foroudi F., Silva L., Gill S., Kron T. Calculating geometrical margins for hypofractionated radiotherapy. Phys Med Biol. 2013;58:319–333. doi: 10.1088/0031-9155/58/2/319. [DOI] [PubMed] [Google Scholar]
- 21.Gordon J.J., Siebers J.V. Convolution method and CTV-to-PTV margins for finite fractions and small systematic errors. Phys Med Biol. 2007;52:1967–1990. doi: 10.1088/0031-9155/52/7/013. [DOI] [PubMed] [Google Scholar]
- 22.Winkel D., Bol G.H., Werensteijn-Honingh A.M., Intven M.P.W., Eppinga W.S.C., Hes J., et al. Target coverage and dose criteria based evaluation of the first clinical 1.5T MR-linac SBRT treatments of lymph node oligometastases compared with conventional CBCT-linac treatment. Radiother Oncol. 2020;146:118–125. doi: 10.1016/j.radonc.2020.02.011. [DOI] [PubMed] [Google Scholar]
- 23.Nijkamp J., Swellengrebel M., Hollmann B., De Jong R., Marijnen C., Van Vliet-Vroegindeweij C., et al. Repeat CT assessed CTV variation and PTV margins for short- and long-course pre-operative RT of rectal cancer. Radiother Oncol. 2012;102:399–405. doi: 10.1016/j.radonc.2011.11.011. [DOI] [PubMed] [Google Scholar]
- 24.van de Lindt T.N., Nowee M.E., Janssen T., van Pelt V., Jansen E.P.M., Schneider C., et al. Evaluation of 4D-MRI Guided Liver SBRT on the MR-Linac. Int J Radiat Oncol Biol Phys. 2020;108:S66. doi: 10.1016/j.ijrobp.2020.07.2201. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.