Kin networks and opportunities for reproductive cooperation and conflict among hunter–gatherers

Abstract

Little is known about the potential for reproductive conflict among hunter–gatherer populations, who are characterized by bilateral kinship ties, flexible residential mobility, and high offspring mortality. To assess the potential for reproductive conflict, we use longitudinal residence and reproductive history data for two bands of South American foragers. Using multilevel logistic regressions (N = 44 women, N = 712 person years), we examine how yearly measures of (i) camp composition, (ii) distribution of female kin and (iii) a woman's position in a female kinship network impact the likelihood of giving birth or experiencing a child's death. We compare conflict models to a demographic model that accounts for the proportion of women giving birth in a given year. Contrary to conflict models, results show that the odds of giving birth increase with the presence of highly related women. However, the odds of experiencing an offspring death are insensitive to the presence of coresident women. Network measures of closeness and centrality in the female kin network also show no significant effect on reproductive outcomes. Furthermore, chances of both births and deaths increase in years when proportionally more women are giving birth. We argue that demographic stochasticity relating to ecological conditions best predicts reproductive outcomes for women.

This article is part of the theme issue ‘Cooperation among women: evolutionary and cross-cultural perspectives’.

1. Introduction: cooperative breeding and the potential for reproductive conflict

Humans are cooperative breeders. Women in hunter–gatherer populations often acquire less food than they themselves need, suggesting an interdependence on others [1–3]. Parents, grandparents, siblings, and older offspring provide significant transfers of food and resources [4–6], with couples rearing children receiving a significant portion of those resources [2]. This cooperation facilitates women having short birth intervals and supporting multiple dependent offspring, a life-history feature unique among great apes [7,8]. A key component of cooperative breeding in humans is that non-breeders (pre- and post-reproductive individuals) play a significant role in providing allocare and resource transfers [5,9].

Despite help from non-breeders, reproductive conflict is also an important dynamic among women. The human pattern of cooperative breeding, with pooled energy budgets [10–12] means that reproducing women may often rely on the same pool of helpers and resources for energetic subsidies and allocare, and that mothers may compete for access to these helpers and resources [13,14]. Indeed, reproductive competition is often being touted as the primary motivation for cooperative breeding [15]. Additionally, cooperative breeding among humans may result in a trade-offs between direct fitness and inclusive fitness payoffs. Rather than engage in competition, women may curtail their own reproduction in order to invest in their close genetic relatives, including younger siblings or their siblings offspring. In such cases, a preference for inclusive fitness benefits may lower direct fitness outcomes with little or no competition between reproducing women.

Competition for helpers and resources can occur within generations among coresident women of similar ages, either related women, co-wives, in-laws or unrelated women. Alternatively, reproductive competition may also occur across generations if there is overlap between mothers' and daughters' reproductive lifespans. In the case of overlap, both a woman and her daughter may have dependent offspring that require subsidies from the same group of kin. Theoretically, this intergenerational conflict has been employed to explain the evolution of key features of the human life history, including menopause [16,17], female dispersal and reproductive scheduling [18].

For humans, the potential for reproductive conflict is expected to vary across socio-ecological contexts, as these shape the pool of helpers and competitors. In contexts where women do not live with natal kin, such as when women disperse at marriage to live with in-laws, competition for reproductive resources may take place among unrelated women, particularly co-wives who have married into a patriline. Indeed, a number of empirical case studies have documented competition between unrelated women in patrilocal populations. One study among the agricultural Dogon of Mali found that greater numbers of co-resident women living in polygynous households and work–eat groups (economic units that pool labour and agricultural resources) contributed to increased child mortality and lower nutritional status among children [19]. Here, the conflict was observed between coresident wives in polygynous marriages, unrelated women in work–eat groups as well as among unrelated women in extended patrilineal families. Interestingly, further work among the Dogon documented effects of competition among relatives, including both within and between generations [20,21].

Another study among pastoralists in Gambia showed similar results; the chances of giving birth for young women declined when more coresident wives lived in the familial compound [22]. However, in this case, mother–daughter dynamics appeared to be the opposite, where reproductive overlap was associated with a reduction in the mother's completed fertility rather than the daughter's. Furthermore, the cost of reproductive overlap to the mother held after controlling for daughter's dispersing at marriage. While reproductive conflict appears to carry a cost, in the same population older women (grandmothers and mother-in-laws) were found to have a positive impact on young women's reproduction [23,24].

Finally, reproductive conflict also has been documented in historical agricultural populations Data from historical Finnish parish records show that the risk of offspring mortality increased by 23% when unrelated coresident women reproduced within 2 years of each other [25]. Follow-up analysis found no evidence that women adopted behaviours, like scheduling births, to avoid the risk of offspring mortality [18].

In these case studies, marriages are characterized as patrilocal and, in some cases, polygynous, where women leave their natal households at marriage and may compete with unrelated co-wives or their husband's kin. In socio-ecological contexts where matrilineal kinship largely structures the flow of resources available to women, and if there is a constraint on sufficient resources to raise children, co-resident female kin would likely be the source of competition. Among the matrilineal Mosuo of China, more reproductive women in a matrilineal household was associated with fewer surviving offspring, which appeared to affect younger women more than older women [14]. An interesting component of this study was the finding that competition between cousins (mother's sister's daughters) can have a stronger negative effect than between sisters.

Theoretical arguments for the importance of reproductive conflict in human evolution have emphasized socio-ecological contexts, with a focus on female dispersal, and the associated consequences of genetic relatedness to the residential group [16,22,26–28]. Current life-history models that incorporate reproductive conflict argue that female dispersal has a deep evolutionary history in humans, which reduces direct conflict among related women. However, there is little supporting evidence for female dispersal as a universal human pattern throughout our history. The ethnographic record shows hunter–gatherer populations having extensive bilateral kin networks and are best characterized by flexible residential mobility [27,29–32]. Under such contexts, reproducing women have both an extended allocare network and the ability to flexibly relocate in ways that may dampen the potential for conflict with other reproducing women. Here, we explore whether the flexible residential mobility and bilateral kin access that characterize mobile hunter–gatherers [29,31,33], are strategies to avoid reproductive conflict.

(a) . Misconceptions about relatedness, dispersal and reproductive conflict among hunter–gatherers

Assumptions about the antiquity and prevalence of patrilocality have informed arguments about relatedness among women in hunter–gatherers. Building upon the assumption of patrilocality, female-biased dispersal is argued to be the primary means women reduce reproductive conflict across generations, which played a pivotal role in the evolution of menopause in humans and other species [16,17,22]. Alternatively, others have suggested that female dispersers forego the benefits of proximity to related women to take advantage of resources controlled by males [15]. That is, women disperse in order to improve access to resources needed for reproduction rather than avoid costly conflict with their mothers. Either way, female dispersal changes the potential pool of both helpers and competitors available to women. Dispersal may lower competition among relatives, but may end up increasing opportunities for conflict among unrelated women.

More importantly, the assumptions of the predominance of patrilocality in hunter–gatherer populations have long been disputed and are not supported empirically [32,34–37]. Demographic studies of hunter–gatherer societies show that groups have a mix of both kin and non-kin [27,31,38], and that band membership is facultative and flexible, changing daily, seasonally, annually and across a woman's reproductive career. Indeed, the phylogenetic depth of arranged marriages and reciprocal exchanges across lineages suggests that bilateral kin recognition and association are key factors shaping human group meta-structure [27,39]. Thus, hunter–gatherer dispersal is not universally sex biased, and is best characterized as highly flexible and facultative in ways that maximize bilateral access to wide ranging kin-networks [29,31]. Additionally, female dispersal does not necessarily mean severing connections to natal kin [40,41], and thus may not fully ameliorate competition with other women in their natal kin group, including both across generations with mothers and daughters.

Lastly, across hunter–gatherers and other small-scale societies, dispersal and residential patterns can be flexible and as such shift relatedness to the residential group considerably over the life course [22,41]. For example, a recent cross-sectional, cross-cultural analyses of 19 small-scale societies (including data from the Savannah Pumé) showed that dispersed women become increasingly more related to their groups with age [26]. While cross-sectional analyses of average relatedness like these can produce a snapshot of kinship structure at a particular point in time, longitudinal studies show that flexibility in residential mobility and camp composition can change kin structure over the life-course [27–29], with implications for competitive dynamics. Temporal variability in group residence, which may be less apparent in non-foraging populations, can remove or add both helpers and competitors over a woman's reproductive lifespan. Moreover, residential mobility is a well-documented hunter–gatherer strategy to reassort people to labour needs or resource constraints, and readjust tensions and conflict as needed [36,42]. For example, Hadza (sub-Saharan hunter–gatherers) women prefer to live with their kin in the first years of marriage when they have young children to care for [43,44], before relocating to affinal camps.

Beside shifting camp residence, a woman's position in her kin network can also influence access to resources and structure opportunities for competition. Network analyses of hunter–gatherer and small-scale populations have identified both costs and benefits to variation within association networks. Recent studies of proximity networks found fitness benefits for women with more indirect connections, or connections to well-connected others [45]. However, increasing indirect connections in hunter–gatherer networks also carried the cost that sickness occurred more commonly among well-connected women. These network studies of hunter–gathers have focused on physical proximity or association (i.e. frequency of direct interactions) between two individuals [45–49]. However, networks can also be constructed from census and pedigree data that capture kinship ties among a group. These networks provide a view of kinship structure in greater detail than average relatedness or distribution of relationships, which have been used to understand social structure in foaging populations [26,38]. While non-kin associations are also important in structuring hunter–gatherer interactions [41,46,48,50], the flow of resources within households, sharing groups, and across generations [4,47,48,51], are largely shaped by kinship. Thus a woman's position in the kinship network may also structure her exposure to potential conflict.

Given the flexibility in hunter–gatherer residential patterns it is unclear whether coresident women help or hinder a woman's reproductive outcomes. In this paper, we explore female kin relations among the mobile Savanna Pumé hunter–gatherers of Venezuela to investigate the opportunities for competition among reproductive-aged women. We focus on three related questions surrounding the opportunities for reproductive conflict. First, how does the total number of reproductive-aged women in the camp shape reproductive outcomes? Second, do women with more female kin ties have better or worse reproductive outcomes? Third, does position in the female kinship network predict reproductive outcomes? While there is a substantial body of theory and literature focusing on the effects of men on reproductive outcomes, as well as the potential conflict between in-laws, these dynamics are beyond the scope of this paper. We focus solely on reproductive-aged women and the female kin network as providing the most direct assessment of competitors.

Using longitudinal census data collected over a 25-year period, we first describe fluctuations in camp composition, the distribution of kin ties, and summary measures of the kin networks. Then with the detailed reproductive histories of 44 women, we model the probability of giving birth and experiencing an offspring death in a given camp in a given year. Our goal is to identify what factors associated with camp composition, distribution of kin, and kin network position influence reproductive outcomes for women. To do so, our analyses focuses on comparing different statistical models that capture exposure to potential female competitors.

2. Methods

(a) . The study population

The Savanna Pumé are mobile hunter–gatherers who live in the west-central Venezuela, in the low plains (llanos) of the Orinoco basin [10,52,53]. They are dispersed in 24 bands of foragers over a 2800 km² area, and are a subset of a larger ethnolinguistic group that includes some sedentary communities. Anthropologists have lived and worked with the Savanna Pumé since the 1990s [52]. The data used here were collected as part of a longitudinal demographic and life-history project [54]. The results of this project have produced a detailed picture of a woman's reproductive lifespan.

Savanna Pumé girls reach menarche on average at 12.9 years, [10] which is comparable to other indigenous South Americans [55]. Girls marry at a young age, typically by the age of 15 years, and though marriages are often arranged by parents, women have autonomy when and whom to marry. Ninety per cent of Savanna Pumé women have their first child between 15 and 19 years [56]. The majority of women (70%) do not disperse at marriage. Non-sex-biased dispersal, and the predominance of residence within an individual's natal community after marriage cultivates bilateral kinship ties (recognition of both mothers' and fathers' kin) among close biological and affinal kin [29]. Natalocality for the Savanna Pumé is sustainable in the short run, in part because individuals and established couples may move between camps, particularly in later life. Additionally, long-term residential data show that every couple of generations, bands migrate and individuals substantially reassort, likely due to population pressures and local resource depletion. Although average completed fertility for women over the age of 40 is 7.0 (±1.3; n = 18), child mortality is high, with 35% of children born not surviving infancy and nearly 50% not surviving to reproductive age [10,57]. Chances of offspring death are greatest among the youngest mothers (less than 14 years), but decline for first time mothers in their mid-teens [56].

(b) . Data collection and variable creation

Census and genealogical data collected between 1982 and 2007 are used to construct detailed descriptions of yearly camp composition for two Savanna Pumé bands—Dora Aná (DA) and Yagurí (YA), whose ranges are in close geographical proximity. These two bands aggregated in their current home ranges in the late 1970s. The first censuses collected shortly after provide a glimpse of founding population dynamics. Residence data are generated from both indigenous censuses conducted in 1982, 1986, 1988, 1989 and 1992, as well as primary interviews conducted by Greaves in 1990, 1992–1993 and again in 2005–2007. Extended descriptions of data collection procedures have been published in previous works [10,52,53].

These data give a yearly snapshot of camp composition for each year between 1983 and 2007 in two bands for which we also have detailed data on marriage, kinship, parentage, reproductive histories, age and subsistence activities. (Note that we use the terms band and camp interchangeably.) Reproductive histories were collected in 2005 and recollected for updates and verification in 2006 and 2007. These data were added to the demographic dataset from 1990 to 1993 when Greaves recorded births, deaths, demographic and genealogical data. From these databases, we construct yearly measures of camp composition, distribution of kin, position in the kin network, and reproductive outcomes (table 1) for women ages 12–49 years who have been recorded in a camp census for at least 2 years. This age range captures a year before the youngest birth (age 13) and a year after the oldest recorded offspring death (age 48). Women may census out due to death, emigration, or because they reach the age of 49. This criterion gives a sample of 712 person years for 44 women (mean observations per woman 18.3, s.d. = 8.98).

Table 1.

Variable descriptions.

variable	description
camp compostion
reproductive-aged females	total number of women (age 12–49 years) in the camp for that year
post-reproductive aged females	total number of women (age 50+ years) in the camp for that year
distribution of kin
mean R	average relatedness of an individual to all other individuals in the camp for that year
distribution of kin	a series of ordinal variables indicating the total number of relationships an individual has at a given range of relatedness
	0.5 = > r (primary kin)
	0.5 > r > = 0.25
	0.25 > r > = 0.125
	0.125 > r > = 0.0625
mother	binary indicator of whether a woman's mother lives in the camp in a given year
sisters	discrete count variable indicating total number of female siblings a woman has in camp in a given year
daughters	discrete count variable indicating the number of reproductive age daughters a woman has in camp at a given time (ages 11–49)
network position
eigen vector centrality	measures centrality of a woman while taking into account the number of ties and the centrality of a woman's primary connections. Eigen vector centrality is interpreted as a measure of influence a woman has given how connected she may be to other well-connected woman
closeness centrality	measures the average length of the shortest path between a woman and all other women in the network. Closeness centrality reflects distance between a woman and all other women in the network
demographic
births per woman	ratio of births to reproductive age women in the camp, calculated as the total number of reproductive age women in the camp at a given year divided by the total number of births in that year. Ranges from 0 (no woman gave birth that year), to 1 (all reproductive age women gave birth that year)

(i) . Camp composition

At the camp level, we sum the total number of reproductive-aged women, which we bracket between ages of 12 and 49 years, and the total number of post-reproductive aged women (women age 50+ years) for each year. Total reproductive-aged women measures the potential number of competitors in a camp in a given year, while women 50+ years provide a proxy for potential allocare. Over the 25-year period, when a woman reaches 49 years, she censuses out of the reproductive age category and into the post-reproductive age category.

(ii) . Distribution of Kin

The censuses are aggregated for the two bands over the 25 years to get a population of 344 men, women and children from which we estimate genetic relatedness between all individuals, using the kinship package in R [58]. We then select only dyads that were resident in the camp in any particular year and take the average relatedness for each individual for each year. A series of discrete variables are then created that track the total number of ties a woman has at different levels of genetic relatedness, starting with primary kin (coef r = ≥ 0.5) and splitting by half until reaching (coef r < 0.0625), generating a total of five count variables. Finally, each woman is associated with a binary variable indicating whether her mother was present in the camp that year (0 = no, 1 = yes), and two discrete variables that totals the number of sisters and reproductive aged daughters present in the camp in a given year.

(iii) . Network position

To estimate position in kin networks, we constructed a network of binary relationships between all women in camp, where the ties reflect relatedness at a coef r ≥ 0.25. From this, two common network measures of centrality are calculated. These network measures have been identified as having fitness-relevant effects in other network studies on hunter–gatherers [45], and represent the number of and distance to potential competitors. First, eigenvector centrality (EC), which accounts for the number of ties a woman has, as well as the number of ties those primary connections have. That is, EC measures how well connected a woman's primary kin are in the kin network. A high EC suggests that the individual is related to well-connected individuals.

Closeness centrality represents a woman's position in the kinship network by assessing the distance, or average number of links connect an individual to all others in the network. In some cases, closeness is interpreted as reflecting the speed or efficiency at which an individual can access any part of the network. Women with high closeness, have shorter distances to reach all other individuals in the network. In graphs with disconnected individuals, there is no shortest path between some women. In these cases, the total number of ties in the graph is imputed to connect the unconnected women. Finally, centrality values tend to be sensitive to the size of the network and the total number of connections, which vary across years. To facilitate comparison across years with different sizes and total ties, both measures were normalized to range from 0 to 1. All network measures were calculated using the R package igraph [59].

(iv) . Births per woman

To assess exogenous conditions in a given year, we calculate the proportion of women giving birth in that year. To do so, we sum the number of births documented in the camp in a particular year and divide by the total number of reproductive-aged women to get a proportion of the number of births per number of women. To avoid autocorrelation in the analyses, this calculation excludes the focal woman, by excluding her in the camp total (the denominator), and the excluding her birth in the total number of births (the numerator).

We include this variable as a proxy for exogenous conditions for two reasons. First, the proportion of other women in camp who gave birth in the same year may reflect annual fluctuations in resource availability for fecundity. For example, in years with a productive dry-season, proportionally more women may give birth, including the focal woman. Second, in models where the outcome is offspring mortality, the proportion of women giving birth in a given year provides a proxy for exogenous conditions that might impact mortality. Thus we treat this variable as capturing demographic and ecological contexts in which we expect competition to occur.

(v) . Reproductive outcomes

To measure reproductive conflict, we use a binary outcome for whether the woman experienced a birth or a child death in a given year. Offspring deaths were limited to children under the age of 5. Additionally, no women gave birth multiple times in a single year and all recorded births were singleton births.

(c) . Analyses

We first describe the composition of both camps, the female kin networks, and their change over time (electronic supplementary material, table S1). To assess how camp composition, distribution of kin, and position in the kin network influence reproductive outcomes, we construct a generalized linear mixed model with a logit link function for the log-odds of experiencing either a birth or an offspring death in a given year. Data were arranged such that each row represented an individual woman present in a band in a given year. Models for birth and death outcomes were constructed independently. For each person-year, the outcome was coded as a 0 or 1, where 0 is the woman did not give birth, or did not experience an offspring death in that year.

First, a baseline model was constructed for each outcome. For births, the baseline model includes age, an age spline, and a camp size variable. The age and age-spline capture known nonlinearities in the probability of giving birth, whereby the proportion of women giving birth at a given age increases from 12 to around 20 years of age, then slowly declines over the course of the reproductive lifespan (see electronic supplementary material, figure S1). The model predictions are then compared to the empirical distribution of the proportion of women at each age giving birth, to show how closely the model captures the effect of age. The probability of giving birth is expected to increase with age, from 12 to 20 followed by a slow decline in the age-specific probability of giving birth. This would result in a positive effect of age and a negative effect of the age spline. Sensitivity analyses were performed using alternative means of capturing the nonlinear effects of age, with no qualitative differences in modelling results (see electronic supplementary material, figure S2 and tables S2 and S3). For deaths, the baseline model includes the variable for age, year and a camp affiliation identifier, as preliminary analyses show higher offspring mortality in YA than in DA.

We test for reproductive competition using four statistical models, where relevant variables are added to the baseline model. For the camp composition model, the total number of reproductive-aged women and the total number of post-reproductive women were included as predictors. For the distribution of kin, we employ two separate models. First the relationship model, two variables were included as predictors, one binary variable indicating the presence of the mother, and an count variable summing the total number of co-resident sisters. For the kinship model, count variables that track the total number of genetic kin at differing levels were included (table 1). For the network model, the estimates of eigen vector centrality and closeness centrality were included as predictors. We treat these four models as our primary test for evidence of reproductive competition among women. Given the goal to explore predictors of reproductive competition, we treat any predictor that lowers the yearly odds of giving birth, or increases the odds of an offspring death as a potential indicator of reproductive conflict.

Finally, for the demographic model, births per woman was the main predictor. We treat this model as an alternative to the competition models, where births and deaths reflect either demographic stochasticity expected in small populations or reflect exogenous ecological conditions that impact women equally.

Individual-level random effects are added to all models to account for inter-individual variation in the odds of giving birth or a child dying. This permits women to differ in their baseline propensity for experiencing either of these outcomes. Additionally, we treat year as a random effect. This permits the baseline propensity for each outcome to vary across years. This captures any underlying exogenous conditions that vary across years. The variance parameters are included for these random intercept and the interclass correlation coefficient are used to assess how much variation is explained within these nested levels. Given the small sample size, predictor groups are assessed independently rather than building a full model with all predictors added. Information theoretic indices (AIC and BIC) are used to assess model improvement when including new groups of predictors. AIC is a common measure to assess model improvement. BIC is similar, but is more conservative by giving a much steeper penalty to each new variable included in a model.

3. Results

(a) . Descriptive statistics

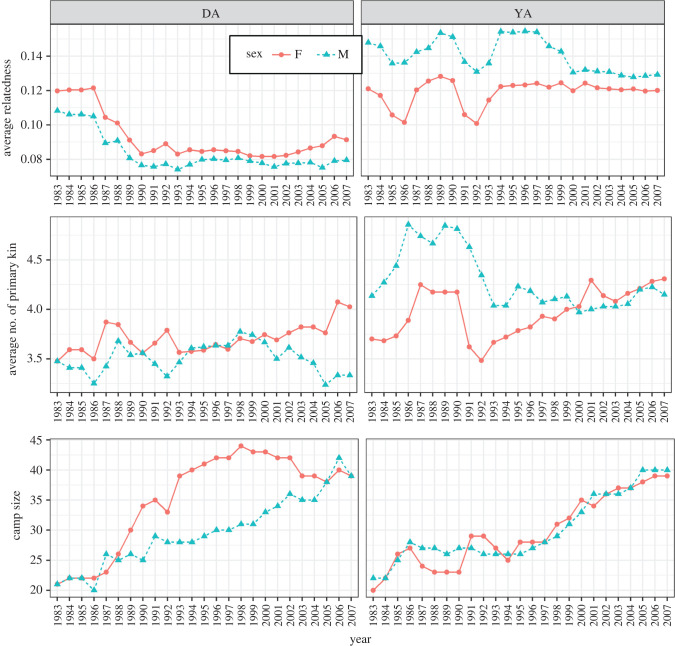
Band size increases steadily from the earliest census in 1983–2007 (figure 1). Both bands had a founder size of 40 members in 1983 (20 women in DA and 19 in YA). By 2007, DA had nearly doubled to 72 members, with 50% female, with 27.8% reproductive-aged women. In 2007, YA had also nearly doubled to 68 members, with 50% female and 22.1% reproductive-aged women. The average number of reproductive-aged women in a given year ranges from 13 to 30 across both camps at a given time (figure 2). Considering the two bands together, the per cent of reproductive-aged women fluctuated across the 25 years, ranging from as low as 15% to a high of 28.9%. Notably, DA shows a larger increase in women from the late 1980s through the 1990s. Over the span of this decade, the band was composed of 55–60% women, before returning to near 50% by the early 2000s. Average relatedness peaks in early years for DA, declines, and remains steady at r ∼ 0.08. Average relatedness is slightly higher for YA and shows minimal fluctuation over the 25 years. Additionally, the average number of primary kin (parents, siblings and offspring) is relatively stable between 3 and 4.5 in both bands, which lies at the upper end of the range for foraging populations [38].

Figure 1.

Average relatedness, distribution of primary kin and camp size (panels bottom to top) of two Savanna Pumé bands (DA and YA) across all census years. (Online version in colour.)

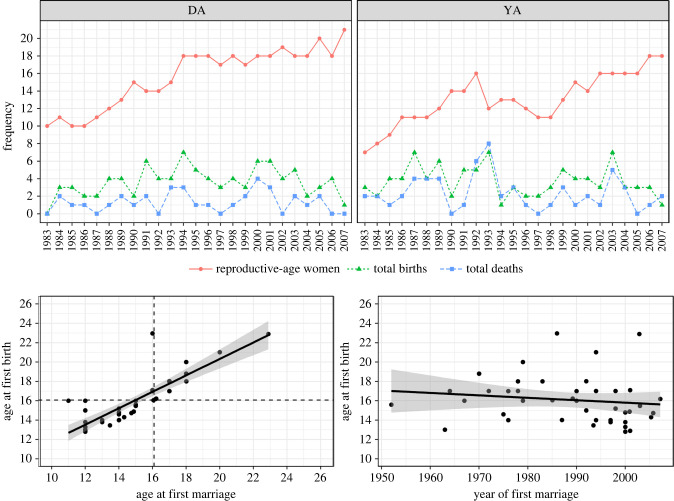
Figure 2.

Total number of reproductive-age women, births and offspring deaths in a given year for each camp (top panels). Joint distribution of age at first birth and age at first marriage (bottom left), showed a strong positive association, indicating marriage and first birth are tightly linked. Dashed lines indicate the mean ages for first marriage and first birth. Age at first birth by year of first marriage (bottom right) showed no evidence of a secular trend of increasing age at birth with time. (Online version in colour.)

All individuals living in either camp over the 25-year period (N = 344) produced 117 992 unique dyads. Average relatedness across this aggregate group was r = 0.023, which is similar to estimates from other small-scale populations [38]. However, this value is lower than a previous estimates from the same groups of Savanna Pumé, where average relatedness was estimated as 0.085 [26]. We attribute this difference to using a much larger, aggregate, longitudinal dataset rather than a cross-sectional dataset (N = 76 versus N = 344). The distribution of siblings across years is relatively stable, with approximately 3–4 primary kin on average for both males and females.

Using the data aggregated across both bands yearly kin networks were built for each camp. While an individual's kin network was allowed to vary across years, averaged estimates remained relatively stable across most years, particularly after the first few years of the census. During the early years, when the groups were smaller, individual networks were denser, with higher average relatedness and greater levels of average individual centrality. Over the years, the distribution of EVC scores was relatively uniform. Closeness measures varied much more across both communities and years (see electronic supplementary material, figure S3).

(i) . Reproductive outcomes

There was a total of 184 births and 92 deaths across the 712 person years of observations (figure 2). The total number of births in a given year ranged from 0 to 7 (mean = 3.68, s.d. = 1.68), with total number of deaths ranging from 0 to 8 (mean = 1.84, s.d. = 1.67). For all years in DA, yearly births exceeded deaths. However, in 1992 and 1993, deaths exceeded births in YA.

The joint distribution of marriage and age at first birth are presented in the two bottom panels of figure 2. Mean age at first marriage was 16.06 (s.d. = 5.17) while mean age at first birth was just slightly older at 16.09 (s.d. = 2.5) (figure 2, bottom left). Additionally, age at first birth was showed no secular trends over time (figure 2, bottom right).

(b) . Modelling probability of birth and offspring death

(i) . Yearly odds of giving birth

The baseline model shows that the odds of giving birth in a given year increase from age 12 years to age 20 years, and then decline from age 20 to 49 years (tables 2 and 3 and figure 3). The model coefficients show the age-specific probabilities of giving birth overlap with the empirical distribution of the proportion of women at each age giving birth (electronic supplementary material, figure S2). Additionally, the odds ratio of giving birth showed a secular trend, declining slightly since the initial year of the census (1983). Camp size was not a significant predictor. Finally, the variance components of the random effects showed a larger proportion of the variance in birth outcomes was captured at the individual-level rather than the yearly level. For the baseline propensity for giving birth, there was more variation between women than between years.

Table 2.

Odds ratio of giving birth in a given year. OR, odds ratio; LCI, lower 95% confidence interval; UCI, upper 95% confidence interval. Bold values indicate p-value <0.05.

fixed effects	baseline model			camp composition model			relationship model			kinship model			network model			demographic model
	OR	LCI	UCI	OR	LCI	UCI	OR	LCI	UCI	OR	LCI	UCI	OR	LCI	UCI	OR	LCI	UCI
intercept	0.07	0.01	0.55	0.07	0.01	0.55	0.09	0.01	0.77	0.07	0.01	0.58	0.06	0.01	0.53	0.04	0.00	0.30
size	0.98	0.97	1.00	0.99	0.94	1.04	0.98	0.97	1.00	1.00	0.97	1.02	0.98	0.97	1.00	0.99	0.97	1.00
age	1.19	1.07	1.31	1.18	1.07	1.31	1.17	1.06	1.30	1.15	1.04	1.27	1.19	1.07	1.31	1.19	1.08	1.31
age2	0.79	0.71	0.89	0.79	0.71	0.89	0.78	0.69	0.88	0.80	0.71	0.90	0.79	0.70	0.89	0.79	0.71	0.88
camp composition
reproductive age women				0.98	0.83	1.15
post-reproductive age women				1.00	0.86	1.16
relationship model
mother present							0.65	0.40	1.07
sisters							1.13	0.84	1.51
daughters							1.29	0.97	1.72
kinship model
r0.5										1.20	1.01	1.43
r0.25										0.99	0.91	1.08
r0.125										0.95	0.88	1.02
r0.0625										0.96	0.92	1.01
network
EVC													1.00	0.50	2.01
closeness													1.13	0.73	1.75
demographic–ecological
births per woman																1.17	1.01	1.36
random effects
woman's ID	0.14			0.14			0.17			0.15			0.13			0.13
year	0.04			0.03			0.03			0.03			0.03			0.03
ICC	0.05			0.05			0.05			0.05			0.05			0.05
N observations (years)	712			712			712			712			712			712
N groups (women)	44			44			44			44			44			44
AIC	792.3			796.2			792.3			790.9			795.9			789.9
BIC	819.7			832.7			833.4			836.6			832.5			821.9

Table 3.

Odds ratio of offspring death in a given year. OR, odds ratio; LCI, lower 95% confidence interval; UCI, upper 95% confidence interval. Bold values indicate p-value <0.05.

	baseline model			camp composition model			relationship model			kinship model			network model			demographic model
fixed effects	OR	LCI	UCI	OR	LCI	UCI	OR	LCI	UCI	OR	LCI	UCI	OR	LCI	UCI	OR	LCI	UCI
intercept	0.31	0.05	1.85	0.35	0.05	2.41	0.46	0.07	2.91	0.43	0.07	2.59	0.37	0.06	2.41	0.10	0.02	0.59
size	0.98	0.95	1.00	0.93	0.86	1.01	0.97	0.95	1.00	0.98	0.95	1.01	0.97	0.95	1.00	0.98	0.96	1.00
age	1.01	0.99	1.04	1.01	0.99	1.04	1.02	0.99	1.05	1.02	0.99	1.05	1.02	0.99	1.04	1.01	0.99	1.04
camp	1.77	1.05	2.97	1.95	1.08	3.54	1.61	0.98	2.65	1.64	0.96	2.82	1.86	1.10	3.16	1.48	0.87	2.52
camp composition
reproductive age women				1.18	0.92	1.52
post-reproductive age women				1.07	0.84	1.36
relationship model
mother present							0.72	0.42	1.23
sisters							0.88	0.60	1.27
daughters							0.81	0.61	1.07
kinship model
r0.5										0.84	0.68	1.03
r0.25										0.99	0.91	1.09
r0.125										0.97	0.90	1.05
r0.0625										0.99	0.93	1.04
network
EVC													0.63	0.27	1.49
closeness													1.18	0.70	1.98
demographic–ecological
births per woman																1.39	1.16	1.67
random effects
woman's ID	0.07			0.07			0.07			0.00			0.06			0.06
year	0.19			0.21			0.18			0.19			0.19			0.00
ICC	0.07			0.07			0.07			0.05			0.07			0.02
N observations (years)	712			712			712			712			712			712
N groups (women)	44			44			44			44			44			44
AIC	536.1			538.2			537.4			537.8			539.0			528.5
BIC	563.5			574.8			578.5			583.5			575.5			560.4

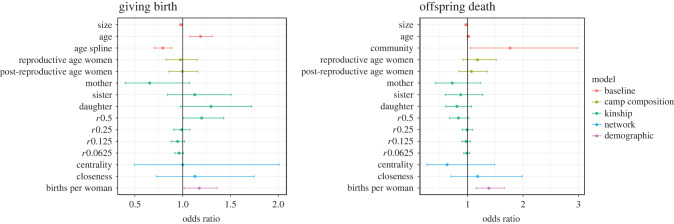
Figure 3.

Odds ratios from each of the models. Error bars represent 95% confidence intervals. (Online version in colour.)

Compared to the baseline model, the predictors of reproductive competition showed no significant negative effects on the probability of giving birth. The only significant predictor was found in the kinship model, which showed the presence of close female kin (coef r = 0.5) had a positive impact on the chance of giving birth. This model showed an improvement in the AIC values compared to the baseline, however the BIC values were still slightly higher.

In contrast to the reproductive conflict models, the demographic–ecological model showed that the births per woman variable was a significant predictor of giving birth. That is, when proportionally more women in camp give birth in a given year, the focal woman is also more likely to give birth. The AIC and BIC values for the demographic–ecological model showed the best fit compared to the reproductive competition models.

(ii) . Yearly odds of experiencing offspring mortality

The baseline model showed women in YA have significantly higher chances of an offspring death compared to DA, while age and camp size showed no significant effects. In contrast to the birth models, the variance components showed a much higher proportion of variance in deaths was captured between years than between women.

The models predicting offspring deaths were similar to those predicting births, in that none of the reproductive competition predictors appeared to have any effect on offspring mortality. Similarly, the demographic–ecological model showed that births per woman within the camp had a large positive effect on the odds a woman experiences an offspring death in a given year. In this model, the effect of year becomes insignificant, suggesting that these variables are capturing shared variance in distribution of deaths. The AIC and BIC values for the baseline were better than all reproductive competition models. However, the demographic–ecological model showed a better fit than the baseline.

4. Discussion

We find little support for direct reproductive conflict among Savanna Pumé women. In years where there are more reproductive-aged women, and thus more potential competitors, no evidence emerges for lower probability of giving birth or increased chance of offspring death. Furthermore, women with more primary female kin are not more likely to experience a birth or an offspring death. Finally, position in the female kin network had no effect on reproductive outcomes. Thus, it appears that coresident women, both kin and non-kin, held no negative impact on the yearly occurrence of reproductive outcomes.

Rather than direct reproductive conflict, we found that women with more close female relatives had a slightly higher chance of giving birth in a year. Outside of this, women seemed to have no impact on other women's reproductive outcomes. Rather, births per woman, our proxy for local ecological conditions, best predicted the yearly probability of giving birth and offspring deaths. In both camps, births per woman were correlated with both total numbers of births and total numbers of offspring deaths in that year (figure 4).

Figure 4.

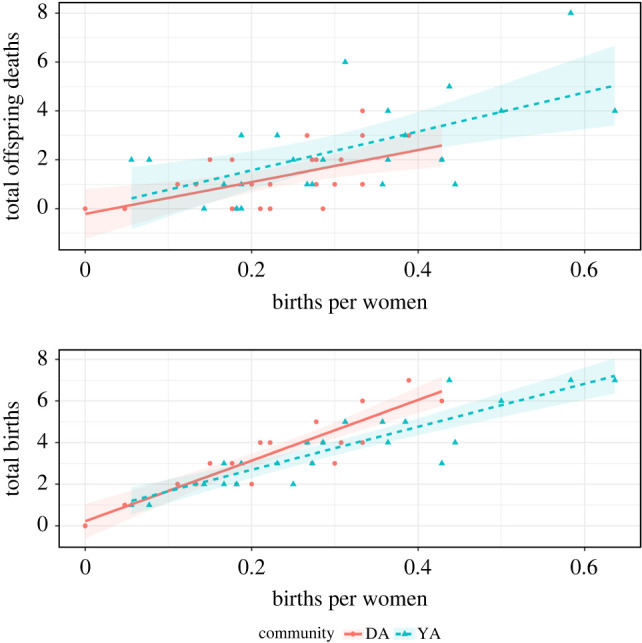
Total number of births and deaths in a given year by proportion of Savanna Pumé women giving birth. (Online version in colour.)

This result suggests that reproductive outcomes are not sensitive to what happens to other women, rather exogenous conditions may create synchronicity among women. If food is plentiful during a dry season, a larger number of women may become pregnant and give birth. With more births, the chances of offspring mortality increase. Under this interpretation, either ecological conditions or demographic stochasticity best explain variance in women's yearly reproductive outcomes. Alternatively, the number of births per woman in a given year may reflect a measure of the potential for conflict, as there will be more women in need support. However, we find no evidence that some women fair better than others (which would indicate successful competitors). That is, women with more kin saw no protective effect nor evidence that they faired worse. Furthermore, mothers, sisters and daughters showed no significant impact on chances of giving birth or experiencing an offspring death. Similarly, we found no evidence that more connected women faired differently than the least connected. The answer to whether some women do better in years with a higher proportion of women giving birth may require a deeper exploration into the ecological conditions and the socioeconomic contexts of the broader kin network. To understand the potential of reproductive conflict among women in foraging populations, a goal for future research would be to examine how ecological conditions produce synchronicity in birth, and whether more connected women do better or worse in those years. Additionally, the potential for conflict is likely less in contexts where infant mortality is more extrinsic. While the loss of young children among the Savanna Pumé is comparable to mortality in other hunter–gatherers [60] much of the mortality appears to be care-independent, meaning that mortality varies independently of the level of care; more parental or alloparental investment does little to buffer against the risks of death as an infant [61]. In such contexts, reproductive competition may not be easily detected as measured by offspring survival. Rather, in situations where offspring survival is more sensitive to parental and alloparental investments, the potential for reproductive conflict is greater.

5. Conclusion

The ethnographic record emphasizes the importance and benefits of kin-based allocare for women in foraging populations [9,62–65]. While this reliance on others sets the stage for reproductive competition, there are good reasons to expect that reproductive conflict is attenuated in hunter–gatherers. First, bilateral kinship recognition, which appears to be a foundation for the large meta structure of hunter–gatherer populations [27], means the potential pool of kin helpers for reproducing women is large and geographically dispersed. Given that allocare networks are diverse in in foraging populations [65–68], having access to a large pool of helpers means there may be less competition for limited help, or less reliance on the same group of low-cost helpers for reproducing women.

Third, among populations where some portion of infant mortality is extrinsic or care-independent, allocare may have little effect on survivorship [61,69]. Additionally, variation in kinship recognition and norms of marriage may be cultural adaptations that reduce reproductive conflict among women. [15,22]. Lastly, in foraging populations women exhibit relatively low levels of reproductive skew, a potential measure of the strength of competition if reproductive competition shapes the control and access to resources needed for reproduction [70]. Variance in reproductive success tends to be larger among food producers than among foragers [71], which may be expected given the greater ability to monopolize resources in food producing societies.

Child care costs are often spread over diverse networks, composed of both kin and alloparents with low opportunity costs. The propensity for reproductive conflict likely increases with more rigid social structures, sex-biased dispersal and when a woman's independent access to resources is more limited, as among intensified agricultural and pastoralist populations. Here, key resources for reproduction are more controlled than in forager populations, with more strict rules governing access. Indeed, most of the evidence for reproductive conflict in small-scale groups comes from non-foraging populations. Female reproductive competition is also more salient in contexts with labour constraints, where women's food acquisition or production trades off with childcare. Indeed, these contexts show not only increased reproductive competition among unrelated women, but competition among siblings as well [72].

Not only does residential mobility enhance resource access, it also serves to dampen competition. Voting with your feet has long been used to describe residential mobility as a mechanism for diffusing tension among hunter–gatherers [37]. Women use a range of mobility strategies, even in more sedentary populations, to both access kin and attenuate conflict [29,31,73]. In a similar vein, low competition can be seen as an extension of the egalitarian ethos of foraging populations [37,42,74,75]. While recent cross-cultural analyses have challenged the egalitarian characterizations of foraging populations, the rates of inequality are among the lowest among human social systems [76,77]. Indeed, ethnographic accounts of hunter–gatherers are rife with descriptions of social and behavioural mechanisms that reduce conflict and accumulation of resources and wealth. It is reasonable to expect that these mechanisms also extend to biological currencies of reproductive success.

Ethics

Informed consent was obtained from participants aged 16 years and over, and in accordance with Venezuelan local legislation and national guidelines. Protocols were approved by the Human Subjects Committees at Harvard University and before that at Stony Brook University.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material [78]. Given the Savanna Pumé are a small population, and the personal nature of the data, we have ensured the data have been anonymized. Additional data are available by reasonable request.

Authors' contributions

J.H.: conceptualization, formal analysis, software, visualization, writing—review and editing; K.L.K.: conceptualization, data curation, resources, supervision, writing—original draft, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

Funding for the Savanna Pumé research was provided by the National Science Foundation (grant nos 0349963 and DBS-9123875, in 2004 and 2006, respectively), the L.S.B. Leakey Foundation (awarded to Russell Greaves, 1991), the Milton Fund and Harvard University.