Flat-Band-Induced Many-Body Interactions and Exciton Complexes in a Layered Semiconductor

Abstract

Interactions among a collection of particles generate many-body effects in solids that result in striking modifications of material properties. The heavy carrier mass that yields strong interactions and gate control of carrier density over a wide range makes two-dimensional semiconductors an exciting playground to explore many-body physics. The family of III–VI metal monochalcogenides emerges as a new platform for this purpose because of its excellent optical properties and the flat valence band dispersion. In this work, we present a complete study of charge-tunable excitons in few-layer InSe by photoluminescence spectroscopy. From the optical spectra, we establish that free excitons in InSe are more likely to be captured by ionized donors leading to the formation of bound exciton complexes. Surprisingly, a pronounced red shift of the exciton energy accompanied by a decrease of the exciton binding energy upon hole-doping reveals a significant band gap renormalization induced by the presence of the Fermi reservoir.

The behavior of electrons in moiré superlattices has attracted tremendous interest because it constitutes a strongly correlated electron system where the mutual interaction energy exceeds the kinetic energy of carriers.¹⁻⁵ Two-dimensional (2D) layered materials are an ideal platform to realize such a system: the maximal kinetic energy of electrons in the moiré mini-bands is limited because of their small bandwidth while, conversely, the reduced dielectric screening leads to strong Coulomb interactions among charge carriers. The crucial factor in further enhancing interactions is the large effective mass of carriers in the host materials, which is determined by the curvature of the relevant bands. The III–VI metal monochalcogenides, such as GaSe and InSe, offer a valid alternative since the effective mass of holes could reach about 2m₀ in the monolayer limit, where m₀ is the electron rest mass.⁶ As a comparison, electrons and holes in monolayer transition metal dichalcogenides (TMDCs) have similar effective masses m_e ≈ m_h ≈ 0.5m₀.⁷ Another intriguing property of III–VI metal monochalcogenides is the Mexican-hat-like inversion near the Γ point at the valence band edge. For example, as the γ-stacked InSe (Figure 1a) is thinned down to the monolayer limit, the valence band maximum (VBM) shifts from the Γ point, which results in a van Hove singularity in the hole density of states (Figure S1). This kind of band dispersion only appears in the thin limit where the thickness of InSe is below seven layers.⁸ Theory has predicted that tuning the Fermi level into the band inversion region could give rise to emergent phenomena such as half-metallicity and ferromagnetism.⁹⁻¹¹

Figure 1.

Few-layer InSe in a field-effect device structure. (a) Top and side views of γ-stacked bilayer InSe. Brown spheres, indium atoms; yellow spheres, selenium atoms. The interlayer distance is about 0.8 nm. (b) Calculated band diagram for six-layer InSe (6L-InSe). CB, conduction band; VB, valence band. (c) Schematic of the hBN-encapsulated 6L-InSe device (device A) with a few-layer graphene contact and bottom gate. (d) Optical microscope image of device A. The orange contour encloses the region of the InSe flake. The dashed line indicates the position of the few-layer graphene contact on the flake. Scale bar, 10 μm. (e) PL count rate as a function of the emission energy at V_g = 0 V using P = 50 μW, measured at position A in (d).

Although thin InSe is not rigorously a direct bandgap semiconductor, the modest momentum mismatch still allows the observation of thickness-dependent photoluminescence (PL) emissions from InSe excitons.^12,13 Combined with the excellent optical properties, we investigate the manifestations of many-body interactions through the PL measurements across a wide range of carrier densities.

Our device consists of a six-layer InSe (6L-InSe) encapsulated in hexagonal boron nitride (hBN), with a few-layer graphene bottom gate. A first-principles calculation of the band diagram, depicted in Figure 1b, shows that for 6L-InSe the VBM is only about 5 meV higher than the Γ point in the valence band. Because of the relatively flat valence band dispersion, the effective mass of holes in InSe is much heavier than that of the electrons.⁶ We calculate effective masses of electrons and holes of m_e ≈ 0.13m₀ and m_h ≈ 0.9m₀ for 6L-InSe (Supplementary Note 1). The corresponding reduced effective mass of excitons in 6L-InSe is 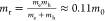. The exciton binding energy E_b and the Bohr radius a_B are directly determined by it as 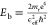and 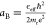, where e is the elementary charge of an electron, and ϵ_eff is the effective dielectric constant. Excitons in few-layer InSe are therefore expected to possess a reduced binding energy E_b and increased Bohr radius a_B compared with excitons in TMDCs.

Figure 1c,d shows a schematic and an optical microscope image of our device A. We use a 720 nm pulsed laser with an 80 MHz repetition rate to excite the sample, unless otherwise specified. All measurements are performed at 4.5 K. Figure 1e presents a typical PL spectrum recorded for gate voltage V_g = 0 V using a laser power P = 50 μW. The exciton peak at 1.48 eV has a line width of 15 meV, which makes it one of the narrowest recorded so far in few-layer InSe (Supplementary Note 3).

Up to now, excitons in thin InSe have been investigated without applying electrostatic gating.¹⁴⁻¹⁶ The embedding of a thin flake into a field-effect structure allows us to tune the Fermi level into the conduction or valence bands. Figure 2a shows a representative PL emission spectrum of our sample as a function of gating with multiple salient features. The bright and narrow peak located at 1.48 eV for V_g between −0.5 and 0 V corresponds to the exciton resonance X₀. As we increase the gate voltage above 0 V, the energy of the exciton peak is reduced by 7 meV (X_–) and a new broad peak (D_–) appears at 1.44 eV. Conversely, as we reduce the gate voltage to between −5.8 and −0.5 V, the exciton peak evolves to 1.47 eV (X₀^′), together with an intensity transfer to a broad peak centered at 1.35 eV (D₀). Further reduction in the gate voltage leads to a rapid decrease in the intensity of the 1.35 eV peak (D₀) and pronounced red shift of the 1.47 eV peak (X₊).

Figure 2.

Charge-tunable excitons in few-layer InSe. (a) PL count rate as a function of the emission energy and gate voltage using P = 50 μW, measured at position A in Figure 1d. The horizontal yellow dashed lines indicate different charging regimes. (b) Upper panel: PL count rate as a function of the gate voltage along the three vertical dashed lines in (a). Red, 1.35 eV; blue, 1.48 eV; green, 1.44 eV. The plateau in the red and green curve correspond to the D₀ and D_– emissions, and the peak in the blue curve corresponds to the X₀ emissions. Lower panel: peak energy as a function of the gate voltage. The vertical yellow dashed lines indicate different charging regimes. Here, “undoped” means unintentionally doped.

These features in the spectra are reproducible in other locations on the same sample (Supplementary Note 4) and a second device (device B). The latter device also has additional electrical contacts that allow us to determine the device charge configurations using electrical transport measurements (Supplementary Note 5). We find that for V_g > 0 V, we have electron doping (n-doped regime); for −5.8 V < V_g < 0 V, the device is in the undoped regime; and for V_g < – 5.8 V, the device is in the hole-doped (p-doped) regime. In accordance with the electrical measurements, the out-of-plane photocurrent (I_g in Figure 1c), acquired during V_g-dependent PL measurements, also exhibits three regimes depending on the gate voltage, which further confirms the assignment of charge configurations (Supplementary Note 6). The upper panel of Figure 2b shows the PL count rate as a function of the gate voltage along the three vertical dashed lines shown in Figure 2a. When the X₀ emission is pronounced, both the D₀ and D_– emissions become less intense. The lower panel of Figure 2b shows the peak energy as a function of the gate voltage. The X₀ emission for −0.5 V < V_g < 0 V is characterized by a small blue shift (∼7 meV). In the p-doped regime, the X₊ emission red shifts by 25 meV as the carrier density is tuned to 1.3 × 10¹² cm^–2.

We first focus on the two peaks in the undoped regime to understand the origins of the various spectral features. Figure 3a shows the emission intensity of X₀^′ (I_X0^′) and D₀ (I_D0) as a function of the excitation power for V_g = −3 V. Compared with the linear increase of I_X0^′ with excitation power, I_D0 increases sublinearly and saturates at about P_sat = 400 μW. At high powers, I_X0^′ keeps growing continuously, and the low-energy tail of X₀ leads to a further linear increase of I_D0 when P > P_sat. We have also performed time-resolved PL (TRPL) measurements on the X₀^′ and D₀ emissions separately (Supplementary Note 7). For the D₀ emission, a slow-decay component with a characteristic time of ∼8 ns dominates. On the basis of the low saturation power, as well as the long radiative lifetime, we identify the D₀ emission as originating from defect-bound excitons, which have been observed in other 2D semiconductors.¹⁷⁻²⁰ Additionally, our first-principles calculations suggest that selenium vacancies in InSe could induce localized states that are about 100–150 meV lower than the conduction band minimum (Figure S1), in agreement with the observed splitting between X₀ and D₀ in the PL spectra (∼120 meV).

Figure 3.

Defect-bound exciton and photoluminescence excitation spectrum. (a) Emission intensity of D₀ (blue) and X₀^′ (red) peaks as a function of the laser power. The black dashed line indicates the linear background originating from the low-energy tail of X₀ at high power. (b) Left: (normalized) total PL counts of X₀^′ and D₀ as a function of temperature using P = 50 μW. Right: PL emission yield of D₀, defined as β = I_D0/(I_D0 + I_X0^′), as a function of temperature. (c) Integrated PL intensity of D₀ as a function of excitation energy (PLE spectrum, blue shaded area) and PL intensity as a function of emission energy (orange shaded area) at V_g = −3 V and −0.2 V. The red solid lines are fits using the 2D Elliott model. For X₀ (V_g = −0.2 V), the fitting parameters are E_g = 1.493 eV and E_b = 12 meV; for X₀ (V_g = −3 V), the fitting parameters are E_g = 1.478 eV and E_b = 6 meV. (d) Schematic of the exciton state and defect-bound exciton state in the quasi-particle picture. Yellow arrows, laser excitation; dashed arrows, relaxations; wave arrows, radiative emissions. VAC stands for the vacuum state.

The presence of ionized defects could strongly influence the properties of optically generated quasi-particles, leading to the formation of bound exciton complexes (BXCs) which have been reported in bulk semiconducting crystals.²¹⁻²⁵ Within their radiative lifetime, free excitons have a probability to be affected by charged impurities, with a capture rate η ∝ n_Dσv_th, where n_D is the defect density, σ is a capture cross-section proportional to a_B², and v_th is the mean thermal velocity of the exciton.²⁶v_th satisfies the Maxwell–Boltzmann distribution, 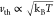, where k_B is the Boltzmann constant, and T is the temperature.²⁷ In experiments, the capture rate η is proportional to the yield of the D₀ emission, which is defined as β = I_D0/(I_D0 + I_X0^′). Figure 3b presents the temperature dependence of β and the (normalized) total PL counts I_D0 + I_X0^′. At T = 80 K, the total PL intensity falls to 20% because of the thermal dissociation of excitons into free electrons and holes. It allows us to estimate the exciton binding energy E_b ∼ k_B × 80 K = 7 meV. As predicted, we observe that the yield of the D₀ emission β increases at elevated temperatures. At T = 50 K, β reaches 80%, which suggests that most of excitons are bound by defects.

Emissions from defect-bound excitons allow us to obtain an absorption spectrum of free excitons and to extract the exciton binding energy. The excitonic absorption edge of InSe has been reported in bulk InSe.^14,28 However, for few-layer InSe, the exciton resonance cannot be observed by performing a reflectance measurement using a broadband white light source (Supplementary Note 8). Instead, we have carried out photoluminescence excitation (PLE) measurements by monitoring I_D0 while tuning the excitation wavelength around the exciton resonance. Here, we use a narrow-line-width tunable continuous-wave laser as a light source to excite the sample. Figure 3c shows the integrated PL intensity of the D₀ peak as a function of the excitation energy (blue shaded area) for V_g = −3 and −0.2 V, as well as the PL spectrum (orange shaded area) obtained at the same gate voltages. The PLE spectra are characterized by an absorption onset with an excitonic resonance at about 1.47 eV and are equivalent to the absorption spectrum of InSe excitons. Furthermore, when the laser energy is tuned below the exciton resonance but still far above the energy of D₀, I_D0 almost vanishes. This indicates that the generation of defect-bound excitons requires the creation of free excitons in InSe and the subsequent relaxation from the exciton state to the defect-bound state (Figure 3d).

The presence of excitonic resonances influences the absorption edge of a semiconductor, which can be described by the Elliott model.²⁹⁻³¹ We apply the 2D Elliott model to the PLE data at V_g = −3 and −0.2 V to extract the exciton binding energy for X₀^′ and X₀ to be 6 and 12 meV, respectively (Supplementary Note 9), consistent with our temperature-dependent measurement presented in Figure 3b.

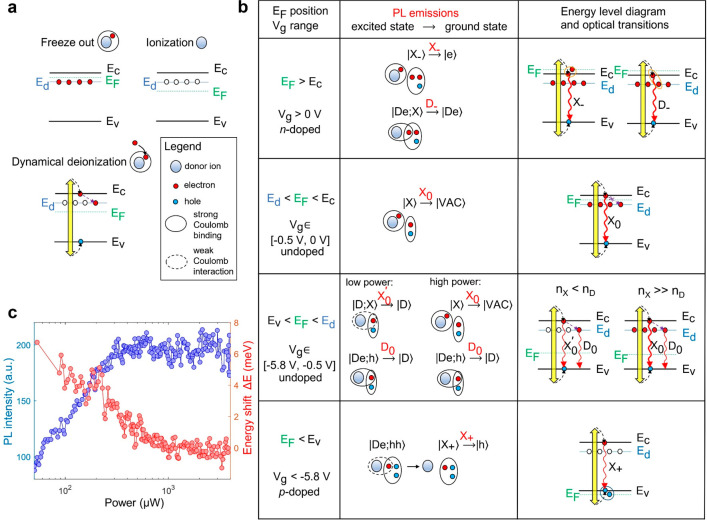
Chalcogen vacancies in 2D semiconductors behave as electron donors because of unsaturated bonds.³²⁻³⁵ Here, we consider how exciton properties change in the presence of neutral and ionized donors. The donor energy levels below the conduction band minimum can be filled or emptied depending on the Fermi level position. As shown in Figure 4a, when the Fermi level is tuned above the donor energy levels (E_F > E_d), all donor electrons remain bound to the donor ions since electrons tend to occupy all lower energy levels. Therefore, the donors are charge neutral, and this is referred to as freeze-out (complete deionization).³⁶ On the contrary, when the Fermi level is below the donor energy levels (E_F < E_d), donors will release the additional electrons to the reservoir (the contact) in the process of donor ionization.³⁶

Figure 4.

Bound exciton complexes associated with neutral and ionized donors. (a) Schematic of donor freeze-out, ionization, and dynamical deionization. Yellow arrow, laser excitation; dashed arrow, carrier relaxations. (b) Table illustrating different quasi-particle (excited and ground) states, relevant PL emissions, and optical transitions for different Fermi level positions. The notation |···⟩ indicates the quasi-particle state: D, donor ion; e, electron; h, hole; X, exciton; VAC, vacuum state. The red words above → indicate the names for PL emissions defined in Figure 2a. (c) Red: energy shift between X₀ and X₀^′ (ΔE = E_X0 – E_X0^′) as a function of the laser power. Blue: PL intensity of defect-bound excitons (D₀) as a function of the laser power at V_g = −3 V, after removing the linear background.

The PLE experiments indicate that the optically excited electrons in the conduction band can relax and fill the donor levels. If the laser excitation is weak (exciton density n_X < n_D), a part of the ionized donor sites will be temporarily occupied by these electrons up to a time scale that is on the order of the emission lifetime of D₀ (∼8 ns), which leads to dynamical deionization. If the laser excitation is sufficiently strong such that n_X ≫ n_D, the donors are in the freeze-out state, even though E_F < E_d. Similarly, we call this process a dynamical freeze-out.

Figure 4b shows a table to illustrate different bound exciton complexes (BXCs) associated with neutral and ionized donors. When E_d < E_F < E_c, the InSe flake is electrostatically undoped, and donors are in the freeze-out state, where E_c (E_v) denotes the energy of the conduction (valence) band edge. The laser-induced electrons in the conduction band cannot relax to donor levels. We thereby assign the X₀ emission in V_g ∈ [−0.5 V, 0 V] to the bare neutral exciton |X⟩. When E_v < E_F < E_d, all donors should be ionized because of the Fermi level position. However, in the presence of laser excitation, the optically generated electrons can be captured by donor ions to form a quasi-particle excited state |De;h⟩ and result in the PL emission of D₀. Here, we use the notation |De⟩ to express the neutral donor state and |D⟩ to express the ionized donor state, where D stands for the donor ion and e/h stands for the electron/hole.

In the low-power regime, the free exciton density is lower than the donor density, and most of the donors are ionized. Electrons in free excitons experience additional attractive interaction with the ionized donors, which induces an energy red shift. Since this type of exciton is not composed of electrons that are captured by donors, we attribute the X₀^′ emission in V_g ∈ [−5.8 V, – 0.5 V] to donor-dressed excitons |D;X⟩. Both |De;h⟩ and |D;X⟩ return to the ionized donor state |D⟩ after emitting photons. However, in the high-power regime, the number of excitons is much larger than that of donors, which leads to a saturation of the |De;h⟩ state. Moreover, the lifetime of |De;h⟩ is much longer than the exciton lifetime, which means that compared with that of excitons, the dynamics of |De;h⟩ can be regarded as a quasi-static process. Because of dynamical freeze-out, the excitons are immersed in an electrostatic environment in which the donors play no role.

On the basis of the above discussion, we expect that the energy difference between X₀ and X₀^′ (ΔE = E_X0 – E_X0^′) should change with the number of ionized donors, and thus, the excitation power. The red curve in Figure 4c depicts the energy difference ΔE as a function of the excitation power. The energy shift that vanishes at large powers constitutes solid evidence for our interpretation. On the basis of our model presented in Figure 4b, P ≈ 500 μW should correspond to n_X ≈ n_D. Therefore, we estimate the donor density is on the order of n_D = ∼10¹²–10¹³ cm^–2. A more detailed analysis can be found in Supplementary Note 10.

The carrier relaxations from the conduction band to the donor levels decrease the probability of generating bare excitons |X⟩. As a result, the intensity of both D₀ and X₀^′ are lower than X₀, as shown in Figure 2a. Finally, recalling that the binding energy of X₀ is double that of X₀, as shown in Figure 3c, we verify that the presence of ionized donors can effectively reduce the exciton binding energy.

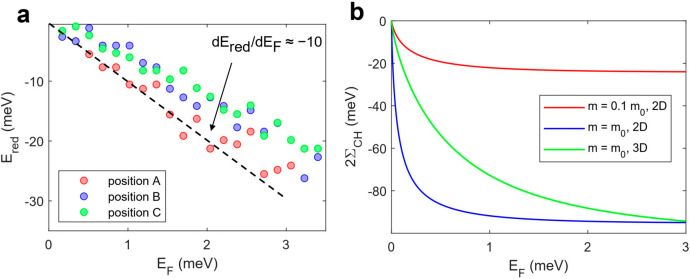
Next, we focus on the prominent red shift in the p-doped regime. To begin with, we quantify the red-shift energy E_red as a function of the Fermi energy E_F (Supplementary Note 11). We find the change of E_red is about 1 order of magnitude larger than the change of the Fermi energy dE_red/dE_F ≈ −10 (Figure 5a). Here, the minus sign denotes the red shift of the PL energy.

Figure 5.

Red shift in the p-doped regime and band gap renormalization. (a) Red-shift energy E_red in the p-doped regime as a function of the Fermi energy E_F, measured on positions A, B, and C in Figure 1d. (b) Calculated Coulomb hole term 2∑_CH as a function of the Fermi energy E_F for m = 0.1m₀ and m = m₀ in 2D (red and blue curve), and for m = m₀ in 3D (green curve).

Generally, the energy of PL emission E_PL can be described as E_PL = E_g – E_b, where E_g is the single-particle band gap. In the presence of a Fermi reservoir, dynamical screening of the electron–hole interactions leads to a lower binding energy E_b as the system approaches the Mott transition.³⁷ As a result, we expect that this gives rise to a vanishing PL intensity together with a blue shift as the carrier density is increased. For excitons in InSe, we expect a modest blue shift since E_b is a small quantity.

However, many-body screening also renormalizes the particle self-energies and results in a reduced E_g, which is referred to as the band gap renormalization (BGR).^38,39 The overall decrease of E_g can be represented in the following form: δE_g = ∑_SX + 2∑_CH, where ∑_SX is the screened exchange term and ∑_CH is the Coulomb hole term.⁴⁰ The former is a consequence of the reduced Coulomb repulsion arising from the exchange interaction due to the Pauli exclusion principle. The latter describes the energy decrease caused by the depletion shell around a charge carrier. The screened exchange term is on the order of the Fermi energy ∑_SX ≈ – 1/2E_F,³⁸ and hence, cannot explain the large red shift in the p-doped regime.

The Coulomb hole term is sensitive to the effective mass of particles in a Fermi liquid. The effect of many-body screening can be represented by introducing a dynamical dielectric function ϵ(q, ω) = V_q/W_q, where q is the wavenumber, V_q is the bare Coulomb potential and W_q is the screened Coulomb potential in momentum space. This allows us to calculate the Coulomb hole term via 2∑_CH = ∑_q(W_q – V_q). For a 2D system in the static limit, ϵ(q, 0) = 1 + κ/q. κ is the screening wavenumber that takes the form of κ = (e²/2ϵ₀ϵ_r)(∂n/∂μ), where μ is the chemical potential, ∂n/∂μ is the DOS, ϵ₀ is the vacuum permittivity, and ϵ_r is the dielectric constant of InSe. It is straightforward to notice that a heavier carrier mass (larger DOS) leads to a larger screening wavenumber and a stronger BGR. It explains our observation that the PL spectrum shows a strong red shift upon hole doping, whereas it almost remains constant upon electron doping (Figure S4f).

According to this picture, we calculate the Coulomb hole term as a function of the Fermi energy for two carrier masses m = 0.1m₀ and m = m₀. From the calculation results depicted in Figure 5b, we expect that the BGR induced by a hole reservoir (m = m₀, blue curve) is about 4–5 times larger than that induced by an electron reservoir (m = 0.1m₀, red curve). Since the calculations are performed in the static approximation, the Coulomb hole term is overestimated³⁸ (Supplementary Note 11). Nevertheless, the BGR model can estimate the red shift within a correct order of magnitude. The value of ∑_CH shows a saturation when E_F > 1 meV. However, our experimental results do not exhibit a clear saturation for the Fermi energies up to E_F = ∼3 meV. This can be explained by the fact that our InSe flake is thicker than a monolayer. The inverse of the screening wavenumber κ (Figure S10), which can be regarded as the screening length in 2D, is on the order of 0.3 nm, similar to the thickness of a monolayer. This means that for thicker flakes (∼5 nm for our sample), the 2D screening model is no longer precise. We develop the 2D model into a 3D model by replacing the expression of the dynamical dielectric function and screening wavenumber with ϵ(q, 0) = 1 + κ²/q² and 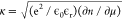(Supplementary Note 11). The green curve in Figure 5b presents the calculation result using the 3D model that predicts a more gradual change of ∑_CH with increasing Fermi energy.

Our results and analysis elucidate the origins of exciton species in different charge regimes and provide an insight into the optical signatures of strong many-body interactions between charge carriers. So far, the research on bound exciton complexes has been conducted mainly on bulk semiconductors. 2D materials have recently emerged as a highly tunable system that allows modifying the carrier density over a large range. Hence, our findings motivate further exploration of bound exciton complexes in charge-tunable 2D semiconductors. Observation of intense emissions from defect-bound excitons motivates the search for individual InSe-hosted single-photon emitters, similar to those that have been discovered in other layered semiconductors.^41,42

Methods

Sample Fabrication

The fabrication of samples was performed completely in an argon-controlled environment with an oxygen level of <0.01 ppm and moisture of <0.1 ppm. The heterostructures presented in this work were fabricated by a three-step dry transfer technique. First, the hBN and few-layer graphene (NGS) building blocks were exfoliated on silicon substrates with a 280 nm oxide layer to optimize the optical contrast. The bottom hBN flake was picked up with the dry-transfer method and released on top of the few-layer graphene (FLG) bottom gate. The few-layer InSe (HQ Graphene) flakes were exfoliated on PDMS (Gelpak), identified by optical contrast, and transferred on top of the previously fabricated hBN/FLG stack. The top hBN and FLG contacts were subsequently picked up, carefully aligned, and released on top of the InSe flake to fully encapsulate the heterostructure. All these steps were performed in an argon environment to avoid any contamination. Once completed, the sample was annealed at 340 °C in high vacuum at 10^–6 mbar for 6 h. Finally, electrical contacts were fabricated by e-beam lithography and metal evaporation (2/80 nm Ti/Au).

Optical and Electrical Measurements

All measurements shown in this work were carried out under vacuum at 4.5 K unless specified otherwise. PL measurements were performed by focusing a laser on a spot of about 1 μm diameter on the sample. Multiple laser sources have been used for this purpose: a tunable femtosecond pulsed laser (Coherent Chameleon) and a narrow-line-width tunable continuous-wave laser (MSquared), which was used for PLE measurements (Figure 3c). The incident power was varied from 1 μW to 5 mW for power dependence measurements (Figure 3a) and kept at 50 μW for the PL measurements shown in Figure 2. Transport measurements were carried out at room temperature with the Keithley 2636 Sourcemeter. TRPL measurements were performed by sending the collected photons to an APD (Excelitas Technologies, SPCM-AQRH-16). A time-correlated photon counting module (TCPCM) with a resolution of 12 ps rms (PicoQuant, PicoHarp 300) was connected to the output of the APD to measure the arrival time of the photons. The instrument resolution (full width at half-maximum) was 300 ps.

First-Principles Calculations

Our first-principles calculations were performed at the density-functional theory level as implemented in VASP.⁴³ We used the semilocal PBE functional⁴⁴ for all structure relaxations and the hybrid HSE06⁴⁵ for accurate band gap estimations of pristine systems. We obtained the correct band gap for defect calculations containing large supercells (where a hybrid functional could not be applied) by using a modified Becke–Johnson exchange potential in combination with LDA-correlation.^46,47 Electron–core interactions were described through the projector augmented wave (PAW) method,^48,49 while Kohn–Sham wave functions were expanded in a plane wave basis set with a cutoff on the kinetic energy of 400 eV. All structures were subjected to periodic boundary conditions, and a 4 × 4 supercell geometry was applied for the defect calculations. A vacuum layer of 10 Å perpendicular to the layers was used to prevent interaction between replica images. The integration over the Brillouin zone was carried out using a 10 × 10 × 1 and 3 × 3 × 1 k-point mesh for pristine and defective systems, respectively. Atomic positions and lattice constants were optimized using the conjugate gradient method, where the total energy and atomic forces were minimized. The convergence criterion for energy was chosen to be 10^–5 eV, and the maximum force acting on each atom was less than 0.01 eV/Å relaxation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.2c02965.

• Details of first-principles calculations, experimental setup, additional characterization of the device, extraction of the binding energy, theoretical model of band gap renormalization, and discussion on the Fermi polaron picture (PDF)

Author Contributions

^¶ G.P. and Z.S. contributed equally to this work. A.K. conceived and supervised the project. Z.S. and G.P. performed the optical and electrical measurements assisted by F.T. G.P. fabricated the samples. Z.S. built the experimental setups. Z.S. analyzed and explained the data with input from R.P.-C, E.M. and all authors. K.Č.. performed first-principles calculations with input from O.V.Y. K.W. and T.T. grew the h-BN crystals. Z.S. and A.K. wrote the manuscript with input from all authors.

We acknowledge support from Swiss National Science Foundation (grant no. 172543, 175822, 177007, and 164015) and the European Union’s Horizon 2020 research and innovation program under grant agreements 785219 and 881603 (Graphene Flagship Core 2 and Core 3). Computations by K.Č. and O.Y. were performed at the Swiss National Supercomputing Centre (CSCS) under project No. s1146 and the facilities of Scientific IT and Application Support Center of EPFL. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan (Grant Number JPMXP0112101001) and JSPS KAKENHI (Grant Numbers JP19H05790 and JP20H00354). E.M. acknowledges funding from Deutsche Forschungsgemeinschaft via CRC 1083.

The authors declare no competing financial interest.