MISL: Multiple Imputation by Super Learning

Abstract

Multiple imputation techniques are commonly used when data are missing, however there are many options one can consider. Multivariate Imputation by Chained Equations (MICE) is a popular method for generating imputations but relies on specifying models when imputing missing values. In this work, we introduce Multiple Imputation by Super Learning (MISL), an update to the MICE method to generate imputations with ensemble learning. Ensemble methodologies have recently gained attention for use in inference and prediction as they optimally combine a variety of user-specified parametric and non-parametric models and perform well when estimating complex functions including interaction terms. Through two simulations we compare inferences made using the MISL approach to those made with other commonly used multiple imputation methods and demonstrate MISL as a superior option when considering characteristics such as bias, confidence interval coverage rate, and confidence interval width.

Introduction

Missing data are ubiquitous in most health research; this is to be expected given questionnaires and research within health sciences require individuals to disclose sensitive information, recall information from the past, complete lengthy surveys, and not become lost to follow-up. From a technical standpoint, missing data can also occur for reasons outside the control of the research participant (data can be mishandled, technology may fail, files may become lost or corrupted, and/or the researcher may not collect the required information). Though reasons explaining why data become missing may never be known, researchers still take particular interest in understanding mechanisms of missingness as their presence and inappropriate handling may detrimentally impact the findings of an analysis^1,2.

Rubin³ first proposed a set of processes by which we could model patterns of missingness: missing completely at random (MCAR), missing at random (MAR), and/or missing not at random (MNAR)⁴. Methods for addressing missing data can be confusing as some are only recommended in specific scenarios⁵. It is thus understandable why missing data are commonly mishandled^6,7. While methods for handling missing data continue to emerge and shape the field (for example, under a causal inference framework^8,9), we broadly categorize missing data approaches into one of three classes: deletion based, single imputation based, and multiple imputation (MI) based methods. Deletion based methods discard incomplete cases which may lead to bias and loss of precision⁴ as well as a potential decrease in statistical power resulting from the reduction in sample size⁵. Single imputation methods are simple to implement however offer no distinction between imputed and observed values which can lead to attenuated variance estimates, inflated degrees of freedom¹⁰, and artificially increased relationships amongst variables⁵.

Multiple Imputation (MI) is superior to both deletion and single imputation-based approaches for at least three reasons. First, the method incorporates both random error and knowledge about the missing data process into the imputation procedure to produce estimates of standard errors that are neither artificially small nor unacceptably large (when compared to single imputation approaches)^11,12. Second, as opposed to deletion based methods, MI is efficient in that it utilizes the entirety of the data rather than discarding incomplete cases¹³. Finally, MI models the missingness within a particular dataset to obtain proper inference while acknowledging differences between observed and imputed values.

Multivariate Imputation by Chained Equations (MICE) (also known as fully conditional specification (FCS)) is a process for multiply imputing data on a variable by variable basis¹⁴. This procedure has been implemented into the R software¹⁵ and has risen in popularity since its release in 2011 (Figure 1). The MICE procedure is general and requires the user to specify a model for generating imputations. The default approaches in the mice package are defined by datatype and are predictive mean matching (PMM) (numeric and/or continuous data), logistic regression imputation (binary data), polytomous regression imputation (unordered categorical data greater than two levels), and proportional odds modeling (ordered categorical data greater than two levels). The mice package is constantly updating as the software is open source¹⁶; such improvements have helped modernize FCS by introducing more flexible non-parametric machine learning approaches like classification and regression trees (CART)¹⁷ and random forests (RF)¹⁸.

Figure 1:

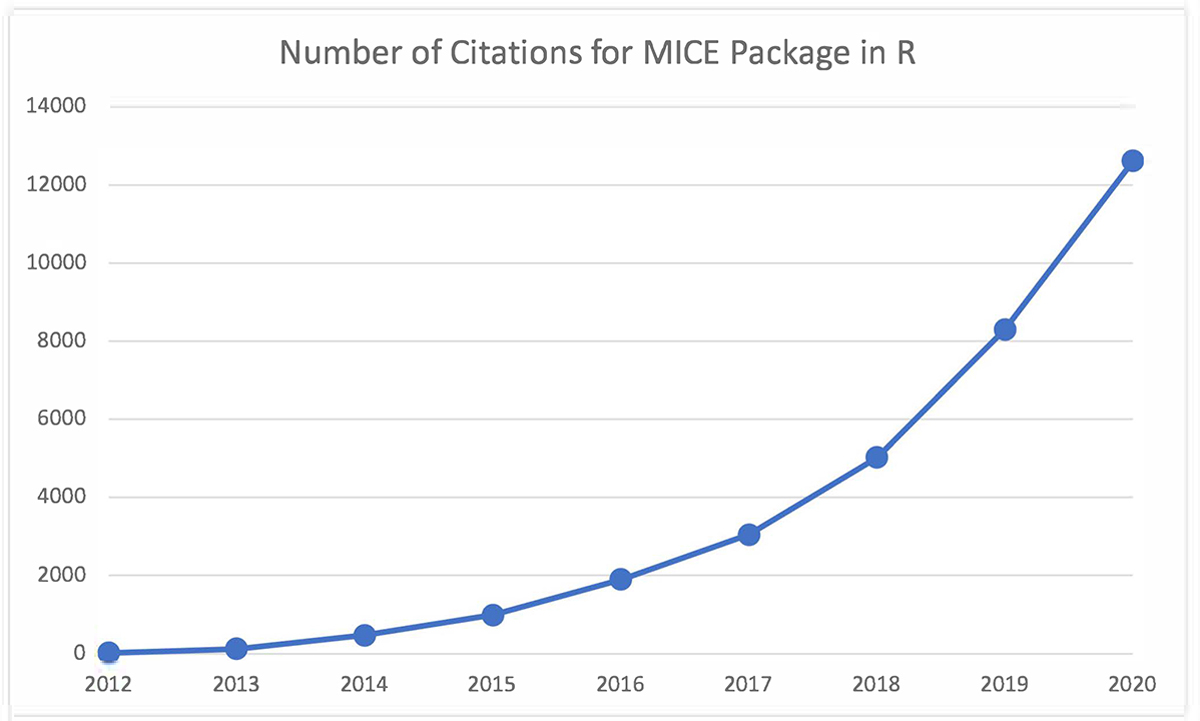
Number of citations for the package MICE in R since release in 2011. Source: www.webofknowledge.com, assessed March 2, 2021

To further improve FCS, this paper introduces Multiple Imputation by Super Learning (MISL), a novel imputation approach for obtaining valid inference from data containing incomplete numeric and/or categorical data. MISL uses super learning¹⁹, an ensemble algorithm capable of mixing both parametric and non-parametric models, to generate more unbiased and efficient parameter estimates in the presence and absence of interaction effects when compared to leading imputation methods. The greatest advantage and distinction of MISL is the lack of explicit modeling assumptions regarding the underlying univariate conditional distributions of the data. This is because MISL combines a user supplied list of candidate algorithms with cross-validation (CV) to independently model relationships between variables. This ensemble approach gives more flexibility and control to the analyst in how missing data are modeled while providing a platform to guarantee variability in imputations. This paper demonstrates through a series of simulations how MISL outperforms existing methodologies for generating multiple imputations under a variety of missing data scenarios while reducing the analyst’s burden in specifying strict conditional relationships amongst variables within an incomplete data set.

Multiple Imputation by Super Learning

Multiple Imputation, Fully Conditional Specification, and Methods for Imputation

MI refers to the procedure by which an incomplete dataset, Y, of dimension n × p, is made complete by generating m plausible values (imputations) for each missing observation, resulting in m distinct datasets, which are then analyzed independently and pooled for inference. This pooling occurs under the assumption the population parameter of interest is normally distributed or otherwise requires some transformation²⁰ (further information on the topic can be found elsewhere²¹). These imputations can be generated by FCS in which variables are imputed sequentially by conditionally modeling the variable containing missing data and the remaining variables of the incomplete dataset¹⁴. This process iterates M times until convergence at which point the imputations are said to be stable²².

The ways to conditionally model the relationship between variables in a dataset are varied dependent on the data type. PMM²³ remains one of the most popular methods for generating imputations for numeric data as it is easy to use and has been shown to produce reliably unbiased estimates of estimands, even in simulations where assumptions for its use have been violated²⁴. PMM is a hot-deck approach where regression coefficients modeling the relationship between the variable requiring imputation and remaining variables in a dataset are first drawn from a posterior distribution to then generate a pool of observed candidate donors from which imputations are sampled. The PMM algorithm can be adjusted in a few ways including the use of bootstrapping (rather than sampling β coefficients from a posterior distribution), specifying one of four differing matching criteria, and altering the number of candidates from which to sample²⁰. When data are not numeric one cannot use PMM and must rely on other methodologies for imputation (i.e., Bayesian imputation using logistic, multinomial, and/or ordered logistic regression, and decision trees).

Current FCS methods have some limitations. Regarding PMM, the method is not reliable where large amounts of data are missing and/or highly skewed²⁴. Further, if the conditional density is incorrectly specified, the resulting inference will be biased²⁵, especially in the presence of nonlinear relationships, namely cross-product and quadratic terms within a regression model (hereafter referred to as interaction effects)²⁶. With categorical data, Van Buuren²⁰ reports mixed results regarding generalized linear models (GLM) for imputation and recommends its use only when parameters can be reasonably well estimated. To capture more complex relationships between variables within an incomplete dataset, CART and RF have been suggested as a viable alternative to PMM and GLM. While these methods have been shown to perform favorably in instances where interaction effects are present²⁷, these methods do not estimate linear main effects well²⁶. Recent advances in statistical modeling present several advantageous methods to consider beyond parametric and semi-parametric modeling; these advances can help update existing tools used for imputation to create a method that can be used both in the presence and absence of interaction effects.

Super Learning

The primary concern with the aforementioned methods is that any sort of conditional modeling may lead to poorly imputed values if the relationship amongst variables is misspecified. In fact, this relationship may be more complex than what any one single algorithm alone could ever capture. Ensemble methodologies, such as super learning¹⁹, directly address this limitation and serve as the foundation for the proposed imputation method.

Super learning is an ensemble technique in which multiple models (“learners”) are combined using cross-validation to generate predictions that are at least as “good” (with respect to the specified loss function) as those from any one of the individual candidate learners¹⁹. For example, if one was interested in predicting a binary outcome, one could choose among: logistic regression, CART, or LASSO regression²⁸ models. While these algorithms each have their own advantages and disadvantages, it can be difficult to ascertain which would best model the true underlying relationship amongst predictors and outcome. Rather than selecting a single model, super learner will create a weighted combination of each individual learner chosen by minimizing the prediction error through cross-validation. The resultant super learner would then consist of an optimal ensemble fit determined by those weights (e.g., 27% logistic regression, 65% LASSO regression, and 8% CART). The super learner algorithm is gaining popularity in applied health research; examples can be seen with predicting acute hypotensive episodes during ICU hospitalization²⁹ and classifying virological failure for HIV-positive patients on antiretroviral therapy³⁰.

Two concerns with super learning and subsequently, MISL, are overfitting and computational efficiency. Overfitting is a common worry with many prediction algorithms³¹, however MISL alleviates this concern by ensuring variability in the process with random sampling (in that predictions are not directly substituted as imputations but merely used as intermediates for generating a pool of suitable matches, or “candidate donors”) and by cross-validation within the super learner³². With regards to computational efficiency, there is some concern with including additional candidate learners in the super learner library. However, both super learner and MISL readily implement parallelization, dramatically cutting down program runtime. Overall, the main advantage of super learner is that a cross validated ensemble will determine the “best” model (as defined by a loss-function) for prediction across all individual learners. This insurance of selecting the best unbiased estimator helps alleviate the concern of incorrectly specified conditional relationships and is the hallmark of both super learning and the proposed MISL method.

Multiple Imputation by Super Learning

The proposed MI approach, MISL, is an update to the already existing PMM and Bayesian GLM imputation methods; rather than strictly relying on linear modeling to define the relationship between the missing variable and remaining variables, an ensemble of candidate algorithms is used. As such, many of the theory-guided decisions supporting the construction of MISL are addressed in relation to other FCS methods (e.g. MICE) discussed elsewhere (e.g. the decision to implement bootstrapping as a means for calculating model weights for the super learner while simultaneously ensuring variability is captured within the process)²⁰. The full procedure for using MISL on an incomplete dataset Y of size n × p (Figure 2) is as follows:

1. For each variable j in j = 1, … p, MISL uses random sampling from the observed data to create a completed version of the data,$\dot{Y}$. (Figure 2: 1)

2. Starting from a random j, MISL selects a bootstrap sample of observations from $\dot{Y}$ for which variable j was originally observed,${\dot{Y}}_j^{boot}$. (Figure 2: 2 and 3)

3. A super learner models the conditional density of variable j using ${\dot{Y}}_j^{boot}$. This model is used to generate predicted values for all ${\dot{Y}}_j$ (both observed and missing). The predicted values for those missing observations in Y_j are denoted ${\widehat{Y}}_j^{mis,boot}$. (Figure 2: 4)

4. Depending on the datatype of variable j, the algorithm continues for each missing observation (i) as follows:

   1. Numeric

      1. A super learner (using the same learners from Step 4) models the conditional density of all observed values for variable j in $\dot{Y}$ and generates corresponding predictions (${\widehat{Y}}_j^{obs}$). (Figure 2: 4)
      2. A (hot-deck) match from the observed values is chosen for each missing value in Y_j by randomly sampling 1 of the 5 corresponding predictions generated using the bootstrapped data closest to the predicted values from the observed data (i.e., 1 of the 5 observations corresponding to the smallest $|{\widehat{Y}}_{j,i}^{mis,boot}-{\widehat{Y}}_j^{obs}|$). (Figure 2: 5 and 6)
   2. Categorical (K categories, K ≥ 2)

      1. Sample u_k, k = 1, …, (K − 1) from a uniform distribution U(0,1).
      2. The imputed category is equal to ${\sum }_{k=1}^{K-1}(u_k\le {\widehat{Y}}_{j,i,k}^{mis\text{,}boot})$, where ${\widehat{Y}}_{j,i,k}^{mis,boot}$ is the predicted probability of the missing observation i from variable j being in category k.

5. Once the entire column for variable j is imputed algorithm completes Steps 2–4 for each remaining variable. (Figure 2: 7)

6. This process iterates M − 1 more times until convergence.

7. The MISL algorithm begins anew (or completes in parallel), generating m − 1 distinct imputed datasets. (Figure 2: 8)

Figure 2:

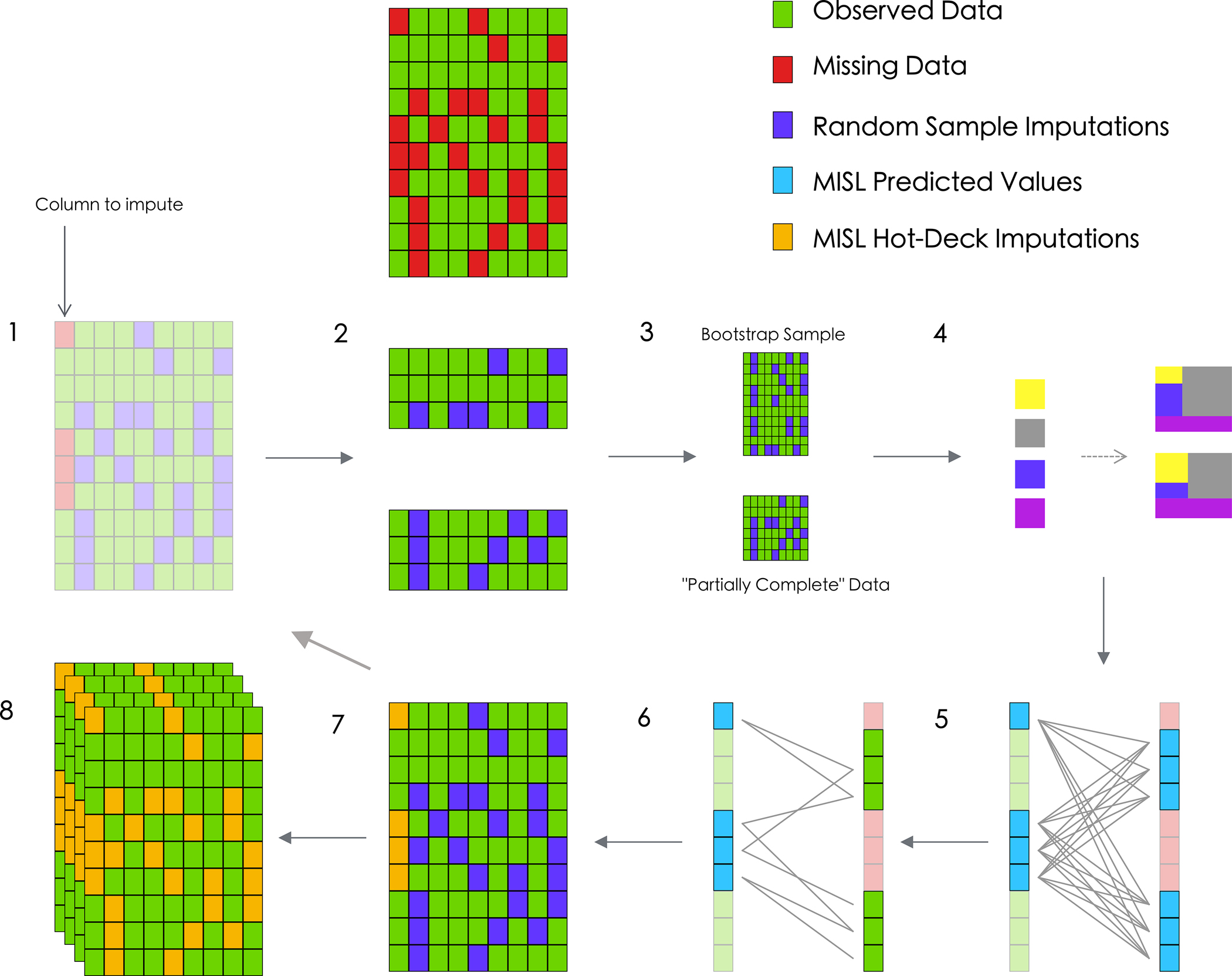
Diagram of the proposed MISL algorithm for a numeric variable. MISL first isolates a random column with missing data and further draws random samples as placeholders for each subsequent incomplete column (1). The algorithm then isolates rows for which data is observed for this column (2) and generates (3) a bootstrap sample from this subset data frame (top) while retaining the “partially complete” data with respect to that column (bottom). Super learner then generates an ensemble (4) predicting the column of interest conditionally using the remaining columns available in the data for both the bootstrap sample (top) and partially complete data (bottom). MISL then generates a distance metric among each of the super learner predictions (the missing values are predicted with the bootstrap super learner (left) and observed values are predicted with the partially complete data (right)) (5). For each MISL prediction, a set of corresponding candidates from the observed data are identified based on a distance metric (6). For each missing value, MISL randomly samples one of the candidate donors and imputes this value (7). The algorithm then continues with the next column containing incomplete data and begins imputation using the newly imputed MISL hot-deck imputations (2–7). Once all columns have been imputed, the algorithm iterates M times until convergence is reached in imputations. What results is a single completed dataset; the algorithm then continues m-1 more times (8) until m distinct (full) datasets are complete.

Simulated Data with Interaction Effects

Two distinct simulations were curated for the evaluation of MISL. First, to compare how MISL performs in instances with interaction effects, synthetic population level data were generated using a regression model as proposed by Burgette and Reiter²⁷ (and further expanded on by Doove, Van Buuren, and Dusseldorp²⁶):

$$\begin{gathered} y_i={\beta }_0+{\beta }_1{x}_{1,i}+{\beta }_2{x}_{2,i}+{\beta }_3{x}_{3,i}+{\beta }_4{x}_{8,i}+{\beta }_5{x}_{9,i}+{\beta }_6{x}_{3,i}^2+{\beta }_7{x}_{1,i}{x}_{2,i}+{\beta }_8{x}_{8,i}{x}_{9,i} \\ {y}_i=0+0.5x_{1,i}+0.5x_{2,i}+0.5x_{3,i}+0.5x_{8,i}+0.5x_{9,i}+0.5x_{3,i}^2+x_{1,i}{x}_{2,i}+x_{8,i}{x}_{9,i} \end{gathered}$$ (1)

Explanatory variables were drawn from a multivariate normal distribution: x₁ through x₄ with a correlation of 0.5 and x₅ through x₁₀ with a correlation of 0.3 of size n = 1,000. For 1,000 simulations, univariate missingness was generated in Y via a MAR mechanism dependent on both x₉ and x₁₀. Specifically, we generated a distribution of probabilities for the missingness in Y for each observation (i) using a weighted sum score (wss) of the values from x₉ and x₁₀ (wss_i = x_9,i + x_10,i) and induced missingness from either the tails, middle, right, or left of the generated joint distribution. Additional information on this procedure for generating missingness can be found elsewhere^15,33. After inducing missingness, roughly 50% of observations were completely observed. Population level data were drawn to remove sampling variability in evaluation of MISL.

For this simulation, four different imputation methods were compared. The first method used the novel MISL approach with the following learners specified: generalized linear modeling, multivariate adaptive regression splines, random forest, and support vector machines using the sl3 package in R³⁴. The remaining three models were PMM (predictive mean matching), CART (classification and regression trees), and RF (random forest) and were implemented using the package mice¹⁵. For all four imputation approaches, five multiply imputed datasets were generated each with five iterations until assumed convergence (m, M = 5). After each completed imputation, a properly specified linear model regressing Y on the remaining variables was fit (in accordance with (1)).

Models were then combined (independently) across each of the imputed datasets using the pool function in the mice package and corresponding bias, coverage rates, and confidence interval widths were calculated for each regression coefficient. These metrics were selected as imputation methods where bias is minimal, and coverage is proper are said to be randomization-valid²¹. Further, the inclusion of three evaluation metrics better describe the performance of any given imputation approach when compared to any single metric alone. For example, the coverage rate for a particular method may consistently be 100% signifying a beneficial technique but the corresponding confidence interval width may be infinitely wide proving the method to be unusable.

Results

The results displaying confidence interval average width, coverage rate, and raw bias for model (1) can be seen in Table 1. For each regression coefficient, MISL has the highest (or, tied for highest) coverage rate and this coverage hovers around 95% for nearly all regression coefficients. MISL further has the smallest average confidence interval width and raw bias closest to zero for each coefficient. PMM tends to have the widest confidence interval widths followed by RF and CART approaches. In no instance did PMM, CART, or RF outperform MISL for any of the evaluation metrics.

Table 1.

Summary of results for simulation 1 for each of the four imputation methods. The imputation methods are described as multiple imputation by super learning (MISL), predictive mean matching (PMM), classification and regression trees (CART), and random forest (RF). Measurements are defined as coverage rate (CR), average confidence interval width (A W), and raw bias (RB).

β	Method	CR	AW	RB
β 0	MISL	0.67	0.08	0.03
	PMM	0.11	0.41	0.37
	CART	0.03	0.21	0.23
	RF	0.03	0.32	0.32
β 1	MISL	0.99	0.08	−0.01
	PMM	0.94	0.39	0.01
	CART	0.74	0.21	−0.02
	RF	0.96	0.34	−0.06
β 2	MISL	0.98	0.09	−0.01
	PMM	0.83	0.39	−0.04
	CART	0.69	0.22	−0.05
	RF	0.93	0.35	−0.06
β 3	MISL	0.99	0.07	0.00
	PMM	0.87	0.37	−0.05
	CART	0.81	0.21	−0.01
	RF	0.99	0.33	−0.01
β 4	MISL	0.97	0.07	−0.01
	PMM	0.57	0.33	−0.09
	CART	0.46	0.18	−0.10
	RF	0.58	0.28	−0.12
β 5	MISL	0.99	0.07	−0.01
	PMM	0.88	0.36	−0.05
	CART	0.61	0.18	−0.07
	RF	0.71	0.29	−0.10
β 6	MISL	0.79	0.06	−0.02
	PMM	0.41	0.23	−0.13
	CART	0.56	0.14	−0.05
	RF	0.67	0.23	−0.09
β 7	MISL	0.82	0.08	−0.02
	PMM	0.10	0.30	−0.27
	CART	0.06	0.18	−0.22
	RF	0.04	0.29	−0.26
β 8	MISL	0.91	0.10	−0.02
	PMM	0.01	0.26	−0.38
	CART	0.01	0.16	−0.29
	RF	0.00	0.26	−0.36

Simulated (Applied) Data without Interaction Effects

Following the advice of previous research^20,35, a second simulation was created to both compare imputation methods in instances where interaction effects were not present and the relationship amongst variables was not known to gain insight into the imputation process. The dataset used for these simulations describe medical expenses for patients in the United States. Of importance, this dataset was simulated from the U.S. Census Bureau and were created for the book, Machine Learning with R³⁶. This dataset was selected as it is complete, adequately sized, contains both numeric and categorical data (both two and three levels), and is readily available via the publisher’s Github page³⁷. This data was not selected to gain meaningful inference about the cost of medical expenses in the United States but to serve as tool for evaluating the proposed imputation approach. The dataset contains 1,338 observations, six covariates: Age (numeric), BMI (numeric), Number of Children (numeric), Smoking Status (binary), Region (categorical), and Sex (binary), and one outcome: Expenses (numeric).

To remove the impact of model variability and to estimate population parameters from a known distribution, we replaced the observed outcome with predictions from a simple main effects linear model (with no interaction effects). This ensured our regression model fit the data and further allowed us to critically evaluate MISL without concern of the observed data being influenced by the sampling mechanism (only the missing data mechanism). This dataset with predicted outcomes served as our complete population level data for all subsequent simulations. Simulations were generated by selecting all permutations from a given organization of how data could be missing. This included specifying the relative proportion of cases with missing data values (0.10, 0.25, 0.50, 0.75), how the missingness was generated (MCAR, MAR), and where the missingness was present (covariates only, outcome only, both covariates and outcome- also known as “mixed”). A similar procedure to simulation one was used to induce missingness with a weighted sum score when data were MAR. This resulted in a total of 24 unique missing data scenarios. Under each missing data scenario, 1,000 unique datasets were generated.

As with the previous simulation, for each iteration a correctly identified linear model was specified and multiply imputed datasets were pooled for inference. MISL was compared to those methods in Table 2 and corresponding bias, coverage rates, and confidence interval widths were reported.

Table 2.

Description of each of the four imputation methods with associated models. Acronyms are as follows: Generalized Linear Model (GLM), Multivariate Adaptive Regression Splines (MARS), Random Forest (RF), Support-vector Machines (SVM), IBR (Independent Binomial Regression), Predictive Mean Matching (PMM), and Recursive Partitioning and Regression Tree (RPART). Implementation of each of the MISL and MICE models are used directly with the SL3³⁴ and MICE¹⁵ packages in R.

Method	Numeric	Binary	Categorical
MISL	GLM, MARS, RF, SVM	GLM, MARS, RF	IBR, RF, SVM
MICE (Default)	PMM	GLM	GLM
CART	RPART	RPART	RPART
Mixed	PMM	GLM	RPART

Results

Results for data where the covariates are MCAR can be seen in Figure 3. In all instances MISL has the narrowest (or, tied for most narrow) average 95% confidence interval width and this width remains relatively unchanged across the percentage of missingness. MISL has approximate 95% coverage foreach regression coefficient though this coverage decreases at high proportions of missingness (0.75) for categorical variables with more than 2 levels. In all instances, MISL has a raw bias closest to zero. In instances of a tied bias, the competing approach has a wider average confidence interval width when compared to MISL. These results are further mimicked with MAR covariate data (see supplemental material).

Figure 3:

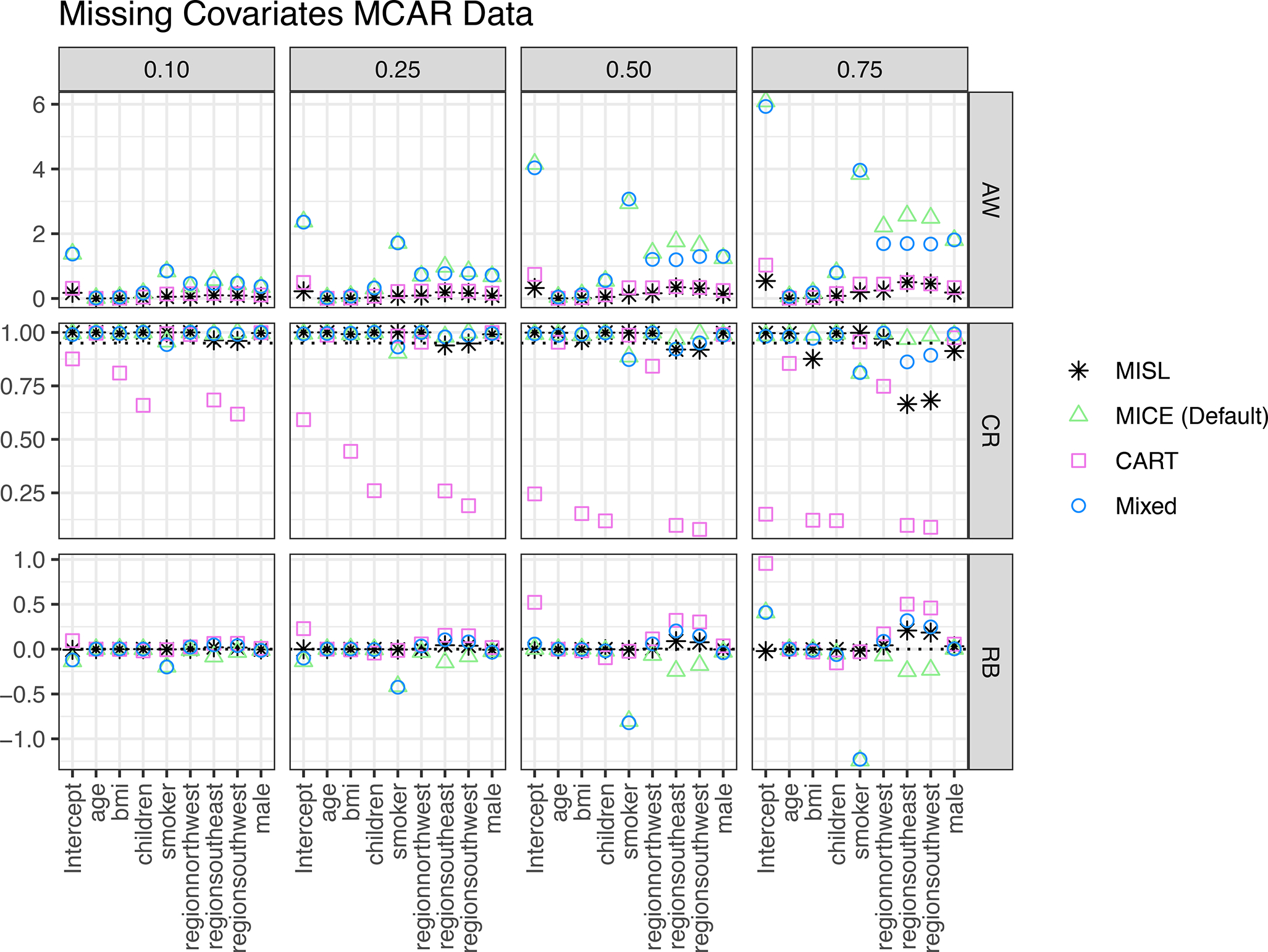
Simulation results including average 95% confidence interval width (AW), coverage rate (CR), and raw bias (RB) for regression coefficients based on 1,000 simulations of MCAR missingness present in covariates (only) across different proportions of missing data (0.10, 0.25, 0.50, 0.75). Methods include MISL, the default methods in MICE (MICE (Default)), classification and regression trees (CART), and a combination of the default imputation methods in MICE along with classification and regression trees (Mixed).

Results for data that were MAR in the outcome of interest (only) can be seen in Figure 4. In all instances (across all percentages of missingness for all measurements), MISL performs identically to the default methods of the MICE package. Specifically, MISL and MICE (Default) have the narrowest 95% confidence interval width, highest coverage rate, and raw bias closest to zero. These results are further mimicked with MCAR outcome data (see supplemental material).

Figure 4:

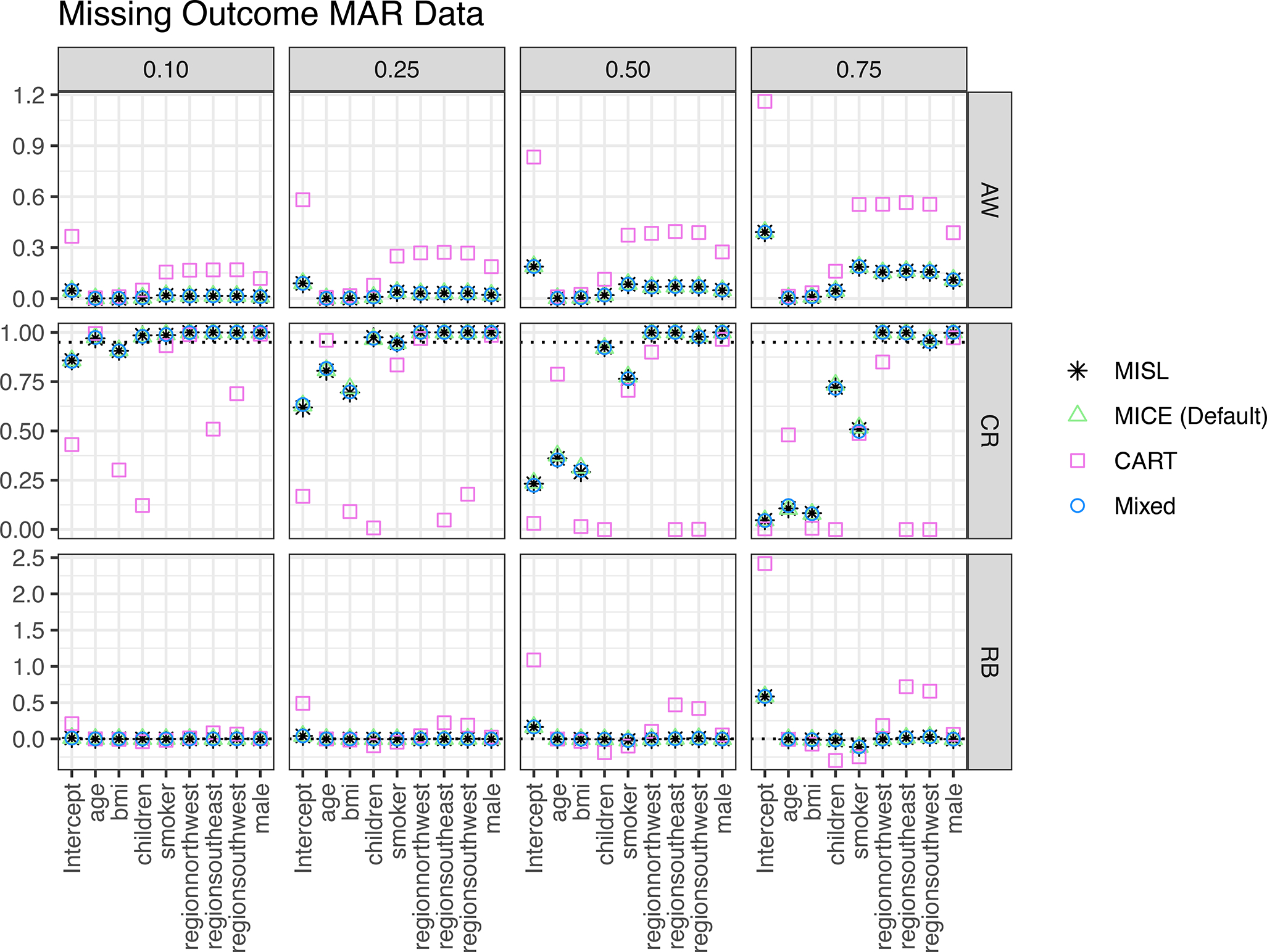
Simulation results including average 95% confidence interval width (AW), coverage rate (CR), and raw bias (RB) for regression coefficients based on 1,000 simulations of MAR missingness present in the outcome (only) across different proportions of missing data (0.10, 0.25, 0.50, 0.75). Methods include MISL, the default methods in MICE (MICE (Default)), classification and regression trees (CART), and a combination of the default imputation methods in MICE along with classification and regression trees (Mixed).

Results for scenarios with MAR data in both covariates and outcome can be seen in Figure 5. In nearly all instances MISL has the narrowest average 95% confidence interval width though this is not true for large amounts of missing data (0.75). In these instances where MISL does not have the narrowest 95% confidence interval, MISL has a superior coverage rate and least biased estimate of the regression coefficient. MISL has approximate 95% coverage for each regression coefficient though this coverage (again) decreases at high proportions of missingness (0.75) for categorical variables with more than two levels. In nearly all instances, MISL has a raw bias closest to zero. When this was not the case, the lesser biased imputation approach has a wider average confidence interval width when compared to MISL. These results are further mimicked with MCAR in both covariates and outcome data (see supplemental material).

Figure 5:

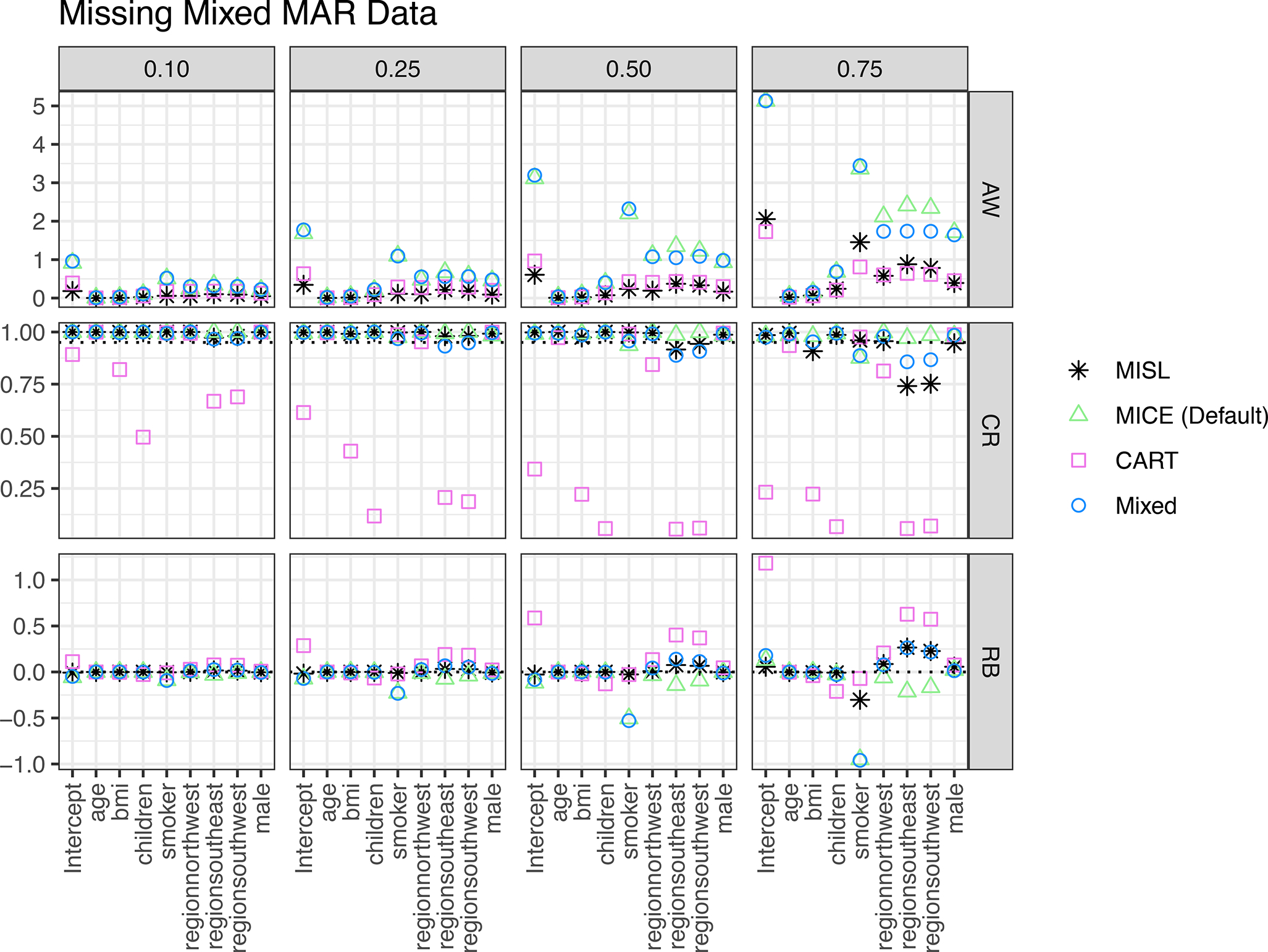
Simulation results including average 95% confidence interval width (AW), coverage rate (CR), and raw bias (RB) for regression coefficients based on 1,000 simulations of MAR missingness present in both the covariates and outcome across different proportions of missing data (0.10, 0.25, 0.50, 0.75). Methods include MISL, the default methods in MICE (MICE (Default)), classification and regression trees (CART), and a combination of the default imputation methods in MICE along with classification and regression trees (Mixed).

Discussion

With two different simulations we have shown MISL to be the preferred approach for imputation when compared to existing FCS methods as it can be used to reliably obtain less biased parameter estimates, both in the presence/absence of interaction effects, under a variety of missing data scenarios when compared to commonly used imputation approaches. MISL is a statistically appropriate and randomization-valid method for generating imputations; the only differences between MISL and existing accepted methods (like, PMM and CART) include how conditional relationships are modeled and how uncertainty is ensured within the procedure. For example, PMM relies on three methods for guaranteeing variability in imputations: generating initial random draws, Bayesian sampling parameter estimates, and sampling from a pool of candidate donors. In addition to generating initial random draws, relying on bootstrapping (rather than Bayesian sampling), and sampling from a pool of candidate donors, MISL adds an additional layer of uncertainty with cross-validation.

The first simulation demonstrates how MISL preserves interaction effects after imputation and generates unbiased and efficient estimates regardless of the underlying data structure for all regression coefficients. In instances where MISL does not achieve 95% coverage, we observe a bias closest to zero – a tradeoff from generating efficient confidence intervals. These results are in agreement with previous research²⁶ showing PMM expectantly generates unbiased estimates for most main effects (β_1,2,3,4,5) though not interaction terms (β_6,7,8). At first glance RF appears to reasonably compete with MISL, as demonstrated by comparable coverage, but at the cost of providing severely biased point estimates and unacceptably wide confidence intervals. CART neither achieves proper coverage nor unbiased point estimates and performs least favorably compared to all three methods. In instances where known interaction effects are present, MISL is the dominant imputation approach.

The second simulation first highlights how MISL prioritizes accuracy and efficiency to reliably obtain inference without large, uninterpretable confidence intervals. These results hold across most proportions of missingness and across different missingness scenarios. When the proportion of missingness is exceptionally high (0.75) and the variable of interest is a categorical variable with more than two levels, MISL’s coverage is less than 95% and subsequent point estimates exhibit slight bias; this may be a direct consequence of MISL both consistently generating precise point estimates, resulting in little uncertainty between datasets giving rise to narrower pooled confidence intervals, but also due to perfectly predicting categorical variables. While potential solutions have been proposed to address “perfect prediction”, it is unclear which method works best²⁰. Techniques in the mice package use a data augmentation method³⁸ whereas MISL uses a bootstrapping method; further research should investigate this phenomenon at such extreme levels of missing data and its impact on imputations generated by MISL.

This simulation further demonstrates the single most valuable aspect of MISL: when a correctly specified model exists among other “extraneous” learners in the candidate library, super learner may generate unbiased point estimates. This flexibility allows researchers to combine inference-based procedures (e.g. linear models) with prediction-based approaches (e.g. neural networks) as super learner generates imputations by choosing the combination of learners (or, single learner) that minimizes the cross-validated risk¹⁹. An example of this phenomenon can be seen in Figure 4 where we believe a simple linear model best describes the relationship among variables in the dataset, explaining why MISL performs identically to MICE (Default). The results from this simulation also show that while the coverage rate appears poor for the coefficients age, BMI, children, and smoker, the raw bias for both MISL and MICE (Default) is almost zero, signifying nearly precise point estimates. Regarding the coefficient smoker, we observe unbiased estimates, poor coverage and (relatively) wider confidence intervals for both MISL and MICE (Default); these results are explained by the generation of a skewed distribution of confidence interval widths in simulations when coverage was not obtained and further depict the importance of considering multiple evaluation metrics when assessing the quality of imputations.

To our knowledge one other competing multiple imputation method using super learning has been developed, SuperMICE³⁹, however we believe the MISL procedure we present is preferable. First, SuperMICE generates imputations from random draws from a normal distribution as parameterized by predictions which does not safeguard against possibly nonsensical imputations (e.g. negative BMI). The hot-deck-based approach employed by MISL will prevent such nonsensical imputations. Likewise, SuperMICE has no explicit/theoretical justification for the kernel function bandwidth, which remains an “area of active research.” Third, unlike MISL, the SuperMICE method cannot be used for categorical variables (only continuous and binary). Fourth, there is no mention of parallelization or code optimization for the SuperMICE function – we believe this method to have a longer runtime than our MISL. Fifth, this SuperMICE code uses an older version⁴⁰ of super learning and not the newer SL3 package³⁴ used by MISL that allows for more customizations and extensions.

There are a few limitations to this study and the proposed MISL algorithm. First, we recognize it is not possible to simulate all possibilities of missingness in datasets of all sizes. We did not vary the number of observations in each of our datasets nor did we exhaust the amount of missingness present in our simulations; these choices were made given the similarity to PMM and prior research reporting both accurate inference when the number of observations vary in size⁴¹ and also possibility of convergence in imputations even in the presence of extreme (> 99%) missingness²⁰. Likewise, we did not vary the number of covariates in simulations. This decision was made as we expect individuals to always use all possible covariates when specifying conditional relationships; a future study should examine the impact of screening algorithms (algorithms within the super learner designed to carry out feature selection) on coverage rate, bias, and efficiency. Second, like any hot-deck approach, MISL cannot impute either beyond the range of observed data nor in-between sparse data; we expect this to likely not be a concern with MISL. Further, we did not evaluate MISL with different candidate learners. This decision was made as there is no risk in adding more learners to the super learner library as the method will always choose an estimator which produces the smallest cross-validated risk, even among misspecified models³². We recommend adding both parametric and non-parametric models to the candidate library, allowing the super learner to model the conditional relationships amongst variables. As previously mentioned, there is some concern with the runtime of MISL however, parallelization has shown to dramatically reduce the method’s average time for computation (from 32 to 6 minutes). We hope to focus future work on making this algorithm more computationally efficient, as seen with the MICE algorithm (6 seconds). Finally, we may only recommend MISL in situations when data are MAR (and optionally MCAR) as further research and simulations are needed to develop adaptations to appropriately generate imputations when data are MNAR. Likewise, given the growing interest in generating imputations created under a causal inference framework^8,9, and its potential for longitudinal missingness, future studies should include investigations with a focus on time-varying covariates and potential outcomes⁴².

Despite these limitations, MISL is preferred over existing methods for imputing numeric, binary, and categorical data as it is flexible, easy to use, and allows the user to specify any conditional relationship they otherwise would with existing methods under the FCS framework. For ease of use and dissemination, we will either incorporate the MISL algorithm into the existing mice package or distribute it as its own R package. Our results demonstrate that MISL is more efficient and less biased when compared to more commonly used methods, and can provide proper estimation in a variety of missing data scenarios both in the presence and absence of interaction effects. MISL provides the groundwork for generating more desirable imputations; as modeling advances so too will our capacity to recover population level estimates in the presence of missing data.