Enhanced quantum sensing with room-temperature solid-state masers

Abstract

Quantum sensing with solid-state electron spin systems finds broad applications in diverse areas ranging from material and biomedical sciences to fundamental physics. Exploiting collective behavior of noninteracting spins holds the promise of pushing the detection limit to even lower levels, while to date, those levels are scarcely reached because of the broadened linewidth and inefficient readout of solid-state spin ensembles. Here, we experimentally demonstrate that such drawbacks can be overcome by a reborn maser technology at room temperature in the solid state. Owing to maser action, we observe a fourfold reduction in the electron paramagnetic resonance linewidth of an inhomogeneously broadened molecular spin ensemble, which is narrower than the same measured from single spins at cryogenic temperatures. The maser-based readout applied to near zero-field magnetometry showcases the measurement signal-to-noise ratio of 133 for single shots. This technique would be an important addition to the toolbox for boosting the sensitivity of solid-state ensemble spin sensors.

Room-temperature masers enable the performance enhancement of quantum sensors by the threshold and amplification effects.

INTRODUCTION

Quantum sensing exploits high sensitivity of quantum systems to external disturbances for measurements of physical quantities. Various systems, such as atomic vapor, Rydberg atoms, and superconducting circuits, have been extensively studied and invoked marked development of a variety of state-of-the-art sensors (1). Most recently, solid-state electron spin systems, e.g., nitrogen-vacancy (NV) defects in diamond (2), without the need for heating, vacuum, or cryogenic conditions, have emerged as an increasingly favorable platform for ultrasensitive quantum sensing of magnetic/electric fields (3–7) and temperature (8, 9), with advantages over other systems in terms of the robustness (10), biocompatibility (11), and spatial resolution (12).

An intriguing feature of quantum sensors is that their ultimate sensitivity, predominantly determined by quantum projection noise, can be further improved by increasing the number of noninteracting spins (12). This approach (using uncorrelated spin ensembles) is nowadays widely used in solid-state spin sensors for sensitivity enhancement (3). However, there are two obstacles existing toward realizing solid-state ensemble spin sensors with a sensitivity approaching the quantum projection noise limit, which fundamentally arises from quantum mechanical uncertainty (13). First, increasing spin density unavoidably introduces complexities and variations in the local environment of individual spins, manifesting as broadened linewidth of the ensemble. Solid-state ensemble spin sensors exploiting slope detection will thus struggle to sense slowly varying physical quantities, such as (near-)dc fields and biotemperature variations (3, 8). Although several pulsed techniques, e.g., pulsed optically detected magnetic resonance (pulsed-ODMR) (3, 14), have been applied to eliminate power broadening of the resonance, solid-state ensemble spin sensors also often suffer from the lack of efficient readout schemes, which is the second obstacle. Optical readout based on the detection of spin state–dependent photoluminescence (PL) is, to date, the most common readout technique but suffers from low readout fidelities arising from nonnegligible photon shot noise (i.e., fluctuations of the collected fluorescence photons) (3). Albeit for spin ensembles, the collected PL signals are magnified, the optical readout fidelity is not necessarily improved because the measurement contrast is degraded by the elevated background luminescence from the spins or impurities not contributing to sensing (15). Overall, inefficient readout of solid-state ensembles results in the sensor sensitivities being limited by photon shot noise about two orders of magnitude worse than the quantum projection noise limit (3).

In this work, we use the recently developed room-temperature maser (an acronym of microwave amplification by stimulated emission of radiation, i.e., the microwave analog of a laser) (16–21) for quantum sensing and demonstrate that the threshold behavior and microwave amplification of maser action can be exploited in solid-state ensemble spin sensors for simultaneously addressing both issues mentioned previously. On the basis of an organic solid-state spin system, constituted by photoexcited triplet electron spins of pentacene in p-terphenyl, we realize masing-assisted narrowing of the pentacene-ensemble magnetic resonance line shape, of which half-width at half-maximum (HWHM) is substantially reduced to about 130 kHz at room temperature, almost a half of that obtained from a single pentacene molecule at cryogenic temperatures (22). As a first application of room-temperature solid-state masers since its invention (16), we exploit the line narrowing and maser-amplified readout in near zero-field magnetometry with a sensitivity of 42 $\text{pT}/\sqrt{\text{Hz}}$, which is one to two orders of magnitude improvement compared with the (near)zero-field magnetometers using nitrogen vacancies in diamond (23, 24).

RESULTS

Theory of masing-enhanced quantum sensing

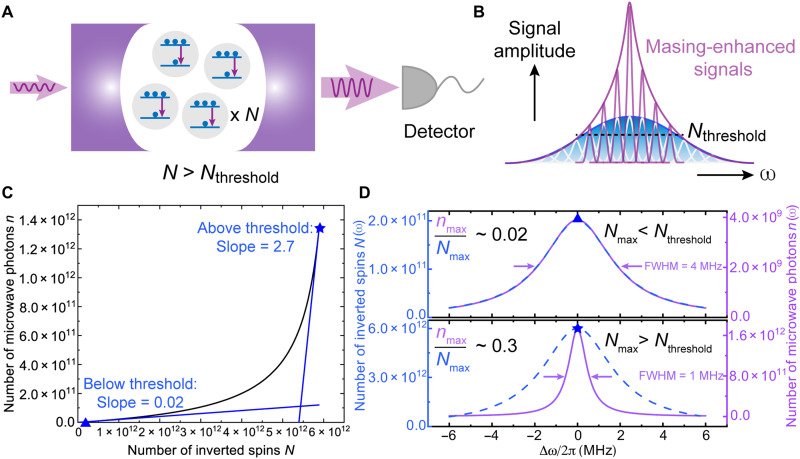
The concept of masing-enhanced quantum sensing is schematically illustrated in Fig. 1 (A and B). We consider a solid-state spin ensemble that comprises N two-level spin systems with microwave transitions. We assume population inversion, which can be achieved by microwave pumping at cryogenic temperatures (25) or optical hyperpolarization protocols (16, 17). Masing occurs when the ensemble is placed in a microwave resonator and the stimulated emission is induced by the injected microwave photons (acting as probe signals) on resonance with the inverted spins, yielding an increased number of microwave photons in the resonator, n. When N is sufficiently large and surpasses a threshold value N_threshold, the stimulated emission will be dominant over loss mechanisms in the resonator resulting in a surge of detected microwave photons, thus substantially enhancing the readout signals (see Fig. 1A). For the solid-state spin ensemble with inhomogeneous broadening, its magnetic resonance line shape can be regarded as a convolution of line shapes of subensembles with different resonance frequencies and amplitudes, as shown in Fig. 1B. The amplitudes are associated with the number of the inverted spins detected via magnetic resonance. Under the condition that certain subensembles near the line center fulfill the requirements of masing, the detected amplitudes are markedly enhanced resulting in overall narrowing of the resonance line shape, which can benefit the slope detection–based quantum sensing (1).

Fig. 1. Concept and simulation results of the masing-enhanced quantum sensing.

(A) Stimulated emission of radiation (downward arrows) occurs when spins with population inversion in a resonator interact coherently with injected microwave photons (left-hand side arrow). The amount of detected microwave photons (right-hand side arrow) is substantially increased, so-called masing, if the inverted spins N is greater than the masing threshold (N_threshold). (B) Schematic illustration of the masing effect on ensemble spin resonance. An ensemble spin resonance spectrum (blue curve) constitutes numerous subensembles (white) with different resonant frequencies. The signal associated with specific subensembles where the amount of inverted spins N is greater than N_threshold can be enhanced by maser action (purple packets). The observed linewidth is narrowed correspondingly (purple envelope). (C) Simulation of the threshold behavior with the predator-prey model. The number of microwave photons n in a resonator increases nonlinearly with the number of inverted spins N. The blue triangle (N = 2 × 10¹¹) and star (N = 6 × 10¹²) representing the typical values of N in the below- and above-threshold regimes are labeled with the associated tangent lines and slopes. (D) Simulation of the masing effect on measured ensemble spin resonance. The distribution of the inverted spins across the resonance N(ω) is set to be Lorentzian (blue dashed lines). On the basis of the correlation of n with N simulated in (C), by varying the amplitude of the distribution N_max [blue triangle and star from (C)], the measured spin ensemble resonance in the below- (top) and above-threshold (bottom) regimes is reflected by distinct distributions of the detected number of microwave photons n(ω) (purple solid lines) in terms of the amplitude and linewidth.

First, we validate the above concept by simulating the effects of maser action on the magnetic resonance feature of a solid-state spin ensemble. The predator-prey model (21, 26) constituted by a pair of first-order nonlinear differential equations (see Materials and Methods) is used to simulate the correlation between N and n in the presence of a high–Purcell factor microwave resonator (27). The threshold behavior is observed in Fig. 1C, clearly revealing the below- and above-threshold regimes in which the two representative N values 2 × 10¹¹ and 6 × 10¹² are chosen, respectively, for the following analysis. The slope at N = 6 × 10¹² is two orders of magnitude larger than that at N = 2 × 10¹¹, indicating the nonlinearity of the correlation between N and n. Therefore, above the threshold, a slight increase in inverted spins results in an exponential increase in detected microwave photons.

We apply the obtained threshold-like correlation to an inhomogeneously broadened spin ensemble with an intrinsic transition linewidth of 4 MHz. When all subensembles have fewer inverted spins than N_threshold, there is no masing. This leads to the measured magnetic resonance line shape, constituted by microwave photons across different frequencies n(ω), identical to the intrinsic transition line shape, as shown in the top Fig. 1D. In contrast to the below-threshold condition (N = 2 × 10¹¹), for the spin ensemble with a central subensemble where N = 6 × 10¹² surpasses the masing threshold, the observed resonance linewidth is markedly reduced to 1 MHz (see Fig. 1D, bottom) because the line shape is dominated by the maser transitions occurring across a narrower frequency range. In addition to the linewidth narrowing, a 30-fold increase of inverted spins N from 2 × 10¹¹ to 6 × 10¹², leading to a transition from the below- to the above-threshold regime, results in a boost of microwave photons n in the resonator by a factor of ∼450. Hence, the obtained ratio of the microwave photons n_max to inverted spins N_max increases by a factor of 15 implying a nonlinear enhancement of peak amplitudes by masing.

Spin system and experimental setup

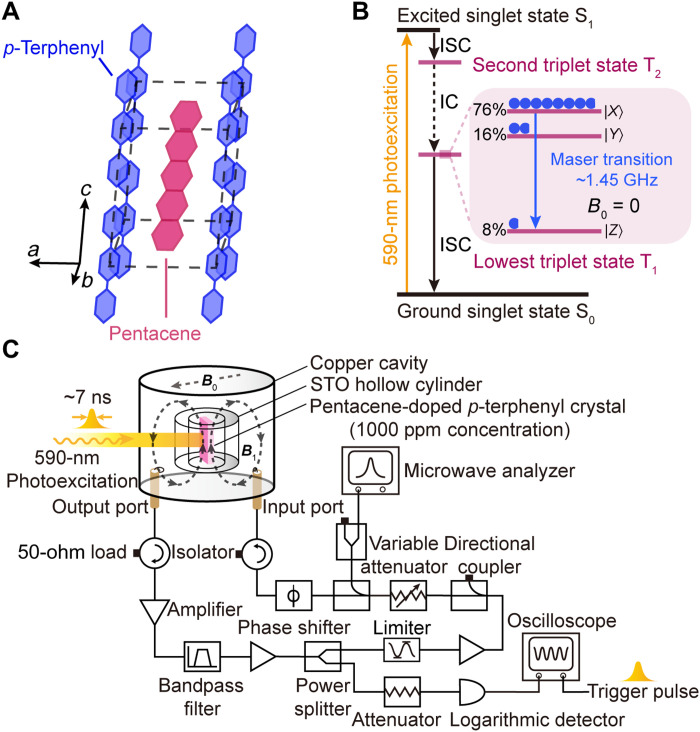
The simulation results drove us to investigate the effects of maser action experimentally. Pentacene-doped p-terphenyl is a suitable testbed because it supports masing at room temperature in solid state at zero magnetic field (16). The maser action is achieved by exploiting the photoexcited triplets of pentacene, which are generated through the triplet mechanism demonstrated in Fig. 2B. The photoexcited triplets are highly polarized, and a maser transition at ∼1.45 GHz is allowed between the ∣X⟩ and ∣Z⟩ sublevels in zero field. It is worth noting that, in contrast to the well-known color center systems such as NV and SiV centers in diamond or silicon carbide, substantially higher doping levels [up to 1000 parts per million (ppm)] can be achieved for pentacene in the lattice of p-terphenyl, see Fig. 2A, facilitating masing.

Fig. 2. Spin system and experimental setup.

(A) Monoclinic crystal structure of pentacene-doped p-terphenyl. (B) Simplified Jablonski diagram depicting the origin of pentacene triplet spins and the ∣X⟩ ↔ ∣Z⟩ maser transition at zero field. The population distributions on the three sublevels ∣X⟩, ∣Y⟩, and ∣Z⟩ of pentacene’s lowest triplet state T₁ are labeled and indicated by the blue circles. ISC, intersystem crossing; IC, internal conversion. (C) Experimental setup for line shape measurements and sensing an external magnetic field. B₁, the microwave field generated in the strontium titanate (STO) resonator; B₀, the static magnetic field applied for sensing.

In this work, a pentacene-doped p-terphenyl crystal with a doping concentration of 1000 ppm is used (see Materials and Methods) in the experiments. A frequency-tunable regenerative microwave oscillator, configured by a strontium titanate (STO) microwave resonator and a feedback loop, shown in Fig. 2C, is used as a zero-field magnetic resonance spectrometer for determining the resonance features of the sample under various conditions, as demonstrated in the next section.

Masing effects on magnetic resonance line shape

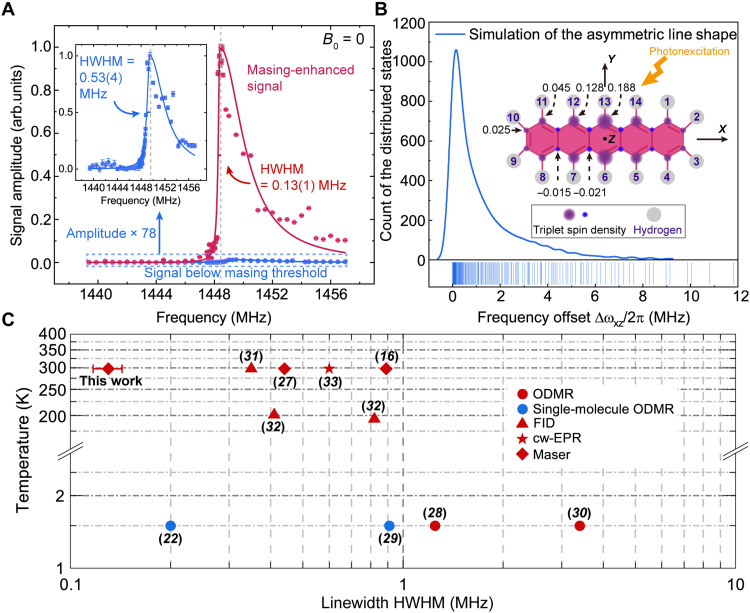
Using the setup shown in Fig. 2C, the zero-field ∣X⟩ ↔ ∣Z⟩ resonance features below and above the masing threshold are investigated using different optical pump energies (see Materials and Methods). As demonstrated in Fig. 3A, the linearly normalized line shape measured with masing reveals a prominent enhancement of the resonance amplitude by a factor of 78, with respect to that detected below the threshold. As the number of pentacene triplet spins is only increased by 50 times from the below- to above-threshold regime, this also confirms the nonlinearity of the threshold behavior and reveals the potential of maser action for nonlinear enhancement of sensitivity.

Fig. 3. Masing effects on the line shape of pentacene’s ∣X⟩ ↔ ∣Z⟩ transition at zero field.

(A) Comparison of the line shapes obtained below (blue) and above (red) the masing threshold. The measured signal amplitudes (dots) with the error bars denoting SEs of the amplitudes are plotted as a function of frequency and fitted with a bi-Lorentzian function (solid lines). The fitted HWHM of the low frequency component of each line shape is labeled. The dashed gray lines indicate the peak positions. Inset: Zoomed-in view of the below-threshold line shape with a 78-fold magnification in its amplitude. (B) Simulated asymmetric line shape of ∣X⟩ ↔ ∣Z⟩ transition at zero field. Frequency offsets of the 2¹⁴ substates arising from the second-order HFIs are calculated and plotted in a kernel density curve with rug. The number of bins is 1000. Inset: The molecular structure of pentacene with the 14 protons (gray circles) labeled. The values of triplet spin densities (purple and blue circles) (57) at different carbon nuclei are partially labeled according to the molecular symmetry. (C) Comparison of the low-frequency side HWHM of zero-field ∣X⟩ ↔ ∣Z⟩ transition line shape measured in different studies. All low-temperature results (22, 28–30) are obtained using optically detected magnetic resonance (ODMR). The free-induction decay (FID) (31, 32), continuous-wave electron paramagnetic resonance (cw-EPR) (33), and masers (16, 27) are used to measure the HWHM at the higher temperatures (≥194 K). Blue, single molecular spin; red, spin ensemble.

On the other hand, the asymmetry of the pentacene transition line shape is a characteristic feature of the zero-field transition (28) arising from the second-order hyperfine interactions (second-order HFIs) between the photoexcited triplet electrons and the 14 protons of pentacene shown in Fig. 3B. The asymmetry of the ∣X⟩ ↔ ∣Z⟩ transition line shape can be theoretically predicted by a second-order perturbation formalism (28) (see Materials and Methods for details), which qualitatively provides the distributions of the second-order HFI–modified energy states of ∣X⟩ and ∣Z⟩.

The other predicted effect of masing-mediated linewidth narrowing is also confirmed. Because of the asymmetry of the measured resonance line shapes shown in Fig. 3A, bi-Lorentzian fitting is used to determine the linewidth. The full-width at half-maximum of the ∣X⟩ ↔ ∣Z⟩ transition line shape is reduced from 3.3(5) to 2.0(2) MHz by maser action, and the HWHM of the steep low-frequency side is narrowed by fourfold from 0.53(4) to 0.13(1) MHz. To the best of our knowledge, such a narrow HWHM is rarely achieved in solid-state spin ensembles with high doping concentrations. Comparing with the reported HWHM values of the same spin transition obtained by different techniques (16, 22, 27–33), the HWHM obtained herein with the aid of masing is the narrowest (see Fig. 3C). Notably, it is 60% of the measured HWHM of a single pentacene molecule in p-terphenyl at cryogenic temperatures (22). Despite two previous works (16, 27) studying the same zero-field transition in the presence of masing as well, the reported HWHM values are slightly larger as the line shapes were measured under different masing conditions. In the previous works (16, 27), two types of microwave resonators were used, while a microwave oscillator is used here that gives rise to different masing thresholds in different studies. Our oscillator is derived from the high–Purcell factor STO resonator used in (27) by driving it in positive active feedback (34), which leads to a much slower damping and thus a substantial reduction of the resonator linewidth from ~180 kHz (35) to ~8 kHz (see section S2). The narrower linewidth implying a boosted quality factor Q (36) (section S2) results in a lower masing threshold (P_threshold) in our setup based on the correlation P_threshold∝1/Q (27). In addition, our detection circuit with the microwave oscillator also offers more accurate frequency selection and better spectral resolution for measuring the magnetic resonance features. On the other hand, although the linewidth of the sapphire resonator (>8 kHz) used in (16) is comparable to ours, its masing threshold is two orders of magnitude higher than that measured in (27) (thus higher than ours as well) due to the smaller Purcell factor (37), as discussed in (27). On the basis of the different masing thresholds and optical pump powers/energies (P_measure) used in all three works, we adopt a figure of merit Λ = P_measure/P_threshold to characterize the masing conditions (i.e., the extent of the optical pumping exceeding the threshold) when the line shape measurements were undertaken. We find Λ ≈ 4 and 30 in (16) and (27), respectively, while Λ = 46 is determined according to P_measure = 4 mJ and P_threshold ~ 86 μJ (see Materials and Methods) in our case. The larger Λ indicating the more pronounced masing effect on the line shape agrees well with the order of HWHM values summarized in Fig. 3C.

Performance of magnetic field sensing

Because the observed masing-enhanced magnetic resonance features are advantageous to quantum sensing with the slope detection protocol (1), e.g., magnetometry (3), we study the feasibility of the spin ensemble (i.e., pentacene-doped p-terphenyl) acting as an organic solid-state magnetometer operating at ambient conditions. The working principle of our magnetometer is similar to continuous-wave optically detected magnetic resonance (cw-ODMR) magnetometry (3) but differs in the type of readout signals and optical initialization. Here, we detect microwave signals (boosted by masing) instead of optical ones. Optical initialization of 7 ns (see Materials and Methods) for generating the pentacene triplet spins is more than one order of magnitude faster than that of the optical readout schemes, by which the shortest initialization times were achieved to be 150 and 600 ns for single (38) and ensemble (39) NV spins, respectively.

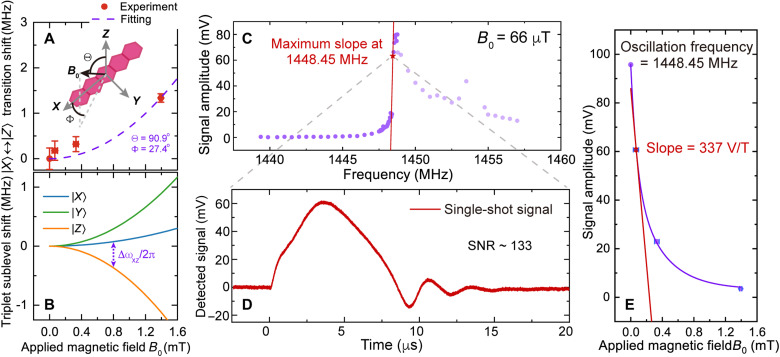
In our experiment, various dc magnetic fields B₀ were applied almost on the XY plane of pentacene molecules with a 27° deviation from the molecular X axis, as shown in Fig. 4A. Because of the Zeeman effect, B₀ can lift up the energy splittings between the pentacene triplet sublevels. Therefore, the magnetic field direction was determined by fitting the Zeeman-induced resonance shifts of the ∣X⟩ ↔ ∣Z⟩ transition with the calculated difference between ∣X⟩ and ∣Z⟩’s energy eigenvalues under various B₀ (see Materials and Methods), as demonstrated in Fig. 4 (A and B). In terms of the magnetometer operation, when the regenerative microwave oscillator shown in Fig. 2C is fixed at a frequency where the steepest magnetic resonance feature is observed (i.e., the working point for our magnetometer), the Zeeman effect–induced shift of pentacene’s ∣X⟩ ↔ ∣Z⟩ transition will lead to a maximum change of the observed signal amplitude. The amplitude change can be further magnified by the masing process, thus enhancing the readout efficiency and mitigating the loss of sensitivity arising from the quadratic Zeeman effect near zero field. Using the microwave circuitry demonstrated in Fig. 2C, the magnetic resonance feature shows a maximum slope at 1448.45 MHz with B₀ = 66 μT where the resonance signal is most sensitive to the dc field variation, shown in Fig. 4C. Owing to the masing process, the single-shot readout at 1448.45 MHz has a signal-to-noise ratio (SNR) of 133 as shown in Fig. 4D. The Rabi oscillations are attributed to the coherent energy exchange between the spin ensemble and microwave photons stored in the microwave oscillator, which are normally observed in STO-based high-power pentacene masers (33, 35).

Fig. 4. Magnetometer performance.

(A) Zeeman effect–induced resonance shifts of pentacene’s ∣X⟩↔∣Z⟩ transition measured under various applied magnetic fields B₀. The alignment of the magnetic field B₀ with respect to pentacene molecular Z and X axes is fitted to be Θ = 90.9° and Φ = 27.4°. (B) Calculated energy shift of each pentacene triplet sublevel when a variable magnetic field B₀ is applied with Θ = 90.9° and Φ = 27.4°. The shift of ∣X⟩↔∣Z⟩ transition frequency associated with (A) is labeled. (C) Signals of the ∣X⟩↔∣Z⟩ transition measured with above-threshold pumping at B₀ = 66 μT. The signals are plotted as a function of frequency (purple dots), in which the steepest rise in signal amplitude, i.e., the maximum slope is determined at 1448.45 MHz (red star). (D) A single-shot time-domain signal with SNR of 133 obtained at 1448.45 MHz. (E) Magnetic field dependence of the signal amplitude measured at 1448.45 MHz. The data are fitted with an exponential curve (purple) with a tangent line used to estimate the slope at B₀ = 66 μT.

By monitoring changes of the readout signal at 1448.45 MHz under different applied magnetic fields, we evaluate the sensitivity of the pentacene-based magnetometer. Figure 4E shows magnetic field increments around 66 μT resulting in maximal changes in the signal amplitude, and the correlation is represented by a slope m_s = 337 V/T. The sensitivity η, defined as the readout signal with an SNR of 1 (3, 12), can thus be estimated according to (40)

$$\mathrm{\eta }=\frac{{\mathrm{\sigma }}_{\mathrm{s}}}{m_{\mathrm{s}}\sqrt{2\mathrm{\Delta }f}}$$ (1)

where σ_s = 4.5 × 10⁻⁴ V is the single-shot SD of the time-domain signal without optical pumping applied measured at 66 μT, and Δf = 500 MHz is the measurement bandwidth used for our data acquisition. Therefore, at this early stage of development, the sensitivity of the pentacene-based magnetometer is 42 $\text{pT}/\sqrt{\text{Hz}}$. Although not better than the state-of-the-art solid-state ensemble magnetometers (e.g., NV-based magnetometers) operating with a bias field of several mT (3, 41, 42), the present device outperforms the latest zero and low-field (<100 μT) NV-ensemble magnetometers whose sensitivities are determined to be 250 pT$/\sqrt{\text{Hz}}$ and 3 nT$/\sqrt{\text{Hz}}$, respectively (23, 24).

The performance could be improved in the future. First, the bias dc magnetic field can be increased to enlarge the magnetic field–dependent slope of the energy shifts, which will improve the sensor by providing a linear zone in which the sensitivity is not limited by the quadratic Zeeman effect shown in Fig. 4 (A and B) (41, 42). Although the resonance linewidth will be broadened by the increased magnetic field (43), the pentacene can be deuterated to suppress the hyperfine interactions, thus compensating for the broadening (28). Moreover, careful tuning of the optical pump energy may give rise to an optimal condition that only triplet subensembles in the immediate vicinity of the resonance reach the masing threshold, leading to further reduction of the magnetic resonance linewidth (44).

Because stimulated emission in lasers and masers is typically nonlinear, the magnetometer demonstrated herein shows nonlinear response to magnetic fields (which is normally undesired) over more than 1 mT. According to the fitting curve in Fig. 4E, we estimate that the dynamic range of the magnetometer with almost linear response is about 3 μT at the optimal operating condition where the sensitivity of 42 $\text{pT}/\sqrt{\text{Hz}}$ can be maintained with a variation of 1%. The obtained dynamic range is comparable to that of other solid-state magnetometers based on lock-in techniques (45), e.g., the zero-field NV-ensemble magnetometer developed recently (23) has a similar dynamic range that is approximately of 2 μT.

To achieve a wider dynamic range with linear response, the magnetometer can be tuned to run above the masing threshold instead of near the threshold. As illustrated in Fig. 1C, there are certain regimes above the threshold revealing almost linear correlations (with large slopes) between the number of inverted spins and generated microwave photons. Thus, adjusting optical pump powers, which modifies the number of inverted pentacene spins to those regimes, may permit linear response of the sensor to magnetic fields. On the other hand, when the optical pumping is kept constant, as microwave driving is used in our setup, tuning the driving amplitudes will change the masing threshold, which can lead to similar effects of adjusting optical pump powers. Similar methodologies for tuning the magnetometer response to magnetic fields have been theoretically validated in laser threshold magnetometry (44, 46), which also implies that high sensitivities and linear response (together with a wide dynamic range) are so far challenging to achieve simultaneously. However, it can also be regarded as an advantage of maser/laser-based magnetometry that multiple parameters of cavities, optical pumping, and microwave driving can be used to adjust the magnetometers to serve specific requirements such as wide dynamic range versus sensitivity (47).

Alternatively, if the maser can work continuously with a large bias magnetic field (about several tens of mT), the maser output frequency f_maser will change linearly with magnetic fields with a correlation that Δf_maser = γ_eΔB, where Δf_maser is the change of maser frequency, γ_e = 28 MHz/mT is the gyromagnetic ratio of electrons, and ΔB is the small change of the magnetic field to be sensed. This strategy was originally proposed by Jin et al. (18) based on cw room-temperature masers, predicting such magnetometer has a sensitivity of 1 ~ 10 $\text{pT}/\sqrt{\text{Hz}}$. Despite that cw pentacene masers have not been realized yet, we have made progress on this topic and recently achieved quasi-cw operation of a pentacene maser at room temperature (48), which is an important step toward cw maser–based pentacene magnetometry.

DISCUSSION

Our study validates the concept of exploiting maser action in solid-state ensemble spin sensors for improvement of the sensitivity. This technique offers a promising path to mitigate the downsides of inhomogeneous broadening limiting the sensitivity of solid-state ensemble spin sensors. The masing-enhanced readout is advantageous over conventional optical readout (3, 39, 49) in terms of the single-shot SNR (∼133). We note that our readout protocol contributes to the nascent field of microwave readout (50, 51) for quantum sensing and enables microwave readout with (i) a higher SNR; (ii) an appealing threshold-like (nonlinear) enhancement of the sensitivity η with increasing number of spins N, whereas the dependence of η on N is linear and square root for alternative microwave readout (50, 51) and conventional optical readout protocols, respectively. Furthermore, this technique is fully compatible with the extensively studied solid-state spin sensors based on NV diamond and V_Si in SiC, which are both candidates for room-temperature solid-state masers (17, 18, 52), and it can also be used to explore new quantum sensors (e.g., the organic solid-state magnetometer demonstrated herein) for broad applications in electric/magnetic field sensing (1) and dark matter searches (53). We note that, recently, the optical counterpart of our work exploiting light amplification by stimulated emission for enhancing the sensitivity of NV-ensemble magnetometers to about 30 $\text{pT}/\sqrt{\text{Hz}}$ was reported independently (54). Both works may open a new avenue toward developing stimulated emission–enhanced quantum sensors.

MATERIALS AND METHODS

Simulation of maser-mediated linewidth narrowing and signal enhancement

The maser-mediated linewidth narrowing and signal enhancement are simulated on the basis of the predator-prey model (also known as the Lotka-Volterra model) (21, 26), which comprises a pair of first-order nonlinear differential equations, as shown below

$$\begin{array}{c}\stackrel{·}{N}=-2\mathit{\text{BnN}}-{\mathrm{\gamma }}_{\mathrm{s}}N\\ \stackrel{·}{n }= -{\mathrm{\kappa }}_{\mathrm{c}}n+\mathit{\text{BnN}}\end{array}$$ (2)

where N and n are the numbers of the inverted spins and microwave photons in a resonator’s electromagnetic mode, and their decay rates are expressed by γ_s and κ_c, respectively. B is the Einstein coefficient of the stimulated emission. The values of these parameters are adopted from previous studies on the pentacene triplet spin system, where γ_s = 4 × 10⁴ s⁻¹ taking both processes of depopulation and spin-lattice relaxation into account (55), B = 11× 10⁻⁸ s⁻¹ and κ_c = 2.1 × 10⁶ s⁻¹ are typical parameters of STO-based pentacene masers (21, 48). For simplicity, the model is solved in steady state, i.e., $\stackrel{·}{N}=\stackrel{·}{n}=0$. Thus, under the conditions of n and N > 0, we arrive at the threshold-like correlation (as depicted in Fig. 1C) between the number of inverted spins and microwave photons

$$n=\frac{{\mathrm{\gamma }}_{\mathrm{s}}N}{{\mathrm{\kappa }}_{\mathrm{c}}-3\mathit{BN}}$$ (3)

On the basis of Eq. 3, we simulate the masing effect on an inhomogeneously broadened spin ensemble with a Lorentzian line shape and intrinsic linewidth of 4 MHz. The line shape can be represented by a distribution of N through different frequencies, i.e., N(ω). The below- and above-threshold regimes are achieved by setting the peak value of the line shape N_max = 2 × 10¹¹ and 6 × 10¹², respectively. Combining with Eq. 3, the distribution of n(ω) is simulated in both regimes revealing the masing effect on the observed linewidth and signal amplitude.

Preparation of pentacene-doped p-terphenyl crystals

The Bridgman method (56) is used to grow pentacene-doped p-terphenyl crystals. Raw p-terphenyl (Alfa Aesar, 99+%) is purified by a home-built zone refiner set at 230°C. The process of zone refining takes 30 iterations, lasting 4 days. Pentacene (TCI Chemicals, purified by sublimation) and purified p-terphenyl powders are mixed in a molar ratio of 1 to 1000 and sealed into a borosilicate tubing under argon. The tubing is loaded inside a vertical furnace (Elite Thermal Systems Ltd.) in which the mixed powders are melted at 217°C. The melt is then lowered to a cold zone for crystallization with an optimized rate of 2 mm/hour. Once the crystallization is completed, the crystal grown is slowly cooled to room temperature with a rate of 10°C/hour to avoid thermal shock. Removed from the tubing, a pentacene-doped p-terphenyl crystal (height, 7.2 mm; width, 4 mm; average thickness, 1.5 mm) with a doping concentration of 1000 ppm is cut for the experiments.

Design of microwave dielectric resonators

The design of the microwave dielectric resonator was accomplished through a finite element method electromagnetic simulation using COMSOL Multiphysics (see section S1 for details).The microwave dielectric resonator comprises a cylindrical oxygen-free copper cavity (inner diameter, 40 mm; internal height, 31mm) and a dielectric hollow cylinder made of monocrystalline STO (inner diameter, 5 mm; outer diameter, 12 mm; height, 7.5mm; all surfaces are finely polished). The STO hollow cylinder, placed concentrically in the cavity, is lifted by 10.5 mm above the floor of the cavity via a Rexolite support. A “piston-like” copper tuning screw, at the top of the cavity, is used to change the distance between the STO cylinder and the cavity’s ceiling so as to adjust the TE_01δ mode’s frequency in the resonator. A 4-mm hole is drilled in the cavity’s wall for firing a laser beam into the cavity to pump the pentacene-doped p-terphenyl crystal optically. Two loop antennas are inserted inside the cavity functioning as an undercoupled input port and an overcoupled output port, respectively. The loaded (Q_L) and unloaded (Q₀) quality factors of the microwave dielectric resonator are determined via a microwave analyzer (Keysight, N9917A) to be Q_L ≈ 800 and Q₀ ≈ 7000.

Line shape measurements

The prepared pentacene-doped p-terphenyl crystal is loaded inside the bore of the STO cylinder with its cleavage plane vertically aligned. The microwave resonator connected with a feedback loop acts as a regenerative microwave oscillator (section S2) as demonstrated in Fig. 2C. The power and frequency of self-oscillation in the microwave circuitry are regulated by the variable attenuator, phase shifter, and tuning screw of the resonator, collectively. For line shape measurements, the microwave power inputted into the resonator is set to be −9 dBm, and the frequency is varied from 1439.375 to 1457 MHz, which are monitored by the microwave analyzer (Keysight, N9917A). An optical parametric oscillator (OPO) (Deyang Tech. Inc., BBOPO-Vis; pulse duration, 7 ns) pumped by a Nd:YAG Q-switched laser (Beamtech Nimma-900; repetition rate, 10 Hz) is used for optically pumping the gain medium (i.e., pentacene-doped p-terphenyl). The OPO output (wavelength, 590 nm) is focused to 2 mm and enters the cavity through the 4-mm hole in its side wall. The data in Figs. 3A and 4C are obtained with the optical pulse energy of 4 mJ, except for the below-threshold measurements (inset of Fig. 3A) in which 80-μJ pulses are used.

Upon photoexcitation of the gain medium, we sweep the frequency of the oscillator in steps of 500 kHz when it is far from the resonance and steps of 50 kHz when we approach the resonance. The signals reflected as power changes of the oscillator are measured by a logarithmic detector (AD8317; scale, 22 mV/dB) AC-coupled to a digital storage oscilloscope (Tektronix MSO64; sampling rate 6.25 GSa/s). The laser pulses monitored by a photodetector (Thorlabs, DET10A2) (not shown in Fig. 2C) are used to trigger the oscilloscope. Because of the limited dynamic range (55 dB) of the logarithmic detector and marked signal enhancement by the masing process, 10- or 35-dB attenuation is added at the input of the detector to avoid signal saturation and/or damage on the detector. All signals near resonance (i.e., masing signals) are collected by single-shot measurements, while weak far-off-resonance signals are averaged and then collected. The background signals introduced by laser-induced microphonics are collected and subtracted when a ∼100 G static magnetic field is applied on the crystal by a neodynium-iron-boron permanent magnet, which completely shifts pentacene’s ∣X⟩ ↔ ∣Z⟩ transition frequency beyond the resonator’s bandwidth. The peak values of the time-domain signals are plotted as a function of frequency, which manifest the line shapes. The line shapes are converted from a logarithm scale to a linear scale and normalized for obtaining the HWHM with a bi-Lorentzian fitting.

Simulation of zero-field asymmetric line shape

The asymmetric line shape of pentacene’s ∣X⟩ ↔ ∣Z⟩ transition can be qualitatively interpreted by calculating the energy shifts of the ∣X⟩ and ∣Z⟩ spin levels arising from the second-order HFIs. Because of the smallest zero-field splitting (ZFS) between the ∣X⟩ and ∣Y⟩ spin levels, the second-order energy shift of ∣X⟩ is much more pronounced than that of ∣Z⟩. Thus, with energy in units of MHz, the shift of ∣X⟩ ↔ ∣Z⟩ transition frequency can be estimated

$$\mathrm{\Delta }{\mathrm{\omega }}_{\text{XZ}}/\text{2π}=\mathrm{\Delta }{E}_{\mathrm{X}}-\mathrm{\Delta }{E}_{\mathrm{Z}}\approx \mathrm{\Delta }{E}_{\mathrm{X}}$$ (4)

According to (28), one obtains

$$\mathrm{\Delta }{E}_{\mathrm{X}}=\frac{1}{4}\frac{{\mid \pm {\mathrm{\rho }}_1{A}_{\mathit{ZZ}}^{(1)}\pm {\mathrm{\rho }}_2{A}_{\mathit{ZZ}}^{(2)}\pm \cdots \pm {\mathrm{\rho }}_{14}{A}_{\mathit{ZZ}}^{(14)}\mid }^2}{E_{\mathrm{X}}-E_{\mathrm{Y}}}$$ (5)

where ρ_i (i = 1,2, ⋯,14) is the triplet spin density (57) at the carbon nucleus bounded with the 14 protons (labeled in Fig. 3B), $A_{\mathit{ZZ}}^{(i)}=-61$ MHz (58) is the associated proton-hyperfine tensor elements where both isotropic and anisotropic parts are included, E_X − E_Y = 107.5 MHz (31) is the ZFS between the ∣X⟩ and ∣Y⟩ spin levels and the “±^” sign implies the two possible states of the protons. The asymmetric line shape of pentacene’s ∣X⟩ ↔ ∣Z⟩ transition at zero field is thus simulated by plotting the 2¹⁴ solutions of Eq. 5 in a kernel density curve with rug, as shown in Fig. 3B.

Sensing of external magnetic fields

We perform the line shape measurements while a small dc magnetic field is applied. The magnetic field is provided by a neodymium-iron-boron permanent magnet and varied by changing the distance between the gain medium and magnet. The applied magnetic field is calibrated by a commercial magnetometer (CH-1600; measurement precision, 10 nT). Its transverse probe (active area, <1 mm by 2.6 mm) is inserted inside the bore of the STO cylinder and moved along the cylindrical axis in steps of 0.1 mm to map the homogeneity of the magnetic flux perpendicular to the gain medium’s cleavage plane.

Calculation of energy eigenvalues of pentacene triplet sublevels

The total Hamiltonian of pentacene triplet spins is given by (59).

$${\mathrm{\mathscr{H}}}_{\text{tot}}={\mathrm{\mathscr{H}}}_{\text{ZFS}}+{\mathrm{\mathscr{H}}}_{\text{Zeeman}}$$ (6)

where ℋ_ZFS and ℋ_Zeeman represent the dipolar interaction between unpaired electrons in the triplet state, i.e., the ZFS interaction and the Zeeman interaction, respectively. Using the {∣X⟩, ∣Y⟩, ∣Z⟩} basis set, the total Hamiltonian matrix is obtained as follows

$${\mathrm{\mathscr{H}}}_{\text{tot}}=\left(\begin{array}{ccc}X& -\mathrm{i}{\mathrm{\gamma }}_{\mathrm{e}}{B}_0\text{cos}\mathrm{\Theta }& \mathrm{i}{\mathrm{\gamma }}_{\mathrm{e}}{B}_0\text{sin}\text{Θsin}\mathrm{\Phi }\\ \mathrm{i}{\mathrm{\gamma }}_{\mathrm{e}}{B}_0\text{cos}\mathrm{\Theta }& Y& -\mathrm{i}{\mathrm{\gamma }}_{\mathrm{e}}{B}_0\text{sin}\text{Θcos}\mathrm{\Phi }\\ -\mathrm{i}{\mathrm{\gamma }}_{\mathrm{e}}{B}_0\text{sin}\text{Θsin}\mathrm{\Phi }& \mathrm{i}{\mathrm{\gamma }}_{\mathrm{e}}{B}_0\text{sin}\text{Θcos}\mathrm{\Phi }& Z\end{array}\right)$$ (7)

where γ_e is the electron gyromagnetic ratio, B₀ is the magnitude of the applied magnetic field, and Θ and Φ are the angles between the applied magnetic field and the molecular axes as shown in Fig. 4A. X, Y, and Z are the energy levels of the triplet sublevels arising from the ZFS, which can be expressed with the ZFS parameters D and E to be

$$\begin{array}{c}X=\frac{1}{3}D-E\\ Y=\frac{1}{3}D+E\\ Z=-\frac{2}{3} D\end{array}$$ (8)

For pentacene-doped p-terphenyl, the ZFS parameters have been determined to be D = 1395.57 MHz and E = −53.35 MHz (31). Therefore, the energy of pentacene triplet sublevels can be obtained as a function of B₀ by calculating the eigenvalues of Eq. 7. Using Θ and Φ as fit parameters, the direction of the dc magnetic field applied on the sample can be determined by fitting the measured resonance shift of the ∣X⟩ ↔ ∣ Z⟩ transition with the calculated difference of ∣X⟩ and ∣Z⟩’s energy levels under various magnetic fields.

Supplementary Materials

This PDF file includes:

Section S1 and S2

Figs. S1 and S2

Table S1

References