Predictive design and analysis of drug transport by multi-scale computational models under uncertainty

Abstract

Computational modeling of drug delivery is becoming an indispensable tool for advancing drug development pipeline, particularly in nanomedicine where a rational design strategy is ultimately sought. While numerous in silico models have been developed that can accurately describe nanoparticle interactions with the bioenvironment within prescribed length and time scales, predictive design of these drug carriers, dosages and treatment schemes will require advanced models that can simulate transport processes across multiple length and time scales from genomic to population levels. In order to address this problem, multi-scale modeling efforts that integrate existing discrete and continuum modeling strategies have recently emerged. These multi-scale approaches provide a promising direction for bottom-up in silico pipelines of drug design for delivery. However, there are remaining challenges in terms of model parametrization and validation in the presence of variability, introduced by multiple levels of heterogeneities in disease state. Parametrization based on physiologically relevant in vitro data from microphysiological systems as well as widespread adoption of uncertainty quantification and sensitivity analysis will help address these challenges.

Introduction

Computational modeling of drug delivery has significantly advanced in recent years. In silico models using discrete or continuum modeling approaches can accurately describe drug’s interactions with the bioenvironment during individual stages of its in vivo journey. In the meantime, advanced nanomedicine has resulted in numerous nanoparticle (NP) formulations offering encapsulation of small molecule drugs and biologics, as well as efficient transport, and delivery of these therapeutics to target sites. Use of NPs as drug carriers, imaging agents, molecular probes, sensors and thermal therapy agents show great potential for therapeutic and diagnostic use with some of these nanomedicines having already found clinical use in critical applications such as anticancer therapy and mRNA vaccine delivery (1,2)(3,4).

A significant amount of continued research on nanomedicine focuses on physiochemical NP characteristics such as particle size, shape, charge and functionalization and efforts to tune these characteristics to realize the biological, transport, optic, magnetic and thermal function desired (5,6). In the NP design process, there are various considerations that can effectively be addressed by computational modeling strategies. These include simulations of NP plasma pharmacokinetics and biodistribution (7), scenarios involving passive and active targeting strategies (8,9), NP interactions with physiological transport barriers (10), and outcomes of therapeutic interventions involving normalization of pathophysiological features of disease (11,12).

While progress has been made towards understanding how multifaceted NP characteristics affect their transport and delivery, predictive design of nanomedicine, dosage and treatment schemes pose challenges for computational models as interactions of NPs with the bioenvironment need to be captured across multiple length and time scales from genomic to population levels to model the transport processes accurately. Integration of existing modeling strategies in a multi-scale modeling setting can enable a bottom-up in silico computation pipeline bridging the scales and shows great promise for building predictive in silico models of drug delivery and efficacy. However, it is still challenging to integrate these multi-scale efforts for broader length and time scales. Another primary challenge remains incorporation of uncertainty arising from heterogeneities within the disease, across different disease states and different patients into the computational models. Systematic verification and validation of computational models based on data from high-fidelity in vitro models such as microphysiological systems and development of models based on anatomically accurate and patient-specific medical imaging data will help address these challenges.

In this review, we summarize the recent progress in computational modeling of drug transport with a focus of nanomedicine, highlight examples of modeling efforts in distinct scales and discuss challenges and opportunities for the next level.

Computational Modeling of Drug Transport Phenomena across Scales

Discrete and Continuum Modeling

Physical phenomena associated with the transport of drugs across the human physiological systems take place at multiple length and time scales (Figure 1). Processes such as drug release from a nanocarrier or partitioning of the drug in the cell plasma membrane typically involve transport over distances on the order of nanometers and times on the order of microseconds or less. A discrete representation of the drug and its surroundings as an ensemble of individual interacting particles is often employed for investigating transport at such a small scale. There are various discrete modeling approaches and the selection of a particular method depends on the level of detail required for the problem of interest. Among the methods with the finest detail, molecular dynamics (MD) involve tracking individual atoms and molecules by the coupled solution of Newton’s second law of motion over a time span, starting from the initial coordinates and velocities of the particles (13–15). The interaction forces between the particles are modeled as gradients of intermolecular potentials. MD techniques are powerful tools that can provide rich information on the structure and motion of individual drug particles and help determine fundamental characteristics relevant to transport based on first principles. Most recent advances in the field enable simulations of time spans on the order of milliseconds, sufficient to observe fundamental biological processes such as protein folding, drug binding, and membrane transport. Particular applications include nanoparticle interaction with the cell membrane (16), aspherical particle modeling (17) and pharmaceutical particle formation (18). MD studies also have potential uses in the discovery of novel binding sites and structure-based drug design. Additionally, drug-resistant disease models may clarify the mechanism of resistance and provide a powerful tool for modifying the drug (19). If electronic motions play an essential role, quantum mechanics (QM) provides a finer approach than MD simulations. On the other hand, averaging electronic properties and assigning partial charges to atoms reduces computational cost compared to QM-based approximation (15). For NPs with a size of 20-200nm within mesoscopic-scale, atomistic detail is mostly not needed. Therefore, in coarse-grained (CG) simulations a number of atoms are grouped into interaction sites called ‘beads’. After coarse-graining the system, a similar method with MD is followed in which a sampling algorithm is used to calculate thermodynamic and structural properties (15).

Figure 1.

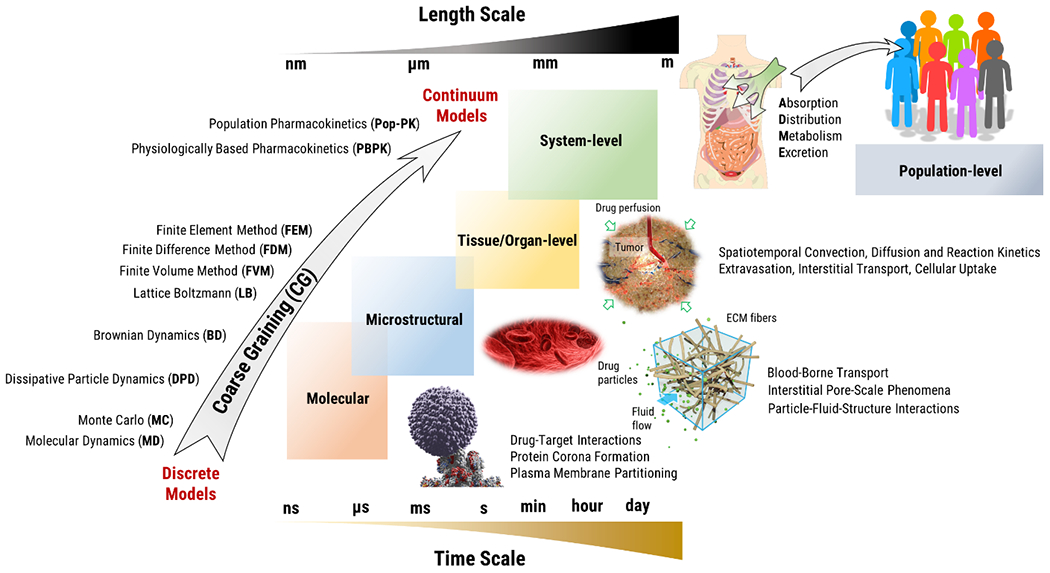
Computational modeling of drug transport phenomena across scales.

Scaling-up of MD simulations to investigate transport phenomena beyond nano/micro-scales is computationally prohibitive (20) and degree of freedom reduction reduces the computational cost. For instance, comparing MARTINI models in the molecular and atomic scales the speed up is proportional to n², i.e. square of the degrees of freedom. It is even greater for models treating solvent as a continuum medium such as Brownian dynamics (21). Mesoscale models average out unimportant microscopic details while keeping the essential ones, resulting in a computationally efficient simulation. Brownian Dynamics (BD), Multi-Particle Collision Dynamics (MPCD) and Dissipative Particle Dynamics (DPD) are common discrete methods used to model mesoscopic phenomena spanning molecular to microstructural processes (14). In general, two classes of mesoscopic methods, namely particle-based (DPD, MPCD) and lattice (LB) methods are utilized (22).

When a small particle is suspended in a fluid, it is subjected to the imbalanced random impacts of the fluid molecules that cause the nanoparticles to move on an erratic path, known as the Brownian motion. A Gaussian white noise stochastic process can model the random impacts of the molecules (23). Particles suspended in a fluid system are subjected to the impacts of the randomly fast-moving fluid molecules. For sub-micron particles, such instantaneously fluctuating momentum transfer from the solvent molecules spurs the particle to yield irregular movements, known as the Brownian motion. The dynamics of such Brownian particles can be described via the (overdamped) Langevin equation (LE) (24).

BD replaces the effect of solvent molecules on particles with a random force, so that solvent molecules are regarded as a continuum medium. Therefore, BD is used when the solvent molecules do not deserve a special interest (25). Being a relatively simpler and computationally cheaper method it is popular, but it does not take momentum transport through the fluid, i.e. hydrodynamic interactions into account. BD method is used in different applications such as the transport of suspended particles within an array of circular objects/obstacles (26), intracellular calcium release (27) and biomolecule association in solutes (28). In DPD, groups of atoms or volumes of fluids are modeled as beads that move according to the Newton’s 2^nd law or LE although the functional forms of forces are slightly different (22). In the most basic form of DPD, there is a conservative, dissipative and random force term between each bead corresponding to soft repulsion, frictional force(drag), and random interaction between neighboring beads. Compared to LBM or MPCD, DPD is more expensive numerically as it accounts for pairwise interactions (22). DPD has been used in nanoparticle targeting kinetics (29), determination of cellular uptake of different NP shapes (30) and drug encapsulation efficiency of Pluroronic micelles (31). An improved version of DPD, smoothed dissipative particle dynamics (SDPD) has the advantage of accounting for fluid compressibility, which might be prominent in specific applications like the collective motion of colloids and flow within complex geometries (32). In multi-particle collision dynamics (MPCD), the solvent molecules are modeled as an ideal gas. The update of particle positions and momentum occurs in two successive time intervals, namely streaming and collision steps. In the most widely used MPCD algorithm, stochastic rotation dynamics (SRD), the coordinates of the particles are updated in the streaming step using Newton’s equation of motion, neglecting solvent-solvent interaction. Then, the system is divided into cells and the relative velocities of particles in the same cell with respect to the center-of-mass are subjected to a random rotation (22,33) in the collision time step. Thanks to the rotation of velocities, the total momentum and energy are conserved while fluid particles transfer momentum. The method might result in misleading results for small temperatures or small collision time steps such that fluid particles remain in the same cell for more than one collision time step (34). MPCD method has been applied for uses such as semiflexible polymer chain dynamic simulation (35) and single rigid spheres with natural buoyancy confined in different geometries under pressure-driven flow (36). Different physical phenomena happening in distinct time-length scales might be represented with the same physics and coarse-graining scheme if the governing set of key non-dimensional numbers is the same (34). Keep in mind that while coarse-graining the molecular system, the thermodynamics of the system must be preserved for a good representation, i.e. the compressibility and solubility of the components should be preserved. There are studies in literature comparing application of MPCD and DPD (37), BD and MPCD (38). Interested reader can refer to reviews and reference texts on the subject for detailed treatment of each method (22,39).

When investigating the transport phenomena at larger length scales such as drug distribution within and across different tissues, a continuum approach is often adopted where the position and motion of the drug particles and the surrounding medium are averaged in space and time and the material is assumed to be distributed continuously in the region of interest. Finite element method (FEM), finite volume method (FVM) and finite difference method (FDM) are numerical techniques that are used to solve differential equations. Such differential equations commonly arise in continuum modeling transport processes and include Navier-Stokes equations for fluid dynamics, Darcy’s Law for fluid dynamics in porous media and species advection diffusion equation for drug transport (40). In FDM, terms of the differential equation are directly estimated at nodal points which yield a set of equations to be solved. In FEM, problem domain is discretized into small regions referred to as finite elements where governing equations are modeled based on variational principles. In FVM also involves discretization of the problem domain into small regions referred to as cells where conservation laws, typically governing fluid or heat transfer are applied over each cell (41,42). Another numerical method for modeling transport problems in the continuum regime is the Lattice Boltzmann Method (LBM). In LBM, the distribution function is discretized to solve Boltzmann equation, a molecular-scale analogue of the Navier-Stokes (NS) equation, such that fluid particles are restricted to move along a lattice vector. LBM method is not a coarse-graining scheme of molecular dynamics; rather, it is evolved from lattice gas cellular automata (22) from which macroscale NS equations can be derived. Although it has streaming and collision time steps similar to MPCD, it cannot represent physics in such small scales. Treating fluids with different length scales challenges lattice-based methods (34).

Modeling of transport process at system-level such as pharmacokinetics associated with drug absorption, distribution, metabolism, and excretion (ADME) are typically done by compartmental models where mass transport and biochemical processes across and within compartments are modeled by coupled differential equations. Physiologically based pharmacokinetic (PBPK) models involve compartments representing individual organs and tissues that are connected by blood or lymphatic circulation (43). The process of mass transport between compartments might be limited by two main factors; namely, blood perfusion and transport across tissue-tissue interfaces, e.g. vascular wall or cell plasma membrane that are repsented by flow-limited and interface-limited models (44,45). One of the key parameters in these models is the tissue-to-plasma partition coefficient that is defined as the ratio of the NP or drug concentration within the tissue to the concentration in the vascular compartment. The partition coefficient is a time dependent parameter estimated individually for the specific NPs or drugs and the environment. Being challenging to measure in vivo, there are in silico approaches developed to predict the partition coefficient (46). Some example applications of these in silico approaches include age dependent organ, portal and hepatic blood flow data adjustments using adult and pediatric simulations for different compounds (47), evaluating the accuracy of different plasma clearance and steady state volume distribution prediction methods (48), analysis of NP distribution to different organs depending on particle size (49), intracellular drug concentration optimization for temperature sensitive liposomes under hyperthermic conditions (50), PEGylated gold nanoparticle internalization modeling (51).

Having a physiologically mechanistic representation of the actual organ level transport, pharmacokinetic models can be used to extrapolate results of animal models to humans or might be helpful in dose determination of specific groups of the population like pediatrics and pregnant women (45). PBPK modeling is indeed widely used in academia and industry to predict dynamics of drug ADME characteristics. In addition it is gaining recognition by regulatory circles as a valid modeling tool for efficacy and toxicity assessment (52). For instance, the effect of focused ultrasound-induced blood-brain/blood-tumor barriers disruption on drug delivery was analyzed (53). Integrating the experimental outcome with a PBPK model, it was pointed out that the disruption alleviates the vascular barriers and enhances interstitial transport. Simulation of population-level variations in pharmacokinetic properties involves nonlinear mixed effects that often utilize generic compartmental models that do not seek physiological mimicry yet provide sufficient explaining power for parameters of interest (54). However, the popularity of PBPK modeling in this area is also increasing (55).

Governing equations for the modeling formulations presented above are provided in Table 1 together with several example applications. It is seen that discrete models are powerful tools that can provide rich information on structure and motion of individual drug particles and help determine fundamental characteristics relevant to transport based on first principles. However, scale-up of discrete methods to investigate transport phenomena beyond nano/micro-scales is currently computationally prohibitive. In cases where length and time scales are sufficiently large, the continuum approach vastly simplifies modeling while maintaining accuracy. However, a critical challenge in continuum modeling is parametrization of the model involving determination of the transport parameters specific for the drug and biological environment considered. These transport parameters include effective diffusivity, retardation and hydraulic conductivity that appear in continuum formulations of fluid and species transport. Likewise, PBPK models require knowledge of interface transport coefficients that themselves arise from parameters defined in smaller scales, e.g. hydraulic conductivity and permeability that govern the convective and diffusive drug transport across the interface as well as geometric parameters such as interface area per unit volume of the compartment. Therefore, transport parameters in continuum models are coarse-grained representations of transport processes and interactions that take place in smaller scales. In the next section, we review examples of multi-scale modeling efforts that integrate discrete and continuum models to address this challenge and build predictive in-silica models of drug delivery.

Table 1.

Governing equations of physical phenomena involving transport of drugs and physiological fluids.

Physical Phenomenon	Mathematical Relation	Definitions	Example Applications
Discrete particle dynamics at atomistic scale	Newton’s 2. Law of Motion $m_i\frac{d^2{\overrightarrow{r}}_i}{d{t}^2}={\overrightarrow{F}}_i$	mi: mass of the ith particle ${\overrightarrow{r}}_i$: position of the ith particle ${\overrightarrow{F}}_i$: external force on ith particle due to intermolecular potentials.	• Aspherical modeling of atoms and coarse-grained particles (MD)(17) • NP-plasma membrane interaction (MD) (16) • NP targeting kinetics (DPD)(29)
Discrete particle dynamics in the presence of time-scale separation	Langevin Equation $m_i\frac{d^2{\overrightarrow{r}}_i}{d{t}^2}=\xi \frac{d{\overrightarrow{r}}_i}{dt}+{\overrightarrow{F}}_{B,i}$	${\overrightarrow{F}}_{B,i}$: random Brownian force exerted on the ith particle ξ: friction coefficient	• Mobility and diffusivity analysis of charged particles (BD) (26) • Increasing speed of brute-force MD while retaining meaningful details (milestoning) (MD) (28) • Estimation of effective diffusivity within porous ECM (61,64)
Continuum fluid dynamics	Navier Stokes Equations $\rho \left(\frac{\partial \overrightarrow{v}}{\partial t}+\left(\overrightarrow{v}\bullet \nabla \right)\overrightarrow{v}\right)=-\nabla p+\mu {\nabla }^2\overrightarrow{v}$	ρ: density of the fluid $\overrightarrow{v}$: velocity field of the fluid p: pressure field of the fluid μ: dynamic viscosity of the fluid	• Analysis of NP distribution within micro-vessels (Coarse-grained MD and IMEFEM)(60) • Flow of interstitial fluid within 3D fiber network (FEM) (61,63)
Continuum fluid dynamics in porous media	Darcy’s Law $\overrightarrow{v}=-K\nabla p$	K: hydraulic conductivity	• Estimation of hydraulic conductivity of porous ECM (FEM) (61,63)
Spatiotemporal distribution of species in continuum	Advection-Diffusion Equation $\frac{\partial C}{\partial t}=-\overrightarrow{v}\bullet f\nabla \mathrm{C}+\nabla \bullet \left(D_{eff}\nabla \mathrm{C}\right)$	C: species concentration Deff: effective diffusivity f: retardation coefficient	• Intra-tissue particle distribution and penetration (BD)(65) • Biotransport in arterial blood clots (FEM) (40)
Dynamics of species transport (accumulation and clearance) in physiological compartments	Compartmental Mass Balance Equations   $\dot{m}={\dot{m}}_{in}-{\dot{m}}_{out}-{\dot{m}}_{elimination}$ Flow-Limited Model $V\frac{dC}{dt}=\sum Q_{in}{C}_{in}-\sum Q_{out}{C}_{out}-R_{cl}V$ Interface-Limited Model    $\frac{dC}{dt}=P{C}_{in}-\frac{P}{K_p}C-R_{cl}$	V: compartment volume C: species concentration within the compartment. Qin, Qout and Cin, Cout: volumetric flow rates into/out of the compartment and corresponding concentrations in fluids Kp: partition coefficient P: interface transport coefficient Rcl: rate of elimination (clearance) per unit volume	• Adaptation of adult PBPK model to analyse paediatric plasma profiles (Interface-Limited PBPK)(47) • Alleviation of vascular barriers using focused ultrasound combined with microbubbles (Flow-Limited PBPK) (53)

Multi-scale Modeling Approaches

Modeling of Vascular and Interstitial Pore-Scale Transport

As drug particles travel through the bloodstream, extravasate and penetrate into a tissue, they are transported across a crowded porous microstructure where significant interactions between the drug, fluid and microstructure take place. These interactions become particularly important for the transport of larger particles such as nanoparticle formulations and are affected by the drug particles’ physiochemical properties, including their size, shape, surface charge, and functionalization (5,6).

While the number of atoms, therefore the degrees of freedom to be solved to resolve these pore-scale interactions are too high for MD approach, the microscopic details such as collisions of particles with the structure and other particles, their hydrodynamic interactions with the fluid as well as the Brownian fluctuations remain significant such that sole use of continuum models is not adequate. Therefore, a hybrid multi-scale approach combining continuum modeling for transport of fluid with discrete modeling for particle trajectory is often utilized to investigate pore-scale transport in vascular and interstitial space (14).

Several examples of earlier studies featuring hybrid modeling approaches are illustrated in Figure 2. There have been several computational efforts to investigate bloodborne NP transport under varying particle and flow conditions such as hematocrit, vessel or NP size, and flow velocity. Intravascular NP transport, considering the effects of both NP characteristics and complex cellular flow is modelled by Liu and coworkers (56) (Figure 2(a)). In order to cover the range of length-scales between NP and RBC, a lattice-Boltzmann (LB) based multi-scale approach was used. The study illustrates that particle total radial diffusivity is the summation of Brownian diffusivity and RBC-enhanced diffusivity. The multi-scale model provides radial diffusivity estimates for varying NP sizes and flow conditions marked by Peclet (Pe) number. These results are particularly significant for blood-borne transport of large NPs. The model recovers Brownian diffusivity if Peclet number is small, e.g., diffusing particle has a diameter less than 100nm.

Figure 2.

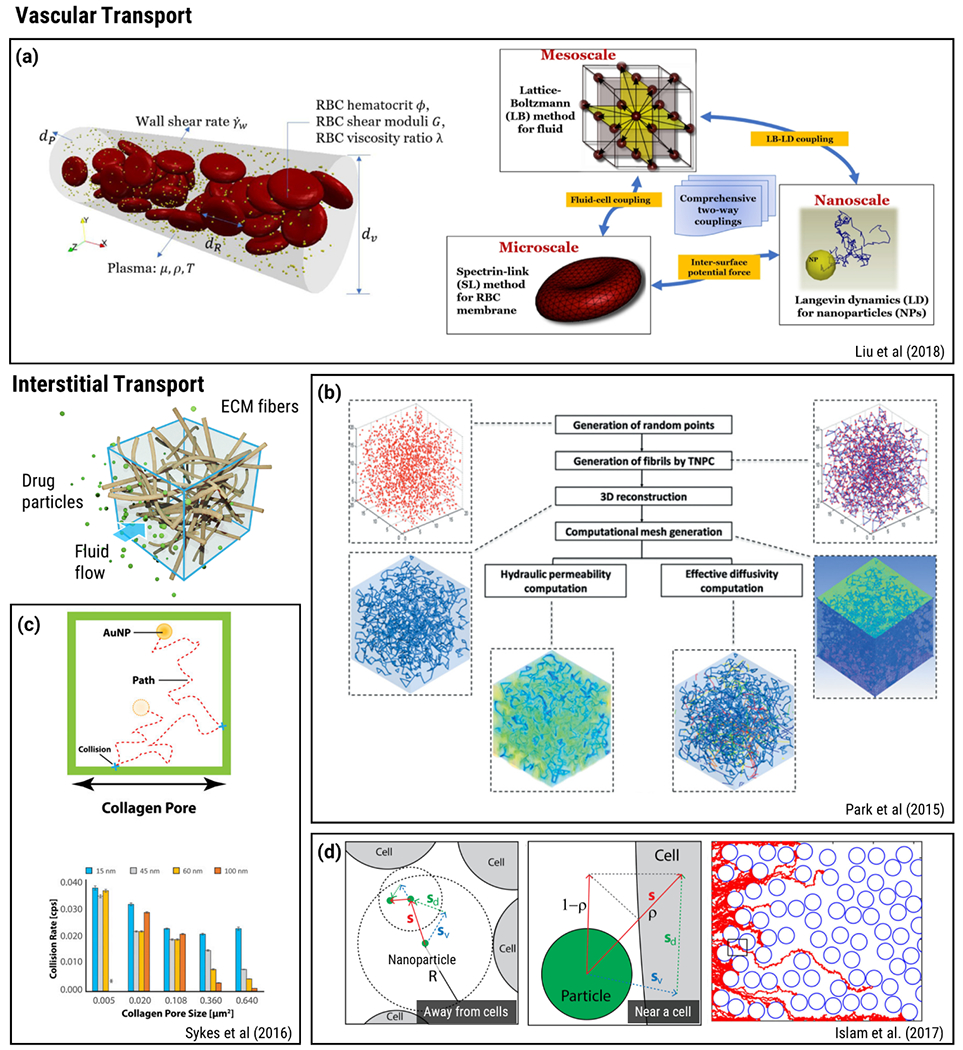
Hybrid discrete and continuum modeling of vascular and interstitial pore-scale transport phenomena. a) A multi-scale approach using LB scheme for the fluid phase, a Spectrin-link method for RBCs and LD to capture NP suspension. Reproduced from Ref (56) with permission from Elsevier. b) Workflow used in a parameter-based 3D microstructural collagen matrix reconstruction and transport property estimation study. Reproduced from Ref (61) with permission from ASME. c) Modelling of NP accumulation and penetration using MC simulations. Reproduced from Ref (64) with permission from PNAS. d) BD simulation of NPs at extracellular space contained with cells. Reproduced from Ref (65) with permission from BMC.

In a similar analysis, dispersion coefficient was investigated using Immersed Finite Element Method (IFEM) (57). IFEM features a Lagrangian solid mesh moving with a Eulerian fluid mesh. Therefore, both the meshing of the computational domain and interpolation of the unknowns are greatly simplified (58). In this manner, IFEM was employed to explore the blood flow and particle dispersion characteristics within the microvasculature (57). Considering the wide variations of the key flow characterizing parameters, i.e., microvascular uncertainty, these simulations were extrapolated using a Bayesian updating algorithm and combined with experimental outcomes to acquire computational prediction. Expansion of the method by incorporation of electrokinetic and molecular interactions was also introduced. This method, designated as Immersed Molecular Electrokinetic Finite Element Method (IMEFEM) (59), was used to investigate effect of RBC aggregates on blood rheology. Within this context, IMEFEM was utilized to simulate RBC-particle interaction using pre-assigned molecular interaction potentials (60). MD or DPD could also be employed for these interactions, enabling molecular scale accounting of cell-cell, cell-particle and particle-particle interactions. Using IMEFEM, it was shown that different hematocrit percentages (0, 15, 30% RBCs) had distinct effects on NP concentration at a cross-section of the blood vessel. At 30% NPs concentrated on regions close to the vessel wall, and as the NP size increased the concentration on this region got even higher.

Park and colleagues (61) developed an image-guided microstructural model of fluid and species transport in fibrous biopolymer networks and applied their model toward estimation of hydraulic conductivity and effective diffusivity of fluorescent tracer molecules (hydrodynamic radius of 5.1 nm) within pig skin collagen hydrogels where microstructures with different branching characteristics could be obtained by varying collagen monomer/oligomer content during polymerization (Figure 2(b)). The computational domain involved a representative unit cell where the geometry was generated from segmentation of confocal reflectance images of the collagen fiber network. Further simulations were performed on artificial fiber networks generated by a parameter-based reconstruction technique to match branching point density and distances in the imaging data. Their model is based on a semi-discrete approach where the flow of physiological fluid is modeled as a continuum by Naiver-Stokes Equations while individual particle trajectories were simulated by BD. Hydrodynamic forces induced by fluid flow on the particles were incorporated based on the empirical Shiller-Nauman Correlation for Stokes drag (62). The model predictions were within the same order of magnitude, yet results were underestimated compared to experimental data. The source of the discrepancy could be attributed to lack of slip flow, particle flexibility and discretization errors in the simulations (61). A similar approach involving volume-averaging theory and FEM were also used to characterize hydraulic permeability of fibrous extracellular matrix (ECM) (63). In another study, Sykes and colleagues (64) investigated whether cancer pathophysiology influences tumor accumulation and nanoparticle penetration using MC simulations (Figure 2(c)). Their model involved stepwise random walk of gold NP within collagen pores and their elastic collision with collagen fibers in 2D and 3D geometries. As illustrated with a bar graph, MC simulations showed that AuNP- fiber collusion frequency decreased with increasing AuNP and pore size. The study helped elicit the particle size and pore size dependence of interstitial diffusion of nanomedicine.

As drug particles penetrate into the tissue they also interact with the cellular compartment. Islam and colleagues (65) developed a hybrid multi-scale model that combined continuum modeling of fluid flow based on Stokes equations with time-adaptive BD to model microscale interactions of particles with cell boundaries in terms of adhesion of particle to cell surface or reflection back into fluid (Figure 2(d)). The model was used to investigate the significance of the particle size in intra-tissue dispersion and penetration. Continuation of this work included consideration of specific and non-specific targeting efficiency and suggested that receptor targeting may result in a marginal efficacy gain (66). As these examples of hybrid modeling approaches indicate, combination of continuum modeling and discrete modeling allows study of drug particle-fluid-structure interactions in dynamic vascular and interstitial flow environments and provides a means to predict key transport properties such as effective diffusivity and hydraulic conductivity that are used in parametrization of continuum-level transport models.

Modeling of Tissue-, Organ- and System-Level Transport

As presented in the previous section, hybrid multi-scale modeling can help estimate effective transport properties in porous microenvironment by simulating fluid and solute transport in a pore-scale domain e.g., an interstitial unit cell containing ECM fibers with certain density and directionality. Theoretical frameworks such as asymptotic homogenization, volume averaging and mixture theory provide alternative means to estimate effective transport properties by recognizing the length-scale separation between the porous microstructure and relatively homogeneous tissue or organ-level structures and developing averaged interpretations of microscale equations that can later be used in homogenized macroscale problems such as simulations over the tissue and organ-scale (Figure 3(a)) (67). As examples of multi-scale modeling, incorporating volume averaging theory and asymptotic homogenization approach, volume-averaging theory was employed to estimate permeability of fiber networks (63). Human stratum corneum, skin’s outermost layer, was modeled to calculate effective diffusivity(68,69). Avascular tumor growth and chemotherapeutic interaction was studied (70). Similarly, angiogenesis during tumor growth was examined using a hybrid approach (71). The role of vascular tortuosity on transport phenomena by bridging micro-macro scales with differential problems and double Darcy model was investigated (72). Capillary network and Darcy’s law were used to investigate Vinblastine and Doxorubicin metabolization within the tumor by Mascheroni and Penta (73). These homogenization techniques have inherent limitations particularly due to local cell-periodicity assumption as mimicking complex-heterogenous ECM or tumor microcapillary network is challenging using periodicity. Indeed, deviations from cell-periodicity near the macroscopic boundary introduce edge effects that result in loss of solution accuracy (73). In addition, direct interactions between the particles, fluid and microstructure due to directional forces, e.g., electrostatic interactions and magnetic stimulation, are challenging to incorporate using spatial homogenization. On the other hand, volume averaging theory and homogenization remain to be useful techniques for estimation of transport properties to be used in macro-scale continuum models without resorting to stochastic approaches while still incorporating microstructure-level geometric details.

Figure 3.

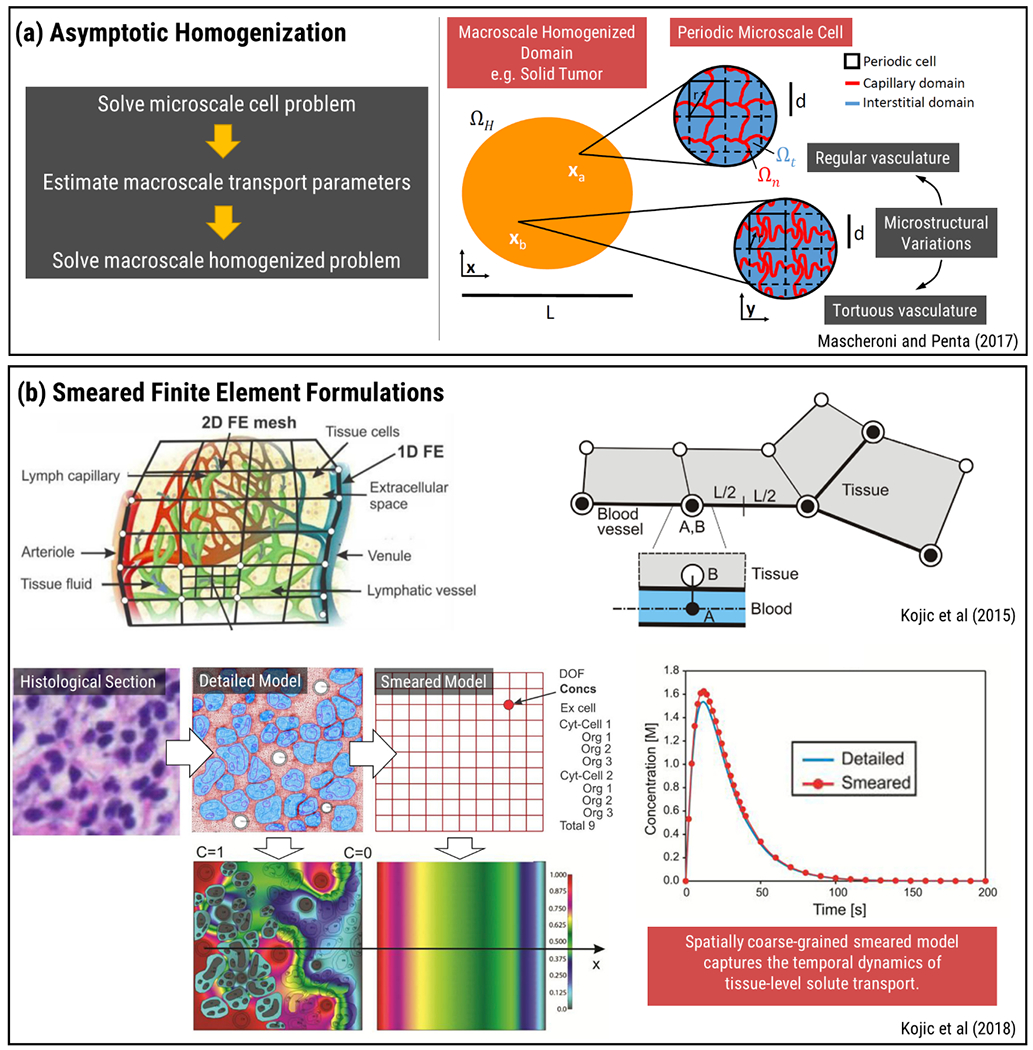
Multi-scale modeling approaches for tissue and organ-level transport. a) Asymptotic homogenization technique utilized to couple periodic microvascular transport properties and macroscale equations. Reproduced from Ref (73) with permission from Wiley. b) Microstructural diffusivity analysis extended to the equivalent continuum diffusion coefficient using numerical homogenization. Coupling of fluid and solid domains accomplished by 1D fictitious elements. Reproduced from Ref (74,77) with permission from Elsevier.

One of the alternative approaches that incorporate the effect of microstructural architecture on tissue and organ-level transport was presented in the work of Kojic and coworkers (74–77). A multi-scale, MD-FE model was used to investigate hierarchical diffusion phenomena for a microstructural architecture. Using MD, interaction effects between molecules and solid microstructure were taken into consideration by using scaling functions. Scaling functions represent the dependence of diffusivity with respect to the bulk diffusivity that is applicable when far away from the surface. Diffusion process taking place in two domains, namely bulk diffusion and hindered diffusion, was calculated using FEM. Following that, a numerical homogenization procedure was utilized in order to make microstructural and continuum level mass release curves identical so that continuum level constitutive diffusion parameters like diffusivity could be determined. The information exchange between continuum FE of tissue, capillary wall and 1D FE of capillaries was analyzed using a “fictitious” element that contained nodes from both FEs at the same position in space (Figure 3(b)). These fictitious elements can be implemented between different elements at lower scales as well, such as between cell cytosol and organelles. The mathematical modeling followed the FE formulation and transport properties for the element were determined from the element of smaller scale and the membrane separating them, such as the cell membrane or the capillary wall. Smeared model was based on transformation of 1D transport equations governing capillary flow in microscale into Darcy’s and diffusion tensors in continuum scale. This smeared FEM formulation, while spatially coarse-grained, can capture the dynamics of tissue-level solute transport and has direct implications of modeling drug pharmacokinetics (74–77).

PBPK and other compartment-based models that are typically used in evaluation of systemic transport of drugs can provide detailed information on dynamics of ADME yet are also highly coarse-grained and remain limited in describing the spatial distribution of drug in sub-tissue level. Recent multi-scale approaches focus on introducing sub-tissue resolution in compartmental models to improve the accuracy of pharmacokinetic and pharmacodynamic modeling. Figure 4 illustrates an annular quasi-3D (Q3D) gastrointestinal tract (GIT) model that is incorporated into a whole body PBPK model and used to study dissolution, transport, adsorption, distribution, metabolism and elimination (DTADME) of orally administered drugs (78). In this study, the GIT was spatially resolved by subdivision into individual Q3D volumes that were modelled as a connection of 1D tubes. These tubes had multiple annular layers which represented the heterogeneous organization of enterocyte and lumen tissues both radially and across the GIT. Therefore, spatiotemporal concentration profile for ibuprofen in the lumen and enterocyte of GIT at different time steps could be obtained.

Figure 4.

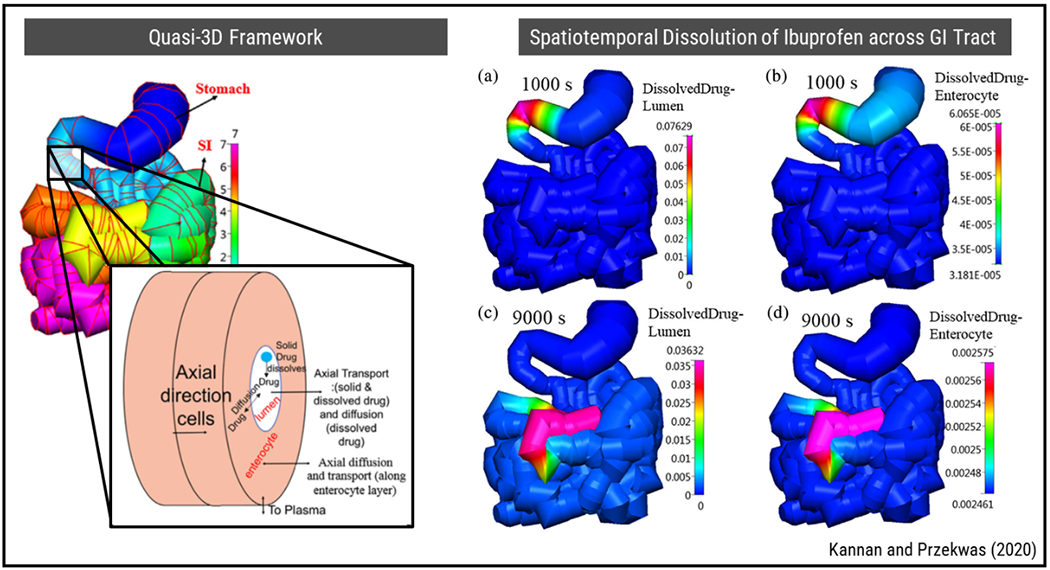
A multi-scale PBPK modeling approach for spatially resolved transport of drugs across GI tract and system-level ADME characteristics. Reproduced from Ref (78) with permission from Wiley.

In another study, a multi-scale PBPK model for the study of cyto-/cardio-toxicity of doxorubicin was introduced (79). The model consisted of a whole body PBPK model utilizing 8 tissue compartments as well as veinous and arterial blood which connected the tissues. In addition, the study featured a compartmental tissue sub-model where each tissue is split into vascular, interstitial, intracellular and nucleus sub-compartments. The model successfully predicted concentration profiles in mice and results were adapted to rats and humans using a cross-species allometric scaling. This multi-scale model enabled sub-tissue resolved pharmacokinetics of doxorubicin in heart and tumor tissue and helped infer about cytotoxicity based on nucleus bound concentrations of the drug.

In another study, PBPK and genome-scale metabolic network (GSMN) models were combined by utilizing drug transport and reaction rates in the intracellular space obtained from the PBPK model to constrain reaction rates in the GSMN model, through which drug perturbation was calculated (80). A multi-scale PK/PD model capable of preclinical to clinical translation to analyze effectiveness of antibody drug conjugates (ADCs) was modeled (81). PK and PD models in cellular and tissue levels were used to obtain parameters that affect ADC distribution, and these parameters were used in the multi-scale, multicompartmental PK/PD model to predict drug concentration in tumors.

A list of selected studies that feature multiscale modeling for drug transport are provided in Table 2.

Table 2.

Selected studies featuring multiscale modeling of drug transport.

Application	Model Scale				Remarks	Reference
	ML	MS	TL	SL
Calculation of effective diffusion coefficient and development of a tumor transport model that accounts for the heterogenous tumor tissue-blood vessel network	+	+	+		Using numerical homogenization, the microstructural diffusivity analysis is extended to the equivalent continuum diffusion coefficient. Fictitious elements that contain nodes from both tumor tissue and vasculature are used for information transfer from lower to higher scales.	(74,183)
Margination of NPs in microvascular network	+		+		RBCs tend to accumulate to the mid-part of the vessel. As a result, NP radial distribution is maximum at regions close to the vessel wall and it gets higher with increasing NP size.	(60)
Uncertainty quantification using Bayesian statistical framework and Immersed Finite Element (IFEM)	+		+		The Immersed Finite Element (IFEM) is employed for simulating both solid and fluid phases, i.e., RBCs, NPs and blood plasma. The study employs computer simulations to explore the blood flow in the microvasculature and particle dispersion characteristics. Considering the wide variations of the key flow characterizing parameters, i.e., microvascular uncertainty, these simulations are extrapolated using Bayesian updating algorithm to acquire computational prediction. It shows that dispersion of NPs is relatively slower than natural diffusion.	(57)
Development of a multi-scale PK/PD model capable of preclinical to clinical translation to analyze antibody drug conjugates (ADCs)		+	+	+	PK and PD models in cellular and tissue levels are used to obtain the parameters that affect ADC distribution in a multi-scale, multicompartmental PK/PD model.	(81)
Estimation of doxorubicin cyto/cardiotoxicity from system to cellular scale		+	+	+	PBPK model having tissue compartments with vascular, interstitial, intracellular and nucleus sub-compartments is utilized to assess doxorubicin cyto/cardiotoxicity. Model predictions agree with rat and human concentration-time profile data.	(79)
Migration of NPs within micro-vessels		+	+		LB for fluid phase is coupled with Spectrin-Link to investigate red blood cell (RBC) - membrane interactions. Langevin Dynamics (LD) approach is used to capture NP motion. The study is particularly critical for transport of large NPs.	(56)
Analysis of drug induced perturbations		+		+	A coupled PBPK-GSMN model is developed to predict drug induced perturbations using cellular scale metabolism and system level pharmacokinetics information.	(80)
Investigation of drug combination effectiveness in realistic brain tumor model		+	+		Efficacy of combination drug treatment is investigated in a realistic brain tumor model, obtained using MR images. Drug concentration in extracellular matrix to intracellular space is described using the mathematical model. Results show that inclusion of anti-angiogenic drug enhances the effect of doxorubicin the most.	(173)
Modelling drug delivery to solid tumor using a 2D computational field reconstructed from tumor image		+	+		A bisected tumor imaged with standard means is utilized to construct the computational domain with heterogeneous tumor vasculature. Results show that circular tumors are easier to eliminate than elliptical tumors and that usage of adjuvant therapy is more effective in eliminating small sized tumors.	(172)
Micro-macro scale governing equations are coupled by homogenization technique		+	+		Capillary and interstitial compartments are modelled on microscale, by local periodicity and smoothing out the macroscopic variations, i.e., using a homogenized domain on the macro-scale to obtain hydraulic conductivity and diffusivities. These tensors are then used in macro-scale equations.	(73)
Study of dissolution, transport, adsorption, distribution, metabolism and elimination (DTADME) of orally administered drugs			+	+	The gastrointestinal tract (GIT) is modelled as a connection of quasi-3D (Q3D) volumes that are made of 1D tubes with annular layers. The model successfully predicts drug concentration at personal and population levels.	(78)

¹ML: molecular, MS: microstructural, TL: tissue-level, SL: system-level

Software tools for Multi-Scale Modeling

Multi-scale modeling generally requires development and interaction of several sub-models specifically developed to simulate processes at separate length and time scales. Progress in this field is currently limited by expertise and resources of individual research groups or small teams of collaborators in developing specific purpose-built models. On the other hand, as outlined above, efforts of the computational research community have led to a large collection of purpose-built models for diverse physical processes. Multi-scale modeling of drug transport can be further advanced by incorporation and reuse of existing models for new multi-scale simulation scenarios. Meta-modeling tools enable coupling of computational models associated with different length and time scales. For example, MUSCLE3 (82) can be used to iteratively couple individual sub-models by automating simulation and transfer of information between models over appropriate solution intervals based on separation of time scales. PK-Sim is an open system pharmacology platform for PBPK modeling that is capable of interfacing with cellular scale models for PD thereby, enabling a mechanistic multi-scale methodology for systems pharmacology (83).

Challenges and Opportunities

Significant advances have been recently made to accurately compute transport of drugs and drug delivery systems. However, there are still several technical challenges to achieve predictive design of drug and delivery systems computationally. These challenges include multiple levels of structural and functional heterogeneity in tissues and organs, capturing the variability introduced by the heterogeneity in model parametrization by reliable transport properties and emergence of needs for integrating omics data into transport simulation. These challenges also pose opportunities for next generation computational models. In this section, these challenges and opportunities are discussed.

Multiple Levels of Heterogeneity

Multiple levels of heterogeneity of tissues and organs escalate the difficulties for accurate computation. The delivery of NPs to the tumor is limited by various physiological barriers alleviating the penetration of the drug and reducing exposure of the tissue to the drug. In order to reach the targeted tissue, NPs first need to circulate for a prolonged duration within the circulatory system, reach and interact with the tumor vasculature, penetrate into the tumor interstitium and get internalized by cancer cells (10). However, features of abnormal tumor physiology such as immature and leaky vasculature compressed lymphatics, elevated interstitial fluid pressure and dense interstitial matrix and large solid stresses together constitute barriers that hinder NP transport. Strategies to overcome these barriers by normalization of the tumor microenvironment are being investigated, however are not applicable for the whole patient population (11,12,84). Therefore, understanding the interactions of NPs with transport barriers at particular stages of delivery continues to be important and heterogeneity of tumor and tumor microenvironment illustrate complexity and challenge to computationally model drug transport. In the following section, we outline features of tumor heterogeneity in some of the prominent types of cancer.

Pancreatic Ductal Adenocarcinoma

Pancreatic ductal adenocarcinoma (PDAC) is one of the most-deadly cancers with a dismal 10% five-year survival rate and remains highly resistant to current therapeutics due to poor drug delivery to cancer cells. The treatment for PDAC is further complicated because of the heterogeneous tumor microenvironment (TME) composed of cancer cells, cancer-associated fibroblasts (CAFs), ECM, immune cells and chaotic microvasculature. This heterogeneity exists at multiple levels including molecular, cellular, tissue and patient levels and also evolves through the course of cancer progression. Thus, incorporating tumor heterogeneity into computational models remains challenging but imperative for next-generation modeling.

Molecular and Cellular Development

PDAC results from prolonged accumulation of oncogenic mutations that drive various transformations in the TME through acinar-to-ductal metaplasia (ADM) leading to various lesions of pancreatic cancer. Most notable oncogenic mutation are Kirsten rat sarcoma virus (KRAS), observed in more than 95% of patients, and tumor suppressor gene mutations CDKN2A/p16, SMAD4, and TP53, observed in 50-80% (85–87). Depending on the accumulated genetic mutations, PDAC may develop into different subtypes which are classified based on the expression of transcription factors and stromal compositions. For instance, PDAC landscape may vary among immune escape, rich, and exhausted phenotypes resulting from variations in genetic mutations (88,89).

Spatial distribution of various stromal cells contributes to significant heterogeneity in cancer phenotype. CAFs are the most prominent stromal component of PDAC and significantly contribute to tumor progression and chemoresistance (90). CAFs have been categorized into multiple subtypes based on their functions and locations (91). Inflammatory CAFs are found to be distant to tumor cells, show lower αSMA expression and induce immunosuppressive and chemo-resistant environment. Myofibroblastic CAFs are adjacent to tumor cells with high αSMA level and promote stiff, hypoxic, and avascular tissue microenvironment. Additionally, current therapy applies selective efficacy in tumors which leads to formation of therapeutically resistant clones and intratumoral heterogeneity. These inter- and intratumoral heterogeneity not only leads to diverse cellular response to therapeutic drugs and clinical outcomes but also results in diverse TME that could significantly alter the transport properties. Moreover, different subtypes of cells within the primary tumor have varying abilities to initiate migration, form colonies in the metastatic lesions, and establish a unique metastatic microenvironment, further complicating the modeling of drug transport in primary and metastatic sites.

Extracellular matrix

PDAC has a characteristic desmoplastic stroma primarily secreted by CAFs which consists of structural glycoproteins, adhesive glycoproteins, and proteoglycans (92,93). The dense stroma is not only a physical obstacle to many drug treatments, but its components are remodeled, and dysregulation triggers biochemical and regulatory pathways that can alter the course of the disease. ECM content is also organ-specific and it is necessary to build distinctive models depending on the tissue type due to varying protein concentrations and the resulting differences in cell-matrix interactions (94). Specifically in the case of pancreas, several proteins and ECM proteins have been recognized to be overexpressed, such as tissue factor, plasminogen, COL1A1,1A2, and 3A1, and hyaluronic acid (HA) (92,95–97). Likewise, several proteins, like matrisome, are upregulated at different stages of pancreatic cancer. ECM proteins are also remodeled throughout tumor progression by enzymes matrix metalloproteases, fibroblasts activation protein, and lysyl oxidases which upregulation have been correlated with dense stroma (98).

The tissue-dependent and evolving ECM composition greatly alters tissue mechanical and transport properties. In this context, studies have shown rearrangement of collagen fibers, increase in collagen density and tissue diffusivity through matrix contraction by pancreatic stellate cells (PSCs) and fibroblasts (99,100). Collagen diffusivity especially decreased in the vicinity of fibroblasts (101) and it is critical to recognize that biomolecule diffusion and uptake may vary due to differential matrix contraction contingent on the cell type. Moreover, HA, one of the most overexpressed PDAC ECM protein along with collagen, inhibited particle diffusion less than collagen in vitro when prepared at physiologically relevant concentrations as in vivo (102). On the other hand, confinement of HA by collagen increased total tissue pressure (sum of growth-induced solids stress and interstitial fluid pressure), reduced active vasculature, and impeded drug delivery in PDAC (103). Histology images have shown this was true only in specific regions where HA was localized within collagen and total tissue pressure was further increased with dense collagen content. This is due to the intrinsic nature of HA to resist compression by retaining interstitial fluid and repulsion of negatively charged monomers and of collagen to confine tumor tissue (104,105). These studies highlight that tumor tissue diffusivity is ECM composition dependent and it is crucial to consider the cellular and matrix spatial heterogeneity even within the same tumor type.

Microvasculature

A significant factor contributing to the highly chemo-resistant nature of PDAC is the limited drug delivery to the TME is abnormal tumor tissue vasculature. Hyperpermeable vasculature increases the fluid transport into the extravascular space thereby increasing the interstitial fluid pressure (IFP). As summarized in Table 3, hypovascular PDAC tissue has microvessel density (MVD) of 20 ~ 50 vessels/mm² (106–108) which is lower compared with other cancer types (109–112) and is hierarchically disorganized, which distinguishes them from normal vasculature system (113,114). Tumor vasculatures are formed from two recognized processes from the mother vessels, known as angiogenesis and arterio-venogenesis, which are stimulated by growth factors and cytokine, secreted by tumor and stromal cells such as VEGF-A signaling driven by transcription factor HIF-1 (115). In PDAC, PSCs play a critical role in controlling the vessel density as collagen concentrations can impose physical stress and hinder vascular formations. Moreover, tumor cells secrete anti-angiogenic signals that exacerbate the vascular damage. Consequently, large diameter blood vessels are collapsed, lymphatic vessels are less functional, and blood flow is decreased by 60% compared with normal pancreas tissue (116). On the other hand, in the normal pancreas adjacent to the tumor, angiogenesis is stimulated by activated stellate cells, promoting diverse vascular formations within the same pancreas (107). Drug transport in the tumor interstitium can be achieved by diffusion and/or convection. The transport from blood vessels to PDAC tissue is typically in the order of 80-220 μm at velocity of 1 μm/s (117). At the given interstitial velocity, elevated IFP and abnormal vasculature, transport of small biomolecules in PDAC becomes largely diffusion dominant. Ultimately, the multifarious nature of PDAC molecular, cellular and ECM properties culminates in the development of heterogeneous microvasculature density that shapes diverse drug delivery patterns.

Table 3.

Human / Murine PDAC Characteristics

Parameter	Value
Microvessel density (MDV)	20 - 50 vessels/mm2
Inter-microvessel distance	80 - 220 μm
Interstitial fluid pressure (IFP)	4 - 130 mmHg
Capillary fluid pressure	10 - 40 mmHg
Lymphatic pressure	< 5 mmHg

Recognizing that drug transport into PDAC TME is a significant limitation to therapy, there has been several efforts to enhance drug delivery by targeting the stromal components. The most notable strategies include targeting CAFs and HA, both of which showed promising results in mouse models. However, inhibiting hedgehog signaling to inhibit CAFs led to antagonistic effects which decreased patient survival and clinical trial terminated in phase II (118,119). Moreover, clinical trials with HA degradation with enzyme pegylated hyaluronidase (PEGPH20) halted in phase III due to failure in increasing overall patient survival (120). These studies demonstrated discrepancies between pre-clinical and clinical models as well as heavily patient-dependent drug responses resulting from heterogeneous PDAC TME. Accurate modeling of the dynamic development and interactions of the cancer cells and the stromal components poses a significant knowledge gap in modeling transport in tumor tissue.

Other Disease States

In addition to the pancreas, the microenvironment of different organs are highly heterogenous including the cellular, extracellular matrix and microvasculature components which collectively lead to heterogeneous drug delivery and distribution. Both experimental and computational models should specifically be tailored to reflect the unique characteristic of the particular organ and the disease. For instance, the brain is composed of neurons, astrocytes, oligodendrocytes, and glial cells. In addition, macrophages, known as microglia, are the most abundant immune cell type. Recent studies have revealed these are phenotypically distinct from macrophages recruited from bone marrow under inflammatory conditions (121). The brain ECM is also vastly different from other organs and is predominantly composed glycoproteins, proteoglycans, and glycosaminoglycans such as hyaluronic acid. Dense deposition of ECM may lead to hypoxia and aggressive tumor in the brain (122). Similar to PDAC, the brain vasculature is also highly disorganized in diseased states leading to further complications such as high interstitial pressure and edema. The distinct brain ECM and vasculature play critical roles in maintaining the blood-brain-barrier leading to significant heterogeneity in drug delivery. Mathematical model to investigate the role of abnormal vasculature on drug delivery to glioblastomas revealed that flow rate, vessel permeability, and tissue diffusion coefficient have nonlinear interaction in producing heterogeneous drug delivery in brain tissue (123). Computational model of brain capillary blood flow heterogeneity demonstrated that perturbations to the capillary network, including to segment diameters or to conductance values, decrease average tissue oxygen levels which could have critical consequences in neuronal function and thereby worsen neurodegenerative diseases and acute ischemic stroke (124). Furthermore, MRI techniques could enhance current computational models by providing templates for three-dimensional construction of the heterogeneous vasculature. Dynamic contrast enhanced-magnetic resonance imaging (DCE-MRI) based computational models allowed accurate modeling of drug delivery depending on the permeability and porosity of brain vasculature and tissue (125,126). Similarly, dynamic contrast enhanced-computerized tomography (DCE-CT) technique allowed measurement of tumor interstitial pressure and modeling of intra-tumoral heterogeneity leading to computational prediction of liposome nanoparticle distribution (127). Such techniques could provide significant benefits in predicting patient specific drug delivery of different chemotherapeutic drugs. Additionally, a study combining MRI of human brain and computational model demonstrated that a significantly greater degree of uncertainty and error is generated by neglecting soft tissue heterogeneity compared with vasculature heterogeneity (128). However, models representing brain tissue heterogeneity is lacking, rendering it a critical knowledge gap. In addition to spatial considerations, mathematical models to predict temporal heterogeneity in glioblastoma revealed novel opportunities to target specific disease states that are patient-specific (129). Temporal variation coming from different mRNA expression of clock genes that are expressed at different levels depending on the circadian rhythm also leads to daily oscillations in vascular permeability and resistance, thrombus formation, and flow conditions that play critical roles in modulating vascular function (130–132). Therefore, perturbations in the circadian rhythm could increase vasculature and blood-brain-barrier vulnerability, increasing the risk of stroke in the morning (133,134). Modelling such temporal heterogeneity in differential gene expression, cellular activities, and the blood-brain-barrier is critically important to understand drug delivery in many brain diseases. Moreover, future models could significantly improve with enhanced understanding of broader patient population brain heterogeneity through disease progression modelling and clustering techniques using neuroimaging (135). Likewise, similar challenges of cellular, tissue, and vascular heterogeneities exist for other organ diseases, such as the lung and the skin, particularly for unique airway architecture of the lung and multiple tissue layers of the skin (136–141). Coupling of the spatial and temporal heterogeneity will provide next generation models to predict tissue specific drug delivery in different organs and present novel therapeutic opportunities.

Uncertainty Quantification and Sensitivity Analysis

Accurate knowledge of model parameters is essential for predictive modeling of drug distribution and efficacy in the organism-level. Hierarchical determination of transport parameters used in macro-scale models based on micro-scale models is a promising approach especially since the expanding landscape of drug design introduces additional factors to consider that affect the delivery performance. In the meantime, various sources of variation in disease conditions such as tumor heterogeneity, patient age and demographics result in significant uncertainty in model parameters including transport properties. Predicting pharmacokinetic parameters like of neonates, infants, and pregnant women can be a particularly challenging task due to limitations of scaling approaches to translate parameters between these interest groups and groups for which data is available (142).

Uncertainty quantification and sensitivity analysis come forward as methodology rapidly gaining importance to tackle this challenge. Incorporation of sensitivity analysis when reporting PBPK model predictions is becoming a common practice where variability in endpoints such as area under curve based on model parameters can be studied (79). A meta-analysis of nanoparticle delivery to tumor revealed that delivery efficiency significantly depended on external sources of heterogeneity such as tumor site and tumor model studies as well as drug design characteristics such as NP hydrodynamic radius, shape, surface charge, material (organic/inorganic) (143). PBPK modeling coupled with sensitivity analysis helped identify low distribution and permeability coefficients to be the most significant factors affecting the delivery efficiency. In addition, in vitro to in vivo extrapolation (IVIVE) to estimate parameters in PBPK models based on in vitro and in silico predictions itself is subject to significant uncertainty. When sensitivity analysis is incorporated into an IVIVE procedure where Rodgers and Rowland model (144) was used to estimate tissue to unbound plasma partition coefficient, it was demonstrated that partition coefficient and fraction unbound in plasma were the most influential parameters affecting the outcome of IVIVE procedure and the process was generally sensitive to tissue composition (145). A promising direction in this context is the simplification of PBPK model parametrization problem by reduction of model dimensionality focusing only on the most influential parameters.

Uncertainty quantification has also been applied to transport models in context other than PBPK modeling. Effect of AIF’s and vascular and tissue transport parameters on interstitial fluid and tracer transport using sensitivity analysis was studied in heterogenous tumor tissue and vasculature by utilizing DCE-MRI data (146). For all cases considered in the analysis IFP was elevated within the tumor and decreased toward tumor boundary, with tumor vessel permeability having the most critical impact on IFP values. Interstitial fluid velocity values were largest near tumor boundaries in all cases and high tumor vessel permeability and low ratio of tumor hydraulic conductivity to normal tissue hydraulic conductivity caused greatest deviations from baseline results. Tracer transport was not affected as much with changing transport parameters and sensitivity analysis showed good agreement between the patterns of simulated and experimental tracer concentrations.

Since UQ and SA mainly involve interrogation of model responses only under changing inputs, these analyses can be applied without the knowledge of implementation specifics of the model, i.e., the model being treated as a blackbox. Therefore, there have been a proliferation of software tools such as DAKOTA (147), UQLab (148), UQ-PyL (149), COSSAN (150), and PUQ (151) as frameworks that provide a general interface to run specific model simulation software or code and perform uncertainty quantification, sensitivity analysis and model parametrization/calibration under uncertainty.

Coupling of PBPK Modeling and Microphysiological Systems

Despite increasing integration of uncertainty quantification using in silico approaches, determination of reliable transport properties for successful predictions of clinical outcomes by in silico models still requires a significant amount of human physiological data that current model system fails to provide. The lack of data is a significant limitation in PBPK models for pediatric applications as well as those for adults (152). Systematic experimental validation of multi-scale models may benefit from novel in-vitro models such as microphysiological systems based on microfluidics (153–157). These include recently emerging interstitial permeability and skin permeability models used to study adsorption, liver models for metabolism, kidney models for elimination/excretion and multiorgan models that provide PK/PD parameters of drugs with higher physiological relevance compared to single organ-on-chips (OoCs) (158,159). These multi-organ-on-chips (MOoC) simulating aspects of drug ADME on coupled microfluidic compartments offer a promising avenue for IVIVE by providing physiologically relevant in-vitro experimental data (160–165). For instance, a recent series of work by Ingber group involved recapitulation of nicotine and cisplatin plasma pharmacokinetics in vivo based on flow and concentration data from fluidically coupled microfluidic devices coupled with a PBPK model for IVIVE (160–162). Despite the promising first results, a primary challenge remains for IVIVE with these MOoC platforms that mirror the discussions on parameter scaling for PBPK models. A consensus on a generalized and systematic approach for scaling individual organs and organs relative to each other is currently yet to be reached (166). Some approaches common in literature are direct scaling, allometric scaling, multifunctional scaling and scaling based on organ mass and residence times (167). Direct scaling directly scales down all organs and their relevant parameters by a factor. While straightforward, this method is not successful at reenacting organ-organ interactions since scaling of individual organs should be different (167). Allometric scaling relates physiological parameters with body mass, usually using an exponential relationship that relies on the assumption that the transport networks within an organism is space-filling and optimized by natural selection, while with organ-on-a-chip devices, the formation of cells and transport networks may not be subject to such optimization (166). Another important point is that cells often show increased metabolism rates on chips compared to their in vivo counterparts due to being given excessive nutrients. This point can be complemented by using allometric scaling but limiting the nutrients given to the cells to obtain realistic metabolism rates (166). Allometric-based scaling methods can be used for extrapolation across age groups, such as developing a PBPK model using adult data and scaling the model for pediatrics (168,169). Scaling based on organ mass and residence times suggests a linear relation between organ mass and physiological parameters, and fluid flow is determined by the in vivo residence times of organs. With this method, flow rates are important in that they should not cause shear deformations to the cells and the compartments should have similar efficiency to the actual organs they are mimicking. Multifunctional scaling aims to replicate a linearly scaled-down version of the functional parameters of real organs such as the amount of blood pumped by the heart with organ-on-a-chip devices (170). This method is advantageous in that parameter measurement and experimental determination of the proper organ-on-a-chip size is easy, but the scaling approach may be an oversimplification. Two multi-MPS devices (gut-liver and gut-liver-kidney) were constructed using multifunctional, direct and allometric scaling approaches and their efficacy were compared by looking at normalized concentration profiles with respect to time (171). When compared to in vivo data, multifunctional scaling showed about a 2-fold deviation in drug exposure whereas direct and allometric scaling showed 50-to-300-fold lower exposure times on average.

Image-Based Modeling

Image-based modeling approaches can be used to obtain patient specific transport properties in the diseased regions as well as to identify heterogeneous structures such as the tumor vasculature which can be implemented to computational models for more accurate representation of the disease. A multi-scale model to estimate drug delivery to solid tumor was constructed using 2D image of a dissected and cleared tumor, which was converted into a computational field where the tumor was simplified as a circler or elliptical region while retaining the heterogenous microvasculature, giving a more realistic representation of the region (172). In another work, MR images were utilized to obtain a realistic 3D brain tumor model through which drug delivery to brain tumor using a multi-scale mathematical model was studied (173). With this model, combination therapy of bevacizumab, an anti-angiogenetic drug, and a total of 6 cytotoxic drugs was investigated. Results showed that inclusion of bevacizumab enhanced the delivery of all cytotoxic drugs albeit at different levels, with doxorubicin seeing the most benefit. A 3D voxelated image of tumor tissue was constructed using DCE-CT, which was utilized to obtain hemodynamic parameters used as inputs in a mathematical model to estimate intra-tumor oxygen concentrations (174). These parameters were checked against values obtained through intravital microscopy and photometric techniques and results were close for voxel sizes under 200μm. Another voxelated numerical model predicted distribution of contrast agent and drugs in brain tumors (126). Data obtained from measurement of the concentration of a contrast agent in a spinal cord injury using DCE-MRI were employed for curve fitting in a multi-compartmental PK model which would track the distribution of the contrast agent (175). DCE-MRI was utilized to obtain permeability and porosity values, and patient specific arterial input function (AIF) was utilized to obtain perfusion kinetic parameters. Using these, heterogenous vasculature of the tumor and selective leakage of drugs due to the heterogeneity were investigated. Results showed that although drug concentration was higher in high permeability areas at first, accumulation was greater in high porosity areas later on.

Emerging Areas

Tumor heterogeneity remains to an outstanding challenge for treatment of cancer that will ultimately be addressed by advanced personalized medicine. In previous sections, we also identified tumor heterogeneity and associated uncertainty in tumor microenvironmental parameters as one of the primary challenges for development and validation of predictive computational models of drug transport. Joint use of emerging technologies in multiscale modeling, microphysiological systems and image-based modeling offer great potential to address these challenges as illustrated in Figure 5. We introduced microphysiological systems as newly emerging in vitro experimental disease models that can incorporate features of the tumor microenvironment including heterogeneity in controlled manner. The transparent operation and ease of read out from microphysiological systems render them suitable benchmark platforms for in vitro validation of computational models while maintaining physiological relevance. In the meantime, further development and parametrization of computational models such as PBPK models can facilitate in vitro to in vivo extrapolation of microphysiological system predictions. In addition, image-based models can provide valuable information in terms of either in vivo structure and function data or transport characteristics that can be used towards model building of both microphysiological systems and computational models. Finally, computational multiscale models are uniquely positioned among the three technologies to provide mechanistic insight into transport processes observed in vivo and in vitro based on first principles. We anticipate that joint use of these three technologies will be pivotal in advancing precision medicine by providing patient-specific evaluation of treatments and treatment planning.

Figure 5.

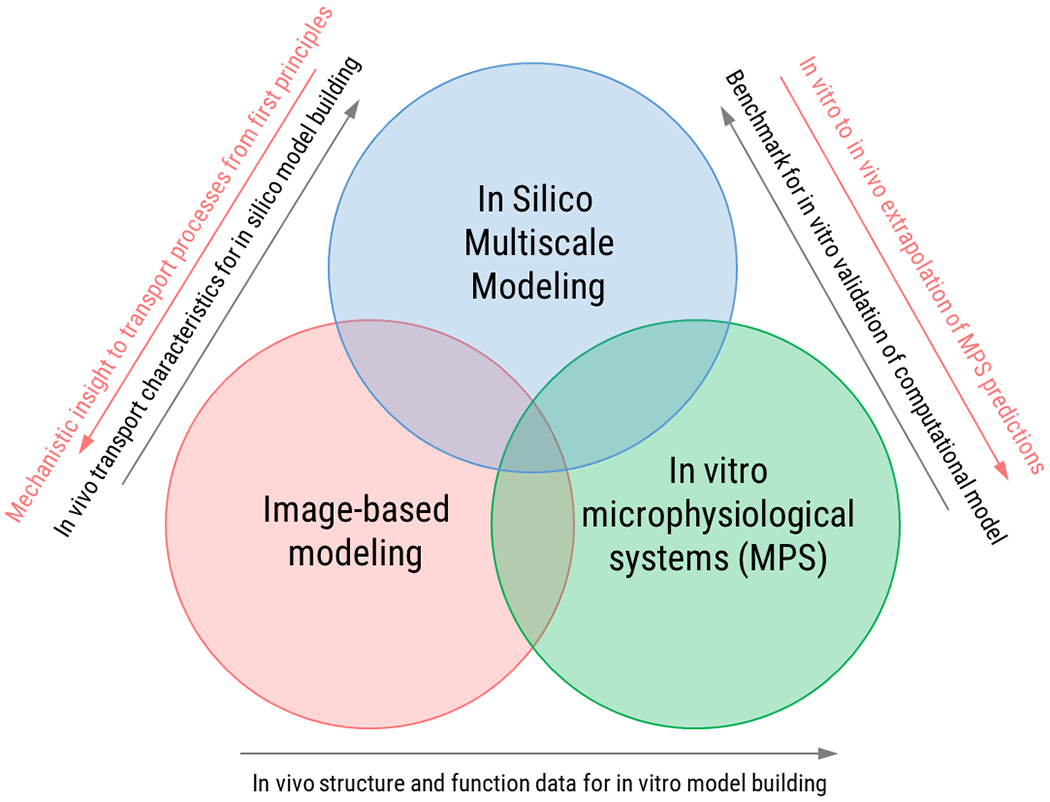
Potential for joint use of emerging technologies in multiscale modeling, microphysiological systems and image-based modeling.

Another emerging trend is the support of UQ/SA efforts by artificial intelligence and machine learning (AIML). Current discovery and development of drugs rely on hands-on traditional in vivo and in vitro experiments which makes the procedure time consuming and unpredictable. With the enhanced computing power and stronger algorithms developed in the last decade, not only multi-scale models but also predictive algorithms based on artificial intelligence are promoted and a new discipline combining these two, computational pharmaceutics has emerged (176). Using machine learning (ML), large volumes of data can be analyzed systematically to find correlations or quantify agreement of correlations (177). ML can also be used in carrying characteristics across the scales, i.e., in the process of information homogenization (178).

There is a growing body of literature adopting data-driven ML approaches for applications such as investigating iron oxide NP cytotoxicity (179), achieving predictive analysis of silver NP protein corona formation (180) and NP property prediction (43). Development of a breast cancer therapy response predictor using a multi-omics model in which the tumor therapy response characteristics were obtained using data integration and ML (181) and development of a ML model to predict 3D printing formulation and drug dissolution properties of FDM printed objects like tablets, films and devices (182) are some other examples. The growing interest and merits of ML-based approaches is also recognized in regulatory circles. In 2019, FDA published an action plan on medical ML algorithms that sets a path for the official approval of such studies. While ML is a powerful tool, caution should be practiced as uninformed and brute-force use of ML might result in unphysical predictions and ill-posed problems (177). It is anticipated that the greatest benefit will come from the combination of ML and multi-scale modeling for an intelligent walk-through drug design landscape for delivery as well as to address challenges in model parametrization and uncertainty quantification.