Abstract
Mutation density patterns reveal unique biological properties of specific genomic regions and shed light on the mechanisms of carcinogenesis. Although previous studies reported insightful mutation density patterns associated with certain genomic regions such as transcription start sites and DNA replication origins, a tool that can systematically investigate mutational spatial patterns is still lacking. Thus, we developed MutDens, a bioinformatic tool for comprehensive analysis of mutation density patterns around genomic features, namely, genomic positions, in humans and model species. By scanning the bidirectional vicinity regions of given positions, MutDens systematically characterizes the mutation density for single-base substitution mutational classes after adjusting for total mutation burden and local nucleotide proportion. Analysis results using MutDens not only verified the previously reported transcriptional strand bias around transcription start sites and replicative strand bias around DNA replication origins, but also identified novel mutation density patterns around other genomics features, such as enhancers and retrotransposon insertion polymorphism sites. To our knowledge, MutDens is the first tool that systematically calculates, examines, and compares mutation density patterns, thus providing a valuable avenue for investigating the mutational landscapes associated with important genomic features.
High-throughput sequencing (HTS) technology has enabled the low-cost identification of numerous genomic variants in personal genomes. Identification and analysis of somatic mutations are critically important in cancer research. In recent years, mutational strand bias in transcribed genes has arisen as an informative and guiding signal that reveals profound cancer mutagenesis mechanisms (Haradhvala et al. 2016). Transcriptional strand bias in somatic mutations is such a phenomenon: A form of single-base substitution (e.g., C > T) significantly outnumbers its complementary mutation form (e.g., G > A) on the transcribed strand or the nontranscribed strand, but the two mutually complementary mutation forms balance out if ignoring the transcription strandedness. Transcriptional strand bias is caused by either stronger transcription-coupled repair on the transcribed strand, stronger transcription-coupled damage to the nontranscribed strand, or both mechanisms combined. As a most representative example of the transcriptional strand bias, skin cancer often has elevated C > T mutations on the nontranscribed strand relative to the transcribed strand (Alexandrov et al. 2013). Moreover, liver cancer displays even more marked divergence, with greater A > G mutations on the nontranscribed strand (Letouzé et al. 2017). Lung cancer also shows transcriptional strand bias by presenting more G > T mutations on the nontranscribed strand (Kucab et al. 2019).
Mutational strand bias associated with DNA replication, termed replicative strand bias, is another intriguing genomic signal that warrants in-depth investigation. Taking in a primitive location data set of DNA replication origins, a study (Haradhvala et al. 2016) revealed global replicative strand bias patterns for 14 tumor types, with specific mutational spectra more prevalent on DNA lagging strand than the leading strand. The data further suggested that the increased APOBEC enzymatic activity and proofreading-compromised POLE were two major mechanisms driving the observed replicative strand bias. This groundbreaking study has inspired successive works on deciphering replicative strand bias, including one from the perspective of mutational signatures (Tomkova et al. 2018). Although they recognized mutational strand bias as a prominent feature in the cancer genome, the previous works did not tackle potential strand bias patterns in localized genomic regions, and in many cases, the studies only reported a global statistic of mutation density ratio between the strands. Without a proper companion statistic test, the severity of the mutational strand bias was not precisely assessed. Furthermore, the replication origin locations mapped in 2016 were far from accurate. Recently, the novel HTS technology SNS-seq was leveraged to map human DNA replication origins (Akerman et al. 2020). This new set of high-resolution location data may propel new replicative strand bias studies in the near future.
Several statistical methods have been applied in recent years to evaluate mutational strand bias in the cancer genome. The majority of them are based on Pearson's Chi-squared test (Jelaković et al. 2015; Lee et al. 2018; Kucab et al. 2019). Although these methods improved the analysis of cancer mutations, several drawbacks have limited their usage in the cancer biology community. First, these approaches were bound with a global analysis strategy that sets the coding regions of all genes as the analysis scope, which cannot be easily adapted to accommodate a localized perspective into limited genomic regions. For example, transcriptional strand bias attenuates as the transcriptional machinery moves far away from transcription start sites (TSSs) (Polak and Arndt 2008), and thus, a proper analytical approach should ideally be built upon the close proximity of the central TSS feature. Second, these approaches summarized widespread mutations in the whole genome but did not account for the varied nucleotide constitution in the local context of each mutation. Last, these studies did not compare mutation asymmetries of different samples and thus did not perform a normalization against the genome-wide mutation abundance (mutation burden). Generally, in-house-developed scripts were used to fulfill research needs. A fully functional, reusable, flexible application to specifically address mutation density patterns (including strand bias and related questions) is still lacking.
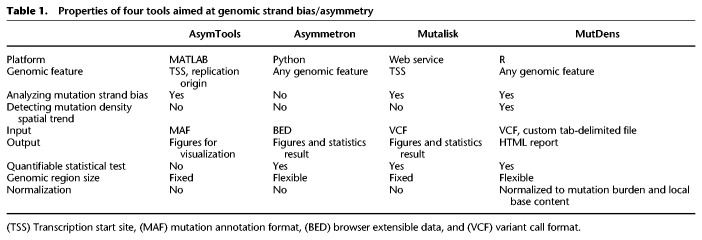
Here, we describe an R application (R Core Team 2022), MutDens, that examines, quantifies, and compares mutation density patterns around any genomic features. MutDens analyzes how somatic mutations spatially distribute in the flanking regions of a concerned genomic feature (e.g., TSSs and replication origins), calibrating local nucleotide composition and global mutation burden in the quantification of mutation density. In comparison to related methods such as AsymTools (Haradhvala et al. 2016), Asymmetron (Georgakopoulos-Soares et al. 2021), and Mutalisk (Lee et al. 2018), MutDens allows flexibility in the proximal vicinity of the focal feature, addresses both transcriptional and replicative strand bias analyses, detects mutation density spatial patterns, and compares between samples or features with proper normalization methods.
Results
MutDens development and availability
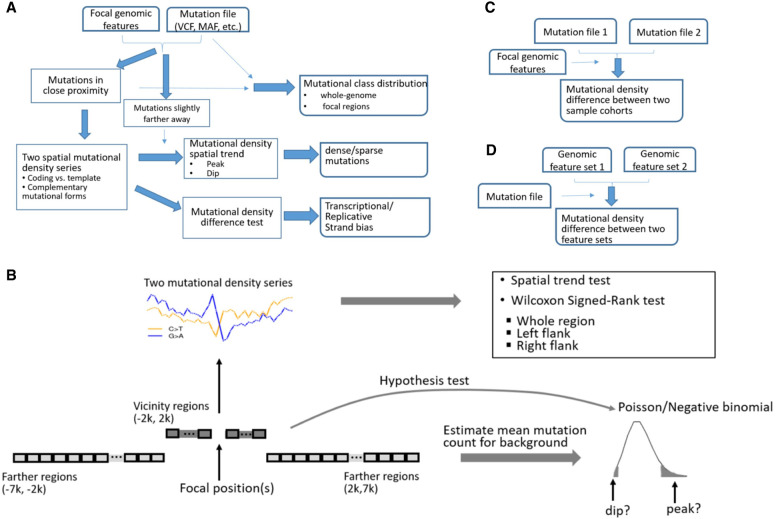
MutDens surveys mutation density spatial trends in specific genomic regions, examining three aspects of mutation data: mutational class distribution, mutation density pattern, and difference in mutation density (Fig. 1A). Extending bidirectionally from the given feature positions, we define immediate flanks as the vicinity and farther flanks as the background and exert statistical models to detect nontrivial mutation density spatial patterns in the vicinity (Fig. 1B). When two patient cohorts or two genomic features are involved, MutDens addresses the problem in comparison modalities (Fig. 1C,D). MutDens presets default values for parameters, including vicinity span limit (2 kb), boundaries of background regions (2 kb and 7 kb), and bin size (100 bp), but these parameters can be changed by the user. Theoretically, any nucleotide substitution can be categorized into six major mutation classes or 96 subclasses of varied trinucleotide contexts (Bergstrom et al. 2019). Mutational mechanisms, such as transcriptional/replicative strand biases, are usually associated with specific mutational classes for different cancers. MutDens can handle multiple mutational classes in parallel and can optionally offer close-up perusal in trinucleotide subclasses. MutDens supports the human genome with the richest built-in genomic features (of defined chromosome coordinates), and it is applicable to eight other model organisms as well, including rhesus, dog, mouse, rat, chicken, zebrafish, fruit fly, and yeast.
Figure 1.
Schema of MutDens. (A) The primary analysis modality entails input of one mutation file and one focal position set. Mutation counts are summarized within close proximity of focal positions (foreground) and over farther flanking regions (background). The foreground mutational counts are converted into two paired spatial mutation density series. MutDens returns three major outputs, elucidating mutational class balance, mutation spatial trend, and mutation density difference. (B) Core modules of MutDens to compare mutation density levels and to detect mutation density spatial patterns. The immediate flanking regions (defaulted to 2 kb in either direction) are sliced into continuous bins (default size, 100 bp); bin-wise mutation counts are converted to mutation density values. A trend test is conducted to detect the existence of a nonrandom spatial trend in the mutation density series. To compare the mutation density levels, a Wilcoxon test is performed between the two complementary mutational forms, in the left, right, and whole flanking region. To detect prominent mutation density spatial patterns, a null Poisson or negative binomial distribution of mutational count per bin is established based on bin-wise mutation counts from background regions (default distal/proximate boundaries, 7 kb and 2 kb). (C) MutDens can compare two sample cohorts on one set of focal positions. (D) MutDens can compare two sets of focal positions for one sample cohort.
Built-in regulatory genomic features: TSSs, replication origins, and enhancers
Transcriptional strand bias of mutation density has been reported for select cancers. Therefore, we included TSSs for human reference genomes GRCh38 and GRCh37 as built-in focal genomic features. Of note, TSSs have variable strand values in accordance with the strandedness of the associated genes, whereas in general, the focal positions are automatically labeled with the forward strand (“+”). Therefore, the spatial mutation density curves derived for TSSs should not be interpreted as left/right flanks on the forward strand; rather, the ostensible left and half sections designate the upstream and downstream regions relative to the TSS, respectively.
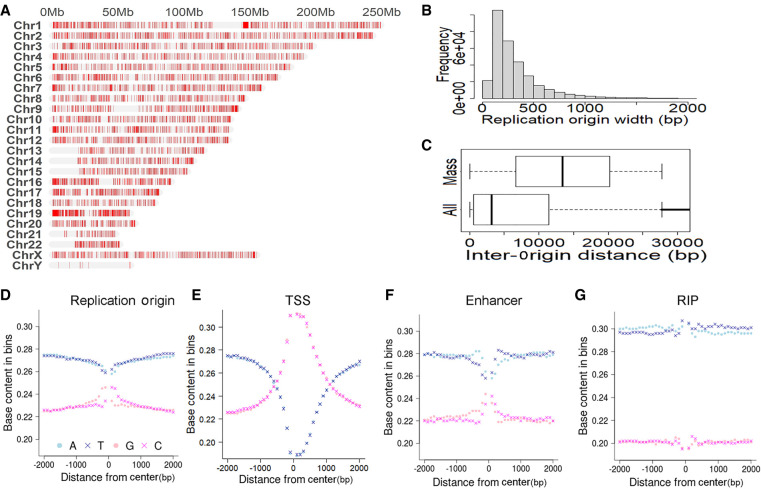
Similar to transcriptional strand bias, replicative strand bias also sheds light on cancer mechanisms. Location of replication origins (abbreviated as Origins hereafter) is key to the analysis of replicative strand bias, but unfortunately, origin locations are not as clear as the annotated TSSs. We noted two major data sources of Origin sites in the field: One was wrapped in the MATLAB application AsymTools in 2016 (Haradhvala et al. 2016), and the other was generated with SNS-seq in 2020 (Akerman et al. 2020). The 2016 location data were based on replication timing transition regions, and it contained 661 rather long Origin segments (median length, 500 kb). The 2020 location data contained 320,748 shorter Origin segments with a median length of 243 bp (Fig. 2B). Landscape views of Origin distribution across 24 human chromosomes were made for both data sets (Fig. 2A; Supplemental Fig. S1), and both landscapes consistently indicate broad barren territories on Chr 13, Chr 14, Chr 15, Chr 21, and Chr 22 p-arm ends and near the centers of Chr 1, Chr 9, and Chr 16 chromosomes. These large blank spots are mostly located in centromeres and telomeres and represent Origin-poor genomic regions. There are two potential reasons leading to sparse Origins in centromeres and telomeres. First, these two types of regions have highly condensed heterochromatin and are associated with late DNA replication. Therefore, they have fewer active Origins than other euchromatin regions. Second, centromeres and telomeres have highly repetitive DNA sequences, which are conceivably difficult for sequencing using SNS-seq. Excluding these long barren gaps, we found the intervals between consecutive Origins had a median length of 13.4 kb in the 2020 data set (Fig. 2C). According to the Origin location of the 2020 data set, G or C content in the 2-kb flanking regions is higher than the genome-wide level of 20% (Piovesan et al. 2019), and it reaches the maximum of 25% at the midpoints of Origins (Fig. 2D). Similarly, G or C content increases toward TSSs, peaking at the center at 31% (Fig. 2E). Such base content trend lines were rather flat with the 2016 Origin data set, where no increasing trend toward Origin center was discernable (Supplemental Fig. S2). Considering data quantity, location resolution, and base content patterns, we adopted the more recent SNS-seq-based Origin data source and took the Origin midpoints as focal positions. Origin locations in both GRCh38 and GRCh37 were included in the MutDens bundle.
Figure 2.
Description of built-in genomic features: replication origins and others. (A) Landscape view of replication origins on human chromosomes. (B) Distribution of width/length of replication origins. (C) Distribution of inter-origin distance. Long, barren intervals appear as outliers in the whole-data set view (All). Thus, we excluded the outliers and showed the distance boxplot for the mass component (Mass). (D) Nucleotide base content in (−2 k, 2 k) flanking regions of replication origins. (E) Nucleotide base content in (−2 k, 2 k) flanking regions of transcription start sites (TSSs). (F) Nucleotide base content in (−2 k, 2 k) flanking regions of enhancers. (G) Nucleotide base content in (−2 k, 2 k) flanking regions of retrotransposon insertion polymorphism (RIP) sites.
In recent years, great research attention was directed to enhancers, a type of cis-elements that is able to affect transcriptional regulation of proximal or distal genes. HACER (Wang et al. 2019) is an online human enhancer portal integrating FANTOM5 CAGE data (Noguchi et al. 2017) and nascent RNA sequencing data. On July 12, 2022, we downloaded the whole data set from HACER and reserved 107,153 enhancers that were supported by ENCODE as well as one of the two projects: Ensembl (Zerbino et al. 2015) and VISTA (Visel et al. 2007). Additionally, we compiled retrotransposon insertion polymorphism (RIP) sites for the human genome. An RIP is a genomic location where the presence or absence of a retrotransposon insertion is observed in the population. Our RIP sites were combined from two sources (Mir et al. 2015; Yu et al. 2017). Enhancer vicinity regions display base content dynamics similar to that of Origin, whereas RIP vicinity regions show a flat trend across the left and right 2-kb flanks (Fig. 2F,G).
Because of the remarkable nucleotide content dynamics in the vicinity of multiple genomic features (Fig. 2D–G), MutDens by default normalizes the mutation density into mutations per megabase (MPM) values accommodating the proportion of specific nucleotide type in each successive 100-bp vicinity bin. The bin-wise base content proportion values for the curated genomic features have been precalculated and can be loaded in session for swift normalization. With the user-supplied custom focal positions, MutDens can calculate the base composition on the fly, as long as the species is among our supported reference genomes. Alternatively, users can use genome-wide base proportion statistics for a global (nonlocal) MPM normalization. In this context, the human genome will use static proportion values of 0.30, 0.30, 0.20, and 0.20, for nucleotide types A, T, G, and C, respectively (Piovesan et al. 2019).
Mutation density patterns in cancers
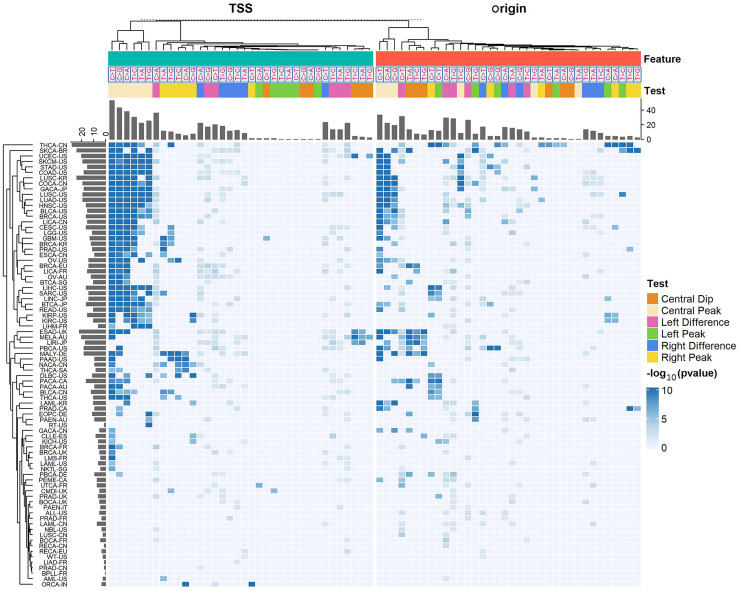
We tested MutDens on individual mutation files of aggregated somatic mutations for 81 International Cancer Genome Consortium (ICGC) cancer cohorts, against whole-genome TSSs and Origin sites, respectively. We generated both the mutation density difference test results and the peak/dip test results for each cohort and each mutational class and showed the P-values in a clustered heatmap (Fig. 3). In the heatmap, 372 and 274 out of the total 2916 tests showed significant results for TSS and Origin, respectively (P < 0.01 for left/right-flank density difference tests and P < 1 × 10−5 for peak/dip tests). A large number of cancer types, including lung cancers (LUSC-US, LUAD-US, and LUSC-KR) and skin cancers (SKCA-BR and SKCM-US), were clustered together, showing extremely low P-values, indicating TSS-coincident mutational peaks for almost all six mutational classes. Many cancers in this cluster also show a mutational peak at Origin, especially for the C > T mutational class. The Australian melanoma cancer cohort (MELA-AU) was isolated from the other skin cancers, possibly because it showed a TSS mutational spike for C > T mutations only. MELA-AU was clustered along with several neighbors (ESAD-UK, LIRI-JP, and PBCA-US), and they all characteristically manifested mutation density dips at Origin sites, especially for the T > A, T > C, and T > G classes. A lung cancer cohort, LUSC-CN, had an overall low mutation density level and did not display apparent peak/dip patterns. LUSC-CN was clustered with other cancers such as ALL-US and NBL-US and placed at the bottom of the heatmap. The cancers arranged at the bottom of the heatmap generally lack notable mutational spatial patterns near TSS or Origin.
Figure 3.
Overview of MutDens bulk analyses across all ICGC cohorts and all six mutational classes. Rows designate 81 ICGC cancer cohorts, and columns designate a total of 72 tests within each cancer cohort, concerning TSS and replication origin. The 72 tests per cohort differed by focal genomic feature (Feature), mutational class, and specific test objective (Test). Intensity in the heatmap is proportional to the inverse P-value (−log10(P)). All insignificant P-values (P > 0.01 for density difference tests and P > 1 × 10−5 for peak/dip tests) were treated as P = 1 and hence shown in the dimmest color.
Examples of mutational strand bias and mutational spatial patterns
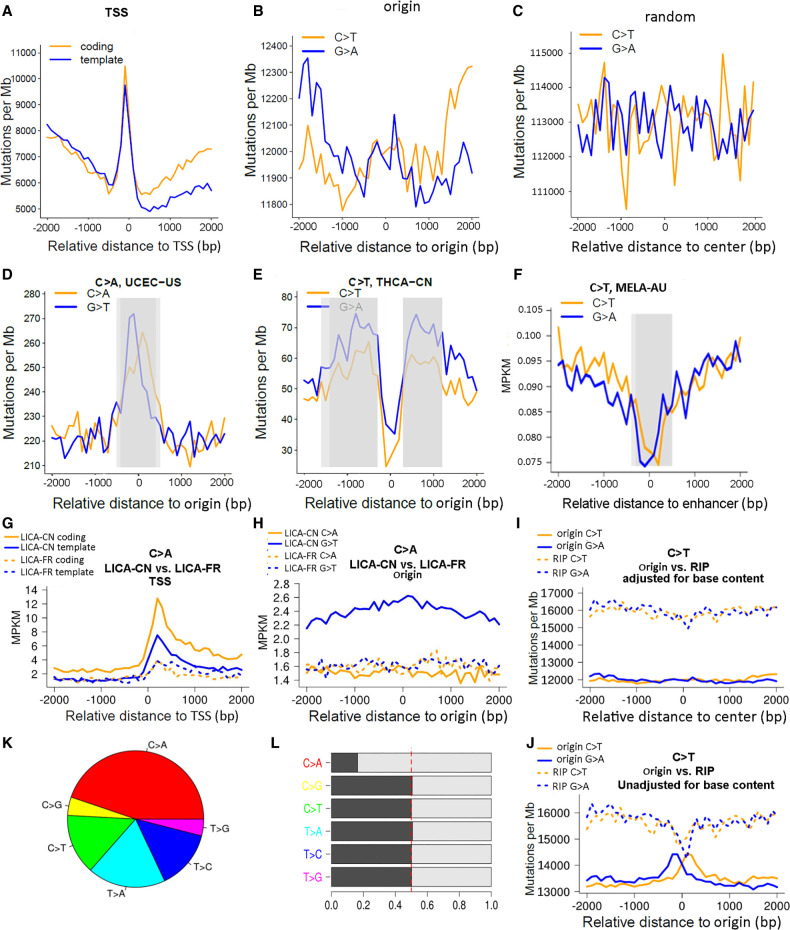
For a specific mutational class, an apparent divergence in the two coupled mutation density curves may indicate transcriptional/replicative strand bias. In the downstream from TSS, if the mutation density curve for the coding strand is higher than the other curve for the template strand, transcriptional strand bias may be postulated. In the left and right flanks of the Origin vicinity, if the mutation density advantage flips from one mutational form to the other, replicative strand bias may be postulated. Our scan of 81 ICGC cancer cohorts for all six mutational classes indeed revealed mutational strand bias in many cases. MELA-AU had the greatest mutation burden among all ICGC cohorts, and it showed remarkable transcriptional (Fig. 4A) and replicative (Fig. 4B) strand biases within the C > T mutational class, as supported by Wilcoxon signed-rank test P-values of 0.0039 for TSS downstream and 3 × 10−6 and 3 × 10−4 for Origin's left/right vicinities. For a negative control, we sampled random genomic positions and excluded those that were within 4-kb proximity of any Origin, thus yielding a set of 67,324 random genomic positions. MELA-AU C > T mutations did not display a strand bias around these random positions (Fig. 4C).
Figure 4.
Representative plots generated by MutDens in case studies of ICGC mutation data sets. (A–C) Mutation density curves of C > T mutations in the MELA-AU cohort, analyzed against three different genomic position sets: TSSs (A), replication origins (B), and random sites (C). (D–F) Distinct mutation density patterns were identified and marked in gray rectangles, including central peak of origins (D), off-center peaks of origins (E), and central dip of enhancers (F). (G–J) Four mutation density curves were aligned side by side as a result of comparing two cohorts (G,H) or comparing two position sets (I,J). When TSSs were in focus, LICA-CN displayed evidently greater C > A mutation density than LICA-FR, for both the coding strands and the template strands (G). When replication origins were in focus, LICA-CN outnumbered LICA-FR only in terms of the G > T mutations but not the C > A mutations (H). Speaking of MELA-AU C > T mutations, mutation density levels around replication origins were lower than those around RIP sites (I). If the background base content near Origins and RIP sites had not been taken into account, two near-center peaks would have shown up for Origin mutation density curves (J). (K) Mutational class distribution in the LICA-CN cohort. (L) Mutations in LICA-CN's each mutational class were divided into two complementary forms, where asymmetry between the C > A and G > T form pairs was prominent.
Similar to TSS-coincident mutational spikes (Fig. 4A), an Origin-coincident mutational peak was commonly seen. The UCEC-US cohort showed an Origin-coincident mutational peak in the C > A class (Fig. 4D). Occasionally, off-center mutational peaks were detected, and representative examples were found in the THCA-CN cohort concerning the C > T class (Fig. 4E). At times, we observed enhancer-coincident mutational dips, such as the one found for C > T in the MELA-AU cohort (Fig. 4F; Supplemental Fig. S3).
Comparison modalities of MutDens
MutDens can be used to compare two mutation cohorts at the same set of genomic positions (Fig. 1C). In such a context, because two sample cohorts are directly compared, the overall mutation burden per cohort should be considered, otherwise the statistical test result may reflect the difference in genome-wide mutation burden, not necessarily the situation within the vicinity of focal positions. Hence, the mutation density is assessed with the metric of “mutations per kilo total mutations per megabase” (MPKM), rather than MPM. The MPKM denotation is coined as an analogy to the well-known RPKM measure in RNA-seq analyses (Li et al. 2015).
To show the between-cohort comparison function, we compared two liver cancer cohorts, LICA-CN and LICA-FR, on TSSs and Origins, respectively. Certain patients displayed exceedingly great mutation burdens (Supplemental Fig. S4; Supplemental Table S1), and thus, the top 10% of patients (40 for LICA-CN and 25 for LICA-FR) were considered hypermutated outliers and were excluded from the analysis. The comparison was set on the C > A mutation class, the predominant class in the LICA-CN cohort (Fig. 4K). The aligned mutation density curves clearly showed that LICA-CN had a higher mutation density around TSSs than LICA-FR, and that LICA-CN showed a more marked TSS-coincident mutational spike than LICA-FR (Fig. 4G). For Origins, we observed that LICA-CN had a comparable mutation density to LICA-FR for C > A mutational form, but the mutation density of the G > T form was drastically different between LICA-CN and LICA-FR (Fig. 4H). The more abundant G > T mutations in LICA-CN over LICA-FR can be attributed to the imbalance between C > A and G > T mutational forms in the whole genome of LICA-CN (Fig. 4L). However, because the MPKM metric had already accounted for the total mutation burden, the imbalance between C > A and G > T forms in the vicinity of Origin must be even more severe than the genome-wide average situation, thus resulting in the evident elevation of LICA-CN G > T mutation density curves above the other three curves (LICA-CN C > A, LICA-FR C > A, and LICA-FR G > T). This assumption was validated by symmetry analysis of the whole genome and focal regions (Supplemental Fig. S5).
MutDens can also be used to compare mutational spatial patterns for two sets of genomic positions (Fig. 1D). To show this, we compared Origins with RIPs using MELA-AU C > T mutations. Mutation density around RIPs was significantly higher than that around Origins in melanoma (Wilcoxon signed-rank test P = 1 × 10−7) (Fig. 4I). A likely mechanism is that repair of UV damage is less efficient in transposons owing to the heterochromatin environment (Rebollo et al. 2011). In contrast, active replication origins are frequently located in open chromatin regions (Audit et al. 2009), where repair of UV damage is generally more efficient (Adar et al. 2016). Excessive C > T mutations in RIP over Origin were also observed in soft-tissue cancer (Supplemental Fig. S6). For the sake of technical analysis, we rendered mutation density curves for Origin in two different ways: with local (Fig. 4I) or global (Fig. 4J) base content normalization. Compared with the local normalization (Fig. 4I), the static, global normalization caused occurrence of central dips and central peaks for RIP and Origin (Fig. 4J), respectively, leading to a misconception that the two genomic features display comparable mutation density levels at their exact sites. This was mainly because the Origin centers harbor a greater portion of G/C bases than the surrounding regions (Fig. 2D), and when we normalized the mutated G/C bases with a greater proportion of constituent G/C bases, the ostensible Origin-center mutational peaks vanished. The local base content normalization also diminished the prominence of the central dip of RIP, although the change was barely noticeable owing to the overall flat base content curves around RIP (Fig. 2G). In this example, with the dissimilar results out of distinct normalization operations, we proved it is a rational and necessary operation to account for constituent base content in local vicinity bins, especially for genomic features like Origin and TSS that display a dynamic base content profile in the flanking regions.
Technical property analyses
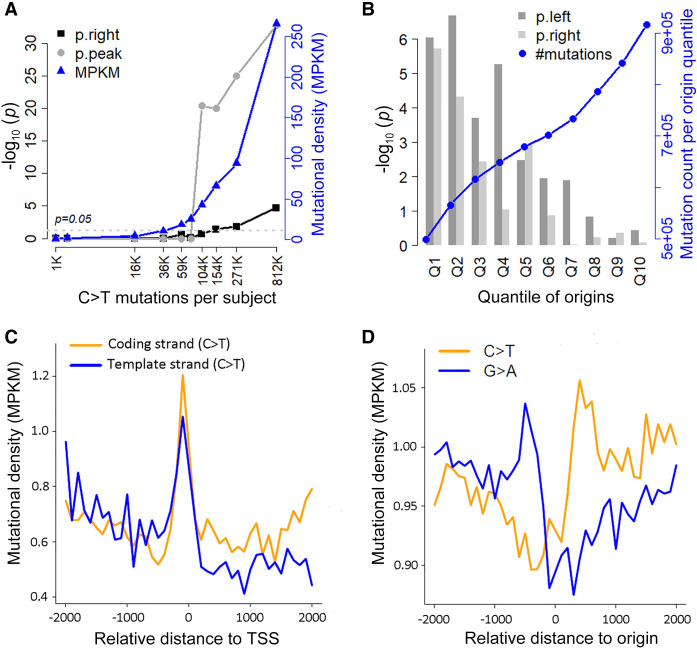
All above case studies made use of all unique mutations identified in a cancer cohort, which typically consisted of tens or even hundreds of subjects. We investigated how sample size and mutation burden impacted MutDens’ performance. MELA-AU had the greatest number of combined mutations (17 million) from 199 subjects, which was a good source for downsizing patient samples and decreasing mutation burden. We randomly selected 50, 10, and one subject(s) from the cohort and combined mutations from only the selected subjects; the random subject selection and follow-up TSS vicinity analysis was repeated five times. The results showed that 10 subjects collectively were enough to manifest a transcriptional strand bias pattern for C > T mutations (Supplemental Fig. S7), and a prominent TSS-coincident peak of C > T mutations was seen in two of five single samples (Supplemental Fig. S8). MELA-AU subjects varied greatly in their mutation burden quantities, ranging from a few thousand to nearly a million. We identified 10 subjects of evenly distributed quantiles (0.1, 0.2, …, 1) in the mutation burden distribution and executed MutDens on the mutations from each individual. Putting the 10 sets of results together, we found that results’ statistical significance increased with mutation burden per subject (Fig. 5A). At the 0.7 and 0.8 quantiles (corresponding to approximately 104,000 and 154,000 total C > T mutations), the Poisson test for central peak and the right-flank Wilcoxon test exceeded the permissive threshold of P = 0.05. This meant that 20%–30% of subjects in the MELA-AU cohort could individually elucidate transcriptional strand bias with their C > T mutations, and an example was shown (Fig. 5C).
Figure 5.
Technical properties of MutDens. (A) Analysis results for C > T mutations from 10 individual MELA-AU samples of increasing mutation burdens. Because the vicinity of TSS was examined, we visualized the transformed P-values out of right-flank Wilcoxon test (p.right) and the Poisson distribution test for central peak (p.peak). (MPKM) Mutations per kilo total mutations per megabase. (B) Analysis results for MELA-AU C > T mutations against 10 equal-sized Origin subsets (Q1–Q10) of decreasing SNS-seq scores. Because replication origins were examined, we visualized the transformed P-values out of both left-flank and right-flank Wilcoxon tests (p.left and p.right). (C) C > T mutations from a single sample in MELA-AU (EXTERN-MELA-20140526-101) led to mutation density curves that clearly reflected transcriptional strand bias. (D) Restricting Origins to the top 10% of highest SNS-seq scores (Q1), the flip of predominant mutational form at Origin center became more apparent, clearly hinting at a replicative strand bias.
On another dimension, we studied if alternate subsets of focal positions would lead to different analysis results. In the original data source (Akerman et al. 2020), the 320,748 Origins were categorized into 10 quantiles (Q1–Q10) based on the normalized SNS-seq score (activity score), with each quantile containing around 32,000 Origins. We executed MutDens on all MELA-AU mutations against each of the 10 Origin subsets and recorded the Wilcoxon test P-values for the left flank and the right flank. As expected, the quantiles of higher normalized SNS-seq scores showed greater statistical significance, with Q1 and Q2 Origins showing P-values lower than 1 × 10−4 (Fig. 5B). Although each quantile had nearly the same number of Origins, their harbored mutations clearly increased with the quantile number, meaning that less active Origins were prone to more mutations. In the paired mutation density curves for MELA-AU C > T mutations using Q1 Origins only (Fig. 5D), the replicative strand bias pattern was more pronounced than using the whole set of Origins, with Wilcoxon test P-values of 1 × 10−6 (left) and 1 × 10−5 (right). This experiment with quantile subsets of Origins indicated that including more relevant or more accurate genomic positions help to sharpen the potential mutation density pattern.
Comparison to similar tools
Currently, there is no dedicated application to explore mutation density spatial trends with complete flexibility on genomic features. Three other tools have partially similar features (Table 1). Asymmetron (Georgakopoulos-Soares et al. 2021) can identify strand asymmetry patterns in biological sequences. However, Asymmetron analyzes the arrangement asymmetry of stranded genomic features; it does not analyze single-base substitutions and does not inspect strand bias of mutations. MATLAB package AsymTools (Haradhvala et al. 2016) is limited to visualizing the strand bias with barplots without providing qualitative judgment on strand bias. The commercial environment of MATLAB and the special input mutation annotation format have impeded the accessibility of AsymTools. Other studies (Tomkova et al. 2018; Degtyareva et al. 2019; Rodin et al. 2021) leveraged only the built-in replication direction data in AsymTools rather than its analysis utility. On the contrary, MutDens is implemented in the more popular open-source platform of R, and it accepts the more widely adopted variant call format (VCF) as input. The web toolkit Mutalisk (Lee et al. 2018) contained a module for transcriptional strand bias, which adopted the general strategy of summarizing and comparing all mutations in transcribed/untranscribed regions. The two tools AsymTools and Mutalisk enrolled the fixed total coding regions in the genome to interrogate mutational strand bias, and they are limited to TSSs and replication origins only. In contrast, MutDens enables mutation density investigation in flexible vicinity regions of any genomic feature. Compared with the few existing related tools, our new application MutDens stresses the close proximity of focal features, empowers both transcriptional and replicative strand bias analyses, and implements proper normalization methods and statistical tests to detect both quantity difference and prominent spatial patterns of mutation density curves.
Table 1.
Properties of four tools aimed at genomic strand bias/asymmetry
Runtime analysis
Finally, we recorded computational time usage on a range of mutation burdens and a range of genomic position quantities. Using the UCEC-US cohort, which reported a total of 880,000 mutations, we executed MutDens on 10 gradually enlarged Origin subsets of 31,000–316,000 positions. On a Linux Ubuntu workstation with Intel Xeon CUP E5-2650 V4 at 2.20-GHz and 32-GB memory, the running time for single-cohort analysis (Fig. 1A) went up roughly linearly from 73 sec to 280 sec (Supplemental Fig. S9). Using the Q1 Origin subset, which consisted of 31,000 positions, we executed MutDens on 10 gradually enlarged mutation subsets of 100,000–17,000,000 mutations from the MELA-AU cohort. The running time went up roughly linearly from 52 sec to 1076 sec (Supplemental Fig. S9). We anticipate that users’ mutation quantity normally will not exceed the ICGC MELA-AU cohort and that the focal positions will typically not outnumber the whole Origin set we tested; therefore, a typical MutDens session in a real application should complete in a few minutes.
Discussion
Somatic mutation is a major factor for tumorigenesis. Instead of studying individual mutations, examining mutations as a whole offers a unique perspective into the tumorigenesis mechanism and history. Methods such as mutation burden (Ping et al. 2020) and mutational signature (Alexandrov et al. 2013) combine all mutations in one subject to describe the overall mutational characteristics. Mutational strand bias represents another holistic perspective on genome-wide mutations, which appeared as a promising approach to tumorigenesis mechanisms. Analyses in this line of research contrast the multitudes of single-base substitutions between the two complementary DNA strands. Insights into mutagenesis mechanisms are revealed by examining the mutation form and quantity only, sparing the step of mutation annotation that is commonly practiced in other research workflows. Currently, the general strategy is to aggregate widespread mutations into summary statistics for the two complementary strands. Such an aggregate strategy cannot emphasize focal genomic regions of the most striking attribute, and it is difficult to accommodate varied nucleotide constitutions in each mutation's local context. The lack of a systematic and quantifiable approach prompted us to develop the novel R application MutDens, which addresses the topic of mutational strand bias by analyzing mutation density spatial trends relative to user-designated focal genomic positions. Although existing approaches typically obtain the total number of mutations present in genomic regions of interest, MutDens delineates the running mutation density curves in the flanking regions of focal genomic positions. Thus, MutDens is able to detect, quantify, and compare special patterns in mutation density spatial trends, including peaks, dips, and density divergence between the complementary mutational forms.
We executed MutDens on somatic mutations of 81 ICGC cancer cohorts spanning 57 cancer types, examining mutation strand bias and mutation density trend around TSSs and replication origins. MutDens successfully revealed well-known transcriptional/replicative strand biases. We recovered evident C > T and G > T transcriptional strand bias patterns from skin cancer cohorts (MELA-AU, SKCA-BR, and SKCM-US) and a lung cancer cohort (LUSC-KR), respectively. In one liver cancer cohort (LICA-FR), we revealed strong transcriptional strand bias for C > A mutations; compared with the more widely known T > C transcriptional strand bias, C > A bias was only occasionally reported before (Brunner et al. 2019). In terms of mutation spatial trend, we found that many cancers show a TSS-coincident mutational peak for multiple mutational classes. The same set of cancers tends to show an Origin-coincident mutational peak for cytosine/guanine-involved substitutions, especially C > T. A small group of cancers including MELA-AU showed Origin-coincident mutational dips for thymine/adenine-involved substitutions. In addition to comprehensively surveying around TSSs and replication origins, we also examined enhancers and RIPs in several cancer types. In a skin cancer cohort (MELA-AU), we observed enhancer-coincident mutational dips for the C > T class; in a liver cancer cohort (LICA-CN), there was a statistically significant predominance of C > A mutations over the complement, G > T; and in skin cancer and soft tissue cancer, RIP displayed higher mutation density than replication origins. These observations show the capability of MutDens to quickly protrude noteworthy mutation patterns or phenomena that are associated with specific cancer cohorts. However, it remains a challenging task to definitively correlate mutational patterns with tumorigenesis, given that the etiologies for many cancers are still elusive. Mechanistic interpretation of the prominent mutation patterns demands domain knowledge on tumorigenesis in specific contexts. Although MutDens may help researchers identify mutational patterns in cancer types of their interest and infer potential risk factors, the hypotheses conceived to explain prominent mutation patterns need to be validated in carefully designed follow-up experiments.
Recently, liver cancers were associated with SBS4 and SBS5 mutation signatures, which featured C > A and C > T as the predominant class, respectively (Degasperi et al. 2022; https://signal.mutationalsignatures.com/explore/studyTissueType/6-11). Our comparison analysis between LICA-CN and LICA-FR found dissimilar mutation density spatial patterns. This difference could be attributed to the batch effect of the technical issue of the HTS analysis pipeline, but it may also reflect the existence of fundamental differences (e.g., genetics, habit, diet, etc.) between the two races, suggesting that disparate mutational signatures likely dictate the two different cancer cohorts from China and France. We observed that LICA-CN and LICA-FR presented distinct predominant mutation classes, namely, C > A and C > T, respectively. Moreover, LICA-CN showed a drastic genome-wide imbalance between the C > A and the G > T mutation forms, and such inter-form imbalances were appreciable in local regions (e.g., TSSs, Origins, and enhancers); this remarkable imbalance was not seen with LICA-FR. The remarkable imbalance between the two complementary mutation forms is not an artifact. First, the asymmetry was revealed in the whole genome, taking full lengths of forward/reverse chromosome strands into account. According to Chargaff's rules, complementary nucleotides (such as cytosine/C and guanine/G) have equivalent amounts in the whole genome. Thus, a genome-wide asymmetry between C > A and G > T must be owing to mutagenesis not to base content disproportionality. Second, such a drastic mutation form asymmetry was only seen in LICA-CN not in patient cohorts of other cancers. Finally, the MPKM metric by design normalizes off uneven base content among the four nucleotide types (A, T, G, and C), as well as variant mutation burdens of each mutation form. Mutation density disparity retained in MPKM curves of focal features thus suggests higher-than-average asymmetry in local regions relative to the global situation.
Although most illustrative analyses in this work used cohort-level mutation files, we showed that one hypermutated individual or a small cohort (n ≥ 10) would generate sufficient mutations for a MutDens analysis. In another perspective, hypermutated patients may represent distinct tumorigenesis mechanisms and are sometimes excluded from the analysis of the majority data-points. As long as the data set shows acceptable mutation burden statistics, it is recommended to look into the majority cohort and the hypermutated outliers separately.
We have strived to incorporate a spectrum of built-in genomic features for users to embark on mutation density analysis in varied tumor cohorts/individuals and even have extended the utility from humans to common model organisms. With novel genomic features, MutDens can calculate the local base content to realize a reasonable mutation density local normalization. With more and more human whole-genome sequencing projects being conducted in research and clinical settings, MutDens can be leveraged to statistically test for transcriptional/replicative strand bias inherent in the mutation data, and moreover, it can reveal potential mutation density spatial patterns around various genomic features for specific patient cohorts.
Methods
MutDens requires two major inputs: a list of somatic mutations and a list of focal genomic positions corresponding to a genomic feature (Fig. 1A). When provided with two mutational files or two position sets, MutDens compares the mutational class distribution and mutation density levels between two sample cohorts or two genomic region sets (Fig. 1C,D). We tested MutDens thoroughly on somatic mutation files for 81 cohorts of 57 cancer types downloaded from the International Cancer Genome Consortium (ICGC; https://dcc.icgc.org/releases/release_28/Summary/).
Mutational class distribution and forward/reverse strand balance
In this work, somatic mutations are limited to single-base substitutions. A total of 12 possible single-nucleotide substitutions exists among four nucleotides (A, T, G, and C). Because of the complementary property of DNA, six mutational classes can be summarized: C > A (C > A & G > T), C > G (C > G & G > C), C > T (C > T & G > A), T > A (T > A & A > T), T > C (T > C & A > G), and T > G (T > G & A > C). MutDens manages each mutational class separately and processes all six possible mutational classes in a single session. Based on the complementarity nature of DNA double-strand structure, it is generally assumed that the two complementary forms of a mutational class should be balanced across the whole genome. The foremost output of MutDens includes a composition overview of the six mutational classes (Fig. 4K) and the balancing situation between the paired forms within each class (Fig. 4L). Such an overview is provided for both the whole genome and within the vicinity (defined below) of focal positions.
Sometimes, it is worthwhile to further distinguish the 5′- and 3′- neighbor base context of the central substitution, as a specific mutational signature may display characteristic peaks for select trinucleotide subclasses only (Alexandrov et al. 2020). Underneath the major six-class classification, MutDens allows for a 16-subclass categorization: A*A, A*C, A*G, A*T, C*A, C*C, C*G, C*T, G*A, G*C, G*G, G*T, T*A, T*C, T*G, and T*T, where the asterisk symbol (*) denotes the central single-base substitution. When the option of trinucleotide context is turned on, each mutation class will be expanded into the 16 foresaid context-specific subclasses. The ensuing analyses (see below), including manifestation of mutation density series, statistical comparisons, and spatial pattern detection, will be conducted within the scope of each subclass.
Spatial mutation density curves in the vicinity of focal features
MutDens aims to analyze the spatial pattern of mutation density in the vicinity of focal genomic features. To this end, MutDens counts mutations in immediate flanking regions (i.e., signal) and more distant regions (i.e., background) and contrasts the signal mutational counts against background mutational counts (Fig. 1B).
The vicinity of a focal position is by default confined to 2 kb in each direction but can be adjusted by the user. Given the set of focal genomic positions, we derive two 2-kb flanking regions in the left and right directions. By default, the total 4-kb vicinity region is dissected into 40 continuous bins, each spanning 100 bp. With assistance from R package GenomicRanges (Lawrence et al. 2013), we count the total number of mutations in each 100-bp bin of each focal position. Merging across all positions, we obtain 40 summed mutational counts for the focal genomic feature. These summed mutational counts are divided by the total number of base pairs of a given type (A/T or G/C) to generate the MPM value, standing for the number of mutations per megabase. The 40 MPM values are connected in order and are visualized as a spatial mutation density curve centered on the genomic feature of interest. Because one mutational class contains two mutually complementary forms, we plot two spatial mutation density curves for the two mutational forms, respectively.
Detecting mutation density peaks and dips in the vicinity of focal features
We generated a statistical protocol for detecting mutation density peaks/dips by following the similar operation in the ChIP-seq software MACS (Zhang et al. 2008). Briefly, we count mutations in each 100-bp bins of the background regions. The background 100-bp bins for all focal positions are aggregated in the same way as we treat foreground bins. With the default inner and outer boundary parameters of 2 kb and 7 kb, we obtain 100 (50 left and 50 right) mutational count numbers, which are used to fit a background count discrete distribution, either negative binomial (default) or Poisson. Because the negative binomial distribution is a generalization of the Poisson distribution, the negative binomial distribution is used as default. The Poisson distribution can be used when we have strong evidence that the mean and variance of the mutational count data are equal. Each of the 40 mutational count numbers summarized from the foreground bins, as expounded above, is tested against the fitted background distribution. If the foreground count number is extremely large, it hints at a mutational peak; if it is extremely small, it hints at a mutational dip (Fig. 1B). We calculated the probability of observing as extreme or more extreme count numbers based on the fitted background distribution, in the left-tail and right-tail directions, respectively. A probability less than 1 × 10−5 was considered statistically significant (Zhang et al. 2008). In our exploration of dozens of cancer cohorts from the ICGC project, we noted that the most striking peaks/dips usually fall upon the exact centers of Origins, and occasionally, we observed two peaks apart from the center. Therefore, as a conservative strategy, MutDens reports at most one qualified dip, which must span the central position. As for peaks, MutDens preferentially seeks a potential central peak; only when a central peak is not statistically affirmed does MutDens further evaluate the most prominent peak in the left/right flanks. In other words, MutDens may commonly assert no peaks or dips at all, and the assertion of a central peak suppresses assertion of noncentral peaks.
In addition, MutDens leverages the local regression-based WAVK test (Wang et al. 2008) via R package funtimes (https://cran.r-project.org/web/packages/funtimes/) to detect the existence of a nonrandom spatial trend in the mutation density series.
Comparing two mutation density series
Because we always summarize the mutational count/density values for the two forms of a mutational class in a paired manner, we use a Wilcoxon signed-rank test to compare the two mutation density series (Fig. 1B). If the test results are both statistically significant in the left and right flanks but are associated with opposite signs of the mean difference values, it suggests the predominance of one mutational form flips to the other mutational form upon crossing the central genomic feature. Previously, such flips of mutational form predominance have signified replicative strand bias in certain cancer cohorts (Haradhvala et al. 2016).
Software availability
The analysis presented here uses publicly available data sources as outlined in the Methods. The R code scripts are contained in Supplemental Code S1–S5. These five R code scripts require simple input configuration files as exemplified in Supplemental Code S6–S8. All R scripts, example input files, and a software manual, are available at our GitHub repository (https://github.com/hui-sheen/MutDens).
Supplementary Material
Acknowledgments
We thank Mr. Wei Wang at The Rockefeller University for parsing the replication origin locations from AsymTools. We also thank Mr. Jiapeng He and Ms. Olufunmilola M. Oyebamiji at University of New Mexico for technical support in coding and debugging. This study was supported by Cancer Center Support grant P30CA118100 from the National Cancer Institute and was also supported by Analytical and Translational Genomics Shared Resource and Bioinformatics Shared Resource of the Comprehensive Cancer Center, University of New Mexico. Y.G. was supported by grant R01ES030993-01A1 from the National Cancer Institute.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.276770.122.
Competing interest statement
The authors declare no competing interests.
References
- Adar S, Hu J, Lieb JD, Sancar A. 2016. Genome-wide kinetics of DNA excision repair in relation to chromatin state and mutagenesis. Proc Natl Acad Sci 113: E2124–E2133. 10.1073/pnas.1603388113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akerman I, Kasaai B, Bazarova A, Sang PB, Peiffer I, Artufel M, Derelle R, Smith G, Rodriguez-Martinez M, Romano M, et al. 2020. A predictable conserved DNA base composition signature defines human core DNA replication origins. Nat Commun 11: 4826. 10.1038/s41467-020-18527-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexandrov LB, Nik-Zainal S, Wedge DC, Aparicio SA, Behjati S, Biankin AV, Bignell GR, Bolli N, Borg A, Børresen-Dale AL, et al. 2013. Signatures of mutational processes in human cancer. Nature 500: 415–421. 10.1038/nature12477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexandrov LB, Kim J, Haradhvala NJ, Huang MN, Tian Ng AW, Wu Y, Boot A, Covington KR, Gordenin DA, Bergstrom EN, et al. 2020. The repertoire of mutational signatures in human cancer. Nature 578: 94–101. 10.1038/s41586-020-1943-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Audit B, Zaghloul L, Vaillant C, Chevereau G, d'Aubenton-Carafa Y, Thermes C, Arneodo A. 2009. Open chromatin encoded in DNA sequence is the signature of ‘master’ replication origins in human cells. Nucleic Acids Res 37: 6064–6075. 10.1093/nar/gkp631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergstrom EN, Huang MN, Mahto U, Barnes M, Stratton MR, Rozen SG, Alexandrov LB. 2019. SigProfilerMatrixGenerator: a tool for visualizing and exploring patterns of small mutational events. BMC Genomics 20: 685. 10.1186/s12864-019-6041-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunner SF, Roberts ND, Wylie LA, Moore L, Aitken SJ, Davies SE, Sanders MA, Ellis P, Alder C, Hooks Y, et al. 2019. Somatic mutations and clonal dynamics in healthy and cirrhotic human liver. Nature 574: 538–542. 10.1038/s41586-019-1670-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degasperi A, Zhou X, Amarante T, Martinez A, Koh G, Dias J, Heskin L, Chmelova L, Rinaldi G, Wang V, et al. 2022. Substitution mutational signatures in whole-genome–sequenced cancers in the UK population. Science 376: science.abl9283. 10.1126/science.abl9283 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Degtyareva NP, Saini N, Sterling JF, Placentra VC, Klimczak LJ, Gordenin DA, Doetsch PW. 2019. Mutational signatures of redox stress in yeast single-strand DNA and of aging in human mitochondrial DNA share a common feature. PLoS Biol 17: e3000263. 10.1371/journal.pbio.3000263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgakopoulos-Soares I, Mouratidis I, Parada GE, Matharu N, Hemberg M, Ahituv N. 2021. Asymmetron: a toolkit for the identification of strand asymmetry patterns in biological sequences. Nucleic Acids Res 49: e4. 10.1093/nar/gkaa1052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haradhvala NJ, Polak P, Stojanov P, Covington KR, Shinbrot E, Hess JM, Rheinbay E, Kim J, Maruvka YE, Braunstein LZ, et al. 2016. Mutational strand asymmetries in cancer genomes reveal mechanisms of DNA damage and repair. Cell 164: 538–549. 10.1016/j.cell.2015.12.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jelaković B, Castells X, Tomić K, Ardin M, Karanović S, Zavadil J. 2015. Renal cell carcinomas of chronic kidney disease patients harbor the mutational signature of carcinogenic aristolochic acid. Int J Cancer 136: 2967–2972. 10.1002/ijc.29338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucab JE, Zou X, Morganella S, Joel M, Nanda AS, Nagy E, Gomez C, Degasperi A, Harris R, Jackson SP, et al. 2019. A compendium of mutational signatures of environmental agents. Cell 177: 821–836.e16. 10.1016/j.cell.2019.03.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence M, Huber W, Pagès H, Aboyoun P, Carlson M, Gentleman R, Morgan MT, Carey VJ. 2013. Software for computing and annotating genomic ranges. PLoS Comput Biol 9: e1003118. 10.1371/journal.pcbi.1003118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Lee AJ, Lee JK, Park J, Kwon Y, Park S, Chun H, Ju YS, Hong D. 2018. Mutalisk: a web-based somatic MUTation AnaLyIS toolKit for genomic, transcriptional and epigenomic signatures. Nucleic Acids Res 46: W102–W108. 10.1093/nar/gky406 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Letouzé E, Shinde J, Renault V, Couchy G, Blanc JF, Tubacher E, Bayard Q, Bacq D, Meyer V, Semhoun J, et al. 2017. Mutational signatures reveal the dynamic interplay of risk factors and cellular processes during liver tumorigenesis. Nat Commun 8: 1315. 10.1038/s41467-017-01358-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li P, Piao Y, Shon HS, Ryu KH. 2015. Comparing the normalization methods for the differential analysis of illumina high-throughput RNA-Seq data. BMC Bioinformatics 16: 347. 10.1186/s12859-015-0778-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mir AA, Philippe C, Cristofari G. 2015. euL1db: the European database of L1HS retrotransposon insertions in humans. Nucleic Acids Res 43: D43–D47. 10.1093/nar/gku1043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noguchi S, Arakawa T, Fukuda S, Furuno M, Hasegawa A, Hori F, Ishikawa-Kato S, Kaida K, Kaiho A, Kanamori-Katayama M, et al. 2017. FANTOM5 CAGE profiles of human and mouse samples. Sci Data 4: 170112. 10.1038/sdata.2017.112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ping J, Oyebamiji O, Yu H, Ness S, Chien J, Ye F, Kang H, Samuels D, Ivanov S, Chen D, et al. 2020. MutEx: a multifaceted gateway for exploring integrative pan-cancer genomic data. Brief Bioinformatics 21: 1479–1486. 10.1093/bib/bbz084 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piovesan A, Pelleri MC, Antonaros F, Strippoli P, Caracausi M, Vitale L. 2019. On the length, weight and GC content of the human genome. BMC Res Notes 12: 106. 10.1186/s13104-019-4137-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polak P, Arndt PF. 2008. Transcription induces strand-specific mutations at the 5′ end of human genes. Genome Res 18: 1216–1223. 10.1101/gr.076570.108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. 2022. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. https://www.R-project.org/. [Google Scholar]
- Rebollo R, Karimi MM, Bilenky M, Gagnier L, Miceli-Royer K, Zhang Y, Goyal P, Keane TM, Jones S, Hirst M, et al. 2011. Retrotransposon-induced heterochromatin spreading in the mouse revealed by insertional polymorphisms. PLoS Genet 7: e1002301. 10.1371/journal.pgen.1002301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodin RE, Dou Y, Kwon M, Sherman MA, D'Gama AM, Doan RN, Rento LM, Girskis KM, Bohrson CL, Kim SN, et al. 2021. The landscape of somatic mutation in cerebral cortex of autistic and neurotypical individuals revealed by ultra-deep whole-genome sequencing. Nat Neurosci 24: 176–185. 10.1038/s41593-020-00765-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomkova M, Tomek J, Kriaucionis S, Schuster-Böckler B. 2018. Mutational signature distribution varies with DNA replication timing and strand asymmetry. Genome Biol 19: 129. 10.1186/s13059-018-1509-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visel A, Minovitsky S, Dubchak I, Pennacchio LA. 2007. VISTA Enhancer Browser: a database of tissue-specific human enhancers. Nucleic Acids Res 35: D88–D92. 10.1093/nar/gkl822 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Akritas MG, Keilegom IV. 2008. An ANOVA-type nonparametric diagnostic test for heteroscedastic regression models. J Nonparametr Stat 20: 365–382. 10.1080/10485250802066112 [DOI] [Google Scholar]
- Wang J, Dai X, Berry LD, Cogan JD, Liu Q, Shyr Y. 2019. HACER: an atlas of human active enhancers to interpret regulatory variants. Nucleic Acids Res 47: D106–D112. 10.1093/nar/gky864 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Q, Zhang W, Zhang X, Zeng Y, Wang Y, Wang Y, Xu L, Huang X, Li N, Zhou X, et al. 2017. Population-wide sampling of retrotransposon insertion polymorphisms using deep sequencing and efficient detection. Gigascience 6: 1–11. 10.1093/gigascience/gix066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zerbino DR, Wilder SP, Johnson N, Juettemann T, Flicek PR. 2015. The Ensembl Regulatory Build. Genome Biol 16: 56. 10.1186/s13059-015-0621-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Liu T, Meyer CA, Eeckhoute J, Johnson DS, Bernstein BE, Nusbaum C, Myers RM, Brown M, Li W, et al. 2008. Model-based Analysis of ChIP-Seq (MACS). Genome Biol 9: R137. 10.1186/gb-2008-9-9-r137 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.