An Efficient Optimization Approach for Glioma Tumor Segmentation in Brain MRI

Abstract

Glioma is an aggressive type of cancer that develops in the brain or spinal cord. Due to many differences in its shape and appearance, accurate segmentation of glioma for identifying all parts of the tumor and its surrounding cancerous tissues is a challenging task. In recent researches, the combination of multi-atlas segmentation and machine learning methods provides robust and accurate results by learning from annotated atlas datasets. To overcome the side effects of limited existing information on atlas-based segmentation, and the long training phase of learning methods, we proposed a semi-supervised unified framework for multi-label segmentation that formulates this problem in terms of a Markov Random Field energy optimization on a parametric graph. To evaluate the proposed framework, we apply it to publicly available BRATS datasets, including low- and high-grade glioma tumors. Experimental results indicate competitive performance compared to the state-of-the-art methods. Compared with the top ranked methods, the proposed framework obtains the best dice score for segmenting of “whole tumor” (WT), “tumor core” (TC ) and “enhancing active tumor” (ET) regions. The achieved accuracy is 94$\%$ characterized by the mean dice score. The motivation of using MRF graph is to map the segmentation problem to an optimization model in a graphical environment. Therefore, by defining perfect graph structure and optimum constraints and flows in the continuous max-flow model, the segmentation is performed precisely.

Introduction

The abnormal growth of glial cells within the brain could cause glioma tumors which can disrupt proper functioning of brain and lead to life-threatening situations. According to the malignancy grade, there are four types of glioma, grades 1 and 2 are known as low-grade glioma (LGG) that grow slowly and they are less harmful and treatable. Grades 3 and 4 are the high-grade glioma (HGG) that are fast developing and harmful [1, 2].

Magnetic resonance imaging (MRI) is widely used in the clinical diagnosis of glioma. The anatomical structure of soft tissue can be reflected in MR images. Also, the location and size of tumors can be characterized by analyzing them.

Due to the intensity inhomogeneity in brain images, more pathological information is needed for precise tumor delineation and description. Therefore, various MRI sequences including $T_1$ weighted, $T_1$ weighted with contrast enhancement ($T_{1C}$), $T_2$ weighted and $T_2$ weighted with fluid-attenuated inversion recovery ($T_{2Flair}$) are necessary for better results [3].

The automatic brain tumor segmentation from multi-modal magnetic resonance images (MRI) is the key step for computer-aided diagnosis in surgery and radiotherapy. The complex pathological changes cause the complex changes in brightness and texture of glioma on MRI images. Different tissues such as normal and tumor, may have similar intensity values, which present challenges to the accurate and stable segmentation of glioma. Hence, an essential clue to simplify this task is a prior anatomical information that can be provided in different ways, for instance, as a set of predefined rules based on known tissue properties, or as a set of manual expert annotations [4].

Regarding to segmentation challenges, numerous algorithms have been developed to perform brain tumor detection and segmentation.

In recent years, learning-based methods have been widely used in MR image segmentation fields, such as the support vector machine (SVM) [5], random forest (RF) [6] and convolutional neural network (CNN) [7]. The automatic and unsupervised segmentation algorithms driven by machine learning ([8, 9]) are presented in other modalities. These methods are suitable for the image analysis of specific anatomical structures due to their advantages in terms of efficiency in pairwise registration and feature description.

Most of the automatic glioma segmentation approaches have learned a discriminative model in offline mode [10, 11]. In these models, image intensity features are computed; then, a machine learning algorithm is trained offline. Most computation time is spent during the learning stage, which should be run again if a new data is added. Moreover, results are highly dependent on the choice of features [12], and feature extraction has to be performed at test time. The generative approach relies on distribution of tissues as a prior knowledge. It builds a probabilistic model of observed image intensity given the tissue type. The latent variable is the spatial distribution of healthy tissues or tumor compartments. Prior knowledge, generally, includes the location and spatial extent of healthy tissues in an atlas.

In the past decade, atlas-based methods have shown superior performance over other automatic brain image segmentation algorithms [13]. The main idea of the atlas-based methods is to use the prior knowledge of the atlas to classify the target pixels. Each atlas contains an intensity image and its label map determined by a radiologist [13].

Many of the atlas-based segmentation techniques rely on label propagation from multiple atlases after nonlinear registration to a target image [14]. The segmentation can be formed by label fusion of the propagated labels, e.g., by applying a majority vote or another combination strategy such as a weighted average based on global or local similarity measures between the target and atlas images [15].

A multi-atlas segmentation method combined with SVM classifiers and super-voxels has been proposed in [16]. This method is not sensitive to pair registration and reduces registration time by using affine transformation. In another study [17], an atlas forest automatic labeling method has been proposed in brain MR images that encodes atlas images into the atlas forest to reduce registration time. Also, [7] proposed a convolutional neural network model combining convolution and prior spatial features for sub-cortical brain structure segmentation and trained the network using a restricted sample selection to increase segmentation accuracy.

Patch-based segmentation methods are another approaches for tumor classification. The author in [18] studied about the glioma labeling using patch based models. A patch-based MR image tissue classification method is presented in [19]. It defines a sparse dictionary learning method and combines the statistical atlas prior to the sparse dictionary learning.

A frequently used method that efficiently solves the labeling problem is to express it as a Markov Random Field energy function [20] and minimize it using min-cut/max-flow techniques [21]. The MRF is normally defined by a graph constructed on a regular grid representing the target image. However, some applications formulate the MRF energy function on graphs connecting multiple images.

Our Contribution

Brain tissue boundary regions are difficult to segment for both multi-atlas segmentation and learning-based segmentation methods [22]. It is mainly because the pixel values of the tissue boundary regions are very similar and it is difficult to identify whether the pixels of these regions belong to the target image. In addition, the segmentation result of one slice does not help in refining the segmentation of its preceding slices.

In order to overcome these shortcomings and make full use of the prior information of the atlas, we introduce an efficient optimization based approach to solve segmentation problem.

The proposed method is defined based on a flexible graph structure that allows optimizing segmentation by using multi-atlas patch-based techniques. More specifically, we introduce a graph that encodes the atlas labels in the unary potential functions and local information propagation in the pairwise potential functions. The proposed graph satisfies Markov Random Field property and its energy function is introduced accordingly. The MRF energy function minimization leads to maximize the label probability of the unlabeled voxels (i.e., target voxel) [21]. Therefore, we define a continuous max-flow model which is equivalent to the formulated related optimization problem. Continuous max-flow algorithm solves the continuous counterpart to the discrete min-cut/max-flow problem, and it can be computed using an inherently parallel multiplier-based algorithm with guaranteed convergence. This makes it suitable for the optimization of large labeling problems. We demonstrate how label propagation, spatial regularization and data models can be expressed simultaneously through this representation.

The proposed method is mainly aimed at improving the segmentation results in the tissue boundary region and improving the segmentation accuracy. We define four types of edges for modeling the information flows in the graph.

To optimize the MRF energy function, we provide an efficient optimization scheme based on continuous max-flow in "The Proposed Framework". "Experimental Results" explains the experiments and comparative analysis of the proposed method. "Discussion" summarizes the discussion and we draw the conclusion in "Conclusion".

The Proposed Framework

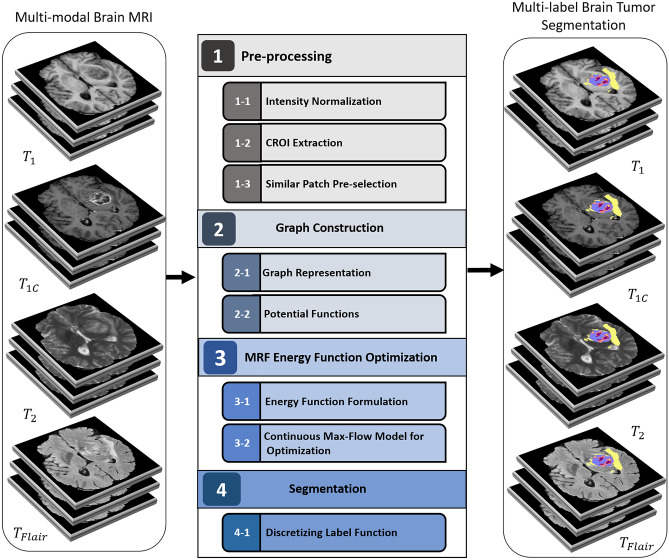
The proposed method relies on learning parameters of a Markov Random Field and optimization of its energy function. A complete architecture of the method is shown in Fig. 1. It consists of four modules as follow:

1. “Preprocessing”: Due to variety of intensity value of a tissue in multi-modal MRI, intensity normalization method is applied on brain MR images. Also, the potentially cancerous region of interest (CROI) is extracted to reduce the size and complexity of graph. In addition, all images (i.e., atlas and unlabeled images) are divided into patches, and similar patches are selected for the next stage.

2. “Graph Construction”: The graph representation and its potential functions are defined in the second module.

3. “MRF Energy Optimization”: In the third module, the MRF energy function is formulated based on the potential functions, and then, it is optimized subject to the constraints using a continuous max-flow model.

4. “Segmentation”: The labeling function is calculated in an iterative optimization procedure. All estimated labels are fused, and the final label is assigned to unlabeled voxels in the final module.

Fig. 1.

Architecture of the proposed method pipeline

Preprocessing

The first module includes three steps: In the first step, the intensity value of voxels is normalized. In the second step, cancerous region of interest (CROI) is extracted. In the third step, the CROI voxels are divided into the patches and they are compared for graph construction.

Intensity Normalization

Intensity normalization is applied to ensure an identical intensity distribution of the same sequence from different patients and scanners.

One of the main disadvantages of brain MRI sequences is that the same type of tissue does not have a specific intensity. Different MRI sequences show different intensity values for the same tissue type even within the same subject. These intensity variations make segmentation and image analysis difficult [23]. Therefore, intensity normalization is an important pre-processing step for MR image analysis [24]. Various intensity normalization methods have been proposed. In this work, we used one of the simplest ones called Gaussian intensity normalization that rescales the intensity values by a global linear scaling. In this method, the primary intensities are divided by the standard deviation of the entire intensity values within one slice: $I_{\mathit{new}}={\displaystyle \frac{I}{\sigma }}$ where I is the primary intensity value and $\sigma$ is the standard deviation of an entire scan. This method assumes each sequence (such as $T_1$, $T_{1C}$, $T_2$ and $T_{2Flair}$) has the same distribution, and the normalization is done based on this assumption [25]. The intensity resolution is typically 12 bits in MRI. We re-scale the intensity values in the range of [0, 1024] in order to present each voxel intensity value with 10 bits. By analyzing the gray level range, we found that re-scaling does not lead to a significant information loss.

Cancerous Region of Interest (CROI) Extraction

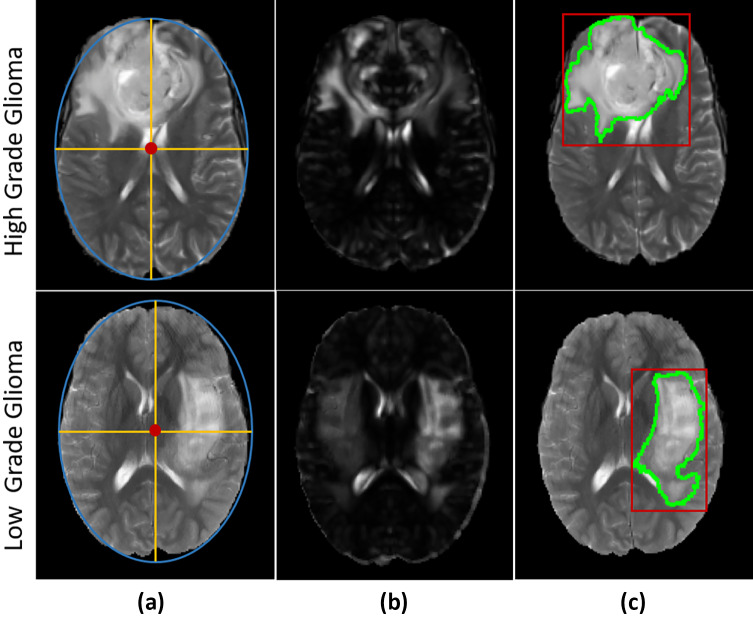
The segmentation methods can achieve competitive running time by extracting the potentially cancerous region of interest and enclosing high-probability tumor regions [18]. In fact, voxels outside of the CROI are directly discarded from the subsequent steps . The purpose of this step is to reduce the search space and restrict it into certain regions where some abnormalities are observed. In this paper, we use an efficient technique to extract regions suspicious to cancer. This technique is based on general symmetry of brain structures in the two hemispheres [26]. First, the symmetry plane of the image is detected using an ellipse fitted to the brain border in MRI slices. The major axis of the fitted ellipse is considered as the symmetry plane. Two hemispheres are distinguished using the detected symmetry plane. Consequently, texture features of hemispheres are extracted and compared using Euclidean distance to calculate the similarity distances between the left and right hemispheres’ voxels. The obtained similarity distances are normalized in [0,1]. Then, the normalized distances are multiplied by the corresponding intensity values of the original image. As a result, the dissimilar regions get higher intensity values. The brighter regions are considered as the cancerous region of interest (CROI). This procedure is illustrated in Fig. 2.

Fig. 2.

“CROI Extraction” steps [26]. a Ellipse fitted to an axial slice, b suspicious hemisphere detection, c estimated tumor border (green) and cancerous region of interest(red)

Similar Patch Pre-selection

The atlas is defined as the combination of a gray-level image (template) and its label map (the atlas labels). Here, training samples are considered as the atlas set that help to segment the unlabeled test images (target images). The fundamental assumption in patch-based methods is that the central voxels of similar patches should have identical labels. Consequently, the target labels could be inferred by finding similar patches in a subset of the atlas images. The CROIs that are extracted from both atlas and target images are divided into overlapping cubic patches of identical size. The corresponding mean $(\mu )$ and standard deviation $(\sigma )$ of each patch are computed and preserved to avoid multiple computations during the labeling procedure.

In order to reduce graph size and complexity, the patches are mutually compared with respect to the first and second statistical moments by means of structural similarity index measure (SSIM) which measures the perceptual difference between two similar patches. Applying a pairwise comparison makes it possible to discard dissimilar patches.

Suppose two patches $P_i(x)$ and $P_j(x)$ centered on voxel x in unlabeled image i and atlas image j, respectively. The similarity of $P_i(x)$ and $P_j(x)$ is calculated according to SSIM defined as follows:

$$\begin{array}{c}\hfill SSIM(P_i(x),P_j(x))={\displaystyle \frac{(2{\mu }_i{\mu }_j+c_1)(2cov(P_i(x),P_j(x))+c_2)}{({\mu }_i^2+{\mu }_j^2+c_1)({\sigma }_i{(x)}^2+{\sigma }_j^2+c_2)}}\end{array}$$ 1

where $\mu$, $\sigma$ and cov represent the mean, standard deviation and covariance of the patches, respectively. The constants $c_1={(k_{1}L)}^2$ and $c_2={(k_{2}L)}^2$ stabilize the division with weak denominator. L is the dynamic range of intensity value, $k_1={10}^{-2}$ and $k_2=3\times {10}^{-2}$ by default.

The similar patch pre-selection procedure based on SSIM can be performed as follows: If the value of SSIM is greater than a given threshold (T), meaning the two patches have acceptable similarity, then vertices corresponding to voxel x in target image i and atlas image j can be connected by an edge in the graph. The value of T is chosen empirically because it should provide an acceptable balance between segmentation accuracy and computational time.

Graph Construction

In the second module, a graph-based structure is introduced to model how the information propagates between the atlas and target images. In the following, we explain graph representation and its potential functions.

Graph Representation

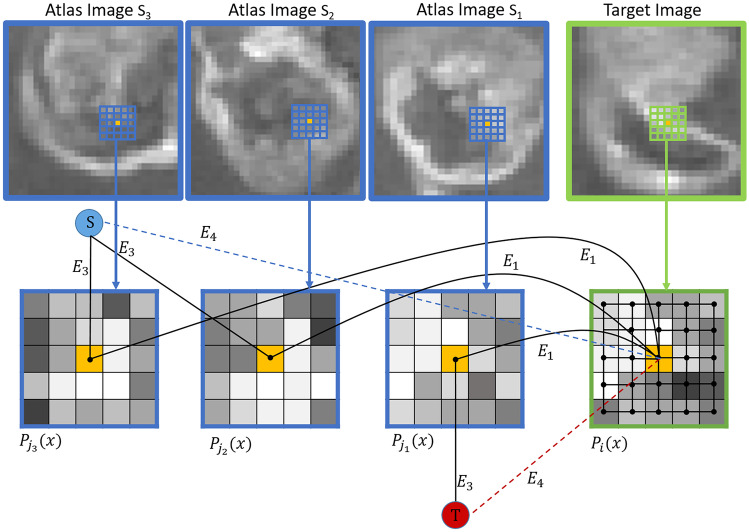
We proposed an undirected graph $G=(V,E)$ consisting of a nonempty vertex set V and an edge set E. The vertex set V consists of all CROI voxels in all images such as atlas and unlabeled images (i.e., $\{V\}=\{V_{\mathit{atlas}}\}\cup \{V_{\mathit{target}}\}$). The proposed graph contains two additional special vertices as well, called terminals. In the context of vision, terminals correspond to the set of labels that can be assigned to a voxel. In case of classification, $L=\{0,1\}$, two terminals are defined: source s, corresponding to $L=1$ and sink t, corresponding to $L=0$. The terminals are illustrated in Fig. 3, where the virtual nodes are shown in red ($L=0$) and blue ($L=1$).

Fig. 3.

Proposed graph representation. All types of edges (N-links and T-links) are displayed and two virtual terminal nodes S and T are shown in blue and red, respectively

There are two types of edges in the edge set E: N-links and T-links.

N-links connect pairs of neighboring voxels. Thus, they represent a neighborhood relation between two vertices. The weight assigned to the N-links defines the local similarity between the voxels.

We propose two different N-links in G:

• $E_1$, the edge between center voxel of $P_i(x)$ and center voxel of $P_j(x)$, with weight $w_{\mathit{ij}}(x)$ calculated based on SSIM. $E_1$ exists only between voxels in similar patches that their calculated SSIM is acceptable and selected in “Similar Patch Pre-selection” step, as described in "Similar Patch Pre-selection". $E_1$ weight, $w_{\mathit{ij}}(x)$, is defined based on the similarity of center voxels of atlas and target patches to express how well label information can be propagated along this edge. The normalized cross-correlation (NCC) is chosen as a similarity metric, which is invariant to linear intensity changes and fast to compute. It is suitable for patch comparison within a large set of images [27]. Consider an unlabeled image patch $P_i(x)$ and similarly an atlas image patch $P_j(x)$, of identical size $n\times n\times n$. The normalized cross-correlation (NCC) between patches $P_i(x)$ and $P_j(x)$ is defined as follows:

  $$\begin{array}{c}\hfill NCC(P_i(x),P_j(x))={\displaystyle \frac{{\sum }_{k\in P_i(x),l\in P_j(x)}(k-{\mu }_i)(l-{\mu }_j)}{n^3\sqrt{{\sigma }_i^2{\sigma }_j^2}}}\end{array}$$ 2

  where k and l refer to intensity value of voxels located in $P_i(x)$ and $P_j(x)$, respectively. $\mu$ and $\sigma$ are mean and standard deviation of patches. To further discard edges between dissimilar patches, the edge weights are defined as:

  $$\begin{array}{c}\hfill w_{\mathit{ij}}(x)=max(0,NCC(P_i(x),P_j(x)))\end{array}$$ 3

  This also ensures all edge weights are positive and in the range [0, 1].
• $E_2$ that connect target voxel x to its neighbors in $P_i(x)$ on a grid structure. The corresponding edge weight ${\alpha }_i(x)$, is calculated based on the intensity gradients:

  $$\begin{array}{c}\hfill {\alpha }_i(x)=exp(-\frac{||\mathrm{\nabla }{P}_i(x){||}^2}{2{\sigma }_i^2})\end{array}$$ 4

T-links connect voxels into the terminals. The weights of T-links depend on penalty for assigning a label to a voxel. Two T-links are defined in the proposed graph G:

• $E_3$, the edge connects center voxel of atlas patch $P_j(x)$ to the source S or sink T corresponding to its label.

• $E_4$, the edges between center voxel of target patch $P_i(x)$ and two terminals source S and sink T, weighted as $w_i^s(x)$ and $w_i^t(x)$, respectively. Both $w_i^s(x)$ and $w_i^t(x)$ are defined based on a prior probability.

Figure 3 shows a sample sub-graph constructed according to the above procedure. Since glioma segmentation is a multi-labeling problem, the above graph structure is replicated for every label. In other words, instead of one source terminal, the proposed graph, G, has L source terminals $\{S_1,...S_L\}$ where L is the number of labels.

Potential Functions

Markov Random Field is an efficient model for solving the segmentation problem [20]. The MRF joint probability distribution is defined as follows:

$$\begin{array}{c}\hfill p(l_i(x))=\frac{1}{Z}\prod _{c\in C}{\varphi }_c(V_c),Z=\sum _V\prod _{c\in C}{\varphi }_c(V_c)\end{array}$$ 5

where C denotes the set of cliques (i.e., fully connected sub-graphs) of G, and ${\varphi }_c(V_c)$ is a non-negative potential function over the variables in a clique. The partition function Z is a normalizing constant that ensures the distribution sums to one. According to graph structure, we define a unary potential function related to the T-links, and two pairwise potential functions corresponding to the N-links. So, (5) becomes:

$$\begin{array}{cc}\hfill p(l_i(x))& =\frac{1}{Z}\prod _{c\in C}\{\phi (l_i(x))\hfill \\ \hfill & +\phi (l_i(x),l_j(x))+\phi (l_i(x),l_i(k))\}\hfill \end{array}$$ 6

As mentioned in "Graph Representation", T-links connect atlas and target vertices to the terminals. $\phi (l(x))$ is the unary potential function, named “data term” that encodes the voxel labels. It is set to 0 for atlas vertices (i.e., voxels in the atlas images). For target vertices (i.e., unlabeled voxels), it is calculated based on an arbitrary prior probability of labels, e.g., uniform distribution:

$$\begin{array}{c}\hfill \phi (l_i(x))=\left\{\begin{array}{cc}0\hfill & i\in V_{\mathit{atlas}}\hfill \\ \frac{1}{L}\hfill & i\in V_{\mathit{target}}\hfill \end{array}\right)\end{array}$$ 7

where L is the number of labels.

$\phi (l_i(x),l_j(x))$ is a pairwise potential function, named “propagation term” related to those edges between an atlas vertex j and a target vertex i (i.e., N-links $E_1$), for label propagation. It penalizes conflicting labels in voxels connected by a high weight $w_{\mathit{ij}}(x)$:

$$\begin{array}{c}\hfill \phi (l_i(x),l_j(x))=w_{\mathit{ij}}(x)\delta (l_i(x)\ne l_j(x))\end{array}$$ 8

where $\delta (.)$ is an indicator function. This assigns a high penalty when the target and atlas labels are different, and the atlas patch $P_j(x)$ is considered similar to the target patch $P_i(x)$, as defined by the similarity measure NCC.

In addition, we define another pairwise potential function between adjacent voxels within a target patch $P_i(x)$ (i.e., N-links $E_2$) that encodes label propagation in form of the spatial regularization through intra-image edges:

$$\begin{array}{c}\hfill \phi (l_i(x),l_i(k))=\sum _{k\in P_i(x)-\{x\}}{\alpha }_i(x)\delta (l_i(x)\ne l_i(k))\end{array}$$ 9

where ${\alpha }_i(x)$ is the regularization weight of N-links $E_2$ calculated in (4).

The “regularization term” enforces spatial consistency by penalizing different label assignment in adjacent voxels. If the regularization weights (${\alpha }_i(x)$) are based on intensity gradients, consistent labels can be enforced in adjacent labels that are similar in appearance, while allowing different labels across intensity boundaries.

MRF Energy Function Optimization

Energy Function Formulation

The joint probability distribution, $p(l_i(x))$, satisfies the independence assumptions and can be found by invoking the Hammersley–Clifford theorem. It states that every Markov Random Field follows a Gibbs distribution of the form (5). The Gibbs distribution $p(l_i(x))$ from (5) can be re-written in an exponential form as shown in (10):

$$\begin{array}{cc}\hfill p(l_i(x))& =\frac{1}{Z}exp(log(\prod _{c\in C}{\varphi }_c(V_c)))\hfill \\ \hfill & =\frac{1}{Z}exp(-\sum _{c\in C}-log({\varphi }_c(V_c)))\hfill \end{array}$$ 10

The MRF energy function $E(l_i(x))$ is then simply the sum of clique energies ${\theta }_c(V_c)=-log{\varphi }_c(V_c)$. So (10) becomes:

$$\begin{array}{c}\hfill p(l_i(x))=\frac{1}{Z}exp(-\sum _{c\in C}{\theta }_c(V_c))=\frac{1}{Z}exp(-E(l_i(x)))\end{array}$$ 11

In our proposed graph, we define the unary potentials to encode voxel labels using (7). The corresponding energy of the data term is defined as:

$$\begin{array}{c}\hfill E_{\mathit{data}}(l_i(x))=\sum _{j\in V_{\mathit{atlas}}}\phi (l_j(x))+\sum _{i\in V_{\mathit{target}}}\phi (l_i(x))\end{array}$$ 12

According to the pairwise potential function defined in (8), the label propagation is encoded in adjacent edges $E_1$ between atlas and target vertices. So, the propagation energy is:

$$\begin{array}{cc}\hfill E_{\mathit{propagation}}(l_i(x))& =\sum _{j\in N_i(x)}\phi (l_i(x),l_j(x))\hfill \\ \hfill & =\sum _{j\in N_i(x)}{w}_{\mathit{ij}}(x)\delta (l_j(x)\ne l_i(x))\hfill \\ \hfill & =\sum _{j\in N_i(x)}{w}_{\mathit{ij}}(x)\delta (l_j(x)=l_i(x))\hfill \\ \hfill & -\sum _{j\in N_i(x)}{w}_{\mathit{ij}}(x)\hfill \end{array}$$ 13

where $N_i(x)$ is the neighborhood set of target voxel x in $P_i(x)$. Another pairwise potential function is defined for spatial regularization in target images (9). The corresponding regularization energy is formulated as follow:

$$\begin{array}{cc}\hfill E_{\mathit{regularization}}(l_i(x))& =\sum _{k\in P_i(x)-\{x\}}\phi (l_i(x),l_i(k))\hfill \\ \hfill & =\sum _{k\in P_i(x)-\{x\}}{\alpha }_i(x)\delta (l_i(x)\ne l_i(k))\hfill \\ \hfill & =\sum _{k\in P_i(x)-\{x\}}{\alpha }_i(x)\delta (l_i(x)=l_i(k))\hfill \\ \hfill & -\sum _{k\in P_i(x)-\{x\}}{\alpha }_i(x)\hfill \end{array}$$ 14

Therefore, the proposed MRF labeling energy function consists of three components corresponding to the data (12), propagation (13) and regularization (14) terms:

$$\begin{array}{cc}\hfill E(l_i(x))& =E_{\mathit{data}}(l_i(x))+E_{\mathit{propagation}}(l_i(x))\hfill \\ \hfill & +E_{\mathit{regularization}}(l_i(x))\hfill \end{array}$$ 15

The above comprehensive formulation handles the multi-labeling segmentation within a single framework and considers all the components simultaneously.

Continuous Max-Flow model for Optimization

As explained in ''Graph Representation", the constructed graph satisfies local Markov property which states that each vertex is independent of any other node given its set of neighbors. On the other hand, the voxels in the target image are conditionally independent given the atlas images.

Since the atlas labels are fixed and assumed to be independent of each other (a common assumption in multi-atlas segmentation), it follows that the target voxels are statistically independent, and the optimal label can be found by minimizing $E(l_i(x))$ independently for all voxels:

$$\begin{array}{cc}\hfill l_i(x)& =arg\underset{\xi }{min}E(l_i(x)=\xi )\hfill \\ \hfill & =arg\underset{\xi }{min}\{E_{\mathit{data}}(l_i(x)=\xi )+E_{\mathit{propagation}}(l_i(x)=\xi )\hfill \\ \hfill & +E_{\mathit{regularization}}(l_i(x)=\xi )\}\hfill \end{array}$$ 16

The goal is to find a label $\xi$ for voxel x in target image i that minimizes the MRF energy. The MRF energy function consists of unary and pairwise terms that can therefore be minimized by finding either the minimum cut or the maximum flow. It yields globally optimal results for classification problems and approximately globally optimal results for multi-labeling problems. In max-flow approach, the energy function on the graph can be optimized by maximizing a source flow through the network, subject to flow conservation and capacity constraints on the edges.

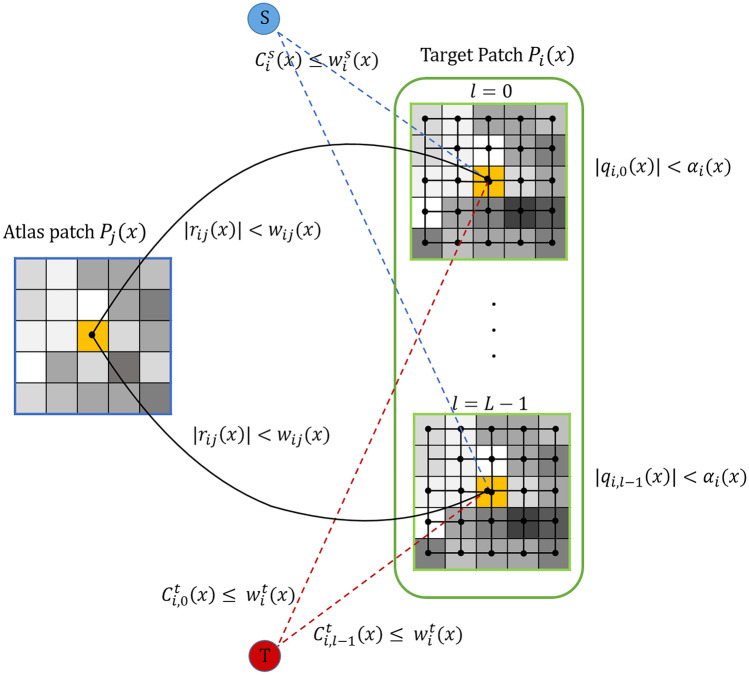
We first introduce the configuration of flows (as illustrated in Fig. 4), such that:

• For each center voxel in target patch $P_i(x)$, two terminal flows $C_i^s(x)$ and $C_i^t(x)$ are added that link the target voxel to the source S and sink T, respectively.

• For each adjacent edge between target voxel i and atlas voxel j, there exists a propagation flow $r_{\mathit{ij}}$.

• Each target voxel links to its grid neighbors in $p_i(x)$ with spatial flows $q_{i,l}$.

With the above flow settings, we formulate the continuous max-flow model by maximizing the total amount of flows subject to the following flow constraints:

• Capacity constraints on terminal flows:

  $$\begin{array}{c}\hfill C_i^s(x)\le w_i^s(x),C_{i,l}^t(x)\le w_i^t(x)\end{array}$$ 17
• Capacity constraints on spatial flows:

  $$\begin{array}{c}\hfill ||q_{i,l}(x)||\le {\alpha }_i(x)\end{array}$$ 18
• Capacity constraints on propagation flows:

  $$\begin{array}{c}\hfill r_{\mathit{ij}}(x)\le w_{\mathit{ij}}(x)\end{array}$$ 19

Considering L labels ($l\in \{0,...,L-1\}$) in this problem, the summation of all input and output flows must be zero :

$$\begin{array}{c}\hfill {\rho }_{i,l}=div{q}_{i,l}(x)-C_i^s(x)+C_{i,l}^t(x)+\sum _{j\in N_i(x)}{r}_{\mathit{ij}}(x)=0\end{array}$$ 20

Fig. 4.

Configuration of flows in Continuous Max-Flow model

Here, div is divergence operator. The next step is to define an augmented lagrangian function as follow:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{L}(\mu ,C^s,C^t,q,r)& =\sum _{V_{\mathit{target}}}({\int }_{\mathrm{\Omega }}{C}_i^s(x)dx\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}\sum _{l=0}^{L-1}{\mu }_{i,l}(x){\rho }_{i,l}dx-\frac{c}{2}\sum _{l=0}^{L-1}||{\rho }_{i,l}{||}^2)\hfill \end{array}\end{array}$$ 21

where $\mathrm{\Omega }$ is denoted as target image space and $c>0$ is constant. ${\mu }_{i,l}(x)$ is lagrange multiplier that represents the labeling function of voxel x in target image i. By means of the augmented lagrangian algorithm, an iterative procedure is defined in which $\mathcal{L}(\mu ,C^s,C^t,q,r)$ is optimized over each variable while the other variables are fixed [21]. Therefore, to update variables in each iteration the following steps are performed:

1. Maximizing $\mathcal{L}(\mu ,C^s,C^t,q,r)$ over the source flow $C_i^s(x)$, subject to the flow constraint $C_i^s(x)\le w_i^s(x)$, while the other variables ${(\mu ,C^t,q,r)}^k$ are fixed, which amounts to:

   $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {C_i^s}^{k+1}(x)& =arg\underset{C_i^s(x)\le w_i^s(x)}{max}{\int }_{\mathrm{\Omega }}{C}_i^s(x)dx-\frac{c}{2}||C_i^s(x)-F^k(x){||}^2\hfill \\ \hfill & =min(F^k(x)+\frac{1}{c},w_i^s(x))\hfill \end{array}\end{array}$$ 22

   where $F^k(x)$ is fixed and summarizes terms independent of $C_i^s(x)$ in iteration k.
2. Maximizing $\mathcal{L}(\mu ,C^s,C^t,q,r)$ over the sink flow $C_{i,l}^t(x)$, subject to $C_{i,l}^t(x)\le w_i^t(x)$, while the other variables ${(\mu ,C^s,q,r)}^k$ are fixed, which amounts to:

   $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {C_{i,l}^t}^{k+1}(x)& =arg\underset{C_{i,l}^t(x)\le w_i^t(x)}{max}-\frac{c}{2}||C_{i,l}^t(x)-G^k(x){||}^2\hfill \\ \hfill & =min(G^k(x)+w_i^t(x))\hfill \end{array}\end{array}$$ 23

   where $G^k(x)$ is fixed and summarizes terms independent of $C_{\mathit{il}}^t(x)$ in iteration k.
3. Maximizing $\mathcal{L}(\mu ,C^s,C^t,q,r)$ over the spatial flows $q_{i,l}(x)$, subject to $||q_{i,l}(x)||\le {\alpha }_i(x)$, while the other variables ${(\mu ,C^s,C^t,r)}^k$ are fixed, which amounts to:

   $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {q_{i,l}}^{k+1}(x)& =arg\underset{||q_{i,l}(x)||\le {\alpha }_i(x)}{max}-\frac{c}{2}||div{q}_{i,l}(x)-H^k{||}^2\hfill \\ \hfill & =proj{}_{||q_{i,l}(x)||\le {\alpha }_i(x)}(q_{i,l}^k+\tau \mathrm{\nabla }(div{q}_{i,l}^k)-H^k)\hfill \end{array}\end{array}$$ 24

   where $H^k(x)$ is fixed and summarizes terms independent of $q_{i,l}(x)$ in iteration k and $\tau$ is some step-size for convergence.
4. Maximizing $\mathcal{L}(\mu ,C^s,C^t,q,r)$ over the propagation flows $r_{\mathit{ij}}(x)$, subject to $r_{\mathit{ij}}(x)\le w_{\mathit{ij}}(x)$, fixing ${(C^s,C^t,q)}^{k+1}$, ${(\mu )}^k$, which gives:

   $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {r_{\mathit{ij}}}^{k+1}(x)& =arg\underset{r_{\mathit{ij}}(x)\le w_{\mathit{ij}}(x)}{max}-\frac{c}{2}||\sum _{j=1,i\ne j}^R{r}_{\mathit{ij}}(x)-J_i^k(x){||}^2\hfill \\ \hfill & -\frac{c}{2}||\sum _{j=1,i\ne j}^R{r}_{\mathit{ij}}(x)-J_j^k(x){||}^2\hfill \end{array}\end{array}$$ 25

   this leads to:

   $$\begin{array}{c}\hfill {r_{\mathit{ij}}}^{k+1}(x)=\frac{J_j^k-J_i^k}{2}\end{array}$$ 26

   where:

   $$\begin{array}{c}\hfill \left\{\begin{array}{c}\begin{array}{cc}\hfill J_i^k& =div{q}_{i,l}^{k+1}-{C_i^s(x)}^{k+1}+{C_{i,l}^t(x)}^{k+1}\hfill \\ \hfill & -\frac{{\mu }_i^k}{c}+{\sum }_{m=1,m\ne i,j}^R{r}_{\mathit{im}}^k(x)\hfill \\ \hfill J_j^k& =div{q}_{j,l}^{k+1}-{C_j^s(x)}^{k+1}+{C_{j,l}^t(x)}^{k+1}\hfill \\ \hfill & -\frac{{\mu }_j^k}{c}+{\sum }_{m=1,m\ne i,j}^R{r}_{\mathit{mj}}^k(x)\hfill \end{array}\hfill \end{array}\right)\end{array}$$ 27
5. Updating the labeling function ${\mu }_{i,l}(x)$ by:

   $$\begin{array}{c}\hfill {\mu }_{i,l}{(x)}^{k+1}={\mu }_{i,l}^k(x)-c{\rho }_{i,l}^k(x)\end{array}$$ 28

The above steps repeat until convergence is achieved. In each iteration, we evaluate the following convergence criterion:

$$\begin{array}{c}\hfill error={\displaystyle \frac{{\mu }_{i,l}{(x)}^{k+1}-{\mu }_{i,l}{(x)}^k}{{\mu }_{i,l}{(x)}^{k+1}}}\end{array}$$ 29

If $error<ϵ$, then it is converged.

Segmentation

Segmentation is a progressive process that becomes accurate through the above iterative procedure. After convergence, a segmentation is performed by discretizing the resulting solution for ${\mu }_{i,l}(x)$, e.g., by threshold $\gamma$:

$$\begin{array}{c}\hfill {\mu }_{i,l}^{\gamma }(x)=\left\{\begin{array}{cc}1\hfill & {\mu }_l(x)>\gamma \hfill \\ 0\hfill & {\mu }_l(x)\le \gamma \hfill \end{array}\right),l=0,..L-1\end{array}$$ 30

Experimental Results

The performance of the proposed framework is evaluated on BRATS datasets provided by the multimodal brain image segmentation challenge. All BRATS datasets are publicly available¹ and they include four MRI modalities ($T_1$, $T_{1C}$, $T_2$, and $T_{2Flair}$). All images are skulls stripped and resampled to 1mm isotropic resolution. Also, all MRI-sequences of each case are co-registered. Further technical details of the datasets are given in Table 1. As mentioned, the BRATS datasets have two sub-sets: high grade glioma (HGG) and low grade glioma (LGG). One third of each sub-set is used for testing and the rest have been used for training using 4-fold cross-validation.

Table 1.

Main attributes of BRATS datasets

Dataset	Grade	Number of patients	Positive voxels	Negative voxels
BRATS 2015	LGG	54	5.46 M*	476.65 M
	HGG	220	24.32 M	1939.8 M
BRATS 2017	LGG	75	8.32M	661.2 M
	HGG	210	20.21 M	1854.6 M
BRATS 2019	LGG	76	8.47 M	670.05 M
	HGG	259	24.39 M	2270 M

*1M is equal to one million

A ground truth segmentation is available which also provides distinguishing different labels including 0) normal tissues, 1) necrosis, 2) edema, 3) non-enhancing tumor and 4) enhancing tumor. To evaluate the performance of segmentation algorithms, different tumor subregions are grouped into three regions that are proper for clinical tasks:

1. WT: The “whole tumor” region (including all four tumor subregions).

2. TC: The “tumor core” region (including all tumor structures except edema).

3. ET: The “enhancing active tumor” region (including only the enhancing core sub-region defined only for high-grade cases) [3].

Framework Evaluation

In order to verify the accuracy of proposed methods, the predicted cancerous region by proposed framework (PR) was compared with manually delineated ground truth (GT). We applied six widely used segmentation metrics to measure the average slice-wise true positive rate (sensitivity), true negative rate (specificity),positive predictive value(PPV), Dice and Jaccard similarity, and Hausdorff distance. These metrics are defined as follows:

$$\begin{array}{c}\hfill Sensitivity(PR,GT)=\frac{|PR\cap GT|}{|GT|}\end{array}$$ 31

$$\begin{array}{c}\hfill Specificity(PR,GT)=\frac{|PR\cap GT|}{|PR|}\end{array}$$ 32

$$\begin{array}{c}\hfill PPV(PR,GT)=\frac{|1-(PR\cup GT)|}{|PR|}\end{array}$$ 33

$$\begin{array}{c}\hfill Dice(PR,GT)=\frac{2|PR\cap GT|}{|PR|+|GT|}\end{array}$$ 34

$$\begin{array}{c}\hfill Jaccard(PR,GT)=\frac{2|PR\cap GT|}{|PR\cup GT|}\end{array}$$ 35

$$\begin{array}{cc}\hfill HD(PR,GT)& =max\{Su{p}_{p\in PR}\{In{f}_{g\in GT}d(p,g)\}\hfill \\ \hfill & ,Su{p}_{g\in GT}\{In{f}_{p\in PR}d(p,g)\}\}\hfill \end{array}$$ 36

The Dice score normalizes the number of true positives to the average size of the two segmented areas. The Jaccard index indicates the similarity between two sets. The higher scores of both Dice and Jaccard show more accurate segmentation [3].

Table 2 represents the sensitivity, specificity,positive predictive value, Dice and Jaccard indexes, and Hausdorff distance for high-grade glioma segmentation with the proposed framework.

Table 2.

Evaluation of proposed method using sensitivity, specificity, Dice and Jaccard similarity indexes and Hausdorff distance for HGG of BRATS 2015, BRATS 2017 and BRATS 2019, where patch pre-selection threshold is 0.9 and patch size is $5\times 5\times 5$

	BRATS 2015			BRATS 2017			BRATS 2019
	WT	TC	ET	WT	TC	ET	WT	TC	ET
Sensitivity	0.9209 ±0.01	0.8921±0.01	0.8782±0.01	0.9212±0.01	0.9002±0.02	0.8965±0.02	0.9304±0.01	0.9104±0.01	0.9019±0.02
Specificity	0.992±0.005	0.988±0.006	0.986±0.009	0.994±0.003	0.993±0.004	0.993±0.003	0.997±0.003	0.995±0.003	0.992±0.006
PPV	0.983±0.01	0.981±0.01	0.978±0.02	0.989±0.01	0.991±0.01	0.984±0.014	0.988±0.012	0.991±0.007	0.987±0.01
Dice	0.9234±0.02	0.9038±0.015	0.9212±0.01	0.9454±0.01	0.9132±0.013	0.9362±0.01	0.9482±0.01	0.9248±0.02	0.9386±0.014
Jaccard	0.895±0.06	0.8707±0.07	0.8816±0.05	0.8919±0.04	0.8765±0.04	0.8873±0.04	0.9042±0.03	0.888±0.05	0.893±0.04
Hausdorff	5.27±1.3	5.77±1.1	5.43±1.3	4.78±2.2	5.06±1.1	5.23±2.1	4.32±2.1	4.63±2.1	4.78±2.5

As shown in Table 2, the “whole tumor” region is better labeled than the “tumor core” and “active tumor” regions. Also, due to better coverage of the glioma tumors in training set available in BRATS 2019 dataset, the results obtained in this dataset are more accurate.

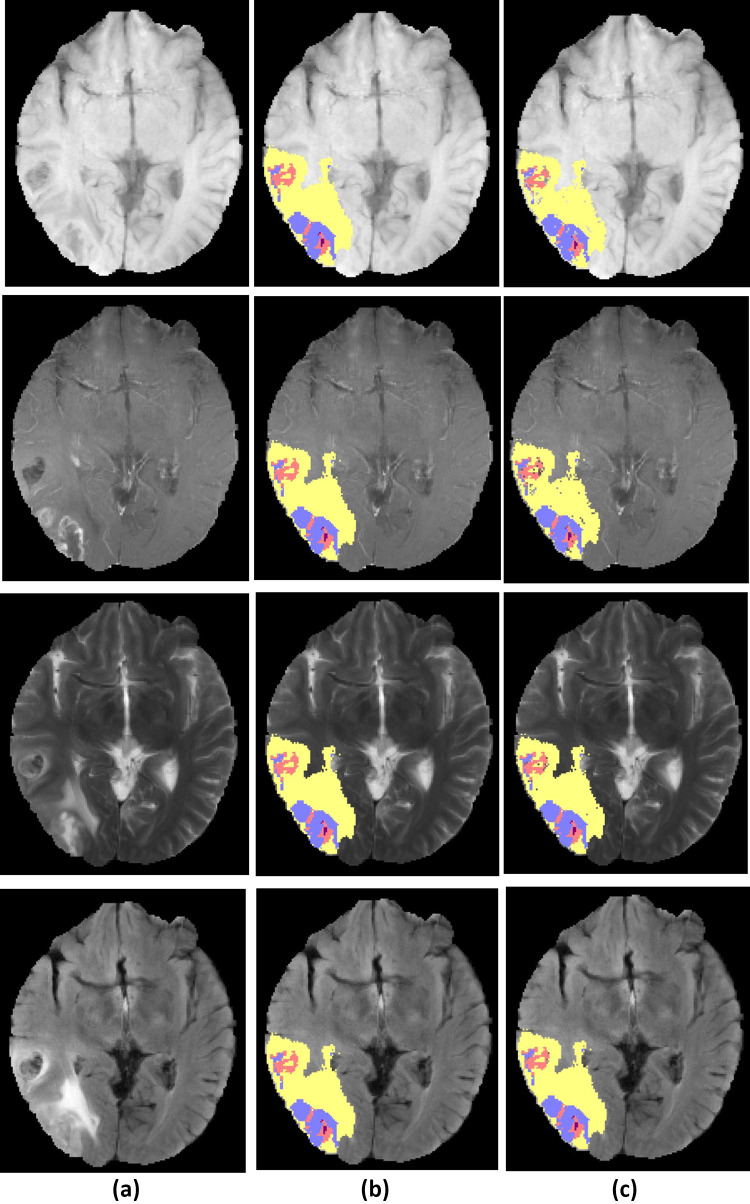
Figure 5 shows a HGG test case examples and a segmentation result of the proposed method.

Fig. 5.

Example of high-grade glioma patient from BRATS dataset, a original image, b ground truth tumor regions, c segmented tumor region result of proposed framework. The row 1$\sim$4 from up to down, show the modalities $T_1$, $T_{1C}$, $T_2$, and $T_{2Flair}$. Tumor structure consists of edema (yellow), non-enhancing core (red), enhancing core (blue) and necrosis (purple)

Influence of the Patch Size

As mentioned in "Similar Patch Pre-selection", the patch size is an important factor in segmentation accuracy. Table 3 shows the performance of the proposed method for different patch sizes.

Table 3.

Accuracy of the proposed method for different patch sizes and patch pre-selection thresholds

Patch Size	WT	TC	ET
3$\times$3$\times$3	0.7761	0.7341	0.7823
5$\times$5$\times$5	0.831	0.8054	0.8093
7$\times$7$\times$7	0.9332	0.9154	0.9011
9$\times$9$\times$9	0.7343	0.7084	0.6528

Regarding to the size of regions in atlas set, it is observed that all regions such as “whole tumor,” “tumor core” and “enhancing active tumor” are segmented with higher accuracy by considering $5\times 5\times 5$ and $7\times 7\times 7$ patches than $3\times 3\times 3$ and $9\times 9\times 9$ patches. Since the size of “tumor core” and “enhancing active tumor” regions in atlas set are approximately smaller than the patch size $9\times 9\times 9$, choosing a smaller patch (i.e., $7\times 7\times 7$) will increase accuracy. Conversely, due to the larger size of “whole tumor” region, choosing the $7\times 7\times 7$ patches lead to less accuracy than $5\times 5\times 5$. The best choice for patch size is $7\times 7\times 7$, as it is possible to segment all three regions with remarkable accuracy.

Segmentation Benchmark

The proposed approach is benchmarked on BRATS datasets against the top-performing documented methods. The comparisons with several state-of-the-art algorithms demonstrate the efficiency of proposed framework for glioma segmentation. The accuracy of proposed method is compared with the existing methods for BRATS datasets; the results are summarized in Table 4.

Table 4.

Comparing Dice score evaluation of the proposed framework with the state-of-the-art methods for HGG in BRATS 2015, BRATS 2017 and BRATS 2019

	Approach	WT	TC	ET
BRATS 2015	Bakas et al. [11]	0.82	0.59	0.74
	Barzegar et al. [23]	0.907	0.853	0.884
	Barzegar et al. [24]	0.89	0.88	0.87
	Barzegar et al. [28]	0.92	0.894	0.902
	Isensee et al. [29]	0.85	0.74	0.64
	Hussain et al. [30]	0.87	0.89	0.92
	our method	0.9234	0.9038	0.9212
BRATS 2017	Isensee et al. [29]	0.895	0.828	0.707
	Barzegar et al. [23]	0.883	0.701	0.748
	Barzegar et al. [28]	0.900	0.872	0.886
	Hussain et al. [30]	0.86	0.87	0.9
	Kamnitsas et al. [31]	0.902	0.82	0.757
	Choudhury et al. [32]	0.905	0.801	0.815
	Guo et al. [33]	0.97	0.77	0.72
	Phophilia et al. [34]	0.64	0.49	0.47
	Bharath et al. [35]	0.833	0.783	0.761
	Lefkovits et al. [36]	0.873	0.689	0.719
	our method	0.9454	0.9132	0.9362
BRATS 2019	Wang et al. [37]	0.83	0.888	0.916
	Barzegar et al. [28]	0.901	0.887	0.89
	Barzegar et al. [23]	0.878	0.808	0.835
	Rafi et al. [38]	0.84	0.8	0.63
	Serranoet al. [12]	0.839	0.733	0.594
	Hamghalam et al. [39]	0.7965	0.8965	0.7901
	our method	0.9482	0.9248	0.9386

As described previously, the “tumor core” (TC) region contains necrosis, enhancing, and non-enhancing tumors labels. The “whole tumor” (WT) region includes edemas as well. Table 4 shows that our framework compares well with the state-of-the-art methods.

In comparison with the top ranked methods applied on BRATS 2015, (except the one based on CNN [30]), our framework could achieve the highest dice score for “whole tumor” and “tumor core” regions. In BRTAS 2017, our framework could achieve the highest dice score for “tumor core” segmentation. The segmentation accuracy of “whole tumor” (WT) in [33] that is based on CNN is better that others. In case of BRATS 2019, the performance of our proposed method in detecting all cancerous regions such as “whole tumor” (WT), “tumor core” (TC) and “enhancing active tumor” (ET) is higher that other methods.

Complexity Analysis

Since the proposed algorithm is a semi-supervised learning algorithm, both atlases (i.e., the training data) and target images (i.e., the test data) contribute to the segmentation concurrently. As mentioned in "The Proposed Framework", the proposed framework has four main stages. The first and second stages (“Pre-processing” and “Graph Construction,” respectively) are performed offline. So, they are not considered in complexity analysis. The time complexity is dominated by the time of third stage, “Energy Function Optimization,” that is an iterative procedure in the core of proposed framework. Suppose N and M are the number of atlas and target voxels, respectively. After CROI extraction, the number of atlas and target voxels become $N^{\prime }$ and $M^{\prime }$, where $N^{\prime }<N$ and $M^{\prime }<M$. Training is performed on a Nvidia GPU RTX 3080 with 12GB memory. In the worst case, all atlas voxels are connected to all target voxels in the constructed graph $G=(V,E)$, and all target voxels of a patch are connected together as well. Each atlas patch, $P_i(x)$, is a $m\times m\times m$ grid. For this grid graph, there are $m\times m\times (m-1)$ edges in each direction. Therefore, the number of edges inside of $P_i(x)$ is $3\times m^2\times (m-1)=3m^3-3m^2$. So, the graph G with $|V|=N^{\prime }+M^{\prime }+(L+1)$, has $E=N^{\prime }\times M^{\prime }+M^{\prime }(3m^3-3m^2)$ edges. For each target voxel i, Eq. (20) must be solved and four variables $C_i^s,C_{i,l}^t,q_{\mathit{il}}$ and $r_{\mathit{ij}}$ must be calculated in each iteration. According to Eq. (28), labeling function is determined based on calculating other variables. Overall, it takes $O(m^3)$ where $m^3$ is the size of neighborhood set of voxel i. Therefore, the upper bound for time complexity of calculating parameters for all target voxels in one iteration is: $O(M^{\prime }\times m^3)$. Considering k as the number of iterations, the overall time complexity is $O(k\times M^{\prime }\times m^3)$. In the worst case, $k\times m^3\approx M^{\prime }$. So, the proposed framework takes $O({M^{\prime }}^2)$. In comparison with the above state-of-the-art methods, convolutional neural networks have much larger computational complexity which highly depends on their architecture (i.e., number of layers and number of nodes in each layer). In addition, compared with 2D network structures, 3D network models are time consuming and takes more GPU memory. Therefore, they require large memory capacity and high-speed advanced processors during both training and testing stages.

Discussion

In this paper, a semi-supervised multi-labeling framework is proposed for automatic glioma segmentation. It uses multi-atlas segmentation concept to take advantage of the prior information of the annotated images (i.e., atlas images). The framework consists of four main modules: image preparation, graph construction, Markov Random Field energy optimization and segmentation as shown in Fig. 1. “MRF Energy Optimization” is the core of proposed framework, in which a continuous max-flow model is defined and its parameters are learned during the iterative procedure.

As mentioned in "Similar Patch Pre-selection", atlas and target voxels are compared based on patch similarity. Due to the patch overlap in patch-based segmentation methods, it is possible to overfit to the atlas labels. The max-flow model parameters that are learned iteratively can reduce the risk of overfitting, since these parameters smooth the labeling procedure.

The motivation of using MRF graph is to map the segmentation problem to an optimization model in a graphical environment. Therefore, by defining perfect graph structure and optimum constraints and flows in the continuous max-flow model, the segmentation is performed precisely.

Conclusion

In this paper, we proposed a reliable brain tumor segmentation framework in multi-modal MRI by formulating the segmentation problem as an MRF energy optimization model. In order to reduce the effects of limited prior information on atlas-based segmentation, we presented a semi-supervised framework that benefits the contribution from both atlases (i.e., the training data) and target images (i.e., the test data).

Among the segmentation approaches, graph-based approaches are powerful tools due to their ability in reflecting general image properties. In addition, they reduce computational complexity of segmentation problem. In this paper, we introduced a fixed-size graph structure. So, the needed memory is fixed and can be estimated beforehand. According to the time analysis, the running time highly depends on the number of samples and their size.

As demonstrated in "Segmentation Benchmark", this approach has compared well enough with the state-of-the-art methods on publicly available BRATS datasets for segmenting high-grade glioma tumors.

In our future work, we will focus on the dynamic graph structures, aiming to reduce overall running time and complexity. We expect that this framework would be suitable for the segmentation of other brain tumors or abnormalities, such as ischemic stroke lesions.