Abstract
Lipophilic persistent environmental chemicals (LPECs) can accumulate in a woman’s body and transfer to her developing child across the placenta and via breast milk. To assess health risks associated with developmental exposures to LPECs, we developed a pharmacokinetic (PK) model that quantifies mother-to-offspring transfer of LPECs during pregnancy and lactation and facilitates internal dosimetry calculations for offspring. We parameterized the model for mice, rats, and humans using time-varying functions for body mass and milk consumption rates. The only required substance-specific parameter is the elimination half-life of the LPEC in the animal species of interest. We used the model to estimate whole-body concentrations in mothers and offspring following maternal exposures to hexachlorobenzene (HCB) and 2,2′,4,4′,5,5′-hexachlorobiphenyl (PCB 153) and compared these with measured concentrations from animal studies. We also compared estimated concentrations for humans to those generated using a previously published human LPEC PK model. Finally, we compared human equivalent doses (HEDs) calculated using our model and an allometric scaling method. Estimated and observed whole-body concentrations of HCB and PCB 153 in offspring followed similar trends and differed by less than 60%. Simulations of human exposure yielded concentration estimates comparable to those generated using the previously published model, with concentrations in offspring differing by less than 12%. HEDs calculated using our PK model were about 2 orders of magnitude lower than those generated using allometric scaling. Our PK model can be used to calculate internal dose metrics for offspring and corresponding HEDs and thus informs assessment of developmental toxicity risks associated with LPECs.
Keywords: pharmacokinetics, biological modeling, mathematical modeling, lipophilic persistent environmental chemicals, pregnancy, lactational transfer
Lipophilic persistent environmental chemicals (LPECs) are resistant to degradation and tend to accumulate in the “body lipids” of animals (Lehmann et al., 2014). These chemicals may be released into the environment directly (eg, via agricultural application as a pesticide), as byproducts (eg, via incineration of a precursor substance), or by leaching from products (eg, through release from plastics or adhesives over time) (El-Shahawi et al., 2010). Once released, LPECs can disperse via air, water, and soil, leading to contamination of a variety of ecosystems (El-Shahawi et al., 2010).
Due to their resistance to degradation and metabolism, LPECs remain in the environment following their introduction, and many of them have half-lives on the order of years in both the environment and in biological organisms (Geyer et al., 2002; Terzaghi et al., 2018). They enter animals through consumption of contaminated food (Di Guardo et al., 2020; Duttagupta et al., 2020), leading to especially high concentrations of LPECs in animals at higher trophic levels (Daley et al., 2014; Han and Currell, 2017). Humans are subject to bioaccumulation of LPECs via dietary exposure (Fromme et al., 2016), and they may also be exposed through inhalation (Ampleman et al., 2015; Iakovides et al., 2021; Lehmann et al., 2015) and dermal absorption (Abdallah and Harrad, 2018; Pius et al., 2020). Because of the many potential routes of exposure and their persistence in the human body, LPECs are ubiquitous in humans (Huetos et al., 2014; Woodruff et al., 2011).
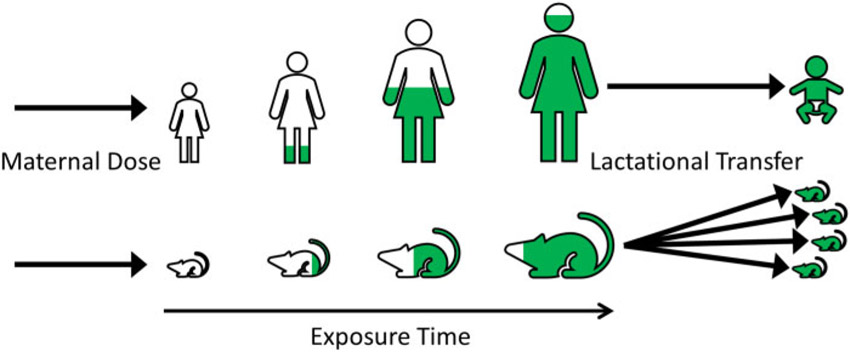
Following absorption, LPECs partition into adipose tissue and they are metabolized and excreted relatively slowly. Scenarios involving continuous or recurring exposure therefore lead to a buildup of LPECs in the body over the course of the life of an individual. Excretion of stored LPECs can occur when lipids are mobilized from the contaminated adipose tissue during lactation (Lerch et al., 2016; Nickerson, 2006) and this can lead to exposure of nursing offspring via breast milk (ATSDR, 2015; Lehmann et al., 2014; Nickerson, 2006). Figure 1 conceptually illustrates how bioaccumulation and lactational transfer can lead to relatively high offspring exposures to LPECs.
Figure 1.
Bioaccumulation (in maternal animals) and lactational transfer (from maternal animals to offspring) of LPECs.
Toxicological studies of prenatal and lactational exposure in laboratory animals are often used as a basis for determining health guidance values such as oral reference doses, minimal risk levels, and tolerable daily intakes. These studies typically report the dosing regimen applied to the maternal animal, but maternal dose may not be an adequate surrogate for the dose that is effectively delivered to offspring due to factors such as placental transport of the substance, partitioning of the substance into maternal lipids, and concentrated delivery of the substance from mother to offspring through nursing. For systemic toxicants, quantifying the association between external and internal doses in both developing laboratory animals and human children is a critical step in determining an appropriate point of departure, and subsequently in calculating a human equivalent dose (HED).
Pharmacokinetic (PK) models allow for translation of applied doses to internal dose metrics, including concentrations in offspring. In fact, multiple PK models have been developed to estimate internal levels of LPECs in pregnant and lactating laboratory animals and their offspring (Lee et al., 2007; Weijs et al., 2010; You et al., 1999), as well as in pregnant and lactating women and their offspring (Emond et al., 2016; Gentry et al., 2003; Redding et al., 2008; Stigum et al., 2015; Trapp et al., 2008; Verner et al., 2009, 2013). However, to our knowledge, no multispecies, multichemical model of gestational and lactational exposure has been previously published, making HED calculations difficult.
We developed a generic, multispecies PK model that quantifies the transfer of LPECs from mother to offspring during gestation and lactation. It is generic in the sense that it can be used for any LPEC if a half-life describing first-order elimination (in animal species of interest) is available. Our model can be used for estimation of HEDs and interspecies comparisons of exposure scenarios that occur before or during pregnancy and nursing; therefore, it may serve as a useful tool for risk assessment of LPECs that bioaccumulate and transfer from mothers to offspring.
MATERIALS AND METHODS
All analyses and simulations described herein were performed using R version 4.0.3 (R Core Team, 2020) on a Dell Latitude E7270 computer running Microsoft Windows 10. Dynamic models were implemented using the MCSim model specification language (Bois, 2009) and were subsequently translated to C (using the MCSim utility “mod”) and compiled for use in R. Supplemental source code and data files are available through the U.S. Environmental Protection Agency’s Environmental Dataset Gateway (https://doi.org/10.23719/1524467).
Pharmacokinetic Models
To analyze in utero and lactational exposure scenarios, we developed a generic PK model for lipophilic substances that describes transfer from a mother to her offspring. We parameterized the model for 2 laboratory animal species (rats and mice) and humans so that it can be used for interspecies dose conversions. This model accounts for the substantial changes (eg, in body mass) associated with pregnancy (for the mother) and in utero and postnatal periods (for the offspring) and can estimate instantaneous concentrations (in mg of substance per kg of body mass) in the mother and offspring following oral or intravenous dosing or dietary intake. Furthermore, this model can be used to calculate various internal “dose metrics” for specific exposure scenarios. By determining an exposure level for humans that produces a dose metric equivalent to that experienced by animals in a well-defined, controlled exposure scenario, one can use the model to compute an HED.
Model assumptions.
The model equations are based on the conservation of the total mass of substance in the mother-offspring system, which consists of a maternal animal and any associated offspring. That is, at any given time the total amount of substance that has entered the system equals the total amount of substance that is in the system plus the total amount that has been eliminated. The following list describes additional assumptions that were made in developing the model.
A fixed percentage of the nominal dose administered to an animal (mother or offspring) is absorbed by that animal. (We assume that the unabsorbed fraction of the administered dose does not enter the system and therefore we do not track the fate of that portion of the dose in our model.)
During gestation and up through the instant birth occurs, the ratio of the fetal concentration (mg of substance per kg of body mass) to the maternal concentration is constant.
Once the substance enters the animal, it is immediately and completely distributed into the lipids of the animal. Although we assume the substance resides only in lipids, average whole-body concentrations (mg/kg) are computed based on total body mass. (This assumption impacts the rate of lactational transfer of the substance as well as estimation of the ratio of fetal concentration to maternal concentration during pregnancy.)
The concentration of the substance in milk lipids equals the concentration of the substance in the lipid fraction of the mother’s body.
The proportion of the mother’s body which is lipid is constant with respect to time.
The proportion of breast milk which is lipid is constant with respect to time.
All (100%) of the substance in the breast milk ingested by the offspring is absorbed by the offspring.
The elimination rates of the substance in mothers and offspring, excluding losses due to birth or lactation, are equal to one another and are proportional to the amount of substance in the body; these rates are characterized by a half-life that is a fixed constant for any given animal species.
For pregnancies that result in the birth of more than one offspring, which are common in nonprimate laboratory mammals, all the sibling offspring are identical. That is, at any given time, they each have the same body mass and milk consumption rate, and each of their bodies contains the same amount of substance.
If there is a decrease in total body mass at birth (ie, if the difference between the mass of mother before birth and the sum of the masses of mother and offspring after birth is greater than zero), then the lost body mass (eg, mass of placenta, amniotic sac, etc.) has the same concentration of substance as does the mother.
Model equations.
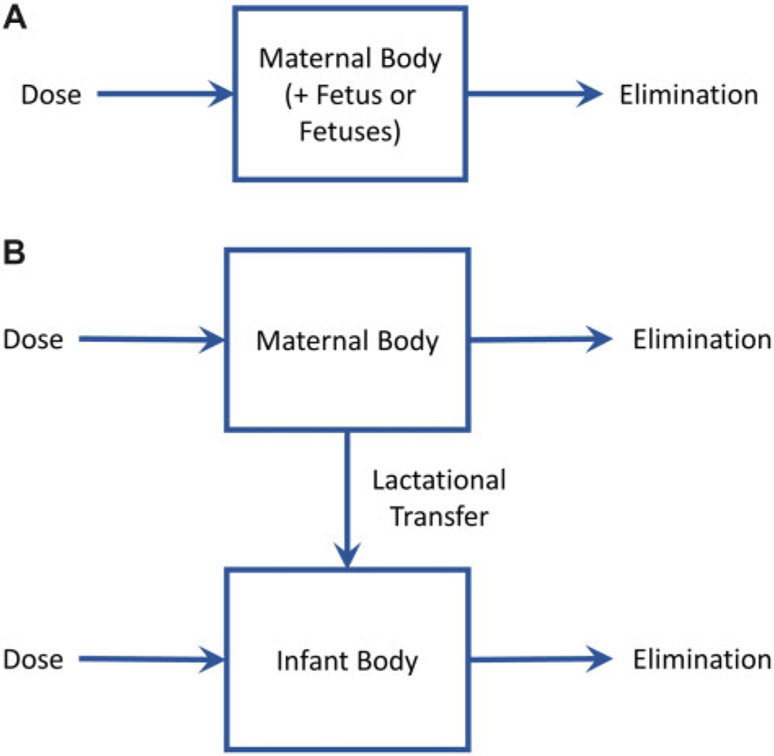
The diagram in Figure 2A illustrates the model for the (nonpregnant) mother at times prior to conception as well as the maternal-fetal system (ie, the mother and any in utero fetuses) during pregnancy. Before conception and during pregnancy, the model can be represented by a single ordinary differential equation (ODE) describing the rate of change of the amount of substance in the maternal body or the maternal-fetal system. The time rate of change of the amount in the maternal body or maternal-fetal system (mg/day) is given by
| (1) |
where Amf(t) is the amount (mg) of substance in the maternal body (prior to conception) or maternal-fetal system (during pregnancy), Fabs is the dose absorption fraction, Dm(t) is the rate of dose administration to the mother (mg/kg/day), Mmf(t) is the mass (kg) of the maternal body (prior to conception) or maternal-fetal system (during pregnancy), 𝓀 is the first-order rate of elimination (days−1) of the substance, and t is the time elapsed (days) since some initial time. The initial time is typically chosen to be the beginning of a controlled exposure study in animals, or the moment of birth of the mother for humans.
Figure 2.
Schematics illustrating the structures of (A) the nonpregnant adult and/or pregnancy and gestation PK model and (B) the lactational transfer PK model.
The diagram in Figure 2B illustrates the model for the mother and “infant(s)” (ie, offspring) after birth. During this time, 2 ODEs are required to track changes in the amount of substance in the mother and the infant(s). The time rate of change of the amount in the mother (mg/day) is given by
| (2) |
where Am(t) is the amount (mg) of substance in the maternal body, Mm(t) is the mass (kg) of the maternal body, ni is the number of infants, Rmilk(t) is the rate of breast milk ingestion by each infant (kg/day), Fmilk is the proportion of breast milk that is lipid, and Fm is the proportion of the maternal body that is lipid. Fabs, Dm(t), 𝓀, and t are all defined as for equation 1. The time rate of change of the amount in each infant (mg/day) is given by
| (3) |
where Ai(t) is the amount (mg) in the infant’s body, Di(t) is the rate of dose administration or exposure (not including breast milk ingestion) for the infant (mg/kg/day), and Mi(t) is the mass (kg) of the infant’s body. The other quantities in this equation (Fabs, 𝓀, Rmilk(t), Fmilk, Fm, Am(t), Mm(t), and t) are defined as described previously.
Equation 1 has a single state variable, Amf (t), and values for this variable at all times t after some initial time t0 (possibly t0 = 0, which corresponds to the moment of conception) up through tgest (the moment of birth) can be obtained by solving the initial value problem that consists of equation 1 and an initial condition, typically Amf(t0) = 0. Similarly, during the post-partum period, equations 2 and 3 and initial conditions that provide values for Am (tgest) and Ai(tgest) describe an initial value problem, so one can compute Am(t) and Ai(t) for all times t > tgest.
As stipulated in the Model Assumptions, the ratio of the concentrations in the fetus(es) and the mother is a fixed constant throughout pregnancy. For continuity, this ratio, denoted by Rfm, also equals the ratio of the concentrations in the infant(s) and the mother at the instant of birth, when t = tgest. Thus,
| (4) |
where Ci (tgest) = Ai(tgest)/Mi(tgest) and Cm(tgest) = Am(tgest)/Mm(tgest) are the concentrations in the infant(s) and mother, respectively, at the instant of birth. Suppose that the total body mass is conserved at the instant of birth (ie, Mmf(tgest) = Mm(tgest) + ni · Mi(tgest)). Then, at this instant, the maternal-fetal system should have an overall concentration given by
This implies
and substituting equation 4, we obtain
Rearranging, we can compute the concentration in the mother at birth as
| (5) |
Also, we can compute the concentration in the infant(s) at the instant of birth as
To compute the concentrations in the mother and in utero fetus(es) throughout pregnancy, we assume that the ratio of concentrations in the mother (ie, in tissues belonging to the mother alone) and the maternal-fetal system transitions linearly from a value of 1 at conception (when the conceptus is very small) to the value shown as a fraction on the right-hand side of equation 5 at the instant of birth. That is,
| (6) |
for t ∈ [0, tgest). Furthermore, the concentration in the fetus(es) can be computed as
| (7) |
for t ∈ [0, tgest). Note that we use the same symbol, Ci(t), to denote concentrations in the fetus(es) during gestation and concentrations in infant(s) (ie, offspring) after birth.
To run a simulation for a period of time that includes the moment of birth, we first solve the initial value problem involving equation 1 up through the instant of birth (ie, when t = tgest). We then compute the concentrations in the mother and fetus(es) at this instant using equations 6 and 7 and use these concentrations to set initial conditions for a second initial value problem involving equations 2 and 3. Specifically, we set Am(tgest) = Cm(tgest) · Mm (tgest) and Ai(tgest) = Ci(tgest) · Mi(tgest), where the values of Cm (tgest) and Ci (tgest) are taken from results of the pregnancy simulation.
If total body mass is not conserved at birth (eg, because products of conception such as placenta and amniotic fluid are discarded and not considered further in simulations) we assume that any lost body mass was “maternal” body mass; thus, that lost body mass is assumed to contain substance at the maternal concentration level Cm (tgest). In this case, the value of Mm(tgest), the “mass of the maternal body,” is decreased by the appropriate amount before starting the simulation of the postnatal period. If we let denote the mass of the maternal body after discarding all products of conception (ie, after subtracting the mass of the placenta, amniotic fluid, etc.), then the initial amount in the mother at the beginning of the postnatal period is .
Model parameters.
We parameterized our PK model for 2 laboratory animal species commonly used in toxicological studies (ie, rats and mice), as well as for humans. Species- and substance-specific values of the model parameters are described in the following paragraphs.
The parameter tgest represents the duration (days) of pregnancy (ie, the time from conception to birth). Default values of this parameter are 273.75 days (approximately 9 months, or 75% of 365 days) for humans, 22 days for rats (U.S. EPA, 1988a), and 18 days for mice (Al Jothery et al., 2014). Note that the default value used for humans (3 quarters of 1 year) is slightly larger than the median number of days from ovulation to birth observed by Jukic et al. (2013), which is 268 days, but is a convenient approximation that can easily be represented as a fraction of a year.
The parameter Fabs, which represents the fraction of the administered dose that is absorbed, can be chosen to reflect a given dosing scenario. For example, one might assume that Fabs = 1.0 for a dose delivered intravenously and that Fabs < 1.0 for a dose delivered orally. In their PK models, Maruyama et al. (2003) used absorption fractions between 80% and 99% for various dioxins (a class of lipophilic substances), citing McLachlan (1993) and Liem and Theelen (1997). We applied a default value of 0.9 for Fabs.
The parameters Fm and Fmilk represent the fraction of the maternal body and the breast milk, respectively, that are lipid. Default values of these parameters are shown in Table 1.
Table 1.
Default Values for Model Parameters Describing Proportion of the Maternal Body and Breast Milk That Are Lipid (Denoted Fm and Fmilk, Respectively) and the Ratio of Concentrations in Fetus(es) and Mother During Pregnancy (Denoted Rfm) in Various Species
Neto Angéloco et al. (2012, Table 3). The value given here is the mean value for a control group of Wistar rats given a “standard AIN-93 diet.”
Reed et al. (2007, Section 2.4). The value given here is the overall mean for female mice from 40 strains.
Borrud et al. (2010, Table 3). The value given here is a weighted average of the mean values listed for females of “all races and ethnicities” for the age categories 8–11, 12–15, 16–19, and 20–39 years. Means for these age categories were converted to a weighted average by multiplying each mean by the sample size for the corresponding age category and then dividing by the sum of the sample sizes.
Nicholas and Hartmann (1991, Table 2). The value given here is the average of the mean values listed for all 5 time points and for both diets.
Johnson et al. (2001). The value given here is the average for milk from 10 female mice (MF1) on day 15 of lactation.
Arcus-Arth et al. (2005, Table 2). The value given here is the mean value for “all measurement periods” (through 12 months post-partum).
The parameter 𝓀, which represents the first-order rate of elimination, can be chosen to reflect the half-life of a given substance in an animal of a given species (eg, rat or human). In practice, we assumed a fixed half-life t1/2 (days) for the chemical in the species of interest, and computed the elimination rate parameter as
where “log” denotes the natural (base e) logarithm. The parameter ni, which represents the number of infants (offspring) born to the mother, can be specified by the user. By default, we assumed ni is 1 for humans, 10 for rats (Chahoud and Paumgartten, 2009), and 6 for mice (Al Jothery et al., 2014), but an alternate value can be substituted for each of the laboratory animal species (eg, if the litter size is specified in a given study). The value of this parameter can be changed at parturition or any time thereafter (eg, to reflect culling of pups in an animal study).
The parameter Rfm, which represents the ratio of the concentrations in the fetus(es) and the mother during pregnancy, will take on default values unless a value is assigned. Ando (1978) observed that newborn rat pups have a total body lipid fraction of 3.3%. Because this number is assumed to be 9.4% for adult rats (cf. Table 1), and because the model assumes the substance resides entirely in the lipids of the animal, the ratio of the concentrations at the end of pregnancy is assumed to be 0.35, which is approximately equal to the ratio of 3.3 and 9.4. We assume that the ratio is the same throughout pregnancy. Deans et al. (1989) observed average human fetal body fat proportion to be 17.15% at 40 weeks of gestation. Because the value for the (adult human) mother is assumed to be 34.6% (cf. Table 1), we estimate the ratio of the concentration in a human fetus and mother to be 0.5, which is approximately equal to the ratio of 17.15 to 34.6. We assumed that the ratio is the same for mice as for rats. All default values of the parameter Rfm are shown in Table 1.
The values of the model parameters Mm(t), Mi(t), Dm(t), Di(t), and Rmilk(t) are all time dependent. The following paragraphs describe these parameters in detail.
Mm(t) and Mi(t) represent the masses of the mother and infant(s) (or offspring), respectively. However, during pregnancy, we let Mm(t) represent the combined mass of the mother and in utero fetus(es); that is, Mmf(t) = Mm(t) for t ∈ [0, tgest). For experiments in laboratory animals, we allow the user to set values for 12 parameters that describe body masses of the mother and the offspring:
, the jth time (days) since conception at which the mass of the mother is observed/known, and
, the mass of the mother at time ,
for j ∈ {1, 2}, and
, the 𝓀th time (days) since birth at which the mass of the infant(s) is observed/known, and
, the mass of one infant at time ,
for 𝓀 2 {1, 2, 3, 4}. Default values for body mass parameters for rats and mice are shown in Table 2.
Table 2.
Default Values for Model Parameters Describing Animal Body Masses
| Quantity (Units) | Rat | Mouse |
|---|---|---|
| (day) | 1 | 1 |
| (kg) | 0.25a | 0.0255b |
| (day) | 44 | 25 |
| (kg) | 0.273c | 0.0318b |
| (day) | 3 | 1 |
| (kg) | 0.0066c | 0.0014d |
| (day) | 10 | 10 |
| (kg) | 0.014c | 0.00608e |
| (day) | 17 | 18 |
| (kg) | 0.028c | 0.00885f |
| (day) | 75g | 45g |
| (kg) | 0.25a | 0.03h |
U.S. EPA (1988b, Table 4-2). The value listed is the “reference body weight” for rats.
Al Jothery et al. (2014, text and Table 2). The values listed for 1 and 25 days are the average mass values for rat dams at baseline (from the first paragraph of the Results section) and during lactation (from Table 2), respectively.
Lehmann et al. (2014, Table 3). The second mass value listed for a rat dam is the “dam weight during lactation” and the pup masses are those for “week 1,” “week 2,” and “week 3.”
U.S. EPA (1988a, Table 3-3). The mouse pup mass value listed for 1 day is the average of the B6C3F1 male and female “Weight at Birth” values.
Al Jothery et al. (2014, Figure 5B). The mouse pup value listed for 10 days is the average of the values for 2 data points (one each for high and low food intake lines) depicted in the figure. Coordinates of the points were digitally extracted using WebPlotDigitizer (Rohatgi, 2021).
Al Jothery et al. (2014, Table 1). The mouse mass listed for 18 days is the average of the mean “pup mass at weaning” values for 2 lines of mice selected for high and low food intake.
U.S. EPA (2002, Table 3-1). The time values listed for the rat and the mouse correspond to the ages of sexual maturity (2.5 months and 1.5 months, respectively) in those species.
U.S. EPA (1988a, Section 3.2.1). The value listed is the reference value for an adult mouse.
For laboratory animals, the body mass functions Mm and Mi are defined in such a way that
they yield the appropriate body masses at certain times (as specified in the above parameter list);
they are piecewise linear and are continuous except at the instant of birth (t = tgest);
the mother gains sufficient body mass during gestation so that losing the mass of the infant(s) at birth will not cause her body mass to fall below the first observed/known body mass prior to birth () if all observations of body mass occurred before birth (ie, ) or the second observed body mass if it occurred after birth (ie, ); and
total body mass of the mother and infant(s) is conserved at birth.
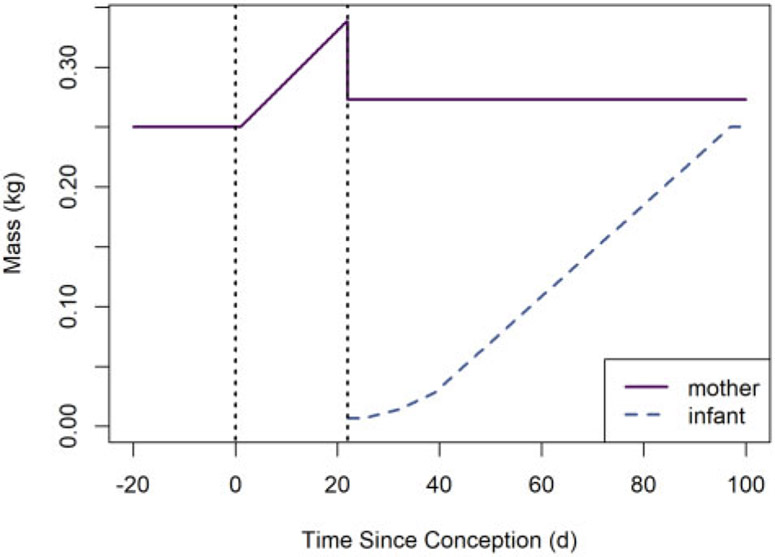
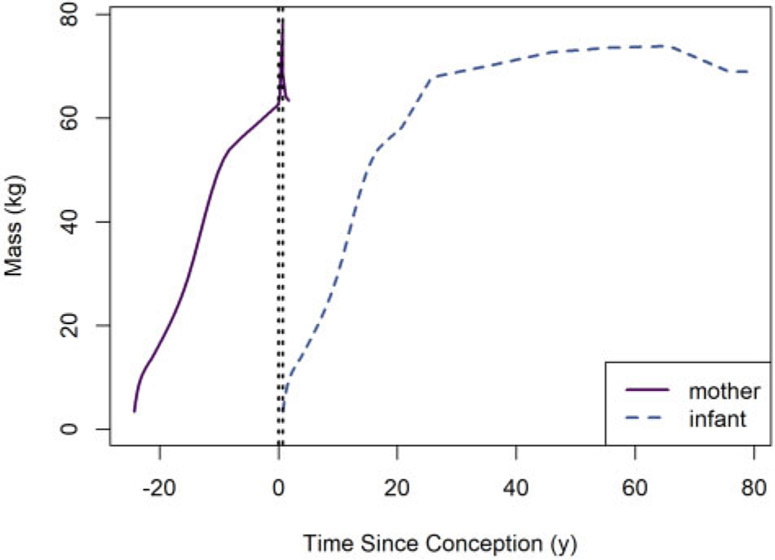
This last condition is achieved by requiring that (1) the mother’s body mass at time tgest is at least greater than the preconception or post-birth body mass, and (2) the mother’s body mass decreases by at tgest. However, note that ni can be changed at any time after the instant of birth to reflect culling. The default body mass functions for rat dams and their offspring (for the default rat mass parameter values) are depicted in Figure 3.
Figure 3.
Default body mass versus time functions for rat dams and their offspring. The left and right vertical dotted lines indicate the times of conception and parturition, respectively.
For a human mother, the body mass function Mm is defined in such a way that
it is piecewise linear and is continuous except at the instant of birth, which corresponds to age 25 years;
it reproduces values from Figure 2 (sampled at 3-month intervals starting with age 0 months and ending with age 36 months) of Kuczmarski et al. (2002), which depicts human female body mass versus age for ages 0–36 months;
it reproduces values from Figure 10 (sampled a 1-year intervals starting with age 4 years and ending with age 20 years) of Kuczmarski et al. (2002), which depicts human female body mass versus age for ages 2–20 years; and
it reproduces values from Table 3 for body mass of an adult woman before, during, and after for a human offspring, the body mass function Mi is defined in such a way that
it is zero before the instant of birth;
it is piecewise linear and continuous for ages greater than zero;
it reproduces values from Figure 2 (sampled at 3-month intervals starting with age 0 months and ending with age 36 months) of Kuczmarski et al. (2002), which depicts human female body mass versus age for ages 0–36 months;
it reproduces values from Figure 10 (sampled at 1-year intervals starting with age 4 years and ending with age 20 years) of Kuczmarski et al. (2002), which depicts human female body mass versus age for ages 2–20 years; and
it has values of 67.9, 70.2, 72.7, 73.6, 73.9, and 69.0 kg at ages 25, 35, 45, 55, 65, and 75 years in agreement with Table 8-5 of Chapter 8 of U.S. EPA (2011a).
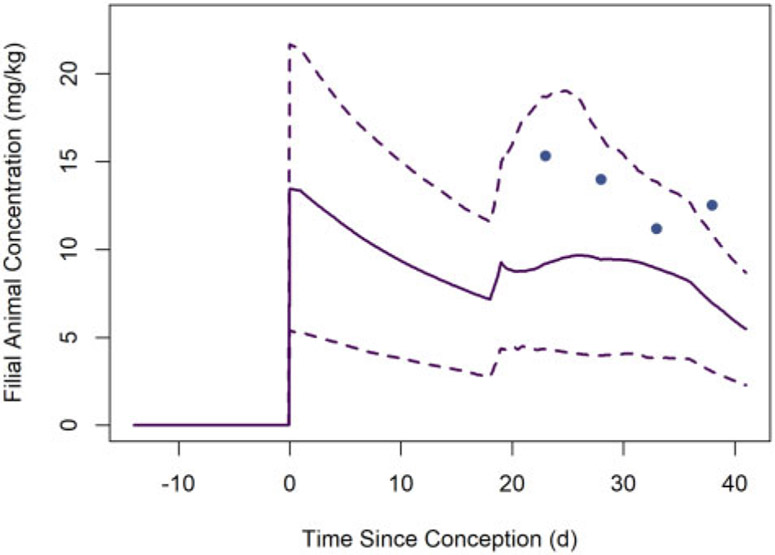
Figure 10.
Whole-body concentrations of PCB 153 in filial animals (mouse pups) observed (solid circles) by Vodicnik and Lech (1980) and estimated (lines) based on model simulations of that study. The solid line represents the median predicted concentrations from the MC simulations, whereas the dashed lines represent the lower and upper bounds of a 95% credible interval for the predicted concentrations.
Table 3.
Time-Dependent Reference Masses for a Woman When Assuming She Conceives at Age 24.25 Years and Gives Birth at Age 25 Years
| Age (Years) | Mass (kg) | Reference | Notes |
|---|---|---|---|
| 24.25 | 62.7 | Portier et al. (2007) | This is the assumed age and mass of the woman at conception. |
| 24.5 | 64.6 | Carmichael et al. (1997) | This reflects an assumption that the woman gains 1.9 kg in the first 3 months of pregnancy. |
| 25.0a | 78.4 | Carmichael et al. (1997) | This reflects an assumption that the woman gives birth at age 25 years, and that she gains a total of 15.7 kg between conception and the moment of birth. |
| 25.0b | 68.3 | Thorsdottir and Birgisdottir (1998) | Women with moderate mass gain during pregnancy return to prepregnancy body mass (or within 0.1 kg of this) by 18–24 months postpartum. Adding the mass losses for 0–6 months and 6–18 months postpartum (see below) to the prepregnancy body mass (see above) results in the body mass shown here. |
| 25.5 | 64.1 | Dewey et al. (1993) | This reflects an assumption that a breastfeeding woman loses 4.2 kg of body mass in the first 6 months postpartum. |
| 26.5 | 62.7 | Dewey et al. (1993) | This reflects an assumption that a breastfeeding woman loses an additional 1.4 kg of body mass between 6 and 18 months postpartum. |
For modeling purposes, the value listed here is a limit as age approaches 25.0 years from below (ages less than 25.0 years). There will be a discontinuity at age 25.0 years, as this coincides with the moment of birth.
For modeling purposes, the value listed here is the exact body mass at age 25.0 years. There will be a discontinuity at age 25.0 years, as this coincides with the moment of birth.
We used human female body mass values for the offspring to allow for multigenerational simulations (ie, cases in which the offspring becomes a mother). The human offspring body mass function is depicted in Figure 4.
Figure 4.
Default body mass versus time functions for human mothers and their offspring. The left and right vertical dotted lines indicate the times of conception and parturition, respectively. Body masses for human mothers after weaning are not shown because this information does not affect offspring dosimetry.
Dm(t) and Di(t) represent the rates of dose administration to the mother and the infant(s) (or offspring), respectively, in mg per kg of body mass per day (mg/kg/day). Typically, these rates will be nonzero and constant during a “dosing” or “exposure” period and will be zero for times outside this period. For experiments in animals, we allow the user to set 6 parameters that define a dosing regimen:
dm, the dose administered to the mother in mg per kg of body mass per day (mg/kg/day) or in mg per kg of food (mg/kg);
, the time (days) since conception at which dose administration to the mother begins;
, the time (days) since conception at which dose administration to the mother ends;
di, the dose administered to the infant(s) (not including lactational transfer) in mg per kg of body mass per day (mg/kg/day) or in mg per kg of food (mg/kg);
, the time (days) since conception at which dose administration to the infant(s) begins; and
, the time (days) since conception at which dose administration to the infant(s) ends.
An additional Boolean (true or false) parameter indicates if the dose is administered in food (and, consequently, whether dm and di have units of mg/kg/day or mg/kg). When the dose (dm or di) is provided in mg/kg/day, we can express the time-dependent dose administration rates as
| (8) |
where x is replaced by m or i for the mother or infant, respectively. On the other hand, when the dose is provided in mg/kg, we use an estimate of food consumption rate (in kg/day) given by
where M is the body mass (in kg) of the animal (cf. equation 6-1 of U.S. EPA [1988a]). Thus, when the dose (dm or di) is provided in mg/kg (ie, mg of chemical per kg of food), we can convert to mg/kg/day (ie, mg of chemical per kg of body mass per day) by using
| (9) |
where x is replaced by m or i for the mother or infant (offspring) respectively.
Rmilk(t) represents the rate at which an offspring consumes breast milk (kg/day). We allow the user to set 5 parameters (for rats or mice) that describe milk consumption rate:
, the starting milk consumption rate in kg milk per day (kg/day);
, the (average) milk consumption rate (kg/day) during the first week of lactation (and nursing);
, the (average) milk consumption rate (kg/day) during the second week of lactation (and nursing);
, the (average) milk consumption rate (kg/day) during the third week of lactation (and nursing); and
tlact, the total duration (days) of the lactation (nursing) period.
For rats and mice, the function Rmilk is defined such that
it is piecewise linear and continuous, except for discontinuities at t = tgest and t = tgest + tlact;
the linear segments are defined on the intervals [tgest, tgest + 7), [tgest + 7, tgest + 14), [tgest + 14, tgest + 21), and [tgest + 21, ∞);
Rmilk(t) = 0 for t < tgest and t > tgest + tlact;
;
, where tgest + 3.5 is the midpoint of the first post-partum week;
, where tgest + 10.5 is the midpoint of the second post-partum week; and
, where tgest + 17.5 is the midpoint of the third post-partum week.
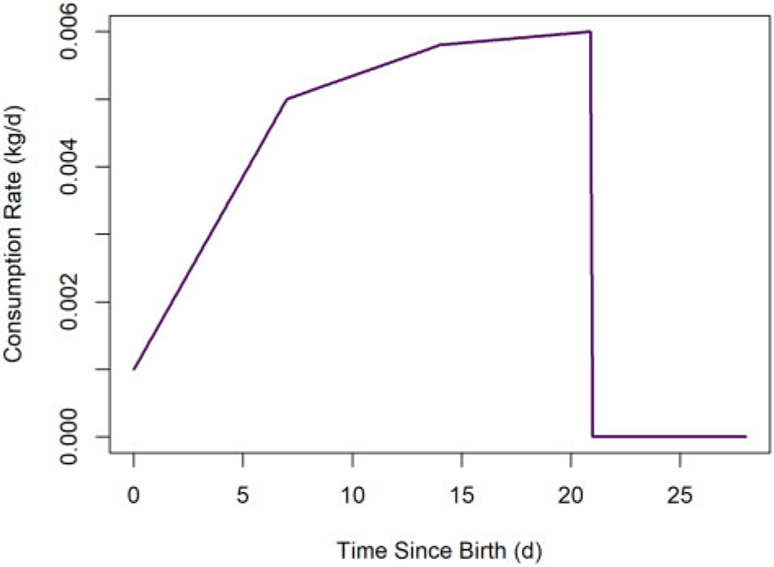
Default values for milk consumption rate parameters for rats and mice are shown Table 4. The animal milk consumption rate function (for the default rat pup milk consumption parameter values) is shown in Figure 5.
Table 4.
Default Values for Model Parameters Describing Animal Milk Consumption Rates (per Individual Offspring)
| Quantity (Units) | Rat | Mouse |
|---|---|---|
| (kg/day) | 0.001 | 0.0001a |
| (kg/day) | 0.003b | 0.0003a |
| (kg/day) | 0.0054b | 0.00054a |
| (kg/day) | 0.0059b | 0.00059a |
| tlact (days) | 21c | 21c |
In general, is the rate of consumption (kg/day) during the 𝓀th week after birth.
For each mouse value, we used 10% of the corresponding rat value based on an assumption that consumption rate is proportional to body mass of the adult of the species. Note that the reference body masses of rats and mice provided in Table 4-2 of U.S. EPA (1988b) are 0.25 kg and 0.025 kg, respectively, so an adult mouse has a body mass approximately 10% of that of an adult rat.
Lehmann et al. (2014, Table 3). The values listed are those for “pup ingestion rate” for “week 1,” “week 2,” and “week3.”
U.S. EPA (1988a, Table 2-2).
Figure 5.
Default rat milk consumption rate versus time. We assume the milk consumption rate decreases to 0 kg/day at weaning.
For humans, the milk consumption function Rmilk is defined such that
it is piecewise linear and continuous, except for discontinuities at t = tgest and t = tgest + tlact, where tgest is assumed to be 273.75 days (as discussed previously) and tlact is assumed to be 365 days;
the linear segments are defined on the intervals [tgest, tgest + 30), [tgest + 30, tgest + 90), [tgest + 90, tgest + 180), [tgest + 180, tgest + 365), and [tgest + 365, ∞);
the milk consumption rates for ages 15, 60, 135, and 272.5 days (which correspond to the midpoints of the intervals defined above) are 0.510, 0.690, 0.770, and 0.620 kg/day, respectively, which correspond to “recommended values for human milk intake rates” for “birth to < 1 month,” “1 to < 3 months,” “3 to < 6 months,” and “6 to < 12 months” as reported in Table 15-1 of Chapter 15 of U.S. EPA (2011a) (assuming a milk density of 1 kg/l);
the milk consumption rate for age 0 day is 0.477 kg/day, which can be extrapolated from the linear function that gives 0.510 kg/day at 15 days and 0.690 kg/day at 60 days; and
the milk consumption rate for ages greater than or equal to 365 days is 0 kg/day.
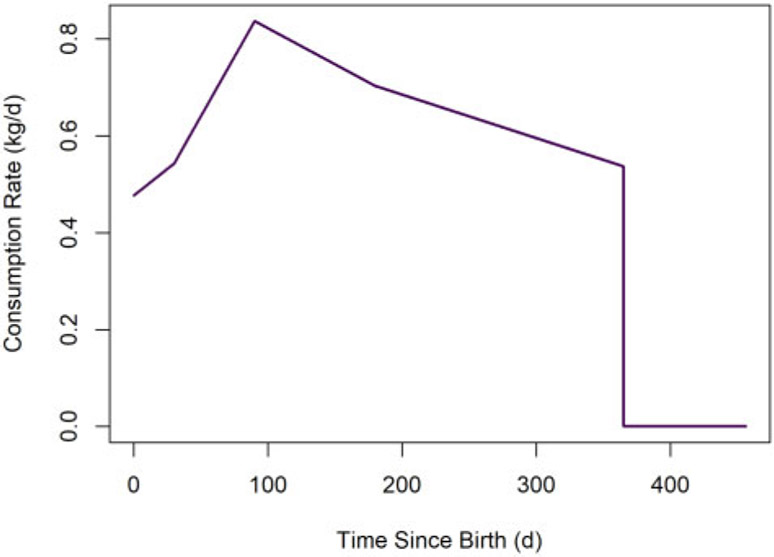
As asserted in the bulleted list above, the default value of tlact for humans is assumed to be 365 days. The human infant milk consumption rate function is depicted in Figure 6.
Figure 6.
Default human milk consumption rate versus time. We assume the milk consumption rate decreases to 0 kg/day at weaning.
Finally, the parameter tage represents the number of days after conception at which the simulation should end. The value of this parameter should reflect the time at which the observation of a particular health outcome in an animal developmental toxicology study occurred, or, for humans, the time at which the possibility of the health outcome ends or concern about the health outcome is greatly diminished (eg, at the end of an expected human lifetime).
Model simulations and output.
PK model simulations generate estimates of amounts (mg), concentrations (mg/kg), and cumulative areas under the concentration curve (mg·day/kg) for the mother and the offspring. The symbol Cx represents a concentration and the symbol AUCx represents area under the concentration curve, where x is replaced by m or i for the mother or infant (offspring), respectively.
The instantaneous concentration of substance in the in utero offspring can be calculated using equation 7 (for 0 ≤ t < tgest) and the comparable concentration in the postnatal offspring can be calculated as
after parturition (ie, for t ≥ tgest). Furthermore, the concentration in offspring is assumed to be zero before conception (ie, for t < 0). The area under the concentration curve for the offspring is computed as
where t = t0 coincides with the beginning of the simulation, and the average concentration (mg/kg) in the offspring during a given period is computed as
where tstart and tend are the start and end times (days) for the period. For example,
for the gestational period, tstart = 0 and tend = tgest;
for the lactation (nursing) period, tstart = tgest and tend = tgest + tlact;
for the entire gestation and lactation period of a given study, tstart = 0 and tend = tgest + tlact; and
for the entire period of a given study, tstart = 0 and tend = tage, where tage is the time (days) since conception corresponding to observation or sacrifice of the offspring.
Dose Metrics
We used 5 distinct dose metrics to compute HEDs for in utero and lactational exposure scenarios. Each dose metric was related to the concentration in the offspring before birth (in utero), after birth, or both. The dose metrics were:
peak concentration (mg/kg) during gestation and the nursing period (ie, the period from conception to weaning);
average concentration (mg/kg) during gestation and the nursing period (ie, the period from conception to weaning);
average concentration (mg/kg) during gestation (ie, the period from conception to birth);
average concentration (mg/kg) during the nursing period (ie, the period from birth to weaning); and
average concentration (mg/kg) during the period from conception to observation of the health outcome of interest (ie, the period from conception to t = tage).
Recall that the parameter tgest represents the duration (days) of pregnancy and gestation (ie, the time from conception to birth). As stated previously, default values of this parameter are 22 days for rats and 18 days for mice. The parameter tlact represents the duration (days) of lactation and nursing (ie, the time from birth to weaning). Default values for this parameter for rats and mice are stated in Table 4. For humans, we assume that pregnancy begins when the mother is exactly 24.25 years old, the birth of the infant occurs when the mother is exactly 25 years old, and the weaning of the infant occurs when the mother is exactly 26 years old. Thus, for humans, tgest and tlact have default values of 273.75 days and 365 days, respectively. For computing dose metric 5, the “observation” of the filial human was assumed to occur at age 78 years, or 78.75 years after conception based on the average human life expectancy value recommended in Chapter 18 of the U.S. EPA’s Exposure Factors Handbook (U.S. EPA, 2011a). However, another age can be provided by the user.
Experimental Data and Model Evaluation
We evaluated our model using PK data from a developmental study of HCB in rats (Nakashima et al., 1997) and a developmental study of PCB 153 in mice (Vodicnik and Lech, 1980). These 2 studies met the following essential criteria: (1) a lipophilic substance (LPEC) was administered to maternal animals; (2) the animals were rats or mice (ie, laboratory animal species for which we had parameterized our PK model); (3) the LPEC was one for which we were able to identify independent PK data sets for determination of an elimination half-life in the relevant animal species; (4) substance concentrations in the maternal animals and/or offspring were observed and reported; and (5) at least some of the concentrations were whole-body concentrations (which can be directly compared with our model predictions). We also compared our PK model predictions for humans to predictions generated using the human PK model of Verner et al. (2013), which was previously evaluated using data from 2 human studies.
Nakashima et al. (1997) dosed 5 rat dams with 35.1 nmol of hexachlorobenzene (HCB) per 100 g of food (0.1 mg/kg food) during pregnancy and lactation. Two dams were sacrificed 1 day before parturition, and concentrations were observed in maternal blood, subcutaneous fat, and perirenal fat, as well as in whole (homogenized) fetuses. Three dams and their pups were sacrificed 16 days after parturition, and concentrations were observed in blood, subcutaneous fat, and perirenal fat of 3 dams and their (suckling) pups. In order to simulate the conditions of the study of Nakashima et al. (1997), we set the simulation parameters as follows:
the concentration in food was dm = 0.1 mg/kg;
the maternal dose start time was day (ie, dosing begins at conception);
the maternal dose end time was days (ie, dosing ends 38 days after conception or 16 days after parturition);
the starting maternal mass was kg at day, which is slightly less than the default value of 0.25 kg, because the dam’s mass after parturition is assumed (in this case) to be equal to both and her mass at the first observation after parturition, which is 0.247 kg based on the average mass of 3 rat dams in the study at 16 days after parturition;
the maternal mass at the end of pregnancy was kg at based on the average mass of 2 rat dams in the study at 1 day prior to parturition;
the number of pups was ni = 14.33 after parturition, as this was the mean number of pups in the 3 litters nursed by the 3 dams in the study;
the number of fetuses was ni = 21.74 (before parturition), as this ensures that the mass of the simulated dam at birth returns the maternal body mass from 0.3905 kg (the average mass of 2 dams just before parturition) to 0.247 kg (the average mass of 3 dams at 16 days after parturition);
the pup mass was kg at days (after birth), as this corresponds to the average mass of the pups at 16 days after parturition;
the default masses (and corresponding times) were used for all other offspring mass parameters;
the half-life was t1/2 = 92.4 days based on a Bayesian analysis (cf. Supplementary Material) of the data of Koss et al. (1983) describing HCB PKs in rats;
the fraction of dose absorbed was Fabs = 0.56 in order to ensure that the total estimated absorption of the nominal dose at 21 days after conception matched 90% (ie, the default absorption fraction) of the total estimated ingestion of HCB for dams between the second day of pregnancy and one day before parturition (ie, 120 nmol or 0.034 mg) reported by Nakashima et al. (1997) for a different but comparably treated group of rat dams;
the end time for the simulation was tage = 38 days after conception because the default gestation duration is tgest = 22 days and the last observation was at 16 days after birth; and
the duration of lactation was set to tlact = 16 days to coincide with the time at which the pups were sacrificed.
Note that the value of the parameter ni was changed (from 21.74 to 14.33) at the moment of birth to account for a loss of body mass greater than that expected based on the number of pups nursed (ni = 14.33) and the (default) initial pup mass ( kg). Essentially, we accounted for a loss of both body mass and substance mass, ostensibly due to the loss of the placenta and other products of conception, by assuming that approximately 7 additional pups were “culled” just after birth. This approach leads to a different treatment of the “other products of conception” than was described previously (at the end of the Model Equations section). For humans, more maternal body mass observations inform the function describing maternal mass, and “other products of conception” are assumed to contain LPECs at the same concentration as maternal tissue (not the same concentration as fetal tissue). For the rats involved in this study, we had only 2 observations of maternal body mass. We used this information to construct a plausible body mass versus time trajectory of the rat dam by setting the maternal mass parameters and adjusting ni at the moment of birth.
The time-varying value of Dm was calculated using equation 9 because the dose was delivered via food. Default values listed in Tables 1, 2, and 4 were used for all other parameters. The Supplementary File “hcb_nakashima1997_study1.R” contains a script that performs the model simulation and generates plots showing the concentration profiles.
To characterize uncertainty in our model predictions, we ran Monte Carlo (MC) simulations using half-lives randomly selected from a Markov chain Monte Carlo (MCMC) sample generated via the previously mentioned Bayesian half-life analysis (cf. Supplementary Material). For the MC simulations, we also randomly selected values for the parameters Fabs, Fm, Fmilk, and Rfm, which we determined to be some of the most influential parameters in determining the values of the dose metrics we considered (cf. Sensitivity Analysis section). We sampled values for those parameters from normal distributions with mean values of 0.56 (the value for Fabs for this study), 0.094, 0.154, and 0.35 (cf. Table 1), respectively, and standard deviations equal to 30% of the mean values. Although the selection of 30% as the value for these coefficients of variation was somewhat arbitrary, this value is typical for distributional representations of PK model parameters (Clewell and Clewell, 2008). The Supplementary File “hcb_nakashima1997_study1_mc.R” contains a script that performs the MC model simulations and generates plots showing the concentration profiles.
We also used data reported by Vodicnik and Lech (1980) to evaluate the model. Briefly, Vodicnik and Lech (1980) provided a bolus dose of 50 mg of 2,4,5,2′,4′,5′-hexachlorobiphenyl (PCB 153) per kg of body mass to mouse dams 2 weeks prior to mating. They then observed whole-body concentrations of PCB 153 in the dams and their fetuses at approximately 21 days after conception and in the dams and pups at 5, 10, 15, and 20 days after birth. In order to simulate the conditions of the study of Vodicnik and Lech (1980), we set the simulation parameters as follows:
the start of the simulation was t0 = −14 days because the bolus dose was administered approximately 2 weeks (ie, 14 days) prior to conception;
the initial amount of substance in the dam was Amf(t0) = (50 mg/kg) · (0.0255 kg) = 1.275 mg because the bolus dose was 50 mg/kg and the default initial mass for a mouse dam is kg;
the maternal dose rate was dm = 0 mg/kg/day because the administered dose was a bolus (1-time) dose;
the half-life was t1/2 = 38.5 days based on a Bayesian analysis (cf. Supplementary Material) of the data of Anderson et al. (1993), de Jongh et al. (1993), and Rignall et al. (2013) describing PCB 153 PKs in mice;
the duration of gestion was tgest = 21 days;
the end time for the simulation was tage = 41 days after conception because the last observation was at 20 days after birth; and
the duration of lactation was set to tlact = 20 days to coincide with the time at which the last pups were sacrificed.
Default values listed in Tables 1, 2, and 4 were used for all other parameters. We also ran simulations using half-lives of 24.4 and 51.6 days, as these were the lower and upper bounds for a 90% highest density credible interval for half-life determined in our half-life analysis (cf. Supplementary Material). The Supplementary File “pcb153_vodicnik1980_study2.R” contains a script that performs the model simulation and generates plots showing the concentration profiles.
To characterize uncertainty in our model predictions, we ran MC simulations using half-lives randomly selected from a sample generated via the previously mentioned Bayesian MCMC half-life analysis (cf. Supplementary Material). For the MC simulations, we also randomly selected values for the parameters Fm, Fmilk, and Rfm, which we determined to be influential in determining the values of the dose metrics we considered (cf. Sensitivity Analysis section). We sampled values for those parameters from normal distributions with mean values of 0.229, 0.264, and 0.35 (cf. Table 1), respectively, and standard deviations equal to 30% of the mean values. The Supplementary File “pcb153_vodicnik1980_study2_mc.R” contains a script that performs the MC model simulations and generates plots showing the concentration profiles.
For comparisons with the human PK model of Verner et al. (2013), we conducted simulations of human mothers exposed to HCB and PCB 153 and their offspring. Like our model, the Verner et al. (2013) model is not a physiologically based pharmacokinetic (PBPK) model, but a simpler PK model with one compartment for the maternal animal and another for the offspring. Both models assume that the substance is immediately and completely distributed into lipids and that elimination of the substance (via metabolism and excretion) can be estimated using a single biological half-life. In the Verner et al. (2013) model, all transfer of substance between mother and offspring occurs either in utero (via placental transfer) or through breast milk lipids (via breast feeding). This is also true of our model, though the 2 models describe in utero transfer differently.
Despite apparent similarities, there are several fundamental differences between our PK model and that of Verner et al. (2013). In many cases, we made different design choices in developing our model because of differences in our intended applications: Verner et al. (2013) focused on estimating bioaccumulation of LPECs in humans, but we designed our PK model for interspecies comparisons of LPEC bioaccumulation and for estimation of HEDs. In our model, there is a single compartment representing the entire body mass of the mother and fetus(es) during pregnancy and there are 2 distinct compartments representing the body of the mother and the body of one of the offspring after birth. In the Verner et al. (2013) model, on the other hand, there are 2 distinct compartments representing the body lipids of the mother and the body lipids of the offspring during pregnancy as well as after birth. Verner et al. (2013) parameterized their model for humans only, but our model can be used to simulate exposure scenarios for humans, rats, and mice (as well as any other animal species for which appropriate parameters can be determined). Our model has been parameterized for simulations that cover the period from the birth of the mother up through the end-of-life of the filial animal for all these species. Verner et al. (2013) were able to develop data-based models for body lipid mass versus time for human mothers, in utero offspring, and postnatal offspring, but we were unable to find data to develop comparable body lipid models for all laboratory animal species of interest. Therefore, we chose to use model compartments that represent the whole bodies of the mother (during pregnancy) or the mother and offspring (after birth of the offspring) rather than compartments that represent only body lipids. The model of Verner et al. (2013) accounts for changes in (human) maternal and child body lipid proportion and the lipid proportion of (human) milk over time, whereas we assumed these lipid proportions are constant (for all species). Furthermore, the model of Verner et al. (2013) accounts for changes in (human) infant milk consumption using an algebraic formula that depends on time, whereas we used a piecewise linear interpolation of data points describing “recommended values for human milk intake rates” reported in Table 15-1 of Chapter 15 of the U.S. EPA Exposure Factors Handbook (U.S. EPA, 2011a). The Verner et al. (2013) model describes the rate of in utero placental transfer as a first-order process, whereas we assumed that the ratio of the concentrations in the in utero fetus(es) and the pregnant mother is a constant (defined by a model parameter). Finally, Verner et al. (2013) assumed 100% absorption of an orally ingested substance, whereas we allow the fraction absorbed to be determined by a user-provided parameter (with a default value of 90%). For substance contained in breast milk, however, our model assumes 100% absorption (like the model of Verner et al. [2013]).
For comparisons with the Verner et al. (2013) model, we set the simulation parameters for our PK model as follows:
the start of maternal dosing was days (ie, 24.25 years before conception) because we assumed exposure of the human mother would begin at her birth and we assumed she would conceive at age 24.25 years;
the maternal dose rate was dm = 1 mg/kg/day; and
the half-life was t1/2 = 2190 days for HCB (To-Figueras et al., 2000; Verner et al., 2013) and t1/2 = 5256 days for PCB 153 (Ritter et al., 2011; Verner et al., 2013).
Default human values (as described in Model Parameters section) were used for all other parameters in our PK model. We conducted comparable simulations using the Verner et al. (2013) model by assuming the same dose rate, dosing start time, and half-lives, as well as the same fractional absorption rate (0.9) and prepregnancy body mass (62.7 kg). Furthermore, to ensure breast milk consumption rates comparable to the defaults used for our model (cf. Figure 6), we set parameters in the Verner et al. (2013) model to effect 3 months of exclusive breastfeeding followed by a gradual decline in the fraction of food intake attributed to breast milk until 12 months of age when performing simulations with that model. The Verner et al. (2013) model estimates concentrations in body lipids rather than whole-body concentrations, so appropriate conversions were made by accounting for body lipid proportions and total body masses used in that model. The Supplementary File “compare_verner2013.R” contains a script that performs model simulations and generates plots showing concentration profiles predicted by the present model and the Verner et al. (2013) model.
Sensitivity Analysis
To assess the relative influence of the various parameters on the output of the PK model, we computed local sensitivity indices. For this analysis, we conducted model simulations of the developmental rat study of Nakashima et al. (1997), the developmental mouse study of Vodicnik and Lech (1980), and a hypothetical exposure scenario in which a human mother receives a continuous dose of 1 mg of HCB per kg of body mass per day from the time she is born up until the weaning of her infant. We adjusted parameter values one at a time and examined the impact on the first 4 dose metrics described above. We did not consider dose metric 5 (the average concentration during the period from conception to observation) because it is equivalent to dose metric 2 (the average concentration during gestation and the nursing period) in the context of the 2 animal studies (because all pups were sacrificed before weaning) and the hypothetical human exposure scenario. The normalized local sensitivity index for each parameter for a given dose metric was computed as
| (10) |
where is a vector containing a “local” set of values for all model parameters, is the value of the dose metric for the parameter values in a vector , is the jth standard basis vector (with a 1 in the jth position and zeros elsewhere), is the local value of the jth parameter (ie, the jth component of the vector ), and hj is a “small” perturbation to the ith parameter. We computed the small perturbation as
where ϵ = 10−2.
The normalized local sensitivity index represents the ratio of the relative change in the dose metric to the relative change in a single parameter. We computed one sensitivity index per dose metric for each model parameter based on the local set of parameter values described for the model evaluation simulations. The sensitivity analysis algorithms can be found in the Supplementary Files “sensitivity_analysis_nakashima1997.R,” “sensitivity_analysis_vodicnik1980.R,” and “sensitivity_analysis_human.R.”
Human Equivalent Dose
To compute an HED for a particular animal study exposure scenario and a specified dose metric, one can first compute the value of the dose metric using the PK model and parameters that correspond to the animal species and the exposure scenario. Then, one can find the exposure dose (mg/kg/day) that would result in the same value of the dose metric when using the PK model parameters that correspond to humans that are exposed continuously.
In the context of our PK model, the HED is a continuous rate of exposure for the human mother (dm) and possibly also for the human infant (di). To demonstrate the overall process, we computed HEDs for the rodent (rat and mouse) dosing regimens described by Nakashima et al. (1997) and Vodicnik and Lech (1980). For the human simulations, we assumed maternal exposure (ie, nonzero values of dm) started at birth of the mother, which was assumed to occur 24.25 years before conception of the filial human. Because all pups were sacrificed before weaning in these studies, we assumed no direct dosing to infants (ie, no nonzero values of di) for the human simulations. In general, one could assume that direct dosing of human infants begins at weaning or at any other time after parturition. For the HED calculations for the Nakashima et al. (1997) and Vodicnik and Lech (1980) studies, we simulated dosing up until the mother was 26 years of age and the infant was 1 year of age, which is the weaning age for humans based on the default duration of breastfeeding (tlact = 365 days). HEDs were computed for the first 4 dose metrics described in the Dose Metrics section of the Materials and Methods.
To compute an HED for the rat HCB dosing regimen described by Nakashima et al. (1997), we used a half-life of 6 years (t1/2 = 2190 days) for HCB in humans (To-Figueras et al., 2000; Verner et al., 2013). To compute an HED for the mouse PCB 153 dosing regimen described by Vodicnik and Lech (1980), we used a half-life of 14.4 years (t1/2 = 5256 days) for PCB 153 in humans (Ritter et al., 2011; Verner et al., 2013). In each case, we calculated an HED that produces the same value of a given dose metric in humans as that estimated for the animals subjected to the relevant dosing regimen. Specifically, we used numerical optimization to find an HED that minimized the square of the difference between the human dose metric and the precomputed animal dose metric for the given animal study. The HED calculations are implemented in the Supplementary Files “hed_nakashima1997.R” and “hed_vodicnik1980.R.”
In order to provide a point of comparison for HEDs, we generated using our PK model, we also calculated an HED for the rat dose level and regimen of Nakashima et al. (1997) using an alternative dosimetry method based on allometric scaling (U.S. EPA, 2011b). We first converted the nominal dose applied to rat dams, 0.1 mg per kg of food, into a dose rate per unit of body mass using equation 9 (which describes food consumption rate as a function of body mass) with the dam body mass reported in the study, 0.247 kg. Next we accounted for PK differences between rats and humans by applying an allometric adjustment factor (Ma/Mh)1/4, where Ma and Mh are the representative body masses of the animal and human, respectively (U.S. EPA, 2011b). To calculate the adjustment factor, we again used 0.247 kg as the rat dam mass (Nakashima et al., 1997) and we used 75 kg as the mass of a pregnant human woman (based on Table 8-29 of Chapter 8 of the U.S. EPA Exposure Factors Handbook [U.S. EPA, 2011a]). We multiplied the rat continuous dose estimate by the PK adjustment factor to obtain an HED.
RESULTS
Model Evaluation
We used our PK model to simulate experiments of Nakashima et al. (1997) and Vodicnik and Lech (1980) and compared simulation results to data reported by those authors. We also compared simulation results generated using our model and the model of Verner et al. (2013) for hypothetical human exposures.
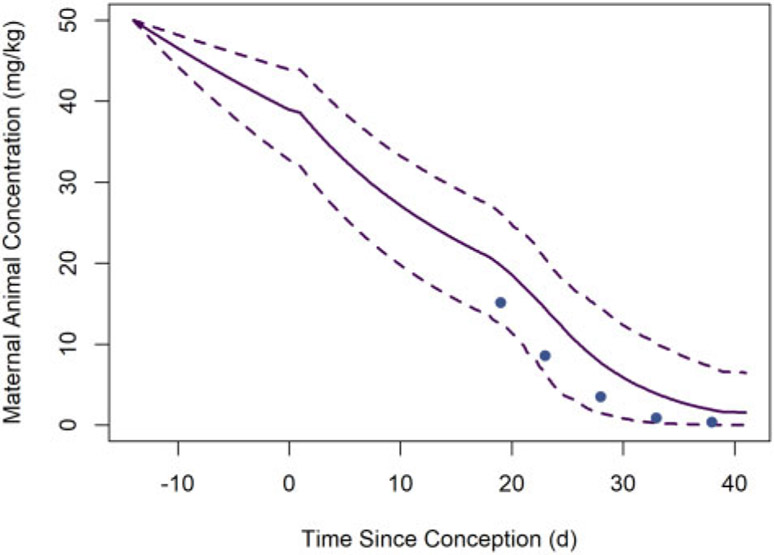
Figure 7 shows HCB concentrations in maternal animal (rat dam) tissues observed by Nakashima et al. (1997) and estimated whole-body HCB concentrations based on MC model simulations of that study design. The model-estimated whole-body concentrations fall within the range of the tissue concentration data at each of the 2 observation time points. Given the high lipid content of subcutaneous and perirenal fat tissues relative to the whole body, we expect HCB concentrations to be higher in these tissues than the average concentrations in the whole body; we also expect the whole-body concentrations to be greater than the observed concentrations blood, which has relatively low lipid content.
Figure 7.
Concentrations of HCB in maternal animal (rat dam) tissues observed by Nakashima et al. (1997) and estimated whole-body concentrations of HCB based on MC model simulations of that study. The solid line represents the median predicted concentrations from the MC simulations, whereas the dashed lines represent the lower and upper bounds of a 95% credible interval for the predicted concentrations. (Note that given the high lipid content of subcutaneous and perirenal fat tissues relative to the whole body, we expect HCB concentrations to be higher in these tissues than the average concentrations in the whole body; we also expect the whole-body concentrations to be greater than the observed concentrations blood, which has relatively low lipid content.)
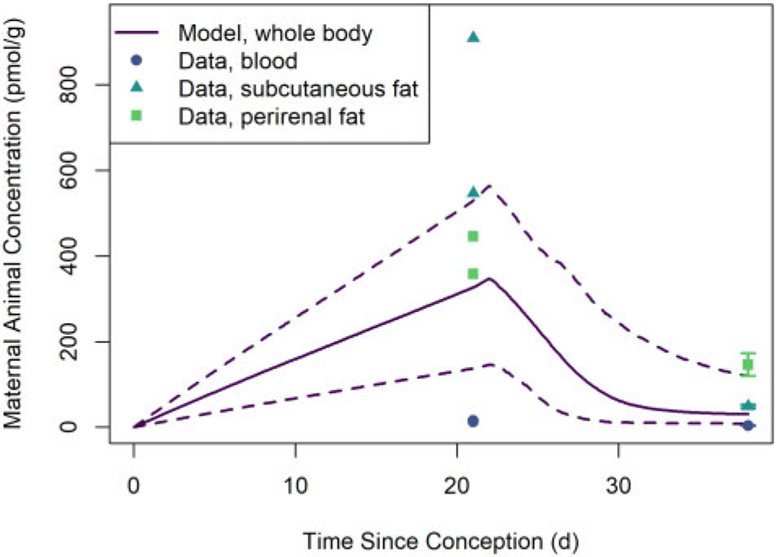
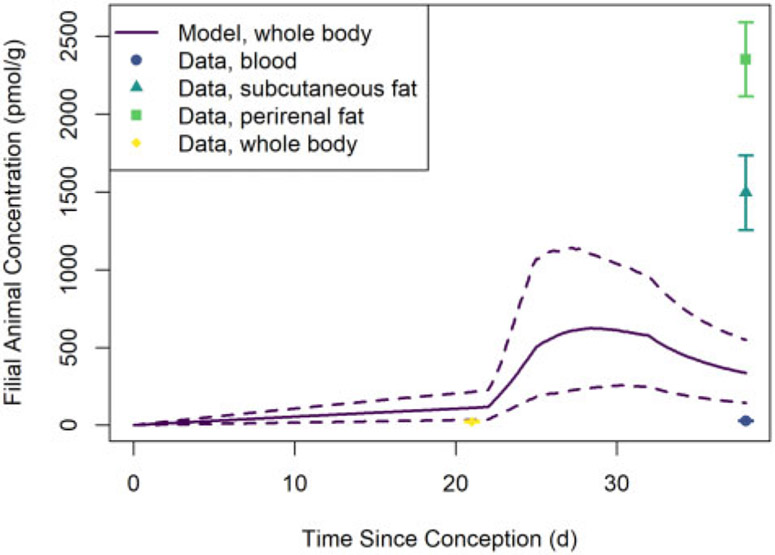
Figure 8 shows HCB concentrations in homogenized (whole) rat fetuses and rat pup tissues observed by Nakashima et al. (1997) and estimated whole-body HCB concentrations based on MC model simulations. The median model-estimated whole-body concentration one day before parturition (at gestation day 21) exceeds the observed whole-body concentration by a factor of about 5 (110.7 vs 22.72 nmol/kg), but the lower-bound 95% credible interval estimate is only about 51% larger than the observed concentration (34.31 vs 22.72 nmol/kg). The model-estimated whole-body concentration at 16 days after parturition falls within the range of observed tissue concentration data.
Figure 8.
Concentrations of HCB in filial animal (rat fetus and pup) whole body and tissues observed by Nakashima et al. (1997) and estimated whole-body concentrations of HCB based on MC model simulations of that study. The solid line represents the median predicted concentrations from the MC simulations, whereas the dashed lines represent the lower and upper bounds of a 95% credible interval for the predicted concentrations. (Note that given the high lipid content of subcutaneous and perirenal fat tissues relative to the whole body, we expect HCB concentrations to be higher in these tissues than the average concentration in the whole body; we also expect the whole-body concentrations to be greater than the observed concentrations for blood, which has relatively low lipid content.)
Figure 9 shows whole-body PCB 153 concentrations in maternal animals (mouse dams) observed by Vodicnik and Lech (1980) and estimated whole-body PCB 153 concentrations based on MC model simulations of that study design (described above). The central (median) estimate whole-body concentrations are all higher than the observed concentrations but they follow a similar trend. Percent differences between central estimates and observations are less than 135% at all observation times, and all observations fall within the 95% credible interval estimate bounds.
Figure 9.
Whole-body concentrations of PCB 153 in maternal animals (mouse dams) observed (solid circles) by Vodicnik and Lech (1980) and estimated (lines) based on MC model simulations of that study. The solid line represents the median predicted concentrations from the MC simulations, whereas the dashed lines represent the lower and upper bounds of a 95% credible interval for the predicted concentrations.
Figure 10 shows PCB 153 concentrations in homogenized (whole) mouse pups observed by Vodicnik and Lech (1980) and estimated whole-body PCB 153 concentrations. The central (median) estimate whole-body concentrations are all lower than the observed concentrations, but the percent differences between central estimates and observations are less than 60% at all observation times and 3 of the 4 observations fall within the 95% credible interval estimate bounds.
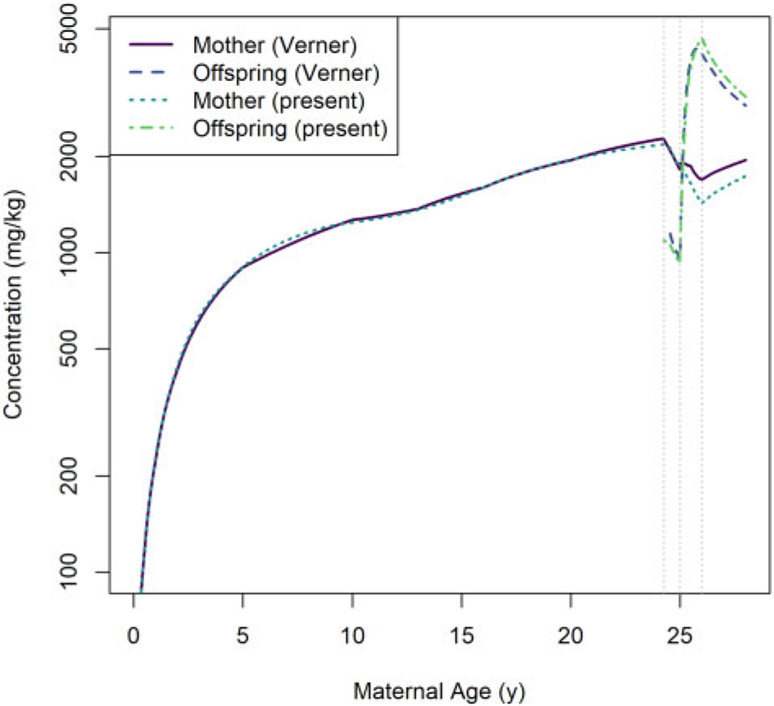
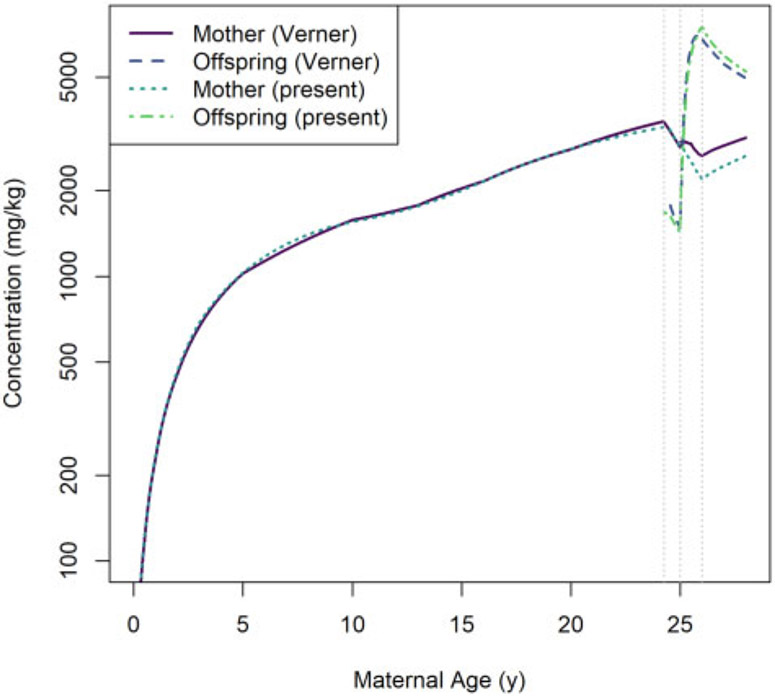
Comparisons of predictions generated using our model and the Verner et al. (2013) human PK model are shown in Figure 11 (for HCB simulations) and Figure 12 (for PCB 153 simulations). In general, the predictions of maternal concentrations differ by less than 19% and the predictions of offspring concentrations differ by less than 12%. We observed the largest disagreements in model predictions during the postnatal period, and these disagreements were most pronounced for maternal concentrations.
Figure 11.
Comparison of whole-body concentrations of HCB in a human mother and her offspring based on a 1 mg per kg of body mass per day dose as estimated using the Verner et al. (2013) model (“Verner”) and the present model (“present”). The vertical dotted lines indicate (from left to right) the times of conception, parturition, and weaning.
Figure 12.
Comparison of whole-body concentrations of PCB 153 in a human mother and her offspring based on a 1 mg per kg of body mass per day dose as estimated using the Verner et al. (2013) model (“Verner”) and the present model (“present”). The vertical dotted lines indicate (from left to right) the times of conception, parturition, and weaning.
In our human model, the birth event results in a decrease in the body mass of the mother that is greater than the mass of the infant (because other products of conception, such as placenta and amniotic fluid, are also lost at that time). As explained in the Model Equations section, we assumed that this lost body mass has the same LPEC concentration (mg per kg of body mass) as the rest of the mother and therefore that the lost body mass contains some LPEC substance, which is consistent with the findings of Vizcaino et al. (2014). In our human simulations, this results in an instantaneous loss of substance mass at the instant of birth while ensuring there is no discontinuity in the maternal concentration coinciding with this event. On the other hand, Verner et al. (2013) assumed that products of conception (other than the newborn infant) do not contain any LPEC substance. Thus, the whole-body concentration for the mother predicted by that model has a discontinuity (an instantaneous increase) at the instant of birth (even though the concentration in maternal body lipid does not). This conceptual difference between the 2 models explains, in part, the discrepancy in predicted concentrations following the birth of the offspring.
Sensitivity Analysis
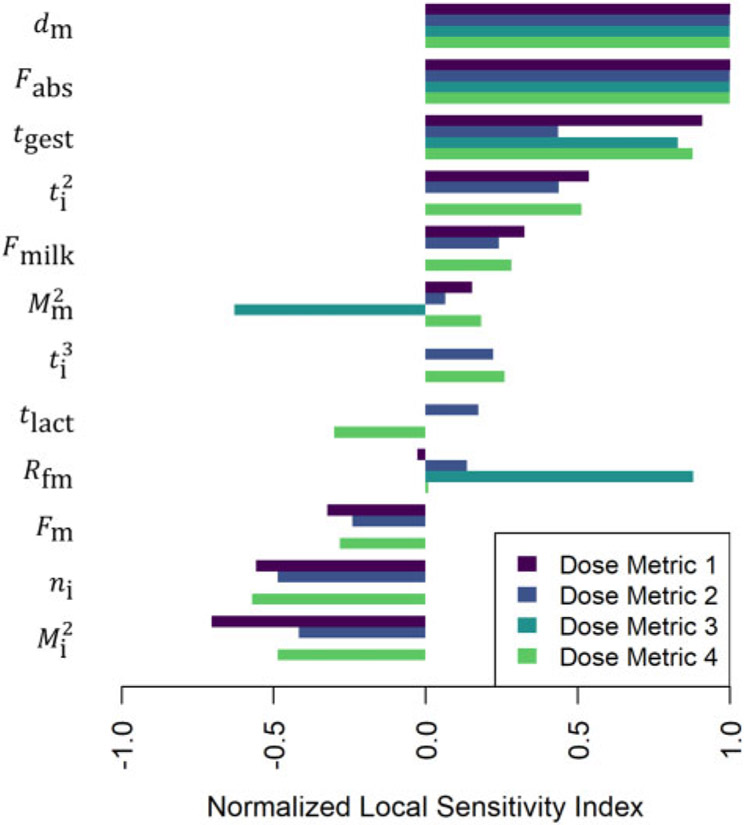
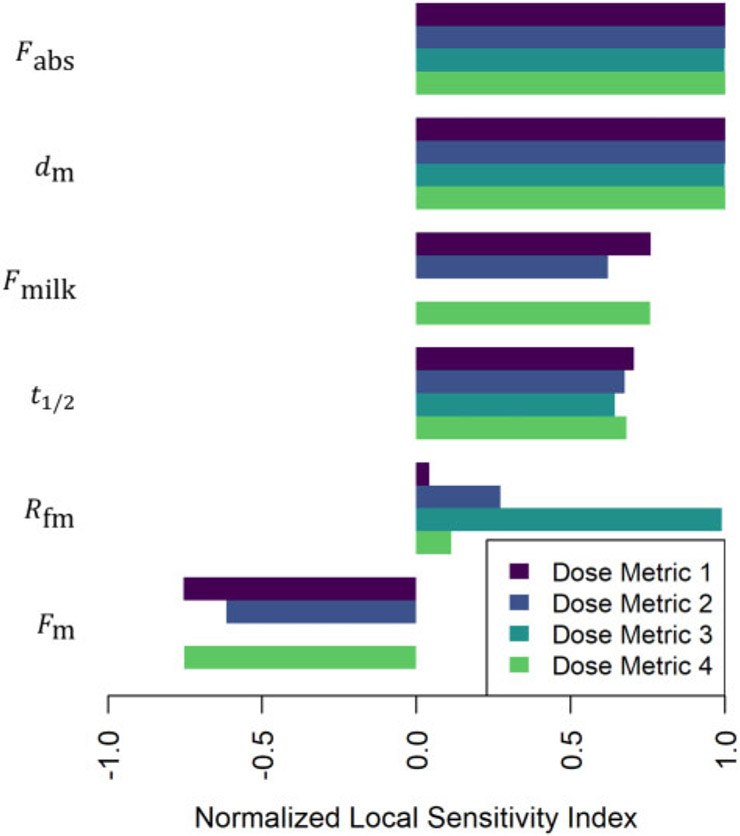
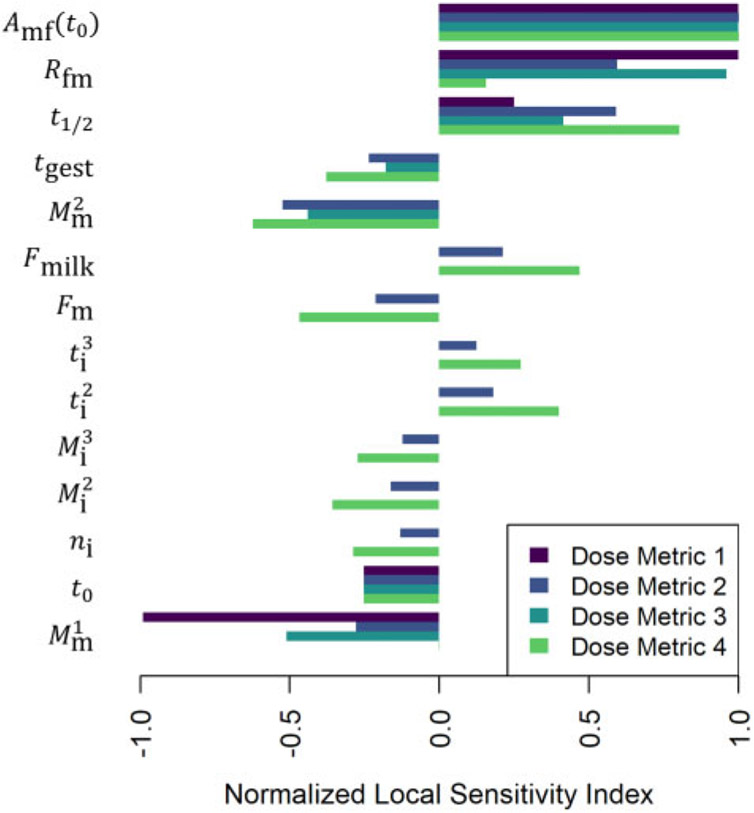
Figures 13-15 illustrate the relative magnitudes of the normalized sensitivity indices for 4 dose metrics: (1) the peak concentration during gestation and the nursing period; (2) the average concentration during gestation and the nursing period; (3) the average concentration during gestation; and (4) the average concentration during the nursing period. The first 2 figures show results for local sensitivity analyses based on the parameter values used for the simulations of the of Nakashima et al. (1997) and Vodicnik and Lech (1980) studies, respectively. The third figure shows sensitivity analysis results for a hypothetical human exposure scenario. In all 3 figures, we have only included those parameters for which at least one of the 4 sensitivity indices had an absolute value greater than 0.25. The values of the sensitivity indices for all parameters and all dose metrics can be found in the Supplementary Files “sens_nakashima1997.csv,” “sens_vodicnik1980.csv,” and “sens_human.csv.”
Figure 13.
Normalized sensitivity indices (cf. equation 10) for dose metric 1 (the peak concentration during gestation and the nursing period), dose metric 2 (the average concentration during gestation and the nursing period), dose metric 3 (the average concentration during gestation), and dose metric 4 (the average concentration during the nursing period). These indices represent the ratio of the relative change in the dose metric to the relative change in a single parameter (shown to the left of each group of bars). We computed one sensitivity index per dose metric for each model parameter based on the local set of parameter values described for the model simulation of the Nakashima et al. (1997) study.
Figure 15.
Normalized sensitivity indices (cf. equation 10) for dose metric 1 (the peak concentration during gestation and the nursing period), dose metric 2 (the average concentration during gestation and the nursing period), dose metric 3 (the average concentration during gestation), and dose metric 4 (the average concentration during the nursing period). These indices represent the ratio of the relative change in the dose metric to the relative change in a single parameter (shown to the left of each group of bars). We computed one sensitivity index per dose metric for each model parameter based on the local set of parameter values described for a hypothetical human exposure scenario involving continuous exposure to HCB.
For simulations of the Nakashima et al. (1997) study, which involved continuous food dosing of rat dams from conception until 16 days after birth of their pups, the maternal dose rate (dm) and dose absorption (Fabs) parameters were most influential for all dose metrics (cf. Figure 13) because these 2 parameters directly affect the amount of substance that enters the system (ie, the dam). Duration of gestation (tgest) was also influential for all dose metrics, though it was less influential for dose metric 2 (the average concentration in the pups during gestation and the nursing period), perhaps because the transfer of LPECs is greater during the nursing period than during the in utero period and so the contribution of the gestational component of that dose metric is relatively small. For dose metric 3 (the average concentration in the pups during gestation), the ratio of fetal concentration to maternal concentration (Rfm) also had relatively high influence. The second maternal mass parameter (), which impacts maternal body mass gain during pregnancy, had a relatively strong negative impact on dose metric 3. This makes sense because larger maternal body mass gain during pregnancy implies more dilution of the substance absorbed during pregnancy, and this leads to lower concentrations of the substance in both the dam and the pups during gestation. On the other hand, this same parameter (), had a relatively weak positive impact on the other dose metrics (1, 2, and 4). This makes sense because nursing (by an equivalent number of offspring of equivalent sizes) will deplete the total amount of substance in a larger dam less rapidly than would be the case for a smaller dam. Both the second offspring mass parameter () and the number of offspring parameter (ni) have a negative influence on the dose metrics that involve postnatal offspring concentrations (1, 2, and 4) because larger offspring bodies will dilute the substance to a greater extent and more nursing offspring will tend to deplete the amount in the mother available for lactational transfer more quickly.
In simulations of the Vodicnik and Lech (1980) study, which involved bolus intravenous dosing of mouse dams 14 days before they conceived, the initial bolus dose to the mother (Amf(t0)) was the most influential parameter (cf. Figure 14). The ratio of fetal concentration to maternal concentration (Rfm) also had relatively high influence for all dose metrics, because most of the mother-to-offspring transfer for this scenario occurred during gestation rather than during the nursing period. The first maternal mass parameter (), which impacts maternal body mass during pregnancy, had a relatively strong negative impact on all dose metrics that involve offspring concentrations during gestation (1, 2, and 3). That’s because the initial bolus dose (Amf (t0)) was assumed to be the same (based on a fixed maternal mass of 0.0255 kg) for local sensitivity analysis calculations for this parameter () and so greater body mass led to greater dilution of the administered dose. A larger value for the half-life parameter (t1/2) had a positive influence on all dose metrics because a longer half-life leads to slower elimination of the substance and therefore concentrations tend to remain higher in both the mother and the offspring.
Figure 14.
Normalized sensitivity indices (cf. equation 10) for dose metric 1 (the peak concentration during gestation and the nursing period), dose metric 2 (the average concentration during gestation and the nursing period), dose metric 3 (the average concentration during gestation), and dose metric 4 (the average concentration during the nursing period). These indices represent the ratio of the relative change in the dose metric to the relative change in a single parameter (shown to the left of each group of bars). We computed one sensitivity index per dose metric for each model parameter based on the local set of parameter values described for the model simulation of the Vodicnik and Lech (1980) study.
As illustrated through the sensitivity analysis for these 2 studies (Nakashima et al., 1997; Vodicnik and Lech, 1980), ranking of parameter influence depends on which dose metric one considers as well as the type of exposure scenario. Thus, we observed different rankings of parameters when considering 2 different dose metrics for the same exposure scenario (eg, when considering sensitivity indices for dose metric 1 versus dose metric 2 in the Nakashima et al. (1997) study. We also observed different rankings of parameters for the continuous oral dosing scenario (Nakashima et al., 1997) and the bolus dosing scenario (Vodicnik and Lech, 1980) for any one dose metric (eg, dose metric 1).
In addition to performing sensitivity analyses for simulations of animal studies, we computed sensitivity indices for model parameters for a human exposure scenario (cf. Figure 15). Our PK model has the same basic structure (cf. Figure 2) for any animal species (including humans), but for human simulations there were fewer model parameters for which we could easily calculate sensitivity indices. This is because the human model uses default time-varying functions for maternal and offspring body mass and breast milk consumption rates (Mm, Mi, and Rmilk, respectively) that are based on relatively large numbers of representative data points. Recall that for animal simulations, we also used time-varying functions to represent these quantities, but the underlying functions are based on relatively small numbers of representative data points for the animal species we considered. We saw that some body mass parameters (eg, , , , and ) were influential in the sensitivity analyses we conducted for simulations of animal studies (cf. Figs. 13 and 14), so we expect that the choice of the time-varying body mass functions used for human simulations should have a strong influence on human dose metrics even though we did not compute sensitivity indices for body masses of human mothers and offspring. For the human exposure scenario sensitivity analysis, we only computed sensitivity indices for parameters that do not vary with time. Among these, the parameters describing maternal dose rate (dm), fractional absorption of dose (Fabs), and elimination half-life (t1/2) were all influential for all dose metrics. The parameters describing the proportions of milk and maternal body that are lipid (Fmilk and Fm, respectively) were influential for dose metrics 1, 2, and 4, but not for dose metric 3. This makes sense because the 2 lipid proportion parameters only impact lactational transfer and dose metric 3 only incorporates information about fetal concentration during gestation (when no lactational transfer occurs). The parameter describing the ratio of fetal to maternal concentration (Rfm) was influential for dose metric 3 (the average concentration in the in utero human fetus during gestation) but less important for the other dose metrics, for which the dominant contributions come from the postnatal lactational transfer period.
Human Equivalent Dose Calculation
Table 5 shows the values of dose metrics 1 through 4 and the corresponding HEDs for the rat HCB dosing regimen described by Nakashima et al. (1997). Table 6 shows the values of dose metrics 1 through 4 and the corresponding HEDs for the mouse PCB 153 dosing regimen described by Vodicnik and Lech (1980). Corresponding dose metrics or HEDs for different studies can be compared more directly than the nominal doses applied in the studies—for example, the 0.1 mg per kg of food administered to rat dams during pregnancy and lactation (Nakashima et al., 1997) and a single bolus dose of 50 mg per kg of body mass applied to mouse dams 14 days before mating (Vodicnik and Lech, 1980). Of course, one would probably not compare these specific studies because they involved different chemicals, but this ex-rcise illustrates how one could compare doses applied at different nominal levels, on different schedules, and even in different animal species by converting them to comparable dose metrics or HEDs. Importantly, the example dose metrics we used reflect exposures experienced by in utero and early postnatal offspring (due to placental and/or lactational transfer) when doses are administered to maternal animals.
Table 5.
Dose Metric Values and Human Equivalent Doses (HEDs) for the Rat HCB Dosing Regimen Described by Nakashima et al. (1997)
| Dose Metric Index | Dose Metric Value (mg/kg) |
HED (mg/kg/day) |
|---|---|---|
| 1 | 0.186 | 3.97 × 10−5 |
| 2 | 0.070 | 2.91 × 10−5 |
| 3 | 0.018 | 1.73 × 10−5 |
| 4 | 0.142 | 4.13 × 10−5 |
The dose metrics are (1) the peak concentration during gestation and the nursing period, (2) the average concentration during gestation and the nursing period, (3) the average concentration during gestation, and (4) the average concentration during the nursing period.
Table 6.
Dose Metric Values and Human Equivalent Doses (HEDs) for the Mouse PCB 153 Dosing Regimen Described by Vodicnik and Lech (1980)
| Dose Metric Index | Dose Metric Value (mg/kg) |
HED (mg/kg/day) |
|---|---|---|
| 1 | 13.6 | 1.81 × 10−3 |
| 2 | 9.21 | 2.43 × 10−3 |
| 3 | 9.81 | 6.23 × 10−3 |
| 4 | 8.57 | 1.58 × 10−3 |
The dose metrics are (1) the peak concentration during gestation and the nursing period, (2) the average concentration during gestation and the nursing period, (3) the average concentration during gestation, and (4) the average concentration during the nursing period.
We computed an alternative HED for the animal dose level and regimen from the Nakashima et al. (1997) study using an allometric scaling method (U.S. EPA, 2011b). Using equation 9 and the dam body mass reported in the study, 0.247 kg, we converted the nominal food dose, 0.1 mg per kg of food, to a continuous daily dose estimate of 0.00870 mg/kg/day. Next, we calculated an interspecies PK adjustment factor of (0.247/75)1/4 = 0.240 (U.S. EPA, 2011b) based on body masses of the rat dam (Nakashima et al., 1997) and a pregnant woman (U.S. EPA, 2011a). Multiplying this factor by the rat continuous dose estimate results in an HED of approximately 2 × 10−3 mg/kg/day.
DISCUSSION
Model Evaluation and Comparison With Verner et al. (2013) PK Model
We evaluated our model using PK data from developmental studies of HCB in rats (Nakashima et al., 1997) and PCB 153 in mice (Vodicnik and Lech, 1980). Although the agreement between model predictions and observed data is reasonable given the limitations of the data and the relative simplicity of the model, additional studies that generate data for whole-body concentrations in rat or mouse dams, fetuses, and pups at multiple time points would allow for a more comprehensive evaluation of model prediction accuracy and precision.
Our model is similar to the PK model of Verner et al. (2013), but also has some key differences. Like the Verner et al. (2013) model, our model uses one compartment to represent the mother and another to represent the offspring, and it assumes that the substance of interest is immediately and completely distributed into lipids upon its introduction to the body. Also like the Verner et al. (2013) model, our model predicts elimination of the substance using a constant elimination half-life and assumes all transfer of substance between the mother and offspring occurs either in utero via placental transfer or during the postnatal period via excretion and consumption of breast milk. Our PK model differs from the human-only model described by Verner et al. (2013) in that it includes parameterizations for mice and rats (as well as humans) and it uses compartments that represent the whole bodies of mother and offspring rather than just “body lipids.” Also, although Verner et al. (2013) assumed 100% absorption of an orally ingested substance, our model allows the fraction absorbed to be specified as a parameter.
We compared simulation results generated using the Verner et al. (2013) PK model and our model and found that corresponding predictions of concentrations in mothers and offspring showed strong concordance (with less than 20% difference) during the period extending from the birth of the mother until 1 year after the birth of the infant for 2 different simulation studies involving 2 different LPECs (cf. Figs. 11 and 12). Verner et al. (2013) evaluated their model using human data from 2 observational studies involving women and infants that collectively considered the period from the birth of infants up until they reached 45 months of age (Hertz-Picciotto et al., 2003; Muckle et al., 2001). Correlation between predictions and concentrations ranged from relatively weak (with a coefficient of determination of R2 = 0.10) to relatively high (R2 = 0.83). The strong agreement between predictions generated using our model and the Verner et al. (2013) model (less than 20% difference) indicates that our model, whereas it does not generate estimates of concentrations in blood lipids that can be directly compared with the observations Verner et al. (2013) used to evaluate their model, should yield similar agreement with human data.
Applications of the PK Model and Implications for Chemical Risk Assessment
Our PK model can be used to estimate whole-body concentrations arising in offspring when a specific dose and dosing regimen are applied to a maternal animal. When analyzing dose-response relationships for developmental toxic effects, dose metrics based on concentrations in offspring may be preferable to measures of doses experienced by maternal animals. We defined 5 dose metrics relevant to developmental exposures and demonstrated how they can be calculated based on the details of a specific study design (cf. Tables 5 and 6 and supporting text), but our PK model could be used to calculate other dose metrics. For example, in the case of a toxic effect with a known “window of susceptibility,” one could use our model to calculate an average or peak concentration in the offspring during the specific time of interest.
Because our PK model has been parameterized for both humans and laboratory animal species, it can be used to com-ute HEDs for a selected dose metric. That is, if one determines (eg, through dose-response analysis) the value of a specific dose metric associated with a toxicity point of departure in an animal study, our PK model can be used to estimate the dose that would be expected to produce the same value of the internal dose metric in humans (ie, the HED). Such HEDs can be used to establish reference values for human health risk assessments for potentially toxic substances. HEDs and internal dose metrics can also serve as useful points of comparison when attempting to evaluate many different studies involving different animal species, different dosing regimens, and different routes of exposure or dose administration.
We used an allometric scaling approach (U.S. EPA, 2011b) to compute an HED for the rat dam dose level and regimen from the Nakashima et al. (1997) study. The HED we obtained using this alternative method, 2 × 10−3 mg/kg/day, is considerably larger (and thus would potentially be less health protective) than the HEDs we calculated for dose metrics 1 through 4 for the Nakashima et al. (1997) study, which were all on the order of 10−5 mg/kg/day (cf. Table 5). Kieskamp et al. (2018) observed similar results when comparing HEDs for developmental toxicity endpoints using PK modeling-based dosimetry and allometric dosimetry based on adult doses. Thus, using our PK model to es-imate mother-to-offspring transfer and dosimetry of LPECs could have substantial impacts on reference values calculated for chemical risk assessments.
Assumptions and Limitations of the PK Model
In developing our PK model, we made several assumptions that allow for relatively simple mathematical descriptions of the PK behavior of LPECs in maternal animals and their offspring. For example, we assumed that the elimination rate (for mothers and offspring) can be described by a single constant parameter for any given LPEC. We also assumed that the lipid proportion of the maternal body, the lipid proportion of the milk, and the ratio of fetal to maternal concentrations can each be described by a single constant parameter.
We assumed that a constant half-life (t1/2) describes elimination of a specific LPEC in any animal of a given species, including adults and very young animals (even fetuses). For exogenous substances in general, elimination half-lives can be very different in younger and older animals due to the ontogeny of metabolizing enzymes (Hines, 2008) and life stage differences in the volume and rate of blood flow to the liver (ICRP, 2002; Kapraun et al., 2019; Kim et al., 2015), which is a primary site of metabolism (Yang, 2021). However, Lehmann et al. (2014) observed that a relatively simple human PK model for LPECs that estimates elimination based on a single constant half-life for mothers and infants (Verner et al., 2013) performed comparably to a more complex human PBPK model for LPECs (Verner et al., 2009) when both models were evaluated using the same data. Estimating elimination rates using a single half-life may work well for certain classes of LPECs, but the validity of the single half-life assumption should be carefully considered when deciding whether to apply our PK model for dosimetry predictions for a particular substance. Even after accepting assumptions about the elimination half-life, it may be difficult to determine an appropriate value. Because the half-life can have a strong influence on model-predicted dose metrics (cf. Figs. 14 and 15), it may be informative to consider a range of values for this parameter (eg, based on a confidence or credible interval estimate) when applying our PK model.
In developing our model, we assumed that the lipid proportion of the maternal body and the lipid proportion of milk (Fm and Fmilk, respectively) are both constants. These 2 parameters can influence dose metrics that reflect postnatal concentrations in offspring (cf. Figs. 13-15), so modifying the model to reflect variations in lipid proportions with respect to time could have a substantial impact on model predictions. However, we note that the Verner et al. (2013) model uses time-varying functions to represent these lipid proportions and that the concentrations predicted by that model and our model nevertheless tend to be very similar (cf. Figs. 11 and 12). Furthermore, as described in the Model Evaluation section, the most substantial differences in concentrations predicted using the 2 models (which occur just after birth of the offspring) can be explained by differences in the way the 2 models describe the birth event.
Our model estimates the time-course concentration of a LPEC in a fetus (in utero) by assuming that the ratio of the fetal concentration to the maternal concentration (ie, the model parameter Rfm) is constant. In developing the model, we assumed that the body lipid fractions for a maternal animal and in utero fetus(es) remain constant (even during the rapid overall growth of their bodies that occurs during pregnancy and gestation) and that LPECs immediately and completely distribute into lipids when they enter an animal. The constant ratio of fetal-to-maternal concentrations follows from these 2 more fundamental assumptions. Our sensitivity analysis indicated that this ratio parameter (Rfm) is influential for the dose metrics we considered, so validity of the constant ratio assumption should be scrutinized. The collection and publication of more robust time-course concentration data for maternal animals dosed with LPECs and their fetuses (involving paired observations at multiple time points during pregnancy) would allow for better evaluation of this assumption.
Because our PK model does not include parameters describing organ volumes and various other anatomical, physiological, and biochemical quantities that could impact the amounts and concentrations of the chemical in various organs and tissues, it cannot predict such distribution. Furthermore, our model does not account for complex changes in distribution that might result from changes in organ volumes and other parameters during pregnancy and other life stages. Nevertheless, the total amount of chemical in the body at any given point in time, which our model does predict, will be the same regardless of distribution (ie, regardless of where in the body the chemical resides). Although we recognize that elimination rate can be impacted by distribution (because overall elimination may depend strongly on chemical concentrations in blood or metabolizing organs or tissues), our objective was to develop and evaluate a relatively simple PK model for mother-to-offspring transfer that only requires one chemical- and animal-specific parameter: a constant half-life describing elimination of the chemical in an animal of interest. To investigate the impacts of changes in body composition and physiology on elimination and dose metrics, one would need to develop a PBPK model (or obtain a previously developed one) that explicitly accounts for such changes.
Although PBPK models are generally preferred over classical compartmental PK models for dosimetry calculations in risk assessment contexts (IPCS, 2010; U.S. EPA, 2006), these more complex models are not available for all LPECs. Even when PBPK models are available for a given LPEC, they may not describe mother-to-offspring transfer or they may not have been parameterized for all animal species of interest (thus limiting their potential use for interspecies dose extrapolation). For example, published PBPK models for PCB 153 (Dzierlenga et al., 2019; Redding et al., 2008; Ulaszewska et al., 2012) and HCB (Lu et al., 2006) exist, but to the best of our knowledge none of the PBPK models for these chemicals describes mother-to-offspring transfer for more than one animal species. In a workshop coordinated by the U.S. Environmental Protection Agency (EPA), a group of scientists with expertise in toxicology, risk assessment, epidemiology, PK modeling, and public health concluded that simpler (eg, classical PK modeling) approaches could be adequate for risk assessment involving lactational transfer of LPECs (ICF, 2013). Furthermore, Farrer et al. (2010) found that estimates of infant lactational doses generated using a relatively simple one-compartment PK model for PCB 153 were comparable to those generated using a more complex PBPK model and that the simpler model was “sufficiently health-protective [for] use in chemical risk assessment.” The conclusions of ICF (2013) and Farrer et al. (2010) and the need for risk assessment methods that quantify mother-to-offspring transfer of LPECs (Lehmann et al., 2014) motivated our development of a generic, multispecies PK model.
Despite its limitations, our PK model for mother-to-offspring transfer of LPECs allows for the calculation of offspring-focused dose metrics based on dosing regimens applied in developmental toxicity studies in laboratory animals. Furthermore, it can be used to calculate HEDs for points of departure identified in such studies. Because the model derives from the fundamental principle of conservation of mass, the impact of uncertainty in the model parameters on errors in model predictions is limited. For example, although there may be uncertainty in the mass of LPEC transferred to the offspring, we know that such transfer reduces the mass of LPEC in the mother by an equal amount. In assessing risks of developmental toxicity for a particular substance and a particular toxicity endpoint, scientists and risk managers must determine whether the assumptions and limitations of this PK model are reasonable and acceptable, but once this determination has been made, the model provides an alternative to allometric scaling methods for computing HEDs that are based only on doses applied to maternal animals.
CONCLUSION
We developed a generic PK model that quantifies the transfer of LPECs from a maternal animal to her offspring during gestation and lactation and parameterized the model for rats, mice, and humans. After comparing our model’s predictions to available PK data for rats (Nakashima et al., 1997) and mice (Vodicnik and Lech, 1980) as well as comparable predictions from a previously published and evaluated human PK model (Verner et al., 2013), we demonstrated how it can be used to calculate dose metrics for offspring based on external (eg, oral) doses experienced by the mother. These offspring dose metrics may be useful for conducting dose-response analyses for developmental toxicity endpoints, as offspring dose metrics may be more directly associated with developmental toxicity than doses applied to maternal animals. The model also provides an alternative to methods for computing HEDs based on allometric scaling of doses of LPECs applied to maternal animals, and we showed that HEDs predicted using our model can be 2 orders of magnitude lower than those generated using such allometric dosimetry calculations. Thus, our LPEC mother-to-offspring transfer PK model may serve as useful tool for scientists assessing developmental toxicity risks associated with LPECs.
Supplementary Material
ACKNOWLEDGMENTS
The authors are grateful to Krista Christensen and Hisham El-Masri for their careful review of an early draft of this manuscript. Also, the authors thank the Toxicological Sciences editors and anonymous peer reviewers, whose comments and suggestions significantly enhanced the final version of this manuscript.
FUNDING
M.-A.V. is the recipient of a Research Scholar J2 Award from the Fonds de Recherche du Québec—Santé (FRQS).
Footnotes
This work is written by US Government employees and is in the public domain in the US.
DECLARATION OF CONFLICTING INTERESTS
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
SUPPLEMENTARY DATA
Supplementary data are available at Toxicological Sciences online.
Disclaimer: The views expressed in this manuscript are those of the authors and do not necessarily represent the views or policies of the U.S. Environmental Protection Agency.
DATA AVAILABILITY
Supplemental source code and data files are available through the U.S. Environmental Protection Agency’s Environmental Dataset Gateway (https://doi.org/10.23719/1524467).
REFERENCES
- Abdallah MA, and Harrad S (2018). Dermal contact with furniture fabrics is a significant pathway of human exposure to brominated flame retardants. Environ. Int 118, 26–33. [DOI] [PubMed] [Google Scholar]
- Al Jothery AH, Król E, Hawkins J, Chetoui A, Saint-Lambert A, Gamo Y, Shaw SC, Valencak T, Bünger L, Hill WG, et al. (2014). Limits to sustained energy intake. Xxii. Reproductive performance of two selected mouse lines with different thermal conductance. J. Exp. Biol 217, 3718–3732. [DOI] [PubMed] [Google Scholar]
- Ampleman MD, Martinez A, Dewall J, Rawn DF, Hornbuckle KC, and Thorne PS (2015). Inhalation and dietary exposure to PCBS in urban and rural cohorts via congener-specific measurements. Environ. Sci. Technol 49, 1156–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson LM, Fox SD, Riggs CW, and Issaq HJ (1993). Selective retention of polychlorinated biphenyl congeners in lung and liver after single-dose exposure of infant mice to Aroclor 1254. J. Environ. Pathol. Toxicol. Oncol 12, 3–16. [PubMed] [Google Scholar]
- Ando M (1978). Transfer of 2,4,5,2′,4′,5′-hexachlorobiphenyl and 2,2-bis-(p-chlorophenyl),1,1,1-trichloroethane (p,p’-DDT) from maternal to newborn and suckling rats. Arch. Toxicol 41, 179–186. [DOI] [PubMed] [Google Scholar]
- Arcus-Arth A, Krowech G, and Zeise L (2005). Breast milk and lipid intake distributions for assessing cumulative exposure and risk. J. Expo. Anal. Environ. Epidemiol 15, 357–365. [DOI] [PubMed] [Google Scholar]
- ATSDR. (2015). Toxicological Profile for Hexachlorobenzene. Agency for Toxic Substances and Disease Registry (ATSDR), U.S. Department of Health and Human Services, Atlanta, GA. [PubMed] [Google Scholar]
- Bois FY (2009). GNU MCSim: Bayesian statistical inference for SBML-coded systems biology models. Bioinformatics 25, 1453–1454. [DOI] [PubMed] [Google Scholar]
- Borrud LG, Flegal KM, Looker AC, Everhart JE, Harris TB, and Shepherd JA (2010). Body Composition Data for Individuals 8 Years of Age and Older: U.S. Population, 1999–2004. National Center for Health Statistics, Hyattsville, MD. Vital and Health Statistics: Series 11, No. 250. [PMC free article] [PubMed] [Google Scholar]
- Carmichael S, Abrams B, and Selvin S (1997). The pattern of maternal weight gain in women with good pregnancy outcomes. Am.J. Public Health 87, 1984–1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chahoud I, and Paumgartten FJ (2009). Influence of litter size on the postnatal growth of rat pups: Is there a rationale for litter-size standardization in toxicity studies? Environ. Res 109, 1021–1027. [DOI] [PubMed] [Google Scholar]
- Clewell RA, and Clewell HJ (2008). Development and specification of physiologically based pharmacokinetic models for use in risk assessment. Regul. Toxicol. Pharmacol 50, 129–143. [DOI] [PubMed] [Google Scholar]
- Daley JM, Paterson G, and Drouillard K (2014). Bioamplification as a bioaccumulation mechanism for persistent organic pollutants (pops) in wildlife. Rev. Environ. Contam. Toxicol 227, 107–155. [DOI] [PubMed] [Google Scholar]
- de Jongh J, Wondergem F, Seinen W, and Van den Berg M (1993). Toxicokinetic interactions between chlorinated aromatic hydrocarbons in the liver of the c57bl/6j mouse: I. Polychlorinated biphenyls (PCBS). Arch. Toxicol 67, 453–460. [DOI] [PubMed] [Google Scholar]
- Deans HE, Smith FW, Lloyd DJ, Law AN, and Sutherland HW (1989). Fetal fat measurement by magnetic resonance imaging. Br. J. Radiol 62, 603–607. [DOI] [PubMed] [Google Scholar]
- Dewey KG, Heinig MJ, and Nommsen LA (1993). Maternal weight-loss patterns during prolonged lactation. Am. J. Clin. Nutr 58, 162–166. [DOI] [PubMed] [Google Scholar]
- Di Guardo A, Raspa G, Terzaghi E, Vergani L, Mapelli F, Borin S, Zanardini E, Morosini C, Anelli S, Nastasio P, et al. (2020). PCB vertical and horizontal movement in agricultural soils of a highly contaminated site: Role of soil properties, cultivation history and PCB physico-chemical parameters. Sci. Total Environ 747, 141477. [DOI] [PubMed] [Google Scholar]
- Duttagupta S, Mukherjee A, Bhattacharya A, and Bhattacharya J (2020). Wide exposure of persistent organic pollutants (PoPS) in natural waters and sediments of the densely populated Western Bengal basin, India. Sci Total Environ. 717, 137187. [DOI] [PubMed] [Google Scholar]
- Dzierlenga MW, Yoon M, Wania F, Ward PL, Armitage JM, Wood SA, Clewell HJ, and Longnecker MP (2019). Quantitative bias analysis of the association of type 2 diabetes mellitus with 2,2′,4,4′,5,5′-hexachlorobiphenyl (PCB-153). Environ. Int 125, 291–299. [DOI] [PubMed] [Google Scholar]
- El-Shahawi MS, Hamza A, Bashammakh AS, and Al-Saggaf WT (2010). An overview on the accumulation, distribution, transformations, toxicity and analytical methods for the monitoring of persistent organic pollutants. Talanta 80, 1587–1597. [DOI] [PubMed] [Google Scholar]
- Emond C, Devito M, Warner M, Eskenazi B, Mocarelli P, and Birnbaum LS (2016). An assessment of dioxin exposure across gestation and lactation using a PBPK model and new data from Seveso. Environ. Int 92–93, 23–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farrer D, Poulsen M, Davoli D, Bailey M, Moffett D, Fowler D, Welsh C, Ayotte P, Verner MA, Muckle G, et al. (2010). Comparison of estimated PCB-153 concentrations in human milk using various pharmacokinetic models [poster]. Society of Toxicology Annual Meeting, Salt Lake City, UT. Archived material available at: https://hero.epa.gov/hero/index.cfm/reference/details/reference_id/1464648. [Google Scholar]
- Fromme H, Becher G, Hilger B, and Völkel W (2016). Brominated flame retardants: Exposure and risk assessment for the general population. Int. J. Hyg. Environ. Health 219, 1–23. [DOI] [PubMed] [Google Scholar]
- Gentry PR, Covington TR, and Clewell HJ III. (2003). Evaluation of the potential impact of pharmacokinetic differences on tissue dosimetry in offspring during pregnancy and lactation. Regul. Toxicol. Pharmacol 38, 1–16. [DOI] [PubMed] [Google Scholar]
- Geyer HJ, Schramm KW, Feicht EA, Behechti A, Steinberg C, Bruggemann R, Poiger H, Henkelmann B, and Kettrup A (2002). Half-lives of tetra-, penta-, hexa-, hepta-, and octachlorodibenzo-p-dioxin in rats, monkeys, and humans-a critical review. Chemosphere 48, 631–644. [DOI] [PubMed] [Google Scholar]
- Han D, and Currell MJ (2017). Persistent organic pollutants in China’s surface water systems. Sci. Total Environ 580, 602–625. [DOI] [PubMed] [Google Scholar]
- Hertz-Picciotto I, Trnovec T, Kocan A, Charles MJ, Ciznar P, Langer P, Sovcikova E, and James R (2003). PCBS and early childhood development in Slovakia: Study design and background. Fresen. Environ. Bull 12, 208–214. [Google Scholar]
- Hines RN (2008). The ontogeny of drug metabolism enzymes and implications for adverse drug events. Pharmacol. Ther 118, 250–267. [DOI] [PubMed] [Google Scholar]
- Huetos O, Bartolomé M, Aragonés N, Cervantes-Amat M, Esteban M, Ruiz-Moraga M, Pérez-Gómez B, Calvo E, Vila M, and Bioambient E (2014). Serum PCB levels in a representative sample of the Spanish adult population: The bioambient.Es project. Sci. Total Environ 493, 834–844. [DOI] [PubMed] [Google Scholar]
- Iakovides M, Iakovides G, and Stephanou EG (2021). Atmospheric particle-bound polycyclic aromatic hydrocarbons, n-alkanes, hopanes, steranes and trace metals: PM2.5 source identification, individual and cumulative multi-pathway lifetime cancer risk assessment in the urban environment. Sci. Total Environ 752, 141834. [DOI] [PubMed] [Google Scholar]
- ICF. (2013). Improving the Risk Assessment of Persistent, Bioaccumulative, and Toxic Chemicals in Breast Milk: Workshop Summary Report. U.S. Environmental Protection Agency, Washington, DC. EPA Contract No. EP-C-09-009, Work Assignment 2-62, 3-62, and 4–62. [Google Scholar]
- ICRP. (2002). Basic Anatomical and Physiological Data for Use in Radiological Protection: Reference Values . Pergamon Press, New York, NY. ICRP Publication No. 89. [Google Scholar]
- IPCS. (2010). Characterization and application of physiologically based pharmacokinetic models in risk assessment. Harmonization Project Document No. 9. International Programme on Chemical Safety (IPCS), World Health Organization, Geneva, Switzerland. [Google Scholar]
- Johnson MS, Thomson SC, and Speakman JR (2001). Limits to sustained energy intake. I. Lactation in the laboratory mouse Mus musculus. J. Exp. Biol 204, 1925–1935. [DOI] [PubMed] [Google Scholar]
- Jukic AM, Baird DD, Weinberg CR, McConnaughey DR, and Wilcox AJ (2013). Length of human pregnancy and contributors to its natural variation. Hum. Reprod 28, 2848–2855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kapraun DF, Wambaugh JF, Setzer RW, and Judson RS (2019). Empirical models for anatomical and physiological changes in a human mother and fetus during pregnancy and gestation. PLoS One. 14, e0215906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kieskamp KK, Worley RR, McLanahan ED, and Verner MA (2018). Incorporation of fetal and child PFOA dosimetry in the derivation of health-based toxicity values. Environ. Int 111, 260–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim IH, Kisseleva T, and Brenner DA (2015). Aging and liver disease. Curr. Opin. Gastroenterol 31, 184–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koss G, Seubert S, Seubert A, Seidel J, Koransky W, and Ippen H (1983). Studies on the toxicology of hexachlorobenzene. V. Different phases of porphyria during and after treatment. Arch. Toxicol 52, 13–22. [DOI] [PubMed] [Google Scholar]
- Kuczmarski RJ, Ogden CL, Guo SS, Grummer-Strawn LM, Flegal KM, Mei Z, Wei R, Curtin LR, Roche AF, and Johnson CL (2002). 2000 CDC Growth Charts for the United States: Methods and Development. National Center for Health Statistics, Hyattsville, MD. Vital and Health Statistics: Series 11, No. 246. [PubMed] [Google Scholar]
- Lee SK, Ou YC, Andersen ME, and Yang RSH (2007). A physiologically based pharmacokinetic model for lactational transfer of PCB 153 with or without PCB 126 in mice. Arch. Toxicol 81, 101–111. [DOI] [PubMed] [Google Scholar]
- Lehmann GM, Christensen K, Maddaloni M, and Phillips LJ (2015). Evaluating health risks from inhaled polychlorinated biphenyls: Research needs for addressing uncertainty. Environ. Health Perspect 123, 109–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann GM, Verner MA, Luukinen B, Henning C, Assimon SA, Lakind JS, McLanahan ED, Phillips LJ, Davis MH, Powers CM, et al. (2014). Improving the risk assessment of lipophilic persistent environmental chemicals in breast milk. Crit. Rev. Toxicol 44, 600–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerch S, Guidou C, Thomé JP, and Jurjanz S (2016). Non-dioxin-like polychlorinated biphenyls (PCBS) and chlordecone release from adipose tissue to blood in response to body fat mobilization in ewe (Ovis aries). J. Agric. Food Chem 64, 1212–1220. [DOI] [PubMed] [Google Scholar]
- Liem AKD, and Theelen RMC (1997). Dioxins: Chemical Analysis, Exposure and Risk Assessment. Utrecht University, Utrecht, Netherlands. [Google Scholar]
- Lu Y, Lohitnavy M, Reddy MB, Lohitnavy O, Ashley A, and Yang RS (2006). An updated physiologically based pharmacokinetic model for hexachlorobenzene: Incorporation of pathophysiological states following partial hepatectomy and hexachlorobenzene treatment. Toxicol. Sci 91, 29–41. [DOI] [PubMed] [Google Scholar]
- Maruyama W, Yoshida K, Tanaka T, and Nakanishi J (2003). Simulation of dioxin accumulation in human tissues and analysis of reproductive risk. Chemosphere 53, 301–313. [DOI] [PubMed] [Google Scholar]
- McLachlan MS (1993). Digestive tract absorption of polychlorinated dibenzo-p-dioxins, dibenzofurans, and biphenyls in a nursing infant. Toxicol. Appl. Pharmacol 123, 68–72. [DOI] [PubMed] [Google Scholar]
- Muckle G, Ayotte P, Dewailly É, Jacobson SW, and Jacobson JL (2001). Prenatal exposure of the northern Québec Inuit infants to environmental contaminants. Environ. Health Perspect 109, 1291–1299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakashima Y, Ohsawa S, Umegaki K, and Ikegami S (1997). Hexachlorobenzene accumulated by dams during pregnancy is transferred to suckling rats during early lactation. J. Nutr 127, 648–654. [DOI] [PubMed] [Google Scholar]
- Neto Angéloco LR, Deminice R, Leme IdA., Lataro RC, and Jordão AA (2012). Bioelectrical impedance analysis and anthropometry for the determination of body composition in rats: Effects of high-fat and high-sucrose diets. Rev. Nutr 25, 331–339. [Google Scholar]
- Nicholas KR, and Hartmann PE (1991). Milk secretion in the rat: Progressive changes in milk-composition during lactation and weaning and the effect of diet. Comp. Biochem. Physiol. A Comp. Physiol 98, 535–542. [DOI] [PubMed] [Google Scholar]
- Nickerson K (2006). Environmental contaminants in breast milk. J. Midwifery Womens Health 51, 26–34. [DOI] [PubMed] [Google Scholar]
- Pius C, Koosaletse-Mswela P, Sichilongo K, and Dikinya O (2020). Mapping polychlorinated dibenzo-p-dioxins/dibenzofurans in soils around Pugu municipal dump site in Dar es Salaam, Tanzania: Implications on dermal and soil ingestion exposure for people in the peripheral. Environ. Pollut 258, 113665. [DOI] [PubMed] [Google Scholar]
- Portier K, Tolson JK, and Roberts SM (2007). Body weight distributions for risk assessment. Risk Anal. 27, 11–26. [DOI] [PubMed] [Google Scholar]
- R Core Team. (2020). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
- Redding LE, Sohn MD, McKone TE, Chen JW, Wang SL, Hsieh DPH, and Yang RSH (2008). Population physiologically based pharmacokinetic modeling for the human lactational transfer of PCB-153 with consideration of worldwide human biomonitoring results. Environ. Health Perspect 116, 1629–1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed DR, Bachmanov AA, and Tordoff MG (2007). Forty mouse strain survey of body composition. Physiol. Behav 91, 593–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rignall B, Grote K, Gavrilov A, Weimer M, Kopp-Schneider A, Krause E, Appel KE, Buchmann A, Robertson LW, Lehmler H-J, et al. (2013). Biological and tumor-promoting effects of dioxin-like and non-dioxin-like polychlorinated biphenyls in mouse liver after single or combined treatment. Toxicol. Sci 133, 29–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritter R, Scheringer M, Macleod M, Moeckel C, Jones KC, and Hungerbühler K (2011). Intrinsic human elimination half-lives of polychlorinated biphenyls derived from the temporal evolution of cross-sectional biomonitoring data from the united kingdom. Environ. Health Perspect 119, 225–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohatgi A (2021). Webplotdigitizer, Version 4.5. Pacifica, CA. Available at: https://automeris.io/WebPlotDigitizer/. [Google Scholar]
- Stigum H, Iszatt N, Polder A, Mandal S, and Eggesbo M (2015). A novel model to characterize postnatal exposure to lipophilic environmental toxicants and application in the study of hexachlorobenzene and infant growth. Environ. Int 85, 156–162. [DOI] [PubMed] [Google Scholar]
- Terzaghi E, Zanardini E, Morosini C, Raspa G, Borin S, Mapelli F, Vergani L, and Di Guardo A (2018). Rhizoremediation half-lives of PCBS: Role of congener composition, organic carbon forms, bioavailability, microbial activity, plant species and soil conditions, on the prediction of fate and persistence in soil. Sci. Total Environ 612, 544–560. [DOI] [PubMed] [Google Scholar]
- Thorsdottir I, and Birgisdottir BE (1998). Different weight gain in women of normal weight before pregnancy: Postpartum weight and birth weight. Obstet. Gynecol 92, 377–383. [DOI] [PubMed] [Google Scholar]
- To-Figueras J, Barrot C, Sala M, Otero R, Silva M, Ozalla MD, Herrero C, Corbella J, Grimalt J, and Sunyer J (2000). Excretion of hexachlorobenzene and metabolites in feces in a highly exposed human population. Environ. Health Perspect 108, 595–598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trapp SM, Bomholtz L, and Legind CN (2008). Coupled mother-child model for bioaccumulation of pops in nursing infants. Environ. Pollut 156, 90–98. [DOI] [PubMed] [Google Scholar]
- U.S. EPA. (1988a). Recommendations for and Documentation of Biological Values for Use in Risk Assessment. Cincinnati, OH. EPA Report No. EPA600687008. [Google Scholar]
- U.S. EPA. (1988b). Reference Physiological Parameters in Pharmacokinetic Modeling. U.S. Environmental Protection Agency, Washington, DC. EPA Report No. EPA/600/6–88/004. [Google Scholar]
- U.S. EPA. (2002). A Review of the Reference Dose and Reference Concentration Processes. Washington, DC. No. EPA630P02002F. [Google Scholar]
- U.S. EPA. (2006). Approaches for the Application of Physiologically Based Pharmacokinetic (pbpk) Models and Supporting Data in Risk Assessment (Final Report). U.S. Environmental Protection Agency, Office of Research and Development, National Center for Environmental Assessment, Washington, DC. EPA Report No. EPA/600/R-05/043F. [Google Scholar]
- U.S. EPA. (2011a). Exposure Factors Handbook: 2011 Edition. U.S. Environmental Protection Agency, Office of Research and Development, National Center for Environmental Assessment, Washington, DC. EPA Report No. EPA/600/R-090/052F. [Google Scholar]
- U.S. EPA. (2011b). Recommended Use of Body Weight 3/4 as the Default Method in Derivation of the Oral Reference Dose. Washington, DC. No. EPA100R110001. [Google Scholar]
- Ulaszewska MM, Ciffroy P, Tahraoui F, Zeman FA, Capri E, and Brochot C (2012). Interpreting PCB levels in breast milk using a physiologically based pharmacokinetic model to reconstruct the dynamic exposure of Italian women. J. Expo. Sci. Environ. Epidemiol 22, 601–609. [DOI] [PubMed] [Google Scholar]
- Verner MA, Ayotte P, Muckle G, Charbonneau M, and Haddad S (2009). A physiologically based pharmacokinetic model for the assessment of infant exposure to persistent organic pollutants in epidemiologic studies. Environ. Health Perspect 117, 481–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verner MA, Sonneborn D, Lancz K, Muckle G, Ayotte P, Dewailly É, Kocan A, Palkovicová L, Trnovec T, Haddad S, et al. (2013). Toxicokinetic modeling of persistent organic pollutant levels in blood from birth to 45 months of age in longitudinal birth cohort studies. Environ. Health Perspect 121, 131–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vizcaino E, Grimalt JO, Fernández-Somoano A, and Tardon A (2014). Transport of persistent organic pollutants across the human placenta. Environ. Int 65, 107–115. [DOI] [PubMed] [Google Scholar]
- Vodicnik MJ, and Lech JJ (1980). The transfer of 2,4,5,2′,4′,5′-hexachlorobiphenyl to fetuses and nursing offspring. I. Disposition in pregnant and lactating mice and accumulation in young. Toxicol. Appl. Pharmacol 54, 293–300. [DOI] [PubMed] [Google Scholar]
- Weijs L, Yang RS, Covaci A, Das K, and Blust R (2010). Physiologically based pharmacokinetic (PBPK) models for lifetime exposure to PCB 153 in male and female harbor porpoises (Phocoena phocoena): Model development and evaluation. Environ. Sci. Technol 44, 7023–7030. [DOI] [PubMed] [Google Scholar]
- Woodruff TJ, Zota AR, and Schwartz JM (2011). Environmental chemicals in pregnant women in the United States: NHANES 2003–2004. Environ. Health Perspect 119, 878–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang LL (2021). Anatomy and physiology of the liver. In Anesthesia for Hepatico-Pancreatic-Biliary Surgery and Transplantation (Milan Z and Goonasekera C, Eds.). pp. 15–40. Springer, Cham, Switzerland. [Google Scholar]
- You L, Gazi E, Archibeque-Engle S, Casanova M, Conolly RB, and Heck HA (1999). Transplacental and lactational transfer of p,p′-DDE in Sprague-Dawley rats. Toxicol. Appl. Pharmacol 157, 134–144. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Supplemental source code and data files are available through the U.S. Environmental Protection Agency’s Environmental Dataset Gateway (https://doi.org/10.23719/1524467).