Phase behavior of disordered proteins underlying low density and high permeability of liquid organelles

Abstract

Many intracellular membraneless organelles form via phase separation of intrinsically disordered proteins/regions (IDPs/IDRs). These include the C elegans protein LAF-1, which forms P-granule-like droplets in vitro. However, the role of protein disorder in phase separation and the macromolecular organization within droplets remain elusive. Here, we utilize a novel technique, ultrafast-scanning fluorescence correlation spectroscopy, to measure the molecular interactions and full coexistence curves (binodals), which quantify the protein concentration within LAF-1 droplets. The binodals of LAF-1 and its IDR display a number of unusual features, including “high concentration” binodal arms that correspond to remarkably dilute droplets. We find that LAF-1 and other in vitro and intracellular droplets are characterized by an effective mesh size of ~3–8 nm, which determines the size scale at which droplet properties impact molecular diffusion and permeability. These findings reveal how specific IDPs can phase separate to form permeable, low-density (semidilute) liquids, whose structural features are likely to strongly impact biological function.

Living cells are complex solutions of thousands of different proteins, nucleic acids, lipids, and small molecules. To organize their contents, cells form many different types of intracellular organelles that localize distinct sets of molecules, allowing spatiotemporal control of molecular interactions. In addition to canonical vesicle-like organelles, there are dozens of non-membrane bound, RNA and protein rich organelles within the cell nucleus^{1, 2} and the cytoplasm^{3, 4}. Despite their lack of an enclosing membrane, these organelles are still able to concentrate molecular components and play important roles in key intracellular functions such as RNA transcription and processing, and in the regulation of protein translation.

It is now recognized that membraneless organelles, including P granules, nucleoli, and stress granules, are condensed liquid-like droplets of RNA and protein that form via phase separation. Indeed, many such organelles exhibit classic signatures of liquids, including rapid exchange dynamics of their contents with their surroundings, spherical shapes, coalescence upon contact, and flowing and dripping in response to shear stresses^{1, 5}. These properties allow membraneless organelles to concentrate molecular reactants while maintaining fluidity to facilitate interactions among the constituent molecules. A growing number of studies have demonstrated the liquid-like nature of membraneless organelles and the relevance of liquid-liquid demixing as a fundamental physical mechanism explaining their formation^{6, 7, 8, 9}. There is also increasing support for a link between the material properties of membraneless organelles and cell physiology as well as disease states^{4, 10, 11, 12, 13, 14}.

A number of key questions remain unanswered regarding the physicochemical driving forces for phase separation and the macromolecular organization within membraneless organelles. Intrinsically disordered proteins or regions (IDPs/IDRs) are, in many cases, the drivers of phase-separation that give rise to membraneless organelles^{12, 14, 15, 16}, although how proteindisorder contributes to phase separation remains unclear. In C. elegans, germ line P granules are RNA and protein rich droplets that are implicated in specification of germ cells. P granule assembly is driven by several proteins with IDRs^{17, 18}, including LAF-1, an abundant DDX3 family protein which contains an arginine/glycine-rich (R/G or RGG) domain that is necessary and sufficient for phase separation¹²; PGL-3 is another P granule protein which contains RGG domains that are important for phase separation¹⁹. R/G-rich IDRs are also found in the nucleolar protein FIB-1⁷, which drives assembly of a core droplet within the nucleolus²⁰. Other examples include WHI3, which contains a Q-rich IDR and drives the formation of liquid-like puncta in the cytoplasm of fungi¹¹. Similarly, the stress granule proteins hnRNPA1 and FUS contain IDRs and are also involved in neurodegenerative diseases^{4, 13, 14}. The molecular concentration within such droplets is expected to influence behaviors including molecular sequestration²¹, promotion of various reactions²², and the nucleation of amyloid-like fibers that are associated with disease^{4, 13, 14}.

Despite the importance of intra-droplet concentration, there are difficulties associated with measuring the full coexistence curves (i.e.,binodals) that define the protein concentrations inside and outside of the droplet. As a result, little is known about how droplet properties emerge from the underlying RNA/protein interactions²². Here, we utilize a novel method based on fluorescence correlation spectroscopy (FCS) measurements to infer second virial coefficients, molecular diffusion coefficients, and binodals for LAF-1 and its intrinsically disordered RGG domain in the presence and absence of RNA molecules. By combining these measurements with a theoretical framework and insights from atomistic simulations, we uncover a rich physical picture of the interactions that underlie the phase behavior and properties of LAF-1 droplets. These results show that intra-droplet concentrations are surprisingly low, and suggest that condensed phases are akin to semidilute polymer solutions. Large-scale conformational fluctuations originating from the intrinsically disordered RGG domain in LAF-1 are critical for the formation of such low-density droplets. We also determine a structural length scale, the mesh size, which characterizes the molecular organization within droplets both in vitro and in vivo. The inferred mesh sizes of P granules in living C.elegans embryos, as well as other membraneless organelles, suggest the broader relevance of our findings for droplets within living cells.

Results

Ultrafast-scanning FCS measurements of coexistence curves

FCS is a powerful technique that relies on measuring the fluorescence intensity fluctuations of labeled molecules within small, femtoliter excitation volumes²³. FCS allows for precise measurements of molecular concentrations and diffusion coefficients, and has been employed for studying protein aggregation²⁴. However, standard FCS methods have well-known limitations²⁵, including the need to calibrate the fluorescence excitation volume. This can become problematic in a droplet-forming system due to refractive index variations. To overcome these limitations, we developed a novel approach, called ultrafast-scanning FCS (usFCS). This approach uses a tunable acoustic gradient index of refraction (TAG)^{26, 27} lens placed in the back focal plane of an oil immersion objective, as shown in Fig. 1a. The TAG lens allows axial scanning of the sample at very high frequency (70 kHz). The axial scan range is adjustable by changing the applied voltage^{28, 29}. The tunable scanning distance serves as an external ruler for measuring the unknown detection volume within droplets. This allows us to estimate the size of the measurement volume and thus determine molecular diffusion coefficients, D, from the characteristic decay times, τ_D, of measured autocorrelation functions (Supplementary Fig. 1). We are also able to measure the internal viscosity and the local molecular concentration within droplets.

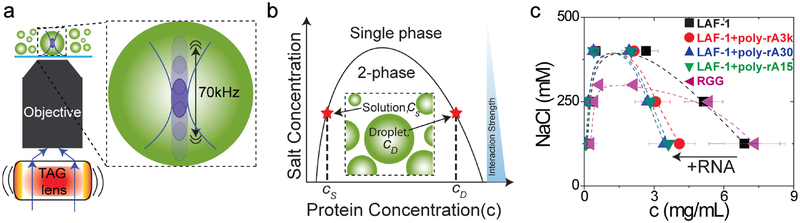
Figure 1: Measured binodals for the RGG domain and LAF-1.

The latter is measured in the absence or presence of RNA using ultrafast-scanning FCS approach. a, A schematic illustration of the microscope with an acoustically modulated beam that is controlled by a tunable acoustic gradient index of refraction (TAG) lens. The system focus can be axially scanned along the optical-axis at a frequency of 70 kHz. b, Schematic showing a typical binodal with increasing protein concentration along the abscissa and increasing salt concentration along the ordinate. Our measurements show that the salt concentration decreases the strengths of two-body interactions for RGG domain/LAF-1 systems. c, The measured binodals of the RGG domain as well as LAF-1 in the presence and absence of RNA. Error bars represent the standard deviation (N=10).

We used usFCS to measure concentrations within the dilute and dense phases, to quantify the low and high concentration arms of the LAF-1binodal, which is the coexistence curve that specifies the envelope of the two-phase region as a function of salt concentration. For a given salt concentration, the equilibrium protein concentration outside the droplet,c_S, The strengths of three-body interactions defines a point on the left arm of the binodal (solid curve in Fig. 1b) whereas the protein concentration inside the droplet, c_D, defines the corresponding point on the right arm of the binodal. At 125 mM NaCl, the value of c_S for LAF-1 is 0.124 ± 0.009 mg/mL (1.5 ± 0.11 μM); the droplets that condense from solution are at a concentration of c_D =6.88 ± 1.52 mg/mL (86.5 ± 19.2 μM; Fig. 1c, Supplementary Fig. 2). These values are surprisingly low, given that the folded proteins lysozyme³⁰ and γ -crystallin³¹, although fundamentally different from IDPs, are also known to phase separate, but at concentrations that are approximately two orders of magnitude higher (~100–500 mg/mL) than what we measure here. We confirmed these low concentration usFCS measurements using different fluorescent labels, as well as an orthogonal three-dimensional confocal microscopy approach (Supplementary Fig. 3). These findings indicate that while LAF-1 droplets are roughly 50 times more concentrated than the dilute phase, they are still at a very low concentration, which corresponds to a number density of 5 × 10⁻⁵ molecules/nm³ (that is, assuming a uniform 3D distribution of protein, the average distance between molecular centers-of-mass is ~27 nm).

The width of the two-phase regime, quantified in terms of the ratio of c_D to c_S, decreases with increasing salt concentrations. This yields a concave down paraboloid binodal for LAF-1 (Fig. 1c), which is characteristic of many polymeric systems³². The RGG domain of LAF-1 is necessary and sufficient to drive phase separation¹². Interestingly, however, the right and left binodal arms of the RGG domain alone are at mass concentrations that are comparable to that of full length LAF-1, although the critical salt concentration is lower than for full-length LAF-1. We also measured binodals in the presence of different types of generic RNA molecules, which may be expected to impact the phase diagram, since they are known to modulate the fluidity of LAF-1 droplets¹². In the presence of polyadenylate RNA (poly-rA) of various lengths, the low concentration arm of the LAF-1 binodal and the concentrations corresponding to the critical region remain essentially invariant. However, upon addition of RNA we observe a marked shift of the high concentration arm of the LAF-1 binodal, toward lower values of c_D (Fig. 1c).

Quantifying the strengths of intermolecular interactions

The remarkably low concentration of LAF-1 droplets must arise from the underlying protein-protein interactions, which can be modulated by RNA. Indeed, in mean field models, such as the Flory-Huggins theory, the sign and magnitude of the effective two-body interactions determine the phase behavior of polymer solutions^{33, 34}. These interactions are quantified using the dimensionless Flory interaction parameter χ, and are measured in terms of molecular dissociation constants K_D or second virial coefficients B₂. We used usFCS to estimate the apparent values of B₂ as a function of salt concentration. For concentrations that are below c_S, the diffusivity of a protein molecule can be influenced by interactions with other proteins^{35, 36}.

Interactions that are, on average, attractive will diminish the protein diffusivities, whereas two-body interactions that are, on average, repulsive will lead to larger effective diffusion coefficients (Fig. 2a). We estimate B₂ by measuring the dependence of the diffusivity on protein concentration (c) and analyzing the data using the relation:³⁵ D ≈D₀ (1+2B₂Mc) (see Supplementary Information for a detailed discussion of this approximation). Here, D is the diffusion coefficient, D₀ is the diffusivity at infinite dilution, and M is the molecular weight of the protein. The B₂ values for LAF-1 extracted using usFCS are numerically equivalent to values obtained using right-angle laser light scattering³² (Supplementary Fig. 4).

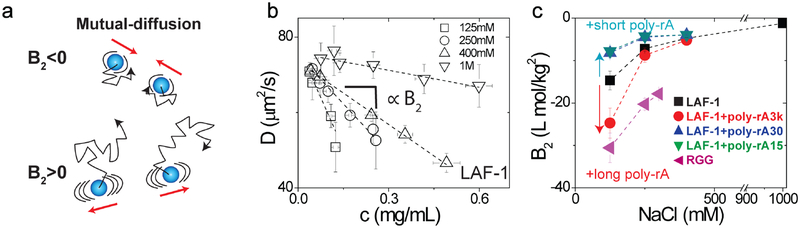
Figure 2: RNA and salt influence intermolecular interactions of LAF-1 and RGG.

a, Schematic illustration of mutual-diffusion. b, Mutual diffusion coefficient of LAF-1 strongly depends on the protein concentration. The dashed lines show the linear fits obtained using the equation shown for D in the text. The slope, which is proportional to B₂, decreases with increasing salt concentration. c, The second virial coefficients, B₂, approach the ideal solution limit of zero with increasing salt concentration. The B₂ values are most negative across the entire salt range for the RGG domain implying stronger effective pairwise interactions for the RGG domain when compared to LAF-1 in the absence or presence of RNA. Error bars represent the standard deviation (N=10).

In the presence of 1 M NaCl, LAF-1 diffusivity is only moderately dependent on protein concentration, with a slope that is near zero, indicating that LAF-1 is only weakly self-associative at high salt concentrations (Fig. 2b, c). However, as salt concentration decreases, LAF-1 diffusivity becomes more strongly dependent on protein concentration, thus yielding negative B₂ values of increasing magnitude. The addition of short unlabeled RNA molecules gives rise to less negative B₂ values, implying that the RNA molecules weaken the strengths of two-body interactions between LAF-1 molecules. In contrast, in the presence of long RNA molecules we obtain more negative B₂ values, implying a strengthening of the effective two-body interactions between LAF-1 molecules. These results are qualitatively consistent with the changes in diffusivities within the droplets (Supplementary Fig. 5). Additionally, measurements of B₂ values for the RGG domain show that these values are the most negative of all the constructs we tested, consistent with this being a highly “sticky” domain that drives phase separation.

Theoretical framework for the measured binodals

The low protein concentration inside LAF-1 droplets comes as a surprise given previous suggestions, including recent measurements of elastin-like-polypeptides (ELPs), which point to concentrations at least two orders of magnitude higher³⁷. Moreover, our findings reveal an unusual invariance of critical points and left binodal arms to the addition of RNA, features that cannot be explained using simple mean-field theories (Supplementary Fig. 6). For example, Flory-Huggins theory suggests that as B₂ becomes more negative (self-interactions are effectively more attractive), c_S should decrease and c_D should increase, but this is not borne out in comparative measurements of the binodals for LAF-1 vs. the RGG domain. A clue to explaining the curious behavior comes from all-atom simulations, which show that the RGG domain exhibits large-scale conformational fluctuations, whereby compact, globular conformations, and expanded coil-like states are sampled with roughly equivalent probabilities (Fig. 3a). The naïve expectation is that these conformational features reflect a lack of preference for interaction of chains with themselves vs. solvent, which would be associated with B₂ values of ≈ 0³²; this is contradicted by our measurements of negative values of B_2. Therefore, the phase behavior of RGG domains appears to derive from a combination of large conformational fluctuations, and negative B₂ values; the latter likely arise from polyvalency of “sticky motifs” comprising charged and aromatic residues. Importantly, the large conformational fluctuations should generate large pervaded volumes, thus dramatically increasing the likelihood that RGG domains will overlap with one another, even at ultra-low concentrations (Supplementary Fig. 7).

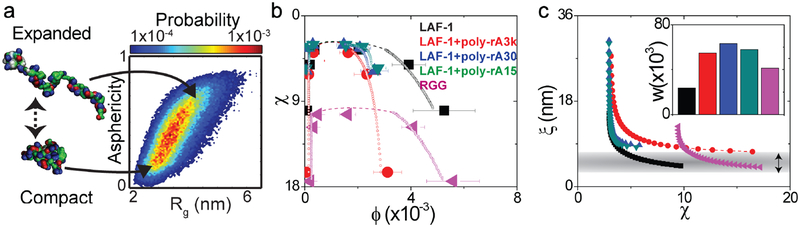
Figure 3: Summary of computational and theoretical analysis.

a, Results from atomistic simulations of the RGG domain. The plot shows a two-dimensional probability density map of chain dimensions in terms of radius of gyration, R_g and asphericities. RGG samples a broad range of conformations leading to large fluctuations and low values for the overlap volume fraction (Supplementary Fig. 7) b, Comparison of the binodals derived from numerical implementation of Muthukumar’s theory³⁸ (open symbols) with experimental data (solid symbols). While the data help to identify the critical χ-region, the precise critical point cannot be reliably located because it is characterized by fluctuations that occur on all length scales. Therefore, the analysis was restricted to reproducing the low and high concentration arms of the binodals away from the critical point. The dashed lines are drawn to guide the eye. C,χ -dependent values of ξ are shown for each of the constructs and are calculated as described in Supplementary Information. The horizontal gray stripe corresponds to values of ξ obtained at 125 mM NaCl. The inset shows inferred values of construct-specific three-body interaction coefficients, w and the color-coding of the bars follows the format used in panels (b) and (c). Error bars represent the standard deviation (N=10).

The concept of overlap volume fraction (φ*) is central to describing the phase behavior of polymer solutions. This is the concentration threshold beyond which inter-chain interactions become more likely than intra-chain interactions – i.e., the concentration at which different chains begin to overlap significantly with one another (Supplementary Figs. 7 and 8). The overlap concentration threshold defines the boundary between the dilute (<φ*) and the semidilute (>φ*) regimes. In a semidilute solution, polymer density fluctuations play a crucial role in determining the interactions between chains³². The large conformational fluctuations associated with the RGG domain combined with the low protein density within droplets points to the direct relevance of the physics and chemistry of polymers in semidilute solutions³⁸.

Numerical reproduction of the measured binodals, for both LAF-1 and the RGG domain alone, requires the adaptation of an advanced theory³⁸ that explicitly accounts for the combined effects of chain density fluctuations, as well as two- and three-body interactions (derived respectively from second and third virial coefficients) (Fig. 3b).

Above the overlap concentration, chain density fluctuations will contribute to screening the interactions between pairs of residues on a single chain, provided the spatial distance between residues is larger than the correlation length, ξ. This characteristic length scale is also referred to as the mesh size because it pertains to the average size of voids between polymer chains. By fitting Muthukumar’s theory³⁸ to the measured binodals, we generate estimates of construct-specific values for ξ and w. The inferred strengths of three-body interactions are encoded in w, which for positive values imply a weakening of attractive inter-molecular interactions (Supplementary Fig. 9). The measured differences between the binodals of the RGG domain and LAF-1 are partially explained by a more positive w associated with RGG compared to LAF-1 (inset of Fig. 3c). Similarly, RNA molecules lead to an increase in w, a result that can be interpreted as the ability of RNA to dilute the attractive interactions between LAF-1 molecules.

The overlap concentration for the RGG domain that we calculate from simulation results, φ*=8.8 ×10^–3, is of the same magnitude as the measured c_D (Supplementary Fig. 6, 7 and associated discussion). This implies that ξ should be quantitatively similar to the dimensions of an individual molecule. Our numerical reproduction of the measured binodals yields estimates for ξ as a function of χ (Fig. 3c). At 125 mM NaCl, the predicted value of ξ is between 3 and 8 nm. These values of ξ are equal to the average dimensions of the RGG domain inferred from simulations (between 3 and 5 nm, see Fig. 3a); the agreement of these two sets of estimates is remarkable given that they were determined through entirely independent approaches. Our analysis thus reveals that protein concentrations in the dense phase are of the same magnitude as the very low overlap concentrations (φ*), which arise from large-scale conformational fluctuations of individual molecules (Supplementary Fig. 7). Therefore, chemical information in the form of sequence-encoded conformational fluctuations controls the dimensions of the disordered RGG domain, and the resulting droplet phase behavior.

Droplet nanorheology

To quantify the impact of low intra-droplet concentration/volume fraction on molecular motions and rheological properties of droplets, we used usFCS to determine the diffusion coefficients of embedded 14 nm fluorescent spherical nanoparticles. We then use the Stokes-Einstein relation to calculate the viscosity, η=k_BT/6πRD, where k_BT is the thermal energy scale, and R is the nanoparticle radius, and D is the measured diffusion coefficient. This gives a LAF-1 droplet viscosity of 27.2 ± 5.9 Pasat 125 mM NaCl, which is consistent with measurements based on particle tracking microrheology¹². Using a similar approach, we find that RGG droplets are roughly twice as viscous as full-length LAF-1 droplets (Fig. 4a), in agreement with the finding that B₂ values for RGG are significantly more negative than full-length LAF-1. Moreover, measurements within RGG droplets show that the RGG domains diffuse more slowly in these droplets when compared to full-length LAF-1 molecules in droplets formed by full-length LAF-1 (Supplementary Fig. 5). Both full-length LAF-1 and RGG droplets exhibit a decreased viscosity and increased molecular diffusivity upon increasing salt concentration (Fig. 4a, Supplementary Fig. 5). This is consistent with the decreasing magnitudes of B₂ values as salt concentrations increase (Fig. 2c).

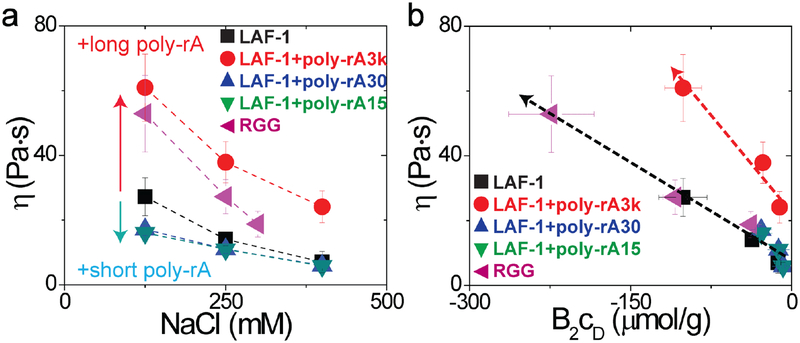
Figure 4: Nano-scale rheology of RGG and LAF-1 condensed droplets.

a, Increasing the concentration of NaCl decreases the viscosity within LAF-1 droplets. Adding short RNA (poly-rA30 and poly-rA15) also decreases the viscosity within LAF-1 droplets. However, adding long RNA (poly-rA3k) increases viscosity of LAF-1 droplets. b, Viscosity within droplets is proportional to the product of B₂c_D. Upon addition of the short RNA (poly-rA) the droplet viscosity decreases and follows the same universal curve with LAF-1 and RGG. Error bars represent the standard deviation (N=20).

When we added RNA of either 15 or 30 nucleotides into LAF-1 droplets in vitro, the droplet viscosity decreased to 16.1 ± 2.8 Pa·s at 125 mM NaCl. Similar mass concentrations of longer 3,000 nucleotide poly-rA cause the opposite effect, whereby the droplet viscosity increases to 60.9 ± 10.3 Pas Nonetheless, in all cases, the droplet viscosity still decreases with increasing salt concentration. These changes are also mirrored in the diffusivities of molecules within the droplets (Supplementary Fig. 5). However, changes in droplet viscosity are not fully captured by considering B₂ alone (Supplementary Fig. 10). Consistent with simple theories of viscosity in polymeric systems³², changes in droplet viscosity also depend on the protein concentration within the droplet, c_D; these combined effects can be captured by plotting viscosity as a product of, B₂c_D, as shown in Fig. 4b. Interestingly, however, the ability to collapse viscosity data as a function of B₂c_D breaks down for the long poly-rA (3,000).

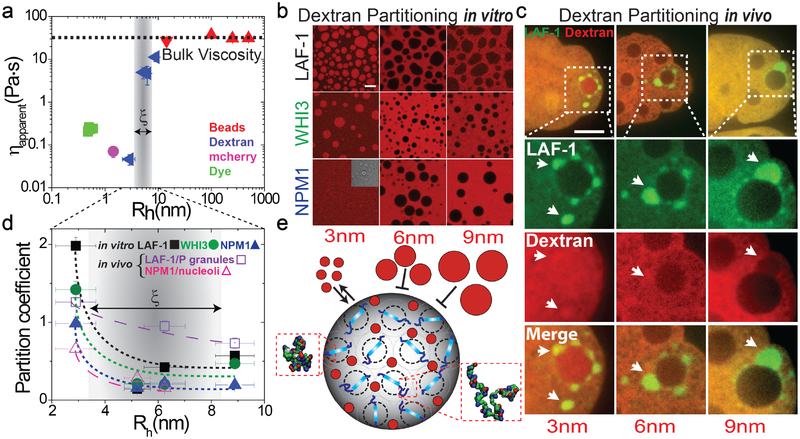
The agreement between the viscosity determined from the diffusive motion of 14 nm particles and micron-sized particles (Fig. 5a) suggests that the effective mesh size (ξ) of the intra-droplet protein network is less than 14 nm. To infer the value of ξ for LAF-1 droplets, we measured the diffusion coefficient for a variety of molecular probes of smaller sizes, and use their hydrodynamic radius R_h to calculate an apparent viscosity as above; we note that using the Stokes-Einstein equation to estimate viscosity is only strictly valid for spherical probe particles (Supplementary Information for a detailed discussion). Small solutes (R_h ~0.5 nm) and the globular protein mCherry (R_h ~1.4 nm) exhibit values in the range of 0.07–0.2 Pas These values are roughly two orders of magnitude lower than the bulk viscosity, consistent with their motion primarily reflecting diffusion through the aqueous solvent that permeates the droplet mesh. To interrogate larger length scales, we used dextran molecules of differing molecular weights. In dilute aqueous buffers, the 10kDa dextran has a hydrodynamic radius (R_h) of ~2.3 nm. By plugging this value of R_h and the measured diffusion coefficient into the Stokes-Einstein equation, we obtain an apparent viscosity value that is comparable to those of the other small probes. However, a similar analysis applied to the measured diffusion coefficients of 40kDa (R_h ~4.5 nm) and larger molecular weight dextran molecules suggests significantly hindered motion, implying that the bulk properties of the droplet become increasingly dominant. Since dextran molecules, especially of higher molecular weights, are not well approximated as spheres, we also analyzed the diffusivity data using the framework of Cai et al.³⁹; this analysis provides additional support for our conclusions (Supplementary Fig. 11). Our dextran diffusivity data are also consistent with the partitioning of different molecular weight dextran into droplets. We find that 10 kDa dextran molecules strongly partition into LAF-1 droplets (Fig. 5c, 5e), while 70 kDa and 155 kDa dextran molecules (> 6 nm) are mostly excluded. These findings suggest that the characteristic mesh size within droplets is between 3 and 6 nm, in agreement with results from our theoretical analysis and simulations (Fig. 3c).

Figure 5: Low-density semidilute liquid droplets.

a, Apparent viscosities extracted from measurements of diffusion coefficients of dyes, mCherry, dextran, and polystyrene beads within LAF-1 droplets at 125 mM NaCl. The gray bar corresponds to ξ in Fig. 3c b, Permeability of different in vitro droplets to fluorescent dextran (red). 10 kDa dextran permeates droplets, while 70 kDa and 155 kDa dextran molecules are excluded from the droplets. The inset figure shows the bright-field image of NPM1 droplets. c, Permeability of in vivo LAF-1::GFP labeled P granules in C. elegans to fluorescent dextran. Perinuclear P granules in ~16-cell embryos are indicated with arrows. (Scale bar, 10 μm). d, Partition coefficients were calculated from fluorescent intensities inside/outside droplets. The dashed lines are drawn to guide the eye. The gray bar corresponds to ξ in Fig. 5a and 3c. e, Schematic illustrating the void-rich nature of LAF-1 droplets, and their probe size-dependent permeability. The RGG domain in LAF-1 is depicted in blue and envelopes defined by the R_g of LAF-1 are shown in black-dash circles. Error bars represent the standard deviation (N=10).

We also measured the partitioning of dextran into LAF-1::GFP labeled P granules in C.elegans embryos (Fig. 5c, 5d). Consistent with our in vitro data, we find that the smaller 10 kDa dextran partitions favorably into P granules, while the larger 155 kDa dextran is significantly excluded; similar in vivo results have been reported for P granules⁴⁰ and for nucleoli⁴¹ (Fig. 5d and Supplementary Fig. 12; LAF-1 labeled P granules in C. elegans and NPM1 labeled nucleoli in oocytes of frog Xenopus laevis, respectively). Moreover, we see similar size-dependent exclusion in vitro for two other well-known droplet forming proteins, WHI3 and NPM1 (Fig. 5b, 5d). These results suggest that the semidilute, void-rich nature of droplets (Fig. 5e) is likely a feature of many liquid phase organelles that are driven by the sequence-encoded conformational fluctuations of IDRs.

Discussion

Phase separation has recently been recognized as a ubiquitous mechanism for organizing the contents of living cells. IDRs of proteins appear to play an important role in driving phase separation. However, there is a lack of clarity regarding the connection between sequence-encoded nanoscale fluctuations of conformationally heterogeneous molecules and the microscale organization and dynamics of droplets that results from phase separation. Here, we begin to uncover these connections using a new usFCS approach to measure the phase behavior and intra-droplet properties of droplets formed by LAF-1, which contains an archetypal disordered R/G-rich domain (Supplementary Fig. 13). By quantifying the strengths of pairwise interactions and resulting coexistence curves, together with measurements of nanoscale viscosity, molecular partitioning, and theoretical analysis, our results provide a holistic picture of how emergent properties of membraneless organelles derive from the amplitudes of conformational fluctuations and interactions of component molecules.

As in many membraneless organelles, LAF-1 and other P granule proteins function by interacting with RNA⁴². Previous work had shown that short (50nt) RNA molecules decrease theviscosity of LAF-1 droplets, consistent with RNA impacting protein-protein interactions¹² However, in that work, RNA had no effect on the saturation concentration required for phase separation, which was unusual since the coexistence curve should arise from the same molecular interactions that govern fluidity. Our results here help resolve this apparent paradox. We find that RNA does indeed impact the coexistence curve, albeit by shifting only the high concentration arm to lower values, while leaving the low concentration arm and critical point invariant. Interestingly, while our results reveal a robust shift in the presence of RNA for all lengths tested (15 – 3000nt), we find that only short RNA decreases droplet viscosity, while long RNA has the opposite effect. This suggests that additional physical processes such as protein-RNA entanglements might be important in describing molecular transport in the presence of longer RNA molecules. Systematic investigations of ternary phase diagrams are needed to obtain a complete understanding of how polydispersity of RNA lengths, sequences, and structural motifs regulate the overall phase behavior of proteins such as LAF-1. This is biologically relevant because RNA molecules of varying lengths are found in P granules. We speculate that their relative abundance could tune P granule viscosity and phase behavior by modulating the effective interactions between LAF-1 molecules or entangling with them.

A surprising finding is that LAF-1 and its IDR phase separate into liquid droplets of ultra-low protein concentrations that correspond to the semidilute regime. We identify the characteristic mesh size within these permeable droplets to be ~3–8 nm (Fig. 3c, 5a, 5c). To account for this behavior, we adapted an analytical model that explicitly accounts for the effects of conformational and chain density fluctuations. For LAF-1, the key region for understanding the multiscale structural features of droplets is the RGG domain, which is necessary and sufficient for phase separation¹², and underlies the intriguing properties of P-granule-like LAF-1 droplets. In particular, the sequence of the RGG domain imparts a unique and unexpected combination of attractive interactions (strongly negative B₂), with large-scale conformational fluctuations and average preference for expanded conformations. These combined effects readily engender overlap among chain molecules, even at very low protein concentrations. This allows the RGG domain to drive the LAF-1-LAF-1 interactions underlying phase separation, while still resulting in remarkably low-density droplets. Our findings provide an interesting contrast with those from another recent study of the phase behavior of elastin-like polypeptides (ELPs), which are IDPs lacking charge residues³⁷. The measured binodals of ELPs correspond to concentrations for c_S and c_D that are at least two orders of magnitude larger than those measured here for LAF-1 and the RGG domain. These differences likely arise from sequence-encoded differences in the amplitudes of conformational fluctuations, and their impact on the resulting droplet phase behavior^{32, 38}.

Our results reveal that LAF-1 droplets, as well as intracellular RNA/protein droplets, are dense when compared to the surrounding solution, but are nevertheless solvent-rich and full of permeable voids that accommodate the free diffusion of small solutes, folded proteins, and flexible polymers up to a specific threshold in size/molecular weight. We find that molecular scale motions within droplets can be decoupled from the mesoscale droplet properties. For example, the bulk viscosity of the droplet has little affect on the diffusion of molecules that are smaller than the mesh size, because they are free to move through the free volume within the droplet (Fig. 5a). By contrast, larger macromolecules and complexes recruited within dropletswill be subject to the viscous drag arising from the dynamic network of IDR-self associations. Since protein sizes span the droplet mesh size, from ~2 nm for an average monomeric protein, to >10 nm for multimeric complexes, these effects are likely to have significant consequences for intracellular droplet functions. We further speculate that low density droplets with large mesh-sizes could allow for size-selective filtering, which could potentially be regulated, in a manner analogous to that of FG Nups in the nuclear pore, which exhibit a comparable passive mesh size (~4 nm)⁴³.

Our findings are likely to shed light not only on P granules, but also many other membraneless organelles. Indeed, IDRs with sequence properties resembling the LAF-1 IDR are found in many RNA binding proteins, including those that are known to drive phase separation^{7, 11, 20, 44}. Our findings provide a new framework for understanding the length scale dependent properties of low-density liquid phase organelles throughout the cell. Changes in these properties will be relevant not only for physiological function, but also in disease-associated pathological aggregation^{4, 11, 13, 14}.

Methods

Ultrafast-Scanning Fluorescent Correlation Spectroscopy.

Samples are excited using a diode-pumped solid-state laser (491 nm, Cobolt Calypso™; Cobolt) with emission wavelengths of 491 nm. After passing through a TAG lens (2.5 BETA; TAG Optics Inc.), the light is focused into the sample using an oil immersion objective (Plan Apo 100X/1.4; Nikon). The fluorescence emission is collected through the same objective, separated from the excitation light by a dichroic mirror (FF495-Di03–25×36; Semrock) and focused into a confocal pinhole unit (MPH16; Thorlabs). The fluorescence light is filtered by a long pass filter (FF01–496/LP; Semrock). Photons are detected by a photomultiplier tube (H10682–210; Hamamatsu), and their arrival times are registered by a data acquisition card (PCI-6115; National Instruments). Here, the scanning distance was kept at ~2 μm, which is an order of magnitude smaller than the size of the liquid droplets.

Protein Preparations.

LAF-1/RGG constructs with a N-terminal His tag were purified on Ni-NTA resin followed by a heparin column (GE) purification step, according to previously published protocols¹². Dylight488 NHS-Ester was conjugated to LAF-1 proteins as needed according to manufacturer protocols (Thermo). Proteins were stored at −80 °C, frozen in high salt buffer (20 mM Tris, pH 7.4, 1 M NaCl, 10% (vol/vol) glycerol, and 1 mM DTT). For droplet experiments, LAF-1/RGG aliquots were centrifuged at 16873g for 2 min and buffer exchanged into high salt buffer (20 mM Tris, pH 7.4, 1 M NaCl, and 1 mM DTT). Then, protein solutions containing ~1% fluorophore labeled LAF-1/RGG were mixed with varying volumes of no salt buffer (20 mM Tris, pH 7.4, and 1 mM DTT). Different lengths of RNA oligonucleotides substrates were added, maintaining the same RNA mass concentration of ~78 μg/mL (15 μM poly-rA15, 7.5 μ M poly-rA30, and 75 nM poly-rA3k).

Data Analysis.

When the measurement volume is axially scanned, Z, at a constant frequency f, the autocorrelation function for simple diffusion is⁴⁵:

$$G(\tau )=G(0){\left(1+\left(\frac{\tau }{{\tau }_D}\right)\right)}^{-1}{\left(1+\left(\frac{\tau }{K^2{\tau }_D}\right)\right)}^{-0.5}exp\left(\frac{-{(Z\text{sin}(\pi f\tau ))}^2}{{\left(2{\omega }_z\right)}^2}\frac{1}{1+\left(\tau /{\kappa }^2{\tau }_D\right)}\right)$$ (1)

Here, G(0) is magnitude at short time scales, τ is the lag time, τ_D is the half decay time, κ is the ratio of axial to radial of measurement volume, and ω_z is the depth of focus. The parameters τ_D, G(0), and ω_z were optimized in the fit while the parameters Z and f were kept fixed. ω_z provides a measurement of the volume, which in turn can be used to determine the diffusion coefficient and molecule concentration in conjunction with τ_D and G(0).

The dependence of the diffusivity (D) on protein concentration (c) can be written as³⁵:

$$D\approx D_0\left[1+\left(2B_{2}M-k_s-\overline{v}\right)c\right]$$ (2)

Here, M is the molecular weight, B₂ is the second virial coefficient, k_s is sedimentation interaction parameter, and ⊽ is partial specific volume. In the presence of 1 M NaCl, LAF-1 diffusivity is only weakly dependent on protein concentration. This indicates that the effective two-body interaction, parameterized in terms of B₂, has a greater contribution to diffusivity than the sedimentation interaction and volume effect, which are expected to depend only weakly on salt concentration. In this approximation, B₂ can be obtained by fitting the observed diffusion coefficient versus protein concentration data to obtain a linear fit (Fig. 2b). For a more extensive discussion, see the Supplementary Information.

Simulation Methods.

All-atom Monte Carlo simulations were run using the CAMPARI software package (campari.sourceforge.net) and the ABSINTH implicit solvent model⁴⁶. Simulations use parameters from the abs_3.2_opls.prm parameter file. Lennard-Jones and electrostatic interactions are subject to 10 Å and 14 Å cutoffs, respectively. CAMPARI uses a range of local and global moves to explore conformational space through a combination of torsional and rigid body moves. The combination of the ABSINTH model and the CAMPARI simulation engine has been extensively used to explore the conformational properties of a wide range of disordered proteins⁴⁷.

Nano- and Microrheology Experiments.

Data for diffusion of micron sized polystyrene beads were obtained using particle tracking-based microrheology and data for diffusion 14nm sized polystyrene beads were obtained using usFCS. Probes larger than ~10 nm accurately probe the bulk viscosity of the droplets, while smaller probes do not. Data for dyes (RhodamineB; Sigma and Alexa488-hydrazide, Alexa488-C5-maleimide, Alexa488-Carboxy, and Alexa488-NHS; Molecular Probes) and mCherry (BioVision) were obtained through standard FCS and corrected for changes to a measurement of the volume based on analysis from usFCS.

Dextran Experiments.

Tetramethylrhodamine dextrans (10k, 40k, 70k; Thermo and 155k; Sigma-Aldrich) were added to droplet solutions of unlabeled LAF-1, WHI3, or NPM1 at final concentrations of ~0.01–0.07 mg/mL. Samples were imaged on a Nikon laser scanning confocal microscope ~2–3 hours after dextran addition. Partition coefficients were calculated from background corrected fluorescent intensities inside/outside droplets. Droplet conditions were as follows: LAF-1 ~3–5μM in 125mM NaCl; WHI3 9 μM with 50 nM BIN1 RNA in 150 mM KCl; NPM1 ~25 μM with 0.1 mg/ml ribosomal RNA in 150 mM NaCl. Cover slips were pretreated with 1%PF127, 30 mg/ml BSA, and SigmaCote for LAF-1, WHI3, and NPM1 respectively. For C. elegans, dextrans were diluted to 4 mg/mL in injection buffer (20 mM KPo4 pH 7.5, 3 mM K citrate, 2% peg-1000) were injected into the syncytial gonad of LAF-1-crispr worms (CPB132[ptnIs077[laf-1::gfp(A206K)]]). After incubation for 4–5 hours at 25°C, worm gonads were dissected and embryos were imaged on a Zeiss spinning disc confocal microscope.

Data availability statement.

The data that support the findings of this study are available from the corresponding author upon reasonable request.